1 Introduction

For a wide range of physicists looking at the universe through the eyes of experts in certain fields, anti-de Sitter/condensed matter (CM) theory (AdS/CMT) correspondence [1, 2] appears (also known as holographic CM physics) to be an appealing subject to dive into. One of the main reasons for this is the fact that AdS/CMT correspondence acts as a bridge between gravitational backgrounds, quantum field theory, and CM physics. Throughout holographic CM physics, non-quasiparticle transport is studied based on experimental phenomena and is compared with black hole and black brane (BB) solutions in large field theories [3]. In 1973, Bardeen et al. [4] showed that black holes obey the laws of thermodynamics; and in the sequel Hawking [5,6,7] stated that black holes are actually not black.

In the years since dynamic critical exponent z and hyperscaling violation parameter \(\theta \) have been proposed, a great many research has been conducted by scientists of many professions, both from observational and theoretical aspects [8, 9]. Throughout Ref. [8], different quantum systems are studied in detail; and consequently, the values that z is allowed to possess are figured out for each case. In addition to being regarded as the main source where the dynamic critical exponent was suggested for the first time, Ref. [8] carries a vital importance in literature, as it provides a linkage between the zero temperature or low temperature behavior of quantum mechanical systems and the associated z values. On the other hand, Ref. [9] is devoted to maintaining arguments on re-normalization and scaling, once a second order transition controlled by a zero-temperature fixed point is achieved for Random-Field Ising systems; and yet the significance of hyperscaling violation parameter for such systems is pointed out. Both studies [8, 9] are supported by experimental phenomena [10,11,12] and a great deal of studies are carried out emphasizing the role of these exponents in CM physics [13,14,15] and in string theory [16, 17]. For a detailed study on the superconducting nature of the boundary theory and investigation of the effect of dynamical exponent on the formation of scalar condensate, the reader is referred to [18]. On the observational side, mainly antiferromagnets situated in fields are investigated in [19,20,21,22,23]; and the aforementioned remarks are achieved. From the perspective of general relativity, however, exploring the effect of these exponents on the wave dynamics of some specific spacetime structures remains intact.

The study of quantum fields propagating in the curved spacetime background predicts particle emission and the thermal black body spectrum is represented by the Hawking temperature [5,6,7, 24,25,26,27,28,29,30,31,32,33,34]. This black body spectrum has its characteristic rate of absorption probability, absorption cross-section, and decay rate which are all frequency-dependent quantities [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. The quasinormal modes (QNMs), on the other hand, disclose how quick a thermal state in the boundary theory will reach thermal equilibrium according to the AdS/CFT (conformal field theory) correspondence [55]. This happens because the relaxation time of a thermal state is inversely proportional to the imaginary part of the QNMs of the dual gravity background that was achieved by the QNMs of the bulk spacetime, which appears from the poles of the retarded correlation function of the corresponding perturbations of the dual CFT [56]. For details on QNMs and stability, one may see the following studies [57,58,59,60,61,62,63]. It is also interesting seeing the linkage between QNMs and the hydrodynamic equations of motion which are conservation laws for the only long-lived excitations expected in a strongly interacting system [64]. The AdS/CFT correspondence makes it possible to derive hydrodynamics from perturbations of bulk spacetime as well as transport coefficients like viscosity, conductivity and resistivity. For experimental results, see for example [65,66,67,68].

Throughout this work, we have taken the opportunity to investigate the influence of z and \(\theta \) on the radiation spectrum, in particular on the the greybody factor (GF) of the 4D Lifshitz-like BB. In the literature, there exist numerous studies on hyperscaling violating metrics among which some can be viewed from [63, 69,70,71,72,73,74,75]. Our work differs from previous studies in the manner that we particularly focus on the analytical computation of GF, absorption cross-section, decay rate, and QNMs for the charged 4D Lifshitz-like spacetimes having the dynamic critical and hyperscaling violation exponents \(z=2\) and \(\theta =-1\), respectively. This non-relativistic case is rather substantial, as systems of \(z=2\) exhibit superconducting fluctuations [8]. It is worth noting that the discovery of superconductivity dates back to 1911 and it has managed to sustain outrageous interest since then [76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97]. Despite being actively used in many different fields of science, the phase transitions of these systems still have mysteries awaiting to be solved. In fact, many of the important properties of superconductors such as Meissner effect and Abrikosov vortices depend on the dynamics of the field. For obtaining more information on holographic superconductor models, one may refer to [98] and [99] and references therein. In the study of [100], it is shown that Lifshitz-like planar spacetimes could indeed be good candidates for revealing significant information regarding the holographic superconductivity. Remarkably, Manikandan and Jordan [101] have recently revealed a mapping between quantum physics of black holes and thermodynamic properties of superconductors. Similarities between the two phenomena are also presented in detail in [102]. As mentioned in Ref. [103], gravitational systems with \(z=2\) can be mapped onto specific CM structures including magnetic materials, liquid crystals, and more specifically; cuprate superconductors. The AdS/CFT correspondence suggests that the boundary value of the bulk field gives a background source for the corresponding dual field theory operator \({\mathcal {O}}\) [104]. At this point, we shall remark that non-relativistic CFTs relevant to nature are strongly coupled and it is a rather challenging task to approach such systems with the usual perturbative techniques. For studies regarding non-relativistic systems, one may refer to [105,106,107,108,109,110,111,112, 114]. Furthermore, as also stated in Ref. [115], the experimental results on many-body properties of non-relativistic CFTs are most commonly supported via numerous numerical simulations and one can get an insight of these observational outcomes via the relevant simulations. However, it is of value noting that constructing analytical methods for those observables of the CFTs remains almost untouched in literature. With the will of finding analytical solutions for the thermal radiation parameters from semi-classical calculations of the 4D Lifshitz-like BB, our pursuit is to address this literature gap via the mapping of the correspondence.

The structure of the paper is as follows. Section 2 includes some details on the geometrical structure of the 4D non-Abelian charged Lifshitz spacetimes with \(z=2\) hyperscaling violation and yet provides the steps for evaluating an analytic solution for the Lifshitz-like BBs under massless scalar perturbation in a clear manner. Then, the massless Klein–Gordon equation (KGE) is analytically solved in this background and the obtained solution is discussed around near horizon and asymptotic regions. Section 3 includes the computations of QNMs and stability analysis. In Sect. 4; GF, absorption cross-section, and decay rate of the concerned BB are analytically computed from the perspective of semi-classical gravitational theory, whereas Sect. 5 touches upon the dual field theory applications. The last section is devoted to summary and conclusions.

2 Behavior of massless scalar field in non-Abelian charged Lifshitz spacetime with \(z=2\) hyperscaling violation

2.1 Geometric structure

For strongly-coupled systems in holographic CM physics, ’t Hooft matrix large N limit needs to be taken into account. The fields, \(\Phi _{k}\), of concern are large \(N\times N\) matrices and the interactions are illustrated in [2] as

$$\begin{aligned} {\mathcal {O}}=tr(\Phi _{{k}_{1}}\Phi _{{k}_{2}}\ldots \Phi _{{k}_{m}}), \end{aligned}$$
(1)

where \(k=1,2,\ldots ,N\). The Lagrangian that characterizes the dynamics of such a system is defined as

$$\begin{aligned} {\mathcal {L}}=\frac{N}{\lambda }tr(\partial ^{\mu }\Phi \partial _{\mu }\Phi +\cdots ), \end{aligned}$$
(2)

in which \(\lambda \) denotes ’t Hooft coupling and for the cases when \( \lambda \) is large, strong interactions occur. In our scenario, there exists a strong coupling between Einstein gravity, the cosmological constant \( \Lambda \), and the fields of concern; namely the dilaton, Maxwell, and N SU(2) Yang–Mills fields which are denoted as \(\phi \), \({\mathcal {A}}\) and \( A_{k}^{a}\), respectively (note that a also runs from 1 to N). Lifshitz spacetime with hyperscaling violation are solutions to the Lagrangian [74]

$$\begin{aligned} {\mathcal {L}}= & {} \sqrt{-g}\left[ R-V\left( \phi \right) -\frac{1}{2}\left( \partial \phi \right) ^{2}-\overset{N}{\underset{k=1}{\sum }}\frac{1}{ 4g_{k}^{2}}e^{\lambda \phi }F_{k}^{2}\right. \nonumber \\&\left. -\frac{1}{4}e^{\lambda \phi }F_{\mu \nu }^{a}F^{a\mu \nu }\right] , \end{aligned}$$
(3)

with \(V(\phi )=\Lambda e^{-\lambda \phi }\) and \(\Lambda =-[D(z-1)^{2}+z-1]\). Equation (3) yields the following line-element:

$$\begin{aligned} ds^{2}=r^{\theta }\left( -r^{2z}f(r)dt^{2}+\frac{dr^{2}}{r^{2}f(r)}+r^{2} \overset{D-2}{\underset{i=1}{\sum }}dx_{i}^{2}\right) , \end{aligned}$$
(4)

where

$$\begin{aligned} f(r)=1-\frac{q^{2}r^{2\left( 1-z\right) }}{2\left( z-1\right) }, \end{aligned}$$
(5)

and

$$\begin{aligned} \theta =\frac{2}{D-2}[z-(D-1)], \end{aligned}$$
(6)

at which q stands for the exact electric charge of concern, \(g_{k}\) is linked to coupling of the Yang Mills term, and R is the Ricci scalar. Furthermore, one shall write \(F_{\mu \nu }^{a}=\partial _{\mu }A_{\upsilon }^{a}-\partial _{\upsilon }A_{\mu }^{a}+\epsilon ^{abc}A_{\mu }^{b}A_{\upsilon }^{c}\).

Holographic correspondence states that the action involves fields propagating on a higher dimensional curved spacetime [74].

2.2 Massless scalar wave equation

Since our focus in this work concerns massless scalar particles, we employ the KGE:

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g}g^{\mu \upsilon }\partial _{\nu }\varphi \right) =0, \end{aligned}$$
(7)

where \(\varphi \) denotes the massless scalar field. By considering the symmetries of metric (4), one may set [63]

$$\begin{aligned} \varphi (t,r,{\vec {x}})=\Phi (r)e^{i{\vec {\kappa }}\cdot {\vec {x}}}e^{-i\omega t}, \end{aligned}$$
(8)

which leads to a more compact form of the KGE that will in turn be used for evaluating the analytical radial solution. Note that \({\vec {\kappa }}\) and \( {\vec {x}}\) represent \((D-2)\)-dimensional wave and spatial vectors, respectively, whereas \(\omega \) denotes frequency of the emitted radiation. After making straight forward computations, one can derive the generic radial equation of Eq. (7) for the metric (4) as

$$\begin{aligned}&\frac{d}{dr}\left[ f(r)r^{2+{\tilde{\eta }} -{\tilde{\theta }}}\frac{d\Phi }{dr}\right] \nonumber \\&\quad +\frac{ 1}{r^{2+{\tilde{\theta }}-{\tilde{\eta }} }}\left( \frac{\omega ^{2}}{r^{2\left( z-1\right) }f(r)}-\kappa ^{2}\right) \Phi (r)=0\,, \end{aligned}$$
(9)

in which \({\tilde{\eta }} =\frac{{\tilde{\theta }}D}{2}+z+D-3\) and \(-\kappa ^{2}\) denotes the eigenvalue of the Laplacian in the flat base submanifold [63]. Furthermore, setting

$$\begin{aligned} \Phi (r)={\mathcal {F}}(r)r^{-\xi }\,, \end{aligned}$$
(10)

where \(\xi =\frac{(D-2)(2+{\tilde{\theta }})}{4}\), and by defining the tortoise coordinate \(r^{*}\) [116] as

$$\begin{aligned} r^{*}=\int r^{-\left( 1+z\right) }\frac{dr}{f(r)}\,, \end{aligned}$$
(11)

one can express the radial equation (9) as a one-dimensional Schr ödinger like equation (or the so-called Zerilli equation [116])

$$\begin{aligned} \frac{d^{2}{\mathcal {F}}(r^{*})}{dr^{*2}}-{\mathcal {V}}(r){\mathcal {F}} (r^{*})=-\omega ^{2}{\mathcal {F}}(r^{*}), \end{aligned}$$
(12)

where \({\mathcal {V}}(r)\) denotes the effective potential:

$$\begin{aligned} {\mathcal {V}}(r)=r^{2\left( z-1\right) }f(r)\left[ \frac{q^{2}}{2}\xi r^{3-z}+\xi (\xi +z)r^{2}f(r)+\kappa ^{2}\right] . \end{aligned}$$
(13)

During this study, based on our current literature knowledge, we have seen that it is not possible to obtain the exact analytical solution of the generic radial equation (9) due to its transcendental form. As already being mentioned in the introduction, throughout this study, we consider the specific case of \(z=2\) and \(D=4\); henceforth \(\theta =-1\) and \(\xi =\frac{1}{2}\). Therefore, metric (4) reduces to

$$\begin{aligned} ds^{2}=-H(r)dt^{2}+\frac{dr^{2}}{H(r)}+r\overset{2}{\underset{i=1}{\sum }} dx_{i}^{2}, \end{aligned}$$
(14)

where \(H(r)=r^{3}f(r)\) and \(f(r)=1-\frac{q^{2}}{2r^{2}}\). For the 4D non-Abelian charged Lifshitz BB (14), the surface gravity [117] can be computed as follows

$$\begin{aligned} \kappa _{s}=\left. \frac{H^{\prime }}{2}\right| _{r=r_{H}}=r_{H}^{2}, \end{aligned}$$
(15)

noting that the outer event horizon obeys \(r_{H}^{2}=q^{2}/2\). The generic radial equation (9) then reduces to

$$\begin{aligned} H(r)\frac{d^{2}\Phi }{dr^{2}}+(4r^{2}-2r_{H}^{2})\frac{d\Phi }{dr}+\left( \frac{ \omega ^{2}}{H(r)}-\frac{\kappa ^{2}}{r}\right) \Phi (r)=0, \end{aligned}$$
(16)

where \(-\kappa ^{2}\) denotes the eigenvalue of the Laplacian in the flat base submanifold [63]. Changing the variable via \(\tilde{z}=r^{-2}(r^{2}-r_{H}^{2})\) and setting

$$\begin{aligned} \Phi (\tilde{z})=\tilde{z}^{\alpha }(1-\tilde{z})^{\beta }G(\tilde{z}), \end{aligned}$$
(17)

with \(\beta =3/2,\) one gets

$$\begin{aligned}&\tilde{z}(1-\tilde{z})G^{\prime \prime }(\tilde{z})+\left( 1-\frac{7\tilde{z} }{2}-\frac{i\omega (1-\tilde{z})}{r_{H}^{2}}\right) G^{\prime }(\tilde{z})\nonumber \\&\quad + \left[ \frac{5i\omega -6r_{H}^{2}-\kappa ^{2}}{4r_{H}^{2}}\right] G(\tilde{z} )=0, \end{aligned}$$
(18)

where \(^{\prime }\) represents the derivative with respect to \( \tilde{z}\). Comparing Eq. (18) with the hypergeometric differential equation [118]

$$\begin{aligned} \tilde{z}(1-\tilde{z})G^{\prime \prime }(\tilde{z})+\left[ c-\left( 1+a+b\right) y\right] G^{\prime }(\tilde{z})-abG(\tilde{z})=0 \end{aligned}$$
(19)

results in

$$\begin{aligned} G(\tilde{z})= & {} C_{1}{}_{2}F_{1}\left( a,b;c;\tilde{z}\right) \nonumber \\&+\, C_{2}\tilde{z}^{1-c} {}_{2}F_{1}\left( a-c+1,b-c+1;2-c;\tilde{z}\right) ,\nonumber \\ \end{aligned}$$
(20)

with the relevant constants

$$\begin{aligned} a= & {} \alpha +\frac{5}{4}\mp \frac{\sqrt{\kappa _{s}^{2}-4\kappa _{s}\kappa ^{2}-4\omega ^{2}}}{4\kappa _{s}}, \end{aligned}$$
(21)
$$\begin{aligned} b= & {} \alpha +\frac{5}{4}\pm \frac{\sqrt{\kappa _{s}^{2}-4\kappa _{s}\kappa ^{2}-4\omega ^{2}}}{4\kappa _{s}}, \end{aligned}$$
(22)
$$\begin{aligned} c= & {} 1+2\alpha , \end{aligned}$$
(23)

where \(\alpha =\pm \frac{i\omega }{2\kappa _{s}}\). Throughout this work, without loss of generality, we choose

$$\begin{aligned} \alpha= & {} -(i\omega /2\kappa _{s}),\nonumber \\ a= & {} \frac{5}{4}-\frac{i}{2\kappa _{s}}\left( \omega +\widehat{\omega }\right) , \end{aligned}$$
(24)
$$\begin{aligned} b= & {} \frac{5}{4}-\frac{i}{2\kappa _{s}}\left( \omega -\widehat{\omega }\right) , \end{aligned}$$
(25)

where

$$\begin{aligned} {\widehat{\omega }}=\sqrt{\omega ^{2}+\kappa _{s}\left( \kappa ^{2}-\frac{ \kappa _{s}}{4}\right) }. \end{aligned}$$
(26)

Thus, Eq. (23) becomes

$$\begin{aligned} c=1-\frac{i\omega }{\kappa _{s}}. \end{aligned}$$
(27)

Then, the general solution for the radial function is obtained as

$$\begin{aligned} \Phi (\tilde{z})= & {} \tilde{z}^{\alpha }(1-\tilde{z})^{\beta }\left[ C_{1}{}_{2}F_{1}\left( a,b;c;\tilde{z}\right) \right. \nonumber \\&\left. +C_{2}\tilde{z} ^{1-c}{}_{2}F_{1}\left( a-c+1,b-c+1;2-c; \tilde{z}\right) \right] .\nonumber \\ \end{aligned}$$
(28)

After this point, one shall split the problem into two parts and investigate the behavior of Eq. (28) near the event horizon and at the spatial infinity regime separately. This will then provide the desired information regarding the flux computation.

2.2.1 Radial solution around near horizon region

To consider the near-horizon property of the solution (28), we reconsider the tortoise coordinate for the metric (16):

$$\begin{aligned} r^{*}=\int \frac{dr}{H(r)}. \end{aligned}$$
(29)

After some algebra, one can obtain the near-horizon tortoise coordinate in terms of \(\tilde{z}\) [recall that \(\tilde{z}=r^{-2}(r^{2}-r_{H}^{2})\)] as follows

$$\begin{aligned} r_{NH}^{*}=\frac{\ln {\sqrt{1-\tilde{z}}-1}}{2r_{H}^{2}}. \end{aligned}$$
(30)

For the case when \(r\rightarrow r_{H}\), or equivalently for \(\tilde{z} \rightarrow 0\), the hypergeometric function becomes identity \([_{2}F_{1}\left( a,b,c;0\right) =1] \) and the general radial solution (28) can be expressed as

$$\begin{aligned} \Phi _{NH}=C_{1}e^{\alpha \ln \tilde{z}}+C_{2}e^{-\alpha \ln \tilde{z}}, \end{aligned}$$
(31)

This enables us to rewrite Eq. (31) as

$$\begin{aligned} \Phi _{NH}\equiv \Phi (r\rightarrow r_{H})= & {} C_{1}e^{-i\omega \frac{\ln \tilde{z}}{ 2r_{H}^{2}}}+C_{2}e^{i\omega \frac{\ln \tilde{z}}{2r_{H}^{2}}}\nonumber \\= & {} \widetilde{ C_{1}}e^{-i\omega r_{NH}^{*}}+\widetilde{C_{2}}e^{i\omega r_{NH}^{*}}, \end{aligned}$$
(32)

where \(\widetilde{C_{1}}=C_{1}e^{\omega \pi /2r_{H}^{2}}\) and \( \widetilde{C_{2}}=C_{2}e^{\omega \pi /2r_{H}^{2}}.\) This implies that the scalar field (8) near horizon region can explicitly be stated as

$$\begin{aligned} \varphi _{NH}=C_{1}e^{-i\omega \left( t+\frac{\ln \tilde{z}}{2r_{H}^{2}} \right) }=\widetilde{C_{1}}e^{-i\omega r_{NH}^{*}}e^{-i\omega t}. \end{aligned}$$
(33)

It is clear from Eq. (33) that the first term corresponds the ingoing wave while the second term is the outgoing wave. In order to match the ingoing boundary condition near the horizon, the coefficient \(C_{2}\) must be vanished. Then, we have the general radial solution with the ingoing boundary condition at the horizon as

$$\begin{aligned} \Phi ({\widetilde{z}})=C_{1}{\widetilde{z}}^{\alpha }(1-{\widetilde{z}})^{\beta }{}_{2}F_{1}\left( a,b;c;\tilde{z}\right) . \end{aligned}$$
(34)

2.2.2 Radial solution around spatial infinity region

We now turn our focus to the computation of the emitted radiation’s flux at spatial infinity. Although there exist a variety of ways for this evaluation, we will be following the method used in [119] which requires finding the asymptotic solution for Eq. (16) followed by performing

$$\begin{aligned} \digamma _{SI}=\frac{\sqrt{-g}g^{rr}}{2i}(\Phi _{SI}^{*}\partial _{r}\Phi _{SI}-\Phi _{SI}\partial _{r}\Phi _{SI}^{*}). \end{aligned}$$
(35)

As stated in Sect. 2, our Lagrangian involves strong coupling which implies that in order for the AdS/CMT correspondence to hold true, the low energy GF should be of interest. Furthermore, our choice of the parameter \( \beta \) (i.e., \(\beta =3/2\)) also supports this requirement, as \(\beta \) being real makes it a challenging task to distinguish between the ingoing and outgoing fluxes [119]. Thus, for \(r\rightarrow \infty \), Eq. (16) reduces to

$$\begin{aligned} \frac{d^{2}\Phi }{dr^{2}}+\frac{4}{r}\frac{d\Phi }{dr}=0, \end{aligned}$$
(36)

which allows us to express the radial solution at spatial infinity as

$$\begin{aligned} \Phi (r)=D_{1}+\frac{D_{2}}{r^{3}}. \end{aligned}$$
(37)

Having obtained the asymptotic radial solution, we will now solve Eq. (28) for \(r\rightarrow \infty \) and compare our solution with the one obtained above so as to be able to find the relevant constants. Hence, it is worthwhile to note that near the spatial infinity \(\tilde{z}\rightarrow 1\) or \(r\rightarrow \infty \), the general radial solution (28) behaves as follows

$$\begin{aligned} \Phi _{SI}(\tilde{z})= & {} C_{1}\tilde{z}^{\alpha }\left[ A_{1} (1-\tilde{z})^{\beta }{}_{2}F_{1}\left( a,b;a{+}b{-}c{+}1;1-\tilde{z}\right) \right. \nonumber \\&+\left. A_{2}\left( \tilde{z}\right) {}_{2}F_{1}\left( c{-}a,c-b;c{-}a{-}b{+}1;1-\tilde{z}\right) \right] .\nonumber \\ \end{aligned}$$
(38)

To this end, the following linear transformation relationship is employed :

$$\begin{aligned} _{2}F_{1}(a,b,c;u)= & {} A_{1}{}_{2}F_{1}(a,b,a+b-c+1;1-u)\nonumber \\&+A_{2}(1-u)^{c-a-b} {}_{2}F_{1}\left( c-a,c\right. \nonumber \\&\left. -b,c-a-b+1;1-u\right) , \end{aligned}$$
(39)

where

$$\begin{aligned} A_{1}= & {} \frac{\Gamma (c)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)}, \end{aligned}$$
(40)
$$\begin{aligned} A_{2}= & {} \frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)}. \end{aligned}$$
(41)

Thus, near the spatial infinity \({\widetilde{z}}\rightarrow 1\) or \( r\rightarrow \infty \), the asymptotic behavior of the radial solution (38) behaves as

$$\begin{aligned} \Phi _{SI}=C_{1}\left[ A_{1}\left( \frac{r_{H}}{r}\right) ^{3}+A_{2}\right] . \end{aligned}$$
(42)

Matching Eq. (37) with Eq. (42) results in \(D_{1}=A_{2}C_{1}\) and \(D_{2}=A_{1}C_{1}r_{H}^{3}\). Finally, the asymptotic flux (35) becomes [119]

$$\begin{aligned} \digamma _{SI}=3\left( \left| D_{out}\right| ^{2}-\left| D_{in}\right| ^{2}\right) , \end{aligned}$$
(43)

in which

$$\begin{aligned} D_{out}=\frac{D_{1}+iD_{2}}{2}, \end{aligned}$$
(44)

and

$$\begin{aligned} D_{in}=\frac{D_{1}-iD_{2}}{2}. \end{aligned}$$
(45)

3 QNMs and stability analysis

In this section, we shall compute the QNMs by using the analytical radial solutions obtained in Sec. II and analyze the stability of the 4D non-Abelian charged Lifshitz BBs with \(z=2\) hyperscaling violation under the scalar field perturbation. QNMs describe perturbations of a field that decay in time. In other words, they are the modes of energy dissipation of a perturbed field.

For QNM analysis, it is necessary to examine the behavior of the effective potential [116] that the wave will be subjected to. Taking cognizance of Eq. (13), one can see that the effective potential of the 4D non-Abelian charged Lifshitz spacetime with \(z=2\) hyperscaling violation reads

$$\begin{aligned} {\mathcal {V}}(r)=H(r)\left( \frac{5r}{4}-\frac{r_{H}^{2}}{4r}+\frac{\kappa ^{2} }{r}\right) . \end{aligned}$$
(46)
Fig. 1
figure 1

The behavior of \({\mathcal {V}}(r)\) with \(q=1\) and \(\kappa =0\)

Full size image

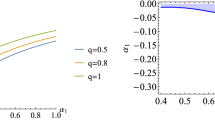
One can check that \(\underset{r\rightarrow \infty }{\lim }{\mathcal {V}}(r){ \rightarrow }\infty \): this can be best seen from Fig. 1. Therefore, the QNMs possess the particular boundary conditions such that scalar field \(\varphi \) is purely ingoing at the horizon and vanishes at spatial infinity (a similar situation was discussed in, for example, [120]). Since the asymptotic (\(\tilde{z}\rightarrow 1\)) radial function is already obtained in Eq. (38), we thus have

$$\begin{aligned} \Phi _{SI}(\tilde{z})\approx & {} C_{1}A_{1}(1-\tilde{z})^{\beta }+C_{1}A_{2},\nonumber \\\cong & {} C_{1}A_{2}=C_{1}\frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)} . \end{aligned}$$
(47)

Therefore, the field at spatial infinity vanishes if \(a=-n\) or \(b=-n\) for \( n=0,1,2,..\). The latter remarks give us the explicit expression for the QNMs:

$$\begin{aligned} \omega =-i\frac{q^{2}(n+1)(2n+3)+\kappa ^{2}}{5+4n}. \end{aligned}$$
(48)

Since the obtained QNMs are purely imaginary and negative, it guarantees that the system is always overdamped. Thus, one concludes that the 4D non-Abelian charged Lifshitz BBs with \(z=2\) hyperscaling violation are stable under the massless scalar field perturbations.

4 Thermal radiation

In this section, we will be carrying out final steps for obtaining analytical expressions for the main focusing point of our study, the thermal radiation parameters \(\gamma \), \(\sigma _{abs}\), and \(\Gamma \), which stand for the GF, absorption cross-section, and decay rate, respectively. To obtain these parameters, we need to start from the GF evaluation, which is described in [119] as follows

$$\begin{aligned} \gamma =1 - \mathfrak {R}= \frac{2i({\mathfrak {D}}-{\mathfrak {D}}^{*})}{{\mathfrak {D}} {\mathfrak {D}}^{*}+i({\mathfrak {D}}-{\mathfrak {D}}^{*})+1}, \end{aligned}$$
(49)

where \(\mathfrak {R}=\left| D_{out}\right| ^{2}/\left| D_{in}\right| ^{2} \) and \({\mathfrak {D}}=D_{1}/D_{2}\). More precisely, we have

$$\begin{aligned} {\mathfrak {D}}=\frac{3}{8}\frac{\Gamma \left( -\frac{1}{4} - i X\right) \Gamma \left( -\frac{1}{4}- i Y \right) }{\Gamma \left( \frac{5}{4}- i Y\right) \Gamma \left( \frac{5}{4} - i X\right) r_{H}^{3}}, \end{aligned}$$
(50)

and hence

$$\begin{aligned}&{\mathfrak {D}} {\mathfrak {D}}^{*}\nonumber \\&\quad =\frac{2304}{\pi ^{4}r_{H}^{6}}[\Gamma (3/4)]^{8} {\displaystyle \prod \limits _{n=0}^{\infty }} \frac{\varepsilon _{n}}{\left[ 1{+} \left( \frac{Y}{ n-1/4}\right) ^{2}\right] \left[ 1{+} \left( \frac{X}{n-1/4}\right) ^{2}\right] },\nonumber \\ \end{aligned}$$
(51)
$$\begin{aligned}&{\mathfrak {D}}-{\mathfrak {D}}^{*} \quad =\frac{24 }{\pi ^{2}r_{H}^{3}} \Xi [\Gamma (3/4)]^{4}{\displaystyle \prod \limits _{n=0}^{\infty }} \varepsilon _{n}. \end{aligned}$$
(52)

Note that the simplifications above are achieved with the aid of the following relations:

$$\begin{aligned} X= & {} \frac{\omega - {\hat{\omega }}}{2r_{H}^{2}}, \end{aligned}$$
(53)
$$\begin{aligned} Y= & {} \frac{\omega + {\hat{\omega }}}{2r_{H}^{2}}, \end{aligned}$$
(54)
$$\begin{aligned} \varepsilon _{n}= & {} \left[ 1+ \left( \frac{Y}{n+5/4}\right) ^{2}\right] \left[ 1+ \left( \frac{X}{n+5/4}\right) ^{2}\right] , \end{aligned}$$
(55)

and

$$\begin{aligned} \Xi =\frac{(\sin {\theta _{1}}\sin {\theta _{2}} - \sin {\theta _{3}} \sin { \theta _{4}})}{\sin {\theta _{1}}\sin {\theta _{2}}\sin {\theta _{3}}\sin {\theta _{4} }}. \end{aligned}$$
(56)

Furthermore, the associated angles can be defined as \(\theta _{1}=\pi \left( \frac{5}{4}-iX\right) \), \(\theta _{2}=\pi \left( \frac{5}{4}-iY\right) \), \( \theta _{3}=\pi \left( \frac{5}{4}+iY\right) \), and \(\theta _{4}=\pi \left( \frac{5}{ 4}+iX\right) \). At this point, one shall record that we have taken the advantage of the following properties of the gamma functions throughout our calculations:

$$\begin{aligned} \frac{\Gamma (x+iy) \Gamma (x-iy)}{[\Gamma (x)]^{2}}= {\displaystyle \prod \limits _{n=0}^{\infty }} \left[ 1+ \left( \frac{y}{x+n}\right) ^{2}\right] ^{-1}, \end{aligned}$$
(57)

and the reflection formula

$$\begin{aligned} \frac{1}{\Gamma (Z)}\frac{1}{\Gamma (1-Z)}= \frac{\sin {\pi Z}}{\pi }, \end{aligned}$$
(58)

where \(Z \in {\mathbb {C}}\) [121]. The aforementioned simplifications allow us to express the GF in anew form as follows:

$$\begin{aligned} \gamma = \frac{2i \Xi { \prod \nolimits _{n=0}^{\infty }} \varepsilon _{n}}{\frac{96 [\Gamma (3/4)]^{4}}{\pi ^{2}r_{H}^{3}}{\prod \nolimits _{n=0}^{\infty }} \frac{ \varepsilon _{n}}{\left[ 1+ \left( \frac{Y}{n-1/4}\right) ^{2}\right] \left[ 1+ \left( \frac{X}{n-1/4}\right) ^{2}\right] } + i \Xi { \prod \nolimits _{n=0}^{\infty }} \varepsilon _{n} + \frac{\pi ^{2}r_{H}^{3}}{ 24[\Gamma (3/4)]^{4}}}. \end{aligned}$$
(59)

Having obtained the GF, one may now have the virtue of evaluating some other thermodynamic quantities. Let us start by computing the 4D absorption cross-section which reads [51,52,53]

$$\begin{aligned} \sigma _{abs}=\sum _{l=0}^{\infty }\frac{i\pi }{\omega ^{2}}\frac{2(2l+1) \Xi {\displaystyle \prod \nolimits _{n=0}^{\infty }} \varepsilon _{n}}{\frac{96 [\Gamma (3/4)]^{4}}{\pi ^{2}r_{H}^{3}} {\displaystyle \prod \nolimits _{n=0}^{\infty }} \frac{ \varepsilon _{n}}{\left[ 1+ \left( \frac{Y}{n-1/4}\right) ^{2}\right] \left[ 1+ \left( \frac{X}{n-1/4}\right) ^{2}\right] } + i \Xi {\displaystyle \prod \nolimits _{n=0}^{\infty }} \varepsilon _{n} + \frac{\pi ^{2}r_{H}^{3}}{ 24[\Gamma (3/4)]^{4}}}. \end{aligned}$$
(60)

Finally, the decay rate of our concerned BB (4) is represented as

$$\begin{aligned} \Gamma =\frac{i \Xi { \prod \nolimits _{n=0}^{\infty }} \varepsilon _{n}d^{3}k}{4 \pi ^{3}(e^{\omega /T_{H}}-1)\left[ \frac{96 [\Gamma (3/4)]^{4}}{ \pi ^{2}r_{H}^{3}} { \prod \nolimits _{n=0}^{\infty }} \frac{\varepsilon _{n}}{\left[ 1+ \left( \frac{Y}{n-1/4}\right) ^{2}\right] \left[ 1+ \left( \frac{X}{n-1/4} \right) ^{2}\right] } + i \Xi {\prod \nolimits _{n=0}^{ \infty }} \varepsilon _{n} + \frac{\pi ^{2}r_{H}^{3}}{ 24[\Gamma (3/4)]^{4}}\right] }. \end{aligned}$$
(61)

5 Duality between analytical results and strongly coupled CFT systems

In the previous sections, we have used the tools of semi-classical methods to compute QNMs, GF, absorption cross section, and decay rate of charged Lifshitz-like background with hyperscaling violation of \(z=2\) and \(\theta =-1\), under scalar perturbations. In the holographic scenario, the dual theory is constructed on the boundary of the bulk spacetime which is located at infinite radial distance away [122]. Thus, the bulk fields in 4D gravitational model are directly linked to dual operators in the dual field theory of two-spatial dimensions on the boundary. It is worth recalling that in our work, the field propagating in the curved spacetime of our concern was chosen to be massless scalar field as \(\varphi (t,r,{\vec {x}})=\Phi (r) e^{i {\vec {\kappa }}\cdot {\vec {x}}} e^{-i \omega t}\). Hence, in the boundary field theory, \(\Phi \) will correspond to \({\mathcal {O}}_{\Phi }\), namely a scalar operator.

We will now be touching upon the relevance of our analytical gravitational results to the strongly coupled systems exhibiting quantum behavior. Let us start from the linkage between QNMs obtained in Eq. (48) and thermalization in the dual strongly coupled CFT. Prior to doing so, we shall take advantage of the membrane paradigm which states that small fluctuations of a stretched horizon have properties corresponding to diffusion of a conserved charge in simple fluids [123,124,125]. In other words, a dispersion relation of the form \(\omega =-i {\mathcal {D}} q^{2}\) suggests the existence of diffusion of a conserved charge [123]. Comparing the dispersion relation with the obtained QNM (48), one can see that

$$\begin{aligned} {\mathcal {D}} =\frac{(n+1)(2n+3)}{5+4n}, \end{aligned}$$
(62)

where \({\mathcal {D}}\) stands for the shear mode diffusion constant [113, 123]. This constant plays a significant role in AdS/CFT correspondence, as its consistency can be investigated via experimental realizations [123, 126]. For the fundamental QNM, i.e. for \(n=0\), our diffusion constant reduces to \({\mathcal {D}}=3/5\). The diffusion constant has a direct relation with the inverse relaxation time. For further details on the numerical analysis of inverse relaxation times for different systems, one may refer to the study of Horowitz et al. [127].

Having calculated the diffusion constant, let us now inspect its relation with the ratio \(\eta /s\). Recall metric (4) for \(D=4\):

$$\begin{aligned} ds^{2}=r^{\theta }\left( -r^{2z}f(r)dt^{2}+\frac{dr^{2}}{r^{2}f(r)}+r^{2} \overset{2}{\underset{i=1}{\sum }}dx_{i}^{2}\right) . \end{aligned}$$
(63)

Letting \(r\rightarrow 1/{\tilde{r}}\) and \(\theta \rightarrow -{\tilde{\theta }}\) leads to

$$\begin{aligned} d{\tilde{s}}^{2}={\tilde{r}}^{{\tilde{\theta }}}\left( -\frac{f({\tilde{r}})}{{\tilde{r}}^{2z}}dt^{2}+\frac{d{\tilde{r}}^{2}}{{\tilde{r}}^{2}f({\tilde{r}})}+ \overset{2}{\underset{i=1}{\sum }}\frac{dx_{i}^{2}}{{\tilde{r}}^{2}}\right) , \end{aligned}$$
(64)

which coincides with the non-relativistic holographic backgrounds considered in [125]. For consistency, we have set the boundary spatial dimension to \(d_{i}=2\). Kolekar et al. [125] derived a universal relation for the shear viscosity to entropy density ratio. We will now be checking how our QNM analysis can be related to this universal relation.

Firstly, we shall record that our choice of exponents (\(d=D-1=3\), \(z=2\) and \({\tilde{\theta }}=1\)) satisfy the null energy conditions [125]

$$\begin{aligned} (d-1-{\tilde{\theta }})((d-1)(z-1)-{\tilde{\theta }})\geqslant 0, (z-1)\,(d-1+z-{\tilde{\theta }})\geqslant 0. \end{aligned}$$
(65)

According to Kolekar, Mukherjee, and Narayan [125], the shear viscosity to entropy density ratio obeys a universal relation derived from the membrane paradigm

$$\begin{aligned} \frac{\eta }{s}= \frac{d-z+1}{4\pi } {\mathcal {D}} {\tilde{r}}_{H}^{2-z}. \end{aligned}$$
(66)

On the other hand, in another study [112] of the same authors, it was reported that the result obtained above applies to uncharged hyperscaling violation theories and may differ for the charged backgrounds. In fact, \(\eta /s\) ratio for the charged BBs is still an active debate topic [113].

For \(d=3\), \(z=2\), and \({\mathcal {D}}=3/5\) (i.e., for the fundamental QNMs), Eq. (66) becomes

$$\begin{aligned} \frac{\eta }{s}= \frac{3}{10 \pi }; \end{aligned}$$
(67)

and yet, satisfies the so-called universal Kovtun–Son–Starinets bound: \(\eta /s\geqslant \frac{1}{4\pi }\) [128]. This result carries importance both in the bulk theory and the dual CFT, as the possible experimental verification of this number from either theory would imply the following: The first implication could be that the system under experimental investigation would highly probably be exhibiting properties of bulk spacetime considered in this work. Furthermore, the experimental verification would suggest that the validity of Eq. (66) proposed by Kolekar et al. can be extended to charged hyperscaling violating Lifshitz-like backgrounds as well. It is also worthwhile mentioning that the experimental constancy of lower bound for the \(\eta /s\) ratio in CM systems is suspected to be an inherent property of semi-classical gravitational theory and should be valid for any theory with a gravitational dual description [126].

Now, let us further investigate the mapping between CM systems and their corresponding bulk spacetime models. In dual strongly coupled CFT, the two-point correlation function which corresponds to the retarded Green’s function, plays a vital role, since its computation allows one to obtain exact or numerical values for physical observables like conductivity, resistivity, flux factor, cross section, shear viscosity, and so on. In order to achieve this, a well-defined boundary value for \(\Phi \) should initially be computed. Then, one can follow the method prescribed by Gubser–Klebanov–Polyakov–Witten (GKPW) [129]. According to the GKPW, we consider an infinitesimal distance \(\epsilon \) away from the boundary of the bulk spacetime. Although this will lead to modifications in the relevant action, the equations of motion remain invariant. Consequently, the UV divergence is avoided and taking \(\epsilon \rightarrow 0 \) results in a well-defined boundary value for \(\Phi \). The flux factor then can be evaluated via [65]

$$\begin{aligned} \digamma ({\vec {\kappa }},\omega )=\underset{r\rightarrow \epsilon }{\lim } \sqrt{g} g^{rr} \Phi (r) \partial _{r}\Phi (r), \end{aligned}$$
(68)

which corresponds to the momentum-space two-point correlation function, i.e,

$$\begin{aligned} \digamma ({\vec {\kappa }},\omega )=\left<{\mathcal {O}}_{\Phi }({\vec {\kappa }},\omega ) {\mathcal {O}}_{\Phi }(-{\vec {\kappa }},-\omega )\right>. \end{aligned}$$
(69)

For further details, the reader is referred to [65, 72, 103, 130] and references therein. This factor carries a major significance in real-world experiments. For instance, for particle physics experiments involving scattering processes, the transitions between states constitute the observables of the system and the model benefits from non-relativistic perturbation theory [131]. Finally, the differential cross-section can be obtained via [131]

$$\begin{aligned} d\sigma =\frac{1}{\digamma }\left| {\mathcal {M}}\right| ^{2} d{\tilde{\Phi }}, \end{aligned}$$
(70)

in which \({\mathcal {M}}\) and \(d{\tilde{\Phi }}\) represent matrix element and phase factor, respectively. Now, let us inspect our case. Recalling Eq. (37):

$$\begin{aligned} \Phi (r)=D_{1}+\frac{D_{2}}{r^{3}}, \end{aligned}$$
(71)

which represents the asymptotic behavior of our radial solution \(\Phi \), one can get the retarded Green’s function as \(G_{O\,+}=D^{-1}\) where \(D^{-1}=D_{2}/D_{1}\) [72]. Then, one can express

$$\begin{aligned} G_{O\,+}=\frac{8}{3}\frac{\Gamma \left( \frac{5}{4}- i Y\right) \Gamma \left( \frac{5}{4} - i X\right) r_{H}^{3}}{\Gamma \left( -\frac{1}{4} - i X\right) \Gamma \left( -\frac{1}{4}- i Y \right) }. \end{aligned}$$
(72)

As one may notice, the Green’s function obtained above is actually the key expression that one needs for being able to evaluate the physical observables in the theory of our concern. For instance, to be able to obtain an analytical solution for the universal \(\eta \) in hydrodynamics, one can use [132]

$$\begin{aligned} \eta =-\underset{\omega \rightarrow 0}{\lim } \frac{1}{\omega } Im G_{O\,+}(\omega ,\kappa =0), \end{aligned}$$
(73)

which would indeed be useful for mapping gravitational results into the dual field theory.

6 Conclusion

The main motivation behind our work was the idea of using the tools of semi-classical gravitational theory to perceive quantum behaviour of strongly-coupled systems of the physical world. Equipped with this motivation, we have evaluated the thermal radiation parameters of hyperscaling violating Lifshitz BB solutions with \(z=2\) to gravity-dilaton-Maxwell–Yang–Mills theories in 4D in the bulk spacetime. Although the parameters we have evaluated do carry significance in gravitational theory, one shall note that they also have intriguing implications in non-relativistic CFTs.

In this study, we have first focused on the scalar perturbations of the non-Abelian Lifshitz spacetime with \(z=2\) hyperscaling violation that have provided us with the analytical expressions for QNMs, GF, absorption cross-section, and decay rate of this Lifshitz BB. We have seen that the obtained exact QNMs are purely imaginary; and one shall note that in such perturbations, an exponential decay behavior is observed. Namely, the system is always over-damped, which results in the mode stability of the non-Abelian Lifshitz spacetime with \(z=2\) hyperscaling violation. Having obtained the gravitational observables, we have then touched upon the linkage between these analytical results and CM systems possessing strong coupling. For the fundamental QNM, the shear viscosity to entropy density ratio in our non-relativistic model is found to be \(\frac{\eta }{s}= \frac{3}{10 \pi }\), which satisfies the universal Kovtun–Son–Starinets bound. Although the ratio of \(\eta /s\) is an ongoing research topic for the charged hyperscaling violating theories [112, 113], we believe that the present study will provide contribution to the relevant discussions. Finally, we have evaluated the thermal Green’s function in the dual theory in terms of the exact expressions we had obtained in the semi-classical gravitational theory.

Our future plans include detailed evaluation of transport coefficients under AdS/CFT correspondence and seeking for relevant experimental evidence for the model of our concern. Furthermore, one can also construct an effective string configuration for verification of the calculations carried out in this work. We are planning to dive into this in the near future with the aid of Ref. [133]. We will then search for comparison of our results with the numerical and experimental studies in literature. We also hope that the exact solutions obtained in this work do get experimentally verified in superconducting systems which can in turn be used throughout gathering more information on strongly coupled fluids. The desire of attaining the exact CM analogue of our analytic results acts as a motivation for further research and discussion, as there exists a broad range of applications of AdS/CMT correspondence in many different areas of physics. Finally, it is worthwhile to re-investigate the outcomes of this study in the presence of back-reaction. We hope to be able to report on this case in the near future.