1 Introduction

Cartan in 1922 introduced an extension of Einstein’s theory of gravity [known as Einstein–Cartan theory (ECT)], interpreting intrinsic angular momentum (i.e, spin) of the matter in terms of torsion [1,2,3]. Later in 1960s introduction of spin of the mater to general relativity [4, 5], showed ECT as the simplest classical modification of Einstein’s theory [see [6] for a general review].

In ECT, the space-time contains asymmetric affine connection in contrast to general relativity having symmetric Christoffel symbols in Riemannian geometry. In particular, torsion is characterized the antisymmetric part of the affine (non-Riemannian) connection. As a result, the gravitational pull is not only described by the metric tensor but also by the independent torsion field. Geometrically, curvature has the tendency of bending the space-time while torsion twists it. In other words, parallel transport of a vector along a closed loop depends on the path due to the curvature of the space-time while presence of torsion may even prevent the formulation of the loop. Further, from the physical point of view, presence of matter causes the curvature of the space-time while intrinsic angular momentum of matter characterizes the torsion.

On the other hand, the introduction of torsion field does not allow the space-time to be maximally symmetric (i.e. homogeneous and isotropic) which is the common choice for standard cosmology, rather it introduces anisotropic degrees of freedom. To overcome this unusual situation, a typical vectorial form of the torsion field has been introduced in recent past [7]. In this specific profile, the space-time torsion fields [8,9,10] and the related matter spin are completely determined by a homogeneous scalar function. Further, this modified torsion field preserves the symmetry of the associated Ricci curvature tensor (in FLRW model) and hence the symmetry of Einstein tensor and energy-momentum tensor. Phenomenologically, torsion play the role of spatial curvature and it has an input in the terms of cosmological constant/ dark energy. So it is speculated that torsion may be responsible for accelerated expansion. However, it is observationally speculated that primordial nucleosynthesis is influenced by torsion and hence it is possible to constraint torsion field from observational point of view.

From an alternative view point, the effect of torsion in space-time can be interpreted as the intrinsic angular momentum of fermionic (i.e. spin) particles [11]. Geometrically, it is related to the asymmetric affine connection of the space-time manifold. Hence matter field acts as a source for torsion and thereby enriching the cosmic descriptions. The well known Einstein–Cartan–Kibble–Sciama (ECKS) gravitational theory is very useful from the perspective of the invariance of local gauge in relation to the group of Poincare [12, 13]. It is to be noted that there is no observational evidence in favour of the existence of torsion field, rather there are suggestions for some experimental tests.

Moreover, the standard cosmology in FLRW model has been a debating issue due to a series of observational evidences [14,15,16] for the last two decades. Attempts to resolve this issue has been continuing in two directions – introduction of exotic matter (known as dark energy) in the frame work of Einstein gravity or modification of Einstein gravity theory itself. The second approach modifies the geometric part of the Einstein field equations and is termed as modified gravity theories. Essentially, a general form of the Lagrangian density than the usual Einstein–Hilbert action or some higher dimensional theories has been considered in this approach. The present torsion theory is an example of this type of modified gravity theory.

The present work shows an extensive study of cosmic evolution in FLRW model with torsion and it is examined whether torsion can be considered as an alternative to dark energy. A complete cosmic description has been presented for a continuous value of the torsion scalar function and thermodynamics of the system has been studied. The paper is organized as follows: Sect. 2 deals with torsion in FLRW model, cosmic solutions and choice of torsion scalar function has been studied in Sect. 3. Section 4 has discussed equivalence with Einstein gravity and non equilibrium thermodynamical prescription. The paper ends with a brief discussion in Sect. 5.

2 Torsion and FLRW model

The Einstein–Cartan theory which is based on the asymmetric affine connection of the space-time, instead of the Riemannian space, is the gravity theory with torsion. In particular, torsion tensor is described by the antisymmetric part of the affine connection, termed by

$$\begin{aligned} S^a_{bc}=\Gamma ^a_{[bc]}, \end{aligned}$$
(1)

which vanishes in absence of torsion. Since the metric tensor is covariantly constant (i.e, \(\nabla _c g_{ab}=0\)), a generalized connection can be decomposed into a symmetric and an antisymmetric part as

$$\begin{aligned} \Gamma ^a_{bc}={\tilde{\Gamma }}^a_{bc}+K^a_{bc}, \end{aligned}$$
(2)

where the symmetric part \({\tilde{\Gamma }}^a_{bc}\) is the usual Christoffel symbols and the antisymmetric part \(K^a_{bc}\) is termed as the contortion tensor with \(K_{abc}=K_{[ab]c}\). This contortion tensor is related to the torsion tensor as

$$\begin{aligned} K_{abc}=S_{abc}+2S_{(bc)a}. \end{aligned}$$
(3)

Thus one can think torsion as a connecting tool between the intrinsic angular momentum (spin) of the matter and the geometry of the space-time.

Due to antisymmetric nature of the torsion tensor one can define torsion vector as

$$\begin{aligned} S_a=S_{~ab}^b\left( =-S_{~ba}^b\right) , \end{aligned}$$
(4)

and consequently, for the contortion tensor we have

$$\begin{aligned} K^b_{~ab}=2S_a=-K^{~~b}_{ab} \end{aligned}$$
(5)

In this work we consider homogeneous and isotropic FLRW space-time having line element

$$\begin{aligned} ds^2 = -dt^2 +a^2(t) \left[ \frac{dr^2}{1-Kr^2}+r^2 \left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) \right] , \end{aligned}$$
(6)

where a(t) is the scale factor with \(H=\frac{\dot{a}}{a}\), H is the Hubble parameter and ‘ \(\cdot {}\) ’ represents differentiation with respect to cosmic time t and K is the curvature index. Also it is assumed that the Universe is consisting of perfect fluid with barotropic equation of state given by \(p= \omega \rho \) and \(\omega =\gamma -1\).

For spatially homogeneous and isotropic FLRW space-time torsion vector fully characterize the torsion tensor (and hence the contortion tensor). For this space-time the torsion vector can be written as [18,19,20,21]

$$\begin{aligned} S_a=-3 \phi u_a, \end{aligned}$$
(7)

where \(\phi =\phi (t)\) is a scalar function, \(h_{ab}\) is the metric of the three space and \(u_a\) is the four velocity field along the tangent to a congruence of time like curves and the torsion tensor and the contortion tensor can be expressed as

$$\begin{aligned} S_{abc}= & {} 2\phi h_{a[b}u_{c]}, \end{aligned}$$
(8)
$$\begin{aligned} K_{abc}= & {} 4\phi u_{[a}h_{b]c}, \end{aligned}$$
(9)

Clearly the torsion vector is a time like vector [17] and (the sign of) the scalar function \(\phi \) indicates the relative orientation between the torsion and the 4-velocity (i.e, torsion vector is future directed for \(\phi <0\) , while it is past directed for \(\phi >0\)).

Further, the matter conservation equation in FLRW model takes the form [18]

$$\begin{aligned} T_{a;b}^b=-4\phi T_{ab}u^b, \end{aligned}$$
(10)

which for perfect fluid has the explicit form

$$\begin{aligned} {\dot{\rho }}+3(H+2\phi )(p+\rho )=4\phi \rho , \end{aligned}$$
(11)

where as usual \(\rho \) is the energy density and p is the thermodynamic pressure of the perfect fluid. Hence, the modified Friedmann equations due to torsion can be written as

$$\begin{aligned} 3H^2= & {} \kappa \rho -3\frac{K}{a^2} -12\phi ^2-12H\phi , \end{aligned}$$
(12)
$$\begin{aligned} 2{\dot{H}}= & {} -\kappa (p+\rho )+2\frac{K}{a^2} -4{\dot{\phi }}+8\phi ^2+4H\phi . \end{aligned}$$
(13)

3 Cosmic solutions and choices of torsion scalar function

In this section, it is found that with proper choices of torsion scalar function, several cosmological solutions are possible in the present modified gravity theories. Throughout the work, the torsion scalar function is chosen in a typical (but general) form as

$$\begin{aligned} \phi =-\lambda (a)H, \end{aligned}$$
(14)

where \(\lambda (a)\) is an arbitrary function of the scale factor. For simplicity, choosing \(K=0\) i.e, flat space-time, the modified Friedmann equations (12) and (13) with the above choice (14) for \(\phi \) takes the form,

$$\begin{aligned} 3H^2 (1-2\lambda )^2&=\kappa \rho , \end{aligned}$$
(15)
$$\begin{aligned} 2{\dot{H}} (1-2\lambda )&=\kappa \rho \left[ \frac{-3\gamma (1-2\lambda )^2+4(a\lambda ^\prime +2\lambda ^2-\lambda )}{3(1-2\lambda )^2}\right] , \end{aligned}$$
(16)

where ‘ \(^\prime \) ’ denotes differentiation with respect to scale factor a.

Now, combining Eqs. (15) and (16) to eliminate \(\rho \), one obtains the cosmic evolution equation as,

$$\begin{aligned} \frac{2{\dot{H}}}{3H^2}=\frac{4a\lambda ^\prime }{3(1-2\lambda )}+2\lambda \left( \gamma -\frac{2}{3}\right) -\gamma . \end{aligned}$$
(17)

3.1 Emergent scenario: non singular universe

In this section it will be examined whether it it is possible to have an emergent scenario (non-singular cosmological solution) for this theory. Now choosing \(\lambda \) in such a way so that

$$\begin{aligned} \frac{2a\lambda ^\prime }{(1-2\lambda )}+3\lambda \left( \gamma - \frac{2}{3}\right) =\frac{\mu }{H}, \end{aligned}$$
(18)

where \(\mu \) is an arbitrary constant.

Equation (17) takes the following form

$$\begin{aligned} {\dot{H}}= \mu H-\frac{3\gamma }{2}H^2, \end{aligned}$$
(19)

Now depending on the signs of \(\mu \) the possible solutions are as follows.

Case 1, \(\mu > 0\),

$$\begin{aligned} \frac{H}{H_0}= & {} \frac{\mu }{\frac{3\gamma }{2}H_0-\left( \frac{3\gamma }{2}H_0-\mu \right) e^{-\mu (t-t_0)}} ,\nonumber \\ \frac{a}{a_0}= & {} \left[ 1+\frac{3\gamma H_0}{2\mu } \left( e^{\mu (t-t_0)}-1\right) \right] ^{\frac{2}{3\gamma }}. \end{aligned}$$
(20)

Case 2, \(\mu = 0 \),

$$\begin{aligned} \frac{H_0}{H}= & {} 1+\frac{3\gamma }{2}H_0 (t-t_0), \nonumber \\ \frac{a}{a_0}= & {} \left[ 1+\frac{3\gamma }{2}H_0 (t-t_0)\right] ^{\frac{2}{3\gamma }}. \end{aligned}$$
(21)

Case 3, \(\mu < 0\) ,

$$\begin{aligned} \frac{H}{H_0}= & {} \frac{\nu ^2}{\left( \nu ^2+\frac{3\gamma }{2}H_0\right) e^{\nu ^2 (t-t_0)}-\frac{3\gamma }{2}H_0} ,\nonumber \\ \frac{a}{a_0}= & {} \left[ 1+\frac{3\gamma H_0}{2\nu ^2} \left( 1-e^{-\nu ^2(t-t_0)}\right) \right] ^{\frac{2}{3\gamma }}, \end{aligned}$$
(22)

with \(\mu =-\nu ^2\).

In the above solutions \(\lambda _0\), \(t_0\), \(a_0\) and \(H_0\) are integration constants with \(\lambda =\lambda _0\), \(a=a_0\), \(H=H_0\) at \(t=t_0\).

Note that Eq. (20) represents big bang singularity for \(\mu <\frac{3\gamma }{2}H_0\), while for \(\mu >\frac{3\gamma }{2}H_0\) the solution (20) represents the emergent scenario of the universe and \(\mu =\frac{3\gamma }{2}H_0\) represents only the inflationary era (i.e. the exponential expansion). The asymptotic limit for emergent scenario are the following:

\(\mathrm{(i)}~a\rightarrow a_0 \left( 1-\frac{3\gamma H_0}{2\mu } \right) ^{\frac{2}{3\gamma }},H\rightarrow 0 ~\text{ as }~t\rightarrow -\infty ,\)

\(\mathrm{(ii)}~a\sim a_0 \left( 1-\frac{3\gamma H_0}{2\mu }\right) ^{\frac{2}{3\gamma }} , H\sim 0~\text{ as }~t\ll t_0,\)

\(\mathrm{(iii)}~a\sim a_0 \left( \frac{3\gamma H_0}{2\mu }\right) ^ {\frac{2}{3\gamma }}e^{\frac{2\mu }{3\gamma } (t-t_0)} , H\sim \frac{2\mu }{3\gamma }~\text{ as }~t\gg t_0. \)

and the parameter \(\lambda \) can be explicitly written \(\left( \text{ for }~\mu =3\gamma H_0\right) \) as

$$\begin{aligned} \frac{1}{1-2\lambda }=\frac{aH}{H_0} \left[ \frac{1}{a_0(1-2\lambda _0)}+\left( \frac{3\gamma }{2}-1\right) H_0\int _{t_0}^{t} \frac{dt}{a(t)} \right] \end{aligned}$$

Also (21) and (22) represent the big bang singularity and the big bang singularity occurs at the time \(t=t_s\) given by,

\(t_s=t_0+\frac{1}{\mu }\ln {\left| 1-\frac{2\mu }{3\gamma H_0}\right| } ~~\text{ for } \text{ the } \text{ equation } (20),\)

\(t_s=t_0-\frac{2}{3\gamma H_0} ~~\text{ for } \text{ the } \text{ equation } (21),\)

\(t_s=t_0-\frac{1}{\mu }\ln {\left| \frac{H_0}{H_0-\frac{2\mu }{3\gamma }}\right| } ~~\text{ for } \text{ the } \text{ equation } (22)\).

3.2 Different cosmological solutions and continuous cosmic evolution

Let \(t_1\) be the time instant in which the universe evolves from inflationary era to matter dominated era. Similarly \(t_2(>t_1)\) is the time instant at which the universe transits into late time acceleration era [22].

Inflationary era \((t<t_1)\)

The choice for \(\lambda \) is

$$\begin{aligned} \frac{1}{1-2\lambda }=1+\frac{H}{H_1}\left[ \frac{a}{a_1}\left( \frac{1}{1-2\lambda _1}-1+\frac{3\gamma \mu _1}{2}\right) -\frac{3\gamma \mu _1}{2}\right] , \end{aligned}$$

and the cosmic solution is given by

$$\begin{aligned} H= & {} \frac{H_1}{\mu _1+(1-\mu _1)\left( \frac{a}{a_1}\right) ^{\frac{3\gamma }{2}}},\nonumber \\ \text{ i.e, }~~H= & {} H_1\left[ \mu _1\left\{ LambertW\left( \frac{1-\mu _1}{\mu _1}\exp \right. \right. \right. \nonumber \\&\left. \left. \left. \quad \times \left\{ \frac{2(1-\mu _1)+3\gamma H_1 (t-t_1)}{2\mu _1}\right\} \right) +1\right\} \right] ^{-1},\nonumber \\ a= & {} a_1\left[ \frac{\mu _1}{1-\mu _1}LambertW\left( \frac{1-\mu _1}{\mu _1}\exp \right. \right. \nonumber \\&\quad \times \left. \left. \left\{ \frac{2(1-\mu _1)+3\gamma H_1 (t-t_1)}{2\mu _1}\right\} \right) \right] ^{\frac{2}{3\gamma }},\nonumber \\ q= & {} \frac{3\gamma }{2}-1-\mu _1\frac{H}{H_1}, \end{aligned}$$
(23)

where \(LambertW(x) e^{LambertW(x)}=x\) and \(q=-\left( 1+\frac{{\dot{H}}}{H^2}\right) \) is the deceleration parameter.

Matter dominated era \((t_1<t<t_2)\)

The choice for \(\lambda \) is

$$\begin{aligned} \frac{1}{1-2\lambda }= & {} \frac{3\gamma -2}{3\gamma (1-\mu _2)-2} \\&+\frac{aH}{a_1 H_1}\left[ \frac{1}{1-2\lambda _1}- \frac{3\gamma -2}{3\gamma (1-\mu _2)-2}\right] , \end{aligned}$$

and the cosmic solution can be written as

$$\begin{aligned} H= & {} H_1\left( \frac{a}{a_1}\right) ^{-\frac{3\gamma }{2}(1-\mu _2)}, \nonumber \\ \text{ i.e, }~~H= & {} H_1\left[ 1+\frac{3\gamma }{2}H_1 (1-\mu _2)(t-t_1)\right] ^{-1},\nonumber \\ a= & {} a_1\left[ 1+\frac{3\gamma }{2}H_1 (1-\mu _2)(t-t_1)\right] ^{\frac{2}{3\gamma (1-\mu _2)}},\nonumber \\ q= & {} \frac{3\gamma }{2}-1-\mu _2. \end{aligned}$$
(24)

Late time acceleration \((t>t_2)\)

The choice for \(\lambda \) is

$$\begin{aligned} \frac{1}{1-2\lambda }=\frac{aH}{H_2}\left[ \frac{1}{ a_2(1-2\lambda _2)}-\left( \frac{3\gamma }{2}-1\right) H_2\int _{t_2}^{t} \frac{dt}{a(t)}\right] , \end{aligned}$$

and the cosmic solution is in the form of

$$\begin{aligned} H= & {} H_2\left[ \mu _2 +(1-\mu _2) \left( \frac{a}{a_2}\right) ^{-3\gamma } \right] ^{\frac{1}{2}},\nonumber \\~~\text{ i.e, }~~ H= & {} \sqrt{\mu _2}H_2\coth {\left\{ \frac{3\gamma }{2}\sqrt{\mu _2}H_2(t-t_i)\right\} } \nonumber \\ a= & {} a_2\left[ \sqrt{\frac{1-\mu _2}{\mu _2}}\sinh \left\{ \frac{3\gamma }{2}\sqrt{\mu _2} H_2 (t-t_i)\right\} \right] ^{\frac{2}{3\gamma }},\nonumber \\ q= & {} \frac{3\gamma }{2}-1-\mu _2 \left( \frac{H_2}{H}\right) ^2. \end{aligned}$$
(25)

where \(t_i\) is the constant of integration. Here \((\lambda _1,a_1,H_1)\) and \((\lambda _2,a_2,H_2)\) are the values of parameter \(\lambda \), scale factor and Hubble parameter respectively at the transition points \(t=t_1\) and \(t=t_2\).

It will be now examined whether this cosmic evolution across these three phases is continuous or not. Then continuity of the deceleration parameter at the transition time \(t=t_1\) and \(t=t_2\), gives

$$\begin{aligned} \mu _1 =\mu _2. \end{aligned}$$

Continuity of physical parameters (i.e Hubble parameter, scale factor) at \(t=t_1\) is obvious while the continuity at \(t=t_2\) provides the following relations:

$$\begin{aligned}&\frac{3\gamma }{2}(1-\mu _2)(t_2-t_1)=\frac{1}{H_2}-\frac{1}{H_1}, \nonumber \\&\left( \frac{a_1}{a_2}\right) ^{\frac{3\gamma (1-\mu _2)}{2}}=\frac{H_2}{H_1}, \end{aligned}$$
(26)
$$\begin{aligned}&\frac{1}{1-2\lambda _2}=\frac{3\gamma -2}{3\gamma (1-\mu _2)-2}\nonumber \\&\qquad \quad \quad \quad +\frac{a_2 H_2}{a_1 H_1}\left[ \frac{1}{1-2\lambda _1} - \frac{3\gamma -2}{3\gamma (1-\mu _2)-2}\right] , \end{aligned}$$
(27)
$$\begin{aligned}&\sinh (\eta _2) = \sqrt{\frac{\mu _2}{1-\mu _2}}, \end{aligned}$$
(28)

where

$$\begin{aligned} \eta _2=\frac{3\gamma }{2}\sqrt{\mu _2} H_2 (t_2-t_i). \end{aligned}$$
Fig. 1
figure 1

The Hubble parameter H(t) is plotted against t

Full size image
Fig. 2
figure 2

The evolution of the scale factor with respect to time t

Full size image
Fig. 3
figure 3

The deceleration parameter q is plotted against t

Full size image
Fig. 4
figure 4

The evolution of the modulus of torsion \(\phi \) with respect to time t

Full size image

Also let \(t=t_0(<t_1)\) be the time instant in which the universe makes a transition from emergent scenario to inflation. Then from the continuity across the transition time \(t=t_0\), we have

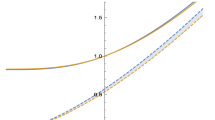
$$\begin{aligned} \frac{1}{1-2\lambda _0}= & {} 1+\frac{H_0}{H_1}\left[ \frac{a_0}{a_1}\left( \frac{1}{1-2\lambda _1}-1+\frac{3\gamma \mu _1}{2}\right) -\frac{3\gamma \mu _1}{2}\right] , \nonumber \\ \frac{H_0}{H_1}= & {} \mu _1+(1-\mu _1)\left( \frac{a_0}{a_1}\right) ^{\frac{3\gamma }{2}}, \end{aligned}$$
(29)

where \(\lambda _0\), \(H_0\) and \(a_0\) are the values of parameter \(\lambda \), Hubble parameter and scale factor at \(t=t_0\) respectively. Also the smoothness of physical parameters H, a, q ans \(\phi \) are shown graphically in Figs. 1, 2, 3 and 4 for the parameter values \(\mu _1 = 0.4\), \(\gamma = \frac{4}{3}\), \(H_1 = 2\), \(a_1=\frac{1}{3}\), \(H_2=1.29\), \(t_1=0.5\), \(t_0=\frac{1}{6}\), \(\lambda _1=\frac{3}{4}\) and \(\mu =3\gamma H_0\).

4 Equivalence to Einstein gravity and non-equilibrium thermodynamical prescription

In this section the thermodynamics of the gravity theory with torsion has been discussed in FLRW model. Also it is checked that, is this theory equivalent to the particle creation in Einstein gravity and temperature of the fluid particles is evaluated. Equation (12) and (13) can be written as

$$\begin{aligned} 3H^2= & {} \kappa \rho -12\phi ^2-12H\phi \nonumber \\= & {} \kappa (\rho +\rho _e)=\kappa \rho _T, \end{aligned}$$
(30)
$$\begin{aligned} 2{\dot{H}}= & {} -\kappa \gamma \rho -4{\dot{\phi }}+8\phi ^2+ 4H\phi \nonumber \\ {}= & {} -\kappa \left[ (p+\rho )+(p_e+\rho _e)\right] =-\kappa (p_T+\rho _T), \end{aligned}$$
(31)

where \(\rho _e,p_e\) are energy density and thermodynamic pressure of the effective fluid particles and are defined as,

$$\begin{aligned} \kappa \rho _e= & {} -12\phi ^2-12H\phi , \end{aligned}$$
(32)
$$\begin{aligned} \kappa p_e= & {} 4\phi ^2+8H\phi +4{\dot{\phi }}. \end{aligned}$$
(33)

From the field equations (30) and (31) due to Bianchi identity one has,

$$\begin{aligned} \dot{\rho _T}+3H(p_T+\rho _T)=0. \end{aligned}$$
(34)

From Eqs. (11) and (34) one have the individual matter conservation equations as,

$$\begin{aligned} {\dot{\rho }}+3H(p+\rho )= & {} Q, \end{aligned}$$
(35)
$$\begin{aligned} \dot{\rho _e}+3H(p_e+\rho _e)= & {} -Q. \end{aligned}$$
(36)

Thus the modified Friedmann equations can be interpreted as Friedmann equations in Einstein gravity for an interacting two fluid system of which one is the usual normal fluid under consideration and other is the effective fluid and the interaction term is given by \(Q=-2(\rho +3p)\phi .\)

For interacting two fluid system the interacting term Q should be positive as the energy is transferred to usual fluid. In this case \(Q>0\implies \phi <0\).

One can write the above conservation Eqs. (35) and (36) in terms of state parameter as

$$\begin{aligned} \omega ^{(eff)}= & {} \omega +2(1+3\omega )\frac{\phi }{3H}, \end{aligned}$$
(37)
$$\begin{aligned} \omega ^{(eff)}_ e= & {} \omega _e-2(1+3\omega )\frac{\phi }{3H}r, \end{aligned}$$
(38)

where \(r=\frac{\rho }{\rho _e}\) is coincidence parameter and \(\omega _e=\frac{p_e}{\rho _e}\) is equation of state parameter of effective fluid.

Equations (35) and (36) can also be written as

$$\begin{aligned} {\dot{\rho }}+3H(p+\rho +p_c)= & {} 0, \end{aligned}$$
(39)
$$\begin{aligned} \dot{\rho _e}+3H(p_e+\rho _e+p_{ce})= & {} 0, \end{aligned}$$
(40)

with

$$\begin{aligned} p_c= & {} \frac{2\phi }{3H}(\rho +3p)=-p_{ce}, \end{aligned}$$
(41)

where \(p_c\), \(p_{ce}\) are the dissipative pressure of the fluid components.

In non-equilibrium thermodynamics this dissipative pressure may be caused by particle creation process. So the particle number conservation equations take the form,

$$\begin{aligned} {\dot{n}}+3Hn= & {} \Gamma n, \end{aligned}$$
(42)
$$\begin{aligned} \dot{n_e}+3Hn_e= & {} \Gamma _e n_e. \end{aligned}$$
(43)

Here n denotes the normal fluid particles density and \(n_e\) represents the number density of effective fluid particles.

If we assume the non-equilibrium thermodynamical process to be adiabatic then the dissipative pressures are related to the particle creation rate linearly as [23],

$$\begin{aligned} p_c= & {} -\frac{\Gamma }{3H}(p+\rho ),\nonumber \\ p_{ce}= & {} \frac{\Gamma _e}{3H}(p_e+\rho _e). \end{aligned}$$
(44)

Comparing Eqs. (41) and (44) we have,

$$\begin{aligned} \Gamma= & {} -2\phi \frac{\rho +3p}{\rho +p}, \end{aligned}$$
(45)
$$\begin{aligned} \Gamma _e= & {} 2\phi \frac{\rho +3p}{\rho _e+p_e}. \end{aligned}$$
(46)

Thus the particle creation rate directly related to \(\phi \). It is also clear that \(\Gamma >0\) i.e, usual fluid particles are created and \(\Gamma _e<0\) i.e, effective particles are annihilated. Also \(p_{ct}=p_c+p_{ce}=0\) so the particle creation rate for resulting fluid particles vanishes identically. Hence resulting fluid forms a closed system.

Further, because of particle creation mechanism there is an energy transfer between the two fluid systems. So these two systems may have different temperatures.

Using Euler’s thermodynamical equation, the evolution of the temperature of the individual fluid is given by [24],

$$\begin{aligned} \frac{{\dot{T}}}{T}= & {} -3H\left( \omega ^{(eff)}+\frac{\Gamma }{3H}\right) +\frac{{\dot{\omega }}}{1+\omega }, \end{aligned}$$
(47)
$$\begin{aligned} \frac{\dot{T_e}}{T_e}= & {} -3H\left( \omega ^{(eff)}_e-\frac{\Gamma _e}{3H}\right) +\frac{{\dot{\omega }}_e}{1+\omega _e}, \end{aligned}$$
(48)

where \(\omega ^{(eff)} \) and \(\omega ^{(eff)}_e \) defined in Eqs. (37) and (38) can be written in terms of particle creation rate as,

$$\begin{aligned} \omega ^{(eff)}= & {} \omega -\frac{\Gamma }{3H}(1+\omega ), \end{aligned}$$
(49)
$$\begin{aligned} \omega ^{(eff)}_e= & {} \omega _e+\frac{\Gamma _e}{3H}(1+\omega ). \end{aligned}$$
(50)

Integrating eqs (47) and (48) we have,

$$\begin{aligned} T= & {} T_0 (1+\omega )exp\left[ -3\int _{a_0}^{a} \omega \left( 1-\frac{\Gamma }{3H}\right) \frac{da}{a}\right] , \end{aligned}$$
(51)
$$\begin{aligned} T_e= & {} T_0 (1+\omega _e)exp\left[ -3\int _{a_0}^{a} \omega _e \left( 1+\frac{\Gamma _e}{3H}\right) \frac{da}{a}\right] , \end{aligned}$$
(52)

where \(T_0\) is the common temperature of the two fluids in equilibrium phase and \(a_0\) is the scale factor in the equilibrium state. In particular, using Eqs. (45) and (51), the temperature of the normal fluid for constant \(\omega \) can be written explicitly in the following form,

$$\begin{aligned} T= & {} T_0 (1+\omega ) \left( \frac{a}{a_0}\right) ^{-3\omega } exp\left[ -2 \int _{t_0}^{t}\frac{\omega (1+3\omega )}{1+\omega } \phi dt\right] .\nonumber \\ \end{aligned}$$
(53)

In general, at very early phases of the evolution of the universe \(T_e<T\) and then when the cosmic fluid attain equilibrium i.e, \(a=a_0\), one has \(T=T_e=T_0\). In the next phase of evolution of universe one has \(a>a_0\) and \(T_e>T\) because energy flows from effective fluid to the usual fluid continuously and hence the thermodynamical equilibrium is violated. Now, from thermodynamical consideration, equilibrium temperature \(T_0\) can be considered as the (modified) Hawking temperature [25] i.e,

$$\begin{aligned} T_0=\frac{H^2 R_h}{2\pi }\Bigg |_{a=a_0}, \end{aligned}$$
(54)

where \(R_h\) is the geometric radius of the horizon, bounding the universe.

5 Brief discussions and concluding remarks

A detailed cosmological study for gravity with torsion is done in present work. At first it is examined that whether a non-singular universe model is possible or not and it is found that for a particular choice of torsion field an emergent scenario is possible. Further it is shown that this gravity model is equivalent to the Einstein gravity with particle creation mechanism. Also it is possible to have a complete cosmic evolution starting from inflationary era to present late time accelerating era through the matter dominated era. Further it is shown that the modified Friedmann equations for this gravity can be considered as the Friedmann equations for the Einstein gravity with interacting two fluid system of which one is the usual fluid and other is effective fluid. The former is created and latter is annihilated in course of cosmic evolution. Also from thermodynamical consideration the temperature of individual fluid particles are evaluated and are found to be distinct. Lastly, different choices of hypothetical fluid component give rise to different cosmic solutions.