Strong decays of the newly observed narrow $\Omega _b$ structures

Abstract

Motivated by the newly observed narrow structures $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ in the $\Xi _b^0 K^-$ mass spectrum, we investigate the strong decays of the low-lying $\Omega _b$ states within the $^3P_0$ model systematically. According to their masses and decay widths, the observed $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ resonances can be reasonably assigned as the $\lambda -$mode $\Omega _b(1P)$ states with $J^P=1/2^-, 3/2^-, 3/2^-$, and $5/2^-$. Meanwhile, the remaining $P-$wave state with $J^P=1/2^-$ should have a rather broad width, which can hardly be observed by experiments. For the $\Omega _b(2S)$ and $\Omega _b(1D)$ states, our predictions show that these states have relatively narrow total widths and mainly decay into the $\Xi _b {\bar{K}}$, $\Xi _b^\prime {\bar{K}}$ and $\Xi _b^{\prime *} {\bar{K}}$ final states. These abundant theoretical predictions may be valuable for searching more excited $\Omega _b$ states in future experiments.

1 Introduction

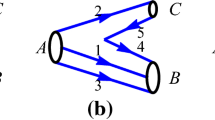
Two kinds of excitations, the $\rho$-mode and $\lambda$-mode, exist for the $\Omega _b$ family. The $\rho$-mode one is the excitation between two strange quarks, while the $\lambda$-mode case is the excitation between the strange quark subsystem and bottom quark. Such a structure is illustrated in Fig. 1. For this system, the $\lambda$-mode is more easily excited due to its heavy reduced mass. To understand the internal structures of these states and establish the low-lying $\Omega _b$ spectrum, experimental and theoretical efforts on their strong decay behaviors are urgently needed.

Although the constituent quark models have predicted plenty of heavy baryons for a long time [1,2,3,4], the experimental information on the $\Omega _c$ and $\Omega _b$ states was scarce in the past years [5]. Before 2017, there were only three $\Omega _c$ and $\Omega _b$ ground states in experiments: $\Omega _c (2695)$, $\Omega _c (2770)$ and $\Omega _b (6046)$ , while the ground state $\Omega _b^*$ was missing. In 2017, the LHCb Collaboration observed five narrow resonances $\Omega _c (3000)$, $\Omega _c (3050)$, $\Omega _c (3066)$, $\Omega _c (3090)$, and $\Omega _c (3119)$ in the $\Xi ^+_c K^-$ channel [6]. Meanwhile, the evidence of a relatively broad signal $\Omega _c (3188)$ was also reported [6]. Subsequently, the Belle Collaboration confirmed most of them except for the $\Omega _c (3119)$ structure [7].

Very recently, the LHCb Collaboration reported four narrow peaks $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ in the $\Xi _b^0 K^-$ mass spectrum [8]. Their measured masses and decay widths are listed as follows:

$$\begin{aligned} m[\Omega _b(6316)^-]= & {} 6315.64\pm 0.31~\pm 0.07\pm 0.50~\mathrm {MeV}, \nonumber \\\end{aligned}$$

(1)

$$\begin{aligned} \Gamma [\Omega _b(6316)^-]< & {} 2.8~\mathrm {MeV}, \end{aligned}$$

(2)

$$\begin{aligned} m[\Omega _b(6330)^-]= & {} 6330.30\pm 0.28\pm 0.07\pm 0.50~\mathrm {MeV}, \nonumber \\\end{aligned}$$

(3)

$$\begin{aligned} \Gamma [\Omega _b(6330)^-]< & {} 3.1~\mathrm {MeV}, \end{aligned}$$

(4)

$$\begin{aligned} m[\Omega _b(6340)^-]= & {} 6339.71\pm 0.26~\pm 0.05\pm 0.50~\mathrm {MeV}, \end{aligned}$$

(5)

$$\begin{aligned} \Gamma [\Omega _b(6340)^-]< & {} 1.5~\mathrm {MeV}, \end{aligned}$$

(6)

$$\begin{aligned} m[\Omega _b(6350)^-]= & {} 6349.88\pm 0.35\pm 0.05\pm 0.50~\mathrm {MeV}, \nonumber \\\end{aligned}$$

(7)

$$\begin{aligned} \Gamma [\Omega _b(6350)^-]= & {} 1.4^{+1.0}_{-0.8}\pm 0.1~\mathrm {MeV}, \end{aligned}$$

(8)

where only the upper limits are determined for the three lower mass states. The experimental data shows that the four resonances are about $6316\sim 6350$ MeV and their mass splittings are rather small. In the constituent quark model, the masses of excited $\Omega _b$ states can be obtained by calculating the eigenvalues of the total Hamiltonian with the QCD inspired potential, and naturally present the small mass splittings due to the small spin-orbit interaction. Compared with the masses predicted by the constituent quark models [9,10,11,12,13,14,15,16,17], these four resonances are good candidates of the $\lambda$-mode $\Omega _b(1P)$ states.

Fig. 1

The $\Omega _b$ system with $\lambda -$ or $\rho -$mode excitation. The $s_1$ and $s_2$ stand for the strange quarks, and b corresponds to the bottom quark

The observations of the low-lying $\Omega _c$ resonances have made an important progress towards a better understanding of the heavy baryon spectrum and aroused widespread interests in hadron physics. Lots of conventional and exotic interpretations on these low-lying states have been done, especially for their strong decays [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. However, the conclusions from various theoretical works with different models and parameters are not consistent with each other, and the spectrum of the low-lying $\Omega _c$ states have not been established so far. The situation is even worse for the low-lying $\Omega _b$ spectrum. Compared with the excited $\Omega _c$ states, the strong decays of the low-lying $\Omega _b$ states were only investigated by several works [15, 32,33,34,35, 43, 44]. Nevertheless, due to the lack of experimental information, the choices of parameters may be adjustable and indeterminate, and the predictions of these different works do not agree with each other. Hence, it is crucial to investigate the strong decays of these low-lying $\Omega _b$ baryons within the unified model and coincident parameters, which has been adopted to describe the excited $\Lambda _{c(b)}$ and $\Sigma _{c(b)}$ states successfully [45,46,47].

In this work, we calculate the strong decay behaviors of the low-lying $\Omega _b$ states within the $^3 P_0$ model systematically. Our results show that the observed $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ resonances can be reasonably assigned as the $\lambda -$mode $\Omega _b(1P)$ states with $J^P=1/2^-, 3/2^-, 3/2^-$, and $5/2^-$. Meanwhile, the remaining $P-$wave state with $J^P=1/2^-$ is predicted to be rather broad, which can hardly be observed by experiments. Moreover, the strong decays of the $\Omega _b(2S)$ and $\Omega _b(1D)$ states suggest that these states have relatively narrow total widths and mainly decay into the $\Xi _b {\bar{K}}$, $\Xi _b^\prime {\bar{K}}$ and $\Xi _b^{\prime *} {\bar{K}}$ final states. We hope these abundant theoretical predictions can provide helpful information for the future experimental searches.

This paper is organized as follows. In Sect. 2, a brief introduction of the $^3 P_0$ model and notations are illustrated. The strong decays of the low-lying $\Omega _b$ states are presented in Sect. 3. A short summary is given in the last section.

2 $^3P_0$ model and notations

In this work, we adopt the $^3P_0$ model to calculate the two-body Okubo-Zweig-Iizuka (OZI) allowed strong decays of the low-lying $\Omega _b$ states. In this model, a quark-antiquark pair with the quantum number $J^{PC}$ =$0^{++}$ is created from the vacuum, and then regroups into two outgoing hadrons by a quark rearrangement process [48]. This model has been successfully employed to study different kinds of the hadron systems for their strong decays with considerable successes [27, 45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. Here, we perform a brief introduction of this model. In the nonrelativistic limit, to describe the decay process $A\rightarrow BC$, the transition operator T in the $^3P_0$ model can be taken as

$$\begin{aligned} T= & {} -3\gamma \sum _m\langle 1m1-m|00\rangle \int d^3\varvec{p}_4d^3\varvec{p}_5\delta ^3 (\varvec{p}_4+\varvec{p}_5)\nonumber \\&\times \mathcal{{Y}}^m_1\left( \frac{\varvec{p}_4-\varvec{p}_5}{2}\right) \chi ^{45}_{1,-m}\phi ^{45}_0\omega ^{45}_0b^\dagger _{4i} (\varvec{p}_4)d^\dagger _{4j}(\varvec{p}_5), \end{aligned}$$

(9)

where $\gamma$ is a dimensionless $q_4\bar{q}_5$ pair-production strength, and $\varvec{p}_4$ and $\varvec{p}_5$ are the momenta of the created quark $q_4$ and antiquark $\bar{q}_5$, respectively. The i and j are the color indices of the created quark and antiquark. $\phi ^{45}_{0}=(u{\bar{u}} + d{\bar{d}} +s{\bar{s}})/\sqrt{3}$, $\omega ^{45}=\delta _{ij}$, and $\chi _{{1,-m}}^{45}$ are the flavor singlet, color singlet, and spin triplet wave functions of the $q_4\bar{q}_5$, respectively. The $\mathcal{{Y}}^m_1(\varvec{p})\equiv |p|Y^m_1(\theta _p, \phi _p)$ is the solid harmonic polynomial reflecting the $P-$wave momentum-space distribution of the created quark pair.

For the strong decay of a baryon $\Omega _b$, there are three possible rearrangements,

$$\begin{aligned} A(s_1,s_2,b_3)+P(q_4,{\bar{q}}_5)&\rightarrow B(s_2,q_4,b_3)+C(s_1,{\bar{q}}_5), \end{aligned}$$

(10)

$$\begin{aligned} A(s_1,s_2,b_3)+P(q_4,{\bar{q}}_5)&\rightarrow B(s_1,q_4,b_3)+C(s_2,{\bar{q}}_5), \end{aligned}$$

(11)

$$\begin{aligned} A(s_1,s_2,b_3)+P(q_4,{\bar{q}}_5)&\rightarrow B(s_1,s_2,q_4)+C(b_3,{\bar{q}}_5). \end{aligned}$$

(12)

These three ways of recouplings are also presented in Fig. 2. It should be mentioned that the first and second ones stand for the heavy baryon plus the light meson channels, while the last one denotes the light baryon plus the heavy meson decay mode.

Fig. 2

The baryon decay process $A\rightarrow B+C$ in the $^3P_0$ model

The S matrix can be written as

$$\begin{aligned} \langle f|S|i\rangle =I-i2\pi \delta (E_f-E_i)\mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}, \end{aligned}$$

(13)

where the $\mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}$ is the helicity amplitude of the decay process $A\rightarrow B+C$. The explicit expression of the helicity amplitude $\mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}$ can be found in Refs. [45,46,47, 54].

In this work, we adopt the simplest vertex which assumes a spatially constant pair production strength $\gamma$, the relativistic phase space, and the simple harmonic oscillator wave functions [48]. Then, the decay width $\Gamma (A\rightarrow BC)$ is calculated directly

$$\begin{aligned} \Gamma = \pi ^2\frac{p}{M^2_A}\frac{1}{2J_A+1}\sum _{M_{J_A},M_{J_B},M_{J_C}}\left| \mathcal{{M}}^{M_{J_A}M_{J_B}M_{J_C}}\right| ^2, \end{aligned}$$

(14)

where $p=|\varvec{p}|=\frac{\sqrt{[M^2_A-(M_B+M_C)^2][M^2_A-(M_B-M_C)^2]}}{2M_A}$, and $M_A$, $M_B$, and $M_C$ are the masses of the hadrons A, B, and C, respectively.

For the $\Omega _b(1P)$ states, we employ the masses of four newly observed structures from LHCb experimental data by assuming that they are possible candidates. For the masses of the $\Omega _b(2S)$ and $\Omega _b(1D)$ states, we adopt the theoretical predictions in the relativistic quark model [9] which are listed in Table 1. For the final ground states, their masses are taken from the Review of Particle Physics [5]. For the harmonic oscillator parameters of mesons, we use the effective values as in Ref. [61]. For the baryon parameters, we use $\alpha _\rho =440~\mathrm {MeV}$ and

$$\begin{aligned} \alpha _\lambda =\Bigg (\frac{3m_Q}{2m_q+m_Q} \Bigg )^{1/4} \alpha _\rho , \end{aligned}$$

(15)

where the $m_Q$ and $m_q$ are the heavy and light quark masses, respectively [20, 45,46,47, 65]. The $m_{u/d}=220~\mathrm {MeV}$, $m_s=419~\mathrm {MeV}$, $m_c=1628~\mathrm {MeV}$ and $m_b=4977~\mathrm {MeV}$ are introduced to consider the mass differences of the heavy and light quarks [61, 66, 67].

The overall parameter $\gamma$ is determined by the well established $\Sigma _c(2520)^{++} \rightarrow \Lambda _c \pi ^+$ process. Then, the $\gamma =9.83$ is obtained by reproducing the width $\Gamma [\Sigma _c(2520)^{++} \rightarrow \Lambda _c \pi ^+]=14.78~\mathrm {MeV}$ [5, 45]. Certainly, it should be checked whether a different parameter $\gamma$ for the bottom sector should be adopted or not. In Ref. [46], we have calculated the decay behaviors of the ground states in bottom sector using $\gamma = 9.83$ compared with the experimental data, which show that the parameter $\gamma$ taken from the charm sector can describe the bottom states well. If we fit the parameter $\gamma$ from these bottom states, a nearly identical value will obtained. To reduce the model parameter, we prefer to use an overall parameter $\gamma$ from charm to bottom sector, which do not affect all the conclusions in present calculations. In the heavy quark limit, the decay behaviors should only depend on the light systems. Due to the finite mass of charm and bottom quarks, the heavy flavor symmetry should also be preserved approximately, which may result in the nearly identical quark pair creation strength $\gamma$ for charm and bottom sectors.

Table 1 Notations, quantum numbers and masses of initial baryons. The $n_\rho$ and $L_\rho$ denote the nodal quantum number and orbital angular momentum between the two strange quarks, respectively. The $n_\lambda$ and $L_\lambda$ represent the the nodal quantum number and orbital angular momentum between the bottom quark and strange quark system. The $S_\rho$ stands for the total spin of the two strange quarks, L is the total orbital angular momentum, j represent total angular momentum of L and $S_\rho$, J is the total angular momentum, and P is the parity. The masses are taken from the theoretical predictions from relativistic quark model [9]. The units are in MeV

Table 2 The decay widths of the four observed resonances as the $\Omega _b(1P)$ states in MeV

3 Strong decay

3.1 $\Omega _b(1P)$ states

There are five $\lambda$-mode $\Omega _b(1P)$ states in the constituent quark model, which are denoted as $\Omega _{b0}(\frac{1}{2}^-)$, $\Omega _{b1}(\frac{1}{2}^-)$, $\Omega _{b1}(\frac{3}{2}^-)$, $\Omega _{b2}(\frac{3}{2}^-)$ and $\Omega _{b2}(\frac{5}{2}^-)$, respectively. From Table 1, the predicted masses of the five $\Omega _b(1P)$ states are around $6330\sim 6340$ MeV. As mentioned in the Introduction, four narrow structures $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ have been observed in the $\Xi _b^0 K^-$ mass spectrum. Given the uncertainties of quark model prediction, these structures are good candidates of the $\Omega _b(1P)$ states. With these experimental masses, all possibilities of these four observed resonances as the $\Omega _b(1P)$ states are considered and the total decay widths are listed in the Table 2. For the $j=0$ state, the total decay width is predicted to be rather large, while for the two $j=1$ states, their OZI-allowed strong decays are forbidden due to the quantum number conservation and the phase space constraint. For the two $j=2$ states, the total decay widths are about several MeV, which may correspond to the experimental observations. Moreover, the decay widths for these excited $\Omega _b(1P)$ states with different quantum numbers show large discrepancy. In the $^3P_0$ model, the formula of decay widths can be divided into the phase factors and amplitudes. Since the masses and final states of these resonances are similar, the phase factors are almost the same. More precisely, the amplitudes include color parts, flavor parts, Clebsch-Gordan coefficients, and spatial overlaps [46, 54]. For the excited $\Omega _b(1P)$ states, these five states have different quantum numbers, and the difference of the decay widths arises from Clebsch–Gordan coefficients of the spin and orbital angular momentum couplings. It can be seen that the pure $\Omega _b(1P)$ assignments can hardly interpret these four resonances simultaneously.

In fact, the physical resonances can be the mixing of the quark model states with the same $J^P$, that is

$$\begin{aligned}&\left( \begin{array}{c}| 1P~{1/2^-}\rangle _1\\ | 1P~{1/2^-}\rangle _2 \end{array}\right) =\left( \begin{array}{cc} \cos \theta &{} \sin \theta \\ -\sin \theta &{}\cos \theta \end{array}\right) \left( \begin{array}{c} |1/2^-,j=0 \rangle \\ |1/2^-,j=1\rangle \end{array}\right) , \nonumber \\\end{aligned}$$

(16)

$$\begin{aligned}&\left( \begin{array}{c}| 1P~{3/2^-}\rangle _1\\ | 1P~{3/2^-}\rangle _2 \end{array}\right) =\left( \begin{array}{cc} \cos \theta &{} \sin \theta \\ -\sin \theta &{}\cos \theta \end{array}\right) \left( \begin{array}{c} |3/2^-,j=1 \rangle \\ |3/2^-,j=2\rangle \end{array}\right) .\nonumber \\ \end{aligned}$$

(17)

Under the heavy quark limit, the mixing angle should equals to zero. Given the finite mass of the bottom quark, the heavy quark symmetry should be approximately preserved, and the mixing angle between the physical states and the quark model states can have a small divergence with the $j-j$ coupling scheme. The total decay widths of various assignments versus the mixing angle $\theta$ in the range $-30^\circ \sim 30^\circ$ are plotted in Fig. 3.

Fig. 3

The total decay widths of various assignments as functions of the mixing angle $\theta$ in the range $-30^\circ \sim 30^\circ$. The red solid lines are the $|1P~{1/2^-}\rangle _1$ and $|1P\;{3/2^-}\rangle _1$ states, and the blue dashed curves correspond to the $|1P~{1/2^-}\rangle _2$ and $|1P\;{3/2^-}\rangle _2$ states. The green bands stand for the measured total decay widths with errors

With the similar masses and total widths, the strong decays of the four resonances are all consistent with the experimental data under the $J^P=1/2^-$ and $J^P=3/2^-$ assignments. However, only three states $| 1P~{1/2^-}\rangle _2$, $| 1P~{3/2^-}\rangle _1$, and $| 1P~{3/2^-}\rangle _2$ belong to the narrow resonances, while the $| 1P~{1/2^-}\rangle _1$ state is too large to be occupied. Fortunately, there is also a $J^P=5/2^-$ state, which is suitable for all four resonances. Hence, four narrow structures $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ can be clarified into the $| 1P~{1/2^-}\rangle _2$, $| 1P~{3/2^-}\rangle _1$, $| 1P~{3/2^-}\rangle _2$, and $| 1P~{5/2^-}\rangle$ states. However, from current experimental information, we can hardly provide the exact correspondence between the physical resonances and theoretical states.

The predicted total decay width of the $| 1P~{1/2^-}\rangle _1$ state is rather large, which can be hardly observed experimentally. This explains why the LHCb experiment only observed four peaks in the $\Xi _b^0 K^-$ mass spectrum. Our present results are consistent with the previous chiral quark model calculations under the $j-j$ coupling scheme [43]. In Ref. [15], the authors predicted one narrow $j=0$ state, two OZI-forbidden $j=1$ states, and two narrow $j=2$ states with the $j-j$ couplings. If the mixing mechanism was considered, the authors could also perform four narrow $\Omega _b(1P)$ states which agree with our present calculations except for the $j=0$ state. Moreover, based on the $L-S$ couplings, the authors predicted five narrow $\Omega _b(1P)$ states within the $^3P_0$ model [35], and three narrow states within the chiral quark model [32], which show different features with our results. Present experiment data suggests that the physical states of these $P-$wave $\Omega _b$ baryons more favor the $j-j$ coupling scheme.

Also, one can determine the mixing angle $\theta$ of the two $J^P=1/2^-$ states. If we choose the normal mass order for the $\Omega _b(1P)$ states, the mixing angle $\theta$ can be constrained by the width of $\Omega _b(6316)^-$ resonance. From Fig. 4, one can see that the mixing angle $\theta$ should lie in $-3.3^\circ \sim 3.3^\circ$ except for zero. When the mixing angle equals to zero, the $| 1P~{1/2^-}\rangle _2$ state corresponds to the $\Omega _{b1}(\frac{1}{2}^-)$, which cannot decay into the $\Xi _b {\bar{K}}$ channel. Thanks to the finite mass of bottom quark, the small mixing between two $J^P=1/2^-$ states can occur, and the narrow one can be observed in the $\Xi _b {\bar{K}}$ final state experimentally. For the two $J^P=3/2^-$ states, the mixing angle cannot be determined by current experimental data. More theoretical and experimental efforts are needed to solve this problem.

Fig. 4

The allowed mixing angle $\theta$ under the assignment of the $\Omega _b(6316)^-$ as $J^P=1/2^-$ state. The red solid line is the $|1P~{1/2^-}\rangle _1$ state, and the blue dashed curve corresponds to the $|1P~{1/2^-}\rangle _2$ state. The green band stands for the measured total decay width with error

Furthermore, the dependence on the harmonic oscillator parameter $\alpha _\rho$ for the pure $J^P=5/2^-$ state is also investigated. With the normal mass order for the $\Omega _b(1P)$ states, the $\Omega _b(6350)$ should be assigned as the pure $J^P=5/2^-$ state. The result is presented in Fig. 5. When the $\alpha _\rho$ varies from 420 to 460 MeV, the decay width of $\Omega _b(6350)$ with $J^P=5/2^-$ lie in the range $2.55 \sim 3.47$ MeV. Compared with the predicted central value 2.98 MeV, the uncertainty of the predicted width is about $16\%$, which show relatively stable prediction.

Fig. 5

The dependence of the decay width on the harmonic oscillator parameter $\alpha _\rho$ for the $J^P=5/2^-$ state

Table 3 Decay widths of the $\Omega _b(2S)$ states in MeV

3.2 $\Omega _b(2S)$ states

In the traditional quark model, there are two $\lambda$-mode $2S-$wave excitations, which are denoted as $\Omega _{b}(2S)$ and $\Omega ^*_{b}(2S)$. From Table 1, the predicted masses of these two $\Omega _{b}(2S)$ states are 6450 MeV and 6461 MeV, respectively. With the calculated masses, their strong decays within the $^3{P_0}$ model are estimated and shown in Table 3.

The total decay width of the $J^P=1/2^+$ state is about 50 MeV and the dominating decay mode is $\Xi _b {\bar{K}}$. The branching ratios are predicted to be

$$\begin{aligned} Br(\Xi ^0_b K^-,\Xi ^-_b {\bar{K}}^0) \thicksim 48\%,45\%. \end{aligned}$$

(18)

For the $J^P=3/2^+$ state, the total width is predicted to be 53 MeV and the $\Xi _b {\bar{K}}$ channel also dominates. The branching ratios of the dominating channels $\Xi ^0_b {\bar{K}}^0$ and $\Xi ^+_b K^-$ are

$$\begin{aligned} Br(\Xi ^0_b K^-,\Xi ^-_b {\bar{K}}^0)\thicksim 48\%, 46\%. \end{aligned}$$

(19)

In Fig. 6, we perform the dependence on the harmonic oscillator parameter $\alpha _\rho$ for these two $\Omega _{b}(2S)$ states. It can be seen that the total and partial decay widths are almost unchanged with the $\alpha _\rho$ variation. Within this reasonable range of the parameter $\alpha _\rho$, all conclusions remain. The total decay widths of our predictions are larger than that of the potential model, but the main decay mode is consistent with each other [15]. With the relatively narrow total widths and dominating decay mode $\Xi _b {\bar{K}}$, these two $\Omega _b(2S)$ states have good potentials to be observed in the $\Xi _b {\bar{K}}$ mass spectrum in future experiments.

Fig. 6

The dependence of the decay widths on the harmonic oscillator parameter $\alpha _\rho$ for the two $\Omega _{b}(2S)$ states

3.3 $\Omega _b(1D)$ states

From Table 1, the masses of the six $\Omega _b(1D)$ states are predicted to be around $6517\sim 6549$ MeV. The strong decay widths for these $D-$wave states are estimated and presented in Table 4. It can be seen that the total decay widths of $\Omega _{b1}(\frac{1}{2}^+)$, $\Omega _{b1}(\frac{3}{2}^+)$, $\Omega _{b2}(\frac{3}{2}^+)$, $\Omega _{b2}(\frac{5}{2}^+)$, $\Omega _{b3}(\frac{5}{2}^+)$ and $\Omega _{b3}(\frac{7}{2}^+)$ states are about 106, 108, 27, 21, 3, and 3 MeV, respectively. For the two $j=1$ states, the dominating decay mode is $\Xi _b {\bar{K}}$, while other decay channels are relatively small. For the two $j=2$ states, the $\Xi ^0_b K^-$ and $\Xi ^-_b \bar{K}^0$ final states are forbidden due to the quantum number conservation, and the main decay modes for the $\Omega _{b2}(\frac{3}{2}^+)$ and $\Omega _{b2}(\frac{5}{2}^+)$ states are $\Xi ^{'}_b {\bar{K}}$ and $\Xi ^{'*}_b {\bar{K}}$, respectively. To distinguish these two $j=2$ states, the partial decay ratios between $\Xi ^{'}_b {\bar{K}}$ and $\Xi ^{'*}_b {\bar{K}}$ modes are helpful. For the two $j=3$ states, the calculated decay widths are about several MeV, which are quite narrow. The main decay mode is $\Xi _b {\bar{K}}$ with the branching ratio up to 97.3% and 98.2% for the $J^P=5/2^+$ and $J^P=7/2^+$ states, respectively. Moreover, the uncertainties raising from the parameter $\alpha _\rho$ for the pure $J^P=1/2^+$ and $7/2^+$ states are studied. From Fig. 7, one can see that our results are relatively stable when the parameter $\alpha _\rho$ varies in a reasonable range.

Table 4 Decay widths of the $\Omega _b(1D)$ states in MeV

Fig. 7

The dependence of the decay widths on the harmonic oscillator parameter $\alpha _\rho$ for the pure $J^P=1/2^+$ and $7/2^+$ states

Within the chiral quark model and the $L-S$ scheme, the authors predicted that the total decay widths of these six states lie in $7\sim 29$ MeV [34], which show different features with ours. Also, our predictions on these $D-$wave $\Omega _b$ states are quite different with the potential model calculations, where six $\Omega _b(1D)$ states all have widths of several MeV [44]. Future experimental searches can help us to clarify these theoretical divergences.

4 Summary

In this work, we study the strong decay behaviors of the low-lying $\lambda -$mode $\Omega _{b}$ states within the $^3P_0$ model systematically. According to the masses and decay modes, four newly observed $\Omega _{b}$ resonances can be reasonably interpreted. It is found that the $\Omega _b(6316)^-$, $\Omega _b(6330)^-$, $\Omega _b(6340)^-$, and $\Omega _b(6350)^-$ can be assigned as the $\lambda -$mode $\Omega _b(1P)$ states with $J^P=1/2^-, 3/2^-, 3/2^-$, and $5/2^-$. Meanwhile, the remaining $P-$wave state with $J^P=1/2^-$ should have a rather broad width, which can hardly be observed by experiments. For the $\Omega _b(2S)$ and $\Omega _b(1D)$ states, our predictions suggest that these states have relatively narrow total widths and mainly decay into the $\Xi _b {\bar{K}}$, $\Xi _b^\prime {\bar{K}}$ and $\Xi _b^{\prime *} {\bar{K}}$ final states. We hope these theoretical calculations are valuable for searching more excited $\Omega _b$ states in future experiments.