Twisted compactifications of 6D field theories from maximal 7D gauged supergravity

Abstract

We study supersymmetric $AdS_n\times \Sigma ^{7-n}$, $n=2,3,4,5$ solutions in seven-dimensional maximal gauged supergravity with $CSO(p,q,5-p-q)$ and $CSO(p,q,4-p-q)$ gauge groups. These gauged supergravities are consistent truncations of eleven-dimensional supergravity and type IIB theory on $H^{p,q}\circ T^{5-p-q}$ and $H^{p,q}\circ T^{4-p-q}$, respectively. Apart from recovering the previously known $AdS_n\times \Sigma ^{7-n}$ solutions in SO(5) gauge group, we find novel classes of $AdS_5\times S^2$, $AdS_3\times S^2\times \Sigma ^2$ and $AdS_3\times CP^2$ solutions in non-compact SO(3, 2) gauge group together with a class of $AdS_3\times CP^2$ solutions in SO(4, 1) gauge group. In SO(5) gauge group, we extensively study holographic RG flow solutions interpolating from the SO(5) supersymmetric $AdS_7$ vacuum to the $AdS_n\times \Sigma ^{7-n}$ fixed points and singular geometries in the form of curved domain walls with $Mkw_{n-1}\times \Sigma ^{7-n}$ slices. In many cases, the singularities are physically acceptable and can be interpreted as non-conformal phases of $(n-1)$-dimensional SCFTs obtained from twisted compactifications of $N=(2,0)$ SCFT in six dimensions. In SO(3, 2) and SO(4, 1) gauge groups, we give a large number of RG flows between the new $AdS_n\times \Sigma ^{7-n}$ fixed points and curved domain walls while, in $CSO(p,q,4-p-q)$ gauge group, RG flows interpolating between asymptotically locally flat domain walls and curved domain walls are given.

1 Introduction

Wrapped branes play an important role in the study of the AdS/CFT correspondence [1,2,3] and its generalization to non-conformal field theories DW/QFT correspondence [4,5,6]. In particular, these brane configurations describe RG flows across dimensions from supersymmetric field theories on the worldvolume of the unwrapped branes to lower-dimensional field theories on the worldvolume of the branes wrapped on internal compact manifolds. For supersymmetric theories, the latter are obtained from twisted compactifications of the former on the internal manifolds. Some amount of supersymmetry is preserved by performing a topological twist along the internal manifolds [7].

In this paper, we are interested in solutions describing wrapped 5-branes in string/M-theory. Rather than searching directly for wrapped brane solutions in string/M-theory, finding supersymmetric solutions of seven-dimensional gauged supergravities in the form of domain walls interpolating between $AdS_7$ and $AdS_n\times \Sigma ^{7-n}$ geometries, with $\Sigma ^{7-n}$ being a $(7-n)$-dimensional compact manifold, is a more traceable task. In many cases, the resulting solutions can be embedded in ten or eleven dimensions by using consistent truncation ansatze. Solutions of this type in the maximal $N=4$ gauged supergravity with SO(5) gauge group in seven dimensions have been extensively studied in previous works [8,9,10,11,12,13,14,15], see also [16,17,18,19] for similar solutions in $N=2$ gauged supergravity. For solutions in other dimensions, see [20,21,22,23,24,25,26,27,28,29,30,31,32,33] for an incomplete list.

We will study this type of solutions within the maximal $N=4$ gauged supergravity constructed in [34] using the embedding tensor formalism, see also [35, 36] for an earlier construction. Unlike the previously known results mentioned above, we will consider more general gauge groups of the form $CSO(p,q,5-p-q)$ and $CSO(p,q,4-p-q)$ obtained respectively from the embedding tensor in $\mathbf {15}$ and $\overline{\mathbf {40}}$ representations of the global symmetry SL(5). Gauged supergravities with these gauge groups can be obtained from consistent truncations of eleven-dimensional supergravity and type IIB theory on $H^{p,q}\circ T^{5-p-q}$ and $H^{p,q}\circ T^{4-p-q}$, respectively, see [37] and [38]. The manifold $H^{p,q}\circ T^r$ is a product of a $(p+q-1)$-dimensional hyperbolic space and an r-torus. The former is in general non-compact unless $p=0$ or $q=0$ in which the $H^{p,0}$ or $H^{0,q}$ become a $(p-1)$-sphere $(S^{p-1})$ or a $(q-1)$-sphere $(S^{q-1})$. To the best of our knowledge, supersymmetric $AdS_n\times \Sigma ^{7-n}$ solutions in $N=4$ gauged supergravity with non-compact and non-semisimple gauge groups have not been considered in the previous studies.

For the aforementioned gaugings of $N=4$ supergravity, only SO(5) gauge group admits a fully supersymmetric $AdS_7$ vacuum dual to $N=(2,0)$ superconformal field theory (SCFT) in six dimensions. The $AdS_n\times \Sigma ^{7-n}$ solutions describe conformal fixed points in $n-1$ dimensions. In this case, these fixed points correspond to $(n-1)$-dimensional SCFTs obtained from twisted compactifications of $N=(2,0)$ SCFT in six dimensions on $\Sigma ^{7-n}$. For all other gauge groups, the vacua are given by half-supersymmetric domain walls dual to six-dimensional $N=(2,0)$ non-conformal field theories. We accordingly interpret the resulting $AdS_n\times \Sigma ^{7-n}$ solutions as conformal fixed points in lower-dimensions of these $N=(2,0)$ non-conformal field theories. We will study various possible RG flows from both conformal and non-conformal field theories in six dimensions to these lower-dimensional SCFTs as well as to non-conformal field theories.

The paper is organized as follows. In Sect. 2, we briefly review the maximal gauged supergravity in seven dimensions. The study of supersymmetric $AdS_n\times \Sigma ^{7-n}$ solutions in gauged supergravities with $CSO(p,q,5-p-q)$ and $CSO(p,q,4-p-q)$ gauge groups is presented in Sects. 3 and 4, respectively. Conclusions and comments on the results are given in Sect. 5. For convenience, we also collect all bosonic field equations of the maximal seven-dimensional gauged supergravity in the appendix.

2 $N=4$ gauged supergravity in seven dimensions

In this section, we briefly review seven-dimensional $N = 4$ gauged supergravity in the embedding tensor formalism constructed in [34]. We will omit all the detail and only collect relevant formulae involving the bosonic Lagrangian and fermionic supersymmetry transformations which are essential for finding supersymmetric solutions. The reader is referred to [34] for more detail.

The only $N=4$ supermultiplet in seven dimensions is the supergravity multiplet with the field content

$$\begin{aligned} \left( e^{{\hat{\mu }}}_\mu , \psi ^a_\mu , A^{MN}_\mu , B_{\mu \nu M}, \chi ^{abc}, {{\mathcal {V}}_M}^A\right) . \end{aligned}$$

(2.1)

The component fields are given by the graviton $e^{{\hat{\mu }}}_\mu$, four gravitini $\psi ^a_\mu$, ten vectors $A^{MN}_\mu =A^{[MN]}_\mu$, five two-form fields $B_{\mu \nu M}$, sixteen spin-$\frac{1}{2}$ fermions $\chi ^{abc}=\chi ^{[ab]c}$ and fourteen scalar fields described by the SL(5)/SO(5) coset representative ${{\mathcal {V}}_M}^A$. In this paper, curved and flat space-time indices are denoted by $\mu$, $\nu ,\ldots$ and ${\hat{\mu }}$, ${\hat{\nu }},\ldots$, respectively. Lower (upper) $M,N=1,\ldots ,5$ indices refer to the (anti-) fundamental representation 5 ($\overline{\mathbf {5}}$) of the global SL(5) symmetry.

Fermionic fields are described by symplectic Majorana spinors subject to the conditions

$$\begin{aligned} {\bar{\psi }}^T_{\mu a}=\Omega _{ab}C\psi _\mu ^b\quad \text {and}\quad {\bar{\chi }}^T_{abc}=\Omega _{ad}\Omega _{be}\Omega _{cf}C\chi ^{def} \end{aligned}$$

(2.2)

where C denotes the charge conjugation matrix obeying

$$\begin{aligned} C=C^T=-C^{-1}=-C^\dagger . \end{aligned}$$

(2.3)

These fermionic fields transform in representations of the local $SO(5)\sim USp(4)$ R-symmetry with USp(4) fundamental or SO(5) spinor indices $a,b,\ldots =1,\ldots ,4$. Accordingly, the four gravitini $\psi ^a_\mu$ and the spin-$\frac{1}{2}$ fields $\chi ^{abc}$ transform as $\mathbf {4}$ and $\mathbf {16}$, respectively. $\chi ^{abc}$ satisfy the following conditions

$$\begin{aligned} \chi ^{[abc]}=0\quad \text {and}\quad \Omega _{ab}\chi ^{abc}=0 \end{aligned}$$

(2.4)

with $\Omega _{ab}=\Omega _{[ab]}$ being the USp(4) symplectic form satisfying

$$\begin{aligned} (\Omega _{ab})^*=\Omega ^{ab}\quad \text {and}\quad \Omega _{ac}\Omega ^{bc}=\delta ^b_a. \end{aligned}$$

(2.5)

Raising and lowering of USp(4) indices by $\Omega ^{ab}$ and $\Omega _{ab}$ correspond to complex conjugation.

The fourteen scalars are described by the SL(5)/SO(5) coset representative ${\mathcal {V}_M}^A$, transforming under the global SL(5) and local SO(5) symmetries by left and right multiplications. Indices $M=1,2,\ldots , 5$ and $A=1,2,\ldots ,5$ are accordingly SL(5) and SO(5) fundamental indices, respectively. The SO(5) vector indices of ${\mathcal {V}_M}^A$ can be described by a pair of antisymmetric USp(4) fundamental indices as ${\mathcal {V}_M}^{ab}={\mathcal {V}_M}^{[ab]}$ satisfying the relation

$$\begin{aligned} {{\mathcal {V}}_M}^{ab}\Omega _{ab}=0. \end{aligned}$$

(2.6)

The inverse of ${{\mathcal {V}}_M}^A$ denoted by ${\mathcal {V}_A}^M$ will be written as ${{\mathcal {V}}_{ab}}^M$ with

$$\begin{aligned} {{\mathcal {V}}_M}^{ab}{{\mathcal {V}}_{ab}}^N= & {} \delta ^N_M \quad \text {and}\nonumber \\ {{\mathcal {V}}_{ab}}^M{{\mathcal {V}}_M}^{cd}= & {} \delta ^{[c}_{a}\delta ^{d]}_{b} -\frac{1}{4}\Omega _{ab}\Omega ^{cd}. \end{aligned}$$

(2.7)

The bosonic Lagrangian of the $N=4$ seven-dimensional gauged supergravity can be written as

$$\begin{aligned} e^{-1}{\mathcal {L}}= & {} \frac{1}{2}R-{\mathcal {M}}_{MP}{\mathcal {M}}_{NQ} {\mathcal {H}}_{\mu \nu }^{(2)MN}{\mathcal {H}}^{(2)PQ\mu \nu }\nonumber \\&-\frac{1}{6}{\mathcal {M}}^{MN}{\mathcal {H}}_{\mu \nu \rho M}^{(3)}{{\mathcal {H}}^{(3)\mu \nu \rho }}_ N\nonumber \\&+\frac{1}{8}(D_\mu {\mathcal {M}}_{MN})(D^\mu {\mathcal {M}}^{MN})-e^{-1} {\mathcal {L}}_{VT}-\mathbf {V} \nonumber \\ \end{aligned}$$

(2.8)

while the supersymmetry transformations of fermions read

$$\begin{aligned} \delta \psi ^a_\mu= & {} D_\mu \epsilon ^a-g\gamma _\mu A^{ab}_1\Omega _{bc}\epsilon ^c\nonumber \\&+\frac{1}{15}{\mathcal {H}}_{\nu \rho \lambda M}^{(3)}\left( {\gamma _\mu }^{\nu \rho \lambda }-\frac{9}{2}\delta ^\nu _\mu \gamma ^{\rho \lambda }\right) \Omega ^{ab}{{\mathcal {V}}_{bc}}^M\epsilon ^c\nonumber \\&+\frac{1}{5}{\mathcal {H}}_{\nu \rho }^{(2)MN}({\gamma _\mu }^{\nu \rho } -8\delta ^\nu _\mu \gamma ^{\rho }){{\mathcal {V}}_M}^{ad}\Omega _{de}{{\mathcal {V}}_N}^{eb}\Omega _{bc}\epsilon ^c, \nonumber \\ \end{aligned}$$

(2.9)

$$\begin{aligned} \delta \chi ^{abc}= & {} 2\Omega ^{cd}{P_{\mu de}}^{ab}\gamma ^\mu \epsilon ^e+gA^{d,abc}_2\Omega _{de}\epsilon ^e \nonumber \\&+2{\mathcal {H}}_{\mu \nu }^{(2)MN}\gamma ^{\mu \nu }\Omega _{de}\nonumber \\&\times \left[ {{\mathcal {V}}_M}^{cd}{{\mathcal {V}}_N}^{e[a}\epsilon ^{b]} -\frac{1}{5}\left( \Omega ^{ab}\delta ^c_g\right. \right. \nonumber \\&\left. \left. -\Omega ^{c[a}\delta ^{b]}_g\right) {{\mathcal {V}}_M}^{gf}\Omega _{fh}{{\mathcal {V}}_N}^{hd}\epsilon ^{e}\right] \nonumber \\&-\frac{1}{6}{\mathcal {H}}_{\mu \nu \rho M}^{(3)}\gamma ^{\mu \nu \rho }{{\mathcal {V}}_{fe}}^M\left[ \Omega ^{af}\Omega ^{be} \epsilon ^c\right. \nonumber \\&\left. -\frac{1}{5}\left( \Omega ^{ab}\Omega ^{cf}+4\Omega ^{c[a}\Omega ^{b]f}\right) \epsilon ^e\right] . \end{aligned}$$

(2.10)

The covariant derivative of the supersymmetry parameters is defined by

$$\begin{aligned} D_\mu \epsilon ^a=\nabla _\mu \epsilon ^a-{Q_{\mu b}}^a\epsilon ^b \end{aligned}$$

(2.11)

with $\nabla _\mu$ being the space-time covariant derivative. The composite connection ${Q_{\mu a}}^b$ and the vielbein on the SL(5)/SO(5) coset ${P_{\mu ab}}^{cd}$ are obtained from

$$\begin{aligned}&{P_{\mu ab}}^{cd}+2{Q_{\mu [a}}^{[c}\delta ^{d]}_{b]}\nonumber \\&\quad = {{\mathcal {V}}_{ab}}^M\left( \partial _\mu {{\mathcal {V}}_M}^{cd} -gA^{PQ}_\mu {X_{PQ,M}}^N{{\mathcal {V}}_N}^{cd}\right) . \end{aligned}$$

(2.12)

The gauge generators in the representation $\mathbf {5}$ of SL(5) can be written in term of the embedding tensor as

$$\begin{aligned} {X_{MN,P}}^Q= {\Theta _{MN,P}}^Q=\delta ^Q_{[M}Y_{N]P}-2\epsilon _{MNPRS}Z^{RS,Q}. \nonumber \\ \end{aligned}$$

(2.13)

Supersymmetry requires that the embedding tensor can have only two components given by the tensors ${Y}_{MN}$ and ${Z}^{MN,P}$ with $Y_{MN}=Y_{(MN)}$, $Z^{MN,P}=Z^{[MN],P}$ and $Z^{[MN,P]}=0$ corresponding to representations $\mathbf {15}$ and $\overline{\mathbf {40}}$ of SL(5), respectively.

The fermion shift matrices $A_1$ and $A_2$ are given by

$$\begin{aligned} A^{ab}_1= & {} -\frac{1}{4\sqrt{2}}\left( \frac{1}{4}B\Omega ^{ab} +\frac{1}{5}C^{ab}\right) , \end{aligned}$$

(2.14)

$$\begin{aligned} A^{d,abc}_2= & {} \frac{1}{2\sqrt{2}}\left[ \Omega ^{ec}\Omega ^{fd}\left( {C^{ab}}_{ef} -{B^{ab}}_{ef}\right) \right. \nonumber \\&\left. +\frac{1}{4}\left( C^{ab}\Omega ^{cd}+\frac{1}{5}\Omega ^{ab}C^{cd} +\frac{4}{5}\Omega ^{c[a}C^{b]d}\right) \right] \nonumber \\ \end{aligned}$$

(2.15)

with

$$\begin{aligned} B= & {} \frac{\sqrt{2}}{5}\Omega ^{ac}\Omega ^{bd}Y_{ab,cd}, \end{aligned}$$

(2.16)

$$\begin{aligned} {{B^{ab}}_{cd}}= & {} \sqrt{2}\left[ \Omega ^{ae}\Omega ^{bf}\delta ^{[g}_c \delta ^{h]}_d-\frac{1}{5}\left( \delta ^{[a}_c \delta ^{b]}_d\right. \right. \nonumber \\&\left. \left. -\frac{1}{4}\Omega ^{ab}\Omega _{cd}\right) \Omega ^{eg}\Omega ^{fh} \right] Y_{ef,gh}, \end{aligned}$$

(2.17)

$$\begin{aligned} C^{ab}= & {} 8\Omega _{cd}Z^{(ac)[bd]}, \end{aligned}$$

(2.18)

$$\begin{aligned} {C^{ab}}_{cd}= & {} 8\left( -\Omega _{ce}\Omega _{df}\delta ^{[a}_g \delta ^{b]}_h+\Omega _{g(c}\delta ^{[a}_{d)} \delta ^{b]}_e\Omega _{fh}\right) Z^{(ef)[gh]}.\nonumber \\ \end{aligned}$$

(2.19)

The “dressed” components of the embedding tensor are defined by

$$\begin{aligned} Y_{ab,cd}= & {} {{\mathcal {V}}_{ab}}^M{{\mathcal {V}}_{cd}}^NY_{MN}, \end{aligned}$$

(2.20)

$$\begin{aligned} \text {and}\quad Z^{(ac)[ef]}= & {} \sqrt{2}{{\mathcal {V}}_M}^{ab}{{\mathcal {V}}_N}^{cd} {{\mathcal {V}}_P}^{ef}\Omega _{bd}Z^{MN,P}. \end{aligned}$$

(2.21)

A unimodular symmetric matrix $\mathcal {M}_{MN}$ describing $SL(5)/SO(5)$ scalars in a manifestly SO(5) invariant manner is defined by

$$\begin{aligned} {\mathcal {M}}_{MN}={{\mathcal {V}}_M}^{ab}{{\mathcal {V}}_N}^{cd}\Omega _{ac}\Omega _{bd} \end{aligned}$$

(2.22)

together with its inverse

$$\begin{aligned} {\mathcal {M}}^{MN}={{\mathcal {V}}_{ab}}^M{{\mathcal {V}}_{cd}}^N\Omega ^{ac}\Omega ^{bd}\,. \end{aligned}$$

(2.23)

The scalar potential is given by

$$\begin{aligned} \mathbf {V}= & {} \frac{g^2}{64}\left[ 2{\mathcal {M}}^{MN}Y_{NP}{\mathcal {M}}^{PQ}Y_{QM} -\left( {\mathcal {M}}^{MN}Y_{MN}\right) ^2\right] \nonumber \\&+g^2Z^{MN,P}Z^{QR,S} \nonumber \\&\times \left( {\mathcal {M}}_{MQ}{\mathcal {M}}_{NR}{\mathcal {M}}_{PS}-{\mathcal {M}}_{MQ}{\mathcal {M}}_{NP}{\mathcal {M}}_{RS}\right) \nonumber \\= & {} -15A_1^{ab}A_{1 ab}+ \frac{1}{8}A_2^{a,bcd}A_{2 a,bcd} \end{aligned}$$

(2.24)

Unlike in the ungauged supergravity in which all three-form fields can be dualized to two-form fields, the field content of the gauged supergravity can incorporate massive two- and three-form fields. The degrees of freedom in the vector and tensor fields of the ungauged theory will be redistributed among massless and massive vector, two-form and three-form fields after gaugings. In general, with a proper gauge fixing of various tensor gauge transformations, there can be t self-dual massive three-form and s massive two-form fields for $s\equiv \text {rank}\ Z$ and $t\equiv \text {rank}\ Y$. In addition, there are $10-s$ massless vectors and $5-s-t$ massless two-form fields. It should be noted that $t+s\le 5$ by the quadratic constraint which ensures that the embedding tensor leads to gauge generators for a closed subalgebra of SL(5). Furthermore, more massive gauge fields can arise from broken gauge symmetry.

The field strength tensors of vector and two-form fields are defined by

$$\begin{aligned} {\mathcal {H}}_{\mu \nu }^{(2)MN}= & {} F^{MN}_{\mu \nu }+gZ^{MN,P}B_{\mu \nu P}, \end{aligned}$$

(2.25)

$$\begin{aligned} {\mathcal {H}}_{\mu \nu \rho M}^{(3)}= & {} gY_{MN}S^N_{\mu \nu \rho }+3D_{[\mu }B_{\nu \rho ]M}+6\epsilon _{MNPQR}A^{NP}_{[\mu } \nonumber \\&\times \Bigg (\partial _\nu A^{QR}_{\rho ]}+\frac{2}{3}g {X_{ST,U}}^QA^{RU}_\nu A^{ST}_{\rho ]}\Bigg ) \end{aligned}$$

(2.26)

with the usual non-abelian gauge field strength

$$\begin{aligned} F^{MN}_{\mu \nu }=2\partial _{[\mu }A^{MN}_{\nu ]}+g{(X_{PQ})_{RS}}^{MN} A^{PQ}_{[\mu }A^{RS}_{\nu ]}. \end{aligned}$$

(2.27)

These field strengths satisfy the following Bianchi identities

$$\begin{aligned} D_{[\mu }{\mathcal {H}}^{(2)MN}_{\nu \rho ]}= & {} \frac{1}{3}gZ^{MN,P} {\mathcal {H}}^{(3)}_{\mu \nu \rho P}, \end{aligned}$$

(2.28)

$$\begin{aligned} D_{[\mu }{\mathcal {H}}^{(3)}_{\nu \rho \lambda ] M}= & {} \frac{3}{2}\epsilon _{MNPQR}{\mathcal {H}}^{(2)NP}_{[\mu \nu } {\mathcal {H}}^{(2)QR}_{\rho \lambda ]}\nonumber \\&+\frac{1}{4}gY_{MN} {\mathcal {H}}^{(4)N}_{\mu \nu \rho \lambda } \end{aligned}$$

(2.29)

where the covariant field strengths of the three-form fields are given by

$$\begin{aligned} Y_{MN}{\mathcal {H}}^{(4)N}_{\mu \nu \rho \lambda }= & {} Y_{MN} \left[ 4D_{[\mu }S^N_{\nu \rho \lambda ]}+6F^{NP}_{[\mu \nu }B_{\rho \lambda ] P}\right. \nonumber \\&\left. +3gZ^{NP,Q}B_{[\mu \nu P}B_{\rho \lambda ] Q}\right. \nonumber \\&+4g\epsilon _{PQRVW}{X_{ST,U}}^VA^{NP}_{[\mu }A^{QR}_\nu A^{ST}_\rho A^{UW}_{\lambda ]}\nonumber \\&\left. +8\epsilon _{PQRST}A^{NP}_{[\mu }A^{QR}_\nu \partial _\rho A^{ST}_{\lambda ]}\right] . \end{aligned}$$

(2.30)

All of these fields interact with each other via the vector-tensor topological term ${\mathcal {L}}_{VT}$ whose explicit form can be found in [34].

3 Solutions from gaugings in $\mathbf {15}$ representation

We now consider supersymmetric $AdS_n\times \Sigma ^{7-n}$ solutions with gauge group $CSO(p,q,5-p-q)$ obtained from gaugings in $\mathbf {15}$ representation. In this case, non-vanishing components of the embedding tensor can be written as

$$\begin{aligned}&Y_{MN}=\text {diag}(\underbrace{1,..,1}_p,\underbrace{-1,..,-1}_q, \underbrace{0,..,0}_r),\nonumber \\&\qquad \qquad p+q+r=5. \end{aligned}$$

(3.1)

We will use the following choice of SO(5) gamma matrices to convert an SO(5) vector index to a pair of antisymmetric spinor indices

$$\begin{aligned} \Gamma _1= & {} -\sigma _2\otimes \sigma _2, \quad \Gamma _2=\mathbf {I}_2\otimes \sigma _1,\quad \Gamma _3=\mathbf {I}_2\otimes \sigma _3,\nonumber \\ \Gamma _4= & {} \sigma _1\otimes \sigma _2, \quad \Gamma _5=\sigma _3\otimes \sigma _2 \end{aligned}$$

(3.2)

where $\sigma _i$ are the usual Pauli matrices. $\Gamma _A$ satisfy the following relations

$$\begin{aligned} \{\Gamma _A,\Gamma _B\}= & {} 2\delta _{AB}\mathbf {I}_4,\quad (\Gamma _A)^{ab}=-(\Gamma _A)^{ba}, \nonumber \\ \Omega _{ab}(\Gamma _A)^{ab}= & {} 0, \quad ((\Gamma _A)^{ab})^*=\Omega _{ac}\Omega _{bd}(\Gamma _A)^{cd}, \end{aligned}$$

(3.3)

and the symplectic form of USp(4) is chosen to be

$$\begin{aligned} \Omega _{ab}=\Omega ^{ab}=\mathbf {I}_2\otimes i\sigma _2. \end{aligned}$$

(3.4)

The coset representative of the form ${\mathcal {V}_M}^{ab}$ and the inverse ${\mathcal {V}_{ab}}^M$ are then given by

$$\begin{aligned} {{\mathcal {V}}_M}^{ab}=\frac{1}{2} {{\mathcal {V}}_M}^A(\Gamma _A)^{ab}\quad \text {and}\quad {{\mathcal {V}}_{ab}}^M=\frac{1}{2} {{\mathcal {V}}_A}^M(\Gamma ^A)_{ab}. \end{aligned}$$

(3.5)

3.1 Supersymmetric $AdS_5\times \Sigma ^2$ solutions with $SO(2)\times SO(2)$ symmetry

We begin with solutions of the form $AdS_5\times \Sigma ^2$ with the metric ansatz given by

$$\begin{aligned} ds_7^2=e^{2U(r)}dx^2_{1,3}+dr^2+e^{2V(r)}ds^2_{\Sigma ^{2}_{k}}. \end{aligned}$$

(3.6)

$\Sigma ^2_k$ is a Riemann surface with the metric given by

$$\begin{aligned} ds^2_{\Sigma ^2_k}=d\theta ^2+f_k(\theta )^2d\varphi ^2, \end{aligned}$$

(3.7)

and $dx^2_{1,3}=\eta _{mn}dx^{m} dx^{n}$ with $m,n=0, \ldots ,3$ is the flat metric on the four-dimensional Minkowski space $Mkw_4$. The function $f_k(\theta )$ is defined by

$$\begin{aligned} f_k(\theta )={\left\{ \begin{array}{ll} \sin {\theta }, \ \ \quad k=+1 \\ \theta , \ \ \ \ \ \ \, \quad k=0\\ \sinh {\theta }, \quad k=-1 \end{array}\right. } \end{aligned}$$

(3.8)

with $k=1,0,-1$ corresponding to $S^2$, ${\mathbb {R}}^2$ and $H^2$, respectively.

With the following choice of vielbein

$$\begin{aligned} e^{{\hat{m}}}= & {} e^{U}dx^m, \quad e^{{\hat{r}}}=dr,\nonumber \\ e^{{\hat{\theta }}}= & {} e^{V}d\theta , \quad e^{{\hat{\varphi }}}=e^{V}f_{k}(\theta )d\varphi , \end{aligned}$$

(3.9)

we find the following non-vanishing components of the spin connection

$$\begin{aligned} \omega _{(1)}^{{\hat{m}}{\hat{r}}}=U'e^{{\hat{m}}}, \quad \omega _{(1)}^{{\hat{i}}{\hat{r}}}= V'e^{{\hat{i}}},\quad \omega _{(1)}^{{\hat{\varphi }}{\hat{\theta }}}=\frac{f'_{k}(\theta )}{f_{k}(\theta )}e^{-V}e^{{\hat{\varphi }}}\,. \end{aligned}$$

(3.10)

The index ${\hat{i}}={\hat{\theta }}, {\hat{\varphi }}$ is a flat index on $\Sigma ^2_{k}$, and $f'_k(\theta )=\frac{df_k(\theta )}{d\theta }$. The r-derivatives will be denoted by $'$ while a $'$ on any function with an explicit argument refers to the derivative of the function with respect to that argument.

We are interested in solutions with $SO(2)\times SO(2)$ symmetry. Among the fourteen scalars in SL(5)/SO(5) coset, there are two $SO(2)\times SO(2)$ singlet scalars corresponding to the following SL(5) non-compact generators

$$\begin{aligned} {\hat{Y}}_1=e_{1,1}+e_{2,2}-2e_{5,5}\quad \text {and}\quad {\hat{Y}}_2=e_{3,3}+e_{4,4}-2e_{5,5}. \end{aligned}$$

(3.11)

We have introduced GL(5) matrices defined by

$$\begin{aligned} (e_{IJ})_{MN}=\delta _{IM}\delta _{JN}. \end{aligned}$$

(3.12)

The SL(5)/SO(5) coset representative is then given by

$$\begin{aligned} {\mathcal {V}}=e^{\phi _1{\hat{Y}}_1+\phi _2{\hat{Y}}_2}\, . \end{aligned}$$

(3.13)

A general form of the embedding tensor for gauge groups with an $SO(2)\times SO(2)$ subgroup can be written as

$$\begin{aligned} Y_{MN}=\text {diag}(+1,+1,\sigma ,\sigma ,\rho ). \end{aligned}$$

(3.14)

This gives rise to SO(5) ($\rho =\sigma =1$), SO(4, 1) ($-\rho =\sigma =1$), SO(3, 2) ($\rho =-\sigma =1$), CSO(4, 0, 1) ($\rho =0$, $\sigma =1$) and CSO(2, 2, 1) ($\rho =0$, $\sigma =-1$) gauge groups.

With all these, we can straightforwardly compute the scalar potential

$$\begin{aligned} \mathbf {V}= & {} -\frac{1}{64}g^2e^{-2(\phi _1+\phi _2)}\left[ 8\sigma -\rho ^2e^{10(\phi _1+\phi _2)}\right. \nonumber \\&\left. +4\rho (e^{4\phi _1+6\phi _2}+\sigma e^{6\phi _1+4\phi _2})\right] . \end{aligned}$$

(3.15)

For SO(5) gauge group, this potential admits two $AdS_7$ critical points given by

$$\begin{aligned} \phi _1=\phi _2=0,\quad \mathbf {V}_0=-\frac{15}{64}g^2 \end{aligned}$$

(3.16)

and

$$\begin{aligned} \phi _1=\phi _2=\frac{1}{10}\ln {2},\quad \mathbf {V}_0=-\frac{5g^2}{16\times 2^{2/5}}. \end{aligned}$$

(3.17)

The former preserves $N=4$ supersymmetry with SO(5) symmetry while the latter is a non-supersymmetric $AdS_7$ vacuum with SO(4) symmetry. We note here that for $\phi _1=\phi _2$ the $SO(2)\times SO(2)$ symmetry is enhanced to SO(4). These two $AdS_7$ vacua have been identified long ago in [36].

To perform a topological twist on $\Sigma ^2_k$, we turn on the following $SO(2)\times SO(2)$ gauge fields

$$\begin{aligned} A^{12}_{(1)}= & {} -e^{-V}\frac{p_{1}}{k}\frac{f'_{k}(\theta )}{f_{k} (\theta )}e^{{\hat{\varphi }}}\quad \text {and}\nonumber \\ A^{34}_{(1)}= & {} -e^{-V}\frac{p_{2}}{k}\frac{f'_{k}(\theta )}{f_{k} (\theta )}e^{{\hat{\varphi }}} \end{aligned}$$

(3.18)

and set all the other fields to zero. By imposing the twist condition

$$\begin{aligned} g(p_1+\sigma p_2)=k \end{aligned}$$

(3.19)

together with the following projection conditions

$$\begin{aligned} \gamma ^{{\hat{\theta }}{\hat{\varphi }}}\epsilon ^a=-{(\Gamma _{12})^a}_b \epsilon ^b=-{(\Gamma _{34})^a}_b\epsilon ^b \end{aligned}$$

(3.20)

and

$$\begin{aligned} \gamma _r\epsilon ^a=\epsilon ^a, \end{aligned}$$

(3.21)

we can derive the BPS equations

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 2e^{-2\phi _1} +\rho e^{4(\phi _1+\phi _2)}+2\sigma e^{-2\phi _2}\right) \nonumber \\&-\frac{2}{5}e^{-2V}\left( e^{2\phi _1}p_1 +e^{2\phi _2}p_2\right) , \end{aligned}$$

(3.22)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 2e^{-2\phi _1} +\rho e^{4(\phi _1+\phi _2)}+2\sigma e^{-2\phi _2}\right) \nonumber \\&+\frac{8}{5}e^{-2V}\left( e^{2\phi _1}p_1 +e^{2\phi _2}p_2\right) , \end{aligned}$$

(3.23)

$$\begin{aligned} \phi _1'= & {} \frac{g}{20}\left( 3e^{-2\phi _1}-\rho e^{4(\phi _1 +\phi _2)}-2\sigma e^{-2\phi _2}\right) \nonumber \\&-\frac{2}{5}e^{-2V}\left( 3e^{2\phi _1}p_1-2e^{2\phi _2}p_2\right) , \end{aligned}$$

(3.24)

$$\begin{aligned} \phi _2'= & {} \frac{g}{20}\left( 3\sigma e^{-2\phi _2}-\rho e^{4(\phi _1+\phi _2)}-2 e^{-2\phi _1}\right) \nonumber \\&+\frac{2}{5}e^{-2V}\left( 2e^{2\phi _1}p_1-3e^{2\phi _2}p_2\right) . \end{aligned}$$

(3.25)

It can be readily verified that these BPS equations together with the twist condition (3.19) imply the second-ordered field equations. The radial component of the gravitino variations $\delta \psi ^a_r$ gives the usual solution for the Killing spinors

$$\begin{aligned} \epsilon ^a=e^{\frac{U}{2}}\epsilon ^a_{(0)} \end{aligned}$$

(3.26)

in which $\epsilon ^a_{(0)}$ are constant spinors.

By imposing the conditions $V'=\phi _1'=\phi _2'=0$ and $U'=\frac{1}{L_{\text {AdS}_5}}$ on the BPS equations, we find a class of $AdS_5$ fixed point solutions given by

$$\begin{aligned} e^{2V}&=-\frac{8\Bigg (e^{4\phi _1}p_1+2e^{2(\phi _1+\phi _2)}p_2\Bigg )}{g}, \end{aligned}$$

(3.27)

$$\begin{aligned} e^{10\phi _1}&=\frac{12p_1^2-24\sigma p_1^2p_2+22\sigma ^2 p_1p_2^2-8\sigma ^3p_2^3 -2K}{3p_1^3\rho \sigma ^2}, \end{aligned}$$

(3.28)

$$\begin{aligned} e^{2\phi _2}&=\frac{6p_1^3-15\sigma p_1^2p_2+13\sigma ^2 p_1p_2^2-4\sigma ^3p_2^3 +K}{p_2(9\sigma p_1p_2-6p_1^2-4\sigma ^2 p_2^2)}e^{2\phi _1}, \end{aligned}$$

(3.29)

$$\begin{aligned} L_{\text {AdS}_5}&=\frac{4(e^{4\phi _1}p_1+2e^{2(\phi _1+\phi _2)}p_2)}{g\left( e^{2\phi _1}p_1+e^{2\phi _2}p_2\right) } \end{aligned}$$

(3.30)

where

$$\begin{aligned} K=\left( 6p_1^2-9\sigma p_1p_2+4p_2^2\sigma ^2\right) \sqrt{(p_1^2-\sigma p_1p_2+\sigma ^2p_2^2)}. \end{aligned}$$

(3.31)

The $AdS_5$ fixed points do not exist in the case of $\rho =0$. Furthermore, it turns out that good $AdS_5$ fixed points exist only in SO(5) and SO(3, 2) gauge groups with $\rho =\sigma =1$ and $\rho =-\sigma =1$, respectively.

For SO(5) gauge group, there exist $AdS_5$ fixed points when

$$\begin{aligned} gp_2\ne -1,0,\quad gp_2\ne 0\quad \text {and}\quad gp_2<0\ \cup \ gp_2>1, \end{aligned}$$

(3.32)

for $\Sigma ^2=H^2, {\mathbb {R}}^2, S^2$, respectively. In deriving the above conditions, we have chosen $g>0$ for convenience. We emphasize here that the $AdS_5\times {\mathbb {R}}^2$ fixed point preserves sixteen supercharges while the $AdS_5\times H^2$ and $AdS_5\times S^2$ preserve only eight supercharges. This is due to the fact that no spin connection on ${\mathbb {R}}^2$ needs to be cancelled by performing a twist. In this case, the projector involving $\gamma _{{\hat{\theta }}{\hat{\varphi }}}$ is not needed. All these $AdS_5\times \Sigma ^2$ fixed points, dual to four-dimensional SCFTs from M5-branes, together with the corresponding RG flows from the supersymmetric $AdS_7$ vacuum have recently been discussed in [13].

In this work, we will extend the study of these RG flows by considering more general RG flows from the $N=4$ $AdS_7$ critical point to $AdS_5$ fixed points and then to singular geometries in the form of curved domain walls with $Mkw_4\times \Sigma ^2$ slices. According to the usual holographic interpretation, these geometries should be dual to non-conformal field theories in four dimensions arising from the RG flows from four-dimensional SCFTs dual to $AdS_5\times \Sigma ^2$ fixed points. The latter are in turn obtained from twisted compactifications of $N=(2,0)$ SCFT in six dimensions dual to the $N=4$ $AdS_7$ vacuum. Examples of these RG flows are given in Figs. 1, 2, and 3 for the cases of $AdS_5\times H^2$, $AdS_5\times {\mathbb {R}}^2$ and $AdS_5\times S^2$ fixed points, respectively. In these solutions, we have chosen the position of the $AdS_5\times \Sigma ^2$ fixed points to be $r=0$ and set $g=16$. We note here that one of the magnetic charges is fixed by the twist condition (3.19). In the numerical solutions, we have chosen $p_2$ to be the independent parameter.

Fig. 1

RG flows from the $N=4$ $AdS_7$ critical point as $r\rightarrow \infty$ to $AdS_5\times H^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $p_2=-\frac{1}{4}, -\frac{1}{24}, \frac{1}{4},4,$ respectively

Fig. 2

RG flows from the $N=4$ $AdS_7$ critical point as $r\rightarrow \infty$ to $AdS_5\times {\mathbb {R}}^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $p_2=-6, -2, \frac{1}{4},4$, respectively

Fig. 3

RG flows from the $N=4$ $AdS_7$ critical point as $r\rightarrow \infty$ to $AdS_5\times S^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $p_2=-12, -1, \frac{1}{8},1$, respectively

We can use the explicit uplift formulae given in [39, 40] to determine whether these IR singularities are physical by considering the (00)-component of the eleven-dimensional metric given by

$$\begin{aligned} {\hat{g}}_{00}=\Delta ^{\frac{1}{3}}g_{00}. \end{aligned}$$

(3.33)

The warped factor $\Delta$ is defined by

$$\begin{aligned} \Delta =\mathcal {M}^{MN}\delta _{MP}\delta _{NQ}\mu ^P\mu ^Q \end{aligned}$$

(3.34)

with $\mu ^M$, $M=1,2,\ldots , 5$, being the coordinates on $S^4$ and satisfying $\mu ^M\mu ^M=1$. Using the coset representative given in (3.13) and the $S^4$ coordinates

$$\begin{aligned} \mu ^M= & {} \left( \cos \xi ,\sin \xi \cos \psi \cos \alpha ,\sin \xi \cos \psi \sin \alpha ,\right. \nonumber \\&\left. \sin \xi \sin \psi \cos \beta ,\sin \xi \sin \psi \sin \beta \right) , \end{aligned}$$

(3.35)

we find the behavior of ${\hat{g}}_{00}$ along the flows as shown in Fig. 4. As can be seen from the figure, ${\hat{g}}_{00}\rightarrow 0$ near the singularities. These singularities are then physical according to the criterion given in [8]. Therefore, the singularities can be interpreted as holographic duals of non-conformal phases of the four-dimensional SCFTs obtained from twisted compactifications of six-dimensional $N=(2,0)$ SCFT on $\Sigma ^2$.

Fig. 4

The behavior of ${\hat{g}}_{00}$ along the RG flows from the $N=4$ $AdS_7$ critical point as $r\rightarrow \infty$ to $AdS_5\times \Sigma ^2$ fixed points and curved domain walls with $SO(2)\times SO(2)$ symmetry for $\Sigma ^2=H^2, {\mathbb {R}}^2, S^2$ in SO(5) gauge group

We now consider SO(3, 2) gauge group. In this case, we find new $AdS_5\times S^2$ fixed points in a small range, with $g>0$,

$$\begin{aligned} -\frac{1}{2}<g p_2<0. \end{aligned}$$

(3.36)

As in the previous case, these $AdS_5\times S^2$ solutions also preserve eight supercharges and are dual to $N=1$ SCFTs in four dimensions. In contrast to SO(5) gauge group, the vacuum solution in this case is given by a half-supersymmetric domain wall, see the solutions given in [41]. According to the DW/QFT correspondence, these solutions are expected to describe $N=(2,0)$ non-conformal field theories in six dimensions. The above $AdS_5\times S^2$ fixed points can be regarded as conformal fixed points in four dimensions arising from twisted compactifications of the $N=(2,0)$ field theories in six dimensions on $S^2$. In Fig. 5, we give examples of RG flows between the $AdS_5\times S^2$ fixed points and curved domain walls with the worldvolume given by $Mkw_4\times S^2$. The latter should describe non-conformal phases of the $N=1$ SCFTs in four dimensions. The two ends of the flows represent two possible non-conformal phases with $(\phi _1\rightarrow \infty ,\phi _2\rightarrow -\infty )$ and $(\phi _1\rightarrow -\infty ,\phi _2\rightarrow \infty )$. In all of these flow solutions, we have set $g=16$.

In Fig. 6, we give the behavior of the eleven-dimensional metric component ${\hat{g}}_{00}$ along the flows. This is obtained by using the consistent truncation of eleven-dimensional supergravity on $H^{p,q}$ given in [37]. The explicit form of ${\hat{g}}_{00}$ is similar to that given in (3.33) but with the warped factor $\Delta$ given by

$$\begin{aligned} \Delta =\mathcal {M}^{MN}\eta _{MP}\eta _{NQ}\mu ^P\mu ^Q. \end{aligned}$$

(3.37)

The tensor $\eta _{MN}=\text {diag}(1,\ldots ,1,-1,\ldots ,-1)$ is the SO(p, q) invariant tensor, and $\mu ^P$ are coordinates on $H^{p,q}$ satisfying $\mu ^P\mu ^Q\eta _{PQ}=1$. For SO(3, 2), we have a truncation of eleven-dimensional supergravity on $H^{3,2}$ with $\eta _{MN}=\text {diag}(1,1,1,-1,-1)$. From Fig. 6, we see that ${\hat{g}}_{00}\rightarrow 0$ on both sides of the flows. Therefore, all of these singularities are physically acceptable. We accordingly interpret these solutions as RG flows between $N=1$ SCFTs and non-conformal field theories in four dimensions obtained from twisted compactifications of $N=(2,0)$ field theory on $S^2$.

Fig. 5

RG flows between $AdS_5\times S^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(3, 2) gauge group. The blue, orange, green and red curves refer to $p_2=-\frac{1}{36}, -\frac{1}{48}, -\frac{1}{64},-\frac{1}{86}$, respectively

3.2 Supersymmetric $AdS_4\times \Sigma ^3$ solutions with SO(3) symmetry

We now carry out a similar analysis for supersymmetric solutions of the form $AdS_4\times \Sigma ^3$ with $\Sigma ^3$ being a 3-manifold with constant curvature. The ansatz for the metric takes the form of

$$\begin{aligned} ds_7^2=e^{2U(r)}dx_{1,2}^2+dr^2+e^{2V(r)}ds^2_{\Sigma ^{3}_{k}} \end{aligned}$$

(3.38)

where $dx^2_{1,2}=\eta _{mn}dx^{m} dx^{n}$, $m,n=0,1,2$ is the metric on the three-dimensional Minkowski space. The metric on $\Sigma ^3_{k}$ is given by

$$\begin{aligned} ds^2_{\Sigma ^3_{k}}=d\psi ^2+f_{k}(\psi )^2\left( d\theta ^2+\sin ^2{\theta }d \varphi ^2\right) \end{aligned}$$

(3.39)

with the function $f_k$ defined in (3.8).

Using the vielbein

$$\begin{aligned} e^{{\hat{m}}}= & {} e^{U}dx^m, \quad e^{{\hat{r}}}=dr,\quad e^{{\hat{\psi }}}= e^{V}d\psi , \nonumber \\ e^{{\hat{\theta }}}= & {} \ e^{V}f_{k}(\psi )d\theta , \quad e^{{\hat{\varphi }}} =e^{V}f_{k}(\psi )\sin {\theta }d\varphi , \end{aligned}$$

(3.40)

we find non-vanishing components of the spin connection as follow

$$\begin{aligned} \omega _{(1)}^{{\hat{m}}{\hat{r}}}= & {} U'e^{{\hat{m}}}, \quad \omega _{(1)}^{{\hat{i}}{\hat{r}}}= V'e^{{\hat{i}}},\quad \omega _{(1)}^{{\hat{\theta }}{\hat{\psi }}}=\frac{f'_{k}(\psi )}{f_{k}(\psi )} e^{-V}e^{{\hat{\theta }}},\nonumber \\ \omega _{(1)}^{{\hat{\varphi }}{\hat{\psi }}}= & {} \frac{f'_{k}(\psi )}{f_{k}(\psi )}e^{-V}e^{{\hat{\varphi }}}, \quad \omega _{(1)}^{{\hat{\varphi }}{\hat{\theta }}}=\frac{\cot \theta }{f_{k}(\psi )} e^{-V}e^{{\hat{\varphi }}} \end{aligned}$$

(3.41)

where ${\hat{i}}={\hat{\psi }}, {\hat{\theta }}, {\hat{\varphi }}$ is a flat index on $\Sigma ^3_{k}$. We will perform the twist by turning on $SO(3)\subset SO(3)\times SO(2)\subset SO(5)_R$ and $SO(3)_+\subset SO(3)_+\times SO(3)_-\sim SO(4)\subset SO(5)_R$ gauge fields with $SO(5)_R$ denoting the R-symmetry.

3.2.1 Solutions with SO(3) twists

We first consider solutions with $SO(3)\subset SO(5)_R$ twists by turning on the following SO(3) gauge fields

$$\begin{aligned} A^{12}_{(1)}= & {} -e^{-V}\frac{p}{k}\frac{f'_{k}(\psi )}{f_{k}(\psi )}e^{{\hat{\theta }}},\quad A^{13}_{(1)}=-e^{-V}\frac{p}{k}\frac{f'_{k}(\psi )}{f_{k}(\psi )}e^{{\hat{\varphi }}}, \nonumber \\ A^{23}_{(1)}= & {} -e^{-V}\frac{p}{k}\frac{\cot \theta }{f_{k}(\psi )}e^{{\hat{\varphi }}}. \end{aligned}$$

(3.42)

There are three SO(3) singlet scalars corresponding to the SL(5) noncompact generators

$$\begin{aligned} {\tilde{Y}}_1= & {} 2e_{1,1}+2e_{2,2}+2e_{3,3}-3e_{4,4}-3e_{5,5},\nonumber \\ {\tilde{Y}}_2= & {} e_{4,5}+e_{5,4},\nonumber \\ {\tilde{Y}}_3= & {} e_{4,4}-e_{5,5}. \end{aligned}$$

(3.43)

The SL(5)/SO(5) coset representative is then given by

$$\begin{aligned} {\mathcal {V}}=e^{\phi _1{\tilde{Y}}_1+\phi _2{\tilde{Y}}_2+\phi _3{\tilde{Y}}_3}. \end{aligned}$$

(3.44)

We will consider gauge groups with an SO(3) subgroup characterized by the embedding tensor of the form

$$\begin{aligned} Y_{MN}=\text {diag}(+1,+1,+1,\sigma ,\rho ). \end{aligned}$$

(3.45)

There are six possible gauge groups given by SO(5) ($\rho =\sigma =1$), SO(4, 1) ($-\rho =\sigma =1$), SO(3, 2) ($\rho =\sigma =-1$), CSO(4, 0, 1) ($\rho =0$, $\sigma =1$), CSO(3, 1, 1) ($\rho =0$, $\sigma =-1$), and CSO(3, 0, 2) ($\rho =\sigma =0$). With this embedding tensor and the coset representative (3.44), the scalar potential reads

$$\begin{aligned} \mathbf {V}= & {} -\frac{g^2}{64}\left[ 3e^{-8\phi _1}+6e^{2\phi _1} \left[ (\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3}\right. \right. \nonumber \\&\left. +(\rho -\sigma ) \sinh {2\phi _3}\right] \nonumber \\&+\frac{1}{4}e^{12\phi _1}\left[ -(\rho +\sigma )^2\cosh {4\phi _2} (1+\cosh {4\phi _3})\right. \nonumber \\&\left. -4(\rho ^2-\sigma ^2)\cosh {2\phi _2}\sinh {4\phi _3}\right. \nonumber \\&\left. \left. +\rho ^2+10\rho \sigma +\sigma ^2\right. \right. \nonumber \\&\left. \left. -(3\rho ^2-2\rho \sigma +3\sigma ^2)\cosh {4\phi _3}\right] \right] \end{aligned}$$

(3.46)

which admits supersymmetric $N=4$ and non-supersymmetric $AdS_7$ critical points given in (3.16) and (3.17) at $\phi _1=\phi _2=\phi _3=0$ and $\phi _1=\frac{1}{20}\ln {2}$, $\phi _2=\pm \frac{1}{4}\ln {2}$, and $\phi _3=0$, respectively.

We now impose a simple twist condition

$$\begin{aligned} gp=k \end{aligned}$$

(3.47)

and the following projectors on the Killing spinors

$$\begin{aligned} \gamma ^{{\hat{\psi }}{\hat{\theta }}} \epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b\quad \text {and} \quad \gamma ^{{\hat{\theta }}{\hat{\varphi }}}\epsilon ^a=-{(\Gamma _{23})^a}_b\epsilon ^b. \end{aligned}$$

(3.48)

With all other fields vanishing and the $\gamma _r$ projector given in (3.21), we obtain the BPS equations

$$\begin{aligned} U'&=\frac{g}{40}e^{6\phi _1}\left[ (\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3} +(\rho -\sigma )\sinh {2\phi _3}\right] \nonumber \\&\quad +\frac{3g}{40}e^{-4\phi _1} -\frac{6}{5}e^{-2(V-2\phi _1)}p, \end{aligned}$$

(3.49)

$$\begin{aligned} V'&=\frac{g}{40}e^{6\phi _1}\left[ (\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3} +(\rho -\sigma )\sinh {2\phi _3}\right] \nonumber \\&\quad +\frac{3g}{40}e^{-4\phi _1} +\frac{14}{5}e^{-2(V-2\phi _1)}p, \end{aligned}$$

(3.50)

$$\begin{aligned} \phi _1'&=\frac{g}{40}e^{6\phi _1}\left[ (\rho -\sigma )\sinh {2\phi _3} -(\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3}\right] \nonumber \\&\quad +\frac{g}{20}e^{-4\phi _1}-\frac{4}{5}e^{-2(V-2\phi _1)}p, \end{aligned}$$

(3.51)

$$\begin{aligned} \phi _2'&=-\frac{g}{8}e^{6\phi _1}(\rho +\sigma )\sinh {2\phi _2}\text {sech}{2\phi _3}, \end{aligned}$$

(3.52)

$$\begin{aligned} \phi _3'&=-\frac{g}{8}e^{6\phi _1}\left( (\rho +\sigma )\cosh {2\phi _2}\sinh {2\phi _3} +(\rho -\sigma )\cosh {2\phi _3}\right) . \end{aligned}$$

(3.53)

From these BPS equations, we find an $AdS_4\times H^3$ fixed point only for SO(5) gauge group given by

$$\begin{aligned} \phi _1= & {} \frac{1}{10}\ln 2,\quad \phi _2= \phi _3=0,\nonumber \\ V= & {} \ln \left[ \frac{16^{3/5}}{g}\right] ,\quad L_{AdS_4}=\frac{4\times 2^{2/5}}{g}. \end{aligned}$$

(3.54)

This is the $AdS_4\times H^3$ solution studied in [11]. The solution preserves eight supercharges and corresponds to $N=2$ SCFT in three dimensions. As in the previous case, in addition to the holographic RG flows from the supersymmetric $N=4$ $AdS_7$ vacuum to this $AdS_4\times H^3$ geometry, we also consider more general RG flows from the $AdS_4\times H^3$ fixed point to curved domain walls with a $Mkw_3\times H^3$ slice dual to $N=2$ non-conformal field theories in three dimensions.

Fig. 6

Profiles of ${\hat{g}}_{00}$ for RG flows between $N=1$ SCFTs and $N=1$ non-conformal field theories in four dimensions from SO(3, 2) gauge group

There are many possible RG flows of this type. The simplest possibility is given by RG flows with $\phi _2=\phi _3=0$ along the entire flows. Examples of these RG flows are given in Figs. 7 and 8 in which $\phi _1\rightarrow \infty$ and $\phi _1\rightarrow -\infty$, respectively. Both types of the singularities are physically acceptable as can be seen from the behavior of the (00)-component of the eleven-dimensional metric ${\hat{g}}_{00}$ given in Fig. 9. These singular geometries are then dual to $N=2$ non-conformal field theories in three dimensions obtained from twisted compactifications of the six-dimensional $N=(2,0)$ SCFT on $H^3$.

Fig. 7

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_4\times H^3$ fixed point and curved domain walls for SO(3) twists with $\phi _1\rightarrow \infty$. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

Fig. 8

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_4\times H^3$ fixed point and curved domain walls for SO(3) twists with $\phi _1\rightarrow -\infty$. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

Fig. 9

Behaviors of the (00)-component of the eleven-dimensional metric for the RG flows given in Figs. 7 and 8

Although $\phi _2$ and $\phi _3$ vanish at both $AdS_7$ and $AdS_4\times H^3$ fixed points, we can consider RG flows to curved domain walls with non-vanishing $\phi _2$ and $\phi _3$. Examples of various possible RG flows are given in Fig. 10. The behavior of ${\hat{g}}_{00}$ near the singularities, ${\hat{g}}_{00}\rightarrow \infty$, indicates that these singularities are unphysical by the criterion of [8].

Fig. 10

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_4\times H^3$ fixed point and curved domain walls for SO(3) twists with $\phi _1$, $\phi _2$ and $\phi _3$ non-vanishing. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

3.2.2 Solutions with $SO(3)_+$ twists

We now consider another twist given by turning on $SO(3)_+$ gauge fields. In this case, the $SO(3)_+$ is identified with the self-dual SO(3) subgroup of $SO(4)\sim SO(3)_+\times SO(3)_-\subset SO(5)$. We will accordingly turn on the following gauge fields

$$\begin{aligned} A^{12}_{(1)}=A^{34}_{(1)}= & {} -e^{-V}\frac{p}{2k}\frac{f'_{k}(\psi )}{f_{k}(\psi )}e^{{\hat{\theta }}},\nonumber \\ A^{13}_{(1)}=A^{24}_{(1)}= & {} -e^{-V}\frac{p}{2k}\frac{f'_{k}(\psi )}{f_{k}(\psi )}e^{{\hat{\varphi }}}, \nonumber \\ A^{23}_{(1)}=A^{14}_{(1)}= & {} -e^{-V}\frac{p}{2k}\frac{\cot \theta }{f_{k}(\psi )}e^{{\hat{\varphi }}}\, . \end{aligned}$$

(3.55)

The gauge groups containing $SO(3)_+\subset SO(4)$ are given by SO(5), SO(4, 1), and CSO(4, 0, 1). These groups can be gauged altogether by the following embedding tensor

$$\begin{aligned} Y_{MN}=\text {diag}(+1,+1,+1,+1,\rho ) \end{aligned}$$

(3.56)

with $\rho =1,-1,0$, respectively.

There is only one $SO(3)_+$ singlet scalar corresponding to the SL(5) non-compact generator

$$\begin{aligned} {\hat{Y}}=e_{1,1}+e_{2,2}+e_{3,3}+e_{4,4}-4e_{5,5}. \end{aligned}$$

(3.57)

It should be noted that this generator is invariant under a larger symmetry SO(4). With SL(5)/SO(5) coset representative of the form

$$\begin{aligned} {\mathcal {V}}=e^{\phi {\hat{Y}}}, \end{aligned}$$

(3.58)

the scalar potential is given by

$$\begin{aligned} \mathbf {V}=-\frac{g^2}{64}e^{-4\phi }\left( 8+8\rho e^{10\phi }-\rho ^2e^{20\phi }\right) . \end{aligned}$$

(3.59)

As expected, there is an $N=4$ supersymmetric $AdS_7$ critical point at $\phi =0$ and a non-supersymmetric, unstable, $AdS_7$ critical point at $\phi =\frac{1}{10}\ln {2}$.

To implement the twist, we impose the following projection conditions given in (3.48) and

$$\begin{aligned} {(\Gamma _{12})^a}_b\epsilon ^b={(\Gamma _{34})^a}_b\epsilon ^b. \end{aligned}$$

(3.60)

Together with the twist condition (3.47) and the $\gamma _r$ projection condition (3.21), we find the following BPS equations

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 4e^{-2\phi }+\rho e^{8\phi }\right) -\frac{6}{5}e^{-2(V-\phi )}p, \end{aligned}$$

(3.61)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 4e^{-2\phi }+\rho e^{8\phi }\right) +\frac{14}{5}e^{-2(V-\phi )}p, \end{aligned}$$

(3.62)

$$\begin{aligned} \phi '= & {} \frac{g}{20}\left( e^{-2\phi }-\rho e^{8\phi }\right) -\frac{3}{5}e^{-2(V-\phi )}p. \end{aligned}$$

(3.63)

As in the SO(3) twist, the BPS equations admit an $AdS_4\times H^3$ fixed point only for SO(5) gauge group. This $AdS_4\times H^3$ vacuum is given by

$$\begin{aligned} V= & {} \frac{1}{2}\ln \left[ \frac{8\times 2^{1/5}\times 5^{3/5}}{g^2}\right] ,\quad \phi =\frac{1}{10}\ln \left[ \frac{8}{5}\right] ,\nonumber \\ L_{\text {AdS}_4}= & {} \frac{2^{3/5}\times 5^{4/5}}{g} \end{aligned}$$

(3.64)

which does not seem to appear in the previously known results.

Unlike the previous case, this $AdS_4\times H^3$ fixed point preserves only four supercharges and corresponds to $N=1$ SCFT in three dimensions. We can similarly study numerical RG flows from the supersymmetric $AdS_7$ vacuum to this $AdS_4\times H^3$ fixed point and to curved domain walls dual to $N=1$ non-conformal field theories in three dimensions. Examples of these RG flows are given in Fig. 11. It can be seen again that the IR singularities are physical since ${\hat{g}}_{00}\rightarrow 0$ near the singularities.

For CSO(4, 0, 1) gauge group, we can analytically solve the BPS equations. The resulting solution is given by

$$\begin{aligned} \phi= & {} C+\frac{g}{160p}(4p{\tilde{r}}+{\tilde{C}})^2-\frac{3}{20} \ln (4p{\tilde{r}}+{\tilde{C}}), \end{aligned}$$

(3.65)

$$\begin{aligned} V= & {} 2\phi +\ln (4p{\tilde{r}}+{\tilde{C}}), \end{aligned}$$

(3.66)

$$\begin{aligned} U= & {} V-\ln (4p{\tilde{r}}+{\tilde{C}})+C'. \end{aligned}$$

(3.67)

The new radial coordinate ${\tilde{r}}$ is defined by $\frac{d{\tilde{r}}}{dr}=e^{-V}$. The integration constants ${\tilde{C}}$ and $C'$ can be neglected by shifting the coordinate ${\tilde{r}}$ and rescaling the coordinates $x^m$ on $Mkw_3$.

Setting $C'={\tilde{C}}=0$, we find the leading behavior of the solution at large ${\tilde{r}}$

$$\begin{aligned} \phi \sim {\tilde{r}}^2\quad \text {and} \quad U\sim V\sim 2\phi . \end{aligned}$$

(3.68)

In this limit, the contribution from the gauge fields to the BPS equations is highly suppressed due to $V\rightarrow \infty$. The asymptotic behavior is then identified with the standard, flat, domain wall found in [41]. Similar to the case of solutions with an asymptotically locally $AdS_7$ space, we will call this limit an asymptotically locally flat domain wall.

On the other hand, as ${\tilde{r}}\rightarrow 0$, we find

$$\begin{aligned}&\phi \sim -\frac{3}{20}\ln (4p{\tilde{r}}),\quad V\sim \frac{7}{10}\ln (4p{\tilde{r}}),\nonumber \\&U\sim -\frac{3}{10}\ln (4p{\tilde{r}}). \end{aligned}$$

(3.69)

We also note that, in this case, the complete truncation ansatz in term of type IIA theory on $S^3$ has been constructed in [42]. Therefore, the solution can be completely embedded in type IIA theory. In this paper, we are only interested in the time component of the ten-dimensional metric given by, see for example [41] for more detail,

$$\begin{aligned} {\hat{g}}_{00}=e^{2U+\frac{3}{2}\phi }. \end{aligned}$$

(3.70)

Using this result, we find that as ${\tilde{r}}\rightarrow 0$, ${\hat{g}}_{00}\rightarrow \infty$, so, in this case, the IR singularity is unphysical.

Fig. 11

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_4\times H^3$ fixed point and curved domain walls for $SO(3)_+$ twists. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

3.3 Supersymmetric $AdS_3\times \Sigma ^4$ solutions

In this section, we move on to the analysis of $AdS_3\times \Sigma ^4$ solutions. We will consider two types of the internal manifold $\Sigma ^4$ namely a Riemannian four-manifold $M^4$ with a constant curvature and a product of two Riemann surfaces $\Sigma ^2\times \Sigma ^2$ with SO(4) and $SO(2)\times SO(2)$ twists, respectively.

3.3.1 $AdS_3\times M^4$ solutions with SO(4) twists

As in the previous section, we will consider SO(4) symmetric solutions for SO(5), SO(4, 1) and CSO(4, 0, 1) gauge groups with the embedding tensor given in (3.56). To find $AdS_3\times M^4_k$ solutions, we use the following ansatz for the seven-dimensional metric

$$\begin{aligned} ds_7^2=e^{2U(r)}dx^2_{1,1}+dr^2+e^{2V(r)}ds^2_{M^{4}_{k}} \end{aligned}$$

(3.71)

with $dx^2_{1,1}=\eta _{mn}dx^{m} dx^{n}$ for $m,n=0,1$ being the metric on two-dimensional Minkowski space. The explicit form of the metric on $M^4_k$ is given by

$$\begin{aligned} ds^2_{\Sigma ^4_k}=d\chi ^2+f_k(\chi )^2\left[ d\psi ^2+\sin ^2{\psi } (d\theta ^2+\sin ^2{\theta }d\varphi ^2)\right] \end{aligned}$$

(3.72)

with $\chi , \psi , \theta \in [0,\frac{\pi }{2}]$, $\varphi \in [0,2\pi ]$ and $f_k(\chi )$ is the function defined in (3.8).

With the vielbein basis of the form

$$\begin{aligned} e^{{\hat{m}}}&= e^{U}dx^{m}, \quad e^{{\hat{r}}}=dr, \nonumber \\ e^{{\hat{\chi }}}&=e^{V}d\chi , \quad e^{{\hat{\psi }}}= e^{V}f_{k}(\chi )d\psi ,\nonumber \\ e^{{\hat{\theta }}}&= e^{V}f_{k}(\chi )\sin {\psi }d\theta , \nonumber \\ e^{{\hat{\varphi }}}&=e^{V}f_{k}(\chi )\sin {\psi }\sin {\theta }d\varphi , \end{aligned}$$

(3.73)

we obtain the following non-vanishing components of the spin connection

$$\begin{aligned} \omega _{(1)}^{{\hat{m}}{\hat{r}}}= & {} U'e^{{\hat{m}}}, \quad \omega _{(1)}^{{\hat{i}}{\hat{r}}}= V'e^{{\hat{i}}}, \nonumber \\ \omega _{(1)}^{{\hat{\psi }}{\hat{\chi }}}= & {} \frac{f'_{k}(\chi )}{f_{k}(\chi )}e^{-V}e^{{\hat{\psi }}},\quad \omega _{(1)}^{{\hat{\theta }}{\hat{\chi }}}=\frac{f'_{k}(\chi )}{f_{k}(\chi )} e^{-V}e^{{\hat{\theta }}},\nonumber \\ \omega _{(1)}^{{\hat{\varphi }}{\hat{\chi }}}= & {} \frac{f'_{k}(\chi )}{f_{k}(\chi )} e^{-V}e^{{\hat{\varphi }}},\quad \omega _{(1)}^{{\hat{\theta }}{\hat{\psi }}}= \frac{\cot \psi }{f_{k}(\chi )}e^{-V}e^{{\hat{\theta }}}, \nonumber \\ \omega _{(1)}^{{\hat{\varphi }}{\hat{\psi }}}= & {} \frac{\cot \psi }{f_{k}(\chi )} e^{-V}e^{{\hat{\varphi }}}, \quad \omega _{(1)}^{{\hat{\varphi }}{\hat{\theta }}}=\frac{\cot \theta }{f_{k}(\chi ) \sin {\psi }}e^{-V}e^{{\hat{\varphi }}} \end{aligned}$$

(3.74)

with ${\hat{i}},{\hat{j}}={\hat{3}},\ldots ,{\hat{6}}={\hat{\chi }}, {\hat{\psi }}, {\hat{\theta }}, {\hat{\varphi }}$ being flat indices on $M^4_k$.

We will perform a twist on $M^4_k$ by turning on SO(4) gauge fields to cancel the spin connection as follow

$$\begin{aligned} A^{IJ}_{(1)}=-\frac{p}{k}\delta ^{I+2}_{[{\hat{i}}}\delta ^{J+2}_{{\hat{j}}]} \left. \omega ^{{\hat{i}}{\hat{j}}}_{(1)}\right| _{M^4_k}. \end{aligned}$$

(3.75)

The corresponding two-form field strengths are given by

$$\begin{aligned} {\mathcal {H}}^{(2)IJ}_{{\hat{i}}{\hat{j}}}=F^{IJ}_{{\hat{i}}{\hat{j}}}= 2\delta ^{I+2}_{[{\hat{i}}}\delta ^{J+2}_{{\hat{j}}]}e^{-2V}p. \end{aligned}$$

(3.76)

For the SO(4) singlet scalar, we use the same coset representative given in (3.58). However, in this case, the three-form field strengths cannot vanish in order to satisfy the Bianchi’s identity for $\mathcal {H}^{(3)}_{\mu \nu \rho M}$ since the above gauge fields lead to non-vanishing $\epsilon _{MNPQR}\mathcal {H}_{(2)}^{NP}\wedge \mathcal {H}_{2}^{QR}$ terms. To preserve the residual SO(4) symmetry, only $\mathcal {H}^{(3)}_{\mu \nu \rho 5}$ is allowed. We also note that for SO(5) and SO(4, 1) gauge groups, the corresponding embedding tensor $Y_{MN}$ is non-degenerate. There are in total $t=\text {rank}Y=5$ massive three-form fields, so for these gauge groups, $\mathcal {H}^{(3)}_{\mu \nu \rho 5}$ is obtained by turning on the massive three-form $S^{(3)}_{\mu \nu \rho 5}$. On the other hand, for CSO(4, 0, 1) gauge group, we have $Y_{55}=0$, so the contribution to $\mathcal {H}^{(3)}_{\mu \nu \rho 5}$ comes from a massless two-form field $B_{\mu \nu 5}$. However, we are not able to determine a suitable ansatz for $B_{\mu \nu 5}$ in order to find a consistent set of BPS equations that are compatible with the second-ordered field equations. Accordingly, we will not consider the non-semisimple CSO(4, 0, 1) gauge group in the following analysis.

For SO(5) and SO(4, 1) gauge groups, the appropriate ansatz for the modified three-form field strength is given by

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{m}}{\hat{n}}{\hat{r}} 5}= -\frac{96}{g}\rho e^{-4(V+2\phi )}p^2\varepsilon _{{\hat{m}}{\hat{n}}}. \end{aligned}$$

(3.77)

Imposing the twist condition (3.47) and the projector in (3.21) together with additional projectors of the form

$$\begin{aligned}&\gamma ^{{\hat{\chi }}{\hat{\psi }}}\epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b,\quad \gamma ^{{\hat{\psi }}{\hat{\theta }}}\epsilon ^a=-{(\Gamma _{23})^a}_b\epsilon ^b,\nonumber \\&\gamma ^{{\hat{\theta }}{\hat{\varphi }}}\epsilon ^a=-{(\Gamma _{34})^a}_b\epsilon ^b, \end{aligned}$$

(3.78)

we find the BPS equations

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 4e^{-2\phi }+\rho e^{8\phi }\right) -\frac{12}{5}e^{-2V+2\phi }p\nonumber \\&+\frac{288}{5g}\rho e^{-4(V+\phi )}p^2, \end{aligned}$$

(3.79)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 4e^{-2\phi }+\rho e^{8\phi }\right) \nonumber \\&+\frac{18}{5}e^{-2V+2\phi }p-\frac{192}{5g}\rho e^{-4(V+\phi )}p^2, \end{aligned}$$

(3.80)

$$\begin{aligned} \phi '= & {} \frac{g}{20}\left( e^{-2\phi }-\rho e^{8\phi }\right) -\frac{6}{5}e^{-2V+2\phi }p\nonumber \\&-\frac{96}{5g}\rho e^{-4(V+\phi )}p^2. \end{aligned}$$

(3.81)

From these equations, we find an $AdS_3$ fixed point only for $k=-1$ and $\rho =1$. The resulting $AdS_3\times H^4$ solution is given by

$$\begin{aligned} V= & {} \frac{1}{2}\ln \left[ \frac{16\times 2^{3/5}\times 3^{2/5}}{g^2}\right] ,\quad \phi =\frac{1}{10}\ln \left[ \frac{3}{2}\right] ,\nonumber \\ L_{\text {AdS}_3}= & {} \frac{2\times 2^{4/5}\times 3^{1/5}}{g}. \end{aligned}$$

(3.82)

This is the $AdS_3\times H^4$ fixed point given in [11] for the maximal SO(5) gauged supergravity. The solution preserves four supercharges and corresponds to $N=(1,1)$ SCFT in two dimensions with SO(4) symmetry. As in the previous cases, we will consider RG flows from the supersymmetric $AdS_7$ vacuum to this $AdS_3\times H^4$ fixed point and curved domain walls. Examples of these RG flows are given in Fig. 12. Unlike the previous cases, the IR singularities in this case are unphysical due to the behavior ${\hat{g}}_{00}\rightarrow \infty$.

Fig. 12

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times H^4$ fixed point and curved domain walls for SO(4) twist in SO(5) gauge group. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

3.3.2 $AdS_3\times \Sigma ^2\times \Sigma ^2$ solutions with $SO(2)\times SO(2)$ twists

In this section, we consider the manifold $\Sigma ^4$ in the form of a product of two Riemann surfaces $\Sigma ^2_{k_1}\times \Sigma ^2_{k_2}$. The ansatz for the metric takes the form of

$$\begin{aligned} ds_7^2=e^{2U(r)}dx^2_{1,1}+dr^2+e^{2V(r)}ds^2_{\Sigma ^{2}_{k_1}} +e^{2W(r)}ds^2_{\Sigma ^{2}_{k_2}}\nonumber \\ \end{aligned}$$

(3.83)

in which the metrics on $\Sigma ^2_{k_1}$ and $\Sigma ^2_{k_2}$ are given in (3.7).

Using the following choice for the vielbein

$$\begin{aligned} e^{{\hat{m}}}&= e^{U}dx^{m}, \quad e^{{\hat{r}}}=dr,\quad e^{{\hat{\theta }}_1}=e^{V}d\theta _1,\nonumber \\ e^{{\hat{\varphi }}_1}&=e^{V}f_{k_1}(\theta _1)d\varphi _1,\quad e^{{\hat{\theta }}_2}=e^{W}d\theta _2, \nonumber \\ e^{{\hat{\varphi }}_2}&=e^{W}f_{k_2}(\theta _2)d\varphi _2, \end{aligned}$$

(3.84)

we obtain all non-vanishing components of the spin connection as follow

$$\begin{aligned} \omega _{(1)}^{{\hat{m}}{\hat{r}}}= & {} U'e^{{\hat{m}}}, \quad \omega _{(1)}^{{\hat{i}}_1{\hat{r}}}= V'e^{{\hat{i}}_1}, \quad \omega _{(1)}^{{\hat{i}}_2{\hat{r}}}= W'e^{{\hat{i}}_2},\nonumber \\ \omega _{(1)}^{{\hat{\varphi }}_1{\hat{\theta }}_1}= & {} \frac{f_{k_1}'(\theta _1)}{f_{k_1}(\theta _1)}e^{-V}e^{{\hat{\varphi }}_1},\quad \omega _{(1)}^{{\hat{\varphi }}_2{\hat{\theta }}_2} =\frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)} e^{-W}e^{{\hat{\varphi }}_2} \end{aligned}$$

(3.85)

with ${\hat{i}}_1={\hat{\theta }}_1, {\hat{\varphi }}_1$ and ${\hat{i}}_2={\hat{\theta }}_2, {\hat{\varphi }}_2$ being flat indices on $\Sigma ^2_{k_1}$ and $\Sigma ^2_{k_2}$, respectively.

As in other cases, we consider all gauge groups of the form CSO(p, q, r) with an $SO(2)\times SO(2)$ subgroup. These gauge groups are obtained from the embedding tensor given in (3.14). To perform the twist, we turn on the $SO(2)\times SO(2)$ gauge fields

$$\begin{aligned} A^{12}_{(1)}= & {} -\frac{p_{11}}{k_1}\frac{f_{k_1}'(\theta _1)}{f_{k_1} (\theta _1)}e^{-V}e^{{\hat{\varphi }}_1}-\frac{p_{12}}{k_2} \frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)}e^{-W}e^{{\hat{\varphi }}_2},\nonumber \\ A^{34}_{(1)}= & {} -\frac{p_{21}}{k_1}\frac{f_{k_1}'(\theta _1)}{f_{k_1} (\theta _1)}e^{-V}e^{{\hat{\varphi }}_1}-\frac{p_{22}}{k_2}\frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)}e^{-W}e^{{\hat{\varphi }}_2}. \nonumber \\ \end{aligned}$$

(3.86)

The corresponding modified two-form field strengths are given by

$$\begin{aligned} {\mathcal {H}}_{(2)}^{12}&=F^{12}_{(2)}= e^{-2V}p_{11}e^{{\hat{\theta }}_1}\wedge e^{{\hat{\varphi }}_1}+e^{-2W}p_{12}e^{{\hat{\theta }}_2}\wedge e^{{\hat{\varphi }}_2}, \nonumber \\ \end{aligned}$$

(3.87)

$$\begin{aligned} {\mathcal {H}}_{(2)}^{34}&=F^{34}_{(2)}= e^{-2V}p_{21}e^{{\hat{\theta }}_1}\wedge e^{{\hat{\varphi }}_1}+e^{-2W}p_{22}e^{{\hat{\theta }}_2}\wedge e^{{\hat{\varphi }}_2}.\nonumber \\ \end{aligned}$$

(3.88)

We also need to turn on the following three-form field strength

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{m}}{\hat{n}}{\hat{r}} 5}= \alpha e^{-2\left( V+W+2\phi _1+2\phi _2\right) }\varepsilon _{{\hat{m}}{\hat{n}}} \end{aligned}$$

(3.89)

in which $\alpha$ is a constant related to the magnetic charges by the relation

$$\begin{aligned} g\rho \alpha =-32(p_{12}p_{21}+p_{11}p_{22}). \end{aligned}$$

(3.90)

For $\rho =0$ corresponding to CSO(2, 2, 1) and CSO(4, 0, 1) gauge groups, we need to impose a relation on the magnetic charges

$$\begin{aligned} p_{12}p_{21}+p_{11}p_{22}=0 \end{aligned}$$

(3.91)

to ensure that the resulting BPS equations are compatible with all the second-ordered field equations.

Using the projection conditions (3.21) and

$$\begin{aligned} \gamma _{\hat{\theta _1}\hat{\varphi _1}}\epsilon ^a =\gamma _{\hat{\theta _2}\hat{\varphi _2}}\epsilon ^a= -{(\Gamma _{12})^a}_b\epsilon ^b=-{(\Gamma _{34})^a}_b\epsilon ^b \end{aligned}$$

(3.92)

together with the twist conditions

$$\begin{aligned} g(p_{11}+\sigma p_{21})=k_1\quad \text {and} \quad g(p_{12}+\sigma p_{22})=k_2, \end{aligned}$$

(3.93)

we obtain the following BPS equations

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 2e^{-2\phi _1}+\rho e^{4(\phi _1+\phi _2)} +2\sigma e^{-2\phi _2}\right) \nonumber \\&-\frac{3\alpha }{5g}e^{-2(V+W+\phi _1+\phi _2)}\nonumber \\&-\frac{2}{5}\left[ e^{-2V}\left( e^{2\phi _1}p_{11}+e^{2\phi _2}p_{21}\right) \right. \nonumber \\&\left. +e^{-2W}\left( e^{2\phi _1}p_{12}+e^{2\phi _2}p_{22}\right) \right] , \end{aligned}$$

(3.94)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 2e^{-2\phi _1}+\rho e^{4(\phi _1+\phi _2)} +2\sigma e^{-2\phi _2}\right) \nonumber \\&+\frac{2\alpha }{5g}e^{-2(V+W+\phi _1+\phi _2)} \nonumber \\&+\frac{2}{5}\left[ 4e^{-2V}\left( e^{2\phi _1}p_{11}+e^{2\phi _2}p_{21}\right) \right. \nonumber \\&\left. -e^{-2W}\left( e^{2\phi _1}p_{12}+e^{2\phi _2}p_{22}\right) \right] , \end{aligned}$$

(3.95)

$$\begin{aligned} W'= & {} \frac{g}{40}\left( 2e^{-2\phi _1}+\rho e^{4(\phi _1+\phi _2)} +2\sigma e^{-2\phi _2}\right) \nonumber \\&+\frac{2\alpha }{5g}e^{-2(V+W+\phi _1+\phi _2)}\nonumber \\&-\frac{2}{5}\left[ e^{-2V}\left( e^{2\phi _1}p_{11}+e^{2\phi _2}p_{21}\right) \right. \nonumber \\&\left. -4e^{-2W}\left( e^{2\phi _1}p_{12}+e^{2\phi _2}p_{22}\right) \right] , \end{aligned}$$

(3.96)

$$\begin{aligned} \phi _1'= & {} \frac{g}{20}\left( 3e^{-2\phi _1}-\rho e^{4(\phi _1+\phi _2)} -2\sigma e^{-2\phi _2}\right) \nonumber \\&+\frac{\alpha }{5g}e^{-2\left( V+W+\phi _1+\phi _2\right) }\nonumber \\&-\frac{2}{5}\left[ 3e^{2\phi _1}\left( e^{-2V}p_{11}+e^{-2W}p_{12}\right) \right. \nonumber \\&\left. -2e^{2\phi _2}\left( e^{-2V}p_{21}+e^{-2W}p_{22}\right) \right] , \end{aligned}$$

(3.97)

$$\begin{aligned} \phi _2'= & {} \frac{g}{20}\left( 3\sigma e^{-2\phi _2}-\rho e^{4(\phi _1+\phi _2)} -2e^{-2\phi _1}\right) \nonumber \\&+\frac{\alpha }{5g}e^{-2(V+W+\phi _1+\phi _2)}\nonumber \\&+\frac{2}{5}\left[ 2e^{2\phi _1}\left( e^{-2V}p_{11}+e^{-2W}p_{12}\right) \right. \nonumber \\&\left. -3e^{2\phi _2}\left( e^{-2V}p_{21}+e^{-2W}p_{22}\right) \right] . \end{aligned}$$

(3.98)

In deriving these equations, we have used the coset representative given in (3.13) for $SO(2)\times SO(2)$ singlet scalars.

From the BPS equations, we find a class of $AdS_3\times \Sigma ^2\times \Sigma ^2$ fixed point solutions

$$\begin{aligned} e^{2V}= & {} -\frac{16\left( e^{2\phi _1}p_{11}+e^{2\phi _2}p_{21}\right) }{ge^{4(\phi _1+\phi _2)}\rho }, \end{aligned}$$

(3.99)

$$\begin{aligned} ^{2W}= & {} -\frac{16\left( e^{2\phi _1}p_{12}+e^{2\phi _2}p_{22}\right) }{ge^{4(\phi _1+\phi _2)}\rho }, \end{aligned}$$

(3.100)

$$\begin{aligned} e^{10\phi _1}= & {} \frac{64\Theta \left[ 32(p_{12}p_{21}+p_{11}p_{22})-g\rho \alpha -64\sigma p_{21}p_{22}\right] ^2}{\left[ 32\sigma (p_{12}p_{21}+p_{11}p_{22}) -g\rho \sigma \alpha -64p_{11}p_{12}\right] ^3},\nonumber \\ \end{aligned}$$

(3.101)

$$\begin{aligned} e^{10\phi _2}= & {} \frac{64\Theta \left[ 32\sigma (p_{12}p_{21}+p_{11}p_{22}) -g\rho \sigma \alpha -64p_{11}p_{12}\right] ^2}{\left[ 32(p_{12}p_{21} +p_{11}p_{22})-g\rho \alpha -64\sigma p_{21}p_{22}\right] ^3},\nonumber \\ \end{aligned}$$

(3.102)

$$\begin{aligned} L_{\text {AdS}_3}= & {} \frac{8e^{2(\phi _1+\phi _2)}}{g(e^{2\phi _2} +e^{2\phi _1}\sigma )} \end{aligned}$$

(3.103)

with

$$\begin{aligned} \Theta= & {} \frac{\Xi \left[ 32\left( p_{12}p_{22} (p_{11}+p_{21}\sigma )-p_{12}^2 p_{21}-p_{11}p_{22}^2\sigma \right) +g\rho \alpha (p_{12}+p_{22}\sigma )\right] }{\rho \left[ 1024 p_{12}^2 p_{21}^2+(32 p_{11}p_{22}-g \rho \alpha )^2-64p_{12}p_{21}(32p_{11}p_{22}+g\rho \alpha )\right] }, \end{aligned}$$

(3.104)

$$\begin{aligned} \Xi= & {} 32\left[ p_{11}p_{21}(p_{12}+p_{22} \sigma )-p_{11}^2p_{22}-p_{12}p_{21}^2\sigma \right] \nonumber \\&+ g\rho \alpha (p_{11}+ p_{21}\sigma ). \end{aligned}$$

(3.105)

Among all the gauge groups with an $SO(2)\times SO(2)$ subgroup, it turns out that $AdS_3\times \Sigma ^2\times \Sigma ^2$ solutions are possible only for SO(5) and SO(3, 2) gauge groups with $\rho =\sigma =1$ and $\rho =-\sigma =1$, respectively. For SO(5) gauge group, the solutions have been extensively studied in [14]. For SO(3, 2) gauge group, all the $AdS_3\times \Sigma ^2\times \Sigma ^2$ solutions given here are new.

Following [14], we define the following two parameters to characterize the possible $AdS_3\times \Sigma ^2\times \Sigma ^2$ solutions

$$\begin{aligned} z_1=g(p_{11}-\sigma p_{21}) \quad \text { and } \quad z_2=g(p_{12}-\sigma p_{22}) \end{aligned}$$

(3.106)

where we have set $\rho =1$. In order for the $AdS_3$ fixed points to exist in SO(5) gauge group with $\sigma =1$, one of the Riemann surfaces must be negatively curved, and $AdS_3\times H^2\times \Sigma ^2$ solutions can be found within the regions in the parameter space $(z_1, z_2)$ shown in Fig. 13. These regions are the same as those given in [14]. The $AdS_3\times \Sigma ^2\times \Sigma ^2$ fixed points preserve four supercharges and correspond to $N=(2,0)$ SCFTs in two dimensions with $SO(2)\times SO(2)$ symmetry. Examples of RG flows with $g=16$ from the $N=4$ supersymmetric $AdS_7$ to $AdS_3\times H^2\times \Sigma ^2$ fixed points and curved domain walls in the IR are shown in Figs. 14, 15 and 16 for $\Sigma ^2=H^2,{\mathbb {R}}^2$ and $S^2$, respectively. All the IR singularities are physical with ${\hat{g}}_{00}\rightarrow 0$ near the singularities.

Fig. 13

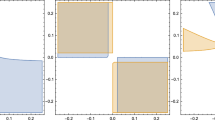
Regions (blue) in the parameter space $(z_1,z_2)$ where good $AdS_3$ vacua exist in SO(5) gauge group. From left to right, these figures correspond to the cases of $(k_1=k_2=-1)$, $(k_1=-1, k_2=0)$, $(k_1=-k_2=-1)$, respectively. The orange regions are obtained from interchanging $k_1$ and $k_2$

Fig. 14

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times H^2\times H^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $(z_1,z_2)=(0,0), (0.3,0.3), (-0.3,-0.3), (-1,0.5)$, respectively

Fig. 15

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times H^2\times {\mathbb {R}}^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $(z_1,z_2)=(1,-0.5), (-1,1), (1,-2), (-8,1)$, respectively

Fig. 16

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times H^2\times S^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $(z_1,z_2)=(-1,5), (1,-2), (1,-4), (-3,8)$, respectively

We now carry out a similar analysis for the case of SO(3, 2) gauge group with $\rho =-\sigma =1$. It turns out that in this case, the $AdS_3$ fixed points exist only for at least one of the two Riemann surfaces is positively curved. For definiteness, we will choose $k_1=1$ and $k_2=-1,0,1$ corresponding to $AdS_3\times S^2\times H^2$, $AdS_3\times S^2\times {\mathbb {R}}^2$ and $AdS_3\times S^2\times S^2$ fixed points, respectively. Using the parameters $z_1$ and $z_2$ defined in (3.106) with $\sigma =-1$, we find regions in the parameter space $(z_1, z_2)$ for $AdS_3$ vacua to exist in SO(3, 2) gauged maximal supergravity as shown in Fig. 17.

For SO(3, 2) gauge group, there is no asymptotically locally $AdS_7$ geometry. We will consider RG flows between the $AdS_3\times S^2\times \Sigma ^2$ fixed points and curved domain walls with $Mkw_3\times S^2\times \Sigma ^2$ slices. These curved domain walls have $SO(2)\times SO(2)$ symmetry and are expected to describe non-conformal field theories in two dimensions obtained from twisted compactifications of $N=(2,0)$ non-conformal field theory in six dimensions. The latter is dual to the half-supersymmetric domain wall of the seven-dimensional gauged supergravity. A number of these RG flows with $g=16$ and different values of $z_1$ and $z_2$ are given in Figs. 18, 19 and 20. We see that all singularities in the flows from $AdS_3\times S^2\times {\mathbb {R}}^2$ fixed points are unphysical while only the singularities on the right (left) with $\phi _1\rightarrow \infty$ and $\phi _2\rightarrow -\infty$ ($\phi _1\rightarrow -\infty$ and $\phi _2\rightarrow \infty$) in the flows from $AdS_3\times S^2\times S^2$ ($AdS_3\times S^2\times H^2$) fixed points are physical.

Fig. 17

Regions (blue) in the parameter space ($z_1$, $z_2$) where good $AdS_3$ vacua exist in SO(3, 2) gauge group. From left to right, these figures correspond to the cases of ($k_1=k_2=1$), ($k_1=1$, $k_2=0$), ($k_1=-k_2=1$), respectively. The orange regions are obtained from interchanging $k_1$ and $k_2$

Fig. 18

RG flows between $AdS_3\times S^2\times S^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(3, 2) gauge group. The blue, orange, green and red curves refer to $(z_1,z_2)=(-0.55,-0.55), (-0.55,-0.6), (-0.35,-0.87), (-1,-0.3)$, respectively

Fig. 19

RG flows between $AdS_3\times S^2\times {\mathbb {R}}^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(3, 2) gauge group. The blue, orange, green and red curves refer to $(z_1,z_2)=(\frac{1}{34},-\frac{1}{34}), (\frac{1}{34},-\frac{1}{26}), (\frac{1}{24},-\frac{1}{18}), (\frac{1}{36},-\frac{1}{8})$, respectively

Fig. 20

RG flows between $AdS_3\times S^2\times H^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(3, 2) gauge group. The blue, orange, green and red curves refer to $(z_1,z_2)=(\frac{1}{24},-18), (\frac{1}{16},-12), (\frac{1}{24},-24), (\frac{1}{16},-24)$, respectively

3.4 $AdS_3$ vacua from Kahler four-cycles

In this section, we consider twisted compactifications of six-dimensional field theories on Kahler four-cycles $K^4_k$. The constant $k=1,0,-1$ characterizes the constant curvature of $K^4_k$ and corresponds to a two-dimensional complex projective space $CP^2$, a four-dimensional flat space ${\mathbb {R}}^4$ and a two-dimensional complex hyperbolic space $CH^2$, respectively. The manifold $K^4_k$ has a $U(2)\sim U(1)\times SU(2)$ spin connection. Therefore, we can perform a twist by turning on $SO(2)\sim U(1)$ or $SO(3)\sim SU(2)$ gauge fields to cancel the U(1) or SU(2) parts of the spin connection.

A general ansatz for the seven-dimensional metric takes the form of

$$\begin{aligned} ds_7^2=e^{2U(r)}dx^2_{1,1}+dr^2+e^{2V(r)}ds^2_{K^{4}_{k}} \end{aligned}$$

(3.107)

in which the explicit form for the metric on the Kahler four-cycle will be specified separately in each case.

3.4.1 $AdS_3\times K^4_k$ solutions with SO(3) twists

We begin with a twist along the $SU(2)\sim SO(3)$ part of the spin connection and choose the following form of the metric on $K_k^4$

$$\begin{aligned} ds^2_{K^4_k}=d\psi ^2+f_k(\psi )^2\left( \tau _1^2+\tau _2^2+\tau _3^2\right) \end{aligned}$$

(3.108)

with $\psi \in [0,\frac{\pi }{2}]$, and $f_k(\psi )$ is the function defined in (3.8). $\tau _i$ are SU(2) left-invariant one-forms satisfying

$$\begin{aligned} d\tau _i=\frac{1}{2}\epsilon _{ijl}\tau _j\wedge \tau _l, \quad i,j,l=1,2,3. \end{aligned}$$

(3.109)

Their explicit forms are given by

$$\begin{aligned} \tau _1= & {} -\sin \vartheta d\theta +\cos \vartheta \sin \theta d \varphi ,\nonumber \\ \tau _2= & {} \cos \vartheta d\theta +\sin \vartheta \sin \theta d \varphi ,\nonumber \\ \tau _3= & {} d\vartheta +\cos \theta d \varphi \end{aligned}$$

(3.110)

where the ranges of the variables are $\theta \in [0,\pi ]$, $\varphi \in [0,2\pi ]$ and $\vartheta \in [0,4\pi ]$.

With the following choice of vielbein

$$\begin{aligned} e^{{\hat{m}}}= & {} e^{U}dx^{m}, \quad e^{{\hat{r}}}=dr, \quad e^{{\hat{3}}}=e^{V}f_k(\psi )\tau _1,\nonumber \\ e^{{\hat{4}}}= & {} e^{V}f_k(\psi )\tau _2, \quad e^{{\hat{5}}}=e^{V}f_k(\psi )\tau _3, \quad e^{{\hat{6}}}=e^{V}d\psi ,\nonumber \\ \end{aligned}$$

(3.111)

we find non-vanishing components of the spin connection

$$\begin{aligned} \omega _{(1)}^{{\hat{m}}{\hat{r}}}= & {} U'e^{{\hat{m}}}, \quad \omega _{(1)}^{{\hat{i}}{\hat{r}}}= V'e^{{\hat{i}}},\nonumber \\ \omega _{(1)}^{{\hat{3}}{\hat{6}}}= & {} f'_k(\psi )\tau _1,\quad \omega _{(1)}^{{\hat{4}}{\hat{5}}}= \tau _1,\nonumber \\ \omega _{(1)}^{{\hat{4}}{\hat{6}}}= & {} f'_k(\psi )\tau _2,\quad \omega _{(1)}^{{\hat{5}}{\hat{3}}}=\tau _2,\nonumber \\ \omega _{(1)}^{{\hat{5}}{\hat{6}}}= & {} f'_k(\psi )\tau _3,\quad \omega _{(1)}^{{\hat{3}}{\hat{4}}}=\tau _3 \end{aligned}$$

(3.112)

where ${\hat{i}}={\hat{3}}, \ldots , {\hat{6}}$ is the flat index on $K^4_k$. $\omega _{(1)}^{{\hat{i}}{\hat{j}}}$ are the SU(2) spin connections.

To perform the twist, we turn on SO(3) gauge fields with the following ansatz

$$\begin{aligned} A_{(1)}^{ij}=-\frac{p}{k}(f'_k(\psi )-1)\varepsilon ^{ijl}\tau _l, \end{aligned}$$

(3.113)

with the modified two-form field strengths given by

$$\begin{aligned} {\mathcal {H}}^{12}_{(2)}= & {} F^{12}_{(2)}=e^{-2V}p(e^{{\hat{3}}}\wedge e^{{\hat{4}}}-e^{{\hat{5}}}\wedge e^{{\hat{6}}}), \end{aligned}$$

(3.114)

$$\begin{aligned} {\mathcal {H}}^{23}_{(2)}= & {} F^{23}_{(2)}=e^{-2V}p(e^{{\hat{4}}}\wedge e^{{\hat{5}}}-e^{{\hat{3}}}\wedge e^{{\hat{6}}}), \end{aligned}$$

(3.115)

$$\begin{aligned} {\mathcal {H}}^{31}_{(2)}= & {} F^{31}_{(2)}=e^{-2V}p(e^{{\hat{5}}}\wedge e^{{\hat{3}}}-e^{{\hat{4}}}\wedge e^{{\hat{6}}}). \end{aligned}$$

(3.116)

Unlike the previous case, we do not need to turn on the three-form field strengths since, in this case, $\epsilon _{MNPQR}\mathcal {H}_{(2)}^{NP}\wedge \mathcal {H}_{(2)}^{QR}=0$.

We then impose the twist condition (3.47) together with the following three projection conditions

$$\begin{aligned}&\gamma ^{{\hat{3}}{\hat{4}}}\epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b,\quad \gamma ^{{\hat{4}}{\hat{5}}}\epsilon ^a=-{(\Gamma _{23})^a}_b\epsilon ^b,\nonumber \\&\gamma ^{{\hat{3}}{\hat{4}}}\epsilon ^a=-\gamma ^{{\hat{5}}{\hat{6}}}\epsilon ^a. \end{aligned}$$

(3.117)

Using the scalar coset representative (3.44) and the projection (3.21), we find the following BPS equations

$$\begin{aligned} U'&=\frac{g}{40}e^{6\phi _1}\left[ (\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3} +(\rho -\sigma )\sinh {2\phi _3}\right] \nonumber \\&\quad +\frac{3g}{40}e^{-4\phi _1} -\frac{12}{5}e^{-2(V-2\phi _1)}p, \end{aligned}$$

(3.118)

$$\begin{aligned} V'&=\frac{g}{40}e^{6\phi _1}\left[ (\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3} +(\rho -\sigma )\sinh {2\phi _3}\right] \nonumber \\&\quad +\frac{3g}{40}e^{-4\phi _1} +\frac{18}{5}e^{-2(V-2\phi _1)}p,\end{aligned}$$

(3.119)

$$\begin{aligned} \phi _1'&=\frac{g}{40}e^{6\phi _1}\left[ (\rho -\sigma )\sinh {2\phi _3}-(\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3}\right] \nonumber \\&\quad +\frac{g}{20}e^{-4\phi _1} -\frac{8}{5}e^{-2(V-2\phi _1)}p,\end{aligned}$$

(3.120)

$$\begin{aligned} \phi _2'&=-\frac{g}{8}e^{6\phi _1}(\rho +\sigma )\sinh {2\phi _2} \text {sech}{2\phi _3},\end{aligned}$$

(3.121)

$$\begin{aligned} \phi _3'&=-\frac{g}{8}e^{6\phi _1}\left( (\rho +\sigma )\cosh {2\phi _2}\sinh {2\phi _3} +(\rho -\sigma )\cosh {2\phi _3}\right) . \end{aligned}$$

(3.122)

It turns out that only SO(5) gauge group admits an $AdS_3\times CH^2$ fixed point given by

$$\begin{aligned} V= & {} \frac{1}{2}\ln \left[ \frac{16\times 3^{4/5}}{g^2}\right] ,\quad \phi _1=\frac{1}{10}\ln 3,\nonumber \\ \phi _2= & {} \phi _3=0,\quad L_{\text {AdS}_3}=\frac{8}{3^{3/5}g}\, . \end{aligned}$$

(3.123)

This is the $AdS_3\times CH^2$ solution found in [11]. The solution preserves four supercharges and corresponds to $N=(2,0)$ SCFT in two dimensions with $SO(3)\times SO(2)$ symmetry. It should be noted that for $\phi _2=\phi _3=0$, the scalar coset representative is invariant under $SO(3)\times SO(2)\subset SO(5)$. Examples of general RG flows from the supersymmetric $AdS_7$ critical point to the $AdS_3\times CH^2$ fixed point and curved domain walls are shown in Figs. 21, 22 and 23. From these figures, we find that both singularities for $\phi _1\rightarrow \pm \infty$ in the flows with $\phi _2=\phi _3=0$ are physical. On the other hand, the IR singularities in the flows with all $\phi _i$’s non-vanishing are unphysical due to ${\hat{g}}_{00}\rightarrow \infty$ near the singularities.

Fig. 21

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times CH^2$ fixed point and curved domain walls with $\phi _1\rightarrow \infty$ and $\phi _2=\phi _3=0$ for $SO(3)\sim SU(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

Fig. 22

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times CH^2$ fixed point and curved domain walls with $\phi _1\rightarrow -\infty$ and $\phi _2=\phi _3=0$ for $SO(3)\sim SU(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

Fig. 23

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times CH^2$ fixed point and curved domain walls with $\phi _1$, $\phi _2$ and $\phi _3$ non-vanishing for $SO(3)\sim SU(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

3.4.2 $AdS_3\times K^4_k$ solutions with $SO(3)_+$ twists

We now move to $AdS_3\times K^4_k$ solutions with the twist given by identifying the SU(2) part of the spin connection with the self-dual $SO(3)_+\subset SO(3)_+\times SO(3)_-\sim SO(4)$. We begin with the $SO(3)\times SO(3)$ gauge fields of the form

$$\begin{aligned} A^{ij}_{(1)}= & {} -\frac{p}{2k}(f'_k(\psi )-1)\epsilon ^{ijl}\tau _l\quad \text {and}\nonumber \\ A^{i4}_{(1)}= & {} -\frac{p}{2k}(f'_k(\psi )-1)\delta ^{ij}\tau _j. \end{aligned}$$

(3.124)

The self-dual SO(3) gauge fields can be defined as

$$\begin{aligned} A^{i}_{(1)}=\frac{1}{2}\epsilon ^{ijk}A^{jk}_{(1)}+ A^{i4}_{(1)}=-\frac{p}{k}(f'_k(\psi )-1)\tau _i. \end{aligned}$$

(3.125)

In this case, we perform the twist by imposing the twist condition (3.47) and the three projections given in (3.117) together with an additional projection for the self-duality of SO(3)

$$\begin{aligned} {(\Gamma _{12})^a}_b\epsilon ^b={(\Gamma _{34})^a}_b\epsilon ^b. \end{aligned}$$

(3.126)

Furthermore, by turning on the above SO(3) gauge fields, we need to turn on the modified three-form field strength of the form

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{m}}{\hat{n}}{\hat{r}} 5}= -\frac{192}{g}\rho e^{-4(V+2\phi )}p^2\varepsilon _{{\hat{m}}{\hat{n}}}. \end{aligned}$$

(3.127)

As in the case of SO(4) symmetric solutions, we will consider only SO(5) and SO(4, 1) gauge group with $\rho \ne 0$. Using the embedding tensor (3.56) and the SO(4) invariant coset representative (3.58), we find the following BPS equations

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 4e^{-2\phi }+\rho e^{8\phi }\right) -\frac{12}{5}e^{-2(V-\phi )}p \nonumber \\&+\frac{144}{5g}\rho e^{-4(V+\phi )}p^2, \end{aligned}$$

(3.128)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 4e^{-2\phi }+\rho e^{8\phi }\right) \nonumber \\&+\frac{18}{5}e^{-2(V-\phi )}p-\frac{96}{5g}\rho e^{-4(V+\phi )}p^2, \end{aligned}$$

(3.129)

$$\begin{aligned} \phi '= & {} \frac{g}{20}\left( e^{-2\phi }-\rho e^{8\phi }\right) \nonumber \\&-\frac{6}{5}e^{-2(V-\phi )}p-\frac{48}{5g}\rho e^{-4(V+\phi )}p^2 \end{aligned}$$

(3.130)

in which we have also imposed the $\gamma _r$ projection (3.21). From these equations, an $AdS_3$ fixed point is obtained only in SO(5) gauge group with $\rho =1$ and $k=-1$. This $AdS_3\times CH^2$ solution is given by

$$\begin{aligned} V= & {} \frac{1}{2}\ln \left[ \frac{4^{7/5}\times 3^{2/5}\times 7^{3/5}}{g^2}\right] ,\nonumber \\ \phi= & {} \frac{1}{10}\ln \left[ \frac{12}{7}\right] ,\quad L_{\text {AdS}_3}=\frac{4^{6/5}\times 3^{1/5}}{g^27^{1/5}} \end{aligned}$$

(3.131)

which is the $AdS_3\times CH^2$ fixed point found in [11]. The solution preserves two supercharges and corresponds to $N=(1,0)$ SCFT in two dimensions with SO(3) symmetry. Supersymmetric RG flows from the $N=4$ $AdS_7$ vacuum to this $AdS_3\times CH^2$ fixed point and curved domain walls in the IR are given in Fig. 24. The IR singularities are physically acceptable as indicated by the behavior ${\hat{g}}_{00}\rightarrow 0$.

Fig. 24

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times CH^2$ fixed point and curved domain walls for $SO(3)_+$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

3.4.3 $AdS_3\times K^4_k$ solutions with $SO(2)\times SO(2)$ twists

As a final case for $AdS_3\times K^4_k$ solutions, we will perform another twist on the Kahler four-cycle by cancelling the U(1) part of the spin connection. To make this U(1) part manifest, we write the metric on $K^4_k$ as

$$\begin{aligned} ds^2_{K^4_k}= & {} \frac{d\psi ^2}{(k\psi ^2+1)^2}+\frac{\psi ^2\tau _3^2}{(k\psi ^2+1)^2}+\frac{\psi ^2}{(k\psi ^2+1)}(\tau _1^2+\tau _2^2)\nonumber \\ \end{aligned}$$

(3.132)

with $\tau _i$ being the SU(2) left-invariant one-forms given in (3.110). The seven-dimensional metric is still given by (3.107) with $ds^2_{K^4_k}$ given by (3.132).

With the following vielbein

$$\begin{aligned} e^{{\hat{m}}}= & {} e^{U}dx^{m}, \quad e^{{\hat{r}}}=dr, \quad e^{{\hat{3}}}=\frac{e^{V}\psi }{\sqrt{k\psi ^2+1}}\tau _1,\nonumber \\ e^{{\hat{4}}}= & {} \ \frac{e^{V}\psi }{\sqrt{k\psi ^2+1}}\tau _2, \quad e^{{\hat{5}}}=\frac{e^{V}\psi }{(k\psi ^2+1)}\tau _3, \nonumber \\ e^{{\hat{6}}}= & {} \frac{e^{V}d\psi }{(k\psi ^2+1)}, \end{aligned}$$

(3.133)

all non-vanishing components of the spin connection are given by

$$\begin{aligned} \omega _{(1)}^{{\hat{m}}{\hat{r}}}= & {} U'e^{{\hat{m}}}, \quad \omega _{(1)}^{{\hat{i}}{\hat{r}}}= V'e^{{\hat{i}}},\quad {\hat{i}}={\hat{3}}, \ldots , {\hat{6}},\nonumber \\ \omega _{(1)}^{{\hat{3}}{\hat{6}}}= & {} \omega _{(1)}^{{\hat{4}}{\hat{5}}}=\frac{\tau _1}{\sqrt{k\psi ^2+1}},\quad \omega ^{{\hat{3}}{\hat{4}}}=\frac{(2k\psi ^2+1)}{(k\psi ^2+1)}\tau _3,\nonumber \\ \omega _{(1)}^{{\hat{5}}{\hat{6}}}= & {} \frac{(1-k\psi ^2)}{(k\psi ^2+1)}\tau _3,\quad \omega _{(1)}^{{\hat{5}}{\hat{3}}}=\omega _{(1)}^{{\hat{4}}{\hat{6}}} =\frac{\tau _2}{\sqrt{k\psi ^2+1)}}.\nonumber \\ \end{aligned}$$

(3.134)

To perform the twist, we turn on the $SO(2)\times SO(2)$ gauge fields

$$\begin{aligned} A^{12}_{(1)}=p_1\frac{3\psi ^2}{\sqrt{k\psi ^2+1}}\tau _3\quad \text {and}\quad A^{34}_{(1)}=p_2\frac{3\psi ^2}{\sqrt{k\psi ^2+1}}\tau _3\nonumber \\ \end{aligned}$$

(3.135)

and impose the following projection conditions on the Killing spinors

$$\begin{aligned} \gamma ^{{\hat{3}}{\hat{4}}}\epsilon ^a=-\gamma ^{{\hat{5}}{\hat{6}}} \epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b=-{(\Gamma _{34})^a}_b\epsilon ^b \end{aligned}$$

(3.136)

together with the twist condition (3.19). The associated two-form gauge field strengths are given by

$$\begin{aligned} {\mathcal {H}}^{12}_{(2)}= & {} F^{12}_{(2)}=3e^{-2V}p_1J_{(2)}\quad \text {and}\nonumber \\ {\mathcal {H}}^{34}_{(2)}= & {} F^{34}_{(2)}=3e^{-2V}p_2J_{(2)} \end{aligned}$$

(3.137)

where $J_{(2)}$ is the Kahler structure defined by

$$\begin{aligned} J_{(2)}=e^{{\hat{3}}}\wedge e^{{\hat{4}}}-e^{{\hat{5}}}\wedge e^{{\hat{6}}}. \end{aligned}$$

(3.138)

With the above non-vanishing $SO(2)\times SO(2)$ gauge fields, we need to turn on the modified three-form field strength of the form

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{m}}{\hat{n}}{\hat{r}} 5}= \frac{576}{g}\rho e^{-4\left( V+\phi _1+\phi _2\right) }p_1p_2 \varepsilon _{{\hat{m}}{\hat{n}}} \end{aligned}$$

(3.139)

with $\rho$ being the parameter in the embedding tensor (3.14) for gauge groups with an $SO(2)\times SO(2)$ subgroup. As in the previous cases, the appearance of $\rho$ in (3.89) implies that the resulting BPS equations are not compatible with the field equations for the case of $\rho =0$. In subsequent analysis, we will accordingly consider only gauge groups with $\rho \ne 0$.

With the $\gamma _r$ projector (3.21) and the scalar coset representative (3.13), the corresponding BPS equations read

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 2e^{-2\phi _1}+\rho e^{4(\phi _1+\phi _2)}+2\sigma e^{-2\phi _2}\right) \nonumber \\&-\frac{12}{5}e^{-2V}\left( e^{2\phi _1}p_1+e^{2\phi _2}p_2\right) \nonumber \\&+\frac{1728}{5g}\rho e^{-2(2V+\phi _1+\phi _2)}p_1p_2,\end{aligned}$$

(3.140)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 2e^{-2\phi _1}+\rho e^{4(\phi _1+\phi _2)}+2\sigma e^{-2\phi _2}\right) \nonumber \\&+\frac{18}{5}e^{-2V}\left( e^{2\phi _1}p_1+e^{2\phi _2}p_2\right) \nonumber \\&-\frac{1152}{5g}\rho e^{-2(2V+\phi _1+\phi _2)}p_1p_2,\end{aligned}$$

(3.141)

$$\begin{aligned} \phi _1'= & {} \frac{g}{20}\left( 3e^{-2\phi _1}-\rho e^{4(\phi _1+\phi _2)}-2\sigma e^{-2\phi _2}\right) \nonumber \\&-\frac{12}{5}e^{-2V}\left( 3e^{2\phi _1}p_1-2e^{2\phi _2}p_2\right) \nonumber \\&-\frac{576}{5g} \rho e^{-2(2V+\phi _1+\phi _2)}p_1p_2,\end{aligned}$$

(3.142)

$$\begin{aligned} \phi _2'= & {} \frac{g}{20}\left( 3\sigma e^{-2\phi _2}-\rho e^{4(\phi _1+\phi _2)}-2 e^{-2\phi _1}\right) \nonumber \\&+\frac{12}{5}e^{-2V}\left( 2e^{2\phi _1}p_1-3e^{2\phi _2}p_2\right) \nonumber \\&-\frac{576}{5g}\rho e^{-2(2V+\phi _1+\phi _2)}p_1p_2. \end{aligned}$$

(3.143)

From these equations, we find the following $AdS_3$ fixed point solutions

$$\begin{aligned} e^{2V}= & {} -\frac{48(p_1e^{2\phi _1}+p_2e^{2\phi _2})}{g\rho e^{4(\phi _1+\phi _2)}}, \end{aligned}$$

(3.144)

$$\begin{aligned} e^{10\phi _1}= & {} \frac{p_2^2\rho \left( (p_1+p_1\rho ^2-p_2\sigma )(p_1 +p_2\sigma )\right) ^2}{p_1^3(2+\rho ^2)(p_2(1+\rho ^2)\sigma -p_1)^3}, \end{aligned}$$

(3.145)

$$\begin{aligned} e^{10\phi _2}= & {} \frac{p_1^2\rho \left( p_1-p_2(1+\rho ^2)\sigma )(p_1 +p_2\sigma )\right) ^2}{p_2^3(2+\rho ^2)(p_1+p_1\rho ^2-p_2\sigma )^3}, \end{aligned}$$

(3.146)

$$\begin{aligned} L_{\text {AdS}_3}= & {} \frac{8e^{-4(\phi _1+\phi _2)}(p_1e^{2\phi _1} +p_2e^{2\phi _2})^2}{g\rho \left( p_1^2e^{4\phi _1}+p_2^2e^{4\phi _2}+2p_1p_2e^{2(\phi _1 +\phi _2)}(1+\rho ^2)\right) }.\nonumber \\ \end{aligned}$$

(3.147)

These solutions preserve four supercharges and are dual to $N=(2,0)$ two-dimensional SCFTs.

For SO(5) gauge group, there exist $AdS_3\times CH^2$ fixed points in the range

$$\begin{aligned} -\frac{2}{3}<gp_2<-\frac{1}{3} \end{aligned}$$

(3.148)

in which we have taken $g>0$ for convenience. Up to some differences in notations, these $AdS_3\times CH^2$ fixed points are the same as the solutions studied in [14]. As in the previous cases, we study RG flows from the supersymmetric $AdS_7$ vacuum to the $AdS_3\times CH^2$ fixed points and curved domain walls in the IR. Some examples of these flows are given in Fig. 25 for $g=16$ and different values of $p_2$. The behaviors of the eleven-dimensional metric component ${\hat{g}}_{00}$ for these RG flows are shown in Fig. 26 which indicates that the singularities are physical.

Fig. 25

RG flows from the $N=4$ $AdS_7$ critical point to the $AdS_3\times CH^2$ fixed point and curved domain walls for $SO(2)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $p_2=-\frac{1}{25}, -\frac{1}{31}, -\frac{1}{40}, -\frac{1}{46}$, respectively

Apart from these $AdS_3\times CH^2$ fixed points, we find new $AdS_3\times CP^2$ fixed points in SO(4, 1) and SO(3, 2) gauge groups respectively in the following ranges, with $g>0$,

$$\begin{aligned} g p_2<0 \ \cup \ g p_2>1 \quad \text {and} \quad -\frac{(3-\sqrt{3})}{6}<g p_2<-\frac{2}{3}.\nonumber \\ \end{aligned}$$

(3.149)

Since there is no supersymmetric $AdS_7$ critical point for SO(4, 1) and SO(3, 2) gauge groups, we will study supersymmetric RG flows between these $AdS_3\times CP^2$ fixed points and curved domain walls with $SO(2)\times SO(2)$ symmetry. Examples of these RG flows in SO(4, 1) and SO(3, 2) gauge groups are shown respectively in Figs. 27 and 28 with $g=16$ and different values of $p_2$. From the behaviors of ${\hat{g}}_{00}$ in Fig. 29, we find that the singularities on the left (right) with $\phi _1\rightarrow \pm \infty$ and $\phi _2\rightarrow \mp \infty$ ($\phi _1\rightarrow \infty$ and $\phi _2\rightarrow - \infty$) of the flows in SO(4, 1) (SO(3, 2)) gauge group are physical.

3.5 Supersymmetric $AdS_2\times \Sigma ^5$ solutions

We end this section by considering solutions of the form $AdS_2\times \Sigma ^5$. $AdS_2\times \Sigma ^5$ solutions for the manifold $\Sigma ^5$ being $S^5$ or $H^5$ have been given in [11]. The twist is performed by turning on SO(5) gauge fields. This is obviously possible only for SO(5) gauge group. In addition, no scalars in SL(5)/SO(5) coset are singlets under SO(5), so the solutions are given purely in term of the seven-dimensional metric. The corresponding RG flows from the supersymmetric $AdS_7$ vacuum and the $AdS_2\times H^5$ or $AdS_2\times S^5$ fixed points have already been analytically given in [11]. We will not repeat the analysis for this case here.

However, if we consider $\Sigma ^5$ as a product of three- and two-manifolds $\Sigma ^3\times \Sigma ^2$, it is possible to perform a twist by turning on $SO(3)\times SO(2)$ gauge fields along $\Sigma ^3\times \Sigma ^2$. In this case, there are two gauge groups with an $SO(3)\times SO(2)$ subgroup namely SO(5) and SO(3, 2). The ansatz for the seven-dimensional metric takes the form of

$$\begin{aligned} ds_7^2=-e^{2U(r)}dt^2+dr^2+e^{2V(r)}ds^2_{\Sigma ^{3}_{k_1}} +e^{2W(r)}ds^2_{\Sigma ^{2}_{k_2}}.\nonumber \\ \end{aligned}$$

(3.150)

The explicit form of the metrics on the $\Sigma ^{3}_{k_1}$ and $\Sigma ^{2}_{k_2}$ are given in (3.39) and (3.7), respectively.

Using the vielbein

$$\begin{aligned} e^{{\hat{t}}}= & {} e^{U}dt, \quad e^{{\hat{r}}}=dr,\quad e^{{\hat{\theta }}_2}=e^{W}d\theta _2,\nonumber \\ e^{{\hat{\varphi }}_2}= & {} e^{W}f_{k_2}(\theta _2)d\varphi _2,\nonumber \\ e^{{\hat{\psi }}_1}= & {} e^{V}d\psi _1, \quad e^{{\hat{\theta }}_1}= e^{V}f_{k_1}(\psi _1)d\theta _1,\nonumber \\ e^{{\hat{\varphi }}_1}= & {} e^{V}f_{k_1}(\psi _1)\sin {\theta _1}d\varphi _1, \end{aligned}$$

(3.151)

we find non-vanishing components of the spin connection as follow

$$\begin{aligned} \omega _{(1)}^{{\hat{t}}{\hat{r}}}= & {} U'e^{{\hat{t}}}, \quad \omega _{(1)}^{{\hat{i}}_1{\hat{r}}}= V'e^{{\hat{i}}_1}, \quad \omega _{(1)}^{{\hat{i}}_2{\hat{r}}}= W'e^{{\hat{i}}_2},\nonumber \\ \omega _{(1)}^{{\hat{\theta }}_1{\hat{\psi }}_1}= & {} \frac{f'_{k_1}(\psi _1)}{f_{k_1}(\psi _1)}e^{-V}e^{{\hat{\theta }}_1},\quad \omega _{(1)}^{{\hat{\varphi }}_1{\hat{\psi }}_1}=\frac{f'_{k_1}(\psi _1)}{f_{k_1}(\psi _1)}e^{-V}e^{{\hat{\varphi }}_1}, \nonumber \\ \omega _{(1)}^{{\hat{\varphi }}_1{\hat{\theta }}_1}= & {} \frac{\cot \theta _1}{f_{k_1}(\psi _1)}e^{-V}e^{{\hat{\varphi }}_1},\quad \omega _{(1)}^{{\hat{\varphi }}_2{\hat{\theta }}_2}=\frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)}e^{-W}e^{{\hat{\varphi }}_2}\nonumber \\ \end{aligned}$$

(3.152)

where ${\hat{i}}_1={\hat{\psi }}_1, {\hat{\theta }}_1, {\hat{\varphi }}_1$ and ${\hat{i}}_2={\hat{\theta }}_2, {\hat{\varphi }}_2$ are flat indices on $\Sigma ^3_{k_1}$ and $\Sigma ^2_{k_2}$, respectively.

Fig. 26

Profiles of the eleven-dimensional metric component ${\hat{g}}_{00}$ for the RG flows given in Fig. 25

Fig. 27

RG flows between $AdS_3\times CP^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(4, 1) gauge group. The blue, orange, green and red curves refer to $p_2=\frac{1}{2}, -\frac{1}{4}, 4, -8, -\frac{1}{47}$, respectively

Fig. 28

RG flows between $AdS_3\times CP^2$ fixed points and curved domain walls for $SO(2)\times SO(2)$ twist in SO(3, 2) gauge group. The blue, orange, green and red curves refer to $p_2=-\frac{1}{23}, -\frac{1}{22}, -\frac{1}{21}, -\frac{2}{41}$, respectively

Fig. 29

Profiles of the eleven-dimensional metric component ${\hat{g}}_{00}$ for the RG flows between $AdS_3\times CP^2$ fixed points and curved domain walls in SO(4, 1) and SO(3, 2) gauge groups

There is only one $SO(3)\times SO(2)$ invariant scalar field corresponding to the following non-compact generator

$$\begin{aligned} {\mathcal {Y}}=2e_{1,1}+2e_{2,2}+2e_{3,3}-3e_{4,4}-3e_{5,5}. \end{aligned}$$

(3.153)

Therefore, the SL(5)/SO(5) coset representative is parametrized by

$$\begin{aligned} {\mathcal {V}}=e^{\phi {\mathcal {Y}}}. \end{aligned}$$

(3.154)

We now turn on the $SO(3)\times SO(2)$ gauge fields of the form

$$\begin{aligned} A^{12}_{(1)}&= -\frac{p_1}{k_1}\frac{f'_{k_1}(\psi _1)}{f_{k_1}(\psi _1)}e^{-V}e^{{\hat{\theta }}_1},\nonumber \\ A^{13}_{(1)}&=-\frac{p_1}{k_1}\frac{f'_{k_1}(\psi _1)}{f_{k_1}(\psi _1)} e^{-V}e^{{\hat{\varphi }}_1},\nonumber \\ A^{23}_{(1)}&= -\frac{p_1}{k_1}\frac{\cot (\theta _1)}{f_{k_1}(\psi _1)}e^{-V}e^{{\hat{\varphi }}_1}, \nonumber \\ A^{45}_{(1)}&=-\frac{p_2}{k_2}\frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)} e^{-W}e^{{\hat{\varphi }}_2} \end{aligned}$$

(3.155)

with the corresponding two-form field strengths given by

$$\begin{aligned} {\mathcal {H}}^{(2)12}_{{\hat{\psi }}_1{\hat{\theta }}_1}&= F^{12}_{{\hat{\psi }}_1{\hat{\theta }}_1}=e^{-2V}p_1,\nonumber \\ {\mathcal {H}}^{(2)23}_{{\hat{\theta }}_1{\hat{\varphi }}_1}&=F^{23}_{{\hat{\theta }}_1{\hat{\varphi }}_1}=e^{-2V}p_1,\nonumber \\ {\mathcal {H}}^{(2)31}_{{\hat{\varphi }}_1{\hat{\psi }}_1}&= F^{31}_{{\hat{\varphi }}_1{\hat{\psi }}_1}=e^{-2V}p_1,\nonumber \\ {\mathcal {H}}^{(2)45}_{{\hat{\theta }}_2{\hat{\varphi }}_2}&=F^{45}_{{\hat{\theta }}_2{\hat{\varphi }}_2}= e^{-2W}p_2. \end{aligned}$$

(3.156)

With all these gauge fields non-vanishing, we also need to turn on the three-form field strengths

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{t}}{\hat{r}}{\hat{i}}_1 M}= -\frac{32}{g}\delta _{{\hat{i}}_1M}e^{4\phi -2V-2W}p_1p_2. \end{aligned}$$

(3.157)

We then impose the twist conditions

$$\begin{aligned} g p_1=k_1 \quad \text {and} \quad \sigma g p_2=k_2 \end{aligned}$$

(3.158)

and the following projectors on the Killing spinors

$$\begin{aligned}&\gamma ^{{\hat{\psi }}_1{\hat{\theta }}_1}\epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b, \quad \gamma ^{{\hat{\theta }}_1{\hat{\varphi }}_1}\epsilon ^a=-{(\Gamma _{23})^a}_b\epsilon ^b, \nonumber \\&\gamma ^{{\hat{\theta }}_2{\hat{\varphi }}_2}\epsilon ^a=-{(\Gamma _{45})^a}_b\epsilon ^b. \end{aligned}$$

(3.159)

Using the embedding tensor in the form

$$\begin{aligned} Y_{MN}=\text {diag}(+1,+1,+1,\sigma ,\sigma ) \end{aligned}$$

(3.160)

for $\sigma =\pm 1$ and the scalar coset representative (3.154), we can derive the following BPS equations

$$\begin{aligned} U'= & {} \frac{g}{40}\left( 3e^{-4\phi }+2\sigma e^{6\phi }\right) +\frac{288e^{2\phi }p_1p_2}{5ge^{2(V+W)}}\nonumber \\&-\frac{2}{5}\left( 3e^{-2V +4\phi }p_1+e^{-2W-6\phi }p_2\right) , \end{aligned}$$

(3.161)

$$\begin{aligned} V'= & {} \frac{g}{40}\left( 3e^{-4\phi }+2\sigma e^{6\phi }\right) -\frac{32e^{2\phi }p_1p_2}{5ge^{2(V+W)}}\nonumber \\&+\frac{2}{5}\left( 7e^{-2V +4\phi }p_1-e^{-2W-6\phi }p_2\right) , \end{aligned}$$

(3.162)

$$\begin{aligned} W'= & {} \frac{g}{40}\left( 3e^{-4\phi }+2\sigma e^{6\phi }\right) -\frac{192e^{2\phi }p_1p_2}{5ge^{2(V+W)}}\nonumber \\&-\frac{2}{5}\left( 3e^{-2V+4\phi }p_1-2e^{-2W -6\phi }p_2\right) , \end{aligned}$$

(3.163)

$$\begin{aligned} \phi '= & {} \frac{g}{20}\left( e^{-4\phi }-\sigma e^{6\phi }\right) +\frac{32e^{2\phi }p_1p_2}{5ge^{2(V+W)}}\nonumber \\&-\frac{2}{5}\left( 2e^{-2V+4\phi }p_1-e^{-2W -6\phi }p_2\right) \end{aligned}$$

(3.164)

in which we have also used the $\gamma _r$ projector in (3.21).

From these equations, we find an $AdS_2$ fixed point only for $k_1=k_2=-1$ and $\sigma =1$. The resulting $AdS_2\times H^3\times H^2$ fixed point is given by

$$\begin{aligned} V= & {} \frac{1}{2}\ln \left[ \frac{16\times 2^{4/5}}{g^2}\right] ,\quad W=\frac{1}{2}\ln \left[ \frac{16}{g^22^{1/5}}\right] ,\nonumber \\ \phi= & {} \frac{1}{10}\ln 2,\quad L_{\text {AdS}_2}=\frac{2\times 2^{2/5}}{g} \end{aligned}$$

(3.165)

which is the solution found in [12]. The three projectors in (3.159) imply that this solution preserves four supercharges. The solution is dual to superconformal quantum mechanics. Examples of RG flows from the supersymmetric $AdS_7$ vacuum to the $AdS_2\times H^3\times H^2$ fixed point and curved domain walls in the IR are given in Fig. 30. From the behavior of the eleven-dimensional metric component ${\hat{g}}_{00}$, we see that the singularity is physically acceptable. Therefore, this singularity is expected to describe supersymmetric quantum mechanics obtained from a twisted compactification of $N=(2,0)$ SCFT in six dimensions.

4 Solutions from gaugings in $\overline{\mathbf {40}}$ representation

In this section, we repeat the same analysis for gaugings from $\overline{\mathbf {40}}$ representation. These result in gauge groups of the form CSO(p, q, r) with $p+q+r=4$. In this case, the embedding tensor is given by

$$\begin{aligned} Y_{MN}=0\quad \text {and}\quad Z^{MN,P}=v^{[M}w^{N]P} \end{aligned}$$

(4.1)

with $w^{MN}=w^{(MN)}$. The SL(5) symmetry can be used to fix $v^M=\delta ^M_5$. Following [34], we will split the index $M=(i,5)$ and set $w^{55}=w^{i5}=0$. The remaining $SL(4)\subset SL(5)$ symmetry can be used to diagonalize $w^{ij}$ in the form

$$\begin{aligned} w^{ij}=\text {diag}(\underbrace{1,..,1}_p,\underbrace{-1,..,-1}_q, \underbrace{0,..,0}_r). \end{aligned}$$

(4.2)

This generates CSO(p, q, r) gauge groups for $p+q+r=4$ with the corresponding gauge generators given by

$$\begin{aligned} {(X_{ij})_k}^l=2\epsilon _{ijkm}w^{ml}. \end{aligned}$$

(4.3)

Fig. 30

RG flows from supersymmetric $AdS_7$ vacuum to the $AdS_2\times H^3\times H^2$ fixed point and curved domain walls with $SO(3)\times SO(2)$ twist in SO(5) gauge group. The blue, orange, green and red curves refer to $g=8,16,24,32$, respectively

With the SL(5) index splitting $M=(i,5)$, it is also useful to parametrize the SL(5)/SO(5) coset in term of the SL(4)/SO(4) submanifold as

$$\begin{aligned} {\mathcal {V}}=e^{b_it^i}\widetilde{{\mathcal {V}}}e^{\phi _0t_0}. \end{aligned}$$

(4.4)

$\widetilde{{\mathcal {V}}}$ is the SL(4)/SO(4) coset representative, and $t_0$, $t^i$ refer respectively to SO(1, 1) and four nilpotent generators in the decomposition $SL(5)\rightarrow SL(4)\times SO(1,1)$. The unimodular matrix ${\mathcal {M}}_{MN}$ decomposes accordingly

$$\begin{aligned} {\mathcal {M}}_{MN}=\begin{pmatrix}e^{-2\phi _0}\widetilde{{\mathcal {M}}}_{ij} +e^{8\phi _0} &{} e^{8\phi _0}b_i \\ e^{8\phi _0}b_j&{} e^{8\phi _0} \end{pmatrix} \end{aligned}$$

(4.5)

with $\widetilde{{\mathcal {M}}}_{ij}=(\widetilde{{\mathcal {V}}} \widetilde{{\mathcal {V}}}^T)_{ij}$. The scalar potential for the embedding tensor (4.1) reads

$$\begin{aligned} \mathbf {V}= & {} \frac{g^2}{4}e^{14\phi _0}b_iw^{ij} \widetilde{{\mathcal {M}}}_{jk}w^{kl}b_l\nonumber \\&+\frac{g^2}{4}e^{4\phi _0}\left( 2\widetilde{{\mathcal {M}}}_{ij}w^{jk} \widetilde{{\mathcal {M}}}_{kl}w^{li}-(\widetilde{{\mathcal {M}}}_{ij}w^{ij})^2\right) . \end{aligned}$$

(4.6)

It can be straightforwardly verified that the nilpotent scalars $b_i$ appear at least quadratically in the Lagrangian. Therefore, these scalars can always be consistently truncated out. In the following analysis, we will consider only supersymmetric solutions with $b_i=0$ for simplicity.

As in the case of gaugings in $\mathbf {15}$ representation, when the compact manifold $\Sigma ^d$ has dimension $d>3$, the modified three-form field strengths need to be turned on in order to satisfy the corresponding Bianchi’s identity. However, with $Y_{MN}=0$, there are no massive three-form fields. In this case, the contribution to $\mathcal {H}^{(3)}_{\mu \nu \rho M}$ arises solely from the two-form fields. There are respectively $5-s$ and s, for $s=\text {rank}\, Z$, massless and massive two-form fields. The latter also appear in the modified gauge field strengths $\mathcal {H}^{(2)MN}_{\mu \nu }$. In particular, with the embedding tensor given in (4.1), we find

$$\begin{aligned} {\mathcal {H}}^{(2)ij}_{\mu \nu }=F^{ij}_{\mu \nu } \quad \text {and} \quad {\mathcal {H}}^{(2)5i}_{\mu \nu }=\frac{g}{2}w^{ij}B_{\mu \nu j} \end{aligned}$$

(4.7)

in which $B_{\mu \nu j}$ are massive two-form fields. However, we are not able to find a consistent set of BPS equations that are compatible with the field equations for non-vanishing massive two-form fields. Therefore, in the following analysis, we will truncate out all the massive two-form fields. Finally, we point out here that the CSO(p, q, r) with $p+q+r=4$ gauge group is not large enough to accommodate SO(5) or $SO(3)\times SO(2)$ subgroups. Consequently, it is not possible to have $AdS_2\times \Sigma ^5$ or $AdS_2\times \Sigma ^3\times \Sigma ^2$ solutions.

4.1 Solutions with the twists on $\Sigma ^2$

We first look for $AdS_5\times \Sigma ^2$ solutions for $\Sigma ^2$ being a Riemann surface. The ansatz for the seven-dimensional metric is given in (3.6). We will consider solutions obtained from $SO(2)\times SO(2)$ and SO(2) twists on $\Sigma ^2$. The procedure is essentially the same as in the gaugings in $\mathbf {15}$ representation, so we will not give all the details here to avoid a repetition.

4.1.1 Solutions with $SO(2)\times SO(2)$ twists

Gauge groups with an $SO(2)\times SO(2)$ subgroup can be obtained from the embedding tensor of the form

$$\begin{aligned} w^{ij}=\text {diag}(1,1,\sigma ,\sigma ) \end{aligned}$$

(4.8)

with the parameter $\sigma =1,-1$ corresponding to SO(4) and SO(2, 2) gauge groups, respectively. There is only one $SO(2)\times SO(2)$ singlet scalar from SL(4)/SO(4) coset described by the coset representative

$$\begin{aligned} \widetilde{{\mathcal {V}}}=\text {diag}(e^\phi ,e^\phi ,e^{-\phi },e^{-\phi }). \end{aligned}$$

(4.9)

The scalar potential is given by

$$\begin{aligned} \mathbf {V}=-2\sigma e^{-4\phi _0}g^2. \end{aligned}$$

(4.10)

In this case, there is no supersymmetric $AdS_7$ fixed point. The supersymmetric vacuum is given by half-supersymmetric domain walls dual to $N=(2,0)$ non-conformal field theories in six dimensions.

We now perform the twist by turning on the following $SO(2)\times SO(2)$ gauge fields

$$\begin{aligned} A^{12}_{(1)}= & {} e^{-V}\frac{p_{2}}{4k}\frac{f'_{k}(\theta )}{f_{k} (\theta )}e^{{\hat{\varphi }}} \quad \text {and} \nonumber \\ A^{34}_{(1)}= & {} e^{-V}\frac{p_{1}}{4k}\frac{f'_{k}(\theta )}{f_{k} (\theta )}e^{{\hat{\varphi }}} \end{aligned}$$

(4.11)

and imposing the projection conditions given in (3.20) and

$$\begin{aligned} \gamma _{{\hat{r}}}\epsilon ^a=-{(\Gamma _{5})^a}_b\epsilon ^b \end{aligned}$$

(4.12)

together with the twist condition (3.19).

With all these, we find the following BPS equations

$$\begin{aligned} U'= & {} \frac{g}{5}e^{-2(\phi _0 +\phi )}(e^{4\phi }+\sigma )\nonumber \\&-\frac{1}{10}e^{-2(V-\phi _0)}\left( e^{-2\phi }p_1 +e^{2\phi }p_2\right) , \end{aligned}$$

(4.13)

$$\begin{aligned} V'= & {} \frac{g}{5}e^{-2(\phi _0 +\phi )}(e^{4\phi }+\sigma )\nonumber \\&+\frac{2}{5}e^{-2(V-\phi _0)}\left( e^{-2\phi }p_1 +e^{2\phi }p_2\right) , \end{aligned}$$

(4.14)

$$\begin{aligned} \phi _0'= & {} \frac{g}{10}e^{-2(\phi _0 +\phi )}(e^{4\phi }+\sigma )\nonumber \\&-\frac{1}{20}e^{-2(V-\phi _0)}\left( e^{-2\phi }p_1 +e^{2\phi }p_2\right) , \end{aligned}$$

(4.15)

$$\begin{aligned} \phi _1'= & {} -\frac{g}{2}e^{-2(\phi _0 +\phi )}(e^{4\phi }-\sigma )\nonumber \\&+\frac{1}{4}e^{-2(V-\phi _0)}\left( e^{-2\phi }p_1 -e^{2\phi }p_2\right) . \end{aligned}$$

(4.16)

From these equations, there are no fixed point solutions satisfying the conditions $\phi '=\phi _0'=V'=0$ and $U'=\frac{1}{L_{\text {AdS}_5}}$. In subsequent analysis, we will consider interpolating solutions between an asymptotically locally flat domain wall and curved domain walls in SO(4) gauge group. Similar solutions can also be found in SO(2, 2) gauge group.

For large V, the contribution from the gauge fields is highly suppressed. In this limit, we find

$$\begin{aligned} \phi \sim \frac{1}{r^5},\quad \phi _0\sim -\frac{1}{10}\log {\phi }, \quad U\sim V\sim 2\phi _0 \end{aligned}$$

(4.17)

which implies that $U\sim V\rightarrow \infty$ as $r\rightarrow \infty$. Examples of flow solutions with this asymptotic behavior are given in Figs. 31, 32 and 33 for $\Sigma ^2=S^2,{\mathbb {R}}^2,H^2$, respectively. In these solutions, we have set $g=16$. We note here that the flows to the flat $Mkw_4\times {\mathbb {R}}^2$-sliced domain walls given in Fig. 32 are possible provided that we set $p_2=-p_1$ as required by the twist condition. It should also be pointed out that the green curve in Fig. 32 is simply the usual flat domain wall since $k=p_1=p_2=0$. In this case, the solution preserves the full SO(4) gauge symmetry due to the vanishing of the $SO(2)\times SO(2)$ singlet scalar $\phi$. This solution has already been given analytically in [41].

As shown in [38], the maximal gauged supergravity in seven dimensions with $CSO(p,q,4-p-q)$ gauge group obtained from the embedding tensor in $\overline{\mathbf {40}}$ representation can be embedded in type IIB theory via a truncation on $H^{p,q}\circ T^{4-p-q}$. For the present discussion, we only need the ten-dimensional metric which, for $SO(p,4-p)$ gauge group, is given by

$$\begin{aligned} {\hat{g}}_{\mu \nu }=\kappa ^{\frac{3}{4}}\Delta ^{\frac{1}{4}}g_{\mu \nu } \end{aligned}$$

(4.18)

with

$$\begin{aligned} \Delta =\mu _i \mu _j\eta ^{ik}\eta ^{jl}\widetilde{\mathcal {M}}_{kl}. \end{aligned}$$

(4.19)

$\eta ^{ij}$ is the $SO(p,4-p)$ invariant tensor, and $\mu _i$ are coordinates on $H^{p,q}$ satisfying $\mu _i\mu _j\eta ^{ij}=1$. In term of the parametrization (4.4), $\kappa$ is identified as follows

$$\begin{aligned} \kappa =e^{2\phi _0}. \end{aligned}$$

(4.20)

For $CSO(p,q,4-p-q)$ gauge group, we decompose the SL(4) indices $i,j,\ldots$ into $({\hat{i}},{\tilde{i}})$ with ${\hat{i}}=1,\ldots p+q$ and ${\tilde{i}}=p+q+1,\ldots , 4$. The ten-dimensional metric and the warped factor are still given by (4.18) and (4.19) but with $\eta ^{ij}=(\eta ^{{\hat{i}}{\hat{j}}},\eta ^{{\tilde{i}}{\tilde{j}}})$ replaced by the SO(p, q) invariant tensor $\eta ^{{\hat{i}}{\hat{j}}}$ and $\eta ^{{\tilde{i}}{\tilde{j}}}=0$. In this case, $\mu _{{\hat{i}}}$ become coordinates on $H^{p,q}$ satisfying $\eta ^{{\hat{i}}{\hat{j}}}\mu _{{\hat{i}}}\mu _{{\hat{j}}}=1$ while $\mu _{{\tilde{i}}}$ are coordinates on $T^{4-p-q}$.

For the present case of SO(4) gauge group, we simply have $\eta ^{ij}=\delta ^{ij}$ for $i,j=1,2,3,4$. The behavior of the time component of the ten-dimensional metric ${\hat{g}}_{00}$ for the flow solutions in Figs. 31, 32 and 33 is shown in Fig. 34. Near the IR singularities, we find ${\hat{g}}_{00}\rightarrow 0$, so the singularities are physically acceptable.

Fig. 31

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_4\times S^2$-sliced curved domain walls for $SO(2)\times SO(2)$ twist in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_2=-0.5, -0.03, 0.03, 0.06, 0.25$, respectively

Fig. 32

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_4\times {\mathbb {R}}^2$-sliced domain walls for $SO(2)\times SO(2)$ twist in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_2=-0.5, -0.03, 0, 0.06, 0.25$, respectively

Fig. 33

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_4\times H^2$-sliced curved domain walls for $SO(2)\times SO(2)$ twist in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_2=-0.5, -0.12, -0.03, 0, 0.25$, respectively

Fig. 34

Profiles of the ten-dimensional metric component ${\hat{g}}_{00}$ for the supersymmetric flows given in Figs. 31, 32 and 33

4.1.2 Solutions with SO(2) twists

We then move to another twist on $\Sigma ^2$ by turning on only an SO(2) gauge field. This can be achieved from the $SO(2)\times SO(2)$ gauge fields given in (4.11) by setting $p_2=0$ and $p_1=p$. In this case, the SL(4)/SO(4) coset representative is given by

$$\begin{aligned} \widetilde{{\mathcal {V}}}=e^{\phi _1\widetilde{{\mathcal {Y}}}_1+\phi _2 \widetilde{{\mathcal {Y}}}_2 +\phi _3\widetilde{{\mathcal {Y}}}_3} \end{aligned}$$

(4.21)

in which $\widetilde{{\mathcal {Y}}}_1$, $\widetilde{{\mathcal {Y}}}_2$, and $\widetilde{{\mathcal {Y}}}_3$ are non-compact generators commuting with the SO(2) symmetry generated by $X_{12}$. The explicit form of these generators is given by

$$\begin{aligned} \widetilde{{\mathcal {Y}}}_1= & {} e_{1,1}+e_{2,2}-e_{3,3}-e_{4,4},\quad \widetilde{{\mathcal {Y}}}_2=e_{3,4}+e_{4,3},\nonumber \\ \widetilde{{\mathcal {Y}}}_3= & {} e_{3,3}-e_{4,4}. \end{aligned}$$

(4.22)

The embedding tensor is taken to be

$$\begin{aligned} w^{ij}=\text {diag}(1,1,\sigma ,\rho ) \end{aligned}$$

(4.23)

corresponding to six gauge groups with an SO(2) subgroup. These are given by SO(4) ($\rho =\sigma =1$), SO(3, 1) ($-\rho =\sigma =1$), SO(2, 2) ($\rho =\sigma =-1$), SO(3, 0, 1) ($\rho =0$, $\sigma =1$), SO(2, 1, 1) ($\rho =0$, $\sigma =-1$), and CSO(2, 0, 2) ($\rho =\sigma =0$).

Imposing the twist condition (3.47) and the projector (4.12) together with

$$\begin{aligned} \gamma ^{{\hat{\theta }}{\hat{\varphi }}}\epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b, \end{aligned}$$

(4.24)

we obtain the BPS equations

$$\begin{aligned} U'= & {} \frac{g}{10}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1} -(\rho -\sigma )\sinh {2\phi _3}\right. \nonumber \\&\left. +(\rho +\sigma )\cosh {2\phi _3} \cosh {2\phi _2}\right] -\frac{1}{10}pe^{-2(V-\phi _0+\phi _1)},\nonumber \\ \end{aligned}$$

(4.25)

$$\begin{aligned} V'= & {} \frac{g}{10}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1} -(\rho -\sigma )\sinh {2\phi _3}\right. \nonumber \\&\left. +(\rho +\sigma )\cosh {2\phi _3}\cosh {2\phi _2} \right] +\frac{2}{5}pe^{-2(V-\phi _0+\phi _1)},\nonumber \\\end{aligned}$$

(4.26)

$$\begin{aligned} \phi _0'= & {} \frac{g}{20}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1} -(\rho -\sigma )\sinh {2\phi _3}\right. \nonumber \\&\left. +(\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3} \right] -\frac{1}{20}pe^{-2(V-\phi _0+\phi _1)},\nonumber \\\end{aligned}$$

(4.27)

$$\begin{aligned} \phi _1'= & {} -\frac{g}{4}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1}\right. \nonumber \\&\left. +(\rho -\sigma ) \sinh {2\phi _3}-(\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3}\right] \nonumber \\&+\frac{1}{4}pe^{-2(V-\phi _0+\phi _1)},\end{aligned}$$

(4.28)

$$\begin{aligned} \phi _2'= & {} -\frac{g}{2}e^{-2(\phi _0+\phi _1)}(\rho +\sigma )\sinh {2\phi _2} \text { sech }{2\phi _3},\end{aligned}$$

(4.29)

$$\begin{aligned} \phi _3'= & {} \frac{g}{2}e^{-2(\phi _0+\phi _1)}\left[ (\rho -\sigma )\cosh {2\phi _3}\right. \nonumber \\&\left. -(\rho +\sigma )\cosh {2\phi _2}\sinh {2\phi _3}\right] . \end{aligned}$$

(4.30)

As in the case of $SO(2)\times SO(2)$ twist, there do not exist any $AdS_5\times \Sigma ^2$ fixed points. The numerical analysis for finding flow solutions interpolating between locally asymptotically flat domain walls and curved domain walls can also be obtained as in the previous case.

4.2 Solutions with the twists on $\Sigma ^3$

In this section, we repeat the same analysis for solutions with the twists on $\Sigma ^3$. We will consider two different twists by turning on SO(3) and $SO(3)_+$ gauge fields.

4.2.1 Solutions with SO(3) twists

In this case, the gauge groups with an SO(3) subgroup are described by the embedding tensor

$$\begin{aligned} w^{ij}=\text {diag}(1,1,1,\rho ) \end{aligned}$$

(4.31)

with $\rho =-1,0,1$ corresponding to SO(3, 1), CSO(3, 0, 1) and SO(4) gauge groups, respectively.

There is one SO(3) singlet scalar from the SL(4)/SO(4) coset with the coset representative given by

$$\begin{aligned} \widetilde{{\mathcal {V}}}=\text {diag}(e^\phi ,e^\phi ,e^\phi ,e^{-3\phi }) \end{aligned}$$

(4.32)

leading to the scalar potential

$$\begin{aligned} \mathbf {V}=-\frac{g^2}{4}e^{-4(\phi _0+3\phi )}\left( 3e^{16\phi }+6\rho e^{8\phi }-\rho ^2\right) . \end{aligned}$$

(4.33)

To perform the twist, we turn on the SO(3) gauge fields

$$\begin{aligned} A^{34}_{(1)}= & {} e^{-V}\frac{p}{4k}\frac{f'_{k}(\psi )}{f_{k}(\psi )} e^{{\hat{\theta }}},\nonumber \\ A^{42}_{(1)}= & {} e^{-V}\frac{p}{4k}\frac{f'_{k}(\psi )}{f_{k}(\psi )} e^{{\hat{\varphi }}}, \nonumber \\ A^{14}_{(1)}= & {} e^{-V}\frac{p}{4k}\frac{\cot (\theta )}{f_{k}(\psi )} e^{{\hat{\varphi }}} \end{aligned}$$

(4.34)

and impose the projectors (3.48) on the Killing spinors together with the twist condition (3.47). With all these and the $\gamma _r$ projector (4.12), the resulting BPS equations read

$$\begin{aligned} U'&=\frac{g}{10}e^{-2(\phi _0+3\phi )}(3e^{8\phi }+\rho ) -\frac{3}{10}e^{-2(V-\phi _0+\phi )}p, \end{aligned}$$

(4.35)

$$\begin{aligned} V'&=\frac{g}{10}e^{-2(\phi _0+3\phi )}(3e^{8\phi }+\rho ) +\frac{7}{10}e^{-2(V-\phi _0+\phi )}p,\end{aligned}$$

(4.36)

$$\begin{aligned} \phi _0'&=\frac{g}{20}e^{-2(\phi _0+3\phi )}(3e^{8\phi }+\rho ) -\frac{3}{20}e^{-2(V-\phi _0+\phi )}p,\end{aligned}$$

(4.37)

$$\begin{aligned} \phi '&=-\frac{g}{4}e^{-2(\phi _0+3\phi )}(e^{8\phi }-\rho ) +\frac{1}{4}e^{-2(V-\phi _0+\phi )}p. \end{aligned}$$

(4.38)

As in the previous case, there do not exist any $AdS_4$ fixed points for these equations. We then look for solutions interpolating between asymptotically locally flat domain walls and curved domain walls.

For CSO(3, 0, 1) gauge group with $\rho =0$, these equations can be analytically solved. First of all, the BPS equations give

$$\begin{aligned} U=2\phi _0. \end{aligned}$$

(4.39)

We have neglected an additive integration constant for U which can be absorbed by rescaling the coordinates on $Mkw_3$. With $\rho =0$, we find that $\phi _0'+\frac{3}{5}\phi '=0$ which gives

$$\begin{aligned} \phi _0=-\frac{3}{5}\phi +C_0 \end{aligned}$$

(4.40)

with an integration constant $C_0$.

Taking a linear combination $V'+\frac{6}{5}\phi '$ and changing to a new radial coordinate ${\tilde{r}}$ given by $\frac{d{\tilde{r}}}{dr}=e^{-\frac{4}{5}\phi }$, we find

$$\begin{aligned} V=\frac{1}{2}\ln (2p{\tilde{r}}+C)-\frac{6}{5}\phi . \end{aligned}$$

(4.41)

The integration constant C can also be set to zero by shifting the coordinate ${\tilde{r}}$. With all these results, the equation for $\phi '$ gives

$$\begin{aligned} \phi =-\frac{1}{4}\ln \left[ \frac{2}{3}g{\tilde{r}}-\frac{{\tilde{C}}}{p\sqrt{p{\tilde{r}}}}\right] \end{aligned}$$

(4.42)

in which we have set $C=0$ for simplicity, and ${\tilde{C}}$ is another integration constant.

As ${\tilde{r}}\rightarrow 0$, we find that the above solution becomes a locally flat domain wall with $U\sim V\rightarrow \infty$. The asymptotic behavior is given by

$$\begin{aligned} \phi \sim \frac{1}{8}\ln {\tilde{r}},\quad \phi _0\sim -\frac{3}{40}\ln {\tilde{r}},\quad U\sim V\sim -\frac{3}{20}\ln {\tilde{r}}. \end{aligned}$$

(4.43)

For ${\tilde{r}}\rightarrow \infty$, we find

$$\begin{aligned}&\phi \sim -\frac{1}{4}\ln {\tilde{r}},\quad \phi _0\sim \frac{3}{20}\ln {\tilde{r}},\nonumber \\&V\sim \frac{4}{5}\ln {\tilde{r}},\quad U\sim \frac{3}{10}\ln {\tilde{r}}. \end{aligned}$$

(4.44)

Computing the type IIB metric, we obtain

$$\begin{aligned} {\hat{g}}_{00}\sim e^{2U+\frac{3}{2}\phi _0+\frac{1}{2}\phi }\sim {\tilde{r}}^{\frac{7}{10}}\rightarrow \infty , \end{aligned}$$

(4.45)

as ${\tilde{r}}\rightarrow \infty$, which implies that the IR singularity is unphysical.

For $\rho \ne 0$, we can only partially solve the BPS equations. As in the $\rho =0$ case, the BPS equations give $U=2\phi _0$. Taking a linear combination $\phi _0'+\frac{3}{5}\phi '$ and defining a new coordinate ${\tilde{r}}$ via $\frac{d{\tilde{r}}}{dr}=e^{-\frac{24}{5}\phi }$, we find

$$\begin{aligned} \phi _0=\frac{1}{2}\ln \left[ \frac{2}{5}(g\rho {\tilde{r}}+C)\right] -\frac{3}{5}\phi . \end{aligned}$$

(4.46)

The complete solutions can be obtained numerically. As $r\rightarrow \infty$, we find

$$\begin{aligned} \phi \sim \frac{1}{r^5},\quad \phi _0\sim -\frac{1}{10}\log {\phi }, \quad U\sim V\sim 2\phi _0. \end{aligned}$$

(4.47)

Examples of these solutions for SO(4) gauge group are given in Figs. 35 and 36 for different values of g. The behavior of the ten-dimensional metric ${\hat{g}}_{00}$ for these flow solutions is shown in Fig. 37 from which only the singularities of $Mkw_3\times H^3$-sliced domain walls are physical. For $Mkw_3\times {\mathbb {R}}^3$-sliced domain walls with $k=0$, the twist condition gives $p=0$ resulting in the usual flat domain walls.

Fig. 35

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_3\times S^3$-sliced curved domain walls for SO(3) twist in SO(4) gauge group. The blue, orange, green and red curves refer to $g=4,8,16,32$, respectively

Fig. 36

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_3\times H^3$-sliced curved domain walls for SO(3) twist in SO(4) gauge group. The blue, orange, green and red curves refer to $g=4,8,16,32$, respectively

Fig. 37

Profiles of the ten-dimensional metric component ${\hat{g}}_{00}$ for the supersymmetric flows given in Figs. 35 and 36

4.2.2 Solutions with $SO(3)_+$ twists

We now consider another twist by turning on the gauge fields for self-dual $SO(3)_+$ gauge symmetry. Only the scalar field $\phi _0$ is $SO(3)_+$ singlet, so we simply have $\widetilde{\mathcal {M}}_{ij}=\delta _{ij}$. Furthermore, we consider only SO(4) gauge group since this is the only gauge group that contains the $SO(3)_+$ subgroup.

The $SO(3)_+$ gauge fields are given by

$$\begin{aligned} A^{12}_{(1)}= & {} A^{34}_{(1)}=e^{-V}\frac{p}{8k}\frac{f'_{k}(\psi )}{f_{k}(\psi )} e^{{\hat{\theta }}},\nonumber \\ A^{13}_{(1)}= & {} A^{42}_{(1)}=e^{-V}\frac{p}{8k}\frac{f'_{k}(\psi )}{f_{k}(\psi )} e^{{\hat{\varphi }}}, \nonumber \\ A^{23}_{(1)}= & {} A^{14}_{(1)}=e^{-V}\frac{p}{8k}\frac{\cot (\theta )}{f_{k}(\psi )} e^{{\hat{\varphi }}}. \end{aligned}$$

(4.48)

With the projectors (3.48), (3.60) and (4.12) together with the twist condition (3.47), the resulting BPS equations are given by

$$\begin{aligned} U'= & {} \frac{2g}{5}e^{-2\phi _0}-\frac{3}{10}e^{-2(V-\phi _0)}p, \end{aligned}$$

(4.49)

$$\begin{aligned} V'= & {} \frac{2g}{5}e^{-2\phi _0}+\frac{7}{10}e^{-2(V-\phi _0)}p, \end{aligned}$$

(4.50)

$$\begin{aligned} \phi _0'= & {} \frac{g}{5}e^{-2\phi _0}-\frac{3}{20}e^{-2(V-\phi _0)}p. \end{aligned}$$

(4.51)

As in the case of SO(3) twist, we do not find any $AdS_4$ fixed points from these equations.

From the BPS equations, we again find that $U=2\phi _0$. By taking a linear combination $V'-2\phi _0'$ and defining a new radial coordinate ${\tilde{r}}$ by $\frac{d{\tilde{r}}}{dr}=e^{-V}$, we obtain

$$\begin{aligned} V=\ln (p{\tilde{r}}+C)+2\phi _0. \end{aligned}$$

(4.52)

Using $\phi _0$ from (4.52) in equation for $V'$, we find, after changing to the coordinate ${\tilde{r}}$,

$$\begin{aligned} V=\frac{g}{5p}(p{\tilde{r}}+C)^2+\frac{7}{10}\ln (p{\tilde{r}}+C). \end{aligned}$$

(4.53)

As ${\tilde{r}}\rightarrow \infty$, we find, with C set to zero by shifting ${\tilde{r}}$,

$$\begin{aligned} U\sim V\sim \frac{1}{5}gp{\tilde{r}}^2\quad \text {and}\quad \phi _0\sim \frac{1}{10}gp{\tilde{r}}^2 \end{aligned}$$

(4.54)

which is identified with a domain wall solution given in [41]. On the other hand, as ${\tilde{r}}\rightarrow 0$, the solution becomes

$$\begin{aligned}&U\sim -\frac{3}{5}\ln (p{\tilde{r}}),\quad V\sim \frac{7}{10}\ln (p{\tilde{r}}),\nonumber \\&\quad \phi _0\sim -\frac{3}{10}\ln (p{\tilde{r}}). \end{aligned}$$

(4.55)

This singularity is unphysical since the ten-dimensional metric gives

$$\begin{aligned} {\hat{g}}_{00}\sim e^{2U+\frac{3}{2}\phi _0}\rightarrow \infty . \end{aligned}$$

(4.56)

We note that this solution is the same as that given in Sect. 3.2.2 for CSO(4, 0, 1) gauge group. The two gauged supergravities can be obtained from truncations of type IIB and type IIA theories on $S^3$, respectively. In fact, there is a duality between these solutions as pointed out in [38].

4.3 Solutions with the twists on $\Sigma ^4$

We finally look for supersymmetric solutions obtained from the twists on a four-manifold $\Sigma ^4$. As in the case of gaugings in $\mathbf {15}$ representation, we will consider two types of $\Sigma ^4$ in terms of a product of two Riemann surfaces $\Sigma ^2\times \Sigma ^2$ and a Kahler four-cycle $K^4$.

4.3.1 Solutions with $SO(2)\times SO(2)$ twists on $\Sigma ^2\times \Sigma ^2$

For solutions with $SO(2)\times SO(2)$ twists, there are two gauge groups to consider, SO(4) and SO(2, 2) with the embedding tensor (4.8). The ansatz for the metric is given in (3.83). To cancel the spin connection on $\Sigma ^2_{k_1}\times \Sigma ^2_{k_2}$, we turn on the following $SO(2)\times SO(2)$ gauge fields

$$\begin{aligned} A^{12}_{(1)}= & {} \frac{p_{11}}{4k_1}\frac{f_{k_1}'(\theta _1)}{f_{k_1}(\theta _1)} e^{-V}e^{{\hat{\varphi }}_1}+\frac{p_{12}}{4k_2}\frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)}e^{-W}e^{{\hat{\varphi }}_2},\nonumber \\ A^{34}_{(1)}= & {} \frac{p_{21}}{4k_1}\frac{f_{k_1}'(\theta _1)}{f_{k_1}(\theta _1)} e^{-V}e^{{\hat{\varphi }}_1}+\frac{p_{22}}{4k_2}\frac{f_{k_2}'(\theta _2)}{f_{k_2}(\theta _2)}e^{-W}e^{{\hat{\varphi }}_2} \end{aligned}$$

(4.57)

with the corresponding two-form field strengths

$$\begin{aligned} F^{12}_{(2)}= & {} -e^{-2V}\frac{p_{11}}{4}e^{{\hat{\theta }}_1}\wedge e^{{\hat{\varphi }}_1}-e^{-2W}\frac{p_{12}}{4}e^{{\hat{\theta }}_2}\wedge e^{{\hat{\varphi }}_2},\nonumber \\ F^{34}_{(2)}= & {} -e^{-2V}\frac{p_{21}}{4}e^{{\hat{\theta }}_1}\wedge e^{{\hat{\varphi }}_1}-e^{-2W}\frac{p_{22}}{4}e^{{\hat{\theta }}_2}\wedge e^{{\hat{\varphi }}_2}\, . \end{aligned}$$

(4.58)

Following a similar analysis for gaugings in $\mathbf {15}$ representation, we also turn on the modified three-form field strength using the ansatz

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{m}}{\hat{n}}{\hat{r}} 5}= \beta e^{-2(V+W+4\phi _0)}\varepsilon _{{\hat{m}}{\hat{n}}} \end{aligned}$$

(4.59)

in which $\beta$ is a constant. We now impose the twist conditions

$$\begin{aligned} g(\sigma p_{11}+p_{21})=k_1\quad \text {and} \quad g(\sigma p_{12}+p_{22})=k_2 \end{aligned}$$

(4.60)

and the projection conditions in (3.92) together with (4.12).

With all these, the resulting BPS equations are given by

$$\begin{aligned} U'= & {} -\frac{e^{2\phi _0}}{10}\left[ e^{-2(V+\phi )}(e^{4\phi }p_{11} +p_{21})\right. \nonumber \\&\left. +e^{-2(W+\phi )}(e^{4\phi }p_{12}+p_{22})\right] \nonumber \\&+\frac{g}{5}e^{-2(\phi _0+\phi )}(e^{4\phi }+\sigma )+\frac{3}{5}e^{-2(V+ W+2\phi _0)} \beta , \end{aligned}$$

(4.61)

$$\begin{aligned} V'= & {} -\frac{e^{2\phi _0}}{10}\left[ 4e^{-2(V+\phi )}(e^{4\phi }p_{11}+p_{21})\right. \nonumber \\&\left. -e^{-2(W+\phi )}(e^{4\phi }p_{12}+p_{22})\right] \nonumber \\&+\frac{g}{5} e^{-2(\phi _0+\phi )}(e^{4\phi }+\sigma )-\frac{2}{5}e^{-2(V+ W+2\phi _0)}\beta ,\end{aligned}$$

(4.62)

$$\begin{aligned} W'= & {} -\frac{e^{2\phi _0}}{10}\left[ e^{-2(V+\phi )}(e^{4\phi }p_{11}+p_{21})\right. \nonumber \\&\left. -4e^{-2(W+\phi )}(e^{4\phi }p_{12}+p_{22})\right] \nonumber \\&+\frac{g}{5} e^{-2(\phi _0+\phi )}(e^{4\phi }+\sigma )-\frac{2}{5}e^{-2(V+ W+2\phi _0)}\beta ,\end{aligned}$$

(4.63)

$$\begin{aligned} \phi _0'= & {} -\frac{e^{2\phi _0}}{20}\left[ e^{-2(V+\phi )}(e^{4\phi }p_{11}+p_{21})\right. \nonumber \\&\left. +e^{-2(W+\phi )}(e^{4\phi }p_{12}+p_{22})\right] \nonumber \\&+\frac{g}{10} e^{-2(\phi _0+\phi )}(e^{4\phi }+\sigma )-\frac{1}{5}e^{-2(V+ W+2\phi _0)}\beta ,\end{aligned}$$

(4.64)

$$\begin{aligned} \phi '= & {} -\frac{e^{2\phi _0}}{4}\left[ e^{-2(V+\phi )}(e^{4\phi }p_{11}-p_{21})\right. \nonumber \\&\left. +e^{-2(W+\phi )}(e^{4\phi }p_{12}-p_{22})\right] \nonumber \\&-\frac{g}{2}e^{-2(\phi _0+\phi )}(e^{4\phi }-\sigma ). \end{aligned}$$

(4.65)

Unlike the similar analysis for gaugings in $\mathbf {15}$ representation, it turns out that compatibility between these BPS equations and the second-ordered field equations requires

$$\begin{aligned} p_{12} p_{21} + p_{11} p_{22}=0 \end{aligned}$$

(4.66)

for any values of $\beta$. This implies that the constant $\beta$ is a free parameter in this case. However, we do not find any $AdS_3$ fixed points from the BPS equations.

For SO(4) gauge group, examples of flow solutions between asymptotically locally flat domain walls and curved domain walls for various forms of $\Sigma ^2\times \Sigma ^2$ are shown in Figs. 38, 39, 40, 41, 42, and 43. In these solutions, we have chosen particular values of $g=16$ and $\beta =2$. The green curve in Fig. 41 is the flat domain wall solution given in [41]. All of the IR singularities are physical as can be seen from the behavior of the ten-dimensional metric given in Fig. 44.

Fig. 38

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times S^2\times S^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_{21}=-0.5, -0.12, 0, 0.12, 0.25$, respectively

Fig. 39

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times S^2 \times {\mathbb {R}}^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_{21}=-0.5, -0.12, 0.03, 0.06, 0.25$, respectively

Fig. 40

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times S^2\times H^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_{21}=-0.5, -0.03, 0, 0.08, 0.25$, respectively

Fig. 41

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times {\mathbb {R}}^2\times {\mathbb {R}}^2$-sliced domain walls in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_{21}=-0.5, -0.12, 0, 0.03, 0.25$, respectively

Fig. 42

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times H^2\times {\mathbb {R}}^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $-0.5, -0.12, -0.03, 0, 0.25$, respectively

Fig. 43

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times H^2\times H^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green, red and purple curves refer to $p_{21}=-0.5, -0.12, -0.01, 0.25, 0.6$, respectively

Fig. 44

Profiles of the ten-dimensional metric component ${\hat{g}}_{00}$ for the supersymmetric flows given in Figs. 38, 39, 40, 41, 42, and 43

We have also considered SO(2) twists on $\Sigma ^2\times \Sigma ^2$ by setting $p_{11}=p_{12}=0$ and obtain more complicated BPS equations. However, we do not find any $AdS_3$ fixed points either. Therefore, we will not give further detail on this analysis.

4.3.2 Solutions with SO(3) twists on $K^4$

For $\Sigma ^4$ being a Kahler four-cycle $K^4_k$, we perform an SO(3) twist to cancel the SU(2) part of the spin connection, given in (3.112), by turning on the SO(3) gauge fields

$$\begin{aligned} A^{i4}_{(1)}=\frac{p}{4k}(f'_k(\psi )-1)\delta ^{ij}\tau _j \end{aligned}$$

(4.67)

with the two-form field strengths given by

$$\begin{aligned} {\mathcal {H}}^{14}_{(2)}= & {} -\frac{p}{4}e^{-2V}\left( e^{{\hat{4}}} \wedge e^{{\hat{5}}}-e^{{\hat{3}}}\wedge e^{{\hat{6}}}\right) ,\nonumber \\ {\mathcal {H}}^{24}_{(2)}= & {} -\frac{p}{4}e^{-2V}\left( e^{{\hat{5}}} \wedge e^{{\hat{3}}}-e^{{\hat{4}}}\wedge e^{{\hat{6}}}\right) ,\nonumber \\ {\mathcal {H}}^{34}_{(2)}= & {} -\frac{p}{4}e^{-2V}\left( e^{{\hat{3}}}\wedge e^{{\hat{4}}}-e^{{\hat{5}}}\wedge e^{{\hat{6}}}\right) . \end{aligned}$$

(4.68)

These field strengths do not lead to any problematic terms in the modified Bianchi’s identity for the three-form field strengths. However, we can have a non-vanishing three-form field strength by using the following ansatz

$$\begin{aligned} {\mathcal {H}}^{(3)}_{{\hat{m}}{\hat{n}}{\hat{r}} 5}= \beta e^{-4(V+\phi _0)}\varepsilon _{{\hat{m}}{\hat{n}}}. \end{aligned}$$

(4.69)

which is a manifestly closed three-form for a constant $\beta$.

With the SL(4)/SO(4) coset representative and the embedding tensor given in (4.32) and (4.31) together with the projections (3.117) and (4.12), we find the following BPS equations

$$\begin{aligned} U'= & {} \frac{g}{10}e^{-2(\phi _0+3\phi )}(3e^{8\phi }+\rho ) -\frac{3}{5}e^{-2(V-\phi _0+\phi )}p\nonumber \\&-\frac{3}{5}e^{-4(V+\phi _0)}\beta , \end{aligned}$$

(4.70)

$$\begin{aligned} V'= & {} \frac{g}{10}e^{-2(\phi _0+3\phi )}(3e^{8\phi }+\rho ) +\frac{9}{10}e^{-2(V-\phi _0+\phi )}p\nonumber \\&+\frac{2}{5}e^{-4(V+\phi _0)}\beta , \end{aligned}$$

(4.71)

$$\begin{aligned} \phi _0'= & {} \frac{g}{20}e^{-2(\phi _0+3\phi )}(3e^{8\phi }+\rho ) -\frac{3}{10}e^{-2(V-\phi _0+\phi )}p\nonumber \\&+\frac{1}{5}e^{-4(V+\phi _0)}\beta , \end{aligned}$$

(4.72)

$$\begin{aligned} \phi '= & {} -\frac{g}{4}e^{-2(\phi _0+3\phi )}(e^{8\phi }-\rho ) +\frac{1}{2}e^{-2(V-\phi _0+\phi )}p \end{aligned}$$

(4.73)

in which we have used the twist condition (3.47). We do not find any $AdS_3$ fixed points from these equations. Examples of supersymmetric flows for $\beta =-2$ are given in Figs. 45 and 46 for $k=1$ and $k=-1$, respectively. From the behavior of the ten-dimensional metric given in Fig. 47, we find that the IR singularities for $k=-1$ are physical. In the case of flat $K^4_k$ with $k=0$, we have $p=0$ by the twist condition resulting in the standard flat domain wall solutions.

Fig. 45

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times CP^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green and red curves refer to $g=4,8,16,32$, respectively

Fig. 46

Supersymmetric flows interpolating between asymptotically locally flat domain walls and $Mkw_2\times CH^2$-sliced curved domain walls in SO(4) gauge group. The blue, orange, green and red curves refer to $g=4,8,16,32$, respectively

Fig. 47

Profiles of the ten-dimensional metric component ${\hat{g}}_{00}$ for the supersymmetric flows given in Figs. 45 and 46

4.3.3 Solutions with SO(2) twists on $K^4$

As the final case, we briefly consider the SO(2) twist by turning on an SO(2) gauge field to cancel the U(1) part of the spin connection for the metric (3.132). This gauge field is given by

$$\begin{aligned} A^{34}_{(1)}=-p\frac{3k\psi ^2}{4\sqrt{f_k(\psi )}}\tau _3. \end{aligned}$$

(4.74)

The SO(2) singlet scalars from SL(4)/SO(4) coset are described by the coset representative (4.21), and the embedding tensor is given in (4.23). We can also turn on the three-form field strength (4.69). With the twist condition (3.47) and the projections (4.12) together with

$$\begin{aligned} \gamma ^{{\hat{3}}{\hat{4}}}\epsilon ^a=-\gamma ^{{\hat{5}}{\hat{6}}} \epsilon ^a=-{(\Gamma _{12})^a}_b\epsilon ^b, \end{aligned}$$

(4.75)

the corresponding BPS equations are given by

$$\begin{aligned} U'= & {} \frac{g}{10}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1}-(\rho -\sigma ) \sinh {2\phi _3}\right. \nonumber \\&\left. +(\rho +\sigma )\cosh {2\phi _3}\cosh {2\phi _2}\right] \nonumber \\&-\frac{3}{5}e^{-2(V-\phi _0+\phi _1)}p-\frac{3}{5}e^{-4(V+\phi _0)}\beta , \end{aligned}$$

(4.76)

$$\begin{aligned} V'= & {} \frac{g}{10}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1}-(\rho -\sigma ) \sinh {2\phi _3}\right. \nonumber \\&\left. +(\rho +\sigma )\cosh {2\phi _3}\cosh {2\phi _2}\right] \nonumber \\&+\frac{9}{10}e^{-2(V-\phi _0+\phi _1)}p+\frac{2}{5}e^{-4(V+\phi _0)}\beta ,\end{aligned}$$

(4.77)

$$\begin{aligned} \phi _0'= & {} \frac{g}{20}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1}-(\rho -\sigma ) \sinh {2\phi _3}\right. \nonumber \\&\left. +(\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3}\right] \nonumber \\&-\frac{3}{10}e^{-2(V-\phi _0+\phi _1)}p+\frac{1}{5}e^{-4(V+\phi _0)}\beta ,\end{aligned}$$

(4.78)

$$\begin{aligned} \phi _1'= & {} -\frac{g}{4}e^{-2(\phi _0+\phi _1)}\left[ 2e^{4\phi _1}+(\rho -\sigma ) \sinh {2\phi _3}\right. \nonumber \\&\left. -(\rho +\sigma )\cosh {2\phi _2}\cosh {2\phi _3}\right] \nonumber \\&+\frac{3}{2}e^{-2(V-\phi _0+\phi _1)}p,\end{aligned}$$

(4.79)

$$\begin{aligned} \phi _2'= & {} \ -\frac{g}{2}e^{-2(\phi _0+\phi _1)}(\rho +\sigma )\sinh {2\phi _2} \text { sech }{2\phi _3},\end{aligned}$$

(4.80)

$$\begin{aligned} \phi _3'= & {} \ \frac{g}{2}e^{-2(\phi _0+\phi _1)}\left[ (\rho -\sigma )\cosh {2\phi _3}\right. \nonumber \\&\left. -(\rho +\sigma )\cosh {2\phi _2}\sinh {2\phi _3}\right] . \end{aligned}$$

(4.81)

As in all of the previous cases for gaugings in $\overline{\mathbf {40}}$ representation, there are no $AdS_3$ fixed points from these equations.

5 Conclusions and discussions

In this paper, we have extensively studied supersymmetric $AdS_n\times \Sigma ^{7-n}$ solutions of the maximal gauged supergravity in seven dimensions with $CSO(p,q,5-p-q)$ and $CSO(p,q,4-p-q)$ gauge groups. These gauged supergravities can be embedded respectively in eleven-dimensional and type IIB supergravities on $H^{p,q}\circ T^{5-p-q}$ and $H^{p,q}\circ T^{4-p-q}$. Therefore, all the solutions given here have higher dimensional origins and could be interpreted as different brane configurations in string/M-theory. This makes applications of these solutions in the holographic context more interesting. Accordingly, we hope our results would be useful along this line of research.

For a particular case of SO(5) gauge group, we have recovered all the previous results on $AdS_n\times \Sigma ^{7-n}$ fixed points with $n=2,3,4,5$. We have provided numerical RG flows interpolating between the supersymmetric $N=4$ $AdS_7$ vacuum dual to $N=(2,0)$ SCFT in six dimensions and all these $AdS_n\times \Sigma ^{7-n}$ fixed points. Some of these flows have not previously been discussed, so our results could complete the list of already known flow solutions. Furthermore, we have extended all these RG flows to singular geometries in the IR. These singularities take the form of curved domain walls with $Mkw_{n-1}\times \Sigma ^{7-n}$ slices and can be interpreted as non-conformal field theories in $n-1$ dimensions. The flow solutions suggest that they describe non-conformal phases of the $(n-1)$-dimensional SCFTs obtained from twisted compactifications of $N=(2,0)$ SCFT in six dimensions.

Table 1 $AdS_n\times \Sigma ^{7-n}$ fixed points from maximal gauged supergravity in seven dimensions together with the corresponding symmetries and numbers of unbroken supercharges. $\Sigma ^2$ can be $S^2$, ${\mathbb {R}}^2$ or $H^2$

We have also discovered novel classes of $AdS_5\times S^2$, $AdS_3\times S^2\times \Sigma ^2$ and $AdS_3\times CP^2$ solutions in non-compact SO(3, 2) gauge group. Unlike in SO(5) gauge group, there do not exist any supersymmetric $AdS_7$ fixed points in this gauge group. The maximally supersymmetric vacua are given by half-supersymmetric domain walls. In this case, we have studied RG flow solutions between these new fixed points and curved domain walls. We have also examined the behavior of the time component of the eleven-dimensional metric and found that many of the singularities are physically acceptable. The singular geometries identified here can be then interpreted as a holographic description of non-conformal field theories obtained from twisted compactifications of $N=(2,0)$ six-dimensional field theories. A similar study has been carried out for SO(4, 1) gauge group in which a new class of $AdS_3\times CP^2$ solutions has been found. For convenience, we summarize all the $AdS_n\times \Sigma ^{7-n}$ fixed points identified here together with all the previously known results in SO(5) gauge group in Table 1.

Flow solutions for non-compact SO(3, 2) and SO(4, 1) gauge groups can also be interpreted as black 3-brane and black strings in asymptotically curved domain wall space-time. These solutions are similar to four-dimensional black holes studied in [43]. In [44], these black hole solutions have been shown to arise from a dimensional reduction of the $AdS_5$ black strings studied in [14]. It has also been pointed out in [44] that the four-dimensional black holes, with curved domain wall asymptotics, should be seen from a higher-dimensional perspective as black strings in $AdS_5$. However, this is not the case for the solutions given in this paper. Our solutions cannot be related to any supersymmetric black objects in eight dimensions with asymptically $AdS_8$ space-time due to the absence of supersymmetric $AdS_d$ vacua for $d>7$.

For $CSO(p,q,4-p-q)$ gauge group which is obtained from a truncation of type IIB theory, we have performed a similar analysis as in the $CSO(p,q,5-p-q)$ gauge group but have not found any $AdS_n$ fixed points. The resulting gauged supergravity admits half-supersymmetric domain walls as vacuum solutions which, upon uplifted to ten dimensions, describe 5-branes in type IIB theory. We have given supersymmetric flow solutions interpolating between asymptotically locally flat domain walls, in which the effect of magnetic charges are small compared to the superpotential of the domain walls, and curved domain walls with $Mkw_{n-1}\times \Sigma ^{7-n}$ worldvolume. By the standard DW/QFT correspondence, these solutions should be interpreted as RG flows across dimensions between non-conformal field theories in six and $n-1$ dimensions. It could be interesting to study these field theories on the worldvolume of the 5-branes in type IIB theory. Our results suggest that these $N=(2,0)$ field theories have no conformal fixed points in lower dimensions. It could be interesting to have a definite conclusion whether this is true in general. On the other hand, if this is not the case, it would also be interesting to extend the analysis of this paper by using more general ansatz in particular with non-vanishing massive two-form fields and find new classes of $AdS_n\times \Sigma ^{7-n}$ solutions of seven-dimensional gauged supergravity.

Appendix A: Bosonic field equations

For convenience, in this appendix, we collect all the bosonic field equations of the maximal gauged supergravity in seven dimensions. These equations are given by

$$\begin{aligned} 0= & {} R_{\mu \nu }-\frac{1}{4}{\mathcal {M}}_{MP}{\mathcal {M}}_{NQ} (D_\mu {\mathcal {M}}^{MN})(D_\nu {\mathcal {M}}^{PQ})\nonumber \\&-\frac{2}{5}g_{\mu \nu } \mathbf {V} -4{\mathcal {M}}_{MP}{\mathcal {M}}_{NQ} \left( {\mathcal {H}}_{\mu \rho }^{(2)MN}{{{\mathcal {H}}^{(2)PQ}}_{\nu }}^\rho \right. \nonumber \\&\left. -\frac{1}{10}g_{\mu \nu }{\mathcal {H}}_{\rho \sigma }^{(2)MN}{\mathcal {H}}^{(2)PQ \rho \sigma }\right) \nonumber \\&-{\mathcal {M}}^{MN}\left( {\mathcal {H}}_{\mu \rho \sigma M}^{(3)} {{\mathcal {H}}_\nu ^{(3)\rho \sigma }}_N-\frac{2}{15}g_{\mu \nu } {\mathcal {H}}_{\rho \sigma \lambda M}^{(3)}{{\mathcal {H}}^{(3)\rho \sigma \lambda }}_N\right) ,\nonumber \\ \end{aligned}$$

(A.1)

$$\begin{aligned} 0= & {} D^\mu ({\mathcal {M}}_{MP}D_\mu {\mathcal {M}}^{PN})-\frac{g^2}{8} {\mathcal {M}}^{PQ}{\mathcal {M}}^{RN}\nonumber \\&\times \left( 2Y_{RQ}Y_{PM}-Y_{PQ}Y_{RM}\right) \nonumber \\&-\frac{4}{6}{\mathcal {M}}^{PN}{\mathcal {H}}_{\mu \nu \rho M}^{(3)} {{\mathcal {H}}^{(3)\mu \nu \rho }}_P\nonumber \\&-8{\mathcal {M}}_{MP}{\mathcal {M}}_{QR} {\mathcal {H}}_{\mu \nu }^{(2)PQ} {\mathcal {H}}^{(2)RN\mu \nu }\nonumber \\&+4g^2Z^{QT,P}Z^{NR,S}{\mathcal {M}}_{QM}(2{\mathcal {M}}_{TR}{\mathcal {M}}_{PS} -{\mathcal {M}}_{TP}{\mathcal {M}}_{RS})\nonumber \\&+4g^2Z^{QT,P}Z^{RS,N}{\mathcal {M}}_{QS}(2{\mathcal {M}}_{TP}{\mathcal {M}}_{RM} -{\mathcal {M}}_{TR}{\mathcal {M}}_{PM})\nonumber \\&-4g^2\delta ^N_MZ^{TU,P}Z^{QR,S}{\mathcal {M}}_{TQ}\left( {\mathcal {M}}_{UR} {\mathcal {M}}_{PS} -{\mathcal {M}}_{UP}{\mathcal {M}}_{RS}\right) \nonumber \\&+\frac{8}{5}\delta ^N_M \left( \mathbf {V}+{\mathcal {M}}_{SP}{\mathcal {M}}_{QR}{\mathcal {H}}_{\mu \nu }^{(2)PQ} {\mathcal {H}}^{(2)RS\mu \nu }\right. \nonumber \\&\left. +\frac{1}{16}{\mathcal {M}}^{PQ} {\mathcal {H}}_{\mu \nu \rho P}^{(3)}{{\mathcal {H}}^{(3)\mu \nu \rho }}_Q\right) ,\nonumber \\&\end{aligned}$$

(A.2)

$$\begin{aligned} 0= & {} 4D_\nu ({\mathcal {M}}_{MP}{\mathcal {M}}_{NQ}{\mathcal {H}}^{(2)PQ\nu \mu })\nonumber \\&-\frac{g}{2}{X_{MNP}}^Q{\mathcal {M}}_{QR}D^\mu {\mathcal {M}}^{PR}\nonumber \\&-2\epsilon _{MNPQR}{\mathcal {M}}^{PS} {{\mathcal {H}}^{(3)\mu \nu \rho }}_S{\mathcal {H}}^{(2)QR}_{\nu \rho }\nonumber \\&+\frac{1}{9}e^{-1}\epsilon ^{\mu \nu \rho \lambda \sigma \tau \kappa } {\mathcal {H}}^{(3)}_{\nu \rho \lambda M}{\mathcal {H}}^{(3)}_{\sigma \tau \kappa N}, \end{aligned}$$

(A.3)

$$\begin{aligned} 0= & {} D_\rho \left( {\mathcal {M}}^{MN}{{\mathcal {H}}^{(3)\rho \mu \nu }}_N\right) \nonumber \\&-2gZ^{NP,M}{\mathcal {M}}_{NQ}{\mathcal {M}}_{PR}{\mathcal {H}}^{(2)QR\mu \nu }\nonumber \\&-\frac{1}{3}e^{-1}\epsilon ^{\mu \nu \rho \lambda \sigma \tau \kappa } {\mathcal {H}}^{(2)MN}_{\rho \lambda }{\mathcal {H}}^{(3)}_{\sigma \tau \kappa N}, \end{aligned}$$

(A.4)

$$\begin{aligned} 0= & {} e^{-1}\epsilon ^{\mu \nu \rho \lambda \sigma \tau \kappa }Y_{MN} {\mathcal {H}}^{(4)N}_{\lambda \sigma \tau \kappa }-6Y_{MN}{\mathcal {M}}^{NP} {{\mathcal {H}}^{(3)\mu \nu \rho }}_P. \end{aligned}$$

(A.5)