Weak field limit and gravitational waves in f(T, B) teleparallel gravity

Abstract

We derive the gravitational waves for $f\left( T, B\right)$ gravity which is an extension of teleparallel gravity and demonstrate that it is equivalent to f(R) gravity by linearized the field equations in the weak field limit approximation. f(T, B) gravity shows three polarizations: the two standard of general relativity, plus and cross, which are purely transverse with two-helicity, massless tensor polarization modes, and an additional massive scalar mode with zero-helicity. The last one is a mix of longitudinal and transverse breathing scalar polarization modes. The boundary term B excites the extra scalar polarization and the mass of scalar field breaks the symmetry of the TT gauge by adding a new degree of freedom, namely a single mixed scalar polarization.

1 Introduction

Albert Einstein, in 1928, made an attempt to formulate a unified theory of gravity and electromagnetism by using the geometric notion of teleparallelism introduced a few years before by Cartan. For this purpose, he relaxed the hypothesis of connection symmetry by Levi Civita and considered a curvature-free connection with torsion, the Weitzenb$\ddot{o}$ck one, and formulated the theory adopting a tangent space basis that had the property to make the spacetime parallelizable. Then, he used the tetrad $\left\{ e_{a}\right\}$ based on the notion of distant or absolute parallelism. This attempt to unify General Relativity (GR) with electromagnetism proved unsuccessful because the components of the electromagnetic field, identified with the additional six components of the tetrad, could be eliminated by imposing the local Lorentz invariance. However, this alternative formulation, based on geometry modification [1,2,3], is equivalent to GR and was named Teleparallel Equivalent General Relativity (TEGR), in the sense that it describes the same physics because it gives the same field equations of GR. In fact, considering the Hilbert–Einstein Lagrangian, linear in the Ricci scalar curvature R [4, 5],

$$\begin{aligned} L_{HE}\left( g\right) =-\frac{1}{2\kappa ^{2}}R\sqrt{-g}, \end{aligned}$$

(1)

with $\kappa ^{2}=8\pi G/c^{4}$ and the teleparallel Lagrangian, linear in the torsion scalar T

$$\begin{aligned} L_{TEGR}\left( e\right) =\frac{e}{2\kappa ^{2}}T, \end{aligned}$$

(2)

they differ from each other by a four divergence which is

$$\begin{aligned} L_{HE}\left( e\right) =L_{TEGR}\left( e\right) +\partial _{\mu }\left( \frac{e}{\kappa ^{2}}T^{\rho \mu }_{\rho }\right) . \end{aligned}$$

(3)

Several issues of today physics can be addressed by extending the geometric sector of the Einstein field equations. For example, f(R) gravity is an extension of GR because it the Hilbert–Einstein Lagrangian, linear in the Ricci curvature scalar R, is extended considering a generic function of it [6]. In the same way it is possible to extend the TEGR by considering an analytical function f(T) of the torsion scalar T [7].

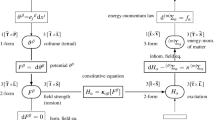
The f(T) teleparallel gravity differs from f(R) gravity because the former leads to second-order field equations while the latter leads to fourth order field equations in metric formalism. Furthermore, f(T) gravity is not invariant under local Lorentz transformation if the spin connection is set to zero. $f\left( T\right)$ gravity can be adopted, for example, to explain the accelerated expansion of the Universe at the present time without the introduction of dark energy (see [5] for a review). If we want to study higher order telepallel theories, equivalent to those expressed in terms of R, we can not limit ourselves to f(T), because it always produces second order dynamical equations. We have to introduce both boundary term $B=2\nabla _{\mu }\left( T^{\mu }\right)$, depending on the derivatives of the torsion vector $T^{\mu }$ and terms like $\Box T$, $\Box ^{k}T$ in the teleparallel Lagrangian [8, 9]. We can therefore start from $f\left( R\right)$ gravity, and find its teleparallel equivalent after observing that the boundary term is $B=-T-R$ and then restore the $f\left( T, B\right)$ gravity [10]. The teleparallel theory of gravity f(T, B) is the teleparallel equivalent of f(R) as the TEGR is the teleparallel equivalent of GR as we will show below by considering the weak field limit and the gravitational wave modes. In the framework of f(T, B) gravity, it is possible to explore the validity of laws of thermodynamics [11] and derive energy constraints for de Sitter (dS), power-law, $\Lambda$CDM and phantom models [12].

The detection of gravitational waves (GWs) opened new perspectives in the study of the alternative theories of gravity and, in general, in relativistic astrophysics. In generic metric theories of gravity, it is possible to show that the GWs polarizations can give, at maximum of six modes in 4D spacetimes. More precisely, according to [13, 14], we have: breathing (b), longitudinal (l), vector-x (x), vector-y (y), plus ($+$) and cross ($\times$) modes.

In order to study the further GW polarizations, beyond the two standards plus and cross modes, it is useful to extend GR to more general theories. If scalar or vector modes are found, it could mean that theory of gravitation should be extended beyond GR and some theoretical models should be excluded.

To this end, the GW170817 event [15] set constraints on viable gravitational theories. In fact, the event was the first to provide constraints on the speed of electromagnetic and gravitational waves. According to this result, it is possible to fix possible masses of further gravitational modes [16]. This fact is important to discriminate among concurring gravitational theories and some alternatives to GR, including some scalar-tensor theories like Brans–Dicke gravity, Horava–Lifshitz gravity, and bimetric gravity, seem excluded [17]. In particular, observational constraints on f(T) gravity can be imposed by the combined observation of GW170817 and its electromagnetic counterpart GRB170817A, as discussed in [18, 19]. In these papers, constraints derived from primordial gravitational waves are also taken into account.

In summary, GWs polarizations are a powerful tool to probe theories of gravity. Moreover, by means of the linearized gravitational energy-momentum pseudo-tensor of f(R), f(T) gravity [20] or more generally of $f(R, R\Box R, \ldots R\Box ^{k}R)$ gravity [21], it is possible to express the pseudo-tensor in terms of the further modes in order to test alternative theories of gravity. In the framework of teleparallelism, gravitational waves have started to be studied recently. These studies led to the interesting possibility to classify teleparallel theories according to their degrees of freedom [22,23,24,25].

In this paper, we investigate GWs generated in theories containing the torsion scalar T and the boundary term B and show, from this point of view, their equivalence with f(R) gravity.

The layout of the article is as follows: in Sect. 2 we obtain the geometrical and physical quantities of interest after the expansion of tetrads around the flat geometry at first order in the weak field approximation. In Sect. 3, we prove the equivalence between f(T, B) and f(R) theories and then we derive the field equations in presence of matter for $f\left( T, B \right)$ gravity in the low energy limit. GWs in vacuum are obtained in Sect. 4 and, finally, in Sect. 5 both polarization and helicity of GWs are studied by mean the equation of geodesic deviation and the Newman–Penrose formalism. Conclusions are drawn in Sect. 6.

Throughout this work we will use conventions by Landau and Lifshitz [26], that is:

• (1) The metric signature is $\left( +, -, -, -\right)$ .

• (2) The Riemann tensor $R^{\rho }_{\lambda \nu \mu }$ for a generic connection $\Gamma$ is defined as

  $$\begin{aligned} R^{\rho }_{\lambda \nu \mu }=\partial _{\nu }\Gamma ^{\rho }_{\lambda \mu }-\partial _{\mu }\Gamma ^{\rho }_{\lambda \nu }+\Gamma ^{\rho }_{\eta \nu }\Gamma ^{\eta }_{\lambda \mu }-\Gamma ^{\rho }_{\eta \mu }\Gamma ^{\eta }_{\lambda \nu }. \end{aligned}$$

  (4)

• (3) The Ricci tensor is defined as the contraction $R_{\mu \nu }=R^{\lambda }_{\mu \lambda \nu }$ .

2 Weak field limit in teleparallel gravity

Dynamical variables used in teleparallelism are the components of tetrad basis $\left\{ e_{a}\right\}$ and dual basis $\left\{ e^{a}\right\}$ which form a local orthonormal basis for the tangent space at each point $\{x_{\mu }\}$ of the spacetime manifold. The components of the vierbein satisfy relations [27,28,29,30,31]

$$\begin{aligned}&e^{a}_{\mu }e_{a}^{\nu }=\delta _{\mu }^{\nu }\ , \qquad \text {and} \qquad e^{a}_{\ \mu }e_{b}^{\ \mu }=\delta _{a}^{b}\ , \end{aligned}$$

(5)

$$\begin{aligned}&\eta _{ab}=g_{\mu \nu }e_{a}^{\ \mu }e_{b}^{\nu }\ ,\qquad \text {and}\qquad g_{\mu \nu }=\eta _{ab}e^{a}_{\mu }e^{b}_{\nu }\ , \end{aligned}$$

(6)

where we are going to use the Greek alphabet to denote indices related to spacetime, and the Latin alphabet to denote indices related to the tangent space. The Weitzenb$\ddot{o}$ck connection is defined as

$$\begin{aligned} {\tilde{\Gamma }}^{\rho }_{\mu \nu }=e_{a}^{\rho }\partial _{\nu }e^{a}_{\mu }, \end{aligned}$$

(7)

and its torsion tensor is

$$\begin{aligned} T^{\nu }_{\rho \mu }={\tilde{\Gamma }}^{\nu }_{\mu \rho }- {\tilde{\Gamma }}^{\nu }_{\rho \mu }=e_{a}^{\nu }\partial _{\rho }e^{a}_{\mu }-e_{a}^{\nu }\partial _{\mu }e^{a}_{\rho }. \end{aligned}$$

(8)

Defined the contortion tensor as the connection of Weitzenb$\ddot{o}$ck minus the Levi Civita connection that is

$$\begin{aligned} K^{\nu }_{ \rho \mu }={\tilde{\Gamma }}^{\nu }_{ \rho \mu }-{\mathop {\Gamma }\limits ^{\circ }}{}^{\nu }_{ \rho \mu }=\frac{1}{2}\left( T_{\rho \mu }^{\nu }+T_{\mu \rho }^{\nu }-T^{\nu }_{\rho \mu }\right) , \end{aligned}$$

(9)

and the superpotential tensor $S^{\rho \mu \nu }$ as

$$\begin{aligned} S^{\rho \mu \nu }=\frac{1}{2}\left( K^{\mu \nu \rho }-g^{\rho \nu }T^{\sigma \mu }_{\sigma }+g^{\rho \mu }T^{\sigma \nu }_{\sigma }\right) , \end{aligned}$$

(10)

we obtain the scalar torsion T

$$\begin{aligned} T=T_{\rho \mu \nu }S^{\rho \mu \nu }, \end{aligned}$$

(11)

from the contraction of the torsion tensor with the superpotential. The curvature of the Weitzenb$\ddot{o}$ck connection is $R[{\tilde{\Gamma }}]=0$, where the Riemann tensor $R^{\rho }_{\lambda \nu \mu }$ for a Weitzenb$\ddot{o}$ck connection is defined as

$$\begin{aligned} R^{\rho }_{\lambda \nu \mu }=\partial _{\nu }{\tilde{\Gamma }}^{\rho }_{\lambda \mu }-\partial _{\mu }{\tilde{\Gamma }}^{\rho }_{\lambda \nu }+{\tilde{\Gamma }}^{\rho }_{\eta \nu }{\tilde{\Gamma }}^{\eta }_{\lambda \mu }-{\tilde{\Gamma }}^{\rho }_{\eta \mu }{\tilde{\Gamma }}^{\eta }_{\lambda \nu }. \end{aligned}$$

(12)

We now express the scalar curvature $R[{\mathop {\Gamma }\limits ^{\circ }}]$ of the Levi-Civita connection in terms of the scalar torsion T and the vector torsion $T^{\sigma }$, that is

$$\begin{aligned} -R[{\mathop {\Gamma }\limits ^{\circ }}]=T+\frac{2}{e}\partial _{\sigma }\left( eT^{\nu \sigma }_{\nu }\right) , \end{aligned}$$

(13)

with $T^{\sigma }$ obtained by contracting the first and third torsion tensor index

$$\begin{aligned} T^{\sigma }=T^{\nu \sigma }_{\nu }, \end{aligned}$$

(14)

where $e=det\left( e^{a}_{\rho }\right)$. If we indicate the boundary term as

$$\begin{aligned} B=\frac{2}{e}\partial _{\sigma }\left( eT^{\nu \sigma }_{\nu }\right) , \end{aligned}$$

(15)

we get the relation¹

$$\begin{aligned} -R[{\mathop {\Gamma }\limits ^{\circ }}]=T+B. \end{aligned}$$

(16)

We now expand the tetrad field around the flat geometry described by the trivial tetrad $e^{a}_{\mu }=\delta ^{a}_{\mu }$ as follows

$$\begin{aligned} e^{a}_{\mu }=\delta ^{a}_{\mu }+E^{a}_{\mu }, \end{aligned}$$

(17)

where $|E^{a}_{\mu } |\ll 1$. Thus perturbing the metric tensor $g_{\mu \nu }$ to first order in $E^{a}_{\mu }$ we obtain

$$\begin{aligned} g_{\mu \nu }= & {} \eta _{\mu \nu }+h_{\mu \nu }+{\mathcal {O}}\left( h^2\right) \nonumber \\= & {} \eta _{\mu \nu }+\eta _{\mu a}E^{a}_{\nu }+\eta _{\nu a}E^{a}_{\mu }+{\mathcal {O}}\left( E^2\right) \ , \end{aligned}$$

(18)

and so

$$\begin{aligned} h_{\mu \nu }=\eta _{\mu a}E^{a}_{\nu }+\eta _{\nu a}E^{a}_{\mu }. \end{aligned}$$

(19)

The Weitzenb$\ddot{o}$ck connection to first order in $E^{a}_{\mu }$ becomes

$$\begin{aligned} {\tilde{\Gamma }}^{\rho \left( 1\right) }_{\mu \nu }=\delta _{a}^{\rho }\partial _{\nu }E^{a}_{\mu }. \end{aligned}$$

(20)

The covariant derivative $\nabla _{\mu }$ and the covariant d’Alembert operator $\Box =g^{\mu \nu }\nabla _{\mu }\nabla _{\nu }$ to zero order become

$$\begin{aligned}&\nabla _{\mu }^{\left( 0\right) }=\partial _{\mu }\ , \end{aligned}$$

(21)

$$\begin{aligned}&\Box ^{\left( 0\right) }=\eta ^{\mu \nu }\partial _{\nu }\partial _{\mu }=\partial ^{\mu }\partial _{\mu }. \end{aligned}$$

(22)

The torsion tensor $T^{\mu }_{\nu \rho }$ and its contraction $T^{\mu \nu }_{\mu }$ can be written as

$$\begin{aligned} T^{\mu \left( 1\right) }_{\nu \rho }=\delta _{a}^{\mu }\left( \partial _{\nu }E^{a}_{\rho }-\partial _{\rho }E^{a}_{\nu }\right) , \end{aligned}$$

(23)

and

$$\begin{aligned} T^{\rho \sigma \left( 1\right) }_{\rho }=\delta _{a}^{\mu }\eta ^{\sigma \nu }\left( \partial _{\nu }E^{a}_{\mu }-\partial _{\mu }E^{a}_{\nu }\right) . \end{aligned}$$

(24)

We compute the contortion tensor as

$$\begin{aligned} K^{\rho \left( 1\right) }_{\mu \nu }=\eta _{\mu \lambda }\delta ^{\lambda }_{a}\partial ^{\rho }E^{a}_{\nu }-\delta _{a}^{\rho }\partial _{\mu }E^{a}_{\nu }, \end{aligned}$$

(25)

and the superpotential $S_{\rho }^{\mu \nu }$, the scalar torsion T and the boundary term B as

$$\begin{aligned} 2S_{\rho }^{\mu \nu \left( 1\right) }= & {} \delta _{a}^{\nu }\partial ^{\mu }E^{a}_{\rho }-\delta _{a}^{\mu }\partial ^{\nu }E^{a}_{\rho }-\delta ^{\nu }_{\rho }\left( \delta _{a}^{\sigma }\partial ^{\mu }E^{a}_{\sigma }-\eta ^{\alpha \mu }\delta ^{a}_{\alpha }\partial _{\sigma }E^{\sigma }_{a}\right) \nonumber \\&+\delta ^{\mu }_{\rho }\left( \delta _{a}^{\sigma }\partial ^{\nu }E^{a}_{\sigma }-\eta ^{\alpha \nu }\delta ^{a}_{\alpha }\partial _{\sigma }E^{\sigma }_{a}\right) \ , \end{aligned}$$

(26)

$$\begin{aligned} T^{\left( 2\right) }= & {} T^{\mu \nu \rho \left( 1\right) }S^{\left( 1\right) }_{\mu \nu \rho }\ , \end{aligned}$$

(27)

$$\begin{aligned} B^{\left( 1\right) }= & {} \left( \frac{2}{e}\partial _{\sigma }\left( e T^{\sigma }\right) \right) ^{\left( 1\right) }=2\delta _{a}^{\nu }\left[ \Box E^{a}_{\nu }-\partial ^{\mu }\partial _{\nu }E^{a}_{\mu }\right] .\nonumber \\ \end{aligned}$$

(28)

The Ricci curvature R, to the first order in $E^{a}_{\mu }$, takes the following form

$$\begin{aligned} R^{\left( 1\right) }=-B^{\left( 1\right) }, \end{aligned}$$

(29)

that is, the first order boundary term $B^{(1)}$ contributes to the Ricci curvature. Finally we obtain the useful relation

$$\begin{aligned} 2\partial _{\nu }S_{\rho }^{\mu \nu (1)}&=\delta _{a}^{\nu }\partial _{\nu }\partial ^{\mu }E^{a}_{\rho }-\delta _{a}^{\mu }\Box E^{a}_{\rho }-\delta _{a}^{\sigma }\partial _{\rho }\partial ^{\mu }E^{a}_{\sigma } \nonumber \\&\quad +\eta ^{\rho \mu }\delta _{a}^{\sigma }\partial _{\rho }\partial _{\sigma }E^{a}_{\rho }\nonumber \\&\quad +\delta ^{\mu }_{\rho }\delta _{a}^{\sigma }\Box E^{a}_{\sigma }-\delta ^{\mu }_{\rho }\delta _{a}^{\sigma }\eta ^{\alpha \nu }\partial _{\nu }\partial _{\sigma }E^{a}_{\alpha }\ , \end{aligned}$$

(30)

and we set

$$\begin{aligned} E_{\mu \nu }=\eta _{\mu a}E^{a}_{\nu }, \qquad E=\delta _{a}^{\mu }E^{a}_{\mu }. \end{aligned}$$

(31)

The first order perturbative tetrad $E^{a}_{\mu }$ is not symmetric because the $f\left( T,B\right)$ gravity is not invariant under a local Lorentz transformation [22, 32]

$$\begin{aligned} \eta _{\mu a}E^{a}_{\nu }\ne \eta _{\nu a}E^{a}_{\mu }, \end{aligned}$$

(32)

and then, we decompose the perturbation tetrad $E_{\mu \nu }$ into symmetric and antisymmetric parts

$$\begin{aligned} E_{\mu \nu }=E_{\left( \mu \nu \right) }+E_{\left[ \mu \nu \right] }. \end{aligned}$$

(33)

However, the antisymmetric part $E_{\left[ \mu \nu \right] }$ have no physical meaning because it is not involved into the Lagrangian $L_{f\left( T,B\right) }$ and field equations, depending on the symmetric part $E_{\left( \mu \nu \right) }$ by means of T and B. Hence, we can set to zero the antisymmetric component $E_{\left[ \mu \nu \right] }$

$$\begin{aligned} E_{\left[ \mu \nu \right] }=0, \end{aligned}$$

(34)

and the metric perturbation becomes

$$\begin{aligned} h_{\mu \nu }=2\eta _{\mu a}E^{a}_{\nu }. \end{aligned}$$

(35)

Now we have all the ingredients to develop the analysis for f(T, B).

3 The weak field limit of f(T, B) teleparallel gravity

Before developing the weak field limit in the context of f(T, B) gravity, let us prove that it is the teleparallel equivalent of f(R) gravity [9]. This statement can be supported by the fact that both theories describe the same physics. It is worth stressing that teleparallel theories are governed by the dynamical variables $e_{a}^{\mu }$, components of the tetrad basis $\left\{ e_{a}\right\}$. After fixing the tetrad, we can express uniquely both the scalar torsion T and the boundary term B. Then we can write the scalar torsion T as

$$\begin{aligned} T=\frac{1}{4}T^{\rho }_{\mu \nu }T_{\rho }^{\mu \nu }+\frac{1}{2}T^{\rho }_{\mu \nu }T^{\nu \mu }_{\rho }-T^{\rho }_{\mu \rho }T^{\nu \mu }_{\nu }. \end{aligned}$$

(36)

From the Weitzenb$\ddot{o}$ck connection ${\tilde{\Gamma }}^{\rho }_{\ \mu \nu }$, defined in (7), and the torsion tensor $T^{\rho }_{\mu \nu }$, defined in (8), both can be expressed in terms of the tetrad $e_{a}^{\mu }$. We get the following expression for the scalar torsion T

$$\begin{aligned} T= & {} e_{a}^{\mu }{\mathop {\nabla ^{\nu }}\limits ^{\circ }}\left( e^{a}_{\alpha }e^{\rho }_{b}e^{\alpha }_{c}\eta ^{bc}\right) e^{b}_{\nu }e^{c}_{\rho }\eta _{bc}e_{a}^{\nu }{\mathop {\nabla }\limits ^{\circ }}_{\mu }e^{a}_{\nu }\nonumber \\&-e_{a}^{\mu }{\mathop {\nabla }\limits ^{\circ }}_{\mu }e^{a}_{\rho }e_{d}^{\sigma }{\mathop {\nabla }\limits ^{\circ }}_{\sigma }e^{d}_{\beta }e^{\beta }_{b}e^{\rho }_{c}\eta ^{bc}\ , \end{aligned}$$

(37)

where ${\mathop {\nabla }\limits ^{\circ }}_{\mu }$ is a covariant derivative for the Levi Civita connection ${\mathop {\Gamma }\limits ^{\circ }}$ given in terms of the tetrad basis. The boundary component B, expressed in terms of vierbein, is given by the relations

$$\begin{aligned} B=\frac{2}{e}\partial _{\sigma }\left( eT^{\nu \sigma }_{\nu }\right) ,\qquad T^{\sigma }=e_{\nu }^{a}\partial ^{\sigma }e^{\nu }_{a}-e^{\sigma }_{b}e^{\tau }_{c}\eta ^{bc}e^{a}_{\tau }\partial _{\nu }e^{\nu }_{a}, \end{aligned}$$

(38)

and then

$$\begin{aligned} B=\frac{2}{e}\partial _{\sigma }\left[ e\left( e_{\nu }^{a}\partial ^{\sigma }e^{\nu }_{a}-e^{\sigma }_{b}e^{\tau }_{c}\eta ^{bc}e^{a}_{\tau }\partial _{\nu }e^{\nu }_{a}\right) \right] . \end{aligned}$$

(39)

Now if we calculate

$$\begin{aligned}&-T-B=-\left[ e_{a}^{\mu }{\mathop {\nabla ^{\nu }}\limits ^{\circ }}\left( e^{a}_{\alpha }e^{\rho }_{b}e^{\alpha }_{c}\eta ^{bc}\right) e^{b}_{\nu }e^{c}_{\rho }\eta _{bc}e_{a}^{\nu }{\mathop {\nabla }\limits ^{\circ }}_{\mu }e^{a}_{\nu }\right. \nonumber \\&\quad \left. -e_{a}^{\mu }{\mathop {\nabla }\limits ^{\circ }}_{\mu }e^{a}_{\rho }e_{d}^{\sigma }{\mathop {\nabla }\limits ^{\circ }}_{\sigma }e^{d}_{\beta }e^{\beta }_{b}e^{\rho }_{c}\eta ^{bc}\right] \nonumber \\&\quad -\frac{2}{e}\partial _{\sigma }\left[ e\left( e_{\nu }^{a}\partial ^{\sigma }e^{\nu }_{a}-e^{\sigma }_{b}e^{\tau }_{c}\eta ^{bc}e^{a}_{\tau }\partial _{\nu }e^{\nu }_{a}\right) \right] \end{aligned}$$

(40)

we get exactly the curvature R of the Levi Civita connection ${\mathop {\Gamma }\limits ^{\circ }}$ expressed in terms of the tetrad basis

$$\begin{aligned} R[{\mathop {\Gamma }\limits ^{\circ }}]=e_{a}^{\theta }e_{b}^{\nu }\eta ^{ab}\left[ \partial _{\rho }{\mathop {\Gamma }\limits ^{\circ }}^{\rho }_{\theta \nu }+{\mathop {\Gamma }\limits ^{\circ }}^{\rho }_{\sigma \rho }{\mathop {\Gamma }\limits ^{\circ }}^{\sigma }_{\theta \nu }-\partial _{\nu }{\mathop {\Gamma }\limits ^{\circ }}^{\rho }_{\theta \rho }-{\mathop {\Gamma }\limits ^{\circ }}^{\rho }_{\sigma \nu }{\mathop {\Gamma }\limits ^{\circ }}^{\sigma }_{\theta \rho }\right] . \end{aligned}$$

(41)

This means that, if we fix the tetrad basis $e_{a}^{\rho }$ both T and B, and therefore R, are uniquely determined. We have no possibility to disentangle the 3 objects T, B, and R once the tetrad is given, then the relation

$$\begin{aligned} R[{\mathop {\Gamma }\limits ^{\circ }}]=-T-B, \end{aligned}$$

(42)

is fixed by the tetrad. If T and B were independent, we could have

$$\begin{aligned} R[{\mathop {\Gamma }\limits ^{\circ }}]\ne -T-B. \end{aligned}$$

(43)

This would be possible, if we could express T in a tetrad basis $e_{(1)a}^{\rho }$ and B in another tetrad basis $e_{(2)a}^{\rho }$, but this is not possible because both T and B must be expressed in terms of the same basis $e_{a}^{\rho }$.

Let us now take into account the action of $f\left( T, B\right)$ gravity in presence of standard matter [9]

$$\begin{aligned} S_{f\left( T,B\right) }=\int _{\Omega }d^{4}x\left[ \frac{1}{2\kappa ^{2}}f\left( T,B\right) +{\mathcal {L}}_{m}\right] e. \end{aligned}$$

(44)

According to the previous considerations, it is that is the teleparallel action equivalent to the f(R) gravity action. The variation of the action (44) with respect to the vierbein fields $e^{a}_{\rho }$ yields the following field equations

$$\begin{aligned}&\frac{4}{e}\partial _{\sigma }\left( ef_{T}S_{a}^{\rho \sigma }\right) +f\left( T,B\right) e_{a}^{\rho }-4f_{T}T^{\mu }_{\nu a}S_{\mu }^{\nu \rho }-Bf_{B}e_{a}^{\rho }\nonumber \\&\quad +4\left( \partial _{\lambda }f_{B}\right) S_{a}^{\lambda \rho }+2e_{a}^{\rho }\Box f_{B}\nonumber \\&\quad -2e_{a}^{\sigma }\nabla _{\sigma }\nabla ^{\rho }f_{B}=2\kappa ^{2}{\mathcal {T}}_{a}^{\rho }\ , \end{aligned}$$

(45)

where ${\mathcal {T}}_{a}^{\rho }$ is the energy momentum tensor of matter defined as

$$\begin{aligned} {\mathcal {T}}_{a}^{\rho }=-\frac{1}{e}\frac{\delta \left( e{\mathcal {L}}_{m}\right) }{\delta e^{a}_{\rho }}. \end{aligned}$$

(46)

Supposing $f\left( T,B\right)$ being an analytic function of T and B we can expand it as

$$\begin{aligned} f\left( T,B\right)= & {} f\left( 0\right) +f_{T}\left( 0\right) T+f_{B}\left( 0\right) B+f_{TB}\left( 0\right) TB\nonumber \\&+f_{TT}\left( 0\right) T^{2}+f_{BB}\left( 0\right) B^{2}\nonumber \\&+{\mathcal {O}}\left( TB, T^2, B^2\right) \ . \end{aligned}$$

(47)

The linearized field equations are

$$\begin{aligned}&4f_{T}\left( 0\right) \partial _{\sigma }S_{\tau }^{\rho \sigma \left( 1\right) }+4f_{B^2}\left( 0\right) \delta ^{\rho }_{\tau }\Box B^{\left( 1\right) }\nonumber \\&\quad -4f_{B^2}\left( 0\right) \partial _{\tau }\partial ^{\rho }B^{\left( 1\right) }=2\kappa ^{2}{\mathcal {T}}_{\tau }^{\rho \left( 0\right) }. \end{aligned}$$

(48)

The field equations (48) are gauge-invariant, namely under transformations of gauge

$$\begin{aligned} E_{\mu \nu }\longrightarrow E_{\mu \nu }+\partial _{\mu }\Lambda _{\nu }+\partial _{\nu }\Lambda _{\mu }, \end{aligned}$$

(49)

remain invariant to first order, with $\Lambda _{\mu }$ infinitesimal. We can use the Lorentz gauge

$$\begin{aligned} \partial _{\mu }\left( E^{\mu \nu }-\frac{1}{2}\eta ^{\mu \nu }E\right) =0, \end{aligned}$$

(50)

where we set

$$\begin{aligned} E_{\mu \nu }=\eta _{\mu a}E^{a}_{\nu }, \qquad E=\delta _{a}^{\mu }E^{a}_{\mu }. \end{aligned}$$

(51)

In the harmonic gauge, $B^{\left( 1\right) }$ and Eq. (30) take the form

$$\begin{aligned} B^{\left( 1\right) }= & {} -\Box \bar{E}, \end{aligned}$$

(52)

$$\begin{aligned} 2\partial _{\nu }S_{\rho }^{\mu \nu (1)}= & {} -\Box \bar{E}^{\mu }_{\rho }\ . \end{aligned}$$

(53)

Thus the Eq. (48) becomes in a simpler form

$$\begin{aligned} \boxed { f_{T}^{(0)}\Box \bar{E}^{\rho }_{\tau }+2f_{B^2}^{(0)}\left( \delta ^{\rho }_{\tau }\Box ^{2}-\partial _{\tau }\partial ^{\rho }\Box \right) \bar{E}=-2\kappa ^{2}{\mathcal {T}}^{\rho \left( 0\right) }_{\tau } }, \end{aligned}$$

(54)

where we called $\bar{E}_{\mu \nu }$

$$\begin{aligned} \bar{E}_{\mu \nu }=E_{\mu \nu }-\frac{1}{2}\eta _{\mu \nu }E. \end{aligned}$$

(55)

Hence the trace of Eq. (54) is

$$\begin{aligned} \boxed { f_{T}^{\left( 0\right) }\Box \bar{E}+6f_{B^2}^{\left( 0\right) }\Box ^{2}\bar{E}=-2\kappa ^{2}{\mathcal {T}}^{\left( 0\right) } }. \end{aligned}$$

(56)

We have now all the ingredients to develop the GW theory for f(T, B) teleparallel gravity.

4 Gravitational Waves in f(T, B) Teleparallel Gravity

Let us now derive the GWs for f(T, B) gravity in vacuum as solutions of Eq. (54). We start from the trace Eq. (56) in vacuum

$$\begin{aligned} f_{T}^{\left( 0\right) }\Box \bar{E}+6f_{B^2}^{\left( 0\right) }\Box ^{2}\bar{E}=0, \end{aligned}$$

(57)

that, in the k-space, becomes the algebraic equation [33] with $f_{B^2}^{\left( 0\right) }\ne 0$

$$\begin{aligned} \left( k^{4}-\frac{f_{T}^{\left( 0\right) }}{6 f_{B^2}^{\left( 0\right) }}k^2\right) {\hat{A}}\left( k_{0},{\mathbf {k}}\right) =0, \end{aligned}$$

(58)

where $k^{2}=\omega ^{2}-{\mathbf {k}}\cdot {\mathbf {k}}=\omega ^{2}-q^{2}$. Here $k^{\mu }=\left( \omega ,\mathbf {k}\right)$ is the wave four-vector. If $f_{B^2}^{\left( 0\right) } =0$, Eq. (48) becomes

$$\begin{aligned} 2f_{T}\left( 0\right) \partial _{\sigma }S_{\tau }^{\rho \sigma \left( 1\right) }=\kappa ^{2}{\mathcal {T}}_{\tau }^{\rho \left( 0\right) }, \end{aligned}$$

(59)

that is the linearized field equations of $f\left( T\right)$ gravity with matter. In the harmonic gauge, we obtain

$$\begin{aligned} f_{T}^{(0)}\Box \bar{E}^{\rho }_{\tau }=-2\kappa ^{2}{\mathcal {T}}^{\rho \left( 0\right) }_{\tau }, \end{aligned}$$

(60)

whose trace equation is

$$\begin{aligned} f_{T}^{\left( 0\right) }\Box \bar{E}=-2\kappa ^{2}{\mathcal {T}}^{\left( 0\right) }. \end{aligned}$$

(61)

The solutions of Eq. (61) are the gravitational waves of f(T) gravity whose polarizations are the two standard $+$ and $\times$ modes of GR, as demonstrated in [50]. Therefore the f(T, B) gravity, for $f_{B^2}^{\left( 0\right) } =0$, reproduces the results of f(T) gravity.

The general solution of Eq. (57) can be expressed as a Fourier integral

$$\begin{aligned} \bar{E}\left( t,{\mathbf {x}}\right) =\int \frac{d^{4}k}{\left( 2\pi \right) ^{2}}{\hat{A}}\left( k_{0}, {\mathbf {k}}\right) e^{i k^{\alpha }x_{\alpha }}. \end{aligned}$$

(62)

Then, we obtain two solutions of Eq. (58) for $A\left( k_{0}, {\mathbf {k}}\right) \ne 0$, that is

$$\begin{aligned} k_{1}^{2}=0, \qquad \text {and} \qquad k_{2}^{2}=\frac{f_{T}^{\left( 0\right) }}{6 f_{B^2}^{\left( 0\right) }}\ne 0, \end{aligned}$$

(63)

and the integral of trace equation (57) in vacuum is

$$\begin{aligned} \bar{E}\left( t,{\mathbf {x}}\right) =\sum _{m=1}^{2}\int \frac{d^{3}{\mathbf {k}}}{\left( 2\pi \right) ^{3/2}}\left( \hat{A}_{m}\left( {\mathbf {k}}\right) e^{ik_{m}^{\alpha }x_{\alpha }}+c. c.\right) . \end{aligned}$$

(64)

Therefore substituting Eq. (64) into Eq. (54), in vacuum, we get

$$\begin{aligned} \Box \bar{E}_{\rho \tau }\left( x\right)= & {} \int \frac{d^{3}{\mathbf {k}}}{(2\pi )^{3/2}}\left\{ \left( -\frac{k_{2}^{2}}{3}\right) \left[ \eta _{\rho \tau }\right. \right. \nonumber \\&\left. \left. -\frac{\left( k_{2}\right) _{\rho }\left( k_{2}\right) _{\tau }}{k_{2}^{2}}\right] \right\} \left( \hat{A}_{2}\left( {\mathbf {k}}\right) e^{ik_{2}^{\alpha }x_{\alpha }}+c.c.\right) \ .\nonumber \\ \end{aligned}$$

(65)

Finally, the general solution of Eq. (54), in vacuum, expressed as a homogeneous plus a particular solution is

$$\begin{aligned}&\bar{E}_{\rho \tau }\left( x\right) =\int \frac{d^{3}{\mathbf {k}}}{(2\pi )^{3/2}}\hat{C}_{\rho \tau }\left( {\mathbf {k}}\right) e^{ik_{1}^{\alpha }x_{\alpha }} \nonumber \\&\quad +\int \frac{d^{3}{\mathbf {k}}}{(2\pi )^{3/2}}\left\{ \left( -\frac{1}{3}\right) \left[ \eta _{\rho \tau }-\frac{\left( k_{2}\right) _{\rho }\left( k_{2}\right) _{\tau }}{k_{2}^{2}}\right] \right\} \hat{A}_{2}\left( {\mathbf {k}}\right) e^{ik_{2}^{\alpha }x_{\alpha }}\nonumber \\&\quad +c.c.\ . \end{aligned}$$

(66)

From Eq. (55), it is possible to derive the GWs for $f\left( T, B\right)$ gravity, that is

$$\begin{aligned} E_{\rho \tau }\left( x\right)&=\int \frac{d^{3}{\mathbf {k}}}{(2\pi )^{3/2}}\hat{C}_{\rho \tau }\left( {\mathbf {k}}\right) e^{ik_{1}^{\alpha }x_{\alpha }} \nonumber \\&\quad +\int \frac{d^{3}{\mathbf {k}}}{(2\pi )^{3/2}}\left\{ \frac{1}{3}\left[ \frac{\eta _{\rho \tau }}{2}+\frac{\left( k_{2}\right) _{\rho }\left( k_{2}\right) _{\tau }}{k_{2}^{2}}\right] \right\} \hat{A}_{2}\left( {\mathbf {k}}\right) e^{ik_{2}^{\alpha }x_{\alpha }}\nonumber \\&\quad +c.c.\ . \end{aligned}$$

(67)

Starting from this solution we can analyze the polarizations and the helicity of GWs.

5 Polarizations and helicity

A useful way to visualize the polarizations of gravitational waves is to derive the geodesic deviation that they generate via the equation for geodesic deviation. Let us consider the wave propagating in $+\hat{z}$ direction, in a local proper reference frame, and take into account the equation for geodesic deviation

$$\begin{aligned} \ddot{x}^{i}=-R^{i}_{0k0}x^{k}, \end{aligned}$$

(68)

where the Latin index range over the set $\left\{ 1,2,3\right\}$ and $R^{i}_{0k0}$ are so-called “electric” components of the Riemann tensor, the only measurable components [30]. Substituting the linearized electric components of the Riemann tensor $R^{\left( 1\right) }_{i0j0}$, expressed in terms of the tetrad perturbation $E_{\mu \nu }$,

$$\begin{aligned} R^{\left( 1\right) }_{i0j0}=\left( E_{i0,j0}+E_{j0,i0}-E_{ij,00}-E_{00,ij}\right) , \end{aligned}$$

(69)

into Eq. (68), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}(t)=-\left( xE_{11,00}+yE_{12,00}\right) \\ \ddot{y}(t)=- \left( xE_{12,00}+yE_{11,00}\right) \\ \ddot{z}(t)=\left( 2E_{03,03}-E_{33,00}-E_{00,33}\right) z \end{array}\right. }. \end{aligned}$$

(70)

From Eq. (67), for $k_{1}^{2}=0$ the massless plane wave, travelling in $+\hat{z}$ direction, whose propagation speed is equal to c, keeping ${\mathbf {k}}$ fixed and $k_{1}^{\mu }=\left( \omega _{1},0,0,k_{z}\right)$, we have

$$\begin{aligned} E^{(k_{1})}_{\mu \nu }\left( t,z\right)= & {} \sqrt{2}\left[ {\hat{\epsilon }}^{(+)}\left( \omega _{1}\right) \epsilon ^{(+)}_{\mu \nu }+{\hat{\epsilon }}^{(\times )}\left( \omega _{1}\right) \epsilon ^{(\times )}_{\mu \nu }\right] \nonumber \\&e^{i\omega _{1}\left( t-z\right) }+c.c. \end{aligned}$$

(71)

where

$$\begin{aligned} \epsilon ^{(+)}_{\mu \nu }= & {} \frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ . \end{aligned}$$

(72)

$$\begin{aligned} \epsilon ^{(\times )}_{\mu \nu }= & {} \frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ , \end{aligned}$$

(73)

and $\omega _{1}=k_{z}$. Furthermore, always from Eq. (67) for $k_{2}^{2}\ne 0$, the massive plane wave propagating in $+\hat{z}$ direction, is

$$\begin{aligned}&E^{(k_{2})}_{\mu \nu }\left( t,z\right) =\Biggl [\left( \frac{1}{2}+\frac{\omega ^{2}_{2}}{k_{2}^{2}}\right) \epsilon _{\mu \nu }^{(TT)}-\frac{\sqrt{2}\omega _{2}k_{z}}{k_{2}^{2}}\epsilon _{\mu \nu }^{(TS)}\nonumber \\&\quad -\frac{1}{\sqrt{2}}\epsilon _{\mu \nu }^{(b)}+\left( \frac{k_{z}^{2}}{k_{2}^{2}}-\frac{1}{2}\right) \epsilon _{\mu \nu }^{(l)}\Biggr ]\frac{\hat{A}_{2}\left( k_{z}\right) }{3}e^{i\left( \omega _{2}t-k_{z}z\right) }\nonumber \\&\quad +c.c.\ . \end{aligned}$$

(74)

Here, the propagation speed is less then c, keeping ${\mathbf {k}}$ fixed and $k_{2}^{\mu }=\left( \omega _{2},0,0,k_{z}\right)$. The polarizations are

$$\begin{aligned} \epsilon ^{(TT)}_{\mu \nu }&= \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ ,&\epsilon ^{(TS)}_{\mu \nu }&=\frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix},\end{aligned}$$

(75)

$$\begin{aligned} \epsilon ^{(b)}_{\mu \nu }&=\frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ ,&\epsilon ^{(l)}_{\mu \nu }&= \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}\ . \end{aligned}$$

(76)

In more compact form, the tetrad linear perturbation $E_{\mu \nu }$, traveling in the $+\hat{z}$ direction assuming ${\mathbf {k}}$ fixed, is

$$\begin{aligned}&E_{\mu \nu }\left( t,z\right) =\sqrt{2}\left[ {\hat{\epsilon }}^{(+)}\left( \omega _{1}\right) \epsilon ^{(+)}_{\mu \nu }+{\hat{\epsilon }}^{(\times )}\left( \omega _{1}\right) \epsilon ^{(\times )}_{\mu \nu }\right] e^{i\omega _{1}\left( t-z\right) }\nonumber \\&\quad +{\hat{\epsilon }}^{\left( s\right) }_{\mu \nu }\left( k_{z}\right) e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\ , \end{aligned}$$

(77)

where ${\hat{\epsilon }}^{\left( s\right) }_{\mu \nu }$ is the polarization tensor associated to the scalar mode

$$\begin{aligned}&{\hat{\epsilon }}^{\left( s\right) }_{\mu \nu }\left( k_{z}\right) =\Biggl [\left( \frac{1}{2}+\frac{\omega ^{2}_{2}}{k_{2}^{2}}\right) \epsilon _{\mu \nu }^{(TT)}-\frac{\sqrt{2}\omega _{2}k_{z}}{k_{2}^{2}}\epsilon _{\mu \nu }^{(TS)}\nonumber \\&\quad -\frac{1}{\sqrt{2}}\epsilon _{\mu \nu }^{(b)}+\left( \frac{k_{z}^{2}}{k_{2}^{2}}-\frac{1}{2}\right) \epsilon _{\mu \nu }^{(l)}\Biggr ]\frac{\hat{A}_{2}\left( k_{z}\right) }{3}\ . \end{aligned}$$

(78)

The only degree of freedom $\hat{A}_{2}$ produces the scalar polarization ${\hat{\epsilon }}^{\left( s\right) }_{\mu \nu }$. It is worth noticing that, for f(R) gravity, we have the three d.o.f.: ${\hat{\epsilon }}^{(+)}$, ${\hat{\epsilon }}^{(\times )}$ and $\hat{A}_{2}$ [34,35,36]. The scalar mode is a combination of longitudinal and breathing scalar modes. In fact, the polarization tensor ${\hat{\epsilon }}^{\left( s\right) }_{\mu \nu }$, restricted to spatial components ${\hat{\epsilon }}^{\left( s\right) }_{i,j}$, is provided by

$$\begin{aligned} {\hat{\epsilon }}^{\left( s\right) }_{i,j}=-\frac{1}{3\sqrt{2}}\hat{A}_{2}\left( k_{z}\right) \epsilon _{i,j}^{(b)}+\frac{1}{3}\left( \frac{k_{z}^{2}}{k_{2}^{2}}-\frac{1}{2}\right) \hat{A}_{2}\left( k_{z}\right) \epsilon _{i,j}^{(l)}, \end{aligned}$$

(79)

where (i, j) range over (1, 2, 3). Hence, for massless plane wave $E_{\mu \nu }^{(k_{1})}$, Eqs.(70) give

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}(t)=\omega _{1}^{2}\left[ {\hat{\epsilon }}^{\left( +\right) }\left( \omega _{1}\right) x+{\hat{\epsilon }}^{\left( \times \right) }\left( \omega _{1}\right) y\right] e^{i\omega _{1}\left( t-z\right) }+c.c. \\ \ddot{y}(t)=\omega _{1}^{2}\left[ {\hat{\epsilon }}^{\left( \times \right) }\left( \omega _{1}\right) x-{\hat{\epsilon }}^{\left( +\right) }\left( \omega _{1}\right) y\right] e^{i\omega _{1}\left( t-z\right) }+c.c.\\ \\ \ddot{z}(t)=0 \end{array}\right. }, \end{aligned}$$

(80)

where we obtain the two standard polarizations of GR, the purely transverse plus and the cross polarization, two-helicity massless tensor modes.

Instead, for a massive plane wave $E^{(k_{2})}$ with $M^2=\omega ^{2}_{2}-k^{2}_{z}$, the geodesic deviation Eq. (70) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}(t)=-\frac{1}{6}\omega ^{2}_{2}\hat{A}_{2}\left( k_{z}\right) x e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\\ \ddot{y}(t)=-\frac{1}{6}\omega ^{2}_{2}\hat{A}_{2}\left( k_{z}\right) y e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\\ \ddot{z}(t)=-\frac{1}{6}M^{2}\hat{A}_{2}\left( k_{z}\right) ze^{i\left( \omega _{2}t-k_{z}z\right) }+c.c. \end{array}\right. }. \end{aligned}$$

(81)

This system of equations can be integrated assuming that $E_{\mu \nu }\left( t,z\right)$ is small. Hence we have

$$\begin{aligned} {\left\{ \begin{array}{ll} x(t)=x(0)+\frac{1}{6}\hat{A}_{2}\left( k_{z}\right) x(0)e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\\ y(t)=y(0)+\frac{1}{6}\hat{A}_{2}\left( k_{z}\right) y(0)e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\\ z(t)=z(0)+\frac{1}{6\omega ^{2}_{2}}M^{2}\hat{A}_{2}\left( k_{z}\right) z(0)e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c. \end{array}\right. }. \end{aligned}$$

(82)

When a GW strikes a sphere of particles of radius $r=\sqrt{x^2(0)+y^{2}(0)+z^{2}(0)}$, this will be distorted into an ellipsoid described by

$$\begin{aligned} \left( \frac{x}{\rho _{1}(t)}\right) ^{2}+\left( \frac{y}{\rho _{1}(t)}\right) ^{2}+\left( \frac{z}{\rho _{2}(t)}\right) ^{2}=r^{2}, \end{aligned}$$

(83)

where $\rho _{1}(t)=1+\frac{1}{3}\hat{A}_{2}\left( k_{z}\right) \cos \left( \omega _{2}t-k_{z}z\right)$ and $\rho _{2}(t)=1+\frac{M^{2}}{3\omega _{2}^{2}}\hat{A}_{2}\left( k_{z}\right) \cos \left( \omega _{2}t-k_{z}z\right)$ both varying between their maximum and minimum values. This swinging ellipsoid represents an additional scalar polarization, zero-helicity which is partly longitudinal and partly transverse [37].

According to these considerations, the d.o.f. of f(T, B) gravity are three: two of these, ${\hat{\epsilon }}^{\left( +\right) }$ and ${\hat{\epsilon }}^{\left( \times \right) }$, generate the tensor modes while the degree of freedom $\hat{A}_{2}$ generates the mixed scalar mode. In summary, $f\left( T,B\right)$ gravity has three polarizations namely, two tensor modes and one mixed scalar mode exactly like f(R) gravity (see [36] for a discussion).

It is possible to derive the same results adopting the Newman–Penrose (NP) formalism. It is not directly applicable to massive waves because it was, in origin, worked out for massless waves. However, it is possible to adopt its generalization to massive waves propagating along non-null geodesics [38]. It is worth noticing that the little group $E\left( 2\right)$ classification fails for massive waves. One can introduce a local quasi-normal null tetrad basis $\left( k, l, m, \bar{m}\right)$ as

$$\begin{aligned} k&=\frac{1}{\sqrt{2}}\left( \partial _{t}+\partial _{z}\right) \ ,&l&=\frac{1}{\sqrt{2}}\left( \partial _{t}-\partial _{z}\right) \ , \end{aligned}$$

(84)

$$\begin{aligned} m&=\frac{1}{\sqrt{2}}\left( \partial _{x}+i\partial _{y}\right) \ ,&\bar{m}&=\frac{1}{\sqrt{2}}\left( \partial _{x}-i\partial _{y}\right) \ , \end{aligned}$$

(85)

which satisfies the relations

$$\begin{aligned} k\cdot l&=-m\cdot \bar{m}=1\ , \nonumber \\ k\cdot k&=l\cdot l=m\cdot m=\bar{m}\cdot \bar{m}=0\ ,\nonumber \\ k\cdot m&=k\cdot \bar{m}=l\cdot m=l\cdot \bar{m}=0\ . \end{aligned}$$

(86)

Let us consider the four-dimensional Weyl tensor $C_{\mu \nu \rho \sigma }$ defined as

$$\begin{aligned} C_{\mu \nu \rho \sigma }=R_{\mu \nu \rho \sigma }-2g_{[\mu |[\rho }R_{\sigma ]|\nu ]}+\frac{1}{3}g_{\mu [\rho }g_{\sigma ]\nu }R. \end{aligned}$$

(87)

The five complex Weyl-NP scalars, classified by the spin weight s, can be expressed from the Weyl tensor in a null tetrad basis as

$$\begin{aligned} s&=+2 \Psi _{0}\equiv C_{kmkm}\ ,\nonumber \\ s&=+1 \Psi _{1}\equiv C_{klkm}\ ,\nonumber \\ s&=0 \Psi _{2}\equiv C_{km\bar{m}}\ ,\nonumber \\ s&=-1 \Psi _{3}\equiv C_{kl\bar{m}l}\ ,\nonumber \\ s&=-2 \Psi _{4}\equiv C_{\bar{m}l\bar{m}l}\ , \end{aligned}$$

(88)

while the ten Ricci-NP scalars, can be expressed from Ricci tensor in a null tetrad basis as

$$\begin{aligned} s= & {} 2 \Phi _{02}\equiv -\frac{1}{2}R_{mm\ ,}\nonumber \\ s= & {} 1\quad {\left\{ \begin{array}{ll} \Phi _{01}\equiv -\frac{1}{2}R_{km}\\ \Phi _{12}\equiv -\frac{1}{2}R_{lm}\\ \end{array}\right. }\ , \nonumber \\ s= & {} 0\quad {\left\{ \begin{array}{ll} \Phi _{00}\equiv -\frac{1}{2}R_{kk}\\ \Phi _{11}\equiv -\frac{1}{4}\left( R_{kl}+R_{m\bar{m}}\right) \\ \Phi _{22}\equiv -R_{ll} \end{array}\right. }\ , \nonumber \\ s= & {} -1\quad {\left\{ \begin{array}{ll} \Phi _{10}\equiv -\frac{1}{2}R_{k\bar{m}}=\Phi _{01}^{*}\\ \Phi _{21}\equiv -\frac{1}{2}R_{l\bar{m}}=\Phi _{21}^{*}\\ \end{array}\right. }\ , \nonumber \\ s= & {} -2 \Phi _{20}\equiv -\frac{1}{2}R_{m\bar{m}}=\Phi _{02}^{*}\ ,\nonumber \\ \Lambda= & {} \frac{R}{24}. \end{aligned}$$

(89)

The driving-force matrix S(t) can be expressed in terms of the six new basis polarization matrices $W_{A}({\mathbf {e}}_{z})$ along the wave direction $\hat{{\mathbf {k}}}={\mathbf {e}}_{z}$, where the index A ranges over $\{1,2,3,4,5,6\}$ [13, 14]. It is

$$\begin{aligned} S\left( t\right) =\sum _{A}p_{A}\left( {\mathbf {e}}_{z},t\right) W_{A}\left( {\mathbf {e}}_{z}\right) , \end{aligned}$$

(90)

where

$$\begin{aligned} W_{1}\left( {\mathbf {e}}_{z}\right) =&-6\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}\ ,&W_{2}\left( {\mathbf {e}}_{z}\right) =&-2\begin{pmatrix} 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ ,\nonumber \\ W_{3}\left( {\mathbf {e}}_{z}\right) =&2\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 \end{pmatrix}\ ,&W_{4}\left( {\mathbf {e}}_{z}\right) =&-\frac{1}{2}\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ ,\nonumber \\ W_{5}\left( {\mathbf {e}}_{z}\right) =&\frac{1}{2}\begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\ ,&W_{6}\left( {\mathbf {e}}_{z}\right) =&-\frac{1}{2}\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}. \end{aligned}$$

(91)

Here $p_{A}\left( {\mathbf {e}}_{z},t\right)$ are the amplitudes of the wave [39,40,41,42,43]. Taking into account that the spatial components of matrix S(t) are the electric components of Riemann tensor, we have

$$\begin{aligned} S_{ij}(t)=R_{i0j0}. \end{aligned}$$

(92)

The amplitudes of six polarizations can be expressed both in terms of the electric components of the Riemann tensor $R_{i0j0}$, and in Weyl and Ricci scalars [34, 44,45,46,47,48,49], that is

$$\begin{aligned} p_{1}^{\left( l\right) }&=-\frac{1}{6}R_{0303}=-\frac{1}{3}\left[ \mathrm {Re}\left( \Psi _{2}\right) +\Phi _{11}-\Lambda \right] \ ,\nonumber \\ p_{2}^{\left( x\right) }&=-\frac{1}{2}R_{0301}=-\frac{1}{2}\left[ -\mathrm {Re}\left( \Psi _{1}\right) +\mathrm {Re}\left( \Psi _{3}\right) -\mathrm {Re}\left( \Phi _{01}\right) \right. \nonumber \\&\quad \left. +\mathrm {Re}\left( \Phi _{12}\right) \right] \ ,\nonumber \\ p_{3}^{\left( y\right) }&=\frac{1}{2}R_{0302}=\frac{1}{2}\left[ -\mathrm {Im}\left( \Psi _{1}\right) -\mathrm {Im}\left( \Psi _{3}\right) -\mathrm {Im}\left( \Phi _{01}\right) \right. \nonumber \\&\quad \left. +\mathrm {Im}\left( \Phi _{12}\right) \right] \ ,\nonumber \\ p_{4}^{\left( +\right) }&=-R_{0101}+R_{0202}=-\mathrm {Re}\left( \Psi _{0}\right) \nonumber \\&-\mathrm {Re}\left( \Psi _{4}\right) -2\mathrm {Re}\left( \Psi _{02}\right) \ ,\nonumber \\ p_{5}^{\left( \times \right) }&=2R_{0102}=\mathrm {Im}\left( \Psi _{0}\right) -\mathrm {Im}\left( \Psi _{4}\right) -2\mathrm {Im}\left( \Psi _{02}\right) \ ,\nonumber \\ p_{6}^{\left( b\right) }&=-R_{0101}-R_{0202}=2\mathrm {Re}\left( \Psi _{2}\right) -\Phi _{00}-\Phi _{22}+4\Lambda \ , \end{aligned}$$

(93)

where the six polarizations modes are: the longitudinal mode $p_{1}^{\left( l\right) }$, the vector-x mode $p_{2}^{\left( x\right) }$, the vector-y mode $p_{3}^{\left( y\right) }$, the plus mode $p_{4}^{\left( +\right) }$, the cross mode $p_{5}^{\left( \times \right) }$, and the breathing mode $p_{6}^{\left( b\right) }$. Under the Lorentz gauge and by Eqs.(71) and (74) for non-null geodesic congruences of gravitational waves, traveling along the $+\hat{z}$ direction, we obtain the six polarization amplitudes $p_{A}\left( {\mathbf {e}}_{z}, t\right)$

$$\begin{aligned} p_{1}^{\left( l\right) }&=-\frac{1}{6}\left[ \frac{\omega ^{2}-k_{z}^{2}}{\omega ^{2}+k_{z}^{2}}\left( \omega ^{2}E_{33}-k_{z}^{2}E_{00}\right) \right] \ ,\\ p_{2}^{\left( x\right) }&=-\frac{1}{2}\left( \omega ^{2}-k_{z}^{2}\right) E_{13}\ ,\\ p_{3}^{\left( y\right) }&=\frac{1}{2}\left( \omega ^{2}-k_{z}^{2}\right) E_{23}\ ,\\ p_{4}^{\left( +\right) }&=\left( \frac{\omega ^{2}-k_{z}^{2}}{\omega ^{2}+k_{z}^{2}}\right) \omega ^{2}\left( E_{00}+E_{33}\right) +2\omega ^{2}E_{22}\ ,\\ p_{5}^{\left( \times \right) }&=2\omega ^{2}E_{12}\ ,\\ p_{6}^{\left( b\right) }&=\left( \frac{\omega ^{2}-k_{z}^{2}}{\omega ^{2}+k_{z}^{2}}\right) \omega ^{2}\left( E_{00}+E_{33}\right) \ . \end{aligned}$$

Finally we get for a massless mode $\omega _{1}$ and massive mode $\omega _{2}$, keeping ${\mathbf {k}}$ fixed, the following amplitudes

$$\begin{aligned} p_{1}^{\left( l\right) }\left( t, z\right)&=\frac{1}{36}\left( \omega _{2}^{2}-k_{z}^{2}\right) \hat{A}_{2}\left( k_{z}\right) e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\ ,\nonumber \\ p_{2}^{\left( x\right) }\left( t, z\right)&=p_{3}^{\left( y\right) }\left( t, z\right) =0\ ,\nonumber \\ p_{4}^{\left( +\right) }\left( t, z\right)&=-2\omega _{1}^{2}{\hat{\epsilon }}^{\left( +\right) }\left( \omega _{1}\right) e^{i\omega _{1}\left( t-z\right) }+c.c.\ ,\nonumber \\ p_{5}^{\left( \times \right) }\left( t, z\right)&=2\omega _{1}^{2}{\hat{\epsilon }}^{\left( \times \right) }\left( \omega _{1}\right) e^{i\omega _{1}\left( t-z\right) }+c.c.\ ,\nonumber \\ p_{6}^{\left( b\right) }\left( t, z\right)&=\frac{\omega _{2}^{2}}{3}\hat{A}_{2}\left( k_{z}\right) e^{i\left( \omega _{2}t-k_{z}z\right) }+c.c.\ . \end{aligned}$$

(94)

It is evident, from Eqs.(94), that the two vector modes $p_{2}^{\left( x\right) }$ and $p_{3}^{\left( y\right) }$ are suppressed while the two standard plus and cross transverse tensor polarization modes $p_{4}^{\left( +\right) }$ and $p_{5}^{\left( \times \right) }$ survive together with the two longitudinal and transverse breathing scalar modes $p_{1}^{\left( l\right) }$ and $p_{6}^{\left( b\right) }$. However only one degree of freedom $\hat{A}_{2}$ intervenes in both b and l scalar modes, giving rise to their mixed state s. This reduces polarizations from four to three.

6 Discussion and conclusions

TEGR is equivalent to Einstein’s GR because they are two representations of the same dynamics. This is not true for their extensions f(T) and f(R) theories and, in general, for higher order gravity theories constructed by the torsion T and curvature R scalars [50]. To restore the equivalence, we must take into account the boundary term B which relates T and R. Because T and B are derived from the same tetrad, R is univocally defined, so $f(T,B)\equiv f(R)$ according to dynamics.

Thus, we have obtained the exact field equations of $f\left( T, B \right)$ gravity (in presence of matter) and then we have linearized them in the low energy limit. This allows to get gravitational waves and then to study their polarization and helicity. To this end, one can adopt the geodesic deviation and the NP formalism.

In this framework. it is possible to show that both f(R) gravity and f(T, B) teleparallel gravity have three polarizations [34, 35, 42, 43, 52]. The third polarization, with respect to the standard $\times$ and $+$ of GR, emerges as a combination of longitudinal and breathing scalar modes.

Same authors claims that the polarization of f(R) theory are four because count two scalar polarizations instead of the single scalar state [53]. This is true for a gravitational wave without mass, where the longitudinal and transverse breathing modes are independent of each other. However, for a massive gravitational wave, both longitudinal and breathing modes are determined by a unique degree of freedom, i.e. $\hat{A}_{2}$ and then cannot be, in principle, disentangled. According to this result, they can be combined giving only a scalar mode.

In $f\left( T, B\right)$ teleparallel gravity, the presence of a massive scalar mode mixes the transverse breathing and the longitudinal modes, in addition to the two standard massless tensor polarizations. This further term is due to the boundary terms B, which survives to first order in $E^{a}_{\mu }$. It is worth stressing that in f(T) gravity only the two standard modes of GR are present [50].

More precisely, it is the first order boundary terms $B^{(1)}$ that generates the massive scalar mode and then adds, to the 2-spin massless tensor modes of GR, an extra 0-spin massive scalar mode. Furthermore, as it is well known, f(R) gravity is equivalent to a scalar-tensor theory [54, 55]. It means that under a conformal transformation, it is equivalent to GR plus a scalar field, justifying the three d.o.f. coinciding with polarizations. It is worth stressing again that, the above analysis includes the sub-cases $f(T,B)= f(-T,-B)=f(R)$ and $f(T,B)=f(T)+B=f(T)$ reported in literature. Clearly, the number of polarizations in f(R) and f(T) gravity are recovered. See [22,23,24,25].

Another motivation for the presence of scalar mode is the symmetry breaking of the TT gauge due to the massive wave, that is, the mass of scalar field brakes the symmetry of the TT gauge. In GR the absence of scalar, longitudinal, and vector modes implies that the response of detectors is governed entirely by the transverse-trace free modes. This fact is relevant to compare alternative theories with GR. In the case of f(T, B) gravity, it is not possible to perform a gauge transformation on $E_{\mu \nu }$ that makes it traceless and completely spatial at the same time, namely performing a TT gauge. According to these considerations, $f\left( T, B\right)$ gravity shows three polarizations: the two standard plus $(+)$ and cross $(\times )$ 2-helicity massless transverse tensor polarization modes and a 0-helicity massive scalar polarization mode (s), resulting as a mixed state of longitudinal and breathing transverse polarizations. Being dynamically equivalent to f(R) gravity, it is possible to show that, in the post-Newtonian limit, a Yukawa-like correction emerges in general [56]. This correction can be considered to put upper bound on the graviton mass as discussed in [57,58,59]. Being f(R) gravity not excluded by observations [15,16,17], this could be a pathway to test also f(T, B) gravity by a possible massive mode.

An important remark is in order at this point. Besides perturbations around the Minkowski background, it is interesting to develop a similar analysis around a cosmological background. This approach results useful to investigate primordial gravitational waves. For example, assuming a Friedmann–Robertson–Walker spatially flat metric as

$$\begin{aligned} ds^2=dt^2-a^2(t)\delta _{ij}dx^{i}dx^{j}, \end{aligned}$$

(95)

with a(t) the scale factor, we can perturb the tetrad $e^{a}_{\mu }=\text {diag}(1,a(t),a(t),a(t))$ obtaining

$$\begin{aligned} e^{a}_{\mu }=\bar{e}^{a}_{\mu }+E^{a}_{\mu }, \end{aligned}$$

(96)

where $\bar{e}^{a}_{\mu }$ is the unperturbed part of the tetrad. See [18, 19] for details. Then, inserting the above cosmological metric into the field Eqs. (45), we obtain the related Friedmann equations. From Eq. (96), it is possible to derive the differential equations for $E^{a}_{\mu }$ giving rise to cosmological gravitational waves as solutions. This kind of analysis has been developed in [51] for f(R). In a forthcoming paper, cosmological gravitational waves for generalized TEGR theories will be discussed.