Cosmological evolution of two-scalar fields cosmology in the Jordan frame

Abstract

In the present article we study the cosmological evolution of a two-scalar field gravitational theory defined in the Jordan frame. Specifically, we assume one of the scalar fields to be minimally coupled to gravity, while the second field which is the Brans-Dicke scalar field is nonminimally coupled to gravity and also coupled to the other scalar field. In the Einstein frame this theory reduces to a two-scalar field theory where the two fields can interact only in the potential term, which means that the quintom theory is recovered. The cosmological evolution is studied by analyzing the equilibrium points of the field equations in the Jordan frame. We find that the theory can describe the cosmological evolution in large scales, while inflationary solutions are also provided.

1 Introduction

Observational data since last 20 years [1,2,3,4,5,6,7] have consistently reported that our universe is currently passing through a phase of accelerating expansion. This has been one of the mysterious discoveries of modern cosmology that thrilled the entire scientific community with a big question mark. Within the paradigm of standard cosmology, it is impossible to fit such accelerating phase since it demands something more in terms of some exotic component having negative pressure enabling the expansion of the universe in an accelerating manner. Usually two distinct but well known approaches are used to introduce such exotic components. Both the approaches essentially need the introduction of new terms in terms of the new degrees of freedom into the Einstein’s field equations. The simplest approach to introduce such new terms is the modifications of the matter distribution of the universe within the context of Einstein gravity, and these new exotic components are usually dubbed as dark energy (DE) fluids [8,9,10,11,12,13,14,15,16,17]. Alternatively, one could introduce such new additional terms through the modifications of the Einstein-Hilbert action [18,19,20,21,22,23,24,25,26,27,28,29]. The resulting exotic terms coming from the gravity modifications are usually designated as the geometrical dark energy (GDE) fluids. According to latest observational estimations [7], the percentage of such exotic dark energy or geometrical dark energy fluids whatever the universe has within it, is around 68% of its total energy budget. Hence, the investigations towards this direction is an essential part of modern cosmological research and we still are looking for an actual cosmological theory fitting the observational results.

The theory of scalar fields have played a significant role in the two different approaches proposed by the cosmologists. When scalar fields are introduced in the gravitational action integral, they provide new degrees of freedom which drives the dynamics of the field equations in a way to explain the observable phenomena and the cosmological history [30]. Scalar fields can be minimally or nonminimally coupled to gravity. When the scalar fields are introduced in such a way where they are minimally coupled to gravity, then we are in Einstein’s General Relativity, where the contribution of the scalar fields is on the energy momentum tensor. The most common known minimally coupled scalar fields are, for instance, the quintessence, phantom, quintom and Chiral cosmological models [8, 31,32,33,34,35,36,37,38,39,40].

Alternatively, scalar fields can be introduced in the gravitational action such that they nonminimally couple to gravity. In these models, the contribution of the scalar field in the field equations includes the terms which correspond to the energy momentum tensor, and in addition, dynamical terms of geometric origin. In these models, usually, the gravitational constant k, is not a constant anywhere, rather it becomes variable. A nonminimally coupled scalar field was introduced by Carl H. Brans and Robert H. Dicke to provide a gravitational theory which satisfies the Machian Principle  [20]. Brans-Dicke theory is a special case of the so called scalar-tensor theory [41]. A main characteristic of the Brans-Dicke field is the parameter $\omega ~$ known as the Brans-Dicke parameter. Indeed, for small values of $\omega$ the contribution of the scalar field in the dynamics of the field equations is significant, while on the other hand, when $\omega$ is large, the main contribution in the dynamics is followed by the tensor part. Someone would expect that as $\omega ~$reaches infinity, the theory of General Relativity will be recovered, however, that is not true, which means that General Relativity and Brans-Dicke gravity are fundamentally different theories [42]. Other well-known nonminimally coupled models are the Galileon and the Hordenski theories [43,44,45,46,47,48].

The nonminimally coupled scalar fields can describe modified theories of gravity by attributing new degrees of freedom in terms of geometric invariants which are introduced to modify the Einstein-Hilbert gravitational action. Indeed, the fourth-order $f\left( R\right)$-gravity is dynamical and physically equivalent to the Brans-Dicke theory in the limit where $\omega$ is zero, such that Brans-Dicke theory reduces to O’Hanlon gravity [49]. For more details in this direction we refer the reader to [50,51,52,53,54] and the references therein.

As we discussed, Brans-Dicke theory is a different theory compared to Einstein’s General Relativity, however, there is a mathematical connection between these two theories. Indeed, the two theories are conformally equivalent [41, 55, 56]. The latter equivalency is a mathematical equivalence between the Jordan and the Einstein frame in the solution space of the field equations while in general the physical properties of the solutions do not remain invariant under the conformal transformation. For instance, a singular universe in the Einstein frame, under a conformal transformation can become a non-singular universe in the Jordan frame which is described by a scalar tensor theory. There is a plethora of studies where the physical quantities have been studied between the Einstein and the Jordan frame for various exact solutions [56,57,58,59]. In addition, the question of which is the preferred frame is still unanswered [60].

In this work we considered a two-scalar field cosmological model where one of the fields is the Brans-Dicke field which is nonminimally coupled to gravity, and the second scalar field is minimally coupled to gravity. The model of our consideration has the Action Integral of the Brans-Dicke Action where the Brans-Dicke field is coupled to the Lagrangian of the quintessence scalar field. Consequently, the two fields interact in the kinetic and in the potential parts. Such a model was investigated before in [61]. Specifically, in [61] the integrability of the cosmological model was investigated and some exact solutions were determined. While our model is defined in the Jordan frame, when we perform a conformal transformation in order to pass to the Einstein frame, we end up with a two-scalar field theory which includes the quintom cosmological model.

Here we study the cosmological evolution of this specific cosmological model in the Jordan frame by investigating the stability of the equilibrium points. For the background space we assume this to be described by the spatially flat Friedmann-Lemaître-Robertson-Walker (FLRW) universe. Under this minimal assumption we shall be able to understand the physical evolution of the universe as it is provided by the field equations and also we will be able to discuss the viability of the cosmological model. Such an analysis has been applied in various cosmological theories with many interesting results [62,63,64,65,66,67,68,69,70,71,72,73,74,75,76]. Any equilibrium point, also known as stationary or critical point, describes a specific phase, i.e., an exact solution, in the evolution of the generic solution. The stability of the critical point indicates the stability of the solution, from where we can draw conclusions for the cosmological evolution.

The plan of the paper is follows. In Sect. 2, we present the cosmological model of our consideration. We derive the field equations and we discuss the mathematical relation of the theory between the Jordan and the Einstein frame, where we show that our model is equivalent with a two-scalar field theory, such is the quintom cosmology, in the Einstein frame. In Sect. 3, we write the field equations in dimensionless variables by using the H-normalization. We end with a five-dimensional algebraic-differential dynamical system. Section 4, includes the main analysis of our work, where we investigate the critical points and their stabilities for the model under consideration in the vacuum case, and in presence of an additional dust fluid source. The scalar field potentials have been selected in order to reduce the number of equations of the dimensionless system under study. However, such selection can also be seen as the limit for other potential forms too. Finally, in Sect. 5, we summarize our results with the main findings.

2 Cosmological model

The gravitation model of our consideration is described by the following Action Integral

$$\begin{aligned} S= & {} \int dx^{4}\sqrt{-g}\left[ \phi \left( \frac{R}{2}-\frac{1}{2}g^{\mu \nu }\psi _{;\mu }\psi _{;\nu }+V\left( \phi ,\psi \right) \right) \right. \nonumber \\&\left. -\frac{1}{2} \frac{\omega }{\phi }g^{\mu \nu }\phi _{;\mu }\phi _{;\nu }\right] , \end{aligned}$$

(1)

which actually describes a two-scalar field cosmology defined in the Jordan frame. More specifically, the scalar field $\phi \left( x^{\mu }\right)$ is the Brans-Dicke field with $\omega \ne \frac{2}{3},$ which is nonminimally coupled to gravity and to the second scalar field $\psi \left( x^{\mu }\right)$ as well, while the second scalar field $\psi \left( x^{\mu }\right)$ is minimally coupled to gravity. The limit $\omega =\frac{2}{3}$ corresponds to a special case where the Brans-Dicke field does not introduce any real degree of freedom and can be neglected by a scale transformation in the metric $g_{\mu \nu }$. Therefore, in the following we shall assume that $\omega \ne \frac{2}{3}$.

An equivalent way to write the Action Integral (1) is by using the Lagrange function for the quintessence, that means,

(2)

where $L_{Q}\left( R,\psi ,\psi _{;\mu }\right)$ is the Lagrangian function for the minimally coupled scalar field theory, that is,

$$\begin{aligned} L_{Q}=\frac{R}{2}-\frac{1}{2}g^{\mu \nu }\psi _{;\mu }\psi _{;\nu }-{\bar{V}}\left( \psi \right) , \end{aligned}$$

(3)

and $W\left( \phi \left( x^{\mu }\right) ,\psi \left( x^{\mu }\right) \right) =V\left( \phi \left( x^{\mu }\right) ,\psi \left( x^{\mu }\right) \right) +\phi \left( x^{\mu }\right) {\bar{V}}\left( \psi \left( x^{\mu }\right) \right) \,$. Consequently, when $\phi \left( x^{\mu }\right) =\phi _{0}$, the gravitational Action Integral (1) reduces to that of a minimally coupled scalar field model.

From (1), one can obtain the gravitational field equations by varying this action with respect to the metric tensor $g_{\mu \nu }$ as follows [61]

$$\begin{aligned} \phi G_{\mu \nu }= & {} \frac{\omega }{\phi }\left( \phi _{;\mu }\phi _{;\nu }-\frac{1}{2}g_{\mu \nu }g^{\kappa \lambda }\phi _{;\kappa }\phi _{;\lambda }\right) \nonumber \\&-\left( g_{\mu \nu }g^{\kappa \lambda }\phi _{;\kappa \lambda }-\phi _{;\mu }\phi _{;\nu }\right) -g_{\mu \nu }V\left( \phi ,\psi \right) \nonumber \\&+\phi \left( \psi _{;\mu } \psi _{;\nu }-\frac{1}{2}g_{\mu \nu }g^{\kappa \lambda }\psi _{;\kappa }\psi _{;\lambda }\right) , \end{aligned}$$

(4)

while the variation of (1) with respect to $\phi \left( x^{\mu }\right)$, and $\psi \left( x^{\mu }\right)$ respectively provide with the equations of motion of the two fields as follows,

$$\begin{aligned}&g^{\kappa \lambda }\phi _{;\kappa \lambda }-\frac{1}{2\phi }g^{\mu \nu }\phi _{;\mu }\phi _{;\nu }+\frac{ \phi }{2\omega }g^{\mu \nu }\psi _{;\mu }\phi _{;\nu }\nonumber \\&\quad +\,\frac{\phi }{2\omega }\left( R-2V_{,\phi }\right) =0, \end{aligned}$$

(5)

$$\begin{aligned}&g^{\kappa \lambda }\psi _{;\kappa \lambda } +\,\frac{1}{\phi }g^{\mu \nu }\phi _{;\mu } \psi _{;\nu }+V_{,\psi }=0. \end{aligned}$$

(6)

It is important to mention here that while someone will expect that for $\phi _{;\kappa }=0$, the limit of General Relativity with a minimally coupled scalar field will be recovered, but that is not true, because of the constraint equation (5) which becomes $R-2V_{,\phi _{0}}=0$.

In order to find an equivalent theory to (1) in the Einstein frame, we consider the conformal transformation $g_{\mu \nu }=\phi {\bar{g}}_{\mu \nu }$, that is, for a four-dimensional manifold, the Ricci scalar R becomes [77]

$$\begin{aligned} R=\phi ^{-2}{\bar{R}}-6\phi ^{-3}\phi _{;\mu \nu }{\bar{g}}^{\mu \nu }. \end{aligned}$$

(7)

Replacing (7) and integrating by pats we end up with the gravitational Action Integral

$$\begin{aligned} {\bar{S}}= & {} \int dx^{4}\sqrt{-g}\left[ \frac{{\bar{R}}}{2}-\frac{1}{2}{\bar{g}} ^{\mu \nu }\psi _{;\mu }\psi _{;\nu }\right. \nonumber \\&\left. +\,U\left( \Phi ,\psi \right) -\frac{1}{2}{\bar{g}}_{;\mu }^{\mu \nu }\Phi _{;\mu }\Phi _{;\nu }\right] , \end{aligned}$$

(8)

where the new scalar field, $\Phi \left( x^{\mu }\right)$, is a functional form of $\phi \left( x^{\mu }\right) ,$ that is, $\Phi =\Phi \left( \phi \left( x^{\mu }\right) \right)$, and specifically, $\Phi \left( x^{\mu }\right) \simeq \phi \left( x^{\mu }\right)$, while the new scalar field potential $U\left( \Phi \left( \phi \right) , \psi \right)$ is defined as $U\left( \phi ,\psi \right) \simeq \phi ^{-2}V\left( \phi ,\psi \right) .~$Consequently, either if we select $V\left( \phi ,\psi \right) =V\left( \psi \right)$ in the Einstein frame, the two scalar fields interact. Therefore, when $U\left( \phi ,\psi \right) =V\left( \psi \right)$, the Action Integral describes a two-scalar field minimally coupled cosmological model, and such model has been studied earlier in the literature [78].

Moreover, if in the Jordan frame, we select $V\left( \phi ,\psi \right) =\phi ^{2}F\left( \psi \right) +Z\left( \phi \right)$, then in the Einstein frame it follows that the two scalar fields are not interacting neither in the kinetic terms nor in the potential terms. In addition, in the latter scenario, by doing the change $\psi \left( x^{\mu }\right) =i\psi \left( x^{\mu }\right)$, the Action integral (8) takes the form of the quintom theory [68, 79].

For the background geometry of our universe we assume that in the large scales it is well described by the spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) spacetime characterized by the following line element

$$\begin{aligned} ds^{2}=-N^{2}\left( t\right) dt^{2}+a^{2}\left( t\right) \left( dx^{2}+dy^{2}+dz^{2}\right) , \end{aligned}$$

(9)

where $N\left( t\right)$ is the lapse function and $a\left( t\right)$ is the expansion scale factor of the universe, i.e. the Hubble function of this universe is defined as $H\left( t\right) =\frac{1}{N}\frac{{\dot{a}}}{a}$. In the following we assume the co-moving observer $u^{\mu }=\frac{1}{N}\delta _{t}^{\mu },~u^{\mu }u_{\mu }=-1$.

For the line element (9), the gravitational field equations (4), (5) and (6) can be expressed as [61]

$$\begin{aligned}&6\phi H^{2}+6H{\dot{\phi }}+\frac{\omega }{\phi }{\dot{\phi }}^{2}+\phi \dot{\psi }^{2}+2V\left( \phi ,\psi \right) =0. \end{aligned}$$

(10)

$$\begin{aligned}&2\phi {\dot{H}}+3\phi H^{2}+2H{\dot{\phi }}-\frac{\omega }{2}\frac{{\dot{\phi }}^{2} }{\phi }-\frac{1}{2}\phi {\dot{\psi }}^{2}+\ddot{\phi }\nonumber \\&\qquad \quad +V\left( \phi ,\psi \right) =0, \end{aligned}$$

(11)

$$\begin{aligned}&3{\dot{H}}+6H^{2}+3\omega H\frac{{\dot{\phi }}}{\phi }-\frac{1}{2}{\dot{\psi }} ^{2}-\frac{\omega }{2}\left( \frac{{\dot{\phi }}^{2}}{\phi ^{2}}-2\frac{\ddot{\phi }}{\phi }\right) \nonumber \\&\qquad +V_{,\phi }\left( \phi ,\psi \right) =0, \end{aligned}$$

(12)

$$\begin{aligned}&\phi \ddot{\psi }+\left( 3H\phi +{\dot{\phi }}\right) {\dot{\psi }}+V_{,\psi }\left( \phi ,\psi \right) =0. \end{aligned}$$

(13)

where without any loss of generality we selected $N\left( t\right) =1$, while additionally, we assumed that the two scalar fields $\phi \left( x^{\mu }\right) ,~\psi \left( x^{\nu }\right)$ inherit the symmetries of the spacetime, that means, $\phi \left( x^{\mu }\right) =\phi \left( t\right)$ and $\psi \left( x^{\mu }\right) =\psi \left( t\right)$.

Let us note that Eq. (10) is the constraint equation, while Eqs. (11), (12) and (13) are the second-order differential equations describing the dynamics of the universe for the two scalar fields $\phi \left( t\right) ,~\psi \left( t\right)$ and the scale factor $a\left( t\right)$.

Now, in presence of an additional matter source, and more specifically, in the presence of a dust fluid term minimally coupled to the Brans-Dicke field $\phi \left( x^{\mu }\right)$ in the gravitational model, the field equations (11), (12), (13) will remain same, except the constraint equation (10) which becomes

$$\begin{aligned} 6\phi H^{2}+6H{\dot{\phi }}+\frac{\omega }{\phi }{\dot{\phi }}^{2}+\phi {\dot{\psi }} ^{2}+2V\left( \phi ,\psi \right) =2\rho _{m}, \end{aligned}$$

(14)

while the continuity equation for the dust fluid is ${\dot{\rho }}_{m}+3H\rho _{m}=0$, from where it follows that, $\rho _{m}=\rho _{m0}a^{-3}$, where $\rho _{m0}$ is an integration constant physically which represents the energy density of the dust fluid at current epoch. We investigate first the vacuum case ($\Omega _{m}=0$), and after that we investigate the matter case.

The gravitational field equations for this particular cosmological model are described by a point-like Lagrangian, however, such an analysis is not necessary in the present work. The purpose of this work is to study the dynamical evolution for this cosmological model. In [61], the specific forms of the scalar field potential were determined such that the field equations admit linear and quadratic conservation laws in the momentum and they are integrable. In addition, exact solutions of special interests, such that the singular solution $a\left( t\right) =a_{0}t^{p}$ and the de Sitter solution $a\left( t\right) =a_{0}e^{H_{0}t},$ were determined in [61].

With the analysis of this work, we will be able to understand the general behavior of the cosmological solution as well as we will be also able to identify the attractors of the cosmological model and to study the stability of the particular solutions. At the same time, we will be able to investigate the similarities and differences of two-scalar field gravitational theories defined in the Einstein and Jordan frames.

Making the selection of the potential for the two scalar field $V\left( \phi ,\psi \right) =V\left( \psi \right) W\left( \phi \right)$, we solve for the higher derivatives (in presence of an additional matter source and more specifically in presence of a dust fluid which is minimally coupled to the Brans-Dicke field) and obtain the field equations:

$$\begin{aligned}&{\dot{H}}=-\frac{3(\omega -2)H^{2}}{2\omega -3}+\frac{\omega H{\dot{\phi }} }{(2\omega -3)\phi }+\frac{V(\psi )W^{\prime }(\phi )}{2\omega -3}\nonumber \\&\qquad +\frac{\omega V(\psi )W(\phi )}{(3-2\omega )\phi }+\frac{(\omega -1){{\dot{\psi }}}^{2}}{4\omega -6}+\frac{(\omega -1)\omega {{\dot{\phi }}}^{2}}{(4\omega -6)\phi ^{2}}, \end{aligned}$$

(15)

$$\begin{aligned}&\ddot{\phi }=-\frac{6(\omega -1)H{\dot{\phi }}}{2\omega -3}+\frac{3H^{2}\phi }{3-2\omega }+\frac{2\phi )V(\psi ))W^{\prime }(\phi )}{3-2\omega }\nonumber \\&\qquad +\frac{3V(\psi )W(\phi )}{2\omega -3}+\frac{\omega {{\dot{\phi }}}^{2}}{(6-4\omega )\phi }+\frac{\phi {\dot{\psi }}^{2}}{6-4\omega }, \end{aligned}$$

(16)

$$\begin{aligned}&\ddot{\psi }=-3H{\dot{\psi }}-\frac{W(\phi )V^{\prime }(\psi )}{\phi }-\frac{{{\dot{\psi }}}{\dot{\phi }}}{\phi }, \end{aligned}$$

(17)

$$\begin{aligned}&{\dot{\rho }}_{m}=-3H\rho _{m}, \end{aligned}$$

(18)

with first integral equation (14).

3 Dimensionless system

In this section we proceed by writing the field equations with the use of dimensionless variables. In particular, we make use of the $H-$normalization [80], which has been applied also in Brans-Dicke theory [81,82,83,84] and in multi scalar field theories [85,86,87,88,89,90]. As far as the scalar field potential is concerned, we make the selection $V\left( \phi ,\psi \right) =V\left( \psi \right) W\left( \phi \right)$.

The new dimensionless variables are

$$\begin{aligned} x=\frac{{\dot{\phi }}}{\sqrt{6} H\phi }~,~y=\frac{{\dot{\psi }}}{\sqrt{6}H} ~,~z=\frac{V\left( \psi \right) W\left( \phi \right) }{3\phi ~H^{2}}, \end{aligned}$$

(19)

or equivalently,

$$\begin{aligned} {\dot{\phi }}=\sqrt{6}x\phi H~,~{\dot{\psi }}=\sqrt{6}yH~,~V\left( \psi \right) =3z\frac{\phi }{W\left( \phi \right) }H^{2}. \end{aligned}$$

(20)

In the new variables, the field equations can be expressed as the following algebraic-differential first-order system

$$\begin{aligned} \frac{dx}{d\tau }&=\frac{-6x^{3}(\omega -1)\omega +\sqrt{6}x^{2} (6-7\omega )-6x\left( (\omega -1)y^{2}+\omega +\mu z-\omega z\right) -\sqrt{6}\left( y^{2}+2\mu z-3z+1\right) }{4\omega -6}, \end{aligned}$$

(21)

$$\begin{aligned} \frac{dy}{d\tau }&=\frac{z\left( \sqrt{6}\lambda (3-2\omega )+6y(\omega -\mu )\right) -6y(\omega -1)\left( x\left( x\omega +\sqrt{6}\right) +y^{2}+1\right) }{4\omega -6}, \end{aligned}$$

(22)

$$\begin{aligned} \frac{dz}{d\tau }&=\frac{z\left( -6x^{2}(\omega -1)\omega +\sqrt{6} x(\mu (2\omega -3)-4\omega +3)-6y^{2}(\omega -1)+\sqrt{6}\lambda y(2\omega -3)+6(\omega -\mu z+\omega z-2)\right) }{2\omega -3}, \end{aligned}$$

(23)

in which the new variables $\lambda$ and $\mu$ are defined as functions of $\phi$

$$\begin{aligned} \lambda =\left( \ln V\left( \psi \right) \right) _{,\psi }~,~\mu =\phi \left( \ln W\left( \phi \right) \right) _{,\phi }~,~\tau =\ln a\left( t\right) , \nonumber \\ \end{aligned}$$

(24)

while the constraint equation (14) becomes

$$\begin{aligned} \Omega _{m}=x\left( x\omega +\sqrt{6}\right) +y^{2}+z+1, \end{aligned}$$

(25)

where $\Omega _{m}$ is the dimensionless density parameter of the dust fluid source defined as $\Omega _{m}=\frac{\rho _{m}}{3\phi H^{2}},$ in which $\Omega _{m}\in \left[ 0,1\right]$. We also have an extra evolution equation

$$\begin{aligned}&\Omega _{m}^{\prime }=\Omega _{m} \nonumber \\&\quad \left[ \frac{-6 x^{2} (\omega -1) \omega +\sqrt{6} x (3-4 \omega )-6 y^{2} (\omega -1)-6 \mu z+6 \omega z-3}{2 \omega -3}\right] .\nonumber \\ \end{aligned}$$

(26)

As far as the variation of the new variables $\mu$ and $\lambda$ is concerned, we find that they should satisfy the following two first-order ordinary differential equations, namely,

$$\begin{aligned}&\frac{d\mu }{d\tau }=\sqrt{6}x h(\lambda ) , \end{aligned}$$

(27)

$$\begin{aligned}&\frac{d\lambda }{d\tau }=\sqrt{6}y f(\lambda ) , \end{aligned}$$

(28)

in which

$$\begin{aligned}&f(\lambda )= (\Gamma \left( \lambda \right) -1) \lambda ^{2}, \quad h(\mu )= \mu ({\bar{\Gamma }}\left( \mu \right) \mu -\mu +1),\nonumber \\&\Gamma \left( \lambda \right) =\frac{V_{,\psi \psi }V}{\left( V_{,\psi }\right) ^{2}}, \quad {\bar{\Gamma }}\left( \mu \right) =\frac{W_{,\phi \phi }W}{\left( W_{,\phi }\right) ^{2}}. \end{aligned}$$

(29)

Consequently, the algebraic-differential system has dimension five, consisting of the first-order differential equations (21), (22), (23), (28) and (27), while for specific forms of the potentials $V\left( \psi \right) ~$ and $W\left( \phi \right)$, it follows that, $\lambda = \text{ const }$ and $\mu = \text{ const }$, which mean that the dimension of the dynamical system can be reduced by one or by two dimensions. In addition, for the vacuum case, i.e., $\Omega _{m}=0$, the algebraic equation (25) can also be used to reduce the dimension of the dynamical system by one dimension.

Any critical point describes a specific universe where the total equation of state is $w_{tot}=-1-\frac{2}{3}\frac{{\dot{H}}}{H^{2}}$, which can be be expressed in terms of the dimensionless parameters as

$$\begin{aligned} w_{tot}=\frac{-2 x \omega \left( 3 x (\omega -1)+\sqrt{6}\right) -6 (\omega -1) y^{2}+6 z (\omega -\mu )-3}{6 \omega -9}. \nonumber \\ \end{aligned}$$

(30)

When $w_{tot}\ne -1$, the scale factor at the critical point is a power-law function, while for $w_{tot}=-1$, the critical point describes a de Sitter universe.

4 Cosmological evolution

In the following, we set $V\left( \psi \right) =V_{0}e^{\lambda \phi }$ and $W\left( \phi \right) =W_{0}\phi ^{\mu }$, and we study the equilibrium points and analyze the stability when $\Omega _{m}=0$ (vacuum case) and when $0<\Omega _{m}\le 1$ (matter case). For the specific functions of the two potentials, variables $\mu$ and $\lambda$ are constants, i.e. the right hand side of equations (27), (28) are zero.

4.1 Vacuum case

In the vacuum case, namely for $\Omega _{m} = 0$, the algebraic equation (25) gives an additional restriction

$$\begin{aligned} x\left( x\omega +\sqrt{6}\right) +y^{2}+z+1=0, \end{aligned}$$

(31)

that can be used to remove one phase-space variable, say z. Hence, we obtain the reduced system:

$$\begin{aligned}&\frac{dx}{d\tau }=\frac{3x^{3}\omega (\mu -2\omega +1)+\sqrt{6}x^{2}(\mu (\omega +3)-8\omega +3)+3x\left( 3\mu +y^{2}(\mu -2\omega +1)-2\omega -3\right) +\sqrt{6}(\mu -2)\left( y^{2}+1\right) }{2\omega -3}, \end{aligned}$$

(32)

$$\begin{aligned}&\frac{dy}{d\tau }=\frac{\left( x\left( x\omega +\sqrt{6}\right) +y^{2}+1\right) \left( \sqrt{6}\lambda (2\omega -3)+6y(\mu -2\omega +1)\right) }{4\omega -6}. \end{aligned}$$

(33)

The total equation of state parameter now becomes,

$$\begin{aligned} w_{tot}=\frac{6 \mu \left( x \left( x \omega +\sqrt{6}\right) +1\right) -2 \omega \left( x \left( 6 x \omega -3 x+4 \sqrt{6}\right) +3\right) +6 y^{2} (\mu -2 \omega +1)-3}{6 \omega -9}. \end{aligned}$$

(34)

For the choices $V\left( \psi \right) =V_{0}e^{\lambda \phi }$ and $W\left( \phi \right) =W_{0}\phi ^{\mu }$, with $\mu$ and $\lambda$ being constants, we study the Equilibrium points and investigate the stability of the two-dimensional system (32), (33).

The (lines of) equilibrium points are the following:

• 1. $A_{\pm }:$ The line

  $$\begin{aligned} x_{c} \left( x_{c} \omega +\sqrt{6}\right) +y^{2}+1=0, \end{aligned}$$

  (35)

  corresponding to the massless fields, exists for $x_{c}<0, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$ or $x_{c}>0, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$.

  The eigenvalues are:

  $\Big \{\frac{1}{2} \left( \sqrt{6} (\mu +1) x_{c}-\sqrt{6} \sqrt{\lambda ^{2} \left( -\left( x_{c} \left( x_{c} \omega +\sqrt{6}\right) +1\right) \right) +(\mu +1) x_{c} \left( \mu x_{c}+x_{c}+2 \sqrt{6}\right) +2 \lambda (\mu +1) x_{c} y+2 \sqrt{6} \lambda y+6}+\sqrt{6} \lambda y+6\right)$,

  $\frac{1}{2} \left( \sqrt{6} (\mu +1) x_{c}+\sqrt{6} \sqrt{\lambda ^{2} \left( -\left( x_{c} \left( x_{c} \omega +\sqrt{6}\right) +1\right) \right) +(\mu +1) x_{c} \left( \mu x_{c} +x_{c}+2 \sqrt{6}\right) +2 \lambda (\mu +1) x_{c} y+2 \sqrt{6} \lambda y+6}+\sqrt{6} \lambda y+6\right) \Big \}$, where $y=\epsilon \sqrt{-x_{c} \left( x_{c} \omega +\sqrt{6}\right) -1}$, $\epsilon =\pm 1$. In Fig.  1 we show the stability conditions of $A_{+}$ for (a) $\omega = 1$, and for (b) $\omega = 0$. For parameters in the red region (upper and lower left graphs of Fig. 1) $A_{+}$ is a source and for parameters in the blue region (upper and lower right graphs of Fig.  1) it is a sink. Similarly, in Fig. 2 we present the stability conditions of $A_{-}$ for (a) $\omega =1$, and for (b) $\omega =0$. For parameters in the red region (upper and lower left graphs of Fig. 2) $A_{-}$ is a source and for parameters in the blue region (upper and lower right graphs of Fig. 2) it is a sink. The total EoS parameter and the fractional matter density at the equilibrium points $A_{\pm }$ are the following: $w_{tot}(A_{\pm })=1+2\sqrt{\frac{2}{3} }x_{c}$. They are accelerating solutions ($w_{tot}<-\frac{1}{3}$) for $x_{c}<-\sqrt{\frac{2}{3}},~\omega <\frac{-\sqrt{6}x_{c}-1}{x_{c}^{2}}$. For $x_{c} =-\sqrt{\frac{3}{2}}$, it is a de Sitter solution ($w_{tot}(A_{\pm })=-1$). It represents a decelerating solution for $-\sqrt{\frac{2}{3}}<x_{c}<0,\omega <\frac{-\sqrt{6}x_{c}-1}{x_{c}^{2}}$, or $x_{c}>0,~\omega <\frac{-\sqrt{6}x_{c}-1}{x_{c}^{2}}$. In particular, it mimics a dust solution ($w_{tot}(A_{\pm })=0$) for $x_{c}=-\frac{1}{2}\sqrt{\frac{3}{2}}$.

• 2. B :  $(x,y)= \left( -\frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -2 \omega +1},\frac{\lambda (3-2 \omega )}{\sqrt{6} (\mu -2 \omega +1)}\right)$.

  Eigenvalues are: $\left\{ \frac{\lambda ^{2} (2 \omega -3)+2 ((\mu -4) \mu +6 \omega -5)}{2 (\mu -2 \omega +1)},\frac{\lambda ^{2} (2 \omega -3)+2 ((\mu -4) \mu +6 \omega -5)}{2 (\mu -2 \omega +1)}\right\}$. The critical point is a stable node for

  • (a) $2 \omega -3\ne 0, \mu =2$, or

  • (b) $\mu =-\frac{1}{2} \left( \lambda ^{2}+2\right) , \left( \lambda ^{2}+6\right) \left( \lambda ^{2}+4 \omega \right) \ne 0$, or

  • (c) $\lambda \in {\mathbb {R}}, -\frac{1}{2} \left( \lambda ^{2}+2\right)<\mu <2, \omega >\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (d) $\lambda \in {\mathbb {R}}, -\frac{1}{2} \left( \lambda ^{2}+2\right)<\mu<2, \omega <\frac{\mu +1}{2}$, or

  • (e) $\lambda \in {\mathbb {R}}, \mu <-\frac{1}{2} \left( \lambda ^{2}+2\right) , \omega >\frac{\mu +1}{2}$, or

  • (f) $\mu>2, \omega >\frac{\mu +1}{2}$, or

  • (g) $\lambda \in {\mathbb {R}}, \mu<-\frac{1}{2} \left( \lambda ^{2}+2\right) , \omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (h) $\lambda \in {\mathbb {R}}, \mu >2, \omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$.

  Fig. 1

  

  Stability of $A_{+}$ for a $\omega =1$, and for b $\omega =0$. For parameters in the red region (left graph of each panel) $A_{+}$ is a source and for parameters in the blue region (right graph of each panel) it is a sink

  The critical point an unstable node for

  • (a) $\lambda \in {\mathbb {R}}, \mu<-\frac{1}{2} \left( \lambda ^{2}+2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega <\frac{\mu +1}{2}$, or

  • (b) $\lambda \in {\mathbb {R}}, -\frac{1}{2} \left( \lambda ^{2}+2\right)<\mu<2, \frac{\mu +1}{2}<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (c) $\lambda \in {\mathbb {R}}, \mu >2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega <\frac{\mu +1}{2}$.

  Otherwise the critical point is nonhyperbolic. The total EoS parameter and the fractional matter density at the equilibrium point B are the following: $w_{tot}(B)=\frac{\lambda ^{2}(2\omega -3)+\mu (2\mu -9)+6\omega +1}{3(\mu -2\omega +1)}$. Therefore, they represent solutions dominated by the scalar field and they are accelerating ($w_{tot}(B)<-\frac{1}{3}$) for

  • (a) $2 \omega -3\ne 0, \mu =2$, or

  • (b) $\mu =\frac{1}{2} \left( 2-\lambda ^{2}\right) , \lambda ^{4}+4 \lambda ^{2} \omega -2 \lambda ^{2}+8 \omega -8\ne 0$, or

  • (c) $\lambda \in {\mathbb {R}}, \frac{1}{2} \left( 2-\lambda ^{2}\right)<\mu <2, \omega >\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 \lambda ^{2}+4}$, or

  • (d) $\lambda \in {\mathbb {R}}, \frac{1}{2} \left( 2-\lambda ^{2}\right)<\mu<2, \omega <\frac{\mu +1}{2}$, or

  • (e) $\lambda \in {\mathbb {R}}, \mu <\frac{1}{2} \left( 2-\lambda ^{2}\right) , \omega >\frac{\mu +1}{2}$, or

  • (f) $\mu>2, \omega >\frac{\mu +1}{2}$, or

  • (g) $\lambda \in {\mathbb {R}}, \mu<\frac{1}{2} \left( 2-\lambda ^{2}\right) , \omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 \lambda ^{2}+4}$, or

  • (h) $\lambda \in {\mathbb {R}}, \mu >2, \omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 \lambda ^{2}+4}$.

  Fig. 2

  

  Stability of $A_{-}$ for a $\omega =1$, and for b $\omega =0$. For parameters in the red region (left graph of each panel) $A_{-}$ is a source and for parameters in the blue region (right graph of each panel) it is a sink

  In particular, we have a de Sitter solution ($w_{tot}(B)=-1$) for

  • (a) $\lambda =0, \mu =1, \omega \ne 1$, or

  • (b) $\lambda =0, \mu =2, 2 \omega \ne 3$, or

  • (c) $\omega =\frac{3}{2}-\frac{(\mu -2) (\mu -1)}{\lambda ^{2}}, \lambda ^{2}+2 \mu >2, \mu <2$, or

  • (d) $\omega =\frac{3}{2}-\frac{(\mu -2) (\mu -1)}{\lambda ^{2}}, \lambda ^{2}+2 \mu <2$, or

  • (e) $\omega =\frac{3}{2}-\frac{(\mu -2) (\mu -1)}{\lambda ^{2}}, \mu >2$.

  The solution B represents decelerating solutions for

  • (a) $\mu<\frac{1}{2} \left( 2-\lambda ^{2}\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 \left( \lambda ^{2}+2\right) }<\omega <\frac{\mu +1}{2}$, or

  • (b) $\frac{1}{2} \left( 2-\lambda ^{2}\right)<\mu<2, \frac{\mu +1}{2}<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 \left( \lambda ^{2}+2\right) }$, or

  • (c) $\mu >2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 \left( \lambda ^{2}+2\right) }<\omega <\frac{\mu +1}{2}$.

  In particular, for $\omega =\frac{3 \lambda ^{2}+(9-2 \mu ) \mu -1}{2 \left( \lambda ^{2}+3\right) }$, it mimics a dust fluid ($w_{tot}(B)=0$).

• 3. $C_{+}:$ $(x,y)=\left( -\frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -2 \omega +1},\frac{\sqrt{\left( 1-\frac{2 \omega }{3}\right) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}\right)$.

  Eigenvalues are: $\left\{ 0,\frac{10-2 (\mu -4) \mu -12 \omega +\sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}\right\}$ Nonhyperbolic critical point with a 1D stable manifold for:

  • (a) $\lambda \le 0, \mu<-1, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{\mu +1}{2}$, or

  • (b) $\lambda \le 0, \mu >2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega \le \frac{3}{2}$, or

  • (c) $\lambda >0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega <\frac{\mu +1}{2}$, or

  • (d) $\lambda >0, \frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu \le -1, \frac{\mu +1}{2}<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (e) $\lambda >0, -1<\mu<2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (f) $\lambda>0, \mu >2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$.

  Nonhyperbolic critical point with a 1D unstable manifold for:

  • (a) $\lambda \le 0, \mu \le -1, \frac{\mu +1}{2}<\omega \le \frac{3}{2}$, or

  • (b) $\lambda \le 0, -1<\mu<2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega \le \frac{3}{2}$, or

  • (c) $\lambda >0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (d) $\lambda >0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{\mu +1}{2}<\omega \le \frac{3}{2}$, or

  • (e) $\mu =\frac{1}{2} \left( -\lambda ^{2}-2\right) , -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (f) $\mu =\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$, or

  • (g) $\frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu \le -1, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{\mu +1}{2}$, or

  • (h) $\frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu \le -1, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$, or

  • (i) $-1<\mu<2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$, or

  • (j) $\mu >2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$.

• 4. $C_{-}:$ $(x,y)=\left( -\frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -2 \omega +1},-\frac{\sqrt{\left( 1-\frac{2 \omega }{3}\right) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}\right)$.

  Eigenvalues are: $\left\{ 0,\frac{10-2 (\mu -4) \mu -12 \omega -\sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}\right\}$.

  Nonhyperbolic critical point with a 1D stable manifold for:

  • (a) $\lambda<0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega <\frac{\mu +1}{2}$,

  • (b) $\lambda<0, \frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu \le -1, \frac{\mu +1}{2}<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$,

  • (c) $\lambda<0, -1<\mu<2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$,

  • (d) $\lambda<0, \mu >2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$

  • (e) $\lambda =0, \mu<-1, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{\mu +1}{2}$,

  • (f) $\lambda =0, \mu >2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega \le \frac{3}{2}$

  • (g) $\lambda >0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{\mu +1}{2}$,

  • (h) $\lambda >0, \mu =\frac{1}{2} \left( -\lambda ^{2}-2\right) , -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$,

  • (i) $\lambda >0, \frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu<-1, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{\mu +1}{2}$,

  • (j) $\lambda>0, \mu >2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega \le \frac{3}{2}$.

  Nonhyperbolic with a 1D unstable manifold for

  • (a) $\lambda<0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$,

  • (b) $\lambda<0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{\mu +1}{2}<\omega \le \frac{3}{2}$,

  • (c) $\lambda<0, \mu =\frac{1}{2} \left( -\lambda ^{2}-2\right) , -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$,

  • (d) $\lambda<0, \mu =\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$,

  • (e) $\lambda<0, \frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu \le -1, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{\mu +1}{2}$,

  • (f) $\lambda \,{<}\,0, \frac{1}{2} \left( -\lambda ^{2}-2\right) \,{<}\,\mu \,{\le }\,-\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }\,{<}\,\omega \,{\le }\,\frac{3}{2}$,

  • (g) $\lambda<0, -1<\mu<2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$,

  • (h) $\lambda<0, \mu >2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$,

  • (i) $\lambda =0, \mu<-1, \frac{\mu +1}{2}<\omega \le \frac{3}{2}$,

  • (j) $\lambda =0, -1\le \mu<2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega \le \frac{3}{2}$,

  • (k) $\lambda >0, \mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{\mu +1}{2}<\omega \le \frac{3}{2}$,

  • (l) $\lambda >0, \mu =\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega \le \frac{3}{2}$,

  • (m) $\lambda >0, \frac{1}{2} \left( -\lambda ^{2}-2\right)<\mu \le -1, \frac{\mu +1}{2}<\omega \le \frac{3}{2}$,

  • (n) $\lambda >0, -1<\mu<2, -\frac{1}{6} (\mu -5) (\mu +1)<\omega \le \frac{3}{2}$.

  The total EoS parameter and the fractional matter density at the equilibrium point $C_{\pm }$ are the following: $w_{tot}(C_{\pm })=-\frac{\mu +6\omega -11}{3(\mu -2\omega +1)}$. They represent solutions dominated by the scalar field and they are accelerating (i.e., $w_{tot}<-\frac{1}{3}$) for

  • (a) $\mu<2, \frac{\mu +1}{2}<\omega <\frac{3}{2}$, or

  • (b) $\mu >2, \frac{3}{2}<\omega <\frac{\mu +1}{2}$.

  In particular, for $\omega = \frac{\mu }{6}+\frac{7}{6}$, it represents a de Sitter solution. It is is decelerating for

  • (a) $\omega <\frac{3}{2}, \mu >2 \omega -1$, or

  • (b) $\omega >\frac{3}{2}, \mu <2 \omega -1$.

  For $\omega = \frac{11}{6}-\frac{\mu }{6}$ it mimics a dust fluid.

4.1.1 Center manifold calculations

Now, we proceed to the center manifold calculation of $C_{+}$, and $C_{-}$.

a. The center manifold of $C_{+}$: For the calculation of the center manifold of $C_{+}$, we introduce the new variables

$$\begin{aligned}&u=\frac{(\mu +1) (2 \omega -3) \left( \frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -2 \omega +1}+x\right) }{\sqrt{2} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}, \end{aligned}$$

(36a)

$$\begin{aligned}&v=\frac{-\sqrt{2} (\mu +1) x (2 \omega -3)+2 y \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+2 \sqrt{3} (3-2 \omega )}{2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}, \end{aligned}$$

(36b)

with inverse

$$\begin{aligned}&x =\frac{\sqrt{2} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)} \left( u-\frac{(\mu -2) (\mu +1) (2 \omega -3)}{\sqrt{3} (\mu -2 \omega +1) \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}\right) }{(\mu +1) (2 \omega -3)}, \end{aligned}$$

(37a)

$$\begin{aligned}&y = -\frac{\sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+3 \mu u-6 u \omega +3 u+3 \mu v-6 v \omega +3 v}{3 (-\mu +2 \omega -1)}. \end{aligned}$$

(37b)

Then, we obtain the dynamical system

$$\begin{aligned}&u^{\prime }=-\frac{9 u^{3} (\mu -2 \omega +1)^{3}}{(\mu +1)^{2} (3-2 \omega )^{2}}+\frac{6 u^{2} v (\mu -2 \omega +1)}{2 \omega -3} +u \left( \frac{3 v^{2} (\mu -2 \omega +1)}{2 \omega -3}+\frac{2 \sqrt{3} v \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) , \end{aligned}$$

(38a)

$$\begin{aligned}&v^{\prime 2 }\left( -\frac{3 (\mu -2 \omega +1)^{2} \left( \sqrt{6} \lambda (2 \omega -3)+2 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (3-2 \omega )^{2}}-\frac{9 v (\mu -2 \omega +1)^{3}}{(\mu +1)^{2} (3-2 \omega )^{2}}\right) \nonumber \\&\quad +u \left( \frac{6 v^{2} (\mu -2 \omega +1)}{2 \omega -3}+v \left( \sqrt{6} \lambda +\frac{2 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) \right) \nonumber \\&\quad +\frac{3 v^{3} (\mu -2 \omega +1)}{2 \omega -3}+v^{2} \left( \sqrt{\frac{3}{2}} \lambda +\frac{3 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) \nonumber \\&\quad +\frac{v \left( \sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}-2 (\mu -4) \mu -12 \omega +10\right) }{\mu -2 \omega +1}. \end{aligned}$$

(38b)

Hence, the center manifold is given by the graph $(u, v)=(u, h(u))$, with $h(0)=0,~h^{\prime }(0)=0$, and satisfying the equation

$$\begin{aligned}&u h^{\prime }(u) \left( \frac{h(u) \left( -3 (\mu +1) (h(u)+2 u)+6 \omega (h(u)+2 u)-2 \sqrt{3} \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}\right) }{2 \omega -3} +\frac{9 u^{2} (\mu -2 \omega +1)^{3}}{(\mu +1)^{2} (3-2 \omega )^{2}}\right) \nonumber \\&\quad -\frac{3 u^{2} (\mu -2 \omega +1)^{2} \left( 6 h(u) (\mu -2 \omega +1)+\sqrt{6} \lambda (2 \omega -3)+2 \sqrt{3} \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (3-2 \omega )^{2}} +\frac{3 h(u)^{3} (\mu -2 \omega +1)}{2 \omega -3}\nonumber \\&\quad +h(u)^{2} \left( \sqrt{\frac{3}{2}} \lambda +\frac{3 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) \nonumber \\&\quad +\frac{h(u) \left( \sqrt{2} \lambda \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}-2 (\mu -4) \mu -12 \omega +10\right) }{\mu -2 \omega +1}\nonumber \\&\quad +\frac{u h(u) \left( 6 h(u) (\mu -2 \omega +1)+\sqrt{6} \lambda (2 \omega -3)+2 \sqrt{3} \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}\right) }{2 \omega -3}=0. \end{aligned}$$

(39)

Fig. 3

Qualitative evolution in the phase plane (u, v) given by (38) for $\omega =1$. The solid red lines denote the implicit function $x(u) \left( x(u) \omega +\sqrt{6}\right) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (37) for $\omega =1$, whereas the dashed black lines represent the approximated center manifold of $C_{+}$. Observe the accuracy for small u

Using the Taylor series expansion we propose the expansion

$$\begin{aligned} h(u)=a u^{2}+b u^{3}+c u^{4}+O\left( u^{5}\right) . \end{aligned}$$

(40)

Substituting this expansion into equation (39), and equating the coefficients of the same powers of u, we obtain

$$\begin{aligned}&a=\frac{3 \sqrt{3} (\mu -2 \omega +1)^{3} \left( \sqrt{2} \lambda (2 \omega -3)+2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (3-2 \omega )^{2} \left( \sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}-2 (\mu -4) \mu -12 \omega +10\right) }, \end{aligned}$$

(41a)

$$\begin{aligned}&b=\frac{9 (\mu -2 \omega +1)^{4}}{2 (\mu +1)^{2} (3-2 \omega )^{2} ((\mu -4) \mu +6 \omega -5)}, \end{aligned}$$

(41b)

$$\begin{aligned}&c= \frac{9 \sqrt{3} (\mu -2 \omega +1)^{5} \left( -4 (2 \mu +5) (\mu +1) \omega +15 (\mu +1)^{2}+12 \omega ^{2}\right) \left( \sqrt{2} \lambda (2 \omega -3)+2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}\right) }{8 (\mu +1)^{4} (3-2 \omega )^{4} ((\mu -4) \mu +6 \omega -5) \left( \sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}-2 (\mu -4) \mu -12 \omega +10\right) }. \end{aligned}$$

(41c)

The evolution equation on the center manifold is reduced to $u^{\prime }=O(u^{6})$, which means that u is approximately constant on the center manifold.

Fig. 4

Qualitative evolution in the phase plane (u, v) given by (38) for $\omega =0$. The solid red lines denote the implicit function $x(u) \left( x(u) \omega +\sqrt{6}\right) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (37) for $\omega =0$, whereas the dashed black lines represent the approximated center manifold of $C_{+}$. Observe the accuracy for small u

In Fig. 3 we show the qualitative evolution in the phase plane (u, v) given by (38) for $\omega = 1$. The solid red line in each plot denotes the implicit function $x(u) \left( x(u) +\sqrt{6}\right) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (63) for $\omega = 1$, whereas the dashed black lines in each plot represent the approximated center manifold of $C_{+}$. In Fig. 4 we show the qualitative evolution (u, v) given by (38) for $\omega =0$. The solid red lines in each plot denote the implicit function $\sqrt{6} x(u) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (37) for $\omega =0$, whereas the dashed black lines shown in each plot represent the approximated center manifold of $C_{+}$. Observe the accuracy for small u.

The numerical solutions suggest that the exact center manifold of $C_{+}$ is the line $x \left( x \omega +\sqrt{6}\right) +y^{2}+1=0$, where x, y are given by the inverse relations of (37).

Indeed, the two branches of this implicit equations are

$$\begin{aligned}&h(u)\equiv v= -u-\frac{\sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\sqrt{3} (\mu -2 \omega +1)}\nonumber \\&\quad -\frac{\sqrt{-\frac{18}{\mu -2 \omega +1}+\frac{2 \omega \left( 3 u^{2} (\mu -2 \omega +1)^{2} ((\mu -4) \mu +6 \omega -5)-(\mu +1)^{2} (2 \omega -3) ((\mu -10) \mu +12 \omega -2)\right) }{(\mu +1)^{2} (2 \omega -3) (\mu -2 \omega +1)^{2}} +\frac{2 \sqrt{3} u \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}+3}}{\sqrt{3}} \end{aligned}$$

(42a)

$$\begin{aligned}&h(u)\equiv v=-u -\frac{\sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\sqrt{3} (\mu -2 \omega +1)}\nonumber \\&\quad +\frac{\sqrt{-\frac{18}{\mu -2 \omega +1}+\frac{2 \omega \left( 3 u^{2} (\mu -2 \omega +1)^{2} ((\mu -4) \mu +6 \omega -5)-(\mu +1)^{2} (2 \omega -3) ((\mu -10) \mu +12 \omega -2)\right) }{(\mu +1)^{2} (2 \omega -3) (\mu -2 \omega +1)^{2}} +\frac{2 \sqrt{3} u \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}+3}}{\sqrt{3}} . \end{aligned}$$

(42b)

Both are solutions of the equation (39). But the only one that satisfies the tangential conditions at the origin, say $h(0)=0, h^{\prime }(0)=0$, is (42b). The exact equation that dictates the dynamics at the center manifold is $u^{\prime }=0$. It means that u is constant at the center manifold.

b. The center manifold of $C_{-}$: For the calculation of the center manifold of $C_{-}$, we introduce the new variables

$$\begin{aligned}&u=-\frac{(\mu +1) (2 \omega -3) \left( \frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -2 \omega +1}+x\right) }{\sqrt{2} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}, \end{aligned}$$

(43a)

$$\begin{aligned}&v=\frac{\sqrt{2} (\mu +1) x (2 \omega -3)+2 y \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+2 \sqrt{3} (2 \omega -3)}{2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}. \end{aligned}$$

(43b)

with inverse

$$\begin{aligned}&x= -\frac{\sqrt{2} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)} \left( \frac{(\mu -2) (\mu +1) (2 \omega -3)}{\sqrt{3} (\mu -2 \omega +1) \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}+u\right) }{(\mu +1) (2 \omega -3)}, \end{aligned}$$

(44a)

$$\begin{aligned}&y= -\frac{-\sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+3 \mu u-6 u \omega +3 u+3 \mu v-6 v \omega +3 v}{3 (-\mu +2 \omega -1)}. \end{aligned}$$

(44b)

Then, we obtain the dynamical system

$$\begin{aligned}&u^{\prime }=-\frac{9 u^{3} (\mu -2 \omega +1)^{3}}{(\mu +1)^{2} (3-2 \omega )^{2}}\nonumber \\&\quad +\frac{6 u^{2} v (\mu -2 \omega +1)}{2 \omega -3}+u \left( \frac{3 v^{2} (\mu -2 \omega +1)}{2 \omega -3}\right. \nonumber \\&\quad +\left. \frac{2 \sqrt{3} v \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{3-2 \omega }\right) , \end{aligned}$$

(45a)

$$\begin{aligned}&v^{\prime 2 }\left( -\frac{3 \sqrt{3} (\mu -2 \omega +1)^{2} \left( \sqrt{2} \lambda (2 \omega -3)-2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (3-2 \omega )^{2}}\right. \nonumber \\&\quad \left. -\frac{9 v (\mu -2 \omega +1)^{3}}{(\mu +1)^{2} (3-2 \omega )^{2}}\right) +u \left( \frac{6 v^{2} (\mu -2 \omega +1)}{2 \omega -3}\right. \nonumber \\&\quad \left. +v \left( \sqrt{6} \lambda -\frac{2 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) \right) \nonumber \\&\quad +\frac{3 v^{3} (\mu -2 \omega +1)}{2 \omega -3}\nonumber \\&\quad +v^{2} \left( \sqrt{\frac{3}{2}} \lambda -\frac{3 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) \nonumber \\&\quad -\frac{v \left( \sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+2 (\mu -4) \mu +12 \omega -10\right) }{\mu -2 \omega +1}. \end{aligned}$$

(45b)

Hence, the center manifold is given by the graph $(u, v)=(u, h(u))$, with $h(0)=0, h^{\prime }(0)=0$, and satisfying the equation

$$\begin{aligned}&u h^{\prime }(u) \left( \frac{h(u) \left( -3 (\mu +1) (h(u)+2 u)+6 \omega (h(u)+2 u)+2 \sqrt{3} \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}\right) }{2 \omega -3}+\frac{9 u^{2} (\mu -2 \omega +1)^{3}}{(\mu +1)^{2} (3-2 \omega )^{2}}\right) \nonumber \\&\quad -\frac{3 u^{2} (\mu -2 \omega +1)^{2} \left( 6 h(u) (\mu -2 \omega +1)+\sqrt{6} \lambda (2 \omega -3)-2 \sqrt{3} \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (3-2 \omega )^{2}}\nonumber \\&\quad +\frac{3 h(u)^{3} (\mu -2 \omega +1)}{2 \omega -3}+h(u)^{2} \left( \sqrt{\frac{3}{2}} \lambda -\frac{3 \sqrt{3} \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{2 \omega -3}\right) \nonumber \\&\quad -\frac{h(u) \left( \sqrt{2} \lambda \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}+2 (\mu -4) \mu +12 \omega -10\right) }{\mu -2 \omega +1}\nonumber \\&\quad +\frac{u h(u) \left( 6 h(u) (\mu -2 \omega +1)+\sqrt{6} \lambda (2 \omega -3)-2 \sqrt{3} \sqrt{-(2 \omega -3) ((\mu -4) \mu +6 \omega -5)}\right) }{2 \omega -3}=0 \end{aligned}$$

(46)

Fig. 5

Qualitative evolution in the phase plane (u, v) given by (45) for $\omega = 1$. The solid red line denotes the implicit function $x(u) \left( x(u) \omega +\sqrt{6}\right) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (44) for $\omega =1$, whereas the dashed black lines represents the approximated center manifold of $C_{+}$. Observe the accuracy for small u

Using the Taylor series we propose the expansion

$$\begin{aligned} h(u)=a u^{2}+b u^{3}+c u^{4}+O\left( u^{5}\right) . \end{aligned}$$

(47)

Substituting this expansion in the equation (46), and equating the coefficients of the same powers of u, to obtain

$$\begin{aligned}&a= -\frac{3 \sqrt{3} (\mu -2 \omega +1)^{3} \left( \sqrt{2} \lambda (2 \omega -3)-2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (3-2 \omega )^{2} \left( \sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+2 (\mu -4) \mu +12 \omega -10\right) }, \end{aligned}$$

(48a)

$$\begin{aligned}&b= \frac{9 (\mu -2 \omega +1)^{4}}{2 (\mu +1)^{2} (3-2 \omega )^{2} ((\mu -4) \mu +6 \omega -5)}, \end{aligned}$$

(48b)

$$\begin{aligned}&c= \frac{9 \sqrt{3} (\mu -2 \omega +1)^{5} \left( \sqrt{2} \lambda (2 \omega -3)-2 \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}\right) }{2 (\mu +1)^{2} (2 \omega -3)^{3} ((\mu -4) \mu +6 \omega -5) \left( \sqrt{2} \lambda \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}+2 (\mu -4) \mu +12 \omega -10\right) }. \end{aligned}$$

(48c)

The evolution equation on the center manifold is reduced to

$$\begin{aligned} u^{\prime }=O\left( u^{5}\right) . \end{aligned}$$

(49)

In Fig. 5, we show the qualitative evolution in the phase plane (u, v) given by (45) for $\omega = 1$. The solid red lines denote the implicit function $x(u) \left( x(u) +\sqrt{6}\right) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (44) for $\omega = 1$. The dashed black lines in Fig. 5 represent the approximated center manifold of $C_{-}$. In Fig. 6, we present the qualitative evolution of (u, v) given by (45) for $\omega =0$. The solid red lines denote the implicit function $\sqrt{6} x(u) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (44) for $\omega =0$, whereas the dashed black lines represent the approximated center manifold of $C_{-}$. Let us observe the accuracy for small u.

Fig. 6

Qualitative evolution in the phase plane (u, v) given by (45) for $\omega =0$. The solid red line denotes the implicit function $x(u) \left( x(u) \omega +\sqrt{6}\right) +y(u,v)^{2}+1=0$, with x(u) and y(u, v) defined by (44) for $\omega =0$, whereas the dashed black lines represents the approximated center manifold of $C_{+}$. Let us observe the accuracy for small u

There are two branches of C:

$$\begin{aligned} v&= h(u):=-u+\frac{\sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\sqrt{3} (\mu -2 \omega +1)}\nonumber \\&+\frac{\sqrt{-\frac{2 (3-2 \omega )^{2} \omega }{(\mu -2 \omega +1)^{2}} -\frac{2 (3-2 \omega )^{2}}{\mu -2 \omega +1}+\frac{36 u^{2} \omega ^{2}}{(\mu +1)^{2} (2 \omega -3)}-\frac{36 u^{2} \omega }{(\mu +1) (2 \omega -3)} +\omega \left( \frac{6 u^{2}}{2 \omega -3}-2\right) -\frac{2 \sqrt{3} u \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}+3}}{\sqrt{3}}, \end{aligned}$$

(50a)

$$\begin{aligned} v&= h(u):= -u+\frac{\sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\sqrt{3} (\mu -2 \omega +1)}\nonumber \\&-\frac{\sqrt{-\frac{2 (3-2 \omega )^{2} \omega }{(\mu -2 \omega +1)^{2}} -\frac{2 (3-2 \omega )^{2}}{\mu -2 \omega +1}+\frac{36 u^{2} \omega ^{2}}{(\mu +1)^{2} (2 \omega -3)}-\frac{36 u^{2} \omega }{(\mu +1) (2 \omega -3)} +\omega \left( \frac{6 u^{2}}{2 \omega -3}-2\right) -\frac{2 \sqrt{3} u \sqrt{(3-2 \omega ) ((\mu -4) \mu +6 \omega -5)}}{\mu -2 \omega +1}+3}}{\sqrt{3} }, \end{aligned}$$

(50b)

Both are solutions of the equation (46). But the only one that satisfies the tangential conditions at the origin, say $h(0)=0, h^{\prime }(0)=0$, is (50b). In this case the exact equation that dictates the dynamics over the center manifold of $C_{-}$ is $u^{\prime }=0$. It means that u is constant at the center manifold.

4.2 Matter case

In this section we determine the equilibrium points of the dimensionless dynamical system (21), (22), (23). For each critical point P we calculate the physical quantities of the solution, which are the equation of state parameter for the effective fluid, i.e. $w_{tot}\left( P\right)$, the energy density of the dust fluid source, $\Omega _{m}\left( P\right)$. As far as concerns the quantity $\Omega =x \left( x \omega +\sqrt{6}\right) +y^{2}+z$, this describes the effective energy density for the two scalar fields. Recall that there is an interaction between the two scalar fields and the interaction in the dynamical term is included in the variable z. Hence, there is no unique definition of $\Omega _{\phi }$ and $\Omega _{\psi }$.

In order to avoid any selection of $\Omega _{\phi }$ and $\Omega _{\psi }$ which can lead to false conclusion of the nature of the two scalar fields at the equilibrium points, we choose to see the two-scalar fields as an effective fluid. The only cases where a conclusion for the nature of the scalar field can be done is, if at the critical point P,  one of the coordinates is zero, that means, $x\left( P\right) =0\,,~$or $y\left( P\right) =0$, or $z\left( P\right) =0$. When $x\left( P\right) =0$, by definition $\phi =\text{ const }\,$ which means that the Brans-Dicke field does not contribute to the physical state of the solution. Moreover, when $y\left( P\right) =0$, it follows $\psi = \text{ const }\,$, where now the scalar field $\psi$ does not contribute in the evolution of the universe. Finally, when $z\left( P\right) =0$, then only the kinetic parts of the two scalar fields, namely, $\phi$ and $\psi$ contribute in the cosmological evolution at the specific point.

Since $\Omega _{m}\ge 0$, therefore, from the restriction

$$\begin{aligned} \Omega _{m}=x \left( x \omega +\sqrt{6}\right) +y^{2}+z+1 \end{aligned}$$

(51)

we have that the phase space is given by

$$\begin{aligned} \left\{ (x,y,z)\in {\mathbb {R}}^{3}: 0\le x \left( x \omega +\sqrt{6}\right) +y^{2}+z+1\le 1\right\} \nonumber \\ \end{aligned}$$

(52)

In this example we study the equilibrium points and their stability of the dimensional system (21), (22), (23).

4.2.1 Equilibrium points for $\omega =1$

• 1. $A_{1\pm }: (x,y,z)=\left( x_{c}, \pm \sqrt{-x_{c} \left( x_{c}+\sqrt{6}\right) -1}, 0\right)$. Eigenvalues: $\left\{ 0,\sqrt{6} x_{c}+3,\sqrt{6} (\mu +1) x_{c}+\sqrt{6} \epsilon \lambda \sqrt{-x_{c} \left( x_{c}+\sqrt{6}\right) -1} +6\right\}$, $\epsilon =\pm 1$. $A_{1+}$ is nonhyperbolic with a 2D stable manifold for

  • (a) $x_{c}=-\frac{1+\sqrt{3}}{\sqrt{2}}, \mu >\frac{\sqrt{3}-1}{1+\sqrt{3}}$, or

  • (b) $\lambda \le 0, -\frac{1+\sqrt{3}}{\sqrt{2}}<x_{c}<-\sqrt{\frac{3}{2}}, \mu >-\frac{x_{c} \sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}+x_{c}+\sqrt{6}}{x_{c}}$, or

  • (c) $\lambda>0, -\frac{1+\sqrt{3}}{\sqrt{2}}<x_{c}<-\sqrt{\frac{3}{2}}, \mu >-\frac{x_{c} \left( -\sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}\right) +x_{c}+\sqrt{6}}{x_{c}}$.

  $A_{1+}$ is nonhyperbolic with a 2D unstable manifold when

  • (a) $\lambda \le 0, -\sqrt{\frac{3}{2}}<x_{c}<-\frac{\sqrt{3}-1}{\sqrt{2}}, \mu <-\frac{x_{c} \sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}+x_{c}+\sqrt{6}}{x_{c}}$, or

  • (b) $\lambda >0, -\sqrt{\frac{3}{2}}<x_{c}<-\frac{\sqrt{3}-1}{\sqrt{2}}, \mu <-\frac{x_{c} \left( -\sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}\right) +x_{c}+\sqrt{6}}{x_{c}}$, or

  • (c) $x_{c}=-\frac{\sqrt{3}-1}{\sqrt{2}}, \mu <\frac{1+\sqrt{3}}{\sqrt{3}-1}$.

  $A_{1-}$ is nonhyperbolic with a 2D stable manifold for

  • (a) $x_{c}=-\frac{1+\sqrt{3}}{\sqrt{2}}, \mu >\frac{\sqrt{3}-1}{1+\sqrt{3}}$, or

  • (b) $\lambda \le 0, -\frac{1+\sqrt{3}}{\sqrt{2}}<x_{c}<-\sqrt{\frac{3}{2}}, \mu >-\frac{x_{c} \left( -\sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}\right) +x_{c}+\sqrt{6}}{x_{c}}$, or

  • (c) $\lambda>0, -\frac{1+\sqrt{3}}{\sqrt{2}}<x_{c}<-\sqrt{\frac{3}{2}}, \mu >-\frac{x_{c} \sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}+x_{c}+\sqrt{6}}{x_{c}}$.

  $A_{1-}$ is nonhyperbolic with a 2D unstable manifold for

  • (a) $\lambda \le 0, -\sqrt{\frac{3}{2}}<x_{c}<-\frac{\sqrt{3}-1}{\sqrt{2}}, \mu <-\frac{x_{c} \left( -\sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}\right) +x_{c}+\sqrt{6}}{x_{c}}$, or

  • (b) $\lambda >0, -\sqrt{\frac{3}{2}}<x_{c}<-\frac{\sqrt{3}-1}{\sqrt{2}}, \mu <-\frac{x_{c} \sqrt{-\frac{\lambda ^{2} \left( x_{c}^{2}+\sqrt{6} x_{c}+1\right) }{x_{c}^{2}}}+x_{c}+\sqrt{6}}{x_{c}}$, or

  • (c) $x_{c}=-\frac{\sqrt{3}-1}{\sqrt{2}}, \mu <\frac{1+\sqrt{3}}{\sqrt{3}-1}$.

• 2. $A_{2}: (x,y,z)=\left( -\frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -1}, \frac{\lambda }{\sqrt{6} (\mu -1)}, -\frac{\lambda ^{2}-2 ((\mu -4) \mu +1)}{6 (\mu -1)^{2}}\right)$. Eigenvalues $\left\{ -\frac{\lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 (\mu -1)} ,-\frac{\lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 (\mu -1)},-\frac{\lambda ^{2}-2 \mu ^{2}+7 \mu -3}{\mu -1}\right\}$. It is a sink for

  • (a) $\mu \le -1, \lambda ^{2}<(\mu -3) (2 \mu -1)$, or

  • (b) $-1<\mu<2-\sqrt{3}, \lambda ^{2}<2 \left( \mu ^{2}-4 \mu +1\right)$, or

  • (c) $1<\mu <3$, or

  • (d) $\mu \ge 3, \lambda ^{2}>(\mu -3) (2 \mu -1)$.

  It is a source for

  • (a) $\mu \le -1, \lambda ^{2}>2 \left( \mu ^{2}-4 \mu +1\right)$, or

  • (b) $-1<\mu \le \frac{1}{2}, \lambda ^{2}>(\mu -3) (2 \mu -1)$, or

  • (c) $\frac{1}{2}<\mu <1, \lambda ^{2}\ge 0$, or

  • (d) $\mu >2+\sqrt{3}, 0\le \lambda ^{2}<2 \left( \mu ^{2}-4 \mu +1\right)$.

  It is a saddle for

  • (a) $\mu<-1, (\mu -3) (2 \mu -1)<\lambda ^{2}<2 \left( \mu ^{2}-4 \mu +1\right)$, or

  • (b) $-1<\mu \le 2-\sqrt{3}, 2 \left( \mu ^{2}-4 \mu +1\right)<\lambda ^{2} <(\mu -3) (2 \mu -1)$, or

  • (c) $(2-\sqrt{3}<\mu<\frac{1}{2}, 0\le \lambda ^{2}<(\mu -3) (2 \mu -1)$, or

  • (d) $3<\mu<2+\sqrt{3}, 0\le \lambda ^{2}<(\mu -3) (2 \mu -1)$, or

  • (e) $\mu =2+\sqrt{3}, 0<\lambda ^{2}<\left( \sqrt{3}-1\right) \left( 3+2 \sqrt{3}\right)$, or

  • (f) $\mu >2+\sqrt{3}, 2 \left( \mu ^{2}-4 \mu +1\right)<\lambda ^{2}<(\mu -3) (2 \mu -1)$.

• 3. $A_{3}: (x,y,z)=\left( -\frac{\lambda ^{2}+3 \mu -3}{\sqrt{6} (\mu -1) \mu }, \frac{\lambda }{\sqrt{6} (\mu -1)}, \frac{\lambda ^{2}-3 (\mu -1)^{2}}{6 (\mu -1)^{2} \mu }\right)$. Eigenvalues

  $\Big \{\frac{\lambda ^{2}-3 (\mu -1)^{2}}{2 (\mu -1) \mu }, \frac{\lambda ^{2}-3 (\mu -1)^{2}-\sqrt{\left( \lambda ^{2}-3 (\mu -1)^{2}\right) \left( \lambda ^{2} (8 \mu -1)+\mu ((59-16 \mu ) \mu -30)+3\right) }}{4 (\mu -1) \mu }$,

  $\frac{\lambda ^{2}-3 (\mu -1)^{2}+\sqrt{\left( \lambda ^{2}-3 (\mu -1)^{2}\right) \left( \lambda ^{2} (8 \mu -1)+\mu ((59-16 \mu ) \mu -30)+3\right) }}{4 (\mu -1) \mu }\Big \}$. This point is physical, i.e., $0\le \Omega _{m}=\frac{3 (\mu -1)^{2} \left( 2 \mu ^{2}-7 \mu +3\right) +\lambda ^{4}+\left( -5 \mu ^{2}+13 \mu -6\right) \lambda ^{2}}{6 (\mu -1)^{2} \mu ^{2}}\le 1$, and it stable, that is, all the eigenvalues have negative real parts for

  • (a) $0<\mu \le 0.0779056, 3 (\mu -1)^{2}<\lambda ^{2}\le \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}$, or

  • (b) $0.0779056<\mu<1, 3 (\mu -1)^{2}<\lambda ^{2}\le \frac{1}{2} \left( 5 \mu ^{2}+\sqrt{\mu ^{2} \left( 25 \mu ^{2}-46 \mu +25\right) }-13 \mu +6\right)$, or

  • (c) $\mu =3.10266, \lambda =0$,

  • (d) $\mu =3.10266, 0<\lambda ^{2}<(\mu -3) (2 \mu -1)$, or

  • (e) $\mu >3.10266, \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}<\lambda ^{2}<(\mu -3) (2 \mu -1)$, or

  • (f) $\mu >3.10266, \lambda ^{2}\le \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}$, or

  • (g) $0<\mu<0.0779056, \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1} <\lambda ^{2}\le \frac{1}{2} \left( 5 \mu ^{2}+\sqrt{\mu ^{2} \left( 25 \mu ^{2}-46 \mu +25\right) }-13 \mu +6\right)$, or

  • (h) $3<\mu<3.10266, \lambda ^{2}<(\mu -3) (2 \mu -1)$.

  This point is physical, i.e., $0\le \Omega _{m}=\frac{3 (\mu -1)^{2} \left( 2 \mu ^{2}-7 \mu +3\right) +\lambda ^{4}+\left( -5 \mu ^{2}+13 \mu -6\right) \lambda ^{2}}{6 (\mu -1)^{2} \mu ^{2}}\le 1$, and it unstable, that is, all the eigenvalues have positive real parts for

  • (a) $\mu =0.240719, \lambda ^{2}=1.10824$, or

  • (b) $\mu =0.240719, \frac{1}{2} \left( 5 \mu ^{2}-13 \mu +6\right) -\frac{1}{2} \sqrt{25 \mu ^{4}-46 \mu ^{3}+25 \mu ^{2}}<\lambda ^{2}<2 \mu ^{2}-7 \mu +3$, or

  • (c) $0.240719<\mu \le \frac{3}{7}, \frac{1}{2} \left( 5 \mu ^{2}-13 \mu +6\right) -\frac{1}{2} \sqrt{25 \mu ^{4}-46 \mu ^{3}+25 \mu ^{2}}\le \lambda ^{2}\le \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}$, or

  • (d) $\frac{3}{7}<\mu <0.450783, \lambda ^{2}\le \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}$, or

  • (e) $\mu =0.450783, \lambda =0$, or

  • (f) $\mu >1, 3 \mu ^{2}-6 \mu +3<\lambda ^{2}\le \frac{1}{2} \left( 5 \mu ^{2}-13 \mu +6\right) +\frac{1}{2} \sqrt{25 \mu ^{4}-46 \mu ^{3}+25 \mu ^{2}}$, or

  • (g) $0<\mu<0.240719, \frac{1}{2} \left( 5 \mu ^{2}-13 \mu +6\right) -\frac{1}{2} \sqrt{25 \mu ^{4}-46 \mu ^{3}+25 \mu ^{2}}\le \lambda ^{2}<2 \mu ^{2}-7 \mu +3$, or

  • (h) $0.240719<\mu \le 0.450783, \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}<\lambda ^{2}<2 \mu ^{2}-7 \mu +3$, or

  • (i) $0.450783<\mu<\frac{1}{2}, \lambda ^{2}<2 \mu ^{2}-7 \mu +3$.

$A_{1\pm }$ are actually surfaces in the plane $\left\{ {x},y\right\}$ ($z=0$) which describe a universe with the cosmological observables $\Omega _{m}(A_{1\pm })=0, w_{tot}=1+2 \sqrt{\frac{2}{3}} x_{c}$. $A_{1\pm }$ are real if and only if $-\sqrt{2+\sqrt{3}}\le {x}_{c}\le -\sqrt{2-\sqrt{3}}$, that is, the total equation of state parameter is bounded as $-1-\frac{2\sqrt{3}}{3}\le w_{tot}\left( A_{1\pm }\right) \le -1+\frac{2\sqrt{3}}{3}$. Therefore, they represent solutions dominated by the scalar field and they are accelerating (i.e., $w_{tot}<-\frac{1}{3}$) for $x_{c}<-\sqrt{\frac{2}{3}}, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$. For $x_{c} -\sqrt{\frac{3}{2}}$ it is a de Sitter solution ($w_{tot}(A_{\pm } )=-1$). It represents a decelerating solution for $-\sqrt{\frac{2}{3}}<x_{c}<0, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$, or $x_{c}>0, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$. In particular, it mimics a dust solution ($w_{tot}(A_{\pm })=0$) for $x_{c}=-\frac{1}{2}\sqrt{\frac{3}{2}}$. In the limits where $\left| {x}_{c}+\frac{1}{2}\sqrt{6}\right| =\frac{\sqrt{2}}{2}$, only the kinetic part of the Brans-Dicke field $\phi$ contributes in the evolution of the universe.

Point $A_{2}$ exists only when $\mu \ne 1$ and it describes a universe with $\Omega _{m}\left( A_{2}\right) =0$ and $w_{tot}\left( A_{2}\right) =-\frac{1}{3}\left( 7-2\mu +\frac{\lambda ^{2}}{\mu -1}\right)$, while for $\lambda =0$, the scalar field $\psi$ does not contribute in the total matter component of the solution. The exact solution at the critical point describes a de Sitter universe when $\lambda ^{2}=7-9\mu +2\mu ^{2}$.

Point $A_{3}$ exists only when $\mu \ne 1$ and $\mu \ne 0.$ In contrary to the rest of the points, the energy density of the dust fluid is nonzero, that is, $\Omega _{m}\left( A_{3}\right) =\frac{\left( \lambda ^{2}-3\left( \mu -1\right) ^{2}\right) \left( \lambda ^{2}-3+\left( 7-2\mu \right) \mu \right) }{\mu ^{2}\left( \mu -1\right) ^{2}}$. Hence, the point is physically accepted when $0\le \Omega _{m}\left( A_{3}\right) \le 1$, and from the latter constraint it follows that for $\mu =-1,~$ parameter $\lambda$ is constrained by

$$\begin{aligned} 12-2\sqrt{6}\le \lambda ^{2}\le 12+2\sqrt{6}. \end{aligned}$$

When $\mu <-1$ and $\mu >0$ we find

$$\begin{aligned}&\left( 5\mu -3\right) \left( \mu -2\right) -\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -46\right) \right) }\\&\quad \le 2\lambda ^{2}\le 6-2\left( 7-2\mu \right) \mu , \\&6\left( \mu -1\right) ^{2}\le 2\lambda ^{2}\le \left( 5\mu -3\right) \left( \mu -2\right) \\&\qquad +\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -46\right) \right) }, \end{aligned}$$

while when $-1<\mu <0$, the parameter $\lambda$ take values in the region

$$\begin{aligned}&\left( 5\mu -3\right) \left( \mu -2\right) -\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -46\right) \right) }\\&\quad \le 2\lambda ^{2}\le 6\left( \mu -1\right) ^{2}, \\&6-2\left( 7-2\mu \right) \mu \le 2\lambda ^{2}\le \left( 5\mu -3\right) \left( \mu -2\right) \\&\qquad +\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -46\right) \right) }. \end{aligned}$$

The latter regions are presented in Fig. 7.

Fig. 7

Region plot in the space $\left\{ \lambda ,\mu \right\}$ where the critical point $A_{3}$ is physically accepted

Fig. 8

Qualitative evolution of the equation of state parameter $w_{tot}$ at the equilibrium points $A_{2}~$ (left graph) and $A_{3}$ (right graph)

As far as the equation of state is concerned for the effective fluid derived to be

$w_{tot}\left( A_{3}\right) =-\frac{1}{\mu } -\frac{\lambda ^{2}}{3\mu \left( \mu -1\right) }$. From the latter it follows that $-1\le w_{tot}\left( A_{3}\right) <1$ when

$$\begin{aligned}&\mu<-1~,\left( 5\mu -3\right) \left( \mu -2\right) \\&\qquad -\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -46\right) \right) }\\&\quad <2\lambda ^{2}\le 6-2\left( 7-2\mu \right) \mu ,\text { and }\lambda ^{2}=3\left( \mu -1\right) ^{2} \end{aligned}$$

or

$$\begin{aligned}&-1\le \mu <0\text { ,~}\left( 5\mu -3\right) \left( \mu -2\right) \\&-\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -46\right) \right) }\\&\le 2\lambda ^{2} \le 6\left( \mu -1\right) ^{2} \end{aligned}$$

      or

$$\begin{aligned}&0<\mu<1~,~6\left( \mu -1\right) ^{2}<2\lambda ^{2}\le \left( 5\mu -3\right) \left( \mu -2\right) \\&+\sqrt{\mu ^{2}\left( 25+\mu \left( 25\mu -6\right) \right) } \end{aligned}$$

or$~\left\{ 1<\mu <3~,~\lambda ^{2}=3\left( \mu -1\right) ^{2}\right\} ;~\left\{ \mu =3,\lambda ^{2}=0,12\right\}$ or $\left\{ \mu >3,~\lambda ^{2}\le 3-\left( 7-2\mu \right) \mu ,~\lambda ^{2}=3\left( \mu -1\right) ^{2}\right\}$.

For large values of $\mu$ and for finite value of $\lambda ^{2}$, $w_{tot}\left( A_{3}\right) \rightarrow 0$, which means that the effective fluid mimics the dust fluid source. On the other hand, point $A_{3}$ describes a de Sitter universe when $\lambda ^{2}=3\left( 1-\mu ^{2}\right) \,\$which can not be true for any value of $\mu$ in order $\left\{ \lambda ,\mu \right\}$ belongs to the region of values where point $A_{3}$ is physically accepted.

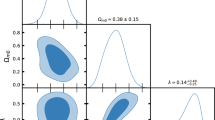
In Fig. 8 we present the contour-plots for the effective equation of state parameters $w_{tot}\left( A_{2}\right)$ and $w_{tot}\left( A_{3}\right)$ in the region space of the variables $\left\{ \lambda ,\mu \right\}$.

Fig. 9

Region plots in the space of variables $\left\{ \lambda ,\mu \right\}$ where the two points $A_{2}$ (left plot) and $A_{3}$ (middle plot) are stable. In the right plot it is superimposed to the stability region, the condition $0\le \Omega _{m}\le 1$, where the critical point $A_{3}$ is physically acceptable

We continue our analysis by studying the stability conditions of the critical points. As we shall see, one can easily conclude about the stability of the equilibrium points $A_{2},~A_{3}$, while for points $A_{1\pm }$ the center manifold theorem should be applied.

The eigenvalues of the linearized system around point $A_{2}$ are found to be

$$\begin{aligned}&e_{1}\left( A_{2}\right) =e_{2}\left( A_{2}\right) =-\frac{\lambda ^{2}-2 \mu ^{2}+8 \mu -2}{2 (\mu -1)}~,\nonumber \\&e_{3}\left( A_{3}\right) =-\frac{\lambda ^{2}-2 \mu ^{2}+7 \mu -3}{\mu -1}, \end{aligned}$$

(53)

from where we infer that the point is stable when

$\left\{ \mu \le -1, \lambda ^{2}<(\mu -3) (2 \mu -1) \right\} ,$ or

$\left\{ -1<\mu<2-\sqrt{3},~ 0\le \lambda ^{2}<2 \left( \mu ^{2}-4 \mu +1\right) \right\} , ~$ or

$\left\{ 1<\mu <3, \lambda \in {\mathbb {R}}\right\} ,$ or

$\left\{ \mu \ge 3,~ \lambda ^{2}>(\mu -3) (2 \mu -1)\right\} .$

As far as the critical point $A_{3}$ is concerned, the eigenvalues of the linearized system are found to be

$$\begin{aligned} e_{1}\left( A_{3}\right)= & {} \frac{\lambda ^{2}-3 (\mu -1)^{2}}{2 (\mu -1) \mu }, \nonumber \\ e_{2\pm }\left( A_{3}\right)= & {} \frac{\lambda ^{2}-3 (\mu -1)^{2}\pm \sqrt{f\left( \lambda ,\mu \right) }}{4 (\mu -1) \mu }, \end{aligned}$$

(54)

where

$$\begin{aligned}&f\left( \lambda ,\mu \right) =\left( 3 (\mu -1)^{2}-\lambda ^{2}\right) \left( \lambda ^{2} (8 \mu -1)\right. \nonumber \\&\quad \left. +\mu ((59-16 \mu ) \mu -30)+3\right) . \end{aligned}$$

(55)

Because of the nonlinear terms one can solve the stability conditions ${\text {Re}}\left( e_{1}\right) <0,$ ${\text {Re}}\left( e_{2\pm }\right) <0$ numerically. The regions of values $\left\{ \lambda ,\mu \right\}$ where the point is an attractor are presented in Fig. 9. In addition in Fig. 9 we show the regions in the space $\left\{ \lambda ,\mu \right\}$ where point $A_{2}$ is stable. For point $A_{3}$ we show also the regions where it is stable and satisfies the condition $0\le \Omega _{m}\le 1$ (physically acceptable). Combining both conditions we obtain that $A_{3}$ “exists” ($0\le \Omega _{m}\le 1$) and it is stable for

$\left\{ 0<\mu \le 0.0779056, 3 (\mu -1)^{2}<\lambda ^{2}\le \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}\right\}$, or

$\left\{ 0.0779056<\mu<1, 3 (\mu -1)^{2}<\lambda ^{2}\le \frac{1}{2} \left( 5 \mu ^{2}+\sqrt{\mu ^{2} \left( 25 \mu ^{2}-46 \mu +25\right) }-13 \mu +6\right) \right\} ,$ or $\left\{ \mu =3.10266, \lambda =0\right\} ,$ or

$\left\{ \mu =3.10266, 0<\lambda ^{2}<(\mu -3) (2 \mu -1)\right\} ,$ or $\left\{ \mu > 3.10266, \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}<\lambda ^{2}<(\mu -3) (2 \mu -1)\right\} ,$ or

$\left\{ \mu >3.10266, 0\le \lambda ^{2}\le \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}\right\} ,$ or

$\left\{ 0<\mu<0.0779056, \frac{16 \mu ^{3}-59 \mu ^{2}+30 \mu -3}{8 \mu -1}<\lambda ^{2}\le \frac{1}{2} \left( 5 \mu ^{2}+\sqrt{\mu ^{2} \left( 25 \mu ^{2}-46 \mu +25\right) }-13 \mu +6\right) \right\} ,$ or

$\left\{ 3<\mu<3.10266, 0\le \lambda ^{2}<(\mu -3) (2 \mu -1)\right) \}.$

a. Center manifold theorem for $A_{1\pm }$: The parametric equation for $A_{1\pm }$ can be derived from

$$\begin{aligned} \left( x+\sqrt{\frac{3}{2}}\right) ^{2}+y^{2}=\frac{1}{2}, \end{aligned}$$

(56)

from which we can define

$$\begin{aligned} x=-\sqrt{\frac{3}{2}}+\frac{\sqrt{2}}{2}\cos \theta , \quad y= \frac{\sqrt{2} }{2}\sin \theta . \end{aligned}$$

(57)

The linearization matrix evaluated at $A_{1\pm }$ is then

$$\begin{aligned} J= \left( \begin{array} [c]{ccc} \sqrt{3} \cos (\theta ) &{} \sqrt{3} \sin (\theta ) &{} \frac{3 (\mu -1) \cos (\theta )-\sqrt{3} \mu }{\sqrt{2}}\\ 0 &{} 0 &{} \frac{3 (\mu -1) \sin (\theta )-\sqrt{3} \lambda }{\sqrt{2}}\\ 0 &{} 0 &{} -3 \mu +\sqrt{3} (\mu +1) \cos (\theta )+\sqrt{3} \lambda \sin (\theta )+3\\ &{} &{} \end{array} \right) , \end{aligned}$$

(58)

with eigenvalues

$$\begin{aligned}&\left\{ 0, \quad \sqrt{3} \cos (\theta ), \quad \sqrt{3} \lambda \sin (\theta )\right. \nonumber \\&\quad \left. +\sqrt{3} (\mu +1) \cos (\theta )-3 \mu +3\right\} \end{aligned}$$

(59)

Due to the dynamics on the sets $A_{1\pm }$, which is essentially two-dimensional, to study the dynamics over $A_{1\pm }$, we project the flow on the plane $(\theta , z)$, where the dynamics is given by

$$\begin{aligned}&\theta ^{\prime }=z \sec (\theta ) \left( 3 (\mu -1) \sin (\theta )-\sqrt{3} \lambda \right) , \end{aligned}$$

(60)

$$\begin{aligned}&z^{\prime }=z \left( \sqrt{3} \lambda \sin (\theta )+\sqrt{3} (\mu +1) \cos (\theta )\right. \nonumber \\&\quad \left. +3 (\mu -1) (2 z-1)\right) . \end{aligned}$$

(61)

For the calculation of the center manifold of $A_{1+}$ we introduce the new variables

$$\begin{aligned}&u=\theta -\theta _{c}+\frac{z \sec ^{2}(\theta _{c}) \left( \sqrt{3} \lambda -3 (\mu -1) \sin (\theta _{c})\right) }{\sqrt{3} (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c})}, \end{aligned}$$

(62a)

$$\begin{aligned}&v=z, \end{aligned}$$

(62b)

with inverse

$$\begin{aligned}&\theta = \frac{\sqrt{3} (\theta _{c}+u) (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c}) (\theta _{c}+u-v \tan (\theta _{c}))-\sqrt{3} \lambda v \sec ^{2}(\theta _{c})}{\sqrt{3} (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c})}. \end{aligned}$$

(63a)

$$\begin{aligned}&z =v, \end{aligned}$$

(63b)

Fig. 10

Phase portrait of (65) for different values of $\lambda , \mu$ ad $\theta _{c}$

where we have used $\theta =\theta _{c}$ to parametrize the system at an specific point of $A_{1\pm }$ with coordinates

$$\begin{aligned} x=-\sqrt{\frac{3}{2}}+\frac{\sqrt{2}}{2}\cos \theta _{c}, \quad y= \frac{\sqrt{2}}{2}\sin \theta _{c} \end{aligned}$$

(64)

Then, we obtain the dynamical system

$$\begin{aligned}&u^{\prime }=\frac{v \sec ^{2}(\theta _{c}) \left( \sqrt{3} \lambda -3 (\mu -1) \sin (\theta _{c})\right) \left( \sqrt{3} \lambda \sin (\theta (u,v))+\sqrt{3} (\mu +1) \cos (\theta (u,v))+3 (\mu -1) (2 v-1)\right) }{\sqrt{3} (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c})} \nonumber \\&\quad +v \sec (\theta (u,v)) \left( 3 (\mu -1) \sin (\theta (u,v))-\sqrt{3} \lambda \right) , \end{aligned}$$

(65a)

$$\begin{aligned}&v^{\prime }= v \left( \sqrt{3} \lambda \sin (\theta (u,v))+\sqrt{3} (\mu +1) \cos (\theta (u,v))\right. \nonumber \\&\quad \left. +3 (\mu -1) (2 v-1)\right) , \end{aligned}$$

(65b)

where

$$\begin{aligned} \theta (u,v)=\frac{\sqrt{3} (\theta _{c}+u) (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c}) (\theta _{c}+u-v \tan (\theta _{c}))-\sqrt{3} \lambda v \sec ^{2}(\theta _{c})}{\sqrt{3} (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c})}. \end{aligned}$$

(66)

In the coordinates u, v, the eigensystem of the linearization is - as expected -

$$\begin{aligned} \left( \begin{array} [c]{cc} 0 &{} -3 \mu +\sqrt{3} (\mu +1) \cos (\theta _{c})+\sqrt{3} \lambda \sin (\theta _{c})+3\\ \{1,0\} &{} \{0,1\}\\ &{} \end{array} \right) , \end{aligned}$$

Hence, the center manifold is given by the graph $(u, v)=(u, h(u))$, with $h(0)=0, h^{\prime }(0)=0$, and satisfying the equation

$$\begin{aligned}&\Big (-h^{\prime }(u) \Big (\frac{\sec ^{2}(\theta _{c}) \left( \sqrt{3} \lambda -3 (\mu -1) \sin (\theta _{c})\right) \left( \sqrt{3} \lambda \sin (\theta (u,h(u)))+\sqrt{3} (\mu +1) \cos (\theta (u,h(u)))+6 (\mu -1) h(u)-3 \mu +3\right) }{\sqrt{3} (\lambda \tan (\theta _{c})+\mu +1)-3 (\mu -1) \sec (\theta _{c})}\nonumber \\&\quad +\sec (\theta (u,h(u))) \left( 3 (\mu -1) \sin (\theta (u,h(u)))-\sqrt{3} \lambda \right) \Big )\nonumber \\&\quad +\sqrt{3} \lambda \sin (\theta (u,h(u))) +\sqrt{3} (\mu +1) \cos (\theta (u,h(u))) +6 (\mu -1) h(u)-3 \mu +3\Big ) h(u) =0. \end{aligned}$$

(67)

For which we have the trivial solution. Now, imposing the compatibility conditions

$$\begin{aligned}&\mu =\frac{2}{\sqrt{3} \cos (\theta _{c})-1}+1, \end{aligned}$$

(68a)

$$\begin{aligned}&\lambda =-\frac{6 \sin (\theta _{c})}{\sqrt{3}-3 \cos (\theta _{c})}, \end{aligned}$$

(68b)

we can seek for another, non-trivial solution using Taylor series

$$\begin{aligned} h(u)=a u^{2}+O\left( u^{3}\right) . \end{aligned}$$

(69)

with results on $a=\frac{1}{4}$. In the two cases the evolution equation on the center manifold is reduced to

$$\begin{aligned} u^{\prime }=O\left( u^{3}\right) , \end{aligned}$$

(70)

that means that u is constant at the invariant manifold.

Fig. 11

Phase portrait of (65) for different values of $\lambda , \mu$ ad $\theta _{c}$

In Figs. 10 and 11 we present some orbits of the phase portraits of (65) for different values of $\lambda , \mu$ ad $\theta _{c}$.

4.2.2 Equilibrium points for $\omega =0$

The case $\omega =0$ is of special interest because the Brans-Dicke field reduces to that of O’Hanlon theory [49]. The latter theory is dynamically equivalent with the fourth-order theory known as $f\left( R\right)$-gravity [50]. The dynamically equivalent scenario can be found easily with the use of a Lagrange multiplier, for more details we refer the reader to [50] and references therein.

For $\omega =0$, we evaluated the cosmological observables

$$\begin{aligned}&\Omega _{m}= \sqrt{6} x+y^{2}+z+1, \end{aligned}$$

(71)

$$\begin{aligned}&w_{tot}=\frac{1}{9} \left( -6 y^{2}+6 \mu z+3\right) , \end{aligned}$$

(72)

and discuss the stability conditions of the equilibrium points of the dimensionless dynamical system (21), (22), (23), as follows.

• 1. $B_{1}: (x,y,z)= \left( -\frac{y_{c}^{2}+1}{\sqrt{6}},y_{c},0\right)$. Eigenvalues: $\left\{ 0,2-y_{c}^{2},-(\mu +1) y_{c}^{2}+\sqrt{6} \lambda y_{c}-\mu +5\right\}$. Nonhyperbolic with a 2D stable manifold for

  • (a) $\lambda \in {\mathbb {R}}, y_{c}<-\sqrt{2}, \mu >\frac{-y_{c}^{2}+\sqrt{6} \lambda y_{c}+5}{y_{c}^{2}+1}$, or

  • (b) $\lambda \in {\mathbb {R}}, y_{c}>\sqrt{2}, \mu >\frac{-y_{c}^{2}+\sqrt{6} \lambda y_{c}+5}{y_{c}^{2}+1}$.

  Nonhyperbolic with a 2D unstable manifold for $\lambda \in {\mathbb {R}}, -\sqrt{2}<y_{c}<\sqrt{2}, \mu <\frac{-y_{c}^{2}+\sqrt{6} \lambda y_{c}+5}{y_{c} ^{2}+1}$. The cosmological observables are $\Omega _{m}(B_{1})=0$, and $w_{tot} (B_{1})=\frac{1}{3} \left( 1-2 y_{c}^{2}\right)$. That means the solution corresponds to a scalar field dominated universe, that is accelerating for $y_{c}^{2}>1$. In particular, it is a de Sitter solution for $y_{c}=\pm \sqrt{2}$. It is decelerating for $y_{c}^{2}<1$. In particular, it mimics a dust solution for $y_{c}=\pm \frac{\sqrt{2}}{2}$.

• 2. $B_{2}: (x,y,z)= \left( -\frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu +1} ,\frac{\sqrt{\frac{3}{2}} \lambda }{\mu +1},1-\frac{3 \left( \lambda ^{2}+4 \mu +4\right) }{2 (\mu +1)^{2}}\right)$. Eigenvalues: $\left\{ -\frac{3 \lambda ^{2}}{2 (\mu +1)}+\mu -5,-\frac{3 \lambda ^{2}}{2 (\mu +1)}+\mu -5,2 \mu -\frac{3 \left( \lambda ^{2}+3 \mu +1\right) }{\mu +1}\right\}$. It is a sink for

  • (a) $\mu =\frac{1}{4} \left( 7+\sqrt{73}\right) , \lambda \ne 0$, or

  • (b) $\mu =\frac{1}{4} \left( 7-\sqrt{73}\right) , \lambda \ne 0$, or

  • (c) $-7<\mu<-1, \lambda ^{2}<\frac{2}{3} (\mu -5) (\mu +1)$, or

  • (d) $\frac{1}{4} \left( 7-\sqrt{73}\right)<\mu <\frac{1}{4} \left( 7+\sqrt{73}\right)$, or

  • (e) $\mu \le -7, \lambda ^{2}<\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (f) $-1<\mu <\frac{1}{4} \left( 7-\sqrt{73}\right) , \lambda ^{2}>\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (g) $\mu>\frac{1}{4} \left( 7+\sqrt{73}\right) , \lambda ^{2}>\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$.

  It is a source for

  • (a) $\mu \le -7, \lambda ^{2}>\frac{2}{3} (\mu -5) (\mu +1)$, or

  • (b) $-7<\mu <-1, \lambda ^{2}>\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (c) $\mu >5, \lambda ^{2}<\frac{2}{3} (\mu -5) (\mu +1)$.

  The cosmological observables are $\Omega _{m}(B_{2})=0$, and $w_{tot} (B_{2})=\frac{-3 \lambda ^{2}+2 \mu ^{2}-9 \mu +1}{3 \mu +3}$. That is, the solution corresponds to a scalar field dominated universe, that is accelerating for

  • (a) $\mu<-1, -\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}<\lambda <\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (b) $-1<\mu<2-\sqrt{3}, \lambda <-\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (c) $-1<\mu <2-\sqrt{3}, \lambda >\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (d) $\mu =2-\sqrt{3}, \lambda <0$, or

  • (e) $\mu =2-\sqrt{3}, \lambda >0$, or

  • (f) $2-\sqrt{3}<\mu <2+\sqrt{3}$, or

  • (g) $\mu =2+\sqrt{3}, \lambda <0$, or

  • (h) $\mu =2+\sqrt{3}, \lambda >0$, or

  • (i) $\mu >2+\sqrt{3}, \lambda <-\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (j) $\mu>2+\sqrt{3}, \lambda >\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$.

  In particular, it is a de Sitter solution for

  • (a) $\mu \ne -1, \lambda =-\sqrt{\frac{2}{3}} \sqrt{\mu ^{2}-3 \mu +2}$, or

  • (b) $\mu \ne -1, \lambda =\sqrt{\frac{2}{3}} \sqrt{\mu ^{2}-3 \mu +2}$.

  Is is decelerating for

  • (a) $\mu<-1, \lambda <-\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (b) $\mu <-1, \lambda >\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (c) $-1<\mu<2-\sqrt{3}, -\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}<\lambda <\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$, or

  • (d) $\mu >2+\sqrt{3}, -\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}<\lambda <\frac{\sqrt{2 \mu ^{2}-8 \mu +2}}{\sqrt{3}}$.

  In particular, it mimics a dust solution for

  • (a) $\mu \ne -1, \lambda =-\frac{\sqrt{2 \mu ^{2}-9 \mu +1}}{\sqrt{3}}$, or

  • (b) $\mu \ne -1, \lambda =\frac{\sqrt{2 \mu ^{2}-9 \mu +1}}{\sqrt{3}}$.

• 3. $B_{3}: (x,y,z)= \left( \frac{\lambda ^{2}+3 \mu -3}{\sqrt{6} \left( \lambda ^{2}-\mu ^{2}+\mu \right) },-\frac{\lambda (\mu +3)}{\sqrt{6} \left( \lambda ^{2}-\mu ^{2}+\mu \right) },\frac{\left( 4 \lambda ^{2}-3 (\mu -1)^{2}\right) (\mu +3)}{6 \left( \lambda ^{2}-\mu ^{2}+\mu \right) ^{2}}\right)$. Eigenvalues: $\left\{ \frac{3 (\mu -1)^{2}-4 \lambda ^{2}}{2 \left( \lambda ^{2}-\mu ^{2}+\mu \right) },-\frac{12 \lambda ^{2}-9 (\mu -1)^{2}+\delta _{1}}{12 \left( \lambda ^{2}-\mu ^{2}+\mu \right) },\frac{-12 \lambda ^{2}+9 (\mu -1)^{2}+\delta _{1}}{12 \left( \lambda ^{2}-\mu ^{2}+\mu \right) }\right\}$,

  where $\delta _{1}=\sqrt{3} {{\sqrt{-\left( 4 \lambda ^{2}-3 (\mu -1)^{2}\right) \left( 12 \lambda ^{2} (2 \mu +5)+\mu ((17-16 \mu ) \mu +174)+81\right) }}}$. It is a sink for

  • (a) $\mu<-7, \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}\le \lambda ^{2}<\frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right)$, or

  • (b) $-3<\mu<-\frac{5}{2}, \frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right) <\lambda ^{2}\le \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}$, or

  • (c) $-\frac{5}{2}\le \mu <-2.48926, \lambda ^{2}>\frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right)$, or

  • (d) $\lambda ^{2}>9.13121, \mu =-2.48926$, or

  • (e) $-2.48926<\mu <-0.501725, \lambda ^{2}\le \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}$, or

  • (f) $-2.48926<\mu <-0.501725, \lambda ^{2}>\frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right)$, or

  • (g) $\lambda ^{2}>1.69138, \mu =-0.501725$, or

  • (h) $-0.501725<\mu \le 1, \lambda ^{2}>\frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right)$, or

  • (i) $1<\mu <4.05349, \lambda ^{2}>\mu ^{2}-\mu$, or

  • (j) $\lambda ^{2}>12.3773, \mu =4.05349$, or

  • (k) $\mu >4.05349, \lambda ^{2}\le \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}$, or

  • (l) $\mu>4.05349, \lambda ^{2}>\mu ^{2}-\mu$, or

  • (m) $\mu<-7, \frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)<\lambda ^{2} <\frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}$, or

  • (n) $-3<\mu<-\frac{5}{2}, 0\le \lambda ^{2}<\mu ^{2}-\mu$, or

  • (o) $-3<\mu <-\frac{5}{2}, \lambda ^{2}>\frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}$, or

  • (p) $-\frac{5}{2}\le \mu<-2.48926, 0\le \lambda ^{2}<\mu ^{2}-\mu$, or

  • (q) $0<\lambda ^{2}<8.68569, \mu =-2.48926$, or

  • (r) $-2.48926<\mu \le -1, \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}<\lambda ^{2}<\mu ^{2}-\mu$, or

  • (s) $-1<\mu<-0.501725, \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}<\lambda ^{2}<\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (t) $0<\lambda ^{2}<0.33851, \mu =-0.501725$, or

  • (u) $-0.501725<\mu<\frac{1}{4} \left( 7-\sqrt{73}\right) , \lambda ^{2} <\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (v) $\frac{1}{4} \left( 7+\sqrt{73}\right)<\mu<4.05349, 0\le \lambda ^{2}<\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (w) $0<\lambda ^{2}<0.495701, \mu =4.05349$, or

  • (x) $\mu >4.05349, \frac{16 \mu ^{3}-17 \mu ^{2}-174 \mu -81}{24 \mu +60}<\lambda ^{2}<\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (y) $\lambda =0, \mu \in \left\{ -2.48926, -0.501725, 4.05349\right\}$.

  It is a source for

  • (a) $-7<\mu<-3, \frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right)<\lambda ^{2}<\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (b) $-3<\mu<-1, \mu ^{2}-\mu<\lambda ^{2}<\frac{1}{3} \left( 2 \mu ^{2}-7 \mu -3\right)$, or

  • (c) $\mu >1, \frac{1}{4} \left( 3 \mu ^{2}-6 \mu +3\right)<\lambda ^{2}<\mu ^{2}-\mu$.

  The cosmological observables are $\Omega _{m}(B_{3})=\frac{\left( 4 \lambda ^{2}-3 (\mu -1)^{2}\right) \left( 3 \lambda ^{2}+(7-2 \mu ) \mu +3\right) }{6 \left( \lambda ^{2}-\mu ^{2}+\mu \right) ^{2}}$, and $w_{tot}(B_{3} )=\frac{\lambda ^{2}+3 \mu -3}{3 \left( \lambda ^{2}-\mu ^{2}+\mu \right) }$. That means, the solution is accelerating for

  • (a) $\lambda<-2 \sqrt{3}, 2-\sqrt{2 \lambda ^{2}+1}<\mu <\frac{1}{2}-\frac{1}{2} \sqrt{4 \lambda ^{2}+1}$, or

  • (b) $\lambda<-2 \sqrt{3}, \frac{1}{2} \sqrt{4 \lambda ^{2}+1}+\frac{1}{2}<\mu <\sqrt{2 \lambda ^{2}+1}+2$, or

  • (c) $-2 \sqrt{3}\le \lambda \le 2 \sqrt{3}, \frac{1}{2}-\frac{1}{2} \sqrt{4 \lambda ^{2}+1}<\mu <2-\sqrt{2 \lambda ^{2}+1}$, or

  • (d) $-2 \sqrt{3}\le \lambda \le 2 \sqrt{3}, \frac{1}{2} \sqrt{4 \lambda ^{2}+1}+\frac{1}{2}<\mu <\sqrt{2 \lambda ^{2}+1}+2$, or

  • (e) $\lambda >2 \sqrt{3}, 2-\sqrt{2 \lambda ^{2}+1}<\mu <\frac{1}{2}-\frac{1}{2} \sqrt{4 \lambda ^{2}+1}$, or

  • (f) $\lambda >2 \sqrt{3}, \frac{1}{2} \sqrt{4 \lambda ^{2}+1}+\frac{1}{2}<\mu <\sqrt{2 \lambda ^{2}+1}+2.$

  In particular, it is a de Sitter solution for

  • (a) $\lambda ^{2}+3 \mu -3\ne 0, \mu =\frac{1}{3} \left( 3-2 \sqrt{3} \lambda \right)$, or

  • (b) $\lambda ^{2}+3 \mu -3\ne 0, \mu =\frac{1}{3} \left( 2 \sqrt{3} \lambda +3\right)$.

  It is decelerating for

  • (a) $\lambda<-2 \sqrt{3}, \mu <2-\sqrt{2 \lambda ^{2}+1}$, or

  • (b) $\lambda<-2 \sqrt{3}, \frac{1}{2}-\frac{1}{2} \sqrt{4 \lambda ^{2}+1}<\mu <\frac{1}{2} \sqrt{4 \lambda ^{2}+1}+\frac{1}{2}$, or

  • (c) $\lambda <-2 \sqrt{3}, \mu >\sqrt{2 \lambda ^{2}+1}+2$, or

  • (d) $-2 \sqrt{3}\le \lambda \le 2 \sqrt{3}, \mu <\frac{1}{2}-\frac{1}{2} \sqrt{4 \lambda ^{2}+1}$, or

  • (e) $-2 \sqrt{3}\le \lambda \le 2 \sqrt{3}, 2-\sqrt{2 \lambda ^{2}+1}<\mu <\frac{1}{2} \sqrt{4 \lambda ^{2}+1}+\frac{1}{2}$, or

  • (f) $-2 \sqrt{3}\le \lambda \le 2 \sqrt{3}, \mu >\sqrt{2 \lambda ^{2}+1}+2$, or

  • (g) $\lambda >2 \sqrt{3}, \mu <2-\sqrt{2 \lambda ^{2}+1}$, or

  • (h) $\lambda >2 \sqrt{3}, \frac{1}{2}-\frac{1}{2} \sqrt{4 \lambda ^{2}+1}<\mu <\frac{1}{2} \sqrt{4 \lambda ^{2}+1}+\frac{1}{2}$, or

  • (i) $\lambda>2 \sqrt{3}, \mu >\sqrt{2 \lambda ^{2}+1}+2$.

  In particular, it mimics a dust solution for $\mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \lambda \left( \lambda ^{2}-12\right) \ne 0$.

• 4. $B_{4}: (x,y,z)= \left( \frac{1}{\sqrt{6}},0,0\right)$. Eigenvalues: $\{-2,-2,\mu +3\}$. Nonhyperbolic for $\mu =-3$, sink for $\mu <-3$, saddle for $\mu >-3$. The cosmological observables are $\Omega _{m}(B_{4})=2$, and $w_{tot}(B_{4})=\frac{1}{3}$. That means, it mimics a radiation dominated universe. But this point has no physical meaning since it satisfies $\Omega _{m}>1$.

Points $B_{1}: (x,y,z)= \left( -\frac{y_{c}^{2}+1}{\sqrt{6}},y_{c},0\right)$ can also be written as $B_{1\pm }=\left( {x}_{c}, \pm \sqrt{-1-\sqrt{6}{x}_{c} },0\right)$, equivalently, points $A_{1\pm }$ for the case $\omega =0$, describe surfaces a family of points in the surface $y^{2}=-\left( 1+\sqrt{6}{x}_{c}\right)$ in the plane $\left\{ x,y\right\}$. The points are real, when $\sqrt{6}{x}_{c}\le -1$. The energy density for the dust fluid is found to be $\Omega _{m}=0$, while the equation of state for the effective fluid is $w_{tot}\left( B_{1\pm }\right) =1+\frac{2}{3}\sqrt{6}{x}_{c}$, similar expression with that of $A_{1\pm }$. In the case where $\sqrt{6}{x}_{c}=-1$ where only the field $\phi$ contributes to the evolution of the universe, we find that $w_{tot}\left( B_{1\pm }\right) |_{\sqrt{6}{x} _{c}\rightarrow -1}=\frac{1}{3}$, where the critical point in which the $f\left( R\right)$-gravity describes the radiation era is recovered.

4.3 Center manifold of $B_{1}$

It is more convenient to use the parametrization $B_{1}: (x,y,z)= \left( -\frac{y_{c}^{2}+1}{\sqrt{6}},y_{c},0\right)$, which is solved globally for x, rather than considering two branches $B_{1\pm }$, which provide with only a local description of the model.

We choose $y_{c}^{2} \ne 2$, in which the center manifold is one dimensional. Next, we introduce the new variables

$$\begin{aligned}&u=-\frac{\sqrt{6} x {y_{c}}}{{y_{c}}^{2}-2}+y \left( -\frac{4}{{y_{c}} ^{2}-2}-1\right) +\frac{{y_{c}}}{{y_{c}}^{2}-2}\nonumber \\&\quad -\frac{\sqrt{6} {y_{c}} z \left( \frac{\mu -(\mu +1) {y_{c}}^{2}-5}{\sqrt{6} \left( \mu +(\mu +1) {y_{c}}^{2}-5\right) -6 \lambda {y_{c}}}+\frac{\left( {y_{c}}^{2}+2\right) \left( -\sqrt{6} \lambda \left( \mu +(3 \mu +2) {y_{c}} ^{2}-3\right) +2 (\mu +1) {y_{c}} \left( \mu +\mu {y_{c}}^{2}-3\right) +6 \lambda ^{2} {y_{c}}\right) }{2 {y_{c}} \left( \sqrt{6} (\mu -5) (\mu -3)+\sqrt{6} \mu (\mu +1) {y_{c}}^{4}-6 {y_{c}}^{3} (2 \lambda \mu +\lambda )+\sqrt{6} {y_{c}}^{2} \left( 6 \lambda ^{2}+\mu (2 \mu -7)-3\right) -12 \lambda (\mu -4) {y_{c}}\right) }\right) }{{y_{c}}^{2}-2}, \end{aligned}$$

(73)

$$\begin{aligned} v&= \frac{\sqrt{6} x {y_{c}}}{{y_{c}}^{2}-2}+y \left( \frac{4}{{y_{c}} ^{2}-2}+2\right) \nonumber \\&\quad \,\, +\frac{{y_{c}} z}{{y_{c}}^{2}-2}+\frac{{y_{c}}-{y_{c}}^{3} }{{y_{c}}^{2}-2}, \end{aligned}$$

(74)

$$\begin{aligned}&w= z, \end{aligned}$$

(75)

with inverse

$$\begin{aligned} x&= -\sqrt{\frac{2}{3}} u {y_{c}}-\frac{v \left( {y_{c}}^{2}+2\right) }{\sqrt{6} {y_{c}}}\nonumber \\&\quad \,\, +\frac{w \left( -\mu +(\mu +1) {y_{c}}^{2}+5\right) }{\sqrt{6} \left( \mu +(\mu +1) {y_{c}}^{2}-5\right) -6 \lambda {y_{c}}} \nonumber \\&\quad \,\, -\frac{{y_{c}}^{2}+1}{\sqrt{6}}, \end{aligned}$$

(76)

$$\begin{aligned}&y= u+v+w +\frac{\left( {y_{c}}^{2}+2\right) {y_{c}}}{2-{y_{c}}^{2}} +\frac{2 {y_{c}}^{3}}{{y_{c}}^{2}-2}+ \Big [\frac{6 \lambda {y_{c}}^{2}-2 \sqrt{6} (\mu +1) {y_{c}}^{3}}{\left( {y_{c}}^{2}-2\right) \left( \sqrt{6} \left( \mu +(\mu +1) {y_{c}}^{2}-5\right) -6 \lambda {y_{c}}\right) }\nonumber \\&\quad +\frac{\left( {y_{c}}^{2}+2\right) \left( -3 \lambda (\mu -3)+\sqrt{6} \mu (\mu +1) {y_{c}}^{3}-3 \lambda (3 \mu +2) {y_{c}}^{2}+\sqrt{6} {y_{c}} \left( 3 \lambda ^{2}+(\mu -3) (\mu +1)\right) \right) }{\left( {y_{c}}^{2}-2\right) \left( \sqrt{6} (\mu -5) (\mu -3)+\sqrt{6} \mu (\mu +1) {y_{c}}^{4}-6 {y_{c}}^{3} (2 \lambda \mu +\lambda )+\sqrt{6} {y_{c}}^{2} \left( 6 \lambda ^{2}+\mu (2 \mu -7)-3\right) -12 \lambda (\mu -4) {y_{c}}\right) }\Big ], \end{aligned}$$

(77)

$$\begin{aligned} z= w. \end{aligned}$$

(78)

The resulting system, which can be written symbolically as

$$\begin{aligned}&u^{\prime }=0. u + f_{1}(u,v,w), \end{aligned}$$

(79)

$$\begin{aligned}&v^{\prime }= (2-{y_{c}}^{2}) v +f_{2}(u,v,w), \end{aligned}$$

(80)

$$\begin{aligned}&w^{\prime }= (-(\mu +1) {y_{c}}^{2}+\sqrt{6} \lambda {y_{c}}-\mu +5) w +f_{3}(u,v,w), \end{aligned}$$

(81)

where $f_{i}$’s ($i = 1, 2, 3$) are at least of second order in (u, v, w). Hence the latter system has the following eigensystem of the linearization

$$\begin{aligned} \left( \begin{array} [c]{ccc} 0 &{} 2-{y_{c}}^{2} &{} -(\mu +1) {y_{c}}^{2}+\sqrt{6} \lambda {y_{c}}-\mu +5\\ \{1,0,0\} &{} \{0,1,0\} &{} \{0,0,1\}\\ &{} &{} \end{array} \right) . \end{aligned}$$

That means, the center manifold of the origin is given locally by the graph $(u,v,w)=(u, h_{1}(u), h_{2}(u))$, where

$$\begin{aligned}&f_{2}(u, h_{1}(u), h_{2}(u))-h_{1}^{\prime }(u) f_{1}(u, h_{1}(u),\nonumber \\&h_{2}(u))=0, h_{1}(0)=0 , h_{1}^{\prime }(0)=0, \end{aligned}$$

(82)

$$\begin{aligned}&f_{3}(u, h_{1}(u), h_{2}(u))-h_{2}^{\prime }(u) f_{1}(u, h_{1}(u),\nonumber \\&h_{2}(u))=0, h_{2}(0)=0 , h_{2}^{\prime }(0)=0. \end{aligned}$$

(83)

Using the Taylor series we propose the expansion

$$\begin{aligned} h_{1}(u)= & {} a_{1} u^{2}+b_{1} u^{3}+c_{1} u^{4}+d_{1} u^{5}+O\left( u^{6}\right) , \nonumber \\ h_{2}(u)= & {} a_{2} u^{2}+b_{2} u^{3}+c_{2} u^{4}+d_{2} u^{5}+O\left( u^{6}\right) . \end{aligned}$$

(84)

Fig. 12

Qualitative evolution in the phase plane (u, v) given by (87) for $\omega =0$. The solid red lines denote the lines $-v\pm \frac{\sqrt{-v \text {yc} \left( \text {yc}^{2}-2\right) }}{\text {yc}}$, whereas the dashed black lines represent the approximated center manifold of $B_{1}$. Observe the accuracy for small u. The solutions typically converge to the unphysical point $B_{4}$

Substituting this expansion in the above equations, and equating the coefficients of the same powers of u, we obtain

$$\begin{aligned} a_{1}&= \frac{y_{c}}{2-y_{c}^{2}},\quad b_{1}= \frac{2 y_{c}^{2}}{\left( y_{c}^{2}-2\right) ^{2}},\nonumber \\ c_{1}&= -\frac{5 y_{c}^{3}}{\left( y_{c} ^{2}-2\right) ^{3}},\nonumber \\ d_{1}&= \frac{14 y_{c}^{4}}{\left( y_{c}^{2}-2\right) ^{4}}, \end{aligned}$$

(85)

$$\begin{aligned} a_{2}&= 0, \quad b_{2}= 0,\quad c_{2}=0,\quad d_{2}=0. \end{aligned}$$

(86)

The evolution at the center manifold is $u^{\prime 7})$. That is, u is constant at the center manifold. In the invariant set $w=0$, the evolution equations in a neighborhood of a point of $B_{1}$ parametrized by $y_{c}$ can be simplified to

$$\begin{aligned}&u^{\prime }= u \left( -(u+v)^{2}-v y_{c}+\frac{2 v}{y_{c} }\right) ,\nonumber \\&v^{\prime }=-\frac{(v+y_{c}) \left( y_{c} (u+v)^{2}+v y_{c}^{2}-2 v\right) }{y_{c}}. \end{aligned}$$

(87)

From the Fig. 12, we see that

$$\begin{aligned} v= & {} h_{1}(u)\nonumber \\:= & {} \frac{\sqrt{y_{c}^{2}-2} \sqrt{4 u y_{c}+y_{c}^{2}-2}-y_{c} (2 u+y_{c})+2}{2 y_{c}},\nonumber \\ w= & {} h_{2}(u):=0, \end{aligned}$$

(88)

is the exact solution for the center manifold, which has the expansion up to fifth order given before (and they satisfy the equations and the initial conditions in (84)). The equation on the center manifold is $u^{\prime }=0$. As before, u is constant at the center manifold.

4.4 Comments on arbitrary $\omega$

For arbitrary $\omega$, we evaluated the cosmological observables

$$\begin{aligned}&\Omega _{m}= x \left( x \omega +\sqrt{6}\right) +y^{2}+z+1, \end{aligned}$$

(89)

$$\begin{aligned}&w_{tot}=\frac{-2 x \omega \left( 3 x (\omega -1)+\sqrt{6}\right) -6 (\omega -1) y^{2}+6 z (\omega -\mu )-3}{6 \omega -9}, \end{aligned}$$

(90)

and discuss the stability conditions of the equilibrium points of the dimensionless dynamical system (21), (22), (23), as follows.

• 1. $A_{1+}:(x, y, z)=(x_{c}, \sqrt{-x_{c} \left( x_{c} \omega +\sqrt{6}\right) -1}, 0)$, with eigenvalues

  $\left\{ 0,\sqrt{6} x_{c}+3,\sqrt{6} \lambda \sqrt{-x_{c} \left( \omega x_{c}+\sqrt{6}\right) -1}+\sqrt{6} (\mu +1) x_{c}+6\right\}$.

  $A_{1+}$ nonhyperbolic with a 2D stable manifold for

  • (a) $\lambda \le 0, x_{c}<-\sqrt{\frac{3}{2}}, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}-\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2} }{x_{c}^{2}}}$, or

  • (b) $\lambda>0, x_{c}<-\sqrt{\frac{3}{2}}, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}+\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}$.

  It is nonhyperbolic with a 2D unstable manifold for

  • (a) $\lambda \le 0, -\sqrt{\frac{3}{2}}<x_{c}<0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu <\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}-\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2} }{x_{c}^{2}}}$, or

  • (b) $\lambda \le 0, x_{c}>0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}+\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}$, or

  • (c) $\lambda >0, -\sqrt{\frac{3}{2}}<x_{c}<0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu <\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}+\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}$, or

  • (d) $\lambda>0, x_{c}>0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}-\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}$.

• 2. $A_{1-}:(x, y, z)=(x_{c}, -\sqrt{-x_{c} \left( x_{c} \omega +\sqrt{6}\right) -1}, 0)$, with eigenvalues

  $\left\{ 0,\sqrt{6} x_{c}+3,\sqrt{6} (\mu +1) x_{c}+6-\sqrt{6} \lambda \sqrt{-x_{c} \left( \omega x_{c}+\sqrt{6}\right) -1}\right\}$.

  $A_{1-}$ nonhyperbolic with a 2D stable manifold for

  • (a) $\lambda \le 0, x_{c}<-\sqrt{\frac{3}{2}}, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}+\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}$, or

  • (b) $\lambda>0, x_{c}<-\sqrt{\frac{3}{2}}, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\frac{-\sqrt{6} x_{c}-6}{\sqrt{6} x_{c}}-\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2} }{x_{c}^{2}}}$.

  Fig. 13

  

  Stability of $A_{3}$ when it is a sink (left panel) and when it is a source (right panel)

  It is nonhyperbolic with a 2D unstable manifold for

  • (a) $\lambda \le 0, -\sqrt{\frac{3}{2}}<x_{c}<0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu <\sqrt{\frac{\lambda ^{2} (-\omega ) x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}+\frac{-x_{c}-\sqrt{6}}{x_{c}}$, or

  • (b) $\lambda \le 0, x_{c}>0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\frac{-x_{c}-\sqrt{6}}{x_{c}}-\sqrt{\frac{-\omega \lambda ^{2} x_{c} ^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}$, or

  • (c) $\lambda >0, -\sqrt{\frac{3}{2}}<x_{c}<0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu <\frac{-x_{c}-\sqrt{6}}{x_{c}}-\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}$, or

  • (d) $\lambda>0, x_{c}>0, \omega \le \frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}, \mu >\sqrt{\frac{-\omega \lambda ^{2} x_{c}^{2}-\sqrt{6} \lambda ^{2} x_{c}-\lambda ^{2}}{x_{c}^{2}}}+\frac{-x_{c}-\sqrt{6}}{x_{c}}$.

  The cosmological observables are $\Omega _{m}(A_{1\pm })=0, w_{tot}=1+2 \sqrt{\frac{2}{3}} x_{c}$. Therefore, they represent solutions dominated by the scalar field and they are accelerating (i.e., $w_{tot}<-\frac{1}{3}$) for $x_{c}<-\sqrt{\frac{2}{3}}, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$. For $x_{c} -\sqrt{\frac{3}{2}}$, it is a de Sitter solution ($w_{tot}(A_{\pm } )=-1$). It represents a decelerating solution for $-\sqrt{\frac{2}{3}}<x_{c}<0, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$, or $x_{c}>0, \omega <\frac{-\sqrt{6} x_{c}-1}{x_{c}^{2}}$. In particular, it mimics a dust solution ($w_{tot}(A_{\pm })=0$) for $x_{c}=-\frac{1}{2}\sqrt{\frac{3}{2}}$.

• 3. $A_{2}: (x,y,z)=\left( -\frac{\sqrt{\frac{2}{3}} (\mu -2)}{\mu -2 \omega +1}, \frac{\lambda (3-2 \omega )}{\sqrt{6} (\mu -2 \omega +1)}, -\frac{(2 \omega -3) \left( (2 \omega -3) \lambda ^{2}+2 ((\mu -4) \mu +6 \omega -5)\right) }{6 (\mu -2 \omega +1)^{2}}\right)$,

  with eigenvalues $\left\{ \frac{(2 \omega -3) \lambda ^{2}+\mu (2 \mu -7)+6 \omega -3}{\mu -2 \omega +1} ,\frac{(2 \omega -3) \lambda ^{2}+2 ((\mu -4) \mu +6 \omega -5)}{2 (\mu -2 \omega +1)},\frac{(2 \omega -3) \lambda ^{2}+2 ((\mu -4) \mu +6 \omega -5)}{2 (\mu -2 \omega +1)}\right\}$. It is a source for

  • (a) $\mu<\frac{1}{2} \left( -\lambda ^{2}-2\right) , \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega <\frac{\mu +1}{2}$, or

  • (b) $-\frac{\lambda ^{2}}{2}<\mu<\frac{1}{6} \left( 6-\lambda ^{2}\right) , \frac{\mu +1}{2}<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+7 \mu +3}{2 \left( \lambda ^{2}+3\right) }$, or

  • (c) $\frac{1}{6} \left( 6-\lambda ^{2}\right) \le \mu<2, \frac{\mu +1}{2}<\omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (d) $\mu >2, \frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }<\omega <\frac{\mu +1}{2}$.

  It is a sink for

  • (a) $\mu <\frac{1}{2} \left( -\lambda ^{2}-2\right) , \omega >\frac{\mu +1}{2}$, or

  • (b) $\frac{1}{2}\left( -\lambda ^{2}-2\right) \le \mu \le -\frac{\lambda ^{2} }{2}, \omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+7 \mu +3}{2 \left( \lambda ^{2}+3\right) }$, or

  • (c) $\frac{1}{2} \left( -\lambda ^{2}-2\right) \le \mu \le -\frac{\lambda ^{2} }{2}, \omega >\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (d) $-\frac{\lambda ^{2}}{2}<\mu \le \frac{1}{6} \left( 6-\lambda ^{2}\right) , \omega <\frac{\mu +1}{2}$, or

  • (e) $-\frac{\lambda ^{2}}{2}<\mu \le \frac{1}{6} \left( 6-\lambda ^{2}\right) , \omega >\frac{3 \lambda ^{2}-2 \mu ^{2}+8 \mu +10}{2 \left( \lambda ^{2}+6\right) }$, or

  • (f) $\frac{1}{6} \left( 6-\lambda ^{2}\right)<\mu<2, \omega <\frac{\mu +1}{2}$, or

  • (g) $\frac{1}{6} \left( 6-\lambda ^{2}\right)<\mu <2, \omega >\frac{3 \lambda ^{2}-2 \mu ^{2}+7 \mu +3}{2 \left( \lambda ^{2}+3\right) }$, or

  • (h) $\mu =2, \omega \ne \frac{3}{2}$, or

  • (i) $\mu >2, \omega <\frac{3 \lambda ^{2}-2 \mu ^{2}+7 \mu +3}{2 \left( \lambda ^{2}+3\right) }$, or

  • (j) $\mu>2, \omega >\frac{\mu +1}{2}$.

  The cosmological observables are $\Omega _{m}(A_{2})=0, w_{tot}(A_{2} )=\frac{\lambda ^{2} (2 \omega -3)+\mu (2 \mu -9)+6 \omega +1}{3 (\mu -2 \omega +1)}$. It corresponds to a scalar field dominated universe. It is an accelerating solution for

  • (a) $\lambda \in {\mathbb {R}}, \mu <1, \omega \ge \frac{3}{2}$, or

  • (b) $\lambda \in {\mathbb {R}}, \mu =2, \omega >\frac{3}{2}$, or

  • (c) $\lambda \in {\mathbb {R}}, \mu>2, \omega >\frac{\mu +1}{2}$, or

  • (d) $\lambda \in {\mathbb {R}}, \mu >2, \omega <\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)$, or

  • (e) $\lambda \in {\mathbb {R}}, \mu<1, \omega <\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)$, or

  • (f) $\lambda \in {\mathbb {R}}, \mu =2, \omega <\frac{3}{2}$, or

  • (g) $\mu>2, \omega =\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right) , \lambda >0$, or

  • (h) $\mu <1, \omega =\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right) , \lambda >0$, or

  • (i) $\lambda \in {\mathbb {R}}, 1\le \mu <2, \omega \ge \frac{3}{2}$, or

  • (j) $\mu >2, \omega =\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right) , \lambda <0$, or

  • (k) $\mu<1, \omega =\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right) , \lambda <0$, or

  • (l) $\lambda \in {\mathbb {R}}, 1\le \mu<2, \omega <\frac{\mu +1}{2}$, or

  • (m) $\mu>2, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega <\frac{3}{2}, \lambda >\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (n) $\mu<1, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega <\frac{\mu +1}{2}, \lambda >\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (o) $\mu >2, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega<\frac{3}{2}, \lambda <-\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (p) $\mu<1, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega<\frac{\mu +1}{2}, \lambda <-\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (q) $\mu<1, \frac{\mu +1}{2}<\omega<\frac{3}{2}, -\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}<\lambda <\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (r) $1\le \mu<2, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega<\frac{3}{2}, -\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}<\lambda <\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$.

  In particular, it mimics a de Sitter solution for

  • (a) $\lambda =-\frac{\sqrt{2} \sqrt{(2-\mu ) (\mu -1)} \sqrt{2 \omega -3}}{3-2 \omega }$, or

  • (b) $\lambda = \frac{\sqrt{2} \sqrt{(2-\mu ) (\mu -1)} \sqrt{2 \omega -3}}{3-2 \omega }$, or

  • (c) $\mu = 1, \omega = \frac{3}{2}$.

  It is a decelerating solution for

  • (a) $\lambda \in {\mathbb {R}}, \mu >2, \frac{3}{2}\le \omega <\frac{\mu +1}{2}$, or

  • (b) $\mu \le 1, \frac{\mu +1}{2}<\omega <\frac{3}{2}, \lambda >\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (c) $1<\mu <2, \omega =\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right) , \lambda >0$, or

  • (d) $\mu \le 1, \frac{\mu +1}{2}<\omega<\frac{3}{2}, \lambda <-\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (e) $\lambda \in {\mathbb {R}}, 1<\mu<2, \frac{\mu +1}{2}<\omega <\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)$, or

  • (f) $1<\mu<2, \omega =\frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right) , \lambda <0$, or

  • (g) $1<\mu<2, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega <\frac{3}{2}, \lambda >\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (h) $\mu >2, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega<\frac{3}{2}, -\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}<\lambda <\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (i) $\mu<1, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega<\frac{\mu +1}{2}, -\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}<\lambda <\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$, or

  • (j) $1<\mu<2, \frac{1}{2} \left( -\mu ^{2}+4 \mu -1\right)<\omega<\frac{3}{2}, \lambda <-\sqrt{2} \sqrt{\frac{-\mu ^{2}+4 \mu -2 \omega -1}{2 \omega -3}}$.

  In particular, it mimics a dust solution for

  • (a) $\omega =\frac{3}{2}, \mu =\frac{5}{2}$, or

  • (b) $\mu +1\ne 2 \omega , 2 \omega \ne 3, \lambda =-\frac{\sqrt{-2 \mu ^{2}+9 \mu -6 \omega -1}}{\sqrt{2 \omega -3}}$, or

  • (c) $\mu +1\ne 2 \omega , 2 \omega \ne 3, \lambda =\frac{\sqrt{-2 \mu ^{2}+9 \mu -6 \omega -1}}{\sqrt{2 \omega -3}}$.

• 4. $A_{3}: (x, y, z)= \left( \frac{-\lambda ^{2}-3 \mu +3}{\sqrt{6} \left( (\omega -1) \lambda ^{2}+(\mu -1) \mu \right) }, \frac{\lambda (\mu -3 \omega +3)}{\sqrt{6} \left( (\omega -1) \lambda ^{2}+(\mu -1) \mu \right) }, -\frac{(\mu -3 \omega +3) \left( (3 \omega -4) \lambda ^{2}+3 (\mu -1)^{2}\right) }{6 \left( (\omega -1) \lambda ^{2}+(\mu -1) \mu \right) ^{2}}\right)$

  with eigenvalues $\Bigg \{\frac{1}{2} \left( \frac{\lambda ^{2}+3 \mu -3}{(\omega -1) \lambda ^{2}+(\mu -1) \mu }-3\right)$,

  $\frac{1}{4} \left( \frac{\lambda ^{2}+3 \mu -3}{(\omega -1) \lambda ^{2}+(\mu -1) \mu }-3-\frac{\sqrt{(8 \mu -21 \omega +20) (2 \omega -3) \lambda ^{2}-144 \omega ^{2}+\mu (\mu (16 \mu -17)-174)+6 (34-7 \mu ) \mu \omega +222 \omega -81} \sqrt{(3 \omega -4) \lambda ^{2}+3 (\mu -1)^{2}}}{\left( (\omega -1) \lambda ^{2}+(\mu -1) \mu \right) \sqrt{2 \omega -3}}\right)$,

  $\frac{1}{4} \left( \frac{\lambda ^{2}+3 \mu -3}{(\omega -1) \lambda ^{2}+(\mu -1) \mu }-3+\frac{\sqrt{(8 \mu -21 \omega +20) (2 \omega -3) \lambda ^{2}-144 \omega ^{2}+\mu (\mu (16 \mu -17)-174)+6 (34-7 \mu ) \mu \omega +222 \omega -81} \sqrt{(3 \omega -4) \lambda ^{2}+3 (\mu -1)^{2}}}{\left( (\omega -1) \lambda ^{2}+(\mu -1) \mu \right) \sqrt{2 \omega -3}}\right) \Bigg \}$. In Fig. 13 we show a portion of the parameters space with stability conditions of P when it is a sink (left panel) and when it is a source (right panel). The cosmological observables are

  $$\begin{aligned}&\Omega _{m}(A_{3})\\&\quad =\frac{\left( \lambda ^{2} (2 \omega -3)+\mu (2 \mu -7)+6 \omega -3\right) \left( \lambda ^{2} (3 \omega -4)+3 (\mu -1)^{2}\right) }{6 \left( \lambda ^{2} (\omega -1)+(\mu -1) \mu \right) ^{2}},\\&w_{tot}(A_{3})=-\frac{\lambda ^{2}+3 \mu -3}{3 \left( \lambda ^{2} (\omega -1)+(\mu -1) \mu \right) }. \end{aligned}$$

  It represents an accelerating universe for

  • (a) $(\omega \in {\mathbb {R}}, \lambda =0, 0<\mu <1$, or

  • (b) $\omega \in {\mathbb {R}}, \lambda =0, 1<\mu <3$, or

  • (c) $\lambda >\sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu \le 0, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (d) $\lambda >0, \mu \ge 3, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (e) $\lambda>0, \mu >1, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (f) $\lambda >0, \mu =1, 1<\omega <2$, or

  • (g) $\lambda<0, \mu \ge 3, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2} }<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (h) $\lambda<-\sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu \le 0, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (i) $\lambda<0, \mu >1, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (j) $\lambda<0, \mu =1, 1<\omega <2$, or

  • (k) $0<\lambda \le \sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu<1, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (l) $\lambda >\sqrt{3}, 0<\mu<1, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2} }<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (m) $\lambda \le -\sqrt{3}, \mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}<\omega <\frac{\lambda ^{2} -\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (n) $-\sqrt{3}<\lambda<0, \mu \le 0, \frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}<\omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (o) $0<\lambda<\sqrt{3}, \mu \le 0, \frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}<\omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (p) $\lambda =\sqrt{3}, \mu<0, \frac{1}{3} \left( -\mu ^{2}+4 \mu +3\right)<\omega <\frac{1}{3} \left( -\mu ^{2}+\mu +3\right)$, or

  • (q) $\lambda >\sqrt{3}, \mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}<\omega <\frac{\lambda ^{2}-\mu ^{2} +\mu }{\lambda ^{2}}$, or

  • (r) $\lambda \le -\sqrt{3}, 0<\mu<1, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (s) $-\sqrt{3}<\lambda<0, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu<1, \frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}<\omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (t) $-\sqrt{3}<\lambda<0, 0<\mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}<\omega <\frac{\lambda ^{2} -\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (u) $0<\lambda<\sqrt{3}, 0<\mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}<\omega <\frac{\lambda ^{2} -\mu ^{2}+\mu }{\lambda ^{2}}$.

  It represents a de Sitter solution for

  • (a) $\omega =\frac{4}{3}, \mu =1, \lambda \ne 0$, or

  • (b) $3 \omega -4\ne 0, (\mu -1) (\mu -3 \omega +3)\ne 0, \lambda =-\frac{\sqrt{3} \sqrt{-(\mu -1)^{2}}}{\sqrt{3 \omega -4}}$, or

  • (c) $3 \omega -4\ne 0, (\mu -1) (\mu -3 \omega +3)\ne 0, \lambda =\frac{\sqrt{3} \sqrt{-(\mu -1)^{2}}}{\sqrt{3 \omega -4}}$.

  It represents a decelerating universe for

  • (a) $(\omega \in {\mathbb {R}}, \lambda =0, \mu >3$, or

  • (b) $\omega \in {\mathbb {R}}, \lambda =0, \mu <0$, or

  • (c) $\lambda>\sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu <0, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (d) $\lambda>0, \mu>3, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (e) $\lambda <0, \mu>3, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (f) $\lambda>0, \mu \ge 1, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (g) $\lambda<-\sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu <0, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (h) $\lambda <0, \mu \ge 1, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (i) $\lambda <-\sqrt{3}, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (j) $\lambda>\sqrt{3}, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (k) $\lambda >\sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu<0, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (l) $\lambda>0, \mu >3, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (m) $\lambda<0, \mu >3, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (n) $\lambda >0, \mu \ge 1, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2} }$, or

  • (o) $\lambda<-\sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu<0, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (p) $\lambda<-\sqrt{3}, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (q) $\lambda >\sqrt{3}, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (r) $\lambda<0, \mu \ge 1, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2} }$, or

  • (s) $0<\lambda \le \sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu <1, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (t) $\lambda>\sqrt{3}, 0\le \mu <1, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (u) $\lambda<-\sqrt{3}, 0\le \mu <1, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (v) $\lambda =-\sqrt{3}, 0<\mu <1, \omega >\frac{1}{3} \left( -\mu ^{2}+4 \mu +3\right)$, or

  • (w) $-\sqrt{3}<\lambda<0, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu <1, \omega >\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (x) $\lambda \le -\sqrt{3}, \mu <\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (y) $-\sqrt{3}<\lambda<0, \mu <0, \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (z) $0<\lambda \le \sqrt{3}, \mu <0, \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (aa) $\lambda>\sqrt{3}, \mu <\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (bb) $-\sqrt{3}\le \lambda <0, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (cc) $0<\lambda \le \sqrt{3}, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (dd) $0<\lambda \le \sqrt{3}, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu<1, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (ee) $\lambda >\sqrt{3}, 0\le \mu<1, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (ff) $\lambda \le -\sqrt{3}, \mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (gg) $-\sqrt{3}<\lambda<0, \mu<0, \omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (hh) $0<\lambda \le \sqrt{3}, \mu<0, \omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (ii) $\lambda >\sqrt{3}, \mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (jj) $\lambda<-\sqrt{3}, 0\le \mu<1, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (kk) $\lambda =-\sqrt{3}, 0<\mu<1, \omega <\frac{1}{3} \left( -\mu ^{2} +\mu +3\right)$, or

  • (ll) $-\sqrt{3}<\lambda<0, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu<1, \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (mm) $-\sqrt{3}\le \lambda<0, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (nn) $0<\lambda \le \sqrt{3}, \mu =\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (oo) $-\sqrt{3}<\lambda<0, 0\le \mu <\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (pp) $0<\lambda<\sqrt{3}, 0\le \mu <\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega >\frac{\lambda ^{2}-\mu ^{2}+\mu }{\lambda ^{2}}$, or

  • (qq) $-\sqrt{3}<\lambda<0, 0\le \mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$, or

  • (rr) $0<\lambda<\sqrt{3}, 0\le \mu<\frac{1}{3} \left( 3-\lambda ^{2}\right) , \omega <\frac{2 \lambda ^{2}-\mu ^{2}+4 \mu -3}{\lambda ^{2}}$.

  It represents a dust solution for

  • (a) $(\mu -1) (\mu -3 \omega +3)\ne 0, \lambda =-\sqrt{3} \sqrt{1-\mu }$, or

  • (b) $(\mu -1) (\mu -3 \omega +3)\ne 0, \lambda =\sqrt{3} \sqrt{1-\mu }$.

• 5. $A_{4}: (x,y,z)=\left( \frac{1}{\sqrt{6} (\omega -1)}, 0, 0\right)$, with eigenvalues $\left\{ \frac{1}{2} \left( \frac{1}{\omega -1}-3\right) ,\frac{1}{2} \left( \frac{1}{\omega -1}-3\right) ,3-\frac{\mu }{\omega -1}\right\}$. It is a sink for

  • (a) $\omega<1, \mu <3 (\omega -1)$, or

  • (b) $\omega>\frac{4}{3}, \mu >3 (\omega -1)$.

  It is a source for $1<\omega<\frac{4}{3}, \mu <3 (\omega -1)$. The cosmological observables are $\Omega _{m}(A_{4})=\frac{(2 \omega -3) (3 \omega -4)}{6 (\omega -1)^{2}}$, $w_{tot}(A_{4})=-\frac{1}{3 (\omega -1)}$. It is associated with an accelerating solution for $1<\omega <2$. It represents a de Sitter solution for $\omega =\frac{4}{3}$. Is corresponds to a decelerated solution for $\omega <1$ por $\omega >2$. For $\omega =0$, it corresponds to a radiation dominated solution.

• 6. For $\omega =\frac{3 \lambda ^{2}+(5-2 \mu ) \mu -3}{2 \lambda ^{2}}$, we have the equilibrium point $A_{5}: (x, y, z)= \left( -\sqrt{\frac{2}{3}}, \frac{2 \mu -3}{\sqrt{6} \lambda }, \frac{3-2 \mu }{6 \lambda ^{2}}\right)$, with eigenvalues

  $\Big \{-\frac{1}{2}, -\frac{1}{4} \left( 1+\frac{\sqrt{(17 \mu -25) \lambda ^{2}+24 (\mu -1) (2 \mu -3)}}{\lambda \sqrt{\mu -1} }\right) , -\frac{1}{4} \left( 1-\frac{\sqrt{(17 \mu -25) \lambda ^{2}+24 (\mu -1) (2 \mu -3)}}{\lambda \sqrt{\mu -1}}\right) \Big \}$. It is a sink for

  • (a) $\lambda<0, \frac{1}{96} \left( -17 \lambda ^{2}-\sqrt{289 \lambda ^{4}+720 \lambda ^{2}+576}+120\right) \le \mu <\frac{1}{3} \left( 3-\lambda ^{2}\right)$, or

  • (b) $\lambda<0, \frac{1}{96} \left( -17 \lambda ^{2}+\sqrt{289 \lambda ^{4}+720 \lambda ^{2}+576}+120\right) \le \mu <\frac{3}{2}$, or

  • (c) $\lambda >0, \frac{1}{96} \left( -17 \lambda ^{2}-\sqrt{289 \lambda ^{4}+720 \lambda ^{2}+576}+120\right) \le \mu <\frac{1}{3} \left( 3-\lambda ^{2}\right)$, or

  • (d) $\lambda >0, \frac{1}{96} \left( -17 \lambda ^{2}+\sqrt{289 \lambda ^{4}+720 \lambda ^{2}+576}+120\right) \le \mu <\frac{3}{2}$.

  It is a saddle point for

  • (a) $\lambda<0, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu <1$, or

  • (b) $\lambda <0, \mu >\frac{3}{2}$, or

  • (c) $\lambda >0, \frac{1}{3} \left( 3-\lambda ^{2}\right)<\mu <1$, or

  • (d) $\lambda>0, \mu >\frac{3}{2}$.

  It is nonhyperbolic otherwise. The cosmological observables are $\Omega _{m}(A_{5})=-\frac{2 \mu -3}{3 \lambda ^{2}}$, $w_{tot}(A_{5})=-\frac{2}{3}$. It is always accelerating.

5 Conclusions

Let us now summarize the main findings of this article. In this work we considered a spatially flat FLRW cosmological model of two scalar fields in the Jordan frame. Specifically, one of the fields is the Brans-Dicke field which is nonminimally coupled to gravity, and the second scalar field is minimally coupled to gravity. The equivalent model in Einstein frame is that of two minimally coupled scalar fields with an interaction only in the potential part of the fields which effectively represents a quintom cosmological model.

We focused on the evolution of the physical quantities of the universe by studying the stationary points of the field equations. Such analysis is important to understand the cosmological viability of the cosmological model, and also we try to conclude about the differences among the Einstein and the Jordan frames.

In the vacuum scenario the field equations admit four stationary points. Two of the points actually, namely $A_{\pm }$, describe two families of stationary points in the phase space of the field equations. The critical points can describe ideal gas solutions, or de Sitter universes for various values of the free parameters.

When we introduce a matter source in the field equations the dynamical analysis differs and in order to perform a complete study we study separate cases where the Brans-Dicke parameter $\omega$ is $\omega =1,~\omega =0$ and $\omega =arbitrary.~$ For $\omega =1$, the dynamical system admits four critical points, when $\omega =0$, we again find four critical points while for arbitrary $\omega$ the dynamical system admits six critical points. In all the cases the physical quantities and the stability of the solutions at the critical points are discussed.

From our analysis we observe that there are many differences between our model and the Brans-Dicke theory with one-scalar field. There are new exact solutions which can describe additional cosmological eras in the evolution of the universe. Consequently, the cosmological evolution differs from the two-scalar field models defined in the Einstein frame.

The cosmological model of our consideration can describe the generic cosmological history, hence, in a future work, we plan to investigate the cosmological viability of the model by using observational constraints.