1 Introduction

Quantum entanglement is identified as the most nonclassical feature of quantum formalism, which plays crucial role in quantum information science [1, 2]. However, the inevitable coupling of quantum system with environment may destroy quantum entanglement, such as a quantum system coupling to the fluctuating quantum field. Recently, the entanglement dynamics is investigated for uniformly accelerated atoms coupling to fluctuating scalar field or electromagnetic field in Minkowski spacetime, and the results show that entanglement exhibit behaviors of degradation, generation, revival and enhancement under the influence of vacuum fluctuation [3, 4]. Lately investigation of entanglement dynamics in curved spacetimes was implemented [5, 6], and the research shows that entanglement behaviors can be utilized to tell the difference between the de Sitter spacetime and the Minkowski spacetime.

On the other side, the cosmic string spacetime is a typical curved spacetime with nontrivial topological defect. The topological defect of cosmic string is produced during the evolution of the early universe due to the symmetry breaking phase transitions [7,8,9,10]. The simplest cosmic string spacetime is characterized by a deficit angle around a straight and infinitely long cosmic string, which is locally flat but not globally [11]. The nontrivial spacetime topology can give rise to some interesting physical effects, for example, bremsstrahlung process [12], gravitational lensing effect [13, 14] and gravitational Aharonov-Bohm effect [15, 16]. Furthermore, for better understanding the effects of the string, some quantum processes in the Minkowski spacetime have been extended to the cosmic string spacetime, for instance, radiative properties [17,18,19], Landau quantization [20, 21], geometric phase [11, 22], the Casimir effect [23] and so on.

As far as we know, entanglement behaviors in the cosmic string spacetime are not studied. In this work, we will investigate the entanglement behaviors for two identical accelerating atoms immersing in fluctuating massless scalar field in the background of the cosmic string spacetime. We are interested in how the nontrivial spacetime topology structure modifies the atom-field interaction and affects the entanglement behaviors, and whether entanglement behaviors can be employed to detect the spacetime topology structure. A uniformly accelerated observer can feel thermal particles in Minkowski vacuum, which is called as Unruh effect [24]; naturally, we also are intriguing with the thermal effect in cosmic string spacetime. Our investigation would throw light on the properties of the cosmic string universe and the quantum field theory of curved spacetime.

In the following, we firstly introduce and calculate the system evolution equation and entanglement measure. And then we make some derivations about the field correlation function for different cases, and examine the entanglement dynamics in the presence of a cosmic string. Finally, we give some conclusions of this paper.

2 Entanglement measure for atoms in the framework of open quantum system

The Hamiltonian of two identical atoms interacting with the massless scalar field is given by [25]

$$\begin{aligned} H=H_{S}+H_{F}+H_{I}. \end{aligned}$$
(1)

The Hamiltonian \(H_{S}\) of the two-level atom reads

$$\begin{aligned} H_{S}={\omega \over 2}\,\sigma _3^{(1)}+ {\omega \over 2}\,\sigma _3^{(2)}, \end{aligned}$$
(2)

where \(\sigma _{i}\) \((i=1,2,3)\) are the Pauli operators and \(\omega \) is the energy-level spacing between the excited state and the ground state of the atom. \(H_{F}\) is the Hamiltonian of the scalar field. The interaction Hamiltonian \(H_{I}\) between atoms and the scalar field is given by [25]

$$\begin{aligned} H_{I}=\mu \left[ \sigma _{2}^{(1)} \phi (t,\mathbf{x}_1) +\sigma _{2}^{(2)}\phi (t, \mathbf{x}_2)\right] , \end{aligned}$$
(3)

where \(\mu \) is the interaction strength, \(\mathbf{x}_1\) and \(\mathbf{x}_2\) denotes the coordinates of the two atoms. The model is of great importance both theoretically and experimental [26,27,28]; by suitable adaptations, it can be applied to other different physical scenes, such as ions in traps, atoms in optical cavities and impurities in phonon fields.

Supposing that initially there is not correlation between the two atoms and the scalar field, the initial state of the total system can be written as \(\rho _{tot}(0)=\rho (0)\otimes |0\rangle \langle 0|\), where \(\rho (0)\) is the initial density matrix of the atoms and \(|0\rangle \) is the vacuum state of the scalar field. In the weak atom-field coupling approximation, the evolution equation of the atoms is given in the Kossakowski–Lindblad form by [29,30,31]

$$\begin{aligned} \frac{\partial \rho (\tau )}{\partial \tau }=-\mathrm {i}[H_{\mathrm{eff}},\rho (\tau )]+{\mathcal {L}}[\rho (\tau )], \end{aligned}$$
(4)

where

$$\begin{aligned} H_{\mathrm{eff}} =H_S-\frac{i}{2}\sum _{\alpha ,\beta =1}^2\sum _{i,j=1}^3 H_{ij}^{(\alpha \beta )}\,\sigma _i^{(\alpha )}\,\sigma _j^{(\beta )}, \end{aligned}$$
(5)

and

$$\begin{aligned} {\mathcal {L}}[\rho ]=&{1\over 2} \sum _{\alpha ,\beta =1}^2\sum _{i,j=1}^3 C_{ij}^{(\alpha \beta )} \Bigg [2\,\sigma _j^{(\beta )}\rho \,\sigma _i^{(\alpha )}\nonumber \\&-\sigma _i^{(\alpha )}\sigma _j^{(\beta )}\, \rho -\rho \,\sigma _i^{(\alpha )}\sigma _j^{(\beta )}\Bigg ]. \end{aligned}$$
(6)

\(C_{ij}^{(\alpha \beta )}\) and \(H_{ij}^{(\alpha \beta )}\) are determined by Fourier transforms \({{{\mathcal {G}}}}^{(\alpha \beta )}(\lambda )\) and Hilbert transforms \({{{\mathcal {K}}}}^{(\alpha \beta )}(\lambda )\) of field correlation function

$$\begin{aligned} \mathrm {}G^{(\alpha \beta )}(\tau -\tau ') =\langle 0|\phi (t,\mathbf {x})\phi (t^{\prime },\mathbf {x}^{\prime })|0 \rangle , \end{aligned}$$
(7)

which are defined as

$$\begin{aligned} {{{\mathcal {G}}}}^{(\alpha \beta )}(\lambda )= & {} \int _{-\infty }^{\infty } d\varDelta \tau \, e^{i{\lambda }\varDelta \tau }\, G^{(\alpha \beta )}, \end{aligned}$$
(8)
$$\begin{aligned} {{{\mathcal {K}}}}^{(\alpha \varDelta \tau ) \beta )}(\lambda )= & {} \frac{P}{\pi i}\int _{-\infty }^{\infty } d\omega \ \frac{{{{\mathcal {G}}}}^{(\alpha \beta )}(\omega )}{\omega -\lambda }, \end{aligned}$$
(9)

with \(\varDelta \tau =\tau -\tau ^{\prime }\). The Kossakowski matrix \(C_{ij}^{(\alpha \beta )}\) can be written explicitly as

$$\begin{aligned} C_{ij}^{(\alpha \beta )} = A^{(\alpha \beta )}\delta _{ij} -iB^{(\alpha \beta )}\epsilon _{ijk}\,\delta _{3k} -A^{(\alpha \beta )}\delta _{3i}\,\delta _{3j}, \end{aligned}$$
(10)

where

$$\begin{aligned} A^{(\alpha \beta )} ={\frac{\mu ^2}{4}}\,\Big [\,{{{\mathcal {G}}}}^{(\alpha \beta )}(\omega ) +{{{\mathcal {G}}}}^{(\alpha \beta )}(-\omega )\Big ],\nonumber \\ B^{(\alpha \beta )}={\frac{\mu ^2}{4}}\,\Big [\,{{{\mathcal {G}}}}^{(\alpha \beta )}(\omega ) -{{{\mathcal {G}}}}^{(\alpha \beta )}(-\omega )\Big ]. \end{aligned}$$
(11)

\(H^{(\alpha \beta )}_{ij}\) can be obtained by replacing \(\mathcal{G}^{(\alpha \beta )}\) with \({{{\mathcal {K}}}}^{(\alpha \beta )}\) in the above equations. Actually, Eq. (10) can be explicitly written as

$$\begin{aligned}&C_{ij}^{(11)}=A_1\,\delta _{ij}-iB_1\epsilon _{ijk}\,\delta _{3k} -A_1\delta _{3i}\,\delta _{3j},\nonumber \\&C_{ij}^{(22)} =A_2\,\delta _{ij}-iB_2\epsilon _{ijk}\,\delta _{3k} -A_2\delta _{3i}\,\delta _{3j},\nonumber \\&C_{ij}^{(12)}=C_{ij}^{(21)} =A_3\,\delta _{ij}-iB_3\epsilon _{ijk}\,\delta _{3k} -A_3\delta _{3i}\,\delta _{3j}. \end{aligned}$$
(12)

Note that the natural units \(c = \hbar = 1\) are adopted in this article.

Supposing that the two atoms initially are prepared in the Werner state \(p|\phi \rangle \langle \phi |+(1-p)\frac{I}{4}, \ p\in [0,1]\), with \(|\phi \rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )\). Werner state is separable when \(p \le \frac{1}{3}\). In this paper, we take \(p=\frac{2}{3}\). Werner state [32] is an important kind of X-type that is written as

$$\begin{aligned} \rho _{X}{=}\frac{1}{4}\left( I\otimes I+\sum _{i}^{3}c_{i}\sigma _{i}\otimes \sigma _{i}{+}c_{4}I\otimes \sigma _{3}+c_{5}\sigma _{3}\otimes I\right) ,\nonumber \\ \end{aligned}$$
(13)

where \(-1\le c_{i}\le 1\). For the X-type state, entanglement can be measured by concurrence [33], which is given by

$$\begin{aligned} E = \max (0,F_{1},F_{2}), \end{aligned}$$
(14)

with \(F_{1} =\frac{1}{2} [| c_1+c_2| -\sqrt{(c_3-c_4-c_5+1) (c_3+c_4+c_5+1)}]\) and \(F_{2} = \frac{1}{2} [| c_1-c_2| -\sqrt{(c_3+c_4-c_5-1) (c_3-c_4+c_5-1)}]\).

Arbitrary two-qubit states can use Pauli matrice to be represented as

$$\begin{aligned} \rho =\frac{1}{4} \sum _{i=0}^3 \sum _{j=0}^3 b_{i,j}(t) \sigma _{i}\otimes \sigma _{j}, \end{aligned}$$
(15)

where \(\sigma _{0}\) denotes the identity matrix. As mentioned above, we considering the initial state of two atoms is Werner state. According to the initial condition, in the interaction presentation, combining Eq. (15) with Eq. (4), we only get the following non-trivial coupled differential equations

$$\begin{aligned} b_{0,0}'(t)&= 0,\end{aligned}$$
(16)
$$\begin{aligned} b_{1,1}'(t)&=2 (-A_1-A_2) b_{1,1}(t)+4 A_3 b_{3,3}(t)\nonumber \\&\quad +2 B_3(b_{0,3}(t)+b_{3,0}(t)),\nonumber \\ b_{0,3}'(t)&=-4 A_2 b_{0,3}(t)-4 B_2 b_{0,0}(t)\nonumber \\&\quad -2 B_3 b_{1,1}(t)-2B_3 b_{2,2}(t),\nonumber \\ b_{2,2}'(t)&=2 (-A_1-A_2) b_{2,2}(t)+4 A_3 b_{3,3}(t)\nonumber \\&\quad +2 B_3(b_{0,3}(t)+b_{3,0}(t)),\nonumber \\ b_{3,0}'(t)&=-4 A_1 b_{3,0}(t)-4 B_1 b_{0,0}(t)\nonumber \\&\quad -2 B_3 b_{1,1}(t)-2B_3 b_{2,2}(t),\nonumber \\ b_{3,3}'(t)&=4 A_3 b_{1,1}(t)+4 A_3 b_{2,2}(t)-4 (A_1+A_2) b_{3,3}(t)\nonumber \\&\quad -4 (B_1 b_{0,3}(t)+B_2 b_{3,0}(t)). \end{aligned}$$
(17)

This indicates that the two-atom evolution state is still X-type state. According to Eq. (14), the concurrence can be expressed as

$$\begin{aligned} E= & {} \max \left[ 0,\frac{1}{2}| b_{1,1}(t)+b_{2,2}(t)|\right. \nonumber \\&\left. -F_1,\frac{1}{2} | b_{1,1}(t)-b_{2,2}(t)| -F_2\right] , \end{aligned}$$
(18)

where \(F_1=\frac{1}{2} \sqrt{(1{+}b_{0,3}(t){-}b_{3,0}(t)-b_{3,3}(t)) (1-b_{0,3}(t)+b_{3,0}(t)-b_{3,3}(t))}\) and \(F_2=\frac{1}{2} \sqrt{(1-b_{0,3}(t){-}b_{3,0}(t){+}b_{3,3}(t)) (1+b_{0,3}(t){+}b_{3,0}(t)+b_{3,3}(t))}\).

3 Quantum entanglement under cosmic string spacetime

In this section, we discuss the entanglement dynamics of two accelerating atom immersed in a bath of fluctuating massless scalar in the background of the cosmic string spacetime. The topological defect like a cosmic string can be analogous to a disclination in crystals [34, 35], so our model might be simulated as moving atoms in a crystal affected by a external quantum field.

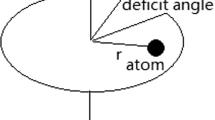
Assuming that the string lies to the z axis, the spacetime line element in the cylindrical coordinates \((t,r,\theta ,z)\) can be written as

$$\begin{aligned} ds^2=dt^2-dr^2-r^2d\theta ^2-dz^2, \end{aligned}$$
(19)

where \(0\le \theta <{2\pi /\nu }\), \(\nu =(1-4G m)^{-1}\) with G and m being the Newton constant and the linear mass density of the string respectively. This metric is derived from the Einstein equations. The value of m is related to the spontaneous symmetry breaking scale. The line element describes a locally flat spacetime with a deficit angle \(8\pi G m\).

The Klein–Gordon equation representing the massless scalar field has the form

$$\begin{aligned} \partial ^2_t-{\frac{1}{r}}\partial _r(r\partial _r) -{\frac{1}{r^2}}\partial ^2_{\theta }-\partial ^2_z\phi (t,\mathbf {x})=0. \end{aligned}$$
(20)

Solving this equation by the method of separation of variables, one can obtain a complete set of normalized field modes:

$$\begin{aligned} u_{n,\kappa ,k_{\perp }}(t,\mathbf {x})={\frac{1}{2\pi }}\sqrt{\frac{\nu }{2\omega }}e^{-i\omega t}e^{i\kappa z}e^{i\nu n\theta }J_{\nu |n|}(k_{\perp }r), \end{aligned}$$
(21)

with \(\kappa \in (-\infty ,\infty )\), \(n\in Z\), \(k_{\perp }\in [0,\infty )\), \(\omega ^2=\kappa ^2+k^2_{\perp }\) and \(J_{\nu |n|}(k_{\perp }r)\) being the first kind Bessel function. According to the field modes, the field operator can be expressed as

$$\begin{aligned} \phi (t,\mathbf {x})=\int d\mu _j[b_j u_j(t,\mathbf {x})+\text {H.c.}], \end{aligned}$$
(22)

with \(j\equiv \{n,\kappa ,k_{\perp }\}\) and

$$\begin{aligned} \int d\mu _j=\sum ^{\infty }_{n=-\infty }\int ^{\infty }_{-\infty }d\kappa \int ^{\infty }_0dk_{\perp }k_{\perp }. \end{aligned}$$
(23)

Then the field correlation function in the cosmic string spacetime can be written as

$$\begin{aligned}&\langle 0|\phi (t,\mathbf {x})\phi (t^{\prime },\mathbf {x}^{\prime })|0 \rangle \nonumber \\&\quad ={\frac{\nu }{8\pi ^2}}\sum ^{\infty }_{n= -\infty }\int ^{\infty }_{-\infty }d\kappa \int ^{\infty }_0dk_{\perp } {\frac{k_{\perp }}{\omega }}e^{-i\omega \varDelta t}e^{i\kappa \varDelta z} \nonumber \\&\qquad \times e^{i\nu n\varDelta \theta }J_{\nu |n|}(k_{\perp }r)J_{\nu |n|}(k_{\perp }r^\prime ), \end{aligned}$$
(24)

where \(\omega =\sqrt{\kappa ^2+k^2_{\perp }}\), \(\varDelta t=t-t^\prime \), \(\varDelta z=z-z^\prime \), and \(\varDelta \theta =\theta -\theta ^\prime \). After some transformations and by use of integral table [18, 36], the correlation function can be obtained

$$\begin{aligned}&\langle 0|\phi (t,\mathbf {x})\phi (t^{\prime },\mathbf {x}^{\prime })|0 \rangle \nonumber \\&\quad =\frac{\nu }{4\pi ^{2}R_{1}R_{2}}\frac{1-\varLambda ^{2\nu }}{1+\varLambda ^{2\nu }-2\varLambda ^{\nu }\cos (\nu \varDelta \theta )}, \end{aligned}$$
(25)

where

$$\begin{aligned}&R_{1}=\sqrt{(r-r^{\prime })^{2}+(z-z^{\prime })^{2}-(t-t^{\prime }-i \varepsilon )^{2}}, \nonumber \\&R_{2}=\sqrt{(r+r^{\prime })^{2}+(z-z^{\prime })^{2}-(t-t^{\prime }-i \varepsilon )^{2}},\nonumber \\&\varLambda =\frac{R_{2}-R_{1}}{R_{2}+R_{1}}. \end{aligned}$$
(26)

The trajectories of two accelerating atoms (vertical to the string) moving along the z-direction can be described as

$$\begin{aligned} t_1(\tau )&=\frac{1}{a}\sinh a\tau ,&z_1(\tau )&=\frac{1}{a}\cosh a\tau , \nonumber \\ r_1(\tau )&=r,&\theta _1(\tau )&=0,\nonumber \\ t_2(\tau )&=\frac{1}{a}\sinh a\tau ,&z_2(\tau )&=\frac{1}{a}\cosh a\tau , \nonumber \\ r_2(\tau )&=r+L,&\theta _2(\tau )&=0. \end{aligned}$$
(27)

If \(\nu \) is a noninteger, the calculation about correlation function is complicated, while for some special cases of integer \(\nu \), the Fourier transform of correlation function can be derived by utilizing contour integration.

Let us firstly assume \(\nu =1\). By Eq. (25), we obtain

$$\begin{aligned} \langle 0|\phi (t,\mathbf {x})\phi (t^{\prime },\mathbf {x}^{\prime })|0 \rangle =\frac{1}{4\pi ^{2}R_{1}^{2}}. \end{aligned}$$
(28)

Substituting the trajectories (27) into Eq. (28), one can obtain the correlation function

$$\begin{aligned} G^{(11)}(\tau -\tau ')&=G^{(22)}(\tau -\tau ')\nonumber \\&=-{1\over 16\pi ^2}{a^2\over \sinh ^2\Big ({a\varDelta \tau \over 2}-i\epsilon \Big )},\nonumber \\ G^{(12)}(\tau -\tau ')&=G^{(21)}(\tau -\tau ')\nonumber \\&=-{1\over 16\pi ^2}{a^2\over \sinh ^2\Big ({a\varDelta \tau \over 2}-i\epsilon \Big )-a^{2}L^{2}/4}. \end{aligned}$$
(29)

Then Fourier transforms of the correlation function are:

$$\begin{aligned}&{{{\mathcal {G}}}}^{(11)}(\lambda )={{{\mathcal {G}}}}^{(22)} (\lambda )=\frac{1}{2\pi }\frac{\lambda }{1-e^{-2\pi \lambda /a}},\nonumber \\&{{{\mathcal {G}}}}^{(12)}(\lambda )={{{\mathcal {G}}}}^{(21)} (\lambda )=\frac{1}{2\pi }\frac{\lambda }{1-e^{-2\pi \lambda /a}}f(\lambda ,L/2). \end{aligned}$$
(30)

where \(f(\lambda ,s)=\frac{\sin [\frac{2\lambda }{a}\sinh ^{-1}(as)]}{2s\sqrt{1+a^2s^2}\lambda }\). In terms of Eq. (11), we get

$$\begin{aligned}&A_1=A_2={\varGamma \coth (\pi \omega /a)\over 4},\quad B_1=B_2={\varGamma \over 4},\nonumber \\&A_3={\varGamma \coth (\pi \omega /a)\over 4} f(\omega ,L/2),\quad B_3= {\varGamma \over 4}f(\omega ,L/2), \end{aligned}$$
(31)

where \(\varGamma = \mu ^2\omega /2\pi \) is the spontaneous emission rate of the atoms. From above equations, we know that the results reduce to the results in Minkowski spacetime [3, 37].

When \(\nu =2\), the correlation function (25) turns to

$$\begin{aligned} G(\tau -\tau ')=\frac{1}{4\pi ^{2}}\left( \frac{1}{R_{1}^{2}}+\frac{1}{R_{2}^{2}}\right) . \end{aligned}$$
(32)

Combining the trajectories (27) with Eq. (32), one can obtain

$$\begin{aligned}&G^{(11)}(\tau -\tau ') =-{1\over 16\pi ^2}{a^2\over \sinh ^2\left( {a\varDelta \tau \over 2}-i\epsilon \right) }\nonumber \\&\quad -{1\over 16\pi ^2}{a^2\over \sinh ^2\left( {a\varDelta \tau \over 2}-i\epsilon \right) -a^{2}r^{2}},\nonumber \\&G^{(22)}(\tau -\tau ')=-{1\over 16\pi ^2}{a^2\over \sinh ^2 \left( {a\varDelta \tau \over 2}-i\epsilon \right) }-\nonumber \\&\quad {1\over 16\pi ^2}{a^2\over \sinh ^2\left( {a\varDelta \tau \over 2}-i\epsilon \right) -a^{2}(r+L)^{2}},\nonumber \\&G^{(12)}(\tau -\tau ') = G^{(21)}(\tau -\tau ')\nonumber \\&=-{1\over 16\pi ^2}{a^2\over \sinh ^2\left( {a\varDelta \tau \over 2}-i\epsilon \right) -a^{2}L^{2}/4}\nonumber \\&\quad -{1\over 16\pi ^2}{a^2\over \sinh ^2\left( {a\varDelta \tau \over 2}-i\epsilon \right) -a^{2}(L+2r)^{2}/4}. \end{aligned}$$
(33)

The corresponding Fourier transforms are

$$\begin{aligned} {{{\mathcal {G}}}}^{(11)}(\lambda )&=\frac{1}{2\pi }\frac{\lambda }{1-e^{-2\pi \lambda /a}}[1+f(\lambda ,r)],\nonumber \\ {{{\mathcal {G}}}}^{(22)}(\lambda )&=\frac{1}{2\pi }\frac{\lambda }{1-e^{-2\pi \lambda /a}}[1+f(\lambda ,r+L)],\nonumber \\ {{{\mathcal {G}}}}^{(12)}(\lambda )&={{{\mathcal {G}}}}^{(21)} (\lambda )\nonumber \\&=\frac{1}{2\pi }\frac{\lambda }{1-e^{-2\pi \lambda /a}}[f(\lambda ,L/2)+f(\lambda ,L/2+r)]. \end{aligned}$$
(34)

By Eq. (11), we obtained

$$\begin{aligned} A_1&={\varGamma \coth (\pi \omega /a)\over 4}[1+f(\omega ,r)],\nonumber \\ B_1&={\varGamma \over 4}[1+f(\omega ,r)],\nonumber \\ A_2&={\varGamma \coth (\pi \omega /a)\over 4}[1+f(\omega ,r+L)],\nonumber \\ B_2&={\varGamma \over 4}[1+f(\omega ,r+L)],\nonumber \\ A_3&={\varGamma \coth (\pi \omega /a)\over 4}[f(\omega ,L/2)+f(\omega ,L/2+r)],\nonumber \\ B_3&={\varGamma \over 4}[f(\omega ,L/2)+f(\omega ,L/2+r)]. \end{aligned}$$
(35)

When an atom is very close to the string (\(r\rightarrow 0\)), we get

$$\begin{aligned} A_1&={\varGamma \coth (\pi \omega /a)\over 2},\quad B_1={\varGamma \over 2},\nonumber \\ A_2&={\varGamma \coth (\pi \omega /a)\over 4}[1+f(\omega ,L)],\nonumber \\ B_2&={\varGamma \over 4}[1+f(\omega ,L)],\nonumber \\ A_3&={\varGamma \coth (\pi \omega /a)\over 2}f(\omega ,L/2),\quad B_3={\varGamma \over 2}f(\omega ,L/2). \end{aligned}$$
(36)
Fig. 1
figure 1

Entanglement as function of \(\varGamma \tau \) with different atomic separations for initial Werner state with p =2/3, \(\nu =2\), \( a/\omega =1/2\) and \( \omega r=1\)

Full size image

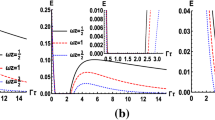
From Fig.  1, it can be seen that entanglement presents a gap of time during which entanglement vanishes. When two-atom distance becomes larger, entanglement decays more faster, the dark period of entanglement becomes longer, and entanglement lifetime becomes shorter; in particular, when two-atom distance is relatively big, entanglement revival no longer occurs. In this sense, we can say small two-atom distance can protect entanglement.

Fig. 2
figure 2

Entanglement as function of \(\varGamma \tau \) with different accelerations for initial Werner state with p =2/3, \(\nu =2\), \( \omega L=1\) and \( \omega r=1\)

Full size image

From Fig. 2, it can be seen that when acceleration becomes greater, entanglement decreases more, entanglement stay longer during dark period, generated entanglement keeps shorter time; in particular, when acceleration is relatively great, entanglement sudden birth no longer appears.

Fig. 3
figure 3

Entanglement as function of \(\varGamma \tau \) with different atom-string distances for initial Werner state with p  = 2/3, \(\nu =2\), \( a/\omega =1/2\) and \( \omega L=1/2\)

Full size image
Fig. 4
figure 4

Entanglement as function of \(\varGamma \tau \) with different atom-string distances for initial Werner state with p = 2/3, \(\nu =3\), \( a/\omega =1/2\) and \( \omega L=1/2\)

Full size image

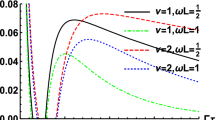
From Fig. 3a, it can be observed that when atom-string distance is relatively small, entanglement firstly declines and then rises with decreasing atom-string distance; specially, when atom is very close to the string, entanglement can last longer time. When acceleration is small and atom-string distance is relatively large, entanglement presents some fluctuations (see Fig. 3b). When two atoms are far away from the string (\(r\rightarrow \infty \)), we exactly obtain the Eq. (31), which indicates the string has no effect on the atoms, and reduces to the case of Minkowski spacetime. Thus the atom-string distance can considerably affects the field vacuum fluctuating and atom-field interplay, and therefore adjusting the atom-string distance could be useful to detect the cosmic string. The different entanglement behaviors can in principle distinguish the cosmic string spacetime and Minkowski spacetime. When \(\nu =3\), the correlation function (25) can be written as

$$\begin{aligned} G(\tau -\tau ')=\frac{1}{4\pi ^{2}}\left( \frac{1}{R_{1}^{2}} +\frac{8}{R_{1}^{2}+3R_{2}^{2}}\right) . \end{aligned}$$
(37)

With similar calculating method and process, we obtained

$$\begin{aligned} A_1&={\varGamma \coth (\pi \omega /a)\over 4}\left[ 1+2f\left( \lambda ,\frac{\sqrt{3}r}{2}\right) \right] ,\nonumber \\ B_1&={\varGamma \over 4}\Big [1+2f\Big (\lambda ,\frac{\sqrt{3}r}{2}\Big )\Big ],\nonumber \\ A_2&={\varGamma \coth (\pi \omega /a)\over 4}\Big [1+2f\Big (\lambda ,\frac{\sqrt{3}r+\sqrt{3}L}{2}\Big )\Big ],\nonumber \\ B_2&={\varGamma \over 4}\Big [1+2f\Big (\lambda ,\frac{\sqrt{3}r+\sqrt{3}L}{2}\Big )\Big ],\nonumber \\ A_3&={\varGamma \coth (\pi \omega /a)\over 4}\Big [f(\omega ,L/2)\nonumber \\&\quad +2f\Big (\lambda ,\sqrt{L^2+3 L r+3 r^2}/2)\Big ],\nonumber \\ B_3&={\varGamma \over 4}\Big [f(\omega ,L/2)+2f(\lambda ,\sqrt{L^2+3 L r+3 r^2}/2)\Big ]. \end{aligned}$$
(38)

When an atom is very close to the string (\(r\rightarrow 0\)), we get

$$\begin{aligned} A_1&={3\varGamma \coth (\pi \omega /a)\over 4},\quad B_1={3\varGamma \over 4},\nonumber \\ A_2&={\varGamma \coth (\pi \omega /a)\over 4}\left[ 1+2f\Big (\lambda ,\frac{\sqrt{3}L}{2}\Big )\right] ,\nonumber \\ B_2&={\varGamma \over 4}\left[ 1+f\Big (\omega ,\frac{\sqrt{3}L}{2}\Big )\right] ,\nonumber \\ A_3&={3\varGamma \coth (\pi \omega /a)\over 4}f(\omega ,L/2),\nonumber \\ B_3&={3\varGamma \over 4}f(\omega ,L/2). \end{aligned}$$
(39)

When atoms are far away from the string (\(r\rightarrow \infty \)), the Eq. (31) is be obtained. Entanglement variations displayed in Fig. 4 are similar with Fig. 3. But entanglement presents more obvious fluctuations.

Finally, we investigate the Unruh thermal effect in the cosmic string spacetime. by letting the rates of change of the coefficients in Eq. (17) to be zero, we can solve the relevant equations and obtain

$$\begin{aligned}&b_{0,3}(\tau )=\frac{(A_1+A_2) (B_1-B_2) B_3^2+2 A_3 B_2 (B_2-B_1) B_3-A_1 [3 (A_1+A_2)+2 A_3] (A_1+A_2-2 A_3) B_2}{(A_1+A_2){}^2 B_3^2-2 A_3 B_3 (A_1 B_1+A_2 B_2)+A_1 A_2 (3 (A_1+A_2)+2 A_3) (A_1+A_2-2 A_3)},\nonumber \\&b_{1,1}(\tau )=-\frac{(A_1+A_2) [B_3 (A_2 B_1+A_1 B_2)-2 A_3 B_1 B_2]}{(A_1+A_2){}^2 B_3^2-2 A_3 B_3 (A_1 B_1+A_2 B_2)+A_1 A_2 [3 (A_1+A_2)+2 A_3] (A_1+A_2-2 A_3)},\nonumber \\&b_{2,2}(\tau )= -\frac{(A_1+A_2) [B_3 (A_2 B_1+A_1 B_2)-2 A_3 B_1 B_2]}{(A_1+A_2){}^2 B_3^2-2 A_3 B_3 (A_1 B_1+A_2 B_2)+A_1 A_2 [3 (A_1+A_2)+2 A_3] (A_1+A_2-2 A_3)},\nonumber \\&b_{3,0}(\tau )=-\frac{(A_1+A_2) (B_1-B_2) B_3^2+2 A_3 B_1 (B_2-B_1) B_3+A_2 [3 (A_1+A_2)+2 A_3] (A_1+A_2-2 A_3) B_1}{(A_1+A_2){}^2 B_3^2-2 A_3 B_3 (A_1 B_1+A_2 B_2)+A_1 A_2 [3 (A_1+A_2)+2 A_3] (A_1+A_2-2 A_3)},\nonumber \\&b_{3,3}(\tau )=\frac{-2 A_3 B_3 (A_2 B_1+A_1 B_2)+(A_1+A_2)[3 (A_1+A_2)-4 A_3] B_1 B_2-(B_1-B_2){}^2 B_3^2}{(A_1+A_2){}^2 B_3^2-2 A_3 B_3 (A_1 B_1+A_2 B_2)+A_1 A_2 [3 (A_1+A_2)+2 A_3] (A_1+A_2-2 A_3)}. \end{aligned}$$
(40)

Substituting Eq. (31), Eq. (35) or Eq. (38) into Eq. (40), we can obtain the equilibrium state

$$\begin{aligned}&\rho _{\infty }=\frac{1}{4}\left( \begin{array}{cccc} \Big (\tanh \frac{\pi \omega }{a}-1\Big )^2 &{} 0 &{} 0 &{} 0 \\ 0 &{} \text {sech}^2\frac{\pi \omega }{a} &{} 0 &{} 0 \\ 0 &{} 0 &{} \text {sech}^2\frac{\pi \omega }{a} &{} 0 \\ 0 &{} 0 &{} 0 &{} \Big (\tanh \frac{\pi \omega }{a}+1\Big )^2 \\ \end{array} \right) \nonumber \\&\quad =\frac{e^{-H_S/T}}{\text {Tr}(e^{-H_S/T})}, \end{aligned}$$
(41)

where \(T=\frac{a}{2\pi }\) denotes the Unruh temperature. The fact that Eq. (41) is a separable state indicates that entanglement can not persist over time. Equation (41) reveals that the two-atom system evolves to a thermal state, and manifests the Unruh thermal effect in the cosmic string spacetime. This demonstrates cosmic string spacetime is locally flat, unlike the de Sitter spacetime shows the Gibbons–Hawking thermal effect of curved spacetime [38].

4 Conclusion

We have investigated the entanglement dynamics for two accelerating atoms immersing in a bath of fluctuating massless scalar field in the cosmic string spacetime. We concretely calculate the entanglement related quantities of different cases for two accelerating atoms vertical to the infinite and straight cosmic string. It is shown that vacuum fluctuation, two-atom separation, acceleration, atom-string distance and deficit angle parameter affect the entanglement behaviors. For deficit angle parameter \(\nu =1\), the cosmic string spacetime reduces to the Minkowski spacetime. Small two-atom separation could make entanglement gain better protection. Great acceleration can quicken entanglement degradation. When atom is near to the string, entanglement behaviors become complicated, which indicates the string can make profoundly modifications to the atom-field interaction and vacuum fluctuation. In general, when atom is relatively close to the string, entanglement decays more slowly and has longer lifetime. The two-atom distance, acceleration, deficit angle parameter and atom-string distance give us more freedom to adjust the entanglement behaviors, which in principle is helpful to detect the different cosmic string spacetimes, and distinguish the cosmic string universe from the Minkowski universe.