1 Introduction

The observations such as Type Ia Supernovae (SNe) [1,2,3], Baryon Acoustic Oscillations (BAO) [4], Large Scale Structures (LSS) [5] and Cosmic Microwave Background (CMB) [6] provide strong evidence that the Universe at present is undergoing an accelerated expansion rather than deceleration (as predicted by the standard cosmology). Since the discovery of the accelerating Universe, people are trying to explain this observational fact in two different ways - either by modifying the Einstein gravity itself or by introducing some unknown kind of matter in the framework of Einstein gravity. Most models consider accelerated expansion as due to a component of the Universe that behaves opposite to gravity, the so called dark energy(DE). The origin and nature of the DE is still unknown, though some of its properties are widely accepted, namely the fact that it has a negative pressure. Cosmological constant is the common choice for this unknown matter but it suffers the serious fine-tuning and cosmic coincidence problems. Recently, many theoretical models have been proposed to describe the Universe with dark energy. A negative pressure can be seen as a possible driving mechanism for this acceleration. One of such mechanism is the adiabatic matter creation which has negative pressure produced by the particle production effects.

Prigogine et al. [7, 8] proposed an interesting type of cosmological history including large-scale entropy production by considering the cosmological thermodynamics of open systems. They used the generalized form of the first law of thermodynamics to describe the flow of energy from the gravitational field to the matter field, resulting in the creation of particles. The authors argued that the creation of matter can occur only as an irreversible process at the expense of the gravitational field. This formalism gives a balance equation for the number of created particles along with Einstein field equations. The combination of this equation with the second law of thermodynamics yields an additional negative pressure which depends on the rate of matter creation. This work actually suggested for the first time to incorporate the particle creation process in the context of cosmology in a self-consistent way. Calvao et al. [9] proposed a generalization of this result to include the variation of specific entropy through a covariant formulation.

A model with adiabatic matter creation was proposed in order to interpret the cosmological entropy and to solve the Big-Bang singularity problem. However, after the discovery of the accelerating expansion of the Universe, this model was reconsidered to explain the expansion of the Universe and got some unexpected results. It has been pointed out that the matter creation can play the role of a dark energy component and lead to drive the accelerating expansion of the Universe.

In this context, Many authors [10,11,12,13,14,15,16,17] have discussed Friedmann-Robertson-Walker line element with matter creation cosmology and analyzed the results through the observations. It has been shown that the matter creation models are consistent with the observations. Zimdahl et al. [18] tested the matter creation models with SNe data and got the result of accelerating Universe. Yuan et al. [19] studied the models with adiabatic matter creation and showed that the model is consistent with SNe data. Many phenomenological models have been proposed in the literature [20,21,22,23,24].

We are mainly interested in the paper of Prigogine and collaborators [7], in which the authors have applied the thermodynamics of open systems to cosmology, allowing both particle and entropy productions. Recently, it has been found that the matter creation cosmology successfully explains the current accelerated expansion [25]. Therefore, this field is very appealing as many important observations are carried out during the past many years with matter creation.

In this paper, we present a matter-dominated cosmological model with matter creation within the framework of Friedmann-Robertson-Walker line element. We propose a generalized form of matter creation rate and investigate the evolution equations by independent/combined observational data of SNe, Observational Hubble data (OHD) and BAO. We observe that the best-fit values of the model parameters give a smooth transition from decelerating phase to the accelerating phase. We study two independent diagnostic tests, namely, the statefinder parameter and the \(\textit{Om}\) diagnostic to discriminate our model from the \(\varLambda \)CDM. We apply AIC and BIC to discriminate the model. We also perform a thermodynamic analysis based on the generalized second law (GSL) of thermodynamics and explore the restrictions on the free parameters of the cosmological model to satisfy the GSL.

The paper is organized as follows. In Sect. 2, we present a brief review of matter creation cosmology and solution of the field equations. In Sect. 3, some observational data like SNe, OHD and BAO are given to find the best-fit values of model parameters. In Sect. 4, we present the result and discussion of the model. In Sect. 5, we discuss the model selection criteria to discriminate the model. We discuss the thermodynamic of the model based on generalized second law of thermodynamics in Sect. 6. Finally, we summarize our findings in Sect. 7. It is to be noted that throughout the paper, we use particle creation and matter creation synonymously.

2 Model with matter creation and solution

Let us start with the homogeneous and isotropic flat Friedmann-Robertson-Walker (FRW) line element

$$\begin{aligned} ds^2 = -dt^2 + a^2(t) \left[ dr^2+r^2(d\theta ^2+sin^2\theta d\phi ^2)\right] , \end{aligned}$$
(1)

where a(t) is the scale factor of the model. Throughout we use units such that the speed of light, \(c=1\) and \(8\pi G=1\). The Einstein field equations are given by

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}R\;g_{\mu \nu }= T_{\mu \nu }. \end{aligned}$$
(2)

The energy momentum tensor \(T_{\mu \nu }\) describes the matter content of the Universe. It is often appropriate to adopt the perfect fluid form. However, we consider the energy-momentum tensor empowered with the mechanism of matter creation of the form

$$\begin{aligned} T_{\mu \nu }=\left( \rho +P\right) u_{\mu }u_{\nu }+P\;g_{\mu \nu }, \end{aligned}$$
(3)

satisfying the covariant conservation equation \(T^{\mu \nu }\;_{;\nu }=0\). In (3), \(u_{\mu }\) is the fluid four-velocity, \(\rho \) is the energy density and P is the dynamics pressure which is given by

$$\begin{aligned} P=p+p_c, \end{aligned}$$
(4)

where p is the equilibrium pressure and \(p_c\) is the pressure due to the matter creation. The particle flux vector has the form

$$\begin{aligned} N^{\mu }=nu^{\mu }, \end{aligned}$$
(5)

where N is the total particle number in a comoving volume V, \(n=N/V\) is the particle density and \(u^{\mu }\) is the usual four velocity vector of the created particles. In the gravitationally induced particle creation mechanism, (5) satisfies the balance equation [8]

$$\begin{aligned} N^{\mu }\;_{;\mu }=\varGamma , \end{aligned}$$
(6)

where \(\varGamma \) is the rate of matter creation from the gravitational field. In principle, \(\varGamma >0\) represents the matter creation, \(\varGamma <0\) is for matter annihilation, and \(\varGamma =0\) is the case when there is no matter creation. In general, the exact form of \(\varGamma \) is unknown, but it should be determined in the context of quantum processes in curved space time.

In this background, the field equations associated with matter creation phenomena for line element (1) are given by [9, 10]

$$\begin{aligned} 3H^2= & {} \rho , \end{aligned}$$
(7)
$$\begin{aligned} 2{\dot{H}}= & {} -\left( \rho +p+p_c\right) , \end{aligned}$$
(8)

where \(H={\dot{a}}/{a}\) is the Hubble parameter, and \(\rho \) and p are energy density and pressure, respectively, of matter existing in the universe in the form of cold dark matter during matter dominated era. An overdot represents the derivative with respect to cosmic time t. The energy conservation law is given by

$$\begin{aligned} {\dot{\rho }}+3(\rho +p+p_c)H=0. \end{aligned}$$
(9)

As the particle number is not conserved (i.e., \(N^{\mu }\;_{;\mu }\ne 0\)), the conservation equation (6) takes the form

$$\begin{aligned} \frac{{\dot{N}}}{N}=\frac{{\dot{n}}}{n}+3H=\varGamma . \end{aligned}$$
(10)

It is to be noted that the creation pressure \(p_c\) must be defined in terms of the creation rate and other physical quantities. In the case of adiabatic particle production, the particles and entropy are generated but the entropy per particle does not vary. Under such ‘adiabatic condition’, the creation pressure can be written as [21]

$$\begin{aligned} p_c=-\frac{\varGamma }{3H}(\rho +p). \end{aligned}$$
(11)

Now, we can describe the dynamics of the Universe only if the matter creation rate is known. The nature of \(\varGamma \) is unknown as the associated quantum field theory (QFT) is yet to be developed. In general, there is no bound to choose some particular choices for \(\varGamma \). Therefore, we can assume some phenomenological but general choices for \(\varGamma \). In the literature, various forms of \(\varGamma \), e.g., \(\varGamma =constant\) [26], \(\varGamma \propto H\) [27], \(\varGamma \propto H^2\) [28, 29], and a linear combination [30], have been presented to explain the early and present day acceleration of the Universe. However, the linear and quadratic forms of \(\varGamma (t)\) are not compatible with the current cosmology, i.e., these models do not show transition redshift. Therefore, a natural extension is to consider the linear combinations of H, \(H^2....\) and the derivative of Hubble parameter. Finally, one can use the observational data to test the viability of such models.

Thus, being motivated, in this work we propose a class of \(\varGamma (t)\) cosmologies in a spatially flat FRW Universe where \(\varGamma (t)\) is assumed to be the function of Hubble rate and its cosmic derivative. We cover a series of \(\varGamma (t)\) (equivalently, \(\varGamma (H_0, H, {\dot{H}})\)) model in order to see their dynamical evolutions and viabilities. We propose the following general form of \(\varGamma \):

$$\begin{aligned} \varGamma =3\alpha H_0+3\beta H+3\gamma \; \frac{\ddot{a}}{{\dot{a}}}, \end{aligned}$$
(12)

which is a linear combination of three terms: the first term is a constant, the second term is proportional to the Hubble parameter, which characterizes the dependence of the matter creation on expansion rate, and the third term is proportional to \(\ddot{a}/{\dot{a}}\), characterizing the effect of acceleration of the expansion. Here, \(\alpha \), \(\beta \) and \(\gamma \) are dimensionless free parameters lying in the interval [0, 1] to be determined by observations, \(H_0\) is the present value of the Hubble parameter and the factor 3 has been maintained for mathematical convenience.

The motivation of considering this form of \(\varGamma \) comes from the matter creation thermodynamics. We know that the transport phenomena is related to velocity, which is related to the Hubble parameter, and the acceleration. Since we don’t know the exact form of \(\varGamma \), so a linear combination of three terms of parametrization of \(\varGamma \) is more physical. The existence of a transition redshift at late time also determines the form of matter creation rate. We may also think the above form from the evolution equation (8).

We are interested in processes that occurred after radiation-dominated phase. Therefore, we neglect radiation and baryons, and consider only the presence (and creation) of pressureless \((p=0)\) dark matter particles. In this case, Eq. (11) reduces to \(p_c=-\rho \;\varGamma / 3H\) for which Eq. (9) reduces to

$$\begin{aligned} \frac{{\dot{\rho }}}{\rho }+3\left( 1-\frac{\varGamma }{3H}\right) H=0, \end{aligned}$$
(13)

Combining (7) and (13), and using (12), we obtain the following dimensionless equation

$$\begin{aligned} \frac{{\dot{h}}}{h}+\frac{3(1-\beta -\gamma )}{(2-3\gamma )}H_0\;h=\frac{3\alpha }{(2-3\gamma )}H_0, \end{aligned}$$
(14)

where \(h=H/H_0\) is the dimensionless Hubble parameter. Using \(\frac{d}{dt}=\frac{{\dot{a}}}{a}\frac{d}{d\;lna}\), the above equation can be written as

$$\begin{aligned} {h^{\prime }}+\frac{3(1-\beta -\gamma )}{(2-3\gamma )}\;h=\frac{3\alpha }{(2-3\gamma )}, \end{aligned}$$
(15)

where a prime denotes the derivative with respect to conformal time \(ln\;a\). Using \(h(a_0)=1\), (15) gives the solution as

$$\begin{aligned} h(a)= & {} \frac{\alpha }{(1-\beta -\gamma )}\nonumber \\&+\left( 1-\frac{\alpha }{(1-\beta -\gamma )}\right) \left( \frac{a}{a_0}\right) ^{-\frac{3(1-\beta -\gamma )}{(2-3\gamma )}}. \end{aligned}$$
(16)

Equation (16) shows that when \(\alpha \), \(\beta \) and \(\gamma \) are all zero, the Hubble parameter, \(H=H_0(a/a_0)^{-3/2}\) which corresponds to the ordinary matter dominated universe. On integration of (16), we obtain the solution of the scale factor a(t) (or the redshift, z) as a function of time, when \((\beta +\gamma )\ne 1\)

$$\begin{aligned} a(t)= & {} \frac{1}{(1+z)}\nonumber \\= & {} \left[ \frac{(1-\beta -\gamma )e^{\frac{3\alpha H_0 }{(2-3\gamma )}(t-t_0)}-1+(\alpha +\beta +\gamma )}{\alpha }\right] ^{\frac{(2-3\gamma )}{3(1-\beta -\gamma )}}.\nonumber \\ \end{aligned}$$
(17)

We have normalized the scale factor so that its present day value is one, \(a(t_0) = 1\). We can study three different cases: \(0<\alpha +\beta +\gamma <1\), \(\alpha +\beta +\gamma =1\) and \(\alpha +\beta +\gamma >1\). In the case \(0<\alpha +\beta +\gamma <1\), we observe that in the early time as \(t\rightarrow 0\), the scale factor \(a(t)\rightarrow \left[ 1+\frac{3(1-\beta -\gamma )H_0}{(2-3\gamma )} (t-t_0)\right] ^{\frac{(2-3\gamma )}{3(1-\beta -\gamma )}}\), which corresponds to an early decelerated expansion and in the late time as \(t\rightarrow \infty \), the scale factor \(a(t)\rightarrow e^{\frac{3\alpha H_0}{(2-3\gamma )}(t-t_0)}\), corresponding to de Sitter like Universe. The model predicts a Big-Bang in the past at cosmic time: \(t_b=t_0+\frac{(2-3\gamma )}{3\alpha H_0}\;ln\left( \frac{1-(\alpha +\beta +\gamma )}{1-\beta -\gamma }\right) \).

The transition time can be obtained by equating to zero the second derivative of scale factor given in (17) with respect to time which is given by

$$\begin{aligned} t_{tr}=t_0+\frac{(2-3\gamma )H^{-1}_{0}}{3\alpha }\;ln\left( \frac{(3-3(\alpha +\beta +\gamma ))}{(2-3\gamma )}\right) . \end{aligned}$$
(18)

The Hubble parameter in terms of redshift z, where \(1+z= a^{-1}\), reads

$$\begin{aligned} H(z)= & {} H_0\left[ \frac{\alpha }{(1-\beta -\gamma )}+\left( 1-\frac{\alpha }{(1-\beta -\gamma )}\right) \nonumber \right. \\&\times \,\left. \left( 1+z\right) ^{\frac{3(1-\beta -\gamma )}{(2-3\gamma )}}\right] . \end{aligned}$$
(19)

When \(\gamma =0\), i.e., \(\varGamma =3\alpha H_0+3\beta H\) (See, Ref. [31]), (17) and (19) reduce to (14) and (13) of [31]. Further, In the limit \(\alpha \rightarrow 0\), the above equation reduces to (16) in [11].

To obtain the transition scale factor \(a_{tr}\) where the transition from decelerated phase to accelerated phase takes place, we take the derivative of (19) with respect to a,

$$\begin{aligned} \frac{d{{\dot{a}}}}{da}= & {} \left[ \frac{\alpha }{1-\beta -\gamma }\nonumber \right. \\&\left. +\frac{(3\beta -1)(1-\alpha -\beta -\gamma )}{(2-3\gamma ) (1-\beta -\gamma )}\;a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}\right] . \end{aligned}$$
(20)

Equating (20) to zero, we obtain the transition scale factor, \(a_{tr}\) as

$$\begin{aligned} a_{tr}=\left[ \frac{(1-3\beta )(1-\alpha -\beta -\gamma )}{\alpha (2-3\gamma )}\right] ^{\frac{2-3\gamma }{3(1-\beta -\gamma )}}. \end{aligned}$$
(21)

It is clear that for \(\alpha +\beta +\gamma =1\) or \(\beta =1/3\), the transition from decelerated phase to accelerated phase occurs at a time corresponds to \(a_{tr}\rightarrow 0\) closer to Big-Bang. In this case, \(a=\exp (H_0(t-t_0))\), corresponds to de Sitter Universe. In this case the model predicts an accelerated expansion from the beginning. For \((\alpha +\beta +\gamma )<1\), the transition occurs in late-time whereas for \((\alpha +\beta +\gamma )>1\), there is no transition and in this case the model always accelerates from very early time.

An important cosmological quantity is the deceleration parameter q, which is an indicator of the accelerating/decelerating nature of the evolution of the Universe. It is straightforward to show from (17) that the deceleration parameter, defined as \(q=-a\ddot{a}/{\dot{a}}^2\), takes the following form in terms of cosmic time t:

$$\begin{aligned} q=-1+\frac{3(1-\alpha -\beta -\gamma )}{2-3\gamma }e^{-\frac{3\alpha H_0}{2-3\gamma }(t-t_0)}. \end{aligned}$$
(22)

The redshift dependence of the deceleration parameter is obtained as

$$\begin{aligned} q=-1+\frac{3(1-\alpha -\beta -\gamma )}{(2-3\gamma )\left[ 1+\frac{\alpha }{1-\beta -\gamma }\left( (1+z)^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}-1\right) \right] }.\nonumber \\ \end{aligned}$$
(23)

It can be observed that \(q(z)\rightarrow -1\) as \(z\rightarrow -1\), i.e., q(z) approaches to \(-1\) in future and for \(z=0\), we get \(q_0=\frac{1-3(\alpha +\beta )}{2-3\gamma }\). This shows that for \(\alpha +\beta =1/3\), the deceleration parameter \(q_0=0\). This implies that the transition into accelerating phase would occur at the present time. In the absence of matter creation, i.e., for \(\alpha =\beta =\gamma =0\), we get \(q=0.5\), a value of q in matter-dominated model. Putting \(q=0\) in (23), the transition redshift is given by

$$\begin{aligned} z_{tr}=\left[ \frac{\alpha (2-3\gamma )}{(1-3\beta )(1-\alpha -\beta -\gamma )}\right] ^{\frac{2-3\gamma }{3(1-\beta -\gamma )}}-1. \end{aligned}$$
(24)

It is to be noted that for \(\alpha =0\), we get \(z_{tr}=-1\), i.e., the transition would be in future which gives the contradiction with SNe data. From (7) and (16), we obtain the mass density parameter \(\varOmega _m=\rho /\rho _{crit}\) and \(\rho _{crit}=3H^{2}_{0}\) as,

$$\begin{aligned} \varOmega _m(a)= & {} \left[ \left( 1-\frac{\alpha }{1-\beta -\gamma }\right) \left( \frac{a}{a_0}\right) ^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}+\frac{\alpha }{1-\beta -\gamma }\right] ^{2}.\nonumber \\ \end{aligned}$$
(25)

We observe that for \(\alpha =\beta =\gamma =0\), the mass density parameter reduces to \(\varOmega _m\sim a^{-3}\), which corresponds to the matter dominated phase with null matter creation. It is also noted that as \(a\rightarrow 0\), the mass density diverges.

In what follows we constrain the free parameters of the model coming from the background tests.

Table 1 The best-fit results of model parameters and free normalization parameter M obtained from the analysis with different combinations of the data sets
Full size table

3 Observational tests: SNe, OHD and BAO data

In this section we briefly present some details of the statistical method and observational sample that we adopt in order to constrain the model. We normalized H(z) using the latest Planck data \(H_0=67.8\pm 0.9\) km s\(^{-1}\) Mpc\(^{-1}\) [32].

First of all, we consider the distant Type Ia Supernova (SNe) compilation on the matter creation matter-dominated model. We use the cJLA data set of 31 check points (30 bins) covering the redshift range \(z=[0.01, 1.3]\) [33]. The best-fit to the set of parameters is found by using a \(\chi ^2\) statistics, i.e.,

$$\begin{aligned} \chi ^2_{SNe}= r^tC^{-1}_b r \end{aligned}$$
(26)

where

$$\begin{aligned} r=\mu _b-M-5\;log_{10}d_L \end{aligned}$$
(27)

in which \(\mu _b\) is the observational distance modulus, M is a free normalization parameter and \(C_b\) is the covariance matrix of \(\mu _b\), see Table F.2 [33]. Also, the dimensionless luminosity distance is defined as

$$\begin{aligned} d_L=\frac{c(1+z)}{H_0} \int _0^z \frac{dz'}{H(z',\theta )} \end{aligned}$$
(28)

where \(\theta \) represents the set of model parameters, \(\theta =(\alpha , \beta , \gamma )\).

Additionally, we also use the observational Hubble parameter dataset (OHD) of 43 measurement points collected in [34] in the redshift range \(0< z < 2.5\). The \(\chi ^2\) for Observational Hubble Data is

$$\begin{aligned} \chi ^2_{OHD}=\sum _{i=1}^n \frac{[H(z_i)-H_{obs}(z_i,\theta )]^2}{\sigma _i^2}, \end{aligned}$$
(29)

where \(H(z_i)\) and \(H_{obs}(z_i)\) are the theoretical and observed values respectively and \(\sigma ^{2}_{i}\) the standard deviation of each \(H_{obs}(z_i)\).

Next, we use the sample of Baryon Acoustic Oscillations (BAO) distances measurements from SDSS(R) [35], the 6dF Galaxy survey [36], \( BOSS\, CMASS \) [37] and three parallel measurements from WiggleZ survey [38].

The angular diameter, \(d_A(z,\theta )\) is given by

$$\begin{aligned} d_A(z_*,\theta )=c\int _{0}^{z_*}\frac{dz'}{H(z',\theta )} \end{aligned}$$
(30)

where \( z_* \) denotes the photons decoupling redshift and according to the Planck 2015 results [32] its value is \(z_*=1090\). Further, the dilation scale, \( D_v(z,\theta ) \) is given by \(D_v(z,\theta )= \big (\frac{d^2_A(z,\theta )c z}{H(z,\theta )}\big )^{\frac{1}{3}}\).

The corresponding \(\chi ^2\) function is given by [40]

$$\begin{aligned} \chi _{BAO}^{2}= A^{T}C^{-1}A \end{aligned}$$
(31)

where A is a matrix given by

$$\begin{aligned} A= \left[ {\begin{array}{cc} \frac{d_A(z_*,\theta )}{D_v(0.106,\theta )}-30.84 \\ \frac{d_A(z_*,\theta )}{D_v(0.35,\theta )}-10.33 \\ \frac{d_A(z_*,\theta )}{D_v(0.57,\theta )}-6.72 \\ \frac{d_A(z_*,\theta )}{D_v(0.44,\theta )}-8.41 \\ \frac{d_A(z_*,\theta )}{D_v(0.6,\theta )}-6.66 \\ \frac{d_A(z_*,\theta )}{D_v(0.73,\theta )}-5.43 \\ \end{array} } \right] \end{aligned}$$

and \( C^{-1} \) is the inverse of covariance matrix [40]. Here, we have adopted the correlation coefficients given in [41].

We can combine the above probes by using a joint likelihood analysis \(\chi ^{2}_{total}=\chi ^{2}_{SNe}+\chi ^{2}_{OHD}+\chi ^{2}_{BAO}\).

4 Results and discussion

Using the observational data of SNe, OHD, BAO, we test the cosmological model with adiabatic matter creation, assuming a spatially flat Universe. We perform a global fitting to determine the model parameters using the MCMC method. We adopt a Python implementation of the ensemble sampler for MCMC, the ‘emcee’, introduced by Foreman-Mackey et al. [42]. The best fitting results of parameters are listed in Table 1. In our statistical analysis, the model parameters can be determined through the \(\chi ^2\) minimization method. We minimize the function \(\chi ^2\) of individual from (26), (29), (31) and jointly.

Fig. 1
figure 1

The contour map of matter creation model using data from SNe with marginalized probability for the parameters. The associated \(1\sigma (68.3{\%})\) and \(2\sigma (95.4{\%})\) confidence contours are shown. In Fig. the symbols e0, e1 and e2 denote the model parameters \(\alpha \), \(\beta \) and \(\gamma \), respectively

Full size image
Fig. 2
figure 2

The contour map of matter creation model based on joint analysis of \(SNe + OHD\) showing contours of \(1\sigma (68.3{\%})\) and \(2\sigma (95.4{\%})\) regions with marginalized probability for the parameters. In Fig. the symbols e0, e1 and e2 denote the model parameters \(\alpha \), \(\beta \) and \(\gamma \), respectively

Full size image

In statistical analysis, we find the best-fit values of model parameters at \(1\sigma (68.3{\%})\) and \(2\sigma (95.4{\%})\) of confidence level, respectively, satisfying the constraints \(0<\alpha <1\), \(0<\beta <1\), \(0<\gamma <1\) and \(0< (\alpha +\beta +\gamma )<1\). We can test the reliability by comparing the result with spatially flat \(\varLambda \)CDM model. We observe that the model provides a very good fit to these data. Figures 1, 2, 3 and 4 show confidence contours and the marginalized likelihood function of model at \(1\sigma (68.3{\%})\) (inner contour) and \(2\sigma (95.4{\%})\) (outer contour) using observational data of SNe, \(SNe+OHD\), \(SNe+BAO\) and \(SNe+OHD+BAO\), respectively.

It can be observed from Table 1 that the result of the free parameters obtained from SNe data are a little different from \(SNe+OHD\), \(SNe+BAO\) and \(SNe+OHD+BAO\). The error bars of free parameters are relatively large in the case of SNe data.

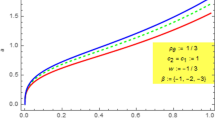
Figure 5 shows the evolution of the scale factor for best-fit values of model parameters. The trajectory of the best-fit values show that the Universe starts its expansion with accelerated rate at very early times. The dots denote the transition point where the transition from decelerated phase to accelerated phase occurs. Using the best-fit values, the transition scale factor, \(a_{tr}\) and the corresponding redshift transition values, \(z_{tr}\) are listed in Table 2. It is observed that the value of \(z_{tr}=2.8619\) obtained from SNe and \(z_{tr}=1.0147\) from \(SNe+BAO\) for the model are substantially higher than the values of \(z_{tr}\) from \(SNe+OHD\), \(SNe+OHD+BAO\) and \(\varLambda \)CDM model.

Fig. 3
figure 3

The contour map of matter creation model based on joint analysis of \(SNe + BAO\) showing contours of \(1\sigma (68.3{\%})\) and \(2\sigma (95.4{\%})\) regions with marginalized probability for the parameters. In Fig. the symbols e0, e1 and e2 denote the model parameters \(\alpha \), \(\beta \) and \(\gamma \), respectively

Full size image
Fig. 4
figure 4

The contour map of matter creation model based on joint analysis of \(SNe + OHD + BAO\), showing contours of \(1\sigma (68.3{\%})\) and \(2\sigma (95.4{\%})\) regions with marginalized probability for the parameters. In Fig. the symbols e0, e1 and e2 denote the model parameters \(\alpha \), \(\beta \) and \(\gamma \), respectively

Full size image

-1The evolution of the deceleration parameter, q with redshift for best-fit values is shown in Fig. 6. The deceleration parameter is a monotonically increasing function of z. It is observed that there is a sign change in each trajectory of q(z) from positive to negative showing that the universe transits from decelerated phase to accelerated phase (positive values of q indicate decelerating expansion while negative values indicate an accelerating evolution). We find that the model transits at around \(z_{tr}=0.8386\) and \(z_{tr}=0.8633\) through joint analysis of \(SNe+OHD\) and \(SNe+OHD+BAO\), respectively. These results are in good agreement with the concordance of \(\varLambda \) cosmology [43]. The present-day value of \(q_0\) and the transition redshift \(z_{tr}\) are listed in Table 2. The values of \(q_0\) lie in range \(-1\le q_0<0\) through each observational data set.

The effective equation of state parameter (EoS), \(\omega _{eff}\) can be obtained using the standard relation [44]

$$\begin{aligned} \omega _{eff}=-1-\frac{1}{3}\frac{2a}{h}\frac{dh}{da}, \end{aligned}$$
(32)

where \(h=H/H_0\) is the weighted Hubble parameter. Using (16) into (32), we get

$$\begin{aligned} \omega _{eff}= & {} -1\nonumber \\&+\frac{2(1-\alpha -\beta -\gamma )}{(2-3\gamma )\left[ 1+\frac{\alpha }{1-\beta -\gamma }\left( (1+z)^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}-1\right) \right] }.\nonumber \\ \end{aligned}$$
(33)

As \(z\rightarrow -1\), \((a\rightarrow \infty )\), we get \(\omega _{eff}\rightarrow -1\), which can also be observed from Fig. 7. This can also be obtained if we take \(\alpha +\beta +\gamma =1\). It means that the model corresponds to \(\varLambda \)CDM in future time. The EoS parameter does not cross the phantom divide line \(\omega \le -1\) which shows that the matter creation model is free from big-rip singularity.

The present value (\(h=1\)) of \(\omega _{eff}\) is found to be

$$\begin{aligned} \omega _{eff}(z=0)=-1+\frac{2(1-\alpha -\beta -\gamma )}{(2-3\gamma )}. \end{aligned}$$
(34)

The present value of \(\omega _{eff}\) are listed in Table 2 using different observational data set. These values are comparatively higher than that predicted by the joint analysis of \(WMAP+BAO+H_0+SNe\) data which is around \(-0.93\) [45].

Let us calculate the age of the universe using best-fit values of parameters. The age of the universe in terms of redshift is given by \(t(z)=T(z)/H_0\), where

$$\begin{aligned} T(z)=\int _{z}^{\infty }\frac{dz'}{(1+z') (H(z')/H_0)}. \end{aligned}$$
(35)

For \(\varLambda CDM\) model, the age parameter is [46]

$$\begin{aligned} T(z)=\int _{z}^{\infty }\frac{dz'}{(1+z') [\varOmega _{m0} (1+z')^3 + (1-\varOmega _{m0} )]^{1/2}} \end{aligned}$$
(36)

Using (19) into (35), the trajectory of the age of the universe with redshift for the best estimates of model parameters is shown in Fig. 8. The current age of the universe is \(t_0\simeq 13.9\) Gyr while the transition point is located at \(a_{tr}\simeq 0.58\) (hence at redshift \(z_{tr}\simeq 0.72\). The ages of the universe corresponding to \(SNe+OHD\) and \(SNe+OHD+BAO\) are found to be 13.9 Gyr. So, the age predicted by the present model is agreeing with the age deduced from \(\varLambda \)CDM model.

We compare our model with the \(\varLambda \)CDM model with the error bar plots of Hubble dataset in the range \(z\in (0,2)\) as shown in Fig. 9. Although at the low redshifts, the cosmological evolution is practically independent on the best-fit values, but at higher redshifts there is a significant effect of the parameter values on the cosmic expansion as can be observed from Fig. 6. The cosmic expansion of \(SNe+OHD\) and \(SNe+OHD+BAO\) differ appreciably in case of SNe and \(SNe+BAO\). It is possible to get good fit using joint statistical analysis of \(SNe+OHD\) and \(SNe+OHD+BAO\). The Hubble function is a monotonically increasing function of the redshift (monotonically decreasing function of time) for all best-fit values of parameters.

Now, we present our analysis on comparing the present model with other standard models of DE. Sahni et al. [47] proposed a geometrical diagnostic tool, known as statefinder parameters \(\{r, s\}\) which allow us to compare the goodness of several DE models with the \(\varLambda CDM\) model. The \(\{r, s\}\) is defined as

$$\begin{aligned} r=\frac{\dot{\ddot{a}}}{aH^3} \quad \text {and} \quad s=\frac{r-1}{3{\left( q-\frac{1}{2}\right) }}, \end{aligned}$$
(37)

where a, H and q have their usual meanings. From (37), we can see parameters (r, s) are just associated with the scale factor a and its higher derivatives. The \(\varLambda CDM\) model corresponds to the fixed point \((r, s) = (1, 0)\). For our model, \(\{r, s\}\) are given by

$$\begin{aligned} r= & {} 1+\frac{9(1-\alpha -\beta -\gamma )^2}{(2-3\gamma )^2\; e^{\frac{6\alpha H_0(t-t_0)}{2-3\gamma }}} \nonumber \\&+ \frac{9(1-\alpha -\beta -\gamma )(-1-\beta +2\gamma )}{(2-3\gamma )^2\; e^{\frac{3\alpha H_0(t-t_0)}{2-3\gamma }}}, \end{aligned}$$
(38)
$$\begin{aligned} s= & {} \frac{2(1-\alpha -\beta -\gamma )\left[ (1+\beta -2\gamma )-(1-\alpha -\beta -\gamma )\; e^{\frac{-3\alpha H_0(t-t_0)}{2-3\gamma }} \right] }{(2-3\gamma ) \left[ (2-3\gamma )\; e^{\frac{3\alpha H_0(t-t_0)}{2-3\gamma }}-2 (1-\alpha -\beta -\gamma ) \right] }.\nonumber \\ \end{aligned}$$
(39)

From the above equations, we observe that as \((t-t_0) \rightarrow \infty \), \(\{r, s\}\rightarrow \{1, 0\}\) which coincide with the \(\varLambda \)CDM model. This can also be achieved by assuming \(\alpha +\beta +\gamma =1\) which gives the de Sitter behaviour. The \(s-r\) plane trajectory of the model for best estimated values of parameters obtained by observational data set are shown in Fig. 10. The direction of trajectories is shown by the arrows. The trajectory obtained through SNe lies in the region \(r<1\), \(s>0\), which is the general behavior of any quintessence model. The other trajectories from \(SNe+OHD\), \(SNe+BAO\) and \(SNe+OHD+BAO\) start from the Chaplygin gas region \((r>1, s<0)\) at early time and in intermediate time pass through quintessence and then ultimately approach to \(\varLambda \)CDM in late time.

The \(\{r,q\}\) trajectory of the model is shown in Fig. 11. The SCDM model and steady state (SS) model correspond to fixed points \(\{r,q\}=\{1, 0.5\}\) and \(\{r,q\}=\{1, -1\}\), respectively. The horizontal line at \(r=1\) corresponds to the time evolution of \(\varLambda \)CDM model. Our model approaches to the standard model like \(\varLambda \)CDM and quintessence model (Q-model) [48] in late time.

The Om is another diagnostic approach to distinguish dark energy. It is defined as [48]

$$\begin{aligned} \textit{Om(z)} = \frac{h^2(z)-1}{(1+z)^3-1}, \end{aligned}$$
(40)

For \(\varLambda CDM\) model, the value of \(\textit{Om(z)}\) is a constant independent of the redshift. Therefore, if \(\textit{Om(z)}\) is variable, it possibly leads to an alternative dark energy or modified gravity model. The \(\textit{Om(z)}\) is sensitive to EoS of DE, namely, a positive slope of \(\textit{Om(z)}\) suggests a phase of phantom \((w < -1)\) while a negative slope of \(\textit{Om(z)}\) represents quintessence \((w > -1)\).

Using (19) into (40), we can write the expression of \(\textit{Om(z)}\). Figure 12 exhibits the evolution of different trajectories of the function \(\textit{Om(z)}\) with respect to the redshift z, corresponding to different best-fit values of model parameters. The negative slope of each trajectory shows that the model behaves like quintessence.

5 Model selection

Reduced chi-squared is a very popular method for model assessment, model comparison, convergence diagnostic, and error estimation in astronomy. If \(\nu \) is the number of degrees of freedom, the reduced \(\chi ^2\) is then defined as

$$\begin{aligned} \chi ^{2}_{red}=\frac{\chi ^{2}_{min}}{\nu }. \end{aligned}$$
(41)

If N is the data points and d is the free parameters, the number of degree of freedom \(\nu =N-d\). If a model is fitted to data and the resulting \(\chi ^2_{red}\) is larger than one, it is considered a “bad” fit, whereas if \(\chi ^2_{red}\) is less than one, it is considered an overfit. The fit model is that one whose value of \(\chi ^2_{red}\) is closest to one.

Fig. 5
figure 5

The scale factor as a function of time. The trajectories show the accelerated expansion after early deceleration for the best-fit values of model parameters obtained from different individual/combined observational data set. The trajectory (dotted curve) is also shown for a matter-dominated model in the absence of matter creation which shows decelerated expansion. A dot denotes the transition point where the transition from decelerated phase to accelerated phase occurs

Full size image
Table 2 The numerical values of \(a_{tr}\), \(z_{tr}\), \(q_0\), \(w_{eff}(z=0)\) and \(t_0\) using best-fit results of model parameters
Full size table

We also use two information criteria, namely the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) to assess the model. For a cosmological model with d degrees of freedom in which N number of data points have been used to fit the model, the AIC parameter is defined through the relation [52]

$$\begin{aligned} AIC=-2\;ln{\mathscr {L}}_{max}+2d, \end{aligned}$$
(42)

where \({\mathscr {L}}_{max}=e^{-{\chi ^2_{tot}}/2}\) is the maximum likelihood obtained for the cosmological model. The “preferred model” for this criterion is the one with the smaller value of AIC. To compare the model k with the model l, we calculate \(\varDelta {AIC_{kl}} = AIC_{k} -AIC_{l}\), which can be interpreted as “evidence in favor” of the model k compared to the model l. For \(0 \le \varDelta {AIC_{kl}} < 2\) we have“strong evidence in favor” of model k, for \(2<\varDelta {AIC_{kl}} < 4\), we have “average evidence in favor” of model k, for \(4< AIC_{kl} \le 7\) there is “less evidence in favor” of the model k, and for \(\varDelta {AIC_{kl}} > 10\) there is basically “no evidence in favor” of model k [53].

On the other hand, the Bayesian criterion is defined through the relation [54]

$$\begin{aligned} BIC=-2\;ln{\mathscr {L}}_{max}+d\; ln N, \end{aligned}$$
(43)

where N is the number of data points. Similar to \(\varDelta {AIC_{kl}}\), \(\varDelta {BIC_{ij}} = BIC_{i} - BIC_{j}\) can be interpreted as “evidence favor” the model i compared to the model j. For \(0\le \varDelta {BIC_{ij}} < 2\) there is “not enough evidence against” the model i, for \(2\le \varDelta {BIC_{ij}} < 6\) there is “evidence against” the model i and for \(6 \le \varDelta {BIC_{ij}} < 10\) there is “strong evidence against” model i [53].

Fig. 6
figure 6

The deceleration parameter as a function of redshift for best-fit values of model parameters obtained from observational data. A dot denotes the current value of q (hence \(q_0\))

Full size image
Fig. 7
figure 7

The variation effective EoS parameter as a function of redshift for best-fit values of model parameters

Full size image
Fig. 8
figure 8

The age of universe as a function of redshift for best-fit values of model parameters

Full size image
Fig. 9
figure 9

Variation of the Hubble function as a function of the redshift z for the best-fit values of the model. The observational 43 H(z) points are shown with error bars (grey colour). The variation of the Hubble function in the standard \(\varLambda \)CDM model is also represented as the solid curve

Full size image
Fig. 10
figure 10

The trajectory of \(\{r, s\}\) in \(s-r\) plane corresponds to best fitted parameters. The arrow shows the direction of the evolution of the trajectory

Full size image
Fig. 11
figure 11

The trajectory of \(\{r, q\}\) in \(q-r\) plane for the best fitted parameters. The arrow shows the direction of the evolution of the trajectory

Full size image
Fig. 12
figure 12

The trajectory of \(\textit{Om(z)}\) for the best fitted parameters

Full size image

Table 3 shows the \(\chi ^2_{min}\)s, \(\chi ^2_{red}\)s, AICs, BICs of the matter creation model with consideration of the \(\varLambda \)CDM as the referring model. It can be observed that the values of \(\chi ^2_{min}\), AIC and BIC for matter creation model are very close to the values of \(\varLambda \)CDM model. Thus, the observational data strongly favor and support the matter creation model from AIC and BIC. The reduced \(\chi ^2_{red}\) also shows that it is very close to the values of \(\varLambda \)CDM model, which is less than one (the model is “over fitting” the data).

6 Thermodynamics analysis

In this section, we find the condition of the thermodynamic stability for the present particle creation model. In [49], it has been demonstrated that cosmological apparent horizons are also endowed with thermodynamic properties. It can relate temperature and entropy to the apparent horizon like to the black hole event horizon.

According to the generalized second law (GSL) of thermodynamic, the total entropy S is the sum of entropy of all sources. Therefore, in this model the total entropy is contributed from the entropy of the apparent horizon (\(S_h\)) and entropy of fluid (\(S_f\)) inside the apparent horizon, i.e., \(S=S_h+S_f\). The entropy of apparent horizon is given by \(S_h=\kappa _B A/4l^2_{pl}\) [50], where \(\kappa _B\) is the Boltzmann’s constant, \(A=4\pi r^2_h\) is the area of horizon in which \(r_h=H^{-1}\) is the horizon radius for flat FRW universe and \(l_{pl}\) is the Planck’s length.

Differentiating \(S_h\) with respect to cosmic time and using (19), we obtain

$$\begin{aligned} \dot{S_h}= & {} -\frac{2\pi \kappa _B}{l^{2}_{pl}}\frac{{\dot{H}}}{H^3}\nonumber \\= & {} \frac{6\pi \kappa _B}{l^2_{pl}H^2}\frac{H_0(1-\alpha -\beta -\gamma )}{(2-3\gamma )}\;a^{-\frac{3(1-\beta -\gamma )}{(2-3\gamma )}}. \end{aligned}$$
(44)

It is observed from the above equation that \(\dot{S_h}\ge 0\) for (\(\alpha +\beta +\gamma ) \le 1\) and \(\gamma < 2/3\).

Now, the Gibb’s equation for the fluid is written as

$$\begin{aligned} TdS_f=d(\rho V)+pdV=V{\dot{\rho }}+\rho {\dot{V}}+pdV, \end{aligned}$$
(45)

where \(V=4\pi r^3_h/3\) is the spatial volume enclosed by the horizon and T is the fluid temperature. Note that we are studying matter-dominated model \(p=0\). Using (19), the above equation gives

$$\begin{aligned} \dot{S_f}=\frac{24\pi ^2 H_0}{H^2}\frac{(1-\alpha -\beta -\gamma )}{(2-3\gamma )}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}, \end{aligned}$$
(46)

where \(T=T_h=1/2\pi r_h\) , i.e., if the temperature of the fluid becomes equal to that of the temperature of the horizon [51]. For \(\dot{S_f}\ge 0\), we must have (\(\alpha +\beta +\gamma ) \le 1\) and \(\gamma < 2/3\).

Thus, from (44) and (46), we observe that \({\dot{S}}=\dot{S_h}+\dot{S_f} \ge 0\) for (\(\alpha +\beta +\gamma ) \le 1\) and \(\gamma < 2/3\). So, the entropy of the horizon plus fluid is an increasing function of the cosmic time.

Differentiating (44) again with respect to cosmic time, we get

$$\begin{aligned} \ddot{S_h}= & {} \frac{18\pi \kappa _B H_0}{l^2_{pl}}\frac{(1-\alpha -\beta -\gamma )}{(2-3\gamma )^2}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}\nonumber \\&\times \,\left[ \frac{2H_0}{H^2}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }} -\frac{(1-\beta -\gamma )}{H}\right] . \end{aligned}$$
(47)

Similarly, differentiating (46) with respect to cosmic time, we get

$$\begin{aligned} \ddot{S_f}= & {} 72\pi ^2 H_0\frac{(1-\alpha -\beta -\gamma )}{(2-3\gamma )^2}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }}\nonumber \\&\times \,\left[ \frac{2H_0}{H^2}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }} -\frac{(1-\beta -\gamma )}{H}\right] . \end{aligned}$$
(48)

Adding (47) and (48), one obtains

$$\begin{aligned} {\ddot{S}}= & {} \ddot{S_h}+\ddot{S_f}\nonumber \\= & {} \left( \frac{18\pi \kappa _B}{l^2_{pl}}+72 \pi ^2 \right) \frac{(1-\alpha -\beta -\gamma )H_0}{(2-3\gamma )^2H}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }} \nonumber \\&\times \left[ \frac{2H_0}{H}a^{-\frac{3(1-\beta -\gamma )}{2-3\gamma }} -(1-\beta -\gamma )\right] . \end{aligned}$$
(49)

The sign of \({\ddot{S}}\) is determined by last bracket in (49) and \(\alpha +\beta +\gamma <1\). Therefore, we find that the generalized second law of thermodynamics is always valid and hence the model is stable under the above constrains.

It is also interesting to discuss the model with adiabatic matter creation like irreversible process. In adiabatic process, the total entropy S increases, but, the specific entropy (per particle), \(\sigma =S/N\), remains constant, i.e., \({\dot{\sigma }}=0\) which implies that

$$\begin{aligned} \frac{{\dot{S}}}{S}=\frac{{\dot{N}}}{N}. \end{aligned}$$
(50)

Using (12) into (10), we get

$$\begin{aligned} N=N_0 a^{3\beta }({\dot{a}})^{3\gamma }\;e^{3\alpha H_0(t-t_0)}, \end{aligned}$$
(51)

where \(N_0\) is the present number of particles. Now, from (50), we get

$$\begin{aligned} S=S_0a^{3\beta }({\dot{a}})^{3\gamma }\;e^{3\alpha H_0(t-t_0)}, \end{aligned}$$
(52)

where \(S_0\) is the present entropy of matter fluid. It is to be noted that if \(\alpha =\beta =\gamma \), i.e., if there is no particle creation, we get \(S=S_0\), i.e., the standard conserved quantities are recovered.

7 Conclusion

We have discussed the matter-dominated model with matter creation cosmology as an alternative to explain the cosmic acceleration. As matter creation models are phenomenological and the literature contains a variety of models, so a generalized model could be a better choice to start for any study. Hence, in the present paper we have generalized the form of matter creation rate assumed by Lima et al. [31].

Table 3 Summary of the reduced \(\chi ^{2}_{red}\), \(\varDelta {AIC}\) and \(\varDelta {BIC}\) for \(\varLambda \)CDM model and matter creation model
Full size table

The assumption \(\varGamma =3\beta H\) [13] always gives accelerating model for \(\beta >1/3\) or decelerating for \(\beta <1/3\), that is, there is no transition redshift from a decelerating to an accelerating regime as required by observational data. In another paper, Abramo and Lima [20] proposed the form of \(\varGamma \) as \(\varGamma =3\beta H^2\), however it also gives no transition redshift. In order to cure such a difficulty, a constant term is added to this expression, i.e., \(\varGamma =3\alpha H_0+ 3\beta H\) [31] to get the transition redshift. Basilakos and Lima [55] have also used the same form to constraints the model. They observed that the age of the Universe to be \(t_0\sim 14.8\) Gyr while the inflection point is located \(a_{tr}\simeq 0.44\) which corresponds to \(z_{tr}\simeq 1.26\). They have found that this form of matter creation rate is endowed with severe difficulties even for the set of background tests because it is unable to adjust simultaneously the observational data at low and high redshift.

In this work, we have generalized the form of \(\varGamma \) in order to produce a clear image about the matter creation models aiming to realize the early physics and its compatibility with the current astronomical data. It covers different matter creation rate, for instance, \(\varGamma \propto H_0\), \(\varGamma \propto H\) and \(\varGamma \propto {\ddot{a}}/{{\dot{a}}}\). Lima et al. [31] have performed best-fit of the free parameters using only SNe data and best -fit values are \(\beta =0\) and \(\alpha =0.65\). We have performed the fitting of free parameters using joint observational data of SNe, OHD and BAO in which none free parameters is zero. However, In our model, the age of universe is found to be 13.8 Gyr from \(SNe+OHD\) and \(SNe+OHD+BAO\), but it is higher with SNe and \(SNe+BAO\). Also, the transition redshift is less than one with \(SNe+OHD\) and \(SNe+OHD+BAO\), which are good fit with \(\varLambda \)CDM model. Our model also generalizes the work of above references and it can be observed from the observational tests that our model gives best -fit values from joint observation of SNe with OHD, and OHD and BAO and fit the data very well with \(\varLambda \)CDM model. We have investigated the model analytically and numerically in which the matter creation process provides the late-time accelerating phase of the cosmic expansion without the need of any dark energy.

We have obtained the exact solutions for the scale factor, Hubble parameter and deceleration parameter. These results have then contrasted with the ones obtained at the background level to find the model parameters. For the background tests we have used SNe in combination with OHD and BAO at different redshifts. The nature of the cosmological evolution is strongly dependent on the numerical values of the model parameters. The best-fit values of model parameters have been listed in Table 1. Figures 1, 2, 3 and 4 show the confidence regions of parameters \(\alpha \), \(\beta \) and \(\gamma \) for different sets of jointly observational data. It has been found that the results of SNe and \(SNe+BAO\) data are little different from other two data. However, the joint analysis of \(SNe+OHD\) and \(SNe+OHD+BAO\) constraint the model parameters very well and are in good agreement with observational data of \(\varLambda \)CDM model. In what follows we summarize the results:

  • The evolutions of the scale factor for best-fit values of model parameters have been plotted in Fig. 5. It has been observed that the model predicts early deceleration and late-time acceleration. The transition points \(a_{tr}\) where the universe transits from decelerated phase to accelerated phase have been listed in Table 2.

  • Figure 6 plots the evolution of deceleration parameter with redshift for best-fit values obtained from independent/combined analysis of observational data. The present-day value of q and transition redshift \(z_{tr}\) have been listed in Table 2. The best-fit values of parameters obtained from different observational data give \(q_0\) in the range of \(-1\le q_0<0\). In general, \(q\rightarrow -1\) as \(z\rightarrow -1\), which corresponds to the de Sitter universe. The deceleration parameter is time dependent and hence shows the transition from positive to negative. The evolution of the universe begins from higher redshift, from a decelerating phase, with \(q>0\). The expansion of the Universe accelerates, and at a finite value of z it reaches the value \(q = 0\), corresponding to the transition to the accelerated phase. The evolution of q is strongly dependent on the numerical values of the model parameters.

  • We have obtained the EoS parameter to discuss the evolution of the model. Figure 7 plots the evolution of EoS parameter with redshift for best-fit values of parameters. It has been observed that the EoS does not cross the phantom-divide line \(\omega =-1\). Irrespective of the values of parameters, \(\omega _{eff}\rightarrow -1\) as \(z\rightarrow -1\) which shows that the model behaves like \(\varLambda \)CDM in late time. The present values of \(\omega \) obtained from independent/combined observational data are listed in Table 2. These values are comparatively higher than that predicted by the joint analysis of \(WMAP+BAO+H_0+SNe\) data which is around \(-0.93\).

  • We have discussed the age of the universe by plotting the trajectory with best-fit values of parameters as shown in Fig. 8. The trajectory shows that the age of the universe obtained by \(SNe+OHD\) and \(SNe+OHD+BAO\) data are found to be approximately 13.9 Gyr. So, the age predicted by the present model is agreeing with the age deduced from \(\varLambda \)CDM model.

  • The Hubble function with the error bar fits in to the \(\varLambda \)CDM model for best-fit values has been plotted in Fig. 9. It has been observed that the curves coincide at low redshifts and differ appreciably at high redshifts. However, it is possible to get good fit using joint analysis of \(SNe+OHD\) and \(SNe+OHD+BAO\).

  • We have studied two diagnostics parameters, namely, statefinder and \(\textit{Om(z)}\) parameters to compare our model with \(\varLambda \)CDM model. In Fig. 10, the trajectories of \(\{r, s\}\) have been plotted in \(s-r\) plane for best-fit values obtained from different observational data set. The model corresponds to \(\varLambda \)CDM model in late-time. The model also approaches to the standard model in late time as shown in \(q-r\) plane (Fig. 11). The trajectory of \(\textit{Om(z)}\) in Fig. 12 shows that the model behaves like quintessence.

  • We have performed the information criterion of AIC and BIC to discriminate our model with \(\varLambda \)CDM model. The values of reduced Chi-square, \(\varDelta {AIC}\) and \(\varDelta {BIC}\) are calculated and have listed in Table 3. The analyses based on the AIC and BIC indicate that there is positive support for the matter creation model when compared to the \(\varLambda \)CDM model. The reduced \(\chi ^2_{red}\) is less than one in each data points which shows that the model gives the best-fit values of model parameters and good support to \(\varLambda \)CDM model.

  • We have discussed the thermodynamic behavior of the model by calculating the total entropy for the matter creation. We have established the general conditions for any matter creation model that ensure the validity of the generalized second law of thermodynamics.

In concluding remarks, the most remarkable feature of this model is that the description of the present acceleration of the universe does not need any dark energy fluid or modified gravity theories. However, this theory is also model dependent. Thus, in this paper, we have proposed a new matter creation model which generalizes the existing models in the literature and constrain them using observational data set. Our analysis shows that the model is close to the standard \(\varLambda \)CDM model.