Higher derivatives driven symmetry breaking in holographic superconductors

Abstract

In this paper, we construct a novel holographic superconductor from higher derivative (HD) gravity involving a coupling between the complex scalar field and the Weyl tensor. This HD coupling term provides a near horizon effective mass squared, which can violates IR Breitenlohner–Freedman (BF) bound by tuning the HD coupling and induces the instability of black brane such that the superconducting phase transition happens. We also study the properties of the condensation and the conductivity in the probe limit. We find that a wider extension of the superconducting energy gap ranging from 4.6 to 10.5 may provide a novel platform to model and interpret the phenomena in the real materials of high temperature superconductor.

1 Introduction

Based on AdS/CFT (Anti-de Sitter/Conformal Field theory) correspondence [1,2,3,4,5], a holographic superconductor model is suggested in [6]. In this model, a complex charged scalar field is introduced in Schwarzschild-AdS (SS-AdS) black brane to spontaneously break the U(1) symmetry and transform to a charged scalar hair black brane. The charged scalar field in the bulk is dual to the “Cooper pair” operator at the boundary and the vacuum expectation value is the order parameter. The symmetry breaking is introduced by a negative mass squared of the scalar field, which is allowed due to the Breitenlohner–Freedman (BF) bound in AdS spacetime [6, 7]. In [8], a positive mass squared situation was studied. It was shown that as $m^{2}$ increase the phase space folds due to the non-linearity of the equations of motion, so the two nearby points in the phase space can represent symmetry breaking. And they show that for a small positive mass squared, the results is not much different from the negative case which has been studied in [9,10,11,12,13].

In [14], they discuss the superconductivity instability by studying the normalisable solution of equations of motion (EOMs) for the charged scalar field on top of RN-AdS black brane geometry. In essence, it is that the near horizon effective mass squared is below the AdS$_2$ BF bound, which induces the instability. At the same time, we also require that the mass squared is above the boundary AdS$_4$ BF bound, which guarantees the stability of scalar field at the boundary. In this paper, we construct a novel holographic superconductor model by introducing a higher derivative (HD) term, which couples the scalar field and Weyl tensor. This HD term provides a near horizon effective mass squared but doesn’t modify the boundary AdS$_4$ BF bound.

The superconducting energy gap is an important characteristic of superconductor models. In the weakly coupled BCS theory, this value is 3.5. In the usual holographic superconductor model [6, 12, 15], this value is approximately 8, which is more than twice the one in the BCS theory, but roughly approximates the value measured in high temperature superconductor materials [16]. The HD term introduced in holographic superconductor model drives the superconducting energy gap running, ranging from 5.5 to 16.2 [17,18,19,20,21].¹. In this paper, we also study the properties of the conductivity of our present model and in particular the running of the superconducting energy gap.

Our paper is organized as what follows. We will introduce the framework of holographic superconductivity in Sect. 2. In Sect. 3, we make a deep analysis for the instabilities. Then we move on to investigate the condensation in Sect. 4. In Sect. 5 we give the results of the conductivity. Conclusion and discussion are given in Sect. 6.

2 Holographic framework

Our starting point is the following actions

$$\begin{aligned} S_0&=\frac{1}{2\kappa ^2}\int d^4x\sqrt{-g}\Big (R+\frac{6}{L^2}\Big ), \end{aligned}$$

(1a)

$$\begin{aligned} S_{\Psi }&=-\int d^4x\sqrt{-g}\Big (|D_{\mu }\Psi |^2+m^2|\Psi |^2-\alpha _1 L^2 C^2|\Psi |^2\Big ), \end{aligned}$$

(1b)

$$\begin{aligned} S_A&=-\int d^4x\sqrt{-g}\frac{L^2}{8g_F^2}F_{\mu \nu }X^{\mu \nu \rho \sigma } F_{\rho \sigma }. \end{aligned}$$

(1c)

$F=dA$ is the Maxwell field strength of gauge field A. $D_{\mu }=\partial _{\mu }-iqA_{\mu }$ is the covariant derivative and $\Psi$ is the charged complex scalar field with mass m and the charge q of the Maxwell field A. We can write $\Psi =\psi e^{i\theta }$ with $\psi$ being a real scalar field and $\theta$ a Stückelberg field. And then, for convenience we choose the gauge $\theta =0$ in what follows. In the action $S_{\Psi }$, a new interaction, which couples the complex scalar field to the Weyl tensor, is added in $S_{\Psi }$. Since the pure AdS geometry is conformally flat, the Weyl tensor vanishes in the UV boundary. But $C^2$ provides a nontrivial source for the scalar in the bulk geometry and gives an effective mass of the scalar. This interaction provides a new mechanism of the symmetry breaking,² for which we shall do in-depth studies in this paper. In the action $S_A$, the tensor X is

$$\begin{aligned} X_{\mu \nu }^{\ \ \rho \sigma }= & {} I_{\mu \nu }^{\ \ \rho \sigma }+\alpha _2|\Psi |^2I_{\mu \nu }^{\ \ \rho \sigma }-8\gamma _{1,1}L^2 C_{\mu \nu }^{\ \ \rho \sigma }\nonumber \\&-4L^4\gamma _{2,1}C^2I_{\mu \nu }^{\ \ \rho \sigma } -8L^4\gamma _{2,2}C_{\mu \nu }^{\ \ \alpha \beta }C_{\alpha \beta }^{\ \ \rho \sigma }\nonumber \\&-4L^6\gamma _{3,1}C^3I_{\mu \nu }^{\ \ \rho \sigma } -8L^6\gamma _{3,2}C^2C_{\mu \nu }^{\ \ \rho \sigma }\nonumber \\&-8L^6\gamma _{3,3}C_{\mu \nu }^{\ \ \alpha _1\beta _1}C_{\alpha _1\beta _1}^{\ \ \ \alpha _2\beta _2}C_{\alpha _2\beta _2}^{\ \ \ \rho \sigma } +\cdots . \end{aligned}$$

(2)

$I_{\mu \nu }^{\ \ \rho \sigma }=\delta _{\mu }^{\ \rho }\delta _{\nu }^{\ \sigma }-\delta _{\mu }^{\ \sigma }\delta _{\nu }^{\ \rho }$ is an identity matrix and $C^n=C_{\mu \nu }^{\ \ \alpha _1\beta _1}C_{\alpha _1\beta _1}^{\ \ \ \alpha _2\beta _2}\ldots C_{\alpha _{n-1}\beta _{n-1}}^{\ \ \ \mu \nu }$ with $C_{\mu \nu \rho \sigma }$ being the Weyl tensor. When $X_{\mu \nu }^{\ \ \rho \sigma }=I_{\mu \nu }^{\ \ \rho \sigma }$, the action $S_A$ reduces to the standard Maxwell theory. The second term introduces the interaction between the scalar field and the gauge field. Starting from the third term, they are an infinite family of HD terms [40]. In this paper, we mainly focus on the top four terms in $X_{\mu \nu }^{\ \ \rho \sigma }$. For convenience sake, we denote $\gamma _{1,1}=\gamma$ and $\gamma _{2,i}=\gamma _i (i=1,2)$. In SS-AdS black brane background, when other parameters are turned off, $\gamma$ and $\gamma _1$ are constrained in the region $-1/12\le \gamma \le 1/12$ [41, 42] and $\gamma _1\le 1/48$ [40], respectively. These constraints come from the instabilities and causality of the vector modes. However, for the black brane with scalar hair, we must reexamine the instabilities and causality of the vector modes and we leave them for future. In this paper, we shall constraint these coupling parameters in small region, which is safe.

3 Superconducting instability

When $\Psi =0$, the system (1) achieves a charged black brane solution, which corresponds to the normal phase. In this section, we shall explore the instability condition for the normal phase towards the development of a hairy black brane under small charged scalar field perturbations. This allows one to determine the superconducting phase structure in the dual boundary field theory. The condition for the formation of the hairy black brane depends on the charge and the mass of the scalar field as well as the background which is specified by the model parameters. For clarity, we first study the role of $\alpha _1$ term in the formation of the hairy black brane. And then, we further explore the joint effect from the $\alpha _1$ term and the $\gamma$ term.

3.1 Case I: $\alpha _1$ HD term

In this subsection, we first want to see what role the $\alpha _1$ term plays in the formation of the hairy black brane. So we only turn on $\alpha _1$ term and turn off other coupling parameters in this section. In this case, the background geometry of the normal phase is RN-AdS black brane,

$$\begin{aligned}&ds^2=\frac{1}{u^2}\Big (-f(u)dt^2+dx^2+dy^2\Big ) +\frac{1}{u^2f(u)}du^2\,,\nonumber \\&f(u)=(1-u)p(u)\,,~~~~~~~ p(u)=1+u+u^2-\frac{\mu ^2u^3}{4},\nonumber \\&A_t(u)=\mu (1-u). \end{aligned}$$

(3)

Here $\mu$ is the chemical potential of the field theory. The Hawking temperature is

$$\begin{aligned} T=\frac{p(1)}{4\pi }=\frac{1}{4\pi }\Big (\frac{\mu ^2}{4}-3\Big ). \end{aligned}$$

(4)

Fig. 1

Left plot: Phase diagram $(\alpha _1,{\hat{T}}_c)$ with $m^2=-2$ for different q. Right plot: QPT diagram in $(\alpha _1,q)$ space for $m^2=-2$. The blue line is the QPT critical line and the blue zone is the superconducting phase at zero temperature

We can estimate the critical temperature for the formation of the superconducting phase by finding static normalizable modes of the scalar field $\psi$ in the above background (3). The procedure has been used in [43,44,45,46]. This problem can be casted into a positive self-adjoint eigenvalue problem for $q^2$ and so we write the equation of motion for the scalar field as the following form:

$$\begin{aligned} \big [\nabla ^2-m^2+\alpha _1L^2C^2\big ]\psi =q^2A^2\psi . \end{aligned}$$

(5)

Without loss of generality, we set the mass of the charged scalar field as $m^2=-2$ here.³ For this case, its asymptotical behavior at infinity is

$$\begin{aligned} \psi =\psi _1 u+\psi _2 u^2. \end{aligned}$$

(6)

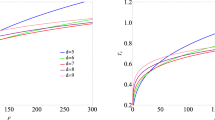
Here, we will treat $\psi _1$ as the source and $\psi _2$ as the expectation value in the dual boundary theory. Also we set $\psi _1=0$ such that the condensation is not sourced. Now, this system is determined by the scaling-invariant Hawking temperature ${\hat{T}}=T/\mu$, the charge of complex scalar field q and the coupling parameter $\alpha$. When the non-trivial scalar profile is developed, the superconducting phase forms. Therefore, we can numerically solve the above Eq. (5) to locate the critical temperature of the superconducting phase as the function of $\alpha _1$ for different q, which is shown in the left plot in Fig. 1. Note that the region above the line is the normal state and the region below the line is the superconducting phase. This plot exhibits that when we reduce the temperature for given parameter q and $\alpha$, an thermodynamic phase transition happens. In addition, at zero temperature, we find that for given q when the coupling parameter $\alpha _1$ increases, the superconducting phase also appears, which is a quantum phase transition (QPT). The phase diagram $(\alpha _1,q)$ is shown in the right plot in Fig. 1. There are several characteristics are summarized as what follows:

• For a given $\alpha _1$, we find that the critical temperature becomes higher with the increase of the charge (left plot in Fig. 1), which means that the increase of the charge make the condensation easier. This tendency is consistent with our intuition and have been observed in [43, 44].

• For a given charge, we find a rise in critical temperature with the coupling parameter $\alpha _1$ (left plot in Fig. 1), which means that the higher derivative term $\alpha _1$ plays the role of driving the superconducting phase transition.

• From the left plot in Fig. 1, we see that for a given charge, if the coupling parameter $\alpha _1$ is relatively small, the system would not undergo a superconducting phase transition no matter how low the temperature. It means that there is a QPT at zero temperature. We show the QPT diagram in $(\alpha _1,q)$ space in the right plot in Fig. 1. The blue line is the QPT critical line and the blue zone is the superconducting phase at zero temperature. The QPT can be also understood by the BF bound. We shall further address this problem in what follows.

Now, we shall analyze the superconducting phase transition at zero temperature by BF bound. To have a superconducting phase transition, the near horizon effective mass squared shall be below the corresponding BF bound, but the UV boundary effective mass squared shall be above the boundary AdS$_4$ BF bound, which guarantees the stability of scalar field at the boundary.

For the RN-AdS black brane, the extremal limit can be arrived at when $\mu =2\sqrt{3}$. At this limit, the near horizon geometry and the gauge field are [47]

$$\begin{aligned} ds^2&=\frac{L_2^2}{\zeta ^2}(-d\tau ^2+d\zeta ^2)+dx^2+dy^2, \end{aligned}$$

(7a)

$$\begin{aligned} A_{\tau }&=\frac{\mu L_2^2}{\zeta }, \end{aligned}$$

(7b)

where $L_2\equiv L/\sqrt{6}$. In deriving the above equations, we have made the transformation $(1-u)=\epsilon \frac{L_2^2}{\zeta }$ and $t=\epsilon ^{-1}\tau$ in the limit $\epsilon \rightarrow 0$ with finite $\zeta$ and $\tau$. It is obvious that at the zero-temperature limit, the near horizon geometry is $\mathrm AdS_2\times {\mathbb {R}}^2$ with the $\mathrm AdS_2$ curvature radius $L_2$.

Fig. 2

Left plot: The blue zone is the allowed region for the superconducting phase transition at $m^2$ vs q plane at the zero temperature for $\alpha _1=0$. Right plot: The blue zone is the allowed region for the superconducting phase transition at the zero temperature for $m^2=-2$

Fig. 3

The blue zone is the allowed region for the superconducting phase transition at $m^2$ vs q plane at the zero temperature (left plot is for $\alpha _1=-0.1$ and right plot is for $\alpha _1=0.1$)

The effective mass of this system is

$$\begin{aligned} m_{eff}^2=m^2+q^2A^2-\alpha _1L^2C^2. \end{aligned}$$

(8)

Since $q^2A^2=q^2g^{tt}A_t^2$, which contributes with minus sign, it tends to destabilize the normal state and induces the superconductivity. While the role plays $\alpha _1$ term depends on the sign of $\alpha _1$, which can stabilize or destabilize the normal state. To have a superconducting phase transition, we require that the near horizon effective mass squared shall be below the corresponding BF bound, but the UV boundary effective mass squared shall be above the corresponding BF bound. Thus we have

$$\begin{aligned} m_{IR}^2<-\frac{1}{4L_2^2}\,, ~~~~~~ m_{UV}^2\ge -\frac{9}{4}, \end{aligned}$$

(9)

where $m_{IR}^2$ and $m_{UV}^2$ denote the near horizon effective mass squared and the bulk mass squared, respectively. Using the expression of the effective mass squared (8) combining with the near horizon geometry (7) and the AdS$_4$ geometry, the above equations can be specifically expressed as

$$\begin{aligned} m^2-2q^2-8\alpha _1<-\frac{3}{2}\,, ~~~~~~ m^2\ge -\frac{9}{4}. \end{aligned}$$

(10)

It has been well studied that for the usual holographic superconductor ($\alpha _1=0$ here), the superconducting instabilities are determined by both the bulk mass squared $m^2$ and the charge q, equivalently, the chemical potential, which can be clearly seen from the above instability condition (10) and have been explored in [8, 14]. Here, we also exhibit the allowed region (blue zone) for the superconducting phase transition with $\alpha _1=0$ at $m^2$ vs q plane at the zero temperature (left plot in Fig. 2). For small q, the superconducting phase transition is forbade if the mass squared is positive. But provided the charge is large, the superconducting phase transition still happen for $m^2=0$ or even positive $m^2$, which is called the density driven symmetry breaking in holographic superconductor in [8].

Subsequently, we turn to explore what role $\alpha _1$ plays. We plot the $\alpha _1$ as the function of q (i.e., QPT diagram) for $m^2=-2$ at zero temperature, which is shown in the right plot in Fig. 2. The result is qualitatively consistent with that above by finding static normalizable modes of the scalar field (see the right plot in Fig. 1).

Further, we plot the allowed region for the superconducting phase transition at $m^2$ vs q plane at the zero temperature for $\alpha _1=-0.1$ and $\alpha _1=0.1$, respectively (Fig. 3). It is obvious that for $\alpha _1=-0.1$, if q is less than some critical value ($q\simeq 0.158$), the superconducting phase transition is forbade regardless of the value of $m^2$ (see the left plot in Fig. 3). For $\alpha _1=0.1$, the allowed range of $m^2$ for the superconducting phase transition becomes larger than $\alpha _1=0$ for the fixed q. To address this point more clearly, we also plot the relation between $m^{2}$ and $\alpha _{1}$ for $q=1$ and $q=2$ in Fig. 4 and a 3D plot for q, $m^2$ and $\alpha _1$ in Fig. 5. It indicates that one can tune $\alpha _1$ to trigger a quantum phase transition. Also, we can infer that for small q, the superconducting phase transition still happen for $m^2=0$ or even positive $m^2$, provided that $\alpha _1$ is large. It is just the role $\alpha _1$ plays and we call the HD driven symmetry breaking in holographic superconductor, which is the focus of our present paper and we shall thoroughly explore this issue in next section.

Fig. 4

The blue zone is the allowed region for the superconducting phase transition at $m^2$ vs $\alpha _1$ plane at the zero temperature (left plot is for $q=1$ and right plot is for $q=2$)

Fig. 5

3D plot of the allowed region for the superconducting phase transition at the zero temperature

3.2 Case II: $\gamma$ HD term

In this subsection, we simultaneously turn on $\alpha _1$ and $\gamma$. Since $\gamma$ term involves the coupling between the Weyl tensor and gauge field, the background geometry of the normal phase is no longer a RN-AdS black brane. We need to solve a set of third order differential equations to obtain the background solution. It is a hard task. However, we can obtain the perturbative solution up to the first order of $\gamma$ as [48]

$$\begin{aligned} ds^2= & {} \frac{f(u)}{u^{2}}dt^{2}+\frac{1}{u^{2}f(u)}du^{2}\nonumber \\&+\left[ \frac{1}{u^{2}}\left( 1+\gamma \frac{u^{2}\mu ^{2}}{9}\right) \right] (dx^{2}+dy^{2}),\nonumber \\ f(u)= & {} (1-u)p(u)\,,\nonumber \\ p(u)= & {} 1+u+u^2-\frac{\mu ^2u^3}{4} +\frac{1}{180}u^{3}\gamma \mu ^{2}\nonumber \\&[240-28\mu ^{2}+26u^{4}\mu ^{2}\nonumber \\&+(u+u^{2}+u^{3})(-100+\mu ^{2})],\nonumber \\ A_t(u)= & {} \frac{1}{90}\mu \{90+74u^{5}\gamma \mu ^{2}+45u^{4}\gamma (-4-\mu ^{2})\nonumber \\&-[90+\gamma (180+29 \mu ^{2})]\}. \end{aligned}$$

(11)

For this black brane, we can obtain the dimensionless Hawking temperature ${\hat{T}}\equiv T/\mu$ with

$$\begin{aligned} T=\frac{12-\mu ^{2}}{16\pi \mu }+\gamma \frac{\mu (\mu ^{2}-60)}{720\pi }. \end{aligned}$$

(12)

At the zero temperature limit, the chemical potential $\mu$ becomes

$$\begin{aligned} \mu =\sqrt{\frac{3}{2}}\sqrt{20+\frac{15}{\gamma } -\frac{\sqrt{5}\sqrt{45+72\gamma +80\gamma ^{2}}}{\gamma }}. \end{aligned}$$

(13)

When $\gamma \rightarrow 0$, $\mu =2\sqrt{3}$, which reduces the case of RN-AdS black brane. At extremal limit, the near horizon geometry of the perturbative solution (11) is also $\mathrm AdS_2\times {\mathbb {R}}^2$ as RN-AdS black brane but with a different $\mathrm AdS_2$ curvature radius $L_2$ as

$$\begin{aligned} L_2^2= \frac{-4000 \gamma ^2+5 \sqrt{5} (40 \gamma +33) \sqrt{80 \gamma ^2+72 \gamma +45}-4956 \gamma -2475}{4 \gamma },\nonumber \\ \end{aligned}$$

(14)

which explicitly dependent on the Weyl parameter $\gamma$.

Following the same procedure in the above subsection, in this case, the constraint on the the near horizon effective mass squared gives

$$\begin{aligned}&m^{2}+\frac{4\alpha _{1}}{3}-\frac{2475+4956\gamma +4000\gamma ^{2} -165w-200w}{16\gamma }\nonumber \\&\qquad +\frac{q^{2}(2355+2860\gamma -161w)^{2}(-15-20\gamma +w)}{600[-4000\gamma ^{2}+165(-15+w)+4\gamma (-1239+50w)]}\nonumber \\&\quad <-\frac{3}{2}. \end{aligned}$$

(15)

For convenience, in the above equation, we have defined w as

$$\begin{aligned} w=\sqrt{5}\sqrt{45+72\gamma +80\gamma ^{2}}. \end{aligned}$$

(16)

In addition, the bulk mass squared satisfies

$$\begin{aligned} m^{2}>-\frac{9}{4}. \end{aligned}$$

(17)

Equations (15) and (17) give the conditions that the superconducting phase happens at zero temperature. We summarize the roles $\alpha _1$ and $\gamma$ play in the superconducting phase transition as what follows.

Fig. 6

3D plot of the allowed region for the superconducting phase transition at the zero temperature for a fixed $\gamma$ (left plot is for $\gamma =-1/12$ and right plot is for $\gamma =1/12$)

Fig. 7

3D plot of the allowed region for the superconducting phase transition at the zero temperature for a fixed $\alpha _1$ (from left to right, $\alpha _1=-0.5, 0, 0.5$)

• In previous subsection, we have observed that for $\gamma =0$, in the phase diagram $(m^2,q,\alpha _1)$, there is a region in which the superconducting phase transition is forbade. When $\gamma =-1/12$, such a region still holds (left plot in Fig. 6). But when $\gamma =1/12$, such a forbidden region of superconducting phase transition vanishes (right plot in Fig. 6). It indicates that we can find a parameter space, the superconducting phase transition can always happen.

• Fig. 7 exhibits 3D plot of the allowed region for the superconducting phase transition at the zero temperature for a fixed $\alpha _1$. When $\alpha _1$ is negative, there is a forbidden region of superconducting phase transition in the phase diagram $(m^2,q,\gamma )$. As $\alpha _1$ increases, this region shrinks and $\alpha _1$ is large, this region vanishes.

In this section, we have made the superconducting instability analysis, from which we clearly see what roles of the HD terms $\alpha _1$ and $\gamma$ play in the superconducting phase transition. However, we would like to point out that the instability analysis is implemented in the probe limit and it only provide a clue of the phase transition. To further confirm the phase transition, we need numerically solve the system (1).

4 Condensation

In this section, we shall numerically solve the system (1) to study the superconducting phase transition. However, it is hard to solve the system (1) with backreaction because it involves solving a set of third order differential equations with high nonlinearity. Therefore, we shall work in the probe limit, i.e., we don’t consider the backreaction of the gauge field and the scalar field on the geometry.

In the probe limit, we consider the metric as

$$\begin{aligned}&ds^2=\frac{1}{u^2}\Big (-f(u)dt^2+dx^2+dy^2\Big ) +\frac{L^2}{u^2f(u)}du^2\,,\nonumber \\&f(u)=(1-u)p(u)\,,~~~~~~~ p(u)=u^2+u+1, \end{aligned}$$

(18)

Fig. 8

The condensation $\sqrt{\langle O_2\rangle }/T_c$ as a function of the temperature $T/T_c$ for different $\alpha _1$. Here the mass of scalar field is $m^2=-2$

which is the SS-AdS black brane. $u=1$ denotes the horizon and $u=0$ is the asymptotically AdS boundary. The Hawking temperature of this system is $T=3/4\pi$. And then, the EOMs of gauge field and scalar field can be derived as

$$\begin{aligned}&\nabla _{\nu }\big (X^{\mu \nu \rho \sigma }F_{\rho \sigma }\big ) -4q^2A^{\mu }\psi ^2 =0,\nonumber \\&\big [\nabla ^2-(m^2+q^2A^2)+\alpha _1 C^2\big ]\psi =0. \end{aligned}$$

(19)

The ansatz for the scalar field and gauge field is taken as

$$\begin{aligned} \psi =\psi (u)\,,\,\,\,\,\, A=\phi (u) dt. \end{aligned}$$

(20)

Under the above ansatz (Eqs. (18) and (20)), the EOMs for $\psi$ and $\phi$ (Eq. (19)) can be explicitly expressed as follows,

$$\begin{aligned}&\psi (u) \left( -\frac{q^2 \phi (u)^2}{u^3-1}+12 \alpha _1 u^4-u\right) \nonumber \\&\quad -\left( u^3-1\right) \psi ''(u)-3 u^2 \psi '(u)=0, \end{aligned}$$

(21a)

$$\begin{aligned}&(u^3-1)(48u^6 \gamma _{1}+8u^3 \gamma -1)\phi ''(u)\nonumber \\&\quad +24u^{2}(u^{3}-1)(\gamma +12u^{3}\gamma _{1})\phi '(u)\nonumber \\&\quad -2q^{2}\psi (u)^{2}\phi (u)=0. \end{aligned}$$

(21b)

Here, we only consider the HD terms up to 6 order. Regardless of any details of the above EOMs, the asymptotical behaviors of $\phi$ and $\psi$ at the conformal boundary are

$$\begin{aligned} \phi =\mu -\rho u,\qquad \psi =\psi _1 u^{3-\Delta }+\psi _2 u^{\Delta }. \end{aligned}$$

(22)

In the dual boundary field theory, $\mu$ and $\rho$ are the chemical potential and the charge density, respectively, as has been mentioned above. This system is depicted by a dimensionless quantity ${\hat{T}}\equiv T/\mu$. We take standard quantization and so $\psi _1$ is treated as the source and $\psi _2$ as the expectation value of the scalar operator, for which we denote $\langle O_2\rangle$. We expect that the condensation is not sourced and so we set $\psi _1=0$. Subsequently, we numerically solve EOMs (21) by the shooting method and study the properties of the condensation $\langle O_2\rangle$ with HD derivative terms.⁴ We shall firstly study the condensation by considering the scalar field with negative mass, $m^2=-2$, which has been well studied in the usual holographic superconductor model.

Figure 8 shows the condensation $\sqrt{\langle O_2\rangle }/T_c$ as a function of the temperature $T/T_c$ for different $\alpha _1$. We observe that as $\alpha _1$ decreases, the condensation value becomes much larger. It indicates that a larger superconducting energy gap $\omega _g/T_c$ emerges, which shall be explicitly addressed in the following study of optical conductivity. Furthermore, we find that with the increase of the $\alpha _1$, the critical temperature $T_c$ goes up (see Table 1). The tendency agrees with that shown in the left plot in Fig. 1. It indicates that the positive $\alpha _1$ term drives the symmetry breaking and makes the condensation easy. While for the negative $\alpha _1$, the condensation becomes hard and when $\alpha _1$ is less than certain value, the condensation is spoiled. The result is consistent with the instability analysis in Sect. 3.

Table 1 The critical temperature ${\hat{T}}_{c}$ with different $\alpha _{1}$ and $\gamma$. Here $\gamma _1=0$

In previous works [17, 20], we have studied the holographic superconductor from the coupling between Weyl tensor and gauge field. We find that the condensation value at low temperature runs and the critical temperature ${\hat{T}}_c$ changes as the coupling parameters $\gamma$ or $\gamma _1$. The tendency is consistent with that from the instability analysis in Sect. 3. Here we further explore the joint effect from $\alpha _1$ term and $\gamma$ or $\gamma _1$ term. The results are exhibited in Tables 1, 2 and Fig. 9. We find that the couplings between $\alpha _1$ and $\gamma$ (or $\gamma _1$) have an enhancement or a competitive effect on the formation of superconducting phase depending on the sign of the coupling parameters. We summarize the properties as what follows.

• From Table 1 and the panels above in Fig. 9, we see that both $\alpha _1$ and $\gamma$ are positive, the critical temperature of the superconducting phase transition is enhanced. If both $\alpha _1$ and $\gamma$ are negative, the critical temperature is reduced. It means that the same sign of $\alpha _1$ and $\gamma$ enhances or reduces the formation of the superconducting phase transition. However, if the signs of $\alpha _1$ and $\gamma$ are opposite, there is a competitive effect on the formation of superconducting phase transition.

• The same analysis from Table 2 and the panels below in Fig. 9 gives that when the signs of $\alpha _1$ and $\gamma _1$ are opposite, the formation of the superconducting phase transition is enhanced or reduced, while for the same signs of $\alpha _1$ and $\gamma _1$, there is a competitive effect on the formation of superconducting phase transition.

5 Conductivity

In this section, we study the optical conductivity of our holographic system with HD terms. For this, we turn on the perturbation of the gauge field along x direction as $\delta A_x(t,u)=e^{-i\omega t}A_x(u)$. And then we can derive the following perturbation equation

Table 2 The critical temperature ${\hat{T}}_{c}$ with different $\alpha _{1}$ and $\gamma _{1}$. Here $\gamma =0$

Fig. 9

The condensation $\sqrt{\langle O_2\rangle }/T_c$ as a function of the temperature $T/T_c$ for different $\alpha _{1}$ and $\gamma$ or $\gamma _1$. Here the mass of scalar field is $m^2=-2$

$$\begin{aligned}&(-1+u^{3})(-1-4u^{3}\gamma +48u^{6}\gamma _{1})A_{x}^{''}\nonumber \\&\quad +(-1+u^{3})(3u^{2}(-1+4\gamma -8u^{3}\gamma -96u^{3}\gamma _{1}\nonumber \\&\quad +144u^{6}\gamma _{1}))A_{x}^{'} +((-1-4u^{3}\gamma +48u^{6}\gamma _{1})\omega ^{2}\nonumber \\&\quad -2q^{2}(-2+u^{3}) \psi ^{2})A_{x}=0. \end{aligned}$$

(23)

We can numerically solve the above equation with the ingoing boundary condition. Once the solution is at hand, we can read off the conductivity in terms of

$$\begin{aligned} \sigma (\omega )=\frac{\partial _u A_x}{i\omega A_x}\Big |_{u=0}\,. \end{aligned}$$

(24)

Fig. 10

Real and imaginary parts of conductivity as a function of the frequency for different $\alpha _{1}$

Fig. 11

Real and imaginary parts of conductivity as a function of the frequency for different $\gamma$

Fig. 12

Real and imaginary parts of conductivity as a function of the frequency for different $\gamma _{1}$

There is no doubt that as the standard version of holographic superconductor model [12], the imaginary part of the conductivity (right plots in Figs. 10, 11 and 12) has a pole at $\omega =0$, which indicates that there is a delta function at $\omega =0$ in the real part of the conductivity according to the Kramers–Kronig (KK) relation. Such a delta function in conductivity means the emergence of superconductivity. The another important property that the superconducting energy gap is also clearly exhibited in the real part of the conductivity (see the left plots in Figs. 10, 11 and 12). Near the gap frequency $\omega _g$, the real part of conductivity quickly goes up, which approximately corresponds to the minimum value in the imaginary part of the conductivity.

In previous works [17,18,19,20], the authors have found that after introducing the coupling between the Weyl tensor and the gauge field, the ratio of the superconducting energy gap frequency over critical temperature $\omega _g/T_c$ ranges from about 5.5 to 16.2. Here we would also like to explore the running of the superconducting energy gap after the coupling term $\alpha _1$, which is the coupling between the complex scalar field and the Weyl tensor. From Fig. 10, we clearly see that the superconducting energy gap runs with the parameter $\alpha _1$. Quantitatively, it ranges from about 7.9, which is less than the value of the standard version holographic superconductor in [12], to 9.5, which is beyond the value of the standard version holographic superconductor, when $\alpha _1\in [-0.2,0.2]$ (see Table 3).

Furthermore, we also study the the joint effect on the running of the superconducting energy gap from $\alpha _1$ term and $\gamma$ or $\gamma _1$ term. The results are exhibited in Figs. 11, 12 and Tables 3 and 4. The enhancement or competitive effect on the running of the superconducting energy gap is similar with that of the formation of the superconducting phase discussed in the previous section. We present a brief summary as what follows.

Table 3 The superconducting energy gap $\omega _{g}/T_{c}$ with different $\alpha _{1}$ and $\gamma$

• The same sign of $\alpha _1$ and $\gamma$ enhances the running of the superconducting energy gap. However, if the signs of $\alpha _1$ and $\gamma$ are opposite, there is a competitive effect on the running of superconducting energy gap.

• When the signs of $\alpha _1$ and $\gamma _1$ are opposite, the running of the superconducting energy gap is enhanced, while for the same signs of $\alpha _1$ and $\gamma _1$, there is a competitive effect on the running of superconducting energy gap.

• The enhancement effect leads to the result that the running range of the superconducting energy gap becomes larger, from 4.6 to 10.5 (see Figs. 11, 12 and Tables 3, 4).

The extension of the energy gap in our holographic model maybe provide a novel platform to model the high temperature superconductor and we pursuit it in future.

Table 4 The superconducting energy gap $\omega _{g}/T_{c}$ with different $\alpha _{1}$ and $\gamma _{1}$

6 Conclusion and discussion

In this paper, we construct a novel holographic superconductor from HD gravity, for which we introduce a coupling between the complex scalar field and the Weyl tensor. The $\alpha _1$ coupling term provides a near horizon effective mass squared but doesn’t modify the boundary AdS$_4$ BF bound. The instability analysis indicates that a quantum phase transition can be triggered by tuning the coupling parameter $\alpha _1$. In particular, even for the positive mass squared, the superconducting phase transition also happens by tuning the $\alpha _1$. Therefore, the $\alpha _1$ HD term plays the role of driving the symmetry breaking and results in the superconducting phase transition. We also explore the instability from the HD terms $\alpha _1$ and $\gamma$, which involves the coupling between the Weyl tensor and gauge field. $\gamma$ coupling term modifies the near horizon AdS$_2$ curvature and thus the near horizon effective mass squared, which provides a mechanism to result in the superconducting phase transition.

The properties of the condensation and the conductivity in our holographic model are also studied. Although in the probe limit, we have the same tendency as the instability analysis. We summarize the main properties of our present model as what follows:

• For the positive $\alpha _1$, the condensation becomes easy. While for the negative $\alpha _1$, the result is just opposite.

• A wider extension of the superconducting energy gap, ranging from 4.6 to 10.5, is observed. We expect that our model provides a novel platform to model and interpret the phenomena in the real materials of high temperature superconductor.

As a novel mechanism, there are some interesting topics deserving further pursuit in future.

• We want to explore whether there is the phenomena of the phase space folding as Ref. [8] due to the introduction of $\alpha _1$ term.

• The Homes’ law can be observed in the holographic superconductor model from HD theory [20], which involves the coupling between Weyl tensor and the gauge field. It is interesting to explore this issue in our present model.

• The transports at full momentum and energy spaces can provide far deeper insights into the holographic system than that at the zero momentum [49, 50]. In future, we shall study this issue in the framework of our present model.

• It is also interesting to study the running of the superconducting energy gap in other HD holographic superconductor model, for example [51].