Impact of generalized polytropic equation of state on charged anisotropic polytropes

Abstract

In this paper, generalized polytropic equation of state is used to get new classes of polytropic models from the solution of Einstein-Maxwell field equations for charged anisotropic fluid configuration. The models are developed for different values of polytropic index $n=1,~\frac{1}{2},~2$. Masses and radii of eight different stars have been regained with the help of developed models. The speed of sound technique and graphical analysis of model parameters is used for the viability of developed models. The analysis of models indicates they are well behaved and physically viable.

1 Introduction

Polytropes are very useful to study the internal structure of stars. They can be used to discuss various astronomical situations and description of compact objects. Chandrasekhar [1] developed the basic theory of Newtonian polytropes by using laws of thermodynamics for polytropic spheres. Tooper [2] derived hydrostatic equilibrium equations for spherically symmetric objects and obtained numerical solutions for adiabatic process with compressible fluid. Irregularities arised in Chandrasekhar’s theory of slowly rotating polytropes were removed by Kovetz [3]. Generalized forms of Lane-Emden equation (LEe) for cylindrical, spherical and planer polytropes were derived by Abramowicz [4]. Ngubelanga and Maharaj [5] obtained new classes of polytropic models for different values of polytropic index. Isayev [6] discussed general relativistic polytropes in anisotropic stars and derived generalized LEe for arbitrary anisotropic parameter.

The discussion of anisotropy factor is essential while studying the formation of stars. Bowers and Liang [7] highlights the importance of locally anisotropic equation of state by generalizing the equation of hydrostatic equilibrium. The change in maximum equilibrium mass and red-shift was found proportional to anisotropic factor. Dev and Gleiser [8] studied effects of pressure anisotropy on stars and found that it has significant effects on the structure and properties. Maurya and Gupta [9] developed a family of anisotropic fluid distributions using spherically symmetric space-time to describe a family of charged perfect fluid distributions. Thirukkanesh and Ragel [10] studied the properties of stellar objects having anisotropic distribution in spherically symmetric space-time. Mardan et al. [11] investigated the gravitational behavior of stellar objects by new classes of anisotropic polytropes for different values of polytropic index. They used GPEoS with anisotropic matter distributions and considered quadratic form of gravitational potential to get the solutions of Einstein field Equations (EFE).

It is important to discuss effects of charge in stellar models for many applications. The effects of electronic forces in hydrostatic equilibrium state of charged stars were initially discussed by Rosseland [12]. Bonner [13, 14] studied the effect of charge on spherically symmetric stellar objects and found that electric repulsion can halt the gravitational collapse. Sharma et al. [15] solved field equations for charged sphere by taking a special class of hyper-surfaces and more general behavior of charged spheres was observed than uncharged spheres. They also presented the presence of charge over wide range of parameters. The red shift, luminosity and mass of the stellar objects were affected in the presence of electric field was presented by Ivanov [16]. Ray et al. [17] analyzed the effect of charge in astronomical objects and found the maximum charge a star can hold is about $10^{20}$ Coulomb. Thirukkanesh and Maharaj [18] obtained solution of field equations in presence electromagnetic field which described anisotropic compact objects having properties similar to SAX J1808.4-3658, a star. To obtain exact solutions for field equations with anisotropic pressure and electromagnetic field Takisa and Maharaj [19] used the polytropic equation of state (PEoS). Sunzu and Danford [20] considered anisotropic charged stellar objects with linear equation of state and generated new exact models for field equations. Noureen et al. [21] studied the effect of charge and anisotropy on gravitational interaction of compact objects using GPEoS. They developed the solutions of Einstein-Maxwell field equations (EMFE) by using linear form of gravitational potential.

The universe is made of radiative fields (photons), matter and vacuum. So the total energy density is sum of energy density of photons, matter and vacuum. Prisco et al. [22] studied the non-adiabatic charged spherically symmetric gravitational collapse as well as the energy density inhomogeneity with shear dissipation. Herrera [23] explored energy density inhomogeneity and stability with dissipative anisotropic fluid. Sharif and Bashir [24] studied effect of charge on energy density inhomogeneity in self gravitating dissipative and non-dissipative fluids using evolution equations of Weyl tensor. Mardan et al. [25] studied anisotropic matter distribution with radiation density using GPEoS in isotropic coordinates. They used quadratic form of gravitational potential to obtain the solutions of EFE.

The stability analysis of stellar objects has significant importance in mathematical modeling. Any mathematical model is worthless if this is unstable against variations in physical parameters. The hydrostatic equilibrium equations were developed by Bondi [26] for stability analysis of compact objects. Herrera et al. [27] used local density perturbation and cracking technique for stability analysis of models. Azam et al. [28] used Tolman mass for the stability analysis of relativistic polytropes. Azam and Mardan [29-31] used local density perturbation technique for stability analysis, by evaluating the cracking points for different compact objects in spherical and cylindrical symmetry.

In this paper, we present physically viable solutions to the EMFE for spherically symmetric spacetimes in isotropic coordinates by using GPEoS. The models are developed for different values of $n=1,~\frac{1}{2},~2$ and they are well behaved. We have plotted graphs of energy density, radial pressure, mass, speed of sound, electric field intensity, and tangential pressure for EXO 1785-248 and explained matter properties of developed model. Discussion and summary is presented in the last section.

2 Einstein Maxwell field equations

The metric in isotropic coordinates for spherically symmetric fluid $(x^{a})=(t,r,\theta ,\phi )$ is of the form

$$\begin{aligned} ds^2=-A^{2}dt^{2}+B^{2}[dr^{2}+r^{2}(d\theta ^{2}+sin^2\theta d \phi ^{2})], \end{aligned}$$

(1)

where A and B are the metric quantities known as gravitational potentials. In general relativity energy momentum tensor acts as source of gravitational field. The anisotropic fluid has energy momentum tensor of following form written as [25]

$$\begin{aligned} T_{\alpha \beta }= & {} (\rho +P_{t})V_{\alpha }V_{\beta }+P_{t}g_{\alpha \beta }\nonumber \\&+(P_{r}-P_{t})\chi _{\alpha }\chi _{\beta }+q_{\alpha }V_{\beta }+V_{\alpha }q_{\beta }+\epsilon \ell _{\alpha }\ell _{\beta }, \end{aligned}$$

(2)

where $\epsilon$ is radiation density, $q_{\mu }$ represents heat flux, V the four velocity, $\chi ^{\alpha }$ unit four vector along the radial direction and $\ell ^ {\alpha }$ is radial null four vector.

$$\begin{aligned} V^{\alpha }= & {} A^{-1}\delta ^{\alpha }_{0},~~q^{\alpha }=q B^{-1}\delta ^{\alpha }_{1},\nonumber \\ l^{\alpha }= & {} A^{-1}\delta ^{\alpha }_{0}+B^{-1}\delta ^{\alpha }_{1},~~ \chi ^{\alpha }=B^{-1}\delta ^{\alpha }_{1},~~q^{\alpha }=q\chi ^\alpha . \end{aligned}$$

(3)

If we have charged fluid, electromagnetic contribution is needed to the fluid distribution. The set of EFE in presence of charge are transformed into EMFE, which can be written as

$$\begin{aligned} G_{\mu \upsilon }=R_{\mu \upsilon }-\frac{1}{2}Rg_{\mu \upsilon }= 8\pi ( T_{\mu \upsilon }+S_{\mu \upsilon }), \end{aligned}$$

(4)

where $G_{\mu \upsilon }$ represents Einstein tensor, $S_{\mu \upsilon }$ electromagnetic energy tensor, written as [22]

$$\begin{aligned} S_{\mu \upsilon }=\frac{1}{4\pi }\left( F_{\mu }^{\sigma }F_{\upsilon \sigma }-\frac{1}{4}F^{\sigma r}F_{\sigma r}g_{\mu \upsilon }\right) , \end{aligned}$$

(5)

in above equation $F_{\upsilon \sigma }$ is the electromagnetic field tensor. The electric charge interior to radius r is time independent and given by

$$\begin{aligned} s(r)=4\pi \int ^{r}_{0} \varsigma Br^{2}dr, \end{aligned}$$

(6)

where $\varsigma$ is charge density. By using Eqs. (2) and (4), the EMFE for line element Eq. (1) takes the form

$$\begin{aligned}&8\pi (\rho +\epsilon )+16\pi ^{2}E^{2}=\frac{-1}{B^{2}}\left[ 2\frac{B^{\prime \prime }}{B}-\frac{B^\prime }{B}\left[ \frac{B^\prime }{B}-\frac{4}{r}\right] \right] ,\nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned}&8\pi (P_r+\epsilon )-16\pi ^{2}E^2=2\frac{A^\prime }{A}\left[ \frac{B^\prime }{B^{3}}+\frac{1}{rB^{2}}\right] \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \quad +\frac{B^\prime }{B^{3}}\left[ \frac{B^\prime }{B}+\frac{2}{r}\right] , \end{aligned}$$

(8)

$$\begin{aligned}&8\pi P_t+16\pi ^2E^2= \frac{1}{B^2}\Bigg [\frac{B^{\prime \prime }}{B}-\frac{B^\prime }{B}\Bigg [\frac{B^\prime }{B}-\frac{1}{r}\Bigg ]\nonumber \\&\qquad \qquad \qquad \qquad \qquad +\Bigg [\frac{A^{\prime \prime }}{A}+\frac{A^\prime }{r A}\Bigg ]\Bigg ], \end{aligned}$$

(9)

$$\begin{aligned}&\sigma =\frac{1}{4\pi r^{2}}B^{-1}(r^2 E)^{\prime }. \end{aligned}$$

(10)

The system of Eqs. (7)–(10) contain four independent equations with five variables $(A,~B,~\rho ,~P_r$ and $P_t)$ and $s=4\pi r^2 EB^2$. The transformations of parameters is used to simplify the system of EMFE

$$\begin{aligned} x\equiv r^2,\quad H\equiv B^{-1},\quad N\equiv HA, \end{aligned}$$

(11)

by using the above transformations the Eqs. (7)–(10) takes the form

$$\begin{aligned}&8\pi \rho +8\pi \epsilon +16\pi ^{2}E^{2}\nonumber \\&\quad = 4\Big [2xHH_{xx}-3H_{x}(xH_{x}-H)\Big ], \end{aligned}$$

(12)

$$\begin{aligned}&8\pi P_{r}+8\pi \epsilon -16\pi ^{2}E^{2}\nonumber \\&\quad =4H(H-2xH_{x})\frac{N_{x}}{N}-4H_{x}[2H-3xH_{x}], \end{aligned}$$

(13)

$$\begin{aligned}&8\pi P_{t}+16\pi ^{2}E^{2}=4xH^2\frac{N_{xx}}{N}+4H(H-2xH_{x})\frac{N_{x}}{N}\nonumber \\&\qquad \qquad \qquad \qquad \qquad -4(2H-3xH_{x})H_{x}-8xHH_{xx}, \end{aligned}$$

(14)

$$\begin{aligned}&\sigma ^2=\frac{1}{4\pi ^{2}x}H^{2}(E+xE_x)^2, \end{aligned}$$

(15)

the subscripts denote the derivatives w.r.t ‘x’.

$$\begin{aligned} P_{r}=\alpha _{o}\rho +\alpha _{1}\rho ^{1+\frac{1}{n}}. \end{aligned}$$

(16)

Using the GPEoS, in Eqs. (14) and (16) gives the anisotropy factor $\Delta =8\pi (P_{t}-P_{r})$ takes the form

$$\begin{aligned} \Delta= & {} 8\pi \left[ \frac{1}{8\pi }\left[ 4xH^{2}\frac{N_{xx}}{N}+4H(H-2xH_{x})\frac{N_{x}}{N}\right. \right. \nonumber \\&\left. -4(2H-3xH_{x})H_{x}-8xHH_{xx}-16\pi ^{2}E^{2}\right] \nonumber \\&-\frac{\alpha _{o}}{8\pi }[4(2xHH_{xx}-3(xH_{xx}-H)H_x)\nonumber \\&-16\pi ^{2}E^{2}-8\pi \epsilon ]-\alpha _{1}\left[ \frac{1}{8\pi }\right] ^{1+\frac{1}{n}}\nonumber \\&\times [4(2xHH_{xx}-3(xH_{x}-H)H_x)\nonumber \\&\left. -16\pi ^{2}E^{2}-8\pi \epsilon ]^{1+\frac{1}{n}}\right] , \end{aligned}$$

(17)

where

$$\begin{aligned} \frac{N_{x}}{N}= & {} \frac{\alpha _{o}}{4H(H-2xH_{x})}\Big [4(2xHH_{xx}-3(xH_{x}\nonumber \\&-H)H_x)-16\pi ^{2}E^{2}-8\pi \epsilon \Big ]+\frac{2\pi \alpha _{1}}{H(H-2xH_{x})}\nonumber \\&\times \left( \frac{1}{8\pi }\right) ^{1+\frac{1}{n}}[4(2xHH_{xx}-3(xH_{x}-H)H_x)\nonumber \\&-16\pi ^{2}E^{2}-8\pi \epsilon ]^{1+\frac{1}{n}}+\frac{8\pi \epsilon }{4H(H-2xH_{x})}\nonumber \\&-\frac{16\pi ^{2}}{4H(H-2xH_{x})}+\frac{4(2H-3xH_{x})H_{x}}{4H(H-2xH_{x})}. \end{aligned}$$

(18)

The measure of anisotropy is, attractive if $\Delta <0$, repulsive if $\Delta >0$ and vanishes for isotropic pressures if $\Delta = 0$. Also for Instantaneous solution the gravitational mass function can be used in following form

$$\begin{aligned} m(x)=2\pi \int ^{x}_{0}\frac{1}{\sqrt{\omega }}\left[ \omega \rho (\omega )+\frac{E^2}{8\pi }\right] d\omega , \end{aligned}$$

(19)

of an electric field intensity in the presence with anisotropy. Here, $\omega$ is an integration variable [19].

3 Integration and polytropic model for $n=1$

To obtain physically viable Instantaneous solution for matter variables, the system of Eqs. (12), (15), (17) and (18) needs to be solved by means of integration. To do so the gravitational potential H in linear form is given by [5]

$$\begin{aligned} H=a+bx, \end{aligned}$$

(20)

and the electric field has the form

$$\begin{aligned} E^2=x^{p}(c+dx)^{q}, \end{aligned}$$

(21)

where p, q are constants and we take $p=0$ and $q=1$, in the process of integration to get exact models. Hence, using Eqs. (20) and (21) in Eqs. (12), (15), (16)–(18) gives

$$\begin{aligned} \rho= & {} \frac{1}{8\pi }\Big [12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon \Big ], \end{aligned}$$

(22)

$$\begin{aligned} P_{r}= & {} \frac{\alpha _{o}}{8\pi }\Big [12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon \Big ] \nonumber \\&+\,\alpha _{1}\Big [\frac{12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon }{8\pi }\Big ]^{1+\frac{1}{n}}, \end{aligned}$$

(23)

$$\begin{aligned} \sigma ^{2}= & {} \frac{(a+bx)^{2}(2c+3dx)^{2}}{16\pi ^{2}x(c+dx)}, \end{aligned}$$

(24)

the generalized form of $\Delta$ can be written as

$$\begin{aligned} \Delta= & {} 4b(-2a+bx)-16\pi ^2(c+dx)-(8\pi )^{-\frac{1}{n}}\nonumber \\&\times \Big (12ab(a+bx)-16\pi ^2(c+dx)-8\pi \epsilon \Big )^{1+\frac{1}{2}} \alpha _1\nonumber \\&-4(3ab-4c\pi ^2+3b^2x-4d\pi ^2x-2\pi \epsilon )\alpha _o\nonumber \\&+(8\pi )^{-\frac{1}{n}}\Big [-2^{4+\frac{3}{n}}d\pi ^{2+\frac{1}{n}}x-b^2x(8\pi )^{-\frac{1}{n}}\nonumber \\&+(8\pi )^{1+\frac{1}{n}}\epsilon +4^{1+\frac{1}{2}}(3ab-2\pi (2\pi c+2\pi dx\nonumber \\&+\epsilon ))^{1+\frac{1}{n}}\alpha _1+2^{2+\frac{3}{n}}\pi ^{\frac{1}{n}}(3ab-2\pi (2\pi c\nonumber \\&+2\pi dx+\epsilon ))\alpha _o\Big ]+\frac{1}{n(a-bx)^2} 2^{-\frac{2(1+n)}{n}}\nonumber \\&\times \pi ^{-\frac{2}{n}}x\Big [16n(3ab-2\pi (2\pi c+2\pi d x+\epsilon ))^{2+\frac{2}{n}}{\alpha ^2}_1\nonumber \\&+2^{3 + \frac{1}{n}}\pi ^{\frac{1}{n}}(3ab-2\pi (2\pi c+2\pi dx+\epsilon ))^{\frac{1}{n}}\alpha _1 a^2(6b^2 n\nonumber \\&-8d(1+n)\pi ^2)+a b n(9b^2x-56\pi ^2 c+ 9 b^2 x\nonumber \\&+4\pi (5\epsilon -14\pi dx)+2 \pi (32 c^2 n \pi ^3 +c (64 d n \pi ^3 x\nonumber \\&-6 b^2 n \pi x ) + b^2x (-2 d(-2 + n) \pi x - 3 n \epsilon )\nonumber \\&+8 n \pi (4 d^2 \pi ^2 x^2 - \epsilon ^2))+4 n (3 a b-2\pi (2 c \pi +2 d\pi x \nonumber \\&+\epsilon ))^2 \alpha _o)+n (2 \pi )^{\frac{2}{n}} (-64 a^2 d \pi ^2 + 256 c^2 \pi ^4 -96\nonumber \\&\times b^2 c \pi ^2 x + 512 c d\pi ^4 x - 3 b^4 x^2-32 b^2 d \pi ^2 x^2 \nonumber \\&+ 256 d^2 \pi ^4 x^2 -256 c \pi ^3 \epsilon +48 b^2 \pi x \epsilon -256 d \pi ^3 x \epsilon \nonumber \\&+ 64 \pi ^2 \epsilon ^2+4 a b (-16 c \pi ^2 + 3 b^2 x +8 \pi (-2 d \pi \nonumber \\&\times x + \epsilon ))+8 (a^2 (6 b^2 - 8 d \pi ^2) +2 \pi (32 c^2 \pi ^3\nonumber \\&+32 d^2 \pi ^3 x^2 +c (-6 b^2 \pi x+64 d \pi ^3 x)-8 \pi \epsilon ^2 \nonumber \\&-b^2 x (2 d \pi x + 3 \epsilon ))+a b (-56 c \pi ^2 + 9 b^2 x +4 \pi \nonumber \\&\times (-14 d \pi x+5 \epsilon )))\alpha _o +16 (3 a b - 2 \pi (2 c \pi + 2 d \pi x\nonumber \\&+ \epsilon ))^2{\alpha ^2}_o)\Big ], \end{aligned}$$

(25)

where

$$\begin{aligned} \frac{N_{x}}{N}= & {} \frac{\alpha _{o}}{4(a+bx)(a-bx)}\nonumber \\&\times \Big [12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon \Big ]\nonumber \\&+\,\frac{2\pi \alpha _{1}}{(a+bx)(a-bx)}\nonumber \\&\times \left[ \frac{12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon }{8\pi }\right] ^{1+\frac{1}{n}}\nonumber \\&+\,\frac{8\pi \epsilon }{4(a+bx)(a-bx)}\nonumber \\&-\,\frac{16\pi ^{2}(c+dx)}{4(a+bx)(a-bx)}\nonumber \\&+\,\frac{(2a-bx)b}{4(a+bx)(a-bx)}. \end{aligned}$$

(26)

It is not easy to integrate above system in the presence of general polytropic index n without specifying its values. To obtain Instantaneous solution, we integrate it for polytropic indices $n=1$ here and polytropic Instantaneous solutions for $n=\frac{1}{2}$ and $n=2$ are given in appendix.

Table 1 Mass, central density, central radial pressure and radiation density $\epsilon =7.5756\times 10^{-16}$, for stars with $\alpha _1=0.931$

Table 2 Variation of radiation density, radial pressure, electric field intensity and mass from center to boundary of realistic star EXO 1785-248

For $n=1$, we can integrate Eq. (26) to give

$$\begin{aligned} N(r)=Ke^{W}(a-br^{2})^{M}(a+br^{2})^{X}, \end{aligned}$$

(27)

where K is constant of integration, here

$$\begin{aligned} W= & {} -\frac{8 d^2 {\pi }^3 r^2 \alpha _1}{b^2}, \end{aligned}$$

(28)

$$\begin{aligned} M= & {} -\frac{1}{8 a b^3}\left[ \frac{(2 (a (-3 b^2 + 4 d {\pi }^2) +2 b {\pi } (2 c \pi + {\epsilon }))^2 \alpha _1)}{\pi }\right. \nonumber \\&+\, b(a(b^2 - 16 d \pi ^2) + 8 b \pi (-2 c \pi + \epsilon ) +4 (a (3 b^2\nonumber \\&\left. -\, 4 d \pi ^2)-2 b \pi (2 c \pi + \epsilon )) \alpha _o)\right] , \end{aligned}$$

(29)

$$\begin{aligned} X= & {} \frac{1}{8 a b^3 \pi }\big [2 (a (3 b^2 + 4 d \pi ^2) -2 b \pi (2 c \pi + \epsilon ))^2\alpha _1\nonumber \\&+\,b \pi (a (3 b^2 + 16 d \pi ^2) +8 b \pi (-2 c \pi + \epsilon ) +4 (a (3 b^2\nonumber \\&+\, 4 d \pi ^2)-2 b \pi (2 c \pi + \epsilon ))\alpha _o)\big ]. \end{aligned}$$

(30)

The degree of anisotropy becomes

$$\begin{aligned} \Delta= & {} \frac{-1}{\pi (a - b r^2)^2} 2((a - b r^2)^2 (-3 a b + 4 c \pi ^2\nonumber \\&-\,3 b^2 r^2 + 4 d \pi ^2 r^2 +2 \pi \epsilon )^2\alpha _1-a^2 b^2 M^2 r^2\nonumber \\&+\,8 a b c \pi ^2 r^2 - 4 a^2 d \pi ^2 r^2 -4 a b^3 r^4 - a b^3 M r^4\nonumber \\&+\, 2 a b^3 M^2 r^4-4 b^2 c \pi ^2 r^4 + 8 a b d \pi ^2 r^4 + b^4 r^6 \nonumber \\&- \,2 b^4 M r^6 + b^4 M^2 r^6 - 4 b^2 d \pi ^2 r^6 + a^3 b X\nonumber \\&-\,4 a^2 b^2 r^2 X - 2 a^2 b^2 r^2 M X + 5 a b^3r^4 X-2 b^4 r^6 X\nonumber \\&+\,2 b^4r^6 M X + a^2 b^2 r^2 X^2 - 2 a b^3 r^4 X^2+ b^4 r^6 X^2\nonumber \\&-\,(a - b r^2)^2 (3 a b - 4 c \pi ^2 + 3 b^2 r^2-4 d \pi ^2 r^2 - 2 \pi \epsilon )\alpha _o\nonumber \\&+\,(a^2 - b^2 r^4) (a^2+ b^2 r^4 (1 - 2 M - 2 X) -2 a b r^2\nonumber \\&\times (1 + M - X))W^\prime +r^2 (a^2- b^2 r^4)^2W^{\prime \prime }+a^4 r^2W^{\prime \prime })\nonumber \\&-\,2 a^2 b^2 r^6W^{\prime \prime }+b^4 r^{10} W^{\prime \prime }. \end{aligned}$$

(31)

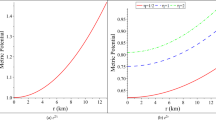
The metric in Eq. (1) takes the form

$$\begin{aligned} ds^{2}= & {} -Ke^{2W}(a+br^{2})^{2(X-1)}(a-br^{2})^{2M}dt^{2}\nonumber \\&+\,(a+br^{2})^{-2}[dr^{2}+r^{2}(d\theta ^{2}+sin^{2}d\phi ^{2})]. \end{aligned}$$

(32)

4 Properties of new solution

To discuss the physical properties of parameters for the polytropic index $n=1$, we obtain from Eq. (23)

$$\begin{aligned} P_{r}= & {} \frac{\alpha _{0}}{8\pi }\left[ 12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon \right] \nonumber \\&+\,\alpha _{1}\left[ \frac{12ab-16\pi ^{2}c-16\pi ^{2}dx-8\pi \epsilon }{8\pi }\right] ^{2}. \end{aligned}$$

(33)

The proper charge density takes the form

$$\begin{aligned} \sigma ^2=\frac{(a+br^{2})^{2}(2c+3dr^{2})^{2}}{16\pi ^{2}r^{2}(c+dr^{2})}. \end{aligned}$$

(34)

The charge density has singularity at $r=0$ (center of star). To avoid singularity $c=0$ is considered

$$\begin{aligned} \sigma ^2=d\left[ \frac{3(a+br^{2})^{2}}{4\pi }\right] ^2. \end{aligned}$$

(35)

For $c=0$ and $n=1$ mass function, energy density and radial pressure are

$$\begin{aligned} m(r)= & {} \frac{r^3}{12}\left[ 24ab-16\pi \epsilon +d\left( \frac{10-96\pi ^{2}r^{2}}{5}\right) \right] \end{aligned}$$

(36)

$$\begin{aligned} 8\pi \rho= & {} 12ab-16\pi ^{2}dr^{2}-8\pi \epsilon , \end{aligned}$$

(37)

$$\begin{aligned} P_{r}= & {} \frac{\alpha _{o}}{8\pi }\left[ 12ab-16\pi ^{2}dr^{2}-8\pi \epsilon \right] \nonumber \\&+\, \alpha _{1}\left[ \frac{12ab-16\pi ^{2}dr^{2}-8\pi \epsilon }{8\pi }\right] ^{2}. \end{aligned}$$

(38)

The energy density, electric field intensity, and the proper charge density remain finite at center of star, so

$$\begin{aligned} \rho _{o}= & {} \frac{1}{8\pi }\left[ 12ab-8\pi \epsilon \right] , \end{aligned}$$

(39)

$$\begin{aligned} P_{r_{o}}= & {} \frac{\alpha _{o}}{8\pi }\left[ 12ab-8\pi \epsilon \right] +\alpha _{1}\left[ \frac{12ab-8\pi \epsilon }{8\pi }\right] ^2, \end{aligned}$$

(40)

$$\begin{aligned} \sigma ^{2}_{o}= & {} d\left( \frac{3a}{4\pi }\right) ^{2}, \end{aligned}$$

(41)

$$\begin{aligned} E^{2}_{o}= & {} 0. \end{aligned}$$

(42)

We take parameter $h=ab$. The mass function also remains finite. The speed of sound is

$$\begin{aligned} \upsilon ^2=\frac{dP_{r}}{d\rho }, \end{aligned}$$

(43)

where $\upsilon ^{2}\le 1$ [5] to maintain causality. For stable configuration of compact object $P_{r}=0$ at boundary. Taking $r=1$, we get

$$\begin{aligned} \alpha _{o}=\frac{-\alpha _{1}}{2\pi }\Big (3h-4\pi ^{2}d-2\pi \epsilon \Big ). \end{aligned}$$

(44)

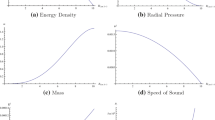
In order show the importance of Instantaneous solution and presence of such situations in realistic stars, we have selected different kinds of stars and obtained their masses and radii for different values of parameters involve in our solutions. Table 1 contain numerical values of all parameters for eight different stars. On varying parameters d, h and $\alpha _{o}$, masses of eight different stars were regained given in Table 1. The acceptable values for $\rho _{0}$ and $P_{r_{0}}$ are given in Table 1 by fixing $\alpha _1=0.931$ and $\epsilon =7.5756\times 10^{-16}$ [32]. Table 2 contains varying values of $\rho$, $P_{r}$, m, $E^{2}$ and $\upsilon ^{2}$ from central point to boundary of stars. No singularity is observed while calculating instantaneous solution for different parametric values given in Table 1. The properties of stars 4U 1820-30, Cen X-3, EXO 1785-248, LMC X-4, SMC X-1, SAX J1808.4-3658, 4U 1538-52 and Her X-1 are similar to this object.

Fig. 1

EXO 1785-248

For detail discussion of physical quantities, we have presented the figures for stellar object EXO 1785-248 with mass $1.30~M_\odot$ and radius 9.701 km here. Figures related to objects 4U 1820-30, Cen X-3, LMC X-4, SMC X-1, SAX J1808.4-3658, 4U 1538-52, Her X-1 show similar profile that is why not included in this work. The energy density, radial pressure and speed of sound are decreasing functions while mass, electric field intensity and tangential pressure are increasing functions with respect to radius. At center of any star $c=0$ the tangential pressure becomes zero. The radial pressure vanishes at boundary of star while tangential pressure attains its maximum value. Any solution for system of stars is not acceptable if it is unstable. Various techniques have been used for analysis of mathematical models. The speed of sound technique and graphical analysis of model parameters is used to check its viability. The speed of sound is decreasing and remains positive inside the star and thus the casuality condition $\upsilon ^{2}\le 1$ is satisfied. The degree of anisotropy was selected in a way that pressure gradient must be less than zero, setting $r = 0$, at the center, $\vartriangle$ will become zero, which is the basic requirement for stability. Graphical analysis shows that all parameters are well behaved and physically acceptable.

4.1 Conclusion and discussion

The models for stars were developed with charged anisotropic inner fluid distribution using GPEoS. The integration is carried out by considering linear form of gravitational potential. Since the process of gravitational collapse is highly dissipative, so it contains massless energy particles forming a radiative field. The main obstacle in astrophysics and general relativity is to develop stable mathematical models that can match with the characteristic of realistic astronomical objects. In this regard numerical values of parameters for eight stars are given in Table 1. The mass of eight stars were regained by varying parameters d, h and $\alpha _{o}$ for given radii with fixed values of $\epsilon =7.5756\times 10^{-16}$ and $\alpha _1=0.931$. The acceptable values for $\rho _{0}$ and $P_{r_{0}}$ are also given in Table 1.

As a test case EXO 1785-248 is chosen to check the variation of physical model parameters. Table 2 contains different values of $\rho$, $P_{r}$, m, $E^{2}$ and $\upsilon ^{2}$ from center of star to its boundary. The subfigures (a), (b), (c), (d), (e) and (f) of Fig. 1 shows that energy density, radial pressure and speed of sound are decreasing functions, have maximum values at center and vanishing at boundary, while mass, electric field intensity and tangential pressure are increasing functions, have minimum values at center and attain maximum values at boundary of astronomical objects. In the interior of all stars the considered matter quantities $\rho$, $P_{r}$, $P_{t}$, $\Delta$ remain positive. The speed of sound remains positive inside the star and thus the casuality condition $\upsilon ^{2}\le 1$ is satisfied. Graphical analysis shows that all the physical quantities are well-behaved and developed models are physically acceptable.

Mardan et al. [11] used GPEoS with anisotropic matter distributions to get exact solutions of EFE. They considered quadratic form of gravitational potential “$L=a x^{2} + b x + c$” to get the solutions of EFE. The solutions of their developed mathematical models contained five parameters. They plotted graphs for unit radius of developed mathematical models. Noureen et al. [21] studied the effect of charge and anisotropy on gravitational interaction of compact objects using GPEoS. They considered linear form of gravitational potential “$L=a + b x$” to get the solutions of EMFE. The solutions of their developed mathematical models contained four parameters. They also plotted graphs for unit radius of mathematical models. Mardan et al. [25] studied anisotropic matter distribution with radiation density using GPEoS in isotropic coordinates. They considered quadratic form of gravitational potential “$M=k x^{2} + g x + h$” to get the solutions of EFE. The solutions of mathematical model contained five parameters. They plotted the graphs of mathematical models for exact value of radius of PSR J0437-4715.

In comparison of [11, 21, 25] our developed models are more general and singularity free. The models presented in [11, 21, 25] are subcases of our work as; (i) if we substitute $``E=0,~\epsilon =0$” our models reduces to the case presented by Mardan et al. [11], (ii) if we put $``\epsilon =0$” we obtained the models developed by Noureen et al. [21], (iii) if we take $``E=0$” the models given by Mardan et al. [25] can be generated. The linear form of gravitational potential Eq. (3.14) considered here is more general to get the solutions of EMFE. The solutions of mathematical models contained four parameters due to which this was easy to get more approximated values of matter quantities (mass, radii, electric field intensity, radial pressure, pressure gradient). The developed models in this thesis contained graphs (of mass, radial pressure, energy density, speed of sound, electric field intensity and tangential pressure) for exact radius of EXO 1785-248.

Appendix

1.1 Polytropic index $n=\frac{1}{2}$

For index $n=\frac{1}{2}$ in Eq. (26) can be integrated to give

$$\begin{aligned} N(r)=K_1 e^{W}(a-br^{2})^{M}(a+br^{2})^{X}, \end{aligned}$$

(A45)

where $K_1$ is constant of integration, here

$$\begin{aligned} W= & {} \frac{4 d^2 \pi ^2 r^2 (-9 a b +2 \pi (6 c \pi + d \pi r^2 + 3 \epsilon ))\alpha _1}{b^2},\nonumber \\ \end{aligned}$$

(A46)

$$\begin{aligned} M= & {} -\frac{1}{8 a b^4 \pi ^2} \left[ (a (3 b^2 - 4 d \pi ^2) -2 b \pi (2 c \pi + \epsilon ))^3 \alpha _1 \right. \nonumber \\&+b^2 \pi ^2 (a (b^2 - 16 d \pi ^2) +8 b \pi (-2 c \pi + \epsilon ) \nonumber \\&+4 (a (3 b^2 - 4 d \pi ^2)-2 b \pi (2 c \pi + \epsilon ))\alpha _o)\Big ], \end{aligned}$$

(A47)

$$\begin{aligned} X= & {} \frac{1}{8 a b^4 \pi ^2}\left[ (a(3 b^2 + 4 d \pi ^2) -2 b \pi (2 c \pi + \epsilon ))^3\alpha _1 \right. \nonumber \\&+b^2 \pi ^2 (a (3 b^2 + 16 d \pi ^2) +8 b \pi (-2 c \pi + \epsilon ) \nonumber \\&\left. +4 (a \times (3 b^2+4 d \pi ^2)-2 b \pi (2 c \pi + \epsilon ))\alpha _o)\right] .\nonumber \\ \end{aligned}$$

(A48)

For $n=\frac{1}{2}$ degree of anisotropy becomes

$$\begin{aligned} \Delta= & {} -\frac{1}{\pi ^2} \left[ (3 a b - 4 c \pi ^2 + 3 b^2 r^2- 4 d \pi ^2 r^2\right. \nonumber \\&-2 \pi \epsilon )^3 \alpha _1 -4 \pi ^2 (4 c \pi ^2 - 3 a b - 3 b^2 r^2\nonumber \\&+4 d \pi ^2 r^2 + 2 \pi \epsilon ) \alpha _o +\frac{4 \pi ^2}{(a - b r^2)^2} \nonumber \\&\times \left( 2 a^3 b + a^3 b M + 4 a^2 c \pi ^2-5 a^2 b^2 r^2\right. \nonumber \\&- a^2 b^2 M^2 r^2 - 8 a b c \pi ^2 r^2 +2 a b^3 M^2 r^4\nonumber \\&+ 4 b^2 c \pi ^2 r^4 - 8 a b d \pi ^2 r^4 -b^4 r^6+ 2 b^4\nonumber \\&\times M r^6- b^4 M^2 r^6 + 4 b^2 d \pi ^2 r^6 -a^3 b X\nonumber \\&+ 4 a^2 b^2 r^2 X + 2 a^2 b^2 r^2 M X - 5 a b^3 r^4 X \nonumber \\&+2 b^4 r^6 X - 2 b^4 r^6 M X- a^2 b^2 r^2 X^2\nonumber \\&+2 a b^3 r^4 X^2 -b^4 r^6 X^2 - (a^2 - b^2 r^4)\nonumber \\&\times (a^2 + b^2 r^4 (1 - 2 M - 2 X) - 2 a b r^2 \nonumber \\&\times (1 + M - X))W^\prime -2 r^2 (a^2 - b^2 r^4)^2 {W^{\prime }}^2\nonumber \\&\left. \left. - r^2 (a^2 - b^2 r^4)^2 W^{\prime \prime }\right) \right] . \end{aligned}$$

(A49)

The metric Eq. (1) takes the form

$$\begin{aligned} ds^{2}= & {} -K_1 e^{2W}(a+br^{2})^{2(X-1)}(a-br^{2})^{2M}dt^{2}\nonumber \\&+\,(a+br^{2})^{-2}[dr^{2}+r^{2}(d\theta ^{2}+sin^{2}d\phi ^{2})]. \end{aligned}$$

(A50)

1.2 Polytropic index n = 2

For index $n=2$ Eq. (26) can be integrated to give

$$\begin{aligned} N=K_2 e^{W}(a-br^{2})^{M}(a+br^{2})^{X}[D]^{T}[V]^{C}, \end{aligned}$$

(A51)

again $K_2$ is constant of integration, here

$$\begin{aligned} W= & {} \frac{4d\pi ^{\frac{3}{2}}\sqrt{6ab-4\pi (2\pi c+2\pi r^2d+\epsilon )}\alpha _1}{b^2}, \end{aligned}$$

(A52)

$$\begin{aligned} M= & {} -\frac{1}{8 a b^2}\left[ a (b^2 - 16 d \pi ^2) + 8 b \pi (-2c\pi +\epsilon )\right. \nonumber \\&\left. +4 (a (3 b^2-4 d \pi ^2)-2 b \pi (2 c \pi + \epsilon ))\alpha _o\right] , \end{aligned}$$

(A53)

$$\begin{aligned} X= & {} \frac{1}{8 a b^2}\left[ a (3 b^2 + 16 d \pi ^2) + 8 b \pi (-2 c \pi + \epsilon ) \right. \nonumber \\&\left. +4 (a (3 b^2 + 4 d \pi ^2)-2 b \pi (2 c \pi + \epsilon ))\alpha _o\right] , \end{aligned}$$

(A54)

$$\begin{aligned} F_1= & {} b(3ab-2\pi (2\pi c+2\pi dr^2+\epsilon )), \end{aligned}$$

(A55)

$$\begin{aligned} D= & {} \frac{\sqrt{a(3b^2-4\pi ^2d)+2b\pi (2\pi c+\epsilon )}+\sqrt{F_1}}{\sqrt{a(3b^2-4\pi ^2d)-2b\pi (2\pi c+\epsilon )}-\sqrt{F_1}}, \end{aligned}$$

(A56)

$$\begin{aligned} T= & {} \frac{\left[ a(3b^2-4\pi ^2d)-2b\pi (2\pi c+\epsilon )^{\frac{3}{2}}\right] \alpha _{1}}{2ab^{\frac{5}{2}}\sqrt{2\pi }}, \end{aligned}$$

(A57)

$$\begin{aligned} V= & {} \frac{\sqrt{a(3b^2+4\pi ^2d)+2b\pi (2\pi c+\epsilon )}+\sqrt{F_1}}{\sqrt{a(3b^2+4\pi ^2d)-2b\pi (2\pi c+\epsilon )}-\sqrt{F_1}}, \end{aligned}$$

(A58)

$$\begin{aligned} C= & {} -\frac{[a(3b^2+4\pi ^2d)-2b\pi (2\pi c+\epsilon )^{\frac{3}{2}}]\alpha _{1}}{2ab^{\frac{5}{2}}\sqrt{2\pi }}. \end{aligned}$$

(A59)

For $n=2$ degree of anisotropy becomes

$$\begin{aligned} \Delta= & {} \frac{1}{\sqrt{\pi }} (-2\sqrt{2} (3 a b - 4 c \pi ^2 + 3 b^2 r^2\nonumber \\&-\, 4 d \pi ^2 r^2 -2 \pi \epsilon ){(3/2)}\alpha _1 +4 \sqrt{\pi }\nonumber \\&\times (4 c \pi ^2 -3 a b - 3 b^2 r^2 + 4 d \pi ^2 r^2 \nonumber \\&+\,2 \pi \epsilon )\alpha _o+4 \sqrt{\pi }\left[ b (-2 a + b r^2)\right. \nonumber \\&-\,4 \pi ^2 (c +d r^2) + \left[ -b (a (M-X)\right. \nonumber \\&+\, b r^2 (M + X))+C (a^2-b^2 r^4)T\nonumber \\&\times (e^W W^\prime )+ r^2 (a + b r^2)^2\nonumber \\&\times \left( b^2 \times \left( \frac{M^2}{(a - b r^2)^2}+\frac{(-1 + X) X}{(a + b r^2)^2}\right. \right. \nonumber \\&\left. +\,M \left( -\frac{1}{(a - b r^2)^2} -\frac{2 X}{a^2 - b^2 r^4}\right) \right) \nonumber \\&+\,(C-1) C T e^WW^\prime +\frac{1}{(a-br^2)(a+br^2)}\nonumber \\&\times C\left( -2 b (a (M - X) +b r^2 (M + X))\right. \nonumber \\&\times \left( T \times \left( e^W W^\prime +(a^2 -b^2 r^4) \right. \right. \nonumber \\&\times \left( Te^W\times \left( (T-1)\left( e^W+D^{1-T} e^W {W^\prime }^2 + W^{\prime \prime }\right) \right) \right) \nonumber \\&\left. \left. \left. \left. \left. \left. \times D^{2-T}\right) \right) \right) \right) \right] \right] . \end{aligned}$$

(A60)

The line element Eq. (1) for $n=2$ takes the form

$$\begin{aligned} ds^{2}= & {} -K_2 e^{2W}(a-br^{2})^{2M}(a+br^{2})^{2(X-1)}[D]^{T}[V]^{2C}dt^{2}\\&+(a+br^{2})^{-2}[dr^{2}+r^{2}(d\theta ^{2}+sin^{2}d\phi ^{2})]. \end{aligned}$$