Vacuum instability in a constant inhomogeneous electric field: a new example of exact nonperturbative calculations

Abstract

Basic quantum processes (such as particle creation, reflection, and transmission on the corresponding Klein steps) caused by inverse-square electric fields are calculated. These results represent a new example of exact nonperturbative calculations in the framework of QED. The inverse-square electric field is time-independent, inhomogeneous in the x -direction, and is inversely proportional to x squared. We find exact solutions of the Dirac and Klein–Gordon equations with such a field and construct corresponding in- and out-states. With the help of these states and using the techniques developed in the framework of QED with x-electric potential steps, we calculate characteristics of the vacuum instability, such as differential and total mean numbers of particles created from the vacuum and vacuum-to-vacuum transition probabilities. We study the vacuum instability for two particular backgrounds: for fields widely stretches over the x-axis (small-gradient configuration) and for the fields sharply concentrates near the origin $x=0$ (sharp-gradient configuration). We compare exact results with ones calculated numerically. Finally, we consider the electric field configuration, composed by inverse-square fields and by an x-independent electric field between them to study the role of growing and decaying processes in the vacuum instability.

1 Introduction

Particle creation from the vacuum by strong electromagnetic and gravitational fields is a remarkable effect predicted by quantum field theory (QFT). In the late 20s and the early 30s, Klein [1, 2] and Sauter [3] considered the effect in the framework of the relativistic quantum mechanics. However, from the very beginning, it became clear that all the questions could be answered only in the framework of QFT. QFT with external backgrounds is, to a certain extent, an appropriate model for such calculations. In the framework of such a model, the particle creation is related to a violation of the vacuum stability with the time. Backgrounds (external fields) that violate the vacuum stability are electric-like fields that are able to produce nonzero work when interacting with charged particles. Depending on the structure of such backgrounds, different approaches for calculating the effect were proposed and realized. From a quantum mechanical point of view, the most clear formulation of the problem of particle production from the vacuum by external fields is possible for time-dependent external electric fields that are switched on and off at infinitely remote times $t\rightarrow \pm \infty$, respectively. Such kind of external fields are called the t-electric potential steps (t-step or t-steps). Scattering, particle creation from the vacuum and particle annihilation by the t-steps were considered in the framework of the relativistic quantum mechanics, see Refs. [4,5,6,7,8], a more complete list of relevant publications can be found in [7, 8]. A general nonperturbative with respect to the external background formulation of QED with t-steps was developed in Refs. [9,10,11].

In contrast to the t-electric potential steps, there are many physically interesting situations where the external backgrounds are constant (time-independent) but spatially inhomogeneous, for example, concentrated in restricted space areas. The simplest type of such backgrounds is the so-called x-electric potential steps (x-step or x-steps), in which the field is inhomogeneous only in one space coordinate and represents a spatial-like step for charged particles. The x-steps can also create particles from the vacuum, the Klein paradox is closely related to this process [1,2,3, 12]. Important calculations of the particle creation by x-steps in the framework of the relativistic quantum mechanics were presented by Nikishov in Refs. [5, 13] and later developed by Hansen and Ravndal in Refs. [14, 15]. A general nonperturbative with respect to the external background formulation of QED with x-steps was developed in Ref. [16]. The corresponding calculation is based on the existence of exact solutions of Dirac or Klein–Gordon equation (wave equations, in what follows) with corresponding external fields. When such solutions can be found and all the calculations can be done, we refer these examples as exactly solvable cases. Until now, there are known only few exactly solvable cases related to t-steps and to x-steps. In the case of the t-steps, these are particle creation in the constant uniform electric field [4, 17], in the adiabatic electric field $E\left( t\right) =E\cosh ^{-2}\left( t/T_{ \mathrm {S}}\right) \,$ [18], in the so-called T-constant electric field [19,20,21], in a periodic alternating in time electric field [21, 22], in an exponentially decaying electric field [23], in an exponentially growing and decaying electric fields [24, 25] (see Ref. [26] for the review), in a composite electric field [27, 28], and in an inverse-square electric field (an electric field that is inversely proportional to time squared [30]). In the case of x-steps these are particle creation in the Sauter electric field [16], in the so-called L-constant electric field [29], and in the inhomogeneous exponential peak field [31].

In this article, we present a new exactly solvable case in QED with x -steps where all nonperturbative characteristics of the vacuum instability can be calculated and analyzed in detail. The electric field that corresponds to this specific step is time-independent, it grows from zero in the interval $x\in \left( -\infty ,0\right)$ inversely proportional to x squared and decreases in the interval $x\in \left[ 0,+\infty \right)$ also inversely proportional to x squared, with x being the coordinate $x=X^{1}$. For brevity, we hereinafter call such a field the inverse potential step. An exact description of this field is given in Sect. 2. There, we present exact solutions of the Dirac and Klein–Gordon equations with such a step and construct corresponding in- and out-states. With the help of these states and using the techniques developed in the work [16], we calculate pertinent quantities for studying all the characteristics of the particle creation effect occurring in the Klein zone, such as differential mean numbers of particles created from the vacuum, total numbers and vacuum-to-vacuum transition probabilities. These results are presented in Sect. 3. Besides processes related to the vacuum instability, in Sect. 4 we calculate amplitudes and probabilities of basic processes occurring beyond the Klein zone, namely reflection and transmission probabilities. Comparisons between exact results (calculated numerically) and corresponding asymptotic estimates are placed in Sect. 5. In Sect. 6, we discuss the role of growing and decaying processes in developing the vacuum instability by considering various electric field configuration, composed by inverse-square fields and by an x-independent electric field between them. The Sect. 7 is devoted to the concluding remarks. Useful formulas involving Whittaker functions and some asymptotic representations of confluent hypergeometric functions are placed in Appendix A. An unitary operator, connecting in- and out-vacua in Klein zone, is described in Appendix B.

2 Solutions of wave equations with inverse potential steps

2.1 Inverse potential steps

Here we consider wave equations with inverse potential steps and their solutions. First of all, we describe more exactly the structure of the electromagnetic field of inverse potential steps. Such a field is an electric field in a $d=D+1$ dimensional Minkowski space-time. The latter space-time is parameterized by coordinates $X=\left( X^{\mu },\mu =0,1,\ldots ,D\right) =\left( X^{0}=t,{\mathbf {r}}\right)$, ${\mathbf {r}}=\left( X^{1}=x,{\mathbf {r}}_{\perp }\right)$, ${\mathbf {r}}_{\perp }=\left( X^{2},\ldots ,X^{D}\right)$, the corresponding metric reads $\eta _{\mu \nu }= \mathrm {diag}\left( 1,-1, \ldots ,-1\right)$. The electric field is constant and has only one component along the x-axis, ${\mathbf {E}}\left( X\right) =\left( E^{1}\left( x\right) =E\left( x\right) ,0,\ldots ,0\right)$. The corresponding electromagnetic potentials $A^{\mu }\left( X\right)$ are:

$$\begin{aligned} A^{\mu }\left( X\right) = ( A^{0}\left( x\right) ,\ \ A^{k}=0, \ \ k=1,\ldots ,D). \end{aligned}$$

It is assumed that the electric field $E\left( x\right) =-\partial _{x}A_{0}\left( x\right) >0$ is positive on the whole interval $x\in \mathbb { R=(}-\infty ,+\infty )$ and switches on and off at $x\rightarrow -\infty$ and $x\rightarrow +\infty$ respectively. At the same time, its potential $A^{0}\left( x\right)$ tends to certain, different in the general case, constants values,

$$\begin{aligned}&\lim _{x\rightarrow \pm \infty }A^{0}\left( x\right) =A_{0}\left( \pm \infty \right) ,\ A_{0}\left( -\infty \right) \ne A_{0}\left( +\infty \right) ,\nonumber \\&\ A_{0}\left( -\infty \right) >A_{0}\left( +\infty \right) . \end{aligned}$$

(1)

The field in question consists of two pieces, the first one is defined on the interval $x\in \mathrm {I}=\left( -\infty ,0\right)$ while the second one is defined on the interval $x\in \mathrm {II}=\left[ 0,+\infty \right)$,

$$\begin{aligned} E\left( x\right) =E\left\{ \begin{array}{ll} \left( 1-x/\xi _{1}\right) ^{-2}, &{} \quad x\in \mathrm {I}, \\ \left( 1+x/\xi _{2}\right) ^{-2}, &{} \quad x\in \mathrm {II}. \end{array} \right. \end{aligned}$$

(2)

The corresponding potential reads:

$$\begin{aligned} A_{0}\left( x\right) =E\left\{ \begin{array}{ll} \xi _{1}\left[ 1-\left( 1-x/\xi _{1}\right) ^{-1}\right] , &{} \quad x\in \mathrm {I }, \\ \xi _{2}\left[ \left( 1+x/\xi _{2}\right) ^{-1}-1\right] , &{} \quad x\in \mathrm { II}. \end{array} \right. \end{aligned}$$

(3)

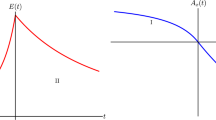
The constants $\xi _{1,2}>0$ are length scales characterizing how “smooth” or “sharp” the electric field evolves from $x=-\infty$ to $x=0$ and from $x=0$ to $x=+\infty$. At the same time, they characterize the magnitude of the potential step. On Fig. 1, we represent an asymmetrical inverse-square electric field, in which $\xi _{2}>\xi _{1}$.

Fig. 1

Inverse-square electric field. In this picture, $\xi _{2}> \xi _{1}$

The potential energy of an electron (with the charge $q=-e,$ $e>0$) in the field of the step is $U\left( x\right) =-eA_{0}\left( x\right)$. It tends to different in the general case constants values $U\left( -\infty \right)$ and $U\left( +\infty \right)$ as $x\rightarrow -\infty$ and $x\rightarrow +\infty$ respectively,

$$\begin{aligned} U\left( -\infty \right) \equiv U_{\mathrm {L}}=-eE\xi _{1},\ \ U\left( +\infty \right) \equiv U_{\mathrm {R}}=eE\xi _{2}. \end{aligned}$$

(4)

The magnitude ${\mathbb {U}}$ of the potential step is given by the difference $U_{\mathrm {R}}-U_{\mathrm {L}}$:

$$\begin{aligned}&{\mathbb {U}}=U_{\mathrm {R}}-U_{\mathrm {L}}=\Delta U_{1}+\Delta U_{2}=eE\left( \xi _{1}+\xi _{2}\right) >0, \nonumber \\&\Delta U_{1}=U\left( 0\right) -U\left( -\infty \right) =eE\xi _{1},\ \nonumber \\&\Delta U_{2}=U\left( +\infty \right) -U\left( 0\right) =eE\xi _{2}\ . \end{aligned}$$

(5)

Depending on the magnitude ${\mathbb {U}}$, the step is called noncritical or critical one, see [16],

$$\begin{aligned} {\mathbb {U}}=\left\{ \begin{array}{l} {\mathbb {U}}<{\mathbb {U}}_{c}=2m, { \text { noncritical step}} \\ {\mathbb {U}}>{\mathbb {U}}_{c}, \qquad \quad \,\, { \text { critical step}} \end{array} \right. . \end{aligned}$$

(6)

As follows from Eq. (5), this classification can be formulated in terms of the sum ($\xi _{2}+\xi _{1}$) of the length scales $\xi _{1,2}$,

(7)

where $E_{c}=m^{2}/e\approx 10^{16}\ \mathrm {V/cm}$ is the Schwinger critical field and is the Compton wave length of the electron. If the length scales $\xi _{1,2}$ are large enough, the particle production from the vacuum could be essential. On Fig. 2 we illustrate the potential energy $U\left( x\right)$ for specific values of $\xi _{1,2}$ and electric field amplitude E.

Fig. 2

Potential energies of an electron $U\left( x\right)$ in critical inverse-square electric fields, corresponding to a “smooth” potential step (solid yellow line) and a “steep” potential step (solid blue line), both with the same asymptotic values $U_{\mathrm {L/R}}$. The smaller (larger) the value of the length scales $\xi _{j}$, the steeper (the smoother) the potential step. In both curves, $\xi _{2}>\xi _{1}$

In the Hamiltonian form, the Dirac equation with the inverse step reads:

$$\begin{aligned}&i\partial _{0}\psi \left( X\right) ={\hat{H}}\psi \left( X\right) , \nonumber \\&{\hat{H}}=\gamma ^{0}\left( -i\gamma ^{j}\partial _{j}+m\right) +U\left( x\right) ,\ \ j=1, \ldots ,D, \end{aligned}$$

(8)

where the spinor field $\psi \left( X\right)$ has $2^{\left[ d/2\right] }$ components¹ and $\gamma ^{\mu }$ are $2^{\left[ d/2\right] }\times 2^{\left[ d/2\right] }$ Dirac matrices in $d=D+1$ dimensions,

$$\begin{aligned} \left[ \gamma ^{\mu },\gamma ^{\nu }\right] _{+}=2\eta ^{\mu \nu },\ \ \eta ^{\mu \nu }=\mathrm {diag}\underset{d}{\underbrace{\left( +1,-1, \ldots ,-1\right) }}. \end{aligned}$$

(9)

Because electromagnetic potentials of the inverse steps have trivial components ${\mathbf {A}}=0$, there exist solutions of the Dirac equation in the form of stationary plane waves propagating along the space-time directions t and ${\mathbf {r}}_{\perp }$. In this case the Dirac spinors can be represented as

$$\begin{aligned} \psi _{n}\left( X\right)= & {} \exp \left( -ip_{0}t+i{\mathbf {p}}_{\perp } {\mathbf {r}}_{\perp }\right) \psi _{n}\left( x\right) ,\ \ n=\left( p_{0}, {\mathbf {p}}_{\perp },\sigma \right) , \nonumber \\ \psi _{n}\left( x\right)= & {} \left\{ \gamma ^{0}\left[ p_{0}-U\left( x\right) \right] +i\gamma ^{1}\partial _{x}-\varvec{\gamma }_{\perp } {\mathbf {p}}_{\perp }+m\right\} \varphi _{n}\left( x\right) v_{\chi ,\sigma }, \nonumber \\ \end{aligned}$$

(10)

where the spinor $\psi _{n}\left( x\right)$ and the scalar function $\varphi _{n}\left( x\right)$ depend exclusively on x while $v_{\chi ,\sigma }$ are eigenspinors of $\gamma ^{0}\gamma ^{1}$, satisfying $\gamma ^{0}\gamma ^{1}v_{\chi ,\sigma }=\chi v_{\chi ,\sigma }$, $\chi =\pm 1$. Here, $\sigma =\left( \sigma _{s}=\pm 1,\ s=1,2,\ldots ,\left[ d/2\right] -1\right)$ denotes a set of eigenvalues of spin operators compatible with $\gamma ^{0}\gamma ^{1}$, whose amount depends on the space-time dimensionality d. For higher dimensions,² $d>3+1$, we may construct $J_{\left( d\right) }=2^{ \left[ d/2\right] -1}$ additional spin operators and subject the constant spinors $v_{\chi ,\sigma }$ to the following supplementary conditions:

$$\begin{aligned}&i\gamma ^{2s}\gamma ^{2s+1}v_{\chi ,\sigma }=\sigma _{s}v_{\chi ,\sigma }, \quad \mathrm {\ \ for\ even\ }d, \nonumber \\&i\gamma ^{2s+1}\gamma ^{2s+2}v_{\chi ,\sigma }=\sigma _{s}v_{\chi ,\sigma }, \quad \mathrm {for\ odd}\ d, \nonumber \\&v_{\chi ^{\prime },\sigma ^{\prime }}^{\dagger }v_{\chi ,\sigma }=\delta _{\chi ^{\prime }\chi }\delta _{\sigma ^{\prime }\sigma }. \end{aligned}$$

(11)

Due to the compatibility of the spin operators with $\gamma ^{0}\gamma ^{1}$ , the eigenvalues $\sigma _{s}$, in addition to $\chi$, parameterize the solutions. Plugging Eqs. (10) into (8), one finds that scalar functions $\varphi _{n}\left( x\right)$ obey the second-order ordinary differential equation

$$\begin{aligned} \left\{ \frac{d^{2}}{dx^{2}}+\left[ p_{0}-U\left( x\right) \right] ^{2}-\pi _{\perp }^{2}+i\chi U^{\prime }\left( x\right) \right\} \varphi _{n}\left( x\right) =0. \nonumber \\ \end{aligned}$$

(12)

Here $\pi _{\perp }=\sqrt{{\mathbf {p}}_{\perp }^{2}+m^{2}}$ and by a prime a differentiation with respect to x, $U^{\prime }\left( x\right) =dU\left( x\right) /dx$, is denoted.

It should be noted that similar solutions of the Klein–Gordon equation can be represented as:

$$\begin{aligned} \psi _{n}\left( X\right) =\exp \left( -ip_{0}t+i{\mathbf {p}}_{\perp }{\mathbf {r}} _{\perp }\right) \varphi _{n}\left( x\right) ,\ \ n=\left( p_{0},{\mathbf {p}} _{\perp }\right) , \nonumber \\ \end{aligned}$$

(13)

where $\varphi _{n}\left( x\right)$ satisfy Eq. (12) with $\chi =0$ . Besides minor modifications in the normalization constants for scalar particles (discussed in the next subsection) a formal transition to the Klein–Gordon case can be done by setting $\chi =0$ in all formulas above.

2.2 Solutions with special left and right asymptotics

Introducing new variables

$$\begin{aligned} z_{1}\left( x\right)= & {} 2i\left| p^{\mathrm {L}}\right| \xi _{1}\left( 1-x/\xi _{1}\right) ,\ \ x\in \mathrm {I}, \nonumber \\ z_{2}\left( x\right)= & {} 2i\left| p^{\mathrm {R}}\right| \xi _{2}\left( 1+x/\xi _{2}\right) ,\ \ x\in \mathrm {II}, \end{aligned}$$

(14)

where $p^{\mathrm {L/R}}=\zeta \left| p^{\mathrm {L/R}}\right|$, $\zeta =\mathrm {sgn}\left( p^{\mathrm {L}}\right)$, $\zeta =\mathrm {sgn}\left( p^{\mathrm {R}}\right)$, $\zeta =\pm$, denotes real asymptotic momenta along the x-axis,³

$$\begin{aligned} \left| p^{\mathrm {L/R}}\right| =\sqrt{\pi _{0}\left( \mathrm {L/R} \right) ^{2}-\pi _{\perp }^{2}},\ \ \pi _{0}\left( \mathrm {L/R}\right) =p_{0}-U_{\mathrm {L/R}}, \nonumber \\ \end{aligned}$$

(15)

differential equation (12) reduces to a Whittaker differential equation⁴ [32],

$$\begin{aligned} \left( \frac{d^{2}}{dz_{j}^{2}}-\frac{1}{4}+\frac{\kappa _{j}}{z_{j}}+\frac{ 1/4-\mu _{j}^{2}}{z_{j}^{2}}\right) \varphi _{n}\left( z_{j}\right) =0, \end{aligned}$$

(16)

whose parameters $\kappa _{j}$, $\mu _{j}$ are given by

$$\begin{aligned}&\kappa _{1}=i\Delta U_{1}\xi _{1}\frac{\pi _{0}\left( \mathrm {L}\right) }{ \left| p^{\mathrm {L}}\right| },\ \ \kappa _{2}=-i\Delta U_{2}\xi _{2}\frac{\pi _{0}\left( \mathrm {R}\right) }{\left| p^{\mathrm {R} }\right| }, \nonumber \\&\mu _{j}=\left( -1\right) ^{j}\left( i\Delta U_{j}\xi _{j}-\chi /2\right) . \end{aligned}$$

(17)

General solutions of Eq. (16) are chosen to be combinations of Whittaker functions with regular asymptotics at infinity [32, 33],

$$\begin{aligned}&W_{\kappa ,\mu }\left( z\right) =e^{-z/2}z^{\kappa }\left[ 1+O\left( z^{-1}\right) \right] ,\ \ z\rightarrow \infty ,\ \ \nonumber \\&\left| \arg z\right| \le \frac{3\pi }{2}-0^{+}, \end{aligned}$$

(18)

such that $\varphi _{n}\left( z_{j}\right) =b_{j}^{1}W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) +b_{j}^{2}W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right)$, with $b_{j}^{1,2}$ being arbitrary constants. The Whittaker functions can be alternatively expressed in terms of confluent hypergeometric functions (CHF) as follows:

$$\begin{aligned}&W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) =e^{-z_{j}/2}z_{j}^{c_{j}/2}\Psi \left( a_{j},c_{j};z_{j}\right) , \nonumber \\&W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) \nonumber \\&\quad =e^{-i\pi c_{j}/2}e^{z_{j}/2}z_{j}^{c_{j}/2}\Psi \left( c_{j}-a_{j},c_{j};e^{-i\pi }z_{j}\right) , \nonumber \\&a_{j}=\mu _{j}-\kappa _{j}+1/2,\ c_{j}=1+2\mu _{j}, \end{aligned}$$

(19)

and the Wronskian of the independent set $W_{\kappa _{j},\mu _{j}}\left( z_{j}\right)$, $W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right)$ is given by Eq. (13.14.30) in [33].

Due to local properties of Eq. (12) at $x\rightarrow \mp \infty$ (where the electric field is zero), the scalar functions $\varphi _{n}\left( x\right)$ have definite left “L ” and right “R ” asymptotics:

$$\begin{aligned} \ _{\zeta }\varphi _{n}\left( x\right)= & {} \ _{\zeta }{\mathcal {N}}e^{i\zeta \left| p^{\mathrm {L}}\right| x}\ {\text {as}}\ x\rightarrow -\infty , \nonumber \\ \ ^{\zeta }\varphi _{n}\left( x\right)= & {} \ ^{\zeta }{\mathcal {N}}e^{i\zeta \left| p^{\mathrm {R}}\right| x}{\text { as}}\ \ x\rightarrow +\infty . \end{aligned}$$

(20)

Here $p^{\mathrm {L}}$, $p^{\mathrm {R}}$ are asymptotic momenta along the x -axis, given by Eq. (15), whereas $_{\zeta }{\mathcal {N}}$ and$\ ^{\zeta }{\mathcal {N}}$ are some normalization constants. We label the scalar functions by $\zeta$ related to the corresponding momenta.

For the Dirac spinors we have:

$$\begin{aligned} {\hat{p}}_{x}\ _{\zeta }\psi _{n}\left( X\right)= & {} \zeta \left| p^{ \mathrm {L}}\right| \ _{\zeta }\psi _{n}\left( X\right) \ \text {as}\ x\rightarrow -\infty , \nonumber \\ {\hat{p}}_{x}\ ^{\zeta }\psi _{n}\left( X\right)= & {} \zeta \left| p^{ \mathrm {R}}\right| \ ^{\zeta }\psi _{n}\left( X\right) \ \text {as }\ x\rightarrow +\infty , \end{aligned}$$

(21)

and

$$\begin{aligned}&{\hat{H}}^{\mathrm {kin}}\ _{\zeta }\psi _{n}\left( X\right) =\pi _{0}\left( \mathrm {L}\right) \ _{\zeta }\psi _{n}\left( X\right) \ \mathrm {as}\ x\rightarrow -\infty , \nonumber \\&{\hat{H}}^{\mathrm {kin}}\ ^{\zeta }\psi _{n}\left( X\right) =\pi _{0}\left( \mathrm {R}\right) \ ^{\zeta }\psi _{n}\left( X\right) \ \mathrm {as}\ x\rightarrow +\infty , \end{aligned}$$

(22)

where ${\hat{H}}^{\mathrm {kin}}={\hat{H}}-U\left( x\right)$ is the one-particle quantum kinetic energy operator. Thus, nontrivial sets of Dirac spinors $\left\{ \ _{\zeta }\psi _{n}\left( X\right) \right\}$, $\left\{ \ ^{\zeta }\psi _{n}\left( X\right) \right\}$ exist for quantum numbers n satisfying the conditions

$$\begin{aligned} \pi _{0}\left( \mathrm {L/R}\right) ^{2}>\pi _{\perp }^{2}\Rightarrow \left\{ \begin{array}{l} \pi _{0}\left( \mathrm {L/R}\right) >\pi _{\perp }\, \\ \pi _{0}\left( \mathrm {L/R}\right) <-\pi _{\perp }\, \end{array} \right. . \end{aligned}$$

(23)

As a result of the above inequalities, the set of quantum numbers n can be divided in specific ranges $\Omega _{k}$, where the index k labels distinct ranges and the corresponding quantum numbers $n_{k}\in \Omega _{k}$ . For critical steps, ${\mathbb {U}}>{\mathbb {U}}_{c}$, there are five ranges of quantum numbers $\Omega _{k}$, $k=1,\ldots ,5$, composed by all spinning degrees-of-freedom $\sigma$, perpendicular momenta ${\mathbf {p}}_{\perp }$, and by certain energies $p_{0}$, whose definitions and general properties are briefly listed below:

• 1. The ranges $\Omega _{1}$ and $\Omega _{5}$ are characterized by energies bounded from below, $\Omega _{1}=\left\{ n:p_{0}\ge U_{\mathrm {R}}+\pi _{\perp }\right\} ,$ and by energies bounded from above $\Omega _{5}=\left\{ n:p_{0}\le U_{\mathrm {L} }-\pi _{\perp }\right\}$. In each one of these ranges, all relations from Eq. (23) are satisfied, which implies that nontrivial complete sets of solutions $\left\{ \ _{\zeta }\psi _{n_{1}}\left( X\right) ,\ _{\zeta }\psi _{n_{5}}\left( X\right) \right\}$ and $\left\{ \ ^{\zeta }\psi _{n_{1}}\left( X\right) ,\ ^{\zeta }\psi _{n_{5}}\left( X\right) \right\}$ do exist.

• 2. The ranges $\Omega _{2}$ and $\Omega _{4}$ are characterized by bounded energies, namely $\Omega _{2}=\left\{ n:U_{\mathrm {R}}-\pi _{\perp }<p_{0}<U_{\mathrm {R}}+\pi _{\perp }\right\}$ and $\Omega _{4}=\left\{ n:U_{\mathrm {L}}-\pi _{\perp }<p_{0}<U_{\mathrm {L}}+\pi _{\perp }\right\}$ if ${\mathbb {U}}\ge 2\pi _{\perp }$ or $\Omega _{2}=\left\{ n:U_{\mathrm {L}}+\pi _{\perp }<p_{0}<U_{ \mathrm {R}}+\pi _{\perp }\right\}$ and $\Omega _{4}=\left\{ n:U_{\mathrm {L} }-\pi _{\perp }<p_{0}<U_{\mathrm {R}}-\pi _{\perp }\right\}$ if ${\mathbb {U}} <2\pi _{\perp }$. The relation $\pi _{0}\left( \mathrm {L}\right) >\pi _{\perp }$ is satisfied only for quantum numbers from $\Omega _{2}$ while the relation $\pi _{0}\left( \mathrm {R}\right) <-\pi _{\perp }$ is satisfied only for quantum numbers from $\Omega _{4}$, which means that in $\Omega _{2}$ there exist solutions only with left asymptotics $\left\{ \ _{\zeta }\psi _{n_{2}}\left( X\right) \right\}$ while in $\Omega _{4}$ there exist solutions only with right asymptotics $\left\{ \ ^{\zeta }\psi _{n_{4}}\left( X\right) \right\}$.

• 3. The range $\Omega _{3}$ is nontrivial only for critical steps and perpendicular momenta ${\mathbf {p}}_{\perp }$ restricted by the inequality $2\pi _{\perp }\le {\mathbb {U}}$. This range is characterized by bounded energies, $\Omega _{3}=\left\{ n:U_{\mathrm {L}}+\pi _{\perp }\le p_{0}\le U_{\mathrm { R}}-\pi _{\perp }\right\}$. In this range, the relations $\pi _{0}\left( \mathrm {L}\right) \ge \pi _{\perp }$ and $\pi _{0}\left( \mathrm {R}\right) \le -\pi _{\perp }$ hold true which means that both sets of solutions $\left\{ \ _{\zeta }\psi _{n_{3}}\left( X\right) \right\}$ and $\left\{ \ ^{\zeta }\psi _{n_{3}}\left( X\right) \right\}$ do exist.

The assumption about the completeness of solutions in some ranges refers to their asymptotic properties at infinitely remote distances. Because of the properties of the Whittaker functions with large arguments (18), sets of solutions in the ranges $\Omega _{1}$, $\Omega _{3}$, and $\Omega _{5}$ are complete asymptotically. Moreover, because of the triviality of right solutions in $\Omega _{2}$ and left solutions in $\Omega _{4}$, certain restrictions on the form of solutions apply in these ranges. The manifold of all the quantum numbers n is denoted by $\Omega =\Omega _{1}\cup \cdots \cup \Omega _{5}$. For noncritical steps ${\mathbb {U}}<{\mathbb {U}}_{c}$, the range $\Omega _{3}$ is absent. For the correct interpretation of the states $\left\{ \ _{\zeta }\psi _{n}\left( X\right) \right\}$ and $\left\{ \ ^{\zeta }\psi _{n}\left( X\right) \right\}$ as wave functions describing electrons and positrons as well as for a complete discussion about the ranges and further properties, see Ref. [16].

In view of the asymptotic behavior of the Whittaker functions with large argument (18) and the properties discussed above, it is possible to classify solutions in the first $\mathrm {I}$ and in the second $\mathrm {II}$ intervals according to the sign $\zeta =\pm$ of the asymptotic momenta $p^{ \mathrm {L/R}}$. Denoting scalar functions in $\mathrm {I}$, $\mathrm {II}$ as$\ _{\zeta }\varphi _{n}\left( x\right)$ and$\ ^{\zeta }\varphi _{n}\left( x\right)$, respectively, we have:

$$\begin{aligned} \ _{+}\varphi _{n}\left( x\right)= & {} \ _{+}{\mathcal {N}}W_{\kappa _{1},\mu _{1}}\left( z_{1}\right) ,\nonumber \\ \ _{-}\varphi _{n}\left( x\right)= & {} \ _{-} {\mathcal {N}}W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) ,\ \ x\in \mathrm {I}, \nonumber \\ \ ^{+}\varphi _{n}\left( x\right)= & {} \ ^{+}{\mathcal {N}}W_{-\kappa _{2},\mu _{2}}\left( e^{-i\pi }z_{2}\right) ,\nonumber \\ ^{-}\varphi _{n}\left( x\right)= & {} \ ^{-}{\mathcal {N}}W_{\kappa _{2},\mu _{2}}\left( z_{2}\right) , \ \ x\in \mathrm {II}. \end{aligned}$$

(24)

Once the electric field is homogeneous in time and in the coordinates perpendicular to the field ${\mathbf {r}}_{\perp }$, the normalization constants $_{\zeta }{\mathcal {N}}$ and$\ ^{\zeta }{\mathcal {N}}$ are calculated with respect to the inner product on the x-constant hyperplane

$$\begin{aligned} \left( \psi ,\psi ^{\prime }\right) _{x}=\int \psi ^{\dagger }\left( X\right) \gamma ^{0}\gamma ^{1}\psi ^{\prime }\left( X\right) dtd{\mathbf {r}} _{\perp }. \end{aligned}$$

(25)

To calculate the inner product, we consider our system in a large space-time box of the volume $V_{\perp }=\prod _{j=2}^{D}K_{j}$ and over time T, where all length scales $K_{j}$, T are macroscopically large. Moreover, we impose periodic boundary conditions on the Dirac spinors $\psi \left( X\right)$ in the variables t and $X^{j}$, $j=2,\ldots ,D$. Then, the integrations over the transverse coordinates are performed from $-K_{j}/2$ to $+K_{j}/2$ and from $-T/2$ to $+T/2$, where the limits $K_{j}\rightarrow \infty$, $T\rightarrow \infty$ are assumed in final expressions; see Ref. [16] for details. Under these conditions, inner product (25) is x-independent and can be expressed in terms of the scalar functions as⁵ follows:

$$\begin{aligned}&\left( \psi _{n},\psi _{n^{\prime }}^{\prime }\right) _{x}=V_{\perp }T\delta _{nn^{\prime }}{\mathcal {I}}_{n}, \nonumber \\&{\mathcal {I}}_{n}=\varphi _{n}^{*}\left( x\right) \left( i\overleftarrow{ \partial }_{x}-i\overrightarrow{\partial }_{x}\right) \left[ p_{0}-U\left( x\right) +i\chi \partial _{x}\right] \varphi _{n}^{\prime }\left( x\right) . \nonumber \\ \end{aligned}$$

(26)

According to general properties of the left and right asymptotics outlined in the previous section, the solutions $\left\{ \ _{\zeta }\psi _{n}\left( X\right) \right\}$ and $\left\{ \ ^{\zeta }\psi _{n}\left( X\right) \right\}$ can be subjected to the orthonormalization conditions

$$\begin{aligned} \left( \ _{\zeta }\psi _{n},\ _{\zeta }\psi _{n^{\prime }}\right) _{x}= & {} \zeta \eta _{\mathrm {L}}\delta _{\zeta \zeta ^{\prime }}\delta _{nn^{\prime }},\ \ n\in \Omega _{1}\cup \Omega _{2}\cup \Omega _{3}\cup \Omega _{5}, \nonumber \\ \left( \ ^{\zeta }\psi _{n},\ ^{\zeta }\psi _{n^{\prime }}\right) _{x}= & {} \zeta \eta _{\mathrm {R}}\delta _{\zeta \zeta ^{\prime }}\delta _{nn^{\prime }},\ \ n\in \Omega _{1}\cup \Omega _{3}\cup \Omega _{4}\cup \Omega _{5}, \nonumber \\ \end{aligned}$$

(27)

where $\eta _{\mathrm {L}}=\mathrm {sgn}\pi _{0}\left( \mathrm {L}\right)$ and $\eta _{\mathrm {R}}=\mathrm {sgn}\pi _{0}\left( \mathrm {R}\right)$. Using asymptotic properties of the Whittaker functions (18) and the above conditions, the normalization constants $_{\zeta }{\mathcal {N}}$ and $\ ^{\zeta }{\mathcal {N}}$ are

$$\begin{aligned}&\ _{\zeta }{\mathcal {N}}=\ _{\zeta }CY,\ \ ^{\zeta }{\mathcal {N}}=\ ^{\zeta }CY,\ \ Y=\left( V_{\perp }T\right) ^{-1/2}, \nonumber \\&\ _{\zeta }C=\frac{\exp \left( -i\pi \kappa _{1}/2\right) }{\sqrt{ 2\left| p^{\mathrm {L}}\right| \left| \pi _{0}\left( \mathrm {L} \right) -\zeta \chi \left| p^{\mathrm {L}}\right| \right| }},\ \ \nonumber \\&^{\zeta }C=\frac{\exp \left( -i\pi \kappa _{2}/2\right) }{\sqrt{ 2\left| p^{\mathrm {R}}\right| \left| \pi _{0}\left( \mathrm {R} \right) -\zeta \chi \left| p^{\mathrm {R}}\right| \right| }}. \end{aligned}$$

(28)

Because spinors $\ _{\zeta }\psi _{n}\left( X\right)$ and $\ ^{\zeta }\psi _{n}\left( X\right)$ with quantum numbers $n\in \Omega _{1}\cup \Omega _{3}\cup \Omega _{5}$ are complete, we can decompose solutions from one set onto another as

$$\begin{aligned} \eta _{\mathrm {L}}\ ^{\zeta }\psi _{n}\left( X\right)= & {} \ _{+}\psi _{n}\left( X\right) g\left( _{+}|^{\zeta }\right) -\ _{-}\psi _{n}\left( X\right) g\left( _{-}|^{\zeta }\right) , \nonumber \\ \eta _{\mathrm {R}}\ _{\zeta }\psi _{n}\left( X\right)= & {} \ ^{+}\psi _{n}\left( X\right) g\left( ^{+}|_{\zeta }\right) -\ ^{-}\psi _{n}\left( X\right) g\left( ^{-}|_{\zeta }\right) , \end{aligned}$$

(29)

where the decomposition coefficients g are given by

$$\begin{aligned}&g\left( ^{\zeta ^{\prime }}|_{\zeta }\right) ^{*}=g\left( _{\zeta }|^{\zeta ^{\prime }}\right) =\left( \ _{\zeta }\psi _{n},\ ^{\zeta ^{\prime }}\psi _{n}\right) _{x},\nonumber \\&n\in \Omega _{1}\cup \Omega _{3}\cup \Omega _{5}. \end{aligned}$$

(30)

Substituting decompositions (29) in normalization conditions (27) we find

$$\begin{aligned}&g\left( ^{\zeta ^{\prime }}|_{+}\right) g\left( _{+}|^{\zeta }\right) -g\left( ^{\zeta ^{\prime }}|_{-}\right) g\left( _{-}|^{\zeta }\right) =\zeta \eta _{\mathrm {L}}\eta _{\mathrm {R}}\delta _{\zeta ,\zeta ^{\prime }}, \nonumber \\&g\left( _{\zeta ^{\prime }}|^{+}\right) g\left( ^{+}|_{\zeta }\right) -g\left( _{\zeta ^{\prime }}|^{-}\right) g\left( ^{-}|_{\zeta }\right) =\zeta \eta _{\mathrm {L}}\eta _{\mathrm {R}}\delta _{\zeta ,\zeta ^{\prime }}. \end{aligned}$$

(31)

The latter relations imply a number of equations on g-coefficients, in particular,

$$\begin{aligned}&\left| g\left( _{-}|^{+}\right) \right| ^{2}=\left| g\left( _{+}|^{-}\right) \right| ^{2},\ \ \left| g\left( _{+}|^{+}\right) \right| ^{2}=\left| g\left( _{-}|^{-}\right) \right| ^{2}, \nonumber \\&\left| g\left( _{+}|^{-}\right) \right| ^{2}-\left| g\left( _{+}|^{+}\right) \right| ^{2}=-\eta _{\mathrm {L}}\eta _{\mathrm {R}}. \end{aligned}$$

(32)

From Eqs. (10) and (29), one finds similar decompositions between the left and right scalar functions,

$$\begin{aligned} \ ^{-}\varphi _{n}\left( x\right) =\left\{ \begin{array}{ll} \eta _{\mathrm {L}}\left[ \ _{+}\varphi _{n}\left( x\right) g\left( _{+}|^{-}\right) -\ _{-}\varphi _{n}\left( x\right) g\left( _{-}|^{-}\right) \right] , &{} x\in \mathrm {I} \\ \ ^{-}{\mathcal {N}}W_{\kappa _{2},\mu _{2}}\left( z_{2}\right) , &{} x\in \mathrm {II} \end{array},\right. \nonumber \\ \end{aligned}$$

(33)

and

$$\begin{aligned} \ _{+}\varphi _{n}\left( x\right) =\left\{ \begin{array}{ll} \ _{+}{\mathcal {N}}W_{\kappa _{1},\mu _{1}}\left( z_{1}\right) , &{} x\in \mathrm {I} \\ \eta _{\mathrm {R}}\left[ \ ^{+}\varphi _{n}\left( x\right) g\left( ^{+}|_{+}\right) -\ ^{-}\varphi _{n}\left( x\right) g\left( ^{-}|_{+}\right) \right] , &{} x\in \mathrm {II} \end{array} \right. \nonumber \\ \end{aligned}$$

(34)

The g-coefficients can be obtained imposing continuity conditions of functions and their derivatives at $x=0$, namely $\ \left. \ _{+}^{-}\varphi _{n}\left( x\right) \right| _{x-0}=\left. \ _{+}^{-}\varphi _{n}\left( x\right) \right| _{x+0}$ and $\left. \partial _{x}\ _{+}^{-}\varphi _{n}\left( x\right) \right| _{x-0}=\left. \partial _{x}\ _{+}^{-}\varphi _{n}\left( x\right) \right| _{x+0}$. Thus, we obtain:

$$\begin{aligned} g\left( _{+}|^{-}\right)= & {} 2\eta _{\mathrm {L}}e^{i\theta _{+}}e^{-i\pi \chi /2}\nonumber \\&\times \sqrt{\frac{\xi _{1}\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| \xi _{2}}{\left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{\mathrm {R}}\right| \right| }}\left( \frac{\left| p^{\mathrm {L}}\right| \xi _{1}}{ \left| p^{\mathrm {R}}\right| \xi _{2}}\right) ^{\chi /2} \nonumber \\&\times \exp \left[ -\frac{\pi }{2}\left( \nu _{1}^{-}+\nu _{2}^{+}\right) \right] \Delta \left( _{+}|^{-}\right) \left( 0\right) , \nonumber \\ \Delta \left( _{+}|^{-}\right) \left( x\right)= & {} \Psi \left( a_{2},c_{2};z_{2}\right) f_{\mathrm {L}}^{+}\left( x\right) \nonumber \\&+\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) f_{\mathrm {R}}^{-}\left( x\right) , \end{aligned}$$

(35)

and

$$\begin{aligned} g\left( ^{-}|_{+}\right)= & {} -2\eta _{\mathrm {R}}e^{i\theta _{-}}e^{i\pi \chi /2}\nonumber \\&\times \sqrt{\frac{\xi _{1}\left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{\mathrm {R}}\right| \right| \xi _{2}}{\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| }}\left( \frac{\left| p^{\mathrm {L}}\right| \xi _{1}}{ \left| p^{\mathrm {R}}\right| \xi _{2}}\right) ^{\chi /2} \nonumber \\&\times \exp \left[ \frac{\pi }{2}\left( \nu _{1}^{+}+\nu _{2}^{-}\right) \right] \Delta \left( ^{-}|_{+}\right) \left( 0\right) , \nonumber \\ \Delta \left( ^{-}|_{+}\right) \left( x\right)= & {} \Psi \left( a_{1},c_{1};z_{1}\right) f_{\mathrm {R}}^{+}\left( x\right) \nonumber \\&+\Psi \left( c_{2}-a_{2},c_{2};e^{-i\pi }z_{2}\right) f_{\mathrm {L}}^{-}\left( x\right) , \end{aligned}$$

(36)

where

$$\begin{aligned} \theta _{\pm }= & {} \pm \left( \left| p^{\mathrm {L}}\right| \xi _{1}-\left| p^{\mathrm {R}}\right| \xi _{2}\right) \\&-eE\xi _{1}^{2}\ln \left( 2\left| p^{\mathrm {L}}\right| \xi _{1}\right) +eE\xi _{2}^{2}\ln \left( 2\left| p^{\mathrm {R}}\right| \xi _{2}\right) , \\ \nu _{1/2}^{\pm }= & {} eE\xi _{1/2}^{2}\left( 1\pm \pi _{0}\left( \mathrm {L/R} \right) /\left| p^{\mathrm {L/R}}\right| \right) , \end{aligned}$$

such that

$$\begin{aligned} f_{\mathrm {L/R}}^{+}\left( x\right)= & {} \left| p^{\mathrm {L/R} }\right| \left[ \frac{1}{2}\left( 1+\frac{c_{1/2}}{z_{1/2}}\right) + \frac{d}{dz_{1/2}}\right] \nonumber \\&\quad \times \Psi \left( c_{1/2}-a_{1/2},c_{1/2};e^{-i\pi }z_{1/2}\right) , \nonumber \\ f_{\mathrm {L/R}}^{-}\left( x\right)= & {} \left| p^{\mathrm {L/R} }\right| \left[ \frac{1}{2}\left( -1+\frac{c_{1/2}}{z_{1/2}}\right) + \frac{d}{dz_{1/2}}\right] \nonumber \\&\quad \times \Psi \left( a_{1/2},c_{1/2};z_{1/2}\right) . \end{aligned}$$

(37)

One can map $g\left( _{+}|^{-}\right)$ onto its complex conjugate $g\left( ^{-}|_{+}\right)$ exchanging $p_{0}\rightleftarrows -p_{0}$ and $\xi _{1}\rightleftarrows \xi _{2}$, simultaneously, to realize that $\left| g\left( _{+}|^{-}\right) \right| ^{2}$ is an invariant. For example, employing Kummer transformations $\Psi \left( a,c;z\right) =z^{1-c}\Psi \left( a-c+1,2-c,z\right)$ to transformed CHF $\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \rightleftarrows \Psi \left( 1-a_{2},2-c_{2};e^{-i\pi }z_{2}\right)$ and $\Psi \left( a_{2},c_{2};z_{2}\right) \rightleftarrows \Psi \left( a_{1}-c_{1}+1,2-c_{1};z_{1}\right)$, one finds that $\Delta \left( _{+}|^{-}\right) \left( x\right) \rightleftarrows e^{i\pi \left( 1-c_{2}\right) }z_{1}^{c_{1}-1}z_{2}^{c_{2}-1}\Delta \left( ^{-}|_{+}\right) \left( x\right)$ to conclude that $g\left( _{+}|^{-}\right) \rightleftarrows g\left( ^{-}|_{+}\right)$ for Fermions. This property simplifies the calculation of differential quantities since one can select a particular sign of $p_{0}$ to study $g\left( _{+}|^{-}\right)$ and generalize results to the opposite sign of $p_{0}$, as shall be discussed in Sect. 3.

To study arbitrary quantum processes, sometimes it is useful to consider other g-coefficients in addition to the coefficients calculated above. For example, to study amplitudes of particle scattering, one may find convenient to use the expression for $g\left( _{+}|^{+}\right)$ rather than the relation (32) once $g\left( _{+}|^{-}\right)$ has been calculated. For such cases, the coefficient $g\left( _{+}|^{+}\right)$ has the form

$$\begin{aligned} g\left( _{+}|^{+}\right)= & {} -2ie^{i{\tilde{\theta }}}\eta _{\mathrm {L}}\nonumber \\&\times \sqrt{ \frac{\xi _{1}\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| \xi _{2}}{\left| \pi _{0}\left( \mathrm {R}\right) -\chi \left| p^{\mathrm {R}}\right| \right| }} \left( \frac{\left| p^{\mathrm {L}}\right| \xi _{1}}{\left| p^{ \mathrm {R}}\right| \xi _{2}}\right) ^{\chi /2} \nonumber \\&\times \exp \left[ -\frac{\pi }{2}\left( \nu _{1}^{-}-\nu _{2}^{-}\right) \right] \Delta \left( _{+}|^{+}\right) \left( 0\right) . \nonumber \\ \Delta \left( _{+}|^{+}\right) \left( x\right)= & {} \Psi \left( c_{2}-a_{2},c_{2};e^{-i\pi }z_{2}\right) f_{\mathrm {L}}^{+}\left( x\right) \nonumber \\&+\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) f_{\mathrm {R} }^{+}\left( x\right) , \end{aligned}$$

(38)

where ${\tilde{\theta }}=\left| p^{\mathrm {L}}\right| \xi _{1}+\left| p^{\mathrm {R}}\right| \xi _{2}-eE\xi _{1}^{2}\ln \left( 2\left| p^{\mathrm {L}}\right| \xi _{1}\right) +eE\xi _{2}^{2}\ln \left( 2\left| p^{\mathrm {R}}\right| \xi _{2}\right)$. It can be obtained through the same continuity conditions considered above but applied to appropriate decompositions between the left and right solutions, similar those given by Eqs. (35) and (36).

With minor modifications, one may extract results from Eqs. (35) and (36) to obtain corresponding expressions for scalar particles. For example, on account of the inner product of the solutions of the Klein–Gordon equation on the hyperplane x-constant [16], the orthonormalization conditions are identical to the ones in Eqs. (27) but with $\eta _{\mathrm {L}}=\eta _{\mathrm {R}}=1$. As a result, relations between the g-coefficients for the scalar case can be extracted from Eqs. (31) and (32) setting $\eta _{\mathrm {L}}=\eta _{\mathrm {R} }=1$. Moreover, the normalization constants $_{\zeta }{\mathcal {N}}=\ _{\zeta }CY$ and $^{\zeta }{\mathcal {N}}=\ ^{\zeta }CY$ are simpler in this case

$$\begin{aligned} \ _{\zeta }C=\frac{\exp \left( -i\pi \kappa _{1}/2\right) }{\sqrt{ 2\left| p^{\mathrm {L}}\right| }},\ \ ^{\zeta }C=\frac{\exp \left( -i\pi \kappa _{2}/2\right) }{\sqrt{2\left| p^{\mathrm {R}}\right| }}, \end{aligned}$$

(39)

such that coefficients (35) and (36) have the form:

$$\begin{aligned} g\left( _{+}|^{-}\right)= & {} 2\sqrt{\xi _{1}\xi _{2}}\exp \nonumber \\&\times \left[ -\frac{\pi }{ 2}\left( \nu _{1}^{-}+\nu _{2}^{+}\right) \right] e^{i\theta _{+}}\left. \Delta \left( _{+}|^{-}\right) \left( 0\right) \right| _{\chi =0}, \nonumber \\ g\left( ^{-}|_{+}\right)= & {} -2\sqrt{\xi _{1}\xi _{2}}\exp \nonumber \\&\times \left[ \frac{\pi }{ 2}\left( \nu _{1}^{+}+\nu _{2}^{-}\right) \right] e^{i\theta _{-}}\left. \Delta \left( ^{-}|_{+}\right) \left( 0\right) \right| _{\chi =0}. \nonumber \\ \end{aligned}$$

(40)

In contrast to Fermions, one can easily show that $g\left( _{+}|^{-}\right) \rightleftarrows -g\left( ^{-}|_{+}\right)$ for Bosons, under the exchanges $p_{0}\rightleftarrows -p_{0}$ and $\xi _{1}\rightleftarrows \xi _{2}$. Hence, the absolute square value $\left| g\left( _{+}|^{-}\right) \right| ^{2}$ is also invariant for Bosons. Due to the opposite signs between $g\left( _{+}|^{-}\right)$ and $g\left( ^{-}|_{+}\right)$ under these exchanges in the Dirac and Klein–Gordon cases, we conveniently introduce a constant⁶ $\kappa$ to represent the transformations as follows⁷:

$$\begin{aligned} g\left( _{+}|^{-}\right) \rightleftarrows \kappa g\left( ^{-}|_{+}\right) ,\ \ \kappa =\left\{ \begin{array}{l} +1\ \mathrm {Fermi} \\ -1\text { Bose} \end{array} \right. . \end{aligned}$$

(41)

Thus, besides the constant $\chi$, the above constant is frequently used to map results from the Dirac to the Klein–Gordon cases, as we will see below. The coefficient $g\left( _{+}|^{+}\right)$ for Bosons can be extracted from Eq. (38) setting $\chi =0$, $\eta _{\mathrm {L}}=\eta _{\mathrm {R} }=0$ and, besides, using the normalization constants (39) instead Eq. (28). Its representation in terms of Whittaker functions can be found in Appendix A; cf. Eq. (118).

2.3 In and out-states

In contrast to time-dependent electric backgrounds,⁸ a quantization of Dirac and Klein–Gordon fields with x-electric potential steps is performed with the help of solutions describing particles moving to the steps from infinitely remote distances or leaving the step to infinitely remote distances. In-solutions are defined as incoming waves (that is, waves going toward the step) while out-solutions are classified as outgoing waves (that is, waves going outwards the step). Since there are five distinct ranges of quantum numbers $\Omega _{k}$, definitions of in- or out-sets are different. For some of the ranges, these definitions are similar to the one-particle relativistic quantum theory. In the case under consideration, the classification is the following⁹:

$$\begin{aligned} \begin{array}{ll} \text {in-solutions:}\! &{} \ _{+}\psi _{n_{1}},\ ^{-}\psi _{n_{1}}; \, \ _{-}\psi _{n_{5}}, \ ^{+}\psi _{n_{5}}\,;\ _{-}\psi _{n_{3}},\ ^{-}\psi _{n_{3}}, \\ \text {out-solutions:}\! &{} \ _{-}\psi _{n_{1}},\ ^{+}\psi _{n_{1}};\ _{+}\psi _{n_{5}}, \ ^{-}\psi _{n_{5}}\,;\ _{+}\psi _{n_{3}},\ ^{+}\psi _{n_{3}}. \end{array} \nonumber \\ \end{aligned}$$

(42)

The sets $\left\{ \ _{+}\psi _{n_{1}},\ ^{-}\psi _{n_{1}}\right\}$ and $\left\{ \ _{-}\psi _{n_{1}},\ ^{+}\psi _{n_{1}}\right\}$ describe incoming and outgoing electron states respectively, while $\left\{ \ _{-}\psi _{n_{5}}, \ ^{+}\psi _{n_{5}}\right\}$ and $\left\{ \ _{-}\psi _{n_{5}},\ ^{+}\psi _{n_{5}}\right\}$ describe incoming and outgoing positron states respectively.

One can demonstrate that the sets of solutions are complete and orthogonal with respect to the inner product on the t-constant hyperplane

$$\begin{aligned} \left( \psi _{n},\psi _{n^{\prime }}^{\prime }\right)= & {} \int _{V_{\perp }}d {\mathbf {r}}_{\perp }\int _{-K^{\left( \mathrm {L}\right) }}^{K^{\left( \mathrm {R }\right) }}dx\psi _{n}^{\dagger }\left( X\right) \psi _{n^{\prime }}^{\prime }\left( X\right) ,\nonumber \\ V_{\perp }= & {} \prod _{j=2}^{D}K_{j}\, \end{aligned}$$

(43)

where the lower/upper cutoffs $K^{\left( \mathrm {L/R}\right) }$ are supposed to admit the limits $K^{\left( \mathrm {L}\right) }\sim T$ and $K^{\left( \mathrm {R}\right) }\sim T$ (and $T\rightarrow \infty$) in final expressions; see Ref. [34] for details. In particular,

$$\begin{aligned}&\left( \ _{\zeta }\psi _{n},\ _{\zeta }\psi _{n^{\prime }}\right) =\left( \ ^{\zeta }\psi _{n},\ ^{\zeta }\psi _{n^{\prime }}\right) =\delta _{n,n^{\prime }}{\mathcal {M}}_{n},\ \ n,n^{\prime }\in \Omega _{1}\cup \Omega _{3}\cup \Omega _{5}, \nonumber \\&\left( \ \psi _{n},\ \psi _{n^{\prime }}\right) =\delta _{n,n^{\prime }},\ \ n,n^{\prime }\in \Omega _{2}\cup \Omega _{4}, \nonumber \\&\left( \ _{\zeta }\psi _{n},\ ^{-\zeta }\psi _{n}\right) =0,\ \ n\in \Omega _{1}\cup \Omega _{5},\ \ \left( \ _{\zeta }\psi _{n},\ ^{\zeta }\psi _{n}\right) =0,\ \ n\in \Omega _{3}, \nonumber \\&{\mathcal {M}}_{n}=\left| g\left( _{+}|^{+}\right) \right| ^{2},\ \ n\in \Omega _{1}\cup \Omega _{5},\ \ {\mathcal {M}}_{n}=\left| g\left( _{+}|^{-}\right) \right| ^{2},\ \ n\in \Omega _{3}, \nonumber \\ \end{aligned}$$

(44)

where we have $\delta _{n,n^{\prime }}=\delta _{\sigma ,\sigma ^{\prime }}\delta \left( p_{0}-p_{0}^{\prime }\right) \delta \left( {\mathbf {p}}_{\perp }-{\mathbf {p}}_{\perp }^{\prime }\right)$ in the limit $K^{\left( \mathrm {L/R} \right) }\rightarrow \infty$. For each set of quantum numbers n there exist one or two complete sets of solutions:

• (a) For $\forall \,n\in \Omega _{1}\cup \Omega _{5}$, there are two $\left( \zeta =\pm \right)$ independent sets of solutions: $\left\{ \ _{\zeta }\psi _{n}\left( X\right) ,\ ^{-\zeta }\psi _{n}\left( X\right) \right\}$;

• (b) For $\forall \,n\in \Omega _{3}$, there are two $\left( \zeta =\pm \right)$ independent sets of solutions: $\left\{ \ _{\zeta }\psi _{n}\left( X\right) ,\ ^{\zeta }\psi _{n}\left( X\right) \right\}$;

• (c) For $\forall \,n\in \Omega _{2}\cup \Omega _{4}$, there is one set of solutions $\left\{ \psi _{n}\left( X\right) \right\}$.

The classification of solutions (42), together with the above properties, allows us to quantize the Dirac and Klein–Gordon fields in terms of particles and antiparticles. To quantize the Dirac field operator ${\hat{\Psi }}\left( X\right)$, we decompose it using the sets of solutions discussed above on the hyperplane $t=\mathrm {const.}$, in which the x -independent decomposition coefficients are creation and annihilation operators of particles or antiparticles. Because there are two independent sets of solutions for states within $\Omega _{1}\cup \Omega _{3}\cup \Omega _{5}$, two possible quantizations exist, one formed exclusively with “in” operators and another formed exclusively with “out” operators, namely

$$\begin{aligned} \begin{array}{ll} {\text {in-set:}} \ _{+}a_{n_{1}}\left( \mathrm {in}\right) , \ ^{-}a_{n_{1}}\left( \mathrm {in}\right) ;\ _{-}b_{n_{5}}\left( \mathrm {in} \right) ,\ ^{+}b_{n_{5}}\left( \mathrm {in}\right) ;\\ \qquad \ _{-}b_{n_{3}}\left( \mathrm {in}\right) , \ ^{-}a_{n_{3}}\left( \mathrm {in}\right) , \\ {\text {out-set:}} \ _{-}a_{n_{1}}\left( \mathrm {out}\right) ,\ ^{+}a_{n_{1}}\left( \mathrm {out}\right) ;\ _{+}b_{n_{5}}\left( \mathrm {out} \right) ,\ ^{-}b_{n_{5}}\left( \mathrm {out}\right) ;\\ \qquad \ _{+}b_{n_{3}}\left( \mathrm {out}\right) , \ ^{+}a_{n_{3}}\left( \mathrm {out} \right) . \end{array} \nonumber \\ \end{aligned}$$

(45)

For states in $\Omega _{2}$, we have only pairs of creation/annihilation operators of particles $\left\{ a_{n_{2}}^{\dagger },a_{n_{2}}\right\}$ whereas for states in $\Omega _{4}$ we have only pairs of creation/annihilation operators of antiparticles $\left\{ b_{n_{4}}^{\dagger },b_{n_{4}}\right\}$. All a’s and b’s are interpreted as annihilation operators of particles and antiparticles, respectively; their adjoints, $a^{\dagger }$’s and $b^{\dagger }$’s, are interpreted as creation operators of particles and antiparticles, respectively. Operators labeled by the argument “in” are in-operators while the ones labeled by the argument “out” are out-operators. All creation and annihilation operators with different quantum numbers or from different ranges $\Omega _{i}$ anticommute between themselves. For example, the only nontrivial anticommutation relations for in-operators are:

$$\begin{aligned} \left[ \ _{+}a_{n_{1}^{\prime }}\left( \mathrm {in}\right) ,\ _{+}a_{n_{1}}^{\dagger }\left( \mathrm {in}\right) \right] _{+}= & {} \left[ \ ^{-}a_{n_{1}^{\prime }}\left( \mathrm {in}\right) ,\ ^{-}a_{n_{1}}^{\dagger }\left( \mathrm {in}\right) \right] _{+}\nonumber \\= & {} \delta _{n_{1}^{\prime }n_{1}}, \nonumber \\ \left[ \ ^{-}a_{n_{3}^{\prime }}\left( \mathrm {in}\right) ,\ ^{-}a_{n_{3}}^{\dagger }\left( \mathrm {in}\right) \right] _{+}= & {} \left[ \ _{-}b_{n_{3}^{\prime }}\left( \mathrm {in}\right) ,\ _{-}b_{n_{3}}^{\dagger }\left( \mathrm {in}\right) \right] _{+}\nonumber \\&=\delta _{n_{3}^{\prime }n_{3}}, \nonumber \\ \left[ \ _{-}b_{n_{5}^{\prime }}\left( \mathrm {in}\right) ,\ _{-}b_{n_{5}}^{\dagger }\left( \mathrm {in}\right) \right] _{+}= & {} \left[ \ ^{+}b_{n_{5}^{\prime }}\left( \mathrm {in}\right) ,\ ^{+}b_{n_{5}}^{\dagger }\left( \mathrm {in}\right) \right] _{+}\nonumber \\= & {} \delta _{n_{5}^{\prime }n_{5}}, \nonumber \\ \left[ a_{n_{2}^{\prime }},a_{n_{2}}^{\dagger }\right] _{+}= & {} \delta _{n_{2}^{\prime }n_{2}},\ \ \left[ b_{n_{4}^{\prime }},b_{n_{4}}^{\dagger } \right] _{+}=\delta _{n_{4}^{\prime }n_{4}}. \nonumber \\ \end{aligned}$$

(46)

Furthermore, the in-vacuum state $\left| 0,\mathrm {in}\right\rangle$,

$$\begin{aligned} \left| 0,\mathrm {in}\right\rangle =\prod _{i=1,3,5}\otimes \left| 0, \mathrm {in}\right\rangle ^{\left( i\right) }\otimes \left| 0\right\rangle ^{\left( 2\right) }\otimes \left| 0\right\rangle ^{\left( 4\right) }, \end{aligned}$$

(47)

is defined as the direct product of partial in-vacuum states $\left| 0, \mathrm {in}\right\rangle ^{\left( i\right) }\$states; all vacua annihilated by corresponding annihilation operators

$$\begin{aligned}&\ _{+}^{-}a_{n_{1}}\left( \mathrm {in}\right) \left| 0,\mathrm {in} \right\rangle ^{\left( 1\right) }=\ _{+}^{-}a_{n_{1}}\left( \mathrm {in} \right) \left| 0,\mathrm {in}\right\rangle =0, \nonumber \\&\ ^{-}a_{n_{3}}\left( \mathrm {in}\right) \left| 0,\mathrm {in} \right\rangle ^{\left( 3\right) }=\ ^{-}a_{n_{3}}\left( \mathrm {in}\right) \left| 0,\mathrm {in}\right\rangle =0, \nonumber \\&\ _{-}b_{n_{3}}\left( \mathrm {in}\right) \left| 0,\mathrm {in} \right\rangle ^{\left( 3\right) }=\ _{-}b_{n_{3}}\left( \mathrm {in}\right) \left| 0,\mathrm {in}\right\rangle =0, \nonumber \\&\ _{-}^{+}b_{n_{5}}\left( \mathrm {in}\right) \left| 0,\mathrm {in} \right\rangle ^{\left( 5\right) }=\ _{-}^{+}b_{n_{5}}\left( \mathrm {in} \right) \left| 0,\mathrm {in}\right\rangle =0, \nonumber \\&\ a_{n_{2}}\left| 0\right\rangle ^{\left( 2\right) }=a_{n_{2}}\left| 0,\mathrm {in}\right\rangle =0,\ \ b_{n_{4}}\left| 0\right\rangle ^{\left( 4\right) }=b_{n_{4}}\left| 0, \mathrm {in}\right\rangle =0. \nonumber \\ \end{aligned}$$

(48)

Anticommutation relations for out-operators and out-vacuum states $\left| 0,\mathrm {out}\right\rangle ^{\left( i\right) }$ can be introduced following the same considerations above.

Due to the quantization of the Dirac/Klein–Gordon fields and the canonical transformations between “in” and “out” sets of creation and annihilation operators in the ranges $\Omega _{1}$, $\Omega _{2}$, $\Omega _{4}$ and $\Omega _{5}$ [16], each partial in-vacuum $\left| 0,\mathrm {in} \right\rangle ^{\left( i\right) },\ i=1,2,4,5$ differs from its corresponding out-vacuum $\left| 0,\mathrm {out}\right\rangle ^{\left( i\right) },\ i=1,2,4,5$ by a complex phase which, without loss of generality, can be selected to match one another, namely $\left| 0, \mathrm {in}\right\rangle ^{\left( i\right) }=\left| 0,\mathrm {out} \right\rangle ^{\left( i\right) }, i=1,2,4,5$. Therefore, we conveniently represent the direct product of all partial vacua by

$$\begin{aligned} \left| 0\right\rangle =\prod _{i=1,2,4,5}\otimes \left| 0,\mathrm {in} \right\rangle ^{\left( i\right) }=\prod _{i=1,2,4,5}\otimes \left| 0, \mathrm {out}\right\rangle ^{\left( i\right) }. \end{aligned}$$

This is not the case for the partial vacua $\left| 0,\mathrm {in} \right\rangle ^{\left( 3\right) }$ and $\left| 0,\mathrm {out} \right\rangle ^{\left( 3\right) }$ in the range $\Omega _{3}$ (Klein zone), which are different by reasons that shall be briefly discussed below. That is why the total vacuum-vacuum transition amplitude $c_{v}$

$$\begin{aligned} c_{v}=\left\langle 0,\mathrm {out}|0,\mathrm {in}\right\rangle =c_{v}^{\left( 3\right) }=\ ^{\left( 3\right) }\left\langle 0,\mathrm {out}|0,\mathrm {in} \right\rangle ^{\left( 3\right) }, \end{aligned}$$

(49)

coincides with the vacuum-vacuum transition amplitude in the Klein zone $c_{v}^{\left( 3\right) }$.

Notice that in the scalar case, all anticommutation relations must be replaced by commutation relations and definitions of in- or out-creation/annihilation operators in $\Omega _{3}$ are different, namely$\ ^{+}a_{n_{3}}\left( \mathrm {in}\right)$ and $_{+}b_{n_{3}}\left( \mathrm {in} \right)$, are in-operators, while$\ ^{-}a_{n_{3}}\left( \mathrm {out}\right)$ and$\ _{-}b_{n_{3}}\left( \mathrm {out}\right)$ out-operators.

3 Processes in the Klein zone

Particle creation from the vacuum occurs exclusively in the Klein zone (the range $\Omega _{3}$), defined by bounded energies $p_{0}$

$$\begin{aligned} U_{\mathrm {L}}+\pi _{\perp }\le p_{0}\le U_{\mathrm {R}}-\pi _{\perp }, \end{aligned}$$

(50)

bounded perpendicular momenta ${\mathbf {p}}_{\perp }$ ($2\pi _{\perp }\le {\mathbb {U}}$), and quantum numbers $\sigma$ that may be arbitrary. We recapitulate below the calculation of main quantities characterizing the vacuum instability as well as elementary processes occurring in the Klein zone.

According to the partial decompositions of the quantized Dirac field ${\hat{\Psi }}\left( X\right)$ in the range $\Omega _{3}$ [16],

$$\begin{aligned} {\hat{\Psi }}_{3}\left( X\right)= & {} \sum _{n\in \Omega _{3}}{\mathcal {M}} _{n}^{-1/2} [ \ ^{-}a_{n}\left( \mathrm {in}\right) \ ^{-}\psi _{n}\left( X\right) \nonumber \\&+\ _{-}b_{n}^{\dagger }\left( \mathrm {in}\right) \ _{-}\psi _{n}\left( X\right) ] , \nonumber \\= & {} \sum _{n\in \Omega _{3}}{\mathcal {M}}_{n}^{-1/2} [ \ ^{+}a_{n}\left( \mathrm {out}\right) \ ^{+}\psi _{n}\left( X\right) \nonumber \\&+\ _{+}b_{n}^{\dagger }\left( \mathrm {out}\right) \ _{+}\psi _{n}\left( X\right) ], \end{aligned}$$

(51)

and the relations (29), specialized to $\Omega _{3}$ (where $\eta _{ \mathrm {L}}=1=-\eta _{\mathrm {R}}$), one may express the independent set $\left\{ \ ^{+}\psi _{n_{3}}\left( X\right) ,\ _{+}\psi _{n_{3}}\left( X\right) \right\}$ in terms of the independent set $\left\{ \ ^{-}\psi _{n_{3}}\left( X\right) ,\ _{-}\psi _{n_{3}}\left( X\right) \right\}$ (or vice-versa) and use inner products on t-constant hyperplane (44) to establish linear canonical transformations between in- and out-operators in $\Omega _{3}$. These transformations are specified by Eqs. (7.4) in [16]. With the aid of these transformations we may introduce, for instance, the differential mean number of in-particles $N_{n_{3}}^{a}\left( \mathrm {in}\right)$ created from the out-vacuum

$$\begin{aligned} N_{n}^{a}\left( \mathrm {in}\right)= & {} \left\langle 0,\mathrm {out}\left| \ ^{-}a_{n}^{\dagger }\left( \mathrm {in}\right) \ ^{-}a_{n}\left( \mathrm {in} \right) \right| 0,\mathrm {out}\right\rangle \nonumber \\= & {} \left| g\left( _{+}|^{-}\right) \right| ^{-2},\ \ n\in \Omega _{3}, \end{aligned}$$

(52)

and use the identity $\left| g\left( _{-}|^{+}\right) \right| ^{2}=\left| g\left( _{+}|^{-}\right) \right| ^{2}$ to realize that Eq. (52) is identically equal to the differential mean number of in-antiparticles created from the out-vacuum $N_{n_{3}}^{b}\left( \mathrm {in} \right)$, the differential mean number of out-particles $N_{n_{3}}^{a}\left( \mathrm {out}\right)$ and out-antiparticles $N_{n_{3}}^{b}\left( \mathrm {out}\right)$ created from the in-vacuum. That is why we denote all these quantities by $N_{n}^{\mathrm {cr}}\equiv N_{n}^{a}\left( \mathrm {in}\right) =N_{n}^{b}\left( \mathrm {in}\right) =N_{n}^{a}\left( \mathrm {out}\right) =N_{n}^{b}\left( \mathrm {out}\right)$. Thus, the total number of particles created $N^{\mathrm {cr}}$ correspond to the summation of the mean numbers $N_{n}^{\mathrm {cr}}$ over the quantum numbers within $\Omega _{3}$

$$\begin{aligned} N^{\mathrm {cr}}=\sum _{n\in \Omega _{3}}N_{n}^{\mathrm {cr}}=\frac{J_{\left( d\right) }V_{\perp }T}{\left( 2\pi \right) ^{d-1}}\int _{\Omega _{3}}dp_{0}d {\mathbf {p}}_{\perp }N_{n}^{\mathrm {cr}}, \end{aligned}$$

(53)

where $V_{\perp }$ is the space volume perpendicular to the direction of the electric field, T its time duration and $J_{\left( d\right) }=2^{\left[ d/2 \right] -1}$ the total number of spinning degrees of freedom ($J_{\left( d\right) }=1$ for scalar particles), that factorizes out as a multiplicative constant since the field does not mix different spin polarizations. In the rightmost equality, the summations were converted into multiple integrals in the standard way, viz. $\left( V_{\perp }T\right) ^{-1}\sum {}_{p_{0}, {\mathbf {p}}_{\perp }\in \Omega _{3}}\leftrightarrow \left( 2\pi \right) ^{1-d}\int dp_{0}d{\mathbf {p}}_{\perp }$, in which $V_{\perp }$, T are macroscopically large.

Besides particle creation, there are other elementary processes in the Klein zone worth of consideration, such as particle scattering, creation of a particle-antiparticle pair and annihilation of a particle-antiparticle pair. The relative (with respect to the in-vacuum $\left| 0,\mathrm {in} \right\rangle$ and the out-vacuum $\left| 0,\mathrm {out}\right\rangle$ ) amplitudes of particle scattering $w_{n}\left( +|+\right)$, antiparticle scattering $w_{n}\left( -|-\right)$, particle-antiparticle creation $w_{n}\left( +-|0\right)$ and particle-antiparticle annihilation $w_{n}\left( 0|-+\right)$ are defined by Eqs. (7.17) and (A9) in [16]. In terms of g-coefficients, the corresponding probabilities can be expressed as follows:

$$\begin{aligned} \left| w_{n}\left( +|+\right) \right| ^{2}= & {} \left| w_{n}\left( -|-\right) \right| ^{2}=\left| g\left( _{+}|^{-}\right) \right| ^{2}\left| g\left( _{+}|^{+}\right) \right| ^{-2}\nonumber \\= & {} \frac{1}{1-\kappa N_{n}^{\mathrm {cr}}}, \nonumber \\ \left| w_{n}\left( +-|0\right) \right| ^{2}= & {} \left| w_{n}\left( 0|-+\right) \right| ^{2}=\left| g\left( _{+}|^{+}\right) \right| ^{-2}\nonumber \\= & {} \frac{N_{n}^{\mathrm {cr}}}{1-\kappa N_{n}^{\mathrm {cr}}}. \end{aligned}$$

(54)

It is noteworthy that total reflection, which is a direct consequence of the quantization of the Dirac and Klein–Gordon fields in $\Omega _{3}$ (51), [16], is the only possible form of particle scattering in $\Omega _{3}$. Particle reflection and particle transmission are allowed beyond the Klein zone, as shall be discussed in Sec. 4.

The most important quantity characterizing the vacuum instability is the vacuum-vacuum transition probability $P_{v}$

$$\begin{aligned} P_{v}=\left| c_{v}\right| ^{2}=\left| \left\langle 0,\mathrm {out} \left| V_{\Omega _{3}}\right| 0,\mathrm {out}\right\rangle \right| ^{2}=\left| \left\langle 0,\mathrm {in}\left| V_{\Omega _{3}}\right| 0,\mathrm {in}\right\rangle \right| ^{2}, \nonumber \\ \end{aligned}$$

(55)

because $P_{v}\ne 1$ $\left( P_{v}<1\right)$ indicates that pairs were created from the vacuum by the external field. Here, $c_{v}$ denotes the vacuum-vacuum transition amplitude and $V_{\Omega _{3}}$ an unitary operator connecting the “in” and “out” vacua $\left| 0,\mathrm {out}\right\rangle =V_{\Omega _{3}}^{\dagger }\left| 0,\mathrm {in}\right\rangle$

$$\begin{aligned} V_{\Omega _{3}}= & {} \exp \left[ -\ ^{-}a_{n}^{\dagger }\left( \mathrm {in} \right) w_{n}\left( +-|0\right) \ _{-}b_{n}^{\dagger }\left( \mathrm {in} \right) \right] \nonumber \\&\times \exp \left[ -\ ^{-}a_{n}\left( \mathrm {in}\right) \ln w_{n}\left( +|+\right) \ ^{-}a_{n}^{\dagger }\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ \ _{-}b_{n}^{\dagger }\left( \mathrm {in}\right) \ln w_{n}\left( -|-\right) \ _{-}b_{n}\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ -\ _{-}b_{n}\left( \mathrm {in}\right) w_{n}\left( 0|-+\right) \ ^{-}a_{n}\left( \mathrm {in}\right) \right] , \end{aligned}$$

(56)

which, in turn, defines a transformation between “in” and “out” operators

$$\begin{aligned}&\left\{ \ ^{+}a_{n}^{\dagger }\left( \mathrm {out}\right) ,\ ^{+}a_{n}\left( \mathrm {out}\right) ,\ _{+}b_{n}^{\dagger }\left( \mathrm {out}\right) ,\ _{+}b_{n}\left( \mathrm {out}\right) \right\} \nonumber \\&\quad =V_{\Omega _{3}}^{\dagger }\left\{ \ ^{-}a_{n}^{\dagger }\left( \mathrm {in}\right) ,\ ^{-}a_{n}\left( \mathrm {in}\right) ,\ _{-}b_{n}^{\dagger }\left( \mathrm {in}\right) ,\ _{-}b_{n}\left( \mathrm {in}\right) \right\} V_{\Omega _{3}}. \nonumber \\ \end{aligned}$$

(57)

The representation of $V_{\Omega _{3}}$ in terms of in-operators (56) is complementary to the one given in terms of out-operators; cf. Eq. (7.20) in Ref. [16]. Details on the calculation of $V_{\Omega _{3}}$ for Bosons can be found in Appendix B.

Using the explicit representations (56) and (129), the probability that the vacuum remains vacuum $P_{v}$ reads

$$\begin{aligned} P_{v}=\exp \left( \sum _{n\in \Omega _{3}}\ln p_{v}^{n}\right) ,\ \ p_{v}^{n}=\left( 1-\kappa N_{n}^{\mathrm {cr}}\right) ^{\kappa }. \end{aligned}$$

(58)

One of the consequences of particle creation occurring exclusively within the Klein zone is the diminishing of $N_{n}^{\mathrm {cr}}$ near the boundaries of $\Omega _{3}$. This is a local property resulting from the behavior of the asymptotic momenta $\left| p^{\mathrm {L}}\right|$, $\left| p^{\mathrm {R}}\right|$ at the boundaries of the Klein zone, namely $\left| p^{\mathrm {R}}\right| \rightarrow 0$ at the vicinity of $\Omega _{2}$ while $\left| p^{\mathrm {L}}\right| \rightarrow 0$ at the vicinity of $\Omega _{4}$. Accordingly, the coefficient $g\left( _{+}|^{-}\right)$ (or $g\left( _{-}|^{+}\right)$) diverges, which means that $N_{n}^{\mathrm {cr}}\rightarrow 0$ near both boundaries. This is more clearly seen if one expresses $g\left( _{+}|^{-}\right)$ in terms of Whittaker functions, whose expressions are given by Eqs. (117) and (118) in Appendix A, because $\left| g\left( _{+}|^{-}\right) \right| ^{-2}=O\left( \left| p^{\mathrm {R} }\right| \left| p^{\mathrm {L}}\right| \right) \rightarrow 0$ near the boundaries. This is also true for the Klein–Gordon case. In the next Sect. 3.1, we study this property in the most favorable configuration for particle creation, wherein the differential mean numbers $N_{n}^{\mathrm {cr}}$ are not necessarily small over a sufficiently wide range of quantum numbers in the Klein zone.

3.1 Small-gradient configuration

Here, we study the case when a strong electric field is concentrated in a wide region on the x-direction with a sufficiently strong amplitude E and sufficiently large length scales $\xi _{j}$ so that the parameters $\left| U_{\mathrm {L}}\right| \xi _{1}$ and $U_{\mathrm {R}}\xi _{2}$ are both large, satisfying the conditions

$$\begin{aligned} \min \left( \left| U_{\mathrm {L}}\right| \xi _{1},U_{\mathrm {R}}\xi _{2}\right) \gg \max \left( 1,\frac{m^{2}}{eE}\right) ,\ \ \frac{\xi _{2}}{ \xi _{1}}={\text {fixed}}. \end{aligned}$$

(59)

This configuration represents an almost symmetrical electric field that is growing “smoothly” from $x=-\infty$ to $x=0$ and then is decreasing “smoothly” to $x=+\infty$. The configuration may be considered as a two-parameter regularization of a uniform electric field.¹⁰ The resulting potential energy of the electron in this field is illustrated by the yellow solid line in Fig. 2.

To study quantities characterizing the vacuum instability, one has to compare the above parameters with parameters involving other quantum numbers. Since particle creation is directly related to the extent of the Klein zone, which is parameterized by the asymptotic potential energies $U_{ \mathrm {L,R}}$ and the perpendicular energies $\pi _{\perp }$, we set an upper bound to the perpendicular momenta ${\mathbf {p}}_{\perp }$ in order to consider a sufficiently wide Klein zone, say $\pi _{\perp }\le K_{\perp }$, where $K_{\perp }$ is a number satisfying the inequality $\min \left( eE\xi _{1}^{2},eE\xi _{2}^{2}\right) \gg K_{\perp }>\max \left( 1,m^{2}/eE\right)$ . As for the parameter $p_{0}/\sqrt{eE}$, we restrict the consideration to positive energies $0\le p_{0}\le U_{\mathrm {R}}-\pi _{\perp }$ and generalize results to negative energies using the properties of the coefficient $g\left( _{+}|^{-}\right)$ (and, therefore, its absolute square value (52)) discussed at the end of SecT. 2.2. In this case, the left kinetic energy is always large and positive $\left| U_{\mathrm {L }}\right| \le \pi _{0}\left( \mathrm {L}\right) \le {\mathbb {U}}-\pi _{\perp }$ , while the right kinetic energy is always negative, $\pi _{\perp }\le \left| \pi _{0}\left( \mathrm {R}\right) \right| \le U_{ \mathrm {R}}$. Within this range, the differential mean numbers $N_{n}^{ \mathrm {cr}}$ are significant only in a subrange $\beta \sqrt{\lambda } <\left| \pi _{0}\left( \mathrm {R}\right) \right| /\sqrt{eE}\le U_{ \mathrm {R}}/\sqrt{eE}$, which can be divided as follows:

$$\begin{aligned}&\left( \mathrm {a}\right) \ \frac{U_{\mathrm {R}}}{\sqrt{eE}}-\frac{\delta }{ \sqrt{2}}\le \frac{\left| \pi _{0}\left( \mathrm {R}\right) \right| }{\sqrt{eE}}\le \frac{U_{\mathrm {R}}}{\sqrt{eE}}, \nonumber \\&\left( \mathrm {b}\right) \ \sqrt{\lambda }+\frac{U_{\mathrm {R}}}{\sqrt{eE}} \left( 1-\Upsilon \right)<\frac{\left| \pi _{0}\left( \mathrm {R}\right) \right| }{\sqrt{eE}}<\frac{U_{\mathrm {R}}}{\sqrt{eE}}-\frac{\delta }{ \sqrt{2}}, \nonumber \\&\left( \mathrm {c}\right) \ \beta \sqrt{\lambda }<\frac{\left| \pi _{0}\left( \mathrm {R}\right) \right| }{\sqrt{eE}}\le \sqrt{\lambda }+ \frac{U_{\mathrm {R}}}{\sqrt{eE}}\left( 1-\Upsilon \right) , \end{aligned}$$

(60)

where $\delta$ is a sufficiently small number $0<\delta \ll 1$, $\Upsilon$ is a fixed number $\pi _{\perp }/U_{\mathrm {R}}<\Upsilon <1,$ and $\beta$ is slightly larger than the unity, $1<\beta \ll 1+\left( 1-\Upsilon \right) U_{\mathrm {R}}/\pi _{\perp }$. To study local properties of the mean numbers $N_{n}^{\mathrm {cr}}$, we introduce two new sets of variables

$$\begin{aligned} \eta _{1}=\frac{e^{-i\pi }z_{1}\left( 0\right) }{c_{1}},\ \ \eta _{2}= \frac{z_{2}\left( 0\right) }{c_{2}},\ \ {\mathcal {Z}}_{j}=\left( \eta _{j}-1\right) {\mathcal {W}}_{j}\sqrt{c_{j}}, \nonumber \\ \end{aligned}$$

(61)

where ${\mathcal {W}}_{j}=\left| \eta _{j}-1\right| ^{-1}\sqrt{2\left( \eta _{j}-1-\ln \eta _{j}\right) }$, sgn${\mathcal {Z}}_{j}=\mathrm {sgn }\left( \eta _{j}-1\right)$, and take into account that $\pi _{0}\left( \mathrm {L}\right) /\sqrt{eE}$ is large and positive for positive energies, which means that $c_{1}-a_{1}$ is fixed while $z_{1}$ and $c_{1}$ are simultaneously large throughout the subranges $\left( \mathrm {a}\right) {-}\left( \mathrm {c}\right)$.

The subrange $\left( \mathrm {a}\right)$ is characterized by sufficiently small energies ($p_{0}/\sqrt{eE}$ small) and $\eta _{1}$ and $\eta _{2}$ are sufficiently close to the unity

$$\begin{aligned} \left( \mathrm {a}\right) \ 1>\eta _{2}\ge 1-\frac{\delta }{\sqrt{2eE}\xi _{2}},\ \ 1<\eta _{1}\le 1+\frac{\delta }{\sqrt{2eE}\xi _{1}}, \nonumber \\ \end{aligned}$$

(62)

such that ${\mathcal {Z}}_{1}$ and ${\mathcal {Z}}_{2}$ are small in this range, $\left| {\mathcal {Z}}_{1}\right| > rsim \left| {\mathcal {Z}} _{2}\right|$, $\left| {\mathcal {Z}}_{2}\right| \approx \delta$. Thus, one can use an asymptotic approximation given by Eq. (66) in [30] and the approximations $\nu _{1}^{-}=-\left( \lambda /2\right) \left[ 1+O\left( \sqrt{eE}\xi _{1}\right) ^{-1}\right]$ and $\nu _{2}^{+}=-\left( \lambda /2\right) \left[ 1+O\left( \sqrt{eE}\xi _{2}\right) ^{-1}\right]$ to show that the mean numbers asymptotically, in the leading-order approximation, are given by the equation

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx e^{-\pi \lambda }. \end{aligned}$$

(63)

This local approximation, holds both for Fermions and for Bosons, and coincides with differential mean numbers of pairs created by a constant electric field [35, 36] and locally by slowly varying time-dependent electric fields (t-electric potential steps), such as the T-constant electric field [20, 26], Sauter-type electric field [20, 26], peak electric field [24] and inverse-square electric field [30]. Moreover, it also coincides with local approximations by some small gradient coordinate-dependent electric fields (x-electric potential steps), namely the L-constant electric field and Sauter electric field [16, 29], and exponential electric step [31]. For t -electric potential steps, the local behavior refers to small values of the longitudinal momentum while for x-electric potential steps refers to small energies, as was seen above. Distribution (63) is an universal feature of the differential mean number of particles created from the vacuum by electric fields, which is uniform (either with respect to the longitudinal momentum or the energy) only for homogeneous (either in time or space) electric fields.

The subrange $\left( \mathrm {c}\right)$ corresponds to finite energies $\min \left( p_{0}/\sqrt{eE}\right) =\Upsilon U_{\mathrm {R}}/\sqrt{eE}-\sqrt{ \lambda }$ and values of parameters $\eta _{1}$ and $\eta _{2}$ slightly distant from the unity $\min \eta _{1}=1+\Upsilon U_{\mathrm {R}}/\left| U_{\mathrm {L}}\right| -\pi _{\perp }/\left| U_{\mathrm {L} }\right|$, $\eta _{2} > rsim 1-\Upsilon$, resulting in sufficiently large values to the variables $\left| {\mathcal {Z}}_{j}\right|$. Hence, we can use Eq. (67) from Ref. [30] for $\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right)$ and the first line of Eq. (68) also from [30] for $\Psi \left( a_{2},c_{2};z_{2}\right)$ to show that the mean numbers are given by the equation

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx \exp \left( 2\pi \nu _{2}^{+}\right) , \end{aligned}$$

(64)

in the leading-order approximation, valid both for Fermions and for Bosons. In the subrange $\left( \mathrm {b}\right)$, the mean numbers vary between the asymptotic forms (63) and (64). More accurate (but less simple) representations for the mean numbers in this subrange can be calculated using the uniform asymptotic approximation given by Eq. (63) from [30]. Despite being a local approximation, the asymptotic form (64) tends to uniform approximation (63) in the limit of small energies, as it can be seen by expanding $\nu _{2}^{+}$ for small $p_{0}/\sqrt{eE}$. Therefore, approximation (64) can be extended over all sub-ranges above.

From the symmetry properties of g-coefficients, we can generalize the above results to negative energies and find approximately differential mean numbers

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx \left\{ \begin{array}{ll} \exp \left( 2\pi \nu _{1}^{-}\right) , &{} \mathrm {if}\ \ U_{\mathrm {L}}+\pi _{\perp }\le p_{0}<0\, \\ \exp \left( 2\pi \nu _{2}^{+}\right) , &{} \mathrm {if\ \ }0\le p_{0}\le U_{ \mathrm {R}}-\pi _{\perp }\, \end{array} \right. . \end{aligned}$$

(65)

The above representation corresponds to dominant contributions. To calculate the total number $N^{\mathrm {cr}}$ dominant in the same approximation, one has to perform integrations over quantum numbers according to Eq. (53). Then we get:

$$\begin{aligned} N^{\mathrm {cr}}= & {} \frac{J_{\left( d\right) }V_{\perp }T}{\left( 2\pi \right) ^{d-1}}\int _{\sqrt{\lambda }<K_{\perp }}d{\mathbf {p}}_{\perp }\left[ I_{ {\mathbf {p}}_{\perp }}^{\left( 1\right) }+I_{{\mathbf {p}}_{\perp }}^{\left( 2\right) }\right] , \nonumber \\ I_{{\mathbf {p}}_{\perp }}^{\left( 1\right) }= & {} \int _{\pi _{\perp }}^{eE\xi _{1}}d\pi _{0}\left( \mathrm {L}\right) \exp \left( 2\pi \nu _{1}^{-}\right) ,\ \ \nonumber \\ I_{{\mathbf {p}}_{\perp }}^{\left( 2\right) }= & {} \int _{\pi _{\perp }}^{eE\xi _{2}}d\left| \pi _{0}\left( \mathrm {R}\right) \right| \exp \left( 2\pi \nu _{2}^{+}\right) . \end{aligned}$$

(66)

Performing a change of variables $-\lambda s_{1}=2\nu _{1}^{-}$ in $I_{ {\mathbf {p}}_{\perp }}^{\left( 1\right) }$ and $-\lambda s_{2}=2\nu _{2}^{+}$ in $I_{{\mathbf {p}}_{\perp }}^{\left( 2\right) }$, one can represent both integrals as follows

$$\begin{aligned} I_{{\mathbf {p}}_{\perp }}^{\left( j\right) }= & {} -\int _{1}^{\infty }ds_{j}F_{j}\left( s_{j}\right) e^{-\pi \lambda s_{j}},\ \ F_{1}\left( s_{1}\right) =\frac{d\pi _{0}\left( \mathrm {L}\right) }{ds_{1}},\ \ \nonumber \\ F_{2}\left( s_{2}\right)= & {} \frac{d\left| \pi _{0}\left( \mathrm {R}\right) \right| }{ds_{2}}. \end{aligned}$$

(67)

Computing the functions $F_{j}\left( s_{j}\right)$ and restricting ourselves to the zeroth order term in powers series of $\lambda /eE\xi _{j}^{2}$, we obtain

$$\begin{aligned} I_{{\mathbf {p}}_{\perp }}^{\left( j\right) }\approx \frac{eE\xi _{j}}{2} e^{-\pi \lambda }G\left( \frac{1}{2},\pi \lambda \right) , \end{aligned}$$

(68)

where $G\left( \alpha ,z\right) =e^{z}z^{\alpha }\Gamma \left( -\alpha ,z\right)$ and $\Gamma \left( -\alpha ,z\right)$ is the incomplete Gamma function [33]. Neglecting exponentially small contributions, one can extend the integration domain over the perpendicular momenta ${\mathbf {p}} _{\perp }$ (66). Thus, one obtains

$$\begin{aligned} N^{\mathrm {cr}}= & {} V_{\perp }Tn^{\mathrm {cr}},\ \ n^{\mathrm {cr}}=r^{ \mathrm {cr}}\frac{{\mathbb {U}}}{2eE}G\left( \frac{d-1}{2},\frac{\pi m^{2}}{eE} \right) , \nonumber \\ r^{\mathrm {cr}}= & {} \frac{J_{\left( d\right) }\left( eE\right) ^{d/2}}{\left( 2\pi \right) ^{d-1}}\exp \left( -\frac{\pi m^{2}}{eE}\right) , \end{aligned}$$

(69)

where $r^{\mathrm {cr}}$ is the rate of pair creation and $n^{\mathrm {cr}}$ denotes the dominant total density of pairs per unit of time T and volume $V_{\perp }$. Then one one can straightforwardly calculate the vacuum-to-vacuum transition probability (58),

$$\begin{aligned}&P_{v}=\exp \left( -\mu N^{\mathrm {cr}}\right) ,\ \ \mu =\sum _{l=0}^{\infty }\frac{\kappa ^{l}\epsilon _{l+1}}{\left( l+1\right) ^{d/2}}\exp \left( -\frac{\pi m^{2}}{eE}l\right) , \nonumber \\&\epsilon _{l}=G\left( \frac{d-1}{2},l\pi \frac{m^{2}}{eE}\right) G\left( \frac{d-1}{2},\pi \frac{m^{2}}{eE}\right) ^{-1}. \end{aligned}$$

(70)

It is worth noticing that Eqs. (69) and (70) are in agreement with universal forms for total dominant densities of particles created from the vacuum and vacuum-to-vacuum transition probabilities by weakly inhomogeneous x-electric potential steps, recently formulated in [37]. It can be readily shown that Eqs. (69) and (70) can be reproduced using universal forms for the above quantities and the explicit form of the external field (2).

According to Eq. (69), the dominant total density of pairs is proportional to the total work done on a charged particle by the electric field, $\pi _{0}\left( \mathrm {L}\right) -\pi _{0}\left( \mathrm {R}\right) = {\mathbb {U}}$. This is a common feature to electric fields in the small-gradient regime and therefore allows us to compare the present results with total quantities obtained in other examples, in particular in the L -constant electric field [29], $E\left( x\right) =E,\ x\in \left[ -L/2,L/2\right]$, where L is the length of the applied constant field.

Recalling its dominant total density of pairs created by the small-gradient regime$\ n^{\mathrm {cr}}=Lr^{\mathrm {cr}}$, one can establish some relations between both fields. For example, considering the electric field E and assuming that the total density of pairs created by the L-constant electric field and by the inverse-square electric field are the same, we conclude that both fields are equivalent in pair production provided the total length of the applied inverse-square electric over the x-direction is given by

$$\begin{aligned} L_{\mathrm {eff}}=\frac{\xi _{1}+\xi _{2}}{2}G\left( \frac{d-1}{2},\frac{\pi m^{2}}{eE}\right) . \end{aligned}$$

(71)

By definition, $L=L_{\mathrm {eff}}$ for the constant field. Thus, one can say that both fields are equivalent in pair production provided that they have the same effective length $L_{\mathrm {eff}}$ over the x-axis.

So far, we have discussed the electric field in an almost symmetrical configuration, characterized by simultaneously large length scales $\xi _{j}$ but slightly close to one another (fixed ratio $\xi _{2}/\xi _{1}$). However, there may be situations where the field is essentially asymmetrical by physical conditions, for instance, growing “smoothly” from infinitely remote negative distances but decreasing “abruptly” to infinitely remote positive distances. Situations like that correspond to cases in which one characteristic length $\xi$ is much larger than another one, in the situation illustrated above, $\xi _{1}/\xi _{2}\gg 1$. More precisely, electric field (2) can be “concentrated” in a “narrow” or “wide” region over the x-axis depending on the length scales $\xi _{1}$ and $\xi _{2}$. The larger the characteristic lengths $\xi _{j}$, the “smoother” the electric field grows from or decreases to asymptotic regions $x=\mp \infty$, respectively. In this way, we qualitatively say that the electric field is concentrated in a “wide” region for $x<0$ if $\xi _{1}$ is sufficiently large or concentrated in a “narrow” vicinity of $x=0$ $\left( x<0\right)$ if $\xi _{1}$ is sufficiently small. For example, for a very asymmetrical configuration specified by very “large” $\xi _{1}$ and very “small” $\xi _{2}$ provided that the parameters $eE\xi _{j}^{2}$ satisfy the relations

$$\begin{aligned}&eE\xi _{1}^{2}\gg \max \left( 1,\frac{m^{2}}{eE}\right) , \ \nonumber \\&eE\xi _{2}^{2}\ll \min \left( 1,\frac{m^{2}}{eE}\right) ,\ \sqrt{eE}\xi _{1} \sqrt{eE}\xi _{2}\ll 1, \end{aligned}$$

(72)

the results concerning particle creation can be formally extracted from Eqs. (65)–(70) considering the limit $\sqrt{eE}\xi _{2}\rightarrow 0$. The last inequality implies that the parameter $eE\xi _{2}^{2}$ is so small that the contribution from the second interval $x\in \mathrm {II}$ is negligible for particle creation. To see that, it is enough to compare the $g\left( _{+}|^{-}\right)$ coefficient calculated for the asymmetrical electric field

$$\begin{aligned} E\left( t\right) =E\left\{ \begin{array}{ll} \left( 1-x/\xi _{1}\right) ^{-2}, &{} \quad x\in \mathrm {I}\, \\ 0, &{} \quad x\in \mathrm {II}\, \end{array} \right. , \end{aligned}$$

(73)

with the one given by Eq. (35) in the limit $\sqrt{eE}\xi _{2}\rightarrow 0$ to conclude that both coefficients coincides in the leading-order approximation.

As a result, dominant contributions to differential and total quantities can be straightforwardly derived from the aforementioned expressions. This can be proved following the same approximations and considerations done for the inverse-square time-dependent electric field [30], due to the close analogy between electric fields (2), (73) and their time-dependent equivalents.

At last but not least, some clarifying remarks concerning the local properties of differential quantities near the boundaries of $\Omega _{3}$ are in order. As we discussed before, the coefficient $g\left( _{+}|^{-}\right)$ (or $g\left( _{-}|^{+}\right)$) diverges near the boundaries, which means that the numbers $N_{n}^{\mathrm {cr}}$ vanish at these regions. For small-gradient fields, this is clearly seen from the asymptotic forms given by Eq. (65). In a vicinity of $\Omega _{2}$, where $p_{0}/\sqrt{eE}=U_{\mathrm {R}}/\sqrt{eE}-\sqrt{\lambda }-\varepsilon$ , or in a vicinity of $\Omega _{4}$, where $p_{0}/\sqrt{eE}=U_{\mathrm {L}}/ \sqrt{eE}+\sqrt{\lambda }+\varepsilon$, with $\varepsilon$ being an infinitesimally small positive number, the parameters

$$\begin{aligned} \nu _{2}^{+}= & {} eE\xi _{2}^{2}\left( -\frac{\lambda ^{1/4}}{\sqrt{2\varepsilon } }+O\left( 1\right) \right) ,\ \ \nonumber \\ \nu _{1}^{-}= & {} eE\xi _{1}^{2}\left( -\frac{ \lambda ^{1/4}}{\sqrt{2\varepsilon }}+O\left( 1\right) \right) , \end{aligned}$$

(74)

diverge as $\varepsilon \rightarrow 0^{+}$, resulting in exponentially small contributions to the mean numbers according to Eq. (65). This result is in agreement with the general theory [16], in which no particle production occurs beyond the Klein zone. This property can also be seen in asymmetrical configurations, corresponding to an electric field growing “smoothly” from $x=-\infty$ but not decreasing “smoothly” nor “abruptly” to $x=+\infty$, so that the parameter $eE\xi _{1}^{2}$ is sufficiently large while $eE\xi _{2}^{2}$ is considered finite. Namely,

$$\begin{aligned} eE\xi _{1}^{2}\gg \max \left( eE\xi _{2}^{2},\frac{m^{2}}{eE}\right) ,\ \ eE\xi _{2}^{2}=O\left( \lambda \right) . \end{aligned}$$

(75)

In a vicinity of $\Omega _{4}$, the mean numbers are exponentially small on account of the behavior of $\nu _{1}^{-}$ given by Eq. (74). As for the vicinity of $\Omega _{2}$, one must take into account that $a_{2}$ is large while $z_{2}$ and $c_{2}$ are finite to use asymptotic approximations (122) from Appendix A to find

$$\begin{aligned}&\left| g\left( _{+}|^{-}\right) \right| ^{2}\nonumber \\&\quad \approx \frac{2\lambda }{ \pi }e^{\pi \left| \nu _{2}^{+}\right| }\sinh \left( \pi \left| \nu _{2}^{+}\right| \right) \nonumber \\&\qquad \times \left| \sqrt{\frac{2\Delta U_{2}}{\pi _{\perp }}}K_{c_{2}-1}\left( 2\sqrt{a_{2}z_{2}}\right) +iK_{c_{2}}\left( 2 \sqrt{a_{2}z_{2}}\right) \right| ^{2}, \end{aligned}$$

(76)

for Fermions and

$$\begin{aligned}&\left| g\left( _{+}|^{-}\right) \right| ^{2}\nonumber \\&\quad \approx \frac{2\lambda }{ \pi }\left( 2\Delta U_{2}\right) e^{\pi \left| \nu _{2}^{+}\right| }\cosh \left( \pi \left| \nu _{2}^{+}\right| \right) \nonumber \\&\qquad \times \left| \sqrt{\frac{2\Delta U_{2}}{\pi _{\perp }}}K_{c_{2}-1}\left( 2\sqrt{a_{2}z_{2} }\right) -iK_{c_{2}}\left( 2\sqrt{a_{2}z_{2}}\right) \right| ^{2}, \end{aligned}$$

(77)

for Bosons, in leading-order approximation. Here, $K_{\nu }\left( z\right)$ are modified Bessel functions of the second kind [33]. According to Eq. (74), both coefficients diverge exponentially in a vicinity of $\Omega _{2}$, which means that $N_{n}^{\mathrm {cr}}\rightarrow 0$ in this region. Note that the combination of the Bessel functions are finite, once $\sqrt{a_{2}z_{2}}=O\left( \lambda ^{7/4}\right)$ and $c_{2}$ is fixed. Using the symmetries discussed in the end of Sect. 2.2, we can generalize these results to a configuration opposite to the one under consideration (75), corresponding to an electric field growing not too “smoothly” nor too “abruptly” from $x=-\infty$ but decreasing “smoothly” to $x=+\infty$, such that $eE\xi _{2}^{2}\gg \max \left( eE\xi _{1}^{2},m^{2}/eE\right) \,$and$\ eE\xi _{1}^{2}=O\left( \lambda \right)$. In particular, the behavior near the range $\Omega _{4}$ can be formally derived from Eqs. (76) and (77) substituting $\xi _{2}\rightarrow \xi _{1}$.

3.2 Sharp-gradient configuration

In contrast to the previous configurations, where one or both length scales are considered large $\xi _{j}$, here we consider the opposite case, characterized by sufficiently small length scales such that the parameters $\left| U_{\mathrm {L}}\right| \xi _{1}$ and $U_{\mathrm {R}}\xi _{2}$ obey the following conditions

$$\begin{aligned} \max \left( \left| U_{\mathrm {L}}\right| \xi _{1},U_{\mathrm {R}}\xi _{2}\right) \ll 1,\ \ \frac{\xi _{2}}{\xi _{1}}=\mathrm {fixed.} \end{aligned}$$

(78)

This configuration corresponds to a very sharp electric field, highly concentrated about the origin $x=0$, described by a very “steep” potential step. The potential energy of an electron in this field is illustrated by the solid blue line in Fig. 2. This configuration has a special interest because it corresponds to a two-parameter regularization of the Klein step and may be useful in a discussion of the Klein paradox.

From condition (78) and the fact that energies in the Klein zone are bounded, see (50), parameters involving kinetic energies

$$\begin{aligned} \max \left( \pi _{0}\left( \mathrm {L}\right) \xi _{1},\left| \pi _{0}\left( \mathrm {R}\right) \right| \xi _{2}\right) \ll 1, \end{aligned}$$

(79)

as well as the asymptotic momenta $\left| p^{\mathrm {L}}\right| \xi _{1}$ and $\left| p^{\mathrm {R}}\right| \xi _{2}$ are also small in this case, since $\left| p^{\mathrm {L/R}}\right| <\left| \pi _{0}\left( \mathrm {L/R}\right) \right|$. Thus, to study differential quantities in the Fermi case it is more convenient to use a representation of the coefficients $g\left( _{+}|^{-}\right)$ in terms of Whittaker functions given by Eq. (117) in Appendix A. Thus, we get¹¹:

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx \frac{4\left| p^{\mathrm {L}}\right| \left| p^{\mathrm {R}}\right| }{\left( \left| p^{\mathrm {L} }\right| -\left| p^{\mathrm {R}}\right| +\chi {\mathbb {U}}\right) ^{2}}\frac{\left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{ \mathrm {R}}\right| \right| }{\left| \pi _{0}\left( \mathrm {L} \right) -\chi \left| p^{\mathrm {L}}\right| \right| }, \end{aligned}$$

(80)

in the leading-order approximation. Distribution (80) has a maximum at $\left| p^{\mathrm {L}}\right| -\left| p^{\mathrm {R} }\right| =0$, i.e., at $p_{0}=\left( U_{\mathrm {R}}^{2}-U_{\mathrm {L} }^{2}\right) /2{\mathbb {U}}$,

$$\begin{aligned} \max N_{n}^{\mathrm {cr}}\approx 1-\left( \frac{2\pi _{\perp }}{{\mathbb {U}}} \right) ^{2}<1, \end{aligned}$$

(81)

which is less than the unity due to the Fermi statistics. Similar results were obtained for other exactly-solvable backgrounds, such as for the Sauter field [16] and the Peak electric field [31].

For scalar particles, one can use a representation of $g\left( _{+}|^{-}\right)$ in terms of Whittaker functions (118) and limiting form (121) to show

$$\begin{aligned} N_{n}^{\mathrm {cr}}\approx & {} 4\pi ^{2}\Delta U_{2}\Delta U_{1} \bigg \{ [ {\mathbb {U}} ( Y_{1}Y_{2}+\pi ^{2}/4)\nonumber \\&- 2 ( \Delta U_{1}Y_{1}+\Delta U_{2}Y_{2} )] ^{2} \nonumber \\&+ \pi ^{2} \bigg [ \frac{{\mathbb {U}}}{2} ( Y_{2}-Y_{1} ) + ( \Delta U_{2}-\Delta U_{1}) \bigg ] ^{2} \bigg \} ^{-1}, \end{aligned}$$

(82)

in the leading-order approximation, where $Y_{2}=\psi \left( 1\right) +\ln 4-\ln \left( 2\left| p^{\mathrm {R}}\right| \xi _{2}\right)$, $Y_{1}=\psi \left( 1\right) +\ln 4-\ln \left( 2\left| p^{\mathrm {L} }\right| \xi _{1}\right)$ and $-\psi \left( 1\right) \approx 0.577$ is the Euler constant. Despite the possibility of a large number of scalar particles be created from the vacuum due to the Bose statistics, the differential mean numbers can be less than the unity due to logarithmic contributions in the denominator. This is more clearly seen considering the symmetric case, $\xi _{1}=\xi _{2}\equiv \xi$ (then $\Delta U_{1}=\Delta U_{2}={\mathbb {U}}/2$), whose maximum at $p_{0}=\left( U_{\mathrm {R}}^{2}-U_{ \mathrm {L}}^{2}\right) /2{\mathbb {U}}$

$$\begin{aligned}&\max N_{n}^{\mathrm {cr}}\approx \left( \frac{\pi }{{\mathbb {Y}}^{2}+2{\mathbb {Y}} +\pi ^{2}/4}\right) ^{2},\ \nonumber \\&{\mathbb {Y}}=-\psi \left( 1\right) -\ln 2+\ln \left( \xi \sqrt{\frac{{\mathbb {U}}^{2}}{4}-\pi _{\perp }^{2}}\right) , \end{aligned}$$

(83)

can be less than the unity depending on the magnitude of the step ${\mathbb {U}}$ and on the length scale $\xi$. This feature, particular to the inverse-square electric field, is not seen in the Sauter electric field [16] nor in the Peak electric field [31], which may create a large number of Bosons in the small-gradient field regime. In Sect. 5, we compare approximations (80) and (82) with numerical calculations and explore further details concerning particle creation.

With the aid of the above results, we may calculate total quantities corresponding to sharp-gradient fields and, in particular, compare them with results obtained through worldline methods. More precisely, it has been recently discovered that in the deeply critical regime, defined by

$$\begin{aligned} 1-\gamma ^{2}\ll \min \left\{ \left( eE/m^{2}\right) ^{2},\left( eE/m^{2}\right) ^{-2},1\right\} ,\ \ \gamma =\frac{2m}{{\mathbb {U}}}, \nonumber \\ \end{aligned}$$

(84)

the imaginary part of the one-loop QED effective action exhibits universal properties similar to those of continuous phase transitions [42, 43]. According to our terminology, this occurs when the Klein zone is sufficiently small, as in the case of strong fields in the sharp-gradient regime. Indeed, assuming $\xi _{1}=\xi _{2}$ for simplicity and rewriting the condition (78) in terms of the Keldysh parameter $\gamma$ we obtain a condition compatible with (84)

$$\begin{aligned} 1-\gamma ^{2}\ll 1, \end{aligned}$$

(85)

provided the field amplitude is strong enough, $E>m^{2}/e$. Thus, to compute total quantities, we simplify calculations by setting $U_{\mathrm {L}}=0$, $U_{\mathrm {R}}={\mathbb {U}}=2m/\gamma$, and introduce new variables

$$\begin{aligned} \frac{p_{0}}{m}=1+\left( 1-\gamma ^{2}\right) \frac{v}{2},\ \ \frac{ {\mathbf {p}}_{\perp }^{2}}{m^{2}}=\left( 1-\gamma ^{2}\right) r, \end{aligned}$$

(86)

so that $\left( p^{\mathrm {L}}\right) ^{2}\approx \left( 1-\gamma ^{2}\right) \left( v-r\right)$ and $\left( p^{\mathrm {R}}\right) ^{2}\approx \left( 1-\gamma ^{2}\right) \left( 2-v-r\right)$ in leading-order, on account of (85). Moreover, using the condition (85) one can expand all quantities in ascending powers of $1-\gamma ^{2}$ to show that the mean number of Fermions created (80) reads

$$\begin{aligned} N_{n}^{\mathrm {cr}}= & {} \left( 1-\gamma ^{2}\right) \sqrt{\left( r-1\right) ^{2}-\left( v-1\right) ^{2}}\nonumber \\&+O\left( \left( 1-\gamma ^{2}\right) ^{3/2}\right) . \end{aligned}$$

(87)

Substituting the leading-order term of (87) into (53) and performing the change of variables (86), the total number of Fermions created can be expressed as follows

$$\begin{aligned} N^{\mathrm {cr}}\approx & {} \frac{J_{\left( d\right) }V_{\perp }T}{\left( 2\pi \right) ^{d}}\frac{m^{d-1}\pi ^{d/2}}{\Gamma \left( d/2-1\right) }\left( 1-\gamma ^{2}\right) ^{1+d/2}\int _{0}^{r_{\max }}\frac{dr}{r^{2}} r^{d/2}\\&\times \int _{v_{\min }}^{v_{\max }}dv\sqrt{\left( r-1\right) ^{2}-\left( v-1\right) ^{2}}, \end{aligned}$$

in which the integration limits $v_{\min }\approx r$, $v_{\max }\approx 2-r$ , $r_{\max }\approx 1$ are determined by restrictions of the Klein zone, given by Eq. (50) and $2\pi _{\perp }\le {\mathbb {U}}$, respectively. Computing the remaining integrals, we finally obtain

$$\begin{aligned} N^{\mathrm {cr}}\approx \frac{J_{\left( d\right) }V_{\perp }T}{\left( 2\pi \right) ^{d-1}}\frac{m^{d-1}\pi ^{d/2}}{\Gamma \left( d/2-1\right) }\frac{4}{ d\left( d^{2}-4\right) }\left( 1-\gamma ^{2}\right) ^{1+d/2}, d>2. \nonumber \\ \end{aligned}$$

(88)

Due to the smallness of the scaling factor $1-\gamma ^{2}$, we observe that the total numbers are substantially small within the Klein zone, which means that the vacuum-vacuum transition probability $P_{v}$, given by the general form (58), can be approximated by the total number of created particles as $P_{v}\approx 1-N^{\mathrm {cr}}$. At the same time, this probability can be represented via the imaginary part of a one-loop effective action $S_{\mathrm {eff}}$ according to Schwinger formula [17],

$$\begin{aligned} P_{v}=\exp \left( -2\mathrm {Im}S_{\mathrm {eff}}\right) . \end{aligned}$$

(89)

Therefore, taking into account that $P_{v}\approx 1-2\mathrm {Im}S_{\mathrm { eff}}$, we can use the result (88) to establish the following expression to the imaginary part of the effective action:

$$\begin{aligned} \mathrm {Im}S_{\mathrm {eff}}\approx N^{\mathrm {cr}}/2\ \ \mathrm {if\ \ }N^{ \mathrm {cr}}\ll 1. \end{aligned}$$

(90)

The above expression coincides, in particular, with results obtained for QED in $d=3+1$ dimensions; cf. Eq. (13) in Ref. [43]. This is an independent confirmation of the universal behavior of pair creation when the Klein zone is sufficiently small (or, near the criticality, according to Refs. [42, 43]). Moreover, it should be noted that particle creation ceases when the step approaches the noncritical configuration ${\mathbb {U}}\rightarrow 2m$, which means $\gamma \rightarrow 1$ and therefore $P_{v}\rightarrow 1$ ($P_{v}\le 1$). Following the same considerations, it can be shown that $\mathrm {Im}S_{\mathrm {eff}}\varpropto \left( 1-\gamma ^{2}\right) ^{1+d/2}$ for the Klein–Gordon case.

Because the Klein paradox is often discussed in particle scattering problems by inhomogeneous potential steps, it is worth considering some relative probabilities listed at the beginning of this section to clarify the absence of the Klein paradox through the correct interpretation of these quantities in $\Omega _{3}$. To this aim, we use Eq. (80) for $\left| g\left( _{+}|^{-}\right) \right| ^{-2}$, the representation (117) for $g\left( _{+}|^{+}\right)$ and the approximations (120) to show that the relative probability of a pair creation $\left| w_{n}\left( +-|0\right) \right| ^{2}$ and of electron scattering $\left| w_{n}\left( +|+\right) \right| ^{2}$ are approximately given by

$$\begin{aligned}&\left| w_{n}\left( +-|0\right) \right| ^{2}\approx \frac{ 4\left| p^{\mathrm {R}}\right| \left| p^{\mathrm {L}}\right| }{ \left( \left| p^{\mathrm {L}}\right| +\left| p^{\mathrm {R} }\right| +\chi {\mathbb {U}}\right) ^{2}}\frac{\left| \pi _{0}\left( \mathrm {R}\right) -\chi \left| p^{\mathrm {R}}\right| \right| }{ \left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L} }\right| \right| }, \nonumber \\&\left| w_{n}\left( +|+\right) \right| ^{2}\approx \left( \frac{ \left| p^{\mathrm {L}}\right| -\left| p^{\mathrm {R}}\right| +\chi {\mathbb {U}}}{\left| p^{\mathrm {L}}\right| +\left| p^{ \mathrm {R}}\right| +\chi {\mathbb {U}}}\right) ^{2}\frac{\left| \pi _{0}\left( \mathrm {R}\right) -\chi \left| p^{\mathrm {R}}\right| \right| }{\left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{\mathrm {R}}\right| \right| }. \nonumber \\ \end{aligned}$$

(91)

These probabilities can be larger than the unity in a sufficiently wide range of energies within $\Omega _{3}$. For example, they reach their maxima at $p_{0}=\left( U_{\mathrm {R}}^{2}-U_{\mathrm {L}}^{2}\right) /2{\mathbb {U}}$

$$\begin{aligned}&\max \left| w_{n}\left( +-|0\right) \right| ^{2}\approx \left( \frac{ {\mathbb {U}}}{2\pi _{\perp }}\right) ^{2}, \ \ \nonumber \\&\max \left| w_{n}\left( +|+\right) \right| ^{2}\approx \left( \frac{{\mathbb {U}}}{2\pi _{\perp }} \right) ^{2}-1, \end{aligned}$$

(92)

and unveil the possibility of particle transmission and particle reflection larger than the unity if interpreted as transmission and reflection coefficients, respectively. Such an interpretation is due to a formal analogy between the above probabilities and reflection and transmission coefficients calculated for the ranges $\Omega _{1}$ and $\Omega _{5}$; cf. Eq. (54) and Eqs. (97), (98) in the next section. In the Klein zone, an in-electron (or an in-positron) is subjected to total reflection, whose amplitude probability is given by $w_{n}\left( +|+\right)$ ($w_{n}\left( -|-\right)$ for positrons), and no transmission occurs in this range. Moreover, from Eqs. (54) and (58) we observe that $\left| w_{n}\left( +|+\right) \right| ^{-2}=1-N_{n}^{\mathrm {cr} }=p_{v}^{n}$ describes the probability that the partial vacuum state, with given quantum numbers n, remains a vacuum while $p_{v}^{n}\left| w_{n}\left( +-|0\right) \right| ^{2}$ denotes the probability that a pair of Fermions, with given quantum numbers n, will be created. Therefore, from the second line of Eq. (32), we obtain the probability conservation

$$\begin{aligned} p_{v}^{n}+p_{v}^{n}\left| w_{n}\left( +-|0\right) \right| ^{2}=1, \end{aligned}$$

(93)

resulting from Pauli’s principle, which states that for given quantum numbers n there are only two possibilities: either the vacuum state remains vacuum or a pair of Fermions be created in a cell of the space. This is the correct interpretation of the coefficients $\left| g\left( _{+}|^{-}\right) \right| ^{-2}$, $\left| g\left( _{+}|^{+}\right) \right| ^{-2}$ and $\left| g\left( _{+}|^{-}\right) \right| ^{2}\left| g\left( _{+}|^{+}\right) \right| ^{-2}$ in the Klein zone.

Similar interpretations of relative probabilities discussed above hold for scalar case, namely $\left| g\left( _{+}|^{-}\right) \right| ^{2}\left| g\left( _{+}|^{+}\right) \right| ^{-2}$ is the relative probability of a particle scattering, while $\left| g\left( _{+}|^{+}\right) \right| ^{-2}$ is the relative probability of a particle-antiparticle creation. To obtain explicit forms for these quantities, one can use Eq. (82) for $\left| g\left( _{+}|^{-}\right) \right| ^{-2}$ and definitions given by Eqs. (54). The essential difference in comparison with the Fermi case is the identification of $p_{v}^{n}$. From Eqs. (54) and (58), the probability that the partial vacuum state with a quantum numbers n remains the vacuum reads: $p_{v}^{n}=\left( 1+N_{n}^{\mathrm {cr}}\right) ^{-1}=\left| w_{n}\left( +|+\right) \right| ^{2}$. From the second line of Eq. (32), we obtain the identity

$$\begin{aligned} p_{v}^{n}\left[ 1-\left| w_{n}\left( +-|0\right) \right| ^{2}\right] ^{-1}=1, \end{aligned}$$

(94)

that can be interpreted as follows: The conditional probability of a pair creation with quantum numbers n is the sum of probabilities of creation for any number l of pairs

$$\begin{aligned} P\left( \mathrm {pairs}|0\right) _{n}=p_{v}^{n}\left[ \sum _{l=1}^{\infty }\left| w_{n}\left( +-|0\right) \right| ^{2l}\right] , \end{aligned}$$

(95)

under the condition that all other partial vacua, labelled by quantum numbers $m\ne n$, remain vacua. Hence, the conservation of probability (94) is the sum of probabilities of all possible events in a cell of the space with quantum numbers n, namely

$$\begin{aligned} P\left( \mathrm {pairs}|0\right) _{n}+p_{v}^{n}=1. \end{aligned}$$

(96)

4 Processes beyond the Klein zone

The most elementary quantum processes beyond the Klein zone are particle scattering in the form of reflection from the potential step and particle transmission through the potential step, both occurring in the ranges $\Omega _{1}$ and $\Omega _{5}$. To study these processes, it is enough to introduce the relative $R_{+,n}$ and absolute ${\tilde{R}}_{+,n}=c_{v}R_{+,n}$ reflection amplitudes of right antiparticles

$$\begin{aligned} R_{+,n_{5}}= & {} \left\langle 0\left| \ ^{-}b_{n_{5}}\left( \mathrm {out} \right) \ ^{+}b_{n_{5}}^{\dagger }\left( \mathrm {in}\right) \right| 0\right\rangle \nonumber \\= & {} g\left( _{+}|^{+}\right) ^{-1}g\left( _{+}|^{-}\right) , \end{aligned}$$

(97)

and the relative $T_{+,n}$ and absolute ${\tilde{T}}_{+,n}=c_{v}T_{+,n}$ transmission amplitudes of right antiparticles

$$\begin{aligned} T_{+,n_{5}}=\left\langle 0\left| \ _{+}b_{n_{5}}\left( \mathrm {out} \right) \ ^{+}b_{n_{5}}^{\dagger }\left( \mathrm {in}\right) \right| 0\right\rangle =\eta _{\mathrm {R}}g\left( _{+}|^{+}\right) ^{-1}, \nonumber \\ \end{aligned}$$

(98)

since all remaining probabilities, corresponding reflection $\left| R_{-,n_{5}}\right| ^{2}$ and transmission $\left| T_{-,n_{5}}\right| ^{2}$ of left antiparticles in $\Omega _{5}$ or else particle reflection $\left| R_{\zeta ,n_{1}}\right| ^{2}$ and particle transmission $\left| T_{\zeta ,n_{1}}\right| ^{2}$ probabilities in $\Omega _{1}$ can be obtained with the aid of the identities

$$\begin{aligned}&\left| R_{+,n}\right| ^{2}=\left| R_{-,n}\right| ^{2}=\left| g\left( _{+}|^{-}\right) \right| ^{2}\left| g\left( _{+}|^{+}\right) \right| ^{-2},\ \ \nonumber \\&\left| T_{+,n}\right| ^{2}=\left| T_{-,n}\right| ^{2}=\left| g\left( _{+}|^{+}\right) \right| ^{-2}, \nonumber \\&\left| R_{\zeta ,n}\right| ^{2}+\left| T_{\zeta ,n}\right| ^{2}=1,\ \ n\in \Omega _{1}\cup \Omega _{5}, \end{aligned}$$

(99)

that follows from Eqs. (31) and (32) specialized to $\Omega _{1}\cup \Omega _{5}$. The representations, in terms of the g-coefficients, in Eqs. (97) and (98) are determined by linear canonical transformations that can be extracted from Eqs. (4.33) in [16] after the formal substitutions$\ _{-}^{+}a_{n}\left( \mathrm {out} \right) \rightarrow \ _{-}^{+}b_{n}^{\dagger }\left( \mathrm {in}\right)$ and $\ _{+}^{-}a_{n}\left( \mathrm {in}\right) \rightarrow \ _{+}^{-}b_{n}^{\dagger }\left( \mathrm {out}\right)$. Moreover, reflection and transmission amplitudes for particles in $\Omega _{1}$ are given by Eqs. (5.3) and (5.5) in [16]. The expressions for Bosons coincide with the above equations setting $\eta _{\mathrm {R}}=\eta _{\mathrm {L}}=+1$.

The above probabilities can be studied for any configurations of the electric field, in particular cases where the field is concentrated over a finite region along the x-axis. Such configurations are characterized by “small” or even “finite” length scales $\xi _{j}$ so that the parameters $\left| U_{\mathrm {L}}\right| \xi _{1}$, $U_{\mathrm {R}}\xi _{2}$ are fixed. First, considering energies and length scales $\xi _{j}$ small enough so that the parameters $\left| p^{\mathrm {L}}\right| \xi _{1}$, $\left| p^{\mathrm {R}}\right| \xi _{2}$ are sufficiently small, the coefficient $\left| g\left( _{+}|^{-}\right) \right| ^{-2}$ formally coincides with Eq. (80) for Fermions and Eq. (82) for Bosons. Therefore, the reflection and transmission probabilities acquire the same form as the relative probabilities in $\Omega _{3}$

$$\begin{aligned} \left| R_{\zeta ,n}\right| ^{2}\approx & {} \left( \frac{\left| p^{ \mathrm {L}}\right| -\left| p^{\mathrm {R}}\right| +\chi {\mathbb {U}} }{\left| p^{\mathrm {L}}\right| +\left| p^{\mathrm {R}}\right| +\chi {\mathbb {U}}}\right) ^{2}\frac{\left| \pi _{0}\left( \mathrm {R} \right) -\chi \left| p^{\mathrm {R}}\right| \right| }{\left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{\mathrm {R}}\right| \right| }, \nonumber \\ \left| T_{\zeta ,n}\right| ^{2}\approx & {} \frac{4\left| p^{ \mathrm {R}}\right| \left| p^{\mathrm {L}}\right| }{\left( \left| p^{\mathrm {L}}\right| +\left| p^{\mathrm {R}}\right| +\chi {\mathbb {U}}\right) ^{2}}\frac{\left| \pi _{0}\left( \mathrm {R} \right) -\chi \left| p^{\mathrm {R}}\right| \right| }{\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| }, \end{aligned}$$

(100)

for Fermions and coincides, in particular, with the reflection and transmission coefficients calculated for the Peak electric field [31] in the sharp-gradient regime. For Bosons, the transmission coefficient can be conveniently calculated using Eq. (82) and the quadratic relations (32) specialized to this case, namely $\left| T_{\zeta ,n}\right| ^{2}=\left[ 1+\left| g\left( _{+}|^{-}\right) \right| ^{2}\right] ^{-1}$. Once the transmission coefficient is obtained, the reflection probability coefficient can be calculated using the conservation of probabilities, $\left| R_{\zeta ,n}\right| ^{2}=1-\left| T_{\zeta ,n}\right| ^{2}$.

Next, considering energies and length scales $\xi _{j}$ large enough so that the parameters $\left| p^{\mathrm {L}}\right| \xi _{1}$, $\left| p^{\mathrm {R}}\right| \xi _{2}$ are sufficiently large, one can use the asymptotic approximations for the Whittaker functions with large argument given by Eq. (13.19.3) in [33] to show that the reflection and transmission probabilities coincide with Eq. (100) for Fermions. Notice that despite the formal coincidence between Eqs. (100) and (91), the reflection and transmission coefficients (100) are less than the unity beyond the Klein zone. For energies in the Klein zone, these coefficients can be larger than unity as we discussed in the previous section. Hence, if interpreted as reflection and transmission coefficients, this suggests that more Fermions are reflected from the potential step than coming in and also more Fermions are transmitted by the potential step than coming in. This is the Klein paradox, which is removed by the correct interpretation of the rhs. of Eqs. (100). As for Bosons, the probabilities acquire substantially different approximations than the previous case, namely

$$\begin{aligned} \left| R_{\zeta ,n}\right| ^{2}\approx \left( \frac{\left| p^{ \mathrm {L}}\right| -\left| p^{\mathrm {R}}\right| }{\left| p^{ \mathrm {L}}\right| +\left| p^{\mathrm {R}}\right| }\right) ^{2},\ \ \left| T_{\zeta ,n}\right| ^{2}\approx \frac{4\left| p^{\mathrm {L}}\right| \left| p^{\mathrm {R}}\right| }{\left( \left| p^{\mathrm {L}}\right| +\left| p^{\mathrm {R}}\right| \right) ^{2}}, \nonumber \\ \end{aligned}$$

(101)

in leading-order approximation. Eq. (101) coincides with reflection and transmission coefficients calculated for the Sauter electric field [16] and the Peak electric field [31] in the sharp-gradient regime. It should be noted that for energies well above or far below the asymptotic potential energies $\left| U_{\mathrm {L} }\right|$, $U_{\mathrm {R}}$, the reflection $\left| R_{\zeta ,n}\right| ^{2}$ and transmission $\left| T_{\zeta ,n}\right| ^{2}$ probabilities tend to zero and one, respectively. Indeed, if $p_{0}\gg U_{\mathrm {R}}$ or $p_{0}\ll -\left| U_{\mathrm {L}}\right|$, one finds $\left| R_{\zeta ,n}\right| ^{2}=O\left( \pi _{\perp }^{2} {\mathbb {U}}^{2}/p_{0}^{4}\right)$ for Fermions and $\left| R_{\zeta ,n}\right| ^{2}=O\left( {\mathbb {U}}^{2}/p_{0}^{2}\right)$ for Bosons, while $\left| T_{\zeta ,n}\right| ^{2}=1+O\left( {\mathbb {U}} ^{2}/p_{0}^{2}\right)$ for both types of particles.

At last, but not least, it is worth comparing the above results with results that can be obtained in the context of nonrelativistic Quantum Mechanics, more precisely, in the study of one-dimensional particle scattering by inverse-square electric fields. To this end, we set $\pi _{\perp }=m$, $p_{0}=m+E$, and choose $\pi _{0}\left( \mathrm {L}\right) =m+E$, $\pi _{0}\left( \mathrm {R}\right) =m+E-{\mathbb {U}}$. To consider the nonrelativistic limit for Bosons, it is enough to study the so-called kinematic factor $k_{b}=\left| p^{\mathrm {R}}\right| /\left| p^{ \mathrm {L}}\right|$, because the reflection and transmission coefficients (101) are expressed in terms of the latter as $\left| R_{\zeta ,n}\right| ^{2}=\left( 1-k_{b}\right) ^{2}/\left( 1+k_{b}\right) ^{2}$ and $\left| T_{\zeta ,n}\right| ^{2}=4k_{b}/\left( 1+k_{b}\right) ^{2}$. In the nonrelativistic limit $E\ll m$, $k_{b}$ is approximately given by [16, 41]

$$\begin{aligned} k_{b}\approx k^{\mathrm {NR}}\left( 1-\frac{{\mathbb {U}}}{4m}\right) ,\ \ k^{ \mathrm {NR}}=\sqrt{\frac{E-{\mathbb {U}}}{E}}. \end{aligned}$$

(102)

It is noteworthy that Eq. (101) formally coincides with reflection and transmission coefficients calculated for the rectangular potential step in the context of the nonrelativistic Quantum Mechanics; see e.g. the textbook [41], Sec. 25.

In contrast to the Klein–Gordon case, the reflection and transmission coefficients for Fermions (100) do not admit simple representations in terms of a kinematic factor because of their more complex representations. Nevertheless, for sufficiently small steps ${\mathbb {U}}\ll E+m$, the ratio

$$\begin{aligned} \frac{\left| \pi _{0}\left( \mathrm {R}\right) -\left| p^{\mathrm {R} }\right| \right| }{\left| \pi _{0}\left( \mathrm {L}\right) -\left| p^{\mathrm {L}}\right| \right| }=1+\frac{{\mathbb {U}}}{ \left| p^{\mathrm {L}}\right| }+O\left( {\mathbb {U}}^{2}/\left| p^{ \mathrm {L}}\right| ^{2}\right) , \end{aligned}$$

(103)

allows us to simplify the transmission coefficient (100) as follows

$$\begin{aligned} \left| T_{\zeta ,n}\right| ^{2}\approx \frac{4k_{b}\left( 1+{\mathbb {U}}/\left| p^{\mathrm {L}}\right| \right) }{\left( 1+k_{b}+{\mathbb {U}} /\left| p^{\mathrm {L}}\right| \right) ^{2}}. \end{aligned}$$

(104)

In Eqs. (103), (104), we selected $\chi =+1$ for simplicity. In the nonrelativistic limit, ${\mathbb {U}}/\left| p^{\mathrm {L}}\right| \approx {\mathbb {U}}/\sqrt{2mE}$ in leading-order. Combining the latter approximation and Eq. (102) with Eq. (104) one can easily obtain a nonrelativistic expression for the transmission coefficient. The reflection coefficient for Fermions can be obtained through the probability conservation (99).

Fig. 3

Differential mean numbers $N_{n}^{\mathrm {cr}}$ of Fermions (left panel) and Bosons (right panel) created from the vacuum by symmetrical inverse-square fields (2). The solid lines refer to numerical calculation of the exact expressions (36), (40) while the dashed curves the asymptotic approximations (65). In a–c, $m\xi _{1}=m\xi _{2}=10$, 50 and 100, respectively, and $E=E_{c}$ in all cases. The horizontal dashed lines denote the uniform distribution $e^{-\pi \lambda }$

Fig. 4

Differential mean numbers of Fermions created from the vacuum $N_{n}^{\mathrm {cr}}$ by symmetrical inverse-square electric fields. The exact results (solid lines) are given by the absolute square value of Eq. (36) and the asymptotic ones (dashed curves), by Eq. (80). In the left panel, $E=250E_{c}$ and $m\xi _{1}=m \xi _{2}=1/50$ while in the right panel, $E=500E_{c}$ and $m\xi _{1}=m\xi _{2}=1/100$. The magnitude of the potential energy step is constant for both plots ${\mathbb {U}}/m=5=\mathrm {const.}$ and so is the extension of the Klein zone, which is $|p_{0}|/m\le 4$. The horizontal dashed lines denote the maximum value (81)

5 Comparing asymptotic estimates with exact results

In this section we supplement the study with comparisons between differential quantities, calculated numerically, and asymptotic approximations discussed throughout the text. To this aim, we simplify computations by setting ${\mathbf {p}}_{\perp }=0$ and work with the system of units where $\hslash =c=m=1$. In all plots below, the length scales $\xi _{j}$, energies $p_{0}$ and electric field amplitudes E are relative to electron’s mass m and Schwinger’s critical field $E_{c}=m^{2}/e$, respectively.

Starting with quantities defined in the Klein zone, we present in Figs. 3, 4, and 5 plots of differential mean numbers $N_{n}^{\mathrm {cr}}$ given by exact expressions (36) and (40) (solid lines) and by specific asymptotic approximations (dashed curves) as functions of the energy $p_{0}$, for some values of the length scales $\xi _{j}$ and field amplitudes E. In Fig. 3, one can compare exact results with asymptotic approximations obtained in small-gradient regime ( 65) while in Figs. 4 and 5, we compare exact results with asymptotic approximations obtained for electric fields in sharp-gradient regime (80) and (82).

Fig. 5

Differential mean numbers of Bosons created from the vacuum $N_{n}^{ \mathrm {cr}}$ by symmetrical inverse-square electric fields. The exact results (solid lines) are given by the absolute square value of Eq. (40) and the asymptotic ones (dashed curves), by Eq. (82). In the left panel, $E=250E_{c}$ and $m\xi _{1}=m\xi _{2}=1/50$ while in the right panel, $E=500E_{c}$ and $m\xi _{1}=m \xi _{2}=1/100$. The magnitude of the potential energy step is constant for both plots ${\mathbb {U}}/m=5=\mathrm {const.}$ and so is the extension of the Klein zone, which is $\left| p_{0}\right| /m\le 4$ . The horizontal dashed lines denote the maximum value (83)

The numerical results represent differential quantities obtained for electric fields near the small-gradient or the sharp-gradient regimes. For example, in Fig. 3, the larger the length scales $\xi _{j}$ the more accurate asymptotic forms (65), which means that electric fields in Fig. 3 are closer to the small-gradient regime. Moreover, we see that the differential means tend to the uniform distribution $e^{-\pi \lambda }$ as $\xi _{j}$ increases. This is expected since inverse-square electric field (2) tends to the L-constant field [29] as the length scales $\xi _{j}$ increase, whose differential means are given by $e^{-\pi \lambda }$ provided it acts on the vacuum over a sufficiently wide region in the space. Still in Fig. 3, we observe that the means $N_{n}^{\mathrm {cr}}$ approach the uniform distribution $e^{-\pi \lambda }$ for small energies, while they approach asymptotic forms (65) as the energy increases, irrespective the value of the length scales $\xi _{j}$. However, increasing the length scales $\xi _{j}$ and the field amplitudes E the parameters $\left| U_{\mathrm {L}}\right| \xi _{1}$, and $U_{\mathrm {R}}\xi _{2}$ increase as well, which significantly improve the accuracy of asymptotic approximations (65) as was discussed in Sect. 3.1. For the values considered on the Fig. 3, the lines $\left( \mathrm {a}\right)$, $\left( \mathrm {b}\right)$ and $\left( \mathrm {c}\right)$ correspond to ${\mathbb {U}}\xi /2=100$, 2500 and $10^{4}$, respectively.

In Figs. 4 and 5 we represent mean numbers in the case of an inverse-square electric field near the sharp-gradient regime. In these plots, we chose sufficiently large electric amplitudes E and sufficiently small length scales $\xi _{j}$, simulating very strong, sharp and critical electric fields. For all plots on the Figs. 4 and 5, the magnitude of the potential energy step is fixed, namely ${\mathbb {U}}/m=5$. According to the above results, we see that the accuracy of asymptotic forms (80) and (82) increases as the length scales $\xi _{j}$ decreases. As discussed in Sect. 3.2, this results from the fact that the parameters $\left| U_{\mathrm {L}}\right| \xi _{1}$ and $U_{ \mathrm {R}}\xi _{2}$ decrease as $\xi _{j}$ decrease and the smaller their values the more accurate the approximations. This explains why the dashed lines are closer to the solid lines on the right panels than on the left panels on the both figures.

Although the asymptotic forms are less accurate in the scalar case, the accuracy of the approximations can be improved incorporating next-to-leading order terms into Eq. (82). Furthermore, it should be noted that for the values of $E/E_{c}$ and $m\xi$ considered on the Fig. 5, the differential mean numbers are less than the unity. However, for inverse-square electric fields in intermediate regimes,¹² this may not be the case: a very large number of Bosons can be created from the vacuum. In these cases, the notion of inverse-square electric fields as an external one is limited.

Besides the differential mean numbers, there are other differential quantities worth of consideration, such as transmission probabilities defined beyond the Klein zone, as was mentioned in the previous section. Thus, on the Figs. 6 and 7 we present transmission probabilities both for scalar and Fermi cases given analytically by exact expressions (99), (38) and by appropriate asymptotic representations discussed in Sec. 4.

Fig. 6

Probabilities of Fermions transmission through symmetrical inverse potential steps in $\Omega _{1}$. Exact results, given by Eqs. (99) and (38), are represented by solid lines while asymptotic ones, given by Eq. (100), are represented by dashed curves. In the left panel, $E=250E_{c}$ and $m\xi _{1}=m\xi _{2}=1/50$ while in the right panel, $E=500E_{c}$ and $m\xi _{1}=m \xi _{2}=1/100$. The lower bound of $\Omega _{1}$ is the same for both plots which, in this system of units, is $p_{0}/m=6$

Fig. 7

Probabilities of Bosons transmission through symmetrical inverse potential steps in $\Omega _{1}$. Exact results, given by Eqs. (99) and (38), are represented by solid lines while the asymptotic ones are represented by dashed curves. $\left( \mathrm {a}\right)$ : approximations given by the coefficient $\left| g\left( _{+}|^{-}\right) \right| ^{-2}$ in Eq. (82) and the identity $\left| T_{\zeta ,n}\right| ^{2}=\left[ 1+\left| g\left( _{+}|^{-}\right) \right| ^{2}\right] ^{-1}$. $\left( \mathrm {b}\right)$: approximations given by Eq. (101). In the left panel, $E=250E_{c}$ and $m\xi _{1}=m\xi _{2}=1/50$ while in the right panel, $E=500E_{c}$ and $m\xi _{1}=m \xi _{2}=1/100$. The lower bound of $\Omega _{1}$ is the same for both plots which, in this system of units, is $p_{0}/m=6$

Thus, one can see that the asymptotic approximations agree with exact results within a certain level of accuracy. In a sufficient wide energy interval, on the Fig. 6 we see that approximations (100) for Fermions are more accurate on the right panel than on the left panel. This is a consequence of the fact that the results on the right panel refer to an electric field sharper than the one of the left panel, which means that the parameter ${\mathbb {U}}\xi /2$ is smaller in the former case than in the latter. According to the discussions presented in the Sect. 4, the smaller the parameter ${\mathbb {U}}\xi /2$ the more accurate are transmission probabilities (100). For the values considered on the Fig 6, we see that ${\mathbb {U}}\xi /2=0.1$ on the left panel while ${\mathbb {U}}\xi /2=0.05$ on the right panel. This explains why the dashed lines on the right panel are closer to the solid lines than on the left panel. Nevertheless, it should be noted that as the energy $p_{0}/m$ grows the parameters $\left| p^{\mathrm {L}}\right| \xi$ and $\left| p^{\mathrm {R} }\right| \xi$ increase as well, which means that approximation (100) becomes more accurate irrespective the value of ${\mathbb {U}}\xi /2$, as long as it is finite. Technically, this follows from the fact that the asymptotic approximations for the Whittaker functions with small or large arguments and fixed parameters notably reproduce the same approximation (100) for Fermions.

The results for Bosons are slightly different than the ones for Fermions, since there are two approximations: one calculated using the coefficients $\left| g\left( _{+}|^{-}\right) \right| ^{-2}$ given by Eq. (82) and the identify $\left| T_{\zeta ,n}\right| ^{2}=\left[ 1+\left| g\left( _{+}|^{-}\right) \right| ^{2}\right] ^{-1}$ and the second one, given by Eq. (101). That is why both panels on the Fig. 7 display two dashed lines. The dashed lines labelled by $\left( \mathrm {a}\right)$ refer to the approximation calculated with the help of Eq. (82) while the ones labelled with $\left( \mathrm {b}\right)$, to Eq. (101). According to the results represented on the left panel, we see that approximations (101) are much more accurate than the ones calculated with the help of Eq. (82). This is quite expected since the electric field parameterized by values considered on that plot is not “sharp” enough. In other words, the parameter ${\mathbb {U}}\xi /2$ is not small enough in comparison to the unity for making results of electric fields in the sharp-gradient regime agree with exact results. Thus, the approximation for electric fields beyond sharp-gradient regime (101) is more accurate in this case. One ought to say that this is a peculiarity of Bosons since for Fermions the approximations obtained for an electric field in the sharp-gradient regime (100) are closer to exact results. The results displayed on the right panel of Fig. 7 are even more interesting since the exact results “interpolate” between both approximations. For sufficiently small energies, the approximations obtained from Eq. (82) are more accurate than the ones calculated with the help of Eq. (101) as was expected, since the parameters $\left| p^{ \mathrm {L}}\right| \xi$, $\left| p^{\mathrm {R}}\right| \xi$ and ${\mathbb {U}}\xi /2$ are small enough. Thus, we may say that an electric field parameterized by the values considered on the right panel are in the sharp-gradient regime. However, as the energy grows, the parameters $\left| p^{\mathrm {L}}\right| \xi$ and $\left| p^{\mathrm {R} }\right| \xi$ grow so that approximation (101) eventually will be more accurate than the one obtained from Eq. (82). This explains why the exact results tend to the dashed lines $\left( \mathrm {b}\right)$ as the energy grows. Finally, based on the numerical values on the Figs. 6 and 7, we conclude that for electric fields characterized by amplitudes $E\lesssim 250E_{c}$ and by length scales $m\xi > rsim 1/50$, approximations for electric fields beyond the sharp-gradient regime (101) agree sufficiently well with exact results for Bosons while for Fermions accuracy approximations (100) is good enough only for large energies. As for electric fields parameterized by $E > rsim 500E_{c}$ and $m\xi \lesssim 1/100$, the field is sharp enough so that approximations (100) agree sufficiently well over a wide range of energies for Fermions. For Bosons, approximations of sharp-gradient regime work sufficiently well only for small energies. For large energies, approximations (101) must be considered instead. Note that similar results can be obtained for negative energies in $\Omega _{5}$. Lastly, one may arrive at the same conclusions studying reflection probabilities instead of transmission probabilities, either in $\Omega _{1}$ or in $\Omega _{5}$.

6 Role of the growing and decreasing regions in the field behavior

As an application of the above results, one can analyze contributions to the vacuum instability from “growing” and “decaying” areas that accompany the arising uniform in space constant electric field. To this end, we consider here a field configuration composed of three independent regions, growing inversely squared in the first region $x\in \mathrm {I}=\left( -\infty ,x_{ \mathrm {L}}\right)$, remaining constant in the second region $x\in \mathrm { Int}=\left[ x_{\mathrm {L}},x_{\mathrm {R}}\right] ,$ and decreasing inversely squared in the last region $x\in \mathrm {II}=\left( x_{\mathrm {R} },+\infty \right)$. Such a field – hereafter referred to as composite electric field – corresponds to a generalization of the inverse-square electric field (2) by having, instead of a peak at $x=0$, an intermediate region. Afterward, we compare the vacuum instability caused by the composite electric field with the one which is caused by the electric field that “suddenly grows” and “suddenly decays” at precise positions on the x-axis, say at $x=x_{\mathrm {L}}$ and $x=x_{\mathrm {R}}$, respectively.

Let us consider the L-constant electric field [29]

$$\begin{aligned} E\left( x\right) =E\left\{ \begin{array}{ll} 0, &{} \quad x\in \mathrm {I}\, \\ 1, &{} \quad x\in \mathrm {Int}\, \\ 0, &{} \quad x\in \mathrm {II}\, \end{array} \right. , \end{aligned}$$

(105)

which, by the definition, “grows” and “decays” sharply at $x=x_{\mathrm {L}}$ and $x=x_{\mathrm {R}}$, respectively, and the composite electric field

$$\begin{aligned} E\left( x\right) =E\left\{ \begin{array}{ll} \left[ 1-\left( x-x_{\mathrm {L}}\right) /\xi _{1}\right] ^{-2}, &{} \quad x\in \mathrm {I}\, \\ 1, &{} \quad x\in \mathrm {Int}\, \\ \left[ 1+\left( x-x_{\mathrm {R}}\right) /\xi _{2}\right] ^{-2}, &{} \quad x\in \mathrm {II}\, \end{array} \right. , \end{aligned}$$

(106)

whose dependence on x, within $\mathrm {I}$ and $\mathrm {II}$, simulate “processes” of “growing” and “decaying” of the electric field. Thus, in what follows, we refer the regions $\mathrm {I}$ and $\mathrm {II}$ as growing and decaying processes for simplicity. For both cases, the constants $x_{\mathrm {L}}=-L/2<0$ and $x_{\mathrm {R}}=L/2>0$ sets the spatial region where the field is constant and shall be the same for both fields. Potential energies of an electron in each field are:

$$\begin{aligned} U\left( x\right) =eE\left\{ \begin{array}{ll} x_{\mathrm {L}}, &{} \quad x\in \mathrm {I}\, \\ x, &{} \quad x\in \mathrm {Int}\, \\ x_{\mathrm {R}}, &{} \quad x\in \mathrm {II}\, \end{array} \right. , \end{aligned}$$

(107)

and

$$\begin{aligned} U\left( x\right) =eE\left\{ \begin{array}{ll} -\left( \xi _{1}-x_{\mathrm {L}}\right) +\xi _{1}\left[ 1-\left( x-x_{\mathrm { L}}\right) /\xi _{1}\right] ^{-1}, &{} \quad x\in \mathrm {I}\, \\ x, &{} \quad x\in \mathrm {Int}\, \\ \xi _{2}+x_{\mathrm {R}}-\xi _{2}\left[ 1+\left( x-x_{\mathrm {R}}\right) /\xi _{2}\right] ^{-1}, &{} \quad x\in \mathrm {II}\, \end{array} \right. , \nonumber \\ \end{aligned}$$

(108)

respectively.

We are interested in differential quantities characterizing vacuum instability, in particular, mean numbers $N_{n}^{\mathrm {cr}}$. To this end, it is enough to analyze relevant g-coefficients within the Klein zone for both examples. For the L-constant field (105), necessary coefficients have been calculated before; see Eqs. (2.27) in Ref. [29]. As for the composite field (106), it should noted that the existence of the intermediate region $\mathrm {Int}=\left[ x_{\mathrm {L} },x_{\mathrm {R}}\right]$ increase the magnitude of the step

$$\begin{aligned} {\mathbb {U}}=eE\left( \xi _{1}+\xi _{2}+L\right) , \end{aligned}$$

(109)

which, in turn, modifies asymptotic kinetic energies $\pi _{0}\left( \mathrm { L/R}\right)$ (15) and variables $z_{j}\left( x\right)$ (14) only by additive constants

$$\begin{aligned} \pi _{0}\left( \mathrm {L}\right)= & {} p_{0}+eE\left( \xi _{1}-x_{\mathrm {L} }\right) ,\ \nonumber \\ \ z_{1}\left( x\right)= & {} 2i\left| p^{\mathrm {L}}\right| \left[ \xi _{1}-\left( x-x_{\mathrm {L}}\right) \right] ,\ \ x\in \mathrm {I} , \nonumber \\ \pi _{0}\left( \mathrm {R}\right)= & {} p_{0}-eE\left( \xi _{2}+x_{\mathrm {R} }\right) ,\ \ \nonumber \\ z_{2}\left( x\right)= & {} 2i\left| p^{\mathrm {R}}\right| \left[ \xi _{2}+\left( x-x_{\mathrm {R}}\right) \right] ,\ \ x\in \mathrm {II }, \end{aligned}$$

(110)

while the asymptotic momenta $\left| p^{\mathrm {L/R}}\right|$ and parameters $\kappa _{j}$, $\mu _{j}$ are defined in the same way as in Eqs. (15), (17)

$$\begin{aligned} \left| p^{\mathrm {L/R}}\right|= & {} \sqrt{\pi _{0}\left( \mathrm {L/R} \right) ^{2}-\pi _{\perp }^{2}},\ \ \mu _{j}=\left( -1\right) ^{j}\left( ieE\xi _{j}^{2}-\chi /2\right) , \nonumber \\ \kappa _{1}= & {} ieE\xi _{1}^{2}\frac{\pi _{0}\left( \mathrm {L}\right) }{ \left| p^{\mathrm {L}}\right| },\ \ \kappa _{2}=-ieE\xi _{2}^{2} \frac{\pi _{0}\left( \mathrm {R}\right) }{\left| p^{\mathrm {R} }\right| }, \end{aligned}$$

(111)

but with $\pi _{0}\left( \mathrm {L/R}\right)$ given by Eq. (110). The above modifications does not interfere on asymptotic properties of the solutions in the intervals $\mathrm {I}$, II and therefore does not change the classification of solutions with special left and right asymptotics. Hence, the exact solutions of wave equations for the intervals $\mathrm {I}$, $\mathrm {II}$ are Whittaker functions, classified according to Eqs. (24) and whose arguments and parameters are given by Eqs. (110), (111).

As for the intermediate region $x\in \mathrm {Int}$, Dirac spinors (or KG wave functions) are proportional to Weber Parabolic Cylinder functions (WPCF) [32] once general solutions of the second-order differential equation (12) are expressed in terms of these functions [29]

$$\begin{aligned} \varphi _{n}\left( x\right) =\alpha _{+}u_{+}\left( {\mathfrak {Z}}\left( x\right) \right) +\alpha _{-}u_{-}\left( {\mathfrak {Z}}\left( x\right) \right) ,\ \ x\in \mathrm {Int}. \end{aligned}$$

(112)

Here $u_{+}\left( {\mathfrak {Z}}\right) =D_{\rho }\left( {\mathfrak {Z}}\right)$ and $u_{-}\left( {\mathfrak {Z}}\right) =D_{-\rho -1}\left( i{\mathfrak {Z}} \right)$ are WPCF while $\alpha _{\pm }$ are arbitrary constants. The argument ${\mathfrak {Z}}$ and parameter $\rho$ are defined as

$$\begin{aligned} {\mathfrak {Z}}\left( x\right)= & {} \left( 1-i\right) \left( \sqrt{eE}x-\frac{p_{0} }{\sqrt{eE}}\right) ,\ \ \nonumber \\ \rho= & {} -\nu -\frac{\chi +1}{2},\ \ \nu =\frac{ i\lambda }{2}. \end{aligned}$$

(113)

Thus, with the aid of (112) and the solutions for the intervals I, II (24) (with the substitutions described above), one may demand continuity of the wave functions and its derivatives at $x=x_{\mathrm {L}}$ and $x=x_{\mathrm {R}}$ [similarly to the derivation of Eqs. (35), (36)] to obtain the following form for the coefficient $g\left( _{+}|^{-}\right)$:

$$\begin{aligned} g\left( _{+}|^{-}\right)= & {} \eta _{\mathrm {L}}\sqrt{\frac{\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| }{8eE\left| p^{\mathrm {L}}\right| \left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{\mathrm {R}}\right| \right| \left| p^{\mathrm {R}}\right| }}\nonumber \\&\quad \times \exp \left[ -\frac{i\pi }{ 2}\left( \kappa _{1}+\kappa _{2}+\nu +\frac{\chi }{2}\right) \right] \nonumber \\&\times \left[ {\mathcal {F}}_{2}^{-}\left( x_{2}\right) {\mathcal {G}} _{1}^{+}\left( x_{1}\right) -{\mathcal {F}}_{2}^{+}\left( x_{2}\right) {\mathcal {G}}_{1}^{-}\left( x_{1}\right) \right] , \end{aligned}$$

(114)

in which

$$\begin{aligned} {\mathcal {G}}_{j}^{\pm }\left( x\right)= & {} u_{\pm }\left( {\mathfrak {Z}}\right) \frac{d}{dx}W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) \nonumber \\&-W_{-\kappa _{j},\mu _{j}}\left( e^{-i\pi }z_{j}\right) \frac{d}{dx}u_{\pm }\left( {\mathfrak {Z}}\right) , \nonumber \\ {\mathcal {F}}_{j}^{\pm }\left( x\right)= & {} u_{\pm }\left( {\mathfrak {Z}}\right) \frac{d}{dx}W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) \nonumber \\&-W_{\kappa _{j},\mu _{j}}\left( z_{j}\right) \frac{d}{dx}u_{\pm }\left( {\mathfrak {Z}}\right) . \end{aligned}$$

(115)

Henceforward, we shall compare mean numbers of particles created from the vacuum $N_{n}^{\mathrm {cr}}$ by the L-constant electric field (105) and by the composite electric field (106) in situations whose intermediate length L and the field amplitude E are larger than the stabilization characteristic number $\max \left( 1,m^{2}/eE\right)$, namely $\sqrt{eE}L>\max \left( 1,m^{2}/eE\right)$. The remaining parameters, related to the length scales $\xi _{j}$, are finite. These configurations allow us to compare and analyze how the mean numbers approach or deviate from the uniform distribution $e^{-\pi \lambda }$, as the field is supplied by growing and decaying regions. Figures 8, 9 and 10 display exact mean numbers $N_{n}^{\mathrm {cr}}$, as a function of the energy $p_{0}$, corresponding to the L-constant field [solid lines, (c) and (d)] and to the composite electric field [solid lines, (a) and (b)] for some values of the parameters $\sqrt{eE}L$, $\sqrt{eE}\xi _{j}$, $E/E_{c}$. For the computation of the mean numbers, we use the coefficient given by Eq. (2.27) in Ref. [29] for the L-constant field while Eq. (114) for the composite field. Energies, length scales and field amplitudes E are expressed in units of the electron mass m and Schwinger’s critical field $E_{c}$, respectively. Moreover, we keep the same conventions employed in Sect. 5, namely we set ${\mathbf {p}}_{\perp }=0$ and work with the system of units where $\hslash =c=m=1$.

Fig. 8

Differential mean numbers $N_{n}^{\mathrm {cr}}$ of particles created from the vacuum by the composite electric field (106) [solid lines (a, b)] and by the L-constant electric field (105) [solid lines (c, d)], with field amplitudes $E=E_{c}$ and length scales $m\xi _{1}=m\xi _{2}=1$. In the left panel (A), $mL=10$, while in the right panel (B), $mL=20$. The distributions have different energy ranges because the extent of the Klein zone depends on the external field under consideration: for the L-constant field, $\left| p_{0}\right| /m\le 4$ in (A) and $\left| p_{0}\right| /m\le 9$ in (B) while for the composite field, $\left| p_{0}\right| /m\le 5$ in (A) and $\left| p_{0}\right| /m\le 10$ in (B). The horizontal dashed lines denote the uniform distribution $e^{-\pi }$

Fig. 9

Differential mean numbers $N_{n}^{\mathrm {cr}}$ of particles created from the vacuum by the composite electric field (106) [solid lines (a, b)] and by the L-constant electric field (105) [solid lines (c, d)], with field amplitudes $E=E_{c}$ and fixed length scale $mL=10$. In the left panel (A), $m\xi _{1}=m\xi _{2}=1$, while in the right panel (B), $m\xi _{1}=m\xi _{2}=2$. The distributions have different energy ranges because the extent of the Klein zone depends on the external field under consideration: for the L-constant field, $\left| p_{0}\right| /m\le 4$ in both panels while for the composite field, $\left| p_{0}\right| /m\le 5$ in (A) and $\left| p_{0}\right| /m\le 6$ in (B). The horizontal dashed lines denote the uniform distribution $e^{-\pi }$

Fig. 10

Differential mean numbers $N_{n}^{\mathrm {cr}}$ of particles created from the vacuum by the composite electric field (106) [solid lines (a, b)] and by the L-constant electric field (105) [solid lines (c, d)] with fixed field amplitudes $E=2E_{c}$ and length $mL=10$. In the left panel (A), $m\xi _{1}=m\xi _{2}=1$ while in the right panel (B), $m\xi _{1}=m\xi _{2}=2$. The distributions have different energy ranges because the Klein zone extent depends on the external field under consideration: for the L-constant field, $\left| p_{0}\right| /m\le 9$ in both panels while for the composite field, $\left| p_{0}\right| /m\le 11$ in (A) and $\left| p_{0}\right| /m\le 13$ in (B). The horizontal dashed lines denote the uniform distribution, $e^{-\pi /2}$

Within the range of values chosen for parameters associated with length scales $L,\xi _{j}$, and field amplitude E, we observe that the mean numbers of particles created $N_{n}^{\mathrm {cr}}$ oscillate around the uniform distribution $e^{-\pi \lambda }$ in all cases. This is a direct consequence of the parameter $\sqrt{eE}L$ being larger than the stabilization characteristic number $\max \left( 1,m^{2}/eE\right)$, which is reduced to the unity here because $E\ge E_{c}$. According to general results obtained for the L-constant field [29], the mean number stabilizes to the uniform distribution $e^{-\pi \lambda }$ provided $\sqrt{eE}L$ is sufficiently large; the larger its value, the closer to the uniform result. This is particularly clear in the plots of Fig. 8, in which the parameters $m\xi _{1}=m\xi _{2}$ and the field amplitude E are fixed but the length L of the intermediate interval is smaller in (A) than in (B).

To understand the role of growing and decaying length scales $\xi _{j}$ on the mean numbers $N_{n}^{\mathrm {cr}}$, we compare results between external fields in two additional configurations, both having the same length of the intermediate region L but field amplitudes E and length scales $\xi _{j}$ assuming the following values: $E=E_{c}$, $m\xi _{1}=m\xi _{2}=1$ and $m\xi _{1}=m\xi _{2}=2$ in Fig. 9 while $E=2E_{c}$, $m\xi _{1}=m\xi _{2}=1$ and $m\xi _{1}=m\xi _{2}=2$ in Fig. 10. According to the results in Fig. 9, we observe that increasing the length scales $\xi _{j}$ lead to results closer to the uniform distribution, as it can be seen comparing the amplitude of oscillations of the lines (a), (b) in the left panel (A) with those in the right panel (B), both in Fig. 9. This feature does not depend on the amplitude of the electric field, as it occurs for different values of the field amplitudes; cf. lines (a) and (b) in the left panel with the ones in the right panel in Fig. 10. Moreover, comparing results from the composite field [lines (a) and (b)] with the ones from the L-constant field [lines (c) and (d)] we see that the former are closer to the uniform distribution $e^{-\pi \lambda }$ than the latter, irrespective the field amplitude E or length scales $\xi _{j}$ . In other words, results from composite fields present smaller – in amplitude – oscillations around $e^{-\pi \lambda }$ as compared to results from the L-constant field. Such a feature can be seen in all cases displayed in Figs. 8, 9, 10 and, besides, does not depend on particle’s statistics, since it occurs both for Fermions as for Bosons. Furthermore, we also observe that increasing the amplitude of the electric field E leads to results closer to the uniform distribution, as it can be seen comparing plots in the left panel of Fig. 9 with those in the left panel of Fig. 10. The same can be concluded comparing right panels. This feature occurs for both external fields.

These results allow us to conclude that growing and decaying processes plays a significant role in the stabilization process of differential quantities, once mean numbers resulting from external fields supplied by growing and decaying processes reach the stabilization distribution $e^{-\pi \lambda }$ more accurately and, as a matter of fact, in a wider range of energies than fields deprived of such processes. The explanation for these results stems from stabilization conditions associated with the composite field (106) and with the L-constant field (105) being different for the same length L of the intermediate region. Recalling that the stabilization condition for the L-constant field is $\sqrt{eE}L\gg \max \left( 1,m^{2}/eE\right)$ [29] and rephrasing it as

$$\begin{aligned} \sqrt{{\mathbb {U}}L}\gg \max \left( 1,\frac{m^{2}}{eE}\right) ,\ \ {\mathbb {U}} =eEL, \end{aligned}$$

(116)

we realize that when applied to symmetric composite fields $\xi _{1}=\xi _{2}$, it leads to a number $\sqrt{{\mathbb {U}}{\tilde{L}}}$ larger than the lhs. of (106) because the length ${\tilde{L}}\equiv 2\xi +L$ and the magnitude of the step ${\mathbb {U}}$, given by Eq. (109), in this case are larger than simply $\sqrt{eE}L$. Therefore, it is not unexpected that the mean numbers of pairs created by the composite field $N_{n}^{\mathrm {cr} }$ are closer to uniform distribution than the ones created by the L -constant field, provided L is the same for both fields. At last, but not least, it is worth pointing out that features similar to the ones above discussed also occur for time-dependent composite electric fields, as reported by us previously in [27, 28, 30].

7 Concluding remarks

Using nonperturbative approach developed in QED with x-electric potential steps [16], we have calculated elementary zero-order processes (with respect to radiative interaction) in inverse-square critical electric fields. Quantities characterizing the vacuum instability and particle scattering are studied in every detail, in particular, in situations where the external field fits in small-gradient and sharp-gradient configurations. The calculations were done in the Klein zone and beyond, mostly in the ranges $\Omega _{1}$ and $\Omega _{5}$. The processes considered in the Klein zone include not only differential mean numbers, total mean numbers and vacuum-to-vacuum transition probabilities, but also relative amplitudes of particle scattering, pair creation and pair annihilation. Results obtained for configurations in the small-gradient regime are consistent with universal expressions for total quantities in arbitrary weakly inhomogeneous x-electric potential steps. For configurations in the sharp-gradient regime, differential quantities are consistent with ones obtained for another exactly-solvable examples in the same regime, such as the Sauter electric field and the Peak electric field. Moreover, computing total quantities within the Klein zone allows us to extract the imaginary part of the QED effective action and confirm, in particular, the universal behavior of pair creation near the criticality, obtained previously in the literature. For sharp-gradient fields, we still studied the nonrelativistic limit of reflection and transmission coefficients beyond the Klein zone whose expressions can be compared, once calculated, with results obtained in scattering problems by inverse-square electric fields in nonrelativistic Quantum Mechanics. We also commented on the absence of the Klein paradox for inverse-square electric fields in sharp-gradient configurations.

Comparing exact results with asymptotic approximations allows us to study parameters characterizing fields in the small-gradient or sharp-gradient regime, as well as the accuracy of the approximations. For fields in the small-gradient regime, the asymptotic approximations agree sufficiently well with exact results over a wide range of energies in the Klein zone. There are no significant differences between results for Fermions and Bosons in this case. This is not true for fields in the sharp-gradient regime, since approximations in the Fermi case are more accurate than in the scalar case in general. However, the accuracy of all approximations increase as the field amplitudes E and the length scales $\xi _{j}$ decrease. Studying transmission probabilities beyond the Klein zone, we find that approximations for fields in the sharp-gradient regime agree sufficiently well with exact results provided the amplitudes E are large enough and the length scales $\xi _{j}$ small enough. For the scalar case, approximations for the sharp-gradient regime represent better results only for small energies while for large energies approximations beyond the sharp-gradient regime leads to more accurate results.

We study the role of growing and decaying processes in the vacuum instability considering various electric field configuration, composed by inverse-square fields and by an x-independent electric field between them. Using exact expressions for differential quantities, we compute mean numbers for cases whose length scales L and field amplitudes E are sufficiently large. Comparing results obtained for the composite field and for the L -constant field with the uniform distribution $e^{-\pi \lambda }$, we conclude that external fields supplied by growing and decaying processes lead to mean numbers closer to the stabilization distribution and in a wider range of energies than fields deprived of such processes. These results are supported by the fact that parameters characterizing the stabilization condition are larger for composite fields than for L-constant fields.

We conclude this work emphasizing that inverse-square electric field is an additional example of external background where all characteristics underlying vacuum instability and particle scattering can be performed exactly. We believe that exact results presented here may be useful in studies of particle creation by electric fields of more complex spatial distributions, which may not be exactly solvable but decreasing spatially as the inverse-square electric field.

Appendices

Some g-coefficients and their asymptotic representations

In this Appendix, we list exact expressions for the coefficients $g\left( _{+}|^{-}\right)$ and $g\left( _{+}|^{+}\right)$ in terms of Whittaker functions as well as some asymptotic representations of CHF that that may be useful in the study of differential quantities, complementary to the ones discussed in our previous publication [30].

Substituting the relations (19) in Eqs. (35) and (38), the coefficients $g\left( _{+}|^{-}\right)$, $g\left( _{+}|^{+}\right)$ for Fermions acquires the following representation

$$\begin{aligned} g\left( _{+}|^{-}\right)= & {} \eta _{\mathrm {L}}\sqrt{\frac{\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| }{\left| p^{\mathrm {R}}\right| \left| \pi _{0}\left( \mathrm {R}\right) +\chi \left| p^{\mathrm {R}}\right| \right| \left| p^{\mathrm {L}}\right| }}\nonumber \\&\times e^{-i\pi \left( \kappa _{1}+\kappa _{2}\right) /2}{\tilde{\Delta }}\left( _{+}|^{-}\right) \left( 0\right) , \nonumber \\ g\left( _{+}|^{+}\right)= & {} \eta _{\mathrm {L}}\sqrt{\frac{\left| \pi _{0}\left( \mathrm {L}\right) -\chi \left| p^{\mathrm {L}}\right| \right| }{\left| p^{\mathrm {R}}\right| \left| \pi _{0}\left( \mathrm {R}\right) -\chi \left| p^{\mathrm {R}}\right| \right| \left| p^{\mathrm {L}}\right| }}\nonumber \\&\times e^{-i\pi \left( \kappa _{1}+\kappa _{2}\right) /2}{\tilde{\Delta }}\left( _{+}|^{+}\right) \left( 0\right) , \end{aligned}$$

(117)

where

$$\begin{aligned} {\tilde{\Delta }}\left( _{+}|^{-}\right) \left( x\right)= & {} \left| p^{ \mathrm {L}}\right| W_{\kappa _{2},\mu _{2}}\left( z_{2}\right) \frac{d}{ dz_{1}}W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) \\&+\left| p^{\mathrm {R}}\right| W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) \frac{d}{dz_{2}}W_{\kappa _{2},\mu _{2}}\left( z_{2}\right) , \\ {\tilde{\Delta }}\left( _{+}|^{+}\right) \left( x\right)= & {} \left| p^{ \mathrm {L}}\right| W_{-\kappa _{2},\mu _{2}}\left( e^{-i\pi }z_{2}\right) \frac{d}{dz_{1}}W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) \\&+\left| p^{\mathrm {R}}\right| W_{-\kappa _{1},\mu _{1}}\left( e^{-i\pi }z_{1}\right) \frac{d}{dz_{2}}W_{-\kappa _{2},\mu _{2}}\left( e^{-i\pi }z_{2}\right) . \end{aligned}$$

The corresponding expressions for Bosons read

$$\begin{aligned} g\left( _{+}|^{\zeta }\right) =\frac{e^{-i\pi \left( \kappa _{1}+\kappa _{2}\right) /2}}{\sqrt{\left| p^{\mathrm {R}}\right| \left| p^{ \mathrm {L}}\right| }}\left. {\tilde{\Delta }}\left( _{+}|^{\zeta }\right) \left( 0\right) \right| _{\chi =0}. \end{aligned}$$

(118)

The above representations are particularly useful for obtaining approximate expressions for differential quantities when the argument of the Whittaker functions are small. For example, using the connection formulae [40]

$$\begin{aligned}&W_{\kappa ,\mu }\left( z\right) \nonumber \\&\quad =\frac{\pi }{\sin 2\pi \mu }\left[ -\frac{ M_{\kappa ,\mu }\left( z\right) }{\Gamma \left( \frac{1}{2}-\mu -\kappa \right) \Gamma \left( 1+2\mu \right) }\nonumber \right. \\&\qquad \left. +\frac{M_{\kappa ,-\mu }\left( z\right) }{\Gamma \left( \frac{1}{2}+\mu -\kappa \right) \Gamma \left( 1-2\mu \right) }\right] , \nonumber \\&W_{-\kappa ,\mu }\left( e^{\pm i\pi }z\right) \nonumber \\&\quad =\frac{\pi }{\sin 2\pi \mu } \left[ -\frac{\exp \left[ \pm i\pi \left( \mu +1/2\right) \right] M_{\kappa ,\mu }\left( z\right) }{\Gamma \left( \frac{1}{2}-\mu +\kappa \right) \Gamma \left( 1+2\mu \right) }\nonumber \right. \\&\qquad \left. +\frac{\exp \left[ \pm i\pi \left( -\mu +1/2\right) \right] M_{\kappa ,-\mu }\left( z\right) }{\Gamma \left( \frac{1}{2}+\mu +\kappa \right) \Gamma \left( 1-2\mu \right) }\right] , \end{aligned}$$

(119)

and the power-series expansion of the Whittaker functions regular at the origin $M_{\kappa ,\mu }\left( z\right) =z^{\mu +1/2}\left[ 1-z\kappa /\left( 1+2\mu \right) +O\left( z^{2}\right) \right]$, one can obtain approximate expressions for the Whittaker functions $W_{\kappa ,\mu }\left( z\right) ,W_{-\kappa ,\mu }\left( e^{\pm i\pi }z\right)$ near the origin, specially when $\kappa$ and $\mu$ are fixed.¹³ Selecting $\chi =+1$ and considering $\Delta U_{j}\xi _{j}\ll 1$, one can expand the Gamma functions and exponents to show that

$$\begin{aligned} W_{\kappa ,\mu }\left( z\right) \approx 1,\ \ W_{-\kappa ,\mu }\left( e^{-i\pi }z\right) \approx 1, \end{aligned}$$

(120)

in leading-order approximation. These approximations are useful for Fermions. Under the same conditions, choosing $\chi =0$ one finds

$$\begin{aligned} W_{\kappa ,\mu }\left( z\right) \approx \sqrt{\frac{z}{\pi }}\left( -\ln z+\psi \left( 1\right) +\ln 4\right) , \end{aligned}$$

(121)

in leading-order approximation. These approximations are useful for Bosons. Here $-\psi \left( 1\right) \approx 0.577$ is Euler’s constant.

For large a, $\left| \arg a\right| \le \pi -0^{+}$, and fixed c , z, the uniform asymptotic representations for the CHF $\Psi \left( a,c;z\right)$ are given in terms of modified Bessel functions of the second kind $K_{\nu }\left( z\right)$, as given by Eq. (13.8.11) in [33]. Using these approximations for z small and az fixed, the CHF and its derivative are approximately given by

$$\begin{aligned}&\Psi \left( a,c;z\right) \sim 2\left( \frac{z}{a}\right) ^{\left( 1-c\right) /2}\frac{e^{z/2}}{\Gamma \left( a\right) }K_{c-1}\left( 2\sqrt{az} \right) , \nonumber \\&\frac{d}{dz}\Psi \left( a,c;z\right) \sim -2\left( \frac{z}{a}\right) ^{-c/2}\frac{e^{z/2}}{\Gamma \left( a\right) }K_{c}\left( 2\sqrt{az}\right) , \end{aligned}$$

(122)

in leading-order approximation.

For z small and a, c fixed, one can use Kummer connection formula [33]

$$\begin{aligned} \Psi \left( a,c;z\right)= & {} \frac{\Gamma \left( 1-c\right) }{\Gamma \left( a-c+1\right) }\Phi \left( a,c;z\right) \nonumber \\&+\frac{\Gamma \left( c-1\right) }{ \Gamma \left( a\right) }z^{1-c}\Phi \left( a-c+1,2-c;z\right) , \nonumber \\ \end{aligned}$$

(123)

and the power series expansion of regular CHF at the origin $\Phi \left( a,c;z\right) =1+\left( a/c\right) z+O\left( z^{2}\right)$ to obtain an approximate expression of $\Psi \left( a,c;z\right)$. If a and c are also small, one may choose a value to $\chi$ ($\chi =+1$ for example) and expand the Gamma functions to obtain

$$\begin{aligned}&\Psi \left( a_{2},c_{2};z_{2}\right) \approx 1,\ \ \frac{d}{dz_{2}}\Psi \left( a_{2},c_{2};z_{2}\right) \approx i\nu _{2}^{+}, \nonumber \\&\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \approx -e^{i\pi c_{1}}z_{1}^{1-c_{1}}, \nonumber \\&\frac{d}{dz_{1}}\Psi \left( c_{1}-a_{1},c_{1};e^{-i\pi }z_{1}\right) \approx e^{i\pi c_{1}}z_{1}^{1-c_{1}}\left( \frac{c_{1}-1}{z_{1}}\right) , \nonumber \\ \end{aligned}$$

(124)

for Fermions, in leading-order approximation.

Unitary operator connecting in- and out-vacua in Klein zone

A fundamental property of linear canonical transformations between sets of creation and annihilation operators is the existence of an unitary operator V [38] that connects both sets in the form $\alpha \left( \mathrm { out}\right) =V^{\dagger }{\tilde{\alpha }}\left( \mathrm {in}\right) V$, where $\alpha \left( \mathrm {out}\right)$ denotes any out-operator and $\tilde{ \alpha }\left( \mathrm {in}\right)$ its corresponding in-operator. The general method for calculating its explicit form has been given in Refs. [9,10,11, 19, 21, 39]. Here we employ this method for calculating the corresponding unitary operator in the Klein zone $V_{\Omega _{3}}$ in terms of in-operators, as a supplement to the representation calculated in terms of out-operators; cf. Eq. (7.20) in Ref. [16]. Starting with the representation

$$\begin{aligned} V_{\Omega _{3}}= & {} \exp \left[ \ ^{-}a_{n}^{\dagger }\left( \mathrm {in} \right) B\ _{-}b_{n}^{\dagger }\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ \ ^{-}a_{n}\left( \mathrm {in}\right) A\ ^{-}a_{n}^{\dagger }\left( \mathrm {in }\right) \right] , \nonumber \\&\times \exp \left[ \ _{-}b_{n}^{\dagger }\left( \mathrm {in}\right) D\ _{-}b_{n}\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ \ _{-}b_{n}\left( \mathrm {in}\right) C\ ^{-}a_{n}\left( \mathrm {in}\right) \right] , \end{aligned}$$

(125)

for Fermions and

$$\begin{aligned} V_{\Omega _{3}}= & {} \exp \left[ \ ^{+}a_{n}^{\dagger }\left( \mathrm {in} \right) B\ _{+}b_{n}^{\dagger }\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ \ ^{+}a_{n}\left( \mathrm {in}\right) A\ ^{+}a_{n}^{\dagger }\left( \mathrm {in }\right) \right] , \nonumber \\&\times \exp \left[ \ _{+}b_{n}^{\dagger }\left( \mathrm {in}\right) D\ _{+}b_{n}\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ \ _{+}b_{n}\left( \mathrm {in}\right) C\ ^{+}a_{n}\left( \mathrm {in}\right) \right] , \end{aligned}$$

(126)

for Bosons, where A, B, C and D are constants, we use the identities

$$\begin{aligned} \exp \left( \pm a_{n}Aa_{n}^{\dagger }\right) \left( \begin{array}{c} a_{i} \\ a_{i}^{\dagger } \end{array} \right) \exp \left( \mp a_{n}Aa_{n}^{\dagger }\right)= & {} \left( \begin{array}{c} e^{\pm \kappa A}a_{i} \\ a_{i}^{\dagger }e^{\mp \kappa A} \end{array} \right) , \nonumber \\ \exp \left( \pm b_{n}^{\dagger }Db_{n}\right) \left( \begin{array}{c} b_{i} \\ b_{i}^{\dagger } \end{array} \right) \exp \left( \mp b_{n}^{\dagger }Db_{n}\right)= & {} \left( \begin{array}{c} e^{\mp D}b_{i} \\ b_{i}^{\dagger }e^{\pm D} \end{array} \right) , \nonumber \\ \exp \left( \pm a_{n}^{\dagger }Bb_{n}^{\dagger }\right) \left( \begin{array}{c} a_{i} \\ b_{i} \end{array} \right) \exp \left( \mp a_{n}^{\dagger }Bb_{n}^{\dagger }\right)= & {} \left( \begin{array}{c} a_{i}\mp Bb_{i}^{\dagger } \\ b_{i}\pm \kappa a_{i}^{\dagger }B \end{array} \right) , \nonumber \\ \exp \left( \pm b_{n}Ca_{n}\right) \left( \begin{array}{c} a_{i}^{\dagger } \\ b_{i}^{\dagger } \end{array} \right) \exp \left( \mp b_{n}Ca_{n}\right)= & {} \left( \begin{array}{c} a_{i}^{\dagger }\pm b_{i}C \\ b_{i}^{\dagger }\mp \kappa Ca_{i} \end{array} \right) , \nonumber \\ \end{aligned}$$

(127)

and the canonical transformations given by Eqs. (7.4), (A3) in Ref. [16], to show that

$$\begin{aligned} A= & {} \left\{ \begin{array}{l} -\ln \left[ g\left( _{+}|^{-}\right) g\left( _{+}|^{+}\right) ^{-1}\right] =-\ln \left[ g\left( ^{+}|_{-}\right) g\left( ^{-}|_{-}\right) ^{-1}\right] ,\ \mathrm {Fermi,} \\ \ln \left[ g\left( _{-}|^{+}\right) g\left( _{-}|^{-}\right) ^{-1}\right] =\ln \left[ g\left( ^{-}|_{+}\right) g\left( ^{+}|_{+}\right) ^{-1}\right] ,\ \mathrm {Bose,} \end{array} \right. \nonumber \\ B= & {} \left\{ \begin{array}{l} -g\left( _{+}|^{+}\right) ^{-1},\ \mathrm {Fermi,} \\ g\left( _{-}|^{-}\right) ^{-1},\ \mathrm {Bose,} \end{array} \right. ,\ \ C=\left\{ \begin{array}{l} g\left( ^{-}|_{-}\right) ^{-1},\ \mathrm {Fermi,} \\ -g\left( ^{+}|_{+}\right) ^{-1},\ \mathrm {Bose,} \end{array} \right. \nonumber \\ D= & {} \left\{ \begin{array}{l} \ln \left[ g\left( _{-}|^{+}\right) g\left( _{+}|^{+}\right) ^{-1}\right] =\ln \left[ g\left( ^{-}|_{+}\right) g\left( ^{-}|_{-}\right) ^{-1}\right] ,\ \mathrm {Fermi,} \\ -\ln \left[ g\left( _{+}|^{-}\right) g\left( _{-}|^{-}\right) ^{-1}\right] =-\ln \left[ g\left( ^{+}|_{-}\right) g\left( ^{+}|_{+}\right) ^{-1}\right] ,\ \mathrm {Bose,} \end{array} \right. \nonumber \\ \end{aligned}$$

(128)

In terms of elementary relative amplitudes of particle scattering $w_{n}\left( +|+\right)$, antiparticle scattering $w_{n}\left( -|-\right)$, creation of a pair $w_{n}\left( +-|0\right)$ and annihilation of a pair $w_{n}\left( 0|-+\right)$ given by Eqs. (7.17) and (A-9) in [16], the unitary operator for Fermions (125) is expressed by Eq. (56) while for Bosons it takes the form

$$\begin{aligned} V_{\Omega _{3}}= & {} \exp \left[ \ ^{+}a_{n}^{\dagger }\left( \mathrm {in} \right) w_{n}\left( +-|0\right) \ _{+}b_{n}^{\dagger }\left( \mathrm {in} \right) \right] \nonumber \\&\times \exp \left[ \ ^{+}a_{n}\left( \mathrm {in}\right) \ln w\left( +|+\right) _{n}\ ^{+}a_{n}^{\dagger }\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ -\ _{+}b_{n}^{\dagger }\left( \mathrm {in}\right) \ln w\left( -|-\right) _{n}\ _{+}b_{n}\left( \mathrm {in}\right) \right] \nonumber \\&\times \exp \left[ \ _{+}b_{n}\left( \mathrm {in}\right) w\left( 0|-+\right) _{n}\ ^{+}a_{n}\left( \mathrm {in}\right) \right] . \end{aligned}$$

(129)

With the help of the representations (56) and (129), the vacuum-vacuum transition probability $P_{v}$ (55) acquires the final form (58).