1 Introduction

Mathematically ideal black holes are usually studied as isolated systems. However, this mathematical idealization cannot be actualized in any real world system. This is because black holes will always interact with matter surrounding it. Even if all the matter around a black hole could be removed, it would still interact with the vacuum around it, and thus cannot be considered an isolated system. So, in any realistic description of a black hole we would have to consider such perturbative effects on the basic parameters describing such a black hole. Such perturbations of a black hole lead to the emission of gravitational waves [1]. Initially there will be an short outburst of radiation, which will be followed by long period of damping oscillations [2,3,4], and finally these oscillations will be suppressed at late times by power-law or exponential tails. These oscillations are called the quasi-normal modes (QNMs) for the black hole.

The study of gravitational wave has become important due to the detection of these wave in events like GW150914 [5]. So, important physical information can be obtained using such data obtained from gravitational antennas like LIGO and VIRGO [6,7,8,9]. It is also expected that in future LISA will also provide important data from gravitational waves. There is an important reason for studying gravitational waves. The existence of extra dimensions in string theory has motivated the study of black hole in large extra-dimensions [10,11,12,13]. These models have been generalized to Randall–Sundrum brane world models with warped extra dimensions [14, 15]. Now there are three possible ways to detect these extra dimensions. The first is by the production of mini black hole at the LHC [16]. The second is by using strong field gravitational lensing from astrophysical black holes [17, 18]. The third is by analyzing QNMs from astrophysical black holes [19,20,21,22].

It may be noted that the Horava–Lifshitz gravity is motivated from a formalism used in condensed matter physics [23, 24]. The space and time scale have different Lifshitz scaling in the Horava–Lifshitz gravity. Motivated by Horava–Lifshitz gravity, the consequences of such different Lifshitz scaling have been studied for various geometrical structures that occur in the string theory. Such a Lifshitz scale has been studied for both type IIA string theory [25] and type IIB string theory [26]. The behavior of dilaton black branes [27, 28] and dilaton black holes [29, 30] with Lifshitz scaling has also been discussed. Furthermore, such black solutions in a BI non-linear action with Lifshitz scaling have also been studied [31]. In [32], the critical behavior of AdS black holes in the presence of BI non-linear electrodynamics has been investigated. The brane world models with warped extra dimensions and Lifshitz scaling have also been constructed [33, 34]. Now as the gravitational waves can also be used to constraint such Lifshitz scaling [35], it is important to study QNMs for theories with Lifshitz scaling.

Now in model with extra dimensions, the effective Planck scale is brought down, and this new scale can be constraint by gravitational antennas like LIGO and VIRGO [36]. As these extra dimensional models are motivated from string theory, and the D-branes action in string theory is described by a Born–Infeld (BI) action coupled to dilaton field [37,38,39,40], we will use such an action for analyzing QNMs.

The QNMs for the charged scalar perturbations have been thoroughly studied [41,42,43,44,45,46]. The QNMs in Lifshitz theories have also been studied for neutral scalar perturbations [47,48,49,50,51,52,53,54]. In fact, QNMs for a charged dilaton-Lifshitz solutions in the four dimensions have also been studied [55]. Recently, QNMs for scalarized black holes in Einstein-Scalar theory with Maxwell electrodynamics have been explored in [56]. As the QNMs can be used to test models with extra dimensions [19,20,21,22], it is important to study the QNMs for such a black hole in extra dimensions. Thus, we will analyze the QNMs from a higher dimensional dilaton-Lifshitz black hole solutions coupled to a non-linear Born–Infeld action.

We organize this paper as follows: In Sect. 2, we will review the dilaton-Lifshitz black hole solutions in the presence of BI nonlinear electrodynamics. In Sect. 3, the wave equations of charged scalar perturbations around our black holes will be presented. In latter section, we will analyze the QNMs analytically. Then, we will use the asymptotic iteration method to analyze QNMs numerically in Sect. 4. Finally, in the last section, we will summarize our results and discuss about them.

2 Lifshitz solutions

In this section, we will analyze a higher dimensional black hole in a UV complete theory. Thus, we will consider a dilaton-Lifshitz black hole coupled to non-linear BI action. The metric for such a d-dimensional Lifshitz black holes can be expressed as [27, 48]

$$\begin{aligned} \mathrm {d}s^{2}=-\frac{r^{2z}f(r)}{l^{2z}}\mathrm {d}t^{2}+\frac{l^{2}}{ r^{2}f(r)}\mathrm {d}r^{2}+r^{2}d{{\varvec{\Omega }}}_{d-2}^{2}, \end{aligned}$$
(1)

where \(d{\varvec{\Omega }}_{d-2}^{2}\) is a (\(d-2\))-dimensional hypersurface with constant curvature \((d-2)(d-3)\), such that

$$\begin{aligned} d{\varvec{\Omega }}_{d-2}^{2}=d\theta _{1}^{2}+\sum \limits _{i=2}^{d-2}d\theta _{i}^{2}\prod \limits _{j=1}^{i-1}\sin ^{2}\theta _{j}. \end{aligned}$$

Here \(\Omega _{d-2}\) is the volume and \(z(\ge 1)\) is dynamical critical exponent. Now it can be observed that in the limit, \(r\rightarrow \infty \), the metric given by Eq. (1) will asymptotically reduce to the Lifshitz metric given by

$$\begin{aligned} ds^{2}=-\frac{r^{2z}dt^{2}}{l^{2z}}+{\frac{l^{2}dr^{2}}{r^{2}}}+r^{2}d {\varvec{\Omega }}_{d-2}^{2}. \end{aligned}$$
(2)

In this paper, we will analyze the coupling of a Lifshitz spacetime to a non-linear BI action. So, first we observe that in the absence of dilaton field, the function L(F) for BI Lagrangian is given by [57]

$$\begin{aligned} L(F)=\frac{4}{\beta ^{2}}\left( 1-\sqrt{1+\frac{F\beta ^{2}}{2}}\right) , \end{aligned}$$
(3)

where \(\beta \) is the BI non-linearity parameter, \(F=F_{\mu \nu }F^{\mu \nu } \) is the Maxwell invariant, as \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) with \(A_{\mu }\) being the U(1) abelian gauge field. The dilaton field can couple to this U(1) abelian gauge field. So, in presence of a dilaton field, the Lagrangian for the BI coupled to a dilaton scalar field \(\Phi \) can be written as [58, 59]

$$\begin{aligned} L(F,\Phi )= \frac{4}{\beta ^{2}}e^{4\lambda \phi /(d-2)}\left( 1{-}\sqrt{1{+} \frac{\beta ^{2}F}{2}e^{{-}8\lambda \Phi /(d{-}2)}}\right) ,\nonumber \\ \end{aligned}$$
(4)

where \(\lambda \) is a constant. In Einstein frame, the Lagrangian density of Einstein-dilaton model with string theory corrections [60], contains two U(1) gauge field’s [27]. So, the Lagrangian for this system can be written as

$$\begin{aligned} 16\pi {\mathcal {L}}= & {} {\mathcal {R}}-\frac{4}{d-2}(\nabla \Phi )^{2}-2\Lambda \nonumber \\&-\sum \limits _{i=1}^{2}e^{-4\Phi \lambda _{i}/(d-2)}H_{i}+L(F,\Phi ), \end{aligned}$$
(5)

where \({\mathcal {R}}\) is the Ricci scalar and \(\Lambda ,\lambda _{i}\) are constants, in this Lagrangian. In the Lagrangian (5), \(H_{i}=\left( H_{i}\right) _{\mu \nu }\left( H_{i}\right) ^{\mu \nu }\), where \(\left( H_{i}\right) _{\mu \nu }=2\partial _{[\mu }\left( B_{i}\right) _{\nu ]}\), and \(\left( B_{i}\right) _{\mu }\) is a gauge field. In the limit, \( \beta \rightarrow 0\), this Lagrangian \({\mathcal {L}}\) reduces to the Einstein-dilaton-Maxwell Lagrangian (at the leading order) [27, 28]

$$\begin{aligned} \lim _{\beta \rightarrow 0}16\pi {\mathcal {L}}= & {} \cdots -e^{-4\lambda \Phi /(d-2)}F\nonumber \\&+\beta ^{2}\frac{e^{-12\lambda \Phi /(d-2)}F^{2}}{8}+O\left( \beta ^{4}\right) . \end{aligned}$$
(6)

By varying the action \(S=\int _{{\mathcal {M}}}d^{d}x\sqrt{-g}{\mathcal {L}}\) with respect to the metric \(g_{\mu \nu }\), the dilaton field \(\Phi \), and U(1) abelian gauge field \(A_{\mu }\), and \(\left( B_{i}\right) _{\mu }\), the following field equations are obtained [61]

$$\begin{aligned}&{\mathcal {R}}_{\mu \nu }-\frac{g_{\mu \nu }}{d-2}\left( 2\Lambda +2L_{F}F-L(F,\Phi )\right. \nonumber \\&\qquad \left. -\sum \limits _{i=1}^{2}e^{-4\Phi \lambda _{i}/(d-2)}H_{i}\right) \nonumber \\&\qquad -\frac{4}{d-2}\partial _{\mu }\Phi \partial _{\nu }\Phi +2L_{F}F_{\mu \lambda }F_{\nu }^{\text { \ }\lambda } \nonumber \\&\quad -2\sum \limits _{i=1}^{2}e^{-4\lambda _{i}\Phi /(d-2)}\left( H_{i}\right) _{\mu \lambda }\left( H_{i}\right) _{\nu }^{\text { \ }\lambda }=0, \end{aligned}$$
(7)
$$\begin{aligned}&\nabla ^{2}\Phi +\frac{d-2}{8}L_{\Phi }+\sum \limits _{i=1}^{2}\frac{{\lambda } _{i}}{2}e^{-{4{\lambda }_{i}\Phi }/(d{-2})}H_{i}=0, \end{aligned}$$
(8)
$$\begin{aligned}&\triangledown _{\mu }\left( L_{F}F^{\mu \nu }\right) =0, \end{aligned}$$
(9)
$$\begin{aligned}&\triangledown _{\mu }\left( e^{-{4\lambda }_{i}{\Phi }/(d{-2})}\left( H_{i}\right) ^{\mu \nu }\right) =0, \end{aligned}$$
(10)

where we use the convention \(X_{Y}=\partial X/\partial Y\). With metric (1), the Eqs. (9) and (10) can be solved for the U(1) abelian gauge field, and thus we obtain

$$\begin{aligned}&F_{rt} =\frac{qe^{4\lambda \Phi /(d-2)}r^{z-d+1}}{\beta \Gamma }, \end{aligned}$$
(11)
$$\begin{aligned}&\left( H_{i}\right) _{rt} =q_{i}r^{z-d+1}e^{4\lambda _{i}\Phi /(d-2)}, \end{aligned}$$
(12)

where \(\Gamma =\sqrt{1+q^{2}l^{2z-2}\beta ^{2}/(r^{2d-4})}\). By subtracting ( tt), and (rr) components of Eq. (7), \(\Phi (r)\) can be obtained, which is given by

$$\begin{aligned} \Phi (r)=\frac{(d-2)\sqrt{z-1}}{2}\ln \left( \frac{r}{b}\right) , \end{aligned}$$
(13)

where b is a constant. By substituting Eqs. (11), (12), and (13) in field equations (7), and (8), the f(r) function for this system is obtained, and this given by

$$\begin{aligned} f(r)=\left\{ \begin{array}{ll} 1-\frac{m}{r^{d+z-2}}+\frac{(d-3)^{2}l^{2}}{(d+z-4)^{2}r^{2}}+\frac{4l^{2}{b} ^{2z-2}}{\beta ^{2}{r}^{2z-2}(d-2)(d-z)}-\frac{4l^{2}b^{2z-2}}{\beta ^{2}(d-2)r^{d+z-2}}\int \Gamma r^{d-z-1}{dr,} &{}\quad \text {for }z\ne d, \\ &{} \\ 1-\frac{m}{r^{2d-2}}+\frac{(d-3)^{2}l^{2}}{4(d-2)^{2}r^{2}}-\frac{ 4b^{2d-2}l^{2}}{\beta ^{2}(d-2)^{2}r^{2d-2}}\left[ 1-\Gamma +\ln \left( \frac{1+\Gamma }{2}\right) \right] , &{}\quad \text {for }z=d. \end{array} \right. \end{aligned}$$
(14)

Here m is a constant, and it is related to the total mass of black brane. Now as this system has to satisfy the field equations, we can write

$$\begin{aligned} \lambda= & {} -\sqrt{z-1},\quad \lambda _{1}=\frac{d-2}{\sqrt{z-1}}, \quad \lambda _{2}=\frac{d-3}{\sqrt{z-1}}, \nonumber \\ q_{1}^{2}= & {} \frac{-\Lambda \left( z-1\right) b^{2(d-2)}}{\left( z+d-3\right) l^{2(z-1)}}, \nonumber \\ q_{2}^{2}= & {} \frac{(d-2)(d-3)(z-1)b^{2(d-3)}}{2(z+d-4)l^{2(z-1)}}, \nonumber \\ \Lambda= & {} -\frac{(d+z-2)(d+z-3)}{2l^{2}}. \end{aligned}$$
(15)

Integrating the last term of f(r) for \(z\ne d\), we obtain

$$\begin{aligned} f(r)&=1-\frac{m}{r^{d+z-2}}+\frac{(d-3)^{2}l^{2}}{(d+z-4)^{2}r^{2}}\nonumber \\&\quad +\frac{4l^{2}b^{2z{-}2}r^{2-2z}\left( 1{-}\Gamma \right) }{\beta ^{2}(d-2)(d-z) }{+}\frac{4q^{2}b^{2z-2}l^{2z}r^{-2(d+z-3)}\Gamma }{(d-z)(d+z-4)} \nonumber \\&\quad \times {\mathbf {F}}\left( 1,\frac{2d+z-6}{2d-4},\frac{3d+z-8}{2(d-2)} ,1-\Gamma ^{2}\right) . \end{aligned}$$
(16)

We can observe from this solution, that in the limit \(r\rightarrow \infty \), f(r) satisfies \(f(r)\rightarrow 1\) (note that \({\mathbf {F}}\left( a,b,c,0\right) =1\)). It may be noted that for \(z=d\), a Schwartzshild-like black hole does not exist in this system, because as \(r\rightarrow 0\), f(r) will go to positive infinity \(f(r)\rightarrow +\infty \). Nevertheless, for \( z\ne d\), the Schwartzshild-like black hole do exists in this system (apart from the extreme and non-extreme black holes and naked singularities). One may note that in the linearly charged limit (\(\beta \rightarrow 0\)), the solutions (14) and (16) for both \(z\ne d\) and \(z=d\) cases reduce to higher-dimensional Lifshitz ones in Einstein-dilaton-Maxwell gravity [27, 28]

$$\begin{aligned} f(r)= & {} 1-\frac{m}{r^{d+z-2}}+\frac{(d-3)^{2}l^{2}}{(d+z-4)^{2}r^{2}} \nonumber \\&+\frac{2q^{2}b^{2z-2}l^{2z}}{(d-2)(d+z-4)r^{2(d+z-3)}} \nonumber \\&-\frac{q^{4}b^{2z-2}l^{4z-2}\beta ^{2}}{2(d-2)(3d+z-8)r^{2(2d+z-5)}} +O( \beta ^{4}) . \end{aligned}$$
(17)

From here on, we fix l and b to unity.

3 Quasi-normal modes

Now in this section, we will analyze the QNMs for the solution discussed in the previous section. So, first we consider a minimally coupled charged massive scalar field in such a spherically symmetric black hole background. It is assumed that this field satisfies the Klein–Gordon equation

$$\begin{aligned} D^{\nu }D_{\nu }\Psi =m_{s}^{2}\Psi , \end{aligned}$$
(18)

where \(D^{\nu }=\nabla ^{\nu }-iq_{s}A^{\nu }\) is the gauge covariant derivative and \(m_{s}\) is the mass of the scalar field \(\Psi \). Now we decompose \(\Psi \) into the following standard form,

$$\begin{aligned} \Psi (t,r,\text {angles})=e^{-i\omega t}R(r)Y(\text {angles}), \end{aligned}$$
(19)

where Y(angles) is the spherical harmonic function related to the angular coordinates, and \(\omega \) is the frequency. As Y is the spherical harmonic function, it satisfies the following equation

$$\begin{aligned} \nabla _{\text {angles}}^{2}Y(\theta ,\phi )=-QY(\text {angles}), \end{aligned}$$
(20)

where Q is the constant of separation. Moreover, the differential equation for the radial function in the d-dimensional Lifshitz-dilaton background (1) is

$$\begin{aligned} fR^{\prime \prime }+ & {} \left( f^{\prime }+\frac{(d+z-1)f}{r}\right) R^{\prime } \nonumber \\+ & {} \left( \frac{q_{s}A_{t}+\omega }{r^{z+1}}\right) ^{2}\frac{R}{f}-\left( m_{s}^{2}+\frac{Q}{r^{2}}\right) \frac{R}{r^{2}}=0, \end{aligned}$$
(21)

So, using a tortoise coordinate \(r_{*}\) as \(dr_{*}/dr=\left[ r^{z+1}f(r)\right] ^{-1}\), and introducing a new radial function R(r) as \( R(r)=K(r)/r\), the Eq. (21) can be transformed into an equation resembling the Schrödinger equation,

$$\begin{aligned} \frac{d^{2}K(r_{*})}{dr_{*}^{2}}+\left[ \left( \omega +q_{s}A_{t}(r)\right) ^{2}-V(r)\right] K(r_{*})=0, \end{aligned}$$
(22)

where the potential V(r) is given by

$$\begin{aligned} V(r)= & {} \left( \frac{d^{2}}{4}+\frac{dz}{2}+1-d-z\right) f^{2}r^{2z}\nonumber \\&+fr^{2z}\left( m_{s}^{2}+\frac{Q}{r^{2}}\right) +ff^{\prime }r^{2z+1}\left( \frac{d}{2}-1\right) . \end{aligned}$$
(23)

By having positive f(r) and \(f^{\prime }(r)\) out of the horizon \(r>r_{h}\), we can observe that \(V(r)>0\) out of horizon, provided that \(m_{s}^{2}>0\). Note that \(m_{s}^{2}\) can be negative as long as it is above Breitenlohner–Freedman(-like) bound. One may read this bound from Eq. (36) in next section.

To perform a general stability analysis for this system, we first transform to Eddington–Finkelstein coordinates, such that \(v=t+r_{*}\). In this new coordinate system, the metric can be written as

$$\begin{aligned} ds^{2}=-r^{2z}fdv^{2}+2r^{z-1}dvdr+r^{2}d{\varvec{\Omega }}_{d-2}^{2}. \end{aligned}$$
(24)

Using the ansatz

$$\begin{aligned} \Psi =e^{-i\omega v}\frac{\psi (r)}{r^{d/2-1}}Y(\text {angles}), \end{aligned}$$
(25)

the differential equation for radial function \(\psi (r)\) can be written as

$$\begin{aligned} \left( r^{d+z-3}f\psi ^{\prime }\right) ^{\prime }-2i\left( \omega +q_{s}A_{t}\right) \psi ^{\prime }-V\psi =0. \end{aligned}$$
(26)

Multiplying above equation by \({\bar{\psi }}\) (the complex conjugate of \(\psi \)) and performing the integration from \(r_{+}\) to infinity, we obtain

$$\begin{aligned} \int _{r_{+}}^{\infty }dr\left[ r^{d+z-3}f\left| \psi ^{\prime }\right| ^{2}+2i\left( \omega {+}q_{s}A_{t}\right) {\bar{\psi }}\psi ^{\prime }{+}V\left| \psi \right| ^{2}\right] {=}0, \nonumber \\ \end{aligned}$$
(27)

where we used the integration by part and applied the Dirichlet boundary condition for \(\psi \) i.e., \(\psi \left( \infty \right) \rightarrow 0\). For (27) to be satisfied, both the real and imaginary parts of integration should vanish. Using the imaginary part, we observeFootnote 1

$$\begin{aligned} 0= & {} \int _{r_{+}}^{\infty }dr\left[ \left( \omega +q_{s}A_{t}\right) {\bar{\psi }}\psi ^{\prime }+\left( {\bar{\omega }}+{\bar{q}}_{s}{\bar{A}}_{t}\right) \psi {\bar{\psi }}^{\prime }\right] \nonumber \\= & {} 2i\int _{r_{+}}^{\infty }dr\mathrm {Im}[\left( \omega +q_{s}A_{t}\right) ] {\bar{\psi }}\psi ^{\prime } \nonumber \\&-{\bar{q}}_{s}\int _{r_{+}}^{\infty }dr\left| \psi \right| ^{2}{\bar{A}} _{t}^{\prime }-{\bar{\omega }}\left| \psi \left( r_{+}\right) \right| ^{2}. \end{aligned}$$
(28)

Here we have again used the integration by part and the Dirichlet boundary condition for \(\psi \). In the case of neutral scalar field (\(q_{s}=0\)), Eq. (28) reduces to

$$\begin{aligned} \int _{r_{+}}^{\infty }dr{\bar{\psi }}\psi ^{\prime }=\frac{{\bar{\omega }} \left| \psi \left( r_{+}\right) \right| ^{2}}{2i\mathrm {Im}[\omega ]} . \end{aligned}$$
(29)

Now we can substitute \(\int _{r_{+}}^{\infty }dr{\bar{\psi }}\psi ^{\prime }\) from Eq. (29) in Eq. (27) and obtain

$$\begin{aligned} \int _{r_{+}}^{\infty }dr\left[ r^{d+z-3}f\left| \psi ^{\prime }\right| ^{2}+V\left| \psi \right| ^{2}\right] =-\frac{ \left| \omega \right| ^{2}\left| \psi \left( r_{+}\right) \right| ^{2}}{\mathrm {Im}[\omega ]}.\nonumber \\ \end{aligned}$$
(30)

Now we observe from this equation that for the potential V to be positive outside the horizon, imaginary part of \(\omega \) is negative. So, for a neutral scalar field, the black hole is stable under scalar field perturbation, if the potential is positive outside the horizon (i.e. as long as \(m_{s}^{2}>0\)). In next section, we proceed more to study charged scalar fields numerically. We investigate the behavior of potential for \( m_{s}^{2}<0 \), as well.

4 Numerical analysis

In the previous section, we analyzed the stability of our black hole system, when the potential was positive outside the horizon and scalar perturbation was neutral. However, we cannot obtain such general results for charged scalar fields as well as negative potential. To understand the behavior of this system generally, we need to analyze it numerically. So, in this section, we will analyze the behavior of QNMs numerically using the asymptotic iteration method (AIM) [62]. Now we first change the variable \(u=1-r_{h}/r\), and write Eq. (21) as

$$\begin{aligned}&\frac{r_{h}^{z+1}f(u)}{(1-u)^{z-1}}R^{\prime \prime }(u) \nonumber \\&\quad +\frac{r_{h}^{z+1}}{(1-u)^{z}}\left[ (d+z-3)f(u)+(1-u)f^{\prime }(u)\right] R^{\prime }(u) \nonumber \\&\quad +\frac{r_{h}^{1-z}l^{2z+2}}{f(u)(1-u)^{1-z}}\left( q_{s}A_{t}(u)+\omega \right) ^{2}R(u) \nonumber \\&\quad -\frac{r_{h}^{z+1}}{(1-u)^{z+1}}\left( m_{s}^{2}+\frac{Q}{r_{h}^{2}} (1-u)^{2}\right) R(u)=0. \end{aligned}$$
(31)

In order to propose an ansatz for (31), we are going to consider the behavior of the function R(u) at horizon \((u=0)\), and boundary \((u=1)\). At horizon \((u=0)\), we have \(f(0)\approx uf^{\prime }(0)\) and \(A_{t}(0)=0\), thus Eq. (31) can be written as

$$\begin{aligned} R^{\prime \prime }(u)+\frac{R^{\prime }(u)}{u}+\frac{R(u)}{ r_{h}^{2z}u^{2}f^{\prime 2}}\omega ^{2}=0. \end{aligned}$$
(32)
Fig. 1
figure 1

The behaviors of real and imaginary parts of QNFs in the case with \( d\ne z\), \(m_{s}^{2}=1/4\) and \(q_{s}=1.5\) for different d, z, and \( \beta \). The increase of the black holes charge q from 0 to near the extreme value in steps of 0.2 are shown with the arrows. Note that for each curve the extreme value of q is different

Full size image
Fig. 2
figure 2

The behaviors of real and imaginary parts of QNFs in the case with \( d=z\), \(m_{s}^{2}=1/4\) and \(q_{s}=1.5\) for different \(\beta \). The increase of the black holes charge q from 0 to near the extreme value in steps of 0.2 are shown with the arrows. Note that for each curve the extreme value of q is different

Full size image
Fig. 3
figure 3

The behaviors of real and imaginary parts of QNFs vs z for different \(\beta \) where \(d=5\), \(m=3\), \(q=1\), \(m_{s}^{2}=1/4\) and \( q_{s}=2\)

Full size image

The solution for this equation can be written as

$$\begin{aligned} R(u\rightarrow 0)\sim C_{1}u^{-\xi }+C_{2}u^{\xi },\quad \xi =- \frac{i\omega }{r_{h}^{z}f^{\prime }(0)}. \end{aligned}$$
(33)

Here we have imposed the ingoing boundary condition at the horizon \((u=0)\), and so we have required \(C_{2}\) to vanish.

At infinity, where \((u=1)\), Eq. (31), can be written as

$$\begin{aligned} R^{\prime \prime }(u)+\frac{(z+d-3)R^{\prime }(u)}{1-u}-\frac{m_{s}^{2}R(u)}{ (1-u)^{2}}=0. \end{aligned}$$
(34)

The solution to this equation can be written as

$$\begin{aligned} R(u\rightarrow 1)\sim D_{1}(1-u)^{\frac{1}{2}\left( z+2+\Pi \right) }+D_{2}(1-u)^{\frac{1}{2}\left( z+2-\Pi \right) }.\nonumber \\ \end{aligned}$$
(35)

where

$$\begin{aligned} \Pi =\sqrt{(d+z-2)^{2}+4m_{s}^{2}}. \end{aligned}$$
(36)

In order to impose Dirichlet boundary condition \(R(u\rightarrow 1)\rightarrow 0\), we can set \(D_{2}=0\).

Using the above solutions at horizon and boundary, the general ansatz for Eq. (31), can be written as

$$\begin{aligned} R(u)=u^{-\xi }(1-u)^{\frac{1}{2}\left( z+2+\Pi \right) }\chi (u). \end{aligned}$$
(37)

Inserting Eq. (37) into (31), we obtain

$$\begin{aligned} \chi ^{\prime \prime }=\lambda _{0}(u)\chi ^{\prime }+s_{0}(u)\chi , \end{aligned}$$
(38)

where the coefficient functions are given by

$$\begin{aligned} \lambda _{0}=\frac{2i\omega }{r_{h}^{z}u+f^{\prime }(0)}-\frac{f^{\prime }(u) }{f(u)}+\frac{\Pi +1}{1-u}. \end{aligned}$$
(39)

Furthermore, \(s_{0}\) is given by

$$\begin{aligned} s_{0}(u)= & {} \frac{r_{h}^{-2(z+1)}}{2(u-1)^{2}u^{2}f(u)^{2}f^{\prime 2}} \nonumber \\&\times \left( -2r_{h}^{2}u^{2}f^{\prime 2}(1-u)^{2z}(q_{s}A_{t}(u)+\omega )^{2}\right. \nonumber \\&+uf(u)f^{\prime }(0)r_{h}^{z}\left( 2uf^{\prime }(0)r_{h}^{z}\left( m_{s}^{2}r_{h}^{2}+Q(u-1)^{2}\right) \right. \nonumber \\&\left. +r_{h}^{2}(u-1)f^{\prime }(u)\right. \nonumber \\&\left. \times \left( -uf^{\prime }(0)r_{h}^{z}\left( \Pi +d+z-2\right) +2i(u-1)\omega \right) \right) \nonumber \\&\left. +2r_{h}^{2}f(u)^{2}\left( i(u-1)\omega f^{\prime }(0)r_{h}^{z}\left( u\Pi +1\right) \right. \right. \nonumber \\&\left. \left. -m_{s}^{2}u^{2}f^{\prime 2}r_{h}^{2z}+(u-1)^{2}\omega ^{2}\right) \right) . \end{aligned}$$
(40)

Now using the improved AIM method, Eq. (38) can be solved numerically. We will derive the charged scalar perturbations, and study the effects of the parameters of the model such as d, and \(\beta \) on the real and imaginary parts of quasi-normal frequencies. In the following, we will set \(Q=0\).

4.1 Numerical results

In this section, we present the numerical results for the QNM of the charged scalar perturbation around Lifshitz black hole and the effective potential \( V(r^{*})\) as a function of tortoise coordinate \(r^{*}\). We will consider two cases, one for the case with \(d\ne z\) (Figs. 1, 4), and the other one with \(d=z\) (Figs. 2, 5).

Fig. 4
figure 4

The behaviors of \(V(r^{*})\) in the case with \(d\ne z\) for different \(\beta \) and \(m_{s}^{2}\)

Full size image
Fig. 5
figure 5

The behaviors of \(V(r^{*})\) in the case with \(d=z\) for different \(\beta \) and \(m_{s}^{2}\)

Full size image

The frequency of quasi-normal modes have both real and imaginary parts, \( \omega =\omega _{R}+i\omega _{I}\). So, the factor \(e^{-i\omega t}\) in scalar field (Eq. (19)) becomes \(e^{-i\omega _{R}t}e^{\omega _{I}t}\). Therefore, \(\omega _{R}\) and \(\omega _{I}\) determine the energy of scalar perturbations and the stability of the system under dynamical perturbations, respectively. If \(\omega _{I}>0\), the scalar field grows with time and therefore the black hole is not stable under this perturbation. If \(\omega _{I}<0\), the black hole system is stable under dynamical perturbation since the scalar field vanishes as time passes. For larger values of \(\left| \omega _{I}\right| \), the perturbation remains longer outside the black hole until it disappears. From holographic point of view, it means that it takes more time for the dual system to go back to equilibrium.

As one can see from Figs. 1 and 2, for both \(d=z\) and \( d\ne z\) cases, for fixed values of \(\beta \), \(\left| \omega _{I}\right| \) decreases as q increases (or equivalently temperature T decreases). According to what explained above, it means that by increasing q, the complete decay of scalar perturbation outside the black hole takes more time. Holographically, it shows that dual system needs more time to return to equilibrium. As Fig. 1a, b show, for \( d\ne z\) case, by increasing q, \(\omega _{R}\) increases up to a maximum value first and then decreases. The value of maximum for a fixed d and z , depends on nonlinear parameter \(\beta \). For larger values of \(\beta \), the maximum value of \(\omega _{R}\) is lower. It means that by increasing the effects of nonlinearity, the maximum energy of perturbation decreases. For specific values of d and z, the influence of \(\beta \) on real and imaginary parts of quasi-normal frequencies disappears as q tends to smaller values (higher T). Moreover, for smaller values of \(\beta \) but fixed d and z, the real part of quasi-normal frequencies is larger in general as q is further away from zero. The latter result shows that the perturbation has more energy in linear electrodynamics case. Furthermore, for larger values of z, the maximum energy of perturbations is lower (Fig. 1a, b). In \(d=z\) case, we have the same behaviors as \(d\ne z\) case (Fig. 2a, b). However, as Fig. 1a, c show, in the case of \(d\ne z\), for fixed z, by increasing d, the behavior of \(\omega _{R}\) with respect to q may change. For \(d=5\) and \(z=2\), \(\omega _{R}\) shows a decreasing trend as q increases.

In Fig. 3, the behaviors of \(\omega _{R}\) and \(\omega _{I}\) with the change of Lifshitz exponent z have been illustrated for different values of \(\beta \) in 5 dimensions. As one can see from Fig. 3a, for fixed values of z, the behavior of \(\omega _{R}\) is different for small and large z. For small values of Lifshitz exponent, \(\omega _{R}\) increases as \(\beta \) increases whereas for large z, \(\omega _{R}\) is lower for higher values of \(\beta \). Furthermore, \(\omega _{R}\) reduces as z becomes big and finally flattens. The value of \(\omega _{R}\) for high z can approach to zero. Now, we discuss the behavior of imaginary part of quasi-normal frequency \(\omega _{I}\) as shown in Fig. 3b. The absolute value of the imaginary part is bigger for bigger values of \(\beta \) for fixed z except for \(z=1\). The difference between values of \(|\omega _{I}|\) for different values of \(\beta \) first increases by increasing z and then reduces.

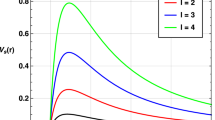
In the case with \(z\ne d\) and \(m_{s}^{2}<0\), the effective potential as a function of \(r^{*}\) are plotted in Fig. 4. In Fig. 4a, with \(d=4\), and \(z=2\), each potential has a well, whose height depends on the value of \(m_{s}^{2}\) and \(\beta \). With the same \(\beta \), the one with lower \(m_{s}^{2}\), has a higher hight of the well. The highest hight of the well in this case is obtained when \(\beta =0.1\) and \( m_{s}^{2}=-26\). Moreover, the same behaviors is obtained by going to higher dimension, such as \(d=5\), as depicted in Fig. 4b. This shows that the particle described by the scalar field is trapped in the potential of the black hole in these cases. Another case is obtained by setting \(d=z\), where the dimension of spacetime equals the dynamical critical exponent z (Fig. 5). For \(d=z\) cases, the same behavior is obtained as in Fig. 4, in which the potential has a well. In order to see the effects of the existence of the extra dimension, in Fig. 5b, we consider the case \(d=z=5\).

5 Summary and conclusion

In this paper, we analyze the behavior of quasi-normal modes (QNMs) for a higher dimensional black hole with Lifshitz scaling. This is important as the QNMs can be used to test models with large extra dimensions with Lifshitz scaling. In this paper, the QNMs for higher dimensional dilaton-Lifshitz black hole solutions coupled to a non-linear Born–Infeld action have been studied. As it is important to study the charged perturbations for such a black hole solution, charged perturbations have been studied for this black hole solution. We first analyzed general conditions for stability analytically, for a positive potential. However, as it was not possible to perform such an analysis for a charged perturbation as well as a negative potential, we numerically analyze this system for these cases. This was done using the asymptotic iteration method for quasi-normal modes. So, we analyze this system for two cases, i.e., when \( d\ne z\), and when \(d=z\). For both cases, it is observed that the absolute value of imaginary parts of quasi-normal frequencies decreases as charge of black hole increase to extremal value. It means that it takes more time for QNMs to completely decay outside the black hole. If one wants to interprete this in AdS/CFT formalism, this result imply that it needs more time for the system to go back to equilibrium under the perturbation. Increasing the charge of black hole, the real part of quasi-normal frequencies first increase up to a maximum and then decreases. The value of this maximum is dependent on the non-linearity parameter \(\beta \) and is higher for lower values of this parameter. In the case of \(d\ne z\), we have a different behavior for real part of quasi-normal frequencies as the dimension of space-time increases. For \(d=5\ne z\), we observed that increase in value of black hole charge (equivalently decrease in black hole temperature) cause the real part of quasi-normal frequencies to decrease. To study the behavior of potential, we depicted the potential in tortoise coordinate with \( m_{s}^{2}<0\), for both \(d\ne z\) and \(d=z\) cases. We observed that potential is partly negative and has a well. For \(d=4 \), each potential has a well whose hight depends on the \(\beta \) and \(m_{s}^{2}\). The same behavior is observed for \(d=5\). It is observed that for the second case, the high of well depends on \(\beta \), and for a fixed \(\beta \), the high depends on the value of \(m_{s}^{2}\). Thus, the behavior of this system depends both on \( \beta \) and \(m_{s}^{2}\) for a fixed dimension.

The QNMs have also become important in string theory, due to the development of AdS/CFT correspondence [63,64,65]. It has been observed that the poles of the retarded Green function in a conformal field theory on the boundary of an AdS space is related to the QNMs of a asymptotically AdS black hole. Thus, QNMs of a higher dimensional AdS black hole can be used to describe the behavior of strongly coupled quark-gluon plasmas [66, 67]. As the AdS/CFT correspondence has been used to analyze the CFT dual to a Lifshitz AdS spacetime [68, 69], it would be interesting to repeat the analysis done in this paper, for an asymptotically AdS black hole. Then such QNMs can be used to analyze various properties of CFT dual to such a black hole in the Lifshitz AdS spacetime. It may be noted that in this paper, we have used an abelian Born–Infeld action, in which a U(1) gauge field was coupled in a non-linear action. The abelian Born–Infeld action has been generalized to a non-abelian Born–Infeld action [70, 71]. Furthermore, black hole solution in such a theory with non-abelian Born–Infeld have also been constructed [72, 73]. It would be interesting to calculate the QNMs for such black holes with a non-abelian Born–Infeld action. It would also be interesting to analyze the QNMs for such black holes in an asymptotically AdS spacetime, and then use the AdS/CFT correspondence to analyze the CFT dual to such a system. Here, we have considered the spherical topology for event horizon. It is also interesting to repeat the study for other topologies such as flat and hyperbolic ones.