Abstract
The cross-sections of \(\psi {(2S)}\) meson production in proton-proton collisions at \(\sqrt{s} =13\text { TeV} \) are measured with a data sample collected by the LHCb detector corresponding to an integrated luminosity of \(275\text { pb} ^{-1} \). The production cross-sections for prompt \(\psi {(2S)}\) mesons and those for \(\psi {(2S)}\) mesons from b-hadron decays (\({\psi {(2S)}} \text{-from- }{b} \)) are determined as functions of the transverse momentum, \(p_{\mathrm {T}}\), and the rapidity, y, of the \(\psi {(2S)}\) meson in the kinematic range \(2<p_{\mathrm {T}} <20\text { GeV/}c \) and \(2.0<y<4.5\). The production cross-sections integrated over this kinematic region are
A new measurement of \(\psi {(2S)}\) production cross-sections in pp collisions at \(\sqrt{s}=7\text { TeV} \) is also performed using data collected in 2011, corresponding to an integrated luminosity of \(614\text { pb} ^{-1} \). The integrated production cross-sections in the kinematic range \(3.5<p_{\mathrm {T}} <14\text { GeV/}c \) and \(2.0<y<4.5\) are
All results show reasonable agreement with theoretical calculations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of hadronic production of heavy quarkonia can provide important information about quantum chromodynamics (QCD). The production of heavy quark pairs, \({Q{\overline{Q}}} \), can be calculated with perturbative QCD, while the hadronisation of \({Q{\overline{Q}}} \) pairs into heavy quarkonia is nonperturbative and must be determined using input from experimental results. Heavy-quarkonium production therefore probes both perturbative and nonperturbative aspects of QCD by providing stringent tests of theoretical models. Knowledge of hadronic production of heavy quarkonium has been significantly improved in the past forty years [1, 2], but the mechanism behind it is still not fully understood. Colour-singlet model calculations [3,4,5,6,7,8,9] require that the intermediate \({Q{\overline{Q}}} \) state is colourless and has the same \(J^{PC}\) quantum numbers as those of the outgoing quarkonium state. In the nonrelativistic QCD (NRQCD) approach [10,11,12], intermediate \({Q{\overline{Q}}} \) states with all possible colour-spin-parity quantum numbers have nonzero probability to be transformed into the desired quarkonium. The transition probability of a \({Q{\overline{Q}}} \) pair into the quarkonium state is described by a long-distance matrix element (LDME), which is assumed to be universal and can be determined from experimental data.
In high-energy proton-proton (pp) collisions, charmonium states can be produced directly from hard collisions of partons inside the protons, through the feed-down from excited states, or via weak decays of \({b} \) hadrons. The first two contributions, which cannot be distinguished experimentally, are referred to as prompt production; while the third component can be separated from prompt production by exploiting the lifetime of \(b \)-hadrons. For prompt \({{\mathrm {J} /\psi }} \) production the feed-down contribution is large, mostly from radiative decays of \({\chi _{{\mathrm {c}} J}} \) (\(J=0,1,2\)) mesons. This complicates the comparison between theoretical calculations and experimental results. On the contrary, the feed-down contribution to \({\psi {(2S)}} \) mesons is negligible [13], thus theoretical calculations can be directly compared with measurements.
The studies of heavy quarkonium production are crucial to separate the contributions of single parton scattering (SPS) [14] and double parton scattering (DPS) [15] to multiple-quarkonium production. Multiple-quarkonium production through the SPS process shares the same LDMEs as the single quarkonium production, thus providing a new method to test the theoretical calculations. The DPS process can reveal the transverse profile of partons inside the proton. Further theoretical and experimental works provide deeper insights on how to interpret the production mechanism of multiple quarkonia. In particular, additional data help in improving the precision of LDME determination.
The differential cross-sections of inclusive \(\psi {(2S)}\) meson production in \({p\overline{p}} \) collisions at centre-of-mass energies of \(\sqrt{s} =1.8\) and \(1.96\text { TeV} \) were measured by the \(\text{ CDF } \) experiment at the Fermilab Tevatron Collider [16, 17], and in \(pp\) collisions at \(\sqrt{s} =7\text { TeV} \) [18,19,20,21,22,23], \(8\text { TeV} \) [23], and \(13\text { TeV} \) [24] with LHC data. This paper presents measurements of \(\psi {(2S)}\) production cross-sections in \({pp} \) collisions using a data sample collected by LHCb in 2015 (2011) corresponding to an integrated luminosity of \(275\pm 11\text { pb} ^{-1} \) at \(\sqrt{s} =13\text { TeV} \) (\(614\pm 11\text { pb} ^{-1} \) at \(\sqrt{s} =7\text { TeV} \)). The \({\psi {(2S)}} \) mesons from prompt production are abbreviated as “prompt \({\psi {(2S)}} \)”, while those from \({b} \)-hadron decays are abbreviated as “\({\psi {(2S)}} \)-from-\({b} \)”. The \(\psi {(2S)}\) mesons are reconstructed through their decay mode \({{\psi {(2S)}} \rightarrow {\mu ^+\mu ^-}} \). The double-differential production cross-sections of prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-\(b \) as functions of transverse momentum \(p_{\mathrm {T}}\) and rapidity y and their integrated production cross-sections are measured, assuming zero polarisation of the \(\psi {(2S)}\) meson. The kinematic region of the measurement at \(13\text { TeV} \) (\(7\text { TeV} \)) is \(2<p_{\mathrm {T}} <20\,\text { GeV/}c \) (\(3.5<p_{\mathrm {T}} <14\,\text { GeV/}c \)) and \(2.0<y<4.5\). Compared to the previous LHCb measurement at \(7\text { TeV} \) using 2010 data [19], the new analysis at \(7\text { TeV} \) has several advantages: the 2011 data sample is much larger than that in the previous measurement corresponding to an integrated luminosity of \(36\text { pb} ^{-1} \), the previous measurement did not provide the \(\psi {(2S)}\) production cross-section as a function of the rapidity y because of the limited sample size, and the same final state and offline selection criteria as those in the \(13\text { TeV} \) measurement are used in the new \(7\text { TeV} \) measurement. This guarantees that the maximum number of systematic uncertainties cancel in the cross-section ratio between \(13\text { TeV} \) and \(7\text { TeV} \), which is measured in the present analysis. This represents a more stringent test of the theoretical models, since many of the experimental and theoretical uncertainties cancel. Finally, the \(\psi {(2S)}\) meson differential production cross-sections are compared with those of the \({\mathrm {J} /\psi }\) meson at \(\sqrt{s} = 13\text { TeV} \) [25].
2 Detector and simulation
The LHCb detector [26, 27] is a single-arm forward spectrometer covering the pseudorapidity range \(2<\eta <5\), designed for the study of particles containing \(b \) or \(\mathrm {c} \) quarks. The detector includes a high-precision tracking system consisting of a silicon-strip vertex detector surrounding the pp interaction region [28], a large-area silicon-strip detector located upstream of a dipole magnet with a bending power of about \(4{\mathrm {\,Tm}}\), and three stations of silicon-strip detectors and straw drift tubes [29, 30] placed downstream of the magnet. The tracking system provides a measurement of the momentum, \(p\), of charged particles with a relative uncertainty that varies from 0.5% at low momentum to 1.0% at 200 \(\text { GeV/}c\). The minimum distance of a track to a primary vertex (PV), the impact parameter (IP), is measured with a resolution of \((15+29/p_{\mathrm {T}})\,\upmu \text {m} \), where \(p_{\mathrm {T}}\) is in \(\text { GeV/}c\). Different types of charged hadrons are distinguished using information from two ring-imaging Cherenkov detectors [31]. Photons, electrons and hadrons are identified by a calorimeter system consisting of scintillating-pad (SPD) and preshower detectors, an electromagnetic calorimeter and a hadronic calorimeter. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers [32]. The online event selection is performed by a trigger [33], which consists of a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage, which applies a full event reconstruction.
Simulated samples are used to evaluate the \(\psi {(2S)}\) detection efficiency. In the simulation, \({pp} \) collisions are generated using Pythia 8 [34, 35] with a specific LHCb configuration [36]. Decays of unstable particles are described by EvtGen [37], in which final-state radiation is generated using Photos [38]. Both the leading-order colour-singlet and colour-octet contributions are included in the generated prompt charmonium states [36, 39]. These states are generated with zero polarisation. The interaction of the generated particles with the detector, and its response, are implemented using the Geant4 toolkit [40, 41] as described in Ref. [42].
3 Selection of \(\psi {(2S)}\) candidates
The decay channel \({\psi {(2S)}} \rightarrow {\mu ^+\mu ^-} \) is used in the measurements of the \(\psi {(2S)}\) production cross-sections at both \(13\text { TeV} \) and \(7\text { TeV} \). The same strategy is used for both analyses, except for different trigger requirements. The hardware trigger selects events that contain two tracks consistent with muon hypotheses, and the product of the transverse momenta of the two muons is required to be greater than \((1.3\,\text { GeV/}c)^2\). At the software trigger stage the two muons are required to be oppositely charged, to have good track quality, to form a good-quality vertex, and to each have a momentum larger than \(6\,\text { GeV/}c \). The invariant mass of the \(\psi {(2S)}\) candidates is required to be within the range \(3566<m_{{\mu ^+\mu ^-}}<3806\text { MeV/}c^2 \). The transverse momentum of each muon is required to be larger than \(0.3\,\text { GeV/}c \) (\(0.5\,\text { GeV/}c \)) and that of the \(\psi {(2S)}\) candidate is required to be larger than \(2\,\text { GeV/}c \) (\(3.5\,\text { GeV/}c \)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) data trigger. Due to the different triggers, the \(\psi {(2S)}\) candidates are selected in different \(p_{\mathrm {T}}\) ranges. For the \(13\text { TeV} \) data taking, an alignment and calibration of the detector is performed in near real-time [43] and updated constants are made available for the trigger.
To suppress the background associated to random combination of tracks (combinatorial) more stringent criteria are applied offline on the \({\psi {(2S)}} \) vertex fit quality, the muon kinematics and particle identification requirements. Each muon must have \(p_{\mathrm {T}} >1.2\,\text { GeV/}c \) and \(2.0<\eta <4.9\). At least one PV should be reconstructed in the event from at least four tracks in the vertex detector.
For events with more than one PV, the \({\psi {(2S)}} \) candidate is associated to the PV for which the difference in the \(\chi ^2 \) of the PV fit with and without the \({\psi {(2S)}} \) candidate is the smallest. This is equivalent to select the vertex with respect to which the signal candidate has the smallest impact parameter, compared to resolution. Using the above procedure, the fraction of candidates associated to the wrong PV is \(0.3\%\), which is negligible. To select \(\psi {(2S)}\) candidates, additional requirements on the pseudo decay time, \(t_z\), \(|t_z|<10\text { ps} \), and its uncertainty, \(\sigma _{t_z}\), \(\sigma _{t_z}<0.3\text { ps} \), are applied. The pseudo decay time \(t_z\) is defined as
where \(z_{\psi {(2S)}} \) (\(z_{\mathrm {PV}}\)) is the z coordinate of the reconstructed \({\psi {(2S)}} \) decay vertex (the PV), \(p_z\) is the z-component of the measured \({\psi {(2S)}} \) momentum, and \(M_{{\psi {(2S)}}}\) is the world average \({\psi {(2S)}} \) mass [13]. The z-axis is the direction of the proton beam pointing downstream into the LHCb acceptance [26]. The pseudo decay time defined above provides a good approximation of the b-hadron decay time [44] and is used to separate prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-\(b \) candidates.
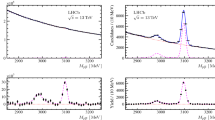
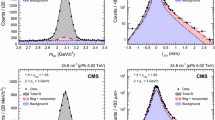
Distributions of (left) the invariant mass \(m_{{\mu ^+\mu ^-}}\) and (right) pseudo decay time \(t_z\) of selected \(\psi {(2S)}\) candidates in the kinematic bin of \(5<p_{\mathrm {T}} <6\,\text { GeV/}c \) and \(2.5<y<3.0\) in the \(13\text { TeV} \) data sample. Projections of the two-dimensional fit result are also shown. The solid (red) line is the total fit function, the shaded (green) area corresponds to the background component. The prompt \(\psi {(2S)}\) contribution is shown in cross-hatched (blue) area, \(\psi {(2S)}\)-from-b in a solid (black) line and the tail contribution due to the association of \(\psi {(2S)}\) with the wrong PV is shown in filled (magenta) area. The tail contribution is invisible in the invariant-mass plot
4 Cross-section determination
The double-differential production cross-section for prompt \(\psi {(2S)}\) or \(\psi {(2S)}\)-from-\({b} \) in a given \((p_{\mathrm {T}},y)\) bin is defined as
where \(N(p_{\mathrm {T}},y)\) is the signal yield, \({\varepsilon _{\mathrm { tot}}} (p_{\mathrm {T}},y)\) is the total detection efficiency of the \({{\psi {(2S)}} \rightarrow {\mu ^+\mu ^-}} \) decay evaluated independently for prompt \(\psi {(2S)}\) or \(\psi {(2S)}\)-from-\({b} \) in the given \((p_{\mathrm {T}},y)\) bin, \(\mathcal {L} _{\text {int}}\) is the integrated luminosity, \({\mathcal {B}} \) is the branching fraction of the decay \({{\psi {(2S)}} \rightarrow {\mu ^+\mu ^-}} \), and \(\Delta p_{\mathrm {T}} =1\,\text { GeV/}c \) and \(\Delta y=0.5\) are the bin widths. The integrated luminosity is determined using the beam-gas imaging and, for the \(7\text { TeV} \) data, also the van der Meer scan methods [45]. Assuming lepton universality in electromagnetic decays, \({\mathcal {B}} ({{\psi {(2S)}} \rightarrow {\mathrm {e} ^+\mathrm {e} ^-}})=(7.89\pm 0.17)\times 10^{-3}\) [46] is used in Eq. 2, taking advantage of the much smaller uncertainty compared to the \({{\psi {(2S)}} \rightarrow {\mu ^+\mu ^-}} \) decay. The difference of the two branching fractions introduced by the mass difference between electrons and muons is negligible.
The yields of prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-\(b \) candidates in each \((p_{\mathrm {T}},y)\) bin are determined from a two-dimensional extended unbinned maximum-likelihood fit to the distributions of the invariant mass, \(m_{{\mu ^+\mu ^-}}\), and \(t_z\) of the \(\psi {(2S)}\) candidates. The correlation between \(m_{{\mu ^+\mu ^-}}\) and \(t_z\) is found to be negligible. The invariant-mass distribution of the signal candidates in each bin is described by the sum of two Crystal Ball (CB) functions [47] with a common mean value and different widths. The parameters of the power-law tails, the relative fractions and the difference between the widths of the two CB functions are fixed to values obtained from simulation, leaving the mean value and the width of one of the CB functions as free parameters. The invariant-mass distribution of the combinatorial background is described by an exponential function with the slope parameter free to vary in the fit. The \(t_z\) distribution of prompt \(\psi {(2S)}\) mesons is described by a Dirac \(\delta \) function at \(t_z=0\), and that of \(\psi {(2S)}\)-from-b by an exponential function, both convolved with the sum of two Gaussian functions. A \(\psi {(2S)}\) candidate can also be associated to a wrong PV, resulting in a long tail component in the \(t_z\) distribution. This shape is modelled from data by calculating \(t_z\) between the \(\psi {(2S)}\) candidate from a given event and the closest PV in the next event of the sample. The background \(t_z\) distribution is parametrised with an empirical function based on the observed shape of the \(t_z\) distribution in the \(\psi {(2S)}\) mass sidebands (\(3566<m_{{\mu ^+\mu ^-}}<3620\text { MeV/}c^2 \) and \(3750<m_{{\mu ^+\mu ^-}}<3806\text { MeV/}c^2 \)). It is parametrised as the combination of a Dirac \(\delta \) function and the sum of five exponential functions, three for positive \(t_z\) and two for negative \(t_z\). This sum is convolved with the sum of two Gaussian functions. All parameters of the background \(t_z\) distribution are fixed to values determined from the \(\psi {(2S)}\) mass sidebands independently in each \((p_{\mathrm {T}},y)\) bin. Figure 1 shows as an example the \(m_{{\mu ^+\mu ^-}}\) and \(t_z\) distributions in the kinematic bin corresponding to \(5<p_{\mathrm {T}} <6\,\text { GeV/}c \) and \(2.5<y<3.0\) for the \(13\text { TeV} \) data sample. The one-dimensional projections of the fit result are also presented. The total signal yields of prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-\(b \) in the kinematic range for the \(13\text { TeV} \) sample are \((440.7\pm 1.2) \times 10^3\) and \((140.0\pm 0.5) \times 10^3\), and for the \(7\text { TeV} \) sample are \((433.9\pm 0.9) \times 10^3\) and \((115.1\pm 0.4) \times 10^3\), respectively.
The total efficiency, \({\varepsilon _{\mathrm { tot}}} \), in each kinematic bin is determined as the product of the geometrical acceptance of the detector and the efficiencies of particle reconstruction, event selection, muon identification and trigger requirements. The detector acceptance, selection and trigger efficiencies are calculated using simulated samples in each \((p_{\mathrm {T}},y)\) bin, independently for prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-b. The trigger efficiencies are also validated using data, as explained in Sect. 5. The track reconstruction and the muon-identification efficiencies are evaluated using simulated samples and calibrated with data. The efficiencies of prompt \(\psi {(2S)}\) and those of \(\psi {(2S)}\)-from-b are very similar.
5 Systematic uncertainties
A variety of sources of systematic uncertainty are studied as described below and are summarised in Table 1. For the uncertainties that vary in kinematic bins, the largest uncertainties always appear in the bins with small sample sizes.
The uncertainty related to the modelling of the signal mass shape is studied by replacing the baseline model with a kernel-density estimated distribution [48] obtained from the simulated sample in each kinematic bin. In order to account for the resolution difference between data and simulation, a Gaussian function is used to smear the shape of the distribution in simulation. The relative difference of the signal yield in each kinematic bin, 0.0–\(4.1\%\) (0.0–\(8.5\%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample, is taken as the systematic uncertainty due to signal mass shape.
Due to the presence of final-state radiation in the \({\psi {(2S)}} \rightarrow {\mu ^+\mu ^-} \) decay, a fraction of \(\psi {(2S)}\) candidates fall outside the mass window used to determine the signal yields. The efficiency of the selection of the mass window is estimated using simulated samples, and the imperfect modelling of the radiation is studied by comparisons of the radiative tails between simulation and data, from which an uncertainty of \(1.0\%\) is assigned to the cross-sections in all kinematic bins.
The track detection efficiencies are determined from a simulated sample in each \((p_{\mathrm {T}},y)\) bin of the \(\psi {(2S)}\) meson, and are corrected by using \({{\mathrm {J} /\psi }} \rightarrow {\mu ^+\mu ^-} \) decays reconstructed in a control data sample and in simulation. These efficiencies are calculated as functions of p and \(\eta \) with a tag-and-probe approach [49]. The uncertainties due to the finite size of the control samples are propagated to the results using a large number of pseudoexperiments. In each pseudoexperiment, a new efficiency-correction ratio in each \((p_{\mathrm {T}},y)\) bin is generated according to a Gaussian distribution where the original ratio and its uncertainty are used as the Gaussian mean and standard deviation, respectively. The contribution to the systematic uncertainty in each kinematic bin of \(\psi {(2S)}\) mesons varies from \(0.1\%\) (\(0.7\%\)) to \(2.4\%\) (\(3.0\%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) data sample. The distribution of the number of SPD hits in simulation is weighted to match that in data to correct the effect of the detector occupancy. As a crosscheck the number of tracks is used as an alternative weighting variable. The tracking efficiencies are found to be different when different variables are used. Therefore, an additional systematic uncertainty of \(0.8\%\) (\(0.4\%\)) per muon track is assigned for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample.
The muon identification efficiency is determined from simulation and calibrated with a data sample of \({{\mathrm {J} /\psi }} \rightarrow {\mu ^+\mu ^-} \) decays. The statistical uncertainty due to the finite size of the calibration sample is propagated to the final results using pseudoexperiments. The resulting uncertainties vary from \(0.1\%\) (\(0.7\%\)) to \(1.1\%\) (\(8.9\%\)) in different \((p_{\mathrm {T}},y)\) bins for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample. The uncertainty related to the kinematic binning scheme of the calibration samples is studied by changing the size and the boundaries of the p and \(\eta \) bins, and number of SPD hits. This leads to systematic uncertainties of 0.1–\(4.6\%\) (0.4–\(5.4\%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample.
The trigger efficiency is determined from simulated samples. To estimate the systematic uncertainty, a tag-and-probe method is used to estimate the trigger efficiencies in each (\(p_{\mathrm {T}},y\)) bin of a \(\psi {(2S)}\) data sample that is independent of the detection of \(\psi {(2S)}\) signals [33]. The same procedure is applied to the simulated \(\psi {(2S)}\) samples, and the relative difference of efficiencies between data and simulation in each kinematic bin, 0.1–\(9.3\%\) (0.0–\(4.4 \%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample, is taken as a systematic uncertainty.
The \(p_{\mathrm {T}}\) and y distributions of \(\psi {(2S)}\) mesons in simulation and in data could be different within each kinematic bin due to the finite bin size, causing differences in efficiencies. The possible discrepancy is studied by weighting the kinematic distribution in simulation to match that in data. All efficiencies are recalculated, and the relative differences of the total efficiencies between the new and the nominal results, which are found to be in the range 0.0–\(2.0\%\) (0.0–\(4.9\%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample, are taken as systematic uncertainties.
The integrated luminosity is determined using the beam-gas imaging method for the \(13\text { TeV} \) data sample, and by a combination of the beam-gas imaging and van der Meer scan methods [45] for the \(7\text { TeV} \) data sample. The uncertainty associated with the luminosity determination is \(3.9\%\) (\(1.7\%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample. The uncertainty of the branching fraction of the \({{\psi {(2S)}} \rightarrow {\mathrm {e} ^+\mathrm {e} ^-}} \) decay, \(2.2\%\), is taken as a systematic uncertainty [46]. The limited size of the simulated sample in each bin leads to uncertainties of 0.7–\(11.5\%\) (1.3–\(13.1\%\)) for prompt \(\psi {(2S)}\) and 0.8–\(5.7\%\) (1.2–\(9.5\%\)) for \(\psi {(2S)}\)-from-\({b} \) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample, and are smaller than or comparable with the data statistical uncertainty in each bin.
There are sources of systematic uncertainties that are related to the \(t_z\) variable, the effects of which are notable for \(\psi {(2S)}\)-from-b and are negligible for prompt \(\psi {(2S)}\). The modelling of the \(t_z\) resolution is modified by adding a third Gaussian to the nominal resolution model. The variation in the \(\psi {(2S)}\)-from-\(b \) fraction \(F_b\) is found to be negligible. An alternative method is adopted to estimate the systematic uncertainty due to the modelling of the background \(t_z\) distribution. In this method, the background distribution is obtained with the \(\text{ sPlot } \) technique [50] using the invariant mass as the discriminating variable. The \(t_z\) distribution is then parametrised for the two-dimensional fits to obtain the fraction \(F_b\). The relative difference of \(F_b\) in each kinematic bin between the two methods is taken as a systematic uncertainty. The total systematic uncertainty on the \({\psi {(2S)}} \text {-from-}b\) cross-section related to the \(t_z\) fit model is 0.1–\(8.4\%\) (0.1–\(9.2\%\)) for the \(13\text { TeV} \) (\(7\text { TeV} \)) sample.
6 Results
6.1 Production cross-sections
The double-differential production cross-sections for prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-b are measured as functions of \(p_{\mathrm {T}}\) and y assuming no polarisation of \(\psi {(2S)}\) mesons. The results are shown in Figs. 2 and 3, respectively. The corresponding values are listed in Tables 2, 3, 4, and 5 in Appendix A.
Double-differential production cross-sections of prompt \(\psi {(2S)}\) as functions of \(p_{\mathrm {T}}\) in bins of y at (left) \(13\text { TeV} \) and (right) \(7\text { TeV} \). The statistical and systematic uncertainties are added in quadrature. The \(\psi {(2S)}\) meson is assumed to be produced unpolarised
Double-differential production cross-sections of \(\psi {(2S)}\)-from-\(b \) as functions of \(p_{\mathrm {T}} \) in bins of y at (left) \(13\text { TeV} \) and (right) \(7\text { TeV} \). The statistical and systematic uncertainties are added in quadrature. The \(\psi {(2S)}\) meson is assumed to be produced unpolarised
By integrating the double-differential results over y in the range \(2.0<y<4.5\), the differential production cross-sections of prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-\(b \) as functions of \(p_{\mathrm {T}} \) are shown in Fig. 4. The results of prompt \(\psi {(2S)}\) production are compared with the theoretical calculations based on NRQCD [52], and those of \(\psi {(2S)}\)-from-\(b \) are compared with the fixed-order-plus-next-leading-logarithm (FONLL) calculations [53]. The differential cross-section as function of y at \(13\text { TeV} \) (\(7\text { TeV} \)) is obtained by integrating the double-differential results over \(p_{\mathrm {T}} \) in the range \(2<p_{\mathrm {T}} <20\,\text { GeV/}c \) (\(3.5<p_{\mathrm {T}} <14\,\text { GeV/}c \)). The results are presented in Fig. 5. The theoretical calculations based on FONLL are shown for \(\psi {(2S)}\)-from-b. The NRQCD calculations are omitted since they are not reliable in the low \(p_{\mathrm {T}}\) region [52]. The values of the differential cross-sections are shown in Tables 6, 7, 8, and 9 in Appendix A. In the NRQCD calculations, only the dominant uncertainties associated with the LDMEs are considered [52]. The FONLL calculations include the uncertainty due to b-quark mass and the scales of renormalisation and factorisation. The NRQCD calculations show reasonable agreement with experimental data for \(p_{\mathrm {T}} >7\,\text { GeV/}c \). The FONLL calculations agree well with the measurements. The production cross-sections of prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-b integrated in the kinematic range \(2.0<y<4.5\) and \(2<p_{\mathrm {T}} <20\,\text { GeV/}c \) at \(13\text { TeV} \), are measured to be:
The production cross-sections of prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-b integrated in the kinematic range \(2.0<y<4.5\) and \(3.5<p_{\mathrm {T}} <14\,\text { GeV/}c \) at \(7\text { TeV} \), are measured to be:
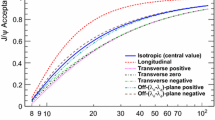
As mentioned above, these results are obtained under the assumption of zero polarisation of \(\psi {(2S)}\) mesons. Possible polarisation of \(\psi {(2S)}\) meson would affect the detection efficiency. This effect is studied for extreme cases of fully transverse and fully longitudinal polarisation corresponding to the parameter \(\alpha \) be equal to \(+1\) or \(-1\), respectively, within the helicity frame [55] approach. Also the polarisation case of \(\alpha = -0.2\), corresponding to a conservative limit of the \(\psi {(2S)}\) polarisation measured at \(7\text { TeV} \) [54], is considered. Resulting scaling factors for prompt \(\psi {(2S)}\) production cross-sections are listed in Appendix B in Tables 16, 17 and 18 for \(13\text { TeV} \) results, and in Tables 19, 20 and 21 for \(7\text { TeV} \) results, respectively.
Differential production cross-sections as functions of \(p_{\mathrm {T}}\) in the range \(2.0<y<4.5\) for the (top) \(13\text { TeV} \) and (bottom) \(7\text { TeV} \) samples. The left-hand figures are for prompt \(\psi {(2S)}\) and the results are compared with the NRQCD calculations [52]; the right-hand figures are for \(\psi {(2S)}\)-from-\(b \) and the results are compared with the FONLL calculations [53]
Differential production cross-sections as functions of y in the range \(2<p_{\mathrm {T}} <20\,\text { GeV/}c \) for the \(13\text { TeV} \) sample (top) and in the range \(3.5<p_{\mathrm {T}} <14\,\text { GeV/}c \) for the \(7\text { TeV} \) sample (bottom). The left figures are for prompt \(\psi {(2S)}\), the right figures are for \(\psi {(2S)}\)-from-\(b \) compared with the FONLL calculations [53]
6.2 Fraction of \(\psi {(2S)}\)-from-\({b} \) mesons
The fraction of \(\psi {(2S)}\)-from-\({b} \) is \(F_b\equiv N_b/(N_b+N_p)\), where \(N_p\) is the efficiency-corrected signal yield of prompt \(\psi {(2S)}\) and \(N_b\) is that of \(\psi {(2S)}\)-from-\({b} \). The fractions \(F_b\) as functions of \(p_{\mathrm {T}}\) and y are shown in Fig. 6. The corresponding values are presented in Table 10 in Appendix A. Only statistical uncertainties are shown owing to the cancellation of most systematic contributions, except for that due to the \(t_z\) fit, which is negligible. For each y bin, the fraction increases with increasing \(p_{\mathrm {T}}\) of the \(\psi {(2S)}\) mesons. For each \(p_{\mathrm {T}}\) bin, the fraction decreases with increasing y of the \(\psi {(2S)}\) mesons.
Ratios of differential cross-sections between prompt \(\psi {(2S)}\) and prompt \({\mathrm {J} /\psi }\) mesons at \(13\text { TeV} \) as functions of (left) \(p_{\mathrm {T}}\) and (right) y. The NRQCD predicted ratio [52] is shown in the left panel for comparison
Ratios of differential cross-sections between \(\psi {(2S)}\)-from-\(b \) and \({\mathrm {J} /\psi }\) mesons from \(b \)-hadron decays at \(13\text { TeV} \) as functions of (left) \(p_{\mathrm {T}}\) and (right) y. The FONLL calculations [57] are shown for comparison
6.3 Comparison with \({{\mathrm {J} /\psi }} \) results at \(13\text { TeV} \)
The production cross-sections of \(\psi {(2S)}\) mesons at \(13\text { TeV} \) are compared with those of \({\mathrm {J} /\psi }\) mesons measured by LHCb at \(\sqrt{s} =13\text { TeV} \) in the range \(0<p_{\mathrm {T}} <14\,\text { GeV/}c \) and \(2.0<y<4.5\) [25], where the \({{\mathrm {J} /\psi }} \) meson is also assumed to be produced with zero polarisation. The ratio, \(R_{{\psi {(2S)}}/{{\mathrm {J} /\psi }}}\), of the differential production cross-sections in the common range between prompt \(\psi {(2S)}\) and prompt \({\mathrm {J} /\psi }\) mesons is shown in Fig. 7 as a function of \(p_{\mathrm {T}} \) (y) integrated over \(2.0<y<4.5\) (\(2<p_{\mathrm {T}} <14\,\text { GeV/}c \)). The NRQCD calculation of \(R_{{\psi {(2S)}}/{{\mathrm {J} /\psi }}}\) for prompt productions [52] is also shown. The ratio of production cross-sections between \(\psi {(2S)}\)-from-\(b \) and \({\mathrm {J} /\psi }\)-from-\(b \) is shown in Fig. 8 as a function of \(p_{\mathrm {T}} \) (y) integrated over \(2.0<y<4.5\) (\(2<p_{\mathrm {T}} <14\,\text { GeV/}c \)). The FONLL calculations [57] are compared to the measured values. To calculate these ratios from the measured cross-sections of \(\psi {(2S)}\) and \({\mathrm {J} /\psi }\) mesons, the systematic uncertainties due to the luminosity, the tracking correction, and the fit model are considered to be fully correlated. All other uncertainties are assumed to be uncorrelated. The numerical results of the measured ratios are listed in Tables 12 and 13 in Appendix A. The FONLL prediction agrees well with the experimental data for the production cross-section ratio between \(\psi {(2S)}\)-from-\(b \) and \({\mathrm {J} /\psi }\) mesons from \(b \)-hadron decays, while the NRQCD predictions show reasonable agreement with the measurements for prompt \(\psi {(2S)}\) and prompt \({\mathrm {J} /\psi }\).
Ratio of differential production cross-sections between the \(13\text { TeV} \) and \(7\text { TeV} \) measurements as a function of (left) \(p_{\mathrm {T}}\) integrated over y and (right) y integrated over \(p_{\mathrm {T}} \) for prompt \(\psi {(2S)}\) production. Theoretical calculations of NRQCD [52] are compared to the data on the left side
Ratio of differential production cross-sections between the \(13\text { TeV} \) and the \(7\text { TeV} \) measurements as a function of (left) \(p_{\mathrm {T}}\) integrated over y and (right) y integrated over \(p_{\mathrm {T}} \) for \(\psi {(2S)}\)-from-\(b \). Theoretical FONLL calculations [57] are compared to the data
6.4 Comparison between \(13\text { TeV} \) and \(7\text { TeV} \)
The production cross-sections of \({\psi {(2S)}} \) mesons in pp collisions at \(13\text { TeV} \) and \(7\text { TeV} \) are compared by means of their ratio, \(R_{13/7}\). Figures 9 and 10 show the ratios as functions of \(p_{\mathrm {T}} \) integrated over \(2.0<y<4.5\) and as functions of y integrated over \(3.5<p_{\mathrm {T}} <14\,\text { GeV/}c \) for prompt \(\psi {(2S)}\) and \(\psi {(2S)}\)-from-\(b \). The NRQCD (FONLL) calculations of \(R_{13/7}\) for prompt \(\psi {(2S)}\) (\(\psi {(2S)}\)-from-b) are also shown in the left (right) panel for comparison. Both FONLL and NRQCD predictions on \(R_{13/7}\) agree well with the corresponding experimental data. The measured ratios are also presented in Tables 14 and 15 in Appendix A.
For both the theoretical calculations and the experimental measurements, some of the uncertainties in the ratio cancel, which allows for a more precise comparison to theory. In the calculation of these ratios from the measured \(\psi {(2S)}\) production cross-sections at \(13\text { TeV} \) and \(7\text { TeV} \) the systematic uncertainty related to the branching fraction is cancelled. The uncertainties due to the luminosity, the fit model and the tracking correction are partially correlated. Other uncertainties are assumed to be uncorrelated.
6.5 Measurement of the inclusive \({b} \rightarrow {\psi {(2S)}} X\) branching fraction
The reported results of the cross-section \(\sigma ({\psi {(2S)}} \text{-from- }{b},13\text { TeV})\), in combination with the previous results about \({\mathrm {J} /\psi }\) production [25], can be used to determine the inclusive branching fraction \(\mathcal {B}(b \rightarrow \psi (2S)X)\). To achieve this, both results must be extrapolated to the full phase space, as they are measured only for a limited range of phase space. The extrapolation factors \(\alpha _{4\pi }({\psi {(2S)}})\) and \(\alpha _{4\pi }({{\mathrm {J} /\psi }})\) are determined with LHCb-tuned versions of Pythia 8 [34] for the \(\psi {(2S)}\) and of Pythia 6 [35] for the \({\mathrm {J} /\psi }\). The factors \(\alpha _{4 \pi }({\psi {(2S)}})\) and \(\alpha _{4\pi }({{\mathrm {J} /\psi }})\) are found to be 7.29 and 5.20, respectively. In the ratio of the two factors,
most of the theoretical uncertainties are expected to cancel. Alternatively, the correction factor \(\xi \) can be obtained using FONLL calculations which uses different parton distribution functions. The values of \(\xi \) obtained from the two methods differ by 2.89 %.
With the definition of the ratio \(\xi \), the \(\mathcal {B}(b \rightarrow {\psi {(2S)}} X)\) branching fraction can be obtained from the ratio
By inserting the value \(\sigma ({{\mathrm {J} /\psi }} \text{-from- }{b},\,\mathrm {13~TeV}) = 2.25 \pm 0.01(\mathrm {stat}) \pm 0.14(\mathrm {syst})\,\upmu \text {b} \) [25] and the value of \(\xi \), the ratio of the branching fractions is
where possible correlations between uncertainties originating from \({\psi {(2S)}} \text {-from-}b\) and \({\mathrm {J} /\psi }\)-from-\(b \), respectively, are taken into account. The last uncertainty is from the uncertainty of the branching fractions \(\mathcal {B}({\psi {(2S)}} \rightarrow e^+e^-)\) and \(\mathcal {B}({{\mathrm {J} /\psi }} \rightarrow \mu ^+ \mu ^-)\). Using the known value \(\mathcal {B}(b \rightarrow {{\mathrm {J} /\psi }} X) = (1.16 \pm 0.10) \times 10^{-2}\) [13], one obtains
This result is in agreement with the world-average value [13]. The \(\mathcal {B}(b \rightarrow {{\mathrm {J} /\psi }} X)\) uncertainty dominates the total uncertainty from the branching fractions.
7 Conclusions
The production cross-sections of \(\psi {(2S)}\) mesons in proton-proton collisions at a centre-of-mass energy of \(13\text { TeV} \) are reported with a data sample corresponding to an integrated luminosity of \(275\pm 11\text { pb} ^{-1} \), collected by the LHCb detector in 2015. The double-differential cross-sections, as functions of \(p_{\mathrm {T}}\) and y of the \(\psi {(2S)}\) meson in the range of \(2<p_{\mathrm {T}} <20\,\text { GeV/}c \) and \(2.0<y<4.5\), are determined for prompt \(\psi {(2S)}\) mesons and \(\psi {(2S)}\) mesons from \({b} \)-hadron decays. A new measurement of the branching fraction \(\mathcal {B}(b \rightarrow \psi (2S)X)\) is presented, which is in agreement with the world average [13]. The measured prompt \(\psi {(2S)}\) production cross-section as a function of transverse momentum is in good agreement in the high \(p_{\mathrm {T}}\) region with theoretical calculations in the NRQCD framework. Theoretical predictions based on the FONLL calculations describe well the measured cross-sections for \(\psi {(2S)}\) mesons from \({b} \)-hadron decays.
A new measurement of \(\psi {(2S)}\) production cross-sections at \(7\text { TeV} \) is performed using the 2011 data sample corresponding to an integrated luminosity of \(614\pm 11\text { pb} ^{-1} \). The new result provides a significantly reduced uncertainty compared to the previous independent LHCb result [19].
The cross section ratios between \(13\text { TeV} \) and \(7\text { TeV} \) show reasonable agreement with theoretical calculations.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: No public data, no additional comments.]
References
A. Andronic et al., Heavy-flavour and quarkonium production in the LHC era: from proton–proton to heavy-ion collisions. Eur. Phys. J. C 76, 107 (2016). arXiv:1506.03981
N. Brambilla et al., Heavy quarkonium: progress, puzzles, and opportunities. Eur. Phys. J. C 71, 1534 (2011). arXiv:1010.5827
C.E. Carlson, R. Suaya, Hadronic production of the \(\psi \)/J meson. Phys. Rev. D 14, 3115 (1976)
A. Donnachie, P.V. Landshoff, Production of lepton pairs, \(J/\psi \) and charm with hadron beams. Nucl. Phys. B 112, 233 (1976)
S.D. Ellis, M.B. Einhorn, C. Quigg, Comment on hadronic production of Psions. Phys. Rev. Lett. 36, 1263 (1976)
H. Fritzsch, Producing heavy quark flavors in hadronic collisions—a test of quantum chromodynamics. Phys. Lett. B 67, 217 (1977)
M. Glück, J.F. Owens, E. Reya, Gluon contribution to hadronic \(J/\psi \) production. Phys. Rev. D 17, 2324 (1978)
C.-H. Chang, Hadronic production of \(J/\psi \) associated with a gluon. Nucl. Phys. B 172, 425 (1980)
R. Baier, R. Rückl, Hadronic production of \(J/\psi \) and \(\varUpsilon \): transverse momentum distributions. Phys. Lett. B 102, 364 (1981)
G.T. Bodwin, E. Braaten, G.P. Lepage, Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 51, 1125 (1995) [Erratum ibid. 55, 5853 (1997)]. arXiv:hep-ph/9407339
P. Cho, A.K. Leibovich, Color-octet quarkonia production. Phys. Rev. D 53, 150 (1996). arXiv:hep-ph/9505329
P. Cho, A.K. Leibovich, Color-octet quarkonia production. II. Phys. Rev. D 53, 6203 (1996). arXiv:hep-ph/9511315
Particle Data Group, M. Tanabashi et al., Review of particle physics. Phys. Rev. D 98, 030001 (2018)
LHCb collaboration, R. Aaij et al., Observation of \(J/\psi \)-pair production in \(pp\) collisions at \(\sqrt{s}=7\,Tev\). Phys. Lett. B 707, 52 (2012). arXiv:1109.0963
LHCb collaboration, R. Aaij et al., Observation of double charm production involving open charm in \(pp\) collisions at \(\sqrt{s}=7\,Tev\). JHEP 06, 141 (2012) [Addendum ibid. 03, 108 (2014)]. arXiv:1205.0975
CDF collaboration, F. Abe et al., \(J/\psi \) and \(\psi (2S)\) production in \(p\bar{p}\) collisions at \(\sqrt{s} = 1.8\,Tev\). Phys. Rev. Lett. 79, 572 (1997)
CDF collaboration, T. Aaltonen et al., Production of \(\psi (2S)\) mesons in \(p\bar{p}\) collisions at \(1.96\,Tev\). Phys. Rev. D 80, 031103 (2009). arXiv:0905.1982
CMS collaboration, S. Chatrchyan et al., \(J/\psi \) and \(\psi (2S)\) production in \(pp\) collisions at \(\sqrt{s}=7\,Tev\). JHEP 02, 011 (2012). arXiv:1111.1557
LHCb collaboration, R. Aaij et al., Measurement of \(\psi (2S)\) meson production in \(pp\) collisions at \(\sqrt{s}=7\,Tev\). Eur. Phys. J. C 72, 2100 (2012). arXiv:1204.1258 (Erratum submitted to Eur. Phys. J. C)
ALICE collaboration, B. Abelev et al., Measurement of quarkonium production at forward rapidity in \(pp\) collisions at \(\sqrt{s} = 7\) Tev. Eur. Phys. J. C 74, 2974 (2014). arXiv:1403.3648
ATLAS collaboration, G. Aad et al., Measurement of the production cross-section of \(\psi (2S) \rightarrow J/\psi ( \rightarrow \mu ^{+} \mu ^{-}) \pi ^{+} \pi ^{-}\) in \(pp\) collisions at \(\sqrt{s}\) = 7 TeV at ATLAS. JHEP 09, 079 (2014). arXiv:1407.5532
CMS collaboration, V. Khachatryan et al., Measurement of \(J/\psi \) and \(\psi (2S)\) prompt double-differential cross sections in \(pp\) collisions at \(\sqrt{s}\)=7 TeV. Phys. Rev. Lett. 114, 191802 (2015). arXiv:1502.04155
ATLAS collaboration, G. Aad et al., Measurement of the differential cross-sections of prompt and non-prompt production of \(J/\psi \) and \(\psi (2S)\) in \(pp\) collisions at \(\sqrt{s} = 7\) and 8 TeV with the ATLAS detector. Eur. Phys. J. C 76, 283 (2016). arXiv:1512.03657
CMS collaboration, A.M. Sirunyan et al., Measurement of quarkonium production cross sections in pp collisions at \(\sqrt{s}= 13\,Tev\). Phys. Lett. B 780, 251 (2018). arXiv:1710.11002
LHCb collaboration, R. Aaij et al., Measurement of forward \(J/\psi \) production cross-sections in \(pp\) collisions at \(\sqrt{s}=13\,Tev\). JHEP 10, 172 (2015) [Erratum ibid. 05, 063 (2017)]. arXiv:1509.00771
LHCb collaboration, A.A. Alves Jr. et al., The LHCb detector at the LHC. JINST 3, S08005 (2008)
LHCb collaboration, R. Aaij et al., LHCb detector performance. Int. J. Mod. Phys. A 30, 1530022 (2015). arXiv:1412.6352
R. Aaij et al., Performance of the LHCb Vertex Locator. JINST 9, P09007 (2014). arXiv:1405.7808
R. Arink et al., Performance of the LHCb Outer Tracker. JINST 9, P01002 (2014). arXiv:1311.3893
P. d’Argent et al., Improved performance of the LHCb Outer Tracker in LHC Run 2. JINST 9, P11016 (2017). arXiv:1708.00819
M. Adinolfi et al., Performance of the LHCb RICH detector at the LHC. Eur. Phys. J. C 73, 2431 (2013). arXiv:1211.6759
A.A. Alves Jr. et al., Performance of the LHCb muon system. JINST 8, P02022 (2013). arXiv:1211.1346
R. Aaij et al., The LHCb trigger and its performance in 2011. JINST 8, P04022 (2013). arXiv:1211.3055
T. Sjöstrand, S. Mrenna, P. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852 (2008). arXiv:0710.3820
T. Sjöstrand, S. Mrenna, P. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arXiv:hep-ph/0603175
I. Belyaev et al., Handling of the generation of primary events in Gauss, the LHCb simulation framework. J. Phys. Conf. Ser. 331, 032047 (2011)
D.J. Lange, The EvtGen particle decay simulation package. Nucl. Instrum. Methods A462, 152 (2001)
P. Golonka, Z. Was, PHOTOS Monte Carlo: a precision tool for QED corrections in \(Z\) and \(W\) decays. Eur. Phys. J. C 45, 97 (2006). arXiv:hep-ph/0506026
M. Bargiotti, V. Vagnoni, Heavy Quarkonia sector in PYTHIA 6.324: tuning, validation and perspectives at LHC(b), LHCb-2007-042. CERN-LHCb-2007-042 (2007)
Geant4 collaboration, J. Allison et al., Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270 (2006)
Geant4 collaboration, S. Agostinelli et al., Geant4: a simulation toolkit. Nucl. Instrum. Methods A 506, 250 (2003)
M. Clemencic et al., The LHCb simulation application, Gauss: design, evolution and experience. J. Phys. Conf. Ser. 331, 032023 (2011)
G. Dujany, B. Storaci, Real-time alignment and calibration of the LHCb Detector in Run II. J. Phys. Conf. Ser. 664, 082010 (2015)
W. Qian, \(J/\psi \) production study at the LHCb experiment, PhD thesis. Tsinghua University, Beijing, CERN-THESIS-2010-307 (2010)
LHCb collaboration, R. Aaij et al., Precision luminosity measurements at LHCb. JINST 9, P12005 (2014). arXiv:1410.0149
Particle Data Group, C. Patrignani et al., Review of particle physics. Chin. Phys. C 40, 100001 (2016)
T. Skwarnicki, A study of the radiative cascade transitions between the Upsilon-prime and Upsilon resonances, PhD thesis, Institute of Nuclear Physics, Krakow, DESY-F31-86-02 (1986)
K.S. Cranmer, Kernel estimation in high-energy physics. Comput. Phys. Commun. 136, 198 (2001). arXiv:hep-ex/0011057
LHCb collaboration, R. Aaij et al., Measurement of the track reconstruction efficiency at LHCb. JINST 10, P02007 (2015). arXiv:1408.1251
M. Pivk, F.R. Le Diberder, sPlot: a statistical tool to unfold data distributions. Nucl. Instrum. Methods A555, 356 (2005). arXiv:physics/0402083
P. Faccioli et al., Quarkonium production in the LHC era: a polarized perspective. Phys. Lett. B 736, 98–109 (2014). https://doi.org/10.1016/j.physletb.2014.07.006
H.-S. Shao et al., Yields and polarizations of prompt \(J/\psi \) and \(\psi (2S)\) production in hadronic collisions. JHEP 05, 103 (2015). arXiv:1411.3300
M. Cacciari, M. Greco, P. Nason, The \(p_{T}\) spectrum in heavy-flavour hadroproduction. JHEP 05, 007 (1998). arXiv:hep-ph/9803400
LHCb collaboration, R. Aaij et al., Measurement of \(\psi (2S)\) polarisation in \(pp\) collisions at \(\sqrt{s}=7\,Tev\). Eur. Phys. J. C 74, 2872 (2014). arXiv:1403.1339
M. Jacob, G.C. Wick, On the general theory of collisions for particles with spin. Ann. Phys. 7, 404 (1959)
M. Jacob, G.C. Wick, On the general theory of collisions for particles with spin. Ann. Phys. 281, 774 (2000)
M. Cacciari, M.L. Mangano, P. Nason, Gluon PDF constraints from the ratio of forward heavy-quark production at the LHC at \(\sqrt{S}=7\) and \(13\, Tev\). Eur. Phys. J. C 75, 610 (2015). arXiv:1507.06197
Acknowledgements
We thank Kuang-Ta Chao and Yan-Qing Ma for frequent and interesting discussions on the production of \({\psi {(2S)}} \) mesons. We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at the LHCb institutes. We acknowledge support from CERN and from the national agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); MOST and NSFC (China); CNRS/IN2P3 (France); BMBF, DFG and MPG (Germany); INFN (Italy); NWO (Netherlands); MNiSW and NCN (Poland); MEN/IFA (Romania); MSHE (Russia); MinECo (Spain); SNSF and SER (Switzerland); NASU (Ukraine); STFC (United Kingdom); DOE NP and NSF (USA). We acknowledge the computing resources that are provided by CERN, IN2P3 (France), KIT and DESY (Germany), INFN (Italy), SURF (Netherlands), PIC (Spain), GridPP (United Kingdom), RRCKI and Yandex LLC (Russia), CSCS (Switzerland), IFIN-HH (Romania), CBPF (Brazil), PL-GRID (Poland) and OSC (USA). We are indebted to the communities behind the multiple open-source software packages on which we depend. Individual groups or members have received support from AvH Foundation (Germany); EPLANET, Marie Skłodowska-Curie Actions and ERC (European Union); ANR, Labex P2IO and OCEVU, and Région Auvergne-Rhône-Alpes (France); Key Research Program of Frontier Sciences of CAS, CAS PIFI, and the Thousand Talents Program (China); RFBR, RSF and Yandex LLC (Russia); GVA, XuntaGal and GENCAT (Spain); the Royal Society and the Leverhulme Trust (United Kingdom).
Author information
Authors and Affiliations
Corresponding author
Additional information
R. Dzhelyadin: Deceased.
Appendices
Appendices
Result tables
See Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15.
Scaling factors for alternative polarisation scenarios
See Tables 16, 17, 18, 19, 20 and 21.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Aaij, R., Beteta, C.A., Adeva, B. et al. Measurement of \({\psi {(2S)}} \) production cross-sections in proton-proton collisions at \(\sqrt{s} =7\) and \(13\text { TeV} \). Eur. Phys. J. C 80, 185 (2020). https://doi.org/10.1140/epjc/s10052-020-7638-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-7638-y