Decay properties of P-wave bottom baryons within light-cone sum rules

Abstract

We use the method of light-cone sum rules to study decay properties of P-wave bottom baryons belonging to the SU(3) flavor $\mathbf {6}_F$ representation. In Cui et al. (Phys Rev D 99:094021, 2019) we have studied their mass spectrum and pionic decays, and found that the $\varSigma _{b}(6097)$ and $\varXi _{b}(6227)$ can be well interpreted as P-wave bottom baryons of $J^P = 3/2^-$. In this paper we further study their decays into ground-state bottom baryons and vector mesons. We propose to search for a new state $\varXi _b({5/2}^-)$, that is the $J^P = 5/2^-$ partner state of the $\varXi _{b}(6227)$, in the $\varXi _b({5/2}^-) \rightarrow \varXi _b^{*}\rho \rightarrow \varXi _b^{*}\pi \pi$ decay process. Its mass is $12 \pm 5$ MeV larger than that of the $\varXi _{b}(6227)$.

1 Introduction

In the past years important progress has been made in the field of heavy baryons, and many heavy baryons were observed in various experiments [2,3,4,5,6,7,8,9]. These heavy baryons are interesting in a theoretical point of view [10,11,12]: the light degrees of freedom (light quarks and gluons) circle around the nearly static heavy quark, so that the whole system behaves as the QCD analogue of the hydrogen bounded by electromagnetic interaction. To understand them, various phenomenological models have been applied, such as the relativized potential quark model [13, 14], the relativistic quark model [15], the constituent quark model [16], the chiral quark model [17], the heavy hadron chiral perturbation theory [18], the hyperfine interaction [19, 20], the Feynman–Hellmann theorem [21], the combined expansion in $1/m_Q$ and $1/N_c$ [22], the pion induced reactions [23], the variational approach [24], the relativistic flux tube model [25], the Faddeev approach [26], the Regge trajectory [27], the extended local hidden gauge approach [28], the unitarized dynamical model [29], the unitarized chiral perturbation theory [30], and QCD sum rules [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47], etc. We refer to reviews [48,49,50,51,52] for their recent progress.

In Refs. [58, 59] we have systematically applied the method of QCD sum rules [53, 54] to study P-wave heavy baryons within the heavy quark effective theory (HQET) [55,56,57], where we systematically constructed all the P-wave heavy baryon interpolating fields, and applied them to study the mass spectrum of P-wave heavy baryons. Later in Ref. [60] we further studied their decay properties using light-cone sum rules, including:

• S-wave decays of flavor ${\bar{\mathbf {3}}}_F$ P-wave heavy baryons into ground-state heavy baryons and pseudoscalar mesons;

• S-wave decays of flavor $\mathbf {6}_F$ P-wave heavy baryons into ground-state heavy baryons and pseudoscalar mesons;

• S-wave decays of flavor ${\bar{\mathbf {3}}}_F$ P-wave heavy baryons into ground-state heavy baryons and vector mesons.

Very quickly, one notices that in order to make a complete study of P-wave heavy baryons, we still need to study:

• S-wave decays of flavor $\mathbf {6}_F$ P-wave heavy baryons into ground-state heavy baryons and vector mesons.

Besides them, we also need to systematically study D-wave and radiative decay properties of P-wave heavy baryons.

In the present study we will study S-wave decays of flavor $\mathbf {6}_F$ P-wave heavy baryons into ground-state heavy baryons and vector mesons. We will further use the obtained results to investigate the $\varSigma _{b}(6097)$ and $\varXi _{b}(6227)$ recently observed by LHCb [7, 8]. Our previous sum rule study in Ref. [1] suggests that they can be well interpreted as P-wave bottom baryons of $J^P = 3/2^-$. This conclusion is supported by Refs. [61,62,63,64,65,66,67], and we refer to Refs. [68,69,70,71,72,73,74,75,76,77,78] for more relevant discussions. The result of Ref. [1] also suggests that they belong to the bottom baryon doublet $[\mathbf {6}_F, 2, 1, \lambda ]$, whose definition will be given below. This doublet contains six bottom baryons, $\varSigma _b({3\over 2}^-/{5\over 2}^-)$, $\varXi ^\prime _b({3\over 2}^-/{5\over 2}^-)$, and $\varOmega _b({3\over 2}^-/{5\over 2}^-)$. We predicted the mass and decay width of the $\varOmega _b(3/2^-)$ state to be

$$\begin{aligned} M_{\varOmega _b(3/2^-)}= & {} 6.46 \pm 0.12 {~\mathrm GeV}, \\ \varGamma _{\varOmega _b(3/2^-)}= & {} 58{^{+65}_{-33}} {~\mathrm MeV}, \end{aligned}$$

and masses of the three $J^P = 5/2^-$ states to be

$$\begin{aligned}&M_{\varSigma _b(5/2^-)} = 6.11 \pm 0.12~\mathrm{GeV}, \\&M_{\varSigma _b(5/2^-)} - M_{\varSigma _b(3/2^-)} = 13 \pm 5~\mathrm{MeV}, \\&M_{\varXi _b^{\prime }(5/2^-)} = 6.29 \pm 0.11~\mathrm{GeV}, \\&M_{\varXi ^\prime _b(5/2^-)} - M_{\varXi ^\prime _b(3/2^-)} = 12 \pm 5~\mathrm{MeV}, \\&M_{\varOmega _b(5/2^-)} = 6.47 \pm 0.12~\mathrm{GeV}, \\&M_{\varOmega _b(5/2^-)} - M_{\varOmega _b(3/2^-)} = 11 \pm 5~\mathrm{MeV} . \end{aligned}$$

The three $J^P = 5/2^-$ states are probably quite narrow, because their S-wave decays into ground-state bottom baryons and pseudoscalar mesons can not happen, and widths of the following D-wave decays are extracted to be zero in Ref. [1]:

$$\begin{aligned} (w^\prime )\,\varGamma _{\varSigma _b^{-}({5/2}^-) \rightarrow \varLambda _b^{0} \pi ^-}= & {} 0, \\ (x^\prime )\,\varGamma _{\varXi _b^{\prime -}({5/2}^-) \rightarrow \varXi _b^{0} \pi ^-}= & {} 0, \\ (y^\prime )\,\varGamma _{\varXi _b^{\prime -}({5/2}^-) \rightarrow \varLambda _b^{0} K^-}= & {} 0, \\ (z^\prime )\,\varGamma _{\varOmega _b^{-}({5/2}^-) \rightarrow \varXi _b^{0} K^-}= & {} 0 . \end{aligned}$$

To further study their decay properties, in this paper we will investigate their S-wave decays into ground-state bottom baryons together with vector mesons $\rho$ and $K^*$.

This paper is organized as follows. In Sect. 2 we study S-wave decays of flavor $\mathbf {6}_F$ P-wave bottom baryons into ground-state bottom baryons and vector mesons, separately in several subsections for the four bottom baryon multiplets, $[\mathbf {6}_F, 1, 0, \rho ]$, $[\mathbf {6}_F, 0, 1, \lambda ]$, $[\mathbf {6}_F, 1, 1, \lambda ]$, and $[\mathbf {6}_F, 2, 1, \lambda ]$. A short summary is given in Sect. 3. Some relevant parameters and formulae are given in Appendix A and Appendix B.

2 Decay properties of P-wave bottom baryons

At the beginning let us briefly introduce our notations. A P-wave bottom baryon (bqq) consists of one bottom quark (b) and two light quarks (qq). Its orbital excitation can be either between the two light quarks ($l_\rho = 1$) or between the bottom quark and the two-light-quark system ($l_\lambda = 1$), so there are $\rho$-type bottom baryons ($l_\rho = 1$ and $l_\lambda = 0$) and $\lambda$-type ones ($l_\rho = 0$ and $l_\lambda = 1$). Altogether its internal symmetries are as follows:

• The color structure of the two light quarks is antisymmetric (${\bar{\mathbf {3}}}_C$).

• The SU(3) flavor structure of the two light quarks is either antisymmetric (${\bar{\mathbf {3}}}_F$) or symmetric ($\mathbf {6}_F$).

• The spin structure of the two light quarks is either antisymmetric ($s_l \equiv s_{qq} = 0$) or symmetric ($s_l = 1$).

• The orbital structure of the two light quarks is either antisymmetric ($l_\rho = 1$) or symmetric ($l_\rho = 0$).

• Due to the Pauli principle, the total symmetry of the two light quarks is antisymmetric.

Fig. 1

Categorization of P-wave bottom baryons. Taken from Ref. [1]

According to the above symmetries, one can categorize the P-wave bottom baryons into eight baryon multiplets, as shown in Fig. 1. We denote these multiplets as $[F(\mathrm{flavor}), j_l, s_l, \rho /\lambda ]$, with $j_l$ the total angular momentum of the light components ($j_l = l_\lambda \otimes l_\rho \otimes s_l$). Every multiplet contains one or two bottom baryons, whose total angular momenta are $j = j_l \otimes s_b = | j_l \pm 1/2 |$, with $s_b$ the spin of the bottom quark. Especially, the heavy quark effective theory tells that the bottom baryons inside the same doublet with $j = j_l - 1/2$ and $j = j_l + 1/2$ have similar masses.

In this section we investigate S-wave decays of flavor $\mathbf {6}_F$ P-wave bottom baryons into ground-state bottom baryons and vector mesons. To do this we use the method of light-cone sum rules within HQET, and investigate the following decay channels (the coefficients at right hand sides are isospin factors):

$$\begin{aligned}&(a1)\, {\varGamma \Big [} \varSigma _b[1/2^-] \rightarrow \varLambda _b + \rho \rightarrow \varLambda _b+\pi +\pi {\Big ]} \nonumber \\&\quad = { \varGamma \Big [} \varSigma _b^{-}[1/2^-] \rightarrow \varLambda _b^{0} +\pi ^0+ \pi ^- {\Big ]} , \end{aligned}$$

(1)

$$\begin{aligned}&(a2)\, { \varGamma \Big [}\varSigma _b[1/2^-] \rightarrow \varSigma _b + \rho \rightarrow \varSigma _b+\pi +\pi {\Big ]} \nonumber \\&\quad = 2 \times { \varGamma \Big [}\varSigma _b^{-}[1/2^-] \rightarrow \varSigma _b^{0} +\pi ^0+ \pi ^-{\Big ]}, \end{aligned}$$

(2)

$$\begin{aligned}&(a3)\,{ \varGamma \Big [}\varSigma _b[1/2^-] \rightarrow \varSigma _b^{*} + \rho \rightarrow \varSigma _b^{*}+\pi +\pi {\Big ]}\nonumber \\&\quad = 2 \times { \varGamma \Big [}\varSigma _b^{-}[1/2^-] \rightarrow \varSigma _b^{*0} +\pi ^0+ \pi ^-{\Big ]}, \end{aligned}$$

(3)

$$\begin{aligned}&(b1)\, { \varGamma \Big [}\varXi _b^{\prime }[1/2^-] \rightarrow \varXi _b + \rho \rightarrow \varXi _b+\pi +\pi {\Big ]}\nonumber \\&\quad = {3\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[1/2^-] \rightarrow \varXi _b^{0} + \pi ^0+\pi ^-{\Big ]}, \end{aligned}$$

(4)

$$\begin{aligned}&(b2)\, { \varGamma \Big [} \varXi _b^{\prime }[1/2^-] \rightarrow \varLambda _b + K^*\rightarrow \varLambda _b+K+\pi {\Big ]}\nonumber \\&\quad ={3\over 2}\times { \varGamma \Big [} \varXi _b^{\prime -}[1/2^-] \rightarrow \varLambda _b^{0} + K^0+\pi ^- {\Big ]}, \end{aligned}$$

(5)

$$\begin{aligned}&(b3)\, { \varGamma \Big [}\varXi _b^{\prime }[1/2^-] \rightarrow \varXi _b^{\prime } + \rho \rightarrow \varXi _b^{\prime }+\pi +\pi {\Big ]}\nonumber \\&\quad = {3\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[1/2^-] \rightarrow \varXi _b^{\prime 0} + \pi ^0+\pi ^-{\Big ]}, \end{aligned}$$

(6)

$$\begin{aligned}&(b4)\, { \varGamma \Big [}\varXi _b^{\prime }[1/2^-] \rightarrow \varSigma _b + K^*\rightarrow \varSigma _b+K+\pi {\Big ]} \nonumber \\&\quad = {9\over 2}\times { \varGamma \Big [}\varXi _b^{\prime -}[1/2^-] \rightarrow \varSigma _b^{0} + K^0+\pi ^-{\Big ]}, \end{aligned}$$

(7)

$$\begin{aligned}&(b5)\, { \varGamma \Big [}\varXi _b^{\prime }[1/2^-] \rightarrow \varXi _b^{*} + \rho \rightarrow \varXi _b^{*}+\pi +\pi {\Big ]}\nonumber \\&\quad = {3\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[1/2^-] \rightarrow \varXi _b^{*0} + \pi ^0+\pi ^-{\Big ]}, \end{aligned}$$

(8)

$$\begin{aligned}&(b6)\,{ \varGamma \Big [}\varXi _b^{\prime }[1/2^-] \rightarrow \varSigma _b^{*} + K^*\rightarrow \varSigma _b^{*}+K+\pi {\Big ]}\nonumber \\&\quad = {9\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[1/2^-] \rightarrow \varSigma _b^{*0} + K^0+\pi ^-{\Big ]}, \end{aligned}$$

(9)

$$\begin{aligned}&(c1)\, { \varGamma \Big [}\varOmega _b[1/2^-] \rightarrow \varXi _b + K^*\rightarrow \varXi _b+K+\pi {\Big ]} \nonumber \\&\quad = 3 \times { \varGamma \Big [}\varOmega _b^{-}[1/2^-] \rightarrow \varXi _b^{0} + K^0+\pi ^-{\Big ]}, \end{aligned}$$

(10)

$$\begin{aligned}&(c2)\, { \varGamma \Big [}\varOmega _b[1/2^-] \rightarrow \varXi _b^{\prime } + K^*\rightarrow \varXi _b^{\prime }+K+\pi {\Big ]}\nonumber \\&\quad = 3 \times { \varGamma \Big [}\varOmega _b^{-}[1/2^-] \rightarrow \varXi _b^{\prime 0} + K^0+\pi ^-{\Big ]}, \end{aligned}$$

(11)

$$\begin{aligned}&(c3)\,{ \varGamma \Big [}\varOmega _b[1/2^-] \rightarrow \varXi _b^{*} + K^*\rightarrow \varXi _b^{*}+K+\pi {\Big ]}\nonumber \\&\quad = 3 \times { \varGamma \Big [}\varOmega _b^{-}[1/2^-] \rightarrow \varXi _b^{*0} + K^0+\pi ^-{\Big ]}, \end{aligned}$$

(12)

$$\begin{aligned}&(d1)\, { \varGamma \Big [} \varSigma _b[3/2^-] \rightarrow \varLambda _b + \rho \rightarrow \varLambda _b+\pi +\pi {\Big ]}\nonumber \\&\quad = { \varGamma \Big [} \varSigma _b^{-}[3/2^-] \rightarrow \varLambda _b^{0} +\pi ^0+ \pi ^- {\Big ]}, \end{aligned}$$

(13)

$$\begin{aligned}&(d2)\, { \varGamma \Big [}\varSigma _b[3/2^-] \rightarrow \varSigma _b + \rho \rightarrow \varSigma _b+\pi +\pi {\Big ]}\nonumber \\&\quad = 2 \times { \varGamma \Big [}\varSigma _b^{-}[3/2^-] \rightarrow \varSigma _b^{0} +\pi ^0+ \pi ^-{\Big ]}, \end{aligned}$$

(14)

$$\begin{aligned}&(d3)\, { \varGamma \Big [}\varSigma _b[3/2^-] \rightarrow \varSigma _b^{*} + \rho \rightarrow \varSigma _b^{*}+\pi +\pi {\Big ]}\nonumber \\&\quad = 2 \times { \varGamma \Big [}\varSigma _b^{-}[3/2^-] \rightarrow \varSigma _b^{*0} + \pi ^0+\pi ^- {\Big ]}, \end{aligned}$$

(15)

$$\begin{aligned}&(e1)\, { \varGamma \Big [}\varXi _b^{\prime }[3/2^-] \rightarrow \varXi _b + \rho \rightarrow \varXi _b+\pi +\pi {\Big ]}\nonumber \\&\quad = {3\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[3/2^-] \rightarrow \varXi _b^{0} + \pi ^0+\pi ^-{\Big ]}, \end{aligned}$$

(16)

$$\begin{aligned}&(e2)\, { \varGamma \Big [} \varXi _b^{\prime }[3/2^-] \rightarrow \varLambda _b + K^*\rightarrow \varLambda _b+K+\pi {\Big ]}\nonumber \\&\quad ={3\over 2}\times { \varGamma \Big [} \varXi _b^{\prime -}[3/2^-] \rightarrow \varLambda _b^{0} + K^0+\pi ^- {\Big ]}, \end{aligned}$$

(17)

$$\begin{aligned}&(e3)\, { \varGamma \Big [}\varXi _b^{\prime }[3/2^-] \rightarrow \varXi _b^{\prime } + \rho \rightarrow \varXi _b^{\prime }+\pi +\pi {\Big ]}\nonumber \\&\quad = {3\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[3/2^-] \rightarrow \varXi _b^{\prime 0} + \pi ^0+\pi ^-{\Big ]}, \end{aligned}$$

(18)

$$\begin{aligned}&(e4)\, { \varGamma \Big [}\varXi _b^{\prime }[3/2^-] \rightarrow \varSigma _b^{\prime } + K^*\rightarrow \varSigma _b^{\prime }+K+\pi {\Big ]} \nonumber \\&\quad = {9\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[3/2^-] \rightarrow \varSigma _b^{\prime 0} + K^0+\pi ^-{\Big ]}, \end{aligned}$$

(19)

$$\begin{aligned}&(e5)\, { \varGamma \Big [}\varXi _b^{\prime }[3/2^-] \rightarrow \varXi _b^{*} + \rho \rightarrow \varXi _b^{*}+\pi +\pi {\Big ]}\nonumber \\&\quad = {3\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[3/2^-] \rightarrow \varXi _b^{*0} + \pi ^0+\pi ^- {\Big ]}, \end{aligned}$$

(20)

$$\begin{aligned}&(e6)\, { \varGamma \Big [}\varXi _b^{\prime }[3/2^-] \rightarrow \varSigma _b^{*} + K^* \rightarrow \varSigma _b^* + K + \pi {\Big ]}\nonumber \\&\quad = {9\over 2} \times { \varGamma \Big [}\varXi _b^{\prime -}[3/2^-] \rightarrow \varSigma _b^{*0} + K^0+\pi ^- {\Big ]}, \end{aligned}$$

(21)

$$\begin{aligned}&(f1)\, { \varGamma \Big [}\varOmega _b[3/2^-] \rightarrow \varXi _b + K^*\rightarrow \varXi _b +K+\pi {\Big ]} \nonumber \\&\quad = 3 \times { \varGamma \Big [}\varOmega _b^{-}[3/2^-] \rightarrow \varXi _b^0 + K^0+\pi ^- {\Big ]}, \end{aligned}$$

(22)

$$\begin{aligned}&(f2) \,{ \varGamma \Big [}\varOmega _b[3/2^-] \rightarrow \varXi _b^{\prime } + K^*\rightarrow \varXi _b^{\prime }+K+\pi {\Big ]} \nonumber \\&\quad = 3 \times { \varGamma \Big [}\varOmega _b^{-}[3/2^-] \rightarrow \varXi _b^{\prime 0} + K^0+\pi ^- {\Big ]}, \end{aligned}$$

(23)

$$\begin{aligned}&(f3)\, { \varGamma \Big [}\varOmega _b[3/2^-] \rightarrow \varXi _b^{*} + K^*\rightarrow \varXi _b^{*}+K+\pi {\Big ]} \nonumber \\&\quad = 3 \times { \varGamma \Big [}\varOmega _b^{-}[3/2^-] \rightarrow \varXi _b^{*0} + K^0+\pi ^- {\Big ]}, \end{aligned}$$

(24)

$$\begin{aligned}&(g1)\, { \varGamma \Big [}\varSigma _b^{}[5/2^-] \rightarrow \varSigma _b^{*}+\rho \rightarrow \varSigma _b^{*}+\pi \pi {\Big ]}\nonumber \\&\quad = 2\times { \varGamma \Big [}\varSigma _b^{-}[5/2^-]\rightarrow \varSigma _b^{*0}+\pi ^0+\pi ^-{\Big ]} , \end{aligned}$$

(25)

$$\begin{aligned}&(h1) \,{ \varGamma \Big [} \varXi _b^{\prime }[5/2^-]\rightarrow \varSigma _b^{*}+K^*\rightarrow \varSigma _b^{*}+K+\pi {\Big ]}\nonumber \\&\quad ={9\over 2}\times {\varGamma \Big [}\varXi _b^{\prime -}[5/2^-]\rightarrow \varSigma _b^{*0}+K^0+\pi ^-{\Big ]}, \end{aligned}$$

(26)

$$\begin{aligned}&(h2) \, { \varGamma \Big [}\varXi _b^{\prime }[5/2^-]\rightarrow \varXi _b^{*}+\rho \rightarrow \varXi _b^{*}+\pi +\pi {\Big ]}\nonumber \\&\quad ={3\over 2}\times {\varGamma \Big [}\varXi _b^{\prime -}[5/2^-]\rightarrow \varXi _b^{*0}+\pi ^0+\pi ^-{\Big ]} , \end{aligned}$$

(27)

$$\begin{aligned}&(i1)\, {\varGamma \Big [}\varOmega _b[5/2^-]\rightarrow \varXi _b^{*}+K^*\rightarrow \varXi _b^{*}+K+\pi {\Big ]}\nonumber \\&\quad =3\times {\varGamma \Big [}\varOmega _b^-[5/2^-]\rightarrow \varXi _b^{*0}+K^0+\pi ^-{\Big ]}. \end{aligned}$$

(28)

We can calculate their decay widths through the following Lagrangians

$$\begin{aligned} {\mathscr {L}}_{X_b({1/2}^-) \rightarrow Y_b({1/2}^+) V}= & {} g {\bar{X}_b}(1/2^-) \gamma _\mu \gamma _5 Y_b(1/2^+) V^\mu , \\ {\mathscr {L}}_{X_b({1/2}^-) \rightarrow Y_b({3/2}^+) V}= & {} g {\bar{X}_{b}}(1/2^-) Y_{b}^{\mu }(3/2^+) V_\mu ,\\ {\mathscr {L}}_{X_b({3/2}^-) \rightarrow Y_b({1/2}^+) V}= & {} g {\bar{X}_{b}^{\mu }}(3/2^-) Y_{b}(1/2^+) V_\mu , \\ {\mathscr {L}}_{X_b({3/2}^-) \rightarrow Y_b({3/2}^+) V}= & {} g {\bar{X}_b}^{\nu }(3/2^-) \gamma _\mu \gamma _5 Y_{b\nu }(3/2^+) V^\mu , \\ {\mathscr {L}}_{X_b({5/2}^-) \rightarrow Y_b({3/2}^+) V}= & {} g {\bar{X}_{b}^{\mu \nu }}(5/2^-) Y_{b\mu }(3/2^+) V_\nu \\&+ g {{\bar{X}}_{b}^{\nu \mu }}(5/2^-) Y_{b\mu }(3/2^+) V_\nu , \end{aligned}$$

where $X_b^{(\mu \nu )}$, $Y_b^{(\mu )}$, and $V^\mu$ denotes the P-wave bottom baryon, ground-state bottom baryon, and vector meson, respectively.

As an example, we study the S-wave decay of the $\varSigma _b^-({1/2}^-)$ belonging to $[\mathbf {6}_F, 1, 0, \rho ]$ into $\varLambda _b^0(1/2^+)$ and $\rho ^-(1^-)$ in the next subsection, and investigate the four bottom baryon multiplets, $[\mathbf {6}_F, 1, 0, \rho ]$, $[\mathbf {6}_F, 0, 1, \lambda ]$, $[\mathbf {6}_F, 1, 1, \lambda ]$, and $[\mathbf {6}_F, 2, 1, \lambda ]$, separately in the following subsections.

2.1 $\varSigma _b^-({1/2}^-)$ of $[\mathbf {6}_F, 1, 0, \rho ]$ decaying into $\varLambda _b^0(1/2^+)$ and $\rho ^-(1^-)$

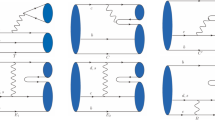
In this subsection we study the S-wave decay of the $\varSigma _b^-({1/2}^-)$ belonging to $[\mathbf {6}_F, 1, 0, \rho ]$ into $\varLambda _b^0(1/2^+)$ and $\rho ^-(1^-)$. To do this we consider the following three-point correlation function:

$$\begin{aligned}&\varPi (\omega , \, \omega ^\prime ) \nonumber \\&\quad = \int d^4 x~e^{-i k \cdot x}~\langle 0 | J_{1/2,-,\varSigma _b^-,1,0,\rho }(0) \bar{J}_{\varLambda _b^{0}}(x) | \rho ^-(q) \rangle \nonumber \\&\quad = {1+v\!\!\!/\over 2} G_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-} (\omega , \omega ^\prime ), \end{aligned}$$

(29)

where $J_{1/2,-,\varSigma _b^-,1,0,\rho }$ and $J_{\varLambda _b^{0}}$ are the interpolating fields coupling to $\varSigma _b^-({1/2}^-)$ and $\varLambda _b^0$:

$$\begin{aligned}&J_{1/2,-,\varSigma _b^-,1,0,\rho } \nonumber \\&\quad = i \epsilon _{abc} \Big ( [{\mathscr {D}}_t^{\mu } d^{aT}] C \gamma _5 d^b - d^{aT} C \gamma _5 [{\mathscr {D}}_t^{\mu } d^b] \Big ) \gamma _t^{\mu } \gamma _5 h_v^c, \end{aligned}$$

(30)

$$\begin{aligned}&J_{\varLambda _b^0}=\epsilon _{abc} [u^{aT} C\gamma _{5} d^{b}] h_{v}^{c}, \end{aligned}$$

(31)

We refer to Refs. [58, 96], where we systematically constructed all the S- and P-wave heavy baryon interpolating fields. In the above expressions $h_v(x)$ is the heavy quark field; $k^\prime = k + q$, with $k^\prime$, k, and q the momenta of the $\varSigma _b^-({1/2}^-)$, $\varLambda _b^0$, and $\rho ^-$, respectively; $\omega = v \cdot k$ and $\omega ^\prime = v \cdot k^\prime$. Note that the definitions of $\omega$ and $\omega ^\prime$ in the present study are the same as those used in Refs. [1, 60], but different from those used in Refs. [58, 59].

At the hadronic level, we write $G_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-}$ as:

$$\begin{aligned}&G_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-} (\omega , \omega ^\prime )\nonumber \\&\quad = g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-} \times { f_{\varSigma _b^-[{1\over 2}^-]} f_{\varLambda _b^{0}} \over ({\bar{\varLambda }}_{\varSigma _b^-[{1\over 2}^-]} - \omega ^\prime ) ({\bar{\varLambda }}_{\varLambda _b^{0}} - \omega )} . \end{aligned}$$

(32)

At the quark and gluon level, we calculate $G_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-}$ using the method of operator product expansion (OPE):

$$\begin{aligned}&G_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^0\rho ^-} (\omega , \omega ^\prime ) \nonumber \\&\quad = \int _0^\infty dt \int _0^1 du e^{i (1-u) \omega ^\prime t} e^{i u \omega t} \times 8 \nonumber \\&\quad \times \Bigg ( \frac{if_\rho ^{\bot }m_\rho ^2}{48}\langle {\bar{q}} q\rangle \psi _{3;\rho }^{||}(u) + \frac{if_\rho ^{||}m_\rho ^3}{8\pi ^2 t^4(v \cdot q)^2}\phi _{2;\rho }^{||}(u) \nonumber \\&\quad - \frac{i f_\rho ^{||} m_\rho ^3}{4\pi ^2t^4(v \cdot q)^2}\phi _{3;\rho }^\bot (u)+\frac{i f_\rho ^{||} m_\rho ^3}{8 \pi ^2 t^4 (v \cdot q)^2} \psi _{4;\rho }^{||}(u)\nonumber \\&\quad -\frac{i f_\rho ^{||} m_\rho }{4 \pi ^2 t^4}\phi _{2;\rho }^{||}(u)+\frac{i f_\rho ^{||} m_\rho }{2 \pi ^2 t^4}\phi _{3;\rho }^\bot (u) \nonumber \\&\quad + \frac{i f_\rho ^\bot m_\rho ^2 t^2}{768} \langle g_s \bar{q} \sigma G q\rangle \psi _{3;\rho }^{||}(u)-\frac{i f_\rho ^{||} m_\rho ^3}{64 \pi ^2 t^2}\phi _{4;\rho }^{||}(u) \Bigg ) \nonumber \\&\quad - \int _0^\infty dt \int _0^1 du \int {\mathscr {D}} {\underline{\alpha }} e^{i \omega ^{\prime } t(\alpha _2 + u \alpha _3)} e^{i \omega t(1 - \alpha _2 - u \alpha _3)} \nonumber \\&\quad \times \Bigg (\frac{i f_\rho ^{||} m_\rho ^3}{8 \pi ^2 t^2}\varPhi _{4;\rho }^{||}({\underline{\alpha }}) + \frac{i f_\rho ^{||} m_\rho ^3}{8 \pi ^2 t^2}{\widetilde{\varPhi }}_{4;\rho }^{||}({\underline{\alpha }}) +\frac{i f_\rho ^{||} m_\rho ^3}{16 \pi ^2 t^2}\varPsi _{4;\rho }^{||}({\underline{\alpha }})\nonumber \\&\quad +\frac{i f_\rho ^{||} m_\rho ^3}{16 \pi ^2 t^2}{\widetilde{\varPsi }}_{4;\rho }^{||}({\underline{\alpha }})+\frac{i f_\rho ^{||} m_\rho ^3 u}{4 \pi ^2 t^2}\varPhi _{4;\rho }^{||}({\underline{\alpha }})+\frac{i f_\rho ^{||} m_\rho ^3 u}{8 \pi ^2 t^2}\varPsi _{4;\rho }^{||}({\underline{\alpha }})\Bigg ).\nonumber \\ \end{aligned}$$

(33)

After Wick rotations and making double Borel transformation with the variables $\omega$ and $\omega ^\prime$ to be $T_1$ and $T_2$, we obtain

$$\begin{aligned}&g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-} f_{\varSigma _b^-[{1\over 2}^-]} f_{\varLambda _b^{0}} e^{- {\bar{\varLambda }_{\varSigma _b^-[{1\over 2}^-]} \over T_1}} e^{ - {\bar{\varLambda }_{\varLambda _b^{0}} \over T_2}} \nonumber \\&\quad = 8 \times \Bigg ( \frac{- f_\rho ^\bot m_\rho ^2}{48}\langle {\bar{q}} q \rangle T f_0\left( {\omega _c \over T}\right) \psi _{3;\rho }^{||}(u_0)\nonumber \\&\qquad -\frac{f_\rho ^{||} m_\rho ^3}{8\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{u_0} du_1 \int _0^{u_1} du_2\phi _{2;\rho }^{||}(u_2) \nonumber \\&\quad +\frac{f_\rho ^{||} m_\rho ^3}{4\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{u_0} du_1 \int _0^{u_1} du_2 \phi _{3;\rho }^\bot (u_2)\nonumber \\&\quad -\frac{f_\rho ^{||} m_\rho ^3}{8\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{u_0} du_1 \int _0^{u_1} du_2 \psi _{4;\rho }^{||}(u_2) \nonumber \\&\quad +\frac{f_\rho ^{||} m_\rho }{4\pi ^2} T^5 f_4\left( {\omega _c \over T}\right) \phi _{2;\rho }^{||}(u_0) - \frac{f_\rho ^{||} m_\rho }{2 \pi ^2} T^5 f_4\left( {\omega _c \over T}\right) \phi _{3;\rho }^\bot (u_0)\nonumber \\&\quad +\frac{f_\rho ^\bot m_\rho ^2}{768}\langle g_s{\bar{q}}\sigma G q \rangle {1 \over T} \psi _{3;\rho }^{||}(u_0) - \frac{f_\rho ^{||} m_\rho ^3}{64} T^3 f_2\left( {\omega _c \over T}\right) \phi _{4;\rho }^{||}(u_0) \Bigg )\nonumber \\&\quad - \Bigg (\frac{f_\rho ^{||} m_\rho ^3}{8\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{1 \over 2} d\alpha _2 \int _{{1 \over 2}-\alpha _2}^{1-\alpha _2} d\alpha _3 {1 \over \alpha _3} \varPhi _{4;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\quad + \frac{f_\rho ^{||} m_\rho ^3}{8\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{1 \over 2} d\alpha _2 \int _{{1 \over 2}-\alpha _2}^{1-\alpha _2} d\alpha _3 {1 \over \alpha _3} {\widetilde{\varPhi }}_{4;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\quad +\frac{f_\rho ^{||} m_\rho ^3}{16 \pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{1 \over 2} d\alpha _2 \int _{{1 \over 2}-\alpha _2}^{1-\alpha _2} d\alpha _3 {1 \over \alpha _3} \varPsi _{4;\rho }^{||}({\underline{\alpha }})\nonumber \\&\quad +\frac{f_\rho ^{||} m_\rho ^3}{16 \pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{1 \over 2} d\alpha _2 \int _{{1 \over 2}-\alpha _2}^{1-\alpha _2} d\alpha _3 {1 \over \alpha _3} {\widetilde{\varPsi }}_{4;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\quad + \frac{f_\rho ^{||} m_\rho ^3 u}{4\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{1 \over 2} d\alpha _2 \int _{{1 \over 2}-\alpha _2}^{1-\alpha _2} d\alpha _3 {1\over \alpha _3} \varPhi _{4;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\quad + \frac{f_\rho ^{||} m_\rho ^3 u}{8\pi ^2} T^3 f_2\left( {\omega _c \over T}\right) \int _0^{1 \over 2} d\alpha _2 \int _{{1 \over 2}-\alpha _2}^{1-\alpha _2} d\alpha _3 {1\over \alpha _3} \varPsi _{4;\rho }^{||}({\underline{\alpha }})\Bigg ).\nonumber \\ \end{aligned}$$

(34)

Here $u_0 = {T_1 \over T_1 + T_2}$, $T = {T_1 T_2 \over T_1 + T_2}$, and $f_n(x) = 1 - e^{-x} \sum _{k=0}^n {x^k \over k!}$. Explicit forms of the light-cone distribution amplitudes contained in the above expression can be found in Refs. [79,80,81,82,83,84,85,86], and we work at the renormalization scale 2 GeV for the parameters involved. More sum rule examples can be found in Appendix B.

In the present study we work at the symmetric point $T_1 = T_2 = 2T$ so that $u_0 = {1\over 2}$. We use the following values for the bottom quark mass and various quark and gluon condensates [2, 87,88,89,90,91,92,93,94,95]:

$$\begin{aligned}&m_b = 4.66 \pm 0.03~\mathrm{GeV}, \nonumber \\&\langle {\bar{q}}q \rangle = - (0.24 \pm 0.01 \text{ GeV })^3, \nonumber \\&\langle {\bar{s}}s \rangle = (0.8\pm 0.1)\times \langle {\bar{q}}q \rangle , \nonumber \\&\langle g_s {\bar{q}} \sigma G q \rangle = M_0^2 \times \langle \bar{q}q \rangle , \nonumber \\&\langle g_s {\bar{s}} \sigma G s \rangle = M_0^2 \times \langle \bar{s}s \rangle , \nonumber \\&M_0^2= 0.8 \text{ GeV }^2, \nonumber \\&\langle g_s^2GG\rangle =(0.48\pm 0.14) \text{ GeV }^4. \end{aligned}$$

(35)

Now the coupling constant $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-}$ only depends on two free parameters, the threshold value $\omega _c$ and the Borel mass T. We choose $\omega _c = 1.$ 485GeV to be the average of the threshold values of the $\varSigma _b(1/2^-)$ and $\varLambda _b^{0}$ mass sum rules (see Appendix A and Ref. [1] for the parameters of the $\varSigma _b(1/2^-)$ and $\varLambda _b^{0}$), and extract the coupling constant $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-}$ to be

$$\begin{aligned}&g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-} \nonumber \\&\quad = 0.17~{^{+0.24}_{-0.17}} =0.17~{^{+0.01}_{-0.00}}~{^{+0.06}_{-0.05}}~{^{+0.06}_{-0.05}}~{^{+0.20}_{-0.17}}~{^{+0.10}_{-0.11}}, \end{aligned}$$

(36)

where the uncertainties are due to the Borel mass, the parameters of the $\varLambda _b^{0}$, the parameters of the $\varSigma _b^-({1/2}^-)$, the light-cone distribution amplitudes of vector mesons [79,80,81,82,83,84,85,86], and various quark masses and condensates listed in Eq. (35), respectively. Besides these statistical uncertainties, there is another (theoretical) uncertainty, which comes from the scale dependence. In the present study we do not consider this, and simply work at the renormalization scale 2 GeV, since $\sqrt{M_{\varSigma _b^-({1/2}^-)}^2 - M_{\varLambda _b^{0}}^2} = 2.4$ GeV. However, it is useful to give a rough estimation on this. Since the largest uncertainty comes from the light-cone distribution amplitudes of vector mesons, we choose the values for the parameters contained in these amplitudes to be at the renormalization scale 1 GeV (see Tables 1 and 2 of Ref. [86]), and redo the above calculations to obtain:

$$\begin{aligned} g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-}(1~\text{ GeV }) = 0.42 . \end{aligned}$$

(37)

Hence, the scale dependence leads to a significant uncertainty, and the total uncertainty of our results can be even larger.

For completeness, we show $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^-}$ in Fig. 2a as a function of the Borel mass T, and find that it only slightly depends on the Borel mass, where the working region for T has been evaluated in the $\varSigma _b(1/2^-)$ mass sum rules [1, 58,59,60] to be 0.31 GeV $<T<0.34$ GeV (we also summarize this in Table 5). Note that the definitions of $\omega$ and $\omega ^\prime$ in this paper are the same as those used in Refs. [1, 60], but different from those used in Refs. [58, 59], so the Borel windows used in this paper are also the same/similar as those used in Refs. [1, 60], but just about half of those used in Refs. [58, 59].

The two-body decay $\varSigma _b^-({1/2}^-) \rightarrow \varLambda _b^{0}\rho ^-$ is kinematically forbidden, but the three-body decay process $\varSigma _b^-({1/2}^-)\rightarrow \varLambda _b^{0}\rho ^- \rightarrow \varLambda _b^{0}\pi ^0\pi ^-$ is kinematically allowed, whose decay amplitude is

$$\begin{aligned}&{\mathscr {M}}\, \left( 0 \rightarrow 3 + 4 \rightarrow 3 + 2 + 1 \right) \nonumber \\&\quad \equiv {\mathscr {M}}\, \left( \varSigma _b^-({1/2}^-) \rightarrow \varLambda _b^{0} + \rho ^- \rightarrow \varLambda _b^{0} + \pi ^0 + \pi ^- \right) \nonumber \\&\quad = g_{0 \rightarrow 3 + 4} \times g_{4 \rightarrow 2 + 1} \times {\bar{u}}_{0} \gamma _\mu \gamma _5 u_3 \times \left( g_{\mu \nu } - { p_{4,\mu } p_{4,\nu } \over m_4^2} \right) \nonumber \\&\qquad \times { 1 \over p_4^2 - m_4^2 + i m_4 \varGamma _4 } \times \left( p_{1,\nu } - p_{2,\nu } \right) . \end{aligned}$$

(38)

Here 0 denotes the initial state $\varSigma _b^-({1/2}^-)$; 4 denotes the intermediate state $\rho ^{-}$; 1, 2 and 3 denote the finial states $\pi ^-$, $\pi ^0$ and $\varLambda _b^{0}$, respectively.

This amplitude can be used to further calculate its decay width

$$\begin{aligned}&\varGamma \left( 0 \rightarrow 3 + 4 \rightarrow 3 + 2 + 1 \right) \nonumber \\&\quad \equiv \varGamma \left( \varSigma _b^-({1/2}^-) \rightarrow \varLambda _b^{0} + \rho ^- \rightarrow \varLambda _b^{0} + \pi ^0 + \pi ^- \right) \nonumber \\&\quad = {1 \over (2\pi )^3} {1 \over 32 m_0^3} \times g^2_{0 \rightarrow 3 + 4} \times g^2_{4 \rightarrow 2 + 1} \times \int d m_{12} d m_{23} \nonumber \\&\qquad \times {1\over 2}~\mathrm{Tr}\Big [ \left( p\!\!\!/_3 + m_3 \right) \gamma _{\mu ^\prime } \gamma _5 \left( p\!\!\!/_0 + m_0 \right) \gamma _{\mu } \gamma _5 \Big ] \nonumber \\&\qquad \times \left( g_{\mu \nu } - { p_{4,\mu } p_{4,\nu } \over m_4^2} \right) \left( g_{\mu ^\prime \nu ^\prime } - { p_{4,\mu ^\prime } p_{4,\nu ^\prime } \over m_4^2} \right) \nonumber \\&\qquad \times {\left( p_{1,\nu } - p_{2,\nu } \right) \left( p_{1,\nu ^\prime } - p_{2,\nu ^\prime } \right) \over |p_4^2 - m_4^2 + i m_4 \varGamma _4|^2 }, \end{aligned}$$

(39)

so that the width of the $\varSigma _b^-({1/2}^-) \rightarrow \varLambda _b^{0}\rho ^- \rightarrow \varLambda _b^{0}\pi ^0\pi ^-$ decay is evaluated to be

$$\begin{aligned}&\varGamma _{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^{0}\rho ^- \rightarrow \varLambda _b^{0}\pi ^0\pi ^-} \nonumber \\&\quad = 8.9~{^{+32.5}_{-8.9}}\mathrm{~keV} = 8.9~{^{+1.1}_{-0.0}}~{^{+6.7}_{-5.0}}~{^{+7.0}_{-4.5}}~{^{+27.9}_{-8.9}}~{^{+13.6}_{-7.5}}\mathrm{~keV}.\nonumber \\ \end{aligned}$$

(40)

In the following subsections we apply the same procedures to separately study the four bottom baryon multiplets, $[\mathbf {6}_F, 1, 0, \rho ]$, $[\mathbf {6}_F, 0, 1, \lambda ]$, $[\mathbf {6}_F, 1, 1, \lambda ]$, and $[\mathbf {6}_F, 2, 1, \lambda ]$.

2.2 The bottom baryon doublet $[\mathbf {6}_F, 1, 0, \rho ]$

The bottom baryon doublet $[\mathbf {6}_F, 1, 0, \rho ]$ consists of six members: $\varSigma _b({1\over 2}^-/{3\over 2}^-)$, $\varXi ^\prime _b({1\over 2}^-/{3\over 2}^-)$, and $\varOmega _b({1\over 2}^-/{3\over 2}^-)$. We use the method of light-cone sum rules within HQET to study their decays into ground-state bottom baryons and vector mesons.

Table 1 S-wave decays of P-wave bottom baryons belonging to the doublet $[\mathbf {6}_F, 1, 0, \rho ]$ into ground-state bottom baryons and vector mesons

There are altogether twenty-four non-vanishing decay channels, whose coupling constants are extracted to be

$$\begin{aligned} (a1)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+] \rho }= & {} 0.17, \nonumber \\ (a2)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho }= & {} 0.35, \nonumber \\ (a3)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+] \rho }= & {} 0.20, \nonumber \\ (b1)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho }= & {} 0.03, \nonumber \\ (b2)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+] K^{*}}= & {} 0.31, \nonumber \\ (b3)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho }= & {} 0.24, \nonumber \\ (b4)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]K^{*}}= & {} 0.38, \nonumber \\ (b5)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 0.14 , \nonumber \\ (b6)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.22, \nonumber \\ (c1)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+]K^{*}}= & {} 0.24, \nonumber \\ (c2)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+]K^{*}}= & {} 0.49 , \nonumber \\ (c3)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.28, \nonumber \\ (d1)\, g_{\varSigma _b[{3\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+]\rho }= & {} 0.29, \nonumber \\ (d2)\, g_{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]\rho }= & {} 0.19 , \nonumber \\ (d3) \,g_{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]\rho }= & {} 0.24, \nonumber \\ (e1)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho }= & {} 0.06, \nonumber \\ (e2)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+]K^{*}}= & {} 0.42 , \nonumber \\ (e3)\, g_{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho }= & {} 0.14, \nonumber \\ (e4)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]K^{*}}= & {} 0.22, \nonumber \\ (e5)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 0.16, \nonumber \\ (e6)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.25, \nonumber \\ (f1)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+]K^{*}}= & {} 0.34, \nonumber \\ (f2)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+]K^{*}}= & {} 0.28, \nonumber \\ (f3)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.33 . \end{aligned}$$

(41)

Then we compute the three-body decay widths, which are kinematically allowed:

$$\begin{aligned} (a1)\, \varGamma _{\varSigma _b[{1\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+] \rho \rightarrow \varLambda _b[{1\over 2}^+]\pi \pi }= & {} 8.9 \mathrm{~keV}, \nonumber \\ (a2)\, \varGamma _{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 2.2\times 10^{-3} \mathrm{~keV}, \nonumber \\ (b1)\, \varGamma _{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho \rightarrow \varXi _b[{1\over 2}^+]\pi \pi }= & {} 0.2 \mathrm{~keV}, \nonumber \\ (b3)\, \varGamma _{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \pi \pi }= & {} 5.1\times 10^{-3} \mathrm{~keV},\nonumber \\ (d1)\, \varGamma _{\varSigma _b[{3\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+]\rho \rightarrow \varLambda _b[{1\over 2}^+]\pi \pi }= & {} 4.1 \mathrm{~keV}, \nonumber \\ (d2)\, \varGamma _{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]\rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 2.1\times 10^{-4} \mathrm{~keV }, \nonumber \\ (e1)\, \varGamma _{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho \rightarrow \varXi _b[{1\over 2}^+]\pi \pi }= & {} 0.2 \mathrm{~keV}, \nonumber \\ (e3)\, \varGamma _{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1 \over 2}^+]\pi \pi }= & {} 5.8\times 10^{-4} \mathrm{~keV}. \end{aligned}$$

(42)

We summarize these results in Table 1. For completeness, we also show the coupling constants as functions of the Borel mass T in Fig. 2.

Fig. 2

The coupling constants a $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^0 \rho ^-}$, b $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varSigma _b^0\rho ^-}$, c $g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^0 \rho ^-}$, d $g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^{\prime 0} \rho ^-}$, e $g_{\varSigma _b^-[{3\over 2}^-] \rightarrow \varLambda _b^0 \rho ^-}$, f $g_{\varSigma _b^-[{3\over 2}^-] \rightarrow \varSigma _b^0 \rho ^-}$, g $g_{\varXi _b^{\prime -}[{3\over 2}^-] \rightarrow \varXi _b^0 \rho ^-}$, and h $g_{\varXi _b^{\prime -}[{3\over 2}^-] \rightarrow \varXi _b^{\prime 0} \rho ^-}$ as functions of the Borel mass T. Here the baryons $\varSigma _b({1\over 2}^-/{3\over 2}^-)$ and $\varXi ^\prime _b({1\over 2}^-/{3\over 2}^-)$ belong to the bottom baryon doublet $[\mathbf {6}_F, 1, 0, \rho ]$, and the working regions for T have been evaluated in mass sum rules [1, 58,59,60] and summarized in Table 5

2.3 The bottom baryon singlet $[\mathbf {6}_F, 0, 1, \lambda ]$

The bottom baryon doublet $[\mathbf {6}_F, 1, 0, \rho ]$ consists of three members: $\varSigma _b({1\over 2}^-)$, $\varXi ^\prime _b({1\over 2}^-)$, and $\varOmega _b({1\over 2}^-)$. We use the method of light-cone sum rules within HQET to study their decays into ground-state bottom baryons and vector mesons.

Table 2 S-wave decays of P-wave bottom baryons belonging to the doublet $[\mathbf {6}_F, 0, 1, \lambda ]$ into ground-state bottom baryons and vector mesons

There are altogether eight non-vanishing decay channels, whose coupling constants are extracted to be

$$\begin{aligned} (a2)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho }= & {} 2.25, \nonumber \\ (a3)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+] \rho }= & {} 7.74, \nonumber \\ (b3)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho }= & {} 1.58, \nonumber \\ (b4)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]K^{*}}= & {} 1.77, \nonumber \\ (b5)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 5.70, \nonumber \\ (b6)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 5.77, \nonumber \\ (c2)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+]K^{*}}= & {} 2.37, \nonumber \\ (c3)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 8.18. \end{aligned}$$

(43)

Then we compute the three-body decay widths, which are kinematically allowed:

$$\begin{aligned} (a2)\, \varGamma _{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 5.9\times 10^{-2} \mathrm{~keV}, \nonumber \\ (b3)\, \varGamma _{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \pi \pi }= & {} 0.2 \mathrm{~keV} . \end{aligned}$$

(44)

We summarize these results in Table 2. For completeness, we also show the coupling constants as functions of the Borel mass T in Fig. 3.

Fig. 3

The coupling constants a $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varSigma _b^0 \rho ^-}$ and b $g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^{\prime 0} \rho ^-}$ as functions of the Borel mass T. Here the baryons $\varSigma _b({1\over 2}^-)$ and $\varXi ^\prime _b({1\over 2}^-)$ belong to the bottom baryon singlet $[\mathbf {6}_F, 0, 1, \lambda ]$, and the working regions for T have been evaluated in mass sum rules [1, 58,59,60] and summarized in Table 5

2.4 The bottom baryon doublet $[\mathbf {6}_F, 1, 1, \lambda ]$

The bottom baryon doublet $[\mathbf {6}_F, 1, 1, \lambda ]$ consists of six members: $\varSigma _b({1\over 2}^-/{3\over 2}^-)$, $\varXi ^\prime _b({1\over 2}^-/{3\over 2}^-)$, and $\varOmega _b({1\over 2}^-/{3\over 2}^-)$. We use the method of light-cone sum rules within HQET to study their decays into ground-state bottom baryons and vector mesons.

Table 3 S-wave decays of P-wave bottom baryons belonging to the doublet $[\mathbf {6}_F, 1, 1, \lambda ]$ into ground-state bottom baryons and vector mesons

There are altogether twenty-four non-vanishing decay channels, whose coupling constants are extracted to be

$$\begin{aligned} (a1)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+] \rho }= & {} 0.83, \nonumber \\ (a2)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho }= & {} 2.21, \nonumber \\ (a3)\, g_{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+] \rho }= & {} 1.28, \nonumber \\ (b1)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho }= & {} 0.59, \nonumber \\ (b2)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+] K^{*}}= & {} 1.60, \nonumber \\ (b3)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho }= & {} 1.45, \nonumber \\ (b4)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]K^{*}}= & {} 0.13, \nonumber \\ (b5)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 0.84, \nonumber \\ (b6)\, g_{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.08, \nonumber \\ (c1)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+]K^{*}}= & {} 2.25, \nonumber \\ (c2)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+]K^{*}}= & {} 0.17, \nonumber \\ (c3)\, g_{\varOmega _b[{1\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.10, \nonumber \\ (d1)\, g_{\varSigma _b[{3\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+]\rho }= & {} 1.62, \nonumber \\ (d2)\, g_{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]\rho }= & {} 0.90, \nonumber \\ (d3)\, g_{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]\rho }= & {} 1.48, \nonumber \\ (e1)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho }= & {} 0.57, \nonumber \\ (e2)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+]K^{*}}= & {} 1.31 , \nonumber \\ (e3)\, g_{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho }= & {} 0.84, \nonumber \\ (e4)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]K^{*}}= & {} 0.08, \nonumber \\ (e5)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 0.97, \nonumber \\ (e6)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.09, \nonumber \\ (f1)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+]K^{*}}= & {} 1.61, \nonumber \\ (f2)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+]K^{*}}= & {} 0.10, \nonumber \\ (f3)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.12. \end{aligned}$$

(45)

Then we compute the three-body decay widths, which are kinematically allowed:

$$\begin{aligned} (a1)\, \varGamma _{\varSigma _b[{1\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+] \rho \rightarrow \varLambda _b[{1\over 2}^+]\pi \pi }= & {} 207.4 \mathrm{~keV}, \nonumber \\ (a2)\, \varGamma _{\varSigma _b[{1\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 5.7 \times 10^{-2} \mathrm{~keV} , \nonumber \\ (b1)\, \varGamma _{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho \rightarrow \varXi _b[{1\over 2}^+]\pi \pi }= & {} 61.0 \mathrm{~keV}, \nonumber \\ (b3)\, \varGamma _{\varXi _b^{\prime }[{1\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \pi \pi }= & {} 0.2 \mathrm{~keV},\nonumber \\ (d1)\, \varGamma _{\varSigma _b[{3\over 2}^-]\rightarrow \varLambda _b[{1\over 2}^+]\rho \rightarrow \varLambda _b[{1\over 2}^+]\pi \pi }= & {} 261.1\mathrm{~keV}, \nonumber \\ (d2)\, \varGamma _{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]\rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 3.2\times 10^{-3} \mathrm{~keV }, \nonumber \\ (e1)\, \varGamma _{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b[{1\over 2}^+] \rho \rightarrow \varXi _b[{1\over 2}^+]\pi \pi }= & {} 18.8 \mathrm{~keV}, \nonumber \\ (e3)\, \varGamma _{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1 \over 2}^+] \pi \pi }= & {} 2.1\times 10^{-2} \mathrm{~MeV} . \end{aligned}$$

(46)

We summarize these results in Table 3. For completeness, we also show the coupling constants as functions of the Borel mass T in Fig. 4.

Fig. 4

The coupling constants a $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varLambda _b^0 \rho ^-}$, b $g_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varSigma _b^0\rho ^-}$, c $g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^0 \rho ^-}$, d $g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^{\prime 0} \rho ^-}$, e $g_{\varSigma _b^-[{3\over 2}^-] \rightarrow \varLambda _b^0 \rho ^-}$, f $g_{\varSigma _b^-[{3\over 2}^-] \rightarrow \varSigma _b^0 \rho ^-}$, g $g_{\varXi _b^{\prime -}[{3\over 2}^-] \rightarrow \varXi _b^0 \rho ^-}$, and h $g_{\varXi _b^{\prime -}[{3\over 2}^-] \rightarrow \varXi _b^{\prime 0} \rho ^-}$ as functions of the Borel mass T. Here the baryons $\varSigma _b({1\over 2}^-/{3\over 2}^-)$ and $\varXi ^\prime _b({1\over 2}^-/{3\over 2}^-)$ belong to the bottom baryon doublet $[\mathbf {6}_F, 1, 1, \lambda ]$, and the working regions for T have been evaluated in mass sum rules [1, 58,59,60] and summarized in Table 5

2.5 The bottom baryon doublet $[\mathbf {6}_F,2,1,\lambda ]$

The bottom baryon doublet $[\mathbf {6}_F, 2, 1, \lambda ]$ consists of six members: $\varSigma _b({3\over 2}^-/{5\over 2}^-)$, $\varXi ^\prime _b({3\over 2}^-/{5\over 2}^-)$, and $\varOmega _b({3\over 2}^-/{5\over 2}^-)$. We use the method of light-cone sum rules within HQET to study their decays into ground-state bottom baryons and vector mesons.

Table 4 S-wave decays of P-wave bottom baryons belonging to the doublet $[\mathbf {6}_F, 2, 1, \lambda ]$ into ground-state bottom baryons and vector mesons

Fig. 5

The coupling constants a $g_{\varSigma _b^-[{3\over 2}^-] \rightarrow \varSigma _b^0 \rho ^-}$, b $g_{\varSigma _b^-[{5\over 2}^-] \rightarrow \varSigma _b^{*0}\rho ^-}$, c $g_{\varXi _b^{\prime -}[{3\over 2}^-] \rightarrow \varXi _b^{\prime 0} \rho ^-}$, and d $g_{\varXi _b^{\prime -}[{5\over 2}^-] \rightarrow \varXi _b^{*0} \rho ^-}$ as functions of the Borel mass T. Here the baryons $\varSigma _b({3\over 2}^-/{5\over 2}^-)$ and $\varXi ^\prime _b({3\over 2}^-/{5\over 2}^-)$ belong to the bottom baryon doublet $[\mathbf {6}_F, 2, 1, \lambda ]$, and the working regions for T have been evaluated in mass sum rules [1, 58,59,60] and summarized in Table 5

There are altogether twelve non-vanishing decay channels, whose coupling constants are extracted to be

$$\begin{aligned} (d2)\, g_{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]\rho }= & {} 5.90~{^{+3.56}_{-3.08}}, \nonumber \\ (d3) \,g_{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]\rho }= & {} 0.69~{^{+0.41}_{-0.35}}, \nonumber \\ (e3)\, g_{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho }= & {} 4.23~{^{+2.42}_{-2.13}}, \nonumber \\ (e4)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+]K^{*}}= & {} 3.17~{^{+2.37}_{-2.20}}, \nonumber \\ (e5)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 0.50~{^{+0.28}_{-0.24}}, \nonumber \\ (e6)\, g_{\varXi _b^{\prime }[{3\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.40~{^{+0.28}_{-0.26}}, \nonumber \\ (f2)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b^{\prime }[{1\over 2}^+]K^{*}}= & {} 4.56~{^{+3.19}_{-2.97}}, \nonumber \\ (f3)\, g_{\varOmega _b[{3\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 0.60~{^{+0.38}_{-0.35}}, \nonumber \\ (g1)\, g_{\varSigma _b[{5\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]\rho }= & {} 3.78~{^{+2.01}_{-1.65}}, \nonumber \\ (h1)\, g_{\varXi _b^{\prime }[{5\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho }= & {} 4.09~{^{+2.08}_{-1.72}}, \nonumber \\ (h2)\, g_{\varXi _b^{\prime }[{5\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]K^{*}}= & {} 2.14~{^{+1.33}_{-1.18}}, \nonumber \\ (i1)\, g_{\varOmega _b[{5\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]K^{*}}= & {} 6.36~{^{+3.75}_{-2.72}}. \end{aligned}$$

(47)

Then we compute the three-body decay widths, which are kinematically allowed:

$$\begin{aligned} (d2)\, \varGamma _{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 0.14~{^{+0.19}_{-0.12}} \mathrm{~keV}, \nonumber \\ (e3)\, \varGamma _{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1 \over 2}^+] \pi \pi }= & {} 0.53~{^{+0.68}_{-0.46}} \mathrm{~keV}, \nonumber \\ (g1)\, \varGamma _{\varSigma _b[{5\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]\rho \rightarrow \varSigma _b^{*}[{3\over 2}^+]\pi \pi }= & {} \left( 3~{^{+4}_{-2}}\right) \times 10^{-6} \mathrm{~keV}, \nonumber \\ (h2)\, \varGamma _{\varXi _b^{\prime }[{5\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho \rightarrow \varXi _b^{*}[{3\over 2}^+]\pi \pi }= & {} 0.29~{^{+0.32}_{-0.23}}\mathrm{~keV }. \end{aligned}$$

(48)

We summarize these results in Table 4. For completeness, we also show the coupling constants as functions of the Borel mass T in Fig. 5.

3 Summary and discussions

To summarize this paper, we have used the method of light-cone sum rules within heavy quark effective theory to study decay properties of P-wave bottom baryons belonging to the flavor $\mathbf {6}_F$ representation. We have studied their S-wave decays into ground-state bottom baryons and vector mesons. The possible decay channels are given in Eqs. (1–28), and the extracted decay widths are listed in Tables 1, 2, 3, and 4. These results are obtained separately for the four bottom baryon multiplets of flavor $\mathbf {6}_F$: $[\mathbf {6}_F, 1, 0, \rho ]$, $[\mathbf {6}_F, 0, 1, \lambda ]$, $[\mathbf {6}_F, 1, 1, \lambda ]$, and $[\mathbf {6}_F, 2, 1, \lambda ]$.

In Ref. [1] we have studied the mass spectrum and pionic decay properties of the $\varSigma _{b}(6097)$ and $\varXi _{b}(6227)$ [7, 8]. Our results suggest that they can be well interpreted as P-wave bottom baryons of $J^P = 3/2^-$, belonging to the bottom baryon doublet $[\mathbf {6}_F, 2, 1, \lambda ]$. This doublet contains altogether six bottom baryons, $\varSigma _b({3\over 2}^-/{5\over 2}^-)$, $\varXi ^\prime _b({3\over 2}^-/{5\over 2}^-)$, and $\varOmega _b({3\over 2}^-/{5\over 2}^-)$. In the present study we further investigate their S-wave decays into ground-state bottom baryons and vector mesons, and extract:

$$\begin{aligned} (d2)\, \varGamma _{\varSigma _b[{3\over 2}^-]\rightarrow \varSigma _b[{1\over 2}^+] \rho \rightarrow \varSigma _b[{1\over 2}^+]\pi \pi }= & {} 0.14~{^{+0.19}_{-0.12}} \mathrm{~keV}, \\ (e3)\, \varGamma _{\varXi _b^{\prime }[{3\over 2}^-] \rightarrow \varXi _b^{\prime }[{1\over 2}^+] \rho \rightarrow \varXi _b^{\prime }[{1 \over 2}^+] \pi \pi }= & {} 0.53~{^{+0.68}_{-0.46}} \mathrm{~keV}, \\ (g1)\, \varGamma _{\varSigma _b[{5\over 2}^-]\rightarrow \varSigma _b^{*}[{3\over 2}^+]\rho \rightarrow \varSigma _b^{*}[{3\over 2}^+]\pi \pi }= & {} \left( 3~{^{+4}_{-2}}\right) \times 10^{-6} \mathrm{~keV}, \\ (h2) \varGamma _{\varXi _b^{\prime }[{5\over 2}^-]\rightarrow \varXi _b^{*}[{3\over 2}^+]\rho \rightarrow \varXi _b^{*}[{3\over 2}^+]\pi \pi }= & {} 0.29~{^{+0.32}_{-0.23}}\mathrm{~keV } . \end{aligned}$$

Hence, these three $J^P = 5/2^-$ states are probably quite narrow, because their S-wave decays into ground-state bottom baryons and pseudoscalar mesons can not happen, and widths of the following D-wave decays are also calculated to be zero in Ref. [1]:

$$\begin{aligned} (w^\prime )\, \varGamma _{\varSigma _b^{-}({5/2}^-) \rightarrow \varLambda _b^{0} \pi ^-}= & {} 0, \nonumber \\ (x^\prime )\, \varGamma _{\varXi _b^{\prime -}({5/2}^-) \rightarrow \varXi _b^{0} \pi ^-}= & {} 0, \nonumber \\ (y^\prime )\, \varGamma _{\varXi _b^{\prime -}({5/2}^-) \rightarrow \varLambda _b^{0} K^-}= & {} 0, \nonumber \\ (z^\prime )\, \varGamma _{\varOmega _b^{-}({5/2}^-) \rightarrow \varXi _b^{0} K^-}= & {} 0. \end{aligned}$$

(49)

We suggest the LHCb and Belle/Belle-II experiments to search for these three narrow states. Especially, we propose to search for the $\varXi _b({5/2}^-)$, that is the $J^P = 5/2^-$ partner state of the $\varXi _{b}(6227)$, in the $\varXi _b({5/2}^-) \rightarrow \varXi _b^{*}\rho \rightarrow \varXi _b^{*}\pi \pi$ decay process. Its mass is $12 \pm 5$ MeV larger than that of the $\varXi _{b}(6227)$.

To end this work, we note that in the present study we have studied S-wave decays of flavor $\mathbf {6}_F$ P-wave heavy baryons into ground-state heavy baryons and vector mesons, which is actually a complement to Ref. [60], where we studied S-wave decays of flavor ${\bar{\mathbf {3}}}_F$ P-wave heavy baryons into ground-state heavy baryons together with pseudoscalar and vector mesons, and S-wave decays of flavor $\mathbf {6}_F$ P-wave heavy baryons into ground-state heavy baryons together with pseudoscalar mesons. To make a complete QCD sum rule studies of P-wave heavy baryons within HQET, we still need to systematically study their D-wave and radiative decay properties, which is currently under investigation.

Appendices

Appendix A: Parameters of S/P-wave bottom baryons and S-wave mesons

We list masses of ground-state bottom baryons used in the present study, taken from PDG [2]:

$$\begin{aligned} \varLambda _{b}(1/2^+) ~:~ m= & {} 5619.60 \text{ MeV }, \\ \varXi _{b}(1/2^+) ~:~ m= & {} 5793.20 \text{ MeV }, \\ \varSigma _{b}(1/2^+) ~:~ m= & {} 5813.4 \text{ MeV }, \\ \varSigma _{b}^{*}(3/2^+) ~:~ m= & {} 5833.6 \text{ MeV }, \, \\ \varXi _{b}^{\prime }(1/2^+) ~:~ m= & {} 5935.02 \text{ MeV }, \\ \varXi _{b}^{*}(3/2^+) ~:~ m= & {} 5952.6 \text{ MeV }, \, \\ \varOmega _b(1/2^+) ~:~ m= & {} 6046.1 \text{ MeV }, \\ \varOmega _b^*(3/2^+) ~:~ m= & {} 6063 \text{ MeV } . \end{aligned}$$

Their QCD sum rule parameters can be found in Refs. [1, 60, 96].

We list masses of P-wave bottom baryons used in the present study, taken from the LHCb experiments [7, 8] as well as our previous QCD sum rule studies [1, 58, 59]:

$$\begin{aligned} M_{\varSigma _b(1/2^-)} = M_{\varSigma _b(3/2^-)}= & {} 6096.9~\mathrm{MeV}, \nonumber \\ M_{\varSigma _b(5/2^-)} - M_{\varSigma _b(3/2^-)}= & {} 13~\mathrm{MeV}, \nonumber \\ M_{\varXi _b^{\prime }(1/2^-)} = M_{\varXi _b^{\prime }(3/2^-)}= & {} 6226.9~\mathrm{MeV}, \nonumber \\ M_{\varXi ^\prime _b(5/2^-)} - M_{\varXi ^\prime _b(3/2^-)}= & {} 12~\mathrm{MeV}, \nonumber \\ M_{\varOmega _b(1/2^-)} = M_{\varOmega _b(3/2^-)}= & {} 6460~\mathrm{MeV}, \nonumber \\ M_{\varOmega _b(5/2^-)} - M_{\varOmega _b(3/2^-)}= & {} 11~\mathrm{MeV} . \end{aligned}$$

(A.1)

Their QCD sum rule parameters can be found in Table 5.

Table 5 Parameters of P-wave bottom baryons belonging to the bottom baryon multiplets $[\mathbf {6}_F, 1, 0, \rho ]$, $[\mathbf {6}_F, 0, 1, \lambda ]$, $[\mathbf {6}_F, 1, 1, \lambda ]$ and $[\mathbf {6}_F, 2, 1, \lambda ]$. Detailed discussions can be found in Refs. [1, 58, 59]

We list masses and decay widths of the pseudoscalar and vector mesons used in the present study, taken from PDG [2]:

$$\begin{aligned} \pi (0^-) ~:~ m= & {} 138.04 \mathrm{~MeV}, \end{aligned}$$

(A.2)

$$\begin{aligned} K(0^-) ~:~ m= & {} 495.65 \mathrm{~MeV}, \nonumber \\ \rho (1^-) ~:~ m= & {} 775.21 \mathrm{~MeV},\, \nonumber \\ \varGamma= & {} 148.2 \mathrm{~MeV},\, {g}_{\rho \pi \pi } = 5.94, \nonumber \\ K^*(1^-) ~:~ m= & {} 893.57 \mathrm{~MeV},\, \nonumber \\ \varGamma= & {} 49.1 \mathrm{~MeV},\, {g}_{K^* K \pi } = 3.20, \end{aligned}$$

(A.3)

where the two coupling constants ${g}_{\rho \pi \pi }$ and ${g}_{K^* K \pi }$ are evaluated using the experimental decay widths of the $\rho$ and $K^*$ [2] through the following Lagrangians

$$\begin{aligned} {\mathscr {L}}_{\rho \pi \pi }= & {} {g}_{\rho \pi \pi } \times \left( \rho _\mu ^0 \pi ^+ \partial ^\mu \pi ^- - \rho _\mu ^0 \pi ^- \partial ^\mu \pi ^+ \right) + \cdots , \nonumber \\ {\mathscr {L}}_{K^* K \pi }= & {} {g}_{K^* K \pi } K^{*+}_\mu \times \left( K^-\partial ^\mu \pi ^0 - \partial ^\mu K^- \pi ^0 \right) +\cdots .\nonumber \\ \end{aligned}$$

(A.4)

Appendix B: Sum rule equations

In this appendix we show several examples of sum rule equations, which are used to extract S-wave decays of P-wave bottom baryons into ground-state bottom baryons and vector mesons.

The sum rule for $\varXi _b^{\prime -}[{1\over 2}^-]$ belonging to $[\mathbf {6}_F, 0, 1, \lambda ]$ is

$$\begin{aligned}&G_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^{*0}\rho ^-} (\omega , \omega ^\prime ) = { g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varXi _b^{*0}\rho ^-} f_{\varXi _b^-[{1\over 2}^-]} f_{\varXi _b^{*0}} \over ({\bar{\varLambda }}_{\varXi _b^-[{1\over 2}^-]} - \omega ^\prime ) ({\bar{\varLambda }}_{\varXi _b^{*0}} - \omega )} \nonumber \\&\quad = \int _0^\infty dt \int _0^1 du e^{i(1-u)\omega ^\prime t} e^{iu\omega t}\times 4\nonumber \\&\qquad \times \Bigg (\frac{if_\rho ^{||} m_\rho }{6\pi ^2 t^4}\phi _{2;\rho }^{||}(u)-\frac{2i f_\rho ^{||} m_\rho }{3\pi ^3 t^4}\phi _{3;\rho }^\perp (u) \nonumber \\&\qquad -\frac{if_\rho ^{||} m_\rho ^3}{12\pi ^2 t^4(v\cdot q)^2}\phi _{2;\rho }^{||}(u)+\frac{if_\rho ^{||} m_\rho ^3}{6\pi ^2 t^4(v\cdot q)^2}\phi _{3;\rho }^{||}(u)\nonumber \\&\qquad -\frac{if_\rho ^{||} m_\rho ^3}{12\pi ^2 t^4(v\cdot q)^2}\psi _{4;\rho }^{||}(u)+\frac{f_\rho ^\perp m_s m_\rho ^2}{12\pi ^2 t^3 v\cdot q}\phi _{2;\rho }^\perp (u) \nonumber \\&\qquad -\frac{f_\rho ^\perp m_s m_\rho ^2}{12\pi ^2 t^3 v\cdot q}\psi _{4;\rho }^\perp (u)-\frac{f_\rho ^{||} m_\rho v\cdot q}{12\pi ^2 t^3}\psi _{3;\rho }^\perp (u)\nonumber \\&\qquad +\frac{if_\rho ^{||} m_\rho ^3}{96\pi ^2 t^2}\phi _{4;\rho }^{||}(u)-\frac{if_\rho ^\perp m_s m_\rho ^2}{24\pi ^2 t^2}\psi _{3;\rho }^{||}(u) \nonumber \\&\qquad -\frac{if_\rho ^\perp m_s u (v\cdot q)^2}{12\pi ^2 t^2}\phi _{2;\rho }^\perp (u)+\frac{i f_\rho ^{||} m_\rho u (v\cdot q)^2}{24\pi ^2 t^2}\psi _{3;\rho }^\perp (u)\nonumber \\&\qquad +\frac{f_\rho ^\perp m_\rho ^2}{36 t v\cdot q}\langle {\bar{s}} s\rangle \phi _{2;\rho }^\perp (u)-\frac{f_\rho ^\perp m_\rho ^2}{36 v\cdot q}\langle {\bar{s}} s\rangle \psi _{4;\rho }^\perp (u) \nonumber \\&\qquad -\frac{i f_\rho ^{||}m_s m_\rho ^3}{288(v\cdot q)^2}\langle {\bar{s}} s\rangle \phi _{2;\rho }^{||}(u)+\frac{i f_\rho ^{||}m_s m_\rho ^3}{144(v\cdot q)^2}\langle {\bar{s}} s\rangle \phi _{3;\rho }^\perp (u)\nonumber \\&\qquad -\frac{i f_\rho ^{||} m_s m_\rho ^3}{288(v\cdot q)^2}\psi _{4;\rho }^{||}(u)+\frac{i f_\rho ^{||} m_s m_\rho }{144}\langle {\bar{s}} s\rangle \phi _{2;\rho }^{||}(u) \nonumber \\&\qquad -\frac{i f_\rho ^{||}m_s m_\rho }{36}\langle {\bar{s}} s\rangle \phi _{3;\rho }^\perp (u)-\frac{i f_\rho ^\perp m_\rho ^2}{72}\langle {\bar{s}} s\rangle \psi _{3;\rho }^{||}(u)\nonumber \\&\qquad -\frac{i f_\rho ^\perp u(v\cdot q)^2}{36}\langle {\bar{s}} s\rangle \phi _{2;\rho }^\perp (u)-\frac{i f_\rho ^\perp m_s m_\rho ^2 u(v\cdot q)^2}{192\pi ^2}\phi _{4;\rho }^\perp (u) \nonumber \\&\qquad +\frac{f_\rho ^\perp m_\rho ^2 t}{576 v\cdot q}\langle g_s{\bar{s}} \sigma G s\rangle \phi _{2;\rho }^\perp (u)-\frac{f_\rho ^\perp m_\rho ^2 t}{576 v\cdot q}\langle g_s{\bar{s}} \sigma G s\rangle \psi _{4;\rho }^\perp (u)\nonumber \\&\qquad -\frac{f_\rho ^{||} m_s m_\rho t v\cdot q}{288}\langle {\bar{s}} s\rangle \psi _{3;\rho }^\perp (u)+\frac{i f_\rho ^{||} m_s m_\rho ^3 t^2}{2304}\langle {\bar{s}} s\rangle \phi _{4;\rho }^{||}(u) \nonumber \\&\qquad -\frac{i f_\rho ^\perp m_\rho ^2 t^2}{1152}\langle g_s{\bar{s}} \sigma G s\rangle \psi _{3;\rho }^{||}(u)\nonumber \\&\qquad -\frac{i f_\rho ^\perp u t^2 (v\cdot q)^2}{576}\langle g_s{\bar{s}} \sigma G s\rangle \phi _{2;\rho }^\perp (u)\nonumber \\&\qquad -\frac{i f_\rho ^\perp m_\rho ^2 u t^2(v\cdot q)^2}{576}\langle {\bar{s}} s\rangle \phi _{4;\rho }^\perp (u) \nonumber \\&\qquad +\frac{i f_\rho ^{||}m_s m_\rho u t^2(v\cdot q)^2}{576}\langle {\bar{s}} s\rangle \psi _{3;\rho }^\perp (u)\nonumber \\&\qquad +\frac{f_\rho ^\perp m_\rho ^2 t^3 v\cdot q}{2304}\langle g_s{\bar{s}} \sigma G s\rangle \phi _{4;\rho }^\perp (u)\nonumber \\&\qquad -\frac{i f_\rho ^\perp m_\rho ^2 u t^4(v\cdot q)^2}{9216}\langle g_s{\bar{s}} \sigma G s\rangle \phi _{4;\rho }^\perp (u)\Bigg ) \nonumber \\&\qquad -\int _0^\infty dt \int _0^1 du \int {\mathscr {D}}{\underline{\alpha }}e^{i\omega ^\prime t(\alpha _2+u\alpha _3)}e^{i\omega t(1-\alpha _2-u\alpha _3)}\nonumber \\&\qquad \times {1\over 2}\times \Bigg (-\frac{i f_\rho ^{||} m_\rho ^3}{24 t^2}\varPsi _{4;\rho }^{||}({\underline{\alpha }})+\frac{i f_\rho ^{||} m_\rho ^3}{24\pi ^2 t^2}{\widetilde{\varPsi }}_{4;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{i f_\rho ^{||}m_\rho ^3 u}{12\pi ^2 t^2}\varPsi _{4;\rho }^{||}({\underline{\alpha }})-\frac{i f_\rho ^{||} m_\rho (v\cdot q)^2}{12\pi ^2 t^2}\varPhi _{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad -\frac{i f_\rho ^{||} m_\rho (v\cdot q)^2}{12\pi ^2 t^2}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad +\frac{i f_\rho ^{||}m_\rho u (v\cdot q)^2}{12\pi ^2 t^2}\varPhi _{3;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad +\frac{i f_\rho ^{||} m_\rho u (v\cdot q)^2}{12\pi ^2 t^2}{\widetilde{\varPhi }}_{3;\rho }^{||}({\underline{\alpha }})+\frac{f_\rho ^{||} m_\rho u (v\cdot q)^3}{12\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_\rho ^{||} m_\rho u (v\cdot q)^3}{12\pi ^2 t}{\widetilde{\varPhi }}_{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_\rho ^{||} m_\rho u\alpha _2(v\cdot q)^3}{12\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_\rho ^{||} m_\rho u\alpha _2(v\cdot q)^3}{12\pi ^2 t}{\widetilde{\varPhi }}_{3;\rho }^{||}({\underline{\alpha }})-\frac{f_\rho ^{||} m_\rho u^2 \alpha _3(v\cdot q)^3}{12\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_\rho ^{||} m_\rho u^2\alpha _3(v\cdot q)^3}{12\pi ^2 t}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }})\Bigg ) . \end{aligned}$$

(B.5)

The sum rule for $\varXi _b^{\prime -}[{1\over 2}^-]$ belonging to $[\mathbf {6}_F, 1, 0, \rho ]$ is

$$\begin{aligned}&G_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varSigma _b^0 K^{*}} (\omega , \omega ^\prime ) = { g_{\varXi _b^{\prime -}[{1\over 2}^-] \rightarrow \varSigma _b^0 K^{*}} f_{\varXi _b^{\prime -}[{1\over 2}^-]} f_{\varSigma _b^0} \over ({\bar{\varLambda }}_{\varXi _b^{\prime -}[{1\over 2}^-]} - \omega ^\prime ) ({\bar{\varLambda }}_{\varSigma _b^0} - \omega )} \nonumber \\&\quad = \int _0^\infty dt \int _0^1 du e^{i(1-u)\omega ^\prime t}e^{iu\omega t}\times 4\nonumber \\&\qquad \times \Bigg (\frac{i f_{K^*}^\perp v\cdot q}{2\pi ^2 t^4}\phi _{2;K^*}^\perp (u)-\frac{i f_{k^*}^\perp m_{K^*}^2}{2\pi ^2 t^4 v\cdot q}\phi _{2;K^*}^\perp (u) \nonumber \\&\qquad +\frac{i f_{K^*}^\perp m_{K^*}^2}{2\pi ^2 t^4 v\cdot q}\psi _{4;K^*}^\perp (u)-\frac{f_{K^*}^\perp u(v\cdot q)^2}{4\pi ^2 t^3}\phi _{2;K^*}^\perp (u)\nonumber \\&\qquad +\frac{if_{K^*}^\perp m_{K^*}^2 v\cdot q}{32\pi ^2 t^2}\phi _{4;K^*}^\perp (u)-\frac{f_{K^*}^\perp m_{K^*}^2 u(v\cdot q)^2}{64\pi ^2 t}\phi _{4;K^*}^\perp (u) \nonumber \\&\qquad -\frac{i f_{K^*}^{||} m_{K^*} v\cdot q}{48}\langle {\bar{q}} q\rangle \psi _{3;K^*}^\perp (u)\nonumber \\&\qquad -\frac{f_{K^*}^{||} m_{K^*} u t(v\cdot q)^2}{96}\langle {\bar{q}} q\rangle \psi _{3;K^*}^\perp (u)\nonumber \\&\qquad -\frac{i f_{K^*}^{||}m_{K^*} t^2 v\cdot q}{768}\langle g_s{\bar{q}} \sigma G q\rangle \psi _{3;K^*}^\perp (u) \nonumber \\&\qquad -\frac{f_{K^*}^{||} m_{K^*} u t^3(v\cdot q)^2}{1536}\langle g_s{\bar{q}}\sigma G q\rangle \psi _{3;K^*}^\perp (u)\Bigg ) \nonumber \\&\qquad -\int _0^\infty dt \int _0^1 du \int {\mathscr {D}}{\underline{\alpha }}e^{i\omega ^\prime t(\alpha _2+u \alpha _3)}e^{i\omega t(1-\alpha _2-u \alpha _3)}\nonumber \\&\qquad \times {1\over 2}\Bigg (-\frac{if_{K^*}^\perp v\cdot q}{8\pi ^2 t^2}\varPhi _{4;K^*}^{\perp (1)}({\underline{\alpha }})+\frac{i f_{K^*}^\perp v\cdot q}{8\pi ^2 t^2}\varPhi _{4;K^*}^{\perp (2)}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{i f_{K^*}^\perp m_{K^*}^2 v\cdot q}{4\pi ^2 t^2}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }})+\frac{i f_{K^*}^\perp m_{K^*}^2 v\cdot q}{4\pi ^2 t^2}\varPhi _{4;K^*}^{\perp (4)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{i f_{K^*}^\perp m_{K^*}^2 v\cdot q}{8\pi ^2 t^2}{{\widetilde{\varPsi }}}_{4;k^*}^\perp ({\underline{\alpha }})+\frac{i f_{K^*}m_{K^*}^2 v\cdot q}{8\pi ^2 t^2}\varPsi _{4;K^*}^\perp ({\underline{\alpha }}) \nonumber \\&\qquad +\frac{i f_{K^*}^\perp m_{K^*}^2 u v\cdot q}{8\pi ^2 t^2}\varPhi _{4;K^*}^{\perp (1)}({\underline{\alpha }})-\frac{i f_{K^*}^\perp u v\cdot q}{8\pi ^2 t^2}\varPhi _{4;K^*}^{\perp (2)}({\underline{\alpha }})\nonumber \\&\qquad -\frac{i f_{K^*} m_{K^*}^2 u v\cdot q}{4\pi ^2 t^2}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }})+\frac{f_{K^*} m_{K^*}^2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (1)}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (2)}({\underline{\alpha }})-\frac{f_{K^*}^\perp m_{K^*}^2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (4)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2(v\cdot q)^2}{16\pi ^2 t}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2(v\cdot q)^2}{16\pi ^2 t}\varPsi _{4;K^*}^\perp ({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2(v\cdot q)^2}{8\pi ^2 t}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u (v\cdot q)^2}{8\pi ^2 t}\varPhi _{4;K^*}^{\perp (4)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u(v\cdot q)^2}{8\pi ^2 t}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 \alpha _2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (1)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 \alpha _2 (v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (2)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 \alpha _2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2\alpha _2(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (4)}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2\alpha _2(v\cdot q)^2}{16\pi ^2 t}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 \alpha _2(v\cdot q)^2}{16\pi ^2 t}\varPsi _{4;K^*}^\perp ({\underline{\alpha }}) \nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _2(v\cdot q)^2}{8\pi ^2 t}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _2(v\cdot q)^2}{8\pi ^2 t}\varPhi _{4;K^*}^{\perp (4)}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _2(v\cdot q)^2}{8\pi ^2 t}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }}) \nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u^2\alpha _3(v\cdot q)^2}{8\pi ^2 t}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u^2\alpha _3(v\cdot q)^2}{8\pi ^2 t}\varPhi _{4;K^*}^{\perp (4)}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u^2\alpha _3(v\cdot q)^2}{8\pi ^2}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _3(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (1)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _3(v\cdot q)^2}{16\pi ^2}\varPhi _{4;K^*}^{\perp (2)}({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _3(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (3)}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _3(v\cdot q)^2}{16\pi ^2 t}\varPhi _{4;K^*}^{\perp (4)}\nonumber \\&\qquad -\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _3(v\cdot q)^2}{16\pi ^2 t}{\widetilde{\varPsi }}_{4;K^*}^\perp ({\underline{\alpha }})\nonumber \\&\qquad +\frac{f_{K^*}^\perp m_{K^*}^2 u\alpha _3(v\cdot q)^2}{16\pi ^2 t}\varPsi _{4;K^*}^\perp ({\underline{\alpha }})\Bigg ). \end{aligned}$$

(B.6)

The sum rule for $\varSigma _b^-[{1\over 2}^-]$ belonging to $[\mathbf {6}_F, 1, 1, \lambda ]$ is

$$\begin{aligned}&G_{\varSigma _b^-[{1\over 2}^-] \rightarrow \varSigma _b^0\rho ^-} (\omega , \omega ^\prime ) = { g_{\varSigma _b^-{1\over 2}^-] \rightarrow \varSigma _b^0\rho ^-} f_{\varSigma _b^-[{1\over 2}^-]} f_{\varSigma _b^0} \over ({\bar{\varLambda }}_{\varSigma _b^-[{1\over 2}^-]} - \omega ^\prime ) ({\bar{\varLambda }}_{\varSigma _b^0} - \omega )} \nonumber \\&\quad = \int _0^\infty dt \int _0^1 du e^{i (1-u) \omega ^\prime t} e^{i u \omega t} \times 8\nonumber \\&\qquad \times \Bigg (-\frac{f_\rho ^{||} m_\rho }{2\pi ^2 t^4}\phi _{2;\rho }^{||}(u)-\frac{f_\rho ^{||} m_\rho }{2\pi ^2 t^4}\phi _{3;\rho }^\perp (u) \nonumber \\&\qquad +\frac{f_\rho ^{||} m_\rho ^3}{4\pi ^2 t^4(v\cdot q)^2}\phi _{2;\rho }^{||}(u)-\frac{f_\rho ^{||} m_\rho ^3}{2\pi ^2 t^4(v\cdot q)^2}\phi _{3;\rho }^\perp (u)\nonumber \\&\qquad +\frac{f_\rho ^{||} m_\rho ^3}{4\pi ^2 t^2(v\cdot q)^2}\psi _{4;\rho }^{||}(u)-\frac{if_\rho ^{||} m_\rho v\cdot q}{8\pi ^2 t^3}\psi _{3;\rho }^\perp (u) \nonumber \\&\qquad -\frac{f_\rho ^{||} m_\rho u(v\cdot q)^2}{16\pi ^2 t^2}\psi _{3;\rho }^\perp (u)-\frac{f_\rho ^{||} m_\rho ^3}{32\pi ^2 t^2}\phi _{4;\rho }^{||}(u)\nonumber \\&\qquad +\frac{if_\rho ^\perp m_\rho ^2}{24 t v\cdot q}\langle {\bar{q}} q\rangle \phi _{2;\rho }^\perp (u)-\frac{if_\rho ^\perp m_\rho ^2}{24 t v\cdot q}\langle {\bar{q}} q\rangle \psi _{4;\rho }^\perp (u) \nonumber \\&\qquad +\frac{f_\rho ^\perp u(v\cdot q)^2}{24}\langle {\bar{q}} q\rangle \phi _{2;\rho }^\perp (u)+\frac{f_\rho ^\perp m_\rho ^2}{24}\langle {\bar{q}} q\rangle \psi _{3;\rho }^{||}(u)\nonumber \\&\qquad +\frac{if_\rho ^\perp m_\rho ^2 t}{384 v\cdot q}\langle g_s{\bar{q}} \sigma G q\rangle \phi _{2;\rho }^\perp (u)-\frac{if_\rho ^\perp m_\rho ^2 t}{384 v\cdot q}\langle g_s{\bar{q}} \sigma G q\rangle \psi _{4;\rho }^\perp (u) \nonumber \\&\qquad +\frac{f_\rho ^\perp u t^2(v\cdot q)^2}{384}\langle g_s{\bar{q}} \sigma G q\rangle \phi _{2;\rho }^\perp (u)\nonumber \\&\qquad +\frac{f_\rho ^\perp m_\rho ^2 u t^2(v\cdot q)^2}{384}\langle {\bar{q}} q\rangle \phi _{4;\rho }^\perp (u)+\frac{f_\rho ^\perp m_\rho ^2 t^2}{384}\langle g_s{\bar{q}} \sigma G q\rangle \psi _{3;\rho }^{||}(u) \nonumber \\&\qquad +\frac{f_\rho ^\perp m_\rho ^2 u t^4 (v\cdot q)^2}{6144}\langle g_s{\bar{q}} \sigma G q\rangle \phi _{4;\rho }^\perp (u)\Bigg ) \nonumber \\&\qquad -\int _0^\infty dt \int _0^1 du\int {\mathscr {D}}{\underline{\alpha }}e^{i\omega ^\prime t(\alpha _2+u\alpha _3)}e^{i\omega t(1-\alpha _2-u\alpha _3)}\nonumber \\&\qquad \times \Bigg (\frac{f_\rho ^{||} m_\rho ^3}{8\pi ^2 t^2}\varPhi _{4;\rho }^{||}({\underline{\alpha }}) -\frac{f_\rho ^{||} m_\rho ^3}{8\pi ^2 t^2}{{\widetilde{\varPhi }}}_{4;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad +\frac{f_\rho ^{||} m_\rho ^3 u}{4\pi ^2 t^2}\varPhi _{4;\rho }^{||}({\underline{\alpha }})-\frac{f_\rho ^{||} m_\rho (v\cdot q)^2}{8\pi ^2 t^2}\varPhi _{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad -\frac{f_\rho ^{||} m_\rho (v\cdot q)^2}{8\pi ^2 t^2}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad +\frac{3f_\rho ^{||} m_\rho u(v\cdot q)^2}{8\pi ^2 t^2}\varPhi _{3;\rho }^{||}({\underline{\alpha }})-\frac{f_\rho ^{||} m_\rho u (v\cdot q)^2}{8\pi ^2 t^2}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad -\frac{i f_\rho ^{||} m_\rho (v\cdot q)^3}{8\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad +\frac{if_\rho ^{||} m_\rho \alpha _2(v\cdot q)^3}{8\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }})-\frac{if_\rho ^{||}m_\rho \alpha _2(v\cdot q)^3}{8\pi ^2 t}{{\widetilde{\varPhi }}}-{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad +\frac{if_\rho ^{||} m_\rho u\alpha _2(v\cdot q)^3}{8\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad -\frac{i f_\rho ^{||} m_\rho u \alpha _2(v\cdot q)3}{8\pi ^2 t}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }})+\frac{if_\rho ^{||} m_\rho u^2\alpha _3(v\cdot q)^3}{8\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }})\nonumber \\&\qquad -\frac{i f_\rho ^{||} m_\rho u^2\alpha _3(v\cdot q)^3}{8\pi ^2 t}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }}) \nonumber \\&\qquad +\frac{if_\rho ^{||} m_\rho u\alpha _3(v\cdot q)^3}{8\pi ^2 t}\varPhi _{3;\rho }^{||}({\underline{\alpha }})-\frac{if_\rho ^{||} m_\rho u\alpha _3(v\cdot q)^3}{8\pi ^2 t}{{\widetilde{\varPhi }}}_{3;\rho }^{||}({\underline{\alpha }})\Bigg ) .\nonumber \\ \end{aligned}$$

(B.7)

The sum rule for $\varOmega _b^-[{1\over 2}^-]$ belonging to $[\mathbf {6}_F, 2, 1, \lambda ]$ is

$$\begin{aligned} G_{\varOmega _b^-[{1\over 2}^-] \rightarrow \varXi _b^{0}K^*} (\omega , \omega ^\prime )= & {} { g_{\varOmega _b^-[{1\over 2}^-] \rightarrow \varXi _b^0K^*} f_{\varOmega _b^-[{1\over 2}^-]} f_{\varXi _b^0} \over ({\bar{\varLambda }}_{\varOmega _b^-[{1\over 2}^-]} - \omega ^\prime ) ({\bar{\varLambda }}_{\varXi _b^0} - \omega )}\nonumber \\= & {} 0 .\nonumber \\ \end{aligned}$$

(B.8)