Transverse momentum and process dependent azimuthal anisotropies in $\sqrt{s_{\mathrm {NN}}}=8.16$ TeV p+Pb collisions with the ATLAS detector

Abstract

The azimuthal anisotropy of charged particles produced in $\sqrt{s_{\mathrm {NN}}}=8.16$ TeV p+Pb collisions is measured with the ATLAS detector at the LHC. The data correspond to an integrated luminosity of 165 $\mathrm {nb}^{-1}$ that was collected in 2016. Azimuthal anisotropy coefficients, elliptic $v_2$ and triangular $v_3$, extracted using two-particle correlations with a non-flow template fit procedure, are presented as a function of particle transverse momentum ($p_\mathrm {T}$) between 0.5 and 50 GeV. The $v_2$ results are also reported as a function of centrality in three different particle $p_\mathrm {T}$ intervals. The results are reported from minimum-bias events and jet-triggered events, where two jet $p_\mathrm {T}$ thresholds are used. The anisotropies for particles with $p_\mathrm {T}$ less than about 2 GeV are consistent with hydrodynamic flow expectations, while the significant non-zero anisotropies for $p_\mathrm {T}$ in the range 9–50 GeV are not explained within current theoretical frameworks. In the $p_\mathrm {T}$ range 2–9 GeV, the anisotropies are larger in minimum-bias than in jet-triggered events. Possible origins of these effects, such as the changing admixture of particles from hard scattering and the underlying event, are discussed.

1 Introduction

The collisions of heavy nuclei at relativistic speeds generate hot and dense droplets of matter composed of deconfined quarks and gluons known as the quark–gluon plasma (QGP) [1, 2]. Studies of the QGP at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) have yielded a wealth of surprising results that reveal a complex set of QGP-related phenomena. Bulk hadron production, occurring mainly at low transverse momentum ($p_{\text {T}} \lesssim 3$ $\text {Ge}\text {V}$), exhibits significant azimuthal anisotropies that are well described in terms of nearly inviscid hydrodynamic flow of the QGP [1]. The final hadron momentum anisotropies arise from inhomogeneities in the initial spatial distribution of the QGP translated to momentum space via strong differential pressure gradients. These anisotropies are characterised in terms of a Fourier decomposition:

$$\begin{aligned} Y(\phi ) = G\Big [1 + 2\sum ^{\infty }_{n=1} v_{n} \cos (n(\phi -\Psi _{n}))\Big ], \end{aligned}$$

where $v_{n}$ are the anisotropy coefficients, $\Psi _{n}$ is the $n^\mathrm {th}$-order orientation of the anisotropy, and the normalization, G, is set by the integral of the distribution. In particular, $v_{2}$ and $v_{3}$ are referred to as the elliptic and triangular coefficients, respectively.

In addition, the production of high transverse momentum hadrons ($p_{\text {T}} \gtrsim 10$ $\text {Ge}\text {V}$) is highly suppressed relative to the yields expected from nuclear thickness scaling of proton–proton collision yields [3]. This suppression is understood to result from high momentum transfer parton–parton interactions followed by the outgoing partons losing energy via radiative and collisional processes in the QGP – processes referred to as jet quenching [4,5,6]. These high-$p_{\text {T}}$ hadrons and associated jets are also observed to have a non-zero azimuthal anisotropy [7,8,9], despite being well outside the nominal domain where the anisotropies are interpreted in terms of hydrodynamic flow. Instead, these anisotropies are understood to also arise from inhomogeneities in the initial spatial distribution of the QGP, but in this case, where the jet quenching effect is stronger for partons traversing longer paths through the QGP and weaker for partons traversing shorter paths [10]. In this way, low- and high-$p_{\text {T}}$ hadrons have a common orientation of their azimuthal anisotropy in a given event, because both are correlated with the orientation of the initial geometry of the colliding nucleons. It is notable that, for more than a decade, an outstanding and challenging theoretical puzzle has been how to quantitatively describe both high-$p_{\text {T}}$ hadron suppression and azimuthal anisotropy in Pb+Pb collisions [11]. There are a number of proposed explanations for resolving this puzzle in heavy-ion collisions – see Refs. [12,13,14,15,16,17] for examples.

Measurements in smaller collision systems, $pp$ and $p$+Pb collisions at the LHC [18,19,20,21,22,23] and $p$+Au, $d$+Au, and ${}^{3}$He+Au at RHIC [24], indicate significant azimuthal anisotropies for low-$p_{\text {T}}$ hadrons with patterns quite similar to those observed in the larger heavy-ion collision systems. For a recent review see Ref. [25]. These observations have raised the question of whether smaller and shorter-lived droplets of QGP are formed in these smaller collision systems. Indeed, models employing nearly inviscid hydrodynamics for the QGP provide a quantitative description of this large body of data at low $p_{\text {T}}$ [26].

In contrast, measurements aimed at observing signatures of jet quenching in small collision systems have found no such effect. Measurements of hadron and jet $p_{\text {T}}$ spectra at high $p_{\text {T}}$ indicate production yields consistent with those in $pp$ collisions scaled up by the expected nuclear thickness in $p$+Pb [27,28,29] and d+Au collisions [30], and that the $p_{\text {T}}$-balance between dijets or hadron–jet pairs is unmodified in $p$+Pb collisions within uncertainties [31, 32]. The ATLAS experiment has also published results for the hadron azimuthal anisotropy up to $p_{\text {T}} \approx 12$ $\text {Ge}\text {V}$ that hint at a non-zero anisotropy extending into the region beyond the usual hydrodynamic interpretation and into the regime of jet quenching [33]. However, it is unlikely that there can be differential jet quenching as a function of orientation relative to the QGP geometry if there is no jet quenching in $p$+Pb collisions as observed in the spectra. Thus, there are two related outstanding puzzles, one being the lack of jet quenching observed in the spectra, if indeed small droplets of QGP are formed, and the other being what mechanism can lead to high-$p_{\text {T}}$ hadron anisotropies other than differential jet quenching.

This paper presents a measurement of the azimuthal anisotropy of unidentified hadrons as a function of $p_{\text {T}}$ and centrality in $\sqrt{s_{_\text {NN}}} = 8.16$ $\text {Te}\text {V}$ $p$+Pb collisions with the ATLAS detector. The measurement is made using two-particle correlations, measured separately for minimum-bias triggered (MBT) events and events requiring a jet with $p_{\text {T}}$ greater than either 75 $\text {Ge}\text {V}$ or 100 $\text {Ge}\text {V}$. There are contributions to the azimuthal correlations from particle decays, jets, dijets, and global momentum conservation, which have traditionally been referred to as ‘non-flow’ [34]. Using this nomenclature, a standard template fitting procedure is applied to subtract non-flow contributions [19, 20]. To decrease the residual influence of the non-flow correlation in the jet events, a novel procedure is used to restrict the acceptance of particles according to the location of jets in the event. Assuming that the two-particle anisotropy coefficients are the products of the corresponding single-particle coefficients (factorisation), the elliptic and triangular anisotropy coefficients, $v_{2}$ and $v_{3}$, are reported as a function of $p_{\text {T}}$. Additionally, $v_{2}$ results are presented as a function of centrality in three different $p_{\text {T}}$ ranges. Finally, the fractional contribution to the correlation functions from jet particles is determined as a function of $p_{\text {T}}$.

2 ATLAS detector

The ATLAS experiment [35] at the LHC is a multipurpose particle detector with a forward–backward symmetric cylindrical geometry and nearly $4\pi$ coverage.¹ This analysis relies on the inner detector, the calorimeter, and the data acquisition and trigger system.

The inner detector (ID) comprises three major subsystems: the pixel detector and the silicon microstrip tracker, which extend up to $\left| \eta \right| = 2.5$, and the transition radiation tracker, which extends to $\left| \eta \right| = 2.0$. The inner detector covers the full azimuth and is immersed in a 2 T axial magnetic field. The pixel detector consists of four cylindrical layers in the barrel region and three discs in each endcap region. A new innermost layer, the insertable B-layer [36, 37], has been operating as a part of the pixel detector since 2015. The silicon microstrip tracker comprises four cylindrical layers (nine discs) of silicon strip detectors in the barrel (endcap) region. The minimum-bias trigger scintillator detects charged particles over $2.07<|\eta |<3.86$ using two hodoscopes of 12 counters positioned at $|z|=3.6$ m.

The calorimeter is a large-acceptance, longitudinally segmented sampling detector covering $\left| \eta \right| < 4.9$ with electromagnetic (EM) and hadronic sections. The EM calorimeter is a lead/liquid-argon sampling calorimeter with an accordion-shaped geometry. It is divided into a barrel region, covering $\left| \eta \right| < 1.475$, and two endcap regions, covering $1.375< \left| \eta \right| < 3.2$. The hadronic calorimeter surrounds the EM calorimeter. It consists of a steel/scintillator-tile sampling calorimeter covering $\left| \eta \right| < 1.7$ and a liquid-argon calorimeter with copper absorber covering $1.5< \left| \eta \right| < 3.2$. The forward calorimeter (FCal) is a liquid-argon sampling calorimeter located on either side of the interaction point. It covers $3.1< \left| \eta \right| < 4.9$ and each half is composed of one EM and two hadronic sections, with copper and tungsten serving as the absorber material, respectively. The FCal is used to characterise the centrality of p+Pb collisions as described below.

In this analysis, a two-level trigger system was used to select events, with a first-level (L1) trigger implemented in hardware followed by a software-based high-level trigger (HLT) which reconstructs the event in a manner similar to the final offline reconstruction. Events used for the measurements presented in this paper were selected using several triggers. MBT events were selected by a trigger that requires a signal in at least one minimum-bias trigger scintillator counter at L1 [38] followed by the requirement of at least one reconstructed track at the HLT stage. Events with a high-$p_\mathrm {T}$ jet were acquired using a high-level jet trigger covering the central region ($\left| \eta \right| < 3.2$). These events were first required to have energy deposits at L1 that are compatible with the presence of a jet and then to pass various thresholds for the jet transverse energy at the HLT stage.

3 Data and event selection

During p+Pb data-taking in 2016, the LHC was configured with a beam composed of protons with an energy of 6.5 $\text {Te}\text {V}$ and a beam of lead ions with an energy per nucleon of 2.51 $\text {Te}\text {V}$. This resulted in a collision system with proton–nucleon centre-of-mass energy $\sqrt{s_{_\text {NN}}} = 8.16~\text {Te}\text {V}$ and a rapidity shift of the centre of mass by +0.465 units in the proton-going direction relative to the laboratory frame. The data were taken over two running periods with different configurations of the LHC beam directions. In the first period of data-taking, comprising a total integrated luminosity of 57 $\mathrm {nb}^{-1}$, the lead ions circulated clockwise in beam 1, while the protons circulated counterclockwise in beam 2. For the second period of data-taking, which comprised 108 $\mathrm {nb}^{-1}$, the beam species were interchanged. The analysed data were provided by the minimum-bias trigger described above, which was prescaled and sampled 0.079 $\mathrm {nb}^{-1}$ of luminosity. In addition, data were selected by the high-level jet triggers with transverse energy thresholds of 75 $\text {Ge}\text {V}$ and 100 $\text {Ge}\text {V}$, which sampled 26 $\mathrm {nb}^{-1}$ and the full 165 $\mathrm {nb}^{-1}$ of $p$+Pb luminosity, respectively.

Events selected by the triggers described above were reconstructed offline following procedures that were optimised for the Run-2 detector configuration [39]. Events are required to have at least one reconstructed vertex. To reduce the contribution from events with multiple in-time $p$+Pb interactions, events with more than one vertex are used only if the additional vertices have fewer than seven associated reconstructed tracks with $p_{\text {T}} > 0.4$ $\text {Ge}\text {V}$. That is, events are only allowed to have one vertex with seven or more associated tracks. Two classes of jet events were defined by requiring an offline jet with $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ or $p_{\text {T}} >100$ $\text {Ge}\text {V}$ respectively, and were drawn from the jet-triggered event samples with the analogous online thresholds. The trigger efficiency, given this offline selection, was greater than 97% for both jet samples.

Events were further characterised by the sum of the transverse energy in the FCal module in the direction of the Pb beam, $\Sigma E_{\text {T}}^\mathrm{{Pb}}$. The event centrality is defined as the $\Sigma E_{\text {T}}^\mathrm{{Pb}}$ percentile of the events in minimum-bias collisions, after accounting for the inefficiency introduced by the trigger and event selection criteria, and was determined in a way similar to previous analyses of Run-1 p+Pb data at $\sqrt{s_{_\text {NN}}} = 5.02~\text {Te}\text {V}$ [27, 40]. Events within the 0–90% centrality range were used in this analysis, with low (high) values corresponding to high-$\Sigma E_{\text {T}}^\mathrm{{Pb}}$ (low-$\Sigma E_{\text {T}}^\mathrm{{Pb}}$) events with large (small) overall particle multiplicity. Since the acceptance of the FCal is separate from that of the ID, this centrality definition has the benefit of reducing event-selection-induced biases in the measured quantities [41].

4 Track and jet reconstruction

The reconstruction, selection, and calibration of charged-particle tracks and calorimetric jets, and their performance as determined using Monte Carlo (MC) simulations, are described below.

Charged-particle tracks and collision vertices are reconstructed in the ID using the algorithms described in Ref. [39]. Inner detector tracks with $p_{\text {T}} >0.4$ $\text {Ge}\text {V}$ and $|\eta |<2.5$ were required to satisfy a set of quality criteria similar to those described in Ref. [19]. The total number of reconstructed ID tracks satisfying these selection criteria in a given event is called the multiplicity or $N_{\mathrm {ch}}^{\mathrm {rec}}$. The reconstruction and selection efficiency for primary [42] charged hadrons to meet these criteria was determined using a sample of 3 million minimum-bias p+Pb events simulated by the Hijing generator [43]. Events were generated with both beam configurations. The ATLAS detector response to the generated events was determined through a full Geant 4 simulation [44, 45], and the simulated events were reconstructed in the same way as the data. Over the measured kinematic range, the efficiency varies from approximately $50\%$ for the lowest-$p_{\text {T}}$ hadrons at large pseudorapidity, to greater than $90\%$ for hadrons with $p_{\text {T}} > 3$ $\text {Ge}\text {V}$ at mid-rapidity.

Jets are reconstructed using energy deposits in the calorimeter system, $\left| \eta \right| < 4.9$, in a range partially overlapping with both the ID and the FCal used to determine centrality. The reconstruction closely follows the procedure used in other measurements for Pb+Pb and pp collisions [46, 47]. Jets are measured by applying the anti-$k_t$ algorithm [48, 49] with radius parameter $R=0.4$ to energy deposits in the calorimeter. No jets with $p_{\text {T}} <15$ $\text {Ge}\text {V}$ are considered. An iterative procedure is used to obtain an event-by-event estimate of the $\eta$-dependent underlying-event energy density, while excluding jets from that estimate. The jet kinematics are corrected for this background and for the detector response using an $\eta$- and $p_{\text {T}}$-dependent calibration derived from fully simulated and reconstructed Pythia 8 [50] hard-scattering events configured with the NNPDF23LO parton distribution function set [51] and the A14 set of tuned parameters [52] to model non-perturbative effects. An additional, small correction, based on in situ studies of jets recoiling against photons, Z bosons, and jets in other regions of the calorimeter, is applied [53, 54]. Simulation studies show that for jets with $p_{\text {T}} > 75$ $\text {Ge}\text {V}$, the average reconstructed jet $p_{\text {T}}$ is within 1% of the generator level jet $p_{\text {T}}$ and has a relative $p_{\text {T}}$ resolution below 10% after the calibration procedure.

5 Analysis procedure

This analysis is based on previous ATLAS two-particle correlation studies [19, 20]. To construct the two-particle correlation functions, the selected inner-detector tracks with $p_{\text {T}} > 0.4$ $\text {Ge}\text {V}$ are divided into two sets, referred to as A- and B-particles in this paper, although they are sometimes referred to as trigger and associated particles in the literature. To reduce the contribution of non-flow correlations from decays and jets, two restrictions are placed on A–B particle pairs drawn from the two sets. First, as was done in previous analyses [19, 20], the particles are required to be separated in pseudorapidity with $|\Delta \eta ^\mathrm {AB}| = |\eta ^\mathrm {B}-\eta ^\mathrm {A}| > 2$. This requirement removes the short-range decay and jet fragmentation structure, while emphasising global, early-time correlations. Due to the enhanced contribution from jet correlations in the jet-triggered events, an additional constraint was developed for this analysis. Namely, B-particles are required to be separated in pseudorapidity by one unit from all reconstructed jets with $p_{\text {T}} ^{\mathrm {jet}}>15$ $\text {Ge}\text {V}$, i.e. $|\Delta \eta ^{\mathrm {jB}}| = |\eta ^\mathrm {B}-\eta ^{\mathrm {jet}}| > 1$. This latter requirement is only applied to the jet-triggered events, and in this way, the jets act as a source of high-$p_{\text {T}}$ A-particles but contribute few B-particles.

The correlation functions, $S(\Delta \phi )$, are defined as the yields of particle pairs passing the above event and pair selection, binned in $\Delta \phi =\phi ^\mathrm {A}-\phi ^\mathrm {B}$, and normalised by the total number of A-particles. Corrections for the imperfect trigger and tracking efficiencies are applied as weights to the entries of the correlation functions. A mixed-event correction, $M(\Delta \phi )$, is generated by correlating A-particles from one event with B-particles from a different event with a vertex z-position differing by less than 10 mm and a number of reconstructed charged particles ($N_{\mathrm {ch}}^{\mathrm {rec}}$) differing by less than 10 for $N_{\mathrm {ch}}^{\mathrm {rec}}<100$ and less than 20 for $N_{\mathrm {ch}}^{\mathrm {rec}}> 100$. Thus, the mixed events contain only trivial detector acceptance effects and no physical correlations. To reduce the statistical uncertainty introduced by the correction, each event is mixed with five others meeting the above vertex z and $N_{\mathrm {ch}}^{\mathrm {rec}}$ conditions. The corrected correlation is, then, $Y(\Delta \phi )=S(\Delta \phi )/M(\Delta \phi )$, where $M(\Delta \phi )$ is normalised such that the ratio preserves the overall integral of $S(\Delta \phi )$. Jet events are mixed with other jet events, and the $|\Delta \eta ^{\mathrm {jB}}|$ condition is applied with respect to the jets in the A-particle event only. Thus, the B-particle acceptance is consistent between the same- and and mixed-event correlations.

To extract the anisotropy coefficients while accounting for residual non-flow, the ATLAS template fitting procedure, as used for previous results [19, 20], is applied to $Y(\Delta \phi )$. In this procedure, $Y(\Delta \phi )$ is found for two different selections of event activity quantified by centrality: a central selection, $Y^{\mathrm {cent}}(\Delta \phi )$, and a peripheral selection, $Y^{\mathrm {peri}}(\Delta \phi )$. In this analysis, the peripheral selection corresponds to the 60–90% centrality interval. Assuming that the shape of the non-flow correlation is independent of centrality, $Y^{\mathrm {cent}}(\Delta \phi )$ is expressed as

$$\begin{aligned} Y^\mathrm {cent}(\Delta \phi ) = FY^\mathrm {peri}(\Delta \phi ) + G\Big [1 + 2\sum ^{4}_{n=2} v_{n,n} \cos (n\Delta \phi ) \Big ]\,, \end{aligned}$$

(1)

where F and each $v_{n,n}$ are parameters of a global $\chi ^2$ fit, and G is fixed by the requirement that the integral of the fit model is that of $Y^\mathrm {cent}$. The parameter F allows for a linear scaling of the non-flow between the two centrality classes. The fit includes the fourth harmonic, $v_{4,4}$, but it is not presented in the results because it is statistically insignificant. The fit $\chi ^2$ function incorporates the statistical uncertainties from both $Y^{\mathrm {cent}}$ and the peripheral template, $Y^{\mathrm {peri}}$, although the examples shown in Figures 1 and 2 do not show the uncertainties of $Y^{\mathrm {peri}}$ for readability. The statistical uncertainties of the extracted $v_{n,n}$ parameters are returned from the MINUIT $\chi ^2$ minimiser [55], accounting for correlations between parameters.

Figure 1 shows an example of two template fits using jet-triggered events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$. The left plot shows the fit for correlations made without the B-particle jet rejection condition, and the right plot shows the same correlation, but with the condition $|\Delta \eta ^{\mathrm {jB}}| > 1$ applied. In this figure, $Y_N^\mathrm {ridge}$ represents the $N^{\mathrm {th}}$-order harmonic component of the fit. The left plot has a dominant non-flow contribution, and a distortion in the resulting subtracted distribution is observed near $\Delta \phi \approx \pi$. Removing much of the jet correlation in this way reduces the overall sensitivity to the template method assumption that the shape of the non-flow contribution is the same for the central and peripheral selections. However, violation of this assumption will introduce distortions that could potentially bias the harmonic coefficients. This is explicitly tested by varying the centrality selection of the peripheral template, as discussed further in Section 6. Two additional examples of template fits from the jet-triggered events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ and with the B-particle jet rejection are plotted in Figure 2. These show the behaviour of the template fits for high A-particle $p_{\text {T}}$.

Fig. 1

Template fitting output for events with jet $p_{\text {T}} >100$ $\text {Ge}\text {V}$. Both require $3.5<p_{\text {T}} ^\mathrm {A}<4.0~\text {Ge}\text {V}$ and are made with 60–90% peripheral selection and 0–5% central selection. The left plot is made with no selection on the B-particles and the right plot is made requiring the B-particles to have $|\Delta \eta ^{\mathrm {jB}}|>1$ relative to all jets with $p_{\text {T}} ^\mathrm {jet} > 15~\text {Ge}\text {V}$ in the event. In the upper panels, the open circles show the scaled and shifted peripheral template with uncertainties omitted, the closed circles show the central data, and the red line shows the fit (template and harmonic functions). The blue dashed line shows the second-order harmonic component, $Y_2^\mathrm {ridge}$, and the orange dotted line shows the third-order harmonic component, $Y_3^\mathrm {ridge}$ (the $n=2$ and $n=3$ contributions to the sum in Eq. 1, respectively). The lower panels show the difference between the central data and the peripheral template along with the second and third harmonic functions. The resulting $v_{2,2}$, $v_{3,3}$, and global fit $\chi ^2$/NDF values are reported in the legends. In these fits, NDF$=35$

Fig. 2

Template fitting output for events with jet $p_{\text {T}} >100$ $\text {Ge}\text {V}$ with 60–90% peripheral selection and 0–5% central selection. The left plot is made with $11<p_{\text {T}} ^\mathrm {A}<16~\text {Ge}\text {V}$ and the right plot with $16<p_{\text {T}} ^\mathrm {A}<100~\text {Ge}\text {V}$. In the upper panels, the open circles show the scaled and shifted peripheral template with uncertainties omitted, the closed circles show the central data, and the red line shows the fit (template and harmonic functions). The blue dashed line shows the second-order harmonic component, $Y_2^\mathrm {ridge}$, and the orange dotted line shows the third-order harmonic component, $Y_3^\mathrm {ridge}$ (the $n=2$ and $n=3$ contributions to the sum in Eq. 1, respectively). The lower panels show the difference between the central data and the peripheral template along with the second and third harmonic functions. The resulting $v_{2,2}$, $v_{3,3}$, and global fit $\chi ^2$/NDF values are reported in the legends. In these fits, NDF$=35$

If the particle momentum correlations originate from a global field, as is the case for collective expansion, the $v_{n,n}$ will factorise such that $v_{n,n}(p_{\text {T}} ^\mathrm {A},p_{\text {T}} ^\mathrm {B}) = v_n(p_{\text {T}} ^\mathrm {A})\cdot v_n(p_{\text {T}} ^\mathrm {B})$. By assuming this relation and making specific $p_{\text {T}}$ selections on A- and B-particles, the single-particle $v_n(p_{\text {T}} ^\mathrm {A})$ can be obtained from

$$\begin{aligned} v_n(p_{\text {T}} ^\mathrm {A})=v_{n,n}(p_{\text {T}} ^\mathrm {A},p_{\text {T}} ^\mathrm {B})/ \sqrt{v_{n,n}(p_{\text {T}} ^\mathrm {B},p_{\text {T}} ^\mathrm {B})}, \end{aligned}$$

where $v_{n,n}(p_{\text {T}} ^\mathrm {A},p_{\text {T}} ^\mathrm {B})$ is determined with A- and B-particles having $p_{\text {T}}$ in range $p_{\text {T}} ^\mathrm {A}$ and $p_{\text {T}} ^\mathrm {B}$, respectively, and $v_{n,n}(p_{\text {T}} ^\mathrm {B},p_{\text {T}} ^\mathrm {B})$ is determined with A- and B-particles both having $p_{\text {T}}$ in range $p_{\text {T}} ^\mathrm {B}$. In this analysis, this range is nominally $p_{\text {T}} ^\mathrm {B}>0.4$ $\text {Ge}\text {V}$, although the dependence of the extracted anisotropy on this choice is explored in Section 7.

The relative yield of particle pairs entering the correlation functions is estimated assuming a simple, two-component model of particle production. Particles are assumed to be produced either by hard scattering (HS) processes, such as jet production, or by soft underlying event (UE) processes. With this assumption, the correlation functions are constructed from pairs pulled from a mixture of the two sources. Particle pairs can be formed in the following four A–B combinations: UE–UE, UE–HS, HS–UE, and HS–HS. The event-by-event yields of the UE and HS processes are estimated by classifying the charged particles according to their azimuthal orientation relative to the leading jet or, in the case of MBT events that contain no jets with $p_{\text {T}} > 15$ $\text {Ge}\text {V}$ and $|\eta |<4.9$, relative to the leading hadron. The following regions are defined relative to this leading vector:

• towards: $(|\phi _\mathrm {B} - \phi _\mathrm {jet}| < \frac{\pi }{4}) \, \cup \, (|\phi _\mathrm {B} - \phi _\mathrm {jet}| > \frac{3\pi }{4})$

• transverse: $\frac{\pi }{4}< |\phi _\mathrm {B} - \phi _\mathrm {jet}| < \frac{3\pi }{4}$.

Then, assuming that HS particles are completely contained in the towards region and the UE particles are distributed uniformly in azimuth, the following relations are inferred:

$$\begin{aligned} N_\mathrm {UE}&= 2 N_\mathrm {trans},\\ N_\mathrm {HS}&= N_\mathrm {toward} - N_\mathrm {trans}, \end{aligned}$$

where $N_\mathrm {UE}$ and $N_\mathrm {HS}$ are the single-particle yields from UE and HS processes, respectively, and $N_\mathrm {trans}$ and $N_\mathrm {toward}$ are the particle yields in the transverse and toward regions, respectively. The quantities $N_\mathrm {UE}$ and $N_\mathrm {HS}$ are statistically determined from the event averaged $N_\mathrm {trans}$ and $N_\mathrm {toward}$ and are, thus, insensitive to event-by-event fluctuations. However, it is not possible to classify individual particles. It should be noted that the assumptions used in this derivation are likely not perfect; for example, the UE is not uniformly distributed in $\phi$, event by event, due to the presence of azimuthal anisotropy. The leading object may be more likely to be oriented with the anisotropy, in which case the UE yield would be underestimated and the HS yield overestimated. However, the analysis proceeds with the assumptions as given and includes no additional uncertainty for this potential effect.

The $\Delta \eta ^\mathrm {AB}$ and $\Delta \eta ^\mathrm {jB}$ rejections produce a geometric correlation between the yields of A- and B-particles and, thus, the number of pairs is not the simple product of the two individual yields. Accounting for the dependencies, the total yield of particle pairs can be expressed in the following way

$$\begin{aligned} Y_\text {X--Z}=\int _{-2.5}^{2.5} \frac{\mathrm {d}N^\mathrm {A}_\mathrm {X}(\eta ^\mathrm {A})}{\mathrm {d}\eta ^\mathrm {A}} \Bigg [ \int _2^5 \frac{\mathrm {d}^2N^\mathrm {B}_\mathrm {Z}(\eta ^\mathrm {A},|\Delta \eta ^\mathrm {AB}|)}{\mathrm {d}\eta ^\mathrm {A} \mathrm {d}|\Delta \eta ^\mathrm {AB}|} \mathrm {d}|\Delta \eta ^\mathrm {AB}| \Bigg ] \mathrm {d}\eta ^\mathrm {A} \, , \end{aligned}$$

(2)

where X–Z could be any pairwise combination of UE and HS. In the case of jet events, the $\Delta \eta ^\mathrm {jB}$ condition is enforced when filling the $\eta ^\mathrm {A}$ and $\Delta \eta ^\mathrm {AB}$ distributions so it’s effects are taken into account.

6 Systematic uncertainties

The systematic uncertainties fall into two categories: those associated with both the MBT and jet events and those associated with only the jet events. The uncertainties are determined by assessing the difference between the nominal value of $v_{2}$ or $v_{3}$ and the value after a given variation. Unless otherwise stated, the uncertainties are defined as asymmetric one-standard-deviation errors. The final uncertainty is the quadrature sum of the uncertainty from each individual source. The relative downward and upward systematic uncertainties from different sources and all sources combined are shown for $v_{2}$ in Table 1 and for $v_{3}$ in Table 2. The rest of this section focuses primarily on the systematic uncertainties of $v_{2}$. While the absolute uncertainties in $v_{2}$ and $v_{3}$ are of similar magnitude, this represents larger relative uncertainties in the $v_{3}$ values since they are generally smaller than the $v_{2}$ values at any given $p_{\text {T}}$.

For both the MBT and jet events, the sensitivity to the trigger and tracking efficiency corrections was assessed by removing each. This variation (‘Track/trig Eff.’ in Table 1) yields a 0–2% (2–4%) difference for MBT (jet) events, depending on track $p_{\text {T}}$, and is subdominant. In the construction of the correlation functions, the uncertainty in the mixed-event correction was again found by removing it from the analysis. This variation results in an uncertainty that vanishes at low $p_{\text {T}}$ but grows to 20% (10%) at high $p_{\text {T}}$ for MBT (jet) events, but remains subdominant to statistical uncertainties over the whole $p_{\text {T}}$ range. Regarding the template fitting procedure, the centrality range for the peripheral reference selection was varied from the nominal 60–90% to 50–70% and 70–90%. This variation (‘Peri. reference’) results in an uncertainty of about 2% at low $p_{\text {T}}$ and increasing to about 10% or 18% in the mid $p_{\text {T}}$ range between 2 and 10 $\text {Ge}\text {V}$ depending on the event trigger. This last uncertainty is dominant in this category for most of the $p_{\text {T}}$ range probed in the measurement. At high $p_{\text {T}}$, the sensitivity of the measurements in MBT events to the mixed event correction and reference selection is significantly higher than in jet events; this is particularly noticeable for the $v_{3}$ values, where the relative uncertainties in the MBT events for $p_{\text {T}} > 10$ $\text {Ge}\text {V}$ are 5–10 times larger than in the jet-triggered events.

The following set of uncertainties is associated with jet events only. To assess the sensitivity to the uncertainty in the jet energy scale and the impact of imperfect trigger efficiency, the jet $p_{\text {T}}$ thresholds used to select events were varied from 75 $\text {Ge}\text {V}$ and 100 $\text {Ge}\text {V}$ to 80 $\text {Ge}\text {V}$ and 105 $\text {Ge}\text {V}$, respectively. This variation (‘Trig jet $p_{\text {T}}$ ’) results in a symmetric uncertainty that is smaller than 1% at low particle $p_{\text {T}}$ and that increases to about 10% with increasing $p_{\text {T}}$. It is subdominant to other sources in this category. The jets used in the B-particle jet rejection were varied to include only jets with $p_{\text {T}}$ greater than 20 $\text {Ge}\text {V}$ instead of the nominal 15 $\text {Ge}\text {V}$ (‘Reject jet $p_{\text {T}}$ ’). The 2% and 10% differences at low and high $p_{\text {T}}$ are incorporated as a symmetric uncertainty that is subdominant to other sources in this category. The $\Delta \eta ^\mathrm {jB}$ rejection allows jets to be composed of only a single particle that may originate in the tail of the UE particle $p_{\text {T}}$ spectrum. Thus, the jets used in this rejection were varied to require at least three tracks in a $\Delta R = 0.4$ cone around the jet axis (‘Reject jet mult.’). The uncertainty associated with this variation is about 5% and subdominant to the others in this category. An additional uncertainty is used to cover the impact of a sector of the hadronic endcap calorimeter (HEC) being disabled for the running period. The disabled sector was in the range $1.5<\eta <3.2$ and $-\pi<\phi <-\pi /2$. This uncertainty (‘Disabled HEC sector’) was assessed by requiring all B-particles to be outside the pseudorapidity region of the disabled HEC. The difference was found to be less than 1% at low $p_{\text {T}}$ and about 20% at high $p_{\text {T}}$, where it is the dominant positive uncertainty. Finally, an uncertainty is assigned to account for the potential of the UE to bias the event selection. The azimuthal modulation of the UE increases the reconstructed $p_{\text {T}}$ of jets aligned with the flow orientation, and, thus, the event-wise jet-$p_{\text {T}}$ threshold will bias the events to have more jets correlated with the flow plane. The impact of this effect on the measured results was assessed in simulation by mixing jet events with a realistic UE containing azimuthal anisotropy. The resulting uncertainty only affects $v_{2}$, is the dominant negative uncertainty for track $p_{\text {T}}$ greater than 3 $\text {Ge}\text {V}$, and is about 30% (20%) for jet-triggered events with jet $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ (100 $\text {Ge}\text {V}$). The effect is larger for lower-$p_{\text {T}}$ jets because the UE energy contribution is independent of jet energy. For a power-law spectrum, a given threshold change has a greater fractional effect on the yield for smaller values of the threshold.

In summary, the uncertainty in $v_{2}$ from the peripheral reference selection was found to be dominant for $p_{\text {T}}$ less than 10 $\text {Ge}\text {V}$ for MBT events, above which, the mixed event correction uncertainty is dominant, and between 2 and 5 $\text {Ge}\text {V}$ for jet events. The uncertainties associated with the jet selection were found to be dominant for $p_{\text {T}} \gtrsim 10$ $\text {Ge}\text {V}$ in jet events. The total uncertainty in MBT events ranges from ($-1\%$, $+2\%$) at low $p_{\text {T}}$ to about ($-10\%$, $+25\%$) at high $p_{\text {T}}$. For jet events, the total uncertainty ranges from about ($-5\%$, $+4\%$) at low $p_{\text {T}}$ to about ($-35\%$, $+50\%$) and ($-30\%$, $+25\%$) at high $p_{\text {T}}$ for events with jet $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ and jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ respectively.

Table 1 Systematic uncertainty summary for anisotropy coefficients $v_2$. The values are approximate, as they represent the average variation in each $p_{\text {T}}$ range, and are reported relative to $v_{2}$. Negative and positive values indicate downward and upward uncertainties respectively. Commas separate the downward and upward uncertainty where applicable

Table 2 Systematic uncertainty summary for anisotropy coefficients $v_3$. The values are approximate, as they represent the average variation in each $p_{\text {T}}$ range, and are reported relative to $v_{3}$. Negative and positive values indicate downward and upward uncertainties respectively. Commas separate the downward and upward uncertainty where applicable

The uncertainties associated with the measurement of particle pair yields are generated from some of the variations discussed above, namely the track and trigger efficiency variation, the trigger jet $p_{\text {T}}$ threshold variation, and each B-particle jet rejection variation. An additional variation was made to test the assumption that the toward region contains all HS particles. The two transverse region sides were tagged as having the minimum and maximum number of tracks out of the two. The pair yields were, then, calculated using the minimum and maximum sides only, as separate variations. This variation produces the dominant uncertainty in the relative pair yields, defined in Eq. (2), for all particle combinations at all $p_{\text {T}}$.

7 Results

Figure 3 shows the extracted second- ($v_{2}$) and third-order ($v_{3}$) anisotropy coefficients for the MBT events compared to those from both selections of jet events plotted as a function of A-particle $p_{\text {T}}$ in the range $0.5<p_{\text {T}} <100$ $\text {Ge}\text {V}$. Each set of values is from events with the same 0–5% centrality selection. Points are located on the horizontal axis at the mean $p_{\text {T}}$ of tracks within any given bin. The $v_{2}$ and $v_{3}$ coefficients increase as a function of $p_{\text {T}}$ in the low $p_{\text {T}}$ region ($p_{\text {T}}<$ 2–3 $\text {Ge}\text {V}$), then decrease (2–3 $< p_{\text {T}}<$ 9 $\text {Ge}\text {V}$), and finally plateau for high $p_{\text {T}}$ ($p_{\text {T}}>$  9 $\text {Ge}\text {V}$). The $v_{2}$ coefficients are consistent with being independent of $p_{\text {T}}$ for $p_{\text {T}} > 9$ $\text {Ge}\text {V}$, while the larger uncertainties in the values of $v_{3}$ preclude any strong conclusion.

Fig. 3

Distribution of $v_{2}$ (left) and $v_{3}$ (right) plotted as a function of the A-particle $p_{\text {T}}$. Values from MBT events are plotted as black squares, and those from events with jet $p_{\text {T}} >75$ $\text {Ge}\text {V}$ and events with jet $p_{\text {T}} >100$ $\text {Ge}\text {V}$ are plotted as blue circles and orange diamonds respectively. Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

The $v_{2}$ results show agreement within uncertainties between the MBT and jet events for the low $p_{\text {T}}$ ($p_{\text {T}} \lesssim 2$ $\text {Ge}\text {V}$) and high $p_{\text {T}}$ ($p_{\text {T}} \gtrsim 9$ $\text {Ge}\text {V}$) regions. For the intermediate $p_{\text {T}}$ region, the MBT events yield a higher $v_{2}$ value than jet events, although the trends are qualitatively similar. Similarly to $v_{2}$, the $v_{3}$ results show agreement between the MBT and jet events for $p_{\text {T}} <2$ $\text {Ge}\text {V}$, and higher values from MBT events for $p_{\text {T}} >2$ $\text {Ge}\text {V}$.

Fig. 4

Measured $v_{2}$ values plotted as a function of the A-particle $p_{\text {T}}$ for MBT events (top), events with jet $p_{\text {T}} >75$ $\text {Ge}\text {V}$ (bottom left), and events with jet $p_{\text {T}} >100$ $\text {Ge}\text {V}$ (bottom right). The nominal values (closed black circles) are overlaid with points generated by making different B-particle $p_{\text {T}}$ selections: $0.4<p_{\text {T}} ^\mathrm {B}<1$ $\text {Ge}\text {V}$ (blue open circles), $1<p_{\text {T}} ^\mathrm {B}<2$ $\text {Ge}\text {V}$ (open violet squares), and $2<p_{\text {T}} ^\mathrm {B}<3$ $\text {Ge}\text {V}$ (open red triangles). The points with different B-particle $p_{\text {T}}$ selections are offset slightly from the nominal horizontal-axis positions to make the uncertainties visible. For clarity, systematic uncertainties are omitted from the three sets of restricted B-particle $p_{\text {T}}$ ranges; they are, however, consistent with those from the inclusive results and are highly correlated between the selections

As mentioned in Section 5, if the measured anisotropy originates from a global momentum field, the $v_{2}$ and $v_{3}$ values, extracted for a given $p_{\text {T}} ^\mathrm {A}$ range, will be independent of B-particle selection. This assumption of factorisation is explicitly tested by carrying out the analysis for different selections of $p_{\text {T}} ^\mathrm {B}$. Figure 4 shows the $v_{2}$ values, from each event trigger, for the nominal results using $p_{\text {T}} ^\mathrm {B}>0.4$ $\text {Ge}\text {V}$ overlaid with results using $0.4<p_{\text {T}} ^\mathrm {B}<1$ $\text {Ge}\text {V}$, $1<p_{\text {T}} ^\mathrm {B}<2$ $\text {Ge}\text {V}$, and $2<p_{\text {T}} ^\mathrm {B}<3$ $\text {Ge}\text {V}$. The test shows factorisation breaking at the level of 5% for $p_{\text {T}} ^\mathrm {A}<5$ $\text {Ge}\text {V}$ in MBT events. However, at higher $p_{\text {T}} ^\mathrm {A}$, the differences grow with $p_{\text {T}} ^\mathrm {A}$ to be 10–100% from the nominal values. For jet events, factorisation holds within about 10–20% for all values of $p_{\text {T}} ^\mathrm {A}$, except for $4<p_{\text {T}} ^\mathrm {A}<9$ $\text {Ge}\text {V}$ in $p_{\text {T}} ^\mathrm {jet}>100$ $\text {Ge}\text {V}$ events, where it is within about 30–40%. Although the large uncertainties prevent strong conclusions from being drawn, there is a hint of a difference in behaviour at high $p_{\text {T}} ^\mathrm {A}$ where the factorisation breaking is greater for MBT events than for jet events. This result could be due to the B-particle jet rejection scheme used for the jet events. Correlations resulting from hard-process, e.g. from back-to-back jets, specifically violate the factorisation assumption, and the B-particle jet rejection dramatically limits the contribution from these processes from entering the correlation functions in jet events. However, the correlations from MBT events have no such rejection, and could, therefore, be more susceptible to hard-process correlations at high $p_{\text {T}} ^\mathrm {A}$.

Fig. 5

Distribution of $v_{2}$ plotted as a function of centrality for MBT events (black squares), events with jet $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ (blue circles), and events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ (orange diamonds). The results are obtained in three different selections of the A-particle $p_{\text {T}}$: $0.5< p_{\text {T}} < 2$ $\text {Ge}\text {V}$ (top left), $2< p_{\text {T}} < 9$ $\text {Ge}\text {V}$ (top right), and $9< p_{\text {T}} < 100$ $\text {Ge}\text {V}$ (bottom). Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

Figure 5 shows $v_{2}$ plotted as a function of centrality for MBT events and both classes of jet events. The results are divided into three regions in A-particle $p_{\text {T}}$: $0.5< p_{\text {T}} < 2$ $\text {Ge}\text {V}$, $2< p_{\text {T}} < 9$ $\text {Ge}\text {V}$, and $9< p_{\text {T}} < 100$ $\text {Ge}\text {V}$. The $v_{2}$ results show agreement, within uncertainties, between the MBT and jet events for $p_{\text {T}}$ selections $0.5<p_{\text {T}} <2$ $\text {Ge}\text {V}$ and $p_{\text {T}} >9$ $\text {Ge}\text {V}$ for all centralities and are found to be nearly independent of centrality. For $2<p_{\text {T}} <9$ $\text {Ge}\text {V}$, the MBT events give a higher $v_{2}$ value than the jet events, and all three sets show a trend to lower values of $v_{2}$ as the collisions become more peripheral.

Focusing on the overall $p_{\text {T}}$ dependence of the anisotropies, Figure 6 (left panel) shows $v_{2}$ and $v_{3}$ coefficients from events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ compared with theoretical calculations from Ref. [14]. This theoretical calculation, within the jet quenching paradigm, invokes a stronger parton coupling to the QGP near the transition temperature, which helps to reduce the tension in simultaneously matching the nucleus–nucleus high-$p_{\text {T}}$ hadron spectrum suppression and the azimuthal anisotropy $v_{2}$. The calculation tests two different initial $p$+Pb geometries referred to as ‘size a’ and ‘size b’, where the latter has a smaller initial QGP volume. The predictions are slightly lower than the data for both $v_{2}$ and $v_{3}$, and the ‘size a’ curve is within two standard deviations of all points. However, in the right panel of Figure 6, the same calculation predicts a substantial suppression of high-$p_{\text {T}}$ hadrons, as expressed by the quantity $R_{p\mathrm {Pb}} = \mathrm {d}^{2}N_{p\mathrm {Pb}}/\mathrm {d}p_{\text {T}} \mathrm {d}y / (T_{p\mathrm {Pb}} \times \mathrm {d}^{2}\sigma _{pp}/\mathrm {d}p_{\text {T}} \mathrm {d}y)$ where $T_{p\mathrm {Pb}}$ represents the nuclear thickness of the Pb nucleus, as determined via a Monte Carlo Glauber calculation [56]. Shown in comparison are published experimental results from ATLAS and ALICE for $R_{p\mathrm {Pb}}$ in central events that are consistent with no nuclear suppression, i.e. $R_{p\mathrm {Pb}} = 1$ [41, 57]. The ALICE experiment uses the notation $Q_{p\mathrm {Pb}}$ for the same quantity to describe a bias that may exist due to the centrality categorisation. There are uncertainties in the experimental measurements related to the centrality or multiplicity selection in $p$+Pb collisions, particularly in determining the nuclear thickness value $T_{p\mathrm {Pb}}$ . However, there is no indication of the large $R_{p\mathrm {Pb}}$ suppression predicted by the jet quenching calculation. Thus, the jet quenching calculation is disfavoured as it cannot simultaneously describe the non-zero high-$p_{\text {T}}$ azimuthal anisotropy and the lack of yield suppression.

Fig. 6

Coefficients $v_{2}$ and $v_{3}$  (left panel) and $R_{p\mathrm {Pb}}$ (right panel) plotted as a function of particle $p_{\text {T}}$ for $p$+Pb collisions. The left panel is for central 0–5% events from the jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ event sample. Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points. The left panel has two sets of curves showing theoretical predictions from a jet quenching framework with two different initial geometries in 0–4% central collisions [14]; the upper two (red/orange) are $v_{2}$ for ‘size a’ (dotted) and ‘size b’ (dash-dotted) configurations, and the lower two (blue) are $v_{3}$ where the ‘size a’ (dash-dotted) and ‘size b’ (dashed) curves are nearly indistinguishable from each other. The right panel shows $R_{p\mathrm {Pb}}$ data from ATLAS [57] and $Q_{p\mathrm {Pb}}$ data from ALICE [41]. Theoretical calculations (red/orange lines) from Ref.  [14] are also shown in this panel; the dotted line gives the results of the ‘size a’ configuration and the dash-dotted line gives the results of the ‘size b’ configuration

Figure 7 shows the MBT $v_{2}$ and $v_{3}$ coefficients compared with theoretical calculations from Ref. [26]. The calculations are derived from two opposite limits of kinetic theory. The low momentum bands represent zeroth-order hydrodynamic calculations for high-multiplicity $p$+Pb events that give quantitative agreement with $v_{2}$ up to $p_{\text {T}} = 2$ $\text {Ge}\text {V}$ while predicting values of $v_{3}$ that are too high. Above some high $p_{\text {T}}$ threshold, hadrons are expected to result, not from hydrodynamics, but instead from jets where the resulting partons have the opposite limit than in hydrodynamics, i.e. a large mean free path. To model this region, a non-hydrodynamic ‘eremitic’ expansion calculation (see Ref. [26] for the detailed calculation), shown as the bands at high $p_{\text {T}}$, indicates slowly declining $v_{2}$ and $v_{3}$ coefficients. The dashed lines are a simple Padé-type fit connecting the two regimes [26]. The trends are qualitatively similar to those in the data, although there is not quantitative agreement. In particular, the calculation predicts values of $v_{2}$ and $v_{3}$ substantially below the experimental results for $p_{\text {T}} =$ 4–15 $\text {Ge}\text {V}$. It should be noted that calculations presented in Ref. [26] are performed, consistently between the hydrodynamic and eremitic components, only for massless partons and with an ideal equation of state. Thus, one does not expect quantitative agreement and is looking for rather qualitative trends. More sophisticated treatments in the hydrodynamic regime result in better quantitative agreement with the anisotropy coefficients at low $p_{\text {T}}$ [58, 59]. It is worth highlighting that traditional parton energy-loss calculations connect the high-$p_{\text {T}}$ $v_{2}$ with a suppression in the overall yield of high-$p_{\text {T}}$ particles. The same is true with this eremitic calculation, and thus, it should also be in contradistinction to $p$+Pb high-$p_{\text {T}}$ experimental data indicating almost no suppression, i.e. jet quenching.

Fig. 7

Coefficients $v_{2}$ and $v_{3}$ plotted as a function of $p_{\text {T}}$ for central 0–5% $p$+Pb collisions from the MBT event sample. Theoretical calculations relevant to the low-$p_{\text {T}}$ regime from hydrodynamics and to the high-$p_{\text {T}}$ regime from an ‘eremitic’ framework from Romatschke [26] are also shown. The lines are Padé-type fits connecting the two regimes, where the red dotted line is for $v_{2}$ and the blue dash-dotted line is for $v_{3}$. Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

Another possible source of the high-$p_{\text {T}}$ anisotropies could lie in an initial-state effect, potentially encoded in a model such as Pythia 8. Shown in Figure 8 is a Pythia 8 calculation with hard² $pp$ events overlaid on minimum-bias $p$+Pb events generated in the default Angantyr framework [60]. It is emphasised that this version of Pythia does not include the recently developed string–string, or so-called string shoving, implementation [61]. The generator-level charged particles are then processed with the entire analysis procedure, including the non-flow template fit. The result is a negative $v_{2,2}$ for all momenta, in contradistinction to the experimental data. Further investigation reveals that Pythia 8 run in ‘hard’ scattering mode has correlations with large pseudorapidity separation between particle pairs as a result of the specific implementation of initial-state radiation. This correlation is reduced in high-multiplicity events because of the large number of uncorrelated UE particles, and thus results in a negative $v_{2,2}$ after subtracting the non-flow contribution.

Fig. 8

Predictions of azimuthal anisotropy from Pythia 8 using the same two-particle formalism used for the data results. The events combine minimum-bias $p$+Pb underlying events generated in the Angantyr framework with hard $pp$ events that require the presence of a jet with $p_{\text {T}} {} > 100$ $\text {Ge}\text {V}$. The two top plots show example correlation functions, with template fits, from a low particle-$p_{\text {T}}$ selection (top left) and a high particle-$p_{\text {T}}$ selection (top right). In the upper panels of the two top plots, the open circles show the scaled and shifted peripheral template with uncertainties omitted, the closed circles show the central data, and the red histogram shows the fit (template and harmonic functions). The blue dashed line shows the second-order harmonic component, $Y_2^\mathrm {ridge}$, and the orange dashed line shows the third-order harmonic component, $Y_3^\mathrm {ridge}$ (the $n=2$ and $n=3$ contributions to the sum in Eq. 1, respectively). The lower panels show the difference between the central data and the peripheral template along with the second and third harmonic functions. The resulting $v_{2,2}$, $v_{3,3}$, and global fit $\chi ^2$/NDF values are reported in the legends, where NDF $=35$. The bottom plot shows the extracted $v_{2,2}$ values as a function of A-particle $p_{\text {T}}$

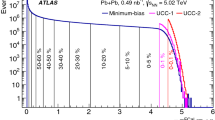
Figure 9 shows the published Pb+Pb results for $v_{2}$ as a function of $p_{\text {T}}$ in the 20–30% centrality selection [62] compared to the $v_{2}$ from both the MBT $p$+Pb data and $p$+Pb containing a jet with $p_{\text {T}} {} > 100$ $\text {Ge}\text {V}$. This Pb+Pb centrality range is selected because the spatial elliptic eccentricity is approximately the same as in 0–5% centrality $p$+Pb collisions [63], despite having a much larger total particle multiplicity. The overall trends for Pb+Pb $v_{2}$ as a function of $p_{\text {T}}$ are qualitatively similar to those presented here for $p$+Pb from MBT events and the jet events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$. Both sets of the $p$+Pb values are scaled by a single multiplicative factor (1.5) to match the Pb+Pb rise at low $p_{\text {T}}$. After scaling, the MBT $p$+Pb results quantitatively agree with those from the Pb+Pb system for $0.5< p_{\text {T}} < 8$ $\text {Ge}\text {V}$, except for a slight difference in the peak value near $p_{\text {T}} \approx 3$ $\text {Ge}\text {V}$. For $p_{\text {T}}$ above about 8 $\text {Ge}\text {V}$, the Pb+Pb results indicate a slow decline of $v_{2}$ values with increasing $p_{\text {T}}$, while the $p$+Pb results exhibit more of a plateau. Strikingly, the overall behaviour of the $v_{2}$ values are quite similar.

As described above, the physics interpretations of the Pb+Pb elliptic anisotropies are hydrodynamic flow at low $p_{\text {T}}$, differential jet quenching at high $p_{\text {T}}$, and a transition between the two in the intermediate region of approximately $2< p_{\text {T}} < 10$ $\text {Ge}\text {V}$. Since these effects all relate to the initial QGP geometric inhomogeneities, a common shape with a single scaling factor for $p$+Pb could indicate a common physics interpretation. This scaling factor of 1.5, as empirically determined, may be the result of slightly different initial spatial deformations, or from the much larger Pb+Pb overall multiplicity, which enables a stronger translation of spatial deformations into momentum space. For the high $p_{\text {T}}$ region, this presents a conundrum in that it is difficult for differential jet quenching to cause the $v_{2}$ anisotropy in $p$+Pb collisions when there is no evidence for jet quenching overall. These measurements showing non-zero high $p_{\text {T}}$$v_{2}$ in $p$+Pb collisions in the absence the jet quenching observed in Pb+Pb collisions suggest there might be additional contributions to $v_{2}$ at high $p_{\text {T}}$ in Pb+Pb collisions.

Fig. 9

Scaled $p$+Pb $v_{2}$ values plotted as a function of the A-particle $p_{\text {T}}$ overlaid with $v_{2}$ from 20–30% central Pb+Pb data at $\sqrt{s_{_\text {NN}}}$ = 5.02 $\text {Te}\text {V}$ [62]. Results from MBT and jet $p_{\text {T}} >100$ $\text {Ge}\text {V}$ $p$+Pb events are plotted as black squares and orange diamonds, respectively, and those from Pb+Pb are plotted as green circles. Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

Returning to the issue of the difference in the intermediate $p_{\text {T}}$ region between the $p$+Pb MBT and jet event results, the source of hadrons in this region should be considered. As detailed previously, in a highly simplified picture one can classify hadrons as originating from hard scatterings (HS) or from the underlying event (UE). Thus, pairs of particles of A and B types can come from the combinations HS–HS, HS–UE, UE–HS, and UE–UE. Figure 10 presents the measured pair fractions for both MBT and jet, 0–5% central events plotted as a function of the A-particle $p_{\text {T}}$. UE–UE pairs dominate the correlation functions at low $p_{\text {T}}$ in each case, and HS–UE combinations dominate at high $p_{\text {T}}$. Combinations with HS B-particles are sub-dominant, because there are fewer jet particles than UE particles in central events; for the jet selected events, these combinations are further suppressed by the B-particle jet rejection condition. Figure 11 shows the dominant contributions from the MBT and jet events overlaid. Although the same qualitative behaviour is found in each case, the point at which the HS–UE pairs become dominant over the other combinations is at a lower $p_{\text {T}}$ for jet events than for MBT events.

This behaviour can also be seen in Figure 12, in which the pair fractions are plotted as a function of centrality, and again, the values for MBT and jet events are overlaid. The centrality-dependent results are plotted for low, medium, and high A-particle $p_{\text {T}}$ ranges in the same way as in Figure 5. At low $p_{\text {T}}$, pair fractions from MBT and jet events agree, and in the mid-$p_{\text {T}}$ transition region, MBT events have a larger UE–UE contribution and smaller HS–UE contribution compared to jet events. At high $p_{\text {T}}$, central events show a difference between UE–UE and HS–UE that is reduced in more-peripheral events and absent for more peripheral than 25% centrality. The overall trend of the pair fractions with centrality is quite similar to that of $v_{2}$ shown in Figure 5; little centrality dependence for low and high $p_{\text {T}}$, and significant centrality dependence in addition to MBT–jet event ordering in the mid-$p_{\text {T}}$ transition region.

Fig. 10

Particle pair yield composition fractions for MBT events (top), events with jet $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ (bottom left), and events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ (bottom right) plotted as a function of the A-particle $p_{\text {T}}$. Green and blue open circles represent HS–HS and UE–HS pairs, respectively, and red and violet closed circles represent UE–UE and HS–UE pairs, respectively. Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

Fig. 11

Underlying event–underlying event (UE–UE) (open circles) and hard scatter–underlying event (HS–UE) (open squares) particle-pair yield composition fractions for MBT events (black), events with jet $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ (blue), and events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ (orange) plotted as a function of the A-particle $p_{\text {T}}$. Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

Fig. 12

Underlying event–underlying event (UE–UE) (open circles) and hard scatter–underlying event (HS–UE) (open squares) particle-pair yield composition fractions for MBT events (black), events with jet $p_{\text {T}} > 75$ $\text {Ge}\text {V}$ (blue), and events with jet $p_{\text {T}} > 100$ $\text {Ge}\text {V}$ (orange) plotted as a function of event centrality. The results are obtained in three different selections of the A-particle $p_{\text {T}}$: $0.5< p_{\text {T}} < 2$ $\text {Ge}\text {V}$ (top left), $2< p_{\text {T}} < 9$ $\text {Ge}\text {V}$ (top right), and $9< p_{\text {T}} < 100$ $\text {Ge}\text {V}$ (bottom). Statistical uncertainties are shown as narrow vertical lines on each point, and systematic uncertainties are presented as coloured boxes behind the points

Thus, a potential explanation for the lower $v_{2}$ and $v_{3}$ in the intermediate $p_{\text {T}}$ region is simply that, in that region, the HS particles have lower anisotropy coefficients than UE particles, and MBT events have a larger fraction of UE–UE pairs than jet-triggered events. In the low and high $p_{\text {T}}$ regions, the same types of pairs dominate in both the MBT and jet-triggered events, namely UE–UE and HS–UE respectively, and hence the anisotropy coefficients agree between the event samples. If this explanation is correct, it also aids in understanding Figure 9 in which there is a significant difference between the $p$+Pb jet event $v_{2}$ and the Pb+Pb $v_{2}$ in the intermediate $p_{\text {T}}$ region, because the relative pair fractions are potentially significantly different.

This particle mixing picture is attractive in that it naturally explains the general shape of the $v_{2}{}{}(p_{\text {T}})$ and $v_{3}{}{}(p_{\text {T}})$ distributions as well as the ordering of the different event samples. However, it is noted that the correspondence between the differences in the flow coefficients and pair fractions is not quantitative; the differences in the flow coefficients are fractionally much larger than the differences in the pair fractions. Thus, there are either additional sources of correlation or our assumptions are violated in some way (e.g. the two assumed HS and UE sources are too simplistic or the measured pair fractions do not accurately represent the sources, as is discussed in Section 5). That said, for particle $p_{\text {T}} >20$ $\text {Ge}\text {V}$, where particle production in any model is thought to arise mainly from jet fragmentation, the non-zero $v_{2}$ demonstrates that a positive correlation exists between hard (high $p_{\text {T}}$) and soft (low $p_{\text {T}}$) particles, irrespective of the pair fractions.

8 Conclusion

This paper presents Fourier coefficients of the azimuthal distribution of unidentified charged particles from 165 $\mathrm {nb}^{-1}$ of $\sqrt{s_{_\text {NN}}} = 8.16$ $\text {Te}\text {V}$ $p$+Pb collisions at the LHC and measured with the ATLAS detector. Results are presented separately for minimum-bias and jet events, with jet $p_{\text {T}}$ thresholds of 75 and 100 $\text {Ge}\text {V}$, as a function of particle $p_{\text {T}}$ and centrality. The results are extracted using two-particle azimuthal correlations combined with a non-flow template fit procedure. The charged particle $p_{\text {T}}$ dependence of $v_{2}$ and $v_{3}$ is found assuming the factorisation of $v_{n,n}$. The $v_{2}$ results are presented for charged-particle transverse momentum $p_{\text {T}}$  = 0.5–20 $\text {Ge}\text {V}$ for minimum-bias events and $p_{\text {T}}$  = 0.5–50 $\text {Ge}\text {V}$ for jet-triggered events, and the $v_{3}$ results are for $p_{\text {T}}$  = 0.5–20 $\text {Ge}\text {V}$ in both cases.

For charged particles with $p_{\text {T}}$ between 0.5 and 2 $\text {Ge}\text {V}$, the $v_n$ results from each event selection are quantitatively consistent with each other, rising steadily with $p_{\text {T}}$ , and the $v_{2}$ coefficients are roughly independent of centrality. The $v_{2}$ values at 0–5% centrality agree with those predicted by hydrodynamic calculations.

Between charged particle $p_{\text {T}}$ of 2 and 9 $\text {Ge}\text {V}$, the $v_n$ values drop in each case, but are ordered with minimum-bias events yielding the highest $v_n$ values and the jet events with jet $p_{\text {T}} > 100~\text {Ge}\text {V}$ the lowest. Charged particles in this $p_{\text {T}}$ range exhibit a significant centrality-dependent $v_{2}$, monotonically decreasing from central to peripheral events. This behaviour can be qualitatively explained within a simplified two-component model of particle production, in which the magnitude of the correlation in this region is determined by the admixture of charged particles originating from soft and hard processes in the given event selection. The measured particle pair yields support this qualitative argument.

For charged particles with $p_{\text {T}}$ above 9 $\text {Ge}\text {V}$, the $v_n$ results are again consistent between MBT and jet events. Although the uncertainties in the $v_{3}$ values make any quantitative statement difficult, $v_{2}$ plateaus at a value of 0.025 up to a $p_{\text {T}}$ of 50 $\text {Ge}\text {V}$. This result cannot be explained in the theoretical context of jet quenching or eremitic expansion calculations while simultaneously describing the observed lack of suppression of high-$p_{\text {T}}$ hadron and jet yields in $p$+Pb collisions.