1. Discovery of neutron–antineutron (\(n-{{\overline{n}}} \)) oscillation [1,2,3,4] would be a clear evidence of the baryon number violation, and can shade more light on the origin of the matter–antimatter asymmetry in the Universe [5, 6]. Nowadays this phenomenon is actively discussed (see [7,8,9] for reviews) and new projects for its experimental search are under consideration [10,11,12,13,14].

In the Standard Model (SM) frames the neutron has only the Dirac mass term \(m \, \overline{n} n\) which conserves baryon number \(\mathrm{B}\). The oscillation \(n-{{\overline{n}}} \) which violates \(\mathrm{B}\) by two units (\(\Delta \mathrm{B}=2\)) can emerge if the neutron has also Majorana mass term originated from new physics

$$\begin{aligned} \frac{ \epsilon _{n{\overline{n}}} }{2} \big ( n^T C n + \overline{n}\, C \overline{n}^T \big ) = \frac{ \epsilon _{n{\overline{n}}} }{2} \big ( \overline{n_c}\, n + \mathrm{h.c.} \big ) \end{aligned}$$
(1)

where n and \(n_c = C \overline{n}^T\) are the neutron and antineutron fields, C being the charge conjugation matrix. The mass terms (1) can be induced via the effective six-fermion operators \(\frac{1}{M^5}(udd)^2\) involving u and d quarks, with M being a large cutoff scale of new physics.Footnote 1

Oscillation \(n-{{\overline{n}}} \) is hampered by the medium effects as interactions with the residual gas and magnetic field. In particular, in the presence of magnetic field B the oscillation probability for a free flight time t is [7]Footnote 2:

$$\begin{aligned} P_{n{{\overline{n}}} }(t) = \frac{ \epsilon _{n{\overline{n}}} ^2 \sin ^2\left( \sqrt{\Omega ^2 + \epsilon _{n{\overline{n}}} ^2}\,t \right) }{\Omega ^2 + \epsilon _{n{\overline{n}}} ^2} \approx \frac{\ \sin ^2\big (\Omega t \big )}{\tau _{n{{\overline{n}}} }^2\Omega ^2} \end{aligned}$$
(2)

where \(\Omega = \vert \mu B \vert = (B/0.5\,\mathrm{G})\times 4581~\mathrm{s}^{-1}\), with \(\mu = 6.031\times 10^{-12}\) eV/G being the neutron magnetic moment, and \(\tau _{n{{\overline{n}}} }= \epsilon _{n{\overline{n}}} ^{-1}= (10^{-23}\, \mathrm{eV}/ \epsilon _{n{\overline{n}}} ) \times 0.66 \times 10^8\) s is characteristic oscillation time. The same formula with \(\Omega \rightarrow \vert U -\bar{U} \vert /2\) applies in the presence of matter, U and \(\bar{U}\) being the matter induced optical potentials for n and \({{\overline{n}}} \). If the medium effects are suppressed so that the quasi-free condition \(\Omega t \ll 1\) is fulfilled, then Eq. (2) gives

$$\begin{aligned} P_{n{{\overline{n}}} }(t) = ( \epsilon _{n{\overline{n}}} \, t)^2 = \left( \frac{t}{0.1~\mathrm{s}}\right) ^2 \left( \frac{10^8~\mathrm{s}}{\tau _{n{{\overline{n}}} }}\right) ^2 \! \times 10^{-18}. \end{aligned}$$
(3)

If medium effects are strong, \(\Omega t \gg 1\), the probability becomes smaller. The time dependent factor in (2) can be averaged and we get:

$$\begin{aligned} \overline{P}_{n{{\overline{n}}} } = \frac{ \epsilon _{n{\overline{n}}} ^2}{2\Omega ^2} = \left( \frac{0.5\, \mathrm{G}}{B}\right) ^2 \left( \frac{10^8~\mathrm{s}}{\tau _{n{{\overline{n}}} }}\right) ^2 \! \times 2.4\times 10^{-24}. \end{aligned}$$
(4)

Experiment on direct search for \(n-{{\overline{n}}} \) oscillations was performed in Institut Laue-Langevin (ILL) using the cold neutron beam with intensity \(10^{11}~n\)/s propagating in a long vessel (80 m) before reaching the antineutron detector, with a mean flight time \(t \simeq 0.1\) s [16]. The quasi-free condition \(\Omega t \ll 1\) was fulfilled by suppressing the magnetic field (\(B< 0.1\) mG) and the residual gas pressure (\(P<2\times 10^{-4}\) Pa) in the drift vessel. No antineutron was detected in a running time of \(2.4\times 10^7\) s, and the lower limit on \(n-{{\overline{n}}} \) oscillation time \(\tau _{n {{\overline{n}}} } > 0.86 \times 10^8\) s (90% CL) was reported which in turn translates into an upper limit on \(n-{{\overline{n}}} \) mass mixing \( \epsilon _{n{\overline{n}}} < 7.7 \times 10^{-24}\) eV.

Somewhat stronger but indirect bounds are obtained from the nuclear stability. E.g. experimental limits on oxygen decay yields \(\tau _{n {{\overline{n}}} } > 2.7 \times 10^8\) s (90% CL) [17], or \( \epsilon _{n{\overline{n}}} < 2.5 \times 10^{-24}\) eV. Due to these bounds, for realistic flight times \(t \le 0.1\) the probability of \(n-{\bar{n}}\) conversion (3) via the direct mixing (1) cannot exceed \(10^{-18}\) or so.

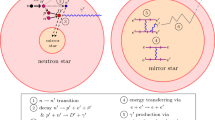
In this paper we show that effective channel for \(n-{\bar{n}}\) conversion can be induced via \(n \rightarrow n'/{{\overline{n}}} ' \rightarrow {{\overline{n}}} \) transitions assuming that the neutron has \(\Delta \mathrm{B}=1\) mixings with the hypothetical neutron \(n'\) and antineutron \({{\overline{n}}} '\) states belonging to dark mirror world. As it was shown in Refs. [18, 19], \(n-n'\) oscillation time \(\tau _{nn'}\) can be smaller than 1 s so that \(n-n'\) mixing mass can be as large as \(\varepsilon _{nn'}\sim 10^{-15}\) eV, or even larger. This possibility is not excluded neither by nuclear stability bounds nor by astrophysical and cosmological limits [18], and it can have observable effects for the propagation of the ultra-high energy cosmic rays at cosmological distances [20, 21]. This phenomenon may manifest in neutron disappearance (\(n\rightarrow n'\)) and regeneration (\(n \rightarrow n' \rightarrow n\)) experiments perfectly accessible to present experimental capabilities [18, 22]. In fact, several dedicated experiments were performed [23,24,25,26,27,28,29], and it is rather intriguing that some of them show anomalous deviations from null hypothesis indicating to \(\tau _{nn'} \sim 20\) s or so [28, 30].

In principle, the neutron can have a mass mixing with both \(n'\) and \({{\overline{n}}} '\) states, with comparable sizes, \(\varepsilon _{n{\overline{n}}'} \sim \varepsilon _{nn'}\). Here we show that if both \(\Delta \mathrm{B}=1\) oscillations \(n-n'\) and \(n-{{\overline{n}}} '\) take place, with the respective probabilities \(P_{nn'}\) and \(P_{n{{\overline{n}}} '}\), then also \(n-{{\overline{n}}} \) oscillation will be induced with the probability \(P_{n{{\overline{n}}} } \simeq P_{nn'} P_{n{{\overline{n}}} '}\). In ‘usual’ experimental conditions the disappearance of free neutrons due to \(n-n'\) and \(n-{{\overline{n}}} '\) oscillations might skip the detection since the probabilities \(P_{nn'}\) and \(P_{n{{\overline{n}}} '}\) are suppressed by environmental effects (as e.g. mirror magnetic field at the Earth [19]), and hence also their doubly suppressed product \(P_{nn'} P_{n{{\overline{n}}} '}\) can be below the experimental bound on \(n-{{\overline{n}}} \) transition [16]. However, in the properly adjusted experimental conditions (e.g. the applied magnetic field) both \(P_{nn'}\) and \(P_{n{{\overline{n}}} '}\) can be resonantly enhanced, and their product \(P_{nn'} P_{n{{\overline{n}}} '} \) can exceed by many orders of magnitude the benchmark value \(P_{n{{\overline{n}}} } = 10^{-18}\) (3) attainable to the direct \(n-{{\overline{n}}} \) mixing (1).

2. There may exist a shadow sector of particles which is a mirror replica of our observable particle sector. Then all known particles: quarks, leptons, Higgs etc. must have their mirror twins: quarks\('\), leptons\('\), Higgs\('\) etc. which are sterile with respect to the SM gauge interactions \(SU(3)\times SU(2)\times U(1)\) but should possess gauge interactions of their own SM\('\) sector \(SU(3)'\times SU(2)'\times U(1)'\) (see e.g. reviews [31,32,33], for a historical overview see [34]). Such shadow matter, invisible in terms of ordinary photons but gravitationally coupled to our matter, can be a part of cosmological dark matter as its asymmetric and atomic (dissipative) fraction, with specific implications for cosmological evolution, formation and structure of galaxies and stars, etc. [35,36,37,38,39,40,41,42,43].

More generically, one can consider the theory based on the product \(G\times G'\) of two identical gauge factors (SM or some its extension), ordinary particles belonging to G and mirror particles to \(G'\). Total Lagrangian of two sectors can be presented as

$$\begin{aligned} {\mathcal L}_{\mathrm{tot}} = {\mathcal L}+ {\mathcal L}' + {\mathcal L}_{\mathrm{mix}} \end{aligned}$$
(5)

where \({\mathcal L}\) and \({\mathcal L}'\) describe two particle sectors whereas \({\mathcal L}_{\mathrm{mix}}\) contains possible cross-interactions between ordinary and mirror particle species.

The identical form of \({\mathcal L}\) and \({\mathcal L}'\) can be guaranteed by discrete \(Z_2\) symmetry \(G\leftrightarrow G'\) when all our particles (fermions, Higgses and gauge fields) exchange places with their mirror twins (‘primed’ fermions, Higgses and gauge fields). If this symmetry is exact, then two sectors should have identical microphysics. In particular, our particles and their mirror twins should have exactly equal masses. The fermions of two sectors can be exchanged with or without the chirality change. Here we shall concentrate on the former case, so called mirror parity \({\mathcal P}\) which exchanges our left-handed (LH) fermions with their right-handed (RH) mirror twins. This symmetry can be interpreted as a generalization of parity.

A direct way to establish the existence of mirror matter is the experimental search for oscillation phenomena between ordinary and mirror particles. In fact, all neutral particles, elementary (as neutrinos) or composite (as the neutron) can have mixings with their mirror twins. Such mixings violate lepton (\(\mathrm{L},\mathrm{L}'\)) or baryon (\(\mathrm{B},\mathrm{B}'\)) numbers of two sectors by one unit, and they can be originated from some relevant effective interactions in the mixed Lagrangian \({\mathcal L}_{\mathrm{mix}}\). Interestingly, such interactions induce \(\mathrm{B}\!-\!\mathrm{L}\) and \(\mathrm{B}'\!-\!\mathrm{L}'\) violating reactions in the early universe which can co-generate baryon asymmetries in both ordinary and mirror worlds [44,45,46].

For warming up, let us consider the lepton sector including three LH families of our lepton doublets \(\ell =(\nu _L,e_L)^T\) and correspondingly three RH families of mirror leptons \(\ell '=(\nu '_R,e'_R)^T\) (family indices are suppressed). As it is well-known, effective D = 5 operators \(\frac{1}{M} \ell ^T C \ell \phi \phi \) (\(\Delta \mathrm{L}=2\)) induce the neutrino Majorana masses \(m_\nu \sim v^2/M\) [47], where M is some large cutoff scale, \(\phi \) is the Higgs doublet of the SM and \(\langle \phi \rangle =v\) is its vacuum expectation value (VEV). Then, by \({\mathcal P}\) parity, mirror Lagrangian \({\mathcal L}'\) should include the analogous operators \(\frac{1}{M} \ell ^{\prime T} C \ell ' \phi ' \phi '\) (\(\Delta \mathrm{L}'=2\)) which induce the Majorana masses of mirror neutrinos \(m_{\nu '} \sim v^{\prime 2}/M\), with \(\phi \) being the Higgs doublet of SM\('\) and \(\langle \phi ' \rangle =v'\) being its VEV.

However, also the mixed Lagrangian \({\mathcal L}_{\mathrm{mix}}\) can include similar D = 5 operators \(\frac{1}{M} \overline{\ell } \ell ' \phi ^\dagger \phi '\) which violate both \(\mathrm{L}\) and \(\mathrm{L}'\) by one unit (but conserve \(\mathrm{L}+ \mathrm{L}'\)) and induce \(\nu -\nu '\) mass-mixings \(m_{\nu \nu '} \sim vv'/M\) [48,49,50]. Hence, mirror neutrinos can be natural candidates for sterile neutrinos, with specific oscillation pattern between three ordinary (active) and three mirror (sterile) neutrinos. In addition, \(\mathrm{L},\mathrm{L}'\)-violating scattering processes \(\ell \phi \rightarrow \ell ' \phi '\) etc. induced by these operators provide a co-leptogenesis mechanism [44, 45] which can explain baryon and dark matter fractions in the universe, \(\Omega '_{\mathrm{B}}/\Omega _{\mathrm{B}}\simeq 5\) [46, 51].

3. Let us discuss now the system of ordinary and mirror neutrons. The neutron and antineutron Dirac masses are equal by fundamental reasons (CPT): \(m \,\overline{n} n=m \,\overline{n_c} n_c\) and \(m' \overline{n'} n'= m' \,\overline{n'_c} n'_c\). As for ordinary and mirror neutron masses, they are equal by mirror parity, \(m'=m\), if the latter is an exact symmetry. (In next section we consider also a situation when n and \(n'\) have a small mass splitting due to spontaneous breaking of \({\mathcal P}\) parity.)

In principle, all four states, n, \(n_c\), \(n'\) and \(n'_c\), can have mixings among each other. Namely, if one introduces the neutron–antineutron mixing (1), then, by mirror parity, analogous mixing between the mirror neutron and mirror antineutron should also exist. Thus, the mass terms describing \(\Delta \mathrm{B}=2\) and \(\Delta \mathrm{B}'=2\) mixings read:

$$\begin{aligned} \frac{ \epsilon _{n{\overline{n}}} }{2} \,\big (\overline{n_c}\, n + \overline{n'_c}\, n' \big ) + \mathrm{h.c.} \end{aligned}$$
(6)

As for mass mixings between ordinary and mirror states, they violate both \(\mathrm{B}\) and \(\mathrm{B}'\) by one unit. However, \(n-n'\) (and \(n_c - n'_c\)) mixing conserves the combination \(\mathrm{B}+ \mathrm{B}'\):

$$\begin{aligned} \frac{\varepsilon _{nn'}}{2} \, \big (\overline{n'} n + \overline{n' _c}\, n_c \big ) + \mathrm{h.c.} \end{aligned}$$
(7)

whereas \(n-n'_c\) and \(n'-n_c\) mixings conserve \(\mathrm{B}- \mathrm{B}'\):

$$\begin{aligned} \frac{\varepsilon _{n{\overline{n}}'} }{2} \big ( \overline{n'_c} \, n + \overline{n_c}\, n' \big ) + \mathrm{h.c.} \end{aligned}$$
(8)

A priori, the mixing masses \( \epsilon _{n{\overline{n}}} \), \(\varepsilon _{nn'}\) and \(\varepsilon _{n{\overline{n}}'} \) are just independent phenomenological parameters which values can be limited only by the experiment or by astrophysical bounds. As already discussed above, the Majorana mass term (6) is limited by the experimental bounds on nuclear stability as \( \epsilon _{n{\overline{n}}} < 2.5 \times 10^{-24}\) eV [17]. As for the mixing terms (7) and (8), they can be much larger: in fact, existing limits (discussed in more details in next sections) do not exclude \(\varepsilon _{nn'}\) and \(\varepsilon _{n{\overline{n}}'} \) as large as \(10^{-15}\) eV or perhaps even larger. All these mixings can be induced by certain effective six-fermion operators, and to understand theoretically how they could naturally fall in the above ranges, one has to analyze how the structures of these operators are constrained by the gauge symmetry.

In ordinary sector \(SU(3)\times SU(2)\times U(1)\) the quarks (\(\mathrm{B}=1/3\)) have the LH components \(q_L=(u_L,d_L)\) transforming as electroweak doublets and the RH ones \(u_R,d_R\) transforming as singlets, whereas the anti-quark fields (\(\mathrm{B}=-1/3\)) have opposite chiralities: \(q^c_R=(u^c_R,d^c_R)\) and \(u^c_L,d^c_L\). Mirror sector \(SU(3)'\times SU(2)'\times U(1)'\) must have exactly the same content modulo the fermion chiralities: mirror quarks are the RH doublets \(q'_R=(u'_R,d'_R)\) and LH singlets \(u'_L,d'_L\) (\(\mathrm{B}'=1/3\)), and antiquarks are \(q^{\prime c}_L = (u^{\prime c}_L,d^{\prime c}_L)\) and \(u^{\prime c}_R,d^{\prime c}_R\) (\(\mathrm{B}'=-1/3\)).

Thus, gauge symmetries allow D = 9 operators with \(\Delta \mathrm{B}=2\) and \(\Delta \mathrm{B}'=2\):

$$\begin{aligned} \frac{1}{\Lambda _2^5} \left[ \overline{ (u^{c} d^{c} d^{c} )_L} (udd)_R + \overline{ (u^{\prime c} d^{\prime c} d^{\prime c} )_R} (u'd'd')_L \right] + \mathrm{h.c.}\nonumber \\ \end{aligned}$$
(9)

as well as the mixed D = 9 operators conserving \(\mathrm{B}+\mathrm{B}'\):

$$\begin{aligned} \frac{1}{\Lambda ^5} \, \overline{ (u'd' d')_L} \, ( u d d) _R+ \mathrm{h.c.} \end{aligned}$$
(10)

where the parentheses contain gauge invariant spin 1/2 chiral combinations of three ordinary quarks which can be composed as e.g. \((u_{R,L}^T Cd_{R,L}) d_R\), and analogous combinations \((u^{\prime T}_{L,R} C d'_{L,R}) d'_L\) of three mirror quarks.

As for the mixed \(\mathrm{B}- \mathrm{B}'\) conserving operators, they cannot be induced without breaking electroweak symmetries in two sectors since \(d_L\subset q_L\) and \(d'_R\subset q'_R\) states reside in weak doublets. Thus, the gauge invariance of these operators requires insertion of the Higgs doublets, \(\phi \) or \(\phi '\), and their minimal dimension is D = 10. After inserting the VEVs \(\langle \phi \rangle = \langle \phi ' \rangle =v\), these operators read:

$$\begin{aligned} \frac{v}{\Lambda _1^6} \left[ \overline{ (u^{\prime c} d^{\prime c} d^{\prime c} )_L} ( u d d)_R + \overline{ (u^{c} d^{c} d^{c} )_R} ( u' d' d') _L \right] + \mathrm{h.c.}\nonumber \\ \end{aligned}$$
(11)

Operators (9), (10) and (11) are explicitly invariant under \({\mathcal P}\) parity \((udd)_{R.L} \leftrightarrow (u'd'd')_{L,R}\).Footnote 3 The cutoff scales \(\Lambda \), \(\Lambda _1\) and \(\Lambda _2\) are a priori independent parameters which can be determined (and related to each other) in the context of UV-complete renormalizable models employing some heavy intermediate particles.

Namely, in the context of the see-saw type models for \(n-n'\) mixing proposed in Refs. [18, 52] one can introduce a gauge singlet Dirac Fermion N which acts as a messenger between two sectors, with the mass term \(M \overline{N}N = M \overline{N_L} N_R + \mathrm{h.c.}\), where \(N_L\) and \(N_R\) are respectively its LH and RH components. Introducing also color-triplet (respectively of SU(3) and \(SU(3)'\)) scalars S and \(S'\) with masses \(M_S=M_{S'}\) (equal due to \({\mathcal P}\) parity), one can write the following Lagrangian terms:

$$\begin{aligned}&{\mathcal L}_{\mathrm{Yuk}} = u_{R,L}^TCd_{R,L} S + S^\dagger N_R^T Cd_R + \mathrm{h.c.} \nonumber \\&{\mathcal L}'_{\mathrm{Yuk}} = u^{\prime T}_{L,R}Cd'_{L,R} S' + S^{\prime \dagger } N_L^T C d'_L + \mathrm{h.c.} \end{aligned}$$
(12)

(the Yukawa constants and gauge indices are suppressed). After integrating out the heavy states \(S,S'\) and N, these terms induce \(\mathrm{B}+\mathrm{B}'\) conserving operator (10) with \(\Lambda ^5 \sim M_N M_S^4\) [18, 52] which gives rise to mixing (7):

$$\begin{aligned} \varepsilon _{nn'}\sim \frac{\Lambda _{\mathrm{QCD}}^6}{\Lambda ^5} \sim \frac{ (10~\mathrm{TeV})^5 }{MM_S^4} \times 10^{-15}~\mathrm{eV}. \end{aligned}$$
(13)

Operator (9) can be induced in this model, with \(\Lambda _2^5 \sim M^2 M_S^4/\mu \), if in addition to Dirac mass \(M\overline{N}N\) the heavy fermion N has also a Majorana mass term \(\mu N C N + \mathrm{h.c.}\) [18, 52]. Provided that \(\mu \ll M\), we get mixings (6) with

$$\begin{aligned} \epsilon _{n{\overline{n}}} \sim \frac{\Lambda _{\mathrm{QCD}}^6}{\Lambda _2^5}\sim \frac{\mu \Lambda _{\mathrm{QCD}}^6}{M^2M_S^4} \sim \frac{\mu }{M} \varepsilon _{nn'}. \end{aligned}$$
(14)

Hence, one can naturally have \( \epsilon _{n{\overline{n}}} \ll \varepsilon _{nn'}\) if the Majorana mass \(\mu \) is much smaller than the Dirac Mass M. In particular, small \(\mu \) can be induced by the low scale spontaneous baryon violation as e.g. in Refs. [52, 53]. Clearly, \( \epsilon _{n{\overline{n}}} \) vanishes if \(\mu =0\).

Finally, also operator (11) can be induced if we introduce an extra vector-like down-type quark D having a Dirac mass term \(M_D (\overline{D_L}D_R + \mathrm{h.c.})\), where both LH and RH components \(D_L\) and \(D_R\) are the weak singlets.Footnote 4 Then, by \({\mathcal P}\) parity, also its mirror twin \(D'\) should be introduced with the same Dirac mass \(M_D (\overline{D'_L}D'_R + \mathrm{h.c.})\). Hence, the following Yukawa terms can be added to Lagrangian (12):

$$\begin{aligned}&\Delta {\mathcal L}_{\mathrm{Yuk}} = S\, N_R^T C D^c_R + \phi D_R^T C q^c_R + \mathrm{h.c.} \nonumber \\&\Delta {\mathcal L}'_{\mathrm{Yuk}} = S' N_L^T C D^{\prime c}_L + \phi ^{\prime } D^{\prime T}_L C q^{\prime c}_L + \mathrm{h.c.} \end{aligned}$$
(15)

In this way, after substituting the Higgs VEVs \(\langle \phi \rangle = \langle \phi ' \rangle =v\), operator (11) is induced with \(\Lambda _1^6 \sim M_D M M_S^4 \sim M_D\Lambda ^5 \). So we get mixing term (8) with

$$\begin{aligned} \varepsilon _{n{\overline{n}}'} \sim \frac{v \Lambda _{\mathrm{QCD}}^6}{\Lambda _1^6} \sim \frac{v}{M_D} \varepsilon _{nn'}. \end{aligned}$$
(16)

Due to the experimental bound on extra quark mass \(M_D > 1\) TeV, one expects \(\varepsilon _{n{\overline{n}}'} /\varepsilon _{nn'}< 0.1\) or so. However, one cannot exclude a situation when \(\varepsilon _{nn'}\) and \(\varepsilon _{n{\overline{n}}'} \) have comparable values, by some conspiracy of the Yukawa constants omitted in couplings (12) and (15). In the following, we conservatively consider the parameter \(r=\varepsilon _{n{\overline{n}}'} /\varepsilon _{nn'}\) to be less than 1 and take \(r=1\) (i.e. \(\varepsilon _{n{\overline{n}}'} = \varepsilon _{nn'}\)) as a marginal case.

Extra color particles, as scalar S and fermion D with the masses of few TeV, can be within the reach of the LHC or future accelerators. This makes our picture potentially testable also at the high energy frontier.

4. In what follows we discuss the oscillation phenomena between the four states \(n,{{\overline{n}}} , n', {{\overline{n}}} '\) due to mass mixings (6), (7) and (8). The time evolution of the wavefunction \(\Psi = (\psi _n, \psi _{{{\overline{n}}} }, \psi _{n'},\psi _{{{\overline{n}}} '})^T\) in medium is determined by the Schrödinger equation \(i d\Psi /dt = H\Psi \) with HamiltonianFootnote 5

$$\begin{aligned} H=\begin{pmatrix} U \! + \! \mu \varvec{B} \varvec{\sigma } &{} \epsilon _{n{\overline{n}}} &{} \varepsilon _{nn'}&{} \varepsilon _{n{\overline{n}}'} \\ \epsilon _{n{\overline{n}}} &{} \! \bar{U}\! - \! \mu \varvec{B} \varvec{\sigma } &{} \varepsilon _{n{\overline{n}}'} &{} \varepsilon _{nn'}\\ \varepsilon _{nn'}&{} \varepsilon _{n{\overline{n}}'} &{} \! U' \! + \! \mu \varvec{B}'\! \varvec{\sigma } &{} \epsilon _{n{\overline{n}}} \\ \varepsilon _{n{\overline{n}}'} &{} \varepsilon _{nn'}&{} \epsilon _{n{\overline{n}}} &{} \! \bar{U}' \! - \! \mu \varvec{B}'\! \varvec{\sigma } \end{pmatrix} \end{aligned}$$
(17)

where each component is in itself a \(2\times 2\) matrix acting on two spin states as far as wavefunctions \(\psi _n,\psi _{{{\overline{n}}} }\) etc. are two component spinors. The terms \(U,\bar{U},U'\) and \(\bar{U}'\) describe the matter induced potentials respectively for \(n,{{\overline{n}}} , n'\) and \({{\overline{n}}} '\) states, \( \varvec{B}\) and \( \varvec{B}'\) are ordinary and mirror magnetic fields and \( \varvec{\sigma }=(\sigma _x,\sigma _y,\sigma _z)\) are the Pauli matrices. Without loss of generality, direction of ordinary magnetic field can be taken as z-axis, i.e. \( \varvec{B}=B (0,0,1)\), and the mirror one can be taken in \(x-z\) plane, i.e. \( \varvec{B}'=B'(\sin \!\beta ,0,\cos \!\beta )\).

The Hamiltonian eigenstates \(n_{1,2,3,4}\) are superpositions of the ‘flavor’ states \(n,{{\overline{n}}} ,n',{{\overline{n}}} '\):

$$\begin{aligned} \left( \begin{array}{c} n_1 \\ n_2 \\ n_3 \\ n_4 \end{array}\right) = \begin{pmatrix} S_{1n} &{} S_{1{{\overline{n}}} } &{} S_{1n'} &{} S_{1{{\overline{n}}} '} \\ S_{2n} &{} S_{2{{\overline{n}}} } &{} S_{2n'} &{} S_{2{{\overline{n}}} '} \\ S_{3n} &{} S_{3{{\overline{n}}} } &{} S_{3n'} &{} S_{3{{\overline{n}}} '} \\ S_{4n} &{} S_{4{{\overline{n}}} } &{} S_{4n'} &{} S_{4{{\overline{n}}} '} \end{pmatrix} \left( \begin{array}{l} n \\ {{\overline{n}}} \\ n' \\ {{\overline{n}}} ' \end{array}\right) . \end{aligned}$$
(18)

This mixing matrix determines the oscillation probabilities, as probability \(P_{n{{\overline{n}}} }(t)=\vert \psi _{{{\overline{n}}} }(t) \vert ^2\) to find antineutron after time t if the initial state at \(t=0\) is the neutron, \(\Psi (0) = (1,0,0,0)^T\), as well as the conversion probabilities \(P_{nn'}(t)\) and \(P_{n{{\overline{n}}} '}(t)\) into mirror states \(n'\) and \({{\overline{n}}} '\).

The oscillations can be averaged in time if their periods are shorter than the flight time. The mean probabilities can be readily deduced, considering that creation of n means to create the eigenstates \(n_{i}\) with the respective probabilities \(\vert S_{in}\vert ^2\). The eigenstates do not oscillate between each other but just propagate, and an eigenstate \(n_i\) is detectable as \({{\overline{n}}} \) with the probability \(\vert S_{i{{\overline{n}}} }\vert ^2\). Hence, for mean probability of \(n-{{\overline{n}}} \) conversion we get \(\overline{P}_{n{{\overline{n}}} }\! = \!\sum _{i}\vert S_{in}\vert ^2 \vert S_{i{{\overline{n}}} }\vert ^2 \), and similarly for \(\overline{P}_{nn'}\) and \(\overline{P}_{n{{\overline{n}}} '}\).

In the rest of this section, we assume that the mirror gas effects at the Earth are negligible, \(U',\bar{U}'=0\), and also suppose that the normal gas density is properly suppressed in laboratory conditions, \(U,{\bar{U}} =0\). So we leave only magnetic contributions in diagonal terms of Hamiltonian (17), denoting their moduli as \(\Omega = \vert \mu B \vert \) and \(\Omega ' = \vert \mu B' \vert \). In addition, we assume that \(\varepsilon _{nn'},\varepsilon _{n{\overline{n}}'} \gg \epsilon _{n{\overline{n}}} \) and neglect direct \(n-{{\overline{n}}} \) mixing taking the limit \( \epsilon _{n{\overline{n}}} =0\).

Let us first discuss the situation under the minimal hypothesis adopted in Ref. [18], assuming that mirror magnetic field \(B'\) is negligibly small at the Earth and setting \(\Omega '=0\). In this case the oscillations are suppressed by ordinary magnetic field B. However, by properly screening the latter, the quasi-free condition \(\Omega t \ll 1\) can be achieved in which case the oscillation probabilities for a flight time t becomeFootnote 6:

$$\begin{aligned}&P_{nn'}(t) = (t/\tau _{nn'})^2, \quad P_{n{{\overline{n}}} '}(t) = (t/\tau _{n{{\overline{n}}} '})^2, \nonumber \\&P_{n{{\overline{n}}} }(t) = P_{nn'}(t) P_{n{{\overline{n}}} '}(t) = ( t^2/\tau _{nn'}\tau _{n{{\overline{n}}} '})^2 \end{aligned}$$
(19)

where \(\tau _{nn'} = \varepsilon _{nn'}^{-1}\) and \(\tau _{n{{\overline{n}}} '} = \varepsilon _{n{\overline{n}}'} ^{-1}\) are characteristic oscillation times. In this case the direct bound \(P_{n{{\overline{n}}} }(t) < 10^{-18}\) from the ILL experiment [16] (performed with \(t\approx 0.1\) s in conditions of screened magnetic field \(B< 0.1\) mG, i.e. \(\Omega t < 0.1\)), merely implies a lower limit for the product of oscillation times:

$$\begin{aligned} \tau _{nn'} \tau _{n{{\overline{n}}} '} > 10^7~\mathrm{s}^2. \end{aligned}$$
(20)

In large magnetic field transition probabilities will be suppressed. Namely, for \(\Omega t \gg 1\), oscillations can be averaged and one gets \(\overline{P}_{nn'}= 2\varepsilon _{nn'}^2/\Omega ^2\), \(\overline{P}_{n{{\overline{n}}} '}= 2\varepsilon _{n{\overline{n}}'} ^2/\Omega ^2\) and \(\overline{P}_{n{{\overline{n}}} } = \overline{P}_{nn'} \overline{P}_{n{{\overline{n}}} '}= 4\varepsilon _{nn'}^2\varepsilon _{n{\overline{n}}'} ^2/\Omega ^4\).

Independent limits on oscillation times can be obtained from dedicated experiments [23,24,25,26,27,28,29] searching for anomalous losses of ultra-cold neutrons (UCN) in different magnetic fields. In the presence of both \(n-n'\) and \(n-{{\overline{n}}} '\) transitions, the neutron disappearance probability \(P_{nn'} + P_{n{\bar{n}}'}\) is proportional to the sum \(\varepsilon _{nn'}^2+\varepsilon _{n{\overline{n}}'} ^2\). Thus the limits of these experiments should be applied to the effective combination \(\tau = (\varepsilon _{nn'}^2+\varepsilon _{n{\overline{n}}'} ^2)^{-1/2}\).

Considering the ratio \(r = \varepsilon _{n{\overline{n}}'} /\varepsilon _{nn'}\) as a free parameter, we have \(\tau _{n{{\overline{n}}} '} = \tau _{nn'}/r\), \(\tau = \tau _{nn'}/\sqrt{1+r^2}\) and so

$$\begin{aligned} \tau _{nn'} \tau _{n{{\overline{n}}} '} = (r + r^{-1})\, \tau ^2 \ge 2 \tau ^2. \end{aligned}$$
(21)

Hence, for typical values \(r \sim 0.1\) one gets \(\tau _{nn'} \approx \tau \) and \(\tau _{nn'} \tau _{n{{\overline{n}}} '} \sim 10\, \tau ^2\). The product (21) becomes minimal for the marginal case \(r=1\), i.e. \(\varepsilon _{n{\overline{n}}'} = \varepsilon _{nn'}\), when \(\tau _{nn'} = \tau _{n{{\overline{n}}} '} = \sqrt{2} \tau \) and \(\tau _{nn'} \tau _{n{{\overline{n}}} '} =2 \tau ^2\).

Under the minimal hypothesis (\(B'=0\)), experiments measuring the UCN losses in the conditions of small (\(\Omega t \ll 1\)) and large (\(\Omega t \gg 1\)) magnetic fields [23,24,25,26,27,28,29] give rather stringent limits on the effective time \(\tau \). Namely, experiments [24, 26] performed at the ILL by Serebrov’s group give a combined lower bound \(\tau > 448\) s (90% CL) [26].Footnote 7 Equation (21) turns this limit into r-dependent limit \( \tau _{nn'} \tau _{n{{\overline{n}}} '} > (r+ r^{-1}) \times 2 \times 10^5\) \(\hbox {s}^2\), which becomes comparable with the lower limit (20) for \(r = 0.02\) or so.

However, these bounds on \(\tau \) as well as the limit (20) become invalid if mirror field \(B'\) is non-zero [19]. In difference from normal magnetic field, it cannot be screened in experiments, and its contribution would block the neutron oscillations into \(n'\) and \({{\overline{n}}} '\) (and also induced \(n-{{\overline{n}}} \) oscillation) even if ordinary field B is suppressed.

Hamiltonian (17), with non-zero magnetic fields \( \varvec{B}\) and \( \varvec{B'}\) having arbitrary directions, can be diagonalized following the techniques described in Refs. [19, 30] and the elements of mixing matrix (18) can be calculated. Let us also remark that the oscillation probabilities do not depend on the neutron spin state (polarization). If the difference of magnetic fields is large enough, \(\vert \Omega -\Omega '\vert t \gg 1\), oscillations can be averaged in time, and the mean probabilities can be presented in a convenient form as

$$\begin{aligned}&\overline{P}_{nn'} = \frac{2\cos ^2(\beta /2)}{ \tau _{nn'}^2 (\Omega - \Omega ^{\prime })^2} + \frac{2 \sin ^2(\beta /2)}{\tau _{nn'}^2(\Omega + \Omega ^{\prime })^2} \, , \nonumber \\&\overline{P}_{n{\bar{n}}'} = \frac{2 \sin ^2(\beta /2)}{\tau _{n{{\overline{n}}} '}^2(\Omega - \Omega ^{\prime })^2} + \frac{2 \cos ^2(\beta /2)}{\tau _{n{{\overline{n}}} '}^2(\Omega + \Omega ^{\prime })^2}, \nonumber \\&\overline{P}_{n{\bar{n}}} = \overline{P}_{nn'} \overline{P}_{n{\bar{n}}'}. \end{aligned}$$
(22)

Namely, in the limit \(B = 0\) we get \(\overline{P}_{nn'}= 2/(\tau _{nn'}\Omega ')^2\), \(\overline{P}_{n{\bar{n}}'} = 2/(\tau _{n{{\overline{n}}} '}\Omega ')^2\) and \(\overline{P}_{n{\bar{n}}} = 4/(\tau _{nn'}\tau _{n{{\overline{n}}} '} \Omega ^{\prime 2})^2\). Hence, in this case the bound from \(n-{{\overline{n}}} \) experiment \(\overline{P}_{n{\bar{n}}} < 10^{-18}\) [16] restricts the product of oscillation times as

$$\begin{aligned} \tau _{nn'} \, \tau _{n{{\overline{n}}} '} > \frac{2 \times 10^9}{\Omega ^{\prime 2}} \approx \left( \frac{0.5\,\mathrm{G}}{B'}\right) ^2 \times 95~\mathrm{s}^2. \end{aligned}$$
(23)

Note that this limit is much weaker than the limit (20) obtained under the minimal hypothesis of vanishing \(B'\).

By increasing ordinary field B, \(\Omega -\Omega '\) dependent terms in \(P_{nn'}\) and \(P_{n{{\overline{n}}} '}\) start to increase and approach the resonance when B gets close to \(B'\). For \(\vert B-B'\vert \) large enough, so that \(\vert \Omega -\Omega ' \vert t \gg 1\), the Eq. (22) for time averaged probabilities remain applicable. However, when B gets so close to \(B'\) that the quasi-free condition \(\vert \Omega -\Omega '\vert t \ll 1\) is satisfied (e.g. \(\vert B- B' \vert < 0.1\) mG for \(t=0.1\) s), oscillation probabilities become maximal. Namely, neglecting contributions of \(\Omega +\Omega '\) dependent terms in (22) we get:

$$\begin{aligned}&P_{nn'}(t) = \frac{t^2 \cos ^2(\beta /2)}{ \tau _{nn'}^2 }, \quad P_{n{{\overline{n}}} '}(t) = \frac{t^2 \sin ^2(\beta /2)}{ \tau _{n{{\overline{n}}} '}^2 }, \nonumber \\&P_{n{{\overline{n}}} }(t) = P_{nn'}(t) P_{n{{\overline{n}}} '}(t) = \left( \!\frac{t^2}{\tau _{nn'}\tau _{n{{\overline{n}}} '}}\! \right) ^2 \frac{\sin ^2\!\beta }{4}. \end{aligned}$$
(24)

For non-vanishing \(B'\), the limits on the effective oscillation time \(\tau \) were obtained by experiments [26,27,28,29] which measured the UCN loss rates for different values and orientations of magnetic field B. Since the neutron disappearance probability is contributed by both \(n-n'\) and \(n-{{\overline{n}}} '\) oscillations, these experiments measure the sum of probabilities \(P_{nn'}+P_{n{{\overline{n}}} '}\). Interestingly, the dependence on the unknown angle \(\beta \) can be excluded by measuring the UCN losses, for a given value of B, for two opposite directions of the magnetic field, \( \varvec{B}\) and \(- \varvec{B}\). The inversion of magnetic field \( \varvec{B}\rightarrow - \varvec{B}\) is equivalent to \(\beta \rightarrow 180^\circ \!-\!\beta \), which exchanges the factors \(\cos ^2(\beta /2)\) and \(\sin ^2(\beta /2)\) between the first and second terms in (22). Hence, the average result between \( \varvec{B}\) and \(- \varvec{B}\) measurements should not depend on \(\beta \). Namely, in the “off-resonance” case \(\vert \Omega -\Omega ' \vert t \gg 1\), for these averages we get:

$$\begin{aligned} \overline{P}^{\mathrm{av}}_{nn'} + \overline{P}^{\mathrm{av}}_{n{{\overline{n}}} '}= \frac{1}{ \tau ^2} \left[ \frac{1}{(\Omega - \Omega ^{\prime })^2} + \frac{1 }{(\Omega + \Omega ^{\prime })^2} \right] \end{aligned}$$
(25)

and in “close to resonance” case \(\vert \Omega -\Omega ' \vert t \ll 1\) , from (24) one analogously gets \(\overline{P}^{\mathrm{av}}_{nn'} + \overline{P}^{\mathrm{av}}_{n{{\overline{n}}} '}= \frac{1}{2}(t/\tau )^2\).

The lower limit on the effective oscillation time \(\tau \) obtained from the UCN experiments [23,24,25,26,27,28,29] depends on the inferred value of \(B'\). The results of these experiments are summarized in Refs. [28, 29] where the respective limits on \(\tau \) are shown (see e.g. Fig. 7 in Ref. [28]) as wiggly functions of \(B'\) with the values varying between \(\tau _{B'}=(20{-} 40)\) s within the interval \(B'= (30 {-} 250)\) mG, excluding narrow peaks with heights exceeding 100 s at \(B'= 100\) mG and \(B'=200\) mG. (Therefore, for certain values of \(B'\) in this interval, the r-dependent limits \(\tau _{nn'}\tau _{n{{\overline{n}}} '} > 400 (r+r^{-1}) \times (\tau _{B'}/20\,\mathrm{s})^2\) obtained from Eq. (21) become competitive to \(n-{{\overline{n}}} \) limit (23).) However, already at \(B'=0.3\) G, the lower limit becomes much smaller, \(\tau \approx 5\) s, and then it drops rapidly as \(\tau \approx (0.5\,\mathrm{G}/B')^2 \times 1\) s or so.

Let us turn now to the induced \(n-{{\overline{n}}} \) oscillation, and investigate how large it probability can be. As noted above, mirror magnetic field cannot be controlled in the experiments and its value is unknown. However, the ordinary field can be varied, and when B gets closer to \(B'\) so that \(\vert \Omega - \Omega ' \vert \) becomes small, the probabilities \(P_{nn'}\) and \(P_{n{{\overline{n}}} '}\) resonantly increase. Then the probability of induced \(n-{{\overline{n}}} \) transition \(P_{n{{\overline{n}}} } = P_{nn'} P_{n{{\overline{n}}} '}\) increases with a double velocity and it can become very large.

For demonstration, let us take e.g. \(B'=0.5\) G and \(\tau _{nn'} \, \tau _{n{{\overline{n}}} '}=100\) \(\hbox {s}^2\), so that in very small magnetic field \(B\ll B'\) the probability of \(n-{{\overline{n}}} \) conversion matches the ILL experimental bound \(\overline{P}_{n{{\overline{n}}} }(B\!=\!0) \simeq 10^{-18}\) [16]. For simplicity, we also take \(\beta =90^\circ \). Let us discuss now what happens when B increases and gets closer to \(B'\), e.g. \(B=0.45\) G (i.e. \(\vert B - B' \vert = 50\) mG). Then from Eq. (22) we get \(\overline{P}_{n{{\overline{n}}} }(B) = 2.5 \times 10^{-15}\) which is more than 3 orders of magnitude larger than \(\overline{P}_{n{{\overline{n}}} }(B\!=\!0)\). Moving closer to the resonance and taking e.g. \(\vert B - B' \vert = 10\) mG, one gets \(\overline{P}_{n{{\overline{n}}} }(B) = 1.5 \times 10^{-12}\), thus gaining another 3 orders of magnitude.

By fine scanning over the magnetic field values one can arrive enough close to the resonance, achieving the quasi-free regime \(\vert \Omega -\Omega '\vert t \ll 1\) (e.g. \(\vert B- B' \vert < 1\) mG for \(t=0.1\) s). In this case \(n-{{\overline{n}}} \) transition probability given by Eq. (24) can be rendered as large as

$$\begin{aligned} P_{n{{\overline{n}}} }(t)= & {} \frac{\sin ^2\!\beta }{4} \left( \frac{t}{0.1~\mathrm{s}}\right) ^{\!4} \! \left( \frac{100~\mathrm{s}^2}{\tau _{nn'} \tau _{n{{\overline{n}}} '} }\right) ^{\!2}\! \times 10^{-8} \nonumber \\&\le \sin ^2\!\beta \left( \frac{t}{0.1~\mathrm{s}}\right) ^{\!4} \left( \frac{B'}{0.5\,\mathrm{G}}\right) ^{\!4} \times 2.5\times 10^{-9} \end{aligned}$$
(26)

where the last row takes in account the limit (23) on \(\tau _{nn'} \tau _{n{{\overline{n}}} '}\). Hence, taking e.g. \(B'=0.5\) G and \(\sin ^2\beta = 1/2\) as random average of unknown angle, we see that, for the neutron flight time \(t\approx 0.1\) s, the probability of \(n-{{\overline{n}}} \) transition induced by \(n-n'\) and \(n-{{\overline{n}}} '\) mixings can be 9 orders of magnitude larger than the benchmark probability (3) due to direct \(n-{{\overline{n}}} \) mixing. The effect can be stronger if \(B'\) is larger than 0.5 G. E.g. for \(B'= 1.5\) G, one could gain another two orders of magnitude.

Therefore, if mirror magnetic field is present at the Earth, the existing experimental limits do not exclude the possibility of enormous enhancement of \(n-{{\overline{n}}} \) conversion probability, by many orders of magnitude. This effect can be searched in experiments similar to the ILL experiment [16] but without suppressing the magnetic field B. Since the value of \(B'\) is unknown, the applied magnetic field should be varied in some proper steps to find the effect of resonant enhancement. As for the its direction (unknown angle \(\beta \)), it can be identified e.g. by changing the direction of applied magnetic field by 90 degrees: if by chance \(\sin ^2\beta \) is small, then \(\sin ^2(\beta +90^\circ )\approx 1\).

Fig. 1
figure 1

\(P_{n{{\overline{n}}} }(t)\) as function of applied magnetic field B for the cases \(B'=0.05,\, 0.17,\, 0.5, \, 1.5\) G (from left to right). Dashed curves correspond to the flight time \(t=0.1\) s, and solid curves correspond to shorter flight time \(t=0.02\) s. For simplicity, \(\beta =90^\circ \) is assumed

Full size image

In Fig. 1 we show how large effects can be obtained by scanning of the magnetic field B in the cases of different inferred values for mirror field \(B'\). For each choice, the product \(\tau _{nn'} \tau _{n{{\overline{n}}} '}\) is taken to saturate the bound (23), so that respective probabilities of \(n-{{\overline{n}}} \) oscillation at vanishing magnetic field are normalized as \(P_{n{{\overline{n}}} }(B\!=\!0) \approx 10^{-18}\), fulfilling the bound from the ILL experiment [16]. The dotted curves of different colors show respective values of \(P_{n{{\overline{n}}} }\) as functions of B in the case of long baseline experiment with cold neutrons assuming a typical flight time \(t=0.1\) s (in some sense, repeating the ILL seminal experiment with about 100 m long vessel [16] but with varying magnetic field). For comparison, we also show the similar expectations for a smaller scale experiment with shorter flight time \(t=0.02\) (solid curves of the same colors). Taking in consideration that similar experiment for the neutron regeneration effect \(n\rightarrow n' \rightarrow n\) [60] is planned at the Oak Ridge National Laboratory (ORNL), with about 20 m baseline [61], the effect \(n\rightarrow n'/{{\overline{n}}} ' \rightarrow {{\overline{n}}} \) regeneration into the antineutron can be searched along the same lines, just substituting the neutron detector by the antineutron one.

We discussed the effect on \(n-{{\overline{n}}} \) oscillations induced by \(n-n'\) and \(n-{{\overline{n}}} '\) mass mixings. Let us remark that such oscillations could occur also via the neutron transitional magnetic (or electric) dipole moments in \(n'\) and \({{\overline{n}}} '\) states [62] which possibility will be discussed in details elsewhere. Let us remind that the Lorentz invariance forbids the transitional moments between n and \({{\overline{n}}} \) states but not between the ordinary and mirror states [63].

Let us briefly discuss now the situation when ordinary and mirror neutrons are not exactly degenerate in mass but they have a mass splitting \(\delta = m'-m \ne 0\) due to a spontaneous breaking of mirror parity which induces a difference between the Higgs VEVs \(\langle \phi \rangle =v\) and \(\langle \phi ' \rangle =v'\). This possibility can related to asymmetric post-inflationary reheating of the ordinary and mirror sectors [38, 39], and in some scenarios this splitting can be rather tiny [64].

Interestingly, \(n-n'\) oscillation with a mass splitting \(\delta \sim 10^{-7}{-}10^{-6}\) eV [65] can be a solution to the neutron lifetime puzzle related to about \(4\sigma \) discrepancy between the neutron decay times measured in the trap and beam experiments. It is based on the idea that \(n-n'\) conversion can be resonantly enhanced in strong (few Tesla) magnetic fields used in beam experiments and thus the deficit of protons is because mirror neutrons decay in invisible channel \(n' \rightarrow p'e'\nu '\).Footnote 8 However, in the following we do not bias ourselves with this range of \(\delta \) and consider it as a free parameter, large enough to satisfy the condition \(\delta \, t \gg 1\) in the oscillation experiments with the neutron flight time t.

Without loss of generality, direction of the magnetic field can be taken as z-axis, i.e. \( \varvec{B}=B (0,0,1)\). Then \(8\times 8\) Hamiltonian (17) can be split two \(4\times 4\) matrices \(H_+\) and \(H_-\) describing separately the neutrons of two polarizations (spin projections \(\pm 1/2\) on z-axis):

$$\begin{aligned} H_\pm =\begin{pmatrix} - \delta \mp \Omega &{} 0 &{} \varepsilon _{nn'}&{} \varepsilon _{n{\overline{n}}'} \\ 0 &{} - \delta \pm \Omega &{} \varepsilon _{n{\overline{n}}'} &{} \varepsilon _{nn'}\\ \varepsilon _{nn'}&{} \varepsilon _{n{\overline{n}}'} &{} 0 &{} 0 \\ \varepsilon _{n{\overline{n}}'} &{} \varepsilon _{nn'}&{} 0 &{} 0 \end{pmatrix} \end{aligned}$$
(27)

where \(\Omega = \vert \mu B \vert \). Now the probabilities of \(n-n'\) and \(n-{{\overline{n}}} '\) oscillations depend on the neutron polarization. In the case when \(\vert \delta \pm \Omega \vert t \gg 1\), the time oscillations can be averaged and the mean probabilities read

$$\begin{aligned}&\overline{P}_{nn'}^\pm = \frac{2 \varepsilon _{nn'}^2}{(\delta \pm \Omega )^2 } , \quad \overline{P}_{n{{\overline{n}}} '}^\pm = \frac{2 \varepsilon _{n{\overline{n}}'} ^2}{(\delta \pm \Omega )^2 } \end{aligned}$$
(28)
$$\begin{aligned}&\overline{P}_{{{\overline{n}}} n'}^\pm = \frac{2 \varepsilon _{nn'}^2}{(\delta \mp \Omega )^2 } , \quad \overline{P}_{{{\overline{n}}} {{\overline{n}}} '}^\pm = \frac{2 \varepsilon _{n{\overline{n}}'} ^2}{(\delta \mp \Omega )^2 }. \end{aligned}$$
(29)

Hence, the neutron disappearance probability \(P_{nn'}^\pm + P_{n{{\overline{n}}} '}^\pm \) resonantly increases for \(\Omega \approx \delta \) only for one spin state (namely for ‘\(+\)’ polarization if \(\delta <0\)).

As for the probability of induced \(n-{{\overline{n}}} \) transition, it is polarization independent:

$$\begin{aligned} P_{n{{\overline{n}}} }^\pm (t) = \frac{4\varepsilon _{nn'}^2\varepsilon _{n{\overline{n}}'} ^2}{(\delta ^2 -\Omega ^2)^2} + \frac{4\varepsilon _{nn'}^2\varepsilon _{n{\overline{n}}'} ^2\delta ^2 }{ (\delta ^2 -\Omega ^2)^2} \, \frac{\sin ^2(\Omega t)}{\Omega ^2}. \end{aligned}$$
(30)

Here the first term is in fact the product \(\overline{P}_{nn'}^\pm \overline{P}_{n{{\overline{n}}} '}^\mp \). However, for small magnetic field, \(\Omega t \ll 1\), the second term is dominant and we get \(P_{n{{\overline{n}}} }(t) = ( \epsilon _{n{\overline{n}}} ^{\mathrm{eff}} t)^2\) which in fact mimics the contribution of direct \(n-{{\overline{n}}} \) mixing (3) with \( \epsilon _{n{\overline{n}}} ^{\mathrm{eff}}=2\varepsilon _{nn'}\varepsilon _{n{\overline{n}}'} /\delta \). Hence, the experimental limit \(\tau _{n{{\overline{n}}} } > 0.86 \times 10^8\) s implies \( \epsilon _{n{\overline{n}}} ^{\mathrm{eff}}< 7.7 \times 10^{-24}\) eV and so

$$\begin{aligned} \varepsilon _{nn'}\varepsilon _{n{\overline{n}}'} < (\delta /10^{-7}~\mathrm{eV}) \times 7.7 \times 10^{-31}~\mathrm{eV}^2 \end{aligned}$$
(31)

We see from Eq. (30) that large magnetic field suppresses \(n-{{\overline{n}}} \) oscillation. Only in quasi-free resonance regime \(\vert \delta - \Omega \vert t < 1\) we get again \(P_{n{{\overline{n}}} }(t) \sim ( \epsilon _{n{\overline{n}}} ^{\mathrm{eff}}\, t)^2\). Thus, the presence of large mass splitting \(\delta \) prevents the possibility of strong enhancement of \(n-{{\overline{n}}} \) oscillation in constant magnetic field. However, larger resonance effect \(P_{n{{\overline{n}}} } \simeq \varepsilon _{nn'}^2\varepsilon _{n{\overline{n}}'} ^2/(\delta -\Omega )^4\) can be obtained in the experiment in which magnetic field direction is changed to the opposite between the first and second parts of the neutron drift vessel. Let us also remark that bound (31) becomes invalid in the presence of reasonably large mirror magnetic field, or if there exist long range fifth forces mediated by hypothetical \(\mathrm{B}\!-\!\mathrm{L}\) baryophotons which could induce level splitting up to \(\sim 10^{-11}\) eV between n and \({{\overline{n}}} \) states [53, 71].

4. In the previous section we have shown that the strong effects of \(n-{{\overline{n}}} \) conversion due to simultaneously present \(n-n'\) and \(n-{{\overline{n}}} '\) mixings are not excluded by existing experimental limits. Let us discuss now whether this possibility can be excluded by the nuclear stability bounds.

As it is well known, the direct \(n-{{\overline{n}}} \) mixing leads to nuclear instability: the neutron inside the nuclei can annihilate with other nucleons into pions with total energy roughly equal to two nucleon masses. The neutron–antineutron oscillations in nuclei via direct \(n-{{\overline{n}}} \) mixing is described by the Hamiltonian

$$\begin{aligned} H =\begin{pmatrix} U &{} \epsilon _{n{\overline{n}}} \\ \epsilon _{n{\overline{n}}} &{} \overline{U} \end{pmatrix} , \quad U=-V,\quad \overline{U} = -\bar{V} - i W \end{aligned}$$
(32)

where V is the nucleon binding energy typically of few MeV, while the antineutron potential \(\overline{U}\) has both real and imaginary (absorptive) parts both being of the order of 100 MeV [72]. The absorptive part W is in fact related to the antineutron annihilation in nuclear medium.

This Hamiltonian can be diagonalized by canonical transformation \(S H S^{-1} = {\widetilde{H}}\) where \({\widetilde{H}}\) is diagonal and unimodular mixing matrix S can be approximated as

$$\begin{aligned} S = \begin{pmatrix}S_{1n} &{} S_{1{{\overline{n}}} } \\ S_{2n} &{} S_{2{{\overline{n}}} } \end{pmatrix} \approx \begin{pmatrix}1 &{} \epsilon _{n{\overline{n}}} /\Delta U \\ - \epsilon _{n{\overline{n}}} /\Delta U &{} 1 \end{pmatrix} \end{aligned}$$
(33)

with the precision up to quadratic terms in small ratio \( \epsilon _{n{\overline{n}}} /\Delta U\), where \(\Delta U = U- \overline{U}\).

The neutron stationary state in nuclei can be viewed as a superposition \(n_1 = S_{1n} n + S_{1 {{\overline{n}}} } {{{\overline{n}}} }\), and corresponding eigenvalue in \({\widetilde{H}}\) also acquires a small imaginary part due to mixing. Thus \(n_1\) contains the antineutron with the weight \(S_{1{{\overline{n}}} }\) and so it can annihilate with other nucleons (\(N=p,n\)) producing pions. The rate of this reaction can be readily estimated as \(\Gamma _{nN} = \vert S_{1{{\overline{n}}} }\vert ^2 \Gamma _{{{\overline{n}}} }\), where \(\Gamma _{{{\overline{n}}} N}= 2W\) is the antineutron annihilation width at nuclear densities. Thus, from (33) we get:

$$\begin{aligned} \Gamma _{nN} = \frac{ \epsilon _{n{\overline{n}}} ^2}{\vert \Delta U \vert ^2}\Gamma _{{{\overline{n}}} N} = \frac{2 \epsilon _{n{\overline{n}}} ^2 W}{(\overline{V}-V)^2 + W^2}. \end{aligned}$$
(34)

Namely, the limit \( \epsilon _{n{\overline{n}}} ^{-1} = \tau _{n{{\overline{n}}} } > 2.7 \times 10^8\) s on \(n-{{\overline{n}}} \) direct mixing (1) can be obtained in this way from the experimental bound on \(^{16}\)O stability \(\Gamma _{nN} < (1.9 \times 10^{32}\,\mathrm{year})^{-1}\) [17]. This limit is about 3 times stronger than the direct experimental limit \(\tau _{n{{\overline{n}}} } > 0.86 \times 10^8\) s [16].

As it was observed in Ref. [18], only \(n-n'\) mixing cannot destabilize the nuclei by kinematical reasons (energy conservation). But in combination with \(n-{{\overline{n}}} '\) mixing it in principle can, as far as \(n-{{\overline{n}}} \) mixing emerges at second order from \(n-n'\) and \(n-{{\overline{n}}} '\) mixings.

Now the neutron oscillations in nuclear medium is described again by Hamiltonian (17) where we take the neutron and antineutron potentials U and \(\overline{U}\) as in (32). Mirror states have vanishing potentials, \(U', \overline{U}'=0\), and the magnetic contributions are negligible. Let us also set \( \epsilon _{n{\overline{n}}} =0\) for excluding the effect of direct \(n-{{\overline{n}}} \) mixing. Then mixing matrix (18) can be directly computed: \(S_{1n'} = -\varepsilon _{nn'}/V\), \(S_{1{{\overline{n}}} '} = -\varepsilon _{n{\overline{n}}'} /V\), and

$$\begin{aligned} \vert S_{1{{\overline{n}}} }\vert = \frac{2\varepsilon _{nn'}\varepsilon _{n{\overline{n}}'} }{\vert V(\overline{V} -iW)\vert } \ll \frac{\varepsilon _{nn'}\varepsilon _{n{\overline{n}}'} }{V^2} = S_{1n'} S_{1{{\overline{n}}} '}. \end{aligned}$$
(35)

Considering now that the neutron stationary state in nuclei is the eigenstate \(n_1=S_{1n} n + S_{1 {{\overline{n}}} } {{{\overline{n}}} }+ S_{1n'} n' + S_{1 {{\overline{n}}} '} {{{\overline{n}}} '}\), it can annihilate with other “spectator” nucleons (\(N=p,n\)) into pions, with the rate \(\Gamma _{nN} = \vert S_{1{{\overline{n}}} }\vert ^2 \Gamma _{{{\overline{n}}} N}\). In addition, two neutrons in the nucleus can also annihilate into (invisible) mirror pions, with the rate \(\Gamma '_{nn} \simeq \vert S_{1n'} S_{1{{\overline{n}}} '}\vert ^2 \Gamma _{{{\overline{n}}} N}\). For our benchmark \(\tau _{nn'}\tau _{n{{\overline{n}}} '} \sim 100\) \(\hbox {s}^2\), both these rates are below \((10^{60}~\mathrm{year})^{-1}\). For comparison, Super-Kamiokande limit on \(^{16}\)O decays yields \(\Gamma _{n N} < (1.9 \times 10^{32}~\mathrm{year})^{-1}\) [17] while KamLAND limit on the pionless \(^{12}\)C decays is \(\Gamma '_{nn} < (1.4 \times 10^{30}~\mathrm{year})^{-1}\) [73, 74]. Thus, we can conclude that our scenario is perfectly safe against the nuclear stability bounds.

Concluding this section, let us briefly discuss the implications for the neutron stars. In difference from nuclei, in this case \(n-n'\) transitions are not forbidden by cinematic reasons, and they would convert a neutron star in a mixed star composed of both ordinary and mirror neutrons. However, as it was noticed in Ref. [18], for \(\tau _{nn'}\sim 1\) s the conversion time would be much larger than the age if the universe \(t_U\). More detailed analysis brings to the conservative lower limit \(\tau _{nn'} > 10^{-2}{-} 10^{-1}\) s or so [75,76,77].

In the case when both \(n-n'\) and \(n-{{\overline{n}}} '\) mixings are present, with \(\varepsilon _{n{\overline{n}}'} < \varepsilon _{nn'}\), then inside the neutron star the neutron should undergo both \(n-n'\) and \(n-{{\overline{n}}} '\) transitions, with different rates respectively proportional to \(\varepsilon _{nn'}^2\) and \(\varepsilon _{n{\overline{n}}'} ^2\). The produced \(n'\) and \(\overline{n}'\) would annihilate into mirror pions and this could eventually bring to the evaporation of the neutron star. However, for \(\tau _{n{{\overline{n}}} '} > 1\) s the evaporation time would me few orders of magnitude larger than \(t_U\). In fact, the evaporation time comparable with \(t_U\) can even have interesting implications. In fact, when the mass of neutron star, due to this evaporation, reduces to \(0.1~M_\odot \) or so, it becomes unstable and should explode producing the hot and relatively dilute neutron rich medium which can be associated to the kilonovae. This phenomenon can be at the origin of r-processes that enrich the universe by rare elements as gold etc.

6. Concluding, we have discussed a fascinating possibility how the neutron could travel to parallel mirror world and then effectively return to our world as the antineutron. The reason why this effect could skip immediate detection in the experiments can be related to the environmental factors, as the existence of the mirror magnetic fields at the Earth [19]. This hypothesis may sound not so weird considering that there can exist dynamical interactions between ordinary and mirror particles mediated e.g. by the photon–mirror photon kinetic mixing \(\frac{1}{2} \epsilon F^{\mu \nu } F'_{\mu \nu }\) [78] which effectively makes mirror particles electrically mini-charged. The cosmological bounds on the mixing parameter imply \(\epsilon > 10^{-9}\) or so [79, 80] while the direct experimental limit from the positronium decay reads \(\epsilon >5 \times 10^{-8}\) [81]. The Rutherford-like interactions between free ordinary and mirror electrons mediated by this kinetic mixing in rotating protogalaxies can induce circular electric currents which may be strong enough to create the observed magnetic fields on the galaxy scales with the help of moderate dynamo amplification [82]. Such interactions can also have interesting implications for the direct detection of dark mirror matter [83, 84] which is expected be rather light as it should be dominated by the helium component [40]. Ordinary and mirror particles can also interact via some common gauge bosons related e.g. to flavor symmetry [85, 86].

The sun and the Earth could capture some tiny amount of mirror matter via these interactions and this captured component should be partially ionized due to the high temperature at the centre of the Earth [87]. Then the drag of free mirror electrons by the Earth rotation can induce reasonably large circular mirror currents via the mechanism of Ref. [82]. These circular currents can give rise to mirror magnetic field which can be further amplified by the dynamo mechanism. In this case, one can generically expect the mirror magnetic field at the Earth to vary in time. In particular, having a dipole character, it can change its direction with a relative periodicity of few years.

The results of the neutron disappearance experiments [23,24,25,26,27,28,29] still allow \(n-n'\) and/or \(n-{{\overline{n}}} '\) oscillations with effective time \(\tau = (\varepsilon _{nn'}^2+\varepsilon _{n{\overline{n}}'} ^2)^{-1/2}\) which can be as small as few seconds provided that mirror magnetic field \(B'\) is larger than 0.5 G or so. Such a short oscillation time can have interesting implications for the propagation of ultra-high energy cosmic rays at cosmological distances [20, 21]. Interestingly, some experiments show deviations from null-hypothesis compatible with \(\tau \simeq 20\) s provided that \(B' \sim 0.1-0.3\) G [28, 30].

A new UCN experiment planned at the PSI can definitely test the existing anomalies with a sensitivity up to \(\tau \sim 100\) s for \(B' < 1\) G or so [88]. Exclusion in this range would imply \(\tau _{nn'} \tau _{n{{\overline{n}}} '} > 10^{4{-}5}\) \(\hbox {s}^2\) in which case Eq. (26) still allows \(P_{n{{\overline{n}}} } \sim 10^{-12}{-} 10^{-14}\), which is anyway orders of magnitude larger than the maximal value \(\sim 10^{-18}\) (3) allowed in the case of direct \(n-{{\overline{n}}} \) mixing (1). Once again, for amplifying the probability of \(n-{{\overline{n}}} \) transition in the direct search experiments, the magnetic field B should be properly scanned for finding the resonant value (unknown mirror field \(B'\)) instead of suppressing it as in the classic experiment [16].

For testing this possibility, experiments on \(n-{{\overline{n}}} \) search should be performed by scanning different values of magnetic field instead of suppressing it as in classic experiment [16]. In particular, this can be done in \(n\rightarrow n' \rightarrow n\) regeneration experiments planned at the ORNL [61], by modifying it for searching \(n\rightarrow n'/{{\overline{n}}} ' \rightarrow {{\overline{n}}} \) process by replacing the neutron detector by the antineutron one.

The discussed possibility of fast \(n-n'\) and \(n-{{\overline{n}}} '\) oscillations points towards the scale \(M\sim 10\) TeV for underlying new physics responsible for operators (10) and (11) which can be reachable in future accelerators. In addition, it could suggest a low scale baryogenesis scenario generating baryon asymmetries in both sectors, Namely, baryon asymmetries can be produced, from the couplings (12) and (15) via out-of equilibrium \(\mathrm{B}\), \(\mathrm{B}'\) and CP violating scattering processes \(dS \rightarrow d'S'\) and \(dS \rightarrow d^{\prime c} \overline{S}'\) involving color scalars S and \(S'\) of two sectors, along the lines of the co-leptogenesis mechanism related to ordinary and mirror neutrino mixings discussed in Refs. [44].