1 Introduction

The study on exotic hadrons is experiencing a renaissance. Dozens of exotic states which do not fit into the conventional quark model predictions are observed since 2003. Most of these exotic states are thought to be tetraquarks, pentaquarks, or hadronic molecules containing a pair of hidden \(c{\bar{c}}\) or \(b{\bar{b}}\). We refer to Refs. [1,2,3,4,5] for some recent reviews about the study on exotic particles. Very recently, the LHCb collaboration reported the observation of two resonance-like structures \(X_0(2900)\) and \(X_1(2900)\) in the \(D^- K^+\) invariant mass distributions in \(B^+\rightarrow D^+ D^- K^+\) decays [6,7,8]. Their masses, widths and spin-parity quantum numbers are

$$\begin{aligned}&M_{X_0}=2866 \pm 7~ \text{ MeV },\\&\quad \Gamma _{X_0}= 57\pm 13~ \text{ MeV },J^P=0^+, \\&\quad M_{X_1}=2904 \pm 5~ \text{ MeV }, \\&\quad \Gamma _{X_1}=110\pm 12~ \text{ MeV }, J^P=1^-, \end{aligned}$$

respectively. Since they are observed in the \(D^-K^+\) channel, the \(X_0(2900)\) and \(X_1(2900)\) could be states with four different valence quarks \({\bar{c}}{\bar{s}}ud\). The two fully open-flavor tetraquark states are quite distinguished from the previously observed XYZ particles. Before the LHCb observation the tetraquark states with four different flavors have been systematically investigated in Ref. [9] using a color-magnetic interaction model. An excited scalar tetraquark state with the mass 2850 MeV and the quark contents \(cs{\bar{u}}{\bar{d}}\) is predicted in Ref. [9], which may account for the \(X_0(2900)\). Another state with the mass 2902 MeV and the same quark contents is also predicted, but its spin-parity is \(1^+\), which is not consistent with the current experiment. Within a coupled channel chiral unitary approach, several isoscalar \(D^*{\bar{K}}^*\) bound states are predicted [10]. The predicted mass and width of one of these states with \(J^P=0^+\) are very close to those of \(X_0(2900)\). In a very recent paper of Ref. [11], the \(X_0(2900)\) is interpreted as a \({\bar{c}}{\bar{s}}ud\) isosinglet compact tetarquark state, but the broader peak \(X_1(2900)\) with \(J^P=1^-\) is not interpreted in the same tetraquark framework.

It should be mentioned that the D0 collaboration in 2016 ever reported the observation of a narrow state X(5568) in the \(B_s^0\pi ^\pm \) invariant mass spectrum [12]. This X(5568) was then thought to be a fully open-flavor exotic hadron with the quark contents \({\bar{b}}{\bar{d}}su\) (or \({\bar{b}}{\bar{u}}sd\)). However, in a later experimental result reported by the LHCb collaboration [13], the existence of X(5568) was not confirmed based on their pp collision data, and the existence of this state was also severely challenged on theoretical grounds [14,15,16]. The possible reason of its appearance in the D0 and absence in LHCb and CMS experiments was discussed in Ref. [17].

Concerning the nature of these exotic states, apart from the genuine resonances interpretations, some non-resonance interpretations were also proposed in literature, such as the cusp effect or the triangle singularity (TS) mechanism. It is shown that sometimes it is not necessary to introduce a genuine resonance to describe a resonance-like peak, because some kinematic singularities of the rescattering amplitudes could behave themselves as bumps in the corresponding invariant mass distributions and simulate genuine resonances, which may bring ambiguities to our understanding about the nature of exotic states. Before claiming that one resonance-like peak corresponds to one genuine particle, it is also necessary to exclude or confirm these possibilities. We refer to Ref. [18] for a recent and detailed review about the threshold cusps and TSs in hadronic reactions.

In this work, we investigate the \(B^+ \rightarrow D^+D^-K^+\) reaction by considering some possible triangle rescattering processes, and try to provide a natural explanation for the exotic hadron candidates \(X_0(2900)\) and \(X_1(2900)\) reported by LHCb.

2 The model

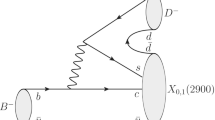
The bottom meson decaying into a charmonium and a kaon meson or a charmed-strange meson and an anti-charmed meson are Cabibbo-favored processes. Therefore it is expected that the rescattering processes illustrated in Fig. 1a, b may play a role in the \(B^+\rightarrow D^+ D^- K^+\) decay. In Fig. 1a, the intermediate state \(\chi _{c1}\) indicates any charmonia with the quantum numbers \(J^{PC}=1^{++}\). For the states (nearly) above \(D{\bar{D}}^*\) threshold, the \(\chi _{c1}\) could be the experimentally observed \(\chi _{c1}(3872)\) (the X(3872) is named \(\chi _{c1}(3872)\) by the Particle Data Group (PDG) [19] according to its quantum numbers), \(\chi _{c1}(4140)\) or \(\chi _{c1}(4274)\) [19]. In Fig. 1b, the intermediate state \(D_{sJ}^+\) indicates a higher charmed-strange meson that can decay into \(D^+ K^0\). The candidates of \(D_{sJ}\) could be \(D_{s1}^{*}(2700)\) and \(D_{s1}^{*}(2860)\), of which the quantum numbers are \(J^{P}=1^{-}\). The \({\bar{D}}_1^0\) in Fig. 1b represents the narrow anti-charmed meson \({\bar{D}}_1(2420)^0\) with \(J^P=1^+\). The thresholds of \(D^{*-}K^{*+}\) and \({\bar{D}}_{1}^{0}K^{0}\) are 2902 and 2918 MeV, respectively. These two thresholds are very close to \(M_{X_0(2900)}\) and \(M_{X_1(2900)}\). It is therefore natural to expect that the \(D^{*-}K^{*+}\) and/or \({\bar{D}}_{1}^{0}K^{0}\) rescattering and the resulting threshold cusps may account for the LHCb observations.

Fig. 1
figure 1

\(B^+\rightarrow D^+ D^- K^+\) via the triangle rescattering diagrams. Kinematic conventions for the intermediate states are a \(K^{*+}(q_1)\), \(\chi _{c1}(q_2)\), \(D^{*-} (q_3)\) and b \({\bar{D}}_1^{0}(q_1)\), \(D_{sJ}^+(q_2)\), \(K^0 (q_3)\)

Full size image

Another intriguing character of the rescattering processes in Fig. 1 is that the \(\chi _{c1}K^{*+}\) and \(D_{sJ}^{+}{\bar{D}}_{1}^0\) thresholds are close to the mass of \(B^+\) meson \(M_{B^+}\), therefore the TSs of rescattering amplitudes in the complex energy plane could be close to the physical boundary, and the TS may enhance the two-body threshold cusp effect or itself may generate a peak in \(D^-K^+\) spectrum. Numerically, if we ignore the widths of intermediate states, when \(4311\le m_{\chi _{c1}} \le 4388\ \text{ MeV }\), the TS of the \(\chi _{c1}K^{*+}D^{*-}\) loop lies on the physical boundary. The observed \(\chi _{c1}(4274)\) is very close to this region. For the \(D_{sJ}^{+}{\bar{D}}_{1}^{0}K^{0}\) loop, when \(2539\le m_{D_{sJ}} \le 2858\ \text{ MeV }\), the TS lies on the physical boundary [18]. There are several charmed-strange mesons whose masses fall in this kinematic range, such as \(D_{s1}^{*}(2700)\) and \(D_{s1}^{*}(2860)\).

Since \(M_{B^+}\) is close to the \(\chi _{c1}K^{*+}\) and \(D_{sJ}^{+}{\bar{D}}_{1}^{0}\) thresholds, the S-wave decays are expected to be dominated. The general S-wave decay amplitudes can be written as

$$\begin{aligned} {\mathcal {A}}(B^+\rightarrow \chi _{c1}K^{*+})= & {} g_{W}^a \epsilon ^*_{\chi _{c1}}\cdot \epsilon ^*_{{K}^{*+}}, \end{aligned}$$
(1)
$$\begin{aligned} {\mathcal {A}}(B^+\rightarrow D_{sJ}^{+}{\bar{D}}_{1}^{0})= & {} g_{W}^b \epsilon ^*_{D_{sJ}^{+}}\cdot \epsilon ^*_{{\bar{D}}_{1}^{0}}, \end{aligned}$$
(2)

where \(g_{W}^a\) and \(g_{W}^b\) represent the weak couplings, and we take the quantum numbers of \(D_{sJ}^{+}\) to be \(J^P=1^-\).

For the processes \(\chi _{c1}\rightarrow D^+ D^{*-}\) and \(D_{sJ}^{+}\rightarrow D^+ K^0\), the amplitudes read

$$\begin{aligned} {\mathcal {A}}(\chi _{c1}\rightarrow D^+ D^{*-})= & {} g_{\chi _{c1} D {\bar{D}}^{*}} \epsilon _{\chi _{c1}}\cdot \epsilon ^*_{{D}^{*-}}, \end{aligned}$$
(3)
$$\begin{aligned} {\mathcal {A}}(D_{sJ}^{+}\rightarrow D^+ K^0)= & {} g_{D_{sJ}DK} p_{K^0}\cdot \epsilon _{D_{sJ}^{+}}. \end{aligned}$$
(4)

The quantum numbers of \(D^- K^+\) system in relative S-, P-, and D-wave are \(J^P=0^+\), \(1^-\) and \(2^+\), respectively. For the rescattering processes in Fig. 1a, b, we are interested in the near-threshold S-wave \(D^{*-} K^{*+}\) (or \({\bar{D}}_{1}^{0} K^{0}\)) scattering into \(D^- K^+\). By taking into account requirements of the parity (strong interaction vertices) and angular momentum conservation, the quantum numbers of \(D^- K^+\) system are \(0^+\) and \(1^-\) for Fig. 1a, b, respectively. The scattering amplitudes for \(D^{*-} K^{*+} \rightarrow D^- K^+\) and \({\bar{D}}_{1}^{0} K^{0} \rightarrow D^- K^+\) can be written as

$$\begin{aligned} {\mathcal {A}}(D^{*-} K^{*+} \rightarrow D^- K^+)= & {} C_{a} \epsilon _{D^{*-}}\cdot \epsilon _{K^{*+}}, \end{aligned}$$
(5)
$$\begin{aligned} {\mathcal {A}}({\bar{D}}_{1}^{0} K^{0} \rightarrow D^- K^+)= & {} C_{b} (p_{K^0}+p_{K^+})\cdot \epsilon _{{\bar{D}}_{1}^{0}}, \end{aligned}$$
(6)

where \(C_a\) and \(C_b\) are coupling constants.

Then, the decay amplitude of \(B^+\rightarrow D^+ D^- K^+\) via the \(\chi _{c1}K^{*+}D^{*-}\) loop in Fig. 1a is given by

$$\begin{aligned}&{\mathcal {A}}_{B^+\rightarrow D^+ D^- K^+}^{[ \chi _{c1}K^{*+}D^{*-} ]} = -{i} \int \frac{d^4q_1}{(2\pi )^4} \frac{{\mathcal {A}}(B^+\rightarrow \chi _{c1}K^{*+}) }{ (q_1^2-m_{{K}^*}^2 +i m_{{K}^*}\Gamma _{{K}^*}) } \nonumber \\&\quad \times \frac{ {\mathcal {A}}(\chi _{c1}\rightarrow D^+ D^{*-}) {\mathcal {A}}(D^{*-} K^{*+} \rightarrow D^- K^+) }{ (q_2^2-m_{\chi _{c1}}^2 +i m_{\chi _{c1}}\Gamma _{\chi _{c1}}) (q_3^2-m_{D^{*}}^2) } , \end{aligned}$$
(7)

where the sum over polarizations of intermediate state is implicit. The amplitude of Fig. 1b is similar to that of Fig. 1a and reads

$$\begin{aligned}&{\mathcal {A}}_{B^+\rightarrow D^+ D^- K^+}^{[ D_{sJ}^{+}{\bar{D}}_{1}^{0}K^{0} ]} = -{i} \int \frac{d^4q_1}{(2\pi )^4} \frac{{\mathcal {A}}(B^+\rightarrow D_{sJ}^{+}{\bar{D}}_{1}^{0}) }{ (q_1^2-m_{{\bar{D}}_{1}}^2 +i m_{{\bar{D}}_{1}}\Gamma _{{\bar{D}}_{1}}) } \nonumber \\&\quad \times \frac{ {\mathcal {A}}(D_{sJ}^{+}\rightarrow D^+ K^0) {\mathcal {A}}({\bar{D}}_{1}^{0} K^{0} \rightarrow D^- K^+) }{ (q_2^2-m_{D_{sJ}}^2 +i m_{D_{sJ}}\Gamma _{D_{sJ}}) (q_3^2-m_{K}^2) }. \end{aligned}$$
(8)

As long as the TS kinematical conditions are satisfied, it implies that one of the intermediate state (here \(\chi _{c1}\) for Fig. 1a and \(D_{sJ}^+\) for Fig. 1b respectively) must be unstable. It is therefore necessary to take into account the width effect. We use the Breit–Wigner (BW) type propagators to account for the width effects of intermediate states, or equivalently replace the real mass m by the complex mass \(m-i\Gamma /2\) [18, 20]. The complex mass in the propagator can remove the TS from physical boundary and makes the physical scattering amplitude finite. Besides, the width effects of \({K}^{*+}\) and \({\bar{D}}_1^0\) are also taken into account in Eqs. (7) and (8) by employing the BW propagators.

3 Numerical results

In order to give the numerical results of the invariant mass spectrum, we firstly estimate some coupling constants in relevant. The experimental data concerning the \(B^+\) decaying into \(D_{sJ}^{+}{\bar{D}}_{1}^{0}\) or \(\chi _{c1}K^{*+}\) with \(\chi _{c1}\) representing a higher axial vector charmonia are not available yet. According to the available data from PDG, we assume that \(\text{ Br }(B^+\rightarrow \chi _{c1}(4274)K^{*+})=1.0\times 10^{-4}\) and \(\text{ Br }(B^+\rightarrow D_{s1}^{*+}(2700){\bar{D}}_{1}^{0})=1.0\times 10^{-3}\). The branching ratio of the open-charm decay mode is set to be lager than that of the charmonium decay mode. This is because that the later one is supposed to be color suppressed. We then have \(|g_W^a|^2/\Gamma _{B^+}\simeq 0.056\) GeV and \(|g_W^b|^2/\Gamma _{B^+}\simeq 0.37\) GeV.

For \(\chi _{c1}(4274)\rightarrow D^+ D^{*-}\), we assume that the partial decay width is around 10 MeV, and obtain \(|g_{\chi _{c1}D{\bar{D}}^*}|\simeq 2.3 \) GeV. For \(D_{s}^{*}(2700)\rightarrow D K\), the coupling constant \(g_{D_{sJ}DK}\) is estimated to be 10.6 in Ref. [21] using the heavy quark effective theory. For \(D^{*-} K^{*+} \rightarrow D^- K^+\), we assume that the interaction is dominated by the one-pion exchange and roughly estimate that \(C_a=g_{D^*D\pi }g_{K^*K\pi }\), with \(g_{D^*D\pi }\simeq 17.9\) and \(g_{K^*K\pi }\simeq 4.6\) determined from the experiments [22]. For \({\bar{D}}_{1}^{0} K^{0} \rightarrow D^- K^+\), we employ the heavy meson chiral lagrangian introduced in Eq. (76) of Ref. [23]. The coupling \(C_b\) then takes the form \(C_b=\frac{\sqrt{6}}{3 f_\pi ^2}\zeta _1 \sqrt{m_{D_1}m_D}\) with the pion decay constant \(f_\pi =132\) MeV. The parameter \(\zeta _1\) has not been determined yet, and we assume that it has the same value as \(\zeta \). Reference [23] gives \(\zeta =0.1\). For the other \(\chi _{c1}\)- and \(D_{sJ}\)-loops, we take the pertinent coupling constants to be the same as those of \(\chi _{c1}(4274)\)-loop and \(D_{s}^{*}(2700)\)-loop, respectively.

Being lacks of the experimental data, it is worth to mention that the above estimations concerning the coupling constants are rather preliminary and large uncertainties will be involved. Although some couplings of the rescattering processes are not well determined yet, in this work we mainly focus on the line-shape of the invariant mass distribution curves, which are independent on the values of these coupling constants.

Fig. 2
figure 2

Invariant mass distribution of \(D^- K^+\) via the rescattering processes in Fig. 1a. The mass and width of intermediate state \(\chi _{c1}\) are taken to be those of \(\chi _{c1}(4274)\) (solid line), \(\chi _{c1}(4140)\) (dotted line), and \(\chi _{c1}(3872)\) (dashed line) given by PDG [19], separately. The width of intermediate state \(K^{*+}\) is set to be a 0 MeV and b 50 MeV, respectively. The bands are obtained by taking into account uncertainties of the mass and width of intermediate particles

Full size image

The theoretical results of the \(D^- K^+\) invariant mass distributions via the rescattering processes of Fig. 1a, b are displayed in Figs. 2 and 3, respectively. If we ignore the \(K^*\) width, it can be seen in Fig. 2a there is a sharp peak when the mass of \(\chi _{c1}\) is taken to be \(m_{\chi _{c1}(4274)}\). This is because \(m_{\chi _{c1}(4274)}\) is in the vicinity of the kinematic region where the TS can be present on the physical boundary. When \(m_{\chi _{c1}}\) becomes smaller, the TS goes further away from the physical boundary, then its influence becomes insignificant and the relevant peak turns to be broader. If we take into account the \(K^*\) width effect, all of the three curves are smoothed to some extent, as illustrated in Fig. 2b. But the solid line is still comparable with the experimental distribution curve.

Fig. 3
figure 3

Invariant mass distribution of \(D^- K^+\) via the rescattering processes in Fig. 1b. The mass and width of intermediate state \(D_{sJ}\) are taken to be those of \(D_{s1}^{*}(2700)\) (solid line) and \(D_{s1}^{*}(2860)\) (dotted line) given by PDG [19], separately. The width of intermediate state \({\bar{D}}_1(2420)^0\) is set to be (a) 0 MeV and (b) 32 MeV, respectively. The bands are obtained by taking into account uncertainties of the mass and width of intermediate particles

Full size image

The \({\bar{D}}_1(2420)\) is relatively narrower compared with \(K^*\), therefore the influence of \({\bar{D}}_1\) width on the line-shape is not quite large, as can be seen from Fig. 3a, b. When the mass of \(D_{sJ}\) is taken to be \(m_{D_{s1}^*(2700)}\), a narrow peak around \({\bar{D}}_1 K\) threshold is obtained, as illustrated with the solid curves in Fig. 3. We input the center value of \(m_{D_{s1}^*(2860)}\) given by PDG, i.e. 2859 MeV, in calculating the dotted curves. Although this mass is just slightly above the kinematic region where the TS can be present on the physical boundary, the mass of \(D_{s1}^*(2860)\) is as large as 159 MeV, and this broad width leads to a broad bump in \(D^-K^+\) spectrum.

From the invariant mass distribution curve line-shape point of view, it can be seen the rescattering effects can simulate the resonance-like structures \(X_0(2900)\) and \(X_1(2900)\). Furthermore, from the discussion in Sect. 2, we know the spin-parity quantum numbers of the two resonance-like structures induced by the \(D^{*-} K^{*+}\) and \({\bar{D}}_{1}^{0} K^{0}\) rescatterings are \(0^+\) and \(1^-\), respectively. This is also consistent with the current experimental results.

4 Summary

In summary, we investigate the \(B^+ \rightarrow D^+ D^- K^+\) decay via the \(\chi _{c1}K^{*+}D^{*-}\) and the \(D_{sJ}^{+}{\bar{D}}_{1}^{0}K^{0}\) rescattering diagrams. Two resonance-like peaks around the \(D^{*-}K^{*+}\) and \({\bar{D}}_{1}^{0}K^{0}\) thresholds are obtained in the \(D^-K^+\) invariant mass spectrum. Without introducing genuine exotic states, the two rescattering peaks may simulate the \(X_0(2900)\) and \(X_1(2900)\) states reported by the LHCb collaboration with consistent spin-parity quantum numbers.Such a special phenomenon is due to the analytical property of the decaying amplitudes with the TS located to the vicinity of the physical boundary. This will enhance the two-body \(D^{*-}K^{*+} \rightarrow D^- K^+\) and \({\bar{D}}^0_1K^0 \rightarrow D^-K^+\) rescatterings and make the peak visible in the \(D^-K^+\) invariant mass distributions.