1 Introduction

The quark potential models, by introducing the interactions respecting the properties of the quantum chromodynamics (QCD), have achieved a general success in predicting many meson states with different quantum numbers [1, 2]. Especially, taking into account the relativistic effect, the Godfrey–Isgur (GI) model provides a unified description of most of mesons and presents fairly reasonable predictions to their masses. The severe deviations from the experimental observation only happen in two regions: the first one is the long-history puzzle of identifying the light scalar sectors; the second one is about the new exotic charmonium-like states starting from the observation of X(3872), especially for the states above the open-flavor thresholds. We are aiming at the former region in this paper, while part of the latter one has been addressed in some other works [3, 4].

The lowest scalar meson predicted in the potential models is located at above 1.0  GeV [2]. However, the \(I=0\) \(\pi \pi \) scattering phase shift rises smoothly and passes \(90^\circ \) at about 850 MeV [5,6,7], so it was believed that there exists a broad structure contributing to the phase shift in the energy region from the \(\pi \pi \) threshold to above 1.0  GeV [8]. Many phenomenological studies have been devoted to proving the existence of this structure which is dubbed \(f_0(500)\) now in the particle data group (PDG) table [9], and its pole position, is confirmed and determined by model-independent methods such as in Refs. [10, 11]. The existence of \(f_0(500)\) and \(f_0(980)\) with clear experimental evidences made people lose faith in the predictions of light scalar mesons in the potential model. Thus, people usually believe that identifications of the light scalar mesons are totally a mess plagued by strong overlap between resonance and background, and the quark model does not work here completely. Moreover, the \(I=1/2\) \(K\pi \) phase shifts measured from about 100 MeV above the threshold in the Kp production also exhibit a similar smoothly-rising behavior [12], which leads to the discovery of another board structure, denoted as \(K_0^*(700)\) or \(\kappa \) now, whose pole position is also determined more and more accurately [13,14,15].

In order to understand such states, several different kinds of methods were introduced. The tetraquark model, proposed by Jaffe [16], regarding them as fourquark states produced by QCD fundamental interaction, was adopt to understand their masses, and \(f_0(500)/\sigma \), \(K_0^*(700)/\kappa \), \(a_0(980)\), and \(f_0(980)\) are regarded as lightest tetraquark nonet [17]. Another idea is that the pseudoscalar-pseudoscalar meson scattering could be well described by the chiral perturbation theory (\(\chi \)PT) [18], and the resonance information could be restored by unitarizing the \(\chi \)PT amplitudes with some unitarization schemes [19, 20]. In this picture, the \(\sigma \), \(\kappa \) resonances can be viewed as dynamically generated from the \(\pi \pi \) or \(\pi K\) interaction rather than the fundamental states produced by QCD. However, this is in the picture of the effective interaction of Goldstones rather than from a constituent quark point of view. Although this kind of method has provided plausible explanations of these resonant states, one still wonders whether these states can really be dynamically generated by the interactions of the meson states consistently from the point of view of the constituent quark model which captures the nature of the mesons with various quantum numbers in a much broader range. In fact, in GI’s paper, they already noticed that the spectra produced by the potential model did not included the interactions between the mesons and the nearby continuum which may modify the mass spectra and produce the width for the mesons. From recent experience in studying the exotic heavy quarkonium-like states like X(3872), it is also demonstrated that by coupling the QCD fundamental \(q\bar{q}\) states with the continuum, not only can the fundamental state itself be modified from the potential model predictions, but also new states can be dynamically generated. This idea was successfully used in explaining the generation of the X(3872) [3, 4, 21,22,23,24,25,26]. Actually, this kind of idea has already been widely used in studying the charmonium state [1] and the low lying scalar mesons [27,28,29,30] with some successes. In fact, even long before these practices, the fact that coupling the discrete state to the continuum will change the spectrum was generalized and demonstrated in the so-called Friedrichs–Lee model [31, 32].

In 1948, Friedrichs established the simplest form of the model in a non-relativistic scenario [31], in which the free Hamiltonian has a discrete eigenstate and a continuum eigenstate, and an interaction between the discrete state and the continuum states is introduced. The eigenvalue of the discrete state is embedded in the continuous mass spectrum of the continuum when the interaction is turned off. Once the discrete state and the continuum state are coupled with each other, the discrete state will dissolve into the continuum state and becomes an unstable state with a certain width. This model is exactly solvable so that some properties of unstable states, such as the wave function of the resonance or scattering amplitudes for the continuum states, could be studied carefully. One of the most important ingredients of the model is the resolvent function \(\frac{1}{\eta (E)}\) as a function of the energy E, with

$$\begin{aligned} \eta (E)=E-\omega _0-\int \mathrm {d}E\frac{\rho (E')}{E-E'}. \end{aligned}$$
(1)

When the function is analytically continued to the complex E plane, zero points of \(\eta (E)\) function represent the poles of the scattering amplitude of the continuum states. When the bare discrete state is below the threshold, there is also a virtual state accompanied with the original discrete state as the interaction is turned on. The importance of the extra virtual-state, bound-state, and resonance poles, which could appear in the amplitude besides the one originally at \(\omega _0\), has been emphasized in Refs. [33,34,35]. These so-called Gamow states, denoted by their complex pole positions on the unphysical Riemann sheets, are generalized eigenstates of the Hamiltonian, which has a good definition in the rigged Hilbert space [36, 37].

Similar excellent ideas were proposed independently by several theorists in different areas in physics. In the quantum field theory, the Lee model is established to study how the processes depicted by \(V\rightleftarrows N+\theta \) could influence the physical state and wave function renormalization [32]. The Feshbach resonance theory [38] and the Anderson model [39] are also different forms with similar spirits in nuclear physics and condensed matter physics. In hadron physics, similar non-relativistic methods originated from this idea have been applied or developed by several different groups [3, 21,22,23, 25, 33, 40, 41], in understanding some charmonium-like state, especially for the enigmatic X(3872) state.

To utilize this Friedrichs–Lee scheme in the low lying mesons states, the relativistic effects need to be considered. This is because in the light meson states with u, d, and s quarks, the constituents are light and might travel very fast, so that the non-relativistic methods might not be self-consistent. There are two aspects of relativistic effects to be considered. The first is related to the Friedrichs–Lee model itself, in particular, the resolvent function. It is well known that the relativistic dispersion relation is expressed in s, the invariant total momentum squared, and thus the corresponding resolvent function should be expressed in s rather than E as in (1). This is due to the presence of antiparticles or annihilation operators in relativistic theory. There are several ways to incorporate the relativistic effects into the Friedrichs model [42, 43] in a more systematical way and we will follow the method in [43] which is most direct and simple by introducing a bilocal operator to simulate the two-particle state. The second aspect is related to the interaction between the discrete state and the continuum, which should be modeled with some relativistic effects taken into account. The well-known nonrelativistic quark pair creation (QPC) model which was used in the discussion of the heavy charmonium states can not be directly used here and should be modified to take into account some relativistic effects. Törnqvist developed a unitarized quark model which introduce a meson propagator with a relativistic dispersion relation [29, 44]

$$\begin{aligned} P(s)^{-1}=s-m_A^2-\int _{s_{th}} \mathrm {d}s\frac{f^{A}_{BC}(s')}{s-s'} \end{aligned}$$
(2)

to describe how the full propagator of meson A be influenced by coupling to the meson pair BC. \(m_A\) is the bare mass of meson A, \(s_{th}\) is the energy squared of the BC threshold, and \(f^{A}_{BC}(s)\) is the spectral function determined by the \(A-BC\) coupling form factor. Although the dispersion relation is a relativistic form, \(f^{A}_{BC}\) is derived from the non-relativistic QPC interaction. In Ref. [27], Beveren et al. took into account the Lorentz transform of the energy in the wavefunction in the QPC model. A more thorough and complete treatment of the relativistic effect on the states and wavefunction in the QPC model was carried out by Fuda, in which the Lorentz transformations are taken into account when the constituent quarks and antiquarks regroup to form a new meson pair [45]. However, his trial study of the \(\rho \) meson coupling to \(\pi \pi \), a non-relativistic dispersion relation was adopt.

In our paper, we will combine Fuda’s relativistic QPC approach and the relativisitic generalization of the Friedrichs–Lee model. This relativistic Friedrichs–Lee–QPC scheme is then applied to study the lowest \(I=0\), \(J^{PC}=0^{++}\), \((u\bar{u}+d\bar{d})/\sqrt{2}\) bound state, with the GI model as the input, coupling to the \(\pi \pi \) continuum state, and it is found that while the discrete state is shifted onto the complex s-plane, a light broad resonance pole corresponding to \(f0(500)/\sigma \) could be generated naturally in the \(\pi \pi \) scattering amplitude. Furthermore, it is observed that the two poles contribute a mild total phase shift of about \(180^\circ \). Their contributions to the smooth rise of the phase shift is consistent with the one measured in the \(\pi p\) experiments [5,6,7].

The paper is organized as follows: the theoretical background is briefly introduced in Sect. 2. To prepare for the relativistic treatment of the Friedrichs–Lee model and QPC model, the definitions of relativistic canonical single-particle and two-particle states are presented in Sect. 2.1. Then the relativistic Friedrichs–Lee model is introduced and solved in Sect. 2.2. The readers could just skip the details of the formal deduction of the solution and jump to the conclusion at the end of this section if they wish. The relativistic QPC model is briefly reviewed in Sect. 2.3 and the coupling form factor is obtained in this scheme. The numerical calculation and its application in studying the \(f_0(500)\) state are briefly discussed in Sect. 3. Some Lorentz transformation and kinematics used in the calculation are described in detail in the Appendix A.

2 Theoretical background

Since both the Friedrichs–Lee model and the QPC model need to deal with relativistic two-particle states, either at the hadron level or at the quark level, we first introduce the definitions of canonical one-particle and two-particle states and their transformation properties under the Lorentz transformation used in this paper. We then present the relativistic Friedrichs–Lee model in the angular momentum representation, and finally review the relativistic quark pair creation (QPC) model, which is used to describe the interaction in the relativistic Friedrichs–Lee model. This section is written in a pedagogical manner to make the presentation self-consistent and easily understandable.

2.1 Definition of one-particle and two-particle states

The one-particle and two-particle states in this paper are represented by the canonical states but not by the helicity states. This means that the third-component of the spin of the state is defined along a fixed direction, the z-axis, in the rest frame of the particle. Such a choice is for the sake of the convenience in the discussion of the QPC model. The relativistic two-particle states have been thoroughly discussed in the textbooks and in many papers, such as in Refs. [45,46,47].

Single-particle state

Since the transformation between different inertial frames will be frequently used in this paper, we first define a general canonical Lorentz boost \(l_c(p)\), symbolized by the four-momentum \(p=(p^0,\mathbf{p})\). If a four-momentum \(q=(q^0,\mathbf{q})\) in an original inertial frame is boosted to an inertial frame moving at the relative velocity \(\mathbf{v}=-\frac{\mathbf{p}}{p^0}\) with respect to the original one, it becomes

$$\begin{aligned} l_c(p)q= & {} l_c(p)\left( \begin{array}{c} q^0 \\ \mathbf {q} \end{array} \right) \nonumber \\= & {} \left( \begin{array}{c} \frac{p^0q^0+\mathbf {p}\cdot \mathbf {q}}{W} \\ \mathbf {q}+\frac{\mathbf {p}}{W}(q^0+\frac{\mathbf {p}\cdot \mathbf {q}}{p^0+W}) \end{array} \right) , \ \ W=(p.p)^{1/2}. \end{aligned}$$
(3)

A general single-particle state with its mass \(\mu \), momentum \(\mathbf{p}\), spin s, and third component of spin m is defined by transforming it from its rest frame to the momentum \(\mathbf{p}\) by a canonical Lorentz boost \(l_c(p)\) as

$$\begin{aligned} |\mathbf{p}; sm\rangle =U(l_c(p))|\mathbf{0};sm\rangle \sqrt{\frac{\mu }{\varepsilon (\mathbf{p})}}, \end{aligned}$$
(4)

where \(p=(\varepsilon (\mathbf{p}),\mathbf{p})\) denotes its on-shell four-momentum, with the energy \(\varepsilon (\mathbf{p})=(\mathbf{p}^2+\mu ^2)^{1/2}\). \(U(l_c(p))\) represents a unitary operator representation of the Lorentz boost, and the factor is to ensure the normalization to be

$$\begin{aligned} \langle \mathbf{p},sm|\mathbf{p}',s'm'\rangle =\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\delta _{ss'}\delta _{mm'}. \end{aligned}$$
(5)

This kind of definition is convenient in presenting the coupling form factor in the relativistic QPC model [45], which is required here in the relativistic Friedrichs–Lee model to describe the coupling between the discrete state and the continuum states.

In the rest frame of a particle, the transformation of the particle state vector under a spatial rotation R is expressed as

$$\begin{aligned} U(R)|\mathbf {0},sm\rangle =\sum _{m'}|\mathbf{0}, sm'\rangle \mathscr {D}^s_{m'm}(R), \end{aligned}$$
(6)

where \(\mathscr {D}^s_{m'm}(R)\) is the standard matrix representation of the rotation R. Then the transformation of a general single-particle state with three-momentum \(\mathbf{p}\) under a general Lorentz transformation a, will be [48]

$$\begin{aligned} U(a)|\mathbf{p}, sm\rangle =\sum _{m'}|\mathbf{p}',sm'\rangle \mathscr {D}^s_{m'm}[r_c(a,p)]\sqrt{\frac{\epsilon (\mathbf{p}')}{\epsilon (\mathbf{p})}}, \end{aligned}$$
(7)

where \(r_c(a,p)=l_c^{-1}(ap)al_c(p)\) is the well-known Wigner rotation.

Two-particle state

Based on the definition of the canonical single-particle state, one could obtain the representation of a two-particle state [45,46,47], by first defining it in the c.m. frame of two-particle system and then boosting it to a general frame. To make it clear, we first define the momenta in this two frames.

Consider two particles 1 and 2 with their masses \(\mu _1, \mu _2\), spins \(s_1, s_2\), and third components \(m_1,m_2\) respectively. In the c.m. frame of a two-particle system, the four-momenta of two particles are respectively

$$\begin{aligned}&k_1\equiv (k_1^0,\mathbf {k}_1)=\left( \varepsilon _1(\mathbf{k}),\mathbf{k}\right) ,\ \nonumber \\&k_2 \equiv (k_2^0,\mathbf {k}_2)=\left( \varepsilon _2(-\mathbf{k}),-\mathbf{k}\right) , \end{aligned}$$
(8)

where \(\mathbf{k}\) is the three-momentum of particle 1 in the c.m. frame of the two-particle system, and \(\varepsilon _i(\mathbf{k})=(\mathbf{k}^2+\mu _i^2)^{1/2}\). In a general frame, the four-momenta of two particles are respectively

$$\begin{aligned}&p_1\equiv (p_1^0,\mathbf {p}_1)=\left( \varepsilon _1(\mathbf{p}_1),\mathbf{p}_1\right) ,\nonumber \\&p_2\equiv (p_2^0,\mathbf {p}_2)=\left( \varepsilon _2(\mathbf{p}_2),\mathbf{p}_2\right) . \end{aligned}$$
(9)

The relation between the two sets of momenta is

$$\begin{aligned} p_1=l_c(p)k_1,\quad p_2=l_c(p)k_2, \end{aligned}$$
(10)

where \(p\equiv (p^0,\mathbf {p})=p_1+p_2=(\varepsilon _1(\mathbf{p}_1)+\varepsilon _2(\mathbf{p}_2),\mathbf{p}_1+\mathbf{p}_2)\).

A general two-particle state could be defined by boosting the two-particle state in the c.m frame by \(l_c(p)\)

$$\begin{aligned} |\mathbf{p}\mathbf{k},s_1s_2 m_1m_2\rangle= & {} U(l_c(p))|\mathbf{k},s_1 m_1\rangle \otimes | -\mathbf{k},s_2m_2\rangle \nonumber \\&\times [W(\mathbf{k})/E(\mathbf{p},\mathbf{k})]^{1/2},\nonumber \\ W(\mathbf{k})= & {} \varepsilon _1(\mathbf{k})+\varepsilon _2(-\mathbf{k}),\ \nonumber \\ E(\mathbf {p},\mathbf {k})= & {} (\mathbf {p}^2+W(\mathbf{k})^2)^{1/2}, \end{aligned}$$
(11)

where the factor is also to ensure the normalization of the states as

$$\begin{aligned}&\langle \mathbf{p}\mathbf{k},s_1s_2 m_1 m_2|\mathbf{p}'\mathbf{k}',s_1's_2' m_1' m_2'\rangle \nonumber \\&\quad =\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\delta ^{(3)}(\mathbf{k}-\mathbf{k}')\delta _{s_1s_1'}\delta _{s_2s_2'}\delta _{m_1m_1'}\delta _{m_2m_2'}. \end{aligned}$$
(12)

According to the Lorentz transformation properties of the single-particle states and the standard derivation, one could find that the two-particle state mentioned above could be expressed as the combination of the direct product of two single-particle states multiplied with extra factors of the matrix representations for the Wigner rotations of the two particles

$$\begin{aligned}&|\mathbf{p}\mathbf{k},s_1s_2 m_1 m_2\rangle =\sum _{m'_1 m'_2}|\mathbf{p}_1,s_1 m_1'\rangle \otimes |\mathbf{p}_2,s_2 m'_2\rangle \nonumber \\&\quad \times {\mathscr {D}}^{s_1}_{m_1'm_1}[r_c(l_c(p),k_1)]\mathscr {D}^{s_2}_{m_2'm_2}[r_c(l_c(p),k_2)]\nonumber \\&\quad \times \left( \frac{\varepsilon _1(\mathbf{p}_1)}{\varepsilon _1(\mathbf{k})}\frac{\varepsilon _2(\mathbf{p}_2)}{\varepsilon _2(-\mathbf{k})}\frac{W(\mathbf{k})}{E(\mathbf{p},\mathbf{k})}\right) ^{1/2}\,. \end{aligned}$$
(13)

Similarly, one can do the partial wave decomposition and couple the orbital angular momentum l and total spin s to be the total angular momentum j in the c.m. frame, and then boost to the general frame to obtain the two-particle state in the angular momentum representation

$$\begin{aligned}&|\mathbf {p}klsjm\rangle \nonumber \\&\quad =\sum _{m_lm_s}\sum _{m_1m_2}\int d\Omega _{\mathbf {k}}Y_l^{m_l}(\hat{\mathbf {k}})|\mathbf {p}\mathbf {k},s_1s_2m_1m_2\rangle \nonumber \\&\qquad \times \langle s_1s_2m_1m_2|sm_s\rangle \langle lsm_lm_s|jm\rangle , \end{aligned}$$
(14)
$$\begin{aligned}&\quad =\sum _{m_lm_s}\sum _{m_1m_2}\sum _{m'_1 m'_2} \int d\Omega _{\mathbf {k}}|\mathbf{p}_1,s_1 m_1'\rangle \nonumber \\&\qquad \otimes |\mathbf{p}_2,s_2 m'_2\rangle Y_l^{m_l}(\hat{\mathbf {k}})\langle s_1s_2m_1m_2|sm_s\rangle \langle lsm_lm_s|jm\rangle \nonumber \\&\qquad \times \mathscr {D}^{s_1}_{m_1'm_1}[r_c(l_c(p),k_1)]\mathscr {D}^{s_2}_{m_2'm_2}[r_c(l_c(p),k_2)]\nonumber \\&\qquad \times \left( \frac{\varepsilon _1(\mathbf{p}_1)}{\varepsilon _1(\mathbf{k})}\frac{\varepsilon _2(\mathbf{p}_2)}{\varepsilon _2(-\mathbf{k})}\frac{W(\mathbf{k})}{E(\mathbf{p},\mathbf{k})}\right) ^{1/2}. \end{aligned}$$
(15)

with the normalization being

$$\begin{aligned}&\langle \mathbf {p}klsjm|\mathbf {p}'k'l's'j'm'\rangle \nonumber \\&=\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\frac{\delta ( k-k')}{k^2}\delta _{ll'}\delta _{ss'}\delta _{jj'}\delta _{mm'}, \end{aligned}$$
(16)

where k is the magnitude of the three-momentum \(\mathbf{k}\) and \(\hat{\mathbf {k}}\) is direction of \(\mathbf{k}\). A rigorous and detailed construction of this state in a common normalization convention could be found in Refs. [46, 47].

2.2 The relativistic Friedrichs–Lee model

The Hamiltonian for the non-relativistic coupling of a discrete state and the continuum state in three dimensional space can be expressed in a Friedrichs model [33, 34] after the partial wave decomposition to the angular momentum representation, where the final solution contains a non-relativistic dispersion relation, and so does the Lee model [32]. To extend the model to a relativistic formalism, we can express the coupling in the creation and annihilation operators for the single-particle state and for a bilocal state representing a two-particle state using the method developed by Antoniou et al. in Ref. [43], where the coupling between a local Klein-Gordan field with a fixed mass and a bilocal Klein-Gordan field with a continuum spectrum is considered. Here, we are going to consider a bare meson coupled to a meson pair, so the bare meson could be represented by a single-particle state and the meson pair could be expressed in the total angular momentum representation \(|\mathbf {p}klsjm\rangle \) and be effectively mimicked by a bilocal field but with more inner degrees of freedom.

Since the normalization of a single-particle state studied here is \(\langle \mathbf {p} jm|\mathbf {p}' j'm'\rangle =\delta ^{(3)}(\mathbf {p}-\mathbf {p}')\delta _{jj'}\delta _{mm'}\), we can define the creation operator of a single-particle as

$$\begin{aligned} |\mathbf {p} jm\rangle =a^\dag _{\mathbf{pjm}}|0\rangle . \end{aligned}$$
(17)

The commutation relation of the annihilation and creation operators of the single particle is

$$\begin{aligned} {[}a_{\mathbf{pjm}},a^\dag _{\mathbf{p}'j'm'}]=\delta ^{(3)}(\mathbf {p}-\mathbf {p}')\delta _{jj'}\delta _{mm'}. \end{aligned}$$
(18)

On the other side, the normalization of two-particle states in the angular momentum representation \(|\mathbf {p}klsjm\rangle \) is

$$\begin{aligned}&\langle \mathbf {p}klsjm|\mathbf {p}'k'l's'j'm'\rangle \nonumber \\&\quad =\delta ^{(3)}(\mathbf {p}-\mathbf {p}')\frac{\delta (k-k')}{k^2}\delta _{ll'}\delta _{ss'}\delta _{jj'}\delta _{mm'}, \end{aligned}$$
(19)

so, we can also define the creation operator of a bilocal field, representing a two-particle state, \(B^\dag _{\mathbf {p}klsjm}\), as

$$\begin{aligned} |\mathbf {p}klsjm\rangle =B^\dag _{\mathbf {p}klsjm}|0\rangle , \end{aligned}$$
(20)

with the commutation relation

$$\begin{aligned}&\left[ B_{\mathbf {p}klsjm},B^\dag _{\mathbf {p}'k'l's'j'm'}\right] \nonumber \\&\quad =\delta ^{(3)}(\mathbf {p}-\mathbf {p}')\frac{\delta (k-k')}{k^2}\delta _{ll'}\delta _{ss'}\delta _{jj'}\delta _{mm'}. \end{aligned}$$
(21)

To simplify the representation of the formula, we define \(a(\mathbf {p})\equiv a_{\mathbf{pjm}}\) and \(B({\mathbf {p},k})\equiv B_{\mathbf {p}klsjm}\) with only the variables \(\mathbf {p}\) and k kept and the other variables lsjm omitted in the derivation procedure and restored finally, since jm should be conserved in the strong interaction between the discrete state and the continuum state and ls will symbolize the coupling form factors involved.

If we introduce an interaction between the single-particle state and the two-particle state, then the full Hamiltonian at \(t=0\) or in Schrödinger picture could be expressed as

$$\begin{aligned} P_0= & {} \int \mathrm {d}^3\mathbf {p}\omega (\mathbf {p})a^\dag (\mathbf {p})a(\mathbf {p})\nonumber \\&+\int \mathrm {d}^3\mathbf {p}k^2\mathrm {d}k E(\mathbf {p},\mathbf {k})B^\dag ({\mathbf {p},k})B({\mathbf {p},k})\nonumber \\&+\int \mathrm {d}^3\mathbf {p}k^2\mathrm {d}k \alpha (k)(a(\mathbf {p})+a^\dag ({-\mathbf {p}}))(B^\dag ({\mathbf {p},k})\nonumber \\&+B({-\mathbf {p},k})), \end{aligned}$$
(22)

where the energy of the single-particle state is \(\omega (\mathbf {p})=(\mathbf {p}^2+\omega _0^2)^{1/2}\) and the total energy of the two-particle state is \(E(\mathbf {p},\mathbf {k})=(\mathbf {p}^2+W(\mathbf {k})^2)^{1/2}\) with the c.m. energy defined by \(W(\mathbf {k})=\varepsilon _1(\mathbf {k})+\varepsilon _2(-\mathbf {k})\). The coupling form factor, \(\alpha (k)\), representing the interaction between the single-particle state and the two-particle state, in principle depends on k, and the sum over l, s quantum numbers in the expression should be understood.

It is clearer and convenient to change the variable k, the magnitude of the relative momentum of two particles, to E, the total energy of the two-particle states, in accordance with the ordinary Friedrichs model. Using the relation

$$\begin{aligned} \frac{\mathrm {d}k}{\mathrm {d}E}=\frac{Ep_1^0p_2^0}{W^2k}, \end{aligned}$$
(23)

one can obtain the relations

$$\begin{aligned} k^2\mathrm {d}k=\frac{kEp_1^0p_2^0}{W^2}\mathrm {d}E,\ \ \frac{\delta (k-k')}{k^2}=\frac{W^2}{kEp_1^0p_2^0}\delta (E-E'),\nonumber \\ \end{aligned}$$
(24)

where \(W=W(\mathbf{k})\) and \(E=E(\mathbf {p},\mathbf {k})\). One can define \(\beta (E)=\frac{kEp_1^0p_2^0}{W^2}\) to simplify the following formula. Then the Hamiltonian could be rewritten as

$$\begin{aligned} P_0= & {} \int \mathrm {d}^3\mathbf {p}\int _{M_{th}}\mathrm {d}E\beta (E) EB^\dag (E,\mathbf {p})B(E,\mathbf {p})\nonumber \\&+\int \mathrm {d}^3\mathbf {p}\omega (\mathbf {p})a^\dag (\mathbf {p})a(\mathbf {p})\nonumber \\&+\int \mathrm {d}^3\mathbf {p}\int _{M_{th}}\mathrm {d}E\beta (E) \alpha (k(E,\mathbf{p}))(a(\mathbf {p})\nonumber \\&+a^\dag (-\mathbf {p}))(B^\dag (E,\mathbf {p})+B(E,-\mathbf {p})), \end{aligned}$$
(25)

and the 3-momentum operator is

$$\begin{aligned} \mathbf{P}= & {} \int \mathrm {d}^3\mathbf {p}\int _{M_{th}}\mathrm {d}E\beta (E) \mathbf {p}B^\dag (E,\mathbf {p})B(E,\mathbf {p})\nonumber \\&+\int \mathrm {d}^3\mathbf {p}\mathbf {p}a^\dag (\mathbf {p})a(\mathbf {p}), \end{aligned}$$
(26)

where \(M_{th}\) is the energy threshold for the continuum. The commutation relation of two-particle operators is

$$\begin{aligned} {[}B(E,\mathbf {p}),B^\dag (E',\mathbf {p}')]=\delta ^{(3)}(\mathbf {p}-\mathbf {p}')\beta (E)^{-1}\delta (E-E').\nonumber \\ \end{aligned}$$
(27)

In the non-relativistic Friedrichs model, solving the problem is to find the solutions of generalized eigenfunction with the complex eigenvalues for the Hamiltonian [4, 33]. Here, in the relativistic case, the eigenvalue problem is equivalent to finding the solution of

$$\begin{aligned} {[}P_\mu ,b^\dag (E,\mathbf {p})]=p_\mu b^\dag (E,\mathbf {p}), \end{aligned}$$
(28)

with the creation operator \(b^\dag (E,\mathbf {p})\) being written as the linear superposition of \(B^\dag (E,\mathbf {p})\),\(B(E,-\mathbf {p})\),\(a^\dag (\mathbf {p})\), and \(a(-\mathbf {p})\) as

$$\begin{aligned} b^\dag (E,\mathbf {p})= & {} \int \beta (E') \mathrm {d}E'[T(E,E',\mathbf {p})B^\dag (E',\mathbf {p})\nonumber \\&+R(E,E',\mathbf {p})B(E',-\mathbf {p})]\nonumber \\&+t(E,\mathbf {p})a^\dag (\mathbf {p})+r(E,\mathbf {p})a(-\mathbf {p}). \end{aligned}$$
(29)

By a direct calculation of the commutation relation in Eq. (28) and comparing the coefficient of each operator, one finds the relations

$$\begin{aligned} (E+\omega (\mathbf {p}))r(E,\mathbf {p})= & {} (E-\omega (\mathbf {p}))t(E,\mathbf {p}),\nonumber \\ (E+E')R(E,E',\mathbf {p})= & {} (E-E')T(E,E',\mathbf {p}). \end{aligned}$$
(30)

After eliminating \(R(E,E',\mathbf {p})\) and \(r(E,\mathbf {p})\), one can obtain

$$\begin{aligned}&(E'-E)T(E,E',\mathbf {p})+\alpha (k)\frac{2\omega (\mathbf {p})}{E+\omega (\mathbf {p})} t(E,\mathbf {p})\nonumber \\&\quad =\gamma (E)(E'-E)\delta (E'-E), \end{aligned}$$
(31)
$$\begin{aligned}&\int \mathrm {d}E'\beta (E')\alpha (k(E',\mathbf{p}))\frac{2E'}{E+E'}T(E,E',\mathbf {p})\nonumber \\&\quad =(E-\omega (\mathbf {p}))t(E,\mathbf {p}), \end{aligned}$$
(32)

and

$$\begin{aligned} T(E,E',\mathbf {p})= & {} \gamma (E)\delta (E'-E)\nonumber \\&-\frac{2\omega (\mathbf {p})\alpha (k(E',\mathbf{p}))}{(E'-E)(E+\omega (\mathbf {p}))}t(E,\mathbf {p}). \end{aligned}$$
(33)

Substituting it back into the equation above, one obtains

$$\begin{aligned} t(E,\mathbf {p})=\frac{\beta (E)\alpha (k(E,\mathbf{p}))\gamma (E)(E+\omega (\mathbf {p}))}{\eta _\pm (E,\mathbf {p})}, \end{aligned}$$
(34)

where \(\eta _\pm (E,\mathbf {p})\) is expressed as

$$\begin{aligned} \eta _\pm (E,\mathbf {p})= & {} E^2-\omega (\mathbf {p})^2\nonumber \\&-\int \mathrm {d}E'^2\left[ \frac{2\omega (\mathbf {p})\beta (E')\alpha (k(E',\mathbf{p}))^2}{(E^2-E'^2\pm i0)}\right] , \end{aligned}$$
(35)

which appears in the denominator of all the coefficients functions. We have introduced the i0 in the integral to make the integral well-defined and the \(+\)(−) sign will correspond to the in(out)-state solution. Similar to the \(\eta _\pm (x)\) in the non-relativistic Friedrichs model [4, 33], \(\eta (E,\mathbf {p})\) is just the inverse of the resolvent function, which has a right hand cut starting from threshold energy squared for the two-particle continuum. In the c.m. frame, \(\mathbf {p}=\mathbf {0}\), the variable is changed to the invariant mass W, and the \(\eta _\pm (W)\) function reads

$$\begin{aligned} \eta _\pm (W)=W^2-\omega _0^2-\int _{s_{th}} \mathrm {d}W'^2 \frac{\rho (W')}{W^2-W'^2\pm i0}\,, \end{aligned}$$
(36)

where \(s_{th}=(\mu _1+\mu _2)^2\) and the spectral function \(\rho (W)=2\omega _0\beta (W)\alpha (k)^2=2\omega _0\frac{k\varepsilon _1\varepsilon _2}{W}\alpha (k)^2\) in which the coupling form factor \(\alpha (k)\) could be obtained using some model as we will show in the next section. In principle, the coupling form factor should include the interaction of the single-particle state and the two-particle state with different L and S, the relative angular momentum and the total spin quantum numbers of the two particles, thus \(\alpha (k)^2=\sum _{LS}\alpha _{LS}(k)^2\). With the variable changed from W to s, Eq. (36) could be expressed as

$$\begin{aligned} \eta _\pm (s)=s-\omega _0^2-\int _{s_{th}} ds' \frac{\rho (s')}{s-s'\pm i0}, \end{aligned}$$
(37)

which is Lorentz invariant and just similar to the relativistic dispersion relation. The main difference from the non-relativistic case is that the relation is in terms of the energy squared s instead of the energy E.

Thus, we have the in-state creation operator:

$$\begin{aligned} b_{in}^\dagger (E,\mathbf{p})&=B^\dagger (E,\mathbf{p})-\frac{2\omega (\mathbf{p})\alpha ( k(E,\mathbf{p}))}{\eta _+(E,\mathbf{p})}\nonumber \\&\quad \times \bigg [\int _{M_{th}} dE'\beta (E')\alpha (k(E',\mathbf{p}))\Bigg (\frac{B^{\dagger }(E',\mathbf{p})}{(E'-E-i0)}\nonumber \\&\quad -\frac{B(E',-\mathbf{p})}{(E'+E+i0)}\Bigg ) \nonumber \\&\quad -\frac{1}{2\omega (\mathbf{p})} \Big ((\omega (\mathbf{p})+E)a^\dagger (\mathbf{p}) -(\omega (\mathbf{p})-E)a(-\mathbf{p})\Big )\bigg ]\,, \end{aligned}$$
(38)

which satisfies \([b_{in}(E,\mathbf{p}),b_{in}^\dagger (E',\mathbf{p}')]=\beta ^{-1}(E)\delta (E-E')\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\), and the normalization \( \gamma (E)=1/\beta (E)\) is determined by this commutation relation. The out-state creation operator is similar with all the signs before i0 reversed and the subscript of \(\eta \) is also reversed. The vacuum \(|\Omega \rangle \) is also different from the free cases, and the in-states and out-states are generated by the creation operators acting on this exact vacuum. The S-matrix of one continuum state can also be obtained by inner product of the in-states and the out-states,

$$\begin{aligned} S(E,\mathbf{p};E',\mathbf{p}')=\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\delta (E-E')\left( 1-2\pi i\frac{\rho (s)}{\eta _+(s)}\right) . \end{aligned}$$
(39)

The discrete states are the solution to the \(\eta (s)=0\) where \(\eta (s)\) is the analytically continued \(\eta _{\pm }\) to the complex s-plane with \(\eta _+\) and \(\eta _-\) on the upper and lower rim of the unitarity cut. The discrete states include the bound states on the real axis of the first sheet, virtual states on the real axis of the second sheet, and resonances on the second Riemann sheet of the complex s-plane. The creation operators for the bound states can also be solved to be

$$\begin{aligned} b^\dagger (E_0,\mathbf{p})&=N\bigg [\frac{(\omega (\mathbf{p})+E_0)}{\sqrt{2\omega (\mathbf{p})}}a^\dagger (\mathbf{p})-\frac{(\omega (\mathbf{p})-E_0)}{\sqrt{2\omega (\mathbf{p})}}a(-\mathbf{p}) \nonumber \\&\quad -\sqrt{2\omega (\mathbf{p})}\int _{M_{th}} dE'\beta (E')\nonumber \\&\quad \times \bigg [\frac{\alpha (k(E',\mathbf{p}))}{E'-E_0} B^\dagger (E',\mathbf{p}) -\frac{\alpha (k(E',\mathbf{p}))}{E'+E_0} B(E',-\mathbf{p})\bigg ]\bigg ], \end{aligned}$$
(40)

where the normalization is chosen to be \(N=\frac{1}{\sqrt{2E_0}}\Big [1+2\omega (\mathbf{p})\int _{M_{th}} dE' \beta (E')\frac{2E'|\alpha (k(E',\mathbf{p}))|^2}{(E'+E_0)^2(E'-E_0)^2}\Big ]^{-1/2}\) such that the commutation relation is \([b(\mathbf{p}),b^\dagger (\mathbf{p}')]=\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\). For resonances and virtual states, similar operators can be found, but since their positions are on the second sheet, the integral contour in the definition of the operator should be deformed and the commutator may not be well-defined.

In general, since there is only one continuum state here, i.e. one unitarity cut, every bare discrete state will generate two poles, either becoming a pair of resonance poles on the second Riemann sheet or remaining on the real axis being virtual or bound state poles. When the coupling is turned down, these poles will move back to the bare position of the discrete state. There could also be dynamically generated poles which does not move to the bare states and normally will run towards the singularities of the form factor when the coupling is switched off [33, 34]. These are dynamically generated by the interaction between the discrete state and the continuum.

This model can easily be generalized to include more discrete bare states and continuum bare states. With more discrete bare states, the \(\eta \) function will become a matrix whose dimension is equal to the number of the discrete bare states. With more continuum bare states, more dispersion integrals will be added in the \(\eta \) functions, with each integral corresponding to a continuum threshold. The number of the continuum solutions and the dimension of the S-matrix is the same as the number of the bare continuum states. If some continuum states come with the same threshold, such as those states with only different isospin but with a degenerate mass when isospin breaking is ignored, the dispersion integrals for them combine into one, and the \(\eta \) function is still similar to the one for a single continuum. The Riemann sheets is doubled when a new threshold for the continuum is added. The discrete state solutions are then the zero points for the determinant of the \(\eta \) matrix. For discrete states originated from the bare discrete states, the number is also doubled when the Riemann sheets is doubled. Also, there could be dynamically generated poles which are also doubled when a new continuum threshold is added. All the poles with the same origin are called shadow poles [49]. In present paper, for simplicity, we will confine ourselves to the cases with a single continuum threshold and one discrete state.

2.3 Coupling form factor from a relativistic QPC model

Now we are going to study the coupling form factor between the bare meson and the meson-pair states. In the quark potential model, a meson state is described as the bound state of a valence quark and a valence anti-quark. Thus, the interaction between a bare meson state and a meson-pair continuum state could be described by the QPC model [50], in which a quark and antiquark pair created from the vacuum and the one in the original meson separate and regroup to form new mesons. Fuda has generalized the QPC model to include the relativistic boost effects of the quarks between different frames [45]. We rewrite the relativistic QPC model in a more convenient version and in a more general case where the mesons can have arbitrary quantum numbers and unequal quark and antiquark masses.

Based on the definition of two-particle state above, we could write down a relativistic mock state of the bare meson A, with three-momentum \(\mathbf{p}\), mass eigenvalue \(\tilde{W}\), orbital angular momentum of two quarks \(l_A\), total spin of quarks \(s_A\), total angular momentum \(j_A\) and its third component \(m_{j_A}\), as

$$\begin{aligned}&|A(\tilde{W},^{2s_A+1}{l_A}_{j_Am_{j_A}})(\mathbf {p})\rangle \nonumber \\&\quad =\sum _{m_lm_s}\sum _{m_1m_2}\int d^3\mathbf {k}\psi _{l_Am_{l_A}}^{A}(\mathbf {k})|\mathbf {p}\mathbf {k}s_1s_2m_1m_2\rangle \nonumber \\&\qquad \times \langle s_1s_2m_1m_2|s_Am_{s_A}\rangle \langle l_As_Am_{l_A}m_{s_A}|j_Am_{j_A}\rangle , \end{aligned}$$
(41)

where \(\psi _{l_Am_{l_A}}^{A}(\mathbf {k})\) is the relative wave function of quarks in the momentum space in the c.m. frame of the meson, which could be obtained by solving the eigenfunction in some potential model as in Ref. [2]. The normalization of the wave function is

$$\begin{aligned} \int d^3\mathbf {k} |\psi _{l_Am_{l_A}}^{A}(\mathbf {k})|^2=1. \end{aligned}$$
(42)
Fig. 1
figure 1

Two kinds of diagrams which could happen in the quark pair creation model. The arrows on the quark lines only represent the directions of fermion lines. Usually only one of the diagrams will contribute to the amplitude, but both of them will have contributions for the \(f_0\) meson discussed here

Full size image

Furthermore, if the flavor and color indices of quarks are considered, according to Eq. (13), the meson mock state could be represented as [45]

$$\begin{aligned}&\Bigg |A\left( \tilde{W},^{2s_A+1}{l_A}_{{j_Am_{j_A}}}\right) (\mathbf {p})\Bigg \rangle \nonumber \\&\quad =\sum _{m_lm_s}\sum _{m_1m_2}\sum _{m'_1 m'_2}\int d^3\mathbf {k}\psi _{l_Am_{l_A}}^{A}(\mathbf {k})|\mathbf{p}_1,s_1 m_1'\rangle \nonumber \\&\qquad \otimes |\mathbf{p}_2,s_2 m'_2\rangle \phi _A^{12}\omega _A^{12}\nonumber \\&\qquad \times \mathscr {D}^{s_1}_{m_1'm_1}[r_c(l_c(p),k_1)]\mathscr {D}^{s_2}_{m_2'm_2} [r_c(l_c(p),k_2)]\nonumber \\&\qquad \times \langle s_1s_2m_1m_2|s_Am_{s_A}\rangle \langle l_As_Am_{l_A}m_{s_A}|j_Am_{j_A}\rangle \nonumber \\&\qquad \times \left( \frac{\varepsilon _1(\mathbf{p}_1)}{\varepsilon _1(\mathbf{k})}\frac{\varepsilon _2(\mathbf{p}_2)}{\varepsilon _2(-\mathbf{k})}\frac{W_{12}(\mathbf{k})}{E_{12}(\mathbf{p},\mathbf{k})}\right) ^{1/2}. \end{aligned}$$
(43)

The subscript 1 and 2 refer to the quark and antiquark in meson A respectively, \(W_{12}(\mathbf{k})=\varepsilon _1(\mathbf{k})+\varepsilon _2(-\mathbf{k})\), and \(E_{12}(\mathbf{p},\mathbf{k})=\sqrt{W_{12}(\mathbf{k})^2+\mathbf{p}^2}\), while \(\phi _A^{12}\) denotes the flavor wave function and \(\omega _A^{12}\) the color wave function of the meson.

In the relativistic QPC model [45], an instant interaction Hamiltonian

$$\begin{aligned} H_I=\gamma \int \mathrm {d}^3x\bar{\psi }(x)\psi (x),\ \ t=0, \end{aligned}$$
(44)

is assumed, where \(\psi (x)\) is a Dirac field operator at x. \(\gamma \) is the strength parameter representing the quark pair production from the vacuum. Then, the transition operator could be derived and written down as

$$\begin{aligned} T= & {} -\sqrt{8\pi }\gamma \int \frac{ d^3\mathbf{p}_3d^3\mathbf{p}_4}{\sqrt{\varepsilon _3(\mathbf{p}_3)\varepsilon _4(\mathbf{p}_4)}}\delta ^{(3)}(\mathbf{p}_3+\mathbf{p}_4)\nonumber \\&\quad \times \sum _m\sum _{m_3m_4}\langle 1,m,1,-m|0,0\rangle \nonumber \\&\quad \times \mathscr {Y}_1^m\left( \frac{\mathbf{p}_3-\mathbf{p}_4}{2}\right) \langle 1/2,m_3,1/2,m_4|1,-m\rangle \phi _0^{34}\omega _0^{34}\nonumber \\&\quad \times b^\dag _{m_3} (\mathbf{p}_3)d^\dag _{m_4}(\mathbf{p}_4), \end{aligned}$$
(45)

where the subscript 3 and 4 refer to the quark and the anti-quark produced from the vacuum respectively. \(\phi _0^{34}\) and \(\omega _0^{34}\) are the flavor and color wave functions of the quark pair from the vacuum. \(\mathscr {Y}_1^m(\frac{\mathbf{p}_3-\mathbf{p}_4}{2})\) is the solid harmonics. \(b^\dag _{m_3}\) and \(d^\dag _{m_4}\) are the creation operators of the quark and the anti-quark.

If we define the S-matrix of \(A\rightarrow BC\) process as

$$\begin{aligned} S= & {} I-2\pi i \delta (E_A-E_B-E_C)\nonumber \\&\times \delta ^{(3)}(\mathbf {P}_A-\mathbf {P}_B-\mathbf {P}_C)\mathscr {M}^{m_{j_A}m_{j_B}m_{j_C}}, \end{aligned}$$
(46)

then the \(A\rightarrow BC\) amplitude in the c.m. frame of meson A could be expressed as

$$\begin{aligned}&\mathscr {M}^{m_{j_A}m_{j_B}m_{j_C}}(\mathbf {q})\nonumber \\&\quad =\sum _{\tiny m_{l_B}m_{s_B}m_{l_C}m_{s_C}m_{l_A}m_{s_A}m}\langle l_As_Am_{l_A}m_{s_A}|j_Am_{j_A}\rangle \nonumber \\&\qquad \times \langle l_Bs_Bm_{l_B}m_{s_B}|j_Bm_{j_B}\rangle \nonumber \\&\qquad \times \langle l_Cs_Cm_{l_C}m_{s_C}|j_Cm_{j_C}\rangle \langle 1,m,1,-m|0,0\rangle \nonumber \\&\qquad \times \{\langle \phi _B^{14}\phi _C^{32}|\phi _0^{34}\phi _A^{12}\rangle \int \mathrm {d}^3\mathbf {k} \frac{(-\sqrt{8\pi }\gamma /3)}{\varepsilon _3(\mathbf{p}_3)}\nonumber \\&\qquad \times \psi ^{B*}_{l_Bm_{l_B}} (\mathbf {k})\psi ^{C*}_{l_Cm_{l_C}}(\mathbf {k}')\psi ^{A}_{l_Am_{l_A}}(\mathbf {p}_1)\mathscr {Y}_1^m(\mathbf {p}_3)\nonumber \\&\qquad \times \sum _{\tiny \begin{array}{c} m_1m_4m_3m_2 \\ m'_1m'_4m'_3m'_2 \end{array} }\langle s_1s_2m_1'm_2'|s_Am_{s_A}\rangle \nonumber \\&\qquad \times \langle s_1s_4m_1m_4|s_Bm_{s_B}\rangle \langle s_3s_2m_3m_2|s_Cm_{s_C}\rangle \langle s_3s_4m_3'm_4'|1,-m\rangle \nonumber \\&\qquad \times \mathscr {D}^{(1/2)*}_{m_1'm_1}[r_c(l_c(q_{1}),k_{1})]\nonumber \\&\qquad \times \mathscr {D}^{(1/2)*}_{m_4'm_4}[r_c(l_c(q_{1}),k_{4})]\mathscr {D}^{(1/2)*}_{m_3'm_3}[r_c(l_c(q_2),k_3)]\nonumber \\&\qquad \times \mathscr {D}^{(1/2)*}_{m_2'm_2}[r_c(l_c(q_2),k_2)]\nonumber \\&\qquad \times \left( \frac{\varepsilon _1(\mathbf{p}_1)}{\varepsilon _1(\mathbf{k})}\frac{\varepsilon _4(\mathbf{p}_4)}{\varepsilon _4(\mathbf{k})}\frac{W_{14}(\mathbf{k})}{E_{14}(\mathbf{q},\mathbf{k})}\right) ^{1/2}\nonumber \\&\qquad \times \left( \frac{\varepsilon _3(\mathbf{k}')}{\varepsilon _3(\mathbf{p}_3)}\frac{\varepsilon _2(\mathbf{k}')}{\varepsilon _2(\mathbf{p}_2)}\frac{E_{32}(-\mathbf{q},\mathbf{k}')}{W_{32}(\mathbf{k}')}\right) ^{1/2}\nonumber \\&\qquad +\left\langle \phi _B^{32}\phi _C^{14}|\phi _0^{34}\phi _A^{12}\right\rangle \nonumber \\&\qquad \!\!\!\times \int \!\!\! \mathrm {d}^3\mathbf {k}' \frac{(\!-\!\sqrt{8\pi }\gamma /3)}{\varepsilon _3(\mathbf{p}_3)}\psi ^{B*}_{l_Bm_{l_B}} \!(\mathbf {k}')\psi ^{C*}_{l_Cm_{l_C}}(\mathbf {k})\psi ^{A}_{l_Am_{l_A}}(\mathbf {p}_1)\mathscr {Y}_1^m(\mathbf {p}_3)\nonumber \\&\qquad \times \sum _{\tiny \begin{array}{c} m_1m_4m_3m_2 \\ m'_1m'_4m'_3m'_2 \end{array} }\langle s_1s_2m_1'm_2'|s_Am_{s_A}\rangle \langle s_3s_2m_3m_2|s_Bm_{s_B}\rangle \nonumber \\&\qquad \times \langle s_1s_4m_1m_4|s_Cm_{s_C}\rangle \langle s_3s_4m_3'm_4'|1,-m\rangle \nonumber \\&\qquad \times \mathscr {D}^{(1/2)*}_{m_3'm_3}[r_c(l_c(q_{1}),k_{3})]\mathscr {D}^{(1/2)*}_{m_2'm_2}[r_c(l_c(q_{1}),k_{2})]\nonumber \\&\qquad \times \mathscr {D}^{(1/2)*}_{m_1'm_1} [r_c(l_c(q_2),k_1)]\mathscr {D}^{(1/2)*}_{m_4'm_4}[r_c(l_c(q_2),k_4)]\nonumber \\&\qquad \times \left( \frac{\varepsilon _3(\mathbf{p}_3)}{\varepsilon _3(\mathbf{k}')}\frac{\varepsilon _2(\mathbf{p}_2)}{\varepsilon _2(\mathbf{k}')}\frac{W_{32}(\mathbf{k}')}{E_{32}(\mathbf{q},\mathbf{k}')}\right) ^{1/2}\nonumber \\&\qquad \times \left( \frac{\varepsilon _1(\mathbf{k})}{\varepsilon _1(\mathbf{p}_1)}\frac{\varepsilon _4(\mathbf{k})}{\varepsilon _4(\mathbf{p}_4)}\frac{E_{14}(-\mathbf{q},\mathbf{k})}{W_{14}(\mathbf{k})}\right) ^{1/2}\} \end{aligned}$$
(47)

with the two terms in the bracket corresponding to two different diagrams in Fig. 1. The factor 1/3 comes from the overlap of the color wave functions. Usually, only one of the diagrams is needed. \(\mathbf {k}\) is the three-momentum of particle 1 in the c.m. frame of 14 system, and \(\mathbf {k}'\) is the three-momentum of particle 3 in the c.m. frame of 32 system. If particle 1 and 2 are of the same mass, \(\mathbf {k}=\mathbf {k}'\), and the normalization factors, such as the one in the last line of Eq. (47), will cancel. Notice that the momenta of the quarks in the integrals are different in the two cases, for example, \(\mathbf{p}_3=\mathbf{p}_1-\mathbf{q}\) for the first case and \(\mathbf{p}_3=\mathbf{p}_1+\mathbf{q}\) for the second one. The case that particle 1 and 2 are not of the same flavor is introduced in the Appendix A. \(\mathbf {p}_1\) is the three-momentum of the quark 1 in the c.m. frame of meson A, and \(\mathbf {q}\) is the three-momentum of meson B in the c.m. frame of A. \(q_1\) and \(q_2\) represent the four-momenta of meson B and C respectively.

If we choose the direction of meson B along the z-direction, the amplitude with the BC system having relative angular momentum L and the total spin S, is expressed as [51]

$$\begin{aligned} \mathscr {M}^{LS}(\mathbf{q}_z)= & {} \frac{\sqrt{4\pi (2L+1)}}{2j_A+1}\sum _{m_{j_B},m_{j_C}}\langle LS0(m_{j_B}+m_{j_C})|j_A(m_{j_B}\nonumber \\&+m_{j_C})\rangle \langle j_B j_C m_{j_B}m_{j_C}|S(m_{j_B}+m_{j_C})\rangle \nonumber \\&\times \mathscr {M}^{(m_{j_A}=m_{j_B}+m_{j_C})m_{j_B}m_{j_C}}(\mathbf{q}_z), \end{aligned}$$
(48)

which corresponds to the coupling form factor \(\alpha _{LS}(k)\) used in the relativistic Friedrichs–Lee model as in Eq. (37) in the center of mass system. Since our normalization for the particle A is \(\langle \mathbf{p}|\mathbf{p}'\rangle =\delta ^{(3)}(\mathbf{p}-\mathbf{p}')\) and the one for particle BC is Eq. (16), the quantity \(\sqrt{2\omega (\mathbf{p}_A)\beta (E)}\alpha _{LS}(E)\) is Lorentz invariant, which is just the \(\sqrt{\rho (s)}\) in Eq. (36).

3 A phenomenological example: low lying \(0^{++}\) scalars with \(I=0\)

In the QPC model described above, the relative wave function of quarks in a meson and the bare mass of the meson state could be obtained by solving the quark potential model. In the GI model [2], the Hamiltonian is modified to incorporate the relativistic effects as

$$\begin{aligned} \tilde{H}= & {} (p^2+m_1^2)^{1/2}+(p^2+m_2^2)^{1/2}+\tilde{H}^{conf}_{12}\nonumber \\&+\tilde{H}^{hyp}_{12}+\tilde{H}^{so}_{12}. \end{aligned}$$
(49)

Thus, the eigenfunction of H can be used in the relativistic QPC model to represent the relative wave functions for the quarks in the c.m. frame and the mass eigenvalues can be identified with the bare masses of the mesons in a consistent manner. After numerically diagonalizing the GI’s Hamiltonian with the original GI’s parameters by choosing a large number of the simple harmonic oscillator (SHO) bases, one could obtain the eigenvalues and eigen-wavefunctions of all the bare \(q\bar{q}\) bound states. The lowest isoscalar \((u\bar{u}+d\bar{d})/\sqrt{2}\) bound state predicted by the GI model is located at about 1.1  GeV. On the other side, the lightest isoscalar state in the PDG table is the \(f_0(500)\), whose pole position is at about \(475^{\pm 75}-i 275^{\pm 75}\) MeV. As was pointed out in the original GI’s paper [2], the meson solutions in the GI potential model are just the quark-antiquark bound states formed by considering the interaction potentials between the quark and antiquark, while the interactions with their decaying channels are omitted. In fact, if the coupling to the continuum states (decaying channels) is considered, two kinds of consequences may happen. The first, which always happens, is the mass shift of the discrete state caused by the “renormalization” effect, and the second, more importantly, is the emergence of extra poles as discussed in Ref. [35]. Thus, the second fact suggests us the possibility that the lightest isoscalar state could be dynamically generated by the interaction between the discrete state and the continuum. In principle, the direct coupling of the continuum to continuum also contributes to the scattering S-matrix. However, since the low energy \(\pi \pi \) interaction is almost saturated by a \(f_0(500)\) resonance, as long as this resonance is produced, almost all low energy \(\pi \pi \) interaction is included and the residual continuum-continuum interaction will not contribute much. We will see that the \(f_0(500)\) really will be automatically generated by the interaction of the lowest isoscalar \((u\bar{u}+d\bar{d})/\sqrt{2}\) bound state and the continuum. Thus the residual continuum-continuum interaction would be weak compared to the seed-continuum interaction and will only renormlize the pole position a little. Technically, including a most general continuum-continuum interaction will render the Friedrichs–Lee model unsolvable. So we will ignore such continuum-continuum interaction in our discussion.

For simplicity, we consider only single channel cases here, i.e. only one continuum state. The lowest isoscalar \((u\bar{u}+d\bar{d})/\sqrt{2}\) bare state is assumed to couple to the \(\pi \pi \) continuum in the QPC model. The wave functions obtained from the GI model are applied to determine the coupling form factors in the Friedrichs–Lee model. The \(\eta (s)\) function of Eq. (37), being the most important ingredient of the Friedrichs–Lee model, will serve to provide most information to be compared with the experiment. When a continuum state (decaying channel) is considered, the \(\eta (s)\) function has a unitarity cut starting from the threshold \(s_{th}\). As the \(\eta (s)\) function is continued to the complex s-plane on the unphysical Riemann sheet,

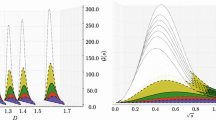
$$\begin{aligned} \eta ^{II}(s)=s-\omega _0^2-\int _{s_{th}} ds' \frac{\rho (s')}{s-s'}-2\pi i\rho (s), \end{aligned}$$
(50)

the zero points of \(\eta ^{II}(s)\) function are just the pole positions of the scattering S-matrix. The spectral function \(\rho (s)\) as a function of \(\sqrt{s}\) is shown in Fig. 3. Secondly, the elastic scattering S-matrix is usually parameterized as \(S(s)=e^{2i\delta (s)}\), where \(\delta (s)\) denotes the scattering phase shift. Since the \(\eta (s)\) function is just the denominator of S(s), the scattering phase shift could be represented by the phase of the \(\eta (s)\) function.

To obtain a better description of the pole positions and experiment phase shifts, we slightly change the bare mass of \((u\bar{u}+d\bar{d})/\sqrt{2}\) state to 1.3  GeV [53] for the reason mentioned above. With the \(\gamma \) parameter increasing from 0 to a certain value, the phase shift of isoscalar \(\pi \pi \) scattering will exhibit different behaviors. We only present three cases with \(\gamma \simeq 1.4,\ 2.9,\ 4.3\) GeV, respectively, as shown in Fig. 2. When \(\gamma \) is small, the phase shift looks like a contribution of a typical narrow resonance or a Breit-Wigner formula, which rises rapidly to about \(180^\circ \) at the vicinity of the mass of the bare state. When \(\gamma \) becomes large, the phase shift will not behave like a narrow resonance. When \(\gamma \) is about 4.3 GeV, the phase shift in the lower region will exhibit a mildly rising behavior which could be identified as a broad \(f_0(500)\), as shown in Fig. 2.

Fig. 2
figure 2

The phase shifts caused by the isoscalar \((u\bar{u}+d\bar{d})/\sqrt{2}\) state with \(\gamma \simeq 1.4~(dashed), 2.9~(dotted), 4.3~(solid)\) GeV, respectively, compared with the experimental data [5,6,7]

Full size image
Fig. 3
figure 3

The spectral function \(\rho (s)\) as a function of \(\sqrt{s}\) for \(\pi \pi \) scattering

Full size image

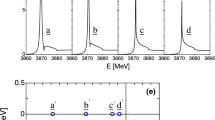
Analysis of the pole positions on the complex s-plane will help us understand the behavior. In fact, two pairs of resonance poles are found on the unphysical Riemann sheet of the complex s-plane. As \(\gamma =4.3\) GeV, two zero points extracted from the \(\eta ^{II}(s)\) function are just located at about

$$\begin{aligned} \sqrt{s_{1}}=390-i 255 \mathrm {MeV},\ \ \sqrt{s_{2}}=1349-i 296 \mathrm {MeV}. \end{aligned}$$
(51)

The lower pole is just close to the average values of \(f_0(500)\) in the PDG table. It is these \(f_0(500)\) and \(f_0(1370)\) poles that contribute a smooth rising of the phase shift, which is the confusing “red dragon” about twenty years ago [8]. Of course, one could tune the parameters to obtain a better description of the data similar to the experimentally measured behavior below the \(K\bar{K}\) threshold, which rises smoothly and approaches \(90^\circ \) at about 850 MeV. However, the more precise way is to do a combined fit together with the other mesons, taking all the bare masses and the universal \(\gamma \) as the parameters and also including the coupled channel effects, which is beyond our present work. In this work, we only wish to present the general properties of scalar mesons, and the results here is enough for our purpose.

Fig. 4
figure 4

Trajectories of the two poles related to the lightest \(I=0\) \((u\bar{u}+d\bar{d})/\sqrt{2}\) bare states on the second sheet of the complex s-plane. As \(\gamma \) increases from 0 to 4.3 GeV, the bare state will move to the complex plane and become a broad resonance. Another pole, which originates from deep in the complex plane, will come to a certain place on the complex s-plane and behave as the \(f_0(500)\)

Full size image

The pole trajectories could provide more insights into the nature of these poles. When \(\gamma \) equals 0, which means that the coupling to the continuum state is not turned on, there is only one pole located at the bare mass of the discrete state on the real axis. Once \(\gamma \) obtains a tiny value, the pole of the discrete state (referred to as the “bare” pole) will move from the real axis to the complex s-plane on the unphysical Riemann sheet and become a resonance. At the same time, another pair of complex poles come into play with very large imaginary parts on the complex s-plane. These poles does not exist when \(\gamma \) vanishes, so they are dynamically generated (referred to as the “dynamical” pole). As the coupling strength \(\gamma \) increases, the “bare” poles move away from the real axis and its imaginary part become larger and larger, while the “dynamical” ones move close to the real axis with its imaginary part decreasing, as shown in Fig. 4.

The higher pole corresponding to the bare isoscalar \((u\bar{u}+d\bar{d})/\sqrt{2}\) state might be the \(f_0(1370)\). Since we only consider one continuum here, the pole position may not be quite precise. It was known that a mysterious property of \(f_0(1370)\) is that there is no phase shift measured so that its existence is questioned [54]. From the point of view here, \(f_0(500)/\sigma \) and \(f_0(1370)\) appear together. \(f_0(500)/\sigma \) is dynamically generated and \(f_0(1370)\) is originated from the bare seed and they both are very broad. Their contributions to the \(IJ=00\) \(\pi \pi \) scattering phase shifts are consistent with the experiment values in quality up to about 0.9  GeV. In the higher region above 0.9  GeV, the contributions of \(f_0(980)\) and \(K\bar{K}\) threshold will be important. Taking the \(f_0(980)\) into account needs the formalism of the Friedrichs–Lee model with multiple bare states and multiple continuous states, which is beyond the scope of this paper. However, roughly speaking, the difference of phase shifts between the single-channel approximation here and the experimental values could just be compensated by another \(180^\circ \) contributed by the \(f_0(980)\). So, it is instructive to look at the total contribution of \(f_0(500)/\sigma \) and \(f_0(1370)\) to the phase shift in this single channel approximation. It can be observed from Fig. 2 that the two poles together contribute a rough \(180^\circ \) phase shift, a very mild phase shift from the \(\pi \pi \) threshold to about 1.5  GeV. In fact, this is a rather general property and can be understood as follows. Since the T matrix is proportional to the spectral function which goes to zero as \(s\rightarrow \infty \), T also goes to zero in this limit. For single channel scatterings, \(T\propto \sin \delta e^{i\delta }\), thus in this limit \(\delta \) can only take the value of \(n\times 180^\circ \), \(n\in \mathbb Z\). In this case, the total phases contributed by the poles falls between 0 and \(180^\circ \) and goes monotonically up. Thus the only limit of the phase shift should be \(180^\circ \). This \(180^\circ \) phase shift can be attributed to the two pair of poles, one from the bare state and the other from the dynamically generated one. Thus, the \(\sigma \) and \(f_0(1370)\) together contribute a total phase shift of \(180^\circ \). This means that they are dynamically related and cannot be treated as independent. In general, the above argument is not limited to this scheme. When single channel approximation is good, similar argument could be applied to the cases where the denominator of the single channel S-matrix is just similar to the \(\eta \) function here, i.e. a real function plus the dispersion relation integral where the spectral function goes to zero as \(s\rightarrow \infty \).

4 Summary

In this paper, we proposed a framework to study the hadron spectrum by generalizing the relativistic Friedrichs–Lee model in a more realistic scenario and combining it with the relativistic QPC model in a consistent way. In the relativistic Friedrichs–Lee model, by assuming the creation and annihilation operators for a single-particle bare state and a two-particle bare state and considering the interaction between them, the exact solution of the creation and annihilation operators for both the single-particle and the two-particle energy eigenstates could be derived. Fuda’s relativistic formulation of the QPC model is also generalized to the cases with unequal quark-antiquark masses. The relativistic exactly-soluble Friedrichs–Lee model combined with the relativistic QPC model and GI’s model, could be used to study the hadron states with light quarks as well as the ones with heavy quarks in a relativistically consistent way and in a unified framework. This scheme may shed more light on the natures of the light scalar states in the constituent quark picture [53]. As an example, we present that the light \(f_0(500)\) and \(f_0(1370)\) could be two poles related to the same bare state, the lightest isoscalar \((u\bar{u}+d\bar{d})/\sqrt{2}\) state: \(f_0(500)\) dynamically generated by the interaction between the bare state and the \(\pi \pi \) continuum, and the \(f_0(1370)\) originated from the bare state. This scheme might also be helpful in studying the other light meson states.