Abstract
We report on a measurement of Spin Density Matrix Elements (SDMEs) in hard exclusive \(\omega \) meson muoproduction on the proton at COMPASS using 160 GeV/c polarised \( \mu ^{+}\) and \( \mu ^{-}\) beams impinging on a liquid hydrogen target. The measurement covers the range 5.0 GeV/\(c^2\) \(< W<\) 17.0 GeV/\(c^2\), with the average kinematics \(\langle Q^{2} \rangle =\) 2.1 (GeV/c)\(^2\), \(\langle W \rangle = 7.6\) GeV/\(c^2\), and \(\langle p^{2}_{\mathrm{T}} \rangle = 0.16\) (GeV/c)\(^2\). Here, \(Q^2\) denotes the virtuality of the exchanged photon, W the mass of the final hadronic system and \(p_T\) the transverse momentum of the \(\omega \) meson with respect to the virtual-photon direction. The measured non-zero SDMEs for the transitions of transversely polarised virtual photons to longitudinally polarised vector mesons (\(\gamma ^*_T \rightarrow V_L\)) indicate a violation of s-channel helicity conservation. Additionally, we observe a sizeable contribution of unnatural-parity-exchange (UPE) transitions that decreases with increasing W. The results provide important input for modelling Generalised Parton Distributions (GPDs). In particular, they may allow to evaluate in a model-dependent way the contribution of UPE transitions and assess the role of parton helicity-flip GPDs in exclusive \(\omega \) production.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, exclusive \(\omega \) meson muoproduction is studied in the process
which in the one-photon-exchange approximation is described by the interaction of a virtual photon \(\gamma ^{*}\) with the target proton p:
This process, which at high virtuality \(Q^2\) of the photon is known as Hard Exclusive Meson Production (HEMP), serves at low values of the squared four-momentum transfer t as an important tool to access Generalised Parton Distributions (GPDs) [1,2,3,4,5] that contain a wealth of new information on the parton structure of the nucleon.
The amplitude for Hard Exclusive Meson Production by longitudinally polarised virtual photons was proven to factorise into a hard-scattering part, which is calculable in perturbative QCD (pQCD), and a soft part [4, 6]. The soft part contains GPDs that describe the structure of the probed nucleon and a distribution amplitude that accounts for the structure of the produced meson. The factorisation is referred to as collinear because parton transverse momenta are neglected. No similar proof of collinear factorisation exists for transversely polarised virtual photons. However, phenomenological pQCD-inspired models have been proposed [7,8,9,10] that go beyond the collinear factorisation by postulating the so called \(k_{\perp }\) factorisation, where \(k_{\perp }\) denotes parton transverse momentum. In the Goloskokov-Kroll model [8,9,10,11,12], hereafter referred to as GK model, cross sections, Spin Density Matrix Elements (SDMEs) as well as target and beam-spin asymmetries for HEMP by both longitudinally and transversely polarised virtual photons can be described simultaneously.
At leading twist, longitudinally polarised vector-meson production by longitudinally polarised virtual photons is described by the chiral-even GPDs \(H^{f}\) and \(E^{f}\), where f denotes a quark of a given flavour or a gluon. When higher-twist effects are included in the three-dimensional light-cone wave function, the production of longitudinally polarised vector mesons by transversely polarised virtual photons is described by the chiral-odd GPDs \(H_T^{f}\) and \({\bar{E}}_T^{f}\), which allow a helicity flip of the “active” quark. Unnatural-parity exchange (UPE) contributes also to transitions from transversely polarised virtual photons to transversely polarised vector mesons or from longitudinally polarised virtual photons to transversely polarised vector mesons. These contributions are described by the GPDs \({\widetilde{H}}^{f}\) and \({\widetilde{E}}^{f}\). Besides these UPE contributions, there is a sizeable pion-pole contribution that is treated as a one-boson exchange in the GK model.
The SDMEs describe the spin structure of the reaction shown in Eq. (1). They are related to helicity amplitudes that describe transitions between specified spin states of virtual photon, target proton, produced vector meson and recoil proton. For an unpolarised nucleon target, after summing over initial and final spin states of the proton, SDMEs only depend on the helicities of virtual photon and produced meson. The measured SDME values can be used to establish a hierarchy of helicity amplitudes, to test the hypothesis of s-channel helicity conservation (SCHC), to evaluate the contribution of unnatural-parity-exchange transitions and to assess the role of chiral-odd, i.e. parton helicity-flip GPDs in exclusive \(\omega \) production. They also allow to determine the phase difference between helicity amplitudes as well as the longitudinal-to-transverse cross-section ratio. The measurements of SDMEs can provide further constraints on GPD parameterisations beyond those from measurements of cross sections and spin asymmetries for HEMP.
The HERMES measurements of SDMEs for exclusive electroproduction of \(\omega \) mesons [13] in the kinematic region 1.0 (GeV/c)\(^2\) \(< Q^{2}<\) 10 (GeV/c)\(^2\), 3.0 GeV/\(c^2\) \(< W < 6.3\) GeV/\(c^2\) and \(|t| < 0.2\) (GeV/c)\(^2\), where t is the squared four-momentum transfer to the target, indicate a sizeable contribution of UPE transitions that can be described by GPDs \({\widetilde{H}}^{f}\) and \({\widetilde{E}}^{f}\) related to quark helicity distributions. Here, \(Q^2\) denotes the virtuality of the exchanged virtual photon and W is the mass of the final hadronic system. In the framework of the GK model it turns out [12] that the pion-pole exchange, which is treated as one-boson exchange, is an important contribution required to reproduce the HERMES results. The effect of such a t-channel \(\pi ^0\) exchange decreases with W while it is predicted still to be measurable at COMPASS. The HERMES results on SDMEs for exclusive \(\omega \) production, as well as those for exclusive \(\rho ^{0}\) production [13, 14], indicate a violation of the SCHC hypothesis, which in the framework of the GK model is attributed to a contribution of chiral-odd GPDs.
Also, an early paper on exclusive \(\omega \) electroproduction [15] contains results on SDMEs obtained at DESY for 0.3 (GeV/c)\(^2\) \(< Q^{2} < 1.4\) (GeV/c)\(^2\) and 0.3 GeV/\(c^2\) \(< W < 2.8\) GeV/\(c^2\). The SDMEs in exclusive \(\omega \) electroproduction were also studied [16] at CLAS in the range 1.6 (GeV/c)\(^2\) \(< Q^2<\) 5.2 (GeV/c)\(^2\) and 1.9 GeV/\(c^2\) \(< W<\) 2.8 GeV/\(c^2\). It was found that the exchange of the pion Regge trajectory dominates exclusive \(\omega \) production, even for \(Q^2\) values as large as 5 (GeV/c)\(^2\).
The present COMPASS results on SDMEs for exclusive \(\omega \) muoproduction, which supplement the published COMPASS results on azimuthal asymmetries for transversely polarised protons [17], have the potential to further constrain GPDs. In the framework of the GK model it may become possible to assess the role of chiral-odd GPDs in the mechanism of SCHC violation and to shed light onto the mechanism of UPE transitions.
2 Theoretical formalism
Adopting the notation from Ref. [13], the theoretical formalism of SDMEs and helicity amplitudes introduced by Schilling and Wolf [18] is used throughout this paper.
2.1 Definition of spin density matrix elements
The helicity amplitudes \(F_{\lambda _{V} \lambda '_{N}\lambda _{\gamma } \lambda _{N}}\) describe the transition of a virtual photon with helicity \(\lambda _{\gamma }\) to a vector meson with helicity \( \lambda _{V}\), where \(\lambda _{N}\) (\(\lambda '_{N}\)) is the nucleon helicity in the initial (final) state. The helicity amplitudes depend on W, \(Q^{2}\), and \(t'\equiv |t| - t_{0}\approx p^{2}_{\mathrm{T}}\), where \(t_{0}\) represents the smallest kinematically allowed value of |t| for given \(Q^{2}\) and meson mass, and \(p^{2}_{\mathrm{T}}\) is the square of the vector-meson transverse momentum with respect to the direction of the virtual photon. In the centre-of-mass (CM) system of virtual photon and nucleon, the vector-meson spin density matrix \(\rho _{\lambda _{V}\lambda _{V}^{'}}\) is related to the helicity amplitude \(F_{\lambda _{V} \lambda '_{N}\lambda _{\gamma } \lambda _{N}}\) as [18]
where \({\mathscr {N}}\) is a normalisation factor [14, 18]. The virtual-photon spin density matrix \(\rho ^{U+L}_{\lambda _{\gamma } \lambda '_{\gamma }}\) [14] describes the subprocess \( \mu \rightarrow \mu ' + \gamma ^{*}\), which is calculable in quantum electrodynamics. It can be decomposed as
where the matrix with superscript L (U) contains elements that are coupled (not coupled) to the beam polarisation \(P_{b}\). In the following the corresponding vector-meson SDMEs, which are related to these elements, will be referred to as “polarised” (“unpolarised”).
The vector-meson spin density matrix \(\rho ^{U+L}_{\lambda _{\gamma } \lambda '_{\gamma }}\) can be decomposed into a set of nine matrices \(\rho ^{\alpha }_{\lambda _V\lambda '_V}\) corresponding to different virtual-photon polarisation states: transverse polarisation (\(\alpha \)=0, ..., 3), longitudinal polarisation (\(\alpha \)=4), and their interference (\(\alpha \)=5, ..., 8) [18]. If it is experimentally not possible to separate the contributions from longitudinally and transversely polarised photons, SDMEs are usually defined as follows:
Here, \(R= d\sigma _{L}/ d\sigma _{T}\) is the differential longitudinal-to-transverse cross-section ratio of virtual photons and \(\epsilon \) is the virtual-photon polarisation parameter, see Eq. (15). The relations between the 23 SDMEs defined in Eq. (5) and the helicity amplitudes are given in Appendix A of Ref. [14].
2.2 Properties of helicity amplitudes
As detailed in Refs. [14, 18], each helicity amplitude can be linearly decomposed into a natural-parity-exchange (NPE) amplitude T and an unnatural-parity-exchange (UPE) amplitude U,
with the following relations [18]:
Using the notation
and the symmetry properties [14, 18] of the amplitudes T, Eq. (9) becomes
Here, both products on the right-hand side represent the contribution of NPE amplitudes, the first without and the second with nucleon-helicity flip. The relations for the UPE amplitudes can be written in an analogous way. In the abbreviated notation used in the text, the nucleon-helicity indices will be omitted for amplitudes with \(\lambda _N=\lambda '_N\), i.e.
The hypothesis of s-channel helicity conservation implies that there exist only diagonal \(\gamma ^{*} \rightarrow V\) transitions (\(\lambda _{V}=\lambda _{\gamma }\)).
3 Experimental access to SDMEs
Spin density matrix elements are extracted from experimental data on exclusive muoproduction of \(\omega \) mesons. The SDMEs are fitted as parameters of the three-dimensional angular distribution \({\mathscr {W}}^{U+L}(\Phi ,\phi ,\) \(\cos \Theta )\) to the corresponding experimental distribution. Here, \(\Phi \) is the azimuthal angle of the produced \(\omega \) meson, while the polar angle \(\Theta \) and the azimuthal angle \(\phi \) describe the three-pion decay of the \(\omega \) meson, see Eqs. (16–21). The angular distribution \({\mathscr {W}}^{U+L}\) is decomposed into contributions that are not coupled (\({\mathscr {W}}^{U}\)) or coupled (\({\mathscr {W}}^{L}\)) to the beam polarisation:
Using the data, which were collected with a longitudinally polarised beam, 15 “unpolarised” SDMEs are extracted from \({\mathscr {W}}^U\):
and 8 “polarised” SDMEs from \({\mathscr {W}}^L\):
Here, the virtual-photon polarisation parameter \(\epsilon \) represents the ratio of fluxes of longitudinal and transverse virtual photons,
where \(y = p\cdot q / p\cdot k {\mathop {=}\limits ^{lab}} \nu / E\). The symbols p, q and k denote the four-momenta of target proton, virtual photon and incident lepton respectively. The energy of virtual photon and incident lepton in the target rest frame is denoted by \(\nu \) and E, respectively.
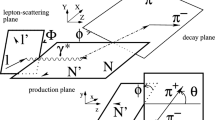
Angles and reference frames are defined in Fig. 1.
Definition of angles in the process \(\mu N \rightarrow \mu N \omega \) with \(\omega \rightarrow \pi ^+ \pi ^- \pi ^0\). Here, \(\Phi \) is the angle between the \(\omega \) production plane and the lepton scattering plane in the centre-of-mass system of the virtual photon and the target nucleon. The variables \(\Theta \) and \(\phi \) are respectively the polar and azimuthal angles of the unit vector normal to the decay plane in the \(\omega \) meson rest frame
The directions of axes of the “hadronic CM system” and the \(\omega \)-meson rest frame coincide with the directions of axes of the helicity frame [14, 15, 18]. Following Ref. [18], the right-handed hadronic CM system of virtual photon and target nucleon, with coordinates XYZ, is defined such that the Z-axis is aligned along the virtual-photon three-momentum \(\mathbf {q}\) and the Y-axis is parallel to \(\mathbf {q} \times \mathbf {v}\), where \(\mathbf {v}\) is the three-momentum of the \(\omega \) meson.
For the convenience of the reader, we give in the following the explicit definitions of angles [13]. The angle \(\Phi \) between \(\omega \) production plane and lepton scattering plane in the hadronic CM system is given by
and
Here \(\mathbf {k}\), \(\mathbf {k'}\), \(\mathbf {q}=\mathbf {k}-\mathbf {k'}\) and \(\mathbf {v}\) are the three-momenta of the incoming and outgoing lepton, the virtual photon and the \(\omega \) meson respectively.
The unit vector normal to the decay plane in the \(\omega \) rest frame is defined by
where \(\mathbf {p}_{\pi ^+}\) and \(\mathbf {p}_{\pi ^-}\) are the three-momenta of the positive and negative decay pion in the \(\omega \) rest frame, respectively.
The polar angle \(\Theta \) of the unit vector \(\mathbf {n}\) in the \(\omega \) meson rest frame, with the z-axis aligned opposite to the outgoing nucleon momentum \(\mathbf {p}'\) and the y-axis directed along \(\mathbf {p}' \times \mathbf {q}\), is defined by
The azimuthal angle \(\phi \) of the unit vector \(\mathbf{n}\) is given as follows:
4 Experimental setup and data selection
The main component of the COMPASS setup is the two-stage magnetic spectrometer. Each spectrometer stage comprises a dipole magnet complemented by a variety of tracking detectors, a muon filter for muon identification and an electromagnetic as well as a hadron calorimeter. A detailed description of the setup can be found in Refs. [20,21,22].
The data used for this analysis were collected within four weeks in 2012. In this period the COMPASS spectrometer was complemented by a 2.5 m long liquid-hydrogen target surrounded by a time-of-flight (TOF) system for the detection of recoiling protons and by a third electromagnetic calorimeter placed directly downstream of the target. The recoil detector restricts the kinematic coverage towards the region of small squared transverse momentum of the \(\omega \)-meson with respect to the virtual-photon direction. Hence it was used only for an additional check of the background correction procedure as explained in Sect. 5.3 and not for the determination of SDMEs.
Data with \(\mu ^{+}\) and \(\mu ^{-}\) beams were taken separately. The natural polarisation of the muon beam provided by the CERN SPS originates from the parity-violating decay-in-flight of the parent meson, which implies opposite polarisations for \(\mu ^{+}\) and \(\mu ^{-}\) beams. Within regular time intervals during data taking, charge and polarisation of the muon beam were swapped simultaneously. In order to equalise the spectrometer acceptance for the two beam charges, also the polarities of the two spectrometer magnets were changed accordingly. For both beams, the absolute value of the average beam polarisation is about 0.8 with an uncertainty of about 0.04.
An event to be accepted for analysis is required to have a topology as that of the observed process

The selected events should have one reconstructed vertex inside the liquid-hydrogen target associated with the incoming and the outgoing muon, and two hadron tracks of opposite charge. The outgoing muon has to have the same charge as the incoming muon and is required to traverse more than 15 radiation lengths to be identified as a muon. The charged hadron tracks are selected by requiring the traversed path to be shorter than 10 radiation lengths.
4.1 \(\pi ^0\) reconstruction
A neutral pion is reconstructed via its dominant decay into two photons that are registered as neutral clusters in the electromagnetic calorimeters. As neutral cluster we denote a reconstructed calorimeter cluster that is not associated to a charged track, thereby including any cluster for the most upstream calorimeter that had no tracking system upstream of it. The method of \(\pi ^0\) reconstruction is similar to the one used in the analysis of azimuthal asymmetries for exclusive \(\omega \) production on a transversely polarised target [23].
In Fig. 2 the distribution of the reconstructed two-photon invariant mass is shown. The \(\pi ^{0}\) peak is prominent. The distribution is fitted by a superposition of the signal, which is described by a Gaussian function, and a linear background. After selection of an event with a \(\pi ^{0}\), the energies of the decay photons are scaled by the factor \( M^{\mathrm {PDG}}_{\pi ^{0}}/M_{\gamma \gamma }\) in order to improve the experimental resolution of the reconstructed three-pion invariant mass. Here \( M^{\mathrm {PDG}}_{\pi ^{0}}\approx \) 0.135 \(\mathrm {GeV/{ c}}^2\) is the nominal \(\pi ^0\) mass. This scaling does not affect the angular distributions of neutral pions.
4.2 Kinematic selections
The following kinematic selections are applied to select exclusively produced \(\omega \) mesons:
-
1.0 (GeV/\({ c})^2< Q^{2} < 10.0\) (GeV/\({ c})^2\), where the lower limit ensures applicability of pQCD and the upper one suppresses background due to hadrons produced in DIS, which hereafter is referred to as “SIDIS background”.
-
\(0.1< \hbox {y} < 0.9\), where the lower limit suppresses events with poorly reconstructed kinematics and the upper one removes events with large radiative corrections.
-
W \(> 5.0~\hbox {GeV}/{ c}^2\) to remove the kinematic region where the cross section changes rapidly due to the production of resonances.
-
0.01 (GeV/\({ c})^2< p_{\mathrm{{T}}}^2 < 0.5\) (GeV/\({ c})^2\), where \(p_{\mathrm{{T}}}\) is the transverse momentum of the \(\omega \) meson with respect to the virtual-photon direction. The lower limit removes events with a poorly determined azimuthal angle of the produced meson and the upper one suppresses SIDIS background.
-
0.1 GeV/\( {c}^2 < M_{\gamma \gamma }<\) 0.17 GeV/\( {c}^2\), where \(M_{\gamma \gamma }\) is the two-photon invariant mass, in order to select \(\pi ^0\) mesons.
-
0.71 GeV/\({ c}^2< M_{\pi ^{+}\pi ^{-}\pi ^{0}} < 0.86\) GeV/\( {c}^2\), where \(M_{\pi ^{+}\pi ^{-}\pi ^{0}}\) is the three-pion invariant mass, in order to select \(\omega \) mesons. In Fig. 3, the \(\omega \) signal is clearly visible above a small background. The invariant mass of the three-pion system is fitted by a Breit–Wigner function and a linear background. As the non-resonant background is found to be small, i.e. about 7% for the used range of three-pion invariant mass, its effect on the extraction of SDMEs is neglected.
-
\( E_{\omega }>\) 14 GeV to reduce the SIDIS background contribution.
The information from the recoil proton detector is not used for the extraction of SDMEs. Instead, in order to enhance the fraction of events with exclusively produced \(\omega \) mesons, the missing energy
is constrained by −3.0 GeV \(< E_{\mathrm{miss}}<\) 3.0 GeV to take into account the experimental resolution. Here M is the proton mass, \( M^{2}_{\mathrm{X}}=({p} + {q}- {p}_{\pi ^+} - {p}_{\pi ^-} -{p}_{\pi ^0})^{2}\) is the missing mass squared, and \({p}_{\pi ^+}\), \( {p}_{\pi ^-}\) and \({p}_{\pi ^0}\) are the four-momenta of the three pions. The \(E_{\mathrm{miss}}\) distribution for the experimental data is shown in Fig. 4 as open histogram. The exclusive peak is apparent.
After applying all kinematic selection criteria, 3060 events are available for further analysis.
4.3 SIDIS background
The \( E_{\mathrm{miss}} \) distribution is used to determine the fraction of SIDIS background under the exclusive peak, following the procedure described in Refs. [17, 23]. For the simulation of background, the LEPTO 6.5.1 generator is used with the COMPASS tuning of parameters [24]. In order to achieve the best possible agreement between experimental and simulated \(E_{\mathrm{miss}}\) distributions, the simulated data are reweighted on a bin-by-bin basis using the weight
Here \(N^{sc}_{rd}(E_{\mathrm{miss}})\) and \(N^{sc}_{MC}(E_{\mathrm{miss}})\) are numbers of events containing same-charge hadron pairs, \(h^{+} h^{+} \gamma \gamma \) and \(h^{-} h^{-} \gamma \gamma \), in the three-pion system for experimental and simulated data, respectively. In order to improve the statistical significance, the constraint on the \(\omega \) invariant mass is not used for the purpose of estimating the weight w. The shaded histogram in Fig. 4 represents the simulated SIDIS background, which is generated by LEPTO and processed through the full simulation of the COMPASS setup [25], followed by the same event reconstruction and selection procedure as for the real data, and then reweighted in the way described above. The distribution is normalised to the experimental data in the region 7 GeV \(<E_{\mathrm{miss}}<\) 20 GeV. The fraction of background in the signal window \(-3.0~\hbox {GeV}< E_\mathrm{miss} < 3.0~\hbox {GeV}\) is found to be \(f_{bg}\)= 0.28 for the total kinematic range. The fraction of SIDIS background increases with increasing \(Q^2\) and \(p^2_{\mathrm{T}}\), and it decreases with increasing W. For the results on kinematic dependences of SDMEs, which are presented in the following, the background fraction \(f_{bg}\) is evaluated separately for each kinematic bin, the values ranging between 0.20 and 0.41.
The missing-energy distribution from experimental data (open histogram) compared to the distribution of SIDIS events from a LEPTO MC simulation (shaded histogram). The MC distribution is normalised to the data in the region 7 GeV \(< E_{\mathrm{miss}} < 20\) GeV. The vertical dashed line denotes the upper limit of the exclusive region. Each LEPTO MC event is reweighted by a \(E_\mathrm{miss}\)-dependent weight that is calculated using both experimental and simulated data with same-charge hadron pairs. See text for a detailed explanation
5 Extraction of SDMEs
5.1 Unbinned maximum likelihood method
The SDMEs are determined by an Unbinned Maximum Likelihood fit of the function \({{\mathscr {W}}} ({{{\mathscr {R}}}};\Phi ,\phi ,\cos \Theta )\) to the experimental three-dimensional angular distribution of \(\omega \) production and decay. The explicit expression for the dependence of \({{\mathscr {W}}}\) on SDMEs was given in Sect. 3 by Eqs. (12, 13, 14). Here \({{\mathscr {R}}}\) denotes the set of 23 SDMEs \(r ^{\alpha }_{\lambda _{V}{\lambda '_{V}}}\). The negative log-likelihood function to be minimised reads
where N is the number of selected events.The likelihood normalisation factor
is calculated numerically using the sample of MC events generated with the HEPGEN++ \(\omega \) generator, in the following denoted by HEPGEN [26, 27]. This generator is used to model the kinematics of exclusive \(\omega \) production. For the purpose of the present analysis, the option with an isotropic three-dimensional angular distribution of \(\omega \) production and decay is chosen. The generated events are passed through a complete description of the COMPASS setup and the resulting data are treated in the same way as it was done for experimental data. The number of HEPGEN events is denoted \(N_{MC}\) in Eq. (25).
5.2 Background-corrected SDMEs
In order to determine SDMEs that are corrected for SIDIS background, a two-step procedure is used. First, the parameterisation of the background angular distributions is obtained by applying the above described maximum likelihood method to selected SIDIS events simulated with the LEPTO generator. These events are required to pass the same selection criteria as experimental data. Performing an unbinned likelihood fit according to Eq. (24) using simulated events in the range \(-3.0~\hbox {GeV}<E_{\mathrm{miss}} < 3.0~\hbox {GeV}\) yields the set \({{\mathscr {B}}}\) of 23 “background SDMEs”.
In the second step, the set \({{\mathscr {B}}}\) of background SDMEs is used to extract the set \({{\mathscr {R}}}\) of background-corrected SDMEs by applying the unbinned maximum likelihood fit to the experimental data. For this purpose the following negative log-likelihood function is fitted:
Here, \(f_{bg}\) is the fraction of background events in the selected experimental data as determined in Sect. 4.2 and \(\widetilde{{\mathscr {N}}}\) is the normalisation factor:
5.3 Systematic uncertainties
The following sources of systematic uncertainties are considered:
-
i)
Difference between results for \(\mu ^+\) and \(\mu ^-\) beams
The \(\mu ^{+}\) beam intensity was about 2.7 times higher than that of the \(\mu ^-\) beam. A possible impact of this difference on the determination of SDMEs is checked by comparing the SDMEs extracted separately for the \(\mu ^{+}\) beam (negative polarisation) and the \(\mu ^{-}\) beam (positive polarisation). For each SDME, half of the difference between the SDME values determined with opposite beam polarisations is taken as systematic uncertainty.
-
ii)
Influence of shifted \(E_{\mathrm{miss}}\) peak position
It was observed in Ref. [28] that certain SDME values depend on the position of the \(E_{\mathrm{miss}}\) peak. The \(E_\mathrm{miss}\) distribution shown in Fig. 4 is not precisely centred at zero, but slightly shifted towards negative values. This results from an imbalance between the energy measured for the incoming muon and the energies of the final-state particles measured in the forward spectrometer. The effect of this shift on the extracted SDMEs is investigated by applying the small kinematic correction (+0.7 GeV/c) to the beam momentum that is needed to centre the \( E_{\mathrm{miss}} \) peak at zero. The difference between the values of final SDMEs and those obtained with corrected kinematics is taken as systematic uncertainty. A similar shift of the \(E_{\mathrm{miss}}\) peak is obtained by rescaling the momenta of the final-state particles measured in the spectrometer. The differences between SDME values obtained without and with the rescaling are comparable to those obtained with corrected beam momentum. In order to avoid double counting, only the differences obtained with corrected beam momentum are taken as systematic uncertainties.
-
iii)
Effect of background subtraction
As detailed in Sect. 5.2, the background-corrected SDMEs are obtained with background SDMEs obtained from LEPTO events in the exclusive region −3.0 GeV \(< E_{\mathrm{{miss}}}<\) 3.0 GeV. As the angular distributions from LEPTO were never experimentally verified for the event selection used in the present analysis, as a check an alternative method is used, in which background SDMEs are estimated from experimental data in the region 7.0 GeV\(< E_{\mathrm{miss}}<\) 20.0 GeV. The difference between SDMEs obtained by these two methods is taken as systematic uncertainty. In addition, the procedure for background correction is checked by using the data from the recoil-proton detector (RPD). These data allow us to apply additional selection criteria on exclusive events [29, 30], which lead to a reduction of the non-exclusive background by a factor of about 10. As a limited \(p^2_{\mathrm{T}}\)-range is covered by the RPD, the same limited kinematic region is used to compare the SDMEs obtained with and without RPD. The results are consistent within statistical uncertainties, hence no systematic uncertainty is assigned here.
-
iv)
Comparison of unbinned and binned maximum likelihood methods
The two fitting methods are expected to yield consistent results for sufficiently large statistics. In this analysis however, when using the unbinned method the background treatment is different from that when using the binned method. In the former case, the angular dependence of the background is parameterised, while in the latter case the background is subtracted in each angular bin on a bin-by-bin basis. Comparing the results from the two methods hence probes a possible systematic uncertainty due to the background-correction procedure. For each SDME, the systematic uncertainty is given by the difference between the final value as obtained using the unbinned method and the value obtained with the binned method.
-
v)
Sensitivity to the shapes of the kinematic distributions generated by HEPGEN
As no experimental data exists on the differential cross section for exclusive \(\omega \) production at COMPASS energies, a model is used to simulate the process in HEPGEN. In order to check the sensitivity of SDMEs to the shapes of kinematic distributions in the HEPGEN generator, the SDME extraction was repeated by reweighting the MC events with weights depending on \(Q^2\) and \(\nu \). The weights are tuned such that the \(Q^2\) and \(\nu \) distributions from the experimental data match those from the reweighted simulated data. The effect of this reweighting on the extracted SDMEs is small in most cases, and the difference between final SDMEs and those obtained with reweighted MC events is taken as systematic uncertainty.
The 23 SDMEs for exclusive \(\omega \) leptoproduction extracted in the total COMPASS kinematic region with \( \langle Q^2 \rangle = 2.13\) (GeV/c)\(^2\), \(\langle W\rangle =7.6\) GeV/\( {c}^2\), \( \langle p^{2}_{\mathrm{T}}\rangle = 0.16\) (GeV/c)\(^2\). Inner error bars represent statistical uncertainties and outer ones statistical and systematic uncertainties added in quadrature. Unpolarised (polarised) SDMEs are displayed in unshaded (shaded) areas
The total systematic uncertainties are obtained by adding the above described components in quadrature. Table 1 gives the values for the total kinematic region. The individual contributions i) - v) to the systematic uncertainty for each SDME are compiled in Table 4 in the Appendix. When averaged over all SDMEs it appears that the group i) systematics dominates by contributing almost half of the systematic uncertainties, while about one-fifth contributions arise from both group ii) and group iv) systematics. In most cases, the statistical uncertainty is comparable to or smaller than the total systematic one.
6 Results
6.1 SDMEs for the total kinematic region
The SDMEs extracted in the total kinematic region 1.0(GeV/c)\(^2\) \(< Q^{2} < 10.0\) (GeV/c)\(^2\), 5.0 GeV/\(c^2\) \(< W < 17.0\) GeV/\(c^2\) and 0.01 (GeV/c)\(^2\) \(<p^{2}_{\mathrm{T}} < 0.5\) (GeV/c)\(^2\), with mean values \(\langle Q^{2} \rangle = 2.13\) (GeV/c)\(^2\), \(\langle W \rangle = 7.6\) GeV/\( {c}^2\) and \(\langle p^{2}_{\mathrm{T}} \rangle = 0.16\) (GeV/c)\(^2\) are presented in Fig. 5 and Table 1. These SDMEs are presented in five classes corresponding to different helicity transitions. For the SDMEs in class A, the dominant contributions are related to the squared amplitudes for transitions from longitudinal virtual photons to longitudinal vector mesons, \(\gamma ^*_L \rightarrow V_L\), and from transverse virtual photons to transverse vector mesons, \(\gamma ^*_T \rightarrow V_T\). In class B, the dominant terms correspond to the interference between amplitudes for the two aforementioned transitions. The main terms in the SDMEs for classes C, D and E are proportional to the products of small amplitudes describing \(\gamma ^*_T \rightarrow V_L\), \(\gamma ^*_L \rightarrow V_T\) and \(\gamma ^*_T \rightarrow V_{-T}\) transitions respectively. In Fig. 5, polarised SDMEs are shown in shaded areas. The experimental uncertainties of these SDMEs are larger than those of the unpolarised SDMEs because the lepton-beam polarisation is smaller than unity (\(|P_{b}| \approx 80\%\)) and in the expressions for the angular distributions (see Eq. (14)) they are multiplied by the small kinematic factor \(|P_{b}|\sqrt{1- \epsilon } \), where \( \epsilon \approx 0.96\). In the calculation of the statistical uncertainty, the correlations between the various SDMEs are taken into account.
6.2 Dependences of SDMEs on \(Q^{2}\), \(p^{2}_{\mathrm{{T}}}\) and W
The kinematic dependences of the SDMEs on \(Q^{2}\), \(p^{2}_{\mathrm{{T}}}\) and W, which have been determined in three bins for each of the variables, are shown in Figs. 6, 7 and 8. In Table 2, the limits of the kinematic bins and the mean values of kinematic variables in the bins are given. The values of SDMEs in bins of \(Q^{2}\), \(p^{2}_{\mathrm{{T}}}\) and W are given in Tables 5, 6 and 7 respectively, in the Appendix.
7 Discussion
7.1 Test of the SCHC hypothesis
In case of SCHC, only the seven SDMEs of classes A and B are not restricted to vanish, while all SDMEs from classes C, D, and E should be equal to zero. Six of the SDMEs in classes A and B have to fulfil the following relations [18]:
Within uncertainties, the extracted SDMEs are consistent with these relations:
However, for the transitions \(\gamma ^*_{\mathrm{T}} \rightarrow V_{\mathrm{L}}\) of class C the non-zero values of SDMEs \(r^5_{00}\) and \(\mathrm {Re}\{r^1_{10}\}\) show SCHC violation at the level of three standard deviations of the statistical uncertainty. In the GK model [10], these SDMEs are related to the chiral-odd GPDs \(H_{\mathrm{T}}\) and \({{{\bar{E}}}}_{\mathrm{T}}\) coupled to the higher-twist wave function of the meson. The kinematic dependences of these SDMEs, as presented in Sect. 6, may help to further constrain the model.
7.2 UPE contribution in exclusive \(\omega \) meson production
The existence of UPE transitions in exclusive \(\omega \) production can be tested by examining linear combinations of SDMEs such as
The quantity \(u_1\) can be expressed in terms of helicity amplitudes as
Since the numerator depends only on UPE amplitudes, a \(u_1\) value different from zero indicates non-zero contribution from UPE transitions. For the total kinematic region of COMPASS \(u_1\) is equal to \(0.830 \pm 0.073\) ± 0.049, which is a clear signal of a large UPE contribution. Additional information on UPE amplitudes is obtained from the SDME combinations
and
which in terms of helicity amplitudes can be combined into
For COMPASS, \(u_2\) = \(-0.033 \pm 0.016 \pm 0.043\) and \(u_3\) = \(-0.114 \pm 0.126 \pm 0.099\) are obtained, which are consistent with zero at the present accuracy of the data.
In Fig. 9 the dependence of the quantities \(u_{1}\), \(u_{2}\), \(u_{3}\) on \(Q^{2}\), \(p^{2}_{\mathrm{{T}}}\), and W is presented. The quantity \(u_{1}\) decreases with increasing W and \(p^{2}_{\mathrm{{T}}}\), which indicates that the UPE contribution becomes smaller, while \(u_{2}\), \(u_{3}\) fluctuate around zero.
More detailed information on the Wdependence of certain UPE transitions in terms of helicity amplitudes can be obtained by considering the difference of the following two class-A SDMEs [14]:
which reads:
For the total kinematic region, both SDMEs and their difference are close to zero. For the present data, \(\mathrm {Im} \{r^2_{1-1}\}-r^1_{1-1}\)= 0.07±0.07 is obtained, hence \({\widetilde{\sum }}|U_{11}|^2 \approx {\widetilde{\sum }}|T_{11}|^2\). By applying Eq. (10), Eq. (35) can be rewritten as follows:
Bilinear contributions of nucleon helicity-flip amplitudes are suppressed by a factor \((\sqrt{-t^{\prime }}/M)^2\), where \(t'\) is a measure of the transverse momentum of the vector meson with respect to the direction of the virtual photon. Neglecting these bilinear contributions yields:
In Table 3, the values of the SDMEs \( r^{1}_{1-1}\) and Im\(\{{r^{2}_{1-1}}\}\) and their difference are shown as a function of \(\langle W \rangle \). The difference is large and positive at \( \langle W \rangle = 5.9\) GeV/\(c^2\), i.e. \( |U_{11}|>|T_{11}|\). For \( \langle W \rangle = 7.1\) GeV/\(c^2\), \( |U_{11}| \approx |T_{11}|\) holds and for \( \langle W \rangle = 9.9\) GeV/\(c^2\) the situation is reversed: \( |U_{11}| < |T_{11}|\).
A substantial contribution of UPE transitions in hard exclusive \(\omega \) meson electroproduction was observed at HERMES [13]. In their total kinematic range , with mean values \(\langle Q^{2} \rangle = 2.4\) (GeV/c)\(^2\), \( \langle W \rangle = 4.8\) GeV/\(c^2\) and \( \langle t' \rangle = 0.08\) (GeV/c)\(^2\), for the proton target they found \(u_1 = 1.1 \pm 0.09 \pm 0.12\) and \(\mathrm {Im} \{r^2_{1-1}\}-r^1_{1-1} = 0.35\pm 0.04\pm 0.05\). The latter value indicates that \(|U_{11}|^2 > |T_{11}|^2\) in their kinematic range. Also they observed that the quantity \(u_1\), when averaged over the total range of W, increases (decreases) with increasing values of \(Q^2\) (\(t'\)).
A quantitative comparison of COMPASS and HERMES results is not straightforward, because the covered kinematic regions only partially overlap, and COMPASS covers significantly wider ranges of W and \(p^2_{\mathrm{T}}\). It is important to note here that, when studying the kinematic dependences of the measured observables, results are extracted in one-dimensional intervals of a given kinematic variable, while averaging over the full ranges of the other two variables. As the two experiments have only partially overlapping kinematic ranges, the results after averaging cannot be directly compared.
When neglecting the observed \(Q^2\) and \(t'\) (\(p^2_{\mathrm{T}}\)) dependences, which exhibit opposite trends, one can compare the HERMES result on \(u_1\) for their total kinematic range to the COMPASS result shown at the lowest W value in Fig. 9. Similarly, HERMES result on \(\mathrm {Im} \{r^2_{1-1}\}-r^1_{1-1}\) can be compared to the corresponding value from COMPASS at \( \langle W \rangle = 5.9\) GeV/\(c^2\) , which is shown in Table 3. Within uncertainties the results from the two experiments are consistent for both observables.
Altogether, the main COMPASS results presented in this subsection, i.e. the W dependence of \(u_1\) as well as that of \(\mathrm {Im} \{r^2_{1-1}\}-r^1_{1-1}\) indicate that the UPE contribution decreases with increasing W without vanishing towards largest W values accessible at COMPASS. In the GK model, UPE is described by the GPDs \({\widetilde{H}}^{f}\) and \({\widetilde{E}}^{f}\) (non-pole), and by the pion-pole contribution treated as a one-boson exchange [12]. The latter one, which is a sizeable contribution, results in a significantly faster decrease of the predicted UPE contribution with increasing W than that measured at COMPASS.
7.3 The NPE-to-UPE asymmetry of the transverse cross section for the transition \(\gamma ^*_T \rightarrow V_T\)
Another observable that is sensitive to the relative contributions of UPE and NPE amplitudes is the NPE-to-UPE asymmetry of the transverse differential cross section for the transition \(\gamma ^*_T \rightarrow V_T\). It is defined [12] asFootnote 1
where the superscript N and U denotes the part of the cross section that is fed by NPE and UPE transitions, respectively.
The value of P obtained in the total kinematic region is \(-0.007 \pm 0.076 \pm 0.125\), which indicates that the UPE and NPE contributions averaged over the whole kinematic range of COMPASS are of similar size. The kinematic dependences of the asymmetry P are shown in Fig. 10. The UPE contribution dominates at small values of W and \(p^2_{\mathrm{T}}\) and decreases with increasing values of these kinematic variables. At large values of W and \(p^2_{\mathrm{T}}\), the NPE contribution becomes dominant, while a non-negligible UPE contribution remains. No significant \(Q^2\) dependence of the asymmetry is observed.
\(Q^{2}\), \(p^{2}_{\mathrm{{T}}}\) and W dependences of the NPE-to-UPE asymmetry of the transverse cross section for the transition \(\gamma ^*_T \rightarrow V_T\). The open symbol represents the value over the total kinematic region. Inner error bars represent statistical uncertainties and outer ones statistical and systematic uncertainties added in quadrature
\(Q^{2}\), \(p^{2}_{\mathrm{{T}}}\) and W dependences of the longitudinal-to-transverse cross-section ratio R. The open symbol represents the value obtained for the total kinematic region. Inner error bars represent statistical uncertainties and outer ones statistical and systematic uncertainties added in quadrature. Note that the additional positive uni-directional systematic uncertainty due to the approximation \(R \approx R'\) is not shown here, see text for details
7.4 Longitudinal-to-transverse cross-section ratio
In order to evaluate the longitudinal-to-transverse virtual-photon differential cross-section ratio
the quantity \(R'\) can be used:
Using expressions defining \(r^{04}_{00}\) and \(1-r^{04}_{00}\) in terms of helicity amplitudes [14, 18], one obtains
The quantity \(R'\) may be interpreted as the longitudinal-to-transverse ratio of “effective” cross sections for the production of vector mesons that are polarised longitudinally or transversely irrespective of the virtual-photon polarisation. In case of SCHC, \(R'\) is equal to R. In spite of the observed clear violation of SCHC at COMPASS, we use the approximate relation \(R \approx R'\). The accuracy of this approximation is estimated using the GK model [11, 12] and the resulting uni-directional systematic uncertainty is found to be about \(+15\%\) on average, while its magnitude ranges between 3% and 47% with increasing W and between 6% and 28% with increasing \(p_T^2\).
For the total kinematic region, the ratio R is found to be \(0.553 \pm 0.044_{\mathrm{stat}} \pm 0.020_{\mathrm{syst}} \ _{- \ 0}^{+ \ 0.082}|_{\mathrm{appr}}\). Here, the third uncertainty is the systematic one due to the approximation \(R \approx R'\). The kinematic dependences of R are shown in Fig. 11. The ratio appears to increase as \(Q^{2}\) and \(p^{2}_{\mathrm{{T}}}\) increase, which indicates an increase of the fraction of longitudinally polarised vector mesons, while it shows no significant change over the W range.
Comparison of the measured SDMEs with calculations of the GPD model of Goloskokov and Kroll [12]. The calculations are obtained for \(Q^{2}= 2.0\) (GeV/c)\(^2\), \(W=7.5\) GeV/\( {c}^2\) and \(p^{2}_{\mathrm{T}}=0.14\) (GeV/c)\(^2\). Inner error bars represent statistical uncertainties and outer ones statistical and systematic uncertainties added in quadrature
7.5 Phase difference between amplitudes
Using Eq. (42), the phase difference between the UPE amplitudes \(U_{11}\) and \(U_{10}\) can be calculated [13]:
The phase difference \(\delta _{U}\) for the total kinematic region is found to be \(\delta _{U} = (-106.1 \pm 53.6 \pm 2.5)\) degrees.
The absolute value of the phase difference \(\delta _{N}\) between the NPE amplitudes \(T_{11}\) and \(T_{00}\) can be calculated using Eq. (43) from Ref. [14]:
The phase difference \(\delta _{N}\) for the total kinematic region is found to be |\(\delta _{N}\)| = (\(33.1 \pm 4.9\) ± 7.2) degrees.
Using the polarised SDMEs, also the sign of \(\delta _{N}\) can in principle be determined using the following equation from Ref. [14]:
However, the large experimental uncertainties of the polarised SDMEs make this presently impossible.
7.6 Comparison with predictions of the GK model
In Fig. 12 the 23 SDMEs for exclusive \(\omega \) production, extracted in the total kinematic region of COMPASS, are compared with the predictions of the GPD model of Goloskokov and Kroll [11, 12] for hard exclusive vector-meson leptoproduction. In this version of the model, contributions from chiral-odd GPDs as well as from pion-pole exchange are included. The model was tuned to HERMES results on SDMEs and spin asymmetries for exclusive \(\rho ^0\) and \(\omega \) production, which led to a satisfactory agreement between the model and the data.
The predictions of the model shown in Fig. 12 were obtained for exclusive \(\omega \) production at \(Q^{2}= 2.0\) (GeV/c)\(^2\), \(W=7.5\) GeV/\( {c}^2\) and \(p^{2}_\mathrm{T}=0.14\) (GeV/c)\(^2\), close to the corresponding average kinematic values for COMPASS. In the following, we concentrate on the most pronounced differences between model predictions and experimental results.
The most noticeable differences are as follows: i) the predicted value of SDME \(r_{00}^{04}\), which represents the fraction of longitudinally polarised mesons in the produced sample, is significantly larger than the measured one; ii) the SDMEs dominated by the transitions \(\gamma ^*_T \rightarrow \omega _L\) (class C) are in general close to zero in the model, while in the data several of them (\(r^5_{00}\), \(\mathrm {Re} \{r^1_{10}\}\)) indicate a clear violation of the SCHC hypothesis.
A characteristic prediction of the model is a strong decrease of the UPE contribution with increasing values of W. The predicted values of the quantity \(u_1\) at \(\langle Q^{2} \rangle = 2.13\) (GeV/c)\(^2\) and \(\langle p^{2}_{\mathrm{T}} \rangle = 0.16\) (GeV/c)\(^2\) are equal to 1.01, 0.39 and 0.07 for W values of 5.0 GeV/\(c^2\), 7.1 GeV/\(c^2\) and 11.0 GeV/\(c^2\) respectively. A comparison of these predictions to the results shown in the lower-left panel of Fig. 9 shows that, while at the smallest accessible value of W the prediction is consistent with the measured \(u_1\), at large values of W the model predicts a much stronger decrease with increasing W and hence underestimates significantly the measured UPE contribution.
8 Summary
Using exclusive \(\omega \) meson muoproduction on protons, we have measured 23 Spin Density Matrix Elements at the average COMPASS kinematics, \(\langle Q^{2} \rangle =\) 2.1 (GeV/c)\(^2\), \(\langle W \rangle = 7.6\) GeV/\(c^2\) and \(\langle p^{2}_{\mathrm{T}} \rangle = 0.16\) (GeV/c)\(^2\). The SDMEs are extracted in the kinematic region \(1.0~(\mathrm{GeV}/c)^2< Q^{2} < 10.0\) \((\mathrm{GeV}/c)^2\), 5.0 GeV/\(c^2< W <17.0\) GeV/\(c^2\) and 0.01 (GeV/c)\(^2\) \(<p^{2}_\mathrm{T} < 0.5\) (GeV/c)\(^2\), which allows us to study their \(Q^2\), \(p^2_{\mathrm{T}}\) and W dependences.
Several SDMEs that are dominated by amplitudes describing \(\gamma ^*_{\mathrm{T}} \rightarrow \omega _{\,\mathrm L}\) transitions indicate a considerable violation of the SCHC hypothesis. These SDMEs are expected to be sensitive to the chiral-odd GPDs \(H_{\mathrm{T}}\) and \({{{\bar{E}}}}_{\mathrm{T}}\), which are coupled to the higher-twist wave function of the meson. A particularly prominent effect is observed for the SDME \(r^5_{00}\), which strongly increases with increasing \(Q^2\) and \(p^2_{\mathrm{T}}\), and decreases with increasing W.
Using specific observables that are constructed to be sensitive to contributions from transitions with unnatural-parity exchanges such as \(u_1\), \(\mathrm {Im} \{r^2_{1-1}\}-r^1_{1-1}\) and the UPE-to-NPE asymmetry for the transverse cross section, a strong W dependence of the UPE contribution is observed. At low values of W, we confirm the earlier observation by HERMES that the amplitude of the UPE transition \(\gamma ^*_{\mathrm{T}} \rightarrow \omega _{\mathrm{T}}\) is larger than the NPE amplitude for the same transition, i.e. \( |U_{11}|>|T_{11}|\). With increasing W the UPE contribution decreases and \( |U_{11}|<|T_{11}|\) at large W, still with a non-negligible UPE contribution at the largest W values accessible at COMPASS.
Altogether, the COMPASS results presented in this paper cover a kinematic range that extends considerably beyond the ranges of earlier experimental data on SDMEs for exclusive \(\omega \) leptoproduction. They provide important input for modelling GPDs, in particular they may help to better constrain the amplitudes for UPE transitions and assess the role of chiral-odd GPDs in exclusive \(\omega \) leptoproduction.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All results/numbers are presented in the paper and in the tables. No further associated data will be deposited elsewhere.]
Notes
In Ref. [13] a different definition of the asymmetry is used.
References
D. Müller et al., Fortschr. Phys. 42, 101 (1994)
X. Ji, Phys. Rev. Lett. 78, 610 (1997)
X. Ji, Phys. Rev. D 55, 7114 (1997)
A.V. Radyushkin, Phys. Lett. B 385, 333 (1996)
A.V. Radyushkin, Phys. Rev. D 56, 5524 (1997)
J.C. Collins, L. Frankfurt, M. Strikman, Phys. Rev. D 56, 2982 (1997)
A.D. Martin, M.G. Ryskin, T. Teubner, Phys. Rev. 55, 4329 (1997)
S.V. Goloskokov, P. Kroll, Eur. Phys. J. C 42, 281 (2005)
S.V. Goloskokov, P. Kroll, Eur. Phys. J. C 53, 367 (2008)
S.V. Goloskokov, P. Kroll, Eur. Phys. J. C 59, 809 (2009)
S.V. Goloskokov, P. Kroll, Eur. Phys. J. C 74, 2725 (2014)
S.V. Goloskokov, P. Kroll, Eur. Phys. J. A 50, 146 (2014)
A. Airapetian et al., (HERMES Collaboration), Eur. Phys. J. C 74, 3110 (2014) Erratum: Eur. Phys. J. C 76, 162 (2016)
A. Airapetian et al., HERMES Collaboration. Eur. Phys. J. C 62, 659 (2009)
P. Joos et al., Nucl. Phys. B 122, 365 (1977)
L. Morand et al., (CLAS Collaboration). Eur. Phys. J. A 24, 445 (2005)
C. Adolph et al., (COMPASS Collaboration). Nucl. Phys. B 915, 454 (2017)
K. Schilling, G. Wolf, Nucl. Phys. B 61, 381 (1973)
M. Diehl, JHEP 0709, 064 (2007)
P. Abbon et al., (COMPASS Collaboration). Nucl. Instrum. Methods A 557, 455 (2007)
P. Abbon et al., (COMPASS Collaboration). Nucl. Instrum. Methods A 779, 69 (2015)
F. Gautheron et al., (COMPASS Collaboration), SPSC-P-340, CERN-SPSC-2019-014
P. Sznajder, PhD thesis, National Centre For Nuclear Research, Otwock -Świerk, March 2015
C. Adolph et al., (COMPASS Collaboration). Phys. Lett. B 718, 922 (2013)
T. Szameitat, PhD thesis, University of Freiburg (2017), https://doi.org/10.6094/UNIFR/11686
A. Sandacz and P. Sznajder, “HEPGEN - generator for hard exclusive leptoproduction”, (2012), arXiv:1207.0333
C. Regali, PhD thesis, University of Freiburg (2016), https://doi.org/10.6094/UNIFR/11449
E. Burtin, N. d’Hose, O.A. Grajek and A. Sandacz, Angular distributions and \(R = \sigma _L / \sigma _T\) for exclusive \(\rho ^0\) production, private communication
R. Akhunzyanov et al., (COMPASS Collaboration). Phys. Lett. B 793, 188 (2019)
M.G. Alexeev et al., (COMPASS Collaboration). Phys. Lett. B 805, 135454 (2020)
Acknowledgements
We are indebted to Sergey Goloskokov and Peter Kroll for numerous fruitful discussions on the interpretation of our results and for providing us with predictions of their model. We gratefully acknowledge the support of CERN management and staff and the skill and effort of the technicians of our collaborating institutions.
Author information
Authors and Affiliations
Consortia
Corresponding authors
Additional information
This article is dedicated to the memory of Bohdan Marianski.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Alexeev, G.D., Alexeev, M.G., Amoroso, A. et al. Spin density matrix elements in exclusive \(\omega \) meson muoproduction. Eur. Phys. J. C 81, 126 (2021). https://doi.org/10.1140/epjc/s10052-020-08740-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08740-y