Generalized absurdly benign traversable wormholes powered by Casimir energy

Abstract

In this work, we explore the connection between Casimir energy and an Absurdly Benign Traversable Wormhole, which in the literature has been considered only in the pioneering paper of Morris and Thorne. To have consistency with the Casimir source, we need to generalize the idea of an Absurdly Benign Traversable Wormhole into a Generalized Absurdly Benign Traversable Wormhole. With this generalization, we have found that the wormhole throat is not more Planckian, but huge. Three profiles have been studied: one of them is directly connected with the Casimir source, while the other two have been obtained approximating the first one close to the throat. In all profiles the wormhole throat size is predicted to be of the order of $10^{17}~\text {m}$. This huge size can be fine tuned by modulating the original Casimir energy source size. We have also found that the traceless and divergenceless property of the original Casimir stress energy tensor is here partially reproduced.

1 Introduction

GW150914 is the acronym associated to the first ever detection of gravitational waves from the merger of two black holes. Advanced LIGO made this first observation during the period running from 12th September 2015 to 19th January 2016 [1] and its second run from 30th November 2016 and 25th August 2017. What is the meaning of such an observation? The meaning is that another prediction of General Relativity has been confirmed and this shows that General Relativity is a quite solid theory for gravitation. Among other things, such a theory predicts other interesting objects: Traversable Wormholes. Traversable Wormholes (TW) are solutions of the Einstein’s Field Equations and even if there is no experimental evidence of their existence, their interest has been growing because potentially they can be considered as black hole mimickers [2]. The interesting feature of a traversable wormhole is its ability in connecting remote regions of space-time in a reasonable amount of time: of course reasonable compared with the duration of human life [3,4,5]. Unfortunately, the traversability is accompanied by unavoidable violations of null energy conditions, namely, the matter threading the wormhole’s throat has to be exotic. Classical matter satisfies the usual energy conditions. Therefore, it is likely that wormholes must belong to the realm of semiclassical or perhaps a possible quantum theory of the gravitational field. In the context of Quantum Field Theory, a possible source of exotic matter could be represented by the Casimir energy [6]. The Casimir energy appears between two plane parallel, closely spaced, uncharged, metallic plates in vacuum. This phenomenon develops an attractive force; it was predicted theoretically in 1948 and experimentally confirmed in the Philips laboratories [7, 8]. However, only in recent years further reliable experimental investigations have confirmed such a phenomenon [9, 10]. As far as we know, the Casimir energy represents the only artificial source of negative energy, whose value in terms of energy density is

$$\begin{aligned} \rho _{0}=-\frac{\hbar c\pi ^{2}}{720d^{4}}. \end{aligned}$$

(1)

Its stress–energy tensor (SET) is represented by

$$\begin{aligned} T_{\mu \nu }=\frac{\hbar c\pi ^{2}}{720d^{4}} [ diag( -1,-3,1,1)] , \end{aligned}$$

(2)

where d is the separation of the plates, and has the following properties: it is divergenceless and traceless. Nevertheless, where is the connection between a TW and the Casimir energy. First of all to describe a spherically symmetric and static TW, we need to introduce a spacetime metric of the form

$$\begin{aligned} ds^{2}=-e^{2\Phi (r)}\,dt^{2}+\frac{dr^{2}}{1-b(r)/r}+r^{2}\,(d\theta ^{2} +\sin ^{2}{\theta }\,d\varphi ^{2})\,, \end{aligned}$$

(3)

where $\Phi (r)$ and b(r) are arbitrary functions of the radial coordinate, r, denoted as the redshift function, and the shape function, respectively [3, 5]. The radial coordinate has a range that increases from a minimum value at $r_{0}$, corresponding to the wormhole throat, to infinity. A fundamental property of a wormhole is that a flaring out condition of the throat, given by $(b-b^{\prime }r)/b^{2}>0$, is imposed [3, 5], and at the throat $b(r_{0})=r_{0}$, the condition $b^{\prime }(r_{0})<1$ is imposed to have wormhole solutions. Another condition that needs to be satisfied is $1-b(r)/r>0$. For the wormhole to be traversable, one must demand that there are no horizons present, which are identified as the surfaces with $e^{2\phi }\rightarrow 0$, so that $\phi (r)$ must be finite everywhere. Using the Einstein Field Equations (EFE) $\left( \kappa =8\pi G/c^{4}\right)$

$$\begin{aligned} G_{\mu \nu }=\kappa T_{\mu \nu }, \end{aligned}$$

(4)

in an orthonormal reference frame, we obtain the following set of equations

$$\begin{aligned} \rho \left( r\right)&=\frac{1}{\kappa }\frac{b^{\prime }}{r^{2}}, \end{aligned}$$

(5)

$$\begin{aligned} p_{r}\left( r\right)&=\frac{1}{\kappa } \left[ \frac{2}{r}\left( 1-\frac{b\left( r\right) }{r}\right) \Phi ^{\prime }-\frac{b}{r^{3}}\right] , \end{aligned}$$

(6)

$$\begin{aligned} p_{t}(r)&=\frac{1}{\kappa }\Bigg \{\left( 1-\frac{b}{r}\right) \left[ \Phi ^{\prime \prime }+\Phi ^{\prime }\left( \Phi ^{\prime } +\frac{1}{r}\right) \right] \nonumber \\&\quad -\frac{b^{\prime }r-b}{2r^{2}} \left( \Phi ^{\prime }+\frac{1}{r}\right) \Bigg \}, \end{aligned}$$

(7)

in which $\rho \left( r\right)$ is the energy density, $p_{r}\left( r\right)$ is the radial pressure, and $p_{t}\left( r\right)$ is the lateral pressure. Using the conservation of the stress–energy tensor, in the same orthonormal reference frame, we get

$$\begin{aligned} p_{r}^{\prime }=\frac{2}{r}\left( p_{t}-p_{r}\right) -\left( \rho +p_{r}\right) \Phi ^{\prime }. \end{aligned}$$

(8)

Finally, the EFE can be rearranged to give

$$\begin{aligned} b^{\prime }&=\kappa \rho \left( r\right) r^{2}, \end{aligned}$$

(9)

$$\begin{aligned} \Phi ^{\prime }&=\frac{b+\kappa p_{r}r^{3}}{2r^{2} \left( 1-\frac{b\left( r\right) }{r}\right) }. \end{aligned}$$

(10)

However, given the quantum nature of the Casimir effect, the EFE must be replaced with the semiclassical EFE, namely

$$\begin{aligned} G_{\mu \nu }=\kappa \left\langle T_{\mu \nu }\right\rangle ^{\mathrm{Ren}}, \end{aligned}$$

(11)

where $\left\langle T_{\mu \nu }\right\rangle ^{\mathrm{Ren}}$ describes the renormalized quantum contribution of some matter fields: in this specific case, the electromagnetic field. In a recent paper [11], a connection between the SET (2) and the spacetime metric (3) has been deduced, obtaining a line element of the form

$$\begin{aligned} ds^{2}&=-{\left( \frac{3r}{3r+r_{0}}\right) }^{2}\,dt^{2} +\frac{dr^{2}}{1-\frac{2r_{0}}{3r}-\frac{r_{0}^{2}}{3r^{2}}}\nonumber \\&\quad +r^{2}\,(d\theta ^{2} +\sin ^{2}{\theta }\,d\varphi ^{2})\,, \end{aligned}$$

(12)

with

$$\begin{aligned} \phi \left( r\right) =\ln \left( \frac{3r}{3r+r_{0}}\right) \quad and\quad {b}\left( r\right) =\frac{2r_{0}}{3}+\frac{r_{0}^{2}}{3r}. \end{aligned}$$

(13)

Such a result has been obtained promoting the plate separation d in the SET to a variable r and an Equation of State (EoS) of the form $p_{r}\left( r\right) =\omega \rho \left( r\right)$ has been used with $\omega =3$. A further investigation about the line element (12) has been done in Refs. [12,13,14]. The purpose of this paper is to establish if other connections between the Casimir energy and a TW can be created. The motivation to insist in this research is dictated by the fact that a TW needs exotic matter and at the moment only the Casimir energy can be used as an appropriate source. However, this time the plate separation d will be considered as fixed and not a variable.¹ Surprisingly, we will obtain an interesting result even in this configuration. The rest of the paper is structured as follows, in Sect. 2 we continue the investigation to determine if the Casimir energy density (1) can be considered as a source for an Absurdly Benign Traversable Wormhole, in Sect. 3 we generalize the definition of an Absurdly Benign Traversable Wormhole, in Sect. 4 we give another profile for the Generalized Absurdly Benign Traversable Wormhole directly connected with the Casimir source (1) but without approximation. We summarize and conclude in Sect. 5. Units in which $\hbar =c=k=1$ are used throughout the paper and will be reintroduced when they are relevant.

2 The absurdly benign traversable wormhole and the equation of state

The original case, that in which, the plate separation d is fixed, has an energy density expressed by Eq. (5). With the help of Eq. (9), we can compute the form of the shape function

$$\begin{aligned} b( r) =r_{0}-\frac{\pi ^{3}}{270d^{4}} \left( \frac{\hbar G}{c^{3}}\right) ( r^{3}-r_{0}^{3}), \end{aligned}$$

(14)

which is not asymptotically flat but asymptotically de Sitter. Indeed, the Casimir energy acts like a “Cosmological Constant”. This means that a TW in a strict sense cannot be formed. On this point we will come back in Sect. 5. However, in proximity of the throat, the shape function (14) can be rearranged in the following way

$$\begin{aligned} b\left( r\right)&=r_{0}-\frac{\pi ^{3}}{270d^{4}} \left( \frac{\hbar G}{c^{3}}\right) \left( r-r_{0}\right) ( r^{2}+r_{0}r+r_{0} ^{2}) \nonumber \\&\simeq r_{0}\left( 1-\frac{r_{0}\pi ^{3}}{90d^{4}} \left( \frac{\hbar G}{c^{3}}\right) \left( r-r_{0}\right) \right) \nonumber \\&=r_{0}\left( 1-\frac{r_{0}l_{P}^{2}\pi ^{3}}{90d^{4}} \left( r-r_{0}\right) \right) . \end{aligned}$$

(15)

The shape function (15) has the same structure of an Absurdly Benign Traversable Wormhole (ABTW) proposed by Morris and Thorne in Ref. [3] except for the exponent. I recall to the reader that an ABTW is defined in such a way to have exotic matter concentrated into the region $r_{0}\le r\le r_{0}+a$ with $a/r_{0}\ll 1$. In practice, the shape function and the redshift functions are defined by

$$\begin{aligned} b(r)&=r_{0}\left( 1-\left( \frac{r-r_{0}}{a}\right) \right) ^{2},\quad \Phi (r)=0;\quad r_{0}\le r\le r_{0}+a\nonumber \\ b(r)&=0,\quad \Phi (r)=0;\quad r\ge r_{0}+a. \end{aligned}$$

(16)

Therefore outside the location $r=r_{0}+a$, the spacetime is Minkowski. If we make the identification

$$\begin{aligned} a=\frac{90d^{4}}{r_{0}l_{P}^{2}\pi ^{3}}, \end{aligned}$$

(17)

then the similarity between (14) and (16) improves and if we put real numbers coming from experiments, we find

$$\begin{aligned} a\simeq \frac{90\left( 10^{-9}~\text {m}\right) ^{4}}{r_{0}\pi ^{3} \left( 1.6\times 10^{-35}~\text {m}\right) ^{2}}\simeq \frac{10^{34} ~\text {m}^{2}}{r_{0}}, \end{aligned}$$

(18)

where we have assumed a plate separation of the order of the nm, which is the actual distance used in laboratories. In order to have a small, we have two possibilities:

(a):

either $r_{0}\gg \ 10^{34}~\text {m}$

or

(b):

the plate separation d must be less of the order of a fm to have a wormhole throat of the order of $10^{10}~\text {m}$, which is bigger of the diameter of the sun.

In both cases, the use of such a source is neither practical nor physically meaningful. If condition (a) or (b) are not satisfied, the exotic matter is not concentrated close to the throat, rather is distributed in a wide area of the space. Therefore, it appears important to establish if a better connection between the Casimir energy and an ABTW exists in order to use such a source. Note that except for Refs. [3, 5, 15, 16], the subject of ABTW has not examined extensively. To further proceed, we introduce an inhomogeneous Equation of State (EoS) of the form

$$\begin{aligned} p_{r}\left( r\right) =\omega \left( r\right) \rho \left( r\right) . \end{aligned}$$

(19)

From Eqs. (5) and (6), by imposing

$$\begin{aligned} b\left( r\right) +\kappa p_{r}\left( r\right) r^{3}=0, \end{aligned}$$

(20)

we find

$$\begin{aligned} \omega \left( r\right) =-\frac{b\left( r\right) }{b^{\prime } \left( r\right) r} \end{aligned}$$

(21)

and the EFE can be solved to give

$$\begin{aligned} b(r)=r_{0}\,\exp \left[ -\int _{r_{0}}^{r}\,\frac{d\bar{r}}{\omega (\bar{r})\bar{r}}\right] \,. \end{aligned}$$

(22)

From the shape function (22), we can compute $\rho \left( r\right)$

$$\begin{aligned} \rho \left( r\right) =-\frac{r_{0}}{\kappa r^{3}\omega \left( r\right) } \,\exp \left[ -\int _{r_{0}}^{r}\,\frac{d\bar{r}}{\omega (\bar{r})\bar{r}}\right] , \end{aligned}$$

(23)

$p_{r}\left( r\right)$

$$\begin{aligned} p_{r}\left( r\right) =-\frac{r_{0}}{\kappa r^{3}}\exp \left[ -\int _{r_{0}}^{r} \,\frac{d\bar{r}}{\omega (\bar{r})\bar{r}}\right] \end{aligned}$$

(24)

and $p_{t}\left( r\right)$

$$\begin{aligned} p_{t}(r)=\frac{r_{0}}{2\kappa r^{3}}\left( \frac{1}{\omega \left( r\right) }+1\right) \exp \left[ -\int _{r_{0}}^{r}\,\frac{d\bar{r}}{\omega (\bar{r})\bar{r}}\right] . \end{aligned}$$

(25)

If the relationship (21) is satisfied, then we have a zero-tidal-force wormhole (ZTF), a condition represented by the choice $\Phi (r)=0$. This is also the same condition assumed for the ABTW. For instance, for the ABTW, it is immediate to obtain that

$$\begin{aligned} \omega \left( r\right)&=\frac{a}{2r}\left( 1-\left( \frac{r-r_{0}}{a}\right) \right) ,\nonumber \\ \omega \left( r_{0}\right)&=\frac{a}{2r_{0}}\quad \omega \left( r_{0}+a\right) =0. \end{aligned}$$

(26)

To complete the discussion we include also the form of the SET²

$$\begin{aligned} T_{\mu \nu }&=\frac{r_{0}}{\kappa r^{3}}diag\left( -\frac{1}{\omega \left( r\right) },-1,\frac{1}{2\omega \left( r\right) }+\frac{1}{2}, \frac{1}{2\omega \left( r\right) }+\frac{1}{2}\right) \nonumber \\&\quad \times \exp \left[ -\int _{r_{0}}^{r}\,\frac{d\bar{r}}{\omega (\bar{r})\bar{r}}\right] \nonumber \\&=-\frac{b(r)}{\kappa r^{3}\omega \left( r\right) }diag\left( 1,\omega \left( r\right) ,-\frac{1}{2}-\frac{\omega \left( r\right) }{2}, -\frac{1}{2}-\frac{\omega \left( r\right) }{2}\right) \nonumber \\&=\rho \left( r\right) diag\left( 1,\omega \left( r\right) , -\frac{1}{2}-\frac{\omega \left( r\right) }{2},-\frac{1}{2} -\frac{\omega \left( r\right) }{2}\right) . \end{aligned}$$

(27)

By construction the SET (27) is divergenceless, but it is not traceless. However, it is always possible to rearrange the previous SET (27) in such a way to extract the traceless part. Indeed

$$\begin{aligned} T_{\mu \nu }&=T_{\mu \nu }^{T}+\frac{T}{4}g_{\mu \nu }=\frac{\rho \left( r\right) }{2}\nonumber \\&\quad \times \left[ diag\left( 1,2\omega \left( r\right) +1,-\omega \left( r\right) , -\omega \left( r\right) \right) -g_{\mu \nu }\right] , \end{aligned}$$

(28)

where $T_{\mu \nu }^{T}$ is the traceless part of the SET (27). It is interesting to observe that by imposing the following condition

$$\begin{aligned} \omega \left( r_{0}\right) =1, \end{aligned}$$

(29)

one finds that

$$\begin{aligned} T_{\mu \nu }^{T}=\frac{\rho \left( r_{0}\right) }{2} \left[ diag\left( 1,3,-1,-1\right) \right] , \end{aligned}$$

(30)

independently on the form of $\omega \left( r\right)$. In the expression (30), we can recognize the Casimir structure of the SET. In the next section, we will examine some specific profiles of $\omega \left( r\right)$ which can lead to a generalized ABTW (GABTW).

3 The generalized absurdly benign traversable wormhole

In Sect. 2, we have derived a form for the shape function directly by the Casimir energy density described by Eq. (14). We have also given the expression in proximity of the throat described by Eq. (15) and we have deduced that it seems to have a connection with the ABTW. However, the connection is not complete, because from Eq. (15), we can easily derive the energy density which has the following form

$$\begin{aligned} \rho \left( r\right) =-\frac{r_{0}^{2}l_{P}^{2}\pi ^{3}}{90d^{4}\kappa r^{2}} =-\frac{r_{0}^{2}\pi ^{2}\hbar c}{720d^{4}r^{2}}\underset{r=r_{0}}{\Longrightarrow } -\frac{\pi ^{2}\hbar c}{720d^{4}}=-\rho _{0}, \end{aligned}$$

(31)

which is exactly the Casimir energy density only on the throat, as it should be. Nevertheless, if we assume the validity of the identification (17), then the associated SET is not the Minkowski SET outside the point $\bar{r}=r_{0}+a$, but it has the following expression

$$\begin{aligned} T_{\mu \nu }=\rho _{0}\frac{r_{0}^{2}}{\bar{r}^{2}}diag \left( -1,0,\frac{1}{2},\frac{1}{2}\right) . \end{aligned}$$

(32)

Furthermore, the assumption (17) is physically meaningless. Therefore, we are going to explore different profiles with the hope they satisfy as much as possible the ABTW form and, at the same time, the form of the Casimir SET. Before going on we have to observe one point: the ABTW shape function is

$$\begin{aligned} b(r)=r_{0}\left( 1-\left( \frac{r-r_{0}}{a}\right) \right) ^{2} \end{aligned}$$

(33)

and close to the throat, the leading term is

$$\begin{aligned} b(r)\simeq r_{0}\left( 1-\frac{2}{a}\left( r-r_{0}\right) \right) , \end{aligned}$$

(34)

which has the same form of (15). This means that the ABTW can be the right prototype to build a better profile. This tentative improvement will be done by means of the inhomogeneous EoS (19) which, in the case of the ABTW obeys the EoS (19) with the following relationship

$$\begin{aligned} \omega \left( r\right) =\frac{1-\mu \left( r-r_{0}\right) }{2\mu r}; \quad \mu =\frac{1}{a}. \end{aligned}$$

(35)

As a first proposal, we will examine the following profile

3.1 Example I $\omega \left( r\right) =\left( 1-\mu \left( r-r_{0}\right) \right) /\alpha \mu r$

When $\omega \left( r\right)$ assumes the following profile

$$\begin{aligned} \omega \left( r\right) =\frac{1-\mu \left( r-r_{0}\right) }{\alpha \mu r};\quad \alpha >1, \end{aligned}$$

(36)

which is an immediate generalization of the relationship (35), one finds

$$\begin{aligned} \omega \left( r\right) \rightarrow \left\{ \begin{array}{cc} 1/\alpha \mu r_{0} &{} r\rightarrow r_{0}\\ -1/\alpha &{} r\rightarrow \infty \end{array}\right. ;\quad r\in \left[ r_{0},\infty \right) , \end{aligned}$$

(37)

where $\mu$ is an inverse length scale. However, it is of much more interest the following assumption

$$\begin{aligned} \omega \left( r\right) =0\quad \text {when} \ r=\bar{r}=r_{0}+\frac{1}{\mu }. \end{aligned}$$

(38)

When choice (38) is adopted, from Eq. (22), one finds

$$\begin{aligned} b(r)&=r_{0}\,\exp \left[ -\int _{r_{0}}^{r}\,\frac{\alpha \mu \bar{r}d\bar{r}}{1-\mu \left( \bar{r}-r_{0}\right) \bar{r}}\right] \nonumber \\&=r_{0} \,\exp \left[ -\alpha \mu \int _{r_{0}}^{r}\,\frac{d\bar{r}}{1-\mu \left( \bar{r}-r_{0}\right) }\right] \nonumber \\&=r_{0}\,\exp \left[ \alpha \ln \left( 1-\mu \left( r-r_{0}\right) \right) \right] =r_{0}\left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha }. \end{aligned}$$

(39)

As we can see, the choice (36) leads to a generalized ABTW, if we adopt also the following further conditions

$$\begin{aligned} b(r)&=r_{0}\left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha } ,\quad \Phi (r)=0;\quad r_{0}\le r\le r_{0}+1/\mu \nonumber \\ b(r)&=0,\quad \Phi (r)=0;\quad r\ge r_{0}+1/\mu . \end{aligned}$$

(40)

Then the components of the stress–energy tensor can be easily computed to obtain

$$\begin{aligned} \rho \left( r\right)&=-\frac{r_{0}\alpha \mu }{\kappa r^{2}} \left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha -1}, \end{aligned}$$

(41)

$$\begin{aligned} p_{r}\left( r\right)&=-\frac{r_{0}\left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha }}{\kappa r^{3}}, \end{aligned}$$

(42)

$$\begin{aligned} p_{t}(r)&=\frac{r_{0}\left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha -1}}{2\kappa r^{3}}\left( 1-\mu \left( r\left( 1-\alpha \right) -r_{0}\right) \right) , \end{aligned}$$

(43)

so that the SET becomes

$$\begin{aligned} T_{\mu \nu }&=\frac{r_{0}}{2\kappa r^{3}} \left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha -1} diag( -2\alpha \mu r,-2,1\nonumber \\&\quad -\mu (r(1-\alpha ) -r_{0}) , 1-\mu ( r( 1-\alpha )-r_{0}) ) . \end{aligned}$$

(44)

However, to have a vanishing $\rho \left( r\right)$ and $p_{t}(r)$ for $r\ge \bar{r}$, we need $\alpha >1$. Note that for $\alpha =2$, we recover the familiar shape function of the ABTW (16). It is easy to see that on the throat the SET (44) becomes

$$\begin{aligned} T_{\mu \nu }=\frac{1}{2\kappa r_{0}^{2}}diag\left( -2\alpha \mu r_{0}, -2,1+\mu r_{0}\alpha ,1+\mu r_{0}\alpha \right) \end{aligned}$$

(45)

and the inhomogeneous EoS function (36) reduces to

$$\begin{aligned} \omega \left( r_{0}\right) =\frac{1}{\alpha \mu r_{0}}, \end{aligned}$$

(46)

while for $r=r_{0}+1/\mu$, one gets

$$\begin{aligned} T_{\mu \nu }=diag\left( 0,0,0,0\right) \quad \alpha >1; \quad \omega \left( r_{0}+1/\mu \right) =0. \end{aligned}$$

(47)

Regarding the energy density on the throat, one finds

$$\begin{aligned} \rho \left( r_{0}\right) =-\frac{\alpha \mu }{\kappa r_{0}} \end{aligned}$$

(48)

and if we impose the constraint (29), one finds

$$\begin{aligned} \rho \left( r_{0}\right) =-\frac{\alpha \mu }{\kappa r_{0}} =-\frac{1}{\kappa r_{0}^{2}}. \end{aligned}$$

(49)

By identifying (49) with the Casimir energy density in (2), one gets

$$\begin{aligned} \rho \left( r_{0}\right) =-\frac{1}{\kappa r_{0}^{2}} =-\frac{\hbar c\pi ^{2}}{720d^{4}}, \end{aligned}$$

(50)

which implies

$$\begin{aligned} r_{0}=\frac{3}{\pi }\sqrt{\frac{10}{\pi }}\frac{d^{2}}{l_{P}} \simeq 1.\,7\times 10^{17}~\text {m} \end{aligned}$$

(51)

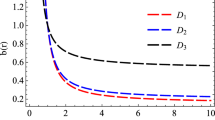
where we have fixed the plate separation at a distance of the order of $10^{-9}~\text {m}$. To have the exotic energy confined close to the throat, $\mu$ must be huge, but the relationship (46) constraints $\alpha$ to be small. Therefore we conclude that even for the first GABTW model, one finds the same problem of the assumption (17) and (18), even if the size of the GABTW is estimated to be $r_{0}\simeq 1.\,7\times 10^{17}~\text {m}$, while for the original Casimir size connected with (17) and (18), the size of the wormhole throat was of the order $r_{0}\simeq 10^{34}~\text {m}$. For this reason, we are going to consider this further generalization.

3.2 Example II $\omega (r) =(1-\mu (r-r_{0}))(1-\nu (r-r_{0})) /r[\alpha \mu ((1-\nu (r-r_{0}))-\beta \nu (1-\mu (r-r_{0})))]$

We now assume the following profile

$$\begin{aligned} \omega \left( r\right) =\frac{\left( 1-\mu \left( r-r_{0}\right) \right) \left( 1-\nu \left( r-r_{0}\right) \right) }{r\left[ \alpha \mu \left( \left( 1-\nu \left( r-r_{0}\right) \right) -\beta \nu \left( 1-\mu \left( r-r_{0}\right) \right) \right) \right] }, \end{aligned}$$

(52)

where $\alpha ,\beta \in {\mathbb {R}}$ and $\mu ,\nu$ are mass scales with $\mu >\nu$. In the range $r\in \left[ r_{0},\infty \right)$, one finds

$$\begin{aligned} \omega \left( r\right) \rightarrow \left\{ \begin{array}{ll} 1/\left( r_{0}\left( \alpha \mu -\beta \nu \right) \right) &{}\quad r\rightarrow r_{0}\\ -1/\left( \alpha +\beta \right) &{}\quad r\rightarrow \infty . \end{array}\right. \end{aligned}$$

(53)

However, like in the Example I, it is of much more interest the following assumption

$$\begin{aligned} \omega \left( r\right) =0\quad \text {when}\ r=\bar{r}=r_{0} +\frac{1}{\mu }. \end{aligned}$$

(54)

When this choice is adopted, from Eq. (22), one finds

$$\begin{aligned} b(r)&=r_{0}\,\exp \left[ -\int _{r_{0}}^{r}\,\frac{\left[ \alpha \mu \left( \left( 1-\nu \left( \bar{r}-r_{0}\right) \right) -\beta \nu \left( 1-\mu \left( \bar{r}-r_{0}\right) \right) \right) \right] \bar{r}d\bar{r}}{\left( 1-\nu \left( \bar{r}-r_{0}\right) \right) \left( 1-\mu \left( \bar{r}-r_{0}\right) \right) \bar{r}}\right] \nonumber \\&=r_{0}\,\exp \left[ -\alpha \mu \int _{r_{0}}^{r}\,\frac{d\bar{r}}{1-\mu \left( \bar{r}-r_{0}\right) }\right. \nonumber \\&\quad \left. +\beta \nu \int _{r_{0}}^{r} \,\frac{d\bar{r}}{1-\nu \left( \bar{r}-r_{0}\right) }\right] \nonumber \\&=r_{0}\,\exp [\alpha \ln \left( 1-\mu \left( r-r_{0}\right) \right) \nonumber \\&\quad -\beta \ln \left( 1-\nu \left( r-r_{0}\right) \right) ]=r_{0} \frac{\left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha }}{\left( 1-\nu \left( r-r_{0}\right) \right) ^{\beta }}. \end{aligned}$$

(55)

As we can see, the choice (36) leads to another generalized ABTW, if we adopt also the following conditions

$$\begin{aligned}&b(r)=r_{0}\frac{\left( 1-\mu \left( r-r_{0}\right) \right) ^{\alpha }}{\left( 1-\nu \left( r-r_{0}\right) \right) ^{\beta }}, \quad \Phi (r)=0; \nonumber \\&\quad r_{0}\le r\le r_{0}+1/\mu \nonumber \\&b(r)=0,\quad \Phi (r)=0;\quad r\ge r_{0}+1/\mu . \end{aligned}$$

(56)

The components of the stress–energy tensor can be easily computed and represented by Eq. (27), while on the throat one finds

$$\begin{aligned} T_{\mu \nu }&=\frac{1}{2\kappa r_{0}^{2}}diag\left( -2\left( \alpha \mu -\beta \nu \right) r_{0},\right. \nonumber \\&\quad \left. -2,1+r_{0}\left( \alpha \mu -\beta \nu \right) , 1+r_{0}\left( \alpha \mu -\beta \nu \right) \right) \end{aligned}$$

(57)

and for $r\ge r_{0}+1/\mu$, the whole SET is vanishing, namely a Minkowski SET. Note that for $\alpha =2$ and $\beta =0$, we recover the familiar shape function of the ABTW (16). On the throat, we can impose that the energy density be

$$\begin{aligned} \rho \left( r_{0}\right) =-\frac{1}{\kappa r_{0}}\left( \alpha \mu -\beta \nu \right) =-\frac{\hbar c\pi ^{2}}{720d^{4}} \end{aligned}$$

(58)

and with the additional condition (29), one finds

$$\begin{aligned} \rho \left( r_{0}\right) =\frac{1}{\kappa r_{0}^{2}} =\frac{\hbar c\pi ^{2}}{720d^{4}} \end{aligned}$$

(59)

leading to

$$\begin{aligned} r_{0}=\frac{3d^{2}}{\pi l_{P}}\sqrt{\frac{10}{\pi }}, \end{aligned}$$

(60)

which is in agreement with the result (51). Note that in proximity of the throat, the shape function (55) can be rewritten as

$$\begin{aligned} b\left( r\right) \simeq r_{0}\left( 1-\left( \alpha \mu -\beta \nu \right) \left( r-r_{0}\right) \right) \end{aligned}$$

(61)

which looks like the shape function (15). Note also that the constraint (29) leads to

$$\begin{aligned} \mu =\frac{\beta }{\alpha }\nu +\frac{\pi l_{P}}{3\alpha d^{2}} \sqrt{\frac{\pi }{10}} \end{aligned}$$

(62)

and by setting

$$\begin{aligned} \alpha =\beta +1;\quad \beta =\beta \quad \text {and}\quad \nu \gg \frac{1}{r_{0}}, \end{aligned}$$

(63)

we can mimic the shape function (15). However, this time the parameter $\mu$ can be large satisfying therefore the request of concentrating the exotic matter close to the throat. One can see that although the original Casimir structure for the SET (30) is reproduced, the whole SET is divided by a factor 2 while the SET (27) becomes on the throat

$$\begin{aligned} \rho \left( r_{0}\right) diag\left( 1,1,-1,-1\right) , \end{aligned}$$

(64)

which is in agreement with the Casimir SET except for the radial pressure. This behavior was present also in the SET of the Ref. [11]. It is important to remark that, differently from the shape function (14) reproducing the Casimir energy density not only on the throat but in every point of the space, the shape function (56) reproduces the Casimir energy density on the throat with the help of the identification (59). This can be done because the throat radius can be fine tuned to give the desired expression. A similar fine tuning is not possible for the shape function (14).

4 Reexamining the original Casimir structure

In this section we are going to reconsider the shape function (14) without the approximation leading to the form (15). We have already observed that, for $r\gg r_{0}$, the shape function assumes a de Sitter profile. However, we can also observe that $b\left( r\right)$ without approximations has one real root. This is located at

$$\begin{aligned} b\left( \bar{r}\right) =0\quad \Longleftrightarrow \quad \bar{r} =r_{0}\root 3 \of {1+\frac{3}{r_{0}^{2}\rho _{0}\kappa }}. \end{aligned}$$

(65)

Therefore, it is straightforward to assume that

$$\begin{aligned} b(r)&=r_{0}-\frac{\rho _{0}\kappa }{3}\left( r^{3}-r_{0}^{3}\right) , \quad \Phi (r)=0;\quad r_{0}\le r\le \bar{r}\nonumber \\ b(r)&=0,\quad \Phi (r)=0;\quad r\ge \bar{r}. \end{aligned}$$

(66)

Nevertheless, this choice does not lead to a Minkowski space outside the region located at $r=\bar{r}$, because the SET has a structure which looks like the SET of Eq. (32). However, it is immediate to realize that the profile described by (66) can be generalized to

$$\begin{aligned} b(r)&=\frac{1}{r_{0}^{\alpha -1}}\left[ r_{0}-\frac{\rho _{0}\kappa }{3\alpha }( r^{3}-r_{0}^{3}) \right] ^{\alpha },\nonumber \\&\quad \alpha >1;\quad \Phi (r)=0;\quad r_{0}\le r\le \bar{r}\nonumber \\ b(r)&=0,\quad \Phi (r)=0;\quad r\ge \bar{r}, \end{aligned}$$

(67)

where, this time

$$\begin{aligned} \bar{r}=r_{0}\root 3 \of {1+\frac{3\alpha }{r_{0}^{2}\rho _{0}\kappa }}. \end{aligned}$$

(68)

In this way by imposing the EoS we find

$$\begin{aligned} \omega \left( r\right)&=\frac{1}{r^{3}\rho _{0}\kappa }\left( r_{0} -\frac{\rho _{0}\kappa }{3\alpha }(r^{3}-r_{0}^{3})\right) \nonumber \\ \omega \left( r\right)&=0\quad r\ge \bar{r},\quad \omega \left( r_{0}\right) =\frac{1}{r_{0}^{2}\rho _{0}\kappa }. \end{aligned}$$

(69)

The corresponding SET can be derived from the Eq. (28) where

$$\begin{aligned}&\rho \left( r\right) =-\frac{\rho _{0}}{r_{0}^{\alpha -1}}\left[ r_{0} -\frac{\rho _{0}\kappa }{3\alpha }( r^{3}-r_{0}^{3})\right] ^{\alpha -1}\nonumber \\&\quad \Longrightarrow \quad \rho \left( r_{0}\right) =-\rho _{0}. \end{aligned}$$

(70)

This is very interesting, because independently on the exponent $\alpha$, on the throat, we can find always the Casimir energy density. A result different compared with (50) and (58). Note that outside the region located at $r=\bar{r}$, the spacetime is Minkowski. Moreover by fixing

$$\begin{aligned} \omega \left( r_{0}\right) =\frac{1}{r_{0}^{2}\rho _{0}\kappa }=1, \end{aligned}$$

(71)

we can recover the Casimir structure of the SET and putting numbers inside the previous relationship, one finds

$$\begin{aligned} r_{0}=\sqrt{\frac{1}{\rho _{0}\kappa }}=\frac{3d^{2}}{\pi l_{P}} \sqrt{\frac{10}{\pi }}, \end{aligned}$$

(72)

which is compatible with what we have investigated in Sect. 3. To determine if the root (68) is close to the throat, we need to evaluate the ratio

$$\begin{aligned} R&=\frac{\bar{r}-r_{0}}{r_{0}}=\root 3 \of {1+\frac{3\alpha }{r_{0}^{2} \rho _{0}\kappa }}-1=\root 3 \of {1+3\alpha }-1 \end{aligned}$$

(73)

$$\begin{aligned}&\Longrightarrow \begin{array}{cc} 0.59 &{} \alpha =1\\ 0.91 &{} \alpha =2 \end{array}, \end{aligned}$$

(74)

where we have used the constraint (71). To have consistency, $1<\alpha \le 2$. For $\alpha >2$, $R>1$: in this case the exotic matter is not confined close tho the throat. Note that it is sufficient to choose $\alpha$ very close to 1 to have the Minkowski space time outside $\bar{r}$. Unfortunately as we can see $R<1$ and not $R\ll 1$. This is due to the constraint induced by (71). If we give up this constraint, we cannot recover the Casimir SET structure.

5 Conclusions

In this paper, we have further extended the study began by Morris and Thorne [3]; Morris et al. in Ref. [4] and, subsequently explored by Visser [5] on the Casimir effect as a possible source for a TW. We have also further extended the results obtained in Ref. [11] and the result of such an extension has revealed an interesting further connection between the Casimir source and a particular TW: an ABTW. However, the structure of the solution directly connected with the Casimir source presents some problems in reproducing the features of an ABTW. One of these problems is the lack of a smooth change between the curved and flat space. For this reason, we have investigated some profiles, termed GABTW, that in some particular cases can mimic the original solution derived by the Casimir source. The first GABTW profile failed to be a good candidate because the constraint (29) and the relationship (46) forbid to fix large values of the parameter $\mu$, a necessary request to have the exotic matter confined close to the throat. For this reason, we have examined another profile defined by Eq. (55), obtained by imposing the inhomogeneous EoS (52). This profile has produced interesting results which go in a completely opposite direction with respect to the results obtained in Ref. [11]: namely in this paper the wormhole throat can be huge, while in Ref. [11] is Planckian. The main difference in this result is that, in case of Ref. [11], the Casimir source has a plate separation which is variable, while in this paper it is not: it is a parameter. A question is in order: why do we insist in analyzing an ABTW and its generalization? Because, by definition, the region of the exotic matter is confined in a very small region and outside of this region, space-time is flat. Therefore, instead of having a long tail that asymptotically becomes flat, the flatness is almost in proximity of the throat. Even if the results related to the profiles (40) and (55) seem not to be encouraging, we have to observe that the estimated size of the wormhole throat obtained in Eq. (18) predicts a wormhole throat of the order of $10^{34}~\text {m}$, but the GABTW described by (40) and (55) predicts a wormhole throat of the order of $10^{17}~\text {m}$. This huge size is essentially due to the request of having imposed $\omega \left( r_{0}\right) =1$. Note also that the size $10^{17}~\text {m}$ is principally due to the plate separation of the order of the nm, which is the actual plate separation used in the experiments, but an interesting improvement can arrive at the next scale, namely a pm scale, which is surely more easier to reach compared to the fm scale. In this case, one obtains

$$\begin{aligned} r_{0}\simeq 10^{11}~\text {m}. \end{aligned}$$

(75)

Note also that the presence of the Planck length square in the expression of the wormhole throat is principally due to the combination of the Newton’s constant G, the Planck constant $\hbar$ and the speed of light c. These last two constants appear in the Casimir energy density calculation. It is interesting to note that in some Casimir experiments, if the plates enter in a superconductive phase, it is possible to show an increase of negative energy [18, 19]. This is promising because from Eq. (60), one finds

$$\begin{aligned} r_{0}=\frac{3d^{2}}{\pi l_{P}}\sqrt{\frac{10}{A\pi }}, \end{aligned}$$

(76)

where A comes from the increase of the negative energy density coming from the superconducting phase. This means that in this particular situation it could be possible to combine the plates separation with the superconducting phase energy density increase to obtain a more realistic wormhole throat size. Finally, we have investigated also the profile generated by the Casimir energy source without approximation, but having in mind a GABTW structure. There are several interesting points about the profile (67): the first one is that the relationships (51) and (60) are confirmed even for this shape function, the second one is the reproduction of the Casimir source for every exponent $\alpha$. Therefore, it seems that with the profile (67), everything seems to go in the right ballpark except for the exotic matter region that cannot be shrunk to a very small region exactly like for the profile (55). At this stage, we do not know how much is important to force the exotic matter to stay in a region very close to the throat to keep the GABTW (67) valid and, at the same time, the reproduction of some features of the Casimir SET, i.e. traceless and divergenceless. To conclude, we have also to point out that in the context of Self-Sustained Traversable Wormholes, namely TW sustained by their own quantum fluctuations [20,21,22,23,24], could be interesting to consider how the Casimir source and the quantum fluctuation carried by the graviton combine to see if the GABTW can be self-sustained in this context. In this picture, the Casimir source could be interpreted as the switch on to power the traversability of the wormhole.

Appendix A: Features of the traversable wormhole of Sect. 3.2

In this section we are going to explore some of the features of the GABTW (55). The motivation of examining only this kind of profile is that it is quite general to include many GABTW profiles in proximity of the throat. We begin to examine the proper length which is defined as

$$\begin{aligned} l\left( r\right) =\pm \int _{r_{0}}^{r}\frac{dr^{\prime }}{\sqrt{1-\frac{b\left( r^{\prime }\right) }{r^{\prime }}}}, \end{aligned}$$

(A1)

where the“±” depends on the wormhole side we are. In this case, one gets

$$\begin{aligned} l\left( r\right) =\pm \int _{r_{0}}^{r}\frac{dr^{\prime }}{\sqrt{1-\frac{r_{0}}{r^{\prime }}\frac{\left( 1-\mu \left( r^{\prime }-r_{0}\right) \right) ^{\alpha }}{\left( 1-\nu \left( r^{\prime }-r_{0}\right) \right) ^{\beta }}}}. \end{aligned}$$

(A2)

The exact evaluation of the integral is really complicated. However, it is sufficient to consider that the amount of exotic matter for the GABTW is concentrated near the throat by construction. Therefore, it is sufficient to consider the expression close to the throat with $\mu$ very large. To this purpose, we can write

$$\begin{aligned}&l\left( r\right) \underset{r\rightarrow r_{0}}{\simeq }\pm \frac{1}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}}\int _{r_{0}}^{r} \frac{\sqrt{r^{\prime }}dr^{\prime }}{\sqrt{r^{\prime }-r_{0}}}\nonumber \\&=\pm \frac{1}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}}\nonumber \\&\quad \times \left[ \sqrt{r}\sqrt{r-r_{0}}+r_{0}{\ln \left( \sqrt{\frac{r}{r_{0}}} +\sqrt{\frac{r}{r_{0}}-1}\right) }\right] \nonumber \\&\qquad r_{0}\le r\le r_{0}+1/\mu \end{aligned}$$

(A3)

and the complete $l\left( r\right)$ is

$$\begin{aligned}&l\left( r\right) =\pm \left\{ \begin{array}{cc} \frac{1}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}} \left[ \sqrt{r}\sqrt{r-r_{0}}+r_{0}{\ln \left( \sqrt{\frac{r}{r_{0}}}+\sqrt{\frac{r}{r_{0}} -1}\right) }\right] &{} r_{0}\le r\le r_{0}+1/\mu \\ \frac{1}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}}\\ \left[ \sqrt{r_{0}+\frac{1}{\mu }}\sqrt{\frac{1}{\mu }}+r_{0}{\ln \left( \sqrt{1+\frac{1}{r_{0}\mu }} +\sqrt{\frac{1}{r_{0}\mu }}\right) }\right] +r-\left( r_{0} +\frac{1}{\mu }\right) &{} r\ge r_{0}+1/\mu \end{array}\right\} . \end{aligned}$$

(A4)

Note that the time lapse dt, and proper time lapse as measured by the observer $d\tau$, for the GABTW are the same, because the redshift function is nought. In a similar way, to compute the embedded surface, we need to evaluate

$$\begin{aligned} z\left( r\right) =\pm \int _{r_{0}}^{r}\frac{dr^{\prime }}{\sqrt{\frac{r^{\prime }}{b\left( r^{\prime }\right) }-1}}, \end{aligned}$$

(A5)

which, for the present case, is

$$\begin{aligned} z\left( r\right) =\pm \int _{r_{0}}^{r}\frac{dr^{\prime }}{\sqrt{\frac{r^{\prime }}{r_{0}}\frac{\left( 1-\nu \left( r^{\prime }-r_{0}\right) \right) ^{\beta }}{\left( 1-\mu \left( r^{\prime }-r_{0}\right) \right) ^{\alpha }}-1}}. \end{aligned}$$

(A6)

By repeating the same procedure adopted for the proper length, we can write

$$\begin{aligned} z\left( r\right)&\underset{r\rightarrow r_{0}}{\simeq }\pm \frac{\sqrt{r_{0}}}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}}\int _{r_{0}}^{r}\frac{dr^{\prime }}{\sqrt{r^{\prime }-r_{0}}}\nonumber \\&=\pm \frac{2\sqrt{r_{0}}\sqrt{r-r_{0}}}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}}. \end{aligned}$$

(A7)

To further investigate the properties of the GABTW, we consider the computation of the total gravitational energy for a wormhole [25], defined as

$$\begin{aligned} E_{G}\left( r\right)&=\int _{r_{0}}^{r}\left[ 1-\sqrt{\frac{1}{1-b \left( r^{\prime }\right) /r^{\prime }}}\right] \rho \left( r^{\prime }\right) dr^{\prime }r^{\prime 2}\nonumber \\&\quad +\frac{r_{0}}{2G}=M-M_{\pm }^{P}, \end{aligned}$$

(A8)

where M is the total mass and $M^{P}$ is the proper mass, respectively. Differently from the case where the Casimir energy was considered variable depending on the radial radius r, here we have no asymptotic mass, since outside the radius $\mu ^{-1}$, spacetime is flat. In particular we find for the total mass

$$\begin{aligned} Mc^{2}&=\int _{r_{0}}^{r_{0}+\frac{1}{\mu }}4\pi \rho \left( r^{\prime }\right) r^{\prime 2}dr^{\prime }\nonumber \\&=\frac{4\pi }{3}\left[ \left( r_{0}+\frac{1}{\mu }\right) ^{3}-r_{0}^{3}\right] \left( \frac{\hbar c\pi ^{2}}{720d^{4}}\right) \end{aligned}$$

(A9)

$$\begin{aligned}&\underset{r\rightarrow r_{0}}{\simeq }\frac{4\pi r_{0}^{2}}{\mu } \left( \frac{\hbar c\pi ^{2}}{720d^{4}}\right) , \end{aligned}$$

(A10)

where we have considered the Casimir energy density as a source and we have momentarily reintroduced the speed of light. For the proper mass, one gets

$$\begin{aligned} M_{\pm }^{P}c^{2}&=\pm \int _{r_{0}}^{r_{0}+\frac{1}{\mu }}\frac{4\pi \rho \left( r^{\prime }\right) r^{\prime 2}}{\sqrt{1-b\left( r^{\prime }\right) /r^{\prime }}}dr^{\prime }\underset{r\rightarrow r_{0}}{\simeq }\nonumber \\&\quad \pm \frac{4\pi r_{0}^{2}}{\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}} \left( \frac{\hbar c\pi ^{2}}{720d^{4}}\right) \int _{r_{0}}^{r_{0}+\frac{1}{\mu }}\frac{dr^{\prime }}{\sqrt{r-r_{0}}}\nonumber \\&\simeq \pm \frac{8\pi r_{0}^{2}\sqrt{r_{0}}}{\sqrt{\mu }\sqrt{1+\alpha \mu r_{0}-\beta \nu r_{0}}}\left( \frac{\hbar c\pi ^{2}}{720d^{4}}\right) \nonumber \\&\underset{\mu r_{0}\gg 1}{\longrightarrow }\qquad \pm \frac{8\pi r_{0}^{2}}{\mu \sqrt{\alpha }}\left( \frac{\hbar c\pi ^{2}}{720d^{4}}\right) , \end{aligned}$$

(A11)

where the “±” depends one the wormhole side we are. Thus the total gravitational energy (A8) becomes

$$\begin{aligned} E_{G}\left( r\right) \simeq \left( \frac{\hbar c\pi ^{2}}{720d^{4}}\right) \frac{4\pi r_{0}^{2}}{\mu }\left[ 1\pm \frac{2}{\sqrt{\alpha }}\right] . \end{aligned}$$

(A12)

For large $\mu$, one finds that $E_{G}$ vanishes, independently on the scale choice we make about $\mu$. Another important traversability condition is that the acceleration felt by the traveller should not exceed Earth’s gravity $g_{\oplus }\simeq 980~\text {cm}/\text {s}^{2}$. In an orthonormal basis of the traveller’s proper reference frame, we can find

$$\begin{aligned} \left| {\mathbf {a}}\right| =\left| \sqrt{1-\frac{b\left( r\right) }{r}}e^{-\Phi (r)}\left( \gamma e^{\Phi (r)}\right) ^{\prime }\right| \le \frac{g_{\oplus }}{c^{2}} \end{aligned}$$

(A13)

and in this case, because $\Phi (r)=0$, the traveller has no acceleration, which is in agreement with Ref. [3]. As regards the lateral tidal forces, we find

$$\begin{aligned}&\left| \frac{\gamma ^{2}c^{2}}{2r^{2}}\left[ \frac{v^{2}\left( r\right) }{c^{2}}\left( b^{\prime }\left( r\right) -\frac{b\left( r\right) }{r}\right) \right. \right. \nonumber \\&\qquad \left. \left. +2r\left( r-b\left( r\right) \right) \Phi ^{\prime } \left( r\right) \right] \right| \left| \eta \right| \nonumber \\&\quad =\left| \frac{\gamma ^{2}c^{2}}{2r^{3}}\left[ -\frac{v^{2} \left( r\right) b\left( r\right) }{c^{2}}\left( \frac{1}{\omega \left( r\right) } +1\right) \right] \right| \left| \eta \right| \le g_{\oplus }, \end{aligned}$$

(A14)

where we have used the relationship (21). This is a constraint about the velocity with which observers traverse the wormhole. $\eta$ represents the size of the traveller which can be fixed approximately equal, at the symbolic value of $2\ m$ [3]. If we assume a constant speed v and $\gamma \simeq 1$, close to the throat, the lateral tidal constraint becomes

$$\begin{aligned}&\left| \frac{\gamma ^{2}c^{2}}{2r_{0}^{2}}\left[ \frac{v^{2} \left( r_{0}\right) }{c^{2}}\left( -r_{0}\left( \alpha \mu -\beta \nu \right) -1\right) \right] \right| \left| 2\right| \nonumber \\&\quad \simeq \left| \left[ \frac{v^{2}\left( r_{0}\right) }{r_{0}^{2}}\right] \right| \lesssim g_{\oplus }\nonumber \\&\qquad \Longrightarrow \qquad v\lesssim r_{0}\sqrt{g_{\oplus }}\nonumber \\&\qquad \Longrightarrow \qquad v\lesssim 3.1r_{0}~\text {m}/\text {s}. \end{aligned}$$

(A15)

If the observer has a vanishing v, then the tidal forces are null. We can use these last estimates to complete the evaluation of the crossing time which approximately is

$$\begin{aligned} \Delta t\simeq 2\times 10^{4}\frac{3r_{0}}{4v}\simeq 5\times 10^{3}~\text {s}, \end{aligned}$$

(A16)

which is in agreement with the estimates found in Ref. [3].The last property we are going to discuss is the “total amount” of ANEC violating matter in the spacetime [26] which is described by Eq. (A17). For the metric (55), one obtains

$$\begin{aligned} I_{V}&=\frac{1}{\kappa }\int _{r_{0}}^{r_{0}+\frac{1}{\mu }} \left( r-b\left( r\right) \right) \left[ \ln \left( \frac{e^{2\phi (r)}}{1-\frac{b\left( r\right) }{r}}\right) \right] ^{\prime }dr\nonumber \\&=\frac{1}{\kappa }\int _{r_{0}}^{r_{0}+\frac{1}{\mu }}\left( \frac{b\left( r\right) }{r} -b^{\prime }\left( r\right) \right) dr \end{aligned}$$

(A17)

$$\begin{aligned}&\simeq \frac{1}{\kappa }\left[ \int _{r_{0}}^{r_{0}+\frac{1}{\mu }}\alpha \mu r_{0}-\beta \nu r_{0}+1+c\left( r\right) \left( r-r_{0}\right) \right] dr, \end{aligned}$$

(A18)

where we have approximated the expression close to the throat and where we have defined

$$\begin{aligned} c\left( r\right)&=-\alpha \mu -r_{0}^{-1}+\beta \nu -{\alpha }^{2}{\mu }^{2}r_{0}\nonumber \\&\quad +\alpha \mu r_{0}\beta \,\nu +\alpha {\mu }^{2}r_{0} -\left( -\alpha \mu r_{0}+\beta \nu r_{0}\right) \beta \nu -\beta {\nu }^{2}r_{0}. \end{aligned}$$

(A19)

After the integration, we find

$$\begin{aligned} I_{V}&=\frac{1}{\kappa }\left( \frac{3}{2}{\alpha }r_{0}-\frac{1}{2} {\alpha }^{2}r_{0}+{\frac{\nu r_{0}\beta \alpha }{\mu }}\right. \nonumber \\&\quad -{\frac{\beta \nu r_{0}}{\mu }}-{\frac{\alpha }{2\mu }}+\frac{1}{\mu } -{\frac{\beta {\nu }^{2}r_{0}}{2{\mu }^{2}}}\nonumber \\&\quad \left. -{\frac{{\beta }^{2}{\nu }^{2}r_{0}}{2{\mu }^{2}}}+{\frac{\beta \nu }{2{\mu }^{2}}}-{\frac{1}{2{\mu } ^{2}r_{0}}}\right) \nonumber \\&\underset{\mu r_{0}\gg 1}{\simeq }\frac{1}{\kappa } \left( \frac{3}{2}{\alpha }r_{0}-\frac{1}{2}{\alpha }^{2}r_{0}\right) , \end{aligned}$$

(A20)

and the result is finite. Therefore we can conclude that, in proximity of the throat the ANEC can be arbitrarily small as it should be.