1 Introduction

The black hole that has received much attention is an extreme phenomenon in the universe. Its existence does not come from actual observations, but the theoretical predictions of general relativity (GR). In 2015, the gravitational wave generated by the collision of two black holes was observed by the laser interferometer gravitational-wave observatory (LIGO) [1,2,3,4,5]. It confirmed the existence of black holes in nature and ushering in a new era of gravitational-wave astronomy. At present, another important scientific project related to the detection of black holes in the world is the Event Horizon Telescope (EHT) [6] Collaboration. One of its main tasks is to capture intuitive images of black holes. Recently, EHT announced their first image of a supermassive black hole at the center of a neighbouring elliptical M87 Galaxy [6]. The images of black holes are of great significance for further verifying the existence of black holes, studying black holes, understanding the process of black holes absorbing matter, and testing various gravitational theories [7].

The black hole shadow is an important phenomenological feature, which is how the black hole looks when a background source of light illuminates it [8]. The size and shape of the black hole shadow depend on the properties of spacetime and also depend on the observer’s position relative to the black hole. Thus, studying the shadow of black holes is a powerful method to verify the existence of black holes and test gravity theories.

For the simplest black hole – the spherical black hole, the shadow’s boundary is a perfect circle. In the sixties of the last century, Synge considered a static observer to calculate the angular radius of the Schwarzschild black hole shadow in his seminal paper [9]. For rotating black holes, the shadow’s shape is no longer circular but somewhat flattened on one side because of the “dragging” of null geodesics by the black holes. Bardeen first gave the shadow’s shape of the Kerr black hole for a distant observer [10, 11]. Since those pioneer works, shadows of objects have been extensively studied [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].

Rotating black holes are of great interesting, because most of the celestial bodies in the universe are rotating. In asymptotic flat spacetime, one can calculate the rotating black hole shadow easily with the celestial coordinates, since the angular radius of the shadow has the same formula with that in Minkowski spacetime [22, 24, 43], namely,

$$\begin{aligned}&\alpha _{d}=\lim _{r_{0} \rightarrow \infty }\left( -r_{0}^{2} \sin \theta _{0} \left. \frac{d \phi }{d r}\right| _{\theta =\theta _{0}}\right) , \end{aligned}$$
(1)
$$\begin{aligned}&\beta _{d}=\lim _{r_{0} \rightarrow \infty } r_{0}^{2} \left. \frac{d \theta }{d r}\right| _{\theta =\theta _{0}}. \end{aligned}$$
(2)

Here, \((r_{0},\theta _{0})\) represents the position of observer; the motion of light rays is described by \(d\phi /dr\) and \(d \theta /dr\). The coordinates \(\alpha _{d} \) and \(\beta _{d}\) are the apparent perpendicular distances of the shadow as seen from the axis of symmetry and its projection on the equatorial plane, respectively [24]. The schematic diagram of celestial coordinates can be obtained in Fig. 1. At present, the cosmological constant has been considered as possible to explain some theoretical and observational problems, for example, as a possible cause of the observed acceleration of the universe. One of the strongest support is the observation results of supernova [49], which shows that there may be a positive cosmological constant in our universe. However, when the cosmological constant exists, we cannot set observers in spatial infinity in the nonasymptotic flat spacetime, which means that (1) and (2) are invalid. Physicists usually put the observers within finite distance and introduce orthonormal tetrads to solve such problems. In Bardeen’s pioneer work on Kerr black hole shadow, he introduced the orthonormal tetrads for zero-angular-momentum-observers (ZAMOs) [11]. This method has also been used to investigate the Kerr–de Sitter black hole shadow [44]. It is worth mentioning that, the authors of Ref. [50] first introduced Carter’s frame [51] to study KerrA Sitter black hole shadow for observers located at a finite distance.

Fig. 1
figure 1

Schematic diagram of a distant observer’s celestial plane and celestial coordinates

Full size image

Very recently, the authors of Refs. [52, 53] proposed a new method for calculating the size and shape of shadow in terms of astrometric observables for observers located at a finite distance, while, they introduced a new distortion parameter to describe the deviation of shadow from circularity. The Kerr–de Sitter black hole shadow for static observers was revisited in this way without introducing tetrads [52]. For distant observers, their results are consistent with those of pioneer works [11, 50]; for near-region, their results are close to Ref. [50]. Furthermore, the appearance of the shadow of a static spherical black hole and the Kerr black hole was discussed in a unified framework [53]. Compared with the previous methods, this new method is more flexible, since, in principle, one can extend to any observers without encountering technical problems. This novel method seems to be a powerful tool for studying the black hole shadow.

On the other hand, the spacetime singularity or naked singularity is the final result of continuous gravitational collapse [54]. It is generally believed that the singularity must be removed through the quantum gravity effect. However, so far, there is no satisfactory theory of quantum gravity. Thus, the research on the properties and meaning of classical black holes with regular or non-singular centers has attracted intense attention in recent years. In particular, Hayward proposed an interesting regular black hole [55] based on the Bardeen’s idea about regular black hole [56]. Regular black holes are solutions of modified Einstein’s equation which behave like a de Sitter spacetime near the center. Over the past few years, there has been an increasing interest in the research of rotating regular black holes, which depend on the mass and spin of the black hole, and on an additional deviation parameter that measure potential deviations from the Kerr metric.

The study of various black hole shadows, as well as current and future observation results, is expected to provide an important method for studying the geometric structure of black holes or small deviations from Kerr metric in the strong gravitational field regime [7]. This paper aims to apply the method proposed in Refs. [52, 53] to construct the rotating Hayward–de Sitter black hole shadow and analyze the effects of different parameters on the shadow. The theoretical study of shadows combined with observation results can determine whether there are rotating Hayward–de Sitter black holes in our universe.

This article is organized as follows: in Sect. 2, we review the method of calculating black hole shadows using astronomical observables briefly. In Sect. 3, we apply this approach to rotating Hayward–de Sitter black holes to analyze the influences of parameters on the shadow’s shape and size. The results and conclusions are in Sect. 4. In this paper we set \( G=c=1 \).

2 Shadows of rotating black holes

In order to make this article self-sufficient, we will briefly introduce some basics in this section. The detailed information can be found in Refs. [52, 53].

In astrometry, the angle \( \epsilon \) between two incident light rays can be expressed by the following formula [57]:

$$\begin{aligned} \cos \epsilon \equiv \frac{\gamma ^{*} w \cdot \gamma ^{*} k}{\left| \gamma ^{*} w \Vert \gamma ^{*} k\right| }=\frac{w \cdot k}{(u \cdot w)(u \cdot k)}+1. \end{aligned}$$
(3)

Here, k and w are tangent vectors of the two light rays, respectively. \( \gamma ^{*} \) is the projection operator, \( \gamma _{\nu }^{\mu }=\delta _{\nu }^{\mu }+u^{\mu } u_{\nu } \), for a given observer, whose 4-velocity is denoted by vector u.

Fig. 2
figure 2

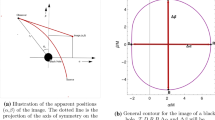
Sketch of measuring the shadow of a spherically symmetric black hole. a The observers are located at \(\theta =0\), and w is a null geodesic. The angle \(\psi \) is the angular radius of shadow. b The observers are located at \(\theta =\pi /2\). k, w, and l are light rays from photon region. \(\alpha \), \(\beta \) and \(\gamma \) are angles between k and l, l and w, k and l respectively

Full size image

Generally speaking, the metric of a rotating black hole can be written as

$$\begin{aligned} \mathrm {d} s^{2}=g_{00} \mathrm {d} t^{2}+g_{11} \mathrm {d} r^{2}+g_{22} \mathrm {d} \theta ^{2}+g_{33} \mathrm {d} \phi ^{2}+2 g_{03} \mathrm {d} t \mathrm {d} \phi .\nonumber \\ \end{aligned}$$
(4)

The 4-velocity of a static observer is \( u=\frac{1}{\sqrt{g_{00}}} \partial _{t} \). For the asymptotically de Sitter spacetime, there is a cosmological horizon. The observers are fixed at the domain of outer communication that is the region between the event horizon and the cosmological horizon [38]. Figure 2 is a schematic diagram of observers located at \(\theta =0\) and \(\theta =\pi /2\) respectively. When the observers located at \( \theta =0 \), they will find that the shadow is a disk and the angular radius is

$$\begin{aligned} \mathrm{cot} \psi =\hbox {sgn }\left( \frac{\pi }{2}-\psi \right) \sqrt{\frac{g_{11}}{g_{22}\left( \frac{l^{2}}{l^{1}}\right) ^{2}+\left( g_{33}-\frac{g_{03}^{2}}{g_{00}}\right) \left( \frac{l^{3}}{l^{2}}\right) ^{2}}}.\nonumber \\ \end{aligned}$$
(5)

Here, we have choose a light ray \( l=\left( l^{0},l^{1},l^{2},l^{3}\right) \) comes from the photon region which is filled by spherical null geodesics [50]. “\( \text {sgn} \)” represents the sign function. For observers located at \( \theta >0 \), the shadow’s silhouette is not a perfect circle as a consequence of the frame dragging effect. As an example, assume the observer located at \( \theta =\pi /2 \). Let \( k=\left( k^{0},k^{1},0,k^{3}\right) \) represent a light ray from a prograde orbit which moves in the same direction as the black hole’s rotation, and \( w=\left( w^{0},w^{1},0,w^{3}\right) \) represent a light ray from a retrograde orbit that moving against the black hole’s rotation. As mentioned in Ref. [58], a prograde photon orbits the black hole at a smaller radius than that of a retrograde photon because of the well-known Lense–Thirring effect. One can get the angle of the two light rays, in such a way that

$$\begin{aligned} \mathrm{cot} \gamma =\hbox {sgn }(k, w) \sqrt{\frac{\left( \frac{g_{11}}{\mathcal {K}-\mathcal {W}}+\left( g_{33}-\frac{g_{03}^{2}}{g_{00}}\right) \frac{1}{\frac{1}{\mathcal {W}}-\frac{1}{\mathcal {K}}}\right) ^{2}}{g_{11}\left( g_{33}-\frac{g_{03}^{2}}{g_{00}}\right) }},\nonumber \\ \end{aligned}$$
(6)

where \(\mathcal {K}\equiv k^{3}/k^{1},\mathcal {W} \equiv w^{3}/w^{1} \), and \( \hbox {sgn }(k, w)={\text {sgn}}\left( \cos \gamma \right) =\hbox {sgn }\left( g_{11}+\left( g_{33}-g_{03}^{2}/g_{00}\right) \mathcal {K} \mathcal {W}\right) \).

Similarly, the angle \( \alpha \) between a light ray \( l=\left( l^{0},l^{1},l^{2},l^{3}\right) \) from the photon region and k is

$$\begin{aligned}&\mathrm{cot} \alpha = {\mathrm{sgn}}(k,l)\sqrt{\frac{{{{\left( {{g_{11}}\frac{1}{{\mathcal {K} - {\mathcal {L}_3}}} + \left( {{g_{33}} - \frac{{g_{03}^2}}{{{g_{00}}}}} \right) \frac{1}{{\frac{{\mathrm{1}}}{{{\mathcal {L}_3}}} - \frac{1}{\mathcal {K}}}}} \right) }^2}}}{{{g_{22}}\left( {{g_{11}}{{\left( {\frac{{{\mathcal {L}_2}}}{{\mathcal {K} - {\mathcal {L}_3}}}} \right) }^2} + \left( {{g_{33}} - \frac{{g_{03}^2}}{{{g_{00}}}}} \right) {{\left( {\frac{{{\mathcal {L}_2}}}{{1 - \frac{{{\mathcal {L}_{\mathrm{3}}}}}{\mathcal {K}}}}} \right) }^2}} \right) + {g_{11}}\left( {{g_{33}} - \frac{{g_{03}^2}}{{{g_{00}}}}} \right) }}} ; \end{aligned}$$
(7)

and the angle \( \beta \) between the light ray l and w is

$$\begin{aligned} \mathrm{cot} \beta = {\mathrm{sgn}} (w,l)\sqrt{\frac{{{{\left( {{g_{11}}\frac{1}{{\mathcal {W} - {\mathcal {L}_3}}} + \left( {{g_{33}} - \frac{{g_{03}^2}}{{{g_{00}}}}} \right) \frac{1}{{\frac{{\mathrm{1}}}{{{\mathcal {L}_3}}} - \frac{1}{\mathcal {W}}}}} \right) }^2}}}{{{g_{22}}\left( {{g_{11}}{{\left( {\frac{{{\mathcal {L}_2}}}{{\mathcal {W} - {\mathcal {L}_3}}}} \right) }^2} + \left( {{g_{33}} - \frac{{g_{03}^2}}{{g_{00}}}} \right) {{\left( {\frac{{{\mathcal {L}_2}}}{{1 - \frac{{{\mathcal {L}_3}}}{{{\mathcal {W}}}}}}} \right) }^2}} \right) + {g_{11}}\left( {{g_{33}} - \frac{{g_{03}^2}}{{{g_{00}}}}} \right) }}}. \end{aligned}$$
(8)

In above equations, \( \mathcal {L}_{2} \equiv l^{2}/l^{1}, \mathcal {L}_{3} \equiv l^{3}/l^{1} \), \( \hbox {sgn }(k, l)={\text {sgn}}\left( \cos \alpha \right) =\hbox {sgn }\left( g_{11}+\left( g_{33}-g_{03}^{2}/g_{00}\right) \mathcal {K} \mathcal {L}_{3}\right) \), and \( \hbox {sgn }(w, l)={\text {sgn}}\left( \cos \beta \right) =\hbox {sgn }\left( g_{11}+\left( g_{33}-g_{03}^{2}/g_{00}\right) \mathcal {W}\mathcal {L}_{3} \right) \). Of course, these rays all come from the photon region.

The angles \( \gamma \), \( \alpha \) and \( \beta \) can provide us the shadow of black hole in the celestial sphere like Fig. 3. One can imagine that an observer at the center of sphere receives light rays from the photon region in Fig. 3. Thus, the tangents of light rays k and w are along \(\mathrm{OB}\) and \(\mathrm{OA}\) respectively, and their included angle is \(\gamma =\angle \mathrm{BOA}\). Similarly, the light ray l is along \(\mathrm{OC}\) and \(\alpha =\angle \mathrm{BOC}\), \(\beta =\angle \mathrm{AOC}\). We can use \(\gamma \) as a representation of the size of shadow, that is, the larger \(\gamma \), the larger the size of shadow.

For the sake of convincing in researching the shadow, one can use the following stereographic projection (Fig. 4) for the celestial coordinates to describe the shape of shadow in a 2D-plane [52].

$$\begin{aligned} Y_{\mathrm {sh}}= & {} \frac{2 \sin \Phi \sin \Psi }{1+\cos \Phi \sin \Psi } \nonumber \\= & {} \frac{2 \cos \beta \sin \gamma -2 \mathrm{cot} \gamma \sqrt{\sin ^{2} \gamma \sin ^{2} \beta +(\cos (\beta +\gamma )-\cos \alpha )(\cos (\beta -\gamma )-\cos \alpha )}}{1+\cos \beta \cos \gamma +\sqrt{\sin ^{2} \gamma \sin ^{2} \beta +(\cos (\beta +\gamma )-\cos \alpha )(\cos (\beta -\gamma )-\cos \alpha )}}, \end{aligned}$$
(9)
$$\begin{aligned} Z_{\mathrm {sh}}= & {} \frac{2 \cos \Psi }{1+\cos \Phi \sin \Psi }\nonumber \\= & {} \frac{2 \csc \gamma \sqrt{(\cos \alpha -\cos (\beta +\gamma ))(\cos (\beta -\gamma )-\cos \alpha )}}{1+\cos \beta \cos \gamma +\sqrt{\sin ^{2} \gamma \sin ^{2} \beta +(\cos (\beta +\gamma )-\cos \alpha )(\cos (\beta -\gamma )-\cos \alpha )}}. \end{aligned}$$
(10)

Here, \( \Phi \equiv \angle \mathrm{BOD} \) and \( \Psi \equiv \pi /2-\angle \mathrm{COD} \) are azimuth angle and polar angle in celestial coordinate system.

In order to quantitatively describe shadow’s shape, a distortion parameter \( \Xi \) in terms of \( \alpha \), \( \beta \) and \( \gamma \) is introduced, which is defined as

$$\begin{aligned} \cos \Xi \equiv \cos (\angle \mathrm{BCA})=\frac{1+\cos \gamma -\cos \alpha -\cos \beta }{2 \sqrt{(1-\cos \alpha )(1-\cos \beta )}}, \end{aligned}$$
(11)

where \( \Xi \) ranges from 0 to \( \pi \). We only care about the hemisphere where the shadow is. If the shadow is not deformed, the boundary is a perfect circle, which means that the shadow is a spherical cap on the hemisphere. In this case, \( \cos \Xi =0 \). If the shadow is deformed, \(\cos \Xi \ne 0\). Specifically, the symbol of \( \cos \Xi \) corresponds to the following two cases:

  • For \( \cos \Xi \) is negative, the boundary point \(\mathrm{C}\) is located in the spherical cap whose bottom surface is a circle with diameter \(l_{\mathrm{AB}}\);

  • For \( \cos \Xi \) is positive, the boundary point \(\mathrm{C}\) is outside the spherical cap whose bottom surface is a circle with diameter \(l_{\mathrm{AB}}\).

Here, \(l_{\mathrm{AB}}\) is the length of the line segment \(\mathrm{AB}\). In addition, the absolute value of \( \cos \Xi \) is proportional to the degree of deformation that can be seen from the graph of the cosine function. The authors of Ref. [53] first proposed this kind of quantity for the shadow. It is not difficult to find that . As shown in Fig. 3, any point \(\mathrm{C}\) on the shadow contour corresponds to the unique \(\cos \Xi \) and \(\Phi /\gamma \). Therefore, considering the symmetry of the shadow, we can obtain the degree of deviation of each point on the shadow contour from the circle through the functional image of \(\cos \Xi \) with respect to \(\Phi /\gamma \). Now, we can use \( \gamma \) and \( \Xi \) to represent the sizes and shapes of shadows without confusion.

3 Application in rotating Hayward–de Sitter black holes

In this section, we will apply the method mentioned above to obtain the rotating Hayward–de Sitter black hole shadow without introducing tetrads.

The metric of rotating Hayward–de Sitter black holes in the Boyer–Lindquist coordinates \( \left( t,r,\theta ,\phi \right) \) is [59, 60]

$$\begin{aligned} d s^{2}= & {} -\frac{\Delta _{r}}{\Sigma }\left( dt-\frac{a \sin ^{2} \theta }{\rho } d \phi \right) ^{2}+\frac{\Sigma }{\Delta _{r}} d r^{2} \nonumber \\&+\frac{\Sigma }{\Delta _{\theta }} d \theta ^{2}+\frac{\Delta _{\theta } \sin ^{2} \theta }{\Sigma }\left( adt-\frac{r^{2}+a^{2}}{\rho } d \phi \right) ^{2}, \end{aligned}$$
(12)

where

$$\begin{aligned} \Sigma= & {} r^2+a^{2}\cos ^{2}\theta ,\quad \rho =1+\frac{\Lambda }{3}a^{2}, \end{aligned}$$
(13)
$$\begin{aligned} \Delta _{r}= & {} \left( r^{2}+a^{2}\right) \left( 1-\frac{\Lambda }{3}r^{2}\right) -2 \tilde{m}\left( r\right) r, \nonumber \\ \Delta _{\theta }= & {} 1+\frac{\Lambda }{3}a^{2}\cos ^{2}\theta , \end{aligned}$$
(14)
$$\begin{aligned} \tilde{m}\left( r\right)= & {} M\left( \frac{r^{3}}{r^{3}+g^{3}}\right) . \end{aligned}$$
(15)

Here, M represents the mass of the black hole, a is the spin parameter of the black hole, \(\Lambda \) is cosmological constant, and the parameter g is the magnetic monopole charge arising from the nonlinear electrodynamics.

Fig. 3
figure 3

Schematic diagram of black hole shadows in terms of astrometrical observables in the celestial sphere. The figure is taken from Ref. [53]

Full size image
Fig. 4
figure 4

Schematic diagram for stereographic projection. The figure is taken from [52]

Full size image
Fig. 5
figure 5

The angular radius \( \psi \) of shadow as a function of the distance from the rotating Hayward–de Sitter black holes for selected parameters, and the observers are located at inclination angle \( \theta =0 \). The vertical dotted lines are the outer boundaries and the cosmological horizons. Here we set \( M=1 \)

Full size image
Fig. 6
figure 6

The angular diameter \( \gamma \) of shadow as a function of the distance from the rotating Hayward–de Sitter black holes for selected parameters, and the observers are located at inclination angle \( \theta =0 \). The vertical dotted lines are the outer boundaries and the cosmological horizons. Here we set \(M=1\)

Full size image
Fig. 7
figure 7

Shadows of rotating Hayward–de Sitter black holes with \( g=0 \) on projective plane \( \left( Y,Z\right) \) for selected parameters. r is the distance from the observer to the black holes. Here we set \( M=1 \). a Shadows of rotating Kerr(-de Sitter) black holes for selected spin parameters for distant observers. b Shadows of rotating Kerr–de Sitter black holes for observers located at \( r=4 \)

Full size image
Fig. 8
figure 8

The shape of shadows and corresponding distortion parameters \( \Xi \) as function of \( \frac{\Phi }{\gamma } \) for selected different parameters for observers located at \( r=4 \). Here we set \( M=1 \). a Shadows and distortion parameters of rotating Hayward–de Sitter black holes of selected different cosmological constants. b Shadows and distortion parameters of rotating Hayward–de Sitter black holes of selected different magnetic monopole charges. c Shadows and distortion parameters of rotating Hayward–de Sitter black holes of selected different the spin parameters

Full size image
Fig. 9
figure 9

The shapes of shadows and corresponding distortion parameters \( \Xi \) as function of \( \frac{\Phi }{\gamma } \) for selected different parameters for distant observers. Here we set \( M=1 \). a Shadows and distortion parameters of rotating Hayward black holes of selected different spin parameters for observers located at \( r=40 \). b Shadows and distortion parameters of rotating Hayward black holes of selected different magnetic monopole charges for observers located at \( r=40 \). c Shadows and distortion parameters of rotating Hayward–de black holes of selected different spin parameters for observers located at \( r=6.31 \). d Shadows and distortion parameters of rotating Hayward–de black holes of selected different the magnetic monopole charges for observers located at \( r=6.31 \)

Full size image
Fig. 10
figure 10

The shapes of shadows and corresponding distortion parameters \( \Xi \) as function of \( \frac{\Phi }{\gamma } \) for observers at selected position r

Full size image

3.1 Null geodesic equations and photon regions

The motion equations of photons in the spacetime, determined by the metric (12), can be given by the Lagrangian,

$$\begin{aligned} \mathcal {L}=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }, \end{aligned}$$
(16)

where an overdot denotes the partial derivative with respect to an affine parameter. For the metric  (12), one can obtain the momenta (\( p_{\mu }=\frac{\partial \mathcal {L}}{\partial \dot{x}^{\mu }}=g_{\mu \nu }\dot{x}^{\nu } \)) as

$$\begin{aligned} p_{t}= & {} \left( \frac{a^{2}\Delta _{\theta }\sin ^{2}\theta }{\Sigma }-\frac{\Delta _{r}}{\Sigma }\right) \dot{t}\nonumber \\&+\left( \frac{a \Delta _{r} \sin ^{2} \theta }{\rho \Sigma }-\frac{a\left( a^{2}+r^{2}\right) \Delta _{\theta } \sin ^{2} \theta }{\rho \Sigma }\right) \dot{\phi }, \end{aligned}$$
(17)
$$\begin{aligned} p_{\phi }= & {} \left( \frac{a \Delta _{r} \sin ^{2} \theta }{\rho \Sigma }-\frac{a\left( a^{2}+r^{2}\right) \Delta _{\theta } \sin ^{2} \theta }{\rho \Sigma }\right) \dot{t}\nonumber \\&+\left( \frac{\left( a^{2}+r^{2}\right) ^{2} \Delta _{\theta } \sin ^{2} \theta }{\rho ^{2} \Sigma }-\frac{a^{2} \Delta _{r} \sin ^{4} \theta }{\rho ^{2} \Sigma }\right) \dot{\phi }, \end{aligned}$$
(18)
$$\begin{aligned} p_{r}= & {} \frac{\Sigma }{\Delta _{r}}\dot{r}, \end{aligned}$$
(19)
$$\begin{aligned} p_{\theta }= & {} \frac{\Sigma }{\Delta _{\theta }}\dot{\theta }, \end{aligned}$$
(20)

where \( p_{t}=-E\), \(p_{\phi }=L_{\phi } \) are integral constants from the null geodesic equations. Combining the momenta and Hamilton–Jacobi equation, we can get null geodesics equations. The Hamilton–Jacobi equation takes the following general form:

$$\begin{aligned} -\frac{\partial S}{\partial \sigma }=\frac{1}{2} g^{\mu \nu }\frac{\partial S}{\partial x^{\mu }}\frac{\partial S}{\partial x^{\nu }}, \end{aligned}$$
(21)

where \( \sigma \) is an affine parameter and S is the Jacobi action which can be decomposed as a sum,

$$\begin{aligned} S=\frac{1}{2}m^{2}\sigma -Et+L_{\phi }\phi +S_{\theta }\left( \theta \right) +S_{r}\left( r\right) , \end{aligned}$$
(22)

if S is separable. m is the mass of particle, which is zero for photons. From (21) and (22), one can get

$$\begin{aligned} \Delta _{\theta }\left( \frac{\partial S_{\theta }}{\partial \theta }\right) ^{2}+\frac{\left( L_{\phi }\rho \csc \theta -aE\sin \theta \right) ^{2}}{\Delta _{\theta }}=\mathcal {Q}, \end{aligned}$$
(23)

and

$$\begin{aligned} \Delta _{r}\left( \frac{\partial S_{r}}{\partial r}\right) ^{2}-\frac{\left( \left( a^{2}+r^{2}\right) E-a\rho L_{\phi }\right) ^{2}}{\Delta _{r}}=-\mathcal {Q}, \end{aligned}$$
(24)

where \( \mathcal {Q} \) is a constant of separation called Carter constant, and \( \partial S/\partial x^{\mu }=p_{\mu } \). We have already set \(m=0\) in equations (23) and (24). With the Hamilton–Jacobi equation (22), it is not difficult to get the null geodesic equations as

$$\begin{aligned} \left( \Sigma \dot{r}\right) ^{2}= & {} R, \end{aligned}$$
(25)
$$\begin{aligned} (\Sigma \dot{\theta })^{2}= & {} \Theta , \end{aligned}$$
(26)
$$\begin{aligned} \Sigma \dot{t}= & {} E\left( \frac{\left( a^{2}+r^{2}\right) \left( a^{2}+r^{2}-a \lambda \rho \right) }{\Delta _{r}} \right. \nonumber \\&\left. +\frac{a\left( \lambda \rho -a \sin ^{2} \theta \right) }{\Delta _{\theta }}\right) , \end{aligned}$$
(27)
$$\begin{aligned} \Sigma \dot{\phi }= & {} \rho E\left( \frac{a\left( a^{2}+r^{2}\right) -a^{2} \lambda \rho }{\Delta _{r}} \right. \nonumber \\&\left. +\frac{\left( \lambda \rho -a \sin ^{2} \theta \right) }{\Delta _{\theta } \sin ^{2} \theta }\right) , \end{aligned}$$
(28)

where

$$\begin{aligned} R= & {} E^{2}\left( \left( a^{2}+r^{2}-a \lambda \rho \right) ^{2}-\eta \Delta _{r}\right) , \end{aligned}$$
(29)
$$\begin{aligned} \Theta= & {} E^{2}\left( \Delta _{\theta } \eta -(\lambda \rho \csc \theta -a \sin \theta )^{2}\right) , \end{aligned}$$
(30)

and

$$\begin{aligned} \lambda \equiv \frac{L_{\phi }}{E},\quad \eta \equiv \frac{\mathcal {Q}}{E^{2}}. \end{aligned}$$
(31)

For spherical orbits,

$$\begin{aligned} R\left( r_{c}\right) =0 \end{aligned}$$
(32)

and

$$\begin{aligned} \left. \frac{dR\left( r\right) }{dr}\right| _{r=r_{c}}=0 \end{aligned}$$
(33)

must be satisfied, which lead to

$$\begin{aligned}&\lambda =\left. \frac{-4 r \Delta _{r}+\left( a^{2}+r^{2}\right) \Delta _{r}^{\prime }}{a \rho \Delta _{r}^{\prime }}\right| _{r=r_{c}}, \end{aligned}$$
(34)
$$\begin{aligned}&\eta =\left. \frac{16 r^{2} \Delta _{r}}{\Delta _{r}^{\prime }\,^2}\right| _{r=r_{c}}, \end{aligned}$$
(35)

where \( \Delta _{r}^{\prime } \) denotes the derivative of \( \Delta _{r} \) with respect to r, and \( r_{c} \) is the location of photon sphere. Furthermore, we can rewrite \( R^{\prime \prime }\left( r_{c}\right) \) as

$$\begin{aligned} R^{\prime \prime }\left( r_{c}\right) =\left. 8 E^{2}\left( r^{2}+\frac{2r\Delta _{r}\left( \Delta _{r}^{\prime }-r\Delta _{r}^{\prime \prime }\right) }{\Delta _{r}^{\prime }\,^{2}}\right) \right| _{r=r_{c}}. \end{aligned}$$
(36)

A spherical null geodesic at \( r=r_{c} \) is unstable with respect to radial perturbations if \( R^{\prime \prime }\left( r_{c}\right) >0 \), and stable if \( R^{\prime \prime }\left( r_{c}\right) <0. \) Unstable photon orbits determine the contour of shadow. The range of \( r_{c} \) (photon region) can be determined by \( \Theta \ge 0 \) from (2627) and (30), which is

$$\begin{aligned} \left( \left( 4 r \Delta _{r}-\Sigma \Delta _{r}^{\prime }\right) ^{2}-16 a^{2} r^{2} \Delta _{r} \Delta _{\theta } \sin ^{2} \theta \right) _{r=r_{c}} \le 0. \end{aligned}$$
(37)

From (36) and (37), we can get \(r_{c-}\le r_{c}\le r_{c+} \), where \( r_{c-} \) and \( r_{c+}\) are the minimum and maximum radial position of the photon region. If limiting the light rays from the photon region, one can regard \( p^{\mu }=\dot{x}^{\mu } \) as functions of \( x^{\mu } \), E, and \( r_{c} \).

3.2 Sizes of shadow

For \( \theta =0 \), one can rewrite (37) as

$$\begin{aligned} \left( 4 r \Delta _{r}-\left( r^{2}+a^{2}\right) \Delta _{r}^{\prime }\right) _{r=r_{c}}=0. \end{aligned}$$
(38)

This means that the photon region becomes photon sphere, and \( r_{c}=r_{c-}=r_{c+} \). Substituting the metric (12) and geodesic equations into (5), one can calculate the angular radius of the shadow in the following form,

$$\begin{aligned} \mathrm{cot} \psi =\sqrt{\frac{\left( a^{2}+r^{2}-a \lambda \rho \right) ^{2}-\eta \Delta _{r}}{\Delta _{r} \eta +a \lambda \rho \left( 2 a^{2}+2 r^{2}-a \lambda \rho \right) }}, \end{aligned}$$
(39)

where \( \lambda \) and \( \eta \) are function of \( r_{c} \). Here, we only consider shadow in the view of observers located outside of the photon region.

In Fig. 5, we plot the shadow’s angular radius as a function of the distance between the observer and the black hole. The figures reflect that the photon sphere radius of the Schwarzschild black hole is the largest, and it’s shadow has the largest size among the shadows observed at the same position. Besides, an increase in a will make the size of shadow smaller, and g and \( \Lambda \) will also have this effect on the shadow.

The situation of the observer locates at the equatorial plane (\( \theta =\pi /2 \)) will be more complicated. In this case, (37) can be rewritten as

$$\begin{aligned} \left( \left( 4 r \Delta _{r}-r^{2} \Delta _{r}^{\prime }\right) ^{2}-16 a^{2} r^{2} \Delta _{r}\right) _{r=r_{c}} \le 0. \end{aligned}$$
(40)

Then one can obtain \( r_{c-}\le r_{c}\le r_{c+} \). From (6), we get the angular diameter \( \gamma \),

$$\begin{aligned}&\mathrm{cot} \gamma =\hbox {sgn }\left( 1+\frac{\Delta _{r}^{2}}{\rho ^{2}\left( \Delta _{r}-a^{2}\right) } \mathcal {K} \mathcal {W}\right) \nonumber \\&\quad \left| \frac{\rho \sqrt{\Delta _{r}-a^{2}}}{\Delta _{r}} \frac{1}{\mathcal {K}-\mathcal {W}} +\frac{\Delta _{r}}{\rho \sqrt{\Delta _{r}-a^{2}} } \frac{1}{\frac{1}{\mathcal {W}}-\frac{1}{\mathcal {K}}}\right| , \end{aligned}$$
(41)

where

$$\begin{aligned}&\mathcal {K}=\left. \frac{p^{\phi }}{p^{r}}\right| _{r_{c}=r_{c-}}, \end{aligned}$$
(42)
$$\begin{aligned}&\mathcal {W}=\left. \frac{p^{\phi }}{p^{r}}\right| _{r_{c}=r_{c+}}. \end{aligned}$$
(43)

From (2627) and (28), we get

$$\begin{aligned} \frac{p^{\phi }}{p^{r}}=\frac{\dot{\phi }}{\dot{r}}=\frac{\rho \left( a^{3}+a\left( r^{2}-\Delta _{r}\right) -a^{2} \lambda \rho +\Delta _{r} \lambda \rho \right) }{\Delta _{r} \sqrt{\left( a^{2}+r^{2}-a \lambda \rho \right) ^{2}-\Delta _{r} \eta }}.\nonumber \\ \end{aligned}$$
(44)

It is worth noting that \( \lambda \) and \( \eta \) can be regarded as functions of \( r_{c} \), so (44) is a function of r and \( r_{c} \). Figure 6 shows that the angular parameter \( \gamma \) changes with the increase of the distance between the observers and the black hole. It is not difficult to find that the angular parameter \( \gamma \) decreases with the increase of a, \( \Lambda \) and g, and the outer boundary of the photon region \( r_{c+} \) is larger than the radius of the photon sphere in Schwarzschild spacetime. Therefore, the size of the black hole shadow will decrease with the increase of a, \( \Lambda \) and g, and the shadow of the Schwarzschild black hole has the largest size.

3.3 Shadow’s shape

In this part, we will consider the shape of shadow in different situations. The observers located at inclination angle \( \theta =0 \) would see the shadows as a perfect circle, while the observers located at \( \theta =\frac{\pi }{2} \) would find that the shadows are distorted. According to (7) and (8), the angular distances \( \alpha \) and \( \beta \) can be read as

$$\begin{aligned}&\mathrm{cot} \alpha =\hbox {sgn }\left( 1+\frac{\Delta _{r}^{2}}{\left( \Delta _{r}-a^{2}\right) \rho ^{2}} \mathcal {K} \mathcal {L}_{3}\right) \nonumber \\&\quad \frac{\left| \frac{\Delta _{r}}{\rho \sqrt{\Delta _{r}-a^{2}}} \frac{1}{\frac{1}{\mathcal {L}_{3}}-\frac{1}{\mathcal {K}}}+\frac{\rho \sqrt{\Delta _{r}-a^{2}}}{\Delta r} \frac{1}{\mathcal {K}-\mathcal {L}_{3}}\right| }{\sqrt{1+\left( \frac{\mathcal {L}_{2}}{1-\frac{\mathcal {L}_{3}}{\mathcal {K}}}\right) ^{2} \Delta r+\frac{\left( \Delta r-a^{2}\right) \rho ^{2}}{\Delta r}\left( \frac{\mathcal {L}_{2}}{\mathcal {K}-\mathcal {L}_{3}}\right) ^{2}}}, \end{aligned}$$
(45)

and

$$\begin{aligned}&\mathrm{cot} \beta =\hbox {sgn }\left( 1+\frac{\Delta _{r}^{2}}{\left( \Delta _{r}-a^{2}\right) \rho ^{2}} \mathcal {W} \mathcal {L}_{3}\right) \nonumber \\&\quad \frac{\left| \frac{\Delta _{r}}{\rho \sqrt{\Delta _{r}-a^{2}}} \frac{1}{\frac{1}{\mathcal {L}_{3}}-\frac{1}{\mathcal {W}}}+\frac{\rho \sqrt{\Delta _{r}-a^{2}}}{\Delta _{r}} \frac{1}{\mathcal {W}-\mathcal {L}_{3}}\right| }{\sqrt{1+\left( \frac{\mathcal {L}_{2}}{1-\frac{\mathcal {L}_{3}}{\mathcal {W}}}\right) ^{2} \Delta _{r}+\frac{\left( \Delta _{r}-a^{2}\right) \rho ^{2}}{\Delta _{r}}\left( \frac{\mathcal {L}_{2}}{\mathcal {W}-\mathcal {L}_{3}}\right) ^{2}}}, \end{aligned}$$
(46)

where \( \mathcal {K} \) and \( \mathcal {W} \) are given by (42), (43) and

$$\begin{aligned}&\mathcal {L}_{2}\equiv \left. \frac{p^{\theta }}{p^{r}}\right| _{r_{c}}, \end{aligned}$$
(47)
$$\begin{aligned}&\mathcal {L}_{3}\equiv \left. \frac{p^{\phi }}{p^{r}}\right| _{r_{c}}, \end{aligned}$$
(48)

with

$$\begin{aligned} \frac{p^{\theta }}{p^{r}}=\frac{\dot{\theta }}{\dot{r}}=\pm \sqrt{\frac{\eta -(\lambda \rho -a)^{2}}{\left( a^{2}+r^{2}-a \lambda \rho \right) ^{2}-\Delta _{r} \eta }}. \end{aligned}$$
(49)

In Fig. 7, we set \(g=0 \) and get the same results as the Kerr(-de Sitter) black holes in Ref. [52]. In Figs. 8 and 9, we scale the shadows appropriately so that the degree of distortion of these shadows can be compared qualitatively from the images. The first row of Figs. 8 and 9 are the shadows after scaling, with different parameters selected, and the second row are the images of the corresponding distortion parameters vary with \( \Phi /\gamma \), which are the quantitative description of the shadow’s distortion. In Fig. 8, the observers are not far from the photon regions of the black holes, and in Fig. 9, the observers are far away from the black holes. As mentioned above, \( \cos \Xi =0 \) means that the shadow is not deformed. Thus, in the functional image of \( \cos \Xi \) respect to \(\Phi /\gamma \), a straight line satisfying \( \cos \Xi =0 \) means the shadow is not deformed and the more deviated from this straight line, the more severe the shadow distortion. From Figs. 8 and 9, the deformation of each position of the shadow contour can be roughly obtained. It is not difficult to find that the shadow’s distortion will decrease as the cosmological constant \(\Lambda \) increases. In contrast, the distortion will increase with the increase of g or a.

In Fig. 10, we plot the shapes and distortion parameters of the shadows for observers at different distances from the center of the black hole. One can see that the distortion parameter would increase with the distance. Through the above discussion, we know that when the parameters g and a reach to their maximum, and the cosmological constant reduce to zero, the distortion of the shadow reaches to its upper limit.

4 Conclusions and discussions

In this article, we have calculated the size and shape of rotating Hayward–de Sitter black hole shadow for static observers at a finite distance in terms of astronomical observables. For the observers on the axis of the black hole, the shadow’s boundary is a perfect circle. For the observers located at the equatorial plane of the black hole, the shadow’s boundary will be distorted. To quantitatively describe the distortion of the shadows, we plotted the distortion parameter affected by the black hole’s parameters. It is found that the shadow will shrink while the parameters increase; the Schwarzschild black hole has the largest shadow. Furthermore, when the magnetic monopole charge and spin parameter of rotating Hayward–de Sitter black holes reach to their maximum, and the cosmological constant reduce to zero, the distortion of the shadow reaches to its upper limit, and the distortion parameter would increase with the distance.

Though this article only considered static observers located at the axis and the equatorial plane of the black hole, this method is suitable for arbitrary observers. Studying the shadows of black holes is an important way for studying the properties of black holes, from which we can obtain rich information about space-time geometry. This work provides a reference for verifying related gravitational theories.