Trapping of null geodesics in slowly rotating spacetimes

Abstract

Extremely compact objects containing a region of trapped null geodesics could be of astrophysical relevance due to trapping of neutrinos with consequent impact on cooling processes or trapping of gravitational waves. These objects have previously been studied under the assumption of spherical symmetry. In the present paper, we consider a simple generalization by studying trapping of null geodesics in the framework of the Hartle–Thorne slow-rotation approximation taken to first order in the angular velocity, and considering a uniform-density object with uniform emissivity for the null geodesics. We calculate effective potentials and escape cones for the null geodesics and how they depend on the parameters of the spacetimes, and also calculate the “local” and “global” coefficients of efficiency for the trapping. We demonstrate that due to the rotation the trapping efficiency is different for co-rotating and retrograde null geodesics, and that trapping can occur even for $R>3GM/c^2$, contrary to what happens in the absence of rotation.

1 Introduction

Recently, there has been increasing interest in “ultra” compact objects (ones which could mimic black holes), in connection with the detection of gravitational waves coming from mergers [1]. Also, a general correlation has been suggested between quasinormal modes and the parameters of unstable circular null geodesics [2], although there could be some exceptions to this [3,4,5,6].

On the other hand, extremely compact objects are important also because of the possible existence of regions of trapped null geodesics that could be relevant for the trapping of gravitational waves [7] or neutrinos [8]. The trapping region is always centered around a stable circular null geodesic whose existence represents a necessary condition for the existence of the trapping zone. Null geodesics inside extremely compact neutron stars may govern the motion of neutrinos, if the neutron stars are sufficiently cool [8], and neutrino trapping can be important for several reasons: it can modify (decrease) the neutrino flow that reaches distant observers during the birth of a neutron star and just afterward; also, trapped neutrinos can substantially influence how it cools – they could modify its internal structure due to induced internal flows, and could cause self-organizing of neutron star matter due to these flows, as discussed in the case of the internal Schwarzschild spacetimes [8], or generalized internal Schwarzschild spacetimes modified by the presence of a cosmological constant [9]; for the relevance of the cosmological constant in astrophysical phenomena see [10].

Models of extremely compact objects with trapping zones (so-called “trapping compact objects”) were until now based on spherically symmetric spacetimes representing non-vacuum solutions of general relativity, or of an alternative gravity theory. The first detailed study of trapping spheres were made for internal Schwarzschild spacetimes, representing objects with uniform energy density [8], for which it was explicitly demonstrated that they can include trapping spheres only if the radius (R) of the object concerned is smaller than $R=3GM/c^2=3r_g/2$, where M is its mass and $r_g$ is the related gravitational radius. Such objects must therefore be really extremely compact - their radius must be smaller than that of the (unstable) circular photon orbit (photosphere) of the external vacuum Schwarzschild spacetime. It has also been shown that the efficiency of the trapping increases monotonically with decreasing radius of the uniform sphere, down to $R = 9r_g/8$ (the minimum allowed for standard internal Schwarzschild spacetimes) [8], for the special case related to gravastars see [11, 12]. Trapping of neutrinos for extremely compact objects in the braneworld scenario has been studied in [13].

It is certainly interesting and relevant, to test the influence of rotation on the trapping of null geodesics. In the present paper, we approach this by making the simplest approximation for rotating compact objects of using the Hartle–Thorne slow-rotation approximation taken to first order in the angular velocity and applying it, once again, for constant-density objects. We thus use the standard internal Schwarzschild spacetime generated by the uniform energy density, but augmented with the off-diagonal term of the Lense–Thirring type arising from the Hartle–Thorne equation for the dragging of inertial frames [14]. Such a solution represents just the simplest way to estimate the role of spacetime rotation in the trapping of null geodesics, but it demonstrates this in a clear and illustrative way. For estimating the efficiency of the trapping, we assume a uniformly distributed, isotropically and uniformly radiating source as in our previous work [8, 9]. Discussion of the applicability of null geodesics to neutrino motion in the interior of neutron stars can be found in [8].

In Sect. 2, we introduce the non-rotating internal Schwarzschild configuration with uniform energy density and the motion of trapped null geodesics connected to the existence of an internal spacetime with a stable sphere of null geodesics. We define the geometry, the effective potential of the motion along null geodesics, and the angles related to directions of emission from local sources needed for the construction of escape cones for null geodesics and their relation to trapping zones. In Sect. 3, we introduce the first-order rotating Hartle–Thorne spacetime with uniform distribution of energy density and with the tetrad formalism being used for the observers (sources) in the rotating spacetime, and we study the null geodesics in both the internal and external first-order Hartle–Thorne spacetimes, constructing the related effective potentials for the null geodesic motion. In Sect. 4 we construct the escape cones (and complementary trapping cones) for the rotating and non-rotating configurations, and calculate their dependence on the compactness of the Hartle–Thorne object, its rotation, and their position in the object. In Sect. 5, we define and calculate the corresponding ‘local’ and ‘global’ trapping efficiencies for null geodesics, and compare the trapping efficiencies of rotating and non-rotating configurations. In Sect. 6, we discuss our results. Throughout, we use geometric units with $c = G = 1$.

2 Internal Schwarzschild spacetime and its null geodesics

We here start by restricting attention to the simplest internal solution for our compact objects, with a uniform distribution of the energy density and with the internal geometry represented by the static and spherically symmetric internal Schwarzschild spacetime [15]. We first present the geometry, its null geodesics, and the trapping of null geodesics occurring when the object is extremely compact.

2.1 Internal Schwarzschild spacetime

In standard Schwarzschild coordinates ($t,r,\theta ,\phi$), the line element of static and spherically symmetric spacetimes takes the form

$$\begin{aligned} {\mathrm {d}}s^2=-e^{2\Phi (r)}{\mathrm {d}}t^2+e^{2\Psi (r)}{\mathrm {d}}r^2 +r^2({\mathrm {d}}\theta ^2 + \sin ^2\theta {\mathrm {d}}\varphi ^2). \end{aligned}$$

(1)

The temporal and radial components of the internal Schwarzschild metric with the uniform energy density, $\rho =const$, are given by

$$\begin{aligned} (-g_{tt})^{1/2}=e^{\Phi }=\frac{3}{2}Y_1-\frac{1}{2}Y(r),\quad (g_{rr})^{1/2}=e^{\Psi }=\frac{1}{Y(r)}, \end{aligned}$$

(2)

where

$$\begin{aligned} Y(r)= & {} \left( 1-\frac{r^2}{a^2}\right) ^{1/2},\nonumber \\ Y_1= & {} Y(R)=\left( 1-\frac{R^2}{a^2}\right) ^{1/2},\quad \frac{1}{a^2}=\frac{8}{3}\pi \rho =\frac{2M}{R^3}, \end{aligned}$$

(3)

with R and M being the total radius and mass of the object. At the surface $r=R$ the internal geometry is smoothly matched to the external vacuum Schwarzschild geometry

$$\begin{aligned} g_{tt}=-e^{2\Phi }=-\left( 1-\frac{2M}{r} \right) ,\quad g_{rr}=e^{2\Psi }=\left( 1-\frac{2M}{r} \right) ^{-1}. \end{aligned}$$

(4)

The radial profile of the pressure for the internal uniform density Schwarzschild spacetimes and its generalization to the case with non-zero cosmological constant is given and discussed in [16, 17]; the internal solutions for polytropic equations of state for the matter are discussed in [18,19,20,21] and their dynamical stability is discussed in [22,23,24].

In order to have a finite central pressure $P_{{\mathrm {c}}} = P(r=0)$, the surface radius has to fulfill the condition $R>R_{{\mathrm {c}}} = 9r_{{\mathrm {g}}} /8 \equiv 9M/4$; of course, at the surface $P(r=R)$ is always zero. Note that the internal Schwarzschild solutions with $R<R_{{\mathrm {c}}}$ are physically unrealistic, but they do have a physical meaning in a modified form with a very interesting interpretation for $R \rightarrow r_{{\mathrm {g}}}$, as they correspond in this limit to gravastars [25]. Here we consider the internal Schwarzschild solutions with $R>9r_{{\mathrm {g}}} /8$, focusing on those in the range $R \in (9/8, 1.6)r_{{\mathrm {g}}}$ corresponding to the so called trapping internal Schwarzschild spacetimes that contain regions of trapped null geodesics [8].

2.2 Effective potentials for the null geodesics

The motion along null geodesics is governed by the relations

$$\begin{aligned} \frac{\mathrm {D}p^{\mu }}{{\mathrm {d}}\tau }=0,\quad p_{\mu }p^{\mu }=0, \end{aligned}$$

(5)

where $p^{\mu }$ is the 4-momentum and $\tau$ is the affine parameter. Two Killing vector fields ($\frac{\partial }{\partial t}\ \mathrm {and} \frac{\partial }{\partial \varphi }$) imply two conserved components of the 4-momentum:

$$\begin{aligned} p_t=-E\quad ({\mathrm {energy}}),\quad p_{\varphi }=\phi \quad (\text {axial angular momentum}) \end{aligned}$$

(6)

which are referred to as “motion constants”. Motion in the spherically symmetric case is limited to a single plane. In the case of only one geodesic, it is convenient to choose that to be the equatorial plane of the coordinate system i.e. we set $\theta =\pi /2=$ const. Introducing the impact parameter $\lambda =\phi /E$ and using the normalisation condition, we obtain the relation

$$\begin{aligned} (p^r)^2=\frac{-1}{g_{tt}g_{rr}}E^2\left( 1+g_{tt} \frac{\lambda ^2}{r^2}\right) . \end{aligned}$$

(7)

It is obvious that the energy is not relevant (we can use it for scaling of the impact parameter $\lambda$). The expression in brackets has to be non-negative [26]. We can then introduce the effective potential determining the turning points of the radial motion along the null geodesics for a given impact parameter $\lambda$.

$$\begin{aligned} \lambda ^2\le {\mathrm {V}}_{\mathrm {eff}}={\left\{ \begin{array}{ll} {\mathrm {V}}_{\mathrm {eff}}^{\mathrm {int}} =\frac{4a^2[1-Y^2(r)]}{[3Y_1-Y(r)]^2}&{}\quad \text {for } r \le R\\ {\mathrm {V}}_{\mathrm {eff}}^{\mathrm {ext}}=\frac{r^3}{r-2M}&{}\quad \text {for } r>R. \end{array}\right. } \end{aligned}$$

(8)

There is a local maximum of $V_{\mathrm {eff}}^{\mathrm {int}}$ corresponding to a stable circular null geodesic (in the interior), given by

$$\begin{aligned} r_{\mathrm {c(i)}}^2=\frac{R^3\left( \frac{4R}{9M}-1 \right) }{R-2M}, \quad \lambda _{\mathrm {c(i)}}^2=\frac{4a^2}{9Y_1^2-1}; \end{aligned}$$

(9)

and a local minimum of $V_{\mathrm {eff}}^{\mathrm {ext}}$ corresponding to an unstable circular null geodesic (in the exterior), given by

$$\begin{aligned} r_{\mathrm {c(e)}}=3M,\quad \lambda _{\mathrm {c(e)}}^2=27M^2. \end{aligned}$$

(10)

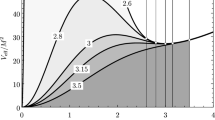
Figure 1 shows the effective potential of the trapping Schwarzschild spacetime with radius $R=2.4M$. The shaded areas indicate the zones of trapped null geodesics: the darker one corresponds to null geodesics fully contained in the internal spacetime (with inner boundary at $r_{\mathrm {b(i)}}$), while the lighter one is related to null geodesics that partially move in the external spacetime (with an inner boundary at $r_{\mathrm {b(e)}}$). The boundaries of the trapping regions lying within the internal Schwarzschild spacetime are given by (see [8]):

$$\begin{aligned} r_{\mathrm {b(i})}= \frac{R}{2R-3} \sqrt{\frac{32R^2-144R+162}{2}} \end{aligned}$$

(11)

and

$$\begin{aligned} \left( \frac{r_\mathrm {b(e)}}{R}\right) ^2=&\frac{ 27(10R^4-18R^3-108R+243) }{ (2R^3+27)^2 }\\ \nonumber&-\frac{ [6R^{3/2}(R-2)^{1/2}(R^4-108R+243)^{1/2}] }{ (2R^3+27)^2 }. \end{aligned}$$

(12)

For our analysis, it is important whether the effective potential is monotonic or not. If it is monotonic, then there cannot be any trapped area present. In other words, only if a local minimum (and a local maximum) of the effective potential exist, can there be a trapped area. For the internal Schwarzschild spacetimes, the analysis of the null geodesics shows that it is impossible to have regions of trapped null geodesics for $R>3M$.

Two types of trapped geodesic are distinguished in Fig. 1. In the darkly-shaded part, the null geodesics are limited to the internal spacetime whereas in the lower lightly-shaded part, the null geodesics can pass through the surface of the object, although they are still bound and trapped (for details see [8]).

Fig. 1

The effective potential for an object with $R=2.4M$; the trapped areas are shaded. The darkly-shaded area, bounded by the radii $r_{\mathrm {b(i)}}$ and R, contains null geodesics trapped completely inside the object, while the lightly-shaded area, bounded by the radii $r_{\mathrm {b(e)}}$ and $r_{\mathrm {c(e)}}$, contains null geodesics, which can temporarily pass through the surface into the vacuum before returning

2.3 Escape cones and trapped null geodesics

In order to treat consistently the trapping of null geodesics in the context of neutrinos emitted by a matter of the trapping configuration, we need to determine the escape cones – the trapped neutrinos are then the proportion of the emitted ones not escaping.

We first briefly summarise the construction of the escape cones in the spherically symmetric internal uniform Schwarzschild spacetimes, as they are a starting point for our paper and provide a test for it. The escape cones need to be related to the static observers (sources) in the static spacetime and they are considered in the corresponding local frames of these static observers. The tetrad of the differential forms is defined as

$$\begin{aligned} e^{(t)}={\mathrm {e}}^\Phi {\mathrm {d}} t,\quad e^{(r)}={\mathrm {e}}^\Psi {\mathrm {d}} r,\quad e^{(\theta )}=r {\mathrm {d}} \theta ,\quad e^{(\varphi )}=r {\mathrm {sin}}\theta {\mathrm {d}} \varphi ,\nonumber \\ \end{aligned}$$

(13)

and the line element then takes the special-relativistic form

$$\begin{aligned} {\mathrm {d}} s^2=-[ e^{(t)}]^2 + [ e^{(r)}]^2 + [ e^{(\theta )}]^2 + [ e^{(\varphi )}]^2. \end{aligned}$$

(14)

The complementary tetrad for the frame of the 4-vector $e_{(\alpha )}$ is given by

$$\begin{aligned} e_{(\alpha )}^{\mu }e_\nu ^{(\alpha )}=\delta ^\mu _\nu , \quad e_\mu ^{(\alpha )}e^\mu _{(\beta )}=\delta ^\alpha _\beta . \end{aligned}$$

(15)

Physically relevant projections of the 4-momentum $p^{\mu }$ are given by

$$\begin{aligned} p^{(\alpha )}=p^{\mu }e_\mu ^{(\alpha )},\quad p_{(\alpha )}=p_\mu e^\mu _{(\alpha )}. \end{aligned}$$

(16)

The neutrinos radiated locally by a static source can be described by the directional angles, as demonstrated in Fig. 2. The angles $\alpha ,~\beta ,~\gamma$ are connected by the relation

$$\begin{aligned} \cos \gamma =\sin \beta \sin \alpha , \end{aligned}$$

(17)

and are related to the outgoing radial direction in the spacetime.

Fig. 2

The definition of angles $\alpha$, $\beta$ and $\gamma$ describing the direction of a null geodesic

The escape cone in the observer (source) frame is determined by the angles corresponding to photon parameters defining the stable and unstable null circular geodesics.

The angle $\alpha$ relates the directions of the null geodesics and the outgoing radial unit vector. In the spherically symmetric internal Schwarzschild spacetime, a cone centered at the point of emission is determined by the angle $\alpha$, while the angle $\beta$ determines the position on the cone. We have to find the angles $\alpha _{\mathrm {c(i)}}$ corresponding to $\lambda _{\mathrm {c(i)}}$ of the stable null circular geodesic and $\lambda _{\mathrm {c(e)}}$ of the unstable null circular geodesic.

Now we have to relate the directional angles to the motion constants (and hence the impact parameters). Due to the spherical symmetry we can consider equatorial null geodesics (when $\beta =\pi /2$, or $\beta =3\pi /2$). The directional angle $\alpha$ is then governed by the relations ($p^{(\theta )}=0$)

$$\begin{aligned} \sin \alpha =\frac{p^{(\varphi )}}{p^{(t)}}, \quad \cos \alpha =\frac{p^{(r)}}{p^{(t)}}. \end{aligned}$$

(18)

As the radial component of the 4-momentum is

$$\begin{aligned} p_r=\pm E{\mathrm {e}}^{\Psi -\Phi }\left( 1-{\mathrm {e}}^{2\Phi } \frac{\lambda ^2}{r^2}\right) ^{1/2}, \end{aligned}$$

(19)

we find the directional angle in the internal Schwarzschild spacetime in the form (putting for simplicity $M=1$)

$$\begin{aligned} \sin \alpha= & {} \left[ \frac{3}{2}\left( 1-\frac{2}{R}\right) ^{1/2} -\frac{1}{2}\left( 1-\frac{2}{R}\left( \frac{r}{R}\right) ^2\right) ^{1/2}\right] \frac{\lambda }{r}\nonumber \\= & {} A(r,R)\frac{\lambda }{r}, \end{aligned}$$

(20)

$$\begin{aligned} \cos \alpha= & {} \pm (1-\sin ^2\alpha )^{1/2}. \end{aligned}$$

(21)

To find the escape (trapping) cone in the region where trapping is possible, defined by the extension of the effective potential barrier, we have to calculate the angles for $\lambda =\lambda _{\mathrm {c(i)}}$ and $\lambda =\lambda _{\mathrm {c(e)}}$

$$\begin{aligned} \sin \alpha _{\mathrm {c(i)}}(r,R)= & {} A(r,R)\frac{R^{3/2}}{r(R-2)^{1/2}}, \end{aligned}$$

(22)

$$\begin{aligned} \sin \alpha _{\mathrm {c(e)}}(r,R)= & {} A(r,R)\frac{3\sqrt{3}}{r}. \end{aligned}$$

(23)

One always has $\alpha _{\mathrm {c(i)}}>\alpha _{\mathrm {c(e)}}$, and the trapping zone lies between these angles, as shown in Fig. 3 where the trapping zone is shaded. The escape cone (zone) is unshaded and null geodesics there can escape to infinity even if originally emitted inwards.¹

The escape and complementary trapping cones have been applied to calculate the trapping efficiency for null geodesics in spherically-symmetric uniform-density internal Schwarzschild spacetimes, and to estimate the neutrino trapping [8]. Here we generalize those results to the simplest case of first-order Hartle–Thorne models based on spherically-symmetric uniform-density internal Schwarzschild spacetimes as the background solution, augmented by the first order rotational off-diagonal metric coefficient. The first-order Hartle–Thorne model is equivalent to the Lense–Thirring metric in the exterior of the compact object, but has a different interior spacetime with regard to both the matter and rotational contributions.

Fig. 3

An example of an escape cone, for a non-rotating configuration with $R/M=2.4$, located at the position of the stable circular photon orbit. The figure emphasizes the positions of the angle $\alpha$ = $\{0, \pi / 4, \pi / 2, 3 \pi / 4, \pi \}$, which has the character of a radial coordinate in a classical polar graph and the angle $\beta$ = $\{0, \pi / 2, \pi , 3 \pi / 2\}$, which has the character of an angular coordinate in a classical polar graph. The figure is also divided into “left” and “right” parts, for null geodesics which are co-rotating ($\beta \in (0, \pi )$) and counter-rotating ($\beta \in (\pi ,2\pi )$)

3 First-order Hartle–Thorne spacetime with uniformly distributed energy density

As already mentioned, the effects of rotation on the trapping internal Schwarzschild spacetime with uniformly distributed energy density is here being treated in the framework of the Hartle–Thorne slow-rotation model taken to first order in the angular velocity. The Hartle–Thorne models treat both the interior and exterior of relativistic perfect-fluid, rotating objects by expanding up to second order in the angular velocity $\Omega$ as measured by distant static observers, with $\Omega$ taken to be constant throughout the model [14]. The case with the uniform internal Schwarzschild spacetime being taken as the reference model about which to perturb, has previously been studied by Chandrasekhar and Miller [28]. For the present purposes, we are including only the first-order term here. We start by summarising the results of [14] that will be applied here.

3.1 Hartle–Thorne spacetimes and their locally non-rotating frames

Using the frame formalism, the internal Hartle–Thorne metric can be written using the 1-forms

$$\begin{aligned} {\mathrm {d}} s^2 = -[{\mathrm {e}}^{(t)} ]^2 + [{\mathrm {e}}^{(r)} ]^2 + [{\mathrm {e}}^{(\theta )} ]^2 +[{\mathrm {e}}^{(\varphi )}]^2 \end{aligned}$$

(24)

where the 1-forms of the metric can be conveniently defined to reflect the so-called locally non-rotating frames (LNRFs) [29], corresponding to observers with zero angular momentum at given $(r,\theta )$ (therefore, the term ZAMO frames is also used) who are locally co-rotating with respect to the internal Hartle–Thorne spacetime, being dragged to corotation with the angular velocity $\omega (r)$ characterizing the spacetime rotation relative to static distant observers:

$$\begin{aligned}&{\mathrm {e}}^{(t)}=\sqrt{-g_{tt({\mathrm {i}})}} {\mathrm {d}} t,\quad {\mathrm {e}}^{(r)}=\sqrt{g_{rr({\mathrm {i}})}} {\mathrm {d}} r, \nonumber \\&{\mathrm {e}}^{(\theta )}=\sqrt{g_{\theta \theta ({\mathrm {i}})}} {\mathrm {d}} \theta ,\quad {\mathrm {e}}^{(\varphi )}=\sqrt{g_{\theta \theta ({\mathrm {i}})}}\sin \theta ({\mathrm {d}} \varphi - \omega {\mathrm {d}} t). \end{aligned}$$

(25)

The metric coefficients are given in [14]; $\omega (r)$ is the angular velocity of the LNRFs reflecting the rotational dragging of the internal spacetime by the gravitation of the object rotating with the angular velocity $\Omega = const$. The motion of the particles constituting the Hartle–Thorne object corresponds to rigid and uniform rotation with angular velocity $\Omega$ relative to distant static observers, so that their 4-velocity $u^\mu$ has components

$$\begin{aligned}&u^t=(-g_{tt} - 2\Omega g_{t\varphi } -g_{\varphi \varphi }\Omega ^2 )^{-1/2},\nonumber \\&\quad u^\varphi =\Omega u^t,\quad u^r=u^\theta =0. \end{aligned}$$

(26)

The angular velocity of the rotating matter relative to the rotating spacetime

$$\begin{aligned} \bar{\omega }(r) \equiv \Omega -\omega (r) \end{aligned}$$

(27)

enters the Einstein gravitational equations – it is of first order in $\Omega$ and satisfies the differential equation

$$\begin{aligned} \frac{1}{4}\frac{{\mathrm {d}}}{{\mathrm {d}}r} \Bigg (r^4f(r)\frac{{\mathrm {d}}\bar{\omega }}{{\mathrm {d}}r}\Bigg ) +\frac{4}{r}\frac{{\mathrm {d}}f(r)}{{\mathrm {d}}r}\bar{\omega }=0, \end{aligned}$$

(28)

where

$$\begin{aligned} f(r)=\Bigg (\frac{-1}{g_{tt(i)}g_{rr(i)}}\Bigg )^{1/2}. \end{aligned}$$

(29)

The solution of this equation needs to be regular at the origin and so we have $\frac{d\bar{\omega }}{dr}=0$ at $r=0$ while $\bar{\omega }$ goes to a finite value $\bar{\omega }_c$ there which is found by matching with the vacuum exterior solution at the surface $r=R$. That matching gives expressions for the angular momentum J and angular velocity $\Omega$ of the object [14]

$$\begin{aligned} J=\frac{1}{6}R^4\Bigg (\frac{{\mathrm {d}}\bar{\omega }}{{\mathrm {d}}r} \Bigg )_{r=R}, \end{aligned}$$

(30)

and

$$\begin{aligned} \Omega =\bar{\omega }(R) + \frac{2J}{R^3}. \end{aligned}$$

(31)

To complete the solution, it is convenient to first solve Eq. (28) for $\bar{\omega }$ measured in units of $\bar{\omega }_c$, then to use (30) and (31) to find $J/\bar{\omega }_c$ and $\Omega /\bar{\omega }_c$, and finally to use these for obtaining J and $\bar{\omega }(r)$ measured in units of $\Omega$. The first of these gives the moment of inertia $I=J/\Omega$ and is related to the radius of gyration by (see [30]):

$$\begin{aligned} \mathcal R_{\mathrm {gyr}}=\left( \frac{J}{\Omega M} \right) ^{1/2}. \end{aligned}$$

(32)

The external Hartle–Thorne geometry can be described in the tetrad frame taking the form [14]

$$\begin{aligned}&{\mathrm {e}}^{(t)}=\sqrt{-g_{tt({\mathrm {e}})}} {\mathrm {d}} t, \quad {\mathrm {e}}^{(r)}=\sqrt{g_{rr({\mathrm {e}})}} {\mathrm {d}} r, \nonumber \\&{\mathrm {e}}^{(\theta )}=\sqrt{g_{\theta \theta ({\mathrm {e}})}} {\mathrm {d}} \theta ,\quad {\mathrm {e}}^{(\varphi )}=\sqrt{g_{\theta \theta ({\mathrm {e}})}}\sin \theta \left( {\mathrm {d}} \varphi - \frac{2J}{r^3} {\mathrm {d}} t\right) .\nonumber \\ \end{aligned}$$

(33)

The form of the metric coefficients can be found in [14] or, in an alternative form, in [31].

3.2 First-order Hartle–Thorne spacetime

The line element of the first-order Hartle–Thorne internal spacetime, with uniformly distributed energy density, considered in the following study takes the form

$$\begin{aligned} {\mathrm {d}}s^2= & {} -e^{2\Phi (r)}{\mathrm {d}}t^2+e^{2\Psi (r)}{\mathrm {d}}r^2 +r^2\big ({\mathrm {d}}\theta ^2\nonumber \\&+ \sin ^2\theta {\mathrm {d}}\varphi ^2\big ) - 2 \omega (r) r^2 \sin ^2\theta {\mathrm {d}}t{\mathrm {d}}\varphi , \end{aligned}$$

(34)

where $\Phi (r)$ and $\Psi (r)$ are the functions governing the static spherically symmetric configuration, here taken to be the internal Schwarzschild spacetime, and $\omega (r)$ is the angular velocity of the LNRF related to those spacetimes. The rotating spacetime geometry is then determined by finding the solution of Eq. (28) for the angular velocity of the rotating matter relative to the spacetime geometry, $\bar{\omega }$, where the characteristic function of the solution is

$$\begin{aligned} f(r)=\Bigg (\frac{4Y^{2}(r)}{(3Y_{1}-Y(r))^{2}}\Bigg )^{1/2}. \end{aligned}$$

(35)

The results of the integration are presented in Fig. 4 – we can see how the frame dragging increases with increasing compactness, if the angular velocity $\Omega$ is kept fixed. The strongest dragging effect, with $\omega (r=0)=\Omega$ and $\bar{\omega }(r=0)=0$, is obtained for the maximally compact case with $R/M=2.25$. Note that this represents a limiting case, with the central pressure going to infinity, which cannot itself be considered as at all physical. In the following, we will focus on the three other cases shown here as being representative of these very compact models.

Fig. 4

Numerical solution for $\bar{\omega }$ scaled by $\Omega$ for $R/M=2.25$ (dotted line), $R/M=2.4$ (solid line), $R/M=2.8$ (dashed line) and $R/M=3.2$ (dash-dotted line)

The metric of the external first-order Hartle–Thorne (or Lense–Thirring) spacetime takes the form

$$\begin{aligned} {\mathrm {d}} s^2= & {} -\left( 1-\frac{2M}{r} \right) {\mathrm {d}}t^2+\left( 1-\frac{2M}{r} \right) ^{-1}{\mathrm {d}}r^2\nonumber \\&+r^2\left( {\mathrm {d}}\theta ^2 + \sin ^2\theta {\mathrm {d}}\varphi ^2\right) - 2 \frac{J}{r} \sin ^2\theta {\mathrm {d}}t{\mathrm {d}}\varphi , \end{aligned}$$

(36)

It is useful to consider also the inverse form of the metric representing the first-order spacetimes. The contravariant form of the internal first-order Hartle–Thorne metric is given by

$$\begin{aligned} \left( \frac{\partial }{\partial s}\right) ^{2}_{\mathrm {int}}= & {} -e^{-2\Phi (r)}_\mathrm {int} \frac{\partial ^2}{\mathrm {\partial }t^2}+\left( 1-\frac{2 r^2}{R^3} \right) \frac{\partial ^2}{\mathrm {\partial }r^2}\nonumber \\&+\frac{1}{r^2}\left( \frac{\partial ^2}{\mathrm {\partial }\theta ^2} + \frac{1}{\sin ^2\theta } \frac{\partial ^2}{\mathrm {\partial }\varphi ^2}\right) \nonumber \\&-\omega (r)e^{-2\Phi (r)}_\mathrm {int} \frac{\partial ^2}{\mathrm {\partial }t\mathrm {\partial }\varphi }, \end{aligned}$$

(37)

where

$$\begin{aligned} e^{-2\Phi (r)}_\mathrm {int}= \left( \frac{2}{\sqrt{1-\frac{2 r^2}{R^3}}-3 \sqrt{\frac{R-2}{R}}} \right) ^2 , \end{aligned}$$

(38)

while the external first-order metric is

$$\begin{aligned} \left( \frac{\partial }{\partial s}\right) ^{2}_{\mathrm {ext}}= & {} -\left( 1-\frac{2M}{r} \right) ^{-1} \frac{\partial ^2}{\mathrm {\partial }t^2}\nonumber \\&+\left( 1-\frac{2M}{r} \right) \frac{\partial ^2}{\mathrm {\partial }r^2} \frac{1}{r^2}\left( \frac{\partial ^2}{\mathrm {\partial }\theta ^2} + \frac{1}{\sin ^2\theta } \frac{\partial ^2}{\mathrm {\partial }\varphi ^2}\right) \nonumber \\&-\frac{2 J}{(r-2) r^2} {\mathrm {d}}t{\mathrm {d}}\varphi . \end{aligned}$$

(39)

It is very important that the $g^{t\phi }$ metric coefficient appears in a form independent of the latitudinal coordinate $\theta$ due to the applied first-order approximation. This fact enables separability of the equations for geodesic motion in the first-order Hartle–Thorne spacetimes of the type being considered here and substantially simplifies the discussion of the trapping effect of null geodesics, as we shall see later.

In the discussion of trapping, we use the fact that the ZAMO observers of the first-order Hartle–Thorne internal spacetime have the simple form of four velocity

$$\begin{aligned}&(U^{\mu })_{\mathrm {ZAMO}} = e^{-\Phi (r)}(1,0,0,\omega ),\nonumber \\&\quad (U_{\mu })_{\mathrm {ZAMO}} = e^{\Phi (r)}(-1,0,0,0) . \end{aligned}$$

(40)

Similarly, the LNRF tetrad of 1-forms takes the simple form

$$\begin{aligned}&e^{(t)}_{\mu } = e^{\Phi (r)}(1,0,0,0),\nonumber \\&e^{(r)}_{\mu } = e^{\Psi (r)}(0,1,0,0), \nonumber \\&e^{(\theta )}_{\mu } = r(0,0,1,0), \nonumber \\&e^{(\varphi )}_{\mu } = r\sin \theta (-\omega ,0,0,1), \end{aligned}$$

(41)

while the tetrad for a comoving frame in 1-forms also takes a simplified form

$$\begin{aligned}&\bar{e}^{(t)}_{\mu }= e^{\Phi (r)}(1,0,0,\bar{\omega }),\nonumber \\&\bar{e}^{(r)}_{\mu }= e^{\Psi (r)}(0,1,0,0),\nonumber \\&\bar{e}^{(\theta )}_{\mu }= r(0,0,1,0),\nonumber \\&\bar{e}^{(\varphi )}_{\mu }= r\sin \theta (-\Omega ,0,0,1). \end{aligned}$$

(42)

3.3 Null geodesics of first-order Hartle–Thorne spacetime

The Lagrangian governing test particle motion along geodesics in both the internal and external first-order Hartle–Thorne spacetimes can be written as [32]²

$$\begin{aligned} 2{\mathcal {L}}=g_{tt}\dot{t}^2+g_{rr}\dot{r}^2 +g_{\theta \theta }\dot{\theta }^2+g_{\varphi \varphi }\dot{\varphi }^2 +2g_{t\varphi }\dot{\varphi }\dot{t}. \end{aligned}$$

(43)

The metric functions (34) and (36) depend only on the radial and latitudinal coordinates, and so there are two Killing vector fields (time and axial) implying the existence of two constants of motion

$$\begin{aligned}&p_t=\frac{\partial {\mathcal {L}}}{\partial \dot{t}} =g_{tt}\dot{t}+g_{t\varphi }\dot{\varphi }=-E={\mathrm {constant}},\nonumber \\&p_{\varphi }=\frac{\partial {\mathcal {L}}}{\partial \dot{\varphi }} =g_{t\varphi }\dot{t}+g_{\varphi \varphi }\dot{\varphi }=\phi ={\mathrm {constant}}. \end{aligned}$$

(44)

These constants correspond to the energy and the axial component of the angular momentum of test particles, as measured by static observers at infinity.

The geodesic motion is governed by the Hamilton–Jacobi equation related to the metric tensor $g^{\mu \nu }$

$$\begin{aligned} 2\frac{\partial S}{\partial \tau }=g^{\mu \nu }\frac{\partial S}{\partial x^{\mu }}\frac{\partial S}{\partial x^{\nu }}, \end{aligned}$$

(45)

where S denotes Hamilton’s principal function, the so-called Action function. Assuming separability of variables, as enabled by the fact that $g^{t\phi }$ is independent of $\theta$, as mentioned above, we seek the principal function in the form

$$\begin{aligned} S=\frac{1}{2}\delta \tau - Et + \phi \varphi + S_r(r) + S_{\theta }(\theta ), \end{aligned}$$

(46)

where $p^{\mu }p_{\mu }=\delta$. After a little algebra and introducing a separation constant L serving as a motion constant related to the total angular momentum, the components of the particle four momentum can be expressed as follows

$$\begin{aligned}&p^r=g^{rr}p_r=g^{rr}\frac{{\mathrm {d}}S_r}{{\mathrm {d}}r}\nonumber \\&\quad =(2g^{t\varphi }g^{rr}E\phi +g^{rr}\delta -g^{tt}g^{rr}E^2 -Lg^{rr}g^{\theta \theta })^{1/2}, \end{aligned}$$

(47)

$$\begin{aligned}&p^{\theta }=g^{\theta \theta }p_{\theta } =g^{\theta \theta }\frac{{\mathrm {d}}S_{\theta }}{{\mathrm {d}}\theta } =g^{\theta \theta }\Bigg (L-\frac{\phi ^2}{\sin ^2\theta } \Bigg )^{1/2}, \end{aligned}$$

(48)

$$\begin{aligned}&p^{\varphi }=\frac{\phi g_{tt}+Eg_{t\varphi }}{g_{tt}g_{\varphi \varphi }-g_{t\varphi }^2},\end{aligned}$$

(49)

$$\begin{aligned}&p^{t}=\frac{\phi g_{t\varphi }+Eg_{\varphi \varphi }}{g_{t\varphi }^2-g_{tt}g_{\varphi \varphi }}. \end{aligned}$$

(50)

Motion along null geodesics corresponds to $\delta =0$. From now on we consider the components of the four-momentum as components of wave-vectors $k^{\mu }$ and $k_{\mu }$, as usual for null geodesics. The null geodesics (neutrino trajectories) are not dependent on the energy and so we can rescale the motion equations in terms of the energy to get new motion constants (impact parameters):

$$\begin{aligned} \lambda =\frac{\phi }{E}\quad \mathrm {and}\quad \mathcal {L}=\frac{L}{E^2}. \end{aligned}$$

(51)

The regions allowed for motion in the radial and latitudinal directions ($r-\theta$) are governed by the turning points, where $k^{r}=0$ or $k^{\theta }=0$. Using (51) in (47) and (48), we arrive at the effective potentials governing the radial and latitudinal motion in the form

$$\begin{aligned}&\mathcal {L}_{r}=2g^{t\varphi }g_{\theta \theta }\lambda -g^{tt}g_{\theta \theta }, \end{aligned}$$

(52)

$$\begin{aligned}&\mathcal {L}_{r}(r,\lambda )={\left\{ \begin{array}{ll} \frac{4 r^2\left( 1-2\omega \lambda \right) }{\left( \sqrt{1-\frac{2 r^2}{R^3}}-3 \sqrt{\frac{R-2}{R}}\right) ^2} &{}\text {for } r \le R\\ \frac{r^3-4J\lambda }{r-2} &{}\text {for } r>R \end{array}\right. } \end{aligned}$$

(53)

and

$$\begin{aligned} \mathcal {L}_{\theta }(\theta ,\lambda )=\frac{\lambda ^2}{\sin ^2\theta }. \end{aligned}$$

(54)

Note that the latitudinal effective potential is independent of the spacetime parameters, whereas the radial effective potential does depend on them, namely on the parameter J of the external spacetime, and on the parameter R/M and the angular velocity function $\bar{\omega }(r)$ of the internal spacetime.

Fig. 5

Restriction for the values of $\lambda$ and the function for $\lambda _c$ in the equatorial plane. The grey area indicates the allowed region for $\lambda$ with the boundaries given by $\lambda _+$ and $\lambda _-$. The bold solid line shows the values of $\lambda _c$ which marks the extremes of $\mathcal {L}$. The first column is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$. The first row is for $R/M=2.4$, the second is for $R/M=2.8$ and the last is for $R/M=3.2$

The reality conditions $k^{r} \ge 0$ and $k^{\theta } \ge 0$ imply restrictions on the impact parameter $\mathcal {L}$ in the form

$$\begin{aligned} \mathcal {L}_r(r,\lambda ) \ge \mathcal {L} \ge \mathcal {L}_{\theta }(\theta ,\lambda ). \end{aligned}$$

(55)

For the behavior of the null geodesics, the character of the effective potential $\mathcal {L}_{r}(r,\lambda )$ is crucial as its extremal points determine the circular null geodesics giving basic restrictions on the trapping effect. The local extrema of the effective potential $\mathcal {L}_{r}(r,\lambda )$ are given by the condition $d\mathcal {L}_{r}/dr=0$ that is fulfilled where $\lambda =\lambda _{c}(r)$. Using the relation (53), we arrive at the general formula

$$\begin{aligned} \lambda _{c}(r)=\frac{\frac{{\mathrm {d}}}{{\mathrm {d}}r}(g^{tt}g_{\theta \theta })}{\frac{{\mathrm {d}}}{{\mathrm {d}}r}(2g^{t\varphi }g_{\theta \theta })}. \end{aligned}$$

(56)

The function $\lambda _c(r)$ determines the locations of the stable circular null geodesics in the internal spacetime (at $r_{\mathrm {c(i)}}$), and of the unstable ones in the exterior (at $r_{\mathrm {c(e)}}$). In the external spacetime, this formula corresponds to minima (if they exist) of the radial effective potential and takes the form

$$\begin{aligned} \lambda _{c}(r,J)=-\frac{(r-3) r^2}{2J} , \end{aligned}$$

(57)

while in the internal spacetime it corresponds to the maxima (if they exist) and has the form

$$\begin{aligned} \lambda _{c}(r;R,\omega )=\frac{R^3 h}{r \left( h R^3 +2 r^2\right) \frac{{\mathrm {d}}\omega (r)}{{\mathrm {d}}r}+R^3 2 \omega (r) h}, \end{aligned}$$

(58)

where

$$\begin{aligned} h(r;R)=3 \sqrt{\frac{R-2}{R}} \sqrt{1-\frac{2 r^2}{R^3}}-1. \end{aligned}$$

(59)

The fundamental limiting condition on the relevance of the local extrema of the radial effective potential is given by the relation $\mathcal {L}_{r} \ge \mathcal {L}_{\theta }$. We thus obtain the limiting functions $\lambda _{r\pm }(r,\theta )$, given by the condition $\mathcal {L}_{r}=\mathcal {L}_{\theta }$, in the general form

$$\begin{aligned} \lambda _{r\pm }=\sin ^2{\theta }\Big ( g^{t\varphi }g_{\theta \theta } \pm \sqrt{(g^{t\varphi }g_{\theta \theta })^2-g^{tt}g_{\theta \theta }\csc ^2\theta } \Big ), \end{aligned}$$

(60)

that, for the internal spacetime, takes the form

$$\begin{aligned} \lambda _{r\pm }^{\mathrm {int}}= & {} \sin ^2\theta \left( -\frac{4 r^2 \omega (r) }{\left( \sqrt{1-\frac{2 r^2}{R^3}}-3 \sqrt{\frac{R-2}{R}}\right) ^2}\right. \nonumber \\&\left. \pm 2 \sqrt{\frac{r^2 \csc ^2\theta }{\left( \sqrt{1-\frac{2 r^2}{R^3}}-3 \sqrt{\frac{R-2}{R}}\right) ^2}}\right) , \end{aligned}$$

(61)

and, for the external spacetime, takes the form

$$\begin{aligned} \lambda _{r\pm }^{\mathrm {ext}}=\sin ^2\theta \left( -\frac{2 J}{r-2}\pm \sqrt{\frac{r^3 \csc ^2\theta }{r-2}} \right) . \end{aligned}$$

(62)

The radial effective function $\mathcal {L}_r$ is thus physically relevant in the regions determined by the condition

$$\begin{aligned} \lambda _{r-}(r,\theta ) \le \lambda \le \lambda _{r+}(r,\theta ). \end{aligned}$$

(63)

In the following discussion we usually consider the most extended region corresponding to the equatorial plane where $\sin \theta =1$. In Fig. 5 we demonstrate the situation corresponding to the trapping of the null geodesics, giving both the functions $\lambda _{r\pm }(r,\theta =\pi /2)$ and $\lambda _{c}(r)$ for a few characteristic values of the spacetime parameters, namely for different rotation rates given by j ($j=J/M^2$ – the dimensionless angular momentum) and for our three highlighted values of the inverse compactness of the object R/M (the compactness being defined as $C=M/R$, with R being measured here in the equatorial plane). The regions allowed for the motion with a fixed value of the impact parameter $\lambda$ are located between the curves given by Eq. (60) (grey area). The location of the extremal points of the radial effective potential, corresponding to the circular null geodesics, is given by the function $\lambda _{c}(r)$.

Note that the stable circular photon orbit for the most highly compact object with $R/M=2.4$ is situated in an almost constant position for most allowed values of $\lambda _c$, while the unstable circular photon orbit changes its position more significantly for allowed $\lambda _c$. We also point out the non-existence of circular photon orbits for low rotations and the less compact objects with $R/M=3.2$ – this is in line with expectations, because for non-rotating configurations with $R/M>3$, there are no circular null geodesics.

3.4 Effective potential of the radial motion

Now we discuss motion along the null geodesics in the radial direction demonstrating the behavior of the radial effective potential $\mathcal {L}_{r}(r)$ given by Eq. (52). In this subsection, we will use the terms $V_{eff}$ and $\mathcal {L}_{r}$ interchangeably. If the rotation is zero ($g^{t\varphi }=0$), Eq. (52) matches (8), the effective potential for the internal (and external) Schwarzschild spacetime.

Fig. 6

The effective potential $\mathcal {L}_r$ for allowed values of the parameter $\lambda$. In the shaded area, we find all possible effective potentials for the allowed values of lambda and $\theta = \pi / 2$. In the darker region, there are effective potentials with allowed values $\lambda$ and $\theta = \pi / 4$ or $3 \pi / 4$, and the curve in the middle of the dark region plots the effective potential as $\theta$ approaches the poles

Fig. 7

Effective potentials for objects with compactness $R/M=2.4$ for several values of j and $\theta$. The solid lines are effective potentials for non-rotating configurations. The dotted and dashed lines denote effective potentials for co-rotating and counter-rotating null geodesics ($\lambda =\lambda _+$ and $\lambda =\lambda _-$ respectively). The first column is for $\theta =\pi /2$, the second is for $\theta =\pi /4$ and the last is for $\theta =1/100$. The first row is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$

Fig. 8

Effective potentials for objects with compactness $R/M=2.8$ for several values of j and $\theta$. The solid lines are effective potentials for non-rotating configurations. The dotted and dashed lines denote effective potentials for co-rotating and counter-rotating null geodesics ($\lambda =\lambda _+$ and $\lambda =\lambda _-$ respectively). The first column is for $\theta =\pi /2$, the second is for $\theta =\pi /4$ and the last is for $\theta =1/100$. The first row is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$

Fig. 9

Effective potentials for objects with compactness $R/M=3.2$ for several values of j and $\theta$. The solid lines are effective potentials for non-rotating configurations. The dotted and dashed lines denote effective potentials for co-rotating and counter-rotating null geodesics ($\lambda =\lambda _+$ and $\lambda =\lambda _-$ respectively). The first column is for $\theta =\pi /2$, the second is for $\theta =\pi /4$ and the last is for $\theta =1/100$. The first row is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$

The effective potential in the first-order Hartle–Thorne spacetime depends on the parameter $\lambda$ that governs the motion in the axial direction. At a given radius r and latitude $\theta =\pi /2$ corresponding to the equatorial plane of the rotating object, the limiting values of $\lambda$ given by the functions $\lambda _{r\pm }(r,\theta =\pi /2)$ govern the maximally (exactly) co-rotating ($\lambda _{r+}(r,\theta =\pi /2)$) and maximally (exactly) counter-rotating ($\lambda _{r-}(r,\theta =\pi /2)$) null geodesics. The effective potentials for those impact parameters (directions) represent the boundary of the effective potentials corresponding to the null geodesics in all other directions with impact parameters $\lambda \in (\lambda _{r-}(r,\theta =\pi /2),\lambda _{r-}(r,\theta =\pi /2))$. If we consider latitudes $\theta \ne \pi /2$, the values of the limiting impact parameters $\lambda _{r\pm }(r,\theta )$ will be governed by the general Eq. (60), where we can observe the shifting factor $\sin ^2\theta$ related to the vanishing of the rotational effects on the rotation axis $\theta =0$, complexified by the additional term depending on the latitude – see Fig. 6.

The positions of the maximum and minimum of the effective potential $\mathcal {L}_{r}(r,\lambda )$, i.e., the positions $r_{\mathrm {c(i)}}$ and $r_{\mathrm {c(e)}}$, can be easily seen from the functions $\lambda _{c}(r)$ and from Fig. 5 (the maximum is always below the surface of the object and the minimum is always above it). Note that these extrema depend on the parameters characterizing the spacetime, but also on the impact parameter $\lambda$ (see Fig. 6), similarly to the values of the radii giving the limits of the trapping region: the radius governing motion fully constrained to the internal spacetime ($r_{\mathrm {c(i)}}$ that is the solution of the equation $\mathcal {L}_{r}(r,\lambda ) = \mathcal {L}_{r}(R,\lambda )$) and the radius allowing for motion in the external spacetime ($r_{\mathrm {c(e)}}$ that is the solution of $\mathcal {L}_{r}(r,\lambda ) = \mathcal {L}_r(r_{\mathrm {c(e)}},\lambda )$). These complexities have to be considered in calculating the coefficient characterizing the trapping effect globally for the whole of the first-order Hartle–Thorne spacetime.

The effective potentials related to the maximally co-rotating and maximally counter-rotating null geodesics (corresponding to the limiting values of the impact parameter $\lambda$) are given in Figs. 7, 8 and 9 for various values of the rotation rate represented by the parameter j, the spacetime inverse compactness R/M, and characteristic latitude $\theta$; their comparison with the non-rotating effective potential is also given. Note how the effective potential near the poles approaches the effective potential related to the non-rotating internal Schwarzschild spacetime due to the fact that $g_{t\varphi }$ goes to zero at the poles.³ We include also relatively high values of the rotational parameter j in order to stress and clearly illustrate the role of the rotation in the trapping effects. We can see that increasing rotation causes increase of trapping of counter-rotating null geodesics, while it decreases trapping of co-rotating null geodesics. This phenomenon is enhanced with increasing compactness.

The monotonicity of the effective potential in the internal Schwarzschild spacetimes with $R/M>3$ implies that rotating configurations with inverse compactness $R/M>3$ have a monotonic effective potential near the poles (independent of the rotation rate), see Fig. 9. In the same figure, we can also see that for inverse compactness $R/M=3.2$ and a small rotation rate there is no minimum and maximum of the effective potential, and there is no trapping of null geodesics as already mentioned in the discussion of Fig. 5. However, with high enough rotation parameter, $j > 0.3$, trapping of counter-rotating null geodesics is possible, but the co-rotating null geodesics cannot be trapped.

For the construction of the trapping cones (complementary escape cones) Fig. 10 is highly instructive and illustrative, as it demonstrates how the characteristic functions of $\lambda$ give the corresponding effective potentials $\mathcal {L}_r$ that enable determination in a given position characterized by coordinates $r,\theta$ of the range of values of the impact parameters $\lambda$ and $\mathcal {L}$ corresponding to the trapped (escaping) null geodesics.

Fig. 10

The left panel shows the restriction on the values of $\lambda$ and the function $\lambda _c$. The middle panel shows the effective potentials $\mathcal {L}_r$ and $\mathcal {L}_\theta$, and the minimum of $\mathcal {L}_r$; the right panel shows the allowed values of $\mathcal {L}$ with their dependence on $\lambda$ (shaded areas, with the trapped region being darker). All of the figures are for the specific case of null geodesics emitted from the equatorial plane at radius $r_0=1$ with $\lambda =-4$

4 Trapping cones in first-order Hartle–Thorne spacetime

In the internal Schwarzschild spherically symmetric spacetimes the trapping (escape) cones are centrally symmetric as they are dependent on a single impact parameter due to the symmetry; in the axially symmetric Hartle–Thorne internal spacetimes the symmetry is naturally broken. In the first-order Hartle–Thorne spacetimes they are dependent on two impact parameters.

Fig. 11

Escape cones for objects with compactness $R/M=2.4$ for several values of $\theta$ and j. The first column is for $\theta =\pi /2$, the second column is for $\theta =\pi /4$ and the last column is for $\theta =1/100$. The first row is for $j=0.1$, the second row is for $j=0.4$ and the last row is for $j=0.7$

Fig. 12

Escape cones for objects with compactness $R/M=2.8$ for several values of $\theta$ and j. The first column is for $\theta =\pi /2$, the second column is for $\theta =\pi /4$ and the last column is for $\theta =1/100$. The first row is for $j=0.1$, the second row is for $j=0.4$ and the last row is for $j=0.7$

Fig. 13

Escape cones for objects with compactness $R/M=3.2$ for several values of $\theta$ and j. The first column is for $\theta =\pi /2$, the second column is for $\theta =\pi /4$ and the last column is for $\theta =1/100$. The first row is for $j=0.1$, the second row is for $j=0.4$ and the last row is for $j=0.7$

4.1 Construction of trapping cones in the first-order Hartle–Thorne spacetime

The motion along the null geodesic is fully determined by the motion constants (impact parameters) $\lambda$ and $\mathcal {L}$ that can be related to any pair of the directional angles {$\alpha ,~\beta ,~\gamma$} defined as shown in Fig. 2. The relation between the tetrad components of the wave four-vector of the null geodesics and the directional angles related to the tetrad is

$$\begin{aligned}&k^{(t)}=-k_{(t)}=1, \end{aligned}$$

(64)

$$\begin{aligned}&k^{(r)}=k_{(r)}=\cos {\alpha },\end{aligned}$$

(65)

$$\begin{aligned}&k^{(\theta )}=k_{(\theta )}=\sin {\alpha }\cos {\beta },\end{aligned}$$

(66)

$$\begin{aligned}&k^{(\varphi )}=k_{(\varphi )}=\sin {\alpha }\sin {\beta }=\cos {\gamma }. \end{aligned}$$

(67)

The directional angle $\alpha$ is determined by the relation

$$\begin{aligned} \cos {\alpha }=\frac{k^{(r)}}{k^{(t)}} =\frac{e^{(r)}_{\mu }k^{\mu }}{e^{(t)}_{\mu }k^{\mu }}. \end{aligned}$$

(68)

Using Eq. (64) in Eq. (51), it turns out that the impact parameter $\lambda$ depends only on the angle $\gamma$

$$\begin{aligned} \lambda= & {} \frac{e_{\varphi }^{(\mu )}k_{(\mu )}}{-e_{t}^{(\mu )}k_{(\mu )}} =\frac{e_{\varphi }^{(t)}k_{(t)} +e_{\varphi }^{(\varphi )}k_{(\varphi )}}{-e_{t}^{(t)}k_{(t)}-e_{t}^{(\varphi )}k_{(\varphi )}}\nonumber \\= & {} \frac{-e_{\varphi }^{(t)}+e_{\varphi }^{(\varphi )}\cos {\gamma }}{e_{t}^{(t)}-e_{t}^{(\varphi )}\cos {\gamma }}. \end{aligned}$$

(69)

In determining the trapping (escaping) cones we strictly follow the method developed and applied in [27, 33, 34] where all details of our approach can be found. By setting $\gamma$ and a given point of the selected first-order Hartle–Thorne spacetime, characterized by coordinates ($r,\theta$), we can determine the impact parameter $\lambda$ and the related effective potential $\mathcal {L}_{r}(r,\lambda )$ giving limits on the impact parameter $\mathcal {L}$. To find out if a photon is trapped (or escapes to infinity) and thus construct the trapping (escape) cone, we have to know the minimum of $\mathcal {L}_r$ coming from d$\mathcal {L}_r/$dr=0. From the intersection of $\mathcal {L}(r_{\mathrm {c(e)}},\lambda )$ ($\mathcal {L}_r$ at the minimum) and $\mathcal {L}_\theta (\lambda )$ (which defines minimal allowed value of $\mathcal {L}$), we get a restriction on the values of $\lambda$ and thanks to Eq. (69) we automatically obtain the restriction on the directional angle $\gamma$. Generally allowed $\lambda$ values can be seen in the right-hand panel of Fig. 10 (grey areas).

The values of the directional angles $\gamma \in \langle \gamma _{min},\gamma _{max}\rangle$ are the cut-off values separating photons escaping to infinity and those trapped by gravity. Using Eq. (68), we get the limiting value of the directional angle $\alpha$ and subsequently from Eq. (64) also the limiting value of the directional angle $\beta$. The trapping cone is formed by plotting all of the limiting angles [$\alpha , \beta$]. Note that the region of co-rotating null geodesics contains the angle $\beta =\pi /2$, while the region of counter-rotating null geodesics contains $\beta =3\pi /2$; the separation line is given by the angles $\beta =0$ and $\beta =\pi$.

The resulting Figs. 11, 12 and 13 are presented for the same selection of the spacetime parameters and the latitudes of the cone position, with the radial coordinate being fixed at $r/M=1$ as in the case of the representative figures for the effective potentials. These figures clearly demonstrate the effects described above, especially the breaking of the central symmetry that increases with increasing values of R/M and, of course, it decreases with decreasing values of the latitudinal coordinate of the position of the trapping cone as the influence of rotation effects is weakened as the apex of the cone approaches the symmetry axis.

The profiles of the effective potentials (co-rotating and counter-rotating) with small rotation rates and $R/M=3.2$ imply that the trapping cone can exist only in a small region of counter-rotating null geodesics and only in spacetimes with a sufficiently high rotation parameter j.

5 Null geodesics trapped in the slowly rotating spacetime

Finally, we are able to study the trapping of neutrinos and the local and global trapping efficiency as they depend on the spacetime parameters and, in the case of the local trapping, also as they depend on the position of the radiation source. We always assume a locally isotropic source of the neutrinos following the null geodesics, as discussed in [8].

5.1 Local trapping

We vary $\theta$, j and R/M in the same way as in the presentation of the representative cases for the effective potential of null geodesic motion $\mathcal {L}_{r}(r,\lambda )$ and the trapping (escape) cones, and we give the radial profiles of the local trapping efficiency at fixed latitudinal coordinates of the compact object, considering the region allowing for the trapping. We follow the methodology introduced in [8], including the assumption of the isotropically radiating sources.

In order to reflect the local properties of the trapping effect we introduce a local trapping efficiency coefficient b, defined at a given point of the compact object determined by the coordinates $r,\theta$, as the ratio of the number of neutrinos emitted from this point and trapped by the object $N_b$ to the total number of neutrinos produced at this point $N_p$ (for details see [8]). Due to the isotropy of the radiation emitted by the local source, the local trapping coefficient is given by the ratio of the surface area of the trapping cone $S_{\mathrm {tr}}$ to the total area $S_\mathrm {tot}=4\pi$. Therefore,

$$\begin{aligned} b(r,\theta ;j,R)\equiv \frac{\mathrm {N_b(r)}}{\mathrm {N_p(r)}} = \frac{S_{\mathrm {tr}}}{4\pi }. \end{aligned}$$

(70)

We use this procedure for all radii r relevant for the trapping, i.e., $r \ge r_\mathrm {b(e)}$, see Fig. 1, where $r_\mathrm {b(e)}(\theta ,R/M,j)$ is the radius where the trapping begins. The resulting local trapping efficiency coefficient is presented in Figs. 14, 15 and 16. For comparison and better insight into the problem, we depict also the analytical solution obtained for the internal Schwarzschild spacetime in [8] (solid line). In order to clearly illustrate the role of the rotation of the object, we calculate separately the trapping coefficients for the co-rotating and counter-rotating neutrinos, thus splitting the coefficient b into two complementary parts denoted as $b_+$ and $b_-$; $b_+$ denotes the local trapping efficiency coefficient for co-rotating null geodesics represented by the right part of the trapping cones (the part containing $\beta =\pi /2$), while $b_-$ denotes the coefficient calculated for counter-rotating null geodesics corresponding to the left part of the trapping cones, containing the angle $\beta =3\pi /2$. We thus define

$$\begin{aligned} b_{+}(r,\theta ;j,R) = \frac{S_{\mathrm {tr}_+}}{2\pi } \text {, } b_{-}(r,\theta ;j,R) = \frac{S_{\mathrm {tr}_-}}{2\pi } . \end{aligned}$$

(71)

In our figures, $b_-$ tends to be located above the analytical function representing the case of the spherically symmetric spacetime (if it exists) and $b_+$ tends to be located below this function.

Fig. 14

The local trapping efficiency coefficient b for $R/M=2.4$ is plotted for several values of j and $\theta$. The solid line shows the local trapping for a non-rotating configuration and the dashed line shows local trapping for the rotating case. For the latter, the points above the dashed line are values for just counter-rotating directions of the null geodesics, and the points below it are those for co-rotating directions. The first column is for $\theta =\pi /2$, the second is for $\theta =\pi /4$ and the last is for $\theta =1/100$. The first row is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$

Fig. 15

The local trapping efficiency coefficient b for $R/M=2.8$ is plotted for several values of j and $\theta$. The solid line shows the local trapping for a non-rotating configuration and the dashed line shows local trapping for the rotating case. For the latter, the points above the dashed line are values for just counter-rotating directions of the null geodesics, and the points below it are those for co-rotating directions. The first column is for $\theta =\pi /2$, the second is for $\theta =\pi /4$ and the last is for $\theta =1/100$. The first row is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$

Fig. 16

The local trapping efficiency coefficient b for $R/M=3.2$ is plotted for several values of j and $\theta$. There is no trapping here for the non-rotating configuration and trapping only for counter-rotating directions in the rotating case. The local trapping for the rotating case is again shown with the dashed lines and the points above them show results for just the counter-rotating directions of the null geodesics (giving twice the values for the dashed curves). The first column is for $\theta =\pi /2$, the second is for $\theta =\pi /4$ and the last is for $\theta =1/100$. The first row is for $j=0.1$, the second is for $j=0.4$ and the last is for $j=0.7$

We can see that generally the local trapping in the rotating Hartle–Thorne spacetime is lower than that for the internal Schwarzschild spacetimes, with the exception of the deepest regions of the trapping that usually reach smaller radii in the rotating spacetimes (especially for the counter-rotating null geodesics). The extension of the trapping region in the rotating spacetimes, in comparison with the related internal Schwarzschild spacetime increases with increasing parameter R/M. As expected, in the first-order Hartle–Thorne spacetimes with $R/M > 3$, the trapping effect can be relevant only for the counter-rotating null geodesics, and we observe the trapping only for sufficiently high rotation parameters, $j > 0.2$.

5.2 Global trapping

The coefficient of global trapping reflects the trapping phenomenon integrated across the whole trapping region, related to the whole radiating object. We thus consider the number of neutrinos radiated along null geodesics by the whole object in unit time for distant static observers, and determine the fraction of these radiated neutrinos that remain trapped by the radiating object. Details of the derivation of the global trapping coefficient are presented in [8], and we apply them here using again the basic assumption that the locally defined radiation intensity is proportional to the energy density of the matter of the object hence being distributed uniformly within all of the object.

The global trapping effects are then reflected by the global trapping efficiency coefficient $\mathcal {B}$ defined by the relation [8]

$$\begin{aligned} \mathcal {B}\equiv \frac{N_b}{N_p} =\frac{\int _{0}^{R}\int ^{\pi }_{0}\int ^{2\pi }_{0}f^{-1}(r) b(r) \, r^2 \, {\mathrm {d}}\varphi \,{\mathrm {d}}\theta \, {\mathrm {d}}r}{\int _{0}^{R}\int _{0}^{\pi }\int _{0}^{2\pi }f^{-1}(r) \, r^2 \, {\mathrm {d}}\varphi \,{\mathrm {d}}\theta \, {\mathrm {d}}r}, \end{aligned}$$

(72)

where we use the radial metric function f(r) defined in Eq. (29).

However, we can simplify the integration process due to the symmetries of the first-order Hartle–Thorne spacetime. The metric coefficients are independent of $\varphi$, and the results of the integration in the upper and lower hemispheres are the same. Also, limits in the radial direction can be shrunk by using knowledge of the position of $r_\mathrm {b(e)}(r,\theta ;R,J,\lambda )$ determining the limits of integration of the trapping effect. The global trapping efficiency coefficient can then be presented in the form

$$\begin{aligned} \mathcal {B}=\frac{\int _{r_{\mathrm {b(i)}}}^{R}\int ^{\pi /2}_{0} f^{-1}(r)b(r) \, r^2 \, {\mathrm {d}}\theta \, {\mathrm {d}}r}{\int _{0}^{R}\int _{0}^{\pi /2}f^{-1}(r) \, r^2 \, {\mathrm {d}}\theta \, {\mathrm {d}}r}. \end{aligned}$$

(73)

Figures 17 and 18 show how the global trapping efficiency coefficient $\mathcal {B}$ depends on the rotation parameter j for fixed characteristic values of the inverse compactness R/M of the object⁴ [35].

Note that for the lowest value of the inverse compactness parameter, namely $R/M=2.4$, the global efficiency parameter $\mathcal {B}(j)$ decreases monotonically with increasing j, while for the middle value, $R/M=2.8$, we observe a decrease of $\mathcal {B}$ up to $j \sim 0.2$ and then a rapid increase for $j>0.2$. For the largest value, $R/M=3.2$, where trapping is impossible in the non-rotating internal Schwarzschild spacetimes, the trapping effect occurs at $j \sim 0.25$ and increases with increasing rotation parameter j, but exclusively for the counter-rotating null geodesics. Nevertheless, we have to say that detailed calculations in the second-order Hartle–Thorne geometry would be necessary in order to obtain a realistic description of the trapping phenomenon for rotation parameters larger than the limit of $j = 0.1$ up to which using the first-order treatment seems to be fully justified.

Fig. 17

The global trapping efficiency coefficient $\mathcal {B}$ for $R/M=2.4$ is shown in the top left panel, with that for $R/M=2.8$ in the top right panel and that for $R/M=3.2$ in the panel below

6 Conclusions

In this introductory study of the role of rotation for the phenomenon of trapping of null geodesics that could be relevant for the motion of neutrinos in the interior of neutron stars, we have used the strongest simplification of taking the first-order Hartle–Thorne spacetime with a uniformly distributed energy density for the matter, in order to obtain simple and easily tractable results. We believe that even such a simplification enables one to find the basic characteristics of the influence of the rotation of radiating compact objects on the effect of trapping in their interior. For these purposes we have considered also values of the dimensionless rotation parameter j exceeding those safe for ensuring the applicability of the first-order approximation (j no larger than around 0.2). Nevertheless, we expect that the results obtained for values of $j > 0.2$ could indicate relevant signatures of realistic effects.

Our results related to the local effects indicate a much stronger trapping coefficient for the counter-rotating null geodesics than for the co-rotating ones and even for the internal Schwarzschild spacetimes with the same parameter R/M. In the rotating Hartle–Thorne spacetimes the region of trapping is always larger than in the related non-rotating internal Schwarzschild spacetimes having the same parameter R/M, and this difference increases with increasing R/M.

Trapping of counter-rotating null geodesics has been found even for $R/M>3$, i.e., for values where trapping does not occur in the internal Schwarzschild spacetimes. It has been shown to be relevant even for objects with $R/M=3.2$, but only for rotation parameters starting at $j \sim 0.25$ for which the validity of using the first-order form of the Hartle–Thorne metric is not secure. Therefore, more detailed models based on the second-order Hartle–Thorne geometry are necessary in order to confirm the possibility of surpassing the limit for trapping effects at the radius $R=3M$, and to follow the occurrence of the trapping for values of the rotation parameter $j\sim 0.2$, where some relevance of the first-order approximation is expected, up to the limiting value of $j\sim 0.5$ appropriate for when the second-order Hartle–Thorne metric is used [35].

Fig. 18

The comparison of the global trapping efficiency coefficients $\mathcal {B}$ from Fig. 17 with the curves being shown together with the same vertical scale

Our study is related to the models of very compact neutron stars (or quark stars) as we are limiting ourselves to internal spacetimes with $R/M\le 3.2$. Surprisingly, it has recently been shown that trapping polytropic spheres can exist with very large extension $R\gg r_g$ – such structures can model dark matter halos related even to galaxy clusters.⁵ The trapping polytropes can exist for polytropic index $n>2.2$ as shown and discussed in [20, 36,37,38,39]. The trapping polytropes with $n>3.3$ can be extended to large radius ($R\sim 100$ kpc) and large mass ($M\sim 10^{12}M_\odot$) corresponding to the extension and mass of large galaxies, while the extension of the trapping zone $R_\mathrm {tr}$ is of order $r_g$, and its mass $M_\mathrm {tr}=M(R_\mathrm {tr})$ is of order $10^9M_\odot$; then gravitational instability of the trapping zone might induce its gravitational collapse and creation of a supermassive black hole having $M\sim 10^9M_\odot$, thus giving a natural explanation for the supermassive black holes observed in quasars at cosmological redshifts $z\ge 6$ (for details see [21]).⁶

Generalization of such spherical trapping polytropes to spacetimes with rotation considered to the first-order level could be of high interest in the framework of models of dark matter halos. This is going to be the scope of further studies.