1 Introduction

The Heisenberg Uncertainty Principle (HUP) plays a crucial rôle within the framework of quantum mechanics (QM) and can be considered as the cornerstone of the theory which successfully describes systems at microscopic level and relatively short distances. On the other hand, general relativity (GR) – the best theory yet of the gravitational interaction – avails of classical laws to explain the physics of macroscopic bodies and large distance scales. These two very different theories manage to share centre stage by keeping clear of each other. Indeed, while quantum mechanical effects are typically negligible when dealing with gravitational phenomena, gravity becomes inconsequential in the quantum realm. In spite of these tensions, it is expected that GR and QM domains have a non-vanishing intersection, and the formulation of a unified theory is by far the greatest challenge in theoretical physics nowadays.

Among the various attempts to incorporate gravity in the quantum world, the quantum field theory in curved space has yielded great development in recent years. In particular, this has been achieved through the prediction of the Hawking [1] and Unruh [2] effects, which emerge from the information loss associated to the appearance of event horizons – the black-hole horizon in the former case, the Rindler ( i.e., uniformly accelerated) horizon in the latter. These two effects are now widely accepted, but concerns about their detectability are still being expressed [3, 4]. Likewise, another fertile arena to explore the interplay between quantum and gravity features is provided by the Generalized Uncertainty Principle (GUP), which accounts for the existence of a minimal length at Planck scale through a suitable modification of the HUP [5,6,7,8,9,10,11]. Duality in phase space have also suggested another extension of the uncertainty relation that should hold on a background with a maximal measurable length. This is known as Extended Uncertainty Principle (EUP) [12,13,14]. However, due to the lack of experimental guidance, physics at the border between GR and QM is largely heuristic and speculative. Therefore, most of the above conjectures should be either tested via in-the-lab analogues [15,16,17] or studied in connection with related phenomena.

In this vein, in Refs. [18, 19] the Unruh effect has been proposed to explain the origin of the inertial mass of bodies. In these works it is predicted that, when objects accelerate in one direction, a Rindler horizon forms on the opposite side, reducing the Unruh radiation by an asymmetric (Rindler-scale) Casimir effect. Hence, more pressure will hit the object coming from the front than from the rear, and this gives rise to a net force which opposes the acceleration, just like inertia. Because of its quantum origin, this model is named quantized inertia (QI). Nevertheless, the implementation of this idea is not given and a priori it seems difficult to find the inertial mass (a constant property of any body) for any value of the acceleration. In fact, only a modification of the inertia is obtained in these works. For the case of a particle of Planck mass, an approximation has been addressed in Ref. [20].

An inherent feature of QI is that, in low acceleration environments (for instance, at the edges of galaxies), the Unruh waves lengthen and are also damped by the cosmic horizon, this time equally in all directions (Hubble-scale Casimir effect) [18]. As a result, the effective mass \(m_I\) of a body should be modified as

$$\begin{aligned} m_I\,=\,m\left( 1-\frac{2c^2}{a\varTheta }\right) , \end{aligned}$$
(1)

where c is the speed of light, a is the magnitude of the acceleration relative to the surrounding matter and \(\varTheta =2R_{\mathrm {U}}\) is twice the cosmic radius \(R_{\mathrm {U}}\). Clearly, for relatively large accelerations (for example equal or greater than Earth’s gravity), the second term in the brackets becomes negligible and the standard inertia is recovered. On the other hand, the minimal value of the acceleration predicted by QI is \(a=2c^2/\varTheta \) [18], which does not allow \(m_I\) to become negative. Recently, a more refined derivation of Eq. (1) has been proposed in Refs. [21, 22] by assuming that the property of inertia is caused by gradients in the energy of the photons of Unruh radiation. In spite of some criticism (see Ref. [23]), QI has been claimed to explain galaxy rotation and cosmic acceleration without invoking dark matter and dark energy, respectively [18, 24, 25].

Starting from the outlined picture, in this paper we provide a novel perspective on the phenomenon (1), showing that it arises from the accelerated expansion of the Universe. In this sense, it can be naturally derived within the framework of the Extended Uncertainty Principle in de Sitter spacetime, where the correction to the standard inertia is found to be related to the background cosmic acceleration and, thus, to the cosmological constant value. By analogy with QI, we shall refer to our model as Modified Inertia. For the sake of completeness, we also consider an alternative generalization of the uncertainty relation, corresponding to a different deformation of the HUP. Our results are then compared with the empirical interpolating functions used in Modified Newtonian Dynamics (MoND) [26, 27]. By requiring consistency between the two approaches, we manage to fix the arbitrary MoND constant, which turns out to be equal to the cosmic acceleration.

The remainder of the work is structured as follows: in Sect. 2 we review the derivation of Eq. (1) presented in Ref. [22] with some improvements and conceptual discussions. The same analysis is extended to the framework of the EUP(s) in Sect. 3. Conclusions and future perspectives are summarized in Sect. 4. The work is completed with an Appendix containing details about the connection between a given background metric and the corresponding form of the EUP.

2 Quantized inertia from HUP

In Refs. [21, 22] QI was derived by assuming that the inertia of accelerated bodies is caused by the gradient in the energy of Unruh radiation perceived as a result of their motionFootnote 1 (we remark that vanishing acceleration is forbidden by QI model). In turn, this energy was estimated by means of the HUP

$$\begin{aligned} \varDelta x\varDelta p\, \sim \, \frac{\hbar }{2}\,\,\Longrightarrow \,\,\varDelta x\varDelta E_p \,\sim \, \frac{\hbar c}{2}, \end{aligned}$$
(2)

where \(E_p=pc\) is the energy of the photons from Unruh radiation.

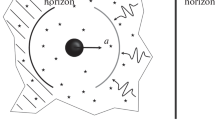
With reference to Fig. 1, let us consider an accelerated body of mass m moving rightwards along the x-axis and denote by a the modulus of its acceleration.Footnote 2 From ordinary considerations of relativistic kinematics, one can infer that a Rindler horizon will appear in the opposite direction to the acceleration, at a distance \(d=c^2/a\) far away from the body. On the other side, a specular rôle is played by the cosmic horizon at a far greater distance \(\varTheta /2\gg d\).

Fig. 1
figure 1

Schematic representation of quantized inertia: a body (black dot) moving rightwards with acceleration a perceives the cosmic horizon far away to its right (at a distance \(\varTheta /2\)) and a closer Rindler horizon to its left (at a distance \(c^2/a\)). Clearly, all the fluctuations originating within a distance \(c^2/a\) on the right side are compensated by the symmetric action of fluctuations in the opposite region. By contrast, photons coming from the strip between the dashed line and the cosmic horizon on the right do not experience any balance. This horizon-scale Casimir effect produces a net force which opposes the acceleration, just like inertia

Full size image

Now, it is well known that the quantum vacuum is filled up with virtual particle-antiparticle pairs randomly popping into existence and disappearing again. Clearly, if one of these fluctuations appears behind the Rindler horizon on the left side, it will never be able to reach the accelerating body. As a consequence, all the quantum fluctuations coming from the strip between the equivalent Rindler horizon (dashed line) and the cosmic horizon on the right side are not balanced by photons in the opposite region, giving rise to an asymmetric Casimir effect (see Fig. 1).

We wonder what is the temperature of this unbalanced radiation. To answer this question, let us observe that fluctuations of Unruh radiation, which come from a distance of the order of Rindler horizon, satisfy

$$\begin{aligned} \varDelta E_{\mathrm {U}}\,\sim \,\frac{\hbar a}{2\pi c}=\,K_BT_{\mathrm {U}}, \end{aligned}$$
(3)

where \(K_B\) is the Boltzmann constant and \(T_{\mathrm {U}}\) is the well-known Unruh temperature [2]

$$\begin{aligned} T_{\mathrm {U}}=\frac{\hbar a}{2\pi c K_B}. \end{aligned}$$
(4)

This relation can be easily obtained by using the HUP (2) and setting \(\varDelta x\sim \pi c^2/a\), where we are assuming a form of half circumference for the Rindler horizon as in Ref. [33]. Furthermore, since a quantum fluctuation is the temporary appearance of a particle-antiparticle pair, we can write \(\varDelta E_{\mathrm {U}}\sim 2 E_{\mathrm {U}}\), with \(E_{\mathrm {U}}\) being the energy of each particle of the pair. Equation (3) then gives

$$\begin{aligned} E_{\mathrm {U}}\sim \frac{K_BT_{\mathrm {U}}}{2}. \end{aligned}$$
(5)

The Unruh temperature is the consequence of the Unruh effect due to the quantum fluctuations near the horizon. However, this is a negligible phenomenon in the present analysis, since photons of the unbalanced radiation originate at distances greater than \(\pi c^2/a\), as discussed above. Clearly, for such particles we have

$$\begin{aligned} \varDelta x\, > rsim \, \frac{\pi c^2}{a}\,\,\Longrightarrow \,\, T\,\lesssim \,T_\mathrm {U}, \end{aligned}$$
(6)

which states that the temperature T of the unbalanced radiation is at most given by the Unruh temperature \(T_\mathrm {U}\). Another different feature between the Unruh and unbalanced radiations is that, while the former is a very tiny effect which can only be detected by an observer comoving with the accelerating body, any inertial observer and everywhere in the space can observe the unbalance between photons coming from the front and the back of the body (the only requirement is that the body has a non-vanishing acceleration relative to its surroundings). Moreover, these photons are expected to produce macroscopic effects on the body, in the same way as vacuum fluctuations manifest themselves through an observable attractive force in the conventional Casimir effect.

Now, the idea proposed by McCulloch [18, 19] is that the asymmetric damping of quantum waves described above would be responsible for QI. Indeed, the unbalanced radiation originated by the appearance of Rindler and cosmic horizons exerts a non-vanishing pressure on the body, giving rise to a net force that pushes it back against its acceleration (see Fig. 1). In turn, such an effect can be rephrased in terms of a modification of the inertial mass of the body, which can be quantified by using the HUP and noticing that the energy uncertainty of fluctuations which impact on the body is

$$\begin{aligned} \varDelta E_p\,\sim \, \frac{\hslash c}{2}\left( \frac{1}{\varDelta x_2}-\frac{1}{\varDelta x_1}\right) , \end{aligned}$$
(7)

where \(\varDelta x_1\) and \(\varDelta x_2\) are the position uncertainties related to the cosmic and Rindler horizons, respectively. Based on the above considerations, we set \(\varDelta x_1\) equal to the half circumference of radius \(R_\mathrm {U}\), i.e., \(\varDelta x_1\sim \pi R_\mathrm {U}=\pi \varTheta /2\), while \(\varDelta x_2\sim \pi d=\pi c^2/a\) as before.Footnote 3 A straightforward substitution into Eq. (7) leads to

$$\begin{aligned} \varDelta E_p\,\sim \, \frac{\hslash a}{2\pi c}\left( 1-\frac{2c^2}{a\varTheta }\right) \,=\, K_B T_{\mathrm {U}}\left( 1-\frac{2c^2}{a\varTheta }\right) , \end{aligned}$$
(8)

which can be expressed in terms of the energy \(E_p=\varDelta E_p/2\) of each particle of the pairs belonging to the unbalanced radiation as

$$\begin{aligned} E_p\,\sim \,E_{\mathrm {U}}\left( 1-\frac{2c^2}{a\varTheta }\right) . \end{aligned}$$
(9)

Now, let \(E_m\sim mc^2\) be approximately the energy of the accelerating body. Here we adopt a corpuscular-like picture for the electromagnetic force [34] akin to the description of gravity proposed in Refs. [35, 36]. Thus, we consider the body as a Bose-Einstein condensate of N photons, which can be interpreted as the resonant parts that interact with the external radiation. Following Ref. [22], we then express N as either the number of photons of Unruh radiation equivalent to the energy \(E_m\) (since the standard mass-energy of the body is mostly determined by fluctuations coming from the Rindler horizon when QI effects are negligbile) or the number of photons of the unbalanced radiation equivalent to the reduced energy \(E'_m\sim m_I c^2\) (given that the modified inertia \(m_I <m\) is due to the fluctuations of the unbalanced radiation in the QI regime). Mathematically speaking, we have \(N=E_m/E_{\mathrm {U}}=E'_m/E_p\).

The above reasoning allows us to get the desired result. Indeed, by multiplying both sides of Eq. (9) by \(N/c^2\), it follows that

$$\begin{aligned} m_I\,\sim \,{m}\left( 1-\frac{2c^2}{a\varTheta }\right) , \end{aligned}$$
(10)

which is the same expression as Eq. (1). Note that, for \(a\rightarrow 2c^2/\varTheta \), the modified inertia \(m_I\) approaches to zero. By referring to the picture described above, this amounts to the physical setting where the Rindler and cosmic horizons emerge approximately at the same distance from the accelerating body. In this case the Unruh wavelengths will be damped in a symmetric way from both the front and the rear of the body, thus leading to an isotropic radiation pressure which cancels the effects of modified inertia.

Now, it is worth noting that Eq. (10) is consistent with the prediction of Modified Newtonian Dynamics (MoND) [26, 27], which has been empirically derived from galaxy rotation data. Indeed, according to the MoND model with the simple interpolating function expanded to the leading order, Newton’s second law of dynamics should be modified as follows

$$\begin{aligned} F_0&= m\left( 1+\frac{a_0}{a}\right) ^{-1}a\\ \nonumber&\approx m\left[ 1-\frac{a_0}{a}+{\mathscr {O}}\left( \frac{a_0}{a}\right) ^2\right] a, \end{aligned}$$
(11)

which can be interpreted in terms of a modification of the inertial mass as

$$\begin{aligned} m_i\,=\,m\left[ 1-\frac{a_0}{a}+{\mathscr {O}}\left( \frac{a_0}{a}\right) ^2\right] . \end{aligned}$$
(12)

Clearly, the agreement between Eqs. (10) and (12) is obtained, provided that the adjustable constant \(a_0\) which marks the transition between the Newtonian and deep-MoND regimes is set equal to \(2c^2/\varTheta \). Hence, the advantage of Modified Inertia is that it predicts corrections to the inertial mass without needing any arbitrary constant.

We also emphasize that the interpolating function is not uniquely fixed by MoND hypothesis, even though it can be partially constrained on empirical basis [37, 38]. Apart from the model (11), another setting commonly found in literature is the so-called standard interpolating function

$$\begin{aligned} F_0&=m\left[ 1+\left( \frac{a_0}{a}\right) ^2\right] ^{-1/2}a\nonumber \\&\approx \, m\left[ 1-\frac{1}{2}\left( \frac{a_0}{a}\right) ^2+{\mathscr {O}} \left( \frac{a_0}{a}\right) ^4\right] a, \end{aligned}$$
(13)

which entails the modified inertia

$$\begin{aligned} m_i\,=\,m\left[ 1-\frac{1}{2}\left( \frac{a_0}{a}\right) ^2 +{\mathscr {O}}\left( \frac{a_0}{a}\right) ^4\right] . \end{aligned}$$
(14)

This differs from the expression in Eq. (12) as for the absence of the linear correction in \(a_0/a\).

In the next section we show how Eqs. (12) and (14) can be straightforwardly derived from proper deformations of the HUP existing in literature.

3 Quantized inertia from EUP(s)

Since a couple of decades, experimental data from supernovae, galaxy clusters and baryon acoustic oscillations have confirmed that our Universe is currently expanding at an accelerated rate. According to the models of inflation and observational evidences, there is quite general agreement that de Sitter spacetime is the most fitting candidate to describe our Universe in its early expanding phase and its far future.

Based on the above picture, we show that the modification in Eq. (14) can be naturally explained in the context of quantum mechanics in de Sitter spacetime, where it arises from the emergence of a characteristic length scale of the order of de Sitter radius. As a further model of modified inertia, we also comment on the possibility to trace Eq. (12) back to some suitable generalization of the uncertainty relation.

3.1 Case I

It has been argued that in the (anti)-de Sitter background, the HUP in Eq. (2) should be modified by introducing a correction proportional to the cosmological constant \(|\varLambda |\sim 1/l_H^2\) [12], i.e.,

$$\begin{aligned} \varDelta x\varDelta p\,\sim \, \frac{\hslash }{2}\left[ 1+\frac{\gamma }{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] . \end{aligned}$$
(15)

Here \(l_H\) is the (anti)-de Sitter radius and \(\gamma \) the (dimensionless) deformation parameter, which is usually taken of order unity so that the extra term only becomes relevant at cosmological scales. In the following, we assume \(\gamma <0\) (\(\gamma >0\)) for de Sitter (anti-de Sitter) spacetime.Footnote 4 Clearly, for \(\gamma =0\) and/or \(\varDelta x/l_H\ll 1\), the Heisenberg uncertainty relation (2) is recovered.

The uncertainty relation (15) is usually referred to as Extended Uncertainty Principle (EUP) [13, 14] by analogy with the Generalized Uncertainty Principle (GUP) [5,6,7,8,9,10,11], which is expected to hold at Planck (rather than cosmological) scales [39,40,41,42,43,44,45,46,47,48]. Phenomenological implications of the EUP have been considered in a variety of contexts, ranging from black hole physics [13, 49,50,51,52], to the thermodynamics of the FRW universe [49], the Unruh effect [52] and the Duffin-Kemmer-Petiau oscillator [53]. From a more theoretical perspective, the EUP has been investigated in Ref. [54], where it has been derived on the basis of first principles.

In order to show how the EUP (15) affects the inertia of an accelerating body, let us retrace the same steps as in Sect. 2. For this purpose, by using \(E_p=pc\) for the photons of the unbalanced radiation, we get

$$\begin{aligned} \varDelta x\varDelta E_p\,\sim \, \frac{\hslash c}{2}\left[ 1+\frac{\gamma }{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] . \end{aligned}$$
(16)

As discussed above, if the body moves with acceleration a, then it will perceive a Rindler horizon at a distance \(d=c^2/a<l_H\). The uncertainty of the crossing point of this horizon determines the uncertainty in the position of photons, which is still given by \(\varDelta x\sim \pi c^2/a\). Notably, this is the only scale we have to consider as a physical input in the present analysis.

From Eq. (16), the energy uncertainty of fluctuations of the environment radiation takes the form

$$\begin{aligned} \varDelta E_p\,\sim \, K_B T_{\mathrm {U}}\left[ 1+\frac{\gamma }{2}\left( \frac{\pi c^2}{l_Ha}\right) ^2\right] , \end{aligned}$$
(17)

which can be recast in terms of the energy \(E_p\) of the single particle of each virtual pair as

$$\begin{aligned} E_p\,\sim \, E_{\mathrm {U}}\left[ 1+\frac{\gamma }{2}\left( \frac{\pi c^2}{l_Ha}\right) ^2\right] . \end{aligned}$$
(18)

The above equation allows us to estimate the EUP-induced modification of the inertial mass of the body. Indeed, by introducing the number N of resonant parts of the body and following the same considerations leading to Eq. (10), we obtain

$$\begin{aligned} m_I\,\sim \,m\left[ 1+\frac{\gamma }{2}\left( \frac{\pi c^2}{l_Ha}\right) ^2\right] . \end{aligned}$$
(19)

At this stage, let us introduce the background cosmic acceleration \(a_H=c^2/l_H\). Then, Eq. (19) takes the form

$$\begin{aligned} m_I\,\sim \,m\left[ 1+\frac{\gamma \pi ^2}{2}\left( \frac{a_H}{a}\right) ^2\right] . \end{aligned}$$
(20)

For \(\gamma =0\) and/or \(a\gg a_H\), the standard inertia is recovered, consistently with the fact that the EUP in Eq. (15) reduces to the usual HUP (2) in these limits.

It is now easy to see that the Modified Inertia (20) has the same behavior as MoND prediction with the standard interpolating function, Eq. (14), provided that the condition

$$\begin{aligned} \gamma \,=\,-\frac{1}{\pi ^2} \end{aligned}$$
(21)

is satisfied. The negative value of the deformation parameter implies that MoND complies with the formulation of the EUP in de Sitter (rather than anti-de Sitter) spacetime, where a positive value of the cosmological constant yields an accelerated Universe expansion. Furthermore, the requirement of consistency between Eqs. (14) and (20) allows us to fix the MoND arbitrary constant \(a_0\) equal to the background cosmic acceleration \(a_H\). Therefore, in our model, Modified Inertia at cosmological scales is ascribed to the accelerating expansion of the Universe. This explains why such an effect is actually negligible in size for local (i.e., large acceleration environments) phenomena, for which \(a\gg a_H\).

Let us now observe that Eq. (19) can be equivalently expressed as

$$\begin{aligned} m_I\,\sim \, m\left( 1-\frac{1}{2}\frac{c^4\varLambda }{a^2}\right) , \end{aligned}$$
(22)

which connects the mass correction to the value of the cosmological constant. Clearly, by use of this relation, one may constrain Modified Inertia by exploiting the current bound on the cosmological constant, that is \(\varLambda \sim 10^{-52}\mathrm {m^{-2}}\). For instance, for typical terrestrial acceleration \(a\sim 10 \mathrm {m/s^2}\), we have

$$\begin{aligned} \left| \frac{m_I - m}{m}\right| \,\sim \ {\mathscr {O}}\left( 10^{-21}\right) , \end{aligned}$$
(23)

that is below the current experimental sensitivity, as expected. However, in environments with much smaller values of the acceleration, (for example at the edges of galaxies or in dwarf galaxies), this bound can be largely improved. For instance, for \(a\sim 10^{-9} \mathrm {m/s^2}\), it follows that

$$\begin{aligned} \left| \frac{m_I - m}{m}\right| \sim {\mathscr {O}}\left( 10^{-1}\right) , \end{aligned}$$
(24)

which in principle may be tested through future high-precision measurements.

Now, an alternative way to derive Eq. (20) can be obtained by directly modelling the interaction between the unbalanced radiation and the test-body. In this regard, let us consider a quantum fluctiation of the unbalanced radiation. From Eq. (16), the energy of each photon of the pair can be estimated as

$$\begin{aligned} E_p\,\sim \,\frac{\hslash c}{4\varDelta x}\left[ 1+\frac{\gamma }{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] . \end{aligned}$$
(25)

The above relation provides us with the value of the energy the photons transmit when impinging on the accelerating body. If the number of transmitted photons is N, then the total absorbed energy is

$$\begin{aligned} E_T\,\sim \,\frac{N\hslash c}{4\varDelta x}\left[ 1+\frac{\gamma }{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] . \end{aligned}$$
(26)

This energy yields a variation of the momentum of the body. In particular, the total transferred momentum is \(p_T=E_T/c\). This transfer of momentum occurs via the exertion of a force

$$\begin{aligned} ma\,=\,F\,=\,-\frac{\partial E_T}{\partial (\varDelta x)}. \end{aligned}$$
(27)

By use of Eq. (26), this becomes

$$\begin{aligned} ma\,\sim \, F_0\left[ 1-\frac{\gamma }{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] , \end{aligned}$$
(28)

where

$$\begin{aligned} F_0\,=\,\frac{N\hslash c}{4 (\varDelta x)^2} \end{aligned}$$
(29)

is the radiation force acting on the body when EUP effects are neglected (i.e., for \(\gamma =0\)). Note that, in the present derivation, the arbitrary number N of photons can be fixed by approximating the unbalanced radiation to a black-body radiation at temperature \(T\lesssim T_\mathrm {U}\) (see Eq. (6)), and equating \(F_0\) to the force exerted by such a radiation.

Equation (27) can be further manipulated by setting \(\varDelta x\sim \pi c^2/a\) and \(l_H=c^2/a_H\), as above. To the lowest order, we then obtain

$$\begin{aligned} ma&\sim \, F_0\left[ 1-\frac{\gamma \pi ^2}{2}\left( \frac{a_H}{a} \right) ^2\right] \end{aligned}$$
(30)
$$\begin{aligned}&\Longrightarrow F_0\,\sim \, m \left[ 1+\frac{\gamma \pi ^2}{2}\left( \frac{a_H}{a}\right) ^2\right] a . \end{aligned}$$
(31)

As remarked in Eq. (14), the above correction can be reinterpreted in terms of a modification induced on the inertia of body as

$$\begin{aligned} m_I\,=\,m\left[ 1+\frac{\gamma \pi ^2}{2}\left( \frac{a_H}{a}\right) ^2\right] , \end{aligned}$$
(32)

consistently with Eq. (20).

3.2 Case II

The extension of the HUP in Eq. (15) is not unique in literature. For instance, we can consider a modified uncertainty relation containing both linear and quadratic terms in \(\varDelta x/l_H\) (see Eq. (A.8) in the Appendix)

$$\begin{aligned} \varDelta x \varDelta p\,\sim \,\frac{\hslash }{2}\left[ 1-\frac{\alpha }{2}\frac{\varDelta x}{l_H}+\frac{3\alpha ^2}{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] , \end{aligned}$$
(33)

where \(\alpha >0\) is the deformation parameter defined as in Eq. (A.5). We remark that a similar EUP has been analyzed in Ref. [54].

Following the same reasoning as in the previous analysis, we apply Eq. (33) to the photons of the unbalanced radiation, yielding

$$\begin{aligned}&\varDelta x \varDelta E_p\,\sim \,\frac{\hslash c}{2}\left[ 1-\frac{\alpha }{2} \frac{\varDelta x}{l_H}+\frac{3\alpha ^2}{2}\left( \frac{\varDelta x}{l_H}\right) ^2\right] \nonumber \\&\quad \Longrightarrow \varDelta E_p\, \sim \,K_B T_\mathrm {U} \left[ 1-\frac{\alpha \pi }{2}\frac{a_H}{a}\,+\,\frac{3 \alpha ^2\pi ^2}{2}\left( \frac{a_H}{a}\right) ^2\right] .\nonumber \\ \end{aligned}$$
(34)

This implies

$$\begin{aligned} E_p\,\sim \,E_\mathrm {U}\left[ 1-\frac{\alpha \pi }{2}\frac{a_H}{a}\,+\,\frac{3\alpha ^2\pi ^2}{2}\left( \frac{a_H}{a}\right) ^2\right] . \end{aligned}$$
(35)

Once again, by expressing the energy of the environment radiation in terms of the the number of photons equivalent to the energy \(E_m\) of the test-body, we obtain

$$\begin{aligned} m_I\,\sim \,m\left[ 1-\frac{\alpha \pi }{2}\frac{a_H}{a}\,+\,\frac{3\alpha ^2\pi ^2}{2} \left( \frac{a_H}{a}\right) ^2\right] . \end{aligned}$$
(36)

This has the same behavior as MoND prediction (12), with the adjustable MoND parameter \(a_0\) being given by the cosmic acceleration \(a_H\), as above (the exact value of the coefficient \(\alpha \) can be determined by equating the leading-order corrections in the two formulas, which gives \(\alpha =2/\pi \)). Clearly, we would arrive at the same result by following the approach based on the direct computation of the radiation force.

A comment is in order here: as discussed in the Appendix, the EUP (33) naturally arises from the first terms in the expansion of a metric which has no evident physical meaning. Hence, the above considerations and the result (36) should only be considered as a mathematical framework to derive Eq. (1) from a deformed commutator. Beyond formal aspects, however, we expect that further details about the actual dependence of Modified Inertia on the acceleration – either linear or quadratic in 1/a – can be provided by future observational data, which will then reinforce the study of the model (20) or (36).

4 Summary and conclusions

The feature of inertial mass of bodies has never been well understood theoretically, but just assumed as empirical Newton’s first law. Based on McCulloch’s idea, which traces the origin of QI back to the combination of relativity (the appearance of the horizons) and quantum mechanics (the Casimir effect), here we have shown that a modification of the inertial mass can be naturally explained within the framework of the Extended Uncertainty Principle. Specifically, we have considered two different deformations of the standard Heisenberg relation. The first one only contains a quadratic correction in the uncertainty position and is the generalization which emerges in (anti)-de Sitter spacetime. In this context, we have found that Modified Inertia is related to the accelerating expansion of the Universe. Moreover, the obtained formula for the modified inertial mass is in agreement with the standard interpolating function used in MoND, but without needing any arbitrary constant. On the other hand, the second EUP exhibits both linear and quadratic corrections, leading to predictions consistent with the simple interpolating function of MoND. Clearly, given that EUP physics is largely heuristic, one should keep any scenario open. Hence, we expect that further hints towards the definitive answer may be provided by future cosmological experiments.

It is worth noting that both MoND and QI are claimed to solve the galaxy rotation problem without dark matter [25], but the latter does it without arbitrary adjustment. Moreover, QI seems also to explain the observed cosmic acceleration without needing dark energy [18, 24]. In spite of these well-understood results, some other issues deserve further attention. As discussed above, the explanation for the modified inertia depends on the peculiar spacetime geometry seen by an accelerating body and, in particular, on the appearance of two relativistic horizons, the cosmic and Rindler ones. Nevertheless, the physical meaning of the latter is quite debated and its real existence often questioned, being related to the idealized notion of eternally accelerating motion (see Refs. [4, 55] for a discussion on the topic). Then, one may wonder to what extent the above predictions are actually testable. In this regard, a clue to a solution has been provided in Refs. [56, 57], where it has been suggested that artificial event horizons might be created by using the metamaterials proposed by Pendry et al. [58] and Leonhardt [59]. The idea is to engineer a material which reflects radiation in such a way an event horizon-like structure is formed. In the same way, another challenging perspective is to derive the intrinsic property of inertial mass of bodies (rather than modifications of its value) starting from similar considerations. These issues will be investigated in more detail in future works.