Automated evaluation of electroweak Sudakov logarithms in SHERPA

Abstract

We present an automated implementation for the calculation of one-loop double and single Sudakov logarithms stemming from electroweak radiative corrections within the SHERPA event generation framework, based on the derivation in Denner and Pozzorini (Eur Phys J C 18:461–480, 2001). At high energies, these logarithms constitute the leading contributions to the full NLO electroweak corrections. As examples, we show applications for relevant processes at both the LHC and future hadron colliders, namely on-shell W boson pair production, EW-induced dijet production and electron–positron production in association with four jets, providing the first estimate of EW corrections at this multiplicity.

1 Introduction

In perturbative electroweak (EW) theory, higher-order corrections include, among other contributions, emissions of virtual and real gauge bosons and are known to have a large effect in the hard tail of observables at the LHC and future colliders [2]. In contrast to massless gauge theories, where real emission terms are necessary to regulate infrared divergences, in EW theory the weak gauge bosons are massive and therefore provide a natural lower scale cut-off, such that finite logarithms appear instead. Moreover, since the emission of an additional weak boson leads to an experimentally different signature with respect to the Born process, virtual logarithms are of physical significance without the inclusion of real radiation terms.

The structure of such logarithmic contributions, referred to as Sudakov logarithms [3], and their factorisation properties were derived in full generality by Denner and Pozzorini [1, 4,5,6,7,8] at leading and next-to-leading logarithmic accuracy at both one- and two-loop order in the EW coupling expansion. In addition, the full set of next-to-next-to-next-to-leading logarithms was calculated at two-loop order in [9] for four-fermion processes. Moreover, Denner and Pozzorini have shown that in the high-energy scattering limit, at least at one-loop order, these logarithmic corrections can be factored as a sum over pairs of external legs in an otherwise process-independent way, hence providing a straightforward algorithm for computing them for any given process. The high-energy limit requires all invariants formed by pairs of particles to be large compared to the scale set by the weak gauge boson masses. In this sense we expect effects due to electroweak corrections in general, and to Sudakov logarithms in particular, to give rise to large effects in the hard tail of observables that have the dimension of energy, such as for example the transverse momentum of a final state particle.

In this work we present an implementation for computing EW Sudakov corrections in the form they are presented in [1] within the SHERPA event generator framework [10]. While Sudakov corrections have been computed for a variety of processes (e.g. [11,12,13,14,15]), a complete and public implementation is, to our knowledge, missing.¹ The one we present here is fully general and automated, it is only limited by computing resources, and it will be made public in the upcoming major release of SHERPA. It relies on the internal matrix element generator COMIX [16] to compute all double and single logarithmic contributions at one-loop order for any user-specified Standard Model process. The correction is calculated for each event individually, and is therefore fully differential in phase-space, such that the logarithmic corrections for any observable are available from the generated event sample. The event-wise correction factors are written out as additional weights [17] along with the main event weight, such that complete freedom is left to the user on how to use and combine these Sudakov correction weights.

As Sudakov EW logarithms are given by the high-energy limit of the full set of virtual EW corrections, they can approximate these effects. Indeed, while NLO EW corrections are now becoming a standard in all general purpose Monte Carlo event generators (see [18] for SHERPA, [19] for MAD GRAPH5_AMC@NLO and process-specific implementations for POWHEG-BOX [20], such as e.g. [21, 22]), the full set of NLO EW corrections for complicated final states may not be available yet or might not be numerically tractable due to the calculational complexity for a given application. Another obstacle for the application of NLO EW corrections is the missing automation of the matching to electromagnetic (let alone EW) showers needed for particle-level event generation, although some process-specific matching implementations exist, e.g. Drell–Yan production [21, 23, 24]. For these reasons, an approximate scheme to deal with NLO EW virtual corrections, dubbed EW$_\text {virt}$, was devised in [25]. Within this approximation NLO EW real emission terms are included only via the endpoint term of the analytic integration over the dipole kernels needed to subtract the infrared singularity of the virtual term. Hence, only the finite parts of the virtual contribution and of the integrated counter-terms remain, which can be taken into account as a local correction to the Born event weight. This approach greatly simplifies the integration of such corrections with more complex event generation schemes, such as matching and merging with a QCD parton shower and higher-order QCD matrix elements. Compared to the Sudakov EW corrections used as an approximation of the virtual NLO EW, the EW$_\text {virt}$ scheme differs due to the inclusion of exact virtual corrections and integrated subtraction terms. These differences are either subleading or constant at high energy in the logarithmic counting, but they can lead to numerically sizeable effects, depending on the process, the observable and the applied cuts.

Alternatively, one can exploit the fact that EW Sudakov logarithms have been shown to exponentiate up to next-to-leading logarithmic accuracy using IR evolution equation [4, 26,27,28] and using Soft-Collinear Effective Theory [29,30,31,32,33,34], and exponentiate the event-wise correction factor to calculate the fully differential next-to-leading logarithmic resummation, as explored e.g. in [35].² This can lead to particularly important effects e.g. at a 100  TeV proton–proton collider [37], where (unresummed) next-to-leading logarithmic corrections can approach O(1) at the high-energy tail due to the increased kinematic reach, hence even requiring resummation to obtain a valid prediction.

The outline of this paper is as follows. In Sect. 2, we present how the algorithm is implemented in the SHERPA event generator, while in Sect. 3 we show a selection of applications of the method used to test our implementation, namely on-shell W boson pair production, EW-induced dijet production, and electron–positron production in association with four jets, providing an estimate of EW corrections for the latter process for the first time and at the same time proving the viability of the method for high multiplicity final states. Finally we report our conclusions in Sect. 4.

2 SHERPA implementation

Electroweak Sudakov logarithms arise from the infrared region of the integration over the loop momentum of a virtual gauge boson exchange, with the lower integration boundary set by the gauge boson mass. If the boson mass is small compared to the process energy scales, they exhibit the same structure of soft and collinear divergences one encounters in massless gauge theories. As such, the most dominant contributions are given by double logarithms (DL) which arise from the soft and collinear limit, and single logarithms (SL) coming instead from less singular regions, as we describe in more detail in the rest of this section. Virtual EW corrections also contain in general non-logarithmic terms (either constant or power suppressed), which are however beyond the accuracy of this work.

Fig. 1

Feynman diagram contributing to double-logarithmic Sudakov corrections

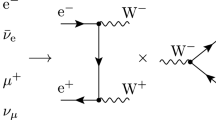
To give a more explicit example, let us consider the DL and SL contributions coming from a diagram of the type shown in Fig. 1. The former correspond to the case of the virtual gauge boson V becoming soft and collinear to one of the external legs i or j of the matrix element ${\mathcal {M}}$, i.e. when $|r_{ij}|\equiv |p_i+p_j|^2\gg m_W^2$. Similarly, as $|p_i+p_j|^2\sim 2\,p_i\cdot \,p_j$, this limit also encodes the case of a collinear, non-soft (and vice-versa) gauge boson which instead gives rise to SL contributions. In turn, these must also be included, since they can numerically be of a similar size as the DL one, see the discussion and the detailed derivation in [1, 7]. The reason for this can also be understood intuitively: while the diagram in Fig. 1 is the only source of double logarithms there are several contributions giving rise to single logarithms, which we discuss later in this section. In all cases, following the conventions in [1], we write DL and SL terms in the following way, respectively:

$$\begin{aligned} L\left( \left| r_{i j}\right| \right) \equiv \frac{\alpha }{4 \pi } \log ^{2} \frac{|r_{i j}|}{m_W^{2}} ,\quad l\left( r_{i j}\right) \equiv \frac{\alpha }{4 \pi } \log \frac{r_{i j}}{m_W^{2}} . \end{aligned}$$

(2.1)

Note that the use of the W mass as a reference scale is only a convention and the same form is indeed also used for contributions coming from Z bosons and photons. Remainder logarithms containing ratios of $m_W$ and $m_Z$ or the vanishing photon mass are taken care of by additional logarithmic terms, as explained in more details below.

After having evaluated all relevant diagrams, and using Ward identities, one can show that the DL and SL contributions factorise off the Born matrix element ${\mathcal {M}}$, and can be written in terms of a sum over pairs of external legs only. Hence, we define these corrections as a multiplicative factor $K_{\text {NLL}}$ to the squared matrix element $|{\mathcal {M}}(\Phi )|^2$ at a given phase space point $\Phi$:

$$\begin{aligned} K_{\text {NLL}}\left( \Phi \right) = 1 + \sum _c \frac{\sum _h 2\,\mathrm{Re}\left\{ (\delta ^c {\mathcal {M}}_h) {\mathcal {M}}_h^* \right\} }{\sum _h \left| {\mathcal {M}}_h \right| ^2}, \end{aligned}$$

(2.2)

where we have written ${\mathcal {M}}_h \equiv {\mathcal {M}}_h(\Phi )$ and the sums go over helicity configurations h and the different types of logarithmic contributions c. Following the original notation, these contributions are divided into Leading and Subleading Soft and Collinear (LSC/SSC) logarithms, Collinear or Soft (C) logarithms and those arising from Parameter Renormalisation (PR). More details about their respective definitions are given below.

Since $\delta ^c$ is in general a tensor in $\text {SU}(2)\times \text {U}(1)$, the $\delta ^c {\mathcal {M}}_h$ are usually not proportional to the original matrix element ${\mathcal {M}}_h$. The tensor structure come from the fact that in general the various $\delta ^c$ are proportional to EW vertices, which in turn means that a single leg or pairs of legs can get replaced with particles of a different kind, according to the relevant Feynman rules. As in [1], we denote the leg index i as a shorthand for the external fields $\phi _{i}$. Denoting with $\{i\}$ the set of all external fields, we therefore have $\delta ^c {\mathcal {M}}_h^{\{i\}} \propto {\mathcal {M}}_h^{\{i'\}}$. In our implementation, the construction and evaluation of these additional amplitudes is taken care of by an interface to the automated tree-level COMIX matrix element generator [16], which is available within the SHERPA framework. Before evaluating such amplitudes, the energy is re-distributed among the particles to put all (replaced) external legs on-shell again. The required auxiliary processes are automatically set up during the initialisation of the framework. Since the construction of additional processes can be computationally non-trivial, we have taken care of reducing their number by re-using processes that are shared between different contributions c, and by using crossing relations when only the order of external fields differs.

In our implementation we consistently neglect purely electromagnetic logarithms which arise from the gap between zero (or the fictitious photon mass) and $m_W$, following [1]. In SHERPA, one can resum soft-photon emissions to all orders through the formalism of Yennie, Frautschi and Suura (YFS) [36] or by a QED parton shower, as is discussed e.g. in [38]. Alternatively, one can compute the purely electromagnetic NLO correction to the desired process, consisting of both virtual and real photon emission, which gives the desired logarithm at fixed order. However, since this is based on dimensional regularisation (at least in SHERPA), one would need to also implement the EW Sudakov logarithms within this scheme to allow for a straightforward combination. This is not part of the current work.

While we ignore the mass gap between 0 and $m_W$, the logarithms originating from the running between the W mass and the Z mass are included, as we explain in the next paragraphs, where we discuss the individual contributions $\delta ^c$.

Leading Soft-Collinear logarithms: LSC The leading corrections are given by the soft and collinear limit of a virtual gauge boson and are proportional to $L(|r_{kl}|)$. By writing

$$\begin{aligned} L\left( \left| r_{k l}\right| \right)= & {} L\left( s\right) +2\,l(s) \log \frac{\left| r_{k l}\right| }{s}\nonumber \\&+L\left( \left| r_{k l}\right| , s\right) , \end{aligned}$$

(2.3)

and neglecting the last term on the right-hand side, which is of order ${\mathcal {O}}(1)$, one has split the soft-collinear contribution into a leading soft-collinear (LSC) and a angular-dependent subleading soft-collinear (SSC) one, corresponding to the first and second term on the right-hand side, respectively. The full LSC correction is then given by

$$\begin{aligned} \delta ^{\mathrm {LSC}} {\mathcal {M}}^{i_{1} \ldots i_{n}} {=}\sum _{k=1}^{n} \delta _{i_{k}^{\prime } i_{k}}^{\mathrm {LSC}}(k) {\mathcal {M}}_{0}^{i_{1} \ldots i_{k}^{\prime } \ldots i_{n}} ,\end{aligned}$$

(2.4)

where the sum runs over the n external legs, and the coefficient matrix on the right-hand side is given by

$$\begin{aligned} \delta _{i_{k}^{\prime } i_{k}}^{\mathrm {LSC}}(k)&{=}-\frac{1}{2}\left[ C_{i_{k}^{\prime } i_{k}}^{\mathrm {ew}}(k) L(s)-2\left( I^{Z}(k)\right) _{i_{k}^{\prime } i_{k}}^{2} \log \frac{M_Z^{2}}{M_W^{2}} l(s) \right] \nonumber \\&= \delta _{i_{k}^{\prime } i_{k}}^{\overline{\mathrm {LSC}}}(k) + \delta _{i_{k}^{\prime } i_{k}}^Z(k). \end{aligned}$$

(2.5)

$C^\text {ew}$ and $I^Z$ are the electroweak Casimir operator and the Z gauge coupling, respectively. The second term $\delta ^Z$ appears as an artefact of writing L(s) and l(s) in terms of the W mass even for Z boson loops, and hence the inclusion of this term takes care of the gap between the Z and the W mass at NLL accuracy. We denote the remaining terms with the superscript “$\overline{\text {LSC}}$”. Note that this term is in general non-diagonal, since $C^\text {ew}$ mixes photons and Z bosons. As is explicit in Eq. (2.2), coefficients need to be computed per helicity configuration; in the case of longitudinally polarised vector boson appearing as external particles, they need to be replaced with the corresponding Goldstone bosons using the Goldstone Boson Equivalence Theorem. This is a consequence of the scaling of longitudinal polarisation vectors with the mass of the particle, which prevents the direct application of the eikonal approximation used to evaluate the high-energy limit, as is detailed in [1]. To calculate such matrix elements we have extended the default Standard Model implementation in SHERPA with a full Standard Model including Goldstone bosons generated through the UFO interface of SHERPA [39, 40]. We have tested this implementation thoroughly against RECOLA [41].³

Subleading Soft-Collinear logarithms: SSC The second term in Eq. (2.3) gives rise to the angular-dependent subleading part of the corrections from soft-collinear gauge-boson loops. It can be written as a sum over pairs of external particles:

$$\begin{aligned} \delta ^{\mathrm {SSC}} {\mathcal {M}}^{i_{1} \ldots i_{n}} {=}\sum _{k=1}^{n} \sum _{l<k} \sum _{V_{a}{=}A, Z, W^{\pm }} \delta _{i_{k}^{\prime } i_{k} i_{l}^{\prime } i_{l}}^{V_{a}, \mathrm {SSC}}(k, l) {\mathcal {M}}_{0}^{i_{1} \ldots i_{k}^{\prime } \ldots i_{l}^{\prime } \ldots i_{n}} , \end{aligned}$$

(2.6)

where the coefficient matrices for the different gauge bosons $V_a=A,Z,W^\pm$ are

$$\begin{aligned} \delta _{i_{k}^{\prime } i_{k} i_{l}^{\prime } i_{l}}^{V_a, \mathrm {SSC}}(k, l)&=2 I_{i_{k}^{\prime } i_{k}}^{V_a}(k) I_{i_{l}^{\prime } i_{l}}^{\bar{V}_a}(l) \, \log \frac{\left| r_{k l}\right| }{s} l(s) . \end{aligned}$$

Note that while the photon couplings $I^A$ are diagonal, the eigenvalues for $I^Z$ and $I^\pm \equiv I^{W^\pm }$ can be non-diagonal, leading again to replacements of external legs as described in the LSC case.

Collinear or soft single logarithms: C The two sources that provide either collinear or soft logarithms are the running of the field renormalisation constants, and the collinear limit of the loop diagrams where one external leg splits into two internal lines, one of which being a vector boson $V_a$. The ensuing correction factor can be written as a sum over external legs:

$$\begin{aligned}&\delta ^{\mathrm {C}} {\mathcal {M}}^{i_{1} \ldots i_{n}} =\sum _{k=1}^{n} \delta _{i_{k}^{\prime } i_{k}}^{\mathrm {C}}(k) {\mathcal {M}}_{0}^{i_{1} \ldots i_{k}^{\prime } \ldots i_{n}} .\end{aligned}$$

(2.7)

For chiral fermions f, the coefficient matrix is given by

$$\begin{aligned} \delta _{f_{\sigma }f_{\sigma ^{\prime }}}^{\mathrm {C}}\left( f^{\kappa }\right)= & {} \delta _{\sigma \sigma ^{\prime }}\left[ \frac{3}{2} C_{f^{\kappa }}^{\mathrm {ew}}\nonumber \right. \\&\left. -\frac{1}{8 s_{\mathrm {w}}^{2}}\left( \left( 1+\delta _{\kappa \mathrm {R}}\right) \frac{m_{f_{\sigma }}^{2}}{M_W^{2}}+\delta _{\kappa \mathrm {L}} \frac{m_{f_{-\sigma }}^{2}}{M_W^{2}}\right) \right] l(s) \nonumber \\= & {} \delta _{f_{\sigma }f_{\sigma ^{\prime }}}^{\mathrm {\overline{C}}}\left( f^{\kappa }\right) + \delta _{f_{\sigma }f_{\sigma ^{\prime }}}^{\mathrm {Yuk}}\left( f^{\kappa }\right) .\end{aligned}$$

(2.8)

We label the chirality of the fermion by $\kappa$, which can take either the value L (left-handed) or R (right-handed). The label $\sigma$ specifies the isospin, its values ± refer to up-type quarks/neutrinos or down-type quarks/leptons, respectively. The sine (cosine) of the Weinberg angle is denoted by $s_w$ ($c_w$). Note that we further subdivide the collinear contributions for fermion legs into “Yukawa” terms formed by terms proportional to the ratio of the fermion masses over the W mass, which we denote by the superscript “Yuk”, and the remaining collinear contributions denoted by the superscript “$\overline{\text {C}}$”. These Yukawa terms only appear for external fermions, such that for all other external particles $\varphi$, we have $\delta ^\text {C}_{\varphi '\varphi } = \delta ^{\overline{\text {C}}}_{\varphi '\varphi }$. For charged and neutral transverse gauge bosons,

$$\begin{aligned} \delta _{W^{\sigma } W^{\sigma ^{\prime }}}^{C}\left( V_{\mathrm {T}}\right)&= \delta _{\sigma \sigma ^{\prime }}\frac{1}{2} b_{W}^{\mathrm {ew}} l(s) \quad \text {and}\quad \nonumber \\ \delta _{N^{\prime }N}^{\mathrm {C}}\left( V_{\mathrm {T}}\right)&=\frac{1}{2}\left[ E_{N^{\prime } N} b_{A Z}^{\mathrm {ew}}+b_{N^{\prime } N}^{\mathrm {ew}}\right] l(s) \quad \text {with}\quad \nonumber \\ E&\equiv \left( \begin{array}{cc}{0} &{} {1} \\ {-1} &{} {0}\end{array}\right) \end{aligned}$$

(2.9)

must be used, where the $b^\text {ew}$ are combinations of Dynkin operators that are proportional to the one-loop coefficients of the $\beta$-function for the running of the gauge-boson self-energies and mixing energies. Their values are given in terms of $s_w$ and $c_w$ in [1].

Longitudinally polarised vector bosons are again replaced with Goldstone bosons. When using the matrix element on the right-hand side of Eq. (2.7) in the physical EW phase, the following (diagonal) coefficient matrices must be used for charged and neutral longitudinal gauge bosons:

$$\begin{aligned} \delta _{W^{\sigma } W^{\sigma ^{\prime }}}^{C}\left( V_{\mathrm {L}}\right) \rightarrow \delta _{\phi ^{\pm } \phi ^{\pm }}^{\mathrm {C}}(\Phi )&=\left[ 2 C_{\Phi }^{\mathrm {ew}}-\frac{N_{\mathrm {C}}}{4 s_{\mathrm {w}}^{2}} \frac{m_t^{2}}{M_W^{2}}\right] l(s), \end{aligned}$$

(2.10)

$$\begin{aligned} \delta _{N^{\prime }N}^{\mathrm {C}}\left( V_{\mathrm {T}}\right) \rightarrow \delta _{\chi \chi }^{\mathrm {C}}(\Phi )&=\left[ 2 C_{\Phi }^{\mathrm {ew}}-\frac{N_{\mathrm {C}}}{4 s_{\mathrm {w}}^{2}} \frac{m_t^{2}}{M_W^{2}}\right] l(s) , \end{aligned}$$

(2.11)

where $N_\text{ C }=3$ is the number of colour charges.

Parameter Renormalisation logarithms: PR The last contribution we consider is the one coming from the renormalisation of EW parameters, such as boson and fermion masses and the QED coupling $\alpha$, and all derived quantities. The way we extract these terms, is by running all EW parameters up to a given scale, $\mu _\text {EW}$, which in all cases presented here corresponds to the partonic scattering centre of mass energy, and re-evaluate the matrix element value with these evolved parameters. We then take the ratio of this ‘High Energy’ (HE) matrix element with respect to the original value, such that, calling $\{p_{\text {ew}}\}$ the complete set of EW parameters,

$$\begin{aligned} \delta ^\text {PR}_{i_1\dots i_n}= & {} \left( \frac{{\mathcal {M}}_{\text {HE}}^{i_1\dots i_n}(\{p_{\text {ew}}\}(\mu _{\text {EW}}))}{{\mathcal {M}}^{i_1\dots i_n}(\{p_{\text {ew}}\})} - 1 \right) \nonumber \\&\sim \frac{1}{{\mathcal {M}}^{i_1\dots i_n}}\sum _{p\in \{p_{\text {ew}}\}}\frac{\delta {\mathcal {M}}^{i_1\dots i_n}}{\delta p}\,\delta p. \end{aligned}$$

(2.12)

The evolution of each EW parameter is obtained through

$$\begin{aligned} p_{\text {ew}}(\mu _{\text {EW}}) = \{p_{\text {ew}}\}\left( 1 + \frac{\delta p_{\text {ew}}}{p_{\text {ew}}} \right) , \end{aligned}$$

(2.13)

and the exact expressions for $\delta p_{\text {ew}}$ can be found in Eqs. (5.4–5.22) of [1].

The right hand side of Eq. (2.12) corresponds to the original derivation of Denner and Pozzorini, while the left hand side is the actual implementation we have used. The two differ by terms that are formally of higher order, $(\alpha \,\log \mu _{\text {EW}}^2/m^2_W)^2$. In fact, although they are logarithmically enhanced, they are suppressed by an additional power of $\alpha$ with respect to the leading terms considered here, $\alpha \,\log ^2\mu _{\text {EW}}^2/m^2_W$.

Generating event samples with EW Sudakov logarithmic contributions After having discussed the individual contributions c, we can return to Eq. (2.2), for which we now have all the ingredients to evaluate it for an event with the phase-space point $\Phi$. Defining the relative logarithmic contributions $\Delta ^c$, we can rewrite it as

$$\begin{aligned} K_{\text {NLL}}\left( \Phi \right)= & {} 1 + \sum _c \Delta ^c = 1 + \Delta ^{\overline{\text {LSC}}} + \Delta ^\text {Z} + \Delta ^\text {SSC}\nonumber \\&+ \Delta ^{\overline{\text {C}}} + \Delta ^\text {Yuk} + \Delta ^\text {PR}. \end{aligned}$$

(2.14)

In the event sample, the relative contributions $\Delta ^c$ are given in the form of named HEPMC weights [17] (details on the naming will be given in the manual of the upcoming SHERPA release). This is done to leave the user freedom on how to combine such weights with the main event weight.

In the context of results, Sect. 3, we employ these corrections in either of two ways. One way is to include them at fixed order,

$$\begin{aligned} \text {d}\sigma ^\text {LO + NLL}\left( \Phi \right) = \text {d}\Phi \,{\mathcal {B}}\left( \Phi \right) \, K_{\text {NLL}}\left( \Phi \right) \, , \end{aligned}$$

(2.15)

where ${\mathcal {B}}$ is the Born contribution. The alternative is to exploit the fact that Sudakov EW logarithms exponentiate (see Refs. [26,27,28,29,30,31,32,33,34]) to construct a resummed fully differential cross section

$$\begin{aligned} \text {d}\sigma ^\text {LO + NLL (resum)}\left( \Phi \right)= & {} \text {d}\Phi \, {\mathcal {B}}\left( \Phi \right) \, K^\text {resum}_{\text {NLL}}\left( \Phi \right) \nonumber \\= & {} \text {d}\Phi \, {\mathcal {B}}\left( \Phi \right) \,e^{\left( 1 - K_\text {NLL}\left( \Phi \right) \right) }\, , \end{aligned}$$

(2.16)

following the approach discussed in [35].

Matching to higher orders and parton showers SHERPA internally provides the possibility to the user to obtain NLO corrections, both of QCD [42] and EW [18] origin, and to further generate fully showered [43, 44] and hadronised events [10]. In addition one is able to merge samples with higher multiplicities in QCD through the CKKW [45], or the MEPS@NLO [46] algorithms. In all of the above cases (except the NLO EW), the corrections implemented here can be simply applied using the K factor methods in SHERPA to one or all the desired processes of the calculations, as there is no double counting between EW Sudakov corrections and pure QCD ones. A similar reasoning can be applied for the combination with a pure QCD parton shower. Although we do not report the result of this additional check here, we have tested the combination of the EW Sudakov corrections with the default shower of SHERPA. Technical checks and physics applications for the combination with matching and merging schemes, and for the combination with QED logarithms, are left for a future publication.

If one aims at matching Sudakov logarithms to higher-order EW effects, such as for example combining fixed order NLO EW results with a resummed NLL Sudakov correction, it is for now required for the user to manually do the subtraction of double counting that one encounters in these cases. An automation of such a scheme is also outside the scope of this publication, and will be explored in the future.

3 Results

Before discussing our physics applications, we report a number of exact comparisons to other existing calculations of NLL EW Sudakov logarithms. A subset of the results used for this comparison for $pp \rightarrow Vj$ processes is shown in Appendix A. They all agree with reference ones on a sub-percent level over the entire probed transverse momentum range from $p_{T,V}=100\,\hbox {GeV}$ to 2000 GeV. In addition to this, the implementation has been guided by passing a number of tests based on a direct comparison of tabulated numerical values for each contribution discussed in Sect. 2 in the high-energy limit, that are given for several electron–positron collision processes in [1] and for quark-induced WZ and $W\gamma$ production processes in [47].⁴ The numerical results for these tests are tabulated in Appendix B.

In the remainder of this section, we present a selection of physics results obtained using our implementation and where possible show comparisons with existing alternative calculations. The aim is twofold, first we wish to show the variety of processes that can be computed with our implementation, and second we want to compare to existing alternative methods to obtain EW corrections to further study the quality of the approximation. In particular, where available, we compare our NLL predictions to full NLO EW corrections, as well as to the EW$_\text {virt}$ approximation defined in [25]. The required virtual matrix elements are provided to SHERPA by the external matrix element generator OPENLOOPS [48]. It is important to note that we only consider EW corrections to purely EW processes here, such that there are no subleading Born corrections that might otherwise complicate the comparison to a full EW NLO calculation or to the EW$_\text {virt}$ approximation. We consider diboson production, dijet production, and Z production in association with 4 jets. In all cases, we focus on the discussion of (large) transverse momentum distributions, since they are directly sensitive to the growing effect of the logarithmic contributions when approaching the high-energy limit.

Fig. 2

The transverse momentum of the individual W bosons in W boson pair production from proton–proton collisions (including photon induced channels) at $\sqrt{s} = 13\,\hbox {TeV}$ (left) and $100\,\hbox {TeV}$ (right). The baseline LO and NLO EW calculations are compared with the results of the LO+NLL calculation and its variant, where the logarithmic corrections are resummed (“LO+NLL (resum)”). In addition, the virtual approximation EW$_\text {virt}$ and a variant of the NLO EW calculation with additional jets vetoed are also included. The ratio plots show the ratios to the LO and to the EW$_\text {virt}$ calculation, and the relative size of each NLL contribution

The logarithmic contributions are applied to parton-level LO calculations provided by the COMIX matrix element generator implemented in SHERPA. The parton shower and non-perturbative parts of the simulation are disabled, including the simulation of multiple interactions and beam remnants, and the hadronisation. Also higher-order QED corrections to the matrix element and by YFS-type resummation are turned off. The contributions to the NLL corrections as defined in Sect. 2 are calculated individually and combined a-posteriori, such that we can study their effects both individually and combined. We consider the fixed-order and the resummed option for the combination, as detailed in Eqs. (2.15) and (2.16), respectively.

For the analysis, we use the Rivet 2 [49] framework, and events are passed to analysis using the HEPMC event record library. Unless otherwise specified, simulations are obtained using the NNPDF3.1, next-to-next-to-leading order PDF set [50], while in processes where we include photon initiated processes we instead use the NNPDF3.1 LUX PDF set [51]. In all cases, PDFs are obtained through the LHAPDF [52] interface implemented in SHERPA. When jets appear in the final state, we cluster them using the anti-$k_T$ algorithm [53] with a jet radius parameter of $R=0.4$, through an interface to FAST JET [54]. The CKM matrix in our calculation is equal to the unit matrix, i.e. no mixing of the quark generations is allowed. Electroweak parameters are determined using tree-level relations using a QED coupling value of $\alpha (m_Z) = 1 / 128.802$ and the following set of masses and decay widths, if not explicitly mentioned otherwise:

$$\begin{aligned} m_W&=80.385\,\hbox { GeV}&m_Z&={91.1876}\,{\hbox {GeV}} \\ m_h&= 125\,\hbox { GeV}&m_t&=173.21\,\hbox { GeV}&\\ \Gamma _W&=2.085\hbox { GeV}&\Gamma _Z&=2.4952\hbox { GeV} \\ \Gamma _h&=0.00407\hbox { GeV}&\Gamma _t&=2.0\hbox { GeV}&. \end{aligned}$$

Note that $\alpha$ is not running in the nominal calculation as running effects are all accounted for by the PR contributions.

3.1 WW production in pp collisions at 13 and 100 TeV

Our first application is the calculation of EW Sudakov effects in on-shell W boson pair production at hadron colliders, which has lately been experimentally probed at the LHC [55, 56], e.g. to search for anomalous gauge couplings. We compare the Sudakov EW approximation to both the full NLO EW calculation and the EW$_\text {virt}$ approximation. The latter has been applied to WW production in [38, 57]. In addition to that, EW corrections for WW production have also been studied in [58,59,60,61,62,63], and NNLL EW Sudakov corrections have been calculated in [58].

We have performed this study at current LHC energies, $\sqrt{s} = 13\hbox { TeV}$, as well as at a possible future hadron collider with $\sqrt{s} = 100\,\hbox {TeV}$. In all cases, we include photon induced channels (they can be sizeable at large energies [59]), and we set the renormalisation and factorisation scales to $\mu _{R,F}^2 = \frac{1}{2}( 2m_W^2 + \sum _i p^2_{T,i})$, where the sum runs over the final-state W bosons, following the choice for gauge-boson pair production in [64]. Lastly, we set the widths of the Z and W boson consistently to 0, as the W is kept on-shell in the matrix elements.

In Fig. 2 we report results for the transverse momentum of each W boson in the final state for both centre of mass energies. Plots are divided into four panels, of which the first one collects results for the various predictions. The second and third panels report the ratio to the leading order and to the EW$_\text {virt}$ approximation, respectively. The aim is to show the general behaviour of EW corrections in the tail of distributions in the former, while the latter serves as a direct comparison between the Sudakov and the EW$_\text {virt}$ approximations. Finally the fourth panel shows the relative impact of the individual contributions $\Delta ^c$ appearing in Eq. (2.14).

Looking at the second panel, we see that all but the full NLO EW calculation show a strong suppression in the $p_T > m_W$ region, reaching between $-70$ and $-90 \%$ at $p_T=2\hbox { TeV}$. This effect is the main effect we discuss in this work, and it is referred to as Sudakov suppression. To explicitly confirm that this behaviour originates from virtual contributions of EW nature, we compare the Sudakov LO+NLL curve to the NLO EW and EW$_\text {virt}$ approximations. Indeed, the latter only takes into account virtual corrections and the minimal amount of integrated counter terms to render the cross section finite. The Sudakov approximation is close to that for both centre of mass energies (see also the third panel), with deviations of the order of a few percent. It begins to deviate more at the end of the spectrum, with similar behaviours observed for both collider setups. However, with a Sudakov suppression of $70\%$ and more, we are already in a regime where the relative corrections become ${\mathcal {O}}(1)$ and a fixed logarithmic order description becomes invalid. In fact, at $p_{T,W} \gtrsim {3}\,\mathrm{TeV}$, the LO+NLL becomes negative both at $\sqrt{s} = {13}\,\mathrm{TeV}$ and 100 TeV, the same being true for the EW$_\text {virt}$ approximation. Note in particular, that this is the main reason for choosing to show the $p_T$ distribution only up to $p_T = {2}\,\mathrm{TeV}$ in Fig. 2 for both collider setups.

It is also clear from the second panel that for both setups, the full NLO EW calculation does not show such large suppressions, and in the context of the question whether to use EW Sudakovs or the EW$_\text {virt}$ to approximate the full corrections, this may be worrisome. However, in the full calculation we have included the real emission matrix elements, which also show a logarithmic enhancement at high $p_T$, as e.g. discussed in [60]. In this case, the real emission contribution almost entirely cancels the Sudakov suppression at $\sqrt{s}={13}\,\mathrm{TeV}$, and even overcompensates it by about 20% in the $p_{T,W}\lesssim {1}\,\mathrm{TeV}$ region for $\sqrt{s}={100}\,\mathrm{TeV}$. To show that this is the case, we have also reported a jet-vetoed NLO EW simulation, which indeed again shows the high $p_T$ suppression as expected. Moreover, we have included a prediction labelled “LO+NLL (resum)”, where we exponentiate the Sudakov contribution using Eq. (2.16). It is similar to the NLL approximation, but resumming these logarithms leads to a smaller suppression in the large $p_T$ tail, which is reduced by about 20% at $p_T={2}\,\hbox { TeV}$, thus increasing the range of validity compared to the non-exponentiated prediction. Moreover, this agrees well qualitatively with the NNLL result reported in [58], and suggests that even higher-order logarithmic effects should be rather small in comparison in the considered observable range.

Lastly, we compare the individual LL and NLL contributions. As expected, we find that the double logarithmic $\overline{\text {LSC}}$ term is the largest contribution and drives the Sudakov suppression. Some single logarithmic terms, in particular the $\overline{\text {C}}$ terms, also give a sizeable contribution, reducing the net suppression. This confirms that the inclusion of single logarithmic terms is needed in order to provide accurate predictions in the Sudakov approximation, with deviations of the order of ${\mathcal {O}} ({10}\%)$ with respect to the EW$_\text {virt}$ calculation. Comparing the individual contributions for the two collider energies, we see qualitatively similar effects. As can be expected from a larger admixture of $b{\bar{b}}$ initial states, the $\Delta ^\text {Yuk}$ is enhanced at the larger collider energy.

Fig. 3

The transverse momentum of the leading jet in EW-induced dijet production in proton–proton collisions (including photon channels), and for the reconstructed Z boson in $e^+ e^-$ plus four jets production, For the dijet production, LO and NLO calculations are shown, whereas for the Z plus jets production only the LO is shown. These baseline calculations are compared with the results of the LO+NLL calculation, both at fixed-order and resummed. In the dijet case, the virtual approximation EW$_\text {virt}$ is shown in addition. The ratio plots show the ratios to the LO and the EW$_\text {virt}$ calculations, and the relative size of each NLL contribution

Fig. 4

The transverse momentum of the vector boson in Vj production for $V=W^+,Z,\gamma$. The baseline LO calculations are compared with the results of our LO+NLL calculation and reference LO+NLL results taken from [11, 12, 14]. The ratio plots show the ratios to the LO calculations, the ratios to the reference LO+NLL calculation, and the relative size of each NLL contribution

3.2 EW-induced dijet production in pp collisions at 13 TeV

For the second comparison in this section, we simulate purely EW dijet production in hadronic collisions at $\sqrt{s} = {13}\,\hbox { TeV}$ at the Born-level perturbative order ${\mathcal {O}}(\alpha ^2\alpha _s^0)$. As for the case of diboson production we add photon initiated channels, and we also include photons in the set of final-state partons, such that $\gamma \gamma$ and $\gamma j$ production is also part of our sample. Partons are thus clustered into jets which are then sorted by their $p_T$. We select events requiring at least two jets, the leading jet (in $p_T$) to have a $p_T > {60}\,\mathrm{GeV}$ and the subleading jet to have a $p_T > {30}\,\mathrm{GeV}$. Note in particular that for all but the real emission case in the full NLO EW simulation, this corresponds to imposing a $p_T$ cut on the two generated partons. The renormalisation and factorisation scales are set to $\mu _{R,F}^2 = {\hat{H}}^2_T = (\sum _i p_{T,i})^2$, where the sum runs over final-state partons.

We compare our LO+NLL EW results, as in the previous subsection, with the LO, the NLO EW and the EW$_\text {virt}$ predictions. NLO EW corrections for dijet production have been first discussed in [65, 66], while [67] discusses those corrections in the context of the 3-to-2-jet ratio $R_{32}$. In this context, we only consider EW corrections to the Born process described above, i.e. we consider the ${\mathcal {O}}(\alpha _s^0\alpha ^3)$ contributions, which is a subset of the contributions considered in the above references.

In Fig. 3 (left), we present the transverse momentum distribution of the leading jet $p_T$ given by the LO+NLL EW calculation, again both at fixed order and resummed, see Eqs. (2.15) and (2.16). As for W pair production, the plot is divided into four panels. However, this time we do not include jet-vetoed NLO results, as in this case we do not observe large real emission contributions. The panels below the main plot give the ratio to the LO calculation, the ratio to the EW$_\text {virt}$ approximation, and the ratio of each NLL contribution to the LO calculation.

Compared to W pair production, we observe a smaller but still sizeable Sudakov suppression, reaching approximately $-{40}\%$ at $p_T={2}\,\mathrm{TeV}$. The NLO contributions not included in the NLO EW$_\text {virt}$ (i.e. mainly real emission terms) are small and cancel the Sudakov suppression only by a few percent and as such both the Sudakov and the EW$_\text {virt}$ approximations agree well throughout the $p_T$ spectrum with the full NLO calculation. The same is true for the resummed NLL case which gives a Sudakov suppression of ${-30}{\%}$ for $p_T={2}\,\mathrm{TeV}$. Note that a small step can be seen for $p_T\sim m_W$ in the Sudakov approximation. The reason for this is that we force, during the simulation, all Sudakov contributions to be zero when at least one of the invariants formed by the scalar product of the external momenta is below the W mass, as Sudakov corrections are technically only valid in the high-energy limit. This threshold behaviour can be disabled, giving a smoother transition between the LO and the LO+NLL, as can be seen for example in Fig. 2.

Comparing the individual NLL contributions we find again that the double logarithmic $\overline{\text {LSC}}$ term is the largest contribution, its size is however reduced by a third compared to the diboson case, since the prefactor $C^\text {ew}$ in Eq. (2.5) is smaller for quarks and photons compared to W bosons. Among the single logarithmic terms the $\overline{\text {C}}$ and PR terms are the most sizeable over the whole range, and are of a similar size compared to the diboson case, while the SSC contribution only give a small contribution. Again, subleading terms must be included to approximate the NLO calculation at the observed 10% level, although we observe an almost entire accidental cancellation, in this case, of the SL terms.

3.3 Off-shell Z production in association with 4 jets in pp collisions at 13 TeV

As a final example, we present for the first time the LO+NLL calculation for $e^+ e^-$ production in association with four additional jets from proton–proton collisions at $\sqrt{s} = {13}\,{\hbox {TeV}}$. The process is one of the key benchmark processes at the LHC to make precision tests of perturbative QCD and is a prominent background constituent for several Standard Model and New Physics processes. In this case, we neglect photon induced contributions, to better compare to the NLL effects in Z plus one-jet production presented in Appendix A, which in turn is set up as a direct comparison to [11]. For the same reason, in this case, we only consider QCD partons in the final state. The factorisation and renormalisation scale are set to $\mu _F^2 = \mu _R^2 = {\hat{H}}_T^{\prime 2} = (M_{T,\ell \ell } + \sum _i p_{T,i})^2/4.0$, where $M_{T,\ell \ell }$ is the transverse mass of the electron–positron pair and the sum runs over the final-state partons. This choice is inspired by [68], where the full next-to-leading QCD calculation is presented.

As we consider here an off-shell Z, the invariant mass formed by its decay products is on average only slightly above the W mass threshold. This means that the high-energy limit discussed in Sect. 2 is not fulfilled, which could introduce sizeable logarithms in particular in Eq. (2.6). However, in practice we only see a small number of large K factors, that only contribute a negligible fraction of the overall cross section. In general, a proper treatment of off-shell configurations must be employed, e.g. via a clustering of the decay products, as described in [69]. Such a treatment is not included in our implementation at this point.

In Fig. 3 (right), we present the LO + NLL EW calculation of the transverse momentum distribution of the reconstructed Z boson. To our knowledge, there is no existing NLO EW calculation to compare it against,⁵ hence we do not have a ratio-to-NLO plot in this case. However, we do show the ratio-to-NLL plot and the plot that shows the different contributions of the LO + NLL calculation, as for the other processes.

Note that the MC errors of the individual bins are of the order of 5%. However, the MC errors of the LO and the LO+NLL calculation are fully correlated, since the NLL terms are completely determined by the phase-space point of the LO event, and the same LO event samples are used for both predictions. Hence the reported ratios are in fact very precise, and we have therefore chosen to omit the otherwise obfuscating MC error bands from the ratio plots. With the aim of additionally making a comparison to the $Z+j$ result reported in Fig. 4 (left panel), we opt for a linear x axis, in contrast with the other results of this section. In both cases we see a similar overall LO+NLL effect, reaching approximately ${-40}\,\%$ for $p_T\lesssim {2}\,\mathrm{TeV}$. This in turn implies that the effects of considering an off-shell Z (as opposed to an on-shell decay) as well as the additional number of jets have very little effect on the size of the Sudakov corrections. Finding similar EW corrections for processes that only differ in their number of additional QCD emissions can be explained by the fact that the sum of EW charges of the external lines are equal in this case. As has recently been noted in [57], this can be deduced from the general expressions for one-loop corrections in [1] and from soft-collinear effective theory [31, 33]. Although the overall effect for Zj and $Z+4j$ is found to be very similar here, the individual contributions partly exhibit a different behaviour between the two, with the SSC terms becoming negative in the four-jet case and thus switching sign, and the C terms becoming a few percent smaller. It is in general noticeable that the SSC terms exhibit the strongest shape differences among all processes considered in this study. Finally, similarly to the previous studied cases, the resummed result gives a slightly reduced Sudakov suppression, reaching approximately ${-30}\%$ for $p_T\lesssim {2}\,{\hbox {TeV}}$, implying that in this case, higher logarithmic contributions should be small.

4 Conclusions

We have presented for the first time a complete, automatic and fully general implementation of the algorithm presented in [1] to compute double and single logarithmic contributions of one-loop EW corrections, dubbed as EW Sudakov logarithms. These corrections can give rise to large shape distortions in the high-energy tail of distributions, and are therefore an important contribution in order to improve the accuracy of the prediction in this region. Sudakov logarithms can provide a good approximation of the full next-to-leading EW corrections. An exponentiation of the corrections can be used to resum the logarithmic effects and extend the region of validity of the approximation.

In our implementation, each term contributing to the Sudakov approximation is returned to the user in the form of an additional weight, such that the user can study them individually, add their sum to the nominal event weight, or exponentiate them first. Our implementation will be made available with the next upcoming major release of the SHERPA Monte Carlo event generator. We have tested our implementation against an array of existing results in the same approximation, and for a variety of processes against full NLO EW corrections and the virtual approximation EW$_\text {virt}$, which is also available in SHERPA. A selection of such tests is reported in this work, where we see that indeed EW Sudakov logarithms give rise to large contributions and model the full NLO corrections well when real emissions are small. We stress that our implementation is not limited to the examples shown here, but it automatically computes such corrections for any Standard Model process. In terms of final-state multiplicity it is only limited by the available computing resources. In terms of theoretical limitations, the same limitations apply that are pointed out in the original formulation of the method [1], namely that it is not valid for cross sections that are dominated by resonances, since in such a case the high-energy limit is not fulfilled. Although there are methods to take care of this issue, such as a clustering of the decay products of such resonances, we have left this generalisation to a future version of the implementation.

In a future publication we also plan to apply the new implementation in the context of state-of-the-art event generation methods, in particular to combine them with the matching and merging of higher-order QCD corrections and the QCD parton shower, while also taking into account logarithmic QED corrections using the YFS or QED parton shower implementation in SHERPA. This will allow for an automated use of the method for the generation of event samples in any LHC or future collider context, in the form of optional additive weights. As discussed towards the end of Sect. 2, we foresee that this is a straightforward exercise, since there is no double counting among the different corrections, and applying differential K factors correctly within these methods is already established within the SHERPA framework. The result should also allow for the inclusion of subleading Born contributions, as the EW$_\text {virt}$ scheme in SHERPA does. The automated combination of (exponentiated) EW Sudakov logarithms with fixed-order NLO EW corrections is another possible follow-up, given the presence of phenomenologically relevant applications.

Appendices

Appendix A: Validation plots for V plus jet production in pp collisions at 13 TeV

Table 1 Comparison of our results (“our”) with reference results (“ref.”) from [1] for the coefficients of the different contributions in lepton-induced diboson production processes, given separately for the helicity configurations that are non-zero in the high-energy limit. Note that the labels for these configurations follow the conventions laid out in [1]. Our results are rounded to the same number of decimal digits before calculating the ratios “our/ref.” whenever the coefficient is just a constant. We give the u-channel and t-channel gauge boson exchange contributions to the SSC coefficients separately. As the SSC coefficients are either dependent on the kinematics or vanish completely we give the ratio only, which is averaged over ten phase-space points. The given uncertainty is the associated standard deviation

Table 2 Same as Table 1, but for lepton-induced quark pair production, with reference values again taken from [1]

Table 3 Same as Table 1, but for diboson production from $u \bar{d}$ initial states, with reference values taken from Sec. 8.4 in [47]. Note that for this process, also LSC, C and PR coefficients are dependent on the kinematics. Hence, instead of giving a reference value, we just indicate that it varies (shortened as “var.”) in such cases, and give an average for the ratio “our/ref.” over ten phase space points

Table 4 Comparison of our K factor results with reference K factor results (“ref.”) from [11] ($u{\bar{u}}\rightarrow Zg$), [14] ($d{\bar{u}}\rightarrow W^- g$) and [12] ($u{\bar{u}}\rightarrow \gamma g$, with the replacement $C^\text {ew} - Q^2 \rightarrow C^\text {ew}$ to reinstate photon-induced contributions) for Vj production processes. Instead of giving the absolute values for our calculation, we give the difference $\Delta$ with respect to the reference value. We use the difference instead of a ratio because the difference is mostly determined by $\sqrt{{{\hat{s}}}}$, while the K factor itself also depends on the other kinematical variables, such that the difference is basically a constant while a ratio would be dependent on the kinematics. Moreover, the reference values and the differences are given as an average over ten random phase space points, in order to exclude a merely accidental agreement. We give averaged differences $\Delta$ for three variants of our calculation. $\Delta _\text {full}$ is our default calculation, with all contributions enabled. $\Delta _{\text {Z}=0}$ sets the Z contribution to zero, which corresponds to setting $m_Z=m_W$, which is assumed in the reference calculations. $\Delta _{\text {Z}=\text {PR}=\text {C}^V=0}$ in addition sets the PR contribution to 0 and ignores the vector-boson induced part of the C contribution. This is because in the scheme of the reference calculations, the PR and the C$^V$ exactly cancel. Hence, with these settings, we can enforce this cancellation and achieve a very close agreement between our calculation and the reference one. The remaining difference should then originate in the fact that in our case the high energy limit is only approximately fulfilled, which corresponds to the observation that the difference increases for smaller $\sqrt{{{\hat{s}}}}$

As an additional validation for our implementation, we show in Fig. 4 the LO+NLL calculation for Z, $W^+$ and $\gamma$ production, each in association with one jet. The setups, the analysis, and the binning are configured to closely match the choices made in [11, 12, 14], respectively, and the reader is referred to these publications for further details. In particular, the photon is not considered to be part of the parton content of the incoming protons, and the MRST01 LO PDF set has been used [70]. The reference result have been included in the plots, and the ratio of our LO+NLL results to the reference results are shown, confirming that both predictions agree at a percent level over the whole range of the observables. In particular, note that the differences visible in the second to last panels between our predictions and the reference values are given by the different treatment of the PR contribution, as discussed in Sect. 2. This is explicitly checked by the comparisons listed in Table 4.

Appendix B: Numerical comparisons with reference calculations

As further validation for our implementation, we have tabulated in this appendix the direct comparison of numerical results for coefficients (Tables 1, 2, 3) and K factors (Table 4) to reference values for a number of processes in the literature.