Interacting generalized anisotropic scalar field models

Abstract

This paper is devoted to investigate the interacting generalized ghost pilgrim dark energy model in the background of anisotropic universe in general relativity. We analyze the two parameters i.e., hubble parameter and equation of state parameter to explore the cosmological evolution of the Bianchi type universe. We study scalar field dark energy models i.e., quintessence, dilaton, K-essence and tachyon to check the consistency of the current universe with their scalar field and corresponding potentials. Further, we check the compatibility of fractional density of matter and dark energy with recent observations of Plank along with their graphical analysis. It is remarkable to conclude that that both fractional densities admits consistency with Plank data 2018 in all cases of Bainchi type universe.

1 Introduction

Recent observational data reveals that we are surviving in the accelerated phase of universe [1,2,3]. The current universe has a finite age of 13.7 billion years, measured by Wilkinson Microwave Anisotropy Probe (WMAP) satellite. The acceptable universe model is known as Big Bang. It is broadly acceptable about the evolution of universe. About 13–14 billion years ago, the universe was scattered only to a few millimeters across. It was very hot and dense, but it expanded regularly and become vast and cool, into cosmos that we know today.

The data also recommends that the universe is also dominated by two dark constituents i.e., dark energy (DE) and dark matter (DM). DM is known as pressureless matter which manipulate the galactic curves and the origination of universe configuration. DE is an energy which opposed the gravity with negative pressure used to explain the accelerated expansion of the universe.

The cosmological constant has been considered as the simplest DE candidate where the cosmological constant model ($\Lambda CDM$) is compatible with current days observations. However, this model has a problem of cosmological issue like “fine tuning”. Two different approaches were introduced in order to inspect the issue, one is the modification in the geometric part of Einstein–Hilbert action which is identified as the modified theories of gravity. The other one is to introduced the different dynamical DE model in the context of general relativity (GR). The matter modification gives candidates of DE such as quintessence [4,5,6,7], phantom [8], k-essence [9], tachyon [10], quintom [11, 12], holographic [13] and pilgrim [14,15,16,17,18] scalar field models etc. The field which naturally found in particle physics like string theory [19] is known as scalar field are utilized as a possible candidate of DE. It plays a vital role to study the cosmic acceleration.

Vacuum energy is ghost field can be utilized to describe the time varying cosmological constant in a space time [20]. In vacuum ghost field, the energy density is directly proportional to $\Lambda ^{3}_{QCD}$, where $\Lambda ^{3}_{QCD}$ is QCD mass scale and H is Hubble parameter, is known as ghost dark energy (GDE) [21]. In QCD, the general vacuum energy of veneziano ghost field have the form $H+O(H^{2})$ [22] is known as generalized GDE (GGDE). It can be revealed that by taking the second term it gives the preferable compatibility with observational data as compared to GDE. In GGDE, the energy density is of the form $\rho _{\Lambda }=H \zeta + H^{2} \varsigma$, where $\zeta$ and $\varsigma$ are constants [23].

Wei introduced a new DE model named as Pilgrim DE (PDE) on this fact that the formation of black hole (BH) can be agnored by strong force of repulsion of the type of DE. In this regard, the phantom DE plays an important role instead of other type of DE. The combination of GGDE and PDE is pronounced as generalized ghost pilgrim DE (GGPDE) and it’s energy density becomes $\rho _{\Lambda }=(H \alpha + H^{2} \beta )^{u}$, where u is constant.

The familiar method to investigate the viability of a DE model is to show the stability against small perturbations. The sign of square speed of sound ($v^{2}_{s}=\frac{{\dot{p}}}{{\dot{\rho }}}=\frac{p'}{\rho '}$) plays an important role for this purpose, its positive sign represents stability and vice versa [24]. The Chaplygin and tachyon Chaplygin are stable gases but holographic and QCD ghost DE models are instable.

There exist some significance in the support of idea of interaction between the DM and DE at observational scale and the conservation equations are used to describe the interaction between energy density and DM [25, 26]. According to the survey of cosmic microwave background radiations (CMBR), the current universe is isotropic and largely homogeneous as indicated by the observations of WMAP. However, the anisotropy is still found in the current universe as CMB temperature. The study of anisotropic models are very useful in order to understand the formation of evolution of universe. Bianchi type universe are spatially homogeneous and anisotropic.

Abdul et al. [27] examined the scalar field models such as quintessence, dilaton, tachyon and k-essence in the background of flat FRW universe. In the presence of interaction, they studied the dynamics of scalar field models with their corresponding potentials. Sheykhi [28] analyzed the DE scalar field models for interacting HDE in flat universe. Sharif and Jawad [29] studied the scalar field and holographic DE (HDE) model for non-flat universe. They discussed the interaction of HDE with quintessence, tachyon, k-essence and dilaton DE models for different values of PDE parameter. Sharif and Shamir [30] examined the solution of Bianchi type I and space-times in the background of f(R) gravity. Sharif and Zubair [31] explained the anisotropic universe models with perfect fluid and scalar field in f(R, T) gravity. They concluded that f(R) reveal identical behavior with different constraints.

In this work, we study the cosmological evolution of anisotropic universe in GR with respect to red-shift parameter z. This paper is outlined as: we provide basic concepts and some cosmological parameters i.e., hubble parameter and Equation of state parameter (EoS) in Sect. 2. In Sect. 3, we explain graphically Bianchi type III model along with scalar field models i.e., quintessence DE model, tachyon DE scalar field model, K-essence scalar field model and dilaton scalar field model. We analyze graphically Bianchi type V and Bianchi type $\hbox {VI}_{{0}}$ along with above mentioned scalar field models in Sects. 4 and 5 respectively. Finally, we conclude the final results in the last section.

2 Anisotropic model and cosmological parameters

Spatially homogeneous and anisotropic model representing Bianchi type-III, V and VI is taken as

$$\begin{aligned} ds^{2}= & {} -dt^{2}+A^{2}(t)dx^{2}+B^{2}(t)e^{-2m_{1}x}dy^{2}\nonumber \\&+C^{2}(t) e^{2m_{2}x}dz^{2}, \end{aligned}$$

(2.1)

here $m_{1}$ and $m_{2}$ are constants and A, B and C are functions of time t.

Equation (2.1) gives

For $m_{1}=0$, the above metric gives Bianchi type-III

For $m_{1}=-m_{2}$, it becomes Bianchi type-V

For $m_{1}=m_{2}$, Bianchi type-VI, respectively.

The Einstein field equations are given by

$$\begin{aligned} R_{ij}-\frac{1}{2}Rg_{ij}=-\kappa ^{2}T_{ij}, \end{aligned}$$

(2.2)

where $R_{ij}$ denotes the Ricci tensor, $g_{ij}$ represents metric tensor and R is Ricci scalar, while $\kappa ^{2} = 1$. The energy momentum tensor $T_{ij}$ of perfect fluid is defined as

$$\begin{aligned}&T^{m}_{ij}=(\rho _{m}+p_{m})u_{i}u_{j}+p_{m}g_{ij}, \end{aligned}$$

(2.3)

$$\begin{aligned}&T^{\Lambda }_{ij}=diag[-\rho _{\Lambda },p_{\Lambda },p_{\Lambda },p_{\Lambda }]. \end{aligned}$$

(2.4)

The four velocity of the fluid particles is taken as $u_{i}=(-1,0,0,0)$. By using Eqs. (2.3) and (2.4), Eq. (2.2) in line element (2.1), the first field equation is given as

$$\begin{aligned} \frac{{\dot{A}}{\dot{B}}}{AB} \!+\!\frac{{\dot{B}}{\dot{C}}}{BC}+\frac{{\dot{A}}{\dot{C}}}{AC}\!-\! \frac{m_{1}^{2}\!-\!m_{1}m_{2}\!+\!m_{2}^{2}}{A^{2}} \!= & {} \! (\rho _{m}\!+\!\rho _{\Lambda }), \end{aligned}$$

(2.5)

where $\rho _{m}$ and $\rho _{\Lambda }$ are cold DM (CDM) and GGPDE densities, respectively. The total amount of energy density can be expressed as fractional energy density. Using Eq. (2.5), fractional density is defined as

$$\begin{aligned} 1+\Omega _{\sigma }=\Omega _{m}+\Omega _{\Lambda }, \end{aligned}$$

(2.6)

here

$$\begin{aligned} \Omega _{m}=\frac{\rho _{m}}{3H^{2}}, \quad \Omega _{\Lambda }=\frac{\rho _{\Lambda }}{3H^{2}}, \quad \Omega _{\sigma }=\frac{\sigma ^{2}}{3H^{2}}. \end{aligned}$$

(2.7)

The shear scalar $\sigma _{ij}$ is given as

$$\begin{aligned} \sigma _{\alpha \beta }= & {} u_{\alpha ,\beta }+\frac{1}{2}( u_{\alpha ;\gamma }u^{\gamma }u_{\beta }\nonumber \\&+ u_{\beta ;\gamma }u^{\gamma }u_{\alpha }) +\frac{1}{3}\theta (g_{\alpha \beta }+u_{\alpha \beta }). \end{aligned}$$

(2.8)

By using Eqs. (2.1) and (2.8), we get

$$\begin{aligned} \sigma ^{2}\!=\!-{\dot{A}}\!+\!A\left( \frac{{\dot{B}}}{B}\!+\!\frac{{\dot{C}}}{C}\right) \!+\!\frac{1}{3} \theta (2A^{2}\!+\!B^{3}e^{-2m_{1}x}\!+\!C^{2}e^{2m_{2}x}). \end{aligned}$$

(2.9)

The equation of continuity can be expressed as

$$\begin{aligned}&{\dot{\rho }}_{m}+\left( \frac{{\dot{A}}}{A} +\frac{{\dot{B}}}{B}+\frac{{\dot{C}}}{C}\right) \rho _{m}=\Delta , \end{aligned}$$

(2.10)

$$\begin{aligned}&{\dot{\rho }}_{\Lambda } +3H\rho _{\Lambda }(1+\omega _{\Lambda })=-\Delta , \end{aligned}$$

(2.11)

where dot is known as derivative of t and Q is the interaction term between the GGPDE and CDM. We consider the interaction term as follow

$$\begin{aligned} \Delta =3d^{2}H\rho _{m}, \end{aligned}$$

(2.12)

where $d^{2}$ is known as interaction parameter. The sign interaction term gives the transformation of energies. It gives negative sign if CDM tends to decompose into DE and gives positive sign when DE decays into CDM. Using Eqs. (2.10) and (2.12), we obtain the following DM density as follows.

$$\begin{aligned} \rho _{m}=\rho _{m0}e^{-(1-d^{2})x}, \end{aligned}$$

(2.13)

where $x=\ln (ABC)$ and $\rho _{mo}$ is the integrating constant. we take the average scale factor as follow

$$\begin{aligned} a=(ABC)^{\frac{1}{3}}. \end{aligned}$$

(2.14)

H is defined as

$$\begin{aligned} H=\frac{1}{3}\left( \frac{{\dot{A}}}{A} +\frac{{\dot{B}}}{B} +\frac{{\dot{C}}}{C}\right) . \end{aligned}$$

(2.15)

By using Eqs. (2.13) and (2.11) in Eq. (2.5), we obtain the differential equation

$$\begin{aligned} {\dot{H}}= & {} \Bigg (\frac{{\ddot{A}}{\dot{B}}}{AB}+\frac{{\dot{A}}{\ddot{B}}}{AB}- \frac{\dot{A^{2}}{\dot{B}}}{A^{2}B}-\frac{{\dot{A}}B^{2}}{AB^{2}} \nonumber \\&+ \frac{{\ddot{C}}{\dot{B}}}{CB}+\frac{{\dot{C}}{\ddot{B}}}{CB}- \frac{{\dot{C}}\dot{B^{2}}}{CB^{2}}+\frac{{\ddot{A}}{\dot{C}}}{AC}\nonumber \\&+ \frac{{\dot{A}}{\ddot{C}}}{AC}-\frac{{\dot{A}}^{2}{\dot{C}}}{A^{2}C}- \frac{{\dot{A}}\dot{C^{2}}}{AC^{2}}\nonumber \\&-\frac{2{\dot{A}}(-m_{1}^{2}-m_{1}m_{2}+ m_{2}^{2})}{A^{3}}+3H^{2}_{0} \Omega _{m0}\nonumber \\&\times e^{-(1-d^{2})x}(1-d^{2})H)\left( \frac{u}{3}\right) (\alpha H+\beta H^{2})^{u-1}\nonumber \\&\times (\alpha +2H \beta )\Bigg )^{-1}. \end{aligned}$$

(2.16)

The Hubble constant calculates the expansion rate of universe along with its total energy density, also the age of universe and the radius of its curvature. Different techniques have been introduced recently to measure the Hubble constant. Recently, the universe seems to have kinetic age less than about 142 billion years for a huge range of cosmological models. Also, the results show consistency with low-matter-density universe for stellar ages. They have a favorable behavior with either an open universe, or a flat universe having a non-zero value of the cosmological constant [32].

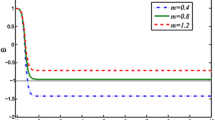
Using Eqs. (2.11), (2.13) and GGPDE, the EoS parameter takes the following form

$$\begin{aligned} \omega _{\Lambda }= & {} -3Hd^{2}\Omega _{m}-\frac{4{\dot{H}}}{H}\left( \frac{\alpha +2\beta H}{\alpha +\beta H}-H\right) (\alpha H+\beta H^{2})^{u}\nonumber \\&\times \, ((\alpha H+\beta H^{2} )^{u})^{-1}. \end{aligned}$$

(2.17)

The deceleration parameter q for the current model is given as

$$\begin{aligned} q= & {} -\frac{a\ddot{a}}{{\dot{a}}^{2}}. \end{aligned}$$

(2.18)

By inserting the values in the above equation, we get the following form of deceleration parameter

$$\begin{aligned} q= & {} (-2)({ABC})^{-1}+(3({\ddot{A}}BC+2{\dot{A}}{\dot{B}}C+2{\dot{A}}B{\dot{C}}+ A{\ddot{B}}\nonumber \\&\times \, C+2A{\dot{B}}{\dot{C}} +AB{\dot{C}}))((ABC)^{\frac{1}{3}}({\dot{A}}BC\nonumber \\&+A{\dot{B}}C+AB{\dot{C}}))^{-1}. \end{aligned}$$

(2.19)

In order to find the average anisotropic parameter $A_{h}$ for the generalized anisotropic model is taken as

$$\begin{aligned} A_{h}=\frac{1}{3}\sum ^{3}_{i=1}\left( \frac{H_{i}-H}{H}\right) ^{2}, \end{aligned}$$

(2.20)

where

$$\begin{aligned} H_{x}=H_{y}=\frac{{\dot{A}}}{A}, \quad H_{z}=\frac{{\dot{B}}}{B}. \end{aligned}$$

(2.21)

Further, we discuss some solutions regarding anisotropic universe models with scalar field models.

3 Reconstruction of scalar field model for Bianchi type-III

If $m_{2}=0$, the Eq. (2.5) gives Bianchi type-III. Other parameters takes the form as

$$\begin{aligned}&A=B=c^{\frac{1}{3}}_{2}(t^{n}e^{t})^{\frac{1}{k}}\exp \left[ \frac{c_{1}}{3}G(t)\right] ,\nonumber \\&C=c^{\frac{-2}{3}}_{2}(t^{n}e^{t})^{\frac{1}{k}}\exp \left[ \frac{-c_{2}}{3}G(t)\right] , \end{aligned}$$

(3.1)

here $c_{1}$ and $c_{2}$ are integrating constant

$$\begin{aligned} G(t)=\int t^{\frac{-3n}{t}}e^{t(\frac{k-3}{k})}dt =\sum ^{\infty }_{i=1}\frac{(k-3)^{i-1}t^{i-\frac{3n}{k}}}{k^{i-2(ki-3n)(i-1)!}}. \end{aligned}$$

(3.2)

Fig. 1

Plot of $\Omega _{m}$ verses z for $u=1$ and $u=2.002$ for Bianchi type-III model

Fig. 2

Plot of $\Omega _{\Lambda }$ verses z for $u=1$ and $u=2.002$ for Bianchi type-III model

Fig. 3

Plot of q verses t for $n=-\,2.8$ and $n=-\,3.8$ for Bianchi type-III model

Fig. 4

Plot of $A_{h}$ verses t for $n=-\,2.8$ and $n=-\,3.8$ for Bianchi type-III model

Fig. 5

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 6

Plot of V verses z for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 7

Plot of $\phi (z)$ verses V(z) for $u=1$ and $u=2.002$ for quintessence scalar field model

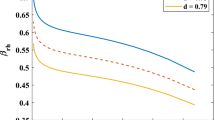
We analyze the behavior of fractional densities corresponding to matter and DE graphically at red-shift scale factor where the scale factor is taken as $a(t)=a_{0}(1+z)^{-1}$ and z is red-shift parameter. We take the values of parameters as $d^{2}=0.05, 0$ and 0.5, $k=1$, $n=-2.85$, $\alpha =100$, $\beta =0.8$, $H_{0}=67$, $c_{1}=1$, $c_{2}=1$, $m_{1}=1$ and $\Omega _{m0}=27$. The evaluation of fractional densities of matter and DE have a great role in cosmos as well as in flat universe. The fractional densities of anisotropic universe is given as $\Omega _m+\Omega _\Lambda =1+\Omega _\sigma$. From the observations of Plank 2018 it is recommended that $\Omega _m\simeq 0.3111$ and $\Omega _\Lambda \simeq 0.6889$. For PDE parameter $u=1$, the fractional density of matter indicates inconsistent behavior as shown in Fig. 1 (left plot). The trajectories of fractional density provide $\Omega _{m}\simeq 0.1$ and 0.3 for PDE parameter $u=2.002$ in the right plot of Fig. 1. In this regard, it provides consistent behavior with Plank 2018. Figure 2 reveals the behavior of fractional density of DE. In the left plot fractional density of DE shows consistent behavior with Plank data whereas in the right plot it exhibits inconsistent behavior. The deceleration parameter is useful to describe the inflation of the model. The negative sign of q indicates the inflation of the universe while the positive sign reveals the deceleration in the standard way. Recent observational data expose that the current universe is expanding having the values of deceleration parameter lie in the range $-\,1\lessapprox q<0$. We examine the behavior of deceleration parameter for different values of $k=0.5, 0.75$ and 1 and $n=-\,2.8$ and - 3.8 in Fig. 3. The trajectories of deceleration parameter lies in the required horizon shows the consistent behavior with the recent observational data. The average anisotropic parameter $A_{h}$ is the function of cosmic time t. Figure 4 depicts the behavior of $A_{h}$ describing that the anisotropic parameter is the decreasing function of time. It indicates that the current model is isotropic in late times.

3.1 Quintessence dynamical field model

Fine tuning problem can be resolved by assuming EoS to be time dependent instead of taking it as a constant which leads toward quintessence scalar field. This model explains the cosmic acceleration when potential dominates over kinetic energy by negative pressure. The energy density and potential of quintessence scalar field is given as [33]

$$\begin{aligned} p_{q}=\frac{1}{2}{\dot{\phi }}^{2}-V(\phi ), \quad \varrho _{q}=\frac{1}{2}{\dot{\phi }}^{2}+V(\phi ), \end{aligned}$$

(3.3)

here ${\dot{\phi }}^{2}$ is kinetic energy and $V(\phi )$ is known as scalar potential where EoS parameter is defined as

$$\begin{aligned} \omega _{q}=\frac{{\dot{\phi }}^{2}-2V(\phi )}{{\dot{\phi }}^{2}+2V(\phi )}. \end{aligned}$$

(3.4)

Fig. 8

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for tachyon scalar field model

Fig. 9

Plot of V verses z for $u=1$ and $u=2.002$ for tachyon scalar field model

Fig. 10

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for tachyon scalar field model

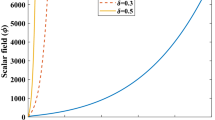
We numerically solve the ${\dot{\phi }}$ and plot $\phi$ against red-shift parameter z by taking initial guess as $\phi (1)=1$ by keeping the other constants same as above. Figure 5 reveals the scalar field increases for PDE parameter $u=1$ and 2.002. Figure 6 represents the trajectories of potential V verses z indicating decreasing behavior for $u=1$ but for $u=2.002$ it shows increasing behavior with time. The comparison of potential and quintessence scalar field is shown in Fig. 7. The potential shows small negative values as compared to $\phi$ showing that the universe is not expanding.

3.2 Tachyon dynamical field model

This model has been originated from the string theory, which is used to discuss the source of DE. The EoS parameter of rolling tachyon has its value between − 1 to 0. It is useful to explain the inflation at high energy. The energy and pressure of this model is given as

$$\begin{aligned} \rho _{t}=\frac{V(\phi )}{\sqrt{1-\dot{\phi ^{2}}}}, \quad p_{t}=-V(\phi )\sqrt{1-\dot{\phi ^{2}}}. \end{aligned}$$

(3.5)

The behavior of tachyon field $\phi$ against z is shown in Fig. 8 representing increasing behavior with time for all values of interacting parameter $d^{2}=0.05, 0$ and 0.5. Figure 9 represents the trajectories of tachyon potential for PDE parameter $u=1$ (left plot) and $u=2.002$ (right plot), it shows decreasing behavior for all values of interacting parameter. Also, we remark that that the negative tachyon potential dominates over the scalar field as shown in Fig. 10 indicating decelerated expansion of the universe.

Fig. 11

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for K-essence scalar field model

Fig. 12

Plot of V verses z for $u=1$ and $u=2.002$ for K-essence scalar field model

Fig. 13

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for K-essence scalar field model

3.3 K-essence dynamical field model

It was observed that quintessence scalar field model is used to describe the present and late time acceleration but later it was noticed that late time acceleration can be defined by the modification of kinetic energy. The idea of K-essence was originated from K-inflation used to explain the inflation at high energies [19]. K-essence has been known as another candidate of DE, gives interesting facts of scaling and attractor solutions [34]. The corresponding energy density and pressure is given as

$$\begin{aligned} \rho _{k}=V(\phi )(-\chi +3\chi ^{2}),\quad p_{k}=V(\phi )(-\chi +\chi ^{2}), \end{aligned}$$

where V($\phi$) is known as the potential of K-essence model. The Eos of K-essence is taken as

$$\begin{aligned} \omega _{k}=\frac{1-\chi }{1-3\chi }. \end{aligned}$$

(3.6)

Fig. 14

Plot of $\chi e^{b_{2} \phi }$ verses z for $u=1$ and $u=2.002$ for dilaton scalar field model

Fig. 15

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for dilaton scalar field model

The scalar field $\phi$ verses z is shown in Fig. 11, representing increasing behavior in present epoch for both values of PDE parameter. The EoS parameter of K-essence DE model is compatible with accelerated universe in the interval $(\frac{1}{3}, \frac{2}{3})$. For kinetic energy $\chi < \frac{1}{2}$, it corresponds to Phantom DE for late time attractor [34]. Trajectories of K-essence potential shows increasing behavior with time in Fig. 12. Figure 13 indicates the increase in potential with increase in scalar field but K-essence scalar field $\phi$ decreases with the expansion of universe.

3.4 Dilaton dynamical field model

It is believed that the dilaton scalar field model avoids the instabilities of DE with respect to the phantom field models. The energy density and pressure of this model is given as

$$\begin{aligned} p_{d}=-\chi +b_{1}e^{b_{2}\phi }\chi ^{2},\quad \rho _{d}=-\chi +3b_{1}e^{b_{2}\phi }\chi ^{2}, \end{aligned}$$

(3.7)

where $b_{1}$ and $b_{2}$ are positive constants. The EoS of this model is given as

$$\begin{aligned} \omega _{d}=\frac{-1+b_{1}e^{b_{2}\phi }\chi }{-1+3b_{1}e^{b_{2}\phi }\chi }. \end{aligned}$$

(3.8)

We observe that the EoS parameter allows $e^{b_{2}\phi }\chi$ to bound in interval $(\frac{20}{3}, \frac{40}{3})$ for the accelerated expansion. Figure 14 shows decelerated expansion in this regard. The inverse relation of field $\phi$ against z is indicated in Fig. 15.

4 Reconstruction of scalar field model for Bianchi-type V

If $m_{1}=-m_{2}$, then the Eq. (2.5)) reduced to Bianchi type-V model whereas, the parameters takes the form

$$\begin{aligned}&A=(e^{t}t^{n})^{\frac{1}{k}}, \quad B=(e^{t}t^{n})^{\frac{1}{kl}}, \quad C=(e^{t}t^{n}) ^{\frac{l-2}{2kl}}. \end{aligned}$$

(4.1)

Fig. 16

Plot of $\Omega _{m}$ verses z for $u=1$ and $u=2.002$ for Bianchi type-V model

Fig. 17

Plot of $\Omega _{\Lambda }$ verses z for $u=1$ and $u=2.002$ for Bianchi type-V model

Fig. 18

Plot of q verses t for $n=-\,2.8$ and $n=-\,3.8$ for Bianchi type-V model

Figure 16 shows the trajectories of fractional density of matter exhibits negative behavior having inconsistent behavior for $u=1$ with recent observations in the left plot. The right plot shows consistent for $d^{2}=0.05$ and 0 but it shows inconsistent behavior for $d^{2}=0.5$ with Plank data 2018. In the Fig. 17, the graphical analysis represents that the DE fractional density admits consistency with Planks data 2018 for $u=1$. The right plot of Fig. 17 shows negative behavior having inconsistent behavior for $u=2.002$. The behavior of deceleration parameter is shown in Fig. 18. It predicts that the deceleration parameter tends to lie in the required span having consistent behavior with current observations. For the Bianchi type V, the anisotropic parameter does not depend on cosmic time t.

4.1 Quintessence dynamical field model

The plot of scalar field $\phi$ verses z for Bianchi-type V is represented in Fig. 19 showing the increasing behavior in the present epoch for $d^{2}= 0.05$ and 0.5. Similarly, the potential indicates the increasing behavior in Fig. 20. In Fig. 21, the Kinetic energy dominates over the potential exhibits accelerated expansion (in the left and right plot) for PDE parameter $u=1$ and 2.002.

4.2 Tachyon dynamical field model

In the left plot of Fig. 22, the field $\phi$ shows increasing behavior but exhibits decreasing behavior in the right plot for PDE parameter $u=2.002$. Similarly, Fig. 23 reveals increasing behavior for $u=1$ (left plot of V) and decreasing behavior for $u=2.002$ (right plot of V). For the expansion of universe, the field $\phi$ rolls down potential, whereas the Fig. 24 represents that the universe is not expanding.

Fig. 19

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 20

Plot of V verses z for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 21

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 22

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for tachyon scalar field model

Fig. 23

Plot of V verses z for $u=1$ and $u=2.002$ for tachyon scalar field model

Fig. 24

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for tachyon scalar field model

4.3 K-essence dynamical field model

K-essence scalar field $\phi$ exhibits increasing behavior for all values of interacting parameter $d^{2}$ having PDE parameter u in Fig. 25. The trajectories of K-essence potential reveals decreasing behavior for PDE parameter $u=1$ and 2.002 in Fig. 26. The kinetic energy $\chi$ does not lie in the required interval indicating that the universe is not in the phase of accelerated expansion as given in Fig. 27.

Fig. 25

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for K-essence scalar field model

Fig. 26

Plot of V verses z for $u=1$ and $u=2.002$ for K-essence scalar field model

Fig. 27

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for K-essence scalar field model

4.4 Dilaton dynamical field model

The plot dilaton field $\phi$ exhibits inverse relation with z for both values of PDE parameter u in Fig. 28 and $\chi e^{b_{2} \phi }$ does not tends to lie in the required interval represents decelerated expansion of the universe as shown in Fig. 29.

Fig. 28

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for dilaton model

Fig. 29

Plot of $\chi e^{b_{2} \phi }$ verses z for $u=1$ and $u=2.002$ for dilaton model

5 Reconstruction of scalar field model for Bianchi-type VI

If $m_{2}=m_{_{1}}$, then the Eq. (2.5) become Bianchi type-VI model and the other parameters reduced to,

$$\begin{aligned}&A=c^{\frac{2}{3}}_{4}(t^{n}e^{t})^{\frac{1}{k}}\exp \left[ \frac{2c_{3}}{3}G(t)\right] ,\nonumber \\&B=C=c^{\frac{-1}{3}}_{4}(t^{n}e^{t})^{\frac{1}{k}}\exp \left[ \frac{-c_{1}}{3}G(t)\right] , \end{aligned}$$

(5.1)

where $c_{3}$ and $c_{4}$ are the constants of integration and G(t) is same as above. Figure 30 represents the incompatible behavior with Plank’s constraints due to small negative value of $\Omega _{m}$ for PDE parameter $u=1$. In the right plot, $\Omega _{m}$ admits compatibility for $u=2.002$ with the recent observations of Plank. Figure 31 reveals consistency with Plank 2018 data whereas it exhibits inconsistent behavior for $u=2.002$. The behavior of deceleration parameter exhibits consistent behavior with the recent observation data that the universe is expanding as in Fig. 32. The anisotropic parameter in Fig. 33 reveals the decrease in behavior which clarify that anisotropic universe evolves into an isotropic one at late times.

5.1 Quintessence dynamical field model

Figure 34 shows the increase in quintessence field against z with the passage of time, whereas the Fig. 35 exhibits the decreasing behavior of quintessence potential. Their comparison plot in Fig. 36 represents decelerated expansion as kinetic energy does not dominate over the potential.

Fig. 30

Plot of $\Omega _{m}$ verses z for $u=1$ and $u=2.002$ for Bianchi type-VI model

Fig. 31

Plot of $\Omega _{\Lambda }$ verses z for $u=1$ and $u=2.002$ for Bianchi type-VI model

Fig. 32

Plot of q verses t for $n=-\,2.8$ and $n=-\,3.8$ for Bianchi type-VI model

Fig. 33

Plot of $A_{h}$ verses t for $n=-\,2.8$ and $n=-\,3.8$ for Bianchi type-VI model

Fig. 34

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 35

Plot of V verses z for $u=1$ and $u=2.002$ for quintessence scalar field model

Fig. 36

Plot of $\phi (z)$ verses V(z) for $u=1$ and $u=2.002$ for quintessence scalar field model

5.2 Tachyon dynamical field model

In Fig. 37, the tachyon field indicates increasing behavior and the tachyon potential exhibits decreasing behavior in Fig. 38. The universe is in the phase of decelerated expansion as revealed by the comparison of tachyon field and potential for all values interacting parameter and PDE parameter in Fig. 39.

Fig. 37

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for tachyon scalar field model

Fig. 38

Plot of V verses z for $u=1$ and $u=2.002$ for tachyon scalar field model

Fig. 39

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for tachyon scalar field model

5.3 K-essence dynamical field model

The K-essence field $\phi$ against z exhibits the increase in behavior as shown is Fig. 40. The potential V also shows increasing behavior in Fig. 41. Figure 42 represents the decelerated expansion as the kinetic energy is not in the required interval.

Fig. 40

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for K-essence scalar field model

Fig. 41

Plot of V verses z for $u=1$ and $u=2.002$ for K-essence scalar field model

Fig. 42

Plot of $\phi$ verses V for $u=1$ and $u=2.002$ for K-essence scalar field model

5.4 Dilaton dynamical field model

$\chi e^{b_{2} \phi }$ does not tends to lie in the required interval for accelerated expansion, so Fig. 43 shows the universe is in accelerated phase. Figure 44 shows decreasing behavior with the passage of time against red-shift parameter z.

Fig. 43

Plot of $\chi e^{b_{2} \phi }$ verses z for $u=1$ and $u=2.002$ for dilaton scalar field model

Fig. 44

Plot of $\phi$ verses z for $u=1$ and $u=2.002$ for dilaton scalar field model

6 Final remarks

In this work, we have discussed the cosmic evolution of anisotropic universe along with GGPDE model in the framework of GR. We have reconstructed two cosmological parameters with the suitable choice of interacting parameter $d^{2}$. Also, we have observed the current cosmic expansion with scalar field DE models i.e., quintessence dynamical field model, tachyon dynamical field model, K-essence dynamical field model and dilaton dynamical field model. We have also analyzed graphically these scalar field models with PDE parameter u.

Currently, two different researches have been introduced to improve the precision of the cosmic distance scale. The usage of HST observations of Cepheid variables has been done for the host galaxies of eight SNe Ia to adjust the relation of supernova magnitude-redshift by Riess et al. [35]. One of the best estimation of Hubble constant, i.e., the fitting of calibrated SNe magnitude-redshift relation is

$$\begin{aligned} H_0=73.8\pm 2.4\, \mathrm{km} \,\mathrm{s}^{-1} \, \mathrm{Mpc}^{-1} \quad (Cepheids+SNe~Ia) , \end{aligned}$$

here $1\sigma$ is the level of error and some systematic errors. Freedman et al. [36] used the Spitzer Space Telescope mid-infrared observations to read just secondary distance methods in the HST key project. They have found the following value of Hubble constant, i.e.,

$$\begin{aligned} H_0= & {} 74.3\pm 1.5~(statistical) \\&\pm ~2.1~(systematic) \, \mathrm{km} \, \mathrm{s}^{-1} \, \mathrm{Mpc}^{-1} \quad (Carnegie~HP) . \end{aligned}$$

The final remarks for Bianchi type III, Bianchi type V and Bainchi type $\hbox {VI}_{{0}}$ are given as

6.1 Bianchi type III model

• For Bianchi type-III the trajectories of fractional density of matter shows compatible behavior with Plank 2018 data for PDE parameter $u=2.002$ for different values of interacting parameter. Recent data of Planks 2018 [37] introduced the different values of $\Omega _{m}$ at $68\%$ limit

  $$\begin{aligned} \Omega _m= & {} 0.289^{+0.026}_{-0.033}\quad \text {(EE + low E)},\\ \Omega _m= & {} 0.3153\pm 0.0073\quad \\&\text {(Planck TT, TE, EE + low E + lensing)},\\ \Omega _m= & {} 0.3111\pm 0.0056\quad \\&\text {(Planck TT, TE, EE + low E + lensing + BAO)}. \end{aligned}$$

• The plot of fractional density of DE reveals consistent behavior with recent data of Plank 2018 for PDE parameter $u=1$. Recent observations of Planck 2018 proposed different values of $\Omega _\Lambda$ at $68\%\,CL$ given by [37]

  $$\begin{aligned} \Omega _\Lambda= & {} 0.711^{+0.033}_{-0.026}\quad \text {(EE + low E)},\\ \Omega _\Lambda= & {} 0.6847\pm 0.0073\quad \\&\text {(Planck TT, TE, EE + low E + lensing)},\\ \Omega _\Lambda= & {} 0.6889\pm 0.0056\quad \\&\text {(Planck TT, TE, EE + low E + lensing + BAO)}. \end{aligned}$$

• The trajectories of deceleration parameter depicts that the universe in expanding.

• The behavior of anisotropic parameter reveals that the current model is isotropic in the late times.

• The quintessence scalar field shows increasing behavior with time against z for PDE parameter and potential V represents decreasing behavior for different values of interacting parameter.

• The comparison plot of field phi $\phi$ and potential V indicates that the universe is in the phase of decelerated expansion.

• The tachyon field $\phi$ shows increasing behavior and potential shows decreasing behavior for all values of interacting parameter.

• The comparison plot indicates that the universe is in the phase of decelerated expansion.

• Both the K-essence scalar field and potential shows increasing behavior against z with time.

• As the kinetic energy does not tends to lie in required interval $(\frac{1}{3}, \frac{2}{3})$, indicating that the universe is not in the era of accelerated expansion.

• For dilaton scalar field model, $e^{b_{2}\phi }\chi$ does not tends to lie in required interval indicating decelerated expansion.

6.2 Bianchi type V

• Fractional density of matter indicates consistent behavior for PDE parameter $u=2.002$ with the recent observations of Plank 2018.

• Fractional density of DE represents compatible behavior with Plank 2018 data for $u=1$.

• The deceleration parameter shows consistent behavior with current observations.

• The anisotropic parameter is independent of time.

• The quintessence scalar field and potential both shows increasing behavior against red-shift parameter z.

• Their comparison plot represents that the universe is in the phase of accelerated expansion.

• Tachyon scalar field represents increasing behavior for PDE parameter $u=1$ and shows decreasing behavior for $u=2.002$.

• Tachyon potential exhibits the increase in behavior for $u=1$ and decreasing behavior for $u=2.002$.

• The comparison plot of scalar field and potential indicates that the universe is not in the phase of accelerated expansion.

• K-essence scalar field shows increasing and potential reveals decreasing behavior against z.

• Their comparison plot exhibits that the universe is not expanding.

• Dilaton scalar field model does not tends to lie in the required interval, showing the universe is not expanding.

6.3 Bianchi type VI

• The fractional density of matter is compatible with Plank data 2018 for $u=2.002$.

• The DE fractional density admits consistency with recent Plank data for $u=1$.

• The plot of deceleration parameter exposes consistency with recent observational data.

• The anisotropic parameter also shows compatible behavior with current observations.

• Quintessence scalar field model indicates that the universe is not in the phase of accelerated expansion as the potential does not dominate over the scalar field.

• Tachyon DE scalar field model reveals that the scalar field does not roll over potential, showing the universe is in decelerated phase.

• K-essence DE scalar field model exhibits the decelerated expansion as the kinetic energy does not lie in the required interval.

• Dilaton scalar field model also shows the deceleration of the universe.

Sharif and Jawad [29] investigated the non-flat universe in the context of interacting HDE model along with dynamical models. They discussed some main features for some values of interaction parameter $d^{2}=0, 0.04, 0.08$. Firstly, they studied about EoS parameter which starts from vacuum region and move towards quintessence region. Secondly, they discussed about the instability of model via speed of sound. Thirdly, they evaluated interacting NHDE for quintessence, tachyon, K-essence and dilaton dynamical models and explained the behavior of potential and dynamics of scalar field for reliable values of the constant parameter. They checked that the scalar field $\phi$ become steeper with the increase in interacting parameter for all scalar field models.

We have studied the Bianchi type universe along with dynamical models in the frame work of interacting GGPDE model in GR. We have investigated that the scalar field models i.e., quintessence, tachyon, K-essence and dilaton DE dynamical model used to check the accelerated and decelerated expansion of the universe. We have concluded that the universe is found to be in decelerated phase of expansion. Also, we have checked the compatibility of fractional density of DE and matter with recent observations of Plank 2018.