Schwarzschild de Sitter and extremal surfaces

Abstract

We study extremal surfaces in the Schwarzschild de Sitter spacetime with real mass parameter. We find codim-2 timelike extremal surfaces stretching between the future and past boundaries that pass through the vicinity of the cosmological horizon in a certain limit. These are analogous to the surfaces in http://arxiv.org/abs/1711.01107 [hep-th]. We also find spacelike surfaces that never reach the future/past boundaries but stretch indefinitely through the extended Penrose diagram, passing through the vicinity of the cosmological and Schwarzschild horizons in a certain limit. Further, these exhibit interesting structure for de Sitter space (zero mass) as well as in the extremal, or Nariai, limit.

1 Introduction and summary

Over the last several years, holographic entanglement entropy [1,2,3,4] has been under substantial investigation, both from the point of view of gaining new insights on strongly coupled field theories as well as on spacetime geometry intertwining with entanglement via gauge/gravity duality [5, 7,8,9]. The RT/HRT proposals involve extremal surfaces whose area encodes entanglement entropy in the dual field theory. In AdS, surfaces anchored at one end of a subsystem dip into the bulk radial direction upto the “deepest” location which is the “turning point”, and then begin to return to the boundary.

It is a fascinating question to extend these explorations to de Sitter space (see e.g. [10] for a review), which is known to possess entropy [11], given by the area of the cosmological horizon. One might imagine this dovetails with attempts to understand de Sitter entropy via gauge/gravity duality for de Sitter space, or dS/CFT [12,13,14], which conjecture dS to be dual to a hypothetical Euclidean non-unitary Conformal Field Theory that lives on ${{\mathcal {I}}}^+$, with the dictionary $\Psi _{dS}=Z_{CFT}$ [14]. $\Psi _{dS}$ is the late-time Hartle–Hawking Wavefunction of the Universe with appropriate boundary conditions and $Z_{CFT}$ the dual CFT partition function. Dual energy–momentum tensor correlation functions reveal a negative central charge $-{R_{dS}^2\over G_4}$ for $dS_4$ suggesting a ghost-like $CFT_3$ dual: this is exemplified in the higher spin $dS_4$ duality involving a 3-dim CFT of anticommuting (ghost) scalars [15]. Bulk expectation values [14] are obtained as $\langle \varphi _k \varphi _{k'}\rangle \sim \int D\varphi \ \varphi _k \varphi _{k'} |\Psi _{dS}|^2$, weighting with the bulk probability $|\Psi _{dS}|^2=\Psi _{dS}^*\Psi _{dS}$: the presence of $\Psi _{dS}$ and $\Psi _{dS}^*$ suggests that bulk de Sitter physics involves two copies of the dual CFT, possibly on the future and past boundaries.

In this context, it is interesting to ask if de Sitter entropy is some sort of generalized entanglement entropy via dS/CFT [16]: a class of investigations in this regard is summarized in [17]. Various explorations of extremal surfaces in de Sitter space were carried out in [18] in the Poincare slicing and in [16] in the static coordinatization, looking for extremal surfaces anchored at $I^+$, since the natural boundary for dS is future/past timelike infinity $I^\pm$. Since the dual CFT is Euclidean and there is no “intrinsic” boundary time, operationally we take some spatial isometry direction as boundary Euclidean time, as a crutch: de Sitter isometries imply that no particular slice is sacrosanct. We then define a subsystem on this slice, which leads to codim-2 bulk extremal surfaces stretching in the time direction. In general it then appears that real surfaces do not exhibit any turning point where a surface starting at $I^+$ begins to return to $I^+$. (There are complex extremal surfaces with turning points that amount to analytic continuation from the Ryu–Takayanagi AdS expressions [18], giving negative area in $dS_4$ consistent with the negative central charge; see also [20, 21]. However their interpretation is not entirely clear.) It is thus interesting to ask if surfaces beginning at $I^+$ stretch all the way to $I^-$: in [16], such codim-2 real timelike surfaces were in fact found. These exhibit an area law divergence ${\pi l^2\over G_4} {1\over \epsilon }$, where $\epsilon ={\epsilon _c\over l}$ is the dimensionless ultraviolet cutoff (with l the de Sitter scale) and the coefficient scales as de Sitter entropy. In more detail, the static patch coordinatization can be recast as

$$\begin{aligned} ds^2 = {l^2\over \tau ^2} \Bigg (-{d\tau ^2\over 1-\tau ^2} + (1-\tau ^2) dw^2 + d\Omega _{d-1}^2\Bigg )\ , \end{aligned}$$

(1)

with the future/past universes F/P parametrized by $0\le \tau \le 1$ with horizons at $\tau =1$, while the Northern/Southern diamonds N/S have $1<\tau \le \infty$. The boundaries at $\tau =0$ are now of the form $R_w\times S^{d-1}$, resembling the Poincare slicing locally. Setting up the extremization for codim-2 surfaces on boundary Euclidean time slices can be carried out: on $S^{d-1}$ equatorial planes for instance we obtain ${\dot{w}}^2 = {B^2\tau ^{2d-2}\over 1-\tau ^2 + B^2\tau ^{2d-2}}$ with real turning points in the Northern/Southern diamonds (N/S). These connected surfaces are analogous to rotated versions of surfaces found by Hartman, Maldacena [22] in the AdS black hole, argued to be dual to a thermofield double state [23]. The existence of the connected surfaces stretching between $I^\pm$, in light of the fact that the bulk de Sitter space has entropy, suggests the speculation [16] that $dS_4$ is approximately dual to an entangled thermofield-double type state $|\psi \rangle = \sum \psi ^{i_n^F,i_n^P} |i_n^F\rangle |i_n^P\rangle$ in two copies $CFT_F\times CFT_P$ of the ghost-CFT, at $I^+$ and $I^-$, the generalized entanglement entropy of the latter scaling as de Sitter entropy. (See also [24] in this regard.) This is also in part motivated by parallel investigations of certain generalizations of entanglement to ghost-like theories, in particular ghost-spins [25], where “correlated” states of this kind, entangling identical states $i_n^F$ and $i_n^P$ in two copies of ghost-spin ensembles, were found to uniformly have positive norm, reduced density matrix and entanglement.

In light of the bulk extremal surface studies above, it is of interest to explore the Schwarzschild de Sitter spacetime. This represents a Schwarzschild black hole in de Sitter space [11], and thus exhibits a cosmological horizon as well as a Schwarzschild horizon, for certain ranges $0< {m\over l} \le {1\over \sqrt{27}}$ of the dimensionless mass parameter ${m\over l}$ where l is the de Sitter scale. An interesting limit here arises for ${m\over l} = {1\over \sqrt{27}}$ : in this extremal or Nariai limit [29], the region between the horizons becomes $dS_2\times S^2$. Schwarzschild de Sitter spacetimes also arise as the dominant contributions to the late-time Hartle–Hawking wavefunction for asymptotically $S^1\times S^2$ geometries in certain limits [30], but with imaginary mass parameter; see also [31] for more on the nearly $dS_2$ limit, the wavefunction and the no-boundary proposal. In what follows, we will mostly be interested in the real mass case: unfortunately this does not appear to have bearing on $dS_4/CFT_3$ so we are mainly studying this as a gravitational question alone. It is then of interest to look for codim-2 real timelike surfaces stretching from $I^+$ to $I^-$. Along the lines of [16], we do find codim-2 real timelike extremal surfaces passing through the vicinity of the cosmological horizon. These are described by ${\dot{w}}^2 = {B^2\tau ^{2d-2}\over f(\tau ) + B^2\tau ^{2d-2}}$ , where $f(\tau )=1-\tau ^2+{2m\over l}\tau ^d$ is the metric factor and $B^2>0$ is a conserved quantity that is a parameter encoding the width boundary conditions at $I^\pm$ as in the de Sitter case. In the limit where the subregion at $I^\pm$ becomes the whole space, we find a limiting surface as in the de Sitter case (described in detail in [32]). As $m\rightarrow 0$, this analysis coincides with the de Sitter case. Along similar lines, one might expect to find similar surfaces passing through the vicinity of the Schwarzschild horizon: we do not find any real surfaces of this kind though, as we explain in detail (Sect. 2).

However we do find that surfaces of the above kind with $B^2<0$ in fact exhibit interesting behaviour (Sect. 3). These end up being spacelike surfaces passing through the vicinity of the Schwarzschild and cosmological horizons in a certain limit. They extend indefinitely through the extended Penrose diagram, and never reach any $I^\pm$. These spacelike surfaces do admit interesting limits in the extremal or Nariai limit of Schwarzschild de Sitter, as we discuss. The de Sitter limit of these spacelike surfaces interestingly has area equal to de Sitter entropy. Finally we show that these spacelike surfaces can also be obtained as certain analytic continuations of certain extremal surfaces in global AdS. Some appendices discuss some technical aspects of the tortoise coordinate and Penrose diagrams, an analysis of the 3-dim Schwarzschild de Sitter spacetime which is a bit special, and some technical aspects of the area integrals that arise in the paper.

2 Schwarzschild de Sitter and extremal surfaces

The Schwarzschild de Sitter spacetime in $d+1$-dimensions is given by the metric

$$\begin{aligned} ds^2= & {} -f(r)dt^2+\frac{dr^2}{f(r)}+r^2d\Omega _{d-1}^2\ , \nonumber \\ f(r)= & {} 1-\frac{2m}{l}\left( \frac{l}{r}\right) ^{d-2}-\frac{r^2}{l^2}\ , \end{aligned}$$

(2)

and describes a Schwarzschild black hole in de Sitter space [11] with an “outer” cosmological horizon as well as an “inner” Schwarzschild horizon. The surface gravity at both horizons is distinct generically and Euclidean continuations can be defined removing a conical singularity at either horizon but not both simultaneously [33] (see also [34, 35]). The periodicities of Euclidean time coincide in an extremal, or Nariai, limit [29], which is degenerate: away from this precise value, the periodicities cannot match. The spacetime develops a nearly $dS_2$ throat in a near extremal limit [33]. Schwarzschild de Sitter spacetimes with large and purely imaginary mass¹ give the dominant contribution to the finite part of the late time Hartle–Hawking wavefunction of the universe for asymptotically $S^1\times S^2$ geometries satisfying the no-boundary proposal in the limit where the $S^1$ size is small [30]. More on the nearly $dS_2$ limit and the wavefunction of the universe appears in [31].

As for the de Sitter case in [16], we find it useful to recast this metric in terms of the coordinates $\tau =\frac{l}{r}, w=\frac{t}{l}$ : this gives

$$\begin{aligned} ds^2= & {} {l^2\over \tau ^2} \left( -{d\tau ^2\over f(\tau )} + f(\tau ) dw^2 + d\Omega _{d-1}^2\right) , \nonumber \\ f(\tau )= & {} 1-\tau ^2+{2m\over l}\tau ^d\ . \end{aligned}$$

(3)

In the $\tau$-coordinate, the future boundary $I^+$ is at $\tau =0$ and singularities arise at $\tau \rightarrow \infty$. Now near $I^+$, the metric locally resembles the Poincare patch. The horizons are given by the zeros of $f(\tau )$. The de Sitter limit with $m=0$ becomes (1): there is a cosmological horizon at $\tau =1$. For $d=3$ i.e. $SdS_4$ with nonzero real mass m, $f(\tau )$ is a cubic function with multiple zeros: two physically interesting roots arise for $0\le {m\over l}\le {1\over \sqrt{27}}$ representing a cosmological and a Schwarzschild horizon [11], as we describe below. The maximally extended Penrose diagram shows an infinitely repeating pattern of “unit-cells”, with cosmological horizons bounding future/past universes F/P, Schwarzschild horizons bounding interior regions $I_F, I_P$ and an intermediate diamond region D.

We will mostly focus on the 4-dim Schwarzschild de Sitter case in what follows (an appendix studies $SdS_3$ in detail). For $SdS_4$, we have

$$\begin{aligned}&SdS_4:\quad f(\tau ) = 1-\tau ^2+{2m\over l}\tau ^3 \nonumber \\&\quad = (1-a_1\tau )(1-a_2\tau )(1+(a_1+a_2)\tau )\ , \nonumber \\&a_1^2+a_2^2+a_1a_2=1\ ,\qquad a_1a_2(a_1+a_2)={2m\over l}\ . \end{aligned}$$

(4)

Thus the roots $a_1,a_2$ are constrained as above, and taking the positive root for $a_2$ gives $a_2={1\over 2} (\sqrt{4-3a_1^2}-a_1)$ . Upto an overall $\tau ^2$ factor, $f(\tau )$ is the same as f(r) in (2) so the zeroes of $f(\tau )$ give the locations of the horizons. Thus in the above, we have $\tau _c={1\over a_1}$ and $\tau _s={1\over a_2}$ as the two physical values, corresponding to the cosmological (de Sitter) and Schwarzschild horizons. (The third zero does not correspond to a physical horizon.) The case with $m=0$, or $a_1=1, a_2=0$, is pure de Sitter space. This structure of horizons is valid for ${m\over l}<{1\over 3\sqrt{3}}$ , beyond which there are no horizons. The limit ${m\over l}={1\over 3\sqrt{3}}$ corresponds to the cosmological and Schwarzschild horizon values coinciding: here we have $a_1=a_2=a_0={1\over \sqrt{3}}$ from (4). This special value leads to the extremal, or Nariai, limit where the near horizon region (between the horizons) becomes $dS_2\times S^2$. Overall the range of physically interesting $a_1, a_2$ satisfies $0< a_2< a_0 < a_1$ for generic values, and ${1\over a_1} < {1\over a_2}$ implies that the cosmological horizon is “outside” the Schwarzschild one.

Fig. 1

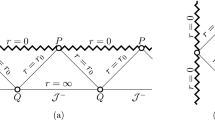
Timelike extremal surfaces $w(\tau )$ in SdS stretching between $I^\pm$, shown as the red curves passing through the vicinity of the cosmological horizon. The dashed blue curves represent hypothetical timelike extremal surfaces of similar nature, but passing near the Schwarzschild horizon in some limit

We want to first consider codim-2 timelike extremal surfaces that stretch from $I^+$ to $I^-$ within a “unit-cell”, as shown in Fig. 1. These lie in some equatorial plane of the $S^2$ and thus wrap an $S^1$ within $S^2$, extend from some fixed boundary subregion at $I^+$ with width $\Delta w$ to an equivalent subregion at $I^-$, stretching in the bulk time direction. For $m=0$, these are identical to the corresponding surfaces in de Sitter discussed in [16]. The area functional for such timelike surfaces is

$$\begin{aligned} S=\ l^{d-1} V_{S^{d-2}} \int {d\tau \over \tau ^{d-1}} \sqrt{{1\over f(\tau )} - f(\tau ) (w')^2}\ , \end{aligned}$$

(5)

where $w'={dw\over d\tau }$ . Extremizing the area integral gives

$$\begin{aligned}&-\frac{f(\tau ) w'}{\sqrt{f(\tau )^{-1}-f(\tau )w'^2}} \frac{1}{\tau ^{d-1}}=B \nonumber \\&\quad \implies f(\tau )^2w'^2=\frac{B^2 \tau ^{2d-2}}{f(\tau )+B^2\tau ^{2d-2}}\ , \end{aligned}$$

(6)

and the extremal surfaces are given by

$$\begin{aligned}&{\dot{w}}^2 \equiv (f(\tau ))^2 (w')^2 = {B^2\tau ^{2d-2}\over f(\tau )+B^2\tau ^{2d-2}}\ , \nonumber \\&S = {2 l^{d-1} V_{S^{d-2}}\over 4G_{d+1}} \int _\epsilon ^{\tau _*} {d\tau \over \tau ^{d-1}}\ {1\over \sqrt{f(\tau )+B^2\tau ^{2d-2}}}\ . \end{aligned}$$

(7)

Here ${\dot{w}}\equiv {dw\over dy}$ with y the tortoise coordinate $y = \int {d\tau \over f(\tau )}$ useful near the horizons: we will discuss this further later. Requiring that ${\dot{w}}^2>0$ near the boundary $\tau \rightarrow 0$ requires $B^2>0$.

The nature of extremal surfaces as timelike or spacelike depends on the local region containing the surface, characterized in particular by the sign of $f(\tau )$. With F/P referring to the future/past universes in the Penrose diagram, $I_F/I_p$ the future/past interior regions and D the diamond shaped region between the horizons, we have

$$\begin{aligned}&F,P,I_F,I_P:\ \ f(\tau )>0 ,\ \ \ 0<\tau<{1\over a_1}\ \ \mathrm{or}\nonumber \\&\quad \tau>{1\over a_2} : {\dot{w}}^2<1\ \mathrm{(timelike)},\ \ {\dot{w}}^2>1\ \mathrm{(spacelike)}, \nonumber \\&D:\quad \ f(\tau )<0 ,\ \ \ {1\over a_1}< \tau< {1\over a_2} : {\dot{w}}^2>1\ \mathrm{(timelike)},\nonumber \\&\quad {\dot{w}}^2<1\ \mathrm{(spacelike)}.\quad \ \ \end{aligned}$$

(8)

In other words, w is a timelike coordinate in D, while it is a spacelike coordinate in $F, P, I_F, I_P$.

Thus the surface (7) satisfies ${\dot{w}}^2<1$ in the future/past universes F, P, and so is timelike. Further, in the diamond D, we have ${\dot{w}}^2>1$, continuing to be timelike. At the horizons, $f=0$ and so ${\dot{w}}^2=1$.

The turning point of an extremal surface such as (20) is the location where ${\dot{w}}^2\rightarrow \infty$ , with the surface roughly beginning to retrace its behaviour until that point: this is typically given by the zero of the denominator in (7). Since $f>0$ in F, P, we have ${\dot{w}}^2<1$ from (20): thus the surface $w(\tau )$ cannot have a turning point there. However a turning point exists in the diamond D since $f<0$ in D. This structure is similar to that of the timelike surfaces in de Sitter in [16]. The turning point in this case satisfies

$$\begin{aligned}&f(\tau _*) + B^2\tau _*^4 = 0 \ ,\nonumber \\&{1\over a_1}< \tau _* < {1\over a_2}\ . \end{aligned}$$

(9)

In the limit where $B\rightarrow 0$, we see that $\tau _*$ approaches a zero of f, i.e. $\tau _*$ approaches either the cosmological ($\tau _*={1\over a_1}$) or the Schwarzschild ($\tau _*={1\over a_2}$) horizon, so we have $B_1^2\tau _{*1}^4=f(\tau _{*1})$ and $B_2^2\tau _{*2}^4=f(\tau _{*2})$ at first sight.

In what follows, we will find surfaces that approach the vicinity of the cosmological horizon: these are shown as the red curves in Fig. 1 and are analogous to the surfaces in [16] in pure de Sitter, with $m=0$ or $a_1=1, a_2=0$. This begs the question of whether there are extremal surfaces that in some limit approach the Schwarzschild horizon: on the face of it, the turning point equation (9) suggests a distinct branch for $\tau _*\rightarrow {1\over a_2}$ as well. Pictorially one might imagine surfaces represented by the dashed blue curves in Fig. 1. If such surfaces exist, one might wonder if there are analogs of “disentangling” transitions observed in holographic mutual information [37]: i.e. for given width $\Delta w$, there would be timelike surfaces passing either near the cosmological or the Schwarzschild horizon (akin to the solid red or dashed blue curves respectively in Fig. 1), with the ones of lower area being picked out by an area minimization prescription. However from Fig. 1, we observe that if the dashed blue curves are timelike but approach the Schwarzschild horizon in some limit, presumably they could only exist for “sufficiently large” width (e.g. a “nearly null” timelike surface would pass close to the Schwarzschild horizon only if it begins near the edge of $I^+$).

Now we will argue that real extremal surfaces of this kind with $B^2>0$ in fact exist only for $\tau _*$ near the cosmological horizon. This is because ${\dot{w}}^2<0$ near the other branch, and more generally between the two turning points: thus it cannot be a real surface. To elaborate, let us recast as

$$\begin{aligned} {\dot{w}}^2 = {B^2\tau ^4\over V(\tau )}\ ,\qquad V(\tau )=f(\tau )+B^2\tau ^4\ , \end{aligned}$$

(10)

and $V(\tau _{*1})=0$ where $\tau _{*1}$ is the turning point near the cosmological horizon ${1\over a_1}$ which satisfies the range in (9). Note that $\tau$ increases from the boundary at $\tau =\epsilon$ to the cosmological horizon ${1\over a_1}$ and then to the Schwarzschild horizon ${1\over a_2}$ in this coordinate parametrization. Since this is a first order zero of $V(\tau )$, expanding near $\tau _{*1}={1\over a_1}$ gives

$$\begin{aligned} {\dot{w}}^2\ \sim \ {B^2\tau ^4\over |V'(\tau _{*1})|\, (\tau _{*1}-\tau )} \end{aligned}$$

(11)

where $V'(\tau _{*1})={dV\over d\tau }|_{\tau _{*1}}$ and we are dropping the higher order terms in this approximation. We know from the explicit form (9) that ${\dot{w}}^2>0$ for $\epsilon<\tau <{1\over a_1}$ and the absolute value in (11) reflects this. We now see that for $\tau > rsim \tau _{*1}$ the sign of ${\dot{w}}^2$ becomes negative. This continues to hold all the way till $V(\tau )$ hits the other zero at ${1\over a_2}$ : this can be seen numerically as in Fig. 2, where we have plotted ${\dot{w}}^2$ as a function of $\tau$ for the representative values $B^2=0.001,\ a_1=0.75$. Further we have $a_2={1\over 2}(\sqrt{4-3a_1^2}-a_1)\sim 0.39,\ {m\over l}={1\over 2} a_1(1-a_1^2) \sim 0.16$, noting that $f(\tau )$ factorizes as (4). In other words, over ${1\over a_1}<\tau <{1\over a_2}$ we have ${\dot{w}}^2<0$ implying that $w(\tau )$ is not real-valued in this range for $B^2>0$. As $B^2$ increases, the two values where ${\dot{w}}^2\rightarrow \infty$ begin to approach each other: at a critical value $B_{max}$ they coincide. We will say more on this later.

Fig. 2

${\dot{w}}^2$ vs $\tau$, for $B^2=0.001$, $a_1=0.75,\ a_2\sim 0.39,\ {m\over l}\sim 0.16$. Here $B^2$ is sufficiently small so that the turning points where ${\dot{w}}^2\rightarrow \infty$ are fairly close to, although not precisely, the horizon values ${1\over a_1}$ and ${1\over a_2}$ . Also plotted is $f(\tau )$ for these values

Overall for $B^2>0$, we see that these surfaces give the red curves in Fig. 1: these are similar to the dS surfaces in [16]. At the horizon ${1\over a_1}$ we have ${\dot{w}}^2=1$. In the limit where $B^2\rightarrow 0$, we see that $\tau _*\sim {1\over a_1}+\delta$: expanding (9) using (4), we obtain

$$\begin{aligned} \tau _*\sim {1\over a_1}+\delta \,:\qquad B^2 \sim \ a_1^5 \Big ( 2 - {a_2(a_1+a_2)\over a_1^2} \Big )\, \delta \equiv \ a_1^5 c \delta .\nonumber \\ \end{aligned}$$

(12)

For $a_1=1, a_2=0$, we have $m=0$ and this becomes $B^2\sim 2\delta$ in agreement with the corresponding expression for the $dS_4$ surface in [16]. More detailed properties of these surfaces can be obtained by using the tortoise coordinate

$$\begin{aligned} y&= \int {d\tau \over f(\tau )}\nonumber \\&= \int \frac{d\tau }{(1-a_1\tau )(1-a_2\tau )(1+(a_1+a_2)\tau )}\ \nonumber \\&\quad \xrightarrow {\,\tau \sim 1/a_1\, }\ \ - {1\over a_1 (2+{a_2\over a_1})(1-{a_2\over a_1})}\, \log |1-a_1\tau |\ \nonumber \\&\equiv \quad -{1\over a_1c} \log |1-a_1\tau |\ , \end{aligned}$$

(13)

with the last approximation valid in the vicinity of the cosmological horizon as $B^2\rightarrow 0$ (more detailed expressions appear in Appendix A). For the region $\tau > rsim {1\over a_1}$ we have $\tau _*\rightarrow {1\over a_1},\ y_*\rightarrow \infty$, so using (12), (13), gives

$$\begin{aligned} c= & {} \Bigg (2+{a_2\over a_1}\Bigg )\Bigg (1-{a_2\over a_1}\Bigg )\ ,\quad \ \ a_1\delta \sim e^{-a_1cy_*}\ ,\nonumber \\&B^2\sim a_1^4c e^{-a_1cy_*}\ ,\quad \ \ \tau \sim {1\over a_1} (1+e^{-a_1cy})\ . \end{aligned}$$

(14)

The area of these surfaces can be evaluated using (7) and the divergent part of the area arises from the region near the boundary ($\tau \sim \epsilon \rightarrow 0$) as

$$\begin{aligned} S= & {} {2 l^2 V_{S^1}\over 4G_4} \int _\epsilon ^{\tau _*} {d\tau \over \tau ^2}\ {1\over \sqrt{1-\tau ^2+{2m\over l}\tau ^3+B^2\tau ^4}}\ ; \nonumber \\ S^{div}\sim & {} {\pi l^2\over G_4} \int _\epsilon ^{1/a_1} {d\tau \over \tau ^2}\nonumber \\&\times {1\over \sqrt{(1-a_1\tau )(1-a_2\tau )(1+(a_1+a_2)\tau )}}\ . \end{aligned}$$

(15)

This gives an area law divergence, scaling as de Sitter entropy ${\pi l^2\over G_4}$, not surprisingly. For $a_1=1, a_2=0$, this matches with the $dS_4$ results in [16]. As in that case, codim-2 surfaces stretching between $I^\pm$ on a $w=const$ slice are difficult to analyse but the area law divergence is straightforward to see, essentially similar to (25). As such, these area integrals are certain kinds of elliptic integrals² and can be evaluated numerically for any particular values of $a_1, a_2$, or equivalently m. This numerical evaluation shows that the area (25) of these surfaces for Schw-dS is always greater than the corresponding area for de Sitter (keeping the same asymptotic structure and cutoff): thus the area law divergence scaling is bigger. In Appendix B, we analyse 3-dim Schwarzschild de Sitter spacetimes and these timelike surfaces: the area of these surfaces in $SdS_3$ can here be seen explicitly to be greater than the corresponding area for $dS_3$ (see (60)).

Analytically speaking, the integral (25) can be expressed in terms of elliptic integrals and functions, as discussed in Appendix C. This agrees with the de Sitter case and has a nonvanishing expression for the physical range of $a_1, a_2$, in (4).

The finite part of the area integral (25) vanishes in the strict $B\rightarrow 0$ limit: for an infinitesimal $\delta B^2\ne 0$ deformation about the $B^2=0$ limit, the finite part of the area can be estimated using the approximations (14) as

$$\begin{aligned}&\delta S\, \sim \ {1\over a_1}\, \delta B^2\ {l^2\over G_4}\ \sim \ {1\over a_1}\, {l^2\over G_4}\ \Bigg (2+{a_2\over a_1}\Bigg )\nonumber \\&\quad \Bigg (1-{a_2\over a_1}\Bigg )\, a_1^5\, \Bigg (\tau _*-{1\over a_1}\Bigg )\ , \end{aligned}$$

(16)

the scaling encoding details of the SdS$_4$ mass m through the parameters $a_1,a_2$.

As stated earlier, the quartic in the denominator of ${\dot{w}}^2$ in (10) has two positive zeros for generic $B^2 > rsim 0$. As $B^2$ increases, these approach each other and finally coincide at $B_{max}$ where ${\dot{w}}^2$ acquires a double zero in the denominator: now $\Delta w \sim \int _0^{y_*} dy\, {\dot{w}}$ acquires a logarithmic divergence and the subregion at $I^\pm$ becomes the whole space. To see what $B_{max}$ is in greater detail, note that B acquires a maximum value at

$$\begin{aligned} B^2 = -{f(\tau _*)\over \tau _*^4}\quad \xrightarrow {\ max\ }\quad {dB^2\over d\tau _*}=0\ \ \Rightarrow \ \ f'(\tau _*) = {4f(\tau _*)\over \tau _*}.\nonumber \\ \end{aligned}$$

(17)

Then expanding near $\tau =\tau _*$ gives

$$\begin{aligned} f(\tau )+B_{max}^2\tau ^4= & {} f(\tau _*)+f'(\tau _*)(\tau -\tau _*)\nonumber \\&-{f(\tau _*)\over \tau _*^4} (\tau _*+\tau -\tau _*)^4+\ldots \end{aligned}$$

(18)

which shows the constant and linear terms in $(\tau -\tau _*)$ cancelling, using (17): this gives a double zero. For instance, $f(\tau )$ in (4) gives

$$\begin{aligned}&{m\over l} = -{2-\tau _*^2\over \tau _*^3} \nonumber \\&\quad \Rightarrow f(\tau _*) = -(3-\tau _*^2)\,,\ B_{max}^2={3-\tau _*^2\over \tau _*^4}\nonumber \\&\quad \Rightarrow \quad f(\tau )+B_{max}^2\tau ^4 = \Bigg (1-{\tau \over \tau _*}\Bigg )^2 \Bigg (1+{2\tau \over \tau _*} \nonumber \\&\qquad + (3-\tau _*^2){\tau ^2\over \tau _*^2}\Bigg )\ , \end{aligned}$$

(19)

with a double zero at $\tau _*$, the expression factorizing. Now $\Delta w$ acquires a logarithmic divergence as $\Delta w \sim {2\over \sqrt{(3-\tau _*^2)(6-\tau _*^2)}} \int ^{\tau _*} {d\tau \over 1-\tau /\tau _*} \sim -{2\tau _*\over \sqrt{(3-\tau _*^2)(6-\tau _*^2)}}\log (1-{\tau \over \tau _*})$ . Beyond $B_{max}$ there is no real solution to $\tau _*$, giving a limiting surface at the $\tau _*(\equiv \tau _*^{max})$ value corresponding to $B_{max}$. This is very similar to the limiting surface in de Sitter space discussed in [32]. At this point, the finite part of the area scales as $S^{fin}\sim \frac{\pi l^2}{G_4}{1\over \tau _*^2\sqrt{6-\tau _*^2} }\int _{1/a_1}^{\tau _*} {d\tau \over 1-\tau /\tau _*} \sim {\pi l^2\over G_4}\frac{\sqrt{3-\tau _*^2}}{2\tau _*^2}\Delta w$ with the same logarithmic divergence, upto numerical factors.

Now we compare the limiting surface at $\tau _*^{max}$ in the Schw-dS space above with the limiting surface in de Sitter space in [32]. From the expression $\frac{m}{l}=-\frac{2-\tau _*^2}{\tau _*^3}$, we see that the value of $\tau _*^{max}$ lies in the range $\sqrt{2}\le \tau _*^{max} < \sqrt{3}$ for $0 \le \frac{m}{l} < \frac{1}{3\sqrt{3}}$. In particular, $\tau _*^{max}=\sqrt{2}$ for $m=0$, corresponding to the limiting surface in de Sitter space. As m increases, $\tau _*^{max}$ increases, showing that the limiting surface in Schw-dS space lies further in the interior, compared to the limiting surface in de Sitter space.

Thus overall, we have obtained timelike extremal surfaces stretching between $I^\pm$ passing through the vicinity of the cosmological horizon. For the case $m=0$, or equivalently $a_1=1, a_2=0$, we obtain empty de Sitter space and recover the results of the timelike extremal surfaces in [16, 32]. As we have seen, similar surfaces passing near the Schwarzschild horizon do not exist: if we insist on surfaces that are anchored at the future boundary $I^+\in F$, the surfaces $w(\tau )$ above do not have the desired behaviour for $B^2>0$ since ${\dot{w}}^2<0$ between the two turning points, thus precluding real surfaces. This appears consistent with the fact that as the subregion becomes the whole space at $I^\pm$, the surfaces approaching the limiting surface and do not go beyond.

Finally, the area functional for codim-1 surfaces in $SdS_{d+1}$ is $S = l^dV_{S^{d-1}} \int {d\tau \over \tau ^d} \sqrt{{1\over f}-f(w')^2}$ , scaling as $l^d$: these wrap the $S^{d-1}$ and stretch in the $(\tau ,w)$-plane. The resulting extremization are similar structurally to (5), (20), except with different $\tau$-factors: as such these can be seen to be equivalent to codim-2 surfaces in $SdS_d$. It may be interesting to analyse these further.

3 Schw-dS extremal surfaces with $B^2<0$

We are looking for surfaces that pass through the vicinity of the Schwarzschild horizon: as we have seen, the surfaces (7) with $B^2>0$ do not do so. However note that the local equation governing extremal surfaces is necessarily given by (20) with the conserved quantity B as a parameter. Thus the only other possibility is to check if the surfaces (7) with $B^2$ continued to $B^2<0$ exhibit any new behaviour. In what follows, we will study this in detail and find that these in fact are spacelike surfaces with interesting behaviour: they pass through the vicinity of the Schwarzschild horizon (as well as the cosmological one), but never reach $I^+$ as real surfaces. Thus consider (20) with $B^2<0$ (focussing on $SdS_4$). This gives the surfaces

$$\begin{aligned} {\dot{w}}^2 \equiv (f(\tau ))^2 (w')^2 = {A^2\tau ^4\over A^2\tau ^4-f(\tau )}\ , \qquad A^2>0\ . \end{aligned}$$

(20)

This can be thought of as the result of extremizing the area functional for spacelike surfaces,

$$\begin{aligned} S=\ l^{d-1} V_{S^{d-2}} \int {d\tau \over \tau ^{d-1}} \sqrt{f(\tau ) (w')^2 - {1\over f(\tau )}}\ . \end{aligned}$$

(21)

As before, these are codim-2 surfaces: they wrap an $S^1$ in some equatorial plane of the $S^2$ and are curves in the $(\tau ,w)$-plane. There is no interpretation for the width $\Delta w$ for these surfaces since as we will see, these surfaces never reach the future/past boundaries $I^\pm$. It thus appears difficult to interpret them via dS/CFT.

Noting (8), we see that the surface (7) satisfies ${\dot{w}}^2<1$ in the diamond D and ${\dot{w}}^2>1$ in $F,P, I_F, I_P$ and is thus a spacelike surface. At the horizons, $f=0$ and ${\dot{w}}^2=1$. Since ${\dot{w}}^2<1$ in D, the surface cannot have a turning point in D. However ${\dot{w}}^2$ can have a turning point in $F, P, I_F, I_P$, where ${\dot{w}}^2\rightarrow \infty$ given by the zero of the denominator in (20): we have

$$\begin{aligned} A^2\tau _*^4 - f(\tau _*) = 0\ ,\qquad \tau _*\in F, P, I_F, I_P\ . \end{aligned}$$

(22)

This has multiple real solutions since $f>0$. Looking near $A\rightarrow 0$ suggests that there are real turning point solutions near the zeros of f. In fact we obtain $\tau _*^1$ near the cosmological horizon and also $\tau _*^2$ near the Schwarzschild one (which can be confirmed numerically). These two turning points satisfy $0<\tau _*^1<{1\over a_1}$ lying in F and $\tau _*^2>{1\over a_2}$ lying in $I_P$, and we note also that

$$ \begin{aligned} A\rightarrow 0\quad \Rightarrow \qquad \quad \tau _*^1\rightarrow {1\over a_1} \qquad \& \qquad \tau _*^2\rightarrow {1\over a_2}\ . \end{aligned}$$

(23)

The surface (7) is real and ${\dot{w}}^2$ is positive between the two turning points near $\tau _*^1 < {1\over a_1}$ and $\tau _*^2 > {1\over a_2}$ .

In addition, an important point to note is that ${\dot{w}}^2$ exhibits a nonzero minimum in D for $A^2\ne 0$: this minimum becomes vanishingly small as $A^2\rightarrow 0$. This behaviour can be seen in the plot of (20) against $\tau$ (which is qualitatively similar to Fig. 2 in the region between the turning points, except for an overall minus sign). The significance of this nonzero minimum is that $w(\tau )$ cannot be tangent to any $w=const$ hypersurface in the D region: for if it were, then ${dw\over d\tau }$ must vanish. This implies that the surface $w(\tau )$ necessarily crosses every $w=const$ slice in D, without being tangent to any slice: thus it cannot approach the future horizon bounding $I_F$. Instead the surface crosses the past horizon bounding $I_p$ and has a turning point $\tau _*^2\rightarrow {1\over a_2}$ in $I_P$ rather than $I_F$. This curious feature of the surface $w(\tau )$ only arises due to the specific cubic form for $f(\tau )$ and the corresponding behaviour of ${\dot{w}}^2$ with nonzero minimum: no such feature arises in the pure de Sitter case, or in the timelike surfaces discussed earlier (which have only one relevant turning point $\tau _*\rightarrow {1\over a_1}$ ).

At the turning points $\tau _*^1\in F$ and $\tau _*^2\in I_P$, the surface can be joined with similar surfaces from the other universes: thus the surface can be extended as a spacelike surface traversing through all the universes (stretching indefinitely). Overall this gives the blue curve in Fig. 3. (Similar spacelike extremal surfaces exist with turning points $\tau _*^1\in P$ and $\tau _*^2\in I_F$, although we have not shown them.) As $A\rightarrow 0$, we have $\tau _*^2\rightarrow {1\over a_2}$ in $I_P$. Thus within the diamond D, we have ${\dot{w}}^2\rightarrow 0$ so that $w(\tau )$ approaches a $w=const$ hypersurface (shown in black in D in Fig. 3). Likewise we have $\tau _*^1\rightarrow {1\over a_1}$ in F: here ${\dot{w}}^2\rightarrow \infty$ with this $\tau =const$ slice approaching $\tau ={1\over a_1}$ . Thus the surface resembles the purple curve: in the strict $A\rightarrow 0$ limit the purple curve asymptotes to a zigzag spacelike curve stretching indefinitely, grazing all the Schwarzschild and de Sitter horizons. On the other hand, as A increases from $A=0$ (which is akin to the limiting purple curve), we find that the two zeros $\tau _*^{1,2}$ of the quartic turning point equation (22) move in opposite directions: i.e. $\tau _*^1 < {1\over a_1}$ and $\tau _*^2 > {1\over a_2}$ . As in the cosmological surfaces case with $B^2>0$, in this case there is a limiting surface with $A=A_{max}$ which is similar in shape to the blue curve, with limiting values for $\tau _*^{1,2}$. This can also be confirmed by numerically evaluating the zeros of (22) for various A values. It is noteworthy that the surfaces here are constrained with regard to two turning points which makes their behaviour/shape different from the cosmological case. In particular, note that the blue and purple curves cross at some nontrivial location, since as A increases from 0 to $A_{max}$ the two zeros move in opposite directions: in the cosmological surfaces there is a single turning point.

Fig. 3

Extremal surfaces in the $(\tau ,w)$-plane of Schw dS: the red curve is timelike, from $I^+$ to $I^-$. The solid blue curve is real and spacelike but does not reach till $I^+$. The blue curve approaches the purple curve as A decreases to a near-vanishing value

These $A^2>0$ surfaces never reach $I^+$ but continue indefinitely as spacelike surfaces, always at some distance from $I^+$. If we require that the surface reaches $I^+$, then it cannot be real-valued at least (if it even exists): it must be interpreted in that vicinity as a complex surface. For instance as $\tau \rightarrow 0$ (approaching $I^+$), we have

$$\begin{aligned} {\dot{w}}^2\sim {A^2\tau ^4\over -f} \sim -A^2\tau ^4 < 0\ , \end{aligned}$$

(24)

which is complex for real $\tau$, or alternatively forces an imaginary time path $\tau =iT$ if we require real $w(\tau )$, interpreting it as the width in the dual CFT and that it be real-valued (this sort of argument was used in [18] to identify complex extremal surfaces in Poincare dS).

The area of the portion of the surface between the two turning points, doubled, is

$$\begin{aligned} S&= 2{l^2 V_{S^1}\over 4G_4} \int _{\tau _*^1}^{\tau _*^2} {d\tau \over \tau ^2}\ {1\over \sqrt{A^2\tau ^4-f(\tau )}}\nonumber \\&\quad \xrightarrow {A\rightarrow 0}\ \ {\pi l^2\over G_4} \int _{1/a_1}^{1/a_2} {d\tau \over \tau ^2}\ {1\over \sqrt{-f(\tau )}}\ , \end{aligned}$$

(25)

where the overall factor of 2 stems from doubling the area so that we cover the “unit cell” fully once, i.e. going from $\tau _*^1$ to $\tau _*^2$ and back to $\tau _*^1$. Since $f<0$ for ${1\over a_1}<\tau <{1\over a_2}$ , this area integral is expected to be well-defined and finite. We confirm this in appendix C, where the last integral in (25) is evaluated. The area integral for spacelike curves is also shown to have a well defined extremal, or Nariai, limit: we discuss further aspects of this extremal limit in what follows.

3.1 The de Sitter limit

It is interesting to note that the de Sitter limit given by $a_1 =1,\ a_2 = 0$ for these spacelike surfaces and the associated turning points are

$$\begin{aligned} {\dot{w}}^2 = {A^2\tau ^4\over A^2\tau ^4-f(\tau )}\ ;\qquad \qquad A^2\tau _*^4=f(\tau _*)=1-\tau _*^2\ , \end{aligned}$$

(26)

with a real solution for $\tau _*$ only in F or P. The spatial “ends” of these surfaces, at $\tau \rightarrow \infty$, appear ill-defined however. Here ${\dot{w}}^2\rightarrow 1$ and the surfaces end on the North/South pole trajectories in N/S but their endpoints appear ill-defined: $\tau =\infty$ corresponds to the poles which have no spatial extent. Pictorially these resemble the portion of the blue curve lying in the de Sitter part of the Penrose diagram in Fig. 3, and so bear resemblance to the Hartman, Maldacena surfaces [22] in the AdS black hole. The present surface here can perhaps be better defined by introducing a cutoff surface at large $\tau$ that encircles the poles.

One can formally calculate the area (25) in the $A\rightarrow 0$ limit where the turning point approaches the horizon at $\tau =1$. This gives

$$\begin{aligned} S\ \rightarrow \ {\pi l^2\over G_4} \int _1^\infty {d\tau \over \tau ^2}\ {1\over \sqrt{\tau ^2-1}}\ \rightarrow \ {\pi l^2\over G_4}\ . \end{aligned}$$

(27)

Interestingly, this is finite and the value is precisely de Sitter entropy.

As stated previously, these are codim-2 spacelike surfaces wrapping an $S^1$ in some equatorial plane of the $S^2$ and stretching as curves in the $(\tau ,w)$-plane. Thus the area arises from the $S^1$ and $\tau$-directions, and is not the $S^2$ area per se. As for all these spacelike surfaces we have been discussing, these ones “hang” at some distance from the future/past boundaries $I^\pm$, which they never reach. It thus appears difficult to interpret them via dS/CFT a priori. These are thus quite different from the connected timelike surfaces stretching between $I^\pm$ in [16]. Those have an area law divergence ${\pi l^2\over G_4} \int _\epsilon ^1 {d\tau \over \tau ^2} {1\over \sqrt{1-\tau ^2}} = {\pi l^2\over G_4} {1\over \epsilon }$ scaling as de Sitter entropy (perhaps consistent with the leading area law divergence expected of entanglement entropy in a CFT in a gravity approximation).

3.2 The extremal, or Nariai, limit

As mentioned earlier, the Schwarzschild de Sitter spacetime admits an interesting extremal, or Nariai, limit, where the values of the cosmological and Schwarzschild horizons coincide,

$$\begin{aligned} a_1=a_2=a_0 :\,\, f(\tau )=(1-a_0\tau )^2(1+2a_0\tau ) > 0 . \end{aligned}$$

(28)

In this case, the near horizon region of the metric (3) becomes $dS_2\times S^2$. The region $\tau \rightarrow 0$ is the asymptotic $dS_4$ region. In this extremal limit, we see that $f(\tau )>0$ always and thus the surfaces (7) satisfy ${\dot{w}}^2<1$ and so do not exhibit any turning point (somewhat similar to the surfaces [18] in Poincare de Sitter). However the spacelike surfaces (20) continue to be interesting: the turning points are

$$\begin{aligned} A^2\tau _*^4 = (1-a_0\tau _*)^2 (1+2a_0\tau _*)\ , \end{aligned}$$

(29)

so that $\tau _*^1\leftrightarrow \tau _*^2$. Thus the blue curves now look symmetric between the two horizons and lead to the purple curve in the $A\rightarrow 0$ limit (Fig. 4).

In more detail in the Nariai limit, ${m\over l}={1\over 3\sqrt{3}}$ so that $a_0 = \frac{1}{\sqrt{3}}$ and

$$\begin{aligned} f(\tau ) = \frac{(\sqrt{3}-\tau )^2 (\sqrt{3}+2\tau )}{3\sqrt{3}}\ . \end{aligned}$$

(30)

The tortoise coordinate $y = \int \frac{d\tau }{f(\tau )}$ in (13) becomes (see Appendix A)

$$\begin{aligned}&y =\frac{1}{\sqrt{3}-\tau } +\frac{2\sqrt{3}}{9}\log \Big |\nonumber \\&\frac{\sqrt{3}+2\tau }{\sqrt{3}-\tau }\Bigg | - \frac{1}{\sqrt{3}}\ \end{aligned}$$

(31)

In the $A\rightarrow 0$ limit, the turning points approach the horizon i.e. $\tau _*^{1,2}\rightarrow \frac{1}{a_0} = \sqrt{3}$. So let us consider the near-horizon region, $\tau \rightarrow \sqrt{3}$, where we have $f(\tau ) \approx (\sqrt{3}-\tau )^2$ and the tortoise coordinate can be approximated as $y \approx \frac{1}{\sqrt{3}-\tau }$ . The equation for spacelike surfaces (7) becomes

$$\begin{aligned} {\dot{w}}^2 = \Big (\frac{dw}{dy}\Big )^2 \approx \frac{A^2(\sqrt{3}\,y-1)^4}{A^2(\sqrt{3}\,y-1)^4-y^2}\ . \end{aligned}$$

(32)

In F with $\tau < \sqrt{3}$ : The turning point with $A>0$ and $y>0$ is given by

$$\begin{aligned} A^2(\sqrt{3}\,y_* - 1)^4-y_*^2 = 0 \,\,\implies \,\, A(\sqrt{3}\,y_* - 1)^2=y_*\ ,\nonumber \\ \end{aligned}$$

(33)

whose roots are

$$\begin{aligned} y_* = \frac{(2\sqrt{3}A+1)\pm \sqrt{1+4\sqrt{3}A}}{6A}\ . \end{aligned}$$

(34)

We see that there is a turning point $y_*^{(1)} = \frac{(2\sqrt{3}A+1) + \sqrt{1+4\sqrt{3}A}}{6A}>0$, which approaches the horizon i.e. $y_*^{(1)} \rightarrow \infty$ as $A\rightarrow 0$.

In I with $\tau > \sqrt{3}$ : The turning point with $A>0$ and $y<0$ is given by

$$\begin{aligned} A^2(\sqrt{3}\,y_* - 1)^4-y_*^2 = 0 \,\,\implies \,\, A(\sqrt{3}\,y_* - 1)^2 = -y_*,\nonumber \\ \end{aligned}$$

(35)

whose roots are

$$\begin{aligned} y_* = -\frac{(1-2\sqrt{3}A)\pm \sqrt{1-4\sqrt{3}A}}{6A}\ . \end{aligned}$$

(36)

We see that there is a turning point $y_*^{(2)} = - \frac{(1-2\sqrt{3}A) + \sqrt{1 - 4\sqrt{3}A}}{6A}<0$ for $0< A < \frac{1}{4\sqrt{3}}$, which also approaches the horizon i.e. $y_*^{(2)} \rightarrow \infty$ as $A\rightarrow 0$.

Thus, we see that for spacelike surfaces described by (20), there are turning points in both $\tau < \sqrt{3}$ and $\tau > \sqrt{3}$ regions for $0< A < \frac{1}{4\sqrt{3}}$. These are the analogs of $\tau _*^{1,2}$ in the previous section, away from the Nariai limit. The upper bound on A i.e. $A < \frac{1}{4\sqrt{3}}$ is approximate as it is obtained by using approximate tortoise coordinate, near the horizon and for $A\rightarrow 0$. To get the exact maximum value $A_{max}$, we maximize $A(\tau _*)$ using (29);

$$\begin{aligned} A^2&= \frac{\big (1-\frac{\tau _*}{\sqrt{3}}\big )^2\big (1+\frac{2\tau _*}{\sqrt{3}}\big )}{\tau _*^4}\nonumber \\&\quad \xrightarrow {\ max\ } \quad \frac{dA^2}{d\tau _*} \nonumber \\&= -\frac{1}{\tau _*^5}\Bigg (\frac{\tau _*^3}{3\sqrt{3}} -\tau _*^2 +2\Bigg ) = 0 \nonumber \\&\quad \implies A_{max}^2 = \frac{2\sqrt{3}-3}{12}\quad \text {at}\quad \tau _* = 3 + \sqrt{3}\ . \end{aligned}$$

(37)

This $A_{max}$ leads to a limiting surface (below).

Fig. 4

Extremal surfaces in the $(\tau ,w)$-plane in the Nariai limit of Schw dS: the blue curve is for generic A, while the $A\rightarrow 0$ limit gives the purple curve

Overall this gives the spacelike extremal surfaces in the Penrose diagram in Fig. 4 for the surfaces (7). The Penrose diagram shows a region F with $0\le \tau \le {1\over a_0}$ containing the asymptotic de Sitter region $\tau \rightarrow 0$, as well as an interior region I with ${1\over a_0}<\tau <\infty$ containing the singularity: this “unit cell” repeats. As we have seen above, there are turning points in both F and I regions. At the horizons, we have $f(\tau )=0$ and ${\dot{w}}^2=1$. Away from the horizon we have $f\ne 0$ so that ${\dot{w}}^2\sim {-A^2\tau ^4\over f}\sim 0$ which implies that this approaches a $w=const$ slice. Since this is true for both F and I regions, we obtain the purple curve in the $A\rightarrow 0$ limit, which runs close to the horizons. For any infinitesimal $A\ne 0$ regulator, the surface is spacelike, not null, and so it only approximately grazes the horizons. As A increases from $A=0$, we find that the two zeros $\tau _*^{1,2}$ of the quartic turning point equation (29) move in opposite directions: i.e. $\tau _*^1 < \sqrt{3}$ and $\tau _*^2 > \sqrt{3}$ . As A approaches $A_{max}$, there is a limiting surface similar in shape to the blue curve, with limiting values for $\tau _*^{1,2}$. The turning points (29) themselves can be seen to never approach the boundary or singularity: there are no real $\tau _*$ solutions for both $\tau _*\rightarrow 0$ (where the quartic term is negligible relative to f) and $\tau _*\rightarrow \infty$ (where the quartic term overpowers f). Thus in some sense, the surfaces (20) are repelled from both near-boundary and near-singularity regions, corresponding to the limiting values for $\tau _*^{1,2}$ where the limiting surface arises.

The area (25) in this Nariai limit must be evaluated carefully, by regulating $a_1=a_0-\epsilon$ and $a_2=a_0+\epsilon$. The limits of the integral then pinch off, which may be expected to cancel a corresponding zero from $\sqrt{-f}$ in the denominator, thereby leading to a finite area. This is confirmed numerically. The recasting of the area (25) in terms of elliptic integrals and functions in Appendix C helps in making this precise. In particular we obtain

$$\begin{aligned} S_{Nariai} = {\pi ^2 l^2\over 3G_4}\ , \end{aligned}$$

(38)

which is ${\pi \over 3}$ times de Sitter entropy. The limiting surface in this case appears to run along the Schwarzschild and cosmological horizons and the area receives contributions from both horizons. The numerical value itself thus does not correspond to any quantity pertaining to either horizon alone.

3.3 Schwarzschild de Sitter and analytic continuations

So far we have been studying the extremization problem in Schwarzschild de Sitter directly. Now we will try to map the $SdS_4$ extremization via analytic continuation to extremization problems in the $AdS_4$ Schwarzschild spacetime. The Poincare version of this was discussed in [18] for the $dS_4$ black brane [36], where these were analytic continuations of the Ryu-Takayanagi expressions in the $AdS_4$ black brane (in this case $f(\tau )=\tau ^2-{C\over \tau }$ with no 1 as is usual for branes, so that the cubic admits no Nariai limit). The discussion below however seems slightly different since the analytic continuation involved is distinct. Note that the analytically continued AdS cases do not appear to admit any Nariai limit.

It is useful to recall the familiar analytic continuation of Euclidean AdS to Poincare dS

$$\begin{aligned}&r\rightarrow -i\tau ,\ R\rightarrow -iR_{dS}\quad \ \Rightarrow \quad \ ds^2={R^2\over r^2} (dr^2+dx_i^2) \nonumber \\&\quad \longrightarrow ds^2={R_{dS}^2\over \tau ^2} (-d\tau ^2+dx_i^2)\ . \end{aligned}$$

(39)

In the present case, consider the 4-dim Schwarzschild de Sitter spacetime in the form

$$\begin{aligned} ds^2= & {} -f(r) dt^2 + {dr^2\over f(r)} +r^2 d\Omega _2^2\ , \nonumber \\ f(r)= & {} 1-{r^2\over l^2}-{2m\over r}\ . \end{aligned}$$

(40)

This can be transformed to the $AdS_4$ Schwarzschild spacetime by analytic continuation

$$\begin{aligned}&l\rightarrow iL\qquad \Rightarrow \qquad ds^2 = -f(r) dt^2 + {dr^2\over f(r)} +r^2 d\Omega _2^2\ , \nonumber \\&f(r)=1+{r^2\over L^2}-{2m\over r}\ , \end{aligned}$$

(41)

which has real mass parameter m. The boundary structure as $r\rightarrow \infty$ is

$$\begin{aligned}&ds^2 \sim {r^2\over L^2} (-dt^2+L^2d\Omega ^2) \nonumber \\&\quad + L^2 {dr^2\over r^2} \equiv {r^2\over L^2} (-dt^2+dx_idx_i) + L^2 {dr^2\over r^2} \end{aligned}$$

(42)

where we are approximating the large $S^2$ by a plane: thus this resembles the Poincare slicing asymptotically. For $m=0$, this simply maps global AdS to $dS_{static}$,

$$\begin{aligned} ds^2&= -\Bigg (1-{r^2\over l^2}\Bigg ) dt^2 + {dr^2\over 1-{r^2\over l^2}} \nonumber \\&\quad + r^2 d\Omega _2^2\ \ \ \xrightarrow {\ l\rightarrow iL\ }\ \ \ ds^2 = -\Bigg (1+{r^2\over L^2}\Bigg ) dt^2 \nonumber \\&\quad + {dr^2\over 1+{r^2\over L^2}} + r^2 d\Omega _2^2\ . \end{aligned}$$

(43)

In terms of the $\tau$-coordinate, Schwarzschild de Sitter is (2), i.e.

$$\begin{aligned} ds^2= & {} {l^2\over \tau ^2} \Bigg (-{d\tau ^2\over f(\tau )} + f(\tau ) dw^2 + d\Omega _{d-1}^2\Bigg ) , \nonumber \\ f(\tau )= & {} 1-\tau ^2+{2m\over l}\tau ^{2d-3}\,,\ \ \tau ={l\over r}\,,\ w={t\over l}\ . \end{aligned}$$

(44)

Note that $\tau , w$ are both dimensionless. It is useful to keep the scales explicit, rewriting as

$$\begin{aligned} ds^2= & {} {l^2\over T^2} \Bigg (-{dT^2\over f(T)} + f(T) dW^2 + l^2d\Omega _2^2\Bigg ), \nonumber \\ f(T)= & {} 1-{T^2\over l^2}+{2m\over l^4}T^3\ ,\ \ T=l\tau ={l^2\over r}\,,\ w={W\over l}\,. \end{aligned}$$

(45)

Now the analytic continuation above gives

$$\begin{aligned}&l\rightarrow iL,\ T\rightarrow -T\ \ \ \longrightarrow \ \ \ ds^2 = {L^2\over T^2} \Bigg (- f(T) dW^2 \nonumber \\&\quad + {dT^2\over f(T)} + L^2d\Omega _2^2\Bigg ), \quad f(T) = 1+{T^2\over L^2}-{2m\over L^4}T^3\ \end{aligned}$$

(46)

We see this is identical to the earlier AdS Schwarzschild metric (41) with $T={L^2\over r}$ being the effective bulk radial coordinate. In terms of $\tau$, this analytic continuation is $l\rightarrow iL\ ,\ \tau \rightarrow i\rho$. Note that the AdS Schwarzschild here does not admit any analog of the Nariai limit: this appears due to the difference in the locations of the minus signs. Thus the Nariai limit in Schwarzschild de Sitter needs to be treated independently, as in our discussion earlier.

The extremal surfaces (7) in the coordinates (45) become

$$\begin{aligned} {(f(T))^2\over l^2} \Big ({dW\over dT}\Big )^2 = {B^2T^4/l^4\over f(T) + B^2T^4/l^4}\ . \end{aligned}$$

(47)

Under the analytic continuation (46) above, these surfaces become

$$\begin{aligned}&-{(f(T))^2\over L^2} \Big ({dW\over dT}\Big )^2 \nonumber \\&\quad = {-A^2T^4/L^4\over f(T) - A^2T^4/L^4}\ \qquad \qquad [B^2=-A^2]\ , \end{aligned}$$

(48)

where we have taken $B^2\rightarrow -A^2$, as for the surfaces (20). The overall minus signs cancel giving real surfaces W(T). This is the analog of the Ryu-Takayanagi extremization in the above AdS background, but on a “time”-slice obtained by taking one of the equatorial planes of $S^2$. Now in the analytically continued AdS-Schw case above, the turning point $T_*$ is given by $f(T_*)-A^2T_*^4=0$ and the width $\Delta l$ scales as $\Delta l\sim {1\over \sqrt{A}}$ in analogy with the AdS case. When $A\rightarrow 0$, it appears that the turning point approaches $f\rightarrow 0$ i.e. $T_*\rightarrow T_h$, in other words the extremal surface wraps the horizon (analogous to the AdS black hole case).

Thus these RT/HRT surfaces in the AdS Schwarzschild under the above analytic continuation map to the spacelike surfaces (7) in Schwarzschild de Sitter. Note by comparison that the surfaces (20) in Schw-dS or dS-static [16] are not analytic continuations of any obvious AdS RT/HRT extremization, although they are analogous to rotated versions of the Hartman, Maldacena surfaces [22]. Note also that this is all with real mass parameter for the AdS Schwarzschild, and so appear distinct from the analytic continuations in [30, 31], arising in the no-boundary proposal. Our goal here is to simply map the extremal surfaces we have discussed to some extremization problems in AdS.

$EAdS_4$ Schw $\rightarrow$ $SdS_4^{im}$ analytic continuation: Consider the Euclidean $AdS_4$ Schwarzschild black hole, which is (41) with $t\rightarrow -it$: the analytic continuation $r\rightarrow -i\tau$ gives

$$\begin{aligned}&ds^2 = f(r)dt^2 + {dr^2\over f(r)} + r^2d\Omega _2^2\ ,\nonumber \\&\qquad f(r) = 1 + {r^2\over l^2} - {2m\over r} \nonumber \\&\quad \xrightarrow {r\rightarrow -i\tau } ds^2 = - {d\tau ^2\over 1 - {\tau ^2\over l^2} - {2mi\over \tau }} \nonumber \\&\qquad + \Bigg (1 - {\tau ^2\over l^2} - {2mi\over \tau }\Bigg ) dt^2 - {\tau ^2\over l^2} (l^2d\Omega _2^2). \end{aligned}$$

(49)

For large $\tau$, this is approximated as

$$\begin{aligned} ds^2= & {} -\left( -{d\tau ^2\over {\tau ^2\over l^2} + {2mi\over \tau }} \right. \nonumber \\&\quad \left. + \Bigg ( {\tau ^2\over l^2} + {2mi\over \tau }\Bigg ) dt^2 + {\tau ^2\over l^2} (l^2d\Omega _2^2)\right) . \end{aligned}$$

(50)

For $m=0$, this becomes $l^2 {d\tau ^2\over \tau ^2} - {\tau ^2\over l^2} (dt^2 + l^2d\Omega _2^2)$. For large $\tau$, approximating the boundary $(t,\Omega _2)$ as $(t,x_i)\equiv R^3$ suggests the analytic continuation $l\rightarrow -il$ to obtain $dS_4$, the overall minus sign being absorbed by this analytic continuation in l. This approximation for nonzero m gives the $dS_4$ black brane [36]

$$\begin{aligned} \xrightarrow {l\rightarrow -il} ds^2 = -{d\tau ^2\over {\tau ^2\over l^2} - {2mi\over \tau }} + \Bigg ( {\tau ^2\over l^2} - {2mi\over \tau }\Bigg ) dt^2 + {\tau ^2\over l^2} dx_i^2\ .\nonumber \\ \end{aligned}$$

(51)

Note that in obtaining this, we have pulled a factor of $l^2$ into the sphere and not continued that: this amounts to approximating the large sphere of size l by a plane. The final complex asymptotically $dS_4$ space can in fact be obtained via analytic continuation from the $EAdS_4$ Schwarzschild black brane $ds^2 = dr^2/({r^2\over R^2}-{2m\over r}) + ({r^2\over R^2}-{2m\over r}) dt^2 + {r^2\over R^2} dx_i^2$.

The Ryu-Takayanagi surface on a $t=const$ slice of $EAdS_4$ Schwarzschild can be mapped to a corresponding surface in this $dS_4$ black brane by analytic continuation [18]. The corresponding surface is parametrized along imaginary time paths: the IR limit where the RT-AdS surface wraps the Schwarzschild horizon maps to an “IR” limit corresponding to $\tau =i\tau _0$ where $\tau _0$ maps to the AdS Schwarzschild horizon. Similarly, other surfaces in the $dS_4$ brane with imaginary mass can be obtained by analytic continuation from the EAdS black brane.

This suggests that similar analytic continuations can be used to map RT surfaces in the EAdS Schwarzschild black hole (49) to those in the Schwarzschild de Sitter space with imaginary mass (49) (with the $l^2d\Omega ^2$ held fixed under analytic continuation). It would be interesting to understand these structures, towards understanding imaginary mass $SdS_4$ spacetimes.

4 Comments

We have studied extremal surfaces in the Schwarzschild de Sitter black hole spacetime $SdS_{d+1}$ with real mass. We find codim-2 timelike surfaces on $S^{d-1}$ equatorial planes stretching from $I^+$ to $I^-$ passing through the vicinity of the cosmological horizon: these are analogs of the future-past surfaces in de Sitter space discussed in [16, 32], described by ${\dot{w}}^2 = {B^2\tau ^{2d-2}\over f(\tau ) + B^2\tau ^{2d-2}}$ with $B^2>0$. There is a limiting surface when the subregion at $I^\pm$ becomes the whole space, as in the de Sitter case. For $B^2<0$, these are spacelike surfaces passing through the vicinity of the Schwarzschild and cosmological horizons in a certain limit: these also admit an interesting Nariai limit. These spacelike surfaces can be obtained as certain analytic continuations of RT/HRT surfaces in AdS Schwarzschild as we have seen: other analytic continuations of (Euclidean) $AdS_4$ Schwarzschild are related to Schwarzschild de Sitter with imaginary mass (related discussions appear for the $dS_4$ black brane [36]). These latter imaginary mass $SdS_4$ spaces arise in certain limits of dS/CFT [30].

The future-past extremal surfaces in de Sitter are perhaps best regarded as encoding some sort of bulk entanglement entropy, as discussed in [32]. From this point of view, although real mass SdS spaces do not appear to arise in dS/CFT, one might consider the black hole as an excitation over de Sitter and thereby expect the area of the cosmological extremal surfaces we have discussed to encode information about SdS spaces. In this regard, we have seen that the area of these surfaces is greater than the corresponding area in de Sitter: as we have seen, $S_{SdS}\ge S_{dS}$ in all cases for the cosmological surfaces (see the discussions after (25) for $SdS_4$ and Appendix B for $SdS_3$). This is reminiscent of the behaviour of extremal surfaces in the AdS black hole (where in the IR limit, the surface hugs the horizon and the finite part of the area is the thermal entropy [1, 2]): here also the area of the surfaces increases $S_{SdS}$ with the mass perturbation to empty de Sitter. However this behaviour is markedly different from the thermodynamic entropy which is known to decrease upon adding mass to de Sitter [10]! Thus while the extremal surfaces do not directly encode the entropy, they do scale as de Sitter entropy and also encode the mass parameter (and thereby the entropy, if only indirectly).

We now make a few comments on the cosmological surfaces, thinking of them as SdS generalizations of the future-past surfaces in de Sitter space [16, 32]. In particular in [32], a codim-1 envelope surface was discussed arising from the family of codim-2 surfaces. This leads to an analog of the entanglement wedge [38,39,40] as the codim-0 interior of the bulk region bounded by the extremal surface and the subregions at $I^\pm$. These exhibit various geometric properties: e.g. the extremal surfaces lie in the causal shadow of the boundary subregions, consistent with causality for entanglement. Further they also lead to an analog of subregion duality in de Sitter space: a boundary subregion maps to the corresponding bulk subregion defined by the entanglement wedge for the corresponding future-past extremal surfaces. Similar arguments can be made for the cosmological surfaces in the present case: since real mass Schwarzschild de Sitter does not appear to have clear interpretation in terms of dS/CFT, these arguments are heuristic here but do reveal similar geometric properties for the surfaces. For instance, a codim-1 envelope surface arises from the family of codim-2 surfaces which then defines an analog of the “entanglement wedge” as the interior of the region bounded by the red extremal surface curve (Fig. 1) and the boundary subregions at $I^\pm$: this is entirely confined to the F, P, D regions of the spacetime. Since these surfaces do not approach the vicinity of the Schwarzschild horizon (recalling the existence of the limiting surface), the “entanglement wedge” also does not access the vicinity of the Schwarzschild horizon. This is perhaps consistent with the geometric fact (and causality) that the Schwarzschild region (in particular its interior) is spacelike separated from all points of $I^\pm$. It is amusing to note that the entanglement wedge region for SdS is “bigger”, in a sense, than that in pure de Sitter. For instance the corresponding limiting surface dips further into the interior (the D region), with the corresponding turning point value $\tau _*^{max}$ larger than that in dS: from the discussion around (17), the limiting surface satisfies $\sqrt{2}\le \tau _*^{max} < \sqrt{3}$, with $\sqrt{2}$ for $m=0$ i.e. dS and approaching $\sqrt{3}$ as m approaches the Nariai value ${m\over l}={1\over 3\sqrt{3}}$ (in this regard, note that the black hole moves the cosmological horizon to $\tau _1={1\over a_1}$ , outward compared with de Sitter). This is perhaps consistent with the area $S_{SdS}$ being bigger as well, as stated above.

Overall, we note that the extremal surfaces we have been discussing are perhaps best regarded as new probes of such cosmological spacetimes, and would be interesting to understand better.

Appendices

Tortoise coordinates and Penrose diagrams

In this appendix, we give constructions of the Penrose diagrams for $SdS_4$ in Fig. 3 and extremal $SdS_4$ in Fig. 4.

Penrose diagram for $SdS_4$

For $SdS_4$ with $f(\tau )$ in (4), the tortoise coordinate $y=\int \frac{d\tau }{f(\tau )}$ in (13) can be integrated in the D region to get [41]

$$\begin{aligned}&y = -\beta _1\log (1-a_1\tau ) +\beta _2\log (1-a_2\tau ) \nonumber \\&\qquad +\beta _3\log (1+(a_1 + a_2)\tau )\ ; \nonumber \\&\beta _1 = \frac{a_1}{3a_1^2 -1}\ , \quad \beta _2 = -\frac{a_2}{3a_2^2 -1}\ , \quad \beta _3 \nonumber \\&\quad = \frac{a_1 + a_2}{3a_1a_2 +2}\ , \qquad \beta _1,\beta _2,\beta _3 > 0\ . \end{aligned}$$

(52)

In the D region, $y\rightarrow \infty$ as $\tau \rightarrow \tau _d=\frac{1}{a_1}$ and $y\rightarrow -\infty$ as $\tau \rightarrow \tau _s=\frac{1}{a_2}$. The ingoing and outgoing radial null coordinates are $(w-y)$ and $(w+y)$ respectively and using these we can define Kruskal-type coordinates. However, the entire Penrose diagram for $SdS_4$ cannot be covered by a single set of Kruskal-type coordinates. We use two sets of coordinates : the Kruskal-type coordinates, $U_2 = -e^{-\frac{w-y}{2\beta _2}}$ and $V_2 = e^{\frac{w+y}{2\beta _2}}$ around the Schwarzschild horizon (i.e. in D and I regions) and Gibbons–Hawking coordinates, $U_1 = e^{\frac{w-y}{2\beta _1}}$ and $V_1 = -e^{-\frac{w+y}{2\beta _1}}$ around the cosmological horizon (i.e. in F and D regions) [41]. From $U_1 V_1 = -e^{-\frac{y}{\beta _1}} \rightarrow -\infty$ as $y\rightarrow -\infty$ at $\tau =\frac{1}{a_2}$, we see the coordinates $(U_1,V_1)$ break down at the Schwarzschild horizon. Similarly, $U_2 V_2 = -e^{\frac{y}{\beta _1}} \rightarrow \infty$ as $y\rightarrow \infty$ at $\tau =\frac{1}{a_1}$ showing that $(U_2,V_2)$ break down at the cosmological horizon.

As $(w-y)$ varies from $-\infty$ to $\infty$, $U_1$ varies from 0 to $\infty$, and as $(w+y)$ varies from $-\infty$ to $\infty$, $V_1$ varies from $-\infty$ to 0. Extending the range of $U_1$, $V_1$ to $U_1\in (-\infty ,\infty )$ and $V_1\in (-\infty ,\infty )$, then covers the 4 regions : F, P and two adjacent D (which include the red curves) in Fig. 3. Similarly, as $(w-y)$ varies from $-\infty$ to $\infty$, $U_2$ varies from $-\infty$ to 0, and as $(w+y)$ varies from $-\infty$ to $\infty$, $V_2$ varies from 0 to $\infty$. Then extending their range to $U_2\in (-\infty ,\infty )$ and $V_2\in (-\infty ,\infty )$ covers the 4 regions : $I_F$, $I_P$ and two adjacent D (which include the blue curve) in Fig. 3.

Penrose diagram for extremal $SdS_4$

For the extremal $SdS_4$ with $f(\tau )$ in (30), the tortoise coordinate $y=\int \frac{d\tau }{f(\tau )}$ can be integrated to get

$$\begin{aligned} y = \frac{1}{\sqrt{3}-\tau } +\frac{2\sqrt{3}}{9}\log \Big |\frac{\sqrt{3}+2\tau }{\sqrt{3}-\tau }\Big | - \frac{1}{\sqrt{3}}\ , \end{aligned}$$

(53)

which is normalized so that at the future boundary $I^+$ at $\tau = 0$, $y = 0$. As we approach the horizon in F and I regions i.e. $\tau \rightarrow \tau _0^-$ and $\tau \rightarrow \tau _0^+$, $y\rightarrow \infty$ and $y\rightarrow -\infty$ respectively. At the singularity $\tau \rightarrow \infty$, $y\equiv y_c = \frac{2\sqrt{3}}{9}\log 2 -\frac{1}{\sqrt{3}} < 0$. The discontinuity in tortoise coordinate y at the degenerate horizon $\tau _0=\sqrt{3}$ suggests that we use different sets of coordinates in the F and I regions.

The Penrose diagram Fig. 4 is for extremal white-holes and following [42], we define the Kruskal-type coordinates $({\tilde{u}},{\tilde{v}})$ as $u=y_c \cot {\tilde{u}}$ and $v=y_c\tan {\tilde{v}}$. Here $u=w-y$ and $v=w+y$ are the ingoing and outgoing null coordinates respectively. In Fig. 4, the ${\tilde{u}}$ and ${\tilde{v}}$ axes are at angles $\frac{3\pi }{4}$ and $\frac{\pi }{4}$ with respect to $I^+$. In the F region, the left and right horizons correspond to $v\rightarrow \infty$, ${\tilde{v}}=-\frac{\pi }{2}$ and $u\rightarrow -\infty$, ${\tilde{u}}=0$ respectively. In the I region, the left and right horizons correspond to $u\rightarrow \infty$, ${\tilde{u}}=0$ and $v\rightarrow -\infty$, ${\tilde{v}}=\frac{\pi }{2}$ respectively.

$SdS_3$ and extremal surfaces

The 3-dim case is somewhat special so we analyze it here separately. The metric (2) for $SdS_3$ is

$$\begin{aligned} ds^2= & {} - f(r) dt^2 + \frac{1}{f(r)} dr^2 + r^2 d\phi ^2\,,\nonumber \\ f(r)= & {} 1 - 8G_3E - \frac{r^2}{l^2}\ . \end{aligned}$$

(54)

Unlike in higher dimensions, there is only one root here where $f(r)=0$, namely

$$\begin{aligned} r_C = l \alpha \,;\qquad \alpha = \sqrt{1 - 8 G_3 E}\ . \end{aligned}$$

(55)

Thus the spacetime admits only one horizon, as in de Sitter. This metric (54) describes an asymptotically de Sitter spacetime with a pointlike object of mass E. When $E=0$, we have $\alpha = 1$ and we recover $dS_3$. On the other hand, $E = \frac{1}{8G_3}$ gives $\alpha =0$: here the horizon pinches off giving a degenerate limit.

Recasting in terms of the $\tau$-coordinate as in (3) gives

$$\begin{aligned} ds^2 = \frac{l^2}{\tau ^2} \left( -\frac{d\tau ^2}{1-\alpha ^2\tau ^2} + (1 - \alpha ^2\tau ^2) dw^2 + d\phi ^2\right) . \end{aligned}$$

(56)

Restricting to the equatorial plane ($\phi = \frac{\pi }{2}$) and simplifying the area functional (5) leads to timelike extremal surfaces (7), which become

$$\begin{aligned}&{\dot{w}}^2 \equiv (f(\tau ))^2 (w')^2 = {B^2\tau ^{2}\over 1-\alpha ^2\tau ^2+B^2\tau ^2}\ , \nonumber \\&\quad S = {l\over G_3} \int _\epsilon ^{\tau _*} {d\tau \over \tau }\ {1\over \sqrt{1-\alpha ^2\tau ^2+B^2\tau ^2}}\ . \end{aligned}$$

(57)

Here ${\dot{w}}$ refers to the y-derivative with y the tortoise coordinate. The turning point $\tau _*$ where ${\dot{w}}\rightarrow \infty$ is, from (57),

$$\begin{aligned} 1 - (\alpha ^2 - B^2) \tau _*^2 = 0\ , \quad {i.e.}\quad \tau _* = \frac{1}{\sqrt{\alpha ^2 - B^2}}\ . \end{aligned}$$

(58)

Thus a real turning point exists only if $B^2 \le \alpha ^2$. For any nonzero B, the turning point satisfies $\tau _*>{1\over \alpha }$ . As $B\rightarrow 0$, we have $\tau _*\rightarrow {1\over \alpha }$ so that the turning point approaches the horizon, while $\tau _*\rightarrow \infty$ as $B\rightarrow \alpha$. The area of the surface (57) becomes

$$\begin{aligned} S = {l\over G_3}\, \log {2\tau _*\over \epsilon }\ \sim \ {l\over G_3}\, \log {2/\sqrt{1-8G_3E}\over \epsilon }\ . \end{aligned}$$

(59)

To compare this with the corresponding area in $dS_3$, we obtain

$$\begin{aligned} S_{SdS_3}-S_{dS_3} = {l\over G_3} \log {1\over \sqrt{1-8G_3E}}\ , \end{aligned}$$

(60)

where we are comparing with the same asymptotic structure and cutoff. We see that the area is larger for the $SdS_3$ case.

The tortoise coordinate in this case has a simple form

$$\begin{aligned} y= & {} \int \frac{d \tau }{1 - \alpha ^2 \tau ^2} \nonumber \\= & {} \frac{1}{2 \alpha }\, \log \left| \frac{1 + \alpha \tau }{1 - \alpha \tau } \right| \ . \end{aligned}$$

(61)

Inverting gives

$$\begin{aligned} \tau= & {} \frac{1}{\alpha }\,\frac{e^{2y\alpha } + 1}{e^{2y\alpha } - 1} \qquad \left[ \tau > \frac{1}{\alpha }\right] ;\nonumber \\ \tau= & {} \frac{1}{\alpha }\,\frac{e^{2y\alpha } - 1}{e^{2y\alpha } + 1} \qquad \left[ \tau < \frac{1}{\alpha }\right] \ . \end{aligned}$$

(62)

To analyse the width in more detail, rewriting (57) as ${\dot{w}}^2 = \frac{1}{1 + \frac{1 - \alpha ^2 \tau ^2}{B^2 \tau ^2}}$ gives

$$\begin{aligned} {\dot{w}}^2= & {} \frac{1}{1 - \frac{4 \alpha ^2 e^{2y\alpha }}{B^2 \left( e^{2y\alpha } + 1\right) ^2}} \qquad \ \left[ \tau > \frac{1}{\alpha }\right] \, ;\nonumber \\ {\dot{w}}^2= & {} \frac{1}{1 + \frac{4 \alpha ^2 e^{2y\alpha }}{B^2 \left( e^{2y\alpha } - 1\right) ^2}} \qquad \ \left[ \tau < \frac{1}{\alpha }\right] \end{aligned}$$

(63)

The turning point relation (58), using (62), can be written as

$$\begin{aligned} B^2 = \alpha ^2-{1\over \tau _*^2} = {4\alpha ^2e^{2\alpha y_*} \over (e^{2\alpha y_*}+1)^2}\ . \end{aligned}$$

(64)

This can be used in (63) to estimate the width scaling. The full width integral can be written as $\Delta w = 2\int _0^{y_*} dy\, {\dot{w}} = 2\int _0^Y dy\, {\dot{w}} + 2\int _Y^{y_*} dy\, {\dot{w}}$ where $Y\rightarrow \infty$ is a cutoff near the horizon $\tau ={1\over \alpha }$ . Then as in [32], the near horizon contributions are smooth and we obtain

$$\begin{aligned} \Delta w \sim \log (\alpha ^2-B^2) \sim \log \tau _* \end{aligned}$$

(65)

so that $\Delta w\rightarrow 0$ as $B\rightarrow 0$ and $|\Delta w|\rightarrow \infty$ as $B\rightarrow \alpha$. In this case, the finite part of the area also scales as $\log \tau _*$ thus scaling linearly with the subregion size.

Analytic expressions for the area integrals

In the text, we have discussed the timelike and spacelike extremal surfaces in the corresponding cases and obtained their areas, respectively in (25) and (25). These integrals in (25) and (25) can in fact be analytically characterized in terms of elliptic integrals and functions. We here mention key definitions and identities needed to discuss the results following the conventions of [43], which we refer to for further details. The usual elliptic integrals of the first and second kind are defined by

$$\begin{aligned} F(\phi ,k)&= \int \limits _{0}^{\phi } \frac{d \theta }{ \sqrt{1- k^2 \, \sin ^2\theta }} \nonumber \\&= \int \limits _{0}^{\sin \,\phi } \frac{d t}{ \sqrt{(1- t^2)(1- k^2 t^2)}}\ , \nonumber \\ E(\phi ,k)&= \int \limits _{0}^{\phi } \sqrt{1- k^2\, \sin ^2\theta } d \theta \nonumber \\&= \int \limits _{0}^{\sin \,\phi } \sqrt{\frac{1- k^2 t^2}{1- t^2}} dt\ . \end{aligned}$$

(66)

The above integrals are functions of a modulus k and an argument, $y = \sin \phi$, where $0 \le y \le 1$, or $0 \le \phi \le \frac{\pi }{2}$. If $\phi = \frac{\pi }{2}$ (or $y=1$), then the above integrals are said to be complete and are denoted by

$$\begin{aligned} K(k) = F\left( \frac{\pi }{2},k\right) \,, \quad E(k) = E\left( \frac{\pi }{2},k\right) \,. \end{aligned}$$

(67)

Further they can be expressed in terms of hypergeometric functions as $K(k) = \frac{\pi }{2} \,_2F_1(\frac{1}{2};\frac{1}{2};1;k^2)$ and $E(k) = \frac{\pi }{2} \,_2F_1(-\frac{1}{2};\frac{1}{2};1;k^2)$ when $k^2<1$.

For all other $\phi$, the elliptic integrals are incomplete. The incomplete elliptic integrals will be denoted by F(v) and E(v), where v denotes $\{\phi ,k\}$. The above elliptic integrals of the first and second kind are real valued when $0 \le k \le 1$.

The expressions involved in the context of elliptic integrals are often described in terms of certain Jacobi elliptic functions. For our purposes, we will be concerned with the elliptic functions $\text {sn} (v)\,, \text {cn} (v)$ and $\text {dn} (v)$, which satisfy

$$\begin{aligned}&\sin \phi \equiv \text {sn} (v) \,,\quad \text {cn} (v) = \sqrt{1 - \text {sn}^2(v)} \,, \nonumber \\&\text {dn} (v) = \sqrt{1 - k^2 \text {sn}^2(v)} \ . \end{aligned}$$

(68)

$$\begin{aligned}&\text {sn}^2(v)+\text {cn}^2(v) =1\, \qquad 1-k^2 \text {sn}^2(v)\nonumber \\&\quad =\text {dn}^2(v)\, \qquad \frac{d}{dv}(\text {sn}(v))\nonumber \\&\quad =\text {cn}(v)\text {dn}(v)\ . \end{aligned}$$

(69)

We will evaluate the integrals in (25) and (25) by performing a transformation which casts the integral in a known form involving these elliptic functions. In general, integrals involving square roots of cubic or quartic expressions of a variable $\tau$ can be simplified by performing a general Mobius transformation $\tau \rightarrow {a+bu\over c+du}$ . This transformation shifts the roots of the original cubic, which can thus be used to remove specific coefficients, such as that of the cubic term etc. The limits in the new integral follow from the inverse transformation $u={a-c\tau \over d\tau -b}$ which is used following the final change in coordinates. Specific simplifications arise e.g. for the cubic case, where we retain only the quadratic and linear terms (or for a quartic, retaining only the quadratic and quartic terms). Additional useful simplifications occur if we ensure well-defined limits in the resulting integral as well as e.g. $0\le k^2\le 1$. If we obtain e.g. limits such that $u\in [0,1]$, then we end up with “definite” elliptic integrals. More generally, we change variables to one of the Jacobi elliptic functions above, which leads to simplifications. Once an integral is recast in sufficiently simple form, it may be possible to look it up in e.g. [43].

Evaluation of the integral (25)

In the case of (25), let us first define

$$\begin{aligned} \beta = \frac{a_2}{a_1} \,, \quad k^2 = \frac{\beta \left( 2+\beta \right) }{1+ 2\beta } \,, \quad \alpha ^2 = \frac{k^2}{\beta }\ . \end{aligned}$$

(70)

We then find that substituting

$$\begin{aligned} \tau = \frac{\frac{1}{a_1} - \frac{k^2}{a_2} \text {sn}^2 v}{1 - k^2 \text {sn}^2 v}\,, \end{aligned}$$

(71)

in 25 provides the following integral

$$\begin{aligned} S = \frac{\pi l^2}{G_4} \frac{2 a_1}{\sqrt{1+2\beta }}\int \limits _{0}^{F\left( {\bar{v}}\right) } dv\frac{\text {dn}^4 (v)}{(1-\alpha ^2\text {sn}^2(v))^2}\ , \end{aligned}$$

(72)

where ${\bar{v}}$ in upper limit $F\left( {\bar{v}}\right)$ of 72 corresponds to

$$\begin{aligned} \text {sn}({\bar{v}}) = \frac{1}{\alpha } \sqrt{\frac{1- a_1 \epsilon }{1 - a_2 \epsilon }}\ . \end{aligned}$$

(73)

The integral in 72 can be expressed in terms elliptic integrals and functions (c.f. Eq. 339 of [43]). Upon considering the limits of the integration, we find the following result

$$\begin{aligned} S&= \frac{\pi l^2}{G_4} \frac{a_1}{\sqrt{1+2\beta }}\Bigg [(1+\beta )F({\bar{v}}) - \left( 1+2\beta \right) E({\bar{v}}) \nonumber \\&\quad + \left( 2+\beta \right) \frac{\text {sn}({\bar{v}}) \,\text {cn}({\bar{v}})\,\text {dn}({\bar{v}})}{1 - \alpha ^2 \text {sn}^2({\bar{v}})}\Bigg ]. \end{aligned}$$

(74)

This is the exact result for the timelike surfaces (25) in Schwarzschild de Sitter. To verify the de Sitter limit $a_1=1, a_2 =0$, note that we now have $\beta \rightarrow 0 ,\ k \rightarrow 0 ,\ \alpha ^2 \rightarrow 2$. We also have $F({\bar{v}}) = \phi = E({\bar{v}})$ and $\text {sn}({\bar{v}}) \rightarrow \sin ({\bar{v}}) ,\ \text {cn}({\bar{v}}) \rightarrow \cos ({\bar{v}}) , \ \text {dn}({\bar{v}}) \rightarrow 1$. Then (74) simplifies to

$$\begin{aligned} S \rightarrow S_{dS}&= \frac{\pi l^2}{G_4}\frac{2 \sin ({\bar{v}}) \,\cos ({\bar{v}})}{1 - 2 \sin ^2({\bar{v}})} = \frac{\pi l^2}{G_4} \tan (2 {\bar{v}})\ . \end{aligned}$$

(75)

From (73) we have $\sin {\bar{v}} = \sqrt{\frac{1 - \epsilon }{2}}$ giving

$$\begin{aligned} S_{dS} = \frac{\pi l^2}{G_4}\frac{1}{\epsilon } + {\mathcal {O}}\left( \epsilon \right) \,, \end{aligned}$$

(76)

in agreement with the area in de Sitter [16].

For $m \ne 0$, i.e. $a_1 > a_2 \ge 0$, we have results for the general Schwarzschild de Sitter case. With the Schwarzschild horizon present, $\frac{\pi }{2} - \frac{\epsilon }{2}(a_1 - a_2) \ge {\bar{v}} \ge \frac{\pi }{4} - \frac{\epsilon }{2}(a_1 - a_2)$ and we can always expand $F({\bar{v}})$, $E({\bar{v}})$ and the elliptic functions $\text {sn}({\bar{v}})\,,\text {cn}({\bar{v}})$ and $\text {dn}({\bar{v}})$ as a power series (c.f. Eqs. 902 and 903 of [43]). The values of $k^2$ and $\alpha ^2$ depend on the choice of $\frac{a_2}{a_1}$, i.e. $\beta$.

Evaluation of the integral (25)

To evaluate the area integral in the spacelike case, we now define

$$\begin{aligned} k^2 = \frac{\left( 1 - \beta ^2\right) }{1+ 2\beta } \,, \quad \alpha ^2 = -\frac{k^2}{1+ \beta }\,, \end{aligned}$$

(77)

with $\beta = \frac{a_2}{a_1}$, as before. We now substitute

$$\begin{aligned} \tau = \frac{\frac{1}{a_1} + \frac{k^2}{a_1(1 + \beta )} \text {sn}^2 v}{1 - k^2 \text {sn}^2 v}\,, \end{aligned}$$

(78)

in (25) and find

$$\begin{aligned} S = \frac{\pi l^2}{G_4}\frac{2 a_1}{\sqrt{1+2\beta }}\int \limits _{0}^{K(k)} dv\frac{\text {dn}^4 (v)}{(1-\alpha ^2\text {sn}^2(v))^2}\ . \end{aligned}$$

(79)

Apart from the coefficient and the limits, the indefinite integral involved in (79) is the same as that in (72). The result on substituting the integration limits is

$$\begin{aligned} S = \frac{\pi l^2}{G_4}\frac{a_1}{\sqrt{1+2\beta }} \left[ -\beta K(k) + \left( 1+2\beta \right) E(k)\right] . \end{aligned}$$

(80)

This result only involves complete elliptic integrals. It is well defined for the entire range of $\beta$, i.e. $0 \le \beta \le 1$.

In the Nariai limit, we have $a_2 = a_1 = \frac{1}{\sqrt{3}}$ , and $\beta \rightarrow 1 \,, \ k \rightarrow 0$, giving $K(0) = \frac{\pi }{2} = E(0)$. This leads to the extremal limit of (80),

$$\begin{aligned} S \rightarrow S_{\text {Nariai}} = \frac{\pi ^2 l^2}{3 G_4}\ . \end{aligned}$$

(81)

As mentioned after (25), the de Sitter limit appears slightly ill-defined. However one can formally calculate the area (80) above in this limit, with $\beta \rightarrow 0 \,, \ k \rightarrow 1$, and $K(1) \rightarrow \infty \,, \ E(1) = 1$, obtaining $S \rightarrow S_{dS} = \frac{\pi l^2}{G_4}$ , which is de Sitter entropy.