1 Introduction

The internal description of the stars, in the context of gravitation, has been approached from different perspectives from the scope of its composition, which determines the structure of the stress-energy tensor and the geometry, which defines the type of gravitational theory that will be considered. In the first of the aspects, the astronomic observations of the accelerated expansion of the universe [1] generate the possibility that the internal matter of the stars is not only formed by ordinary matter but also by matter with negative pressure, like quintessence [2]. Although its origin is cosmological, and that is where its presence is more transcendental, it is interesting to analyze what would happen at a stellar level, as minimal as its effects may be.

There are diverse investigations around quintessence; for more than a decade it has been considered that quintessence is a good candidate to solve some problems in cosmolog. For example it has been argued that quintessence may explain the ’cosmic coincidence’ problem and may fit the observational data better than the cosmological constant [3], while its possible existence has already been shown based on the observations [4, 5]. Quintessential dark matter has been used to explain the asymptotic behavior of rotation curves in spiral galaxies; in some cases the theoretical approach is the only work done [6,7,8]. In other cases there has been reported that the theoretical model matches the observations, where the Einstein and Klein–Gordon equations for distances smaller than the optical radius have been solved [9].

In relation to the formation of large scale structures quintessence has also been successful [10,11,12]. Considering a scalar field and the cosmic microwave background (CMB) anisotropies match CMB and large scale structure data very well [10]. For quintessence with a speed of sound equal to zero, quintessence perturbations induce effects on the evolution of structures particularly when the dark energy component comes to dominate the energy density of the universe [11], just to mention an example. Other more recent work shows elements in favor of quintessence both from the theoretical point of view and as regards their consistency with the observations [13,14,15,16,17,18,19].

On the other hand there have been some approaches at a stellar level to describe compact objects [20,21,22,23], considering that the interior of the stars is formed by ordinary neutral matter [24,25,26,27,28,29,30], ordinary charged matter [31,32,33,34,35,36,37], and also by sources which are a combination of ordinary matter and quintessence dark energy, consistent with neutron stars [38]. Neutron or quark stars are not exclusively composed of neutrons or quarks, respectively, but rather these stars are formed predominantly by one of those particles. Generally their interior contains matter with a greater density than the nuclear density, which generates an enormous pressure causing in some cases its collapse and the formation of black holes [39, 40]. There are alternative proposals to describe the case in which collapse can be avoided. One of these considers the interior of the star to be formed by dark energy (\(P=-c^2\rho \)) with a shell of normal matter (\(P=c^2\rho \)), where \(\rho \) and P represent the density and pressure, respectively. The core of exotic matter would avoid the gravitational collapse and it may be similar in appearance to a black hole, but without an event horizon [41].

Another possibility for avoiding the collapse is the presence of quintessence dark matter, characterized by a negative pressure, described by the equation of state \(P_q(\rho )=wc^2\rho _q\), where \((P_q,\;\rho _q)\) represents the pressure and the energy density, respectively, with \(w\in (-1,-\frac{1}{3})\), which would allow for more compact stars. Unlike the dark energy in gravastars, the quintessence and the ordinary matter inside the stars do not generate a core with negative pressure and another region with monotonically decreasing positive pressure, which has a similar structure to stars with ordinary matter. Its effect is present in the whole region of the star allowing the star to be denser. When the density in the star is greater than the nuclear density, there exists the possibility that the radial pressure \(P_r\) and the tangential pressure \(P_t\) are different [42], a situation relevant in the stellar structure [43], which allows one to represent stars with a greater compactness [44]. So it is to be expected that the equation of state which describes quark stars with perfect fluid \((P_t=P_r)\), given by \(P_r=\frac{1}{3}(c^2\rho -4B_g)\) where \(B_g\) is the MIT Bag constant [45], is modified in such a way that the radial and tangential pressures are not equal. Now considering the possibility that inside the stars there exists quintessence matter, a natural question would be which equation of state holds for the tangential pressure.

In this work we propose a stellar model in which its interior is formed by the interaction of quarks with the quintessence dark matter; as a result of this interaction we suggest a new state equation for the tangential pressure, and this proposal is discussed in Sect. 3. For this equation, in the absence of quintessence the anisotropy in the pressures ceases to exist; in other words, in our model the quintessence dark matter is responsible of this anisotropy and in consequence of the possibility that the star has a greater density than the nuclear density. From this proposal of an equation of state in this work we present a new stellar model that, when it is applied to the data of a star that is a quark star candidate, allows one to determine its internal behavior and in particular its MIT Bag constant.

The work is organized in the following manner: in Sect. 2 we present the system of equations for an anisotropic stellar model with quintessence. In Sect. 3 we discuss two theorems that allow one to build solutions for the MIT Bag model with quintessence, starting from a stellar solution with perfect fluid. In Sect. 4 a physically acceptable and potentially stable model is presented, generated by the direct application of the theorem 1. Section 5 is dedicated to realizing a graphic analysis of the model. In Sect. 6 we determine the MIT Bag constant and its hydrostatic values, taking as data the observational values of mass and radius of the star HerX-1. Finally in Sect. 7 we present the conclusions and discussion of our results, and the possibility of new work is pointed out.

2 The field equations

The metric that describes the geometry in the case of a static and spherically symmetric time space can be represented by [46]

$$\begin{aligned} \mathrm{d}s^2=-y(r)^2\mathrm{d}t^2 + \frac{\mathrm{d}r^2}{B(r)} + r^2\mathrm{d}\varOmega ^2, \end{aligned}$$
(1)

where \(\mathrm{d}\varOmega ^2=\mathrm{d}\theta ^ {2}+\sin ^2 \theta \mathrm{d}\phi ^2\) is the standard line element on the second sphere. In our case the metrical components will be determined by Einstein’s equations:

$$\begin{aligned} G_{\mu \nu }=kT_{\mu \nu }+kT_{\mu \nu }^{(Q)}, \end{aligned}$$

where \(k= \frac{8 \pi G}{c^4}\) and

$$\begin{aligned} T_{\mu \nu }= (c^2\rho +{ P}_t ) u_{\mu }u_{\nu }+ { P}_t g_{\mu \nu }+({ P}_r-P_t) \chi _{\mu }\chi _{\nu } \end{aligned}$$
(2)

represents the source of matter of an anisotropic fluid, with \(\rho \) the density, \(P_r\) and \(P_t\) the radial and tangential pressures respectively; \(u^\mu \) is the fluid 4-velocity and \(\chi ^\mu \) is the unit vector in the radial direction. \(T_{\mu \nu }^{(Q)}\) stands for the energy-momentum tensor of the quintessence type with components

$$\begin{aligned} T^{(Q)\,t }\,_{t}= & {} T^{(Q)\,r }\,_{r}=-c^2\rho _{q},\\ T^{(Q)\,\theta }\,_{\theta }= & {} T^{(Q)\,\phi }\,_{\phi }=\frac{1+3w}{2}c^2\rho _{q}, \end{aligned}$$

with w satisfying the constraint \(-1< w < -\frac{1}{3} \) [47], thus \(P_{rq}=-c^2\rho _{q}\) and \(P_{tq}=\frac{1+3w}{2}c^2\rho _{q}\). The Einstein equations with this form of the stress-energy tensors generate the following system:

$$\begin{aligned}&kc^2\rho +kc^2\rho _q = -\frac{B'}{r}+\frac{1-B}{r^2}, \end{aligned}$$
(3)
$$\begin{aligned}&kP_r-kc^2\rho _q = \frac{2By'}{ry}-\frac{1-B}{{r}^{2}}, \end{aligned}$$
(4)
$$\begin{aligned}&k{ P_t}+\frac{1+3w}{2}kc^2\rho _q = \frac{( ry''+y')B }{ry}-\frac{( ry'+y)B'}{2ry }, \end{aligned}$$
(5)

where \('\) denotes the derivative with respect to the coordinate r. Of the equation for the conservation of the effective stress-energy tensor we have the relation

$$\begin{aligned} { P_r}'= & {} c^2{\rho }_q'-\left( { P}_r +c^2\rho \right) {\frac{y'}{y }} \nonumber \\&+\frac{2}{r}\left[ P_t-P_r+\frac{3}{2}(1+w)c^2\rho _q\right] . \end{aligned}$$
(6)

3 The theorems

Our interest is to get an exact solution of the system (3)–(5) with an anisotropic strange quark matter distribution described by the MIT Bag equation of state for the radial pressure [45],

$$\begin{aligned} P_r=\frac{1}{3}(c^2\rho -4B_g), \end{aligned}$$
(7)

and a modified equation for the tangential pressure:

$$\begin{aligned} P_t=\frac{1}{3}(c^2\rho -4B_g)-\frac{3}{2}(1+w)c^2\rho _q, \end{aligned}$$
(8)

where \(B_g\) is the MIT Bag constant. From the form of the state equation for the tangential pressure it can be observed that it is reduced to the perfect fluid case in the absence of a quintessence field, so in the proposed equation of state (8), the quintessence density represents the effect of the interaction of quintessence with ordinary matter.

This is the cause of the anisotropy in the pressures, an effect which arises when the matter density is of the same or higher order of magnitude than the nuclear density. Then due to the anisotropic pressure it is possible to have objects in equilibrium with a greater density and compactness than in the case of a perfect fluid [44, 48]. In this case that would be the result of quintessence, which generates a negative pressure counteracting the gravitational attraction caused by ordinary matter.

On the other hand, the existence of the quintessence field can be justified as a consequence of the accelerated expansion of the universe and the consistency with the rotation curves of the galaxies. However, their detection has not been proved in an alternative manner, it would seem that it can be confused with the ordinary matter and only its effects are perceptible. Starting from the equation of state proposed for the tangential pressure (8) a similar effect occurs in the case of stellar models, since the same metric components (y, B), associated to the geometry for the case of a perfect fluid in the absence of the quintessence density, describe the anisotropic case with sources of ordinary matter in the presence of the quintessence field.

Furthermore, the possibility of a new form of an equation of state is not ruled out, since the theorems remain valid if the state equations are replaced by \(P_r=P_r(\rho )\) and \(P_t(\rho )=P_r(\rho )-3(1+w)c^2\rho _q/2\), giving rise to a diversity of work that could help to understand in a clearer manner the effect of quintessence on the stellar models. Now we focus on the implications of these equation of states on our system. Replacing the form of \(P_r\) and subtracting Eq. (4) from Eq. (5) we obtain

$$\begin{aligned}&k{ P_t}-\frac{k}{3}(c^2\rho -4B_g) +\frac{3}{2}k(1+w)c^2\rho _q \nonumber \\&\quad = \frac{( ry''-y')B }{ry}-\frac{( ry'+y)B'}{2ry} +\frac{1- B}{{r}^{2}}. \end{aligned}$$
(9)

Of the equation of state (8) for the tangential equation, we find that the term to the left is zero and the term to the right generates a relation between the functions (B, y):

$$\begin{aligned} \frac{( ry''-y')B }{ry}-\frac{( ry'+y)B'}{2ry} +\frac{1- B}{{r}^{2}}=0, \end{aligned}$$
(10)

which matches the restriction that we have between (B, y) for the case of a model formed with only a perfect fluid [49]. On the other hand, adding Eqs.  (3) and (4), and considering the equation of state (7), we obtain the density in terms of the functions (y, B) and their derivatives, that is to say,

$$\begin{aligned} k{c}^{2}\rho =-\,{\frac{ 3 { B'}}{4r}}+\, {\frac{3B{ y' }}{2ry }}+kB_g. \end{aligned}$$
(11)

Replacing this form of the density in the Eq. (3) there results

$$\begin{aligned} k{c}^{2}\rho _{{q}}=-\,{\frac{{ B'}}{4r}}-\, {\frac{3B{ y' }}{2ry }}+{\frac{1-B }{{r}^{2} }}-kB_g. \end{aligned}$$
(12)

This allows us to obtain a new solution once we have determined the functions (B, y) in such a way that it satisfies (10). In summary, we have the following theorem.

Theorem 1

Let (M, g) be a differentiable manifold that describes a static and spherically symmetric spacetime, regular, with metric g given by

$$\begin{aligned} \mathrm{d}s^2=-y(r)^2\mathrm{d}t^2 + \frac{\mathrm{d}r^2}{B(r)} + r^2\left[ \mathrm{d}\theta ^ {2}+\frac{}{}\sin ^2 \theta \mathrm{d}\phi ^2\right] , \end{aligned}$$
(13)

such that the metric functions (B, y) satisfy Einstein’s equations with a perfect fluid, that is to say,

$$\begin{aligned} G_{\mu \nu }= k[ (c^2\rho _0 +{ P}_0) u_{\mu }u_{\nu }+ { P}_0 g_{\mu \nu }] , \end{aligned}$$
(14)

or equivalently

$$\begin{aligned} kc^2\rho _0= & {} -\frac{B'}{r}+\frac{1-B}{r^2} , \end{aligned}$$
(15)
$$\begin{aligned} kP_0= & {} \frac{2By'}{ry}-\frac{1-B}{{r}^{2}}, \end{aligned}$$
(16)
$$\begin{aligned} k{ P}_0= & {} \frac{( ry''+y')B }{ry}-\frac{( ry'+y)B'}{2ry }. \end{aligned}$$
(17)

Then any regular solution (B, y) of (15)–(17) is a regular solution of the system (3)–(5) with state equations for the radial and tangential pressures described by (7) and (8), with densities \((\rho ,\rho _q)\) determined by Eqs. (11) and (12) respectively.

The condition of regularity means that the Kretschmann scalar is regular, that is to say [50],

$$\begin{aligned} R^{\alpha \beta \sigma \delta }R_{\alpha \beta \sigma \delta }= & {} 4\left[ \frac{1-B}{r^2}\right] ^2+ \frac{2B'^2}{r^2}+\frac{8B^2}{y^2}\frac{y'^2}{r^2}\nonumber \\&+\left[ \frac{B'y'}{y} +\frac{2y''}{y}B \right] ^2 \end{aligned}$$
(18)

is finite. Since both sets of solutions (B, y, \(P_0\), \(\rho _0\)) and (B, y, \(P_r,P_t,\rho ,\rho _w\)) are described by the same metric functions (B, y), geometrically they are equivalent although with different sources of matter. This property of the same metric form being associated to two stress-energy tensors, is not exclusive of this system, another example of this is the Reissner–Nordstrom extreme solution, for the case of electrovacuum, and Bekenstein’s solution for a scalar field with compliant coupling [51], which has the same metric form.

An important point to emphasize is that if we put aside the geometrical aspect and the regularity of the geometry we have the following theorem.

Theorem 2

Let (B, y) be differentiable function such as that they satisfy Eq. (10) then the system (3)–(5) admits a solution with equation of state for the tangential pressure \(P_t\) given by (8) and densities \((\rho ,\rho _q)\) determined by the Eqs. (11) and (12), respectively.

Theorem 1 could be applied to the set of known regular solutions for a perfect fluid [49, 52,53,54,55] and we obtain for each one of these a model that tentatively describes stars formed by quintessence and MIT Bag matter. The existence of these with the equations for the radial and tangential pressures given by (7) and (8) is a new theoretical proposal presented in this work., Its possible physical existence is justified by the astrophysics observations related to the accelerated expansion of the universe. In previous work stellar models with quintessence dark energy have already been approached [20,21,22,23, 38] as well as proposals based on the MIT Bag model for strange stars [56,57,58,59,60]. One substantial difference in our case is the proposal of the equation of state (8), which can be understood as the consequence of the interaction between ordinary matter and the quintessence.

3.1 Physical conditions

The physical conditions to impose on the geometry determined by (B, y) and the functions \((P_r,P_t,\rho )\) are in part the ones known for the case without quintessence, the only difference being that the condition, near the origin, required for \(\varDelta = P_t-P_r\approx \alpha r^2\), now is not present and additionally one is required to impose conditions on \(\rho _q\). In general, we find that a solution for the system (3)–(5) is physically acceptable if the following conditions are met [50, 61,62,63]:

  1. (a)

    Regularity conditions

    1. (i)

      The solution should be free from physical and geometric singularities i.e. Kretschmann’s scalar given by (18) must be finite and \(y^2(r) > 0\) and \(B(r)> 0\) in the range \(0\le r\le R\). This implies, based on the relation for Kretschmann’s scalar given by (18), near the origin [50]

      $$\begin{aligned} B(r)\approx & {} 1-\alpha r^2,\quad y(r)\approx \beta +\gamma r^2,\\ y'\approx & {} \sigma r ,\quad B' \approx \delta r. \end{aligned}$$

      The conditions on B and \(B'\) are obtained from the first two terms of Eq. (18) by imposing the requirement that each must be finite, since this expression is the sum of squares. Meanwhile the requirement for y and \(y'\) has to be imposed and the regularity of the third and fourth terms in (18).

    2. (ii)

      The radial and tangential pressures and density are positive, \((P_r \ge 0), (P_t \ge 0) \,and\, (\rho >0)\).

    3. (iii)

      The radial pressure \(P_r\) should be zero at boundary \(r = R\), i.e. \(P_r(r = R) = 0\), the energy density and tangential pressure may obey \(\rho (r=R)\ge 0\) and \(P_t(r=R)\ge 0\).

  2. (b)

    Causality condition

    1. (iv)

      The conditions \(0\le v_r^2\equiv \frac{\mathrm{d}P_r}{\mathrm{d}\rho } \le 1\) and \(0\le v_r^2\equiv \frac{\mathrm{d}P_t}{\mathrm{d}\rho } \le 1\) entail the conditions that the radial and tangential speed of sound should not exceed the speed of light.

  3. (d)

    Energy conditions

    1. (v)

      A physically reasonable energy-momentum tensor has to obey the conditions \(\left( c^2\rho \ge P_r\right) , \left( c^2\rho \ge P_t\right) and \left( c^2\rho +P_r +2P_t\ge 0\right) \).

  4. (e)

    Monotone decrease of physical parameters

    1. (vi)

      The radial pressure and density should be maximum at the center and monotonically decreasing towards the pressure free interface (i.e. boundary of the fluid sphere). Mathematically,

      $$\begin{aligned}&\left. P_r'(r)\right| _{r=0}=0, \qquad \left. \rho '(r)\right| _{r=0}=0,\\&\left. P_r''(r)\right| _{r=0}<0, \qquad \left. \rho ''(r)\right| _{r=0}<0. \end{aligned}$$

      Thus

      $$\begin{aligned} \left[ \begin{aligned} P_r'<0, \qquad \quad \rho '<0,\qquad \quad 0<r\le R. \end{aligned}\right] \end{aligned}$$
  5. (f)

    Matching condition

    1. (vii)

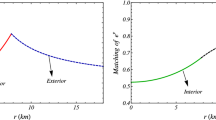
      The interior solution should match continuously with an exterior Schwarzschild geometry, \( r\ge R \),

      $$\begin{aligned} \mathrm{d}s^2= & {} \left( 1-\frac{2GM}{c^2r}\right) \mathrm{d}t^2-\left( 1-\frac{2GM}{c^2r} \right) ^{-1}\mathrm{d}r^2 \\&+r^2\mathrm{d}\varOmega ^2, \end{aligned}$$

      where M represents the total mass inside the fluid sphere, respectively. This requires the continuity of \(y^2(r)\) and B(r) across the boundary \(r = R\).

  6. (g)

    Quintessence distribution

    1. (viii)

      The regularity of the geometry, in particular \(y'(0)\approx \sigma r\) and the behavior required of the radial pressure and density in the origin being positive and finite, that is, \(P'_r(0)=0\), in conjunction with Eq. (6) imply that near the origin

      $$\begin{aligned} P_t-P_r+\frac{3}{2}(1+w)c^2\rho _q\approx \nu r^2; \end{aligned}$$

      the behavior required for this case is different from the case in which there is no quintessence matter. In the absence of this it is seen as a result that near the origin \(P_t-P_r \approx \nu r^2\).

  7. (h)

    Stability conditions

    1. (iiix)

      In order to have an equilibrium configuration the matter must be stable against the collapse of local regions. \(v_t^2-v_r^2<0\) [64].

3.2 The Schwarzschild’s interior solution

The previous theorem does not guarantee that the solutions obtained for the quintessence and MIT Bag matter system are physically acceptable and that these are stable. Here we will show that for the case in which Schwarzschild’s internal solution is taken, the corresponding solution for (3)–(5) is not stable since this does not satisfy the condition \(v_t^2-v_r^2<0\). To show this we start from Eq. (3), with (B, y) the corresponding functions to the solution with constant density \(\rho _S\), in that case \( B = 1-kc ^ 2 \rho _Sr ^ 2/3 \), so

$$\begin{aligned} \rho +\rho _q=\rho _S \quad \Rightarrow \quad \rho _q=\rho _S-\rho . \end{aligned}$$

Subtracting Eqs.  (7) and (8), and replacing the form obtained from \(\rho _q \) we arrive at

$$\begin{aligned} P_t(\rho )-P_r(\rho )= & {} -\frac{3}{2}(1+w)c^2\nonumber \\ \rho _q= & {} \frac{3}{2}(1+w)c^2(\rho -\rho _S). \end{aligned}$$
(19)

Taking the derivative of this equation with regard to the density we have

$$\begin{aligned} v^2_t-v^2_r=\frac{3}{2}(1+w)c^2, \end{aligned}$$
(20)

and since the admissible values of w are given by \(-1<w<-\frac{1}{3}\), there results \( 0<v^2_t-v^2_r<c^2 \). This implies that the solution is not stable. A detailed analysis is not presented in this work; here we focus on a model which is stable and allows us to describe the Her X-1 star.

4 The model

The metric functions (y, B) that we choose were previously proposed to describe compact stars like quark stars or neutron stars. According to the requirement of Theorem 1, these satisfy Einstein’s equations with a perfect fluid [65]:

$$\begin{aligned} y \left( r \right)= & {} \frac{C( 5+{4}a{r}^{2 } )}{ \sqrt{1+a{r}^{2} } },\end{aligned}$$
(21)
$$\begin{aligned} B (r)= & {} \frac{( 5+11a{r}^{2}+6\,{a}^{2}{r}^{4}-4 a{r}^{2} S(r) ) ( 1+a{r}^{2}) }{5+12a{r}^{2}+8{a}^{2}{r}^{4}}, \end{aligned}$$
(22)

where

$$\begin{aligned} S\left( r \right) = \frac{( 1+a{r}^{2}) ^{2} \left[ A+\arctan {\text{ h }}\left( {\frac{1+2a{r}^{2}}{\sqrt{5+12a{r}^{2}+8{a}^{2}{r}^{4}}}} \right) \right] }{\sqrt{5+12\,a{r}^{2}+8\,{a}^{2}{r}^{4}}}, \end{aligned}$$

and (C, A, a) are constants. The solution mentioned depends on a the parameter \(\left( W\in (0,2.0375509325]\right) \) related to the compactness of the star \(u=GM/c^2R\), with maximum value \(u=0.2660858316\). This choice guarantees that at least in the absence of quintessence matter we have the representation of a model for compact stars. Replacing this in Eqs. (11) and (12) we obtain

$$\begin{aligned} \rho (r)= & {} {\frac{B_{{g}}}{{c}^{2}}} -{\frac{3a( 25+40a{r}^{2}+28{a}^ {2}{r}^{4}+16{a}^{3}{r}^{6})( 1+a{r}^{2}) }{2k{c}^{2} ( 5+12a{r}^{2}+8{a}^{2}{r}^{4}) ^{2}( 5+4a{r}^{2}) }} \nonumber \\&+{\frac{6a(25+75a{r}^{2}+70{a}^{2}{r}^{4}+24{a}^{3}{r}^{6}){S}( r ) }{ k{c}^{2}( 5+12a{r}^{2}+8{a}^{2}{r}^{4}) ^{2} ( 5 +4a{r}^{2}) }},\end{aligned}$$
(23)
$$\begin{aligned} \rho _{{q}}(r)= & {} -{\frac{B_{{g}}}{{c}^{2}}} - { \frac{ \left( 525+2935a{r}^{2}+6776{a}^{2}{r}^{4}+H(r) \right) a}{ 2 k{c}^{2} ( 5+ 12a{r}^{2}+8{a}^{2}{r}^{4})^{2} ( 5+4a{r}^{ 2}) }}\nonumber \\&+{\frac{6a ( 1+a{r}^{2}) ( 5+8a{r}^{2})( 5+10a{r}^{2}+8{a}^{2}{r}^{4} )S(r) }{ k{c}^{2}( 5+12a{r}^{2}+8{a}^{2}{r}^{4})^{2}( 5+4a{r}^{2}) }},\nonumber \\ \end{aligned}$$
(24)

where \(H(r)=7996{a}^{3}{r}^{6} +4784\,{a}^{4}{r}^{8}+1152\,{a}^{5}{r}^{10} \). The radial and tangential pressures are given by (7) and (8). Due to this the radial and tangential speeds are

$$\begin{aligned} v_r^2(r)=\frac{1}{3}c^2,\quad v_t^2(r)=\frac{1}{3}c^2-\frac{3}{2}(1+w)c^2\frac{\mathrm{d} \rho _q}{\mathrm{d}r}\left[ \frac{\mathrm{d} \rho }{\mathrm{d}r} \right] ^{-1},\nonumber \\ \end{aligned}$$
(25)

where we see that the condition for stability,

$$\begin{aligned} v_t^2(r)-v_r^2(r)=-\frac{3}{2}(1+w)c^2\frac{\mathrm{d} \rho _q}{\mathrm{d}r}\left[ \frac{\mathrm{d} \rho }{\mathrm{d}r} \right] ^{-1} <0, \end{aligned}$$
(26)

requires that the function \(\rho _q(r)\) is monotonic decreasing, that is,

$$\begin{aligned} \frac{\mathrm{d} \rho _q}{\mathrm{d}r}<0. \end{aligned}$$
(27)

This is due to the parameter \(w\in (-1,-1/3)\) so that \(0<w+1\) and, since the density must be a monotonic decreasing radial function, \(\frac{d \rho }{\mathrm{d}r}<0\). Also, by Eq.  (26) and the condition (27) we see that the tangential speed of sound is lower than \(c^2/3\).

5 Analysis of the solution

Once that we have found the functions \((P_r,\) \(P_t,\) \(\rho ,\) \(\rho _q)\) and the form of the radial and tangential speeds of sound we proceed to realize the graphical representation of the solution. This requires that we set the constants (A,  a,  C,  w,  \(B_g)\) or that we determine the validity intervals of these, although we already know that \(w\in (-1,-\frac{1}{3})\) and \(B_g\in (80,120)\,\mathrm{Mev}/\mathrm{fm}^3\). Of the condition that the pressure is zero on the surface of the star, we obtain A:

$$\begin{aligned} A= & {} {\frac{ \left( 25+40\,\nu +28\,{\nu }^{2}+16\,{\nu }^{3} \right) \sqrt{5+12\,\nu +8\,{\nu }^{2}}}{4 \left( 25+75\,\nu +70\,{\nu }^ {2}+24\,{\nu }^{3} \right) \left( 1+\nu \right) }}\nonumber \\&+{\frac{ \left( 5+12\,\nu +8\,{\nu }^{2} \right) ^{5/2} \left( 5+4\,\nu \right) \sigma }{ 2\left( 1+\nu \right) ^{2} \left( 25+75\,\nu +70\,{\nu }^{2}+24 \,{\nu }^{3} \right) \nu }}\nonumber \\&-\mathrm{arctanh} \left( {\frac{1+2\,\nu }{\sqrt{5+12\,\nu +8\,{\nu }^{2} }}}\right) , \end{aligned}$$
(28)

where \(\nu =a{R}^{2}\) and \(\sigma =k B_{{g}}{R}^{2}\). Applying the coupling condition of the solution with Schwarzschild’s metric on the surface of the star there results

$$\begin{aligned} u= & {} \frac{GM}{c^2R}\nonumber \\= & {} {\frac{ \left( 1+\nu \right) \left( 5+12\,\nu +8\,{\nu }^{2} \right) \left( 5+4\,\nu \right) \sigma }{25+75\,\nu +70\,{\nu }^{2}+24 \,{\nu }^{3}}}\nonumber \\&-{\frac{ \left( 15+51\,\nu +48\,{\nu }^{2}+16\,{\nu }^ {3} \right) \nu }{ 2(25+75\,\nu +70\,{\nu }^{2}+24\,{\nu }^{3}) }}, \end{aligned}$$
(29)
$$\begin{aligned} C= & {} \frac{(1-2u)\sqrt{1+u }}{ ( 5+u ) }, \end{aligned}$$
(30)

where u is the compactness value. From these conditions on the surface we have determined the constants A and C, together with \(\nu =aR^2\), w and \(\sigma =k{R}^{2}B_{{g}}\); these are the parameters of the solution. Although there exists the possibility that \(\rho _q<0\) in the whole interior or in certain regions, we will analyze solutions for which \(\rho _q>0\) in the whole region, in concordance with what happens to the quintessence matter in cosmology where \(\rho _q>0\) and \(P_q<0\). The property that we impose, that \(\rho _q>0\), and Eq. (8) evaluated in the surface of the star imply \(P_t(R)=-\frac{3}{2}(1+w)\rho _q(R)\) and since we require that \(P_t(R)\ge 0\), we have \(\rho _q(R)=0\), which gives us a relation between \(\nu \) and \(\sigma \):

$$\begin{aligned} \sigma ={\frac{\nu \, \left( 45+145\,\nu +144\,{\nu }^{2}+48\,{\nu }^ {3} \right) }{2 \left( 5+12\,\nu +8\,{\nu }^{2} \right) \left( 5+15\,\nu +12\,{\nu }^{2} \right) }}. \end{aligned}$$
(31)

Since \(\sigma =k{R}^{2}B_{{g}}>0\) this relation determines the values of the MIT Bag constant given \(\nu \). Replacing (31) in Eq. (30) we arrive at the finding that the rate of compactness u for this model matches the one obtained for the case of a perfect fluid with (y, B), given by (22) and (21) [65]:

$$\begin{aligned} u={\frac{ \left( 3+4\,\nu \right) \nu }{5+15\,\nu +12\,{\nu }^{2}}}. \end{aligned}$$
(32)

This occurs because the effective mass is given by

$$\begin{aligned} m_{ef}(r)= & {} \frac{kc^2}{2}\int _0^r \rho _{ef}y^2\mathrm{d}y\nonumber \\= & {} {\frac{\left( 4S\left( r \right) \left( 1+a{r}^{2} \right) -4-9\,a{r}^{2}-6\,{a}^{2}{r}^{4} \right) a{r}^{3}}{2(5+12\,a{r}^{2}+8\,{a}^{2}{r}^{4} )}},\nonumber \\ \end{aligned}$$
(33)

and this function of the effective mass is the same as that for the case of a perfect fluid analyzed in [65].

5.1 Graphical representation of the solution

As regards the function’s algebraic representation \((\rho ,\rho _q)\) and the radial and tangential pressures it is not clear that these show the required behavior (of being monotone decreasing functions). Graphical analysis shows that these do meet the required properties. Although we only represent the graphics for specific values of \(( \nu ,w)\) this behavior is similar for \(\nu \in (0,0.78787)\).

Fig. 1
figure 1

Graphical representation of the density

Full size image
Fig. 2
figure 2

Graphical representation of the quintessence matter’s density

Full size image
Fig. 3
figure 3

Graphical representation of the radial pressure

Full size image

Figures 1, 2 and 3 represent the behavior of the densities and the radial pressure. For a set value of \(\nu \) they are the same, independently of the value w. Each one of these functions decreases as the parameter \(\nu \) decreases. They also show that \(0 \le kR^2c^2\rho _q\le kR^2P_r<kR^2c^2\rho \), or equivalently, \(0 \le c^2\rho _q \le P_r<c^2\rho \).

Fig. 4
figure 4

Graphical representation of tangential pressure for \(w=-0.34\)

Full size image
Fig. 5
figure 5

Graphical representation of tangential pressure for \(w=-0.9\)

Full size image

The behavior of the tangential pressure depends of w, in Figs. 4 and  5 its behavior is presented for the values of \(w=-0.34\) and \(w=-0.9\) from which we see that for an equal value of \(\nu \) the pressure is lower if w is lower.

Fig. 6
figure 6

Graphical representation of the tangential speed of sound for \(w=-0.34\)

Full size image
Fig. 7
figure 7

Graphical representation of the tangential speed of sound for \(w=-0.9\)

Full size image

In Figs. 6 and 7 we observe the behavior of the tangential speed of sound, and just like in the case of the tangential pressure this depends of the parameters \((\nu ,w)\) showing that it approximates \(\frac{1}{3}c^2\) when \(w \rightarrow -1\). The radial speed of sound \(v_r^2=\frac{1}{3}c^2\) and in conjunction with Figs. 6 and 7 we see that \(v_t^2-v_r^2<0\), implying that the solution is potentially stable.

6 Application to the star Her X-1

The form of the function’s behavior for the presented model is adequate according to the characteristics imposed for it to be physically acceptable, except for the orders of magnitude that may have been considered. To determine the orders of magnitude and see if these are consistent with what we expect for strange quark stars we take the data of the star Her X-1 being a candidate to be strange quark star [66] to obtain its associated values. We know that its mass is \(M =0.87M_\odot \) and its radius \(R=7.866km\), replacing this in (32) we obtain \(\left( \nu =0.51192\right) \), and replacing this value in Eq. (31) and since \(\sigma =kR^2 B_g\) we determine the value of \(B_g\) to be

$$\begin{aligned} B_g= 97.00476509 \,\frac{\mathrm{Mev}}{\mathrm{fm}^3}. \end{aligned}$$

The value that we obtained differs a little from the one obtained previously for the same star, considering a model without quintessence, which was \(B_g=99.7207866 \,\mathrm{Mev}/\mathrm{fm}^3\) [66] . Figures 1, 2, 3, 4, 5, 6 and 7 with the value of \(\nu =0.51192\) describe the behavior for the data for the star Her X-1.

Table 1 Values of the hydrostatic variables for the star Her-X1
Full size table
Table 2 Values of the hydrostatic variables for the star Her X-1
Full size table

One point to highlight is that the order of magnitude of the quintessence matter’s density is two orders lower than the energy for the ordinary matter. Both pressures are zero on the surface, just like the density of quintessence. The densities, central and in the surface, reported in Table 1, match with those expected for this type of stars. The magnitude of the radial and tangential pressures reported in Table 2 do not match in the center; however, both are nullified on the surface, the tangential pressure being lower than the radial pressure for any value of \(w\in (-1,-\frac{1}{3})\).

7 Conclusions

(a) We have proposed a model with an equation of state for the tangential pressure that reflects the interaction between ordinary matter composed of quarks and quintessence. (b) It was demonstrated that this equation of state in the presence of quintessence leads to the geometry that it describes being equivalent to the one that represents a stellar solution with perfect fluid. Its content is reflected in Theorem 1, which guarantees the regularity of the geometry. In the case of new solutions for the system of quintessence with an MIT Bag equation for the radial pressure and a modified MIT Bag for the tangential pressure the one of the theorem does not guarantee the existence of regular solutions. (c) For the case of Schwarzschild’s internal solution it was proven that the solution to the new model is not stable in the sense of cracking [64], which shows that although there exists a way to obtain a model for quintessence, starting from a solution with a perfect fluid, this is not necessarily physically acceptable or potentially stable. (d) A physically acceptable and potentially stable model was constructed; for its construction we started, according to Theorem 1, from a solution that represents compact stars with a compactness rate of \(u\in (0 ,a)\), and its analysis was done in a complementary manner in a graphical form. (e) As an application of the constructed model we obtained the MIT Bag constant for the candidate to strange quark star Her X-1. (f) It is shown that at a stellar level, the possible existence with the proposed radial and tangential equations of state generates a quintessence density which is two orders of magnitude lower than the density of ordinary matter. As a result of this work a question arises. What conditions must the solutions of a perfect fluid satisfy for them to allow them to represent quintessence stars? This work represents a milestone for the generation of new solutions associated with quintessence matter as well as its generalization for other equations of state different from the MIT Bag one. Particularly it is natural to ask the following questions. What type of star represent the perfect fluid models in the context of the model posed in this investigation [67,68,69]? How is the spectrum of solutions modified if we allow \(\rho _q\) to admit regions where it is negative? It is not clear that \(\rho _q\ge 0\). If stars constituted by this type of matter did exist, what is their formation mechanism? What is the way to detect them? This work is a starting point for future work in different directions, both theoretical and observational, which may allow one to solve the questions we present here and those that would arise as a result of these investigations.