Study on wormhole geometry with $\rho (R, R^{'})$ matter in modified gravity

Abstract

In this work, static traversable wormholes are investigated in $R^2$ gravity with logarithmic trace term T, where R denotes the Ricci scalar, and $T=-\rho +p_r+2p_t>0$, the trace of the energy momentum tensor. The connection between energy density of the matter component and the Ricci scalar is taken into account. Exact wormhole solutions are determined for three different novel forms of energy density: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$, $\rho =\alpha _2 R e^{\xi _2 R}$ and $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$, where prime denotes derivative with respect to r. The parameters $\alpha _1$, $\beta _1$, $\xi _1$, $\alpha _2$, $\xi _2$, $\alpha _3$, $\xi _3$ and $\beta _2$ play an important role for the absence of exotic matter inside the wormhole geometry. The parameter space is separated into numerous regions where the energy conditions are obeyed.

1 Introduction

The notion of wormhole was first proposed by L. Flamm in 1916 [1]. After Flamm, the more detailed nature of wormhole was explored by Einstein and Rosen [2], which is famously called as Einstein–Rosen bridge. A wormhole is a geometrical piece of space-time, which is supposed as a shortcut to join two distinct points in the same space-time or two distinct space-times. The shape of wormhole is considered like a tube, which is asymptotically flat at both sides. The radius of the throat of wormhole can be either constant or variable. If it is constant, then wormholes are termed as static wormholes otherwise these are termed as non-static wormholes. Further, investigation revealed that the Einstein–Rosen wormhole is opposing to outward appearances. For an observer trying to pass through, the wormhole opens up and closes too quickly for even a photon to get through [3]. Further, investigation by Morris et al. [4] suggested that exotic forms of matter threaded through a wormhole might keep it open, however, it remains unclear whether such provisions are physically possible. Finally, Morris and Thorne introduced static traversable wormholes that describe interstellar travel [5] and are exact solutions of the Einstein field equations in general relativity. After Morris and Thorne, Visser [6] deeply studied in wormhole construction and showed that the key factor in the wormhole geometry is the destruction of classical energy conditions near the throat of wormhole, i.e. for the matter contained near the throat of wormhole radial tension must exceed the mass energy density ($\tau _0>\rho _0 c^2$). So far no known matter has this property and such type of matter must violate null energy condition. The matter that violates Null Energy Condition (NEC) stated by $T_{\mu \nu }k^{\mu }k^{\nu }\ge 0$, in which $k^{\mu }$ is any null vector and $T_{\mu \nu }$ stress-energy tensor, is called exotic matter. Hence, the exotic matter is one of the necessary components to form a wormhole geometry in general relativity [4,5,6]. So far laboratory and ordinary matters obey energy conditions, so, several researchers attempt to explain the problem of exotic matter in studying wormhole theory. In scalar–tensor theories, scalar fields play the part of exotic matter, in precise, wormhole solutions can be found if scalar fields play as a role of phantom fluid [7,8,9]. Many classes of efforts have been built on the modified gravity theories such as f(R) gravity [10,11,12,13], curvature matter coupling [14, 15] and brane-world [16,17,18,19,20,21]. In these theories, the effective stress energy tensor causes the violation of energy conditions. Since in these theories the higher order curvature terms have been used instead of an ordinary stress energy tensor. For example, in the brane-world scenario, the Einstein field equations are modified because the four-dimensional brane is embedded in five-dimensional bulk, so in this consequence, the ordinary matter satisfies NEC and violation of the NEC is because of the terms coming from the bulk effects [20]. Nevertheless, there are extended theories in which a traversable wormhole respect NEC [22,23,24,25,26]. Recently, Samanta and Godani [27] studied static traversable wormhole in viable f(R) model and showed that the presence of exotic matter near the throat could be avoided by suitable choice of throat size. In fact, the study of traversable wormholes in generalized theories is a major and noticeable concern and many authors have carried out it from various angles [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46](mentioned few, only).

The theory of general relativity is modified in several aspects in literature [47,48,49,50,51]. The modified theory of f(R) gravity [52] is one which is adopted by various researchers to describe the expanding scenario of the universe. This theory replaces the scalar curvature R with an arbitrary function f(R) in gravitational action. Starobinsky [53] studied f(R) model with $f(R)=R+\alpha R^2$, where $\alpha >0$ and found it to represent the inflationary epoch of the early universe. Furthermore, the scenario to unify inflation with dark energy in a consistent way was proposed in [54]. Bertolami et al. [55] discussed a coupling between function f(R) and the matter Lagrangian which leads towards the presence of an extra force in the geodesic equation of a perfect fluid. Further, this force is found to be responsible factor for the accelerated and expanding nature of our universe [56,57,58]. Moreover, the cosmological models in the context of modified theories are explored in [59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79]. Many f(R) models are also ruled out because they do not pass solar system tests [80]. Nevertheless, a number of realistic consistent f(R) gravities which pass the solar tests were proposed in [81,82,83]. Further, f(R, T) theory of gravity [84] is another modified theory of gravity that includes an arbitrary function of both R and T, where T denotes the trace of the stress-energy tensor, in gravitational action. Several forms of f(R, T) function are defined and studied in literature. Its split-up $f(R, T)=f_1(R)+f_2(T)$, where $f_1(R)$ and $f_2(T)$ are arbitrary functions of R and T respectively, has attracted the attention of cosmologists in different perspectives [85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106].

In nature, the presence of wormholes can be anticipated in extreme conditions. These may be found around either black holes at the center of our galaxy or binary black hole systems. In literature, efforts are put to discuss the possibilities for the detection of wormholes. Bambi [107] analyzed the iron $k\alpha$ line and explored the possibility of distinguishing black holes and wormholes. Further, the same author [108] suggested the possibility to examine through observations the idea that the supermassive objects in galactic nuclei are wormholes. They explained that the observations of the shadow of $\hbox {Sgr A}^*$, having mass of $4\times 10^6$ $M_\odot$ with the corresponding Schwarzchild radius of $r_g=0.084$ AU, could test the possibility that $\hbox {Sgr A}^*$ is a wormhole rather than black hole. Li and Bambi [109] discussed the possibility of testing the existence of a wormhole at the center of our galaxy through the observations of a hot blob of plasma orbiting near the ISCO of $\hbox {Sgr A}^*$. It is known that $\hbox {Sgr A}^*$ harbors a super massive black hole at the center of our galaxy. Dai and Stojkovic [110] investigated the possibility that $\hbox {Sgr A}^*$ might be a wormhole. They studied the motion of star $S_2$ orbiting a super massive black hole in $\hbox {Sgr A}^*$ at the center of our galaxy and found that the near future data would soon inform the harboring of a wormhole by black hole.

The purpose of this article is to explore the traversable wormholes filled with non-exotic matter in f(R, T) gravity by defining energy density in following forms: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$, $\rho =\alpha _2 R e^{\xi _2 R}$ and $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$. The parameters $\alpha _1$, $\beta _1$, $\xi _1$, $\alpha _2$, $\xi _2$, $\alpha _3$, $\xi _3$ and $\beta _2$ are found to play an important role to provide the existence of non-exotic matter for the development of wormhole solutions. The structure of the paper is as follows: In Sect. 2, the general field equations for f(R, T) gravity are mentioned. In Sect. 3, a new form of f(R, T) function, non-linear in R and logarithmic in T, is defined and field equations are derived. In Sect. 4, three forms of energy density are defined and wormhole solutions are obtained for each form. Further, the results are also discussed for each form. Finally, the findings are concluded in Sect. 5.

2 f(R, T) gravity

The f(R, T) theory, proposed by Harko et al. [84] is an extended theory of relativity in which the gravitational action is defined as

$$\begin{aligned} S=S_G + S_m=\dfrac{1}{16\pi }\int f(R,T)\sqrt{-g}d^4x +\int \sqrt{-g}{\mathcal {L}} d^4x, \end{aligned}$$

(1)

where f(R, T) stands for an arbitrary function of Ricci scalar R and trace of the energy momentum tensor T. We have used $G=c=1$. The energy momentum tensor is defined in terms of the matter action as [111]:

$$\begin{aligned} T_{\mu \nu }=-\frac{2\delta (\sqrt{-g}{\mathcal {L}})}{\sqrt{-g}\delta g^{\mu \nu }}. \end{aligned}$$

(2)

which yields

$$\begin{aligned} T_{\mu \nu }=g_{\mu \nu }{\mathcal {L}}-2\frac{\partial {\mathcal {L}}}{\partial g^{\mu \nu }}, \end{aligned}$$

(3)

where ${\mathcal {L}}$ denotes the matter Lagrangian density. The trace of stress energy momentum tensor T and its variation with respect to metric, respectively, are defined as $T=g^{\mu \nu }T_{\mu \nu }$ and

$$\begin{aligned} \frac{\delta (g^{\alpha \beta }T_{\alpha \beta })}{\delta g^{\mu \nu }}=T_{\mu \nu }+\Theta _{\mu \nu }, \end{aligned}$$

(4)

where $\Theta _{\mu \nu }=g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}$. Varying action (1) with respect to the metric tensor $g^{\mu \nu }$, yields

$$\begin{aligned}&f_R(R,T)R_{\mu \nu } -\frac{1}{2}f(R,T)g_{\mu \nu } + (g_{\mu \nu } \square -\triangledown _\mu \triangledown _\nu )f_R(R,T)\nonumber \\&\quad =8\pi T_{\mu \nu } -f_T(R, T)T_{\mu \nu }- f_T(R,T) \Theta _{\mu \nu }, \end{aligned}$$

(5)

where $f_R(R,T) \equiv \dfrac{\partial f(R, T)}{\partial R}$ and $f_T(R,T) \equiv \dfrac{\partial f(R,T)}{\partial T}$. For $f(R, T)=R$, the Eq. (5) reduces to Einstein’s field equations of general relativity and for $f(R, T)=f(R)$, (5) reduces to Einstein’s field equations of f(R) gravity. We consider the stress-energy tensor in the form of

$$\begin{aligned} T_{\mu \nu }=(p+\rho )u_\mu u_\nu -p g_{\mu \nu }, \end{aligned}$$

(6)

and the matter Lagrangian ${\mathcal {L}}$ as ${\mathcal {L}}=-p$. The four velocity $u_{\mu }$ satisfies the conditions $u_{\mu }u^{\mu }=1$ and $u^{\mu }\triangledown _{\nu }u_{\mu }=0$. If the matter source is a perfect fluid, then $\Theta _{\mu \nu }=-2T_{\mu \nu }-pg_{\mu \nu }$.

In this present study, we consider $f(R, T)=f(R)+2f(T)$, where f(R) and f(T) are arbitrary functions of R and T.

3 $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ and field equations

In the present section, we define f(R, T) function as

$$\begin{aligned} f(R, T)=R+\alpha R^2+2\beta \ln (T), \end{aligned}$$

(7)

where $T=-\rho +p_r+2p_t>0$ and, $\alpha$ and $\beta$ are constants.

The metric of static, spherical and symmetric wormhole geometry is defined as

$$\begin{aligned} ds^2=-e^{2\Phi (r)}dt^2+\frac{dr^2}{1-b(r)/r} + r^2(d\theta ^2+\sin ^2\theta d\phi ^2),\nonumber \\ \end{aligned}$$

(8)

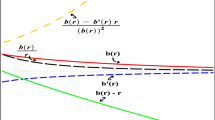
where r is the radial coordinate that can take values from $r_0\ne 0$ to $\infty$, where $r_0$ stands for the radius of the throat. In metric (8), b(r) is called shape function and $\Phi (r)$ is called redshift function. The values of angles $\theta$ and $\phi$ lie from 0 to $\pi$ and 0 to $2\pi$, respectively. The red shift function must be finite everywhere in order to avoid the existence of singularities and horizons. The shape function b(r) must fulfill the following characteristics: (i) $\frac{b(r)}{r}<1$ for $r>r_0$, (ii) $b(r_0)=r_0$ at $r=r_0$, (iii) $\frac{b(r)}{r}\rightarrow 0$ as $r\rightarrow \infty$, (iv) $\frac{b(r)-b'(r)r}{b(r)^2}>0$ for $r>r_0$ and (v) $b'(r_0)\le 1$. The condition (i) is necessary for the radial metric component to be negative. The shape function possesses minimum value equal to $r_0$ given by condition (ii). To obtain asymptotically flat space time as $r\rightarrow \infty$, the condition (iii) is required. Conditions (iv) and (v) are known as flaring out condition which are required to obtain traversable wormholes.

For the matter source of wormholes, the energy momentum tensor is defined as

$$\begin{aligned} T_{\mu \nu } = (\rho + p_t)u_\mu u_\nu - p_tg_{\mu \nu }+(p_r-p_t)X_\mu X_\nu , \end{aligned}$$

(9)

such that

$$\begin{aligned} u^{\mu }u_\mu =-1 \text{ and } X^{\mu }X_\mu =1, \end{aligned}$$

(10)

where $\rho$ denotes the energy density, $p_r$ and $p_t$ stand for the radial and tangential pressures respectively.

For the metric (8), the Ricci scalar $R=\frac{2b'(r)}{r^2}$. The field equations with $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ for the metric (8) are:

$$\begin{aligned}&\frac{b'(r)}{r^2} + A(r)=8\pi \rho -2\beta -\beta \ln (-\rho +p_r+2p_t) \end{aligned}$$

(11)

$$\begin{aligned}&\frac{-b(r)}{r^3}+B(r)=8\pi p_r\nonumber \\&\quad +\frac{4\beta (p_r+p_t)}{-\rho +p_r+2p_t} +\beta \ln ({-\rho +p_r+2p_t}) \end{aligned}$$

(12)

$$\begin{aligned}&\frac{b(r)-rb'(r)}{2r^3}+C(r)=8\pi p_t\nonumber \\&\quad +\frac{2\beta (3p_t+p_r)}{-\rho +p_r+2p_t} +\beta \ln ({-\rho +p_r+2p_t}), \end{aligned}$$

(13)

where $A(r)=\frac{1}{r^5}\bigg [6r\alpha b'(r)^2+b'(r)\Big (4\alpha b(r)+r^3-8\alpha r-2r^2\alpha b''(r)\Big )+r\Big (8r\alpha b''(r)-6\alpha b(r)b''(r)-4r^2\alpha b'''(r)+4r\alpha b(r)b'''(r)\Big )\bigg ]$,

$B(r)=\frac{1}{r^5}\bigg [12\alpha b(r)b'(r)-8r\alpha b(r)b''(r)-16\alpha r b'(r)+2r\alpha b'(r)^2+8r^2\alpha b''(r)\bigg ]$

and $C(r)=\frac{1}{2r^5}\bigg [-20\alpha b(r)b'(r)+20\alpha b(r)b''(r)-8r\alpha b(r)b'''(r)-8r\alpha b'(r)^2+32r\alpha b'(r)+4r^2\alpha b'(r)b''(r)+24r\alpha b''(r)-8r^2\alpha b'''(r)\bigg ]$.

4 Different forms of matter density

In this section, some new exact static traversable wormhole solutions sustained by non-exotic matter, by assuming different hypotheses for their matter content in $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ gravity, are found. In particular, we would like to construct exact traversable wormhole models assuming that the energy density of the matter contained in wormhole could be described by one of the following terminologies: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$, $\rho =\alpha _2 R e^{\xi _2 R}$ and $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$, respectively, where prime stands for derivative with respect to r and R denote the Ricci scalar. In our first form of $\rho$, if we consider $\xi _1=0$, then our first form of the $\rho (r)$ will be reduced to the model studied by [42], i.e. $\rho =\alpha _1 R+\beta _1 R^{'}$, in this particular model if we consider $\alpha _1=1$ and $\beta _1=\frac{r}{2}$, then the matter content of the wormhole will depend on the second derivative of shape function, i.e. $\rho =\frac{b^{''}}{r}$. In our second form of $\rho$, if we neglect the higher degree of $e^{\xi _2 R}$ terms, then the form of $\rho$ will be reduced to the model discussed by [42]. In our third form of $\rho$, if we consider $\xi _3=0$, then the form of $\rho$ will be reduced to the model discussed by [42]. The more detailed and comparisons of the models are discussed in the next section.

The wormhole modeling with power-law shape function have been studied by several authors [10, 27, 112,113,114,115,116]. Samanta and Godani [27] considered power law shape function, which is defined as

$$\begin{aligned} b(r)={r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }, \end{aligned}$$

(14)

where $0<\gamma <1$. They obtained wormhole solutions using the framework of f(R) gravity and found the satisfaction of energy conditions for wormholes having the radius of throat greater 1.7. So the following natural questions arise: (i) What are the wormhole solutions in the setting of f(R, T) gravity? (ii) Are the energy conditions satisfied in the new setting of f(R, T) gravity? (iii) What should be the radius of throat for the validation of energy conditions? To answer all these questions, we have taken the same shape function (14) with a novel function $f(R, T)=R+\alpha R^2+2\beta \ln (T)$, where $\alpha$ and $\beta$ are constants. To obtain the explicit form of the radial and tangential pressure, we would like to consider one more condition $p_t=kp_r$.

Model-I: In this model, we assumed the following form of the energy density for the wormhole geometry:

$$\begin{aligned} \rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R} \end{aligned}$$

(15)

Let us use the shape function defined in Eq. (14) and the condition $p_t=kp_r$, to obtain the explicit form of $\rho$ and $p_r$.

$$\begin{aligned} \rho= & {} \frac{2 \gamma {r_0}}{r^4} \left( \frac{r}{r_0}\right) ^{\gamma } \left( {\alpha _1} (-r)-{\beta _1} (\gamma -3) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned} p_r= & {} \bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&+ \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&+ \left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\nonumber \\&\left( {\beta _1} (\gamma -3)+{\alpha _1} r e^{\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \bigg ]\nonumber \\&\div \bigg [r^4 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma \right. \right. \nonumber \\&+\left. \left. (4 \gamma -2) k-1)-8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&+\left. \left. (\gamma -4) (\gamma -3) k-2)\right) +4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+ \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+19 k-4))\left. \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]. \end{aligned}$$

(17)

The wormhole sustain by non-exotic matter is a major part in this study, so we try to minimize exotic matter in the wormhole geometry. Hence we need to check all energy conditions to minimize exotic matter. The terms $\rho +p_r$, $\rho +p_t$, $\rho +p_r+2p_t$, $\rho -|p_r|$ and $\rho -|p_t|$ are computed below:

$$\begin{aligned} \rho +p_r= & {} \frac{2 \gamma {r_0}}{r^4} \left( \frac{r}{r_0}\right) ^{\gamma } \nonumber \\&\times \left( {\alpha _1} (-r)-{\beta _1} (\gamma -3) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \nonumber \\&+ \left[ 2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma + (\gamma -3) r^3 \right. \right. \right. \nonumber \\&+ \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&+\left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\nonumber \\&\left. \times \left( {\beta _1} (\gamma -3)+{\alpha _1} r e^{\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \right] \nonumber \\&\div \bigg [r^4 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma \right. \right. \nonumber \\&+ \left. \left. (4 \gamma -2) k-1)-8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&+\left. \left. (\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+ \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+19 k-4))\left. \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(18)

$$\begin{aligned} \rho +p_t= & {} \frac{2 \gamma {r_0}}{r^4} \left( \frac{r}{r_0}\right) ^{\gamma } \nonumber \\&\times \left( {\alpha _1} (-r)-{\beta _1} (\gamma -3) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \nonumber \\&+\,k\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&+ \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&+\left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\nonumber \\&\times \left( {\beta _1} (\gamma -3)+{\alpha _1} r e^{\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \bigg ] \nonumber \\&\div \bigg [r^4 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma \right. \right. \nonumber \\&+\left. \left. (4 \gamma -2) k-1)-8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&+\left. \left. (\gamma -4) (\gamma -3) k-2)\right) +4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+ \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+19 k-4))\left. \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(19)

$$\begin{aligned}&\rho +p_r+2p_t=\frac{2 \gamma {r_0}}{r^4} \left( \frac{r}{r_0}\right) ^{\gamma } \nonumber \\&\quad \times \left( {\alpha _1} (-r)-{\beta _1} (\gamma -3) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) +(1+2k)\nonumber \\&\quad \times \bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&\quad + \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&\quad +\left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\nonumber \\&\quad \left. \times \left( {\beta _1} (\gamma -3)+{\alpha _1} r e^{\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \right] \nonumber \\&\div \bigg [r^4 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma \right. \right. \nonumber \\&\quad +\left. \left. (4 \gamma -2) k-1)-8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&\quad +\left. \left. (\gamma -4) (\gamma -3) k-2)\right) +4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&\quad + \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&\quad + \left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(20)

$$\begin{aligned}&\rho -|p_r|=\frac{2 \gamma {r_0}}{r^4} \left( \frac{r}{r_0}\right) ^{\gamma } \nonumber \\&\quad \times \left( {\alpha _1} (-r)-{\beta _1} (\gamma -3) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \nonumber \\&\quad -\Bigg |\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&\quad +\left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&\quad +\left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\nonumber \\&\quad \times \left( {\beta _1} (\gamma -3)+{\alpha _1} r e^{\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \bigg ]\nonumber \\&\quad \div \bigg [r^4 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma \right. \right. \nonumber \\&\quad +\left. \left. (4 \gamma -2) k-1)-8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&\quad +\left. \left. (\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&\quad + \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&\quad +\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+19 k-4))\left. \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\Bigg | \end{aligned}$$

(21)

$$\begin{aligned}&\rho -|p_t|=\frac{2 \gamma {r_0}}{r^4} \left( \frac{r}{r_0}\right) ^{\gamma } \nonumber \\&\quad \times \left( {\alpha _1} (-r)-{\beta _1} (\gamma -3) e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \nonumber \\&\quad -\Bigg |k\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&\quad + \left. \left. (\gamma -3) r^3\right. \right. \nonumber \\&\quad + \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&\quad +\left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\quad \times e^{-\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\nonumber \\&\quad \times \left( {\beta _1} (\gamma -3)+{\alpha _1} r e^{\frac{2 \gamma {\xi _1} {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\right) \bigg ] \nonumber \\&\quad \div \bigg [r^4 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma \right. \right. \nonumber \\&\quad + \left. \left. (4 \gamma -2) k-1)\right. \right. \nonumber \\&\quad - \left. \left. 8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&\quad +\left. \left. (\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&\quad + \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&\quad + \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&\quad +19 k-4))\left. \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\Bigg |. \end{aligned}$$

(22)

Discussion for Model-I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

The parameter $\alpha _1$, $\beta _1$ and $\xi _1$ are the controlling parameters for the model $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$. The function $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ is dependent on constants $\alpha$ and $\beta$. The constant $\xi _1$ can be zero, positive or negative. So, there are three possible cases:

• Case-I: $\xi _1=0$

• Case-II: $\xi _1>0$

• Case-III: $\xi _1<0$

For each case, there are following eight possible subcases: (i) $\alpha _1>0$, $\beta _1>0$, $\alpha >0$, (ii) $\alpha _1>0$, $\beta _1>0$, $\alpha <0$, (iii) $\alpha _1<0$, $\beta _1<0$, $\alpha >0$, (iv) $\alpha _1<0$, $\beta _1<0$, $\alpha <0$, (v) $\alpha _1>0$, $\beta _1<0$, $\alpha >0$, (vi) $\alpha _1>0$, $\beta _1<0$, $\alpha <0$, (vii) $\alpha _1<0$, $\beta _1>0$, $\alpha >0$, (viii) $\alpha _1<0$, $\beta _1>0$, $\alpha <0$.

Thus, there are total 24 following subcases for Model-I.

Table 1 Results for Model-I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

Table 2 Results for Model-I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

1.   $\xi _1=0$, $\alpha _1>0$, $\beta _1>0$, $\alpha >0$,     2.   $\xi _1=0$, $\alpha _1>0$, $\beta _1>0$, $\alpha <0$,

3.   $\xi _1=0$, $\alpha _1<0$, $\beta _1<0$, $\alpha >0$,     4.   $\xi _1=0$, $\alpha _1<0$, $\beta _1<0$, $\alpha <0$,

5.   $\xi _1=0$, $\alpha _1>0$, $\beta _1<0$, $\alpha >0$,     6.   $\xi _1=0$, $\alpha _1>0$, $\beta _1<0$, $\alpha <0$,

7.   $\xi _1=0$, $\alpha _1<0$, $\beta _1>0$, $\alpha >0$,     8.   $\xi _1=0$, $\alpha _1<0$, $\beta _1>0$, $\alpha <0$,

9.   $\xi _1>0$, $\alpha _1>0$, $\beta _1>0$, $\alpha >0$,     10.  $\xi _1>0$, $\alpha _1>0$, $\beta _1>0$, $\alpha <0$,

11.  $\xi _1>0$, $\alpha _1<0$, $\beta _1<0$, $\alpha >0$,    12.  $\xi _1>0$, $\alpha _1<0$, $\beta _1<0$, $\alpha <0$,

13.  $\xi _1>0$, $\alpha _1>0$, $\beta _1<0$, $\alpha >0$,    14.  $\xi _1>0$, $\alpha _1>0$, $\beta _1<0$, $\alpha <0$,

15.  $\xi _1>0$, $\alpha _1<0$, $\beta _1>0$, $\alpha >0$,    16.  $\xi _1>0$, $\alpha _1<0$, $\beta _1>0$, $\alpha <0$,

17.  $\xi _1<0$, $\alpha _1>0$, $\beta _1>0$, $\alpha >0$,    18.  $\xi _1<0$, $\alpha _1>0$, $\beta _1>0$, $\alpha <0$,

19.  $\xi _1<0$, $\alpha _1<0$, $\beta _1<0$, $\alpha >0$,    20.  $\xi _1<0$, $\alpha _1<0$, $\beta _1<0$, $\alpha <0$,

21.  $\xi _1<0$, $\alpha _1>0$, $\beta _1<0$, $\alpha >0$,    22.  $\xi _1<0$, $\alpha _1>0$, $\beta _1<0$, $\alpha <0$,

23.  $\xi _1<0$, $\alpha _1<0$, $\beta _1>0$, $\alpha >0$,    24.  $\xi _1<0$, $\alpha _1<0$, $\beta _1>0$, $\alpha <0$.

The all possible studies of the model have been taken into account. The energy conditions and geometry are investigated for each subcase with the variation of r and k. In Subcases 3, 5, 6, 12, 13, 14, 19, 21 and 22, the energy density and NEC terms are found to be negative near and outside the throat of the wormhole, which implies that whole geometry filled with exotic matter. As per the requirement for the construction of wormhole, the NEC could be violated near the throat, which indicates the presence of exotic matter near the throat. However, outside throat the wormhole must be filled with normal matter, which implies that all energy condition must be satisfied. Therefore, these subcases are either unrealistic or beyond of our knowledge to judge the nature, so we ignore these subcases for our discussion.

Table 3 Results for Model-I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

Table 4 Results for Model-I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

Table 5 Results for Model-I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

For remaining subcases, the results are summarized in Tables 1, 2, 3, 4 and 5. In Subcase 1, both WEC and DEC are satisfied for all $r>0$ and $k\in [0,1]$, however SEC is dissatisfied. In Subcase 2, if $k=0$, both WEC and SEC are satisfied and DEC is not satisfied for all $r>0$. If $k\ne 0$, both WEC and DEC are satisfied everywhere and SEC is not. In Subcase 4, WEC and SEC validate for $r>2.4$ and $k\le 0$, so in this subcase if we assume the minimum size of the throat is $r_0=2.4$, then we can avoid exotic matter, unless exotic matter could be available near throat. In Subcase 7, WEC and SEC are satisfied for $r<1.6$ and $k<0$ and DEC is violated everywhere, which implies that the huge amount of exotic matter is threaded in the wormhole geometry. In Subcase 8, although WEC and SEC are valid for all r and $k\le 0$, however DEC is invalid everywhere, so we are not about the presence or absence of exotic matter.

In Subcase 9, WEC and DEC are obeyed for $r\in (0.2,1.6)$ and for all k and all WEC, SEC and DEC are obeyed for $r\in (0.2,0.6)$ and for all k. In Subcase 10, WEC and DEC are satisfied for $r\in (0.2,5)$ and $k<0$ and all WEC, DEC and SEC are also satisfied for $r\in (0.2,5)$ and $k<-2$. In Subcase 11, SEC and DEC is satisfied nowhere, however WEC is satisfied for $r\in (2.5,3.1)$ and $k\ne 0$. In Subcase 15, DEC is not violated for $r<8$. WEC is valid for all r and k and SEC is valid for all r and $k\le 0$. Thus, both WEC and SEC are valid for all r and $k\le 0$. In Subcase 16, WEC holds everywhere for every k. SEC also holds everywhere but for $k\in [-1,0]$. DEC holds for $r\in (0.6,\infty )$ and $k\in (-\infty ,0]\cup (1,\infty )$. Thus, all WEC, SEC and DEC hold for $r>0.6$ and $k\in [-1,0]$, so in this subcase, if we consider the minimum throat size of the wormhole is $r_0=0.6$, then the presence of exotic matter could be avoidable.

In Subcase 17, WEC is obeyed everywhere for every k. SEC is also obeyed everywhere but for $k\le 0$. DEC is obeyed for $r>2.5$ and for all k. Thus, all WEC, SEC and DEC are obeyed for $r>2.5$ and $k\le 0$, so in this subcase, if we assume the minimum throat size is $r_0=2.5$, then all ECs are valid and consequently we can say that the wormhole could be sustained without exotic matter. In Subcase 18, WEC and SEC are satisfied everywhere for every k. DEC is obeyed for $r>2.6$ and for all k. Thus, all WEC, SEC and DEC are obeyed for $r>2.6$ and for all k, so in this subcase, if we assume the throat size is $r_0=2.6$ or more, then the exotic matter can be removed for the development of wormhole structure. In Subcase 20, NEC, WEC and DEC are validated for $r>2.5$ and for all k. SEC validates for $r>9$ and for all k. Thus, all ECs NEC, WEC, SEC and DEC validate for $r>9$ and for all k. In Subcase 23, WEC and SEC are satisfied everywhere for $k<0$, however DEC is satisfied for $r>0.9$. So, all ECs are satisfied for $r>0.3$ and $k<0$. In Subcase 24, all WEC, SEC and DEC hold for any range of r, and $k\ne 0$. The results for subcases discussed above are also shown in Fig. 1a–o. Hence, it is observed that the energy conditions are satisfied in various subcases of Model-I. The highest ranges of r and k for the validation of desired properties are found in Subcase 24, i.e. $\xi _1<0$, $\alpha _1<0$, $\beta _1>0$, $\alpha <0$. In this subcase, the energy conditions are valid forevery r and $k\ne 0$. The geometry is repulsive near the throat till $r=0.6$ and then it is attractive. In this subcase, the value of EoS parameter $\omega >-1$, i.e. the wormhole geometry is filled with non-phantom fluid.

Fig. 1

Plots of EC terms for 15 subcases of model I: $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$

Model-II: In this model, we assumed the energy density in the following form:

$$\begin{aligned} \rho =\alpha _2 R e^{\xi _2 R} \end{aligned}$$

(23)

Let us use the shape function defined in Eq. (14) and the condition $p_t=kp_r$, then

$$\begin{aligned} \rho= & {} -\frac{2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}}{r^3} \end{aligned}$$

(24)

$$\begin{aligned} p_r= & {} \bigg [2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&+\left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&+\left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\bigg ]\nonumber \\&\div \bigg [r^3 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+\left. \left. r^3 (-3 \gamma +(4 \gamma -2) k-1)-8 \alpha \gamma r (-(\gamma -5) \gamma \right. \right. \nonumber \\&+\left. \left. (\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+\left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)+r (-2 (\gamma -4) \gamma \right. \nonumber \\&+ \left. (\gamma -8) \gamma k+19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]. \end{aligned}$$

(25)

Table 6 Results for Form II: $\rho =\alpha _2 R e^{\xi _2 R}$

Table 7 Results for Form II: $\rho =\alpha _2 R e^{\xi _2 R}$

The wormhole sustain by non-exotic matter is a major part in this study, so we try to minimize exotic matter in the wormhole geometry. Hence we need to check all energy conditions to minimize exotic matter. The terms $\rho +p_r$, $\rho +p_t$, $\rho +p_r+2p_t$, $\rho -|p_r|$ and $\rho -|p_t|$ are computed as below:

$$\begin{aligned} \rho + p_r= & {} -\frac{2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}}{r^3}\nonumber \\&+\bigg [2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ (\gamma -3) r^3+\left. \left. 16 \alpha (\gamma -5) \gamma r\right) \right. \nonumber \\&- \left. 4 \alpha \gamma {r_0} \left( 11 \gamma + \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\bigg ]\div \bigg [r^3 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k-1) \right. \right. \nonumber \\&-\left. \left. 8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right. \right. \nonumber \\&+ \left. \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right) \right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+ \left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(26)

$$\begin{aligned} \rho + p_t= & {} -\frac{2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}}{r^3}\nonumber \\&+k\bigg [2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ (\gamma -3) r^3+\left. \left. 16 \alpha (\gamma -5) \gamma r\right) \right. \nonumber \\&- \left. 4 \alpha \gamma {r_0} \left( 11 \gamma + \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\bigg ]\div \bigg [r^3 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k-1) \right. \right. \nonumber \\&-\left. \left. 8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right. \right. \nonumber \\&+ \left. \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right) \right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+\left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(27)

$$\begin{aligned} \rho + p_r + 2p_t= & {} -\frac{2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}}{r^3}\nonumber \\&+(1+2k)\bigg [2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ (\gamma -3) r^3+\left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&+ \left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\bigg ]\div \bigg [r^3 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k-1) \right. \right. \nonumber \\&-\left. \left. 8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right. \right. \nonumber \\&+ \left. \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9))\right. \right. \nonumber \\&+ \left. \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \right. \nonumber \\&+ \left. \left. 19 k-4)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(28)

$$\begin{aligned} \rho - |p_r|= & {} -\frac{2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}}{r^3}\nonumber \\&+\Bigg |\bigg [2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ (\gamma -3) r^3+\left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \left( 11 \gamma \right. \right. \nonumber \\&+ \left. \left. \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\bigg ]\div \bigg [r^3 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k-1) \right. \right. \nonumber \\&-\left. \left. 8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right. \right. \nonumber \\&+ \left. \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9))\right. \right. \nonumber \\&+ \left. \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \right. \nonumber \\&+ \left. \left. 19 k-4)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\Bigg | \end{aligned}$$

(29)

$$\begin{aligned} \rho - |p_t|= & {} -\frac{2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}}{r^3}\nonumber \\&+\Bigg |k\bigg [2 {\alpha _2} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+\left. \left. (\gamma -3) r^3+16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0} \right. \nonumber \\&\left. \left( 11 \gamma + \gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 \gamma {\xi _2 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^3}}\bigg ]\div \bigg [r^3 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k-1) \right. \right. \nonumber \\&-\left. \left. 8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right. \right. \nonumber \\&+ \left. \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9))\right. \right. \nonumber \\&+ \left. \left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \right. \nonumber \\&+ \left. \left. 19 k-4)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\Bigg |. \end{aligned}$$

(30)

Discussion for Model-II: $\rho =\alpha _2 R e^{\xi _2 R}$

This form of $\rho$ is dependent on constants $\alpha _2$ and $\xi _2$ and $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ is dependent on constants $\alpha$ and $\beta$. For the detail study of the model, we can consider the constant $\xi _2$ to be zero, positive or negative. So, there are three possible cases:

• Case-I: $\xi _2=0$

• Case-II: $\xi _2>0$

• Case-III: $\xi _2<0$

For each case, there are following four possible subcases: (i) $\alpha _2>0$, $\alpha >0$, (ii) $\alpha _2>0$, $\alpha <0$, (iii) $\alpha _2<0$, $\alpha >0$ and (iv) $\alpha _2<0$, $\alpha <0$.

Thus, there are total 12 following subcases for Model-II.

1.   $\xi _2=0$, $\alpha _2>0$, $\alpha >0$,     2.   $\xi _2=0$, $\alpha _2>0$, $\alpha <0$,     3.   $\xi _2=0$, $\alpha _2<0$, $\alpha >0$

4.   $\xi _2=0$, $\alpha _2<0$, $\alpha <0$,     5.   $\xi _2>0$, $\alpha _2>0$, $\alpha >0$,     6.   $\xi _2>0$, $\alpha _2>0$, $\alpha <0$,

7.   $\xi _2>0$, $\alpha _2<0$, $\alpha >0$,     8.   $\xi _2>0$, $\alpha _2<0$, $\alpha <0$,     9.   $\xi _2<0$, $\alpha _2>0$, $\alpha >0$,

10.  $\xi _2<0$, $\alpha _2>0$, $\alpha <0$    11.   $\xi _2<0$, $\alpha _2<0$, $\alpha >0$,    12.   $\xi _2<0$, $\alpha _2<0$, $\alpha <0$.

The energy conditions and geometry are investigated for each subcase with the variation of r and k. It is found that the energy density and NEC terms are negative in Subcases 1, 2, 5, 6, 9 and 10. Furthermore it is found that the NEC is violated for entire region of the wormhole geometry which implies that the whole geometry is threaded with exotic matter. Therefore, those subcases are either physically unrealistic or beyond of our knowledge to study.

For remaining subcases, the results are summarized in Tables 6 and 7. In Subcase 3, WEC is satisfied for $r<4.7$ and $k\in (-\infty ,0)\cup (1,\infty )$. SEC is valid for $r\le 5$ and $k\le 0$. DEC is valid for $1.5<r<4.7$ and $k\le -1$. Thus, WEC & DEC are valid for $1.5<r<4.7$ and $k\le -1$ and WEC & SEC are valid for $r\le 1$ and $k\le 0$. In Subcase 4, WEC is satisfied for all r and $k\ne 1$. SEC is satisfied for all r and $k\in (-4,0)$. DEC is satisfied for all r and $k\in (-\infty ,0)\cup (1,\infty )$. All, WEC, SEC and DEC are satisfied for all r and $k\in (-4,0)$, so in this subcase, we realized that the wormhole could be sustained without exotic matter. In Subcase 7, WEC is obeyed for all r and $k\in (-\infty ,0)\cup (1,\infty )$. SEC is obeyed for $r\ge 6$ and $k<0$. DEC is obeyed for all r and $k\le 0$. So, WEC, SEC and DEC are obeyed for $r\ge 6$ and $k\le 0$, so in this subcase, to avoid exotic matter, we require to assume the minimum throat size $r_0=6$. In Subcase 8, WEC is valid for $r>0.5$ and $k\ne 1$. SEC is valid for $r>0.5$ and $k\le 0$. DEC is valid for $r>0.5$ and $k\in (-\infty ,0)\cup (1,\infty )$. Thus, all WEC, SEC and DEC are validated for $r>0.5$ and $k<0$, so, to avoid exotic matter in the wormhole, the minimum throat size will be $r_0=0.5$. In Subcase 11, WEC holds for $r>0.3$ and for all k. SEC holds for $r>4$ and $k\ge 0$. DEC holds for all r and $k>0$. Thus, all WEC, SEC and DEC hold for $r>4$ and $k>0$, so, to avoid exotic matter in the wormhole construction, the minimum throat size will be $r_0=4$. In Subcase 12, WEC is not violated for $r>0.2$ and $k\ne 1$. SEC is not violated for $r>0.2$ and $k\in [0,1)\cup (1,\infty )$. DEC is not violated for $r>0.55$ and for all k. Hence, all WEC, SEC and DEC are not violated for $r>0.55$ and $k\in [0,1)\cup (1,\infty )$. The results for subcases discussed above are shown in Fig. 2a–f.

Thus, it can be seen that in Subcase 4 i.e. $\xi _2=0$, $\alpha _2<0$, $\alpha <0$, all energy conditions are satisfied for all $r>0$ and $k\in [-4,0)$. The wormholes are filled with ordinary fluid having repulsive geometry for $r<0.1$ and attractive geometry for $r\ge 1$.

Fig. 2

Plots of EC terms for 6 subcases of model II: $\rho =\alpha _2 R e^{\xi _2 R}$

Model-III: In this model, we assumed the energy density in the following form:

$$\begin{aligned} \rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}} \end{aligned}$$

(31)

Let us use the shape function defined in equation (14) and the condition $p_t=kp_r$, then

$$\begin{aligned} \rho= & {} \frac{2 \gamma {r_0}}{r^6} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( 2 {\alpha _3} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\right. \nonumber \\&-\left. {\beta _2} (\gamma -3) r^2 e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \end{aligned}$$

(32)

$$\begin{aligned} p_r= & {} \bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&+ \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0}\right. \nonumber \\&\times \left. \left( 11 \gamma +\gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}} \left( {\beta _2} (\gamma -3) r^2-2 {\alpha _3} \gamma {r_0}\right. \nonumber \\&\times \left. \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \bigg ]\nonumber \\&\ \div \bigg [r^6 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k\right. \right. \nonumber \\&-\left. \left. 1)-8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+ \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+ \left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]. \end{aligned}$$

(33)

The wormhole sustain by non-exotic matter is a crucial part in this study, so we try to minimize exotic matter in the wormhole geometry. Hence we need to check all energy conditions to minimize exotic matter. The expressions for $\rho +p_r$, $\rho +p_t$, $\rho +p_r+2p_t$, $\rho -|p_r|$ and $\rho -|p_t|$ are computed below:

$$\begin{aligned} \rho +p_r= & {} \frac{2 \gamma {r_0}}{r^6} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( 2 {\alpha _3} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\right. \nonumber \\&- \left. {\beta _2} (\gamma -3) r^2 e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \nonumber \\&+\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&+ \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0}\right. \nonumber \\&\times \left. \left( 11 \gamma +\gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}} \left( {\beta _2} (\gamma -3) r^2-2 {\alpha _3} \gamma {r_0}\right. \nonumber \\&\times \left. \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \bigg ]\div \bigg [r^6 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k\right. \right. \nonumber \\&-\left. \left. 1)-8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+ \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k+19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned} \rho +p_t= & {} \frac{2 \gamma {r_0}}{r^6} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( 2 {\alpha _3} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\right. \nonumber \\&- \left. {\beta _2} (\gamma -3) r^2 e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \nonumber \\&+k\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&\quad + \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0}\right. \nonumber \\&\times \left. \left( 11 \gamma +\gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}} \left( {\beta _2} (\gamma -3) r^2-2 {\alpha _3} \gamma {r_0}\right. \nonumber \\&\times \left. \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \bigg ]{\div }\bigg [r^6 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. r^3 (-3 \gamma +(4 \gamma -2) k\right. \right. \nonumber \\&-\left. \left. 1)-8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+\left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+\left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(35)

$$\begin{aligned} \rho +p_r+2p_t= & {} \frac{2 \gamma {r_0}}{r^6} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( 2 {\alpha _3} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\right. \nonumber \\&-\left. {\beta _2} (\gamma -3) r^2 e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) +(1+2k)\nonumber \\&\times \bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma {+}(\gamma -3) r^3\right. \right. \nonumber \\&+\left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0}\right. \nonumber \\&\times \left. \left( 11 \gamma +\gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}} \left( {\beta _2} (\gamma -3) r^2-2 {\alpha _3} \gamma {r_0}\right. \nonumber \\&\times \left. \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \bigg ]\nonumber \\&\div \bigg [r^6 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma {+}r^3 (-3 \gamma {+}(4 \gamma -2) k\right. \right. \nonumber \\&-\left. \left. 1)-8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+ \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+\left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ] \end{aligned}$$

(36)

$$\begin{aligned} \rho -|p_r|= & {} \frac{2 \gamma {r_0}}{r^6} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( 2 {\alpha _3} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\right. \nonumber \\&- \left. {\beta _2} (\gamma -3) r^2 e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \nonumber \\&-\Bigg |\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +(\gamma -3) r^3\right. \right. \nonumber \\&+ \left. \left. 16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0}\right. \nonumber \\&\times \left. \left( 11 \gamma +\gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}} \left( {\beta _2} (\gamma -3) r^2-2 {\alpha _3} \gamma {r_0}\right. \nonumber \\&\left. \times \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \bigg ]\nonumber \\&\div \bigg [r^6 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma +(4 \gamma -2) k\right. \right. \nonumber \\&-\left. \left. 1)-8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&\quad + \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+ \left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\Bigg | \end{aligned}$$

(37)

$$\begin{aligned} \rho -|p_t|= & {} \frac{2 \gamma {r_0}}{r^6} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( 2 {\alpha _3} \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }\right. \nonumber \\&-\left. {\beta _2} (\gamma -3) r^2 e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \nonumber \\&-\Bigg |k\bigg [2 \gamma {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma } \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma \right. \right. \nonumber \\&+ \left. \left. (\gamma -3) r^3+16 \alpha (\gamma -5) \gamma r\right) -4 \alpha \gamma {r_0}\right. \nonumber \\&\times \left. \left( 11 \gamma +\gamma ^2 (r-2)-3 (5 r+3)\right) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \nonumber \\&\times e^{-\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}} \left( {\beta _2} (\gamma -3) r^2-2 {\alpha _3} \gamma {r_0}\right. \nonumber \\&\times \left. \left( \frac{r}{{r_0}}\right) ^{\gamma } e^{\frac{2 (\gamma -3) \gamma {\xi _3 } {r_0} \left( \frac{r}{{r_0}}\right) ^{\gamma }}{r^4}}\right) \bigg ]\nonumber \\&\div \bigg [r^6 \left( r \left( 8 \alpha (\gamma -5) (\gamma -1) \gamma +r^3 (-3 \gamma +(4 \gamma -2) k\right. \right. \nonumber \\&-\left. \left. 1)-8 \alpha \gamma r (-(\gamma -5) \gamma +(\gamma -4) (\gamma -3) k-2)\right) \right. \nonumber \\&+ \left. 4 \alpha \gamma {r_0} ((\gamma -1) (2 \gamma -9)\right. \nonumber \\&+\left. r (-2 (\gamma -4) \gamma +(\gamma -8) \gamma k\right. \nonumber \\&+ \left. 19 k-4)) \left( \frac{r}{{r_0}}\right) ^{\gamma }\right) \bigg ]\Bigg |. \end{aligned}$$

(38)

Table 8 Results for Form III: $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$

Table 9 Results for Form III: $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$

Discussion for Model-III: $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$

This form of $\rho$ is dependent on constants $\alpha _3$, $\beta _2$ and $\xi _3$ and $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ is dependent on constants $\alpha$ and $\beta$. Like first two forms, our model consists of four constants $\alpha _3$, $\beta _2$, $\xi _3$ and $\alpha$. The constant $\xi _3$ can be zero, positive or negative. So, there are three possible cases:

• Case-I: $\xi _3=0$,

• Case-II: $\xi _3>0$,

• Case-III: $\xi _3<0$

For each case, there are following eight possible subcases: (i) $\alpha _3>0$, $\beta _2>0$, $\alpha >0$, (ii) $\alpha _3>0$, $\beta _2>0$, $\alpha <0$, (iii) $\alpha _3<0$, $\beta _2<0$, $\alpha >0$, (iv) $\alpha _3<0$, $\beta _2<0$, $\alpha <0$, (v) $\alpha _3>0$, $\beta _2<0$, $\alpha >0$, (vi) $\alpha _3>0$, $\beta _2<0$, $\alpha <0$, (vii) $\alpha _3<0$, $\beta _2>0$, $\alpha >0$, (viii) $\alpha _3<0$, $\beta _2>0$, $\alpha <0$.

Thus, there are total 24 following subcases for Model-III.

1.   $\xi _3=0$, $\alpha _3>0$, $\beta _2>0$, $\alpha >0$,     2.   $\xi _3=0$, $\alpha _3>0$, $\beta _2>0$, $\alpha <0$,

3.   $\xi _3=0$, $\alpha _3<0$, $\beta _2<0$, $\alpha >0$,     4.   $\xi _3=0$, $\alpha _3<0$, $\beta _2<0$, $\alpha <0$,

5.   $\xi _3=0$, $\alpha _3>0$, $\beta _2<0$, $\alpha >0$,     6.   $\xi _3=0$, $\alpha _3>0$, $\beta _2<0$, $\alpha <0$,

7.   $\xi _3=0$, $\alpha _3<0$, $\beta _2>0$, $\alpha >0$,     8.   $\xi _3=0$, $\alpha _3<0$, $\beta _2>0$, $\alpha <0$,

9.   $\xi _3>0$, $\alpha _3>0$, $\beta _2>0$, $\alpha >0$,    10.   $\xi _3>0$, $\alpha _3>0$, $\beta _2>0$, $\alpha <0$,

11.  $\xi _3>0$, $\alpha _3<0$, $\beta _2<0$, $\alpha >0$,    12.   $\xi _3>0$, $\alpha _3<0$, $\beta _2<0$, $\alpha <0$,

13.  $\xi _3>0$, $\alpha _3>0$, $\beta _2<0$, $\alpha >0$,    14.   $\xi _3>0$, $\alpha _3>0$, $\beta _2<0$, $\alpha <0$,

15.  $\xi _3>0$, $\alpha _3<0$, $\beta _2>0$, $\alpha >0$,    16.   $\xi _3>0$, $\alpha _3<0$, $\beta _2>0$, $\alpha <0$,

17.  $\xi _3<0$, $\alpha _3>0$, $\beta _2>0$, $\alpha >0$,    18.   $\xi _3<0$, $\alpha _3>0$, $\beta _2>0$, $\alpha <0$,

19.  $\xi _3<0$, $\alpha _3<0$, $\beta _2<0$, $\alpha >0$,    20.   $\xi _3<0$, $\alpha _3<0$, $\beta _2<0$, $\alpha <0$,

21.  $\xi _3<0$, $\alpha _3>0$, $\beta _2<0$, $\alpha >0$,    22.   $\xi _3<0$, $\alpha _3>0$, $\beta _2<0$, $\alpha <0$,

Table 10 Results for Form III: $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$

Table 11 Results for Form III: $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$

23.  $\xi _3<0$, $\alpha _3<0$, $\beta _2>0$, $\alpha >0$,    24.   $\xi _3<0$, $\alpha _3<0$, $\beta _2>0$, $\alpha <0$.

Like first two models, the energy conditions and geometry are investigated for each subcase with the variation of r and k. In Subcases 3, 4, 5, 6, 11, 12, 13, 14, 19, 20, 21, and 22 the energy density and NEC terms are found to be negative for entire region. Therefore, in those subcases the entire wormhole geometry completely filled with exotic matter, which is unrealistic. So, these subcases are not of our interest. For remaining subcases, the results are summarized in Tables 8, 9, 10 and 11. In Subcase 1, WEC is satisfied for $r>0.2$ and $k\in (-\infty ,0)\cup (1,\infty )$, SEC is satisfied for $r>0.2$ and $k\in (-\infty ,0)$ and DEC is satisfied for $r>0.22$ and $k\ne 0$. All WEC, SEC and DEC are satisfied for $r>0.22$ and $k\in (-\infty ,0)$. So, in this subcase, the existence of exotic matter can be avoided by choosing size of the throat as $r_0=0.22$.

In Subcase 2, WEC and SEC hold for all r and $k\le 0$ and DEC holds for all r and $k=0$. $k=0$, means the tangential pressure $p_t$ is zero. In this subcase, we can say that the matter could be avoided by taking zero tangential pressure, however, which could be unrealistic.

In subcase 7, WEC is valid for $r>0.5$ and for all k. SEC is invalid everywhere. DEC is valid for $0.5<r<2.7$ and $k\in (-\infty ,-1)\cup (0,\infty )$. All WEC, SEC and DEC are valid for $0.5<r<2.7$ and $k\in (-\infty ,-1)\cup (0,\infty )$, which implies that the wormhole geometry is filled with normal matter for very small region $0.5<r<2.7$, elsewhere, the geometry filled with exotic matter.

In Subcase 8, WEC holds for $r>0.2$ and for all k. SEC holds for $r>0.2$ and $k\in (-1,0)$. DEC holds for $r>0.25$ and $k\ne 0$. Thus, all WEC, SEC and DEC hold for $r>0.25$ and $k\in (-1,0)$, so in this subcase, if we assume the minimum size of the throat is $r_0=0.25$, then we can remove the necessity of exotic matter.

In Subcase 9, WEC is satisfied for $0.3<r<3.7$ and $k\in [0,1)$. SEC is satisfied for $r<1$ and $k=0$. DEC is satisfied for $0.4<r<3.7$ and for all k. All WEC, SEC and DEC are satisfied $0.4<r<1$ and $k=0$. This subcase may be irrelevant for the study of the wormhole, because we obtained very small region where all ECs are satisfied with the zero tangential pressure.

In Subcase 10, WEC is not violated for $r>0.2$ and for all k. SEC is not violated for $r>0.2$ and $k\in (-1,0)$. DEC is not violated for $r>0.3$ and $k\ne 0$. Hence, WEC, DEC and SEC are not violated for $r>0.3$ and $k\in (-1,0)$, so in this subcase we may choose the minimum size of the throat is $r_0=0.3$ to avoid the presence of exotic matter.

In Subcase 15, WEC and DEC are obeyed for $r>0$ and $k\ne 0$. SEC is obeyed for $r>2.4$ and for all k. Thus, all WEC, SEC and DEC are obeyed for $r>2.4$ and $k\ne 0$.

In Subcase 16, WEC is valid for $r>0.2$ and for all k. SEC is valid for $r>0.2$ and $k\in (-1,0)$. DEC is valid for $r>0.3$ and $k\ne 0$. All WEC, SEC and DEC are valid for $r>0.3$ and $k\in (-1,0)$.

In Subcase 17, WEC holds for $0.3<r<3.7$ and for all k. Both SEC and DEC hold for $0.3<r<3.7$ and $k\in (-1,0)$. All WEC, SEC and DEC hold for $0.3<r<3.7$ and $k\in (-1,0)$.

In Subcase 18, WEC is satisfied for all r and $k\ne 1$. SEC is satisfied for all r and $k=0$. DEC is satisfied for $r>4$ and $k\ne 0$. Thus, all ECs are valid for $r>4$ and $k\notin \{0,1\}$.

In Subcase 23, WEC is obeyed for $r>0.9$ and $k\in (-\infty ,0)\cup (1,\infty )$. SEC is obeyed for $r>6$ and $k\in (-\infty ,0)\cup (1,\infty )$. DEC is obeyed for $r>0.9$ and for all k. All WEC, SEC and DEC are obeyed for $r>6$ and $k\in (-\infty ,0)\cup (1,\infty )$.

In Subcase 24, WEC validates for $r>0.9$ and for all k, SEC validates for $r>0.9$ and $k\ne 0$ and DEC validates for $r>3$ and $k\ne 0$. Thus, both WEC and SEC are validated for $r>0.9$ and $k\ne 0$ and both WEC and DEC are validated for $r>3$ and $k\ne 0$. All WEC, SEC and DEC are satisfied nowhere. The results for subcases discussed above are plotted in Fig. 3a–l. It can be observed that the highest range of r for the validity of energy conditions is $r>0$ in Subcase 2 but only for $k=0$. This implies the zero tangential pressure which is not preferable. In Subcases 8, 10 and 16, we have same results for energy conditions. In these subcases, energy conditions are valid for $r>0.3$ ad $k\in (-1,0)$. In Subcase 8, the geometry is attractive, in Subcase 10, it is repulsive for $0.3<r<0.6$ and attractive for $r\ge 0.6$ and in Subcase 16, it is also attractive. In Subcase 8 and 16, $\omega >0$ for $r> 0.5$ and in Subcase 10, $\omega >0$ for $r> 0.1$. Since we are finding the existence of wormholes filled with ordinary fluid having repulsive geometry near the throat and attractive away from the throat, we have all desired geometrical properties in Subcase 10 of Model-III.

Fig. 3

EC terms for 15 subcases of $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$

Thus, we have most favourable results for (i) $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$ with $r>0$ & $k\ne 0$ (Subcase 24 in Model-I), (ii) $\rho =\alpha _2 R e^{\xi _2 R}$ with $r>0$ & $k\in (-4,0)$ (Subcase 4 in Model-II) and (iii) $\rho =\alpha _3 R^2+\beta _2 R^{'}e^{\xi _3 R^{'}}$ with $r>0.3$ & $k\in (-1,0)$ (Subcase 10 in Model-III).

5 Conclusion

The present paper is aimed at the investigation of traversable wormhole solutions in f(R, T) gravity with novel function $f(R, T)=R+\alpha R^2+2\beta \ln (T)$, where $\alpha$ and $\beta$ are constants and $T=-\rho +p_r+2p_t>0$. Using this f(R, T) function, the field equations are derived in Sect. 3. To solve these field equations, the shape function b(r) is considered as $b(r)=r_0\Big (\frac{r}{r_0}\Big )^\gamma$, where $0<\gamma <1$. Further, the radial pressure $p_r$ and tangential pressure $p_t$ are considered to be related as $p_t=kp_r$. Furthermore, the connection between Ricci scalar and energy density of the matter component is taken into account. We have defined three new forms of energy density: I. $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$, II. $\rho =\alpha _2 R e^{\xi _2 R}$ and III. $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$, where $\alpha _1$, $\alpha _2$, $\alpha _3$, $\beta _1$, $\beta _2$, $\xi _1$, $\xi _2$ and $\xi _2$ are constants. For each $\rho$ function, the solutions are obtained in preceding section.

In our first form of $\rho$, if we consider $\xi _1=0$, then our first form of the $\rho$ will be reduced to $\rho =\alpha _1 R+\beta _1 R^{'}$, which is studied by [42]. For this particular model, Elizalde and Khurshudyan [42] showed that the violation of the NEC and DEC at the throat which implies that the existence of exotic matter is not avoidable in their work. However, in our model results are quite different and interesting. From the Tables 1 and 2, subcases-1, 2, 4, 7 and 8, it is observed that NEC, WEC and SEC are valid for different range of r, moreover the DEC term is violated for some particular range of r. For $\rho =\alpha _1 R+\beta _1 R^{'}$, if we consider $\alpha _1=1$ and $\beta _1=\frac{r}{2}$, then the matter content of wormhole will depend on the second derivative of shape function, i.e $\rho =\frac{b^{''}}{r}$. Hence from the Model-I, it is observed that the subcase-24 (Table 5) is more interesting, i.e. for $\rho =\alpha _1 R+\beta _1 R^{'}e^{\xi _1 R}$ with $\xi _1 <0$, $\alpha _1<0$, $\beta _1>0$ and $\alpha <0$, for this particular model, the validation of all energy conditions are achieved throughout the wormhole geometry for $r>0$ & $k\ne 0$. In this subcase, the wormhole geometry is found to be supported by non-exotic matter within $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ gravity for the aforesaid particular form of energy density.

In our second form of $\rho$, if we neglect the higher degree of $e^{\xi _2 R}$ terms, then the form of $\rho$ will be reduced to the model discussed by [42]. In Model-II, the most favorable form of energy density is: $\rho =\alpha _2 R e^{\xi _2 R}$, where $\xi _2=0$, $\alpha _2<0$ and $\alpha <0$, for this particular model, the validation of all energy conditions are achieved throughout the wormhole geometry for $r>0$ & $k\in (-4,0)$ (subcase 4 in Model-II, Table 6). Hence, the wormhole geometry could be supported by non-exotic matter within $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ gravity for the aforesaid particular form of energy density.

In our third form of $\rho$, if we consider $\xi _3=0$, then the form of our $\rho$ will be reduced to the model discussed by [42]. In Model-III, the most feasible form of energy density is: $\rho =\alpha _3 R^2+\beta _2 R^{'} e^{\xi _3 R^{'}}$, where $\xi _3>0$, $\alpha _3>0$, $\beta _2>0$, $\alpha <0$, for this particular model, the validation of all energy conditions are achieved throughout the wormhole geometry for $r>0.3$ & $k\in (-1,0)$ (Subcase 10 in Model-III). Hence, the wormhole geometry could be supported by non-exotic matter within $f(R, T)=R+\alpha R^2+2\beta \ln (T)$ gravity for the aforesaid particular form of energy density by choosing minimum throat size is $r_0=0.3$, unless exotic matter is required. Eventually, in all the cases it is observed that our solutions are asymptotically flat. Hence, from the results of the above three models, we conclude that the Model-I is more general and reliable than other two.

Thus, for every possible case, we have divided the space of controlling parameters and explored the regions where the energy conditions are respected. We have determined exact traversable wormhole solutions supported by non-exotic matter. The new models are considered by specifying new forms of energy density in terms of Ricci scalar. We have studied the validity of ECs and found the regions where NEC, WEC, SEC and DEC are respected. Consequently, it shows a good performance of the obtained solutions. Other than this, the regions where we have found the violation of some ECs may also provide useful information in future. Hence, in the present work, some efforts are put for the exploration of wormhole geometries that may lead towards their deeper investigation.