Anisotropic generalization of isotropic models via hypergeometric equation

Abstract

We study Einstein’s field equations to describe static spherically symmetric relativistic compact objects with anisotropic matter distribution, and generate two classes of exact solutions by choosing a generalized form for one of the gravitational potentials and a particular form for the measure of anisotropy. This is achieved by transforming the Einstein’s field equation to a hypergeometric equation. The generated models generalize the isotropic models of Durgapal–Bannerji, Tikekar and Vaidya–Tikekar. The physical viability of the model is examined and compared with observational results of strange star candidates.

1 Introduction

The modeling of relativistic astrophysical objects composed of anisotropic matter distribution in strong gravitational fields has been of growing interest. In modeling such high-density stellar structures above the nuclear density, one can expect the appearance of unequal principal stresses, the so-called anisotropic fluid. This usually means that two different kinds of pressures inside these compact objects; i.e. the radial pressure component is not equal to the components in the transverse direction [1]. Ivanov [2] pointed out that influences of shear and/or electromagnetic field on self-bound stellar body can be represented by incorporating a gross anisotropic parameter into the system of field equations.

The anisotropy effect was first predicted in 1922 by Jeans [3] for self-gravitating objects in the Newtonian regime. Later Ruderman [4] gave an interesting picture about more realistic stellar models where nuclear interactions need to be treated relativistically when a star with matter density $\rho > 10^{15} \text{ gcm }^{-3}$. Ruderman [4] and Canuto [5] observed that material distribution in the highly dense core of a compact star might exhibit unequal stresses. Bowers and Liang [6] have extensively analyzed the sources of anisotropy at the stellar interior. Subsequently, the origin and effects of local anisotropy on astrophysical objects have been reported by many authors [7,8,9,10,11] and Herrera and Santos [1] have reviewed and discussed possible causes for local anisotropy in self gravitating systems with examples of both Newtonian and general relativistic contexts. Pressure anisotropy in compact star may arise due to various factors which includes exotic phase transitions during gravitational collapse, pion condensation [12, 13], the existence of a solid core or the presence of a type-3A superfluid [14], strong electromagnetic fields [15,16,17], viscosity [2], slow rotation of a fluid [18], etc. Chan et al [19] studied in detail the role played by the local pressure anisotropy in the onset of instabilities and showed that small anisotropies might in principle drastically change the stability of the system.

Such structurally anisotropic physical systems are boson stars [20], wormholes [21] and gravastars [22, 23]. There have been significant experimental developments in recent years to identify astrophysical objects by measuring the radii and masses; e.g. observations on double neutron star [24], glitches in radio pulsars [25], thermal emission [26, 27] from accreting neutron star and from millisecond X-ray pulsars, pressure on neutron star matter at supranuclear density [28], etc. Mass-to-radius ratio of astrophysical objects emanating from such experimental studies provides a vital clue to distinguish different stars such as white dwarf, neutron stars and strange stars from one another [29]. There has been extensive literature devoted to model anisotropic, spherically symmetric, static relativistic matter distributions [9, 30,31,32,33,34,35,36,37], in particular, modeling anisptropic compact stars with a barotropic equation of state [9, 32,33,34, 37]. In this work, we seek new class of solutions to the Einstein field equations to describe static spherically symmetric anisotropic matter distribution and we analyse the physical viability of the model generated and compared with strange star candidates reported through experimental data.

The paper has been organized as follows: In Sect. 2, we formulate the Einstein field equations to describe static spherically symmetric anisotropic matter distribution and obtained an equivalent system of equations with the use of Durgapal and Bannerji [38] transformation. In Sect. 3, we choose a physically reasonable form for the gravitational potential $g_{rr}$ and a prescribed form of the anisotropic parameter, and obtained a general solution in series form by transforming the master equation into hypogeometric equation. In Sect. 4, by restricting the parameters involved in the series solution, we generate two classes of exact solutions in terms of elementary and algebraic functions. In Sect. 5, we extracted two simple solutions as examples from the class of exact solutions obtained. In Sect. 6, we regain a number of anisotropic and isotropic physically reasonable known models reported in literature from our generalized model. In Sect. 7, we analyse the physical viability of the model generated and compared with strange star candidates reported through experimental data.

2 The field equations

The gravitational field for static, spherically symmetric spacetime can be describe by the metric

$$\begin{aligned} ds^{2}=-e^{2\nu (r)}dt^{2}+e^{2\lambda (r)}dr^{2}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$

(1)

in Schwarzschild coordinates $x^{a}=(t, r, \theta , \phi ).$ For an anisotropic imperfect fluid the energy momentum tensor can be taken as

$$\begin{aligned} T_{ij}=diag(-\rho , p_{r}, p_{t}, p_{t}). \end{aligned}$$

(2)

The energy density $\rho$, the radial pressure $p_{r}$ and the tangential pressure $p_{t}$ are measured relative to the comoving four fluid velocity $u^{i}=e^{-\nu }\delta ^{i}_{0}.$ For the line element (1) and matter distribution (2), the Einstein field equations can be expressed as

$$\begin{aligned}&\frac{1}{r^{2}}[r(1-e^{-2\lambda })]'=\rho , \end{aligned}$$

(3)

$$\begin{aligned}&-\frac{1}{r^{2}}(1-e^{-2\lambda })+\frac{2\nu '}{r}e^{-2\lambda } =p_{r}, \end{aligned}$$

(4)

$$\begin{aligned}&e^{-2\lambda }\bigg (\nu ''+\nu '^{2}+\frac{\nu '}{r}-\nu '\lambda '-\frac{\lambda '}{r}\bigg )=p_{t}, \end{aligned}$$

(5)

where primes denote differentiation with respect to r. We employ the coupling constant $\frac{8\pi G}{c^{4}}=1$ with speed of light $c=1$. The system of equations (3)–(5) govern the behaviour of the gravitational field of an anisotropic imperfect fluid sphere.

The mass contained within a radius r of the sphere is defined as

$$\begin{aligned} m(r)=\frac{1}{2}\int ^r_0 \omega ^{2}\rho (\omega )d\omega . \end{aligned}$$

(6)

Using the transformation

$$\begin{aligned} x=Cr^{2},~~Z(x)=e^{-2\lambda (r)}~~\text{ and }~~ A^{2}y^{2}(x)=e^{2\nu (r)} \end{aligned}$$

(7)

where A and C are arbitrary constants, introduced by Durgapal and Bannerji [38] , the system (3)–(5) takes an equivalent form

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{1-Z}{x}-2{\dot{Z}}, \end{aligned}$$

(8)

$$\begin{aligned} \frac{p_{r}}{C}= & {} 4Z\frac{{\dot{y}}}{y}+\frac{Z-1}{x}, \end{aligned}$$

(9)

$$\begin{aligned} p_{t}= & {} p_r + \varDelta , \end{aligned}$$

(10)

$$\begin{aligned} 0= & {} 4x^{2}Z\ddot{y}+2x^{2}{\dot{Z}}{\dot{y}}+\left( {\dot{Z}}x-Z+1-\frac{\varDelta }{C}x\right) y, \end{aligned}$$

(11)

where $\varDelta =p_{t}-p_{r}$ is the measure of anisotropy and dots denote differentiation with respect to x. The mass function (6) becomes

$$\begin{aligned} m(x)=\frac{1}{4C^{3/2}} \int ^x_0\sqrt{\omega }\rho (\omega )d\omega , \end{aligned}$$

(12)

in terms of the new variables in (7).

3 Method of generating solutions

The Einstein system (8)–(11) comprises four independent equations with six independent variables  y, Z, $\rho$,$p_{r}$, $p_{t}$ and  $\varDelta$. Therefore we have the freedom to specify two of the variables on physical ground. It is noted that the work of Herrera et al [39] had shown that all static spherically symmetric anisotropic solutions to Einstein field equations could be obtained by making use of two generating functions, namely the gravitational potential $g_{tt}$ (i.e., z(r)) and $\varPi =p_r-p_t$ by considering the master equation in view of first order differential equation in terms of the gravitational potential $g_{rr}$. In this treatment we view the master equation (11) as a second order linear differential equation in terms of the gravitational potential $g_{tt} (i.e., y)$ and integrate by choosing suitable forms for the gravitational potential $g_{rr}$ (i.e., Z(x))) and the measure of anisotropy $\varDelta$ on physical ground as:

$$\begin{aligned} Z= & {} \frac{1+ax}{1+bx} \end{aligned}$$

(13)

$$\begin{aligned} \varDelta= & {} \frac{kCbx}{(1+bx)^{2}} \end{aligned}$$

(14)

where a, b and k are real constants. This form of Z has been used to study neutron star models with isotropic matter distribution previously [40, 41]. Also this choice contains Durgapal and Bannerji model [38] for the particular values $a=-\frac{1}{2},b=1$ and Tikekar super dense star model [42] for the values $a=-1,b=7$. The form chosen for $\varDelta$ ensures that anisotropy vanishes at the center of the star (i.e., $p_{r}=p_{t}$ at the center). Therefore the choices made in (13) and (14) are physically reasonable. Our objective is to confirm that this type of potential is also consistent with anisotropic matter.  Substituting (13) and (14) into (11) we obtain

$$\begin{aligned}&4(1+ax)(1+bx)\ddot{y}+2(a-b){\dot{y}}\nonumber \\&\quad +(b^{2}-ab-kb)y=0 \end{aligned}$$

(15)

As the equation (15) is difficult to integrate in the above form, we intoduce a transformation

$$\begin{aligned} X=\frac{a(1+bx)}{(a-b)},~~~~~Y(X)=y(x),~~~a\ne b \end{aligned}$$

(16)

to obtain a convenient form. Use of transformation (16), (15) becomes

$$\begin{aligned} X(X-1)\frac{d^{2}Y}{dX^{2}}+\frac{1}{2}\frac{dY}{dX}+\bigg [\frac{b-a-k}{4a}\bigg ]Y=0, \end{aligned}$$

(17)

which is a Gaussian type hypergeometric equation. In the limit of vanishing anisotropy (i.e., $k=0$) (17) becomes

$$\begin{aligned} X(X-1)\frac{d^{2}Y}{dX^{2}}+\frac{1}{2}\frac{dY}{dX}+\bigg [\frac{b-a}{4a}\bigg ]Y=0, \end{aligned}$$

(18)

which describe the behaviour of an isotropic fluid sphere and has been studied by Thirukkanesh and Ragel [41].

General solution of the equation (17) is given by

$$\begin{aligned} Y= & {} C_{1}F\bigg (\alpha ,-(\alpha +1),-\frac{1}{2};X\bigg )\nonumber \\&+C_{2}X^{\frac{3}{2}}F\bigg (\alpha +\frac{3}{2},\frac{1}{2} -\alpha ,\frac{5}{2};X\bigg ) \end{aligned}$$

(19)

in terms of hypergeometric functions, where $C_{1}$ and $C_{2}$ are constants of integration and $\alpha =\displaystyle (-1\pm \sqrt{(2a-b+k)/a})/2$. In general (19) can be written in series form as

$$\begin{aligned} Y= & {} C_{1}\left[ 1+\sum _{j=1}^{\infty }\frac{(\alpha )_{j}(-\alpha -1)_{j}}{(-\frac{1}{2})_{j}}\frac{X^{j}}{j!}\right] \nonumber \\&+C_{2}X^{3/2}\left[ 1+\sum _{j=1}^{\infty }\frac{(\frac{3}{2}+\alpha )_{j} (\frac{1}{2}-\alpha )_{j}}{(\frac{5}{2})_{j}}\frac{X^{j}}{j!}\right] , \end{aligned}$$

(20)

where $(\alpha )_{j}=\alpha (\alpha +1)...(\alpha +j-1).$

4 Exact solutions

It is noted that in some special cases a hypergeometric function can be expressed in terms of elementary or algebraic functions [43]. This is possible because the series (20) terminate for restricted values of a, b and k. We demonstrate two of such cases below.

4.1 Case I :

If we set $\displaystyle (2a-b+k)/a=4n^{2}~$(i.e., $\alpha =\frac{2n-1}{2}$) and using the properties of hypergeometric functions, (19) becomes

$$\begin{aligned} Y= & {} C_{1}(1-X)^{1/2}F\bigg (-n,n,-\frac{1}{2};X\bigg )\nonumber \\&+C_{2}X^{3/2}F\bigg (n+1,1-n,\frac{5}{2};X\bigg ) \end{aligned}$$

(21)

This can be expressed as

$$\begin{aligned} Y= & {} C_{1}(1-X)^{1/2}\nonumber \\&\times \left[ 1+\displaystyle \sum _{j=1}^{n} \frac{(-1)^{j-1}2^{2j-1}n}{j}\frac{(n+j-1)!X^{j}}{(n-j)!(2j-2)!}\right] \nonumber \\&+C_{2}X^{3/2} \left[ 1+\displaystyle \sum _{j=1}^{n-1} \frac{(-1)^{j}2^{2j+2}3(j+2)(j+1)}{n}\right. \nonumber \\&\left. \times \frac{(n+j)!X^{j}}{(n-j-1)!(2j+4)!}\right] , ~\text{ for }~n\ge 1. \end{aligned}$$

(22)

In terms of variable x, this solution takes the form

$$\begin{aligned} y= & {} C_{1}\bigg (1-\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{1/2} \left[ 1+\displaystyle \sum _{j=1}^{n}\frac{(-1)^{j-1}2^{2j-1}n}{j}\right. \nonumber \\&\left. \times \frac{(n+j-1)!}{(n-j)!(2j-2)!} \bigg (\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{j}\right] \nonumber \\&+C_{2}\bigg (\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{3/2}\nonumber \\&\times \left[ 1+\displaystyle \sum _{j=1}^{n-1}\frac{(-1)^{j}2^{2j+2}3(j+2)(j+1)}{n}\right. \nonumber \\&\displaystyle \left. \times \frac{(n+j)!}{(n-j-1)!(2j+4)!} \displaystyle \bigg (\frac{a(1+bx)}{a-b}\bigg )^{j}\right] ,\nonumber \\&\text{ for }~n\ge 1. \end{aligned}$$

(23)

4.2 Case II :

If we set $\displaystyle (2a-b+k)/{a}=(2n-1)^{2}~$(i.e., $\alpha =n-1$) and using the properties of hypergeometric functions, (19) becomes

$$\begin{aligned} Y= & {} C_{1}F\bigg (n-1,-n,-\frac{1}{2};X\bigg )\nonumber \\&+C_{2}X^{3/2}(1-X)^{1/2}F\bigg (2-n,n+1,\frac{5}{2};X\bigg ) \end{aligned}$$

(24)

This can be expressed as

$$\begin{aligned} Y= & {} C_{1}\left[ 1+\sum _{j=1}^{n}\frac{(-1)^{j-1}2^{2j-1}n(n-1)}{j}\right. \nonumber \\&\times \left. \frac{(n+j-2)!X^{j}}{(n-j)!(2j-2)!}\right] +C_{2}X^{3/2}(1-X)^{1/2}\nonumber \\&\times \left[ 1+\sum _{j=1}^{n-2}\frac{(-1)^{j}2^{2j+2}3(j+2)(j+1)}{n(n-1)}\right. \nonumber \\&\left. \times \frac{(n+j)!X^{j}}{(n-j-2)!(2j+4)!}\right] ,~\text{ for }~n\ge 2. \end{aligned}$$

(25)

In terms of variable x, this solution takes the form

$$\begin{aligned} y= & {} C_{1}\left[ 1+\sum _{j=1}^{n}\frac{(-1)^{j-1}2^{2j-1}n(n-1)}{j}\right. \nonumber \\&\left. \times \frac{(n+j-2)!}{(n-j)!(2j-2)!} \bigg (\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{j}\right] \nonumber \\&+C_{2}\bigg (\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{3/2} \bigg (1-\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{1/2} \nonumber \\&\times \left[ 1+\sum _{j=1}^{n-2}\frac{(-1)^{j}2^{2j+2} 3(j+2)(j+1)}{n(n-1)}\right. \nonumber \\&\left. \times \frac{(n+j)!}{(n-j-2)!(2j+4)!} \bigg (\displaystyle \frac{a(1+bx)}{a-b}\bigg )^{j}\right] ,\nonumber \\&\text{ for }~n\ge 2. \end{aligned}$$

(26)

It is remarkable that the solutions (23) and (26) are completely expressed in terms of polynomial and algebraic function. It is noted that our treatment has combined both the isotropic and anisotropic cases. If we switch off the anisotropic factor (i.e., $k=0$) into (23) and (26) then we can obtain the solution for isotropic case directly.

5 Examples

It is interesting to observe that variety of solutions can be obtained from (23) and (26) by substituting particular values for n. Here we illustrate two of such sample solutions as examples.

5.1 Example I:

If we set $n=1$ (i.e., $(k-b)/a=2,~\alpha =\frac{1}{2}$), from (23)

we obtain

$$\begin{aligned} y= & {} e_{1}\,[5b-3k+2b(b-k)x]\sqrt{b(2+(k-b)x)}\nonumber \\&+e_{2}\,(1+bx)^{3/2}, \end{aligned}$$

(27)

where $e_{1}$ and $e_{2}$ are new arbitrary constants.

Consequently, the solution to the system (3)–(5) can be written as

$$\begin{aligned} e^{2\lambda }= & {} \frac{2(1+bx)}{2+(k-b)x} , \end{aligned}$$

(28)

$$\begin{aligned} e^{2\nu }= & {} A^{2}y^{2}, \end{aligned}$$

(29)

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{3b-k}{2(1+bx)}+\frac{3b-k}{(1+bx)^{2}}, \end{aligned}$$

(30)

$$\begin{aligned} \frac{p_{r}}{C}= & {} \frac{k-3b}{2(1+bx)}+\frac{2(2+(k-b)x)}{(1+bx)}\frac{{\dot{y}}}{y}, \end{aligned}$$

(31)

$$\begin{aligned} p_{t}= & {} p_{r}+\varDelta , \end{aligned}$$

(32)

$$\begin{aligned} \varDelta= & {} \frac{kCbx}{(1+bx)^{2}}, \end{aligned}$$

(33)

where y is given in (27), and the mass contain within the sphere of radius R is given by

$$\begin{aligned} M=m(R)=\frac{C(3b-k)R^{3}}{4(1+bCR^{2})} \end{aligned}$$

(34)

5.2 Example II:

If we set $n=2$ (i.e., $(k-b)/a=7,~\alpha =1$), from (26)

we obtain

$$\begin{aligned} y= & {} d_{1}\,[(8b-k)^{2}+4(b-k)(8b-k)\nonumber \\&\times (6b+k-2b(b-k)x)]\nonumber \\&+d_{2}\,(1+bx)^{\frac{3}{2}}\sqrt{7b-b(b-k)x)}, \end{aligned}$$

(35)

where $d_{1}$ and $d_{2}$ are new arbitrary constants. Consequently, the solution to the system (3)–(5) can be written as

$$\begin{aligned} e^{2\lambda }= & {} \frac{7(1+bx)}{7+(k-b)x}, \end{aligned}$$

(36)

$$\begin{aligned} e^{2\nu }= & {} A^{2}y^{2}, \end{aligned}$$

(37)

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{8b-k}{7(1+bx)}+\frac{2(8b-k)}{7(1+bx)^{2}}, \end{aligned}$$

(38)

$$\begin{aligned} \frac{p_{r}}{C}= & {} \frac{k-8b}{7(1+bx)}+\frac{4(7+(k-b)x)}{7(1+bx)}\frac{{\dot{y}}}{y}, \end{aligned}$$

(39)

$$\begin{aligned} p_{t}= & {} p_{r}+\varDelta , \end{aligned}$$

(40)

$$\begin{aligned} \varDelta= & {} \frac{kCbx}{(1+bx)^{2}}, \end{aligned}$$

(41)

where y is given in (35), and the mass contain the sphere of radius R is given by

$$\begin{aligned} M=m(R)=\frac{C(8b-k)R^{3}}{14(1+bCR^{2})}. \end{aligned}$$

(42)

6 Known solutions

It is possible to regain a number of physically reasonable anisotropic and isotropic ($\varDelta =0$) models from our general class solutions (22) and (25) for particular values of parameters. We regain the following particular models of physical intrest.

6.1 Anisotropic model

If we set $a=-1$, $k=-\beta$ and $b=-d$, (22) and (25) becomes

$$\begin{aligned} Y= & {} C_{1}(1-X)^{1/2}\left[ 1+\displaystyle \sum _{j=1}^{n}\frac{(-1)^{j-1}2^{2j-1}n}{j}\right. \nonumber \\&\left. \times \frac{(n+j-1)!X^{j}}{(n-j)!(2j-2)!}\right] +C_{2}X^{3/2}\nonumber \\&\times \left[ 1+\displaystyle \sum _{j=1}^{n-1}\frac{(-1)^{j}2^{2j+2}3(j+2)(j+1)}{n}\right. \nonumber \\&\left. \times \frac{(n+j)!X^{j}}{(n-j-1)!(2j+4)!}\right] ,~~\text{ for }~n\ge 1. \end{aligned}$$

(43)

where $d-\beta =2-4n^{2}$ and $X=\displaystyle \frac{1-dx}{1-d}$.

$$\begin{aligned} Y= & {} C_{1}\left[ 1+\displaystyle \sum _{j=1}^{n}\frac{(-1)^{j-1}2^{2j-1}n(n-1)}{j}\right. \nonumber \\&\left. \times \frac{(n+j-2)!X^{j}}{(n-j)!(2j-2)!}\right] +C_{2}X^{3/2}(1-X)^{1/2}\nonumber \\&\times \left[ 1+\displaystyle \sum _{j=1}^{n-2}\frac{(-1)^{j}2^{2j+2}3(j+2)(j+1)}{n(n-1)}\right. \nonumber \\&\left. \times \frac{(n+j)!X^{j}}{(n-j-2)!(2j+4)!}\right] ,~~\text{ for }~n\ge 2. \end{aligned}$$

(44)

where $d-\beta =2-(2n-1)^{2}$ and $X=\displaystyle \frac{1-dx}{1-d}$.

The solutions (43) and (44) correspond to the anisotropic model of Thirukkanesh et al. [44].

6.2 Isotropic models

6.2.1 Durgapal and Bannerji neutron stars

If we set $k=0$ and $a=-\frac{1}{2}$ (i.e. $b=1$), then (27) becomes

$$\begin{aligned} y=e_{3}(2-x)^{1/2}(5+2x)+e_{4}(1+x)^{3/2}, \end{aligned}$$

(45)

where $e_{3}$ and $e_{4}$ are new arbitrary constants. Thus we have regained Durgapal and Bannerji [38] neutron star model. This model satisfies all physical requirements and has been utilized by many researchers to study the behaviour of neutron stars.  Note that the Durgapal and Bannerji model (45) cannot be regained from Thirukkanesh et al. [44] model because the parameter $a=-1$ is fixed in their treatment. This indicates that our model generalizes the Thirukkanesh et al. [44] model with more general behaviour in the gravitational field.

6.2.2 Tikekar superdence stars

If we set $k=0$, $a=-1$ (i.e. $b=7$), (35) becomes

$$\begin{aligned} y=d_{3}(1+7x)^{\frac{3}{2}}\sqrt{1-x} +d_{4}\bigg [1+\frac{1}{2}(1+7x)-\frac{1}{8}(1+7x)^{2}\bigg ], \end{aligned}$$

where $d_{3}$ and $d_{4}$ are new arbitrary constants.

If we set $C=1/R^{2}$ and ${\tilde{x}}=\sqrt{1-x}=\sqrt{1-\displaystyle \frac{r^{2}}{R^{2}}}$,  this becomes

$$\begin{aligned} y=d_{5}{\tilde{x}}\bigg (1-\frac{7}{8}{\tilde{x}}^{2}\bigg )^{3/2}+d_{6}\bigg (1-\frac{7}{2}{\tilde{x}}^{2}+\frac{49}{24}{\tilde{x}}^{4}\bigg ), \end{aligned}$$

(46)

where $d_{5}$ and $d_{6}$ are new arbitrary constants, which is the Tikekar [42] model for superdense neutron star. The Tikekar model plays an impotent role in describing highly dense stars and cold compact stars.

6.2.3 Vaidya–Tikekar superdence stars

When $k=0$, $a=-1$ (i.e. $b=2$), (27) becomes

$$\begin{aligned} y=e_{3}(5+4x)\sqrt{1-x}+e_{4}(1+2x)^{\frac{3}{2}}, \end{aligned}$$

where $e_{3}$ and $e_{4}$ are new arbitrary constants.

This becomes

$$\begin{aligned} y=e_{5}{\tilde{x}}\bigg (1-\frac{4}{9}{\tilde{x}}^{2}\bigg )+e_{6}\bigg (1-\frac{2}{3}{\tilde{x}}^{2}\bigg )^{3/2}, \end{aligned}$$

(47)

where $e_{5}$ and $e_{6}$ are new arbitrary constants. Thus we have regained the Vaidya and Tikekar [45] model for superdense neutron star which is relevant for developing physically realizable stellar models.

7 Physical analysis

Any new solution generated should satisfy the following physical conditions to represent a realistic anisotropic stellar model [9, 46]:

• (i) Regularity of the gravitational potentials at the center of the star $r=0$.

• (ii) Positive definiteness of the density $\rho$ and the radial pressure $p_{r}$ throughout the interior of the star.

• (iii) Vanishing of radial pressure $p_{r}$ at some finite radius $r=R$,  i.e. $p _{r}(R)=0$.

• (iv) Monotonic decrease of the density $\rho$, the radial pressure $p_{r}$ and the tangential pressure $p_{t}$ with increasing radius.

• (v) Junction condition: Interior metric matches smoothly with the Schwarzschild exterior metric

  $$\begin{aligned} ds^{2}= & {} -\bigg (1-\frac{2M}{r}\bigg )dt^{2}+\bigg (1-\frac{2M}{r}\bigg )^{-1}dr^{2}\\&+r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2}) \end{aligned}$$

  at the boundary $r=R$,  where M is total mass of the sphere.

• (vi) Casuality condition:  the radial and tangential speed of sound should be less than the speed of light throughout the interior of the star.

  i.e., $\displaystyle 0\le V^{2}_{Sr}=\frac{dp_{r}}{d\rho }\le 1~\text{ and }~\displaystyle 0\le V^{2}_{St}=\frac{dp_{t}}{d\rho }\le 1$, where $V_{Sr}$ is the radial sound speed and $V_{St}$ is the tangential sound speed.

• (vii) Condition for not cracking [47, 48]:  $-1\le V^{2}_{St}-V^{2}_{Sr}\le 0$.

• (viii) Adiabatic index  $\displaystyle \varGamma = \frac{\rho +p}{p}\frac{dp}{d\rho }>\gamma$,

  where  $\gamma =\displaystyle \frac{4}{3}-\bigg [\frac{4(p_{r}-p_{t})}{3|p'_{r}|r}\bigg ]_{max}.$

• (ix) Energy conditions:  the energy momentum tensor should obey the conditions  $\displaystyle \rho -p_{r}-2p_{t}\ge 0$  and  $\displaystyle \rho +p_{r}+2p_{t}\ge 0$.

Now we show that the model generated satisfy the above listed criteria. As an example we check these for the particular model (28)–(33). Since $(e^{2\nu })_{r=0}'=(e^{2\lambda })_{r=0}'=0$,  and $e^{2\lambda (0)}=1$,  $e^{2\nu (0)}=A^{2}[e_{1}(5b-3k)\sqrt{2b}+e_{2}]^{2}$ which are constants, the condition (i) satisfied. The condition (iii) impose the restriction on the parameters $b, k, C, e_1$ and $e_2$ as

$$\begin{aligned}&e_{1}\sqrt{b[2-(b-k)CR^{2}]}\\&\quad \times \bigg [(5b-3k)+[8b^{2}-2bk-6k^{2}-2b(b-k)^{2}]CR^{2}\bigg ]\\&\quad +e_{2}\sqrt{1+bCR^{2}}\bigg [(k-3b){+}(7bk-9b^{2}{+}12b)CR^{2}\bigg ]=0 \end{aligned}$$

The junction condition (v) implies

$$\begin{aligned} \bigg (1-\frac{2M}{R}\bigg )^{-1}= & {} \frac{2(1+bCR^{2})}{2+(k-b)CR^{2}} \end{aligned}$$

(48)

$$\begin{aligned} \bigg (1-\frac{2M}{R}\bigg )= & {} A^{2}y^{2}(CR^{2}). \end{aligned}$$

(49)

The condition (48) does not impose any restriction on the parameters while condition (49) restricts the parameter A as

$$\begin{aligned} A^{2}=\displaystyle \frac{2+(k-b)CR^{2}}{2(1+bCR^{2})} \times \displaystyle \frac{1}{[e_{1}\xi +e_{2}\,(1+bx)^{3/2}]^{2}} \end{aligned}$$

where

$$\begin{aligned} \xi =[5b-3k+2b(b-k)CR^{2}]\sqrt{b(2+(k-b)CR^{2})} \end{aligned}$$

Due to the complexity of the solution, we use graphical approach to verify if the matter variables of the model satisfy the above criteria for realistic star. The variables of the model $e_{1}$, C and R has been chosen in view of comparing our model with various strange star candidates RXJ 1856-37, Her. X-1, SAX J1808.4-3658, SMC X-1 and Cen X-3, and the physical quantities are given in respective order are given in the Table 1. Taking $k=0.2$ and $b=1$ as an example, we show that this model satisfy the necessary physical requirements. In the calculation of numerical values for the physical parameters in the Table 1, we fixed values for parameters $b=1$ , $k=0.2$ and $e_{2}=5.00879$ and values for the parameters $e_{1}$ and C as given in the Table 1 are chosen such that to satisfy above listed physical requirements.

Table 1 Pressure, density and mass for different stellar models

Our calculated mass $1.49M_{\odot }$ for radii $7.07~\text{ km }$ corroborates with theoretical model [49] reported analysing pulsars SAX J1808.4-3658, which is also shown to be consistent with observational data and remarkable accord with the strange star models [49]. Moreover, Mass-radius relation studies using different theoretical models to analyze the original experimental observations associated with cyclotron line data from the X-ray pulsar Her X-1 have shown that they are good strange star candidates [50, 51]. Moreover, our calculated masses for respective strange star candidates are compared with the classification of Tikekar and Jotania [29] based on mass-to-radius ratio: $u > 0.3$ for pulsars SAX J1808.4-3658 suggests to be strange stars of type I, and Her X-1 and RXJ 1856-37 are of type II ($0.2< u < 0.3$), and the u value for neutron star counterparts are considered to be still lower.

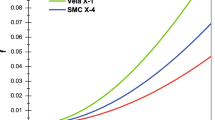
To illustrate the radial dependence of physical quantities of the model, Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14 were plotted for the same parameter values utilised in Table 1. Figures 1 and 2 show that for all five radii, the density and the radial pressure are positive at the center and the density is non zero at the surface while the radial pressure vanishes, satisfying conditions (ii) and (iii) above. Figures 1, 2 and 3 illustrate that the density, the radial pressure and the tangential pressure are continuous and monotonically decreasing towards the surface of the star satisfying requirement (iv) for all radii. The behavior of anisotropy is plotted in Figure 4 which shows the pressure anisotropy is directed outwards ($\triangle >0$) for all cases. Further the anisotropy at the boundary of the star is non-zero, which is physically admissible [46]. In Figs. 1, 2, and 3, except the stellar object with largest radius, the magnitude of physical quantity values of others seems to have a proportional relationship to mass-to-radius ratio. It is illustrated from Figs. 5 and 6 respectively that the radial and tangential speed of sound are less than the speed of light $c = 1$ throughout the interior of the stars and hence the causality condition (vi) is satisfied. Figure 7 illustrates that condition (vii) is satisfied everywhere within the interior of all stars, and cracking will not occur. Figures 8, 9, 10, 11 and 12 show that the radial adiabatic index $\varGamma _r$ and transverse adiabatic index $\varGamma _t$ are greater than $\gamma$ throughout the interior for all stars, satisfying condition (viii). Figures 13 and 14 illustrate that the energy momentum tensor of all radii obey the condition (ix).

Fig. 1

Energy density

Fig. 2

Radial pressure

Fig. 3

Tangential pressure

Fig. 4

Measure of anisotropy

Fig. 5

Radial speed of sound

Fig. 6

Tangential speed of sound

Fig. 7

Cracking condition

Fig. 8

Adiabatic Index for RXJ 1856-37

Fig. 9

Adiabatic Index for Her X-1

Fig. 10

Adiabatic Index for SAX J1808.4-3658

Hence for the model parameters chosen the solution comply with requirements (i)–(ix) of a realistic star and in corroboration with reported physical quantities determined by experimental observation on strange star candidates RXJ 1856-37, Her X-1, SAX J1808.4-3658, SMC X-1 and Cen X-3 [52,53,54].

Fig. 11

Adiabatic Index for SMC X-1

Fig. 12

Adiabatic Index for Cen X-3

Fig. 13

Energy condition

Fig. 14

Energy condition

Fig. 15

Behavior of forces in RXJ 1856-37

Fig. 16

Behavior of forces in Her X-1

Fig. 17

Behavior of forces in SAX J1808.4-3658

Fig. 18

Behavior of forces in SMC X-1

Fig. 19

Behavior of forces in Cen X-3

The Tolman-Oppenheimer-Volkoff equaion (TOV)

Equilibrium of our generalized models can be analysed using generalized TOV equation. This defines the internal structure of the static spherically symmetric compact object with anisotropic matter distribution and has a relationship between three forces such as gravitational force, hydrostatic force and anisotropic force. TOV equation in the presence of anisotropy [55, 56] can be written as

$$\begin{aligned} -\frac{M_{G}(\rho + p_{r})}{r^{2}}e^{\frac{\lambda - \nu }{2}}-\frac{dp_{r}}{dr}+\frac{2}{r}(p_{t}-p_{r})=0, \end{aligned}$$

(50)

where

$$\begin{aligned} M_{G}(r)=r^{2}e^{\frac{\nu - \lambda }{2}}\nu ' \end{aligned}$$

(51)

is the effective gravitational mass of the star within the interior, which can be derived from the Tolman-Whittakar formula and the Einstein field equations. By substituting (51), TOV equation (50) becomes,

$$\begin{aligned} -\nu '(\rho + P_{r})-\frac{dp_{r}}{dr}+\frac{2}{r}\varDelta =0 \end{aligned}$$

(52)

Using equations (28)–(33), (52) can be written as,

$$\begin{aligned} F_{g}+F_{h}+F_{a}=0 \end{aligned}$$

(53)

where $F_{g}$,$F_{h}$ and $F_{a}$ are gravitational force, hydrostatic force and anisotropic force respectively and are given by,

$$\begin{aligned} F_{g}= & {} -\nu '(\rho + p_{r})\nonumber \\= & {} -2C^{2}r\nonumber \\&\times \bigg [\frac{3b-k}{(1+bCr^{2})^{2}}\frac{{\dot{y}}}{y} +\frac{2(2+(k-b)Cr^{2})}{(1+bCr^{2})} \bigg (\frac{{\dot{y}}}{y}\bigg )^{2}\bigg ],\nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned} F_{h}= & {} -\frac{dP_{r}}{dr}\nonumber \\= & {} -C\frac{d}{dr}\bigg (\frac{k-3b}{2(1+bCr^{2})}+\frac{2(2+(k-b)Cr^{2})}{(1+bCr^{2})}\frac{{\dot{y}}}{y}\bigg ),\nonumber \\ \end{aligned}$$

(55)

$$\begin{aligned} F_{a}= & {} \frac{2}{r}\varDelta =\frac{(2 b C^2 k r)}{(1 + b C r^2)^2}, \end{aligned}$$

(56)

where y is given by (27).

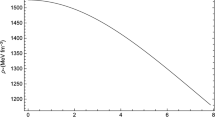
The behavior of $F_{g}$,$F_{h}$ and $F_{a}$ of all stars are plotted in Figs. 15, 16, 17, 18 and 19 for chosen parameters in Table 1, which shows that hydrostatic force and anisotropic forces are positive and is dominated by the gravitational force that is negative which keep the respective stars in static equilibrium.

8 Conclusion

By studying the Einstein field equations to describe static spherically symmetric relativistic compact objects with anisotropic matter distribution, we generate two classes of exact solutions by choosing a generalized form for the gravitational potential $g_{rr}$ and a particular form for the measure of anisotropy on physical ground. We transform the master equation involved in the integration process to hypergeometric equation. In general, the solution is given in hypergeometric series form and we extracted two classes of exact solutions by restricting the parameters involved in the series solution. Our treatment has combined both the isotropic and anisotropic cases, so that if we switch-off the anisotropic factor we can obtain the isotropic case directly. The generated models generalize the isotropic models of Durgapal–Bannerji,Tikekar and Vaidya–Tikekar. The physical analysis show that the model satisfy all major physical properties of a realistic star and compares with observational results of strange star candidates RXJ 1856-37, Her X-1, SAX J1808.4-3658, SMC X-1 and Cen X-3.