1 Introduction

Einstein’s Theory of General Relativity (GR) is one of the most successful theories in physics. This theory has passed all precision tests in a medium-energy scale, and has a substantial conceptual foundation. However, this theory is still not perfect. In a low-energy scale, additional ingredients, such as dark matter and a nonzero cosmological constant (dark energy) should be introduced to fit with a variety of astrophysical observations of galaxies and clusters as well as with the cosmic acceleration of the universe. These ingredients raise two additional questions related to the cosmological constant and coincidence problems. In a high-energy scale, GR as a classical theory, also yields a singularity, which is slightly unpleasant for some people. Therefore, until now, much interest has been observed in the study of alternative or modified theories of GR (Please see the reports of a recent review in modified gravity theories [2,3,4,5,6,7] and the references therein). After passing very stringent sets of some commonly accepted fundamental physical requirements, BH and EiBI theories can now be classified as plausible alternatives or modified gravity theories in the context of strong gravitation field tests (Please see details, in Ref. [2].). The EiBI and a broad class of BH theories of the \(G^3\) type yield modifications of the Newtonian hydrostatic equilibrium equations. These modifications affect the properties of non-relativistic stars, such as white dwarfs (WDs), main sequences, and brown dwarfs (BDs). We need to note some recent works concerning the BH and EiBI theories and their applications in astronomical and cosmology objects. For BH theory, they can be found in Refs. [8,9,10,11,12,13,14,15,16,17,18] while those for EiBI theory, can be found in Refs. [19,20,21,22,23,24,25,26,27,28,29]). We also need to note that the recent review of the cosmological test of modified gravities has been discussed in Refs. [30, 31], while the discussion about cosmological constraint on Horndeski gravity in the light of GW170817 can be found in Ref. [32].

BDs were theoretically predicted for the first time in 1963 by Kumar [33] and Hayashi and Nakano [34]. BDs are known as faint self-gravitating bodies. A BD generally has a sufficiently low mass, and its radius is almost independent to the mass. However, the BD elemental composition is substantially uniform. A BD’s core is composed of hydrogen, helium, and other chemical compositions, and its body is mainly supported by a repulsive force from degenerate electrons with respect to gravitational collapse. However, detailed structure of the atmosphere and the surface luminosity of BDs is quite complex (Please see a recent review of the BD theory in [35,36,37] and the references therein.). A BD was detected for the first time more than 30 years later after its prediction. Since then hundreds of BDs have been observed (Please see details in Ref. [38] and the references therein.). Much progress has recently been made and reported from the observation investigations (Please see Ref. [1] and the references therein.). For example, the most precise masses and radii of BDs (LHS 6343A and LHS6343C) have been reported in [39, 40] ( i.e., BD with a mass of \(62.7 \pm 2.4 M_{Jup}\) and a corresponding radius of \(0.833 \pm 0.021 R_{Jup}\) and BD with a mass of \(62.1 \pm 1.2 M_{Jup}\) and a radius of \(0.782 \pm 0.013 R_{Jup}\) (\(M_{\odot }\) = \(10^3 M_{Jup}\) and \(R_{\odot }\) = \(9.735 R_{Jup}\))). Note that, these results depended on the calculated mass with a precision of \(1.9 \%\) and on the calculated radius with an accuracy of \(1.4 \%\) [1, 39, 40]. One crucial challenge is to distinguish BDs and very low-mass stars (VLMs) from their maximum mass because from the BD models, the features are degenerate with their age, radius, and metallicity [41]. The maximum mass of BDs is known as the hydrogen-burning limit maximum mass (MMHB), where the corresponding mass is approximately \(\sim 0.08 M_{\odot }\). The MMHB shows the limit where the collapse will not occur as far as the star’s surface luminosity is still supplied by nuclear fusion. The precise value of the MMHB depends, but not significantly, on the corresponding elemental composition. A recent study using analytical models within GR theory [42] has shown an acceptable MMHB in the range of \(0.064-0.087 M_{\odot }\). BD Kepler-503b has also recently reported to sit right at the hydrogen-burning limit mass, straddling the boundary between BDs and VLMs [43]. Another study [44] reported that objects that behave exactly like BDs are evidence, with their masses exceeding MMHB. These objects, which are termed “overmassive BDs,” form a continuous sequence with traditional BDs in any property, such as mass, effective temperature, radius, and luminosity. Similar to the MMHB limit, a distinction between the planetary-mass objects below and the BDs above is also needed. The corresponding minumum mass limit of a BD is known as the deuterium-burning limit mass (MMDB). The MMDB value is generally \(\sim 0.013 M_{\odot }\). The MMDB strongly depends on the elemental composition, such as helium abundance, the initial deuterium abundance, and model metallicity. Even though the MMDB value is \(\sim 0.013 M_{\odot }\) for most BDs, models ranging from zero metallicity to more than three times of solar metallicity have recently been reported to have a corresponding MMDB ranging from \(\sim 0.011\) to \(\sim 0.016 M_{\odot }\) [45]. Moreover, note that a recent study on deuterium burning in objects forming through the core accretion scenario has shown that the value of the MMDB (\(0.013 M_{\odot }\)) does not change much when none of the corresponding investigated parameters was able to change this mass limit by more than \(0.0008 M_{\odot }\). Furthermore, the luminosity of hot and cold stars caused by hydrogen burning becomes comparable only after \(\sim \) 200 Myr [46].

Studies on WDs within modified gravity theories, including the EiBI and BH theories have been done by many authors (please see Refs. [12, 18, 29, 47, 48] for examples). Constraining the parameters of several modified gravity theories, such as the EiBI, BH, scalar-tensor-vector gravity, f(R), and forth-order gravity theories, WD masses and radii data from observations have also been used and reported in Refs. [12, 18, 29, 48]. These studies, used chi-squared analysis to determine the allowed region of parameter space with its corresponding confidence. This analysis is very robust determining the acceptable parameter of the modified gravity theories from the observation data of WD properties. However, such study has not been done before for the case of BDs because of the limited masses and radii data. Therefore, it is interesting to know how robust the BD properties from the masses and radii observation data in extracting the acceptable parameter of modified gravity theories. Sakstein [10, 16] recently studied the impact of modified gravity within BH theory on the MMHB. He found that the MMHB increases when the free parameter \(\gamma \) value of BH theory increases. He stated that the MMHB of BDs has the potential to provide an extremely stringent limit to constraint the \(\gamma \) value of BH theory.

The present study constrains the parameter of the EiBI and BH theories using the current masses and radii observation data of BDs [1]. We also use Chi-squared analysis to determine the allowed region of parameter space of both theories and the acceptable parameters with their confidences. The obtained free parameters are used to calculate the mass limits determined from the equivalence of nuclear and photon sphere luminosities for the pp (hydrogen burning) and pp+pd (deuterium burning) reactions predicted by the EiBI and HB theories and compared to the ones of GR. The results can be used to study the impact of both modified gravity theories to the BD mass limits from hydrogen and deuterium burning.

Section 2, briefly discusses the BD equation of states (EOS), which is the modified hydrostatic equilibrium equation of both theories presented. We also discuss the chi-squared analysis on BDs and the EOS profile of both theories. Section 3 presents the hydrogen and deuterium-burning mass. Finally, Sect. 4 provides the conclusions.

2 BDs in the EiBI and BH theories

We need to solve a modified hydrostatic equilibrium equation to calculate the mass and radius of non-relativistic stars, such as BDs, within a modified gravity theory. However, the EOS of stars as input for the hydrostatic equilibrium equation is still similar to that used for Newtonian. We discuss herein the EOS of BDs and the modification of the hydrostatic equilibrium equations within the EiBI and BH theories, chi-squared test of the mass and radius, and the corresponding EOS profiles of a BD.

2.1 Equation of states

The density of BDs is estimated between the range of \(\mathrm 10^3 ~kg/m^3\) and \(\mathrm 10^6 ~kg/m^3\) [48]. BDs preserve their lives from gravitational collapse mostly from the contribution of a repulsive Fermi pressure from degenerate electrons. The corresponding Fermi pressure in a non-relativistic limit is presented as follows:

$$\begin{aligned} P_F = \alpha \int _{0}^{\infty } \frac{\epsilon ^{3/2} d\epsilon }{1+e^{\beta (\epsilon -\mu )}}, \end{aligned}$$
(1)

where \(\alpha = (2/3)[4\pi (2m_e)^{3/2}/(2\pi \hbar )^3]\), \(\beta =(k_B T)^{-1}\), and \(\epsilon \) and \(\mu \) are energy density and chemical potential of electrons. \(K_B\) and T are the Boltzmann constant and temperature, respectively. The \(P_F\) integral equation can be analytically solved and compactly expressed using dilogaritmic \(Li_2\) and trilogaritmic \(Li_3\) functions. The result is as follows:

$$\begin{aligned} P_F= & {} \frac{2}{5} \alpha \mu ^{5/2} - \frac{1}{8} \alpha \mu ^{3/2} Log(1+e^{-\beta \mu }) + \frac{3}{2} \alpha \beta ^{-2} \mu ^{1/2} \frac{\pi ^2}{6} \nonumber \\&+\frac{3}{4} \alpha \beta ^{-2} \mu ^{1/2} Li_2(-e^{-\beta \mu })\nonumber \\&- \frac{3}{4} \alpha \beta ^{-3} \mu ^{-1/2} Li_3 (-e^{-\beta \mu })\nonumber \\&+\bigg (\frac{\pi ^2}{6}-\frac{9}{4}\bigg ) \alpha \beta ^{-1} \mu ^{3/2} + \bigg (\frac{9}{8}-\frac{\pi ^2}{3}\bigg ) \alpha \beta ^{-2} \mu ^{1/2} \nonumber \\&+ \bigg (\frac{\pi ^2}{2} \frac{3}{8}\bigg ) \alpha \beta ^{-3} \mu ^{-1/2} +\frac{1}{8} \alpha \mu ^{5/2}. \end{aligned}$$
(2)

We define the degeneracy parameter \(\psi \) for simplification. This parameter can link the central density and the central temperature of a BD and make the expression of the EOS in a polytropic form, then \(\psi \) is defined as:

$$\begin{aligned} \psi \equiv \frac{k_B T}{\mu _F} = \frac{2 m_e}{\hbar ^2} \bigg (\frac{m_H \mu _e}{3 \pi ^2 \rho }\bigg )^{2/3} k_B T, \end{aligned}$$
(3)

where \(\mu _F\) is the Fermi electron energy in the degeneracy limit, \(\mu _e=1.143\), \(\frac{1}{\mu _e}= X +\frac{Y}{2}\); X and Y are mass fractions from hydrogen and helium, respectively. \(m_e\) and \(m_H\) are the electron and hydrogen masses, respectively. Parameter \(\psi \) is a function of temperature and density. The BDs interior consisted of hydrogen and helium hence the total pressure has the combination effects of electrons and ions, where \(P_{ion} = \frac{\kappa \rho T}{\mu _1 m_H}\) and \(\mu _1\) is the average molecular mass for the hydrogen and helium mixture. The explicit expression for the total pressure \(P=P_F+P_{ion}\) can be written as:

$$\begin{aligned} P= & {} \frac{2}{5} \alpha A^{5/2} \bigg (\frac{\rho }{\mu _e}\bigg )^{5/3} \bigg \{1- \frac{5}{16} \psi Log \left( 1+e^{-\frac{1}{\psi }}\right) \nonumber \\&+\frac{15}{8} \psi ^2 \bigg (\frac{\pi ^2}{3}+Li_2\left( -e^{-\frac{1}{\psi }}\right) \bigg ) - \frac{15}{16} \psi ^3 Li_3 \left( -e^{-\frac{1}{\psi }}\right) \nonumber \\&+ \frac{5}{2} \bigg (\frac{\pi ^2}{6}-\frac{9}{4} \psi \bigg )+\frac{5}{2} \bigg (\frac{9}{8}-\frac{\pi ^2}{3}\bigg ) \psi ^2 \nonumber \\&+ \frac{5}{2} \bigg ( \frac{3\pi ^2}{16}\bigg ) \psi ^3 +\frac{5}{16} \bigg \} + \alpha \psi , \end{aligned}$$
(4)

with now \(\alpha \) is \(\frac{5 \mu _e}{2 \mu _1}\). Equation (4) can now be recast into a polytropic form as:

$$\begin{aligned} P = K \rho ^{\varGamma }, \end{aligned}$$
(5)

where \(\varGamma =1+\frac{1}{n}\) with \(n=3/2\). K takes the following form:

$$\begin{aligned} K = \frac{(3 \pi ^2)^{2/3} \hbar ^2}{5 m_e m_H^{5/3} \mu _e^{5/3}} (1+\varUpsilon +\alpha \psi ). \end{aligned}$$
(6)

The term \(\varUpsilon \) is defined herein as:

$$\begin{aligned} \varUpsilon= & {} - \frac{5}{16} \psi Log(1+e^{-1/\psi }) \nonumber \\&+ \frac{15}{8} \psi ^2 \bigg (\frac{\pi ^2}{3}+ Li_2(-e^{-1/\psi })\bigg )\nonumber \\&-\frac{15}{16}\psi ^3 Li_3(-e^{-1/\psi })+\frac{5}{2} \bigg (\frac{\pi ^2}{6}-\frac{9}{4}\bigg ) \psi \nonumber \\&+ \frac{5}{2} \bigg (\frac{9}{8}-\frac{\pi ^2}{3} \bigg ) \psi ^2 +\frac{5}{2} \bigg (\frac{\pi ^2}{2} \frac{3}{8}\bigg ) \psi ^3 +\frac{5}{16}. \end{aligned}$$
(7)

We use the polytropic expression of the EOS to convert the form of the hydrostatic equilibrium equation from a gradient of the pressure form into a gradient of the density form.

2.2 BH and EiBI gravity theories

BH theory is a modified gravity theory containing the screening mechanism if \(R<< r_V\). \(r_V\) is the Vainshtein radius and R is the radius of the corresponding astrophysical body. In other words \(r_V\) defined as the transition between the screened and unscreened regimes inside astrophysical bodies (Please see the discussion of the Vainshtein mechanism in Ref. [14] and the references therein.). The action of BH theory is presented as [14]:

$$\begin{aligned} S = \int \sqrt{-g} M^2_{pl} \left( \frac{R}{2} + X + \frac{\mathcal {L}_4}{\varLambda ^4}\right) d^4 x + S_M. \end{aligned}$$
(8)

\(M_{pl}= (8 \pi G_N)^{-1}\) is the Planck mass, R is the Ricci scalar, and g is a metric determinant. \(X = - \frac{1}{2} \partial _a \phi \partial ^b \phi \) and \( \mathcal {L}_4 = X [(\Box \phi ^2)-\phi _{ab}\phi ^{ab}]-(\phi ^a\phi ^b\phi _{ab}\Box \phi -\phi ^a\phi _{ab}\phi _c \phi ^{cb})\), while \(\varLambda \) is the cosmological constant. Note that \(\phi \) is a scalar field, \(\phi _a\)=\(\nabla _a \phi \), and \(\phi _{ab}\)=\(\nabla _a \nabla _b\phi \). If \(\phi (r,t)\) \(\equiv \) \(\phi _0 (t) ~+~ \pi (r,t)\) and use the Newtonian form of Friedmann–Robertson–Walker (FRW) space-time metric.

$$\begin{aligned} ds^2=-[1+2\varPhi (r,t)] dt^2+a(t)[ 1-2\varPsi (r,t)]\delta _{ij}dx^i dx^j, \end{aligned}$$
(9)

with \(r^2=\delta _{ij}~x^i ~x^j\) and \(\varPhi (r,t)\) as well as \(\varPsi (r,t)\) are time dependent gravitation potentials, the non-relativistic limit of the static gravitation potential \(\varPhi (r)\) of BH theory derived from Eq. (8) yields a modified Poisson equation. Note that the BH dimensionless parameter is defined as \(\gamma \)= \(\epsilon ^2\varLambda ^4\) with \(\epsilon \)= \(\frac{\dot{\phi }_0}{\varLambda ^4}\). The expression of the corresponding modified Poisson equation of BH theory is presented as [16]:

$$\begin{aligned} \nabla ^2\varPhi (r)=4 \pi G_N \rho (r) + \frac{\gamma }{4} G_N \frac{d^3M(r)}{dr^3}. \end{aligned}$$
(10)

Please see the detail derivation in Ref. [14]. We can extract the radial acceleration from the Poisson equation in Eq. (10) to obtain the Euler equation. From the Euler equation, we can obtain the hydrostatic equilibrium equation represented as:

$$\begin{aligned} \frac{d\rho (r)}{dr}=\frac{-\left[ \frac{G_N M(r)}{r^2}+2 \pi \gamma G_N r \rho (r)\right] \rho (r)}{K \varGamma \rho (r)^{\varGamma -1}+\gamma G_N \pi r^2 \rho (r)}. \end{aligned}$$
(11)

The EiBI theory of gravity belongs to one type of Born-Infeld gravity modification introduced by Banados and Ferreira [19], who used the auxiliary field approach. This theory can regularize the gravitational dynamics, leading to non-singular cosmologies, and predict regular black hole space-time without resorting to quantum gravity. The EiBI action is presented as [19]:

$$\begin{aligned} S= & {} \frac{1}{8 \pi G_N \kappa } \int d^4 x (\sqrt{|g_{ab}+\kappa R_{ab}(\varGamma )|} \nonumber \\&- \lambda \sqrt{-g}) + S_m (g_{ab}, \chi _m), \end{aligned}$$
(12)

where |.| denotes a determinant. Here \(\kappa \) is a free parameter of the EiBI theory. \(S_m (g_{ab}, \chi _m)\) is the matter action, \(\chi _m\) denotes the matter field, \(g_{ab}\) is a metric tensor and \(R_{ab}\) is the symmetric part of the Ricci tensor, while \(\lambda \) is related to the cosmological constant, \(\varLambda = \frac{(\lambda -1)}{\kappa }\) so that we can obtain the asymptotically flat solutions when \(\lambda = 1\). The EiBI modified Poisson equation is obtained as follows from the non-relativistic limit of the EiBI field equation [19, 20]:

$$\begin{aligned} \nabla ^2\varPhi (r)=4 \pi G_N \rho (r) + \frac{\kappa }{4}\nabla ^2\rho (r). \end{aligned}$$
(13)

Similar to that of BH theory, we can easily arrive to the hydrostatic equilibrium equation:

$$\begin{aligned} \frac{d\rho (r)}{dr}=- \frac{G_N M(r)}{r^2} \rho (r) \frac{1}{K \varGamma \rho (r)^{\varGamma -1}+\frac{\kappa }{4} \rho (r)}. \end{aligned}$$
(14)

The gradients of the mass of both theories are the same in the non-relativistic limit:

$$\begin{aligned} \frac{d m(r)}{dr}= 4 \pi r^2 \rho (r). \end{aligned}$$
(15)

Together with Eq. (11) for BH theory or Eq. (14) for EiBI theory and using Eq. (5) as input, Eq. (15) can be numerically solved using the fourth-order Runge-Kutta method. We used herein \(M(\approx 0) \approx 0\), \(\rho (\approx 0)=\rho _c\) and \(\rho (R) \approx 0\) as the the boundary conditions.

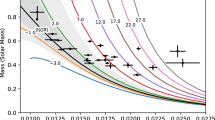
The upper panel of Fig. 1 shows the mass-radius relation of the BDs for the current epoch predicted by BH theory, while the top panel of Fig. 2 depicts that for EiBI theory. The corresponding figures also illustrate those predicted by Newtonian and the observation data taken from Ref. [1] for comparison. The \(\gamma \) parameter can be positive or negative for BH theory. For \(\gamma > 0\), the gravity correction term in the hydrostatic equation plays a role as an additional repulsive force. Meanwhile, for \(\gamma < 0\), it plays a position as another additional attractive force. As a result, the mass and radius relation is modified because of the role of \(\gamma \), where for the fixed mass value, the radius is increased or decreased by increasing or decreasing the \(\gamma \) value. This situation is also applicable to EiBI theory, where the role of the dimensionless parameter \(\gamma \) in BH is replaced by the role of parameter \(\kappa \). However, the trend of the mass changes with respect to the radii of both theories because the functional form of the gravity correction of both theories is different. Note that for the mass-radius data taken from the observation [1], three points have rather a large error bar.

2.3 Chi-squared analysis and mass-radius relation

In this section, we determine whether or not the appropriate parameter values of the BH and EiBI theories which are the masses and the radii predictions, are compatible with the 12 observational masses and radii of BD data in Ref. [1] using chi-squared analysis. We selected one point from our theoretical mass and radius relation results of each theory with a variety of parameter values that have smaller deviation to the mass and radius observational data point of Ref. [1]. For each theory, we also collected all masses and radii having a small deviation together with the corresponding data from the observation. Subsequently, we used the following equation to calculate the chi-square (\(\varDelta \chi ^2_i\)) of each BD:

$$\begin{aligned} \varDelta \chi _i^2 = \frac{[M_{th}(R_{th})-M_i]^2}{\sigma _{M,i}^2}+ \frac{(R_{th}-R_i)^2}{\sigma _{R,i}^2}, \end{aligned}$$
(16)

where \(M_{th}\) is the mass from the theoretical calculation point with a small deviation to \(M_i\), which is the mass of the corresponding observational of the \(i{\mathrm{th}}\) BD. \(R_{th}\) is the theoretical radius, and \(R_i\) is the radius of observational \(i{\mathrm{th}}\) BD. \(\sigma _{M,i}^2\) and \(\sigma _{R,i}^2\) are the corresponding mass and radius standard deviations, respectively. We then summed up the results of Eq. (16) for all 12 BDs using the following equation:

$$\begin{aligned} \chi ^2 = \sum _{i=1}^N \varDelta \chi _i^2. \end{aligned}$$
(17)

To this end, we obtained the chi-squared result in every free parameter of the used modified gravity theories shown in the lower panels of Figs. 1 and 2 for the BH and EiBI theories, respectively. Figure 2 shows that for the EiBI model, the chi-squared limits of the corresponding parameter were in the range of \(-2.375 \le \kappa \rho _A \le 1.266\) or \((-1.51 \times 10^2 \le \kappa \le 0.81 \times 10^2) ~\mathrm{m}^5 \mathrm{kg}^{-1} \mathrm{s}^{-2} \) for the \(1 \sigma \) confidence level and \(-2.5 \le \kappa \rho _A \le 1.822\) or \((-1.59 \times 10^2 \le \kappa \le 1.16 \times 10^2) ~\mathrm{m}^5 \mathrm{kg}^{-1} \mathrm{s}^{-2} \) for the \(5 \sigma \) confidence level. The minimum of the chi-square was \(\kappa \rho _A=0.274\) or \(\kappa = 0.17 \times 10^2 ~\mathrm{m}^5 \mathrm{kg}^{-1} \mathrm{s}^{-2} \), which was quite close to that of Newtonian. Figure 1 also depicts that the chi-squared limits of the \(\gamma \) parameter for BH theory were in the range of \(-0.565 \le \gamma \le 0.234\) for the \(1\sigma \) confidence level and \(-0.6 \le \gamma \le 0.391\) for the \(5 \sigma \) confidence level. This theory showed two minimums but the true minimum of the chi-square was for \(\gamma =-0.12072\). This result was also quite close to that of Newtonian. However, note that the three data points taken from Baylisset al. [1] had quite a large error bar in radius. If in the future we have more data points with the values of the average error bar smaller than the one used herein, we will have a better prediction of \(\gamma \) and \(\kappa \) based on the BD properties.

For comparison for EiBI theory, we need to note that the authors of Ref. [29] obtained from WDs mass and radius constraints, a quite close \(\kappa \) range to the ones of BDs i.e., \((-16.0 \times 10^2< \kappa < 0.35 \times 10^2) ~\mathrm{m}^5\,\mathrm{kg}^{-1}\,\mathrm{s}^{-2} \) for the \(1 \sigma \) confidence level. From neutron stars properties, it is reported by the authors of Ref. [21]that \(\kappa \lesssim 10^{-3} ~\mathrm{m}^5\,\mathrm{kg}^{-1}\, \mathrm{s}^{-2} \) and using the recent maximum mass constraints, it is reported a more restricted \(\kappa \) constraint i.e., \((2.7 \times 10^{-4}< \kappa < 0.35 \times 10^{-4}) ~\mathrm{m}^5\,\mathrm{kg}^{-1}\,\mathrm{s}^{-2} \) [24]. This leads to the fact that constraints from NS are tighter than those of WD and BD. While stellar equilibrium and solar constraints lead to \(|\kappa | \lesssim 3 \times 10^{5} ~\mathrm{m}^5 \,\mathrm{kg}^{-1}\,\mathrm{s}^{-2} \) [26]. \(|\kappa | \lesssim 6 \times 10^{8} ~\mathrm{m}^5\,\mathrm{kg}^{-1}\,\mathrm{s}^{-2} \) constraint comes from primordial nucleosynthesis [23]. It is also reported recently that in EiBI theory, the speed of gravitation waves in matter deviates to c. Therefore, from the time delay in the arrival gravitation wave signals at Earth-based detectors, can be estimated that \(|\kappa | \lesssim 10^{11} ~\mathrm{m}^5\, \mathrm{kg}^{-1}\,\mathrm{s}^{-2} \), while from time delay between the signals of GW170817 and GRB170817A in a background FRW universe \(|\kappa | \lesssim 10^{27} ~\mathrm{m}^5 \mathrm{kg}^{-1} \mathrm{s}^{-2} \) [28]. Therefore, based on the variety predictions of free parameter of EiBI theory \(\kappa \), we might suspect that the values of \(\kappa \) could depend on the compactness of the corresponding stellar and cosmological objects and compact objects provide tighter constraint than those of cosmological objects.

For the case of BH theory, several works [10, 12,13,14, 16] have assessed the behavior of less compact stars using a non-relativistic form of BH theory. They have found the corresponding \(\gamma \) constraint is \(-0.51< \gamma < 0.027\) at red-shift zero. \(\gamma =-0.51\) lower limit comes from the consistency of the lowest mass of WD with Chandrasekhar mass [12], while \(\gamma =0.027\) upper limit comes from the minimum mass for hydrogen burning [10, 16] (Please see also the discussion of this \(\gamma \) constraint range in Ref. [17]). The constraints from BDs with \(1 \sigma \) confidence is quite compatible with this \(\gamma \) constraint range. Furthermore, using the most recent, complete, and independent measurements of masses and radii of WDs as well as using a realistic EOS of WD, the authors of Ref. [18] has found tighter constraint than that of the upper limit from Hydrogen burning, i.e., \(\gamma <0.14\). Furthermore, the analysis of weak lensing and X-ray profiles of 58 galaxy clusters with an averaged red-shift of 0.33 have done by the authors of Ref. [17] obtain the constraint \(\gamma = -0.11^ {0.93}_{-0.67}\). It is interesting to observe that the true minimum of the chi-square obtained in our result is quite compatible with this galaxy cluster constraint. Note that \(\gamma \) is related to the parameters appearing in the effective field theory (EFT) of dark energy. The EFT parameters characterize the linear cosmology of BH theory. Therefore, \(\gamma \) constrain deviation from GR on cosmological scale [17]. We also need to note that in the case of neutron stars, the authors of Ref. [8] have found that the configuration with \(\gamma \gtrsim \,-0.05\) predict reasonable maximum masses \(M~\sim 3~M_{\odot }\) and radii \(R \lesssim 14 ~\mathrm{km}\).

Fig. 1
figure 1

The upper and lower panels show the mass-radius relation of the BD calculations for the current epoch based on BH theory with a variety of \(\gamma \) values and the corresponding chi-square per d.o.f vs \(\gamma \) relation. The corresponding observation data of [1] with the associated error bars are also given. Here, \(d.o.f=22\). The shaded area with the blue region contours shows 1 to \(5 \sigma \) confidence levels

Full size image
Fig. 2
figure 2

The upper and lower panels show the mass-radius relation of the BD calculations for the current epoch based on EiBI theory with a variety of \(\kappa \rho _A\) values and the corresponding chi-square per d.o.f vs \(\gamma \) relation. The corresponding observation data of [1] with the associated error bars are also given. Here, \(d.o.f=22\). The shaded area with the blue region contours shows 1 to \(5 \sigma \) confidence levels. \(\rho _A=\rho _{\odot } \times 10^{12}\)

Full size image

2.4 Brown dwarf profiles

For completeness, we also provide herein the contour plots of the EOS profiles (\(\rho \)-T-P plots) for a certain \(\rho _c\) in the range of \(10^4{-}10^6\) \(\mathrm kg/m^3\) [37] in Fig. 3 as predicted by the BH and EiBI theories using the \(\gamma \) and \(\kappa \) values with the minimum of the chi-square. The results of Newtonian were also given for comparison. The patterns of the results of the EiBI, and BH theories and Newtonian are quite similar because we used quite small values of \(\gamma \) for BH and \(\kappa \) for EiBI. The profiles will look more different if we used relatively large values of \(\gamma \) and \(\kappa \).

Fig. 3
figure 3

Profile of the BD predicted by BH, and EiBI theories for a certain \(\rho _c\) using the \(\gamma \) and \(\kappa \) values with the minimum of the chi-square. The figures show the distribution of the temperature, energy density, and pressure of each gravity theory

Full size image

3 Brown dwarf limiting masses

One must clearly determine the mass boundaries of WDs to determine the mass range where the WDs exist. The maximum and minimum masses of WDs can be used to differentiate BDs from other stars or planets. BDs maintain their shapes with respect to gravitational collapse using the pressure degeneracy of electrons and the role of any other ions. The core burning of hydrogen and helium significantly acts to determine the nuclear luminosity. The nuclear luminosity limit needs to be equal to the photosphere luminosity to prevent balance. The requirement is \(L_{N} = L_e\). In this section, we want to know how further modifying the gravity will shift the limiting masses of BDs.

Fig. 4
figure 4

Nuclear and photosphere luminosities are utilized to categorize the BD area predicted by the BH and EiBI theories using \(\kappa \rho _A =0.274\) and \(\gamma =-0.1207\). Those of GR with their corresponding hydrogen- and deuterium-limiting mass boundaries are provided for comparison

Full size image

3.1 Nuclear burning luminosity

The primary reaction to differentiating BD and VLS is \(p + p ~\rightarrow ~ d + e^+ + \nu _e \). The next important reaction is \(p + d ~\rightarrow ~ ^3He + \gamma \). One can always parameterize the thermonuclear rates to power laws in T and \(\rho \). This parameterization is valid only for a narrow range in T and \(\rho \), but is quite good in providing a clear indication of the sensitivities of the energy generation rates. If we set,

$$\begin{aligned} \epsilon _{N} = \epsilon _c \bigg ( \frac{T}{T_c} \bigg )^s \bigg ( \frac{\rho }{\rho _c} \bigg )^{u-1} \end{aligned}$$
(18)

with \(s=6.31\), \(u=2.28\), and \(\epsilon _c= \epsilon _{pp}\) for hydrogen burning (Please see details in [10]) and \(\epsilon _c= \epsilon _{pp} + \epsilon _{pd}\) for deuterium burning (e.g., discussed in [44]). The detailed process explains that the energy generation rates depend on T and \(\rho \) [37]. We use the following expression of the energy generation rates taken from Refs. [37, 44]:

$$\begin{aligned} \epsilon _{pp}= & {} 2.5 \times 10^6 (\rho X^2/T_6^{2/3}) e^{-33.8/T_6^{1/3}} erg g^{-1} s^{-1} \end{aligned}$$
(19)
$$\begin{aligned} \epsilon _{pd}= & {} 1.4 \times 10^24 (\rho X D /T_6^{2/3}) e^{-37.2/T_6^{1/3}} erg g^{-1} s^{-1}, \end{aligned}$$
(20)

where \(T_6\) is defined as \(T/(10^6 K)\). Deuterium is produced by the weak interaction in the p–p reaction. The two reactions mentioned in the earlier section are accountable for the deuterium chain production. The equilibrium value for deuterium production is presented as [44]:

$$\begin{aligned} D_{eq} = 1.79 \times 10^{-18} X e^{3.4/T_6^{1/3}} \frac{Q_{pd}}{Q_{pp}}, \end{aligned}$$
(21)

where \(Q_{pd}=5.494~\mathrm{MeV}\) and \(Q_{pp}=1.442-0.262 ~\mathrm{MeV}= 1.18 ~\mathrm{MeV}\). The p-p reaction also shows that the average neutrino energy lost is \(0.262 ~\mathrm{MeV}\) [36].

3.2 Luminosity of hydrogen and deuterium burning

We can obtain the nuclear luminosity as follows:

$$\begin{aligned} L_{N} = \int _0^R \epsilon _{N} dm, \end{aligned}$$
(22)

This becomes the following when we substitute the gradient mass into Eq. (22)

$$\begin{aligned} \frac{dL_{N}}{dr} = 4 \pi \epsilon _c r^2 \rho (r) \epsilon _c \bigg ( \frac{T}{T_c} \bigg )^s \bigg ( \frac{\rho }{\rho _c} \bigg )^{u-1} \end{aligned}$$
(23)

with \(T/T_c = (\rho /\rho _c)^{2/3}\). This equation will be solved together with other differential equations to obtain \(L_{N}\). Note that we use \(L_{N}( r\approx 0)\) \(\approx 0\) as an initial boundary [49].

Fig. 5
figure 5

MMHB and M (DB limit) as a function of the \(\gamma \) parameter of BH theory

Full size image

3.3 Photosphere luminosity

When comparing the star radius, the surface can be really thin. The surface gravity \(g = GM/r^2\). We will use the approximation from \(dM/dr = 2M/r\) and \(d^2M/dr^2 = 2M/r^2\) [10] to find the modified surface gravity \(g_{eff}\) from the BH and EiBI gravity theories. Accordingly, \(g_{eff}\) in BH theory is given as follows:

$$\begin{aligned} g_\mathrm{eff} = \frac{GM}{R^2} \bigg ( 1 + \frac{\gamma }{4}\bigg ). \end{aligned}$$
(24)

Meanwhile in the EiBI theory \(g_{eff}\) is obtain as:

$$\begin{aligned} g_\mathrm{eff} = \frac{GM}{R^2} \bigg ( 1 - \frac{1}{2 \pi } \frac{\kappa }{4} \frac{1}{G R^2} \bigg ) \end{aligned}$$
(25)

We used the ideal gas law \(P_e = \frac{\rho _e k_B T_e}{\mu m_H}\), where the mean molecular mass \(\mu = 0.593\) and we can obtain the following equation using the polytropic EOS to find the effective temperature in the surface

$$\begin{aligned} T_e^{1.42} = 1.8 \times 10^6 \bigg [ \frac{2}{3} \frac{g_\mathrm{eff} ~\mu ~m_H}{k_R k_B}\bigg ]^{0.42} \psi ^{1.545}, \end{aligned}$$
(26)

with \(k_R = 10^{-2} \mathrm{cm}^2/\mathrm{g}\). With this effective temperature in hand we can calculate the photo sphere luminosity as follows:

$$\begin{aligned} L_e = 4 \pi R^2 \sigma T_e^4. \end{aligned}$$
(27)
Fig. 6
figure 6

MMHB and M (DB limit) as a function of the \(\kappa \rho _A\) parameter of EiBI theory

Full size image

Figure 4 shows the nuclear and photo sphere luminosities as a function of the BD mass predicted by the BH and EiBI theories using \(\kappa \) and \(\gamma \) with the minimum chi-squared values. Those of GR with their corresponding hydrogen- and deuterium-limiting mass boundaries were also given for comparison. Figure 4 further illustrates that for those of GR, our hydrogen-limiting mass result was compatible with the known standard MMHB value. However, our deuterium-burning limit mass (M (DB limit)) results were larger than those of the standard MMDB value. Therefore, the calculation of M (DB limit) using this procedure only roughly approximates the MMDB. A further refined calculation, such as a more realistic EOS, and a better approximation for \(L_N\) and Le are needed to reproduce a correct MMDB value. By using \(\kappa \) and \(\gamma \) with the minimum chi-squared values, we found that the corresponding hydrogen- and deuterium-burning limits were not significantly changed. However, for EiBI theory, the range slightly shifted to a larger mass. In contrast, for BH, it slightly shifted to a smaller mass. Figure 5 shows the masses and the radii of the hydrogen- and deuterium-burning mass limits predicted by BH theory as a function of parameter \(\gamma \). For that of hydrogen-burning, our mass and radius results were compatible to those obtained in Ref. [10]. the radii and the masses of hydrogen- and deuterium-burning limits increased with the increasing \(\gamma \). Figure 6 shows those of EiBI theory. A similar trend was also evidenced from Fig. 6, wherein the radii of the hydrogen- and deuterium-burning mass limits increased with the increasing \(\kappa \). The impact of the contribution of the corresponding modified gravity terms more significantly appeared in BH theory than in EiBI theory for the case of \(\kappa \) and \(\gamma \) with the minimum chi-squared values. Figures 5 and 6 also show the impacts of the maximum and minimum \(\gamma \) and \(\kappa \) values with the 1\(\sigma \) and 5\(\sigma \) confidences in the masses and the radii of the hydrogen- and deuterium-burning mass limits. The maximum allowed parameter \(\kappa \) value (the one within 1\(\sigma \) confidence) of EiBI had a more significant effect on the masses of the hydrogen- and deuterium-burning limits compared to the corresponding \(\gamma \) value of BH. For BH, \(0.071 \le MMHB/M_\odot \le 0.08\), and \(0.042 \le M (\mathrm DB~limit)/M_\odot \le 0.049\), while for EiBI, \(0.052 \le MMHB/M_\odot \le 0.09\), and \(0.038 \le M (\mathrm DB ~limit)/M_\odot \le 0.045\). The situation was reversed for the corresponding radius. The maximum allowed \(\gamma \) value of BH had a more significant impact compared to that the corresponding \(\kappa \) of EiBI. For BH, \(0.074 \le R_\mathrm{MMHB}/R_\odot \le 0.1\) and \(0.06 \le R_{M (\mathrm DB~limit)}/R_\odot \le 0.08\), while for EiBI, \(0.088 \le \) \(R_\mathrm{MMHB}/R_\odot \) \(\le 0.098\) and \(0.072 \le R_{M (\mathrm DB~limit)}/R_\odot \le 0.078\).

4 Conclusion

Using compact and less-compact stars to study the modified gravity theory is important. In this way we can check the possible deviation signature of the standard gravity theory and the dependency of the corresponding free parameter of modified gravity theories with the compactness of the stellar and cosmological objects. We studied herein the mass and the radius of BDs as a representation of less-compact stars predicted by BH and EiBI gravity theories by numerically solving the modified hydrostatic equations predicted by both theories. We used the most recent compilation of BD masses and radii obtained from Ref. [1] to constrain the free parameter of the BH and EiBI theories using a minimum chi-squared analysis. We found that for EiBI theory, the chi-squared limit \(\kappa \) parameter is in the range of \((-1.51 \times 10^2 \le \kappa \le 0.81 \times 10^2) ~\mathrm{m}^5\mathrm{kg}^{-1}\mathrm{s}^{-2} \) for the \(1\sigma \) confidence level and in the range of \((-1.59 \times 10^2 \le \kappa \le 1.16 \times 10^2) ~\mathrm{m}^5\mathrm{kg}^{-1}\mathrm{s}^{-2} \) for the \(5\sigma \) confidence level. Meanwhile for BH theory, the chi-squared limit \(\gamma \) parameter is in the range of \(-0.565 \le \gamma \le 0.234\) for the \(1\sigma \) confidence level and in the range of \(-0.6 \le \gamma \le 0.391\) for the \(5\sigma \) confidence level, while \(\kappa = 0.17 \times 10^2 ~\mathrm{m}^5\mathrm{kg}^{-1}\mathrm{s}^{-2} \) for the EiBI and \(\gamma \)=-0.1207 for the BH theories can yield minimum chi-squared values. The value of \(\kappa \) and \(\gamma \) parameters with minimal \(\chi ^2\) were relatively small. Therefore, they cannot significantly provide effects to increase or decrease the MMHB and MMDB limits of a BD. We also obtained the hydrogen and approximate deuterium mass limits by calculating the BD nuclear and surface luminosity using \(\epsilon _c= \epsilon _{pp}\) for hydrogen burning and \(\epsilon _c= \epsilon _{pp} + \epsilon _{pd}\) for deuterium-burning reactions. Also, we have found that the EiBI free parameter \(\kappa \) constraint from BDs is tighter than that from cosmological objects, while the BH free parameter \(\gamma \) constraint from BDs is compatible with the one from cosmological objects.