1 Introduction

Quantum coherence originating from quantum state superposition is an essential physical resource for quantum theory and quantum technology, such as quantum optics [1,2,3], quantum thermodynamics [4,5,6,7], quantum information [8,9,10,11,12] and quantum biology [13,14,15,16]. QC is intrinsically related to other quantum resources, such as entanglement and quantum correlation [17,18,19,20]. Recently, Baumgratz et al. [21] introduced a rigorous framework for quantifying QC. Based on such a framework, some QC measures are proposed which satisfy the necessary criteria for well QC measure [21], such as the relative entropy of coherence and \(l_1\) norm of coherence [21].

Quantum gravity theory is the cross discipline of classical gravity theory, quantum mechanics and quantum field theory. Recently, gravitational wave predicted by Einstein a hundred years ago is observed by LIGO from black hole merging objects [22]. Naturally, one may wonder whether there is similar nature between gravitational wave and electromagnetic wave, and what would happen when gravitational field is quantized analogous to quantized electromagnetic field. According to Einstein’s general relativity, gravity is described as a consequence of the curvature of spacetime. If we quantized the gravity, the vacuum fluctuation of quantum gravitational field means the space-time fluctuation itself. Recently, some studies show, analogous to the fluctuation of matter field (such as scalar field and electromagnetic field), the fluctuation of gravitational field may also cause the Casimir-like force [23, 24] and quantum gravitational decoherence [25, 26]. Vacuum fluctuation has great influence on quantum system under it. Liu et al. [27] investigated the QC dynamics of a static polarizable two-level atom coupling with a thermal bath of fluctuating electromagnetic field. Huang et al. [28] studied the dynamics of QC for an uniformly accelerated atom interacting with fluctuating electromagnetic field. Cheng et al. [29] examined the spontaneous emission and excitation of an atom under fluctuating gravitational field.

Inspired by these works, we would study the QC behaviors in the framework of open quantum system that an uniformly accelerated gravitationally polarizable two-level object couples with fluctuating quantum gravitational field. We are very interested in how gravitational fluctuation would affect the QC behaviors and whether accelerated object interacting with fluctuating gravitational field can yield Unruh-like effect [30]. Our study indicates that an uniformly accelerated object interacting with fluctuating quantum gravitational field can produce the similar QC behaviors and Unruh-like effect analogous to matter field, which would be useful for improving our understanding of quantum gravity theory and quantum field theory of curved space-time.

In the following, we firstly introduce the evolution physical model and related concept about QC. And then we derive the master equation that describes the system evolution, and discuss the behaviors of QC affected by gravitational vacuum fluctuation. Finally, we present a brief conclusion of this paper.

2 Preliminaries

We consider that a two-level gravitationally polarizable object weakly couples with a bath of fluctuating quantum gravitational field. The gravitationally polarizable system can be any quantum system that carries nonzero quadrupole polarizability. For example, a Bose–Einstein condensate (BEC), which is a multilevel system in a harmonic trap as a gravitationally polarizable object. The BEC will be stretched and squeezed when it couples with gravitational wave [24].

The whole Hamiltonian of such a system takes the form

$$\begin{aligned} H=H_{S}+H_{F}+H_{I}. \end{aligned}$$
(1)

\( H_{S}\) denotes the Hamiltonian of the gravitationally polarizable object, which is given by

$$\begin{aligned} H_{S}=\frac{\omega }{2}\sigma _{3}, \end{aligned}$$
(2)

where \(\sigma _{i} (i=1,2,3)\) are the Pauli matrices and \(\omega \) is the energy level spacing. \(H_{F}\) is the Hamiltonian of the gravitational field. \(H_{I}\) is the quadrupolar interaction Hamiltonian between gravitationally polarizable object and fluctuating gravitational field, which takes the form

$$\begin{aligned} H_{I}=-\frac{1}{2}Q_{ij}(t)E_{ij}(x(t)), \end{aligned}$$
(3)

where \(Q_{ij}\) is the induced quadrupole moment of the object. By analogy to the linearized Einstein field equations and the Maxwell equations, one can obtain the gravito-electric tensor [31]

$$\begin{aligned} E_{ij}=R_{0i0j}, \end{aligned}$$
(4)

where \(R_{\mu \nu \alpha \beta }\) is the Riemann tensor defined in terms of the metric tensor. In the Newtonian limit, Eq. (4) coincides with the expression \(-\frac{\partial ^2\varPhi }{\partial x_i\partial x_j} +\frac{1}{3}\delta _{ij}\nabla ^2\varPhi \) [32], where \(\varPhi \) is the external gravitational potential.

In the interaction picture, the quadrupole operator can be expressed as

$$\begin{aligned} Q_{ij}(t)=q_{ij}\sigma _{-}e^{-\mathrm {i}\omega t}+q_{ij}^{*}\sigma _{+}e^\mathrm{{i}\omega t}, \end{aligned}$$
(5)

where \(\sigma _+, \sigma _-\) are the raising and lowering operators of the object respectively, \(q_{ij}=\langle {0|Q_{ij}|1}\rangle \) are the transition matrix elements of the quadrupole operator and denote the polarizations of the object, which is symmetric and traceless, i.e., \(\sum _{i}q_{ii}=0\) and \(q_{ij}=q_{ji}\). In this paper, we assume that the gravitational quadrupole polarizabilities are real, and the gravito-electric field \(E_{ij}\) is also supposed to be quantized. The metric for a flat space-time metric with a perturbation can be written as \(g_{\mu \nu }=\eta _{\mu \nu }+h_{\mu \nu }\), where \(\eta _{\mu \nu }\) denotes the flat space-time metric, and linearized perturbation \(h_{\mu \nu }\) describes the fluctuating vacuum gravitational field. Taking the transverse traceless (TT) gauge, the quantized space-time perturbation has the form

$$\begin{aligned} h_{ij}=\sum _{\mathbf {k},\lambda }\left[ a_{\mathbf {k},\lambda }e_{ij}(\mathbf {k},\lambda )f_{\mathbf {k}}+H.c.\right] , \end{aligned}$$
(6)

where \(a_{\mathbf {k},\lambda }\) are the gravitational field operator, \(f_{\mathbf {k}}=\frac{1}{4 \pi ^{3/2} \sqrt{2\omega }}e^\mathrm{{i}(\mathbf {k}\cdot \mathbf {x}-\omega t)}\) are the field modes and \(e_{\mu \nu }(\mathbf {k},\lambda )\) are the polarization tensors with \(\omega =|\mathbf {k}|=(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})^{\frac{1}{2}}\). \(\lambda \) labels the polarization state, and note that \(\hbar =c=32\pi G=1\) through this paper. From the definition of \(E_{ij}\) (4), one can obtain

$$\begin{aligned} E_{ij}=\frac{1}{2}\ddot{h}_{ij}, \end{aligned}$$
(7)

where a dot denotes a derivative with respect to time t. According to Eqs. (6) and (7), the correlation function can written as

$$\begin{aligned}&{\langle {E_{ij}(x)E_{kl}(x')}\rangle }\nonumber \\&\quad =\frac{1}{8(2\pi )^{3}}\int d^{3}\mathbf {k}\sum _{\lambda }e_{ij}(\mathbf {k},\lambda )e_{kl}(\mathbf {k},\lambda ) {\omega ^{3}}\nonumber \\&\qquad \times e^\mathrm{{i}\mathbf {k}\cdot (\mathbf {x}-\mathbf {x'})}e^{-\mathrm {i}\omega (t-t')}, \end{aligned}$$
(8)

where

$$\begin{aligned} \sum _{\lambda }e_{ij}(\mathbf {k},\lambda )e_{kl}(\mathbf {k},\lambda )&=\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}-\delta _{ij}\delta _{kl}+\hat{k_{i}}\hat{k_{j}}\hat{k_{k}}\hat{k_{l}}\nonumber \\&\quad +\hat{k_{i}}\hat{k_{j}}\delta _{kl}+\hat{k_{k}}\hat{k_{l}}\delta _{ij}-\hat{k_{i}}\hat{k_{l}}\delta _{jk}\nonumber \\&\quad -\hat{k_{i}}\hat{k_{k}}\delta _{jl}-\hat{k_{j}}\hat{k_{l}}\delta _{ik}-\hat{k_{j}}\hat{k_{k}}\delta _{il}, \end{aligned}$$
(9)

with \(\hat{\mathbf {k}}={\mathbf {k}}/|\mathbf {k}|\).

For simplicity, we assume the initial state of the whole system is the form \(\rho _{tot}(0)=\rho (0)\otimes |0\rangle \langle 0|\), where \(\rho (0)\) is the initial state of the object and \(|0\rangle \) is the vacuum state of the external gravitational field. Under the Born approximation (weak-coupling approximation), assuming that the strength of coupling between the object and gravitational field is very small and the wavelength of the gravity wave is larger than the geometric size of the object, at any time, the state of the whole system can always be expressed as a product state [33, 34]. Further we make the Markov approximation assumption, assuming that the evolution time scale of the object is much longer than time scale of information memory and feedback of gravitational fluctuating bath, the memory effect in the evolution process can be ignored. Under the Born–Markov approximation and rotating wave approximation, in terms of the proper time \(\tau \) of the object, the evolution process of the object obeys the Kossakowski–Lindblad master equation [34,35,36]

$$\begin{aligned} \frac{\partial \rho (\tau )}{\partial \tau }=-\mathrm {i}\left[ H_{\text {eff}},\rho (\tau )\right] +\mathcal {L}[\rho (\tau )], \end{aligned}$$
(10)

where

$$\begin{aligned} H_{\text {eff}}=\frac{1}{2}\varOmega \sigma _{3}=\frac{1}{2}\left\{ \omega +\frac{i}{2}[\mathcal {K}(-\omega )-\mathcal {K}(\omega )]\right\} \sigma _{3}, \end{aligned}$$
(11)

and

$$\begin{aligned} \mathcal {L}[\rho ]=\frac{1}{2}\sum _{i,j=1}^{3}S_{ij}\left[ 2\sigma _{j}\rho \sigma _{i}-\sigma _{i}\sigma _{j}\rho -\rho \sigma _{i}\sigma _{j}\right] . \end{aligned}$$
(12)

\(S_{ij}\) and \(H_{\text {eff}}\) are determined by the gravitational field correlation functions:

$$\begin{aligned} G_{ijkl}(\tau -\tau ')=\left\langle {E_{ij}(\tau ,x)E_{kl}(\tau ',x)}\right\rangle . \end{aligned}$$
(13)

\(\mathcal {G}_{ijkl}(\omega )\) and \(\mathcal {K}_{ijkl}(\omega )\) denote Fourier and Hilbert transforms of field correlation function respectively, defined as [34,35,36,37,38]

$$\begin{aligned} \mathcal {G}_{ijkl}(\omega )&=\int ^{\infty }_{-\infty }d\varDelta \tau e^\mathrm{{i}\omega t}G_{ijkl} (\varDelta \tau ), \end{aligned}$$
(14)
$$\begin{aligned} \mathcal {K}_{ijkl}(\omega )&=\frac{P}{\pi \mathrm {i}}\int _{-\infty }^{\infty }d\lambda \frac{\mathcal {G}_{ijkl}(\lambda )}{\lambda -\omega }. \end{aligned}$$
(15)

Then Kossakowski matrix \(S_{ij}\) can be expressed explicitly as [38,39,40]

$$\begin{aligned} S_{ij} = A\delta _{ij} -iB\epsilon _{ijk}\,\delta _{3k} -A\delta _{3i}\,\delta _{3j} , \end{aligned}$$
(16)

where

$$\begin{aligned} A={\frac{1}{16}}\,\left[ \,\mathcal{G}(\omega ) +\mathcal{G}(-\omega )\right] ,\quad B ={\frac{1}{16}}\,\left[ \,\mathcal{G}(\omega ) -\mathcal{G}(-\omega )\right] , \end{aligned}$$
(17)

with

$$\begin{aligned} \mathcal {G}(\omega )=\sum _{i,j,k,l=1}^{3}q_{ij}^{*}q_{kl}\mathcal {G}_{ijkl}(\omega ). \end{aligned}$$
(18)

Replacing the \(\mathcal {G}_{ijkl}(\omega )\) with \(\mathcal {K}_{ijkl}(\omega )\) in above equation, one can obtain \(\mathcal {K}(\omega )\).

A rigorous framework for quantifying QC recently was proposed by Baumgratz et al. [21]. By specifying a particular basis \(\{|i\rangle \}\) in the d-dimensional Hilbert space, all density operators like \(\hat{\delta }=\sum _{i=1}^{d}p_{i}|i\rangle \langle i|\) are called incoherent states, labeled as \(\mathcal {I}\). A quantum operation \(\varLambda :\ \rho \rightarrow \sum _n K_n\rho K_n^\dagger \) is called an incoherent operation if \(K_n \mathcal {I} K_n^\dagger \subset \mathcal {I}\) is satisfied for all n. A bone fide QC measure Q should satisfy the following properties [21]:

  1. 1.

    \(Q(\rho )=0\) iff \(\rho \in \mathcal {I}\).

  2. 2.

    Monotonicity under non-selective incoherent completely positive and trace preserving (ICPTP) maps: \(Q(\rho )\ge Q(\varLambda _{\text {ICPTP}}(\rho ))\), where \(\varLambda _{\text {ICPTP}}(\rho )=\sum _n K_n\rho K_n^\dagger \) with \(K_n^\dagger K_n=I\) and \(K_n \mathcal {I} K_n^\dagger \subset \mathcal {I}\).

  3. 3.

    Monotonicity under selective measurements on average: \(Q(\rho )\ge \sum _n p_n Q(\rho _n)\), where \(\rho _{n}= K_n\rho K_n^\dagger /p_{n}\), \(p_{n}=\text {Tr}(K_n\rho K_n^\dagger )\) with \(K_n^\dagger K_n=I\) and \(K_n \mathcal {I} K_n^\dagger \subset \mathcal {I}\).

  4. 4.

    Convexity: \(\sum _n p_n Q(\rho _n)\ge Q(\sum _n p_n \rho _n)\) for any set of states \(\{\rho _n\}\) with probability \(p_{n}\ge 0\) and \(\sum _n p_n=1\).

There are several QC measures that meet the above criteria, such as the relative entropy of coherence and \(l_1\) norm of coherence [21]. QC of a quantum state is usually attributed to the off-diagonal elements of its density matrix with respect to a specified basis, and the \(l_1\) norm of coherence is an intuitive QC measure related to the off-diagonal elements of the considered quantum state, given by

$$\begin{aligned} Q=\sum _{\begin{array}{c} i\ne j \end{array}}|\rho _{i,j}|. \end{aligned}$$
(19)

Compared with other QC measures, for example, relative entropy of coherence, \(l_1\) norm of coherence is easier to calculate since it just needs to add all of the off-diagonal elements of the considered quantum state.

3 QC dynamics

In this section, we explore the dynamics of QC for a gravitationally polarizable two-level object coupling to gravitational vacuum fluctuation. The trajectory of the moving object with a constant proper acceleration a along the x axis is

$$\begin{aligned} t(\tau )&=\frac{1}{a}\sinh a\tau , \quad x(\tau )=\frac{1}{a}\cosh a\tau ,\nonumber \\ y(\tau )&=0, \quad z(\tau )=0 . \end{aligned}$$
(20)

With a Lorentz transformation from the laboratory frame to the frame of the object [40], according to Eq. (8), the two point correlated functions can be written as

$$\begin{aligned} G_{1111}(\varDelta \tau )&=-\frac{a^6 }{16 \pi ^2 \sinh ^{6}(\frac{a \varDelta \tau }{2}-i \epsilon )}, \nonumber \\ G_{1122}(\varDelta \tau )&=-\frac{1}{2}G_{1111}(\varDelta \tau ), \quad G_{1212}(\varDelta \tau )=\frac{3}{4}G_{1111}(\varDelta \tau ), \end{aligned}$$
(21)

where \(\varDelta \tau =\tau -\tau '\). Correspondingly, according to the residue theory, the Fourier transforms (14) of field correlation functions can be calculated as

$$\begin{aligned} \mathcal {G}_{1111}(\omega )&=\frac{\omega (a^2+\omega ^2) (4 a^2+\omega ^2) (\coth \frac{\pi \omega }{a}+1)}{30 \pi }, \nonumber \\ \mathcal {G}_{1122}(\omega )&=-\frac{1}{2}\mathcal {G}_{1111}(\omega ), \quad \mathcal {G}_{1212}(\omega )=\frac{3}{4}\mathcal {G}_{1111}(\omega ). \end{aligned}$$
(22)

For the other nonzero components have the following relations,

$$\begin{aligned} \mathcal {G}_{1111}(\omega )&=\mathcal {G}_{2222}(\omega )=\mathcal {G}_{3333}(\omega ), \nonumber \\ \mathcal {G}_{1122}(\omega )&=\mathcal {G}_{1133}(\omega )=\mathcal {G}_{2233}(\omega )=\mathcal {G}_{2211}(\omega )\nonumber \\&=\mathcal {G}_{3311}(\omega )=\mathcal {G}_{3322}(\omega ),\nonumber \\ \mathcal {G}_{1212}(\omega )&=\mathcal {G}_{1313}(\omega )=\mathcal {G}_{2323}(\omega )=\mathcal {G}_{1221}(\omega )=\mathcal {G}_{1331}(\omega )\nonumber \\&=\mathcal {G}_{2332}(\omega )=\mathcal {G}_{2112}(\omega )\nonumber \\&=\mathcal {G}_{3113}(\omega )=\mathcal {G}_{3223}(\omega )=\mathcal {G}_{2121}(\omega )\nonumber \\&=\mathcal {G}_{3131}(\omega )=\mathcal {G}_{3232}(\omega ). \end{aligned}$$
(23)

According to Eqs. (17), (18) and (23), we can obtain the coefficients of \(S_{ij}\) (16)

$$\begin{aligned} A&=\frac{30\pi \varGamma }{ \omega ^5} \sum _{i,j,k,l=1}^{3}\hat{q}_{ij}^{*}\hat{q}_{kl}\left[ \mathcal {G}_{ijkl}(\omega )+\mathcal {G}_{ijkl}(-\omega )\right] ,\nonumber \\ B&=\frac{30\pi \varGamma }{ \omega ^5} \sum _{i,j,k,l=1}^{3}\hat{q}_{ij}^{*}\hat{q}_{kl}\left[ \mathcal {G}_{ijkl}(\omega )-\mathcal {G}_{ijkl}(-\omega )\right] , \end{aligned}$$
(24)

where \(\varGamma = \omega ^5 |\mathbf {q}|^2 /480\pi \) is the spontaneous emission rate of object, and \(\hat{q}_{ij}=q_{ij}/|\mathbf {q}|\) are a unit vector.

Now, we consider to solve the evolution Eq. (10). Any single qubit states can be represented with Pauli operators

$$\begin{aligned} \rho =\frac{1}{2}\left( I+ \sum _{i=1}^3 b_{i}(\tau ) \sigma _{i}\right) . \end{aligned}$$
(25)

By substituting Eq. (25) into Eq. (10), we can obtain the coupled differential equations

$$\begin{aligned} b_{1}'(\tau )&=-2 A b_1(\tau )-\varOmega b_2(\tau ),\nonumber \\ b_{2}'(\tau )&=\varOmega b_1(\tau )-2 A b_2(\tau ),\nonumber \\ b_{3}'(\tau )&=-4 (A b_3(\tau )+B). \end{aligned}$$
(26)

Before examining the QC behaviors, we firstly consider the case of equilibrium state. By letting the left side of Eq. (26) to be zero, we can obtain the Bloch vector of the equilibrium state

$$\begin{aligned} b_1(\tau )= 0,\quad b_2(\tau )= 0,\quad b_3(\tau )= -\frac{B}{A}. \end{aligned}$$
(27)

Plugging Eq. (27) into Eq. (25), the equilibrium state is given by

$$\begin{aligned} \rho (\infty )= \left( \begin{array}{cc} \frac{A-B}{2 A} &{} 0 \\ 0 &{} \frac{A+B}{2 A} \\ \end{array} \right) . \end{aligned}$$
(28)

This is an incoherent state, which implies that QC can not maintain for a long time under the effect of gravitational vacuum fluctuation. Substituting Eq. (24) into Eq. (28), we can exactly obtain the equilibrium state

$$\begin{aligned} \rho (\infty )= \left( \begin{array}{cc} \frac{1}{1+e^{\frac{2 \pi \omega }{a}}} &{} 0 \\ 0 &{} \frac{1}{1+e^{-\frac{2 \pi \omega }{a}}} \\ \end{array} \right) =\frac{e^{-H_S/T}}{\text {Tr}(e^{-H_S/T})}, \end{aligned}$$
(29)

From the equation, we can see that an uniformly accelerating gravitationally polarizable object in a fluctuating gravitational field is driven to a thermal state with Unruh-like temperature \(T =\frac{a}{2\pi }\) [28, 41, 42], which manifests the Unruh-like effect that an uniformly accelerated observer feeling the gravitational vacuum as a thermal bath [30]. This might stem from spontaneous emission of the object due to the gravitational fluctuations and radiation reaction [29].

Now, we assume the initial state of the gravitationally polarizable object is a maximal coherent state \(|\psi (0)\rangle =\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )\). By solving above differential equations (26) with the initial state, we can obtain the Bloch vector of the evolved state

$$\begin{aligned} b_{1}(\tau )&=e^{-2 A \tau } \cos (\tau \varOmega ),\nonumber \\ b_{2}(\tau )&=e^{-2 A \tau } \sin (\tau \varOmega ),\nonumber \\ b_{3}(\tau )&=\frac{B (e^{-4 A \tau }-1)}{A}. \end{aligned}$$
(30)

Substituting Eq. (30) into Eq. (25), according to Eq. (19), we can obtain QC of the evolution state

$$\begin{aligned} Q=e^{-2 A \tau }. \end{aligned}$$
(31)

When \(a\rightarrow 0\), \(A=B=\varGamma (M_1-M_2)\) with

$$\begin{aligned} M_{1}&=2 | \hat{q}_{1,1}| {}^2+6 | \hat{q}_{1,2}| {}^2+6 | \hat{q}_{1,3}| {}^2+2 | \hat{q}_{2,2}| {}^2\nonumber \\&\quad +6| \hat{q}_{2,3}| {}^2+2 | \hat{q}_{3,3}| {}^2,\nonumber \\ M_{2}&=(\hat{q}_{1,1}+\hat{q}_{2,2}) q_{3,3}^*+(\hat{q}_{1,1}+\hat{q}_{3,3}) \hat{q}_{2,2}^*\nonumber \\&\quad +(\hat{q}_{2,2}+\hat{q}_{3,3}) \hat{q}_{1,1}^*. \end{aligned}$$
(32)

The evolution model reduces to the evolution model of an inertia object. From Eqs. (31) and (32), we know that QC decreases exponentially with evolution time due to the influence of gravitational fluctuating. The decay rate is equal to the spontaneous emission rate of the object in gravitational vacuum. When \(a\ne 0\), we have

$$\begin{aligned} A&=\frac{\varGamma (a^2+\omega ^2) (4 a^2+\omega ^2) \coth \frac{\pi \omega }{a}}{\omega ^4}(M_1-M_2),\nonumber \\ B&=\frac{\varGamma (a^2+\omega ^2) (4 a^2+\omega ^2) }{\omega ^4}(M_1-M_2). \end{aligned}$$
(33)
Fig. 1
figure 1

QC as function of \(\varGamma \tau \) with different accelerations for the object is polarized along the x axis and y axis (\(\hat{q}_{11}=-\hat{q}_{22}=\frac{1}{\sqrt{2}}\))

Full size image

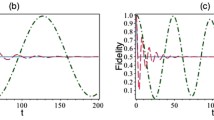
Figure 1 demonstrates the QC exponentially decays as acceleration and evolution time grow, which is similar to the matter field [27, 28] where QC quickly decreases as acceleration (or temperature) and evolution time increase.

4 Conclusion

In this literature, we have investigated the QC behaviors for an accelerated gravitationally polarizable two-level object weakly coupling with a bath of fluctuating quantum gravitational field. The master equation that governs the system evolution is derived. We find that in the paradigm of open quantum system, an accelerating gravitationally polarizable object is driven to a thermal state, which indicate that an accelerating object interacting with a bath of fluctuating quantum gravitational field can produce Unruh-like effect. For the asymptotic equilibrium state, vanishing QC means QC can not maintain for a long evolution time. In addition, QC exponentially degrades with increasing evolution time and acceleration. Under gravitational vacuum fluctuation, that the gravitationally polarizable object shows similar QC behaviors and Unruh-like effect as that of matter field [27, 28, 41, 42] would enlighten us that quantum gravitational field may have similar essence with matter field.