1 Introduction

Very recently, LHCb Collaboration reported the discovery of a narrow state \(P_{c}(4312)^{+}\) with a statistical significance of \(7.3\sigma \) in a data sample of \(\Lambda _{b}^{0}\rightarrow J/\psi p K^{-}\) decays [1]. Moreover, \(P_{c}(4450)^{+}\) formerly announced by LHCb is confirmed and observed to consist of two narrow overlapping peaks, \(P_{c}(4440)^{+}\) and \(P_{c}(4457)^{+}\). Soon after the LHCb’s new observation, many works [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] have been promptly triggered. Among these new experimental results, the most exciting point should attribute to the freshly discovered \(P_{c}(4312)^{+}\). After all, there already have existed plenty of researches on \(P_{c}(4450)^{+}\) [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] (one can also see a recent review e.g. [35]). Besides, \(P_{c}(4312)^{+}\) is narrow and below the \(\Sigma _{c}^{+}\bar{D}^{0}\) threshold within a plausible hadron-hadron binding energy, hence it provides the strongest experimental evidence to date for the existence of a \(\Sigma _{c}\bar{D}\) bound state [1]. Meanwhile, some different opinion has also appeared in Ref. [16], in which the authors could find evidence for the attractive effect of the \(\Sigma _{c}^{+}\bar{D}^{0}\) channel, however not strong enough to form a bound state and they infer that the \(P_{c}(4312)^{+}\) peak is more likely to be a virtual (unbound) state instead. Whether or no, to realize the nature of \(P_{c}(4312)^{+}\), it certainly requires more theoretical scrutiny.

In this work, we focus all our attention on the newly discovered \(P_{c}(4312)^{+}\) and would investigate the possibility of \(P_{c}(4312)^{+}\) being a \(\Sigma _{c}\bar{D}\) state, if the \(\Sigma _{c}\bar{D}\) state does exist. While studying a baryon-meson state, one inevitably has to confront and treat nonperturbative QCD problem. As one reliable method for evaluating nonperturbative effects, the QCD sum rule [36,37,38] is an analytic formalism firmly established on QCD theory and has been successfully applied to different hadronic systems [39,40,41,42,43]. As a matter of fact, there have appeared some related works on these \(P_{c}\) hadrons basing on baryon-meson configuration QCD sum rules [2, 44,45,46,47]. In QCD sum rule analysis, it is of great importance to carefully inspect both the operator product expansion (OPE) convergence and the pole dominance in order to ensure the extracted result authentic. In practice, one could note that some condensate may play an important role in some multiquark cases [48,49,50,51,52], which causes that it is of difficulty to find conventional work windows. Specially for the four-quark condensate, a general factorization \(\langle \bar{q}q\bar{q}q\rangle =\varrho \langle \bar{q}q\rangle ^{2}\) has been hotly discussed [53,54,55,56,57,58,59,60,61,62], where \(\varrho \) is a constant, which may be equal to 1, to 2, or be smaller than 1. Moreover, the factorization parameter \(\varrho \) could be about \(3{\sim }4\) [63,64,65]. Compromisingly, the parameter \(\varrho \) is taken as 2 in this work.

The rest paper is organized as follows. In Sect. 2, \(P_{c}(4312)^{+}\) is studied as a \(\Sigma _{c}\bar{D}\) state through the QCD sum rule approach. Numerical analysis and discussions are given in Sect. 3. The last part is a brief summary.

2 QCD sum rule study of \(P_{c}(4312)^{+}\) as a \(\Sigma _{c}\bar{D}\) state

Mass sum rules for a \(\Sigma _{c}\bar{D}\) state can be derived from the two-point correlator

$$\begin{aligned} \Pi (q^{2})=i\int d^{4}x\text{ e }^{iq.x}\langle 0|T[j(x)\overline{j}(0)]|0\rangle . \end{aligned}$$
(1)

To represent the \(\Sigma _{c}\bar{D}\) state, one can construct its interpolating current j from baryon-meson type of fields adopting currents for the heavy baryon [66, 67] and for the heavy meson [42]. Concretely, the current can be written as

$$\begin{aligned} j=\epsilon _{abe}(q_{a}^{T}C\gamma _{\mu }q_{b})\gamma ^{\mu }\gamma _{5}c_{e}\bar{c}_{f}i\gamma _{5}q_{f}. \end{aligned}$$

Here q could be the light u or d quark, c denotes the heavy charm quark, T means matrix transposition, C is the charge conjugation matrix, and the subscript a, b, e, and f are color indices.

Lorentz covariance implies that the two-point correlator (1) has the general form

$$\begin{aligned} \Pi (q^{2})=\Pi _{1}(q^{2})+/\!q\Pi _{2}(q^{2}). \end{aligned}$$
(2)

In phenomenology, it can be expressed as

$$\begin{aligned} \Pi (q^{2})= & {} \lambda ^{2}_H\frac{M_{H}+/\!q}{M_{H}^{2}-q^{2}}\nonumber \\&+\frac{1}{\pi }\int _{s_{0}} ^{\infty }ds\frac{\text{ Im }\Pi _{1}^{\text{ phen }}+/\!q\text{ Im }\Pi _{2}^{\text{ phen }}}{s-q^{2}}+ \cdots \end{aligned}$$
(3)

where \(M_{H}\) is the hadron’s mass, and \(\lambda _{H}\) denotes the coupling of the current to the hadron \(\langle 0|j|H\rangle =\lambda _{H}u(p,s)\). In the OPE side, one can write the correlator as

$$\begin{aligned} \Pi (q^{2})=\int _{4m_{c}^{2}}^{\infty }ds\frac{\rho _{1}}{s-q^{2}}+/\!q\int _{4m_{c}^{2}}^{\infty }ds\frac{\rho _{2}}{s-q^{2}}+ \cdots \end{aligned}$$
(4)

where spectral densities are \(\rho _{i}=\frac{1}{\pi }\text{ Im }\Pi _{i}^{\text{ OPE }}\), with \(i=1,2\). After equating the two expressions, applying quark-hadron duality, and making a Borel transform, the sum rules are

$$\begin{aligned} \lambda ^{2}_HM_{H}e^{-M_{H}^{2}/M^{2}}= & {} \int _{4m_{c}^{2}}^{s_{0}}ds\rho _{1}e^{-s/M^{2}}, \end{aligned}$$
(5)

and

$$\begin{aligned} \lambda ^{2}_He^{-M_{H}^{2}/M^{2}}= & {} \int _{4m_{c}^{2}}^{s_{0}}ds\rho _{2}e^{-s/M^{2}}, \end{aligned}$$
(6)

where \(M^2\) indicates the Borel parameter. Taking the derivative of Eqs. (5) or (6) with respect to \(1/M^{2}\) and dividing the equation itself, one can obtain mass sum rules

$$\begin{aligned} M_{H}^{2}= & {} \int _{4m_{c}^{2}}^{s_{0}}ds\rho _{1}s e^{-s/M^{2}}/ \int _{4m_{c}^{2}}^{s_{0}}ds\rho _{1}e^{-s/M^{2}}, \end{aligned}$$
(7)

and

$$\begin{aligned} M_{H}^{2}= & {} \int _{4m_{c}^{2}}^{s_{0}}ds\rho _{2}s e^{-s/M^{2}}/ \int _{4m_{c}^{2}}^{s_{0}}ds\rho _{2}e^{-s/M^{2}}. \end{aligned}$$
(8)

In the deriving of spectral densities, one can utilize the similar techniques as Refs. e.g. [43, 68,69,70]. The heavy-quark propagator in momentum-space [42] can be used to keep the heavy-quark mass finite, and the correlator’s light-quark part can be obtained in the coordinate space, which is then Fourier-transformed to the D dimension momentum space. The resulting light-quark part is combined with the heavy-quark part before it is dimensionally regularized at \(D=4\). As follows, we concretely present spectral densities \(\rho _{i}\) deduced from \(\Pi _{i}(q^{2})\) and put them forward to further numerical analysis, with

$$\begin{aligned} \rho _{i}= & {} \rho _{i}^{\text{ pert }}+\rho _{i}^{\langle \bar{q}q\rangle }+\rho _{i}^{\langle g^{2}G^{2}\rangle }+\rho _{i}^{\langle g\bar{q}\sigma \cdot G q\rangle }+\rho _{i}^{\langle \bar{q}q\rangle ^{2}}\\&+\rho _{i}^{\langle g^{3}G^{3}\rangle }+\rho _{i}^{\langle \bar{q}q\rangle \langle g^{2}G^{2}\rangle }+\rho _{i}^{\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle } \end{aligned}$$

up to dimension 8. In detail,

$$\begin{aligned} \rho _{1}^{\text{ pert }}= & {} -\frac{1}{5\cdot 2^{14}\pi ^{8}}m_{c}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{5}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{4}}(1-\alpha -\beta )^{3} [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{5},\\ \rho _{1}^{\langle \bar{q}q\rangle }= & {} \frac{\langle \bar{q}q\rangle }{2^{10}\pi ^{6}}m_{c}^{2}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{3}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{3}}(1-\alpha -\beta )^{2} [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{3},\\ \rho _{1}^{\langle g^{2}G^{2}\rangle }= & {} -\frac{\langle g^{2}G^{2}\rangle }{3\cdot 2^{15}\pi ^{8}}m_{c}\int _{\alpha _{min}}^{\alpha _{max}} \frac{d\alpha }{\alpha ^{5}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{4}}(1-\alpha -\beta )^{3} [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{2}\\&\times \,[(\alpha +\beta )(\alpha ^{2}-\alpha \beta +2\beta ^{2})m_{c}^{2}-\alpha \beta ^{3}s],\\ \rho _{1}^{\langle g\bar{q}\sigma \cdot G q\rangle }= & {} \frac{3\langle g\bar{q}\sigma \cdot G q\rangle }{2^{11}\pi ^{6}}m_{c}^{2}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{2}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{2}}(1-\alpha -\beta )\\&\times [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{2},\\ \rho _{1}^{\langle \bar{q}q\rangle ^{2}}= & {} \frac{\varrho \langle \bar{q}q\rangle ^{2}}{2^{6}\pi ^{4}}m_{c}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{2}} \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta }\\&\times [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{2},\\ \rho _{1}^{\langle g^{3}G^{3}\rangle }= & {} -\frac{\langle g^{3}G^{3}\rangle }{3\cdot 2^{17}\pi ^{8}}m_{c} \int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{5}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{4}}(1-\alpha -\beta )^{3} [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]\\&\times \Big \{(\alpha ^{3}+6\beta ^{3})[(\alpha +\beta )m_{c}^{2} -\alpha \beta s]+4m_{c}^{2}(\alpha ^{4}+\beta ^{4})\Big \},\\ \rho _{1}^{\langle \bar{q}q\rangle \langle g^{2}G^{2}\rangle }= & {} \frac{\langle \bar{q}q\rangle \langle g^{2}G^{2}\rangle }{3\cdot 2^{12}\pi ^{6}}m_{c}^{2} \int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{3}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{3}}\\&\times \{[\alpha ^{2}\beta ^{2}+3(\alpha ^{2}+\beta ^{2})(1-\alpha -\beta )^{2}]\\&\times [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]\\&+(\alpha ^{3}+\beta ^{3})(1-\alpha -\beta )^{2}m_{c}^{2}\},\\ \rho _{1}^{\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle }= & {} \frac{\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle }{2^{6}\pi ^{4}}m_{c}\\&\times \int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha }[m_{c}^{2}-\alpha (1-\alpha )s],\\ \rho _{2}^{\text{ pert }}= & {} -\frac{1}{5\cdot 2^{13}\pi ^{8}}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{4}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{4}}(1-\alpha -\beta )^{3}[(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{5},\\ \rho _{2}^{\langle \bar{q}q\rangle }= & {} \frac{\langle \bar{q}q\rangle }{2^{9}\pi ^{6}}m_{c}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{2}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{3}}(1-\alpha -\beta )^{2}[(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{3},\\ \rho _{2}^{\langle g^{2}G^{2}\rangle }= & {} -\frac{\langle g^{2}G^{2}\rangle }{3\cdot 2^{14}\pi ^{8}}m_{c}^{2}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{4}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{4}}(\alpha ^{3}+\beta ^{3})(1-\alpha -\beta )^{3}\\&\times [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{2},\\ \rho _{2}^{\langle g\bar{q}\sigma \cdot G q\rangle }= & {} \frac{3\langle g\bar{q}\sigma \cdot G q\rangle }{2^{10}\pi ^{6}}m_{c}\\&\times \int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha }\int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{2}}(1-\alpha -\beta )\\&\times [(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{2},\\ \rho _{2}^{\langle \bar{q}q\rangle ^{2}}= & {} \frac{\varrho \langle \bar{q}q\rangle ^{2}}{2^{7}\pi ^{4}}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha }\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta }[(\alpha +\beta )m_{c}^{2}-\alpha \beta s]^{2},\\ \rho _{2}^{\langle g^{3}G^{3}\rangle }= & {} -\frac{\langle g^{3}G^{3}\rangle }{3\cdot 2^{16}\pi ^{8}}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{4}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{4}}(1-\alpha -\beta )^{3}[(\alpha +\beta )m_{c}^{2}-\alpha \beta s]\\&\times \Big \{\beta ^{3}[(\alpha +5\beta )m_{c}^{2}-\alpha \beta s]\\&+\alpha ^{3}[(5\alpha +\beta )m_{c}^{2}-\alpha \beta s]\Big \},\\ \rho _{2}^{\langle \bar{q}q\rangle \langle g^{2}G^{2}\rangle }= & {} \frac{\langle \bar{q}q\rangle \langle g^{2}G^{2}\rangle }{3\cdot 2^{11}\pi ^{6}}m_{c}\int _{\alpha _{min}}^{\alpha _{max}}\frac{d\alpha }{\alpha ^{2}}\\&\times \int _{\beta _{min}}^{1-\alpha }\frac{d\beta }{\beta ^{3}}\\&\times \Big \{(\alpha +\beta )(4\alpha ^{2}-\alpha \beta +\beta ^{2})(1-\alpha -\beta )^{2}m_{c}^{2}\\&-\alpha ^{3}\beta [\beta ^{2}+3(1-\alpha -\beta )^{2}]s\Big \}, \end{aligned}$$

and

$$\begin{aligned} \rho _{2}^{\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle }= & {} \frac{\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle }{2^{7}\pi ^{4}}\int _{\alpha _{min}}^{\alpha _{max}}d\alpha [m_{c}^{2}\!-\!\alpha (1\!-\!\alpha )s], \end{aligned}$$

in which the general \(\langle \bar{q}q\bar{q}q\rangle =\varrho \langle \bar{q}q\rangle ^{2}\) factorization has been used. The integration limits are \(\alpha _{min}=\Big (1-\sqrt{1-4m_{c}^{2}/s}\Big )/2\), \(\alpha _{max}=\Big (1+\sqrt{1-4m_{c}^{2}/s}\Big )/2\), and \(\beta _{min}=\alpha m_{c}^{2}/(s\alpha -m_{c}^{2})\). Those condensates higher than dimension 8 are not involved here, as one could expect that kind of high dimension contributions may not radically influence the OPE’s character [71,72,73,74].

Fig. 1
figure 1

The relative contributions of various OPE as a function of \(M^2\) in sum rule (6) for \(\sqrt{s_{0}}=4.8~\text{ GeV }\) for \(\Sigma _{c}\bar{D}\)

Full size image

3 Numerical analysis and discussions

In this part, we firstly perform the numerical analysis of sum rule (8) to extract the value of \(M_{H}\), and take \(m_{c}\) as the running charm quark mass \(1.275_{-0.035}^{+0.025}~\text{ GeV }\) [75] along with other input parameters as \(\langle \bar{q}q\rangle =-(0.24\pm 0.01)^{3}~\text{ GeV }^{3}\), \(\langle g\bar{q}\sigma \cdot G q\rangle =m_{0}^{2}~\langle \bar{q}q\rangle \), \(m_{0}^{2}=0.8\pm 0.1~\text{ GeV }^{2}\), \(\langle g^{2}G^{2}\rangle =0.88\pm 0.25~\text{ GeV }^{4}\), and \(\langle g^{3}G^{3}\rangle =0.58\pm 0.18~\text{ GeV }^{6}\) [36,37,38, 40]. Steering a middle course, the factorization parameter \(\varrho \) is set to be 2. According to a standard procedure, both the OPE convergence and the pole dominance should be considered to find appropriate work windows for the threshold \(\sqrt{s_{0}}\) and the Borel parameter: the lower bound of \(M^{2}\) is gained by analyzing the OPE convergence, and the upper one is obtained by viewing that the pole contribution should be larger than QCD continuum contribution. Besides, \(\sqrt{s_{0}}\) characterizes the beginning of continuum states and should not be taken at will. It is correlated to the next excited state energy and empirically \(400{\sim }600~\text{ MeV }\) above the eventually achieved value \(M_{H}\).

In Fig. 1, the relative contributions of various OPE in sum rule (6) are compared as a function of \(M^2\) for the \(\Sigma _{c}\bar{D}\) state. Visually, there four main condensate contributions could play an important role on the OPE side, i.e. the two-quark condensate \(\langle \bar{q}q\rangle \), the mixed condensate \(\langle g\bar{q}\sigma \cdot G q\rangle \), the four-quark condensate \(\langle \bar{q}q\rangle ^{2}\), and the \(\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle \) condensate. The direct consequence is that it is not easy to find the standard Borel window, in which the low dimension condensate contribution should be bigger than the high dimension one. To say the least, these four main condensates could cancel each other out to some extent. In this way, the perturbative term still plays an important role on the OPE side and the OPE’s convergence could be under control at the relatively low value of \(M^{2}\). Thus, the lower bound of \(M^{2}\) is taken as \(2.0~\text{ GeV }^{2}\) for the sum rule (6).

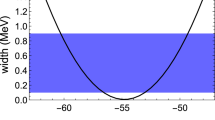
Phenomenologically, a comparison between pole contribution and continuum contribution of sum rule (6) for \(\sqrt{s_{0}}=4.8~\text{ GeV }\) is shown in Fig. 2, which manifests that the relative pole contribution is about \(50\%\) at \(M^{2}=2.7~\text{ GeV }^{2}\) and decreases with \(M^{2}\). In a similar way, the upper bounds of Borel parameters are \(M^{2}=2.6~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.7~\text{ GeV }\) and \(M^{2}=2.9~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.9~\text{ GeV }\). Thus, Borel windows are taken as \(2.0{\sim }2.6~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.7~\text{ GeV }\), \(2.0{\sim }2.7~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.8~\text{ GeV }\), and \(2.0{\sim }2.9~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.9~\text{ GeV }\). The mass \(M_{H}\) of \(\Sigma _{c}\bar{D}\) is shown in Fig. 3 as a function of \(M^2\) from sum rule (8). In the chosen work windows, \(M_{H}\) is calculated to be \(4.35\pm 0.07~\text{ GeV }\). Furthermore, in view of the uncertainty due to the variation of quark masses and condensates, we have \(4.35\pm 0.07^{+0.55}_{-0.21}~\text{ GeV }\) (the first error is resulted from the variation of \(\sqrt{s_{0}}\) and \(M^{2}\), and the second error reflects the uncertainty rooting in the variation of QCD parameters) or briefly \(4.35^{+0.62}_{-0.28}~\text{ GeV }\) for \(\Sigma _{c}\bar{D}\).

Fig. 2
figure 2

The phenomenological contribution in sum rule (6) for \(\sqrt{s_{0}}=4.8~\text{ GeV }\) for \(\Sigma _{c}\bar{D}\). The solid line is the relative pole contribution (the pole contribution divided by the total, pole plus continuum contribution) as a function of \(M^2\) and the dashed line is the relative continuum contribution

Full size image
Fig. 3
figure 3

The mass of \(\Sigma _{c}\bar{D}\) state as a function of \(M^2\) from sum rule (8). The continuum thresholds are taken as \(\sqrt{s_0}=4.7{\sim }4.9~\text{ GeV }\). The ranges of \(M^{2}\) are \(2.0{\sim }2.6~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.7~\text{ GeV }\), \(2.0{\sim }2.7~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.8~\text{ GeV }\), and \(2.0{\sim }2.9~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.9~\text{ GeV }\)

Full size image
Fig. 4
figure 4

The relative contributions of various OPE as a function of \(M^2\) in sum rule (5) for \(\sqrt{s_{0}}=4.8~\text{ GeV }\) for \(\Sigma _{c}\bar{D}\)

Full size image

Furthermore, one could put forward the numerical analysis of sum rule (7) analogously. In Fig. 4, the relative contributions of various OPE in sum rule (5) are shown as a function of \(M^2\) for \(\sqrt{s_{0}}=4.8~\text{ GeV }\). Similarly, four main condensates (i.e. \(\langle \bar{q}q\rangle \), \(\langle g\bar{q}\sigma \cdot G q\rangle \), \(\langle \bar{q}q\rangle ^{2}\), and \(\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle \)) could cancel each other out to some extent. For the sum rule (5), the lower bound of \(M^{2}\) is taken as \(2.2~\text{ GeV }^{2}\) at which the OPE’s convergence could still be controllable. In Fig. 5, a comparison between pole and continuum contribution of sum rule (5) is shown for \(\sqrt{s_{0}}=4.8~\text{ GeV }\), which indicates that the relative pole contribution is about \(50\%\) at \(M^{2}=2.9~\text{ GeV }^{2}\) and decreases with \(M^{2}\). Thereby, the ranges of \(M^{2}\) are fixed as \(2.2{\sim }2.9~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.7~\text{ GeV }\), \(2.2{\sim }3.1~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.8~\text{ GeV }\), and \(2.2{\sim }3.2~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.9~\text{ GeV }\). The mass of \(\Sigma _{c}\bar{D}\) state is shown in Fig. 6 as a function of \(M^2\) from sum rule (7). In the chosen work windows, \(M_{H}\) is calculated to be \(4.38\pm 0.09~\text{ GeV }\). In view of the uncertainty due to the variation of quark masses and condensates, we have \(4.38\pm 0.09^{+0.13}_{-0.07}~\text{ GeV }\) (the first error is resulted from the variation of \(\sqrt{s_{0}}\) and \(M^{2}\), and the second error reflects the uncertainty rooting in the variation of QCD parameters) or briefly \(4.38^{+0.22}_{-0.16}~\text{ GeV }\) for \(\Sigma _{c}\bar{D}\).

Fig. 5
figure 5

The phenomenological contribution in sum rule (5) for \(\sqrt{s_{0}}=4.8~\text{ GeV }\) for \(\Sigma _{c}\bar{D}\). The solid line is the relative pole contribution (the pole contribution divided by the total, pole plus continuum contribution) as a function of \(M^2\) and the dashed line is the relative continuum contribution

Full size image
Fig. 6
figure 6

The mass of \(\Sigma _{c}\bar{D}\) state as a function of \(M^2\) from sum rule (7). The continuum thresholds are taken as \(\sqrt{s_0}=4.7{\sim }4.9~\text{ GeV }\). The ranges of \(M^{2}\) are \(2.2{\sim }2.9~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.7~\text{ GeV }\), \(2.2{\sim }3.1~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.8~\text{ GeV }\), and \(2.2{\sim }3.2~\text{ GeV }^{2}\) for \(\sqrt{s_0}=4.9~\text{ GeV }\)

Full size image

In the end, combining the eventual results from both (7) and (8), one could arrive at a conservative mass range \(4.07{\sim }4.97~\text{ GeV }\) for the \(\Sigma _{c}\bar{D}\) state, which is consistent with the data of \(P_{c}(4312)^{+}\) and could support its explanation as a \(\Sigma _{c}\bar{D}\) state.

4 Summary

Motivated by LHCb’s new discovery of \(P_{c}(4312)^{+}\), we study that whether \(P_{c}(4312)^{+}\) could be a \(\Sigma _{c}\bar{D}\) state in QCD sum rules. In order to insure the quality of sum rule analysis, contributions of condensates up to dimension 8 have been computed to test the OPE convergence. We find that some condensates, i.e. the two-quark condensate, the mixed condensate, the four-quark condensate, and the \(\langle \bar{q}q\rangle \langle g\bar{q}\sigma \cdot G q\rangle \) condensate are of importance to the OPE side. Not bad, those main condensates could cancel each other out to some extent, which brings that the OPE convergence is still controllable. By combining those results from two sum rules, we finally obtain that a conservative mass range for \(\Sigma _{c}\bar{D}\) is \(4.07{\sim }4.97~\text{ GeV }\), which is in agreement with the experimental value of \(P_{c}(4312)^{+}\). This result supports that \(P_{c}(4312)^{+}\) could be explained as a \(\Sigma _{c}\bar{D}\) state.

In the future, one can expect that further experimental observations may shed more light on the nature of \(P_{c}(4312)^{+}\) and the inner structure of \(P_{c}(4312)^{+}\) could be further revealed by continual efforts in both experiment and theory.