1 Introduction

Particle detectors making use of superheated liquids are currently employed in the search for dark matter in the form of WIMPs [1,2,3,4,5,6]. Any of these devices is a variant of the standard bubble chamber developed by Glaser [7], in which the bubble nucleation is the result of a highly localized energy deposition by an interacting particle, as described by Seitz [8]. Indeed, the employment of bubble chambers in direct dark matter searches has a number of advantages. The most important is that the critical energy of bubble formation commonly required for a WIMP search is high enough to allow reaching an approximate \(10^{-11}\) intrinsic rejection against minimum ionizing backgrounds [9], whose contribution to nucleation can therefore be neglected. Additionally, neutron and cosmic ray induced activity can be strongly attenuated by an appropriate shielding application, as well as a deep underground operation of the detector. This means that the only remaining significant background source is represented by the alpha-decay events.

The current approach to alpha background rejection is based on the fact that the radiation-induced nucleation of a vapour bubble in a superheated liquid is accompanied by sound emission, first observed by Glaser and Rahm [10], and that the alpha decays are normally louder than nuclear recoils. Therefore, the acquisition and analysis of the acoustic signals associated with the bubble nucleation play a crucial role in WIMP search experiments.

Acoustic signatures of bubble nucleations were originally measured by Martynyuk and Smirnova [11], and more recently recorded by a number of investigators - see, e.g., Aubin et al. [12], Felizardo et al. [13], Behnke et al. [9], Mondal and Chatterjee [14], Archambault et al. [15], Amole et al. [16], and Sarkar et al. [17] - , most of them being involved in dark matter searches. According to these works, the amplitude of the acoustic signal - and then its clarity - increases as the pressure of the sensitive liquid is decreased and its temperature is increased, yet no direct correlation between the thermodynamic operating conditions of the detector and the acoustic signature of the bubble nucleation is readily available in the literature. On the other hand, since the acoustic signals are usually captured using piezoelectric transducers, their limited sensitivity settles the threshold of the acoustic signals detectable above the electronics background noise, which needs being translated into suitable conditions of temperature and pressure of the superheated liquid.

In this framework, a study is executed to establish a computational procedure aimed at determining in what measure the sound emission associated with a bubble nucleation occurrence is related to the thermodynamic state at which the superheated liquid is maintained, which could be helpful in defining the operating conditions of the detector and to provide a first-approach description of the higher loudness of the alpha-decay sound emission.

2 Bubble nucleation

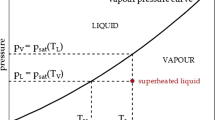
A superheated liquid is a liquid kept in a metastable state \(({T_{L}},{p_{L}})\) such that its temperature \({T_{L}}\) is higher than the saturation temperature \({T_{V}}\) at pressure \({p_{L}}\) or, that is the same, its pressure \({p_{L}}\) is lower than the saturation pressure \({p_{V}}\) at temperature \({T_{L}}\), the metastability being typically quantified either in terms of superheat, \(\,\mathrm {\Delta }{T}= {T_{L}}- {T_{V}}\), or in terms of underpressure, \(\,\mathrm {\Delta }{p}= {p_{V}}- {p_{L}}\).

In a particle detector in which the sensitive liquid is kept superheated at temperature \({T_{L}}\) and pressure \({p_{L}}\), if a minimum amount of energy, called critical energy and denoted as \({E_{c}}\), is released by an ionizing particle into a restricted volume of liquid, then a vapour bubble of critical radius \({R_{c}}\) nucleates, its subsequent growth being ensured by the energy supplied by the surrounding liquid.

Homogeneous nucleation in superheated liquids has been the subject of several studies carried out in past decades, each proposing a different expression for the critical energy, as well as for the critical radius [8, 18,19,20,21,22,23]. A reasoned review of these relations has recently been carried out by Bruno et al. [24], who also obtained a pair of equations for the calculation of \({E_{c}}\) and \({R_{c}}\), which will be used in the present work.

The critical energy is given by the sum of the energy required to vaporize the mass of liquid involved in the phase change and the energy required to form the bubble surface, that is

$$\begin{aligned} {E_{c}}=\frac{4}{3}{\pi }{R_{c}}^3{\rho _{V}}{L}+4{\pi }{R_{c}}^2\left( {\sigma }-{T_{L}}\frac{\mathrm {d}{\sigma }}{\mathrm {d}{T}}\right) , \end{aligned}$$
(1)

while the critical radius, regarded as the size of the vapour bubble corresponding to the maximum of the free enthalpy variation associated with the phase change, can be expressed as

$$\begin{aligned} {R_{c}}=\frac{2{\sigma }}{{\rho _{V}}{L}\frac{{T_{L}}-{T_{V}}}{{T_{V}}}}. \end{aligned}$$
(2)

In the above equations, \({\rho _{V}}\) is the mass density of the saturated vapour phase, \({L}\) is the latent heat of vaporization, and \({\sigma }\) is the surface tension of the liquid. Both \({\rho _{V}}\) and \({L}\) must be evaluated at the saturation temperature \({T_{V}}\), whereas \({\sigma }\) must be calculated at the liquid temperature \({T_{L}}\).

Notice that the two terms in the right-hand side of Eq.  (1) are the same as the vaporization and surface formation terms included in the relationships proposed by Bugg [19], Norman and Spiegler [20], Tenner [21], and Peyrou [22]. On the other hand, these authors included also an expansion work term or a kinetic energy term, which need not being considered. Additionally, they assumed that all the physical properties had to be evaluated at the liquid temperature.

Furthermore, it is worth pointing out that, should the superheat degree be sufficiently low, which allows for approximating the temperature derivative of the saturation pressure in the Clapeyron-Clausius equation using the corresponding ratio between the underpressure \(\,\mathrm {\Delta }{p}\) and the superheat \(\,\mathrm {\Delta }{T}\), then Eq.  (2) resolves into the commonly used expression of \({R_{c}}\) given by the Young-Laplace relation wherein the pressure inside the bubble is assumed to be the same as the saturation pressure \({p_{V}}\) at temperature \({T_{L}}\).

3 Sound emission

Sound waves are produced during the growth of the nucleated vapour bubble.

In the hypothesis that a growing bubble can be treated as a pulsating body [11, 15, 25] and that the wavelength \({\lambda }\) of the emitted sound is large compared to the bubble size, the fluid velocity \({U}\) in the wave region at any radial distance \({r}\) from the center of the bubble such that \({r}\gg {\lambda }\) is related to the second time derivative of the bubble volume \(\mathrm {d}^2{V}/\mathrm {d}{\tau }^2\) by the equation [26]

$$\begin{aligned} {U}=\frac{1}{4{\pi }{c_{s}}{r}}\left( \mathrm {d}^2{V}/\mathrm {d}{\tau }^2\right) , \end{aligned}$$
(3)

where \({c_{s}}\) is the speed of sound in the liquid.

Correspondingly, the amplitude \(\,\mathrm {\Delta }{p}\) of the sound pressure at a distance \({r}\) from the center of the bubble and the related emitted acoustic power \({W}\) are

$$\begin{aligned} \,\mathrm {\Delta }{p}= & {} \frac{{\rho _{L}}}{4{\pi }{r}}\left( \mathrm {d}^2{V}/\mathrm {d}{\tau }^2\right) , \end{aligned}$$
(4)
$$\begin{aligned} {W}= & {} \frac{{\rho _{L}}}{4{\pi }{c_{s}}}\left( \mathrm {d}^2{V}/\mathrm {d}{\tau }^2\right) ^2, \end{aligned}$$
(5)

in which \({\rho _{L}}\) is the mass density of the liquid.

Notice that, once \(\mathrm {d}^2{V}/\mathrm {d}{\tau }^2\) is calculated at time \({\tau }\), then \({W}\) is the acoustic power emitted at time \({\tau }\), whereas \({U}\) and \(\,\mathrm {\Delta }{p}\) are the fluid velocity and the amplitude of the sound pressure at the subsequent time \({\tau }+ {r}/{c_{s}}\), which accounts for the time interval required by the wave to cover the distance \({r}\) propagating at velocity \({c_{s}}\).

Finally, the acoustic energy \({AE_{{\tau }}}\) radiated during the bubble formation and growth up to time \({\tau }\) is obtained by integrating W in the time interval 0–\({\tau }\):

$$\begin{aligned} {AE_{{\tau }}}=\frac{{\rho _{L}}}{4{\pi }{c_{s}}}\int _0^{\tau }\left( \mathrm {d}^2{V}/\mathrm {d}{\tau }^2\right) ^2\,\mathrm {d}{\tau }, \end{aligned}$$
(6)

Obviously, the calculation of the time evolution of \(\,\mathrm {\Delta }{p}\), \({W}\) and \({AE_{{\tau }}}\) requires the knowledge of the time evolution of the bubble radius \({R}\), whose value, as well as the values of its first and second time derivatives, enter into the computation of the second time derivative of the bubble volume

$$\begin{aligned} \mathrm {d}^2{V}/\mathrm {d}{\tau }^2=4{\pi }\left( 2{R}\left( \mathrm {d}{R}/\mathrm {d}{\tau }\right) ^2 + {R}^2 \left( \mathrm {d}^2{R}/\mathrm {d}{\tau }^2\right) \right) . \end{aligned}$$
(7)

Leaving aside the very first growth stage during which the newborn proto-bubble becomes a vapour bubble surpassing the critical size, having a time scale of the order of \(10^{-8}\) ms [27], three subsequent growth regimes can be identified, called the surface tension-controlled regime, the inertia-controlled regime and the heat diffusion-controlled regime. In the surface tension-controlled regime, the opposition exerted by the surface tension to the growth of the bubble results in what is generally referred to as the delay period of the bubble growth, due to the extremely small increase of the bubble size. In the subsequent inertia-controlled regime, the expansion of the bubble is determined by its ability to push back the surrounding liquid using the energy available in its interior, which results in a pressure drop, and then a decrease of the vapour temperature. In the last heat diffusion-controlled regime, the bubble growth is due to the continuous evaporation of the liquid layer located just behind its surface, the necessary heat being supplied by the superheated liquid.

Intuitively, once the surface tension stresses are relaxed and the growth of the bubble volume sets definitely in, the inertia-controlled regime of growth is faster than the heat diffusion-controlled regime, which is clearly limited by the rate of evaporation, dictated by the rate of heat transfer through the liquid to the bubble surface. Actually, in the inertia-controlled regime the bubble radius increases linearly with time, as described by the Rayleigh-Plesset relationship [28]. Conversely, in the heat diffusion-controlled regime the bubble radius increases as the square root of time, as described by the relations obtained by Plesset and Zwick [28] or by Scriven [29], which apply whether the thermal boundary layer surrounding the vapour bubble is sufficiently thin or not, respectively. Details on the vapour bubble growth can be found in the studies performed by Lee and Merte [30], and Robinson and Judd [31], to cite a few.

Moreover, it is equally intuitive that the growth rate in the inertia-controlled regime must depend on the resistance of the liquid to be pushed back by the expanding vapour bubble, meaning that, since the energy stored within the bubble is transferred to the surrounding liquid by mechanical work, the higher is the liquid pressure, the smaller will be the volume increase experienced by the bubble up to the start of the subsequent heat diffusion-controlled regime.

Another parameter which should significantly affect the rate of the bubble volume increase, and then the acoustic signature of the bubble nucleation, is the metastability degree. In fact, the higher is the metastability degree, the more “explosively” the phase change is expected to take place. On the other hand, such a metastability degree cannot be expressed simply in terms of the absolute distance from saturation, i.e., in terms of \(\,\mathrm {\Delta }{T}\) or \(\,\mathrm {\Delta }{p}\). Actually, the same \(\,\mathrm {\Delta }{T}\) or \(\,\mathrm {\Delta }{p}\) plays a different role whether the related saturation temperature or pressure is close or far from its critical value, since the maximum theoretical distance from saturation, represented by the spinodal limit of stability, increases as the saturation temperature or pressure is decreased. Therefore, it is not the absolute superheat that counts, but how close to the limit of stability the sensitive liquid is maintained thanks to the imposed superheat. Such an information is usefully delivered by the so-called superheat parameter \({SH}\) introduced by d’Errico [32]

$$\begin{aligned} {SH}=\frac{{T_{L}}-{T_{V}}}{{T_{c}}-{T_{V}}}, \end{aligned}$$
(8)

where \({T_{c}}\) denotes the critical temperature.

Finally, it is important that the time-length of the delay period is properly accounted for, as it must unquestionably play a meaningful role in determining the growth characteristics of the vapour bubble. In fact, the larger is the amount of internal energy used to reduce the surface tension stresses during the surface tension-controlled regime, the smaller will be the availability of energy to be transferred from the bubble to the liquid in the subsequent inertia-controlled regime before the commencement of the heat diffusion-controlled regime.

The time evolution of the bubble radius along the three growth regimes discussed above is reliably described by the following correlation proposed by Robinson and Judd [31]

$$\begin{aligned} {R}\left( {\tau }\right) ={R_{c}}+\frac{2}{3}{C_{0}}\left( \left( {\tau }+4{C}\right) ^{3/2}-{\tau }^{3/2}-\left( 4{C}\right) ^{3/2}\right) , \end{aligned}$$
(9)

where the constants \({C_{0}}\) and \({C}\) are

$$\begin{aligned} {C_{0}}= & {} \sqrt{\frac{{\pi }}{27{\alpha _{L}}}}\left( \frac{\,\mathrm {\Delta }{p}}{{\rho _{L}}\left( {Ja}\right) }\right) , \end{aligned}$$
(10)
$$\begin{aligned} {C}= & {} \frac{9{\rho _{L}}{\alpha _{L}}\left( {Ja}\right) ^2}{2{\pi }\,\mathrm {\Delta }{p}}. \end{aligned}$$
(11)

In the above equations, \({\alpha _{L}}\) is the thermal diffusivity of the liquid and \({Ja}\) is the Jakob number defined as

$$\begin{aligned} {Ja}=\frac{{\rho _{L}}{c_{L}}\,\mathrm {\Delta }{T}}{{\rho _{V}}{L}}, \end{aligned}$$
(12)

in which \({c_{L}}\) is the specific heat at constant pressure of the liquid and \({\rho _{V}}\) is the mass density of the vapour phase.

Indeed, Eq. (9) is a revisitation of the well-known Mikic–Rohsenhow–Griffith growth equation [33], modified to include the delay period among the growth regimes, to take into account that the description of the bubble growth starts when the bubble radius is just larger than \({R_{c}}\), to extend the solution to low Jakob numbers, and to recognize the non-linearity of the relationship existing between the saturation pressure and the temperature.

According to Eq. (9) the first and second time derivatives of the bubble radius are

$$\begin{aligned} \frac{\mathrm {d}{R}}{\mathrm {d}{\tau }}= & {} {C_{0}}\left( \left( {\tau }+4{C}\right) ^{1/2}-{\tau }^{1/2}\right) , \end{aligned}$$
(13)
$$\begin{aligned} \frac{\mathrm {d}^2{R}}{\mathrm {d}{\tau }^2}= & {} \frac{1}{2}{C_{0}}\left( \left( {\tau }+4{C}\right) ^{-1/2}-{\tau }^{-1/2}\right) . \end{aligned}$$
(14)

The substitution of Eqs. (9)–(14) into Eq.  (7) allows for the calculation of \(\mathrm {d}^2{V}/\mathrm {d}{\tau }^2\), that, replaced into Eqs.  (4)–(6), provides for the evaluation of \(\,\mathrm {\Delta }{p}\), \({W}\) and \({AE_{{\tau }}}\), whose time-distributions can be used to describe the acoustics of the vapour bubble growth.

4 Results and discussion

The computational procedure discussed earlier is applied to a number of refrigerants rich in Fluorine, which has by far the largest enhancement factor in the spin-dependent cross section for the scattering of WIMP particles, with the main aim to determine the effects of the thermodynamic conditions of metastability on the sound emission associated with a bubble nucleation.

Typical time-distributions of the bubble radius calculated for \(\mathrm {C_{3}F_{8}}\), which is the sensitive liquid currently used for WIMP-recoil detection in the experiments carried out by PICO [5] and MOSCAB [6], are reported in Fig.  1 for different operating conditions selected to obtain the same critical energy \({E_{c}}= 10\) keV, the values of the physical properties being extracted from the NIST Chemistry WebBook [34]. Notice that, as the operating pressure \({p_{L}}\) - and then the saturation temperature \({T_{V}}\) - is decreased, the superheat \(\,\mathrm {\Delta }{T}= {T_{L}}-{T_{V}}\) to be imposed to reach the same critical energy must be increased, which, despite the growth of the difference between the critical temperature and the saturation temperature, results in an increase of the superheat parameter \({SH}\), as shown in Fig. 2 for different values of \({E_{c}}\). According to the distributions of \({R}({\tau })\) shown in Fig. 1, the duration of the delay period, having a time scale of the order of \(10^{-6}\) ms, increases as \({p_{L}}\) is reduced, due to the decrease of \({T_{L}}\) and the consequent increase of the surface tension, whose opposition to the bubble growth enhances. On the other hand, it can be seen that the bubble growth in the two regimes of growth subsequent to the delay period occurs at a rate that increases as \({p_{L}}\) is reduced, due to the smaller opposition exerted by the liquid to the expansion of the vapour bubble.

Fig. 1
figure 1

Distributions of the bubble radius (\({R}> {R_{c}}\)) vs. time at \({E_{c}}= 10\) keV using \({p_{L}}\) as a parameter

Full size image
Fig. 2
figure 2

Distributions of \({SH}\) vs. \({p_{L}}\) using \({E_{c}}\) as a parameter

Full size image

The corresponding time-distributions of the emitted acoustic power \({W}\), calculated using Eqs. (5), (7) and (9)–(14), are displayed in Fig. 3, while the related time-distributions of the acoustic energy \({AE_{{\tau }}}\) radiated up to time \({\tau }\), calculated using Eqs.  (6), (7) and (9)–(14), are represented in Fig. 4. Notice that, for any assigned distance \({r}\) from the bubble center, in a \(\mathrm {Log}\)-\(\mathrm {Log}\) plot the time-distributions of \(\,\mathrm {\Delta }{p}\) have the same trend as those of \({W}\). In fact, based on the relationship existing between the pressure amplitude and the power of the radiated sound, which can be obtained by the combination of Eqs. (4) and (5), we can write \(\mathrm {Log}(\,\mathrm {\Delta }{p}) = 0.5 \times \mathrm {Log}({W}) + {K}\), where the constant is \({K}= 0.5 \times \mathrm {Log}({\rho _{L}}{c_{s}}/4{\pi }{r}^2)\).

Fig. 3
figure 3

Distributions of \({W}\) vs. time at \({E_{c}}= 10\) keV using \({p_{L}}\) as a parameter

Full size image
Fig. 4
figure 4

Distributions of \({AE}\) vs. time at \({E_{c}}= 10\) keV using \({p_{L}}\) as a parameter

Full size image

It can be seen that \({W}\) - and then also \(\,\mathrm {\Delta }{p}\) - increases in the inertia-controlled regime and decreases in the heat diffusion-controlled regime, owing respectively to the increasing and decreasing velocity of the bubble growth. Furthermore, at higher liquid pressures, the rate of the increase is lower, and also the inertia-controlled regime, whose typical time scale is of the order of \(10^{-5}\)–\(10^{-3}\) ms, is shorter, tending to vanish at very high liquid pressures, with a consequent noticeably reduced sound emission. Finally, since at time \({\tau }= 1\) ms the emitted acoustic power is reduced by at least three orders of magnitude, the time interval 0–1 ms can be assumed as a characteristic time interval over which the integration of the acoustic power of the emitted sound can be executed to calculate the acoustic energy conventionally associated with the bubble nucleation, which is in line with the duration of the signals captured by Martynyuk and Smirnova [11], Barnabé-Heider et al. [35] and Jordan et al. [36].

In this regard, it is worth pointing out that, according to Fig.  1, the size reached by the vapour bubble at time \({\tau }= 1\) ms is of the order of 0.1–0.5 mm, which is the typical size of the vapour bubble when it can be seen for the first time. This means that, when the vapour bubble is visually recognized, its acoustic history has already been almost totally written, which emphasizes how rich of physical details can be the acoustic bubble detection compared with the visual inspection technique.

More importantly, as shown in Fig. 4, it can be noticed that at \({p_{L}}= 2\) bar and \({SH}= 0.333\) the emitted acoustic energy is 4–5 orders of magnitude higher than that radiated at \({p_{L}}\) = 6 bar and \({SH}= 0.204\), which requires a brief discussion on the relative importance of the role played by the decrease of \({p_{L}}\) and the increase of \({SH}\) on the generation of a detectable acoustic signature of bubble nucleation.

Indeed, if a well defined value of \({E_{c}}\) has to be obtained, \({p_{L}}\) and \({SH}\) are not independent of one another, as mentioned earlier. Thus, in order to evaluate in what measure \({p_{L}}\) and \({SH}\) affect the acoustic signal, the distributions of the emitted acoustic power and the related emitted acoustic energy, plotted against time, are displayed in Figs. 5 and 6, using both \({p_{L}}\) and \({SH}\) as parameters. Naturally, in this case a different critical energy is associated to any combination of values of \({p_{L}}\) and \({SH}\).

It is apparent that the increase of \({W}\) and \({AE_{{\tau }}}\) consequent to the increase of \({SH}\) is practically independent of \({p_{L}}\), yet, by the point of view of the clarity of the acoustic signature of bubble nucleation, the increase of \({SH}\) is beneficial only if \({p_{L}}\) is sufficiently low. In fact, only at low pressures, thanks to the increased superheat, the radiated acoustic energy can reach values such that the related acoustic signals are high enough to be easily detectable, which emphasizes the crucial role played by the liquid pressure.

Fig. 5
figure 5

Distributions of \({W}\) vs. time using \({p_{L}}\) and \({SH}\) as parameters

Full size image
Fig. 6
figure 6

Distributions of \({AE}\) vs. time using \({p_{L}}\) and \({SH}\) as parameters

Full size image

This effect can be much better appreciated if the acoustic energy emitted in the time interval 0–1 ms \({AE_{\mathrm {1ms}}}\) is plotted versus \({SH}\) using \({p_{L}}\) as a parameter, as displayed in Fig.  7, which points out that the experimental data obtained by Felizardo et al. [13] and Archambault et al. [15] through the increase of \({T_{L}}\) - and then \({SH}\) - at \({p_{L}}\approx 1\) atm followed a markedly increasing distribution due to their low operating pressure. A comparison between our calculations and the amplitudes of the acoustic signals measured by Archambault et al. [15] using \(\mathrm {C_{4}F_{10}}\) is shown in Fig.  8, where, according to Eq. (4), the theoretical prediction of the peak of the instantaneous sound pressure, which the piezoelectric transducers are sensitive to, is calculated using a direct proportionality to the second time derivative of the bubble volume. It can be seen that a good degree of agreement is obtained between the predictions of our computational procedure and the experimental data.

Fig. 7
figure 7

Distributions of \({AE_{\mathrm {1ms}}}\) vs. \({SH}\) using \({p_{L}}\) as a parameter

Full size image
Fig. 8
figure 8

Predicted vs. measured acoustic signal amplitudes for \(\mathrm {C_{4}F_{10}}\) at \({p_{L}}\approx 1\) atm

Full size image

Same type of results shown in Fig. 7 for \(\mathrm {C_{3}F_{8}}\) can be achieved also for other fluids, as shown in Fig. 9, in which the distributions of \({AE_{\mathrm {1ms}}}\) versus \({SH}\) at \({p_{L}}= 2\) bar and 4 bar are for example displayed for two widely diffused refrigerants, i.e., \(\mathrm {C_2Cl_2F_4}\), also known as R114, and \(\mathrm {C_2HF_5}\), also known as R125.

Fig. 9
figure 9

Distributions of \({AE_{\mathrm {1ms}}}\) vs. \({SH}\) for R114 and R125 using \({p_{L}}\) as a parameter

Full size image

Therefore, a high value of the superheat parameter \({SH}\) describes the potentiality of the bubble to grow enough in the inertia-controlled regime, which is the condition required to radiate an intense acoustic signal, but this potentiality is quite difficult to be put into effect when the liquid pressure \({p_{L}}\) is such that the liquid hardly accepts to be pushed back by the growing bubble. All in all, from the acoustic detection viewpoint, the lower pressure effect overwhelms the higher metastability effect, which means that, since a lower operating pressure asks for a higher superheat degree to reach the same assigned critical energy, any requirement of increase of the clarity of the acoustic signals should result into dark matter detectors designed to bear increasingly higher superheat degrees.

The computational procedure illustrated above can be used for a first-approach quantitative description of the usually higher loudness of the alpha-decay events compared with the events originating from neutron-induced nuclear recoils. Actually, being reasonable to assume that the sound generated by the growing vapour bubble after the critical size has been surpassed is substantially particle-independent, this means that a nucleation produced by a stopping recoiled ion, for example \(\mathrm {^{12}C}\) or \(\mathrm {^{19}F}\) in \(\mathrm {C_{3}F_{8}}\), is acoustically indistinguishable from a nucleation produced by a stopping recoiled daughter of the \(\mathrm {^{222}Rn}\) decay chain, which is what has been found experimentally at low to moderate metastability degrees of the superheated liquid [12, 15]. On the other hand, should the thermodynamic conditions be such that the critical stopping force required for nucleation is lower than the stopping force for alpha-particles in the region of the Bragg peak - typically in the range 200–220 keV/\(\mu \)m depending on the liquid temperature - which occurs at sufficiently high metastability degrees, then also a stopping alpha-particle could generate one or more nucleations in addition to that produced by the stopping daughter of the \(\mathrm {^{222}Rn}\) chain. In such a case, due to the contribution of the additional nucleations produced along the alpha track, the acoustic energy emission associated with the alpha decay would prevail over that associated with the nucleation produced by a neutron-induced nuclear recoil, which is the customary explanation for the higher loudness of the alpha-decay events [12, 15].

Indeed, this is not an absolute rule. In fact, since the stopping force of \(\mathrm {^{12}C}\) and \(\mathrm {^{19}F}\) is much higher than that of an alpha-particle, multiple nucleations are likely to take place also along their track for sufficiently low values of the critical stopping force, provided that the energy of the recoiled \(\mathrm {^{12}C}\) or \(\mathrm {^{19}F}\) ion is high enough. Conversely, the daughters of the \(\mathrm {^{222}Rn}\) decay chain are expected to produce almost always a single nucleation, due to the extremely limited length of their tracks. This would imply that if the critical stopping force is such that an alpha-particle cannot produce any nucleation whereas a recoiled \(\mathrm {^{12}C}\) or \(\mathrm {^{19}F}\) ion is able to generate a multiple nucleation, thus meaning that the critical stopping force is just higher than the cited 200–220 keV/\(\mu \)m, then, in these thermodynamic conditions, the nuclear recoil would be louder than an alpha-decay event. Indeed, sets of acoustic signals due to nuclear recoils louder than those due to alpha-decay events were recorded in a number of experiments [5, 12, 15]. However, based on the spectra of the neutron sources usually employed for calibration purposes, the probability that a recoiled \(\mathrm {^{12}C}\) or \(\mathrm {^{19}F}\) ion has such a high energy to produce multiple nucleations is relatively low. On the other hand, when the critical stopping force is lower than approximately 200–220 keV/\(\mu \)m the number of nucleations produced along the alpha track is expected to be much larger than that for a recoiled \(\mathrm {^{12}C}\) or \(\mathrm {^{19}F}\) ion, due to the significantly greater track length.

The situation for \(\mathrm {C_{3}F_{8}}\) at \({p_{L}}= 2\) bar is schematically described in Fig. 10 for the alpha-decay \(\mathrm {^{222}Rn}\) \(\rightarrow \) \(\mathrm {^{218}Po}\) (101 keV) +  \(\alpha \) (5.49 MeV) and three \(\mathrm {^{19}F}\) ions with recoil energies of 50, 100 and 200 keV, which reflects the increasing higher loudness of the alpha-decay signals detected experimentally for increasing superheat degrees [12, 15].

Fig. 10
figure 10

Distributions of \({AE_{\mathrm {1ms}}}\) vs. \({SH}\) for alpha decays and nuclear recoils in \(\mathrm {C_{3}F_{8}}\) at \({p_{L}}= 2\) bar

Full size image

Notice that the distributions of \({AE_{\mathrm {1ms}}}\) versus \({SH}\) have been obtained as the product of the acoustic energy associated with a single nucleation event multiplied by the number of bubbles of critical size generated along the particle track, assuming that a nucleation event occurs when the energy of the ionizing particle exceeds the critical energy and the stopping force of the particle is higher than the critical stopping force calculated as \({E_{c}}/2{R_{c}}\). The number of nucleations and the related acoustic energy associated with an alpha decay is calculated as the sum of the nucleations produced by the alpha-particle and the recoiled \(\mathrm {^{218}Po}\) ion. It is apparent that above \({SH}\) = 0.251, which corresponds to a critical energy of 29.2 keV and a critical stopping force of 215 keV/\(\mu \)m, the loudness of the alpha decays increases steeply, due to the multiple nucleations occurring along the alpha track as a consequence of the decrease of the critical stopping force below the stopping force for the alpha-particles at the Bragg peak. In contrast, as shown in the close-up of Fig. 11, in which a Log-scale is used to represent the acoustic energy \({AE_{\mathrm {1ms}}}\), for \({SH}\) =  0.250–0.251, i.e., when the critical stopping force is just slightly higher than 215 keV/\(\mu \)m, the amount of acoustic energy injected into the liquid by the nuclear recoils is somewhat larger than that associated with the alpha-decay events.

Fig. 11
figure 11

Close-up of the distributions of \({AE_{\mathrm {1ms}}}\) in Log-scale vs. \({SH}\) for alpha decays and nuclear recoils in \(\mathrm {C_{3}F_{8}}\) at \({p_{L}}= 2\) bar

Full size image

Of course, this is just a simplified first approach to the problem, as the real situation is certainly different, being affected by the coalescence of the consecutive bubbles, as well as by potential ineffective energy release by the stopping particle and/or ineffective usage of the released energy by the superheated liquid. These matters, falling outside the scope of the present paper, will be the subject of a future work.

5 Conclusions

The use of superheated liquids in searches for dark matter in the form of WIMPs requires to know the effects of the thermodynamic operating conditions of the detector on the acoustic signature of bubble nucleation, which is useful both to carry out an acoustic bubble recognition additional to the visual inspection and to discriminate alpha-decay events from the events originating from nuclear recoils.

A computational procedure has then been established to determine in what measure the sound emission associated with the growth of a vapour bubble is related to the thermodynamic state at which the superheated liquid is maintained. The acoustic energy injected into the liquid by the growing vapour bubble has been found to increase with decreasing the operating pressure and increasing the metastability degree expressed in terms of the superheat parameter, the lower pressure effect giving the major contribution. A good agreement has also been found between the predictions of our computational procedure and a set of experimental data available in the literature for the amplitude of the detected acoustic signals, which seems encouraging enough to schedule further investigations on this topic.

Finally, according to the results obtained through a first-approach application of the proposed computational procedure, the increasingly higher loudness of the alpha-decay events detected by increasing the metastability degree at constant pressure is consistent with the idea that the increase of the emitted acoustic energy is due to the increasing number of vapour bubbles generated in the region of the Bragg peak and along the track of the alpha-particle, consequent to the decrease of the critical stopping force required for nucleation.