Exploring $\hbox {CE}\nu \hbox {NS}$ with NUCLEUS at the Chooz nuclear power plant

Abstract

Coherent elastic neutrino–nucleus scattering ($\hbox {CE}\nu \hbox {NS}$) offers a unique way to study neutrino properties and to search for new physics beyond the Standard Model. Nuclear reactors are promising sources to explore this process at low energies since they deliver large fluxes of anti-neutrinos with typical energies of a few MeV. In this paper, a new-generation experiment to study $\hbox {CE}\nu \hbox {NS}$ is described. The NUCLEUS experiment will use cryogenic detectors which feature an unprecedentedly low-energy threshold and a time response fast enough to be operated under above-ground conditions. Both sensitivity to low-energy nuclear recoils and a high event rate tolerance are stringent requirements to measuring $\hbox {CE}\nu \hbox {NS}$ of reactor anti-neutrinos. A new experimental site, the Very-Near-Site (VNS), at the Chooz nuclear power plant in France is described. The VNS is located between the two 4.25 $\hbox {GW}_{\mathrm {th}}$ reactor cores and matches the requirements of NUCLEUS. First results of on-site measurements of neutron and muon backgrounds, the expected dominant background contributions, are given. In this paper a preliminary experimental set-up with dedicated active and passive background reduction techniques and first background estimations are presented. Furthermore, the feasibility to operate the detectors in coincidence with an active muon veto at shallow overburden is studied. The paper concludes with a sensitivity study pointing out the physics potential of NUCLEUS at the Chooz nuclear power plant.

1 Introduction

The existence of neutral-current neutrino interactions implies the existence of elastic neutrino–nucleus scattering [1]. The Standard Model (SM) $\hbox {CE}\nu \hbox {NS}$ cross-section can be approximated by [2]

$$\begin{aligned} \frac{\mathrm {d}\sigma }{\mathrm {d}\mathrm {E}_{\mathrm {R}}}\,=\,\frac{\mathrm {G}^2_{\mathrm {F}}}{4\,\pi }\,\mathrm {Q}^2_{\mathrm {W}}\,\mathrm {F}^2(\mathrm {q}^2)\,\cdot \,\mathrm {m}_{\mathrm {N}}\, \left( 1\,-\,\frac{\mathrm {E}_{\mathrm {R}}}{\mathrm {E}^{\mathrm {max}}_{\mathrm {R}}}\right) \end{aligned}$$

(1)

where $\mathrm {G}_{\mathrm {F}}$ is the Fermi constant, $\mathrm {Q}_{\mathrm {W}}$ is the nuclear weak charge, $\mathrm {m}_{\mathrm {N}}$ is the total mass of the nucleus, $\mathrm {E}_{\mathrm {R}}$ is the nuclear-recoil energy, and $\mathrm {F}(\mathrm {q}^2)$ is the nuclear form factor as a function of the momentum transfer q. The weak charge is given by $\mathrm {Q}_{\mathrm {W}}\,=\,\mathrm {N}\,-\,\mathrm {Z}\cdot (1-4\cdot \mathrm {sin}^2\theta _{\mathrm {W}})$, with N and Z being the number of neutrons and protons of the target nucleus, and $\theta _{\mathrm {W}}$ the Weinberg angle. The maximum nuclear-recoil energy $\mathrm {E}_{\mathrm {R}}$ is given by $\mathrm {E}^{\mathrm {max}}_{\mathrm {R}}\,=\,2\,\mathrm {E}_{\nu }^2/(\mathrm {m}_{\mathrm {N}}\,+\,2\,\mathrm {E}_{\nu })$, where $\mathrm {E}_{\nu }$ is the incident neutrino energy. Equation (1) assumes the absence of radiative corrections and coherent neutrino scattering off a spin-0 nucleus. The latter assumption is valid, as for large nuclei the neutron and proton spins cancel out [2]. For scattering off spin-1/2 nuclei, a small correction of $\mathscr {O}(\mathrm {E}_{\mathrm {R}}^2/\mathrm {E}_{\nu }^2)$ is needed which is negligible for heavy nuclei [2]. For momentum transfers smaller than the inverse of the nuclear radius (typically for $\mathrm {E}_{\nu }\,\lesssim \,30$ MeV) the form factor is close to unity and the scattering is coherent over all nucleons in a nucleus [1]: this process is called coherent elastic neutrino nucleus scattering ($\hbox {CE}\nu \hbox {NS}$). For larger momentum transfers the full coherence is no longer given and the form factor drops below unity.

Fig. 1

Differential $\hbox {CE}\nu \hbox {NS}$ count rate on $\hbox {Li}_2\hbox {WO}_4$ (solid green line), $\hbox {CaWO}_4$ (dashed blue line), germanium (dash-dotted red line) and $\hbox {Al}_2\hbox {O}_3$ (dotted orange line), calculated with the anti-neutrino flux expected at the VNS from both Chooz-B reactor cores. The reactor neutrino flux model follows [3] as parameterized in [4]. The NUCLEUS experiment aims to reach a background count rate of 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$), indicated by the gray band

The coherent cross-section is boosted by a factor of N$^2$, and can exceed the cross-section of the standard neutrino detection methods, such as inverse beta decay (IBD), by more than two orders of magnitude [5]. Contrary to the enhancement of the cross-section, the experimental signature, i.e. the nuclear recoil, is suppressed in energy by the nucleus mass, $\mathrm {m}_{\mathrm {N}}$.

Figure 1 shows the differential count rate of coherently scattered anti-neutrinos in different targets. For $\mathrm {E}_{\mathrm {R}}\,\le \,100$ eV, the $\hbox {CE}\nu \hbox {NS}$ count rate in a $\hbox {CaWO}_4$ or $\hbox {Li}_2\hbox {WO}_4$ crystal exceeds the rate on lighter nuclei such as present in $\hbox {Al}_2\hbox {O}_3$ by more than an order of magnitude. However, as the $\hbox {CE}\nu \hbox {NS}$ count rate decreases rapidly with increasing energy, an energy threshold well below 100 eV is necessary to explore the $\hbox {CE}\nu \hbox {NS}$ signal with heavy targets.

While for IBD the kinetic energy of the anti-neutrino needs to be at least 1.8 MeV, $\hbox {CE}\nu \hbox {NS}$ does not have an energy threshold. Thus, $\hbox {CE}\nu \hbox {NS}$ provides a unique probe of the Standard Model (SM) at low energies: e.g. measuring the Weinberg angle, $\theta _{\mathrm {W}}$, at low momentum transfer [6] or exploring fundamental neutrino properties such as the existence of a neutrino magnetic dipole moment [7]. Moreover, as a neutral-current interaction, $\hbox {CE}\nu \hbox {NS}$ is flavor insensitive, and, thus, a new probe to search for sterile neutrinos [8]. Any deviation from the SM prediction may reveal new physics beyond the SM, such as non-standard neutrino interactions, i.e. modified V-A quark-neutrino couplings, or new exotic neutral currents; see e.g. [2, 9]. $\hbox {CE}\nu \hbox {NS}$ offers a broad spectrum of possible applications in nuclear physics [10, 11] and supernovae detection [6, 12]. The enhancement of the $\hbox {CE}\nu \hbox {NS}$ cross-section allows for a miniaturization of neutrino detectors, from the typical tonne-size to kilogram- or even gram-scale in the case of NUCLEUS, and thus, a possible practical application in nuclear reactor monitoring [13]. Furthermore, $\hbox {CE}\nu \hbox {NS}$ of solar and atmospheric neutrinos will become an irreducible background for future dark matter experiments searching for weakly interacting massive particles, which thus profit from an independent measurement of the cross-section.

Due to its rich physics program, $\hbox {CE}\nu \hbox {NS}$ is a very active field of research, and numerous experiments based on different technologies and target materials are planned or under way: e.g. CONUS [14] and TEXONO [15] based on high purity germanium detectors, MINER [16] and Ricochet [17] using cryogenic detector technology, the CCD-based experiment CONNIE [18], and RED-100 [19] using a liquid xenon dual phase technology. The first observation of $\hbox {CE}\nu \hbox {NS}$ was reported by the COHERENT collaboration at a $6.7\sigma$ confidence level [5]. The COHERENT detector [20], operating at the Spallation Neutron Source (SNS) in a neutrino flux of $4.3\times 10^{7}\nu /(\mathrm {s}\,\,\mathrm {cm}^2 )$, uses a 14.6 kg CsI[Na] scintillating crystal target. In contrast to reactor neutrinos, the neutrino beam produced at the SNS features a well defined energy spectrum reaching up to 50 MeV, i.e. partially above the coherence regime of elastic neutrino–nucleus scattering.

This paper describes the NUCLEUS experiment at the Chooz Very-Near-Site (VNS), designed to study $\hbox {CE}\nu \hbox {NS}$ using reactor anti-neutrinos. The VNS is presented in Sect. 2, together with on-site muon and neutron attenuation measurements. Section 3 focuses on the concept of the NUCLEUS experiment at the VNS, whereas the NUCLEUS target detectors are described in detail in Ref. [13]. Section 4 demonstrates that the NUCLEUS detectors can be operated at the VNS with a moderate dead time induced by the muon veto. First Monte Carlo (MC)-based background studies are presented in Sect. 5. The potential to measure the $\hbox {CE}\nu \hbox {NS}$ process with the NUCLEUS experiment at the VNS is presented in Sect. 6.

2 The Very-Near-Site at the Chooz nuclear power plant

The VNS is a new experimental site between the two power reactors of the Chooz-B plant, planned to host the NUCLEUS experiment. The nuclear power plant, shown in Fig. 2, is operated by the French company Electricité de France (EDF). The two N4-type pressurized water reactors, hereafter identified as B-1 and B-2, are separated by 160 m, and their respective cores are located about 7 m above the Chooz ground level. Each reactor runs at a nominal thermal power of 4.25 $\hbox {GW}_{\mathrm {th}}$ and features a high duty cycle. The two cores are switched off for refueling approximately one month per year during alternating periods.

Nuclear reactors are one of the strongest artificial continuous neutrino sources. Reactor-$\bar{\nu _{e}}$ are produced via the beta decays of the fission products of $^{235}$U, $^{238}$U, $^{239}$Pu and $^{241}$Pu with energies up to 10 MeV. The mean $\bar{\nu _{e}}$ energy is around 1.5 MeV [21]. Thus, reactor-$\bar{\nu _{e}}$ are expected to be in the fully coherent region for typical nuclear target elements, maximizing the $\hbox {CE}\nu \hbox {NS}$ cross-section. Assuming an average number of six $\bar{\nu _e}$ per fission with an average energy release of 200 MeV, about $8\times 10^{20}\,\bar{\nu _e}/\mathrm {s}$ are produced by a 4.25 $\hbox {GW}_{\mathrm {th}}$ power reactor [22].

Until 1998, the Chooz power plant hosted the long baseline ($\sim 1000\,\mathrm {m}$) neutrino oscillation experiment CHOOZ [23]. The main result was an upper limit on neutrino oscillation in the $\bar{\nu _{e}}$ disappearance mode. Since 2008 the Chooz laboratory site is used by the neutrino oscillation experiment Double Chooz to measure the neutrino mixing angle $\theta _{13}$ [24].

Thanks to these previous neutrino experiments, the Chooz reactor site has an existing infrastructure for scientists, including office, meeting and storage rooms, which can be made available for future projects. The acquired expertise and relationship developed in past collaborations with EDF greatly helps to establish the new site for a future neutrino experiment.

Fig. 2

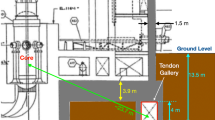
Sketch of the Chooz nuclear power plant and of the Very-Near-Site (VNS). The VNS is located in-between the two reactor buildings B-1 and B-2. Since 2008, the power plant hosts the Double Chooz experiment with two experimental sites, denoted the near and the far site. Office buildings close to the Double Chooz sites can be used in the future. The inset on the top right shows the office building between the reactor cores hosting the VNS. Figure credit to EDF CNPE de Chooz

2.1 Description of the VNS

The VNS is a 24 m$^2$ room situated in the basement of a five-story office building at the Chooz power plant (see inset of Fig. 2). The small size of the room requires that the full set-up does not exceed a volume of several cubic meters and a weight of the order of $\mathscr {O}(10\,\mathrm {t})$. To support loads on the floor of $\mathscr {O}(5\,\mathrm {t}/\mathrm {m}^2)$, as expected for the NUCLEUS shielding, a weight support platform will be installed. Furthermore, minor modifications of the VNS are foreseen to meet the safety regulations.

Mechanical vibrations are a known cause of disturbance in cryogenic detectors. Vibrations can arise within the cryostat necessary to operate the detectors. In addition, vibrations may be introduced to the set-up at the VNS by the turbines and generators of the nuclear power plant in the close vicinity. Further external sources of vibrations can be of seismic origin, as well as introduced by the elevator system, or movements in the office building. A vibration measurement campaign is planned for 2019. Based on the campaign results, a system to attenuate the vibrations will be designed.

The baseline of the VNS to the two reactor cores is 72 m to B-1, and 102 m to B-2, respectively. The expected neutrino flux at the VNS is about $3\,\times 10^{12}\,\bar{\nu _{\mathrm {e}}}/(\mathrm {s} \,\mathrm {cm}^{2})$. At this distance, no neutron background from the reactor cores is expected (see Sect. 3.1). However, for an expected overburden of less than 10 m of water equivalent (m.w.e.), see section below, special care of the cosmic-ray induced background needs to be taken.

Therefore, a campaign to determine the relative reduction of the cosmic muon and atmospheric neutron flux at the VNS with respect to the surface was performed from October 2017 until May 2018. The campaign results are presented below and used to estimate the upper limit on the trigger rate of the NUCLEUS muon veto in Sect. 4. To be conservative, the background simulations presented in Sect.  5 use the fluxes at surface level.

Fig. 3

Measurement of the muon rate at the surface (open data points) and at the VNS (filled data points) as a function of zenith angle for different azimuthal orientations. The muon flux at the surface follows the expected cos$^2\theta$-law. Uncertainties are statistical only

Fig. 4

Left: sketch of the office building hosting the VNS and the reactor buildings B-1 and B-2 as seen from the top. Right: overburden map over the VNS. The azimuth angle is measured counter-clockwise with respect to the direction opposite to the reactor buildings. The projections of the zenith angle are indicated by circles. The red markers represent the zenith angles in the measurements with $0^{\circ }/180^{\circ }$ azimuthal orientation

2.2 Measurement of the muon flux attenuation

The muon rate at the location of the VNS was measured with the cosmic wheel developed by the Centre de physique des particules de Marseille (CPPM) for the “Science à l’école” outreach program [25]. The device consists of three (26 $\times$ 14) cm$^{2}$ plastic scintillator plates separated by 10 cm. Each plastic scintillator is read out by a photo-multiplier tube (PMT). Time-coincident signals in all three scintillators are interpreted as a cosmic muon event. Therefore, the number of background events from external gamma-rays or random coincidences are expected to be negligible. The mechanical structure allows one to measure different zenith positions with an opening angle of 70 $^{\circ }$.

Figure 3 shows the measured muon rate above ground (open red markers) and four different azimuthal orientations at the VNS (filled markers). The angular zenithal distribution of the muon rate above ground follows the expected cos$^2\theta$ law for cosmic muons at the surface [26], shown by the red line. Based on the attenuation $a_{\mu }$ of the muon rate at the VNS, $\hbox {R}_{\mathrm {VNS}}$, with respect to the surface, $\hbox {R}_{\mathrm {surface}}$, the overburden $m_0$ is approximated with the following relation:

$$\begin{aligned} a_{\mu }\,=\,\frac{\mathrm {R}_{\mathrm {VNS}}}{\mathrm {R}_{\mathrm {surface}}}\,=\,10^{-1.32\,\mathrm {log}d\,-\,0.26\,(\mathrm {log}d)^2} \end{aligned}$$

(2)

where $d\,=\,1\,+\,m_0/10$, and $m_0$ is given in m.w.e. [27].

Figure 4 shows a projection of the overburden over the VNS as obtained from the muon-attenuation measurements. Since the VNS is not centered with respect to the building, the angular distribution of the overburden is asymmetric. For zenith angles smaller than 50$^{\circ }$, the overburden ranges from 2.1 to  4.1 m.w.e.

For each measurement, i.e. same azimuthal orientation at the VNS and at the surface, the measured muon rates are integrated over the zenith angle to obtain $\widehat{\mathrm {R}}_{\mathrm {surface}}$ and $\widehat{\mathrm {R}}_{\mathrm {VNS,i}}$, where i $=$  $0^{\circ }/180^{\circ }$, $45^{\circ }/225^{\circ }$, $90^{\circ }/270^{\circ }$, and $135^{\circ }/315^{\circ }$ (see Table 1). The averaged attenuation factor is given by $\overline{a}_{\mu }\,=\, 1/4\,\cdot \,\sum _{\mathrm {i}} \widehat{\mathrm {R}}_{\mathrm {VNS,i}}/\widehat{\mathrm {R}}_{\mathrm {surface}} \,=\,0.71\,\pm \,0.01$, where the error is given by the standard deviation. This attenuation corresponds to an overburden of $m_{0}$ $=$ (2.9 ± 0.1) m.w.e.

Table 1 Muon-attenuation factor, $\hbox {a}_{\mu }$, at the VNS for different azimuthal angles $\phi$. $\phi$ and $\phi \,+\,180^{\circ }$ are considered as one orientation. Only statistical uncertainties are considered

Fig. 5

Left: schematic drawing of the neutron detectors used in the neutron set-up (see text). Right: detector array box

2.3 Measurement of the fast neutron flux reduction

Neutrons are a potentially harmful background (discussed in Sect. 3.1). To evaluate the reduction of the neutron flux at the VNS, an array of neutron counters from Technische Universität München was deployed at Chooz. Each detector consists of a hexagonal cell with a diameter of $91~\hbox {mm}$ and a height of ${\sim }\,50~\hbox {mm}$. It is filled with approximately $300~\hbox {g}$ of liquid scintillator (EJ-301 from Eljen Technology [28]) which has a high discrimination capability between gamma-ray induced electronic and neutron-induced proton recoil. In order to collect the scintillation light the detectors are equipped with Philips XP- 3461-B PMTs which are optically coupled to a perspex window. Cell and PMT are enclosed in a plastic tube. A schematic drawing of the detectors can be seen in Fig. 5.

The set-up is not only sensitive to neutrons but also to atmospheric protons. However, the flux of protons is reduced by a factor of $\sim 38$ compared to the neutron flux whereby the protons are neglected in this measurement [29].

An array of seven such neutron detectors was operated at the Chooz power plant, at the surface and at the VNS location. The surface measurements were performed in a hut close to the Double Chooz near site (see Fig. 2) and at negligible overburden. During the measurement campaign, the detectors were operated for a cumulative time of $15~\hbox {h}$ at the surface and $21~\hbox {h}$ at the VNS location.

A reduced data set of three detectors, selected for discrimination threshold and performance stability, was used for the final analysis. The detectors were calibrated by identifying the Compton edges of various gamma sources ($^{22}$Na, $^{137}$Cs), wherefore the energy is given in units of electron equivalent, $\hbox {keV}_{ee}$, in the following. The discrimination thresholds of the used detectors are $100~\hbox {keV}_{ee}$, $400~\hbox {keV}_{ee}$ and $650~\hbox {keV}_{ee}$, respectively. Neutron-induced nuclear recoils in the liquid scintillator are unambiguously identified by a generic pulse-shape parameter based on the difference in the pulse decay time with respect to electron recoils. The cut is defined using an AmBe neutron calibration data set and then applied to the background data.

The data show a statistically compatible shape of the neutron recoil spectra at the VNS and surface. Thus, an energy-independent neutron reduction factor for the range $100~\hbox {keV}_{ee}$–$2~\hbox {MeV}_{ee}$ is found: at the VNS the neutron flux is reduced by a factor of $8.1\pm 0.4$ compared to the surface (see Fig. 6).

Fig. 6

Neutron-induced recoil rate in the liquid scintillator detectors up to an energy of $2~\hbox {MeV}_\mathrm {ee}$ observed at the VNS (green histogram, solid line) and a nearby surface location (blue histogram, dashed line). For the calculation the best three detectors in terms of discrimination threshold and stability are used. Each bin displays the exposure-weighted average of the rates from all detectors with a sufficiently low threshold, along with error bars following Poissonian statistics. The histogram uses logarithmic binning with small bins at low energy to display the shape of the spectrum and large bins at high energy to account for the low statistics

3 The NUCLEUS experiment at the VNS

A high signal-to-background ratio is one of the key requirements for the success of a $\hbox {CE}\nu \hbox {NS}$ experiment. The primary $\hbox {CE}\nu \hbox {NS}$ target material in NUCLEUS will be $\hbox {CaWO}_{4}$. The enhanced cross-section for heavy nuclei such as tungsten, together with an envisioned detector threshold of $\mathscr {O}(10\,\mathrm {eV})$, will give a strong $\hbox {CE}\nu \hbox {NS}$ signal (see Fig. 1 and Eq. (1)). One of the main experimental challenges is to achieve a sufficiently low background level in the $\hbox {CE}\nu \hbox {NS}$ target detector. To reach the desired background count rate of the order of $10^2$ counts/($\hbox {keV } \hbox {kg } \hbox {day}$), the NUCLEUS experiment will apply passive and active background suppression methods.

In the following section, the potential background sources for the NUCLEUS experiment at the VNS are discussed. A first concept of the NUCLEUS experiment is presented in Sect. 3.2 with focus on active and passive background suppression. The BASKET R&D project, presented in Sect. 3.3, gives the opportunity to complement the $\hbox {CE}\nu \hbox {NS}$ detection concept of NUCLEUS with a unique idea to characterize the neutron background, one of the most challenging backgrounds for $\hbox {CE}\nu \hbox {NS}$ experiments.

3.1 Sources of background

Experimental sites close to nuclear reactors are usually located at shallow depth, typically corresponding to an overburden of $\mathscr {O}(10\mathrm {\,m.\,w.\,e.})$. The background sources of interest for the NUCLEUS experiment are here categorized into external, internal, cosmic-ray induced and reactor-correlated backgrounds. The dominant sources are briefly summarized below; for a more detailed description the reader is referred to [30, 31].

The external background is dominated by gamma-rays from $\alpha$- and $\beta$-decaying nuclides in the $^{232}$Th, $^{238}$U and $^{235}$U decay chains, as well as $^{40}$K which is present in material surrounding the experiment. Gamma-rays originating in the concrete of the laboratory building can be shielded by high-Z material, such as lead. Materials used for components close to the target detectors, such as mounting and support structures or electronic components, need to be carefully selected, e.g. by exploiting $\gamma$-ray spectroscopy, and undergo cleaning and purification processes [31].

Nuclides from the thorium and uranium decay chains may also be present in the detector target itself. In the case of NUCLEUS, this internal contamination can be reduced e.g. by special measures during crystal production [32]. In the uranium and thorium decay chains, radon is produced which escapes by diffusion or nuclear recoil accompanying the ejection of an $\alpha$-particle. Radon is the strongest source of airborne radioactivity [31]. To prevent radon deposition on the detector surface, special cleaning procedures are needed during detector assembly and installation.

The above-mentioned decays typically produce $\gamma$-rays with energies up to 2.6 MeV, which is the highest naturally occurring $\gamma$-line from the decay of $^{208}$Tl (a progeny of $^{232}$Th). $\gamma$-rays of MeV energies predominantly interact via Compton scattering, thus the energy deposited in the target detector ranges from zero up to the energy of the Compton edge. Since $\gamma$-rays likely interact via multiple Compton scattering, a fiducialization of the NUCLEUS detector is a promising tool to actively suppress the external $\gamma$-background (see Sect. 3.2 for further details).

The energies of $\alpha$- and $\beta$-particles typically reach up to several MeV. In $\beta$-decays, the available energy is split between the emitted $\nu$ and the $e^{+/-}$. While a $\beta$-particle is typically absorbed within a few mm in a solid, the neutrino remains undetected. If the $\beta$-decay occurs on the surface of the detector or is followed by the emission of $\gamma$-rays, the fiducialization of the detector volume allows one to discriminate this background from $\hbox {CE}\nu \hbox {NS}$ events. The range of an $\alpha$-particle does not exceed a few tens of $\mu$m in a solid. If released in the bulk of the target detector, $\alpha$-particles are fully absorbed, and the event exhibits an energy well above the (sub-)keV signal of a $\hbox {CE}\nu \hbox {NS}$ event. However, if the $\alpha$-decay happens on or close by the detector surface a significant fraction of the energy remains undetected and such an energy deposit may mimic a (sub-)keV event. By instrumenting the surrounding material surface events can be discriminated from $\hbox {CE}\nu \hbox {NS}$ events (see Sect. 3.2).

Most of the secondary cosmic rays from air showers like electrons, $\gamma$-rays, protons and pions are absorbed by the building structure or a dedicated lead shielding. The remaining muons and neutrons are the main components of cosmic-ray induced background at shallow overburden [30].

Besides a source of background via ionization, pair production and Bremsstrahlung, muons also produce neutrons in nuclear reactions, especially in high-Z materials like lead. The flux of neutrons caused by air showers decreases rapidly with increasing overburden. Already with an overburden of 3 m.w.e. the neutron flux starts to be dominated by neutrons produced by muons in a massive lead shielding [30]. The experimental signature of a neutron is a nuclear recoil, and thus, neutrons are a particularly dangerous source of background for any $\hbox {CE}\nu \hbox {NS}$ experiments. Furthermore, they can be highly penetrating and difficult to shield. Neutrons may also produce radio-nuclides by inelastic scattering and neutron capture in the detector or surrounding materials.

To reduce the muon-induced background, an active muon veto, typically based on plastic scintillators is used: all events in coincidence with a muon event are discarded. In this way, muon-induced events, which are e.g. induced by ionization or Bremsstrahlung, or by neutrons produced in the shielding material, are vetoed. Neutron-induced radio-isotopes with lifetimes much shorter than the coincidence window are rejected as well. In order to decrease the time for thermalization and capture of neutrons in the shielding, moderators, e.g. polyethylene (PE), are used. To attenuate neutrons produced inside the shielding, it is most efficient to place a neutron absorber inside the high-Z shielding material [30].

Nuclear reactors emit a large number of $\gamma$-rays and neutrons. $\gamma$-rays are produced in the fission process as well as the subsequent $\beta$-decay, neutron capture or de-excitation of the fission products. High energy $\gamma$-rays may produce neutrons in photo-nuclear reactions e.g. in the concrete of the reactor building [33]. The VNS is located at a distance of more than 70 m from the cores, with $\mathscr {O}$(10 m) of rock and concrete in the line of sight. Furthermore, the reactor vessel is shielded by a thick layer of steel. Therefore, $\gamma$-ray induced neutron background is negligible.

Fission induced neutrons are emitted with a mean energy of 2 MeV. Most of these primary neutrons are thermalized in the reactor. The expected reactor-correlated fast neutron background at the VNS is estimated to be negligible (see Sect. 5). This assumption is further supported by recent neutron measurements at the experimental sites of the TEXONO experiment at the Kuo-Sheng Reactor Neutrino Laboratory [34] and CONUS at the Brokdorf nuclear reactor [14]. Both experiments conclude that the reactor-correlated background is negligible. Both detector set-ups feature a multi-layer shielding similar to the one envisioned by NUCLEUS, however, the CONUS (TEXONO) experiment is located at 17 m (28 m) from the reactor core while NUCLEUS has a baseline of 72 m and 102 m.

Fig. 7

Sketch of the NUCLEUS experiment at the VNS. The set-up consists of a cryostat (1), where the target detectors are installed in its lower part, the experimental volume (2). The latter is surrounded by a passive shielding (3) consisting of alternating layers of borated PE and lead. The top part will be completed by a cold shield inside the cryostat. The outermost layer is the active muon veto (4) made from plastic scintillator panels. The full set-up with a footprint of approximately 1 m$^2$ is placed on a weight support platform (5). Further support structures, e.g. for the cryostat, are omitted for clarity. The schematics shows an example set-up of a multi-layer passive shielding

3.2 The NUCLEUS experiment

A promising technology for the study of $\hbox {CE}\nu \hbox {NS}$ are cryogenic calorimeters. Cryogenic detectors measure the temperature rise $\varDelta \mathrm {T}\,=\,\varDelta \mathrm {E}/\mathrm {C}$ following an energy deposition $\varDelta \mathrm {E}$ in a target with a heat capacity C. For crystalline material kept at a temperature $\mathscr {O}(\mathrm {mK})$, C is small enough to achieve a measurable $\varDelta \mathrm {T}$ even for small energy depositions. The detector technology of NUCLEUS is based on CRESST cryogenic detectors [36] which have world-leading sensitivity in the field of direct low mass dark matter search and are driven by requirements similar to the study of $\hbox {CE}\nu \hbox {NS}$: a sub-keV energy threshold as well as a low intrinsic background. The CRESST experiment has developed $\hbox {CaWO}_{4}$ and $\hbox {Al}_{2}\hbox {O}_{3}$ crystals as targets with masses between 24 and 300 g.

The NUCLEUS concept expands this technology to an ultra-low-threshold ($\mathscr {O}$(10 eV)) gram-scale cryogenic calorimeter [37] as a target detector for $\hbox {CE}\nu \hbox {NS}$ combined with cryogenic veto detectors for active background discrimination. The experiment will proceed in two phases: in a first step, NUCLEUS-10g, a detector with a 10 g $\hbox {CE}\nu \hbox {NS}$ target will be deployed. A later stage, NUCLEUS-1kg, foresees an upgrade to a total target mass of 1 kg. Figure 7 shows a first design of the proposed $\hbox {CE}\nu \hbox {NS}$ experiment at the VNS. The NUCLEUS target detectors are installed in a cryostat. The experimental volume is surrounded by a shielding for active and passive background reduction.

3.2.1 The NUCLEUS target detectors

The NUCLEUS detector concept is a fiducial-volume cryogenic detector (see Fig. 8) based on three individual calorimeter systems: (1) an array of gram-scale cryogenic calorimeters with ultra-low-energy threshold as target detector, (2) a low-threshold inner veto holding and encapsulating the target, and (3) a surrounding kg-scale cryogenic detector used as outer veto.

Fig. 8

3D sketch of the NUCLEUS-10g detector. It consists of three different types of cryogenic calorimeters – two 3$\times$3 arrays of gram-scale cryogenic calorimeters as $\hbox {CE}\nu \hbox {NS}$ target (1), an inner veto (2) and an outer veto (3) with a diameter of 10 cm. The assembly is held mechanically by a non-instrumented support structure (4). The target is operated in anti-coincidence with the inner and the outer veto. See text for details

$\hbox {CaWO}_4$, $\hbox {Al}_2\hbox {O}_3$, Si and Ge are well known materials for cryogenic detectors and suitable candidates for the target volume of the experiment. Detectors with a total mass of $\mathscr {O}(1~\hbox {g})$ enable ultra-low thresholds [37] and imply a total event rate per crystal of ${\lesssim }1~\hbox {Hz}$ which is crucial to keep the dead time at a value of $\mathscr {O}(1\%)$. In the CRESST experiment [36], transition edge sensors (TESs) have proven to be a highly sensitive thermometer able to measure the low recoil energies produced in $\hbox {CE}\nu \hbox {NS}$. With a 0.5 g prototype detector made from a (5 mm)$^3$ $\hbox {Al}_2\hbox {O}_3$ cubic crystal, an unprecedented ultra-low threshold of $\hbox {E}_{\mathrm {th}}$ $=$ (19.7 ± 0.9) eV has been reached [13], one order of magnitude lower than previous devices. Such gram-scale crystals exploit the full potential of the $\hbox {CE}\nu \hbox {NS}$ signal (see Fig. 1). Arrays of these gram-scale cryogenic calorimeters allow deploying a larger total target mass. Figure 8 shows a schematic view of NUCLEUS-10g: a 3$\times$3 array of $\hbox {CaWO}_4$ (6 g) and a 3$\times$3 array of $\hbox {Al}_2\hbox {O}_3$ (4 g). This multi-target approach will provide an in-situ background characterization: while the $\hbox {CE}\nu \hbox {NS}$ scattering rate ($\sim$N$^2$) is strongly enhanced for $\hbox {CaWO}_4$, fast neutrons are expected to induce comparable signatures in $\hbox {CaWO}_4$ and $\hbox {Al}_2\hbox {O}_3$ due to scattering on O nuclei [13]. Furthermore, coincident background events in several target detectors can efficiently be discriminated from $\hbox {CE}\nu \hbox {NS}$ events, which are single scatters.

The target detectors will be embedded within cryogenic veto detectors which allow for an efficient active background reduction. The NUCLEUS detector support structures are made of Si-wafers read out by TESs which enable a 4$\pi$ low-threshold inner veto. Background events originating from surface $\alpha$ and $\beta$ contamination of the detector components can be rejected by anti-coincidence [13]. Both target and inner veto will be enclosed in a kg-scale outer veto which is operated in anti-coincidence mode to reject neutron and $\gamma$-ray backgrounds. Ge and $\hbox {CaWO}_4$ are established materials for cryogenic detectors with masses up to $1~\hbox {kg}$ and typically reach energy thresholds of a few keV. Ge single crystals are commercially available in extremely high purity and large sizes. $\hbox {CaWO}_4$ is especially interesting due to the presence of tungsten with a high cross-section for $\gamma$-radiation, and oxygen which enables efficient neutron moderation. An outer veto from $\hbox {CaWO}_{4}$ would require R&D into large-diameter crystal production. Studies based on Monte Carlo simulations show that with the outer and inner vetos a background suppression of $\mathscr {O}(10^3)$ can be achieved [13].

The NUCLEUS detector concept foresees to scale the total target mass from gram to kilogram. The production of the cryogenic detectors is based on well-established techniques of the semiconductor industry. In particular, the capability to produce multiple target elements simultaneously before cutting and polishing has been demonstrated, which is crucial for the later stages of NUCLEUS.

3.2.2 The cryostat

The base temperature of $\mathscr {O}$(10 mK) required to operate cryogenic detectors is typically provided by “wet” dilution refrigerators relying on a continuously evaporating bath of liquid helium at 4 K. At the VNS, the handling of cryogenic liquids can be avoided using a “dry” dilution refrigerator which replaces the helium bath with a pulse-tube cryocooler integrated into the cryostat. Though much simpler in operation and infrastructure requirements, this feature makes a “dry cryostat” a challenging environment for cryogenic detectors due to vibrations induced by the pulse-tube, which will degrade the detector performance if not addressed. This challenge can be met by dedicated work on vibration decoupling [38], which is mandatory for the NUCLEUS set-up. The $\hbox {CE}\nu \hbox {NS}$ target detectors are installed in the experimental volume inside the cryostat. The cryogenic infrastructure is chosen such as to host both NUCLEUS phases. The experimental cryogenic volume is surrounded by a compact passive and active shielding.

3.2.3 Active and passive shielding

Many examples in the literature demonstrate that a low-background count rate can be reached with a shallow overburden of $\mathscr {O}(10\,\mathrm {m.w.e.})$. Two promising examples are GIOVE, a highly sensitive HPGe spectrometer in the shallow depth laboratory (15 m.w.e.) at the Max-Planck-Institut für Kernphysik [39], and the Dortmund low-background facility with an overburden of 10 m.w.e. [29]. Both set-ups feature an active muon veto and passive shields of lead, copper, and borated PE. With these graded shielding structures background rates of 0.13 counts/(keV kg day) for GIOVE and 1.4 counts/(keV kg day) for the Dortmund low-background facility are reached in the 40–2700 keV energy range.

The goal of the NUCLEUS experiment is to achieve a background count rate of $10^{2}\,\mathrm {counts}/(\mathrm {keV} \,\mathrm {kg}\,\mathrm {day})$ in the sub-keV region. At present, this energy range has never been probed in a shallow depth laboratory. Based on the experience of the aforementioned experiments operating in the keV region, the passive shielding of NUCLEUS will consist of several alternating layers of borated PE and lead. To avoid a hole directly above the detectors, a part of the shielding has to be mounted inside the cryostat and kept cold during operation. Neutrons produced in nuclear reactions are moderated by the PE and captured on boron. External gamma-rays and such produced in radiative neutron captures (for boron the most intense line is at 478 keV [40]) are attenuated by the lead. As copper can be produced with very low intrinsic radioactive contamination compared to lead (see e.g. [41]), copper may be used as innermost shielding layer.

As discussed in Sect. 3.1, cosmic-ray induced events are an unavoidable source of background. Cosmic muons cannot be sufficiently attenuated by a passive shielding, thus, muon-induced background events need to be identified and removed from the data. An active muon veto consisting of 5 cm thick plastic scintillator plates is planned. With an energy loss of $\sim 2\,\mathrm {MeV}/\mathrm {cm}$ a 4 GeV muon (mean energy of the cosmic muons at the surface) deposits about 10 MeV in a veto panel [26]. The most energetic gamma-ray from natural radioactivity is at 2.6 MeV; see Sect. 3.1. Thus, cosmic muons can efficiently be discriminated by a simple energy cut. An event in the muon veto that exceeds the energy threshold, causes a muon trigger. Events in the target detector in coincidence with a muon trigger are disregarded.

The cubic passive shielding will have an edge length between 0.8 and 1.2 m, since a larger shielding is not feasible due to the increase of dead time for large active veto areas; see Sect. 4.2. In this work, a preliminary two-layer passive shielding consisting of 10 cm of 5% borated PE and 5 cm lead (from outside to inside) is used. First background Monte Carlo (MC) simulations with this configuration are presented in Sect. 5.

3.3 The BASKET detectors

BASKET (Bolometers At Sub-KeV Energy Threshold) is an R&D program started in 2017 at CEA in collaboration with CSNSM (Centre de Sciences Nucléaires et Sciences de la Matière) to develop innovative detectors for neutrinoless double beta decay and $\hbox {CE}\nu \hbox {NS}$ [42]. For the latter, the project focuses on the development of $\hbox {Li}_2\hbox {WO}_4$ crystals as a new absorber material together with new thermal sensors to optimize the time response and energy resolution. First tests on an 11-g crystal, which was read out with a Neutron Transmutation Doped Ge sensor and a Ge Neganov-Luke light detector, showed that $\hbox {Li}_2\hbox {WO}_4$ exhibits good bolometric and scintillation properties. Furthermore, it could be demonstrated that $\alpha$-particles can be discriminated from $\beta$-particles and $\gamma$-rays with a discrimination power of more than five sigma [43]. Further tests with 1-g crystals coupled to metallic magnetic calorimeters [44] and NbSi TES [45] are currently performed. The goal is to reach an energy threshold of $\mathscr {O}$(10 eV) and a time response of $\mathscr {O}$(100 $\upmu$s). A possible synergy of BASKET with the NUCLEUS experiment is the deployment of gram-size $\hbox {Li}_2\hbox {WO}_4$ crystals as target detectors. The $\hbox {CE}\nu \hbox {NS}$ rate is similar to the one expected for $\hbox {CaWO}_4$. Moreover, an additional target compound to $\hbox {CaWO}_4$ and $\hbox {Al}_2\hbox {O}_3$ may yield supplementary information on the background yet to be explored at a few tens of eV.

Furthermore, $\hbox {Li}_2\hbox {WO}_4$ is a very interesting material to monitor neutron backgrounds and could be used for the outer veto of NUCLEUS. The heavy element tungsten has a high attenuation power for $\gamma$-rays. Neutrons can be tagged using the neutron capture on $^6$Li which has a natural abundance of about 7.4%, allowing for an in-situ characterization of the neutron background [46]. The reaction $^6$Li $+$ n $\rightarrow$ $^3$H $+$ $^4$He, with an energy release of E $=$ 4.78 MeV $+$ $\hbox {E}_{\mathrm {n}}$, where $\hbox {E}_{\mathrm {n}}$ is the kinetic energy of the neutron, produces only heavy charged particles. The latter are well separated from electronic recoils ($\beta$, $\gamma$, $\mu$) by the reduced light signal. Thus, the identified $^{6}$Li neutron-capture events can be used to constrain the neutron rate and allow fast neutron spectroscopy. In order to increase the capture rate, isotopically enriched $^6\hbox {Li}_2\hbox {WO}_4$ may be used. Currently, techniques to grow large-sized $\hbox {Li}_2\hbox {WO}_4$ crystals as well as the possibility of enrichment are under investigation.

4 Muon-induced dead time considerations

To reach the required background level for NUCLEUS at a shallow experimental site, a compact passive shielding in combination with an efficient muon veto is compulsory (see Sect. 3.2.3). At the Earth’s surface the count rate of cosmic muons is $\sim$100 Hz/m$^2$ [26]. Hence, to avoid significant detector dead time the timing of the coincident events has to be sufficiently fast. While typical muon-veto panels feature pulse rise times $<1\,\upmu$s, pulses of cryogenic detectors as the one used for NUCLEUS are typically orders of magnitude slower, which makes the detector operation at shallow depth challenging.

4.1 Monte Carlo simulations of cosmic muons at the VNS

A MC simulation tool based on GEANT4 [47] was used to simulate cosmic muons at the VNS and to estimate an upper limit on the trigger rate of the muon veto. Muons are randomly generated on a plane tangent to a half-sphere centered at the detector whereas the distribution of the point of tangency follows the cos$^2\theta$-distribution of muons on the surface. The direction of the generated muons is parallel to the normal vector of the plane, pointing towards the detector.

To validate the MC simulations, a shielding configuration similar to the one used in the NUCIFER experiment [35] was simulated and the amount of simulated hits in the shield was compared to the published experimental data. The differential flux of incident atmospheric muons $\mathrm{d}\varPhi /\mathrm{d}E \mathrm{d}\varOmega$ is approximated according to an adapted Gaisser parametrization [48, 49]. For simplicity, only mono-energetic muons between 4.5 MeV and 450 GeV in logarithmic binning were simulated. The results were weighted according to the flux within the given energy range with respect to the total flux. The trigger rate of the muon veto is calculated by

$$\begin{aligned} \mathrm {R}\,=\,\frac{\mathrm {N}_{\mu }}{\mathrm {N}_{\mathrm {MC}}}\cdot 2\pi \cdot \varPhi _{\mu }\cdot \mathrm {A}\cdot \mathrm {a}_{\mu } \end{aligned}$$

(3)

where $N_\mathrm {MC}$ is the number of generated muons in the simulation, $N_\mu$ is the number of energy depositions in the muon veto (i.e. a muon trigger) which pass the 10 MeV threshold [35] of the NUCIFER experiment, $\varPhi _{\mu }$ $=$ $70/(\mathrm {sr} \,\mathrm {s}\,\mathrm {m}^{2})$ is the total muon flux at the surface [26], $A=(3.5\,\mathrm {m})^2$ is the surface of the plane where the muons are generated, and $a_\mu$ is the muon attenuation at the experimental site. In total $10^{4}$ muons were generated for each muon energy bin.

Table 2 summarizes the simulated muon-trigger rates in the NUCIFER set-up. The muon simulations with the simplified NUCIFER geometry yield a total muon-trigger rate of (535 ± 9) Hz, by taking into account a veto efficiency of 97% the trigger rate is reduced to (519 ± 9) Hz. The MC result is about 50% higher than the measured muon-trigger rate of 350 Hz [35]. This deviation may originate in the simplifications of the detector geometry, and in further unaccounted-for inefficiencies. It is believed that the applied approximations to the muon energy spectrum give the largest systematic uncertainty. The simulation assumes a uniform overburden of 12 m.w.e., and it does not account for any changes in the muon energy spectrum with respect to the surface. Furthermore, the rough binning may be over-simplified.

Table 2 Number of simulated muon triggers, $\hbox {N}_{\mu }$, for the NUCIFER experiment for different muon energies E. In total 10$^{4}$ muons were simulated for each energy. The weights are given within the logarithmic energy bin centered at the energy E with respect to the total flux. The total number of triggers is given by the weighted sum of the mono-energetic simulations

As the goal is to estimate an upper limit on the trigger rate for the actual NUCLEUS muon veto, a verified overestimation of 50% in the simulated trigger rate is not an obstacle. To estimate the muon rate, a simplified cubic geometry with six plates, i.e. at the top, bottom and four side faces, of equal size was implemented in the simulation tool. Each plate of the muon veto is made from standard PE ($\hbox {C}_2\hbox {H}_4$) with a density of 0.96 g/cm$^3$. For simplicity the generated muons have an energy of 4 GeV which corresponds to the mean energy of cosmic muons at the surface. For the muon attenuation, a uniform factor of $\hbox {a}_{\mu }$ $=$ 0.71 is assumed; see Sect. 2.2. No trigger threshold is applied, which is legitimate as only an upper limit on the trigger rate is estimated. The muon rate is calculated using Eq. (3). As seen in Fig. 9, the rate is proportional to the surface of the muon veto. For a shielding covering a volume of 1 m$^3$, as envisioned by NUCLEUS, the simulation yields an upper limit on the muon-trigger rate of (487 ± 38) Hz.

4.2 Estimation of muon-induced dead time

The overall detector dead time is governed by the timing of the cryogenic pulses, since the timing of the muon veto panels is orders of magnitude faster and, therefore, can be neglected. In the following, the pulse timing, i.e. the uncertainty $\sigma _\tau$ of the determination of the pulse’s onset is assumed to be proportional to the rise time. In cryogenic detectors, the rise time is given by the thermalization of the signal phonons at the surface of the absorber crystal, and is thus expected to scale roughly with the linear dimension of the target. The pulse rise time of the 0.5 g NUCLEUS detector prototype is $\tau _r\approx 300\,\upmu$s [37], significantly faster than CRESST-II detectors with a mass of 300 g and a typical rise time of several ms [50], and with other cryogenic detector technology.

For the estimation of the detector dead time, a time window of $\pm 5\sigma _\tau$ is defined around every event in the muon veto and removed from the total exposure time. For example, in the case of a cubic muon veto of 1 m side length with a count rate of $R=(487\,\pm \,38)$ Hz the pulse’s onset has to be determined with $\sigma _\tau \lesssim 20\,\upmu$s to restrict the dead time to $\lesssim 10\%$. The precision of the pulse onset of a fast cryogenic detector with a rise time of 100 $\upmu$s has been measured using a pulsed neutron beam from an accelerator in [51]. The uncertainty of the onset determination is $\sigma _\tau =(4.8\pm 0.4)\,\upmu$s corresponding to a time window of $48\,\upmu$s around every event in the muon veto to be removed from the exposure time.

Fig. 9

Simulated rate of incident muons with 4 GeV energy for a cubic muon veto at the VNS with varying edge length l. The rate shows a quadratic increase with the edge length (red line). Uncertainties are statistical only

Using the results of the dedicated MC simulation (see Sect. 4.1) for the muon count rate of different shielding dimensions, the resulting dead time can be calculated with respect to the side length of the cubic-shaped muon veto. Figure 10 shows the resulting dead time for a number of detector technologies with different pulse rise times. For a cryogenic bolometer of CRESST-II with a mass of 300 g, its slow signal implies a dead time above 10% even for small set-ups (red line in Fig. 10). For the existing NUCLEUS prototype detector, the dead time is predicted to be about 7% for a cubic muon veto of 1 m side length.

The rise time in NUCLEUS detectors can be influenced by changing the phonon collection area of the TES. A larger area leads to a quicker collection of signal phonons and thus a faster pulse rise time. For the NUCLEUS experiment, a rise time of 100 $\upmu$s is envisioned. Under these conditions, the dead time, e.g. for a cubic-shaped muon veto of 1 m side length, is about 2% and stays below 10% even for a dimension of (2 m)$^3$.

5 Background studies

A detailed background model of the detectors is crucial to obtain a realistic sensitivity projection for the NUCLEUS experiment. Dedicated simulations on muon-induced and atmospheric neutrons have been performed in the framework of this work, based on the preliminary set-up presented in Sect. 3.2.3. Furthermore, previous work on external gammas, surface and detector-intrinsic backgrounds, as well as an estimation for reactor-correlated backgrounds are included in the study. Table 3 summarizes the different background contributions to the region-of-interest (ROI) defined between 10 eV and 1 keV. The count rates of the considered background sources are well below our benchmark background model of 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$), which shows that the sensitivity study presented in Sect. 6 is based on conservative assumptions. The choice of the benchmark background appears to be conservative also when being compared to results from neutron measurements performed by the TEXONO collaboration at a nuclear power reactor [34].

Fig. 10

Detector dead time vs. dimension of the cubic-shaped muon veto. The lines indicate the predicted values for the NUCLEUS prototype detector (300 $\upmu$s rise time, blue line) and a CRESST-II detector (1.3 ms rise time, red line) based on TES technology. The relation between rise time and timing uncertainty is taken from a neutron beam coincidence measurement (see text). For comparison, expected dead times of slower detectors with 5 ms rise time (black dashed line) and 10 ms rise time (black dotted line), as well as a NUCLEUS detector with an envisioned rise time of 100 $\upmu$s (blue dashed line) are shown

The study presented in the following is a first evaluation of the expected NUCLEUS background. This section concludes that muon-induced neutrons generated in the passive shielding are the dominant background source for the NUCLEUS experiment.

5.1 Atmospheric neutrons

The contribution of atmospheric neutrons on the overall background level of the NUCLEUS detectors has been investigated with a dedicated GEANT4 MC simulation. Although neutron measurements suggest a reduction of the neutron flux at the VNS by a factor of $8.1\pm 0.4$ (see Sect. 2.3), the neutron flux at surface level as measured in [52] is considered here in order to be conservative.

In a first step the neutrons are shot onto bare $\hbox {CaWO}_{4}$ and $\hbox {Al}_{2}\hbox {O}_{3}$ crystals of size ($5\times 5\times 5$) mm$^3$ as foreseen for NUCLEUS-10g. For the energy regions between 10 eV and 1 keV, the simulation yields a background count rate of $3\,\times \,10^{3}$ counts/($\hbox {kg}\,\hbox {day}$) for both targets. Introducing the preliminary NUCLEUS shielding with 10 cm of borated (5%) PE and 5 cm of Pb reduces the flux by more than four orders of magnitude. This results in a background rate of $6\,\times \,10^{-2}$ counts/($\hbox {kg}\,\hbox {day}$) for $\hbox {CaWO}_{4}$(similar values for $\hbox {Al}_{2}\hbox {O}_{3}$). Compared to the other background rates shown in Table 3, the contribution from atmospheric neutrons is expected to be negligible for NUCLEUS.

5.2 Muon-induced neutrons

To study muon-induced neutron production in the shielding surrounding the detectors, atmospheric muons were simulated according to Sect. 4.1. The muons are propagated through the preliminary NUCLEUS passive shielding of PE and lead (see Sect. 3.2.3). The induced secondary neutrons are further shot onto the full NUCLEUS target detector, consisting of the outer veto, the inner veto and the $\hbox {CaWO}_{4}$ and $\hbox {Al}_{2}\hbox {O}_{3}$ target detector arrays (see Sect. 3.2). Conservatively, no overburden and thus no attenuation of the surface muon flux is considered.

Assuming a muon-veto efficiency of 99%, as aimed for by NUCLEUS, the muon-induced neutron background can be reduced up to two orders of magnitude to a level of $\lesssim 1$ counts/($\hbox {kg}\,\hbox {day}$). Despite being the dominant external background source, muon-induced neutrons can be reduced to values well below the benchmark background rate of 90 counts/($\hbox {kg}\,\hbox {day}$) all over the ROI.

Table 3 Expected integral background count rates in $\hbox {CaWO}_{4}$ and $\hbox {Al}_{2}\hbox {O}_{3}$ in the energy regions 10–100 eV and 100 eV–1 keV for muon-induced neutrons, atmospheric neutrons, external $\gamma$-rays, and surface backgrounds. For muon-induced and atmospheric neutrons a preliminary shielding configuration (see Sect. 3.2.3) has been considered. The background count rate for muon-induced neutrons is given after outer- and inner-cryogenic veto, and anti-coincidence cut of the NUCLEUS detector array. For the muon veto an efficiency of 99% is assumed. The background rate from external $\gamma$-rays has been determined only for $\hbox {CaWO}_{4}$ crystals in the ROI, while for surface events the MC simulations were performed with a $\hbox {Al}_{2}\hbox {O}_{3}$ NUCLEUS array. The benchmark background is the background count rate used in the sensitivity studies presented in Sect. 6. The $\hbox {CE}\nu \hbox {NS}$ signal count rate is calculated for the nominal reactor power. See text for details

5.3 External $\gamma$-rays

In a previous publication [13], the background contribution originating from external gammas in a shallow underground laboratory has been studied by a MC simulation. The gamma background spectrum as measured in the Dortmund Low Background Facility [29], which has a shielding configuration and location comparable to that planned for NUCLEUS, has been propagated through the full NUCLEUS detector (including active outer and inner vetoes). Due to the high rejection power of the active outer veto made of a $\hbox {CaWO}_{4}$ crystal (see Sect. 3.2.1), the gamma rate is expected to be reduced to $\lesssim 1\,\, \times \,\,10^{-3}$ counts/($\hbox {kg}\,\hbox {day}$) in the ROI of NUCLEUS, completely negligible with respect to the neutron backgrounds studied above.

5.4 Surface events

The background contribution due to surface events originating from radioactive isotopes implanted in the direct vicinity of the NUCLEUS detector have been studied for NUCLEUS in a previous work [13]. The detector configuration is similar to the one described in Sect. 5.3 using inner and outer cryogenic veto detectors. Typically, decays of isotopes following the implantation of Rn from the air are a dominant source of surface radiation (see Sect. 3.1). For example an activity of 1 counts/($\hbox {kg}\,\hbox {day}$), a value measured with typical low-background CRESST detectors [53], of the beta-emitter $^{210}$Pb is considered on the surface directly surrounding the NUCLEUS detectors. Since these surfaces, i.e. the inner-cryogenic veto, are fully active (see Sect. 3.2.1), a significant part of the beta decays can be rejected. The simulation results in a remaining surface background rate of $\lesssim 1\,\, \times \,10^{-2}$ counts/($\hbox {kg}\,\hbox {day}$) in the ROI, again being negligible compared to neutron backgrounds.

5.5 Intrinsic background of $\hbox {CaWO}_4$ crystals

The intrinsic background of $\hbox {CaWO}_4$ crystals has been studied in great detail for the CRESST experiment [53, 54]. Decay rates of beta/gamma-emitters from natural decay chains are determined by measuring the intrinsic alpha activities of the crystals. This analysis is subsequently combined with a MC simulation to estimate the background rate in the energy region below 40 keV. Extrapolating the results down to energies below 1 keV, the studies yield a (flat) background rate of $\lesssim 2$ counts/($\hbox {keV } \hbox {kg } \hbox {day}$) below 1 keV for typical $\hbox {CaWO}_4$ crystals. The total rate is well below the NUCLEUS benchmark background of 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) and in the same order of magnitude as the muon-induced neutron background after muon veto. However, due to its flat shape, the intrinsic background is well distinguishable from the exponential rising neutron background. Therefore, at low energies, muon-induced neutron background is expected to dominate.

5.6 Cosmogenic activation of $\hbox {CaWO}_4$ crystals

The hadronic component of the cosmic radiation can cause an activation of target materials which may lead to successive decays. In the case that long-lived decay products emit particles of low energies, cosmogenic activation may contribute significantly to the background in the ROI of NUCLEUS. For $\hbox {CaWO}_4$ so far only isotopes that are produced by proton capture on tungsten isotopes and that are decaying by electron capture (EC) have been identified (see [53] for details). These decays are visible as distinct gamma lines exactly at the energies of the shell electrons of the daughter isotopes in the EC process (extending to below 1 keV), therefore, clearly distinguishable from the exponentially falling $\hbox {CE}\nu \hbox {NS}$ signal. Since cosmogenic activation depends on the individual history of the crystal, special care is taken for the storage of NUCLEUS crystals.

5.7 Reactor-correlated neutrons

The expected reactor-correlated fast neutron background at the VNS is estimated referring to the results obtained with the NUCIFER [35] experiment, a project designed for online monitoring of nuclear reactors. The NUCIFER detector was based on Gd-loaded liquid scintillator and was operated 7.2 m from the core of the Osiris research reactor (70 MW) in Saclay, France. The estimated neutron elastic scattering rate on hydrogen in the whole NUCIFER target volume was $4\,\, \times \,\,10^{-5}\,\mathrm{events}/(\mathrm{day})$ for energies above 2 MeV [35]. Scaling this result to the relevant parameters of NUCLEUS, i.e. reactor power of 2$\, \cdot \,$4.25 GW$_{\mathrm{th}}$, distance of 72 m between the detector and the core, and assuming the same scattering cross-section on each nuclide of $\hbox {CaWO}_4$ as on hydrogen, indicates that the neutron background from the reactor core is negligible.

6 Sensitivity of NUCLEUS to $\hbox {CE}\nu \hbox {NS}$ at the VNS

The NUCLEUS experiment will proceed in a staged approach, as presented in Sect. 3.2: a first phase called NUCLEUS-10g, and an upgrade called NUCLEUS-1kg. At the VNS, with distances of 72 m and 102 m to the two 4.25 $\hbox {GW}_\mathrm {th}$ cores of the CHOOZ nuclear power plant, NUCLEUS-10g will observe 0.33 (0.03) $\hbox {CE}\nu \hbox {NS}$-induced nuclear-recoil events per day above 10 eV in the $\hbox {CaWO}_{4}$ ($\hbox {Al}_{2}\hbox {O}_{3}$) array. The high $\hbox {CE}\nu \hbox {NS}$ rate in the $\hbox {CaWO}_4$ array, induced by the large tungsten nuclei, allows for a fast discovery of $\hbox {CE}\nu \hbox {NS}$ at the VNS. The strongly suppressed $\hbox {CE}\nu \hbox {NS}$ rate in the $\hbox {Al}_2\hbox {O}_3$ array provides an effective “neutrino-off” reference spectrum, which is of great advantage in the case of an unknown background shape, as discussed in Sect. 6.3.

Although Sect. 5 suggest that the expected background is of the order of $10^{-1}$, the following sensitivity studies use the benchmark background of 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) to be conservative.

Fig. 11

Statistical significance of $\hbox {CE}\nu \hbox {NS}$ observation as a function of live time for NUCLEUS-10g, for different background indices, using the expected neutrino flux at the VNS and an energy threshold of 10 eV. For each background index, the median line and 90% probability bands (computed from 600 simulated random spectra at each point) are shown. For the background index of 10 counts/($\hbox {keV } \hbox {kg } \hbox {day}$), only the median line is shown for clarity

6.1 Sensitivity of NUCLEUS-10g for different flat backgrounds

The results of a sensitivity study for NUCLEUS-10g, similar to the sensitivity study of Reference [13], are shown in Fig. 11 for different background indices. For each background index and exposure time, 600 random spectra with a flat background and the Standard Model $\hbox {CE}\nu \hbox {NS}$ expectation at the VNS are generated for the two target materials $\hbox {CaWO}_{4}$ and $\hbox {Al}_{2}\hbox {O}_{3}$ in the energy range from 10 eV to 2 keV. To each pair of spectra, a flat-background-plus-$\hbox {CE}\nu \hbox {NS}$ signal strength model (”free model“) and a flat-background-only model (“null model”) are fit. The “null model” has only one free parameter, the flat-background rate, which is common to both target materials. The “free model” has one additional parameter, the signal normalization, for which a value of 1 corresponds to the Standard Model $\hbox {CE}\nu \hbox {NS}$ expectation in each target material. The ratio of the maximum likelihood for these nested models ($\mathscr {L}_\mathrm {free}$ and $\mathscr {L}_\mathrm {null}$ respectively) is converted to a significance of $\hbox {CE}\nu \hbox {NS}$ observation using $Z = \sqrt{2 \log (\mathscr {L}_\mathrm {free} / \mathscr {L}_\mathrm {null})}$. The median, 5$\mathrm {th}$ and 95$\mathrm {th}$ percentile of the resulting Z distribution are used to draw the color bands (corresponding to a 90% probability interval).

For the most pessimistic background index of 1000 counts/($\hbox {keV } \hbox {kg } \hbox {day}$), the signal rate in $\hbox {CaWO}_{4}$ exceeds the background rate only close to the assumed energy threshold of 10 eV, so that long exposures are necessary to distinguish the contributions by spectral shape. Below around 10 counts/($\hbox {keV } \hbox {kg } \hbox {day}$), the experiment is background-free over most of the region of interest, so that the necessary live time becomes limited by signal statistics.

For a benchmark background rate of 100 counts/($\hbox {keV } \hbox {kg}\, \hbox {day}$), a 5$\sigma$ observation of $\hbox {CE}\nu \hbox {NS}$ at VNS can be achieved in less than 40 days of measurement time.

6.2 Achievable precision of NUCLEUS-10g and -1kg

As an absolute-rate experiment with the goal of studying the $\hbox {CE}\nu \hbox {NS}$ cross-section, NUCLEUS has to rely on reactor neutrino flux predictions which will contribute a significant systematic uncertainty to the measurement. At energies above the IBD threshold, the reactor anti-neutrino spectrum is modeled with an uncertainty of 2–3% [55, 56]. As nuclear recoils on tungsten induced by neutrinos below the IBD threshold extend up to 38 eV in nuclear-recoil energy, NUCLEUS has the potential to become sensitive to this as yet unobserved low-energy part of the spectrum. An effort to predict the fluxes of reactor anti-neutrinos below the IBD threshold is thus necessary to interpret the NUCLEUS data at these lowest recoil energies.

Assuming a flat background of 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) and an energy threshold of 10 eV, the statistical precision achievable with NUCLEUS-10g after one year is 11%. Therefore, NUCLEUS-10g is expected to be limited by statistics over its complete measurement time. On the contrary, for NUCLEUS-1kg (with an assumed improved background index of 1 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) and an energy threshold of 4 eV) the achievable statistical precision with one year of data is 0.64%, so that this stage of the experiment will be limited by systematics early on in the measurement campaign.

Fig. 12

Relative precision of the $\hbox {CE}\nu \hbox {NS}$ cross-section measurement as a function of live time for the experimental stages NUCLEUS-10g (composed of $\hbox {CaWO}_{4}$ and $\hbox {Al}_{2}\hbox {O}_{3}$ detectors), and NUCLEUS-1kg (modeled as a Ge detector array). The solid lines show statistical uncertainties (one standard deviation) only, for the dashed lines a systematic uncertainty of 10% (1%) is added in the case of NUCLEUS-10g (NUCLEUS-1kg). The dotted horizontal line indicates the 32% precision achieved by COHERENT (adding in quadrature the 16% experimental uncertainty and the 28% uncertainty of the rate prediction [5])

Figure 12 shows the precision (one standard deviation) on the $\hbox {CE}\nu \hbox {NS}$ cross-section achievable by NUCLEUS, compared to the best current precision achieved by COHERENT [5] (black dashed line). For NUCLEUS-10g (blue), the solid line shows statistical precision only, while the dashed line adds a 10% systematical uncertainty in quadrature. NUCLEUS-10g can approach the expected systematic limit within few years of live time. The continuous green line in Fig. 12 shows the statistical precision achievable with a 1 kg Ge target at the VNS. Adding an optimistic 1% systematical uncertainty (dashed green line) shows that NUCLEUS-1kg can reach a percent-level measurement of the $\hbox {CE}\nu \hbox {NS}$ cross-section within few years of measurement time. The final precision on the $\hbox {CE}\nu \hbox {NS}$ cross-section that can be reached by NUCLEUS-1kg depends strongly on the control of systematics, such as neutrino flux normalization, precise knowledge of the energy scale and modeling of backgrounds.

6.3 NUCLEUS-10g in the case of a non-flat background

Since NUCLEUS is aiming to measure a signal in a previously unexplored energy range in a radiogenically challenging environment, assuming a flat background down to threshold may well be overly optimistic. Accepting a background model with a free shape parameter drastically reduces the detection significance in a single target material, as the signal can then also be fit reasonably well with the background-only model.

The multi-target approach of NUCLEUS-10g (i.e. deploying $\hbox {CaWO}_4$ as well as $\hbox {Al}_2\hbox {O}_3$ target arrays) has the potential to mitigate the impact of a background of unknown shape. While the $\hbox {CE}\nu \hbox {NS}$ signal in $\hbox {Al}_{2}\hbox {O}_{3}$ is more than an order of magnitude below the one in $\hbox {CaWO}_4$ (see Fig. 1), first MC simulations show that the background count rate of muon-induced neutrons in $\hbox {Al}_{2}\hbox {O}_{3}$ are compatible to the one of $\hbox {CaWO}_{4}$ in the ROI of NUCLEUS (see Table 3). Furthermore, below 200 eV, i.e. the region where the $\hbox {CE}\nu \hbox {NS}$ signal is most prominent, the two background spectra agree better than 20%. Assuming for simplicity an identical appearance of backgrounds in $\hbox {Al}_{2}\hbox {O}_{3}$ and $\hbox {CaWO}_{4}$ allows one to study the power of this multi-target approach in NUCLEUS-10g. To demonstrate the advantage of combining materials with different expected $\hbox {CE}\nu \hbox {NS}$ signal strength, a scenario is considered here in which the background is non-flat and, more importantly, of unknown shape.

As a simple non-flat-background model an exponential + flat model with the functional form $R(E)=C+A\, \mathrm {e}^{-E/B}$ is considered, where C is the flat-background rate, A is the amplitude and B is the slope of the exponential. Changing the slope of the exponential background while keeping the total integral fixed and the flat-background level constant at 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$), shows the strongest impact on the sensitivity of NUCLEUS-10g after one year to occur for a slope of around 45 eV. Therefore, to be conservative, a background of this slope is chosen for the non-flat scenario. An amplitude of 1500 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) is set for the exponential background (see Fig. 13) so that the background level is higher than the signal rate at all observed energies. In this scenario, there are 120 (636) $\hbox {CE}\nu \hbox {NS}$ (background) interactions in the 6 g $\hbox {CaWO}_{4}$ array expected between 10 eV and 2 keV within one year. In the 4 g $\hbox {Al}_{2}\hbox {O}_{3}$ array, these numbers change to 12 (415) $\hbox {CE}\nu \hbox {NS}$ (background) interactions.

Fig. 13

Comparison of $\hbox {CE}\nu \hbox {NS}$ recoil spectra and background models discussed in Sect. 6 in the context of NUCLEUS-10g. The flat background of 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) taken as a benchmark model in Sect. 6.1 is well above $\hbox {CE}\nu \hbox {NS}$ on $\hbox {Al}_{2}\hbox {O}_{3}$, while the $\hbox {CaWO}_{4}$ recoil spectrum rises above it below 110 eV. The exponential background model (see text) with an amplitude of 1500 counts/($\hbox {keV } \hbox {kg } \hbox {day}$) and a slope of 45 eV is similar in shape and normalization to the $\hbox {CaWO}_{4}$ $\hbox {CE}\nu \hbox {NS}$ signal, therefore it is adopted for the study of NUCLEUS-10g with a non-flat background in Sect. 6.3 (see text)

The $\hbox {CaWO}_{4}$ spectrum alone is fit nearly equally well by both the (three parameter) background-only model and the (four parameter) model including the signal. Thus no sensitivity to the $\hbox {CE}\nu \hbox {NS}$ cross-section can be derived from $\hbox {CaWO}_{4}$ alone. The simultaneous fit of both spectra uses the same background model in both materials (three parameters) and the SM $\hbox {CE}\nu \hbox {NS}$ expectation for each material scaled by a common strength parameter. In this way, the $\hbox {Al}_{2}\hbox {O}_{3}$ array helps constraining the background rate and shape, so that an expected preference for the background $+$ $\hbox {CE}\nu \hbox {NS}$ model of more than 4 $\sigma$ can be extracted after 1 year.

This result shows the crucial advantage of the multi-target approach: the sensitivity is significantly improved even without any prior knowledge of the background shape (apart from the flat $+$ exponential parameterization). Even in the case of a background with a signal-like shape and strength, $\hbox {CE}\nu \hbox {NS}$ becomes observable through its characteristic dependence on the nuclear composition of the target. This advantage is complementary to the traditional concept of particle identification, i.e. distinction of electron recoil and nuclear-recoil events. While the multi-target approach is statistical only, it can be used to constrain neutron background which features an identical experimental signature as $\hbox {CE}\nu \hbox {NS}$, i.e. a nuclear recoil, but a distinct dependence on the nuclear composition of different materials.

7 Conclusion

The VNS at the Chooz nuclear plant is a promising new experimental site for the planned $\hbox {CE}\nu \hbox {NS}$ experiment NUCLEUS. The site is located in close distance to the two 4.25 $\hbox {GW}_{\mathrm {th}}$ reactor cores of the Chooz nuclear power plant in France, providing an anti-neutrino flux of $3\,\, \times \,10^{12}~\overline{\nu }/(\mathrm {s}\cdot \mathrm {cm}^2 )$. First muon-attenuation measurements on-site indicate a shallow overburden of about 3 m.w.e. at the VNS.

The NUCLEUS detector concept provides a suitable technology for a new-generation $\hbox {CE}\nu \hbox {NS}$ experiment at the VNS. Thanks to its unprecedentedly low-energy threshold of $\le ~20~\mathrm {eV}$, a strong $\hbox {CE}\nu \hbox {NS}$ signal is expected which allows a significant miniaturization of the detector size. Dedicated MC simulations show that the muon-induced dead time is expected to stay well below 10%, given the fast rise time of the NUCLEUS detectors. The small size of the target detectors and the envisioned compact set-up, which consists of passive and active shielding material, greatly reduce the overall size of the experiment matching the space constraints of the VNS. Using active and passive background reduction techniques, the NUCLEUS experiment aims to reach a background count rate of $\le$ 100 counts/($\hbox {keV } \hbox {kg } \hbox {day}$).

In the first phase of the experiment, NUCLEUS-10g aims at a first observation of $\hbox {CE}\nu \hbox {NS}$ at a nuclear reactor with a total target mass of 10 g. Due to the demonstrated threshold in the 10 eV regime, NUCLEUS will probe the reactor anti-neutrino spectrum for the first time below 1.8 MeV—below the threshold of inverse beta decay. The reach of NUCLEUS strongly depends on the achieved background level at low energy. NUCLEUS-10g will explore this background for the first time at energies below 100 eV and at shallow overburden. A statistical analysis shows that $\hbox {CE}\nu \hbox {NS}$ can be observed within two weeks of live time assuming our benchmark background model. Even in a scenario in which shape and rate of the background are similar to that of the $\hbox {CE}\nu \hbox {NS}$ signal, NUCLEUS-10g reaches a sensitivity of more than 4$\sigma$ for $\hbox {CE}\nu \hbox {NS}$ after one year of measuring time. NUCLEUS-10g, which is expected to take data from 2021 on, has the potential to achieve a final precision of $\sim$10% on the $\hbox {CE}\nu \hbox {NS}$ cross-section.

The second phase, NUCLEUS-1kg, is planned for commissioning in 2023 and aims for precision measurements of the $\hbox {CE}\nu \hbox {NS}$ cross-section at a level of 1%. Harnessing the full potential of NUCLEUS-1kg requires a significant reduction of systematic uncertainties. Particularly, to take advantage of the achievable statistical precision, an improved prediction of the reactor anti-neutrino spectrum is needed. This opens the door for the study of physics beyond the Standard Model of particle physics such as the search for non-standard neutrino interactions, the electro-magnetic properties of neutrinos or exotic neutral currents, as well as a test of the reactor anti-neutrino anomaly [57].

NUCLEUS will demonstrate a new detector technology with ultra-low thresholds and allow to study fundamental properties of the neutrino, pushing the low-energy frontier in neutrino observations.