1 Introduction

One of the most fascinating phenomena which cosmology has encountered so far is the expansion of the universe. It has become a source of information about the nature and composition of the universe. Observational data has confirmed that currently universe is undergoing a phase of acceleration [1,2,3,4]. But the source of this acceleration is still a challenge in cosmology, to identify this ambiguous source many suggestions have been put forward [5, 6]. Untill yet the existence of dark energy (DE) is the most significant cause for this expansion. Dark matter (DM) is another dark component of the universe that leaves impression on astrophysical observations. DM plus DE both compose 95 percent of energy -matter content of the universe.

Many theoretical ideas have been suggested to explore the nature and origin of the dark energy, they include the cosmological constant, modified matter models, modified gravity models. An appealing idea that the DM and DE both demonstrate a single dark component leads to the unified models of dark energy and dark matter. These type of models are referred to as quintessence [7, 8]. Chaplygin gas model is also a unified model of dark matter and dark energy [9]. Chaplygin gas behaves as dark matter in early times and dark energy in late times. Different unified models using chaplygin gas have been suggested such as modified chaplygin gas model [10, 11], hybrid chaplygin gas [12]. The relationship between the perfect fluid model and the speed of sound has been used in [37]. The unified DE-DM with scalar fields are discussed in [14, 15].

Historically, fractal cosmology was first discussed by Andrew linde [16]. His theory describes that evolution of the scalar fields creates peaks which results in making universe fractal on a very large scale. The recent theories of quantum gravity has a profound connection with fractal cosmology , according to these theories dimensionality of space evolves with time. Calcogni [17, 18] studied quantum gravity in the framework of fractal universe, he formulated a power counting renormalizable field theory which exists in fractal space time and without ultraviolet divergence. In this scenario near the two topological dimensions, the renormalizability of perturbative quantum gravity theories draw attention to \(D = 2+\epsilon \) models which can improve the understanding of four dimensions \(D = 4\) [19,20,21]. Fractal characteristics of quantum gravity in D dimension, for \(D = 3\) and \(D < 3\) are investigated in [22,23,24].

It is worthwhile to understand this universe in the context of fractal cosmology. Various dark energy models have been proposed in this framework. Lemets et al. [25] presented the main aspects for the fractal cosmology models. They discussed the model with the interaction of DE and DM. A generalized HDE model [26] and a ghost dark energy model [27] and nonlinear interacting dark energy [28] are discussed. Furthermore, thermodynamic features of apparent horizon are studied in [29] and fractal analysis with the distribution of galaxies is investigated in [30]. The goal of the present work is to discuss the cosmic acceleration in the framework of fractal cosmology. This paper is organized in the following way. In the second section, basics of fractal cosmology are focused, the third section contains the discussions of a barotropic fluid defined in terms of speed of sound and the models with the constant and variable forms of squared speed of sound. In the fourth section, cosmological parameters are investigated. The fifth section closes paper with concluding remarks.

2 Basics of fractal universe

Let us consider an isotropic and homogeneous FLRW model of the universe. In fractal cosmology, it is required that space and time coordinates scale isotropically. The standard measure in the action of fractal space time is replaced by a non trivial measure, which comes in Lebesgue stieltjes integrals. We assume that gravity and matter are minimally coupled in the fractal universe. The total action is written as [17, 18, 31]

$$\begin{aligned} S=S_G+S_m. \end{aligned}$$
(1)

The gravitational part of the action is given by

$$\begin{aligned} S_G = \frac{1}{16\pi G}\int d\varrho (x)\sqrt{-g}(R-2\Lambda -\xi \partial _\mu \nu \partial ^\mu \nu ), \end{aligned}$$
(2)

while, the action of of the matter part is

$$\begin{aligned} S_m= \int d\varrho (x)\sqrt{-g}L_m, \end{aligned}$$
(3)

where \(\xi \) is the fractal parameter and \(\nu \) is the fractal function and g is the determinant of the metric \(g_{\mu \nu }\). The cosmological constant and Ricci scalar are denoted by \(\Lambda \) and R respectively. \(L_m\) indicate lagrangian density of matter field. The variation of Eq. (1) with respect to \(g_{\mu \nu }\) gives Friedmann equation as follows

$$\begin{aligned} H^2+\frac{k}{a^2}+H\frac{\dot{\nu }}{\nu } -\frac{\xi }{6}\dot{\nu ^2}=\frac{8\pi G}{3}\rho +\frac{\Lambda }{3}, \end{aligned}$$
(4)

where \(H=\frac{\dot{a}}{a}\) is the Hubble parameter and \(\rho \) is the energy density. Equation of continuity in the fractal universe takes the following form [17, 18]

$$\begin{aligned} \dot{\rho }+\left( 3H+\frac{\dot{\nu }}{\nu }\right) (\rho +p)=0. \end{aligned}$$
(5)

The fractal function is either timelike or spacelike. By plugging a timelike fractal function i.e. \({\nu } = a^{-\gamma }\) and \(\dot{\nu }=-\gamma a^{-\gamma -1}\dot{a}\) in Eq. (4) the Hubble parameter is expressed as

$$\begin{aligned} H^2=\frac{8\pi G}{3}\bigg (\frac{\rho }{1-\gamma -\frac{\gamma ^2}{6}\xi (1+z)^{2\gamma }}\bigg ), \end{aligned}$$
(6)

and Eq. (5) takes the following form

$$\begin{aligned} \dot{\rho }+(3-\gamma )H(\rho +p)=0. \end{aligned}$$
(7)

Here, we choose the curvature constant as \(k=0\) for the flat universe, \(\Lambda =0\) and \(z=-1+\frac{1}{a}\) and dot denotes the derivative w.t.t time.

3 Models of squared speed of sound

The equation of state (EoS) of barotropic fluid relates the pressure and density, so it can be implicitly expressed as

$$\begin{aligned} G(\rho ,p)=0. \end{aligned}$$
(8)

The EoS parameter \(w=\frac{p}{\rho }\) is utilized to replace pressure so the Eq. (8) is rewritten as \(F(\rho ,w)=0\) and hence \( G(\rho ,w)=F(\rho ,p)\). We can consider the density \(\rho =\rho (w)\) and pressure \(p=p(w)=w\rho (w)\) as functions of w. Further the inversion of the relation \(F(\rho ,w)=0\) implies that various solutions for p(w) and \(\rho (w)\) can be found, especially for some values of w there might be several values of \(\rho (w)\). In barotropic cosmic fluid, the squared speed of sound (\( c^2_s\)) is defined as

$$\begin{aligned} c^{2}_{s}=\frac{d p}{d\rho }. \end{aligned}$$
(9)

By taking differential of Eq. (8) we have

$$\begin{aligned} \frac{\partial G}{\partial \rho }d \rho +\frac{\partial G}{\partial p}d p=0, \end{aligned}$$
(10)

which leads to

$$\begin{aligned} c^{2}_{s}=-\frac{\frac{\partial G}{\partial \rho }}{\frac{\partial G}{\partial p}}. \end{aligned}$$
(11)

We insert the expression \(p=w\rho \) in Eq. (10) and use Eq. (11) to obtain

$$\begin{aligned} \frac{d\rho }{\rho }=\frac{d w}{c^2_s-w}, \end{aligned}$$
(12)

by combining Eqs. (12) and (7), we get

$$\begin{aligned} d\rho +(3-\gamma )(1+w)\rho \frac{da}{a}=0, \end{aligned}$$
(13)

further, it is transformed as

$$\begin{aligned} \frac{dw}{(c^2_s-w)(1+w)}=(3-\gamma )\frac{dz}{1+z}. \end{aligned}$$
(14)

As we know that the \(\rho \) and p are the functions of w so the speed of sound \(c^2_s\) can also be considered as functions of w i.e. \(c^2_s=c^2_s(w)\).

$$\begin{aligned} c^{2}_{s}=\frac{d p}{d \rho }=\frac{\frac{d p}{d w}}{\frac{d \rho }{d w}}. \end{aligned}$$
(15)

Therefore, the dynamics of equation of state parameter w is governed by the Eq. (14). Moreover, the characteristics of the solutions of Eq. (14) is based on the zeros of function \(c^2_s(w)-w\), especially EoS parameter w(z) is restricted to intervals fixed by the zeros of \(c^2_s(w)-w\) and \(w=-1\). Speed of sound as function of EoS parameter \(c^2_s(w)\) can plays an important role in modeling a cosmic fluid as unified dark mater and dark energy because according to the definition of \(c^2_s\) there are some constraint on its value such as it should be positive and smaller than the squared speed of light. Due to these limitations this sort of modeling becomes more suitable. some models with variable speed of sound are discussed in literature [33,34,35,36]. In the following, we discuss the models with some specific forms of \(c^2_s\).

3.1 Model 1 with constant speed of sound

A constant speed of sound is being discussed in [37]. see also [38,39,40,41]. Integration of Eq. (14) with \(c^2_s= constant\) generate the parameter of EoS as

$$\begin{aligned} w_1=\frac{c^{2}_{s} \frac{1+w_o}{c^{2}_{s}-w_o}(1+z)^{(3-\gamma ) (1+c^2_s)}-1}{\frac{1+w_o}{c^{2}_{s}-w_o}(1+z)^{(3-\gamma )(1+c^2_s)}+1}. \end{aligned}$$
(16)

By integrating Eq. (12), we get the following relation

$$\begin{aligned} \rho =\rho _o\frac{c^2_s-w_o}{c^2_s-w}, \end{aligned}$$
(17)

and

$$\begin{aligned} p= c^2_s\rho -\rho _o(c^2_s-w_o), \end{aligned}$$
(18)

where \(w(0)=w_o\), we put the value of w in Eqs. (17) and (18) to obtain density and pressure as

$$\begin{aligned} \rho _1=\rho _o\frac{c^2_s-w_o}{1+c^2_s} \bigg (\frac{1+w_o}{c^2_s-w_o}(1+z)^{(3-\gamma )(1+c^2_s)}+1\bigg ), \end{aligned}$$
(19)
$$\begin{aligned} p_1=\rho _o \frac{c^2_s-w_o}{1+c^2_s}\bigg (c^2_s\frac{1+w_o}{c^2_s-w_o}(1+z)^{(3-\gamma )(1+c^2_s)}-1\bigg ),\nonumber \\ \end{aligned}$$
(20)

consequently, we have

$$\begin{aligned} p_1+\rho _1=\rho _o(1+w_o)(1+z)^{(3-\gamma )(1+c^2_s)}. \end{aligned}$$
(21)

3.2 Models with power law form \(c^2_s=\alpha (-w)^\beta \)

Now consider a general parametrization

$$\begin{aligned} c^2_s=\alpha (-w)^\beta , \end{aligned}$$
(22)

it is required to solve Eq. (14) numerically to obtain \(w=w(z)\). However analytic solution is also possible for some particular values of \(\alpha \) and \(\beta \). From the definition we have

$$\begin{aligned} c^2_s=\frac{d p}{d\rho }=\alpha \left( -\frac{p}{\rho }\right) ^\beta , \end{aligned}$$
(23)

for \(\beta \ne 1\), we readily obtains

$$\begin{aligned} \rho =\rho _o\bigg [\frac{\alpha +(-w_o)^{1-\beta }}{\alpha +(-w_o)^{1-\beta }}\bigg ]^\frac{1}{1-\beta }, \end{aligned}$$
(24)

for \(\beta =1\), the equation of state becomes

$$\begin{aligned} p=A\rho ^{-\alpha }. \end{aligned}$$
(25)

The result (25) shows that for \(\beta =1\), the parametrization in Eq. (22) is equivalent to the generalized chaplygin gas, whereas the EoS of chaplygin gas is reproduced for \(\beta =1,~\alpha =1\). One can solve Eq. (14) analytically for \(\beta =2\) and \(\alpha \ne -1\) and present in a closed form as

$$\begin{aligned} \frac{w_0}{w}\bigg (\frac{w+1}{w_0+1}\bigg )^{\frac{1}{\alpha +1}}\bigg (\frac{w-\frac{1}{\alpha }}{w_o-\frac{1}{\alpha }}\bigg )^ {\frac{\alpha }{\alpha +1}}=(1+z)^{(3-\gamma )}. \end{aligned}$$
(26)

3.2.1 Model 2

For an explicit expression of Eos parameter, we take a special case \(\alpha =1\) and Eq. (26) yields

$$\begin{aligned} w_2= & {} -\frac{1}{\sqrt{1+\frac{1-w^2_{o}}{w^2_{o}}(1+z)^{6-2\gamma }}}, \end{aligned}$$
(27)

furthermore, density and pressure takes the following form

$$\begin{aligned} \rho _2= & {} (-w_o\rho _o)\frac{1+\sqrt{{1+\frac{1-w_{o}^{2}}{w_{o}^{2}}}(1+z)^{6-2\gamma }}}{-w_{o}+1}, \end{aligned}$$
(28)
$$\begin{aligned} p_2= & {} \rho _ow_o\frac{1+\frac{1}{\sqrt{1+\frac{1-w^2_{o}}{w^2_{o}}(1+z)^{6-2\gamma }}}}{-w_{o}+1}. \end{aligned}$$
(29)

3.2.2 Model 3

Next by inserting \(\alpha =-\frac{1}{2}\) in Eq. (26), we obtain Equation of state parameter as

$$\begin{aligned} w_3=-1+\frac{1}{\sqrt{1+\frac{1-(w_o+1)^2}{(w_o+1)^2} (1+z)^{-({3-\gamma })}}}, \end{aligned}$$
(30)

expressions for energy density and pressure are given as

$$\begin{aligned} \rho _3=\rho _o\frac{-w_o}{w_o+2}\frac{\sqrt{1+\frac{1-(w_o+1)^2}{ (w_o+1)^2}(1+z)^{-({3-\gamma })}}+1}{\sqrt{1+\frac{1-(w_o+1) ^2}{(w_o+1)^2}(1+z)^{-({3-\gamma })}}-1}, \end{aligned}$$
(31)

and

$$\begin{aligned} p_3=\rho _o\frac{w_o}{w_o+2}\left( 1+\frac{1}{\sqrt{1+\frac{1-(w_o+1)^2}{(w_o+1)^2}(1+z)^{-(3-\gamma )}}}\right) .\nonumber \\ \end{aligned}$$
(32)

respectively.

3.3 Model 4 with \(c^2_s(w)= w+A(1+w)^B\)

This model is centered on a specific form of \(c^2_s\) given as

$$\begin{aligned} c^2_s(w)= w+A(1+w)^B, \end{aligned}$$
(33)

where A and B are the constant values, by plugging this value in Eq. (14) and after integration we get the expression for \(w_4\)

$$\begin{aligned} w_4(z)= & {} -1+\bigg ((1+w_o)^{-B}\nonumber \\&+(3-\gamma )ABln(1+z)\bigg )^{\frac{-1}{B}}, \end{aligned}$$
(34)

Finally, the density and pressure are given as

$$\begin{aligned}&\rho _4 =\rho _oe^{\frac{1}{A(1-B)}((1+w_o)^{-B}-(3-\gamma ) AB\ln (1+z))^\frac{B-1}{B}-(1+w_o)^{-B+1}},\nonumber \\ \end{aligned}$$
(35)
$$\begin{aligned}&p_4=\rho _o\bigg (-1+\bigg ((1+w_o)^{-B}\nonumber \\&\qquad +(3-\gamma )ABln(1+z)\bigg ) ^{\frac{-1}{B}}\bigg )\nonumber \\&\qquad e^{\frac{1}{A(1-B)}((1+w_o)^{-B}-(3-\gamma )AB\ln (1+z)) ^\frac{B-1}{B}-(1+w_o)^{-B+1}}. \end{aligned}$$
(36)

4 Cosmological parameters

To investigate the expansion dynamics of the universe the study of cosmological parameters have received a lot of attraction in present day cosmology. In this section, we discuss the cosmological parameters including Hubble parameter, EoS parameter, deceleration parameter and Om-diagnostic for the prior constructed models.

4.1 Hubble parameter

We obtain the Hubble parameter for Model 1 from Eq. (6) by Replacing \(\rho \) with \(\rho _1\) which is given in Eq. (19)

$$\begin{aligned}&H_1^2=\frac{8\pi G}{3}\nonumber \\&\quad \times \left( \frac{\rho _o \frac{c^2_s-w_o}{c^2_s+1}\bigg (\frac{1+w_o}{c^2_s-w_o} (1+z)^{(3-\gamma )(1+c^2_s)}+1\bigg )}{1-\gamma - \frac{\gamma ^2}{6}\xi (1+z)^{2\gamma }}\right) . \end{aligned}$$
(37)

In the similar way Hubble parameter for the model 2, 3 and 4 are calculated by inserting Eqs. (28), (31) and (35) in (6) respectively

$$\begin{aligned} H_2^2= & {} \frac{8\pi G}{3}\left( \frac{-w_o\rho _o \frac{1+\sqrt{1+\frac{1-w_o^{2}}{w_o^{2}}(1+z) ^{6-2\gamma }}}{-w_o+1}}{1-\gamma -\frac{\gamma ^2}{6}\xi (1+z)^{2\gamma }}\right) , \end{aligned}$$
(38)
$$\begin{aligned} H_3^2= & {} \frac{8\pi G}{3}\left( \frac{\frac{\rho _o \frac{-w_o}{w_o+2}\sqrt{1+\frac{1-(w_o+1)^{2}}{(w_o+1)^{2}} (1+z)^{-(3-\gamma )}}+1}{\sqrt{1+\frac{1-(w_o+1)^{2}}{(w_o+1)^{2}} (1+z)^{-(3-\gamma )}}-1}}{1-\gamma -\frac{\gamma ^2}{6}\xi (1+z)^ {2\gamma }}\right) , \end{aligned}$$
(39)
$$\begin{aligned} H_4^2= & {} \frac{8\pi G}{3}\nonumber \\&\times \left( \rho _o\frac{e^{{\frac{1}{A(1-B)}\big ((1+w_o) ^{-B}-(3-\gamma )AB\ln (1+z)\big )^\frac{B-1}{B}-(1+w_o)^{-B+1}}} }{1-\gamma -\frac{\gamma ^2}{6}\xi (1+z)^ {2\gamma }}\right) .\nonumber \\ \end{aligned}$$
(40)

4.2 Equation of state parameter

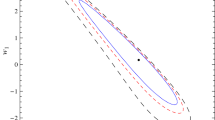
This parameter is extensively utilized to categorize the various phases of the growing universe. We have already constructed EoS parameters for all the four models. Now, the graphs of these parameters with respect to redshift parameter are being plotted. We choose \(\gamma =0.6\) and get three different trajectories by setting three different values of \(w_o\) as \(-0.4,-0.5,-0.6\). Figure 1 shows the behavior of EoS parameter for the model 1, it is found that all three trajectories correspond to \(\Lambda \)CDM model for the lower values of z and for the higher values, it shows quintessence like behavior of the universe. Figure 2 display the graph of EoS parameter for model 2 and we can observe a similar behavior as discussed in model 1. For model 2, it approaches to -1 near \(z=-0.7\) and below, whereas Eos parameter fall in quintessence region for \(z>-0.7\). The plot for the model 3 shown in Fig. 3 indicates that it remains in the quintessence region for early, present and later times. For the model 4 all three trajectories of EoS parameter as shown in Fig. 4 also remains in quintessence region.

Fig. 1
figure 1

Plot of w versus z for Model 1

Full size image
Fig. 2
figure 2

Plot of w versus z for Model 2

Full size image
Fig. 3
figure 3

Plot of w versus z for Model 3

Full size image
Fig. 4
figure 4

Plot of w versus z for Model 4

Full size image

4.3 Deceleration parameter

Deceleration parameter q is one of the important parameters which are required to discuss the behavior of the universe. The sign (negative or positive) of the q indicates wether the universe accelerates or decelerates, it is defined as

$$\begin{aligned} q=-1-\frac{\dot{H}^2}{{H^2}}, \end{aligned}$$
(41)

it can be further expressed in terms of z

$$\begin{aligned} q=-1+\frac{(1+z)}{2\tilde{H^2}}\frac{d\tilde{H^2}}{dz}, \end{aligned}$$
(42)

where \(\frac{H}{H_o}\equiv \tilde{H}\) and \(H_o\) is the present value of Hubble parameter. Hubble parameter is being utilized to get the expression of q, for the model 1

$$\begin{aligned}&q_1=-1+3(1+c^2_s)H_o(1+z)\nonumber \\&\left( 1-\gamma -\frac{(1+z)^{2\gamma } \gamma ^{2}\xi }{6}\right) \bigg (8G\pi (1+w_o)\nonumber \\&\times (1+z)^{-1+(1+c^2_s)(3-\gamma )}(3-\gamma )\rho _o\bigg )\nonumber \\&\left( 3H_o\left( 1-\gamma -\frac{(1+z)^{2\gamma }\gamma ^{2}\xi }{6}\right) \right) ^{-1}\nonumber \\&+\left. \frac{16G\pi (c^2_s-w_o)(1+z)^{-1+2\gamma }\bigg (1 +\frac{(1+w_o)(1+z)^{(1+c^{2}_s)(3-\gamma )}}{c^2_s-w_o}\bigg ) \gamma ^{3}\xi \rho _o}{3(1+c^{2}_s)H_o\bigg (1-\gamma -\frac{(1+z)^{2\gamma }\gamma ^{2}\xi }{6}\bigg )^{2}6}\right) \nonumber \\&\times \bigg (16G\pi (c^2_s-w_o)\nonumber \\&\bigg (1+\frac{(1+w_o)(1+z)^{(1+c^2_s) (3-\gamma )}}{c^2_s-w_o}\bigg )\rho _o\bigg )^{-1}. \end{aligned}$$
(43)

Similarly, equation of q for model 2 is as follows

$$\begin{aligned}&q_2=-1-3 (1+z) \nonumber \\&\times \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6 }\right) H_o \left( 1-w_o\right) \nonumber \\&\times \bigg ( (-4 G \pi (1+z)^{5-2 \gamma } (6-2 \gamma ) \left( 1-w_o^2\right) \rho _o)\nonumber \\&(H_o \left( 1-w_o\right) w_o)^{-1}\nonumber \\&\times \bigg (3 \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6 }\right) \nonumber \\&\sqrt{1+\frac{(1+z)^{6-2 \gamma } \left( 1-w_o^2\right) }{w_o^2}}\bigg )^{-1}\nonumber \\&-\left. \frac{16 G \pi (1+z)^{-1+2 \gamma } \gamma ^3 \xi w_o \left( 1+\sqrt{1+\frac{(1+z)^{6-2 \gamma } \left( 1-w_o^2\right) }{w_o^2}}\right) \rho _o}{3 \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6 }\right) ^2 6 H_o \left( 1-w_o\right) }\right) \nonumber \\&\times \bigg (16 G \pi w_o \left( 1{+}\sqrt{1{+}\frac{(1+z)^{6-2 \gamma } \left( 1-w_o^2\right) }{w_o^2}}\right) \rho _o\bigg ). \end{aligned}$$
(44)

For Model 3, we have

$$\begin{aligned}&q_3=\frac{-1}{2 \left( -6+\gamma \left( 6+(1+z)^{2 \gamma } \gamma \xi \right) \right) \sqrt{1-\frac{(1+z)^{-3+\gamma } w_o \left( 2+w_o\right) }{\left( 1+w_o\right) {}^2}}}\nonumber \\&\times \bigg (18-12 \sqrt{1-\frac{(1+z)^{-3+\gamma } w_o \left( 2+w_o\right) }{\left( 1+w_o\right) {}^2}}\nonumber \\&+\gamma \bigg (12 \bigg (-2+\sqrt{1-\frac{(1+z)^{-3+\gamma } w_o \left( 2+w_o\right) }{\left( 1+w_o\right) {}^2}}\bigg )\nonumber \\&+\gamma \bigg (6+(1+z)^{2 \gamma } \xi \nonumber \\&\times \bigg (-3+\gamma +2 \sqrt{1-\frac{(1+z)^{-3+\gamma } w_o \left( 2+w_o\right) }{\left( 1+w_o\right) {}^2}}\nonumber \\&+2 \gamma \sqrt{1-\frac{(1+z)^{-3+\gamma } w_o \left( 2+w_o\right) }{\left( 1+w_o\right) {}^2}}\bigg )\bigg )\bigg )\bigg ). \end{aligned}$$
(45)

For model 4, it takes the following form

$$\begin{aligned}&q_4=-1 +\frac{1}{16 G \pi \rho _o}3 e^{\left( 1+w_o\right) {}^{1-B}-\frac{\left( -A B (3-\gamma ) \text {Log}[1+z]+\left( 1+w_o\right) {}^{-B}\right) {}^{\frac{-1+B}{B}}}{A (1-B)}} (1+z) \nonumber \\&\times \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6 }\right) \left( \frac{16 e^{-\left( 1+w_o\right) {}^{1-B}+\frac{\left( -A B (3-\gamma ) \text {Log}[1+z]+\left( 1+w_o\right) {}^{-B}\right) {}^{\frac{-1+B}{B}}}{A (1-B)}} G \pi (1+z)^{-1+2 \gamma } \gamma ^3 \xi \rho _o}{3 \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6}\right) ^2 6 H_o}-(8 (-1+B)\right. \nonumber \\&\times \left. e^{-\left( 1+w_o\right) {}^{1-B}+\frac{\left( -A B (3-\gamma ) \text {Log}[1+z]+\left( 1+w_o\right) {}^{-B}\right) {}^{\frac{-1+B}{B}}}{A (1-B)}}G \pi (3-\gamma ) \left( -A B (3-\gamma ) \text {Log}[1+z]+\left( 1+w_o\right) {}^{-B}\right) {}^{-1+\frac{-1+B}{B}} \rho _o)\right. \nonumber \\&\times \left. \big (3 (1-B) (1+z) \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6 }\right) H_o\big )^{-1}\right) H_o. \end{aligned}$$
(46)
Fig. 5
figure 5

Plot of q versus z for Model 1

Full size image
Fig. 6
figure 6

Plot of q versus z for Model 2

Full size image

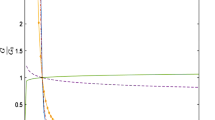
In order to discuss the graphical variation of q versus z, we set the values of constants as \(\rho =0.23,~\xi =0.1,~\gamma =0.6,~H_o=0.7\) and \(c^2_s=0.25\). The trajectories of q for model 1 represent positive behavior for higher values of z as shown in Fig. 5, as the value of z deceases, we get the negative behavior of the deceleration parameter. This implies that q for model 1 shows the decelerated phase in early times and for decreasing z an accelerated phase of the universe is obtained. We can observe the same behavior of q for model 2 as shown in Fig. 6. For the model 3 in Fig. 7 the deceleration parameter is negative that indicates the accelerated phase of the universe. For the Model 4 , values of two additional constants are taken as \(A=1.5\), \(B=1.4\) and the plot in Fig. 8 exhibit both accelerated and decelerated phase of the universe for all the choices of \(w_o\) .

4.4 Om diagnostic

Hubble parameter H and deceleration parameter q cannot discriminate the several DE models in an effective manner, for the better understanding of DE models higher order derivatives of scale factor is required, so taking into account this need Sahani et al. [42] and Alam et al. [43] introduced a geometrical diagnostic pair, it is known as statefinder pair (r,s). Another very useful geometrical diagnostic has been proposed as Om-diagnostic [42] to elaborate different phases of the universe. It relies on first order derivative so it is simpler diagnostic as compare to the statefinder diagnostic when it is applied to the cosmological observation [47]. Many authors [48,49,50] applied Om-analysis to DE models. The constant behavior of Om-diagnostic shows DE is cosmological constant \(\Lambda \)CDM, the positive slope of Om trajectory indicates that DE behaves like phantom and negative slope of trajectories indicate that DE behaves like quintessence. The Om-diagnostic in terms of z is defined as [42]

$$\begin{aligned} Om(x)=\frac{h^{2}(x)-1}{x^{3}-1}, \end{aligned}$$
(47)

where \(x=z+1\) and \(h(x)=\frac{H(x)}{H_o}\). The equation of Om for model 1 is as follows

$$\begin{aligned} Om_1=\frac{-1+\frac{8 G \pi \left( c_s^2-w_o\right) \left( 1+\frac{(1+z)^{(3-\gamma ) \left( 1+c_s^2\right) } \left( 1+w_o\right) }{c_s^2-w_o}\right) \rho _o}{3 \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6}\right) \left( 1+c_s^2\right) H_o}}{-1+(1+z)^3}, \end{aligned}$$
(48)
Fig. 7
figure 7

Plot of q versus z for Model 3

Full size image
Fig. 8
figure 8

Plot of q versus z for Model 4

Full size image
Fig. 9
figure 9

Plot of Om versus z for Model 1

Full size image

we obtain the expression of Om for model 2, 3 and 4 as

$$\begin{aligned} Om_2=\frac{-1-\frac{48 G \pi w \left( 1+\sqrt{1-\frac{\left( -1+w^2\right) (1+z)^{6-2 \gamma }}{w^2}}\right) \rho }{3 \text {h0} (-1+w) \left( (1+z)^{2 \gamma } \gamma ^2 \xi +(-1+\gamma )6 \right) }}{-1+(1+z)^3}. \end{aligned}$$
(49)
Fig. 10
figure 10

Plot of Om versus z for Model 2

Full size image
$$\begin{aligned} Om_3=\frac{-1+\frac{48 G \pi \left( -2+w_o \left( -1+\sqrt{1-\frac{(1+z)^{3-\gamma } w_o \left( 2+w_o\right) }{\left( 1+w_o\right) {}^2}} \rho _o\right) \right) }{3 \left( -1+\sqrt{1-\frac{w (2+w) (1+z)^{3-\gamma }}{(1+w)^2}}\right) \left( (1+z)^{2 \gamma } \gamma ^2 \xi +(-1+\gamma ) 6 \right) H_o \left( 2+w_o\right) }}{-1+(1+z)^3}.\nonumber \\ \end{aligned}$$
(50)
Fig. 11
figure 11

Plot of Om versus z for Model 3

Full size image
$$\begin{aligned} Om_4=\frac{-1+\frac{8 e^{-\left( 1+w_o\right) {}^{1-B}+\frac{\left( -A B (3-\gamma ) \text {Log}[1+z]+\left( 1+w_o\right) {}^{-B}\right) {}^{\frac{-1+B}{B}}}{A (1-B)}} G \pi \rho _o}{3 \left( 1-\gamma -\frac{(1+z)^{2 \gamma } \gamma ^2 \xi }{6 }\right) H_o}}{-1+(1+z)^3}.\nonumber \\ \end{aligned}$$
(51)
Fig. 12
figure 12

Plot of Om versus z for Model 4

Full size image

By taking same values of the constants as mentioned above the behavior of Om trajectories is analyzed. For the model 1 and 2, Om trajectories with respect to z are displayed in Figs. 9 and 10 respectively, the plots exhibit the negative curvature i.e. the model 1 and 2 behaves as quintessence. The slopes of the all three trajectories for model 3 and 4 are positive as shown in Figs. 11 and 12, hence it shows the phantom phase of the universe.

5 Concluding remarks

In this paper, we have studied FRLW universe that is the combination of dark matter and dark energy. In various theories of quantum gravity, universe is described as a dimensional flow which has become a motivation for the fractal cosmology. One of the important features of fractal cosmology is that it can remove ultraviolet divergencies and provide a better understanding of the universe in different dimensions. We have developed the unified models in fractal universe involving the squared speed of sound. In the present scenario, a barotropic cosmic fluid is expressed in terms of speed of sound and utilization of the four different forms of \(c^2_s(w)\) as function of w leads us to the construction of energy densities and pressures for the four models. Further, the EoS parameter and various cosmological parameters in terms of red shift are explored for these models. Figures 1, 2, 3 and 4 show the evolution of Eos parameter with respect to redshift parameter, it is observed that for the model 1 and 2, w approaches to the \(\Lambda \)CDM limit for the lower values of z and corresponds to quintessence era for the higher values of z. However for model 3 and 4, w exhibit quintessence like behavior. Graphical behavior of deceleration parameter is shown in Figs. 5, 6, 7, and 8. For the models 1, 2 and 4, q is showing both accelerated and decelerated phase and for the model 3 (Fig. 7), only an accelerated phase is indicated. om-diagnostic parameter represents the quintessence like era for the models 1 and 2 as shown in the Figs. 9 and 10 respectively and it corresponds to the phantom era for the models 3 (Fig. 11) and 4 (Fig. 12). Our results are summarized as follows

 

\(\text {EoS Parameter}\)

Deceleration Parameter

\(\text {om Digonostic}\)

Model1

Quintessence

Accelerated and Decelerated Phase

\(\text {Quintessence }\)

Model2

\(\text {Quintessence }\)

Accelerated and Decelerated Phase

\(\text {Quintessence }\)

Model3

Quintessence

Accelerated Phase

\(\text {Phantom }\)

Model4

Quintessence

Accelerated and Decelerated Phase

\(\text {Phantom }\)

Shahzad et al. [51] considered fractal FRW universe filled with interacting dark energy and dark matter. They discussed three types of dark energy models and explored the cosmological parameters (equation of state, deceleration parameter, Om-diagnostic) and cosmological planes for all the selected models. They observed that equation of state parameter lies within the range given by observational schemes and deceleration parameter shows transition from decelerated phase to accelerating phase and plots for Om-diagnostic leads to the phantom behavior of the models. Chattopadhyay et al. [52] investigated modified and extended Holographic Ricci dark energy in the framework of fractal universe. They reconstructed Hubble parameter, energy density, EOS parameter and deceleration parameter for both of dark energy candidates. They observed the accelerated expansion of the universe through deceleration parameter and EOS parameter for the modified Holographic and extended Holographic dark energy shows quintessence like behavior and quintom like behavior respectively. Sadri et al. [53] considered interacting Holographic dark energy model in fractal cosmology. They studied the cosmological consequences of the model and found that it is compatible with the recent observational data. These results obtained in above mentioned works support the models constructed in the present scenario. We have utilized different from above mentioned works and found interesting results which are comparable with observational data sets.