Scotogenic cobimaximal Dirac neutrino mixing from $\Delta (27)$ and $U(1)_\chi$

Abstract

In the context of $SU(3)_C \times SU(2)_L \times U(1)_Y \times U(1)_\chi$, where $U(1)_\chi$ comes from $SO(10) \rightarrow SU(5) \times U(1)_\chi$, supplemented by the non-Abelian discrete $\Delta (27)$ symmetry for three lepton families, Dirac neutrino masses and their mixing are radiatively generated through dark matter. The gauge $U(1)_\chi$ symmetry is broken spontaneously. The discrete $\Delta (27)$ symmetry is broken softly and spontaneously. Together, they result in two residual symmetries, a global $U(1)_L$ lepton number and a dark symmetry, which may be $Z_2$, $Z_3$, or $U(1)_D$ depending on what scalar breaks $U(1)_\chi$. Cobimaximal neutrino mixing, i.e. $\theta _{13} \ne 0$, $\theta _{23} = \pi /4$, and $\delta _{CP} = \pm \pi /2$, may also be obtained.

1 Introduction

Whereas there exist powerful theoretical arguments that neutrinos are Majorana, there is yet no incontrovertible experimental evidence that they are so, i.e. no definitive measurement of a nonzero neutrinoless double beta decay [1], with the best present experimental upper limit [2] on the Majorana electron neutrino mass in the range 61 to 165 meV. To make a case for neutrinos to be Dirac, the existence of a right-handed neutrino $\nu _R$ must be justified, which is of course not required in the standard model (SM) of quarks and leptons. The canonical choice is to extend the SM gauge symmetry $SU(3)_C \times SU(2)_L \times U(1)_Y$ to the left-right symmetry $SU(3)_C \times SU(2)_L \times SU(2)_R \times U(1)_{(B-L)/2}$ [3]. In that case, the $SU(2)_R$ doublet $(\nu ,e)_R$ is required, and the charged $W_R^\pm$ gauge boson is predicted along with a neutral $Z'$ gauge boson.

A more recent choice is to consider $U(1)_\chi$ which comes from $SO(10) \rightarrow SU(5) \times U(1)_\chi$, with SU(5) breaking to the SM at the same grand unified scale. Assuming that $U(1)_\chi$ survives to an intermediate scale, the current experimental bound on the mass of $Z_\chi$ being about 4.1 TeV [4, 5], then $\nu _R$ must exist for the cancellation of gauge anomalies. Now $\nu _R$ is a singlet and $W_R^\pm$ is not predicted. In this context, new insights into dark matter [6, 7] and Dirac neutrino masses [8, 9] have emerged. In particular, the breaking pattern was fully discussed in Ref. [6].

To make sure that $\nu _R$ itself does not have a Majorana mass, the breaking of $U(1)_\chi$ should not come from a scalar which couples to $\nu _R \nu _R$. This simple idea was first discussed [10] in 2013 in the case of singlet fermions charged under a gauge $U(1)_X$. If the latter is broken by a scalar with three units of X charge, it is impossible for these fermions with one unit of X charge to acquire Majorana masses. Hence the residual symmetry is global U(1) in this case. It is straightforward then to apply this idea to lepton number [11]. Another possible residual lepton symmetry is $Z_4$ which was first pointed out in Ref. [12].

A second issue regarding Dirac neutrinos is that the corresponding Yukawa couplings linking $\nu _L$ to $\nu _R$ through the SM Higgs boson must be very small. To avoid these tree-level couplings, it is often assumed that some additional symmetry exists which forbids these dimension-four couplings, but Dirac neutrino masses may be generated radiatively as this symmetry is broken softly by dimension-three terms. For a generic discussion, see Ref. [13], which is patterned after that for Majorana neutrinos [14]. In some applications [15,16,17], the particles in the loop belong to the dark sector. This is called the scotogenic mechanism, from the Greek ‘scotos’ meaning darkness, the original one-loop example [18] of which was applied to Majorana neutrinos.

Table 1 Particle content of model

Instead of the ad hoc extra symmetry which forbids the tree-level couplings, exotic assignments of the gauge charges of $\nu _R$ may be used [11, 19,20,21,22,23,24,25] instead. However, a much more efficacious idea is to use a non-Abelian discrete family symmetry, which is softly broken in the dark sector. In this paper, $\Delta (27)$ [26,27,28,29,30] is shown to be useful in achieving the goal of having scotogenic Dirac neutrino masses with a mixing pattern [31,32,33] called cobimaximal [34,35,36,37,38,39], i.e. $\theta _{23} = \pi /4$ and $\delta _{CP} = \pm \pi /2$, which is consistent with present neutrino oscillation data [40] for $\delta _{CP} = -\pi /2$.

2 Outline of model

The particles of this model are shown in Table 1. In the adopted notation, all fermion fields are left-handed. The usual right-handed fields are denoted by their charge conjugates. The SM particles transform under $U(1)_\chi$ according to their SO(10) origin, as well as the particles of the dark sector $(N, N^c, \eta , \sigma )$. Note that although many large representations of SO(10) are shown, there is no commitment to grand unification, only to the $U(1)_\chi$ assignments of the particles added. The basic assumption is that they are relevant at low energies, without understanding their true origin. In other words, instead of extending the SM with an unknown U(1) gauge symmetry which has been done in many studies, the known $U(1)_\chi$ which has predetermined couplings to the SM fermions (and orthogonal to $U(1)_Y$) is chosen here. Note further that the often discussed $U(1)_{B-L}$ is NOT orthogonal to $U(1)_Y$. The input family symmetry is $\Delta (27)$. The gauge $U(1)_\chi$ is broken by $\zeta _2$ or $\zeta _3$ or $\zeta _4$. In each case, a residual $U(1)_L$ symmetry remains for lepton number whereas the dark symmetry becomes $Z_2^D$ or $Z_3^D$ or $U(1)_D$ respectively. The complete Lagrangian is invariant under gauge $U(1)_\chi$ in all its terms, as well as $\Delta (27)$ in all the dimension-four terms. Whereas the breaking of gauge $U(1)_\chi$ must only be spontaneous, through the vacuum expectation value of $\zeta _2$ or $\zeta _3$ or $\zeta _4$, the breaking of $\Delta (27)$ is both spontaneous, through the vacuum expectation values of $\phi ^0_{1,2}$, and explicit, through soft dimension-three terms as shown below.

The key feature of this model is the interplay between $U(1)_\chi$ and $\Delta (27)$ for restricting the interaction terms among the various fermions and scalars. The irreducible representations of $\Delta (27)$ and their character table are given in Ref. [27]. The important point is that if a set of 3 complex fields transforms as the 3 representation of $\Delta (27)$, then its conjugate transforms as $3^*$, which is distinct from 3. The basic multiplication rules are

$$\begin{aligned} 3 \times 3 = 3^* + 3^* + 3^*, ~~~ 3 \times 3^* = \sum ^9_{i=1} 1_i. \end{aligned}$$

(1)

From Table 1, the Yukawa term $e e^c \phi _1^0$ is allowed, but not $\nu \nu ^c \phi _2^0$ because of $\Delta (27)$. Furthermore, the usual dimension-five operator for Majorana neutrino mass, i.e. $\nu \nu \phi _2^0 \phi _2^0$, is forbidden as well as the usual singlet Majorana mass term $\nu ^c \nu ^c$. Note that without $U(1)_\chi$, $\nu ^c \nu ^c$ is a soft term breaking $\Delta (27)$ and would then have been allowed by itself. To obtain Dirac neutrino masses, the scalar doublet $\eta$ and singlet $\sigma$ with odd $Q_\chi$ as well as the fermion singlets $N,N^c$ with even $Q_\chi$ are added. Note that they belong to the dark sector because SM fermions have odd $Q_\chi$ and the SM Higgs doublet has even $Q_\chi$, as pointed out in Ref. [6].

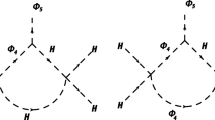
Since $\Phi _1^\dagger$ transforms exactly like $\Phi _2$, the linear combination $\Phi = (v_1 \Phi _1^\dagger + v_2 \Phi _2)/\sqrt{v_1^2+v_2^2}$ is the analog of the standard-model Higgs doublet, where $\langle \phi ^0_{1,2} \rangle = v_{1,2}$. In the following, only $\Phi$ is used, and because it is a 3 under $\Delta (27)$, it is denoted as $\Phi _{1,2,3}$. The dark scalars and fermions have allowed interactions with $\nu ,\nu ^c$ and $\Phi$ under $U(1)_\chi$. The soft breaking of $\Delta (27)$ then allows the one-loop generation of radiative Dirac neutrino masses as shown in Fig. 1. The dimension-four terms, i.e. $\nu N^c \eta ^0$, $\nu ^c N \sigma$, respect both $U(1)_\chi$ and $\Delta (27)$. The dimension-three scalar trilinear couplings $\eta ^0 \sigma {\bar{\phi }}^0$ respect $U(1)_\chi$ but not $\Delta (27)$. The dimension-three $N^c N$ terms are also allowed to break $\Delta (27)$. They are in fact the only two such terms available.

Consider now the spontaneous breaking of $U(1)_\chi$. First, because $\nu , N \sim 3$ and $\nu ^c, N^c \sim 3^*$ under $\Delta (27)$, they cannot obtain Majorana masses through any scalar which is a singlet. Hence $U(1)_L$ lepton number holds as indicated in Table 1. If $\zeta _2$ is used, then the term $\zeta _2^* \sigma ^2$ is allowed, hence the residual dark symmetry is $Z_2^D$. Similarly, $\zeta _3 \sigma ^3$ yields $Z_3^D$ with $\omega = \exp (2\pi i/3)$, and $\zeta _4$ yields $U(1)_D$ because $\zeta _4^* \sigma ^4$ is not allowed by renormalizability, and cannot be generated by the given particle content of the model. In the case of $Z_3^D$ from $\zeta _3$, there is an equivalent assignment of lepton number and dark symmetry. Instead of the conventional thinking that $N,N^c$ must carry lepton number, the latter may be assigned [41] to the scalars $\eta$ and $\sigma$. Hence lepton number becomes $Z_3^L$ [42] with $\nu , \sigma \sim \omega$; $\nu ^c, \eta \sim \omega ^2$; $N, N^c, \phi \sim 1$; whereas dark symmetry remains $Z_3^D$ with $\sigma , N^c \sim \omega$; $\eta , N \sim \omega ^2$; $\nu , \nu ^c, \phi \sim 1$.

3 Cobimaximal neutrino mixing

Using the decomposition $3 \times 3^*$ and $\langle \phi ^0_i \rangle = v_i$, with $1_1,1_7,1_4$ as defined in Ref. [27], instead of the usual $1_1,1_2,1_3$ of the original $A_4$ model [43] of neutrino mixing, the charged-lepton mass matrix is given by

$$\begin{aligned} {{{\mathcal {M}}}}_l = \begin{pmatrix} f_e v_1^* &{} f_\mu v_3^* &{} f_\tau v_2^* \\[2mm] f_e v_2^* &{} f_\mu v_1^* &{} f_\tau v_3^* \\[2mm] f_e v_3^* &{} f_\mu v_2^* &{} f_\tau v_1^* \end{pmatrix} = \begin{pmatrix} m_e &{} 0 &{} 0 \\[2mm] 0 &{} m_\mu &{} 0 \\[2mm] 0 &{} 0 &{} m_\tau \end{pmatrix}, \end{aligned}$$

(2)

where $v_2=v_3=0$ has been assumed for the spontaneous breaking of $\phi ^0_{1,2,3}$. This ${{{\mathcal {M}}}}_l$ is diagonal and different from that of Ref. [43]. It allows also three independent masses for the charged leptons, and the emergence of lepton flavor triality [44, 45] in the Yukawa interactions of the three charged leptons with the three Higgs doublets.

In the neutrino sector, the tree-level Yukawa couplings $\nu \nu ^c \phi ^0$ are forbidden by $\Delta (27)$. Hence the $3 \times 3$ Dirac neutrino mass matrix ${{{\mathcal {M}}}}_\nu$ is generated through dark matter (scotogenic) as shown in Fig. 1. Since $\eta ^0 \sigma {\bar{\phi }}^0$ is just one coupling, the flavor structure of ${{{\mathcal {M}}}}_\nu$ comes from the $N^cN$ mass terms which break $\Delta (27)$ softly. Assuming the residual symmetry to be generalized $N_2 - N_3$, $N^c_2 - N^c_3$, and $N_{1,2,3} - N^c_{1,3,2}$ exchange with complex conjugation [32], the $3 \times 3$ $N^cN$ mass matrix is of the form

$$\begin{aligned} {{{\mathcal {M}}}}_N = \left( \begin{array}{lll} A &{} D &{} D^* \\ D &{} B &{} C \\ D^* &{} C &{} B^*, \end{array}\right) \end{aligned}$$

(3)

where A, C are real. The above is exactly of the form [31,32,33] required for cobimaximal mixing [34,35,36,37,38,39], i.e. $\theta _{13} \ne 0$, $\theta _{23} = \pi /4$, and $\delta _{CP} = \pm \pi /2$, because the neutrino basis is also the one where the charged leptons are diagonal. As with all previous derivation of a neutrino mixing pattern, there are two steps in this process. First is the choice of a symmetry such as $A_4$ or $\Delta (27)$ and the particle content transforming under this symmetry. Second is the residual symmetry assumed. Together they “predict” a neutrino mixing pattern. The second step is always an assumption in all previous claims, such as tribimaximal mixing. The claim here of cobimaximal mixing is no different.

As is well-known, only 5 of the 6 real parameters of Eq. (3) are independent because the phase of either B or D could be rotated away. These 5 parameters yield 3 masses (with no Majorana phases) and two mixing angles, i.e. $\theta _{12}$ and $\theta _{13}$. The two predictions are thus $\theta _{23}=\pi /4$ and $\delta _{CP}=\pm \pi /2$ as stated above. If $B_I=D_I=0$, then $\theta _{13}=0$ and $\theta _{23} = \pi /4$. If

$$\begin{aligned} A-B_R-C+D_R=0 \end{aligned}$$

(4)

in addition, then $\tan ^2 \theta _{12} = 1/2$ as well, i.e. tribimaximal mixing is obtained. Since neutrino oscillation data are close to this limit, the above quantities may be considered small if not zero, hence the neutrino mass eigenvalues are approximately given by

$$\begin{aligned} m_{\nu _1}\simeq & {} (2A + B_R + C - 4D_R)/3, \nonumber \\ m_{\nu _2}\simeq & {} (A + 2B_R + 2C + 4D_R)/3, ~~ m_{\nu _3} \simeq B_R - C. \end{aligned}$$

(5)

If $B_I \ne 0$ or $D_I \ne 0$ or both, cobimaximal mixing is obtained. However, $\theta _{13}$ and $\theta _{12}$ are not fixed. If Eq. 4 is valid together with $B_I = 2D_I$, then [46]

$$\begin{aligned} \tan ^2 \theta _{12} = {1 - 3 \sin ^2 \theta _{13} \over 2} < {1 \over 2}, \end{aligned}$$

(6)

in good agreement with data.

Fig. 1

One-loop diagram for scotogenic $U(1)_\chi$ Dirac neutrino mass

4 Dark sector

To compute the Dirac neutrino mass matrix of Fig. 1, assume first that $\eta ^0 \sigma$ couples only to ${\bar{\phi }}^0_{1}$, leading to the possibility of lepton flavor triality [44, 45] which may be tested experimentally. Note then that the one-loop calculation is equivalent to taking the difference of the exchanges of two scalar mass eigenstates

$$\begin{aligned} \chi _1 = \cos \theta ~\sigma - \sin \theta ~{\bar{\eta }}^0, ~~~ \chi _2 = \sin \theta ~\sigma + \cos \theta ~{\bar{\eta }}^0, \end{aligned}$$

(7)

where $\theta$ is the mixing angle due to the ${\bar{\phi }}^0 \eta ^0 \sigma$ term. Let the $\nu _i N^c_k \eta ^0$ Yukawa coupling be $h_L {U}_{ik}$ and the $\nu ^c_j N_k \sigma$ Yukawa coupling be $h_R {U}^T_{kj}$, then the Dirac neutrino mass matrix is given by

$$\begin{aligned} ({{{\mathcal {M}}}_\nu })_{ij}= & {} {h_L h_R \sin 2 \theta \over 16 \pi ^2} \sum _k {U}_{ik} M_k \nonumber \\&\left[ {m_2^2 \over m_2^2-M_k^2} \ln {m_2^2 \over M_k^2} - {m_1^2 \over m_1^2-M_k^2} \ln {m_1^2 \over M_k^2} \right] {U}^T_{kj}, \end{aligned}$$

(8)

where $m_{1,2}$ are the masses of $\chi _{1,2}$ and $M_k$ is the mass of $N_k$. If $|m_2^2-m_1^2|<< m_2^2 + m_1^2 = 2m_0^2<< M_k^2$, then the $M_k$ contribution reduces to

$$\begin{aligned}&M_k \left[ {m_2^2 \over m_2^2-M_k^2} \ln {m_2^2 \over M_k^2} - {m_1^2 \over m_1^2-M_k^2} \ln {m_1^2 \over M_k^2} \right] \nonumber \\&\quad = {(m_2^2-m_1^2) \over M_k} \left[ \ln {M_k^2 \over m_0^2} - 1 \right] . \end{aligned}$$

(9)

This expression is of the radiative seesaw form. On the other hand, if $M_k<< m_{1,2}$, then [47]

$$\begin{aligned}&M_k \left[ {m_2^2 \over m_2^2-M_k^2} \ln {m_2^2 \over M_k^2} - {m_1^2 \over m_1^2-M_k^2} \ln {m_1^2 \over M_k^2} \right] \nonumber \\&\quad = \ln (m_2^2/m_1^2) M_k. \end{aligned}$$

(10)

This is no longer a seesaw formula. It shows that the three Dirac neutrinos $\nu$ may have masses which are proportional to those of the three dark Dirac fermions N.

If Eq. 9 holds, then the lighter of $\chi _{1,2}$ is dark matter. It should not have a large $\eta ^0$ component because it would then have significant interactions with nuclei through the Z gauge boson and be ruled out by underground direct-search experiments. Assuming $\theta$ in Eq. 7 to be very small, then it should be $\chi _1$. If its mass is greater than that of the SM Higgs boson, its annihilation to the latter is a well-known mechanism [48] for generating the correct dark-matter relic abundance of the Universe. It is assumed that the particles in the dark sector are not accidentally degenerate so that coannihilation is not a factor in this discussion.

If Eq. 10 holds, then the lightest N is dark matter, i.e. $N_1$ for the normal hierarchy of neutrino masses $(m_{\nu _1}< m_{\nu _2} < m_{\nu _3})$ or $N_3$ for the inverse hierarchy $(m_{\nu _3}< m_{\nu _1} < m_{\nu _2})$. In either case, the other two Ns will decay to the lightest N plus a neutrino pair or charged lepton pair, through $\chi _{1,2}$ or $\eta ^\pm$. The annihilation of $N {\bar{N}} \rightarrow \nu {\bar{\nu }}$ through $\chi _1$ exchange has a cross section $\times$ relative velocity given by

$$\begin{aligned} \sigma \times v_{rel} = {h_R^4 \over 32 \pi } {M_N^2 \over (m_1^2 + M_N^2)^2}, \end{aligned}$$

(11)

assuming again that $\theta$ is very small. As a numerical example, let $M_N =150$ GeV, $m_1 = 400$ GeV, $h_R = 0.62$, then this is about 1 pb, which is a typical value for obtaining the correct dark-matter relic abundance of the Universe, i.e. $\Omega h^2 = 0.12$.

At the mass of 150 GeV, the constraint on the elastic scattering cross section of N off nuclei per nucleon is about $1.5 \times 10^{-46}$ $\hbox {cm}^2$ from the latest XENON result [49]. This puts a lower limit on the mass of $Z_\chi$, i.e.

$$\begin{aligned} \sigma _0 = {\mu _N^2 \over 64 \pi } {[Z f_P +(A-Z) f_N]^2 \over A^2} < 1.5 \times 10^{-10}~\mathrm{pb}, \end{aligned}$$

(12)

where $\mu _N$ is the reduced mass of N, and

$$\begin{aligned} f_P= & {} g^2_{Z_\chi } N_V (2u_V + d_V)/M^2_{Z_\chi }, \nonumber \\ f_N= & {} g^2_{Z_\chi } N_V (u_V + 2d_V)/M^2_{Z_\chi }, ~~~ \end{aligned}$$

(13)

and $Z=54$, $A=131$ for xenon. In $U(1)_\chi$, the vector couplings are

$$\begin{aligned} N_V = \sqrt{5 \over 2}, ~~~ u_V =0, ~~~ d_V = {-1 \over \sqrt{10}}. \end{aligned}$$

(14)

Using $\alpha _\chi = g^2_{Z_\chi }/4\pi = 0.0154$ from Ref. [6], the bound $M_{Z_\chi } > 34$ TeV is obtained.

5 Concluding remarks

The $U(1)_\chi$ gauge symmetry and a minimal particle content with a softly broken $\Delta (27)$ family symmetry are the ingredients for the radiative generation of Dirac neutrino masses through dark matter. Both symmetries are broken, but the resulting residual symmetries, i.e. global $U(1)_L$ and $Z_2^D$ or $Z_3^D$ or $U(1)_D$, maintain the Dirac nature of neutrinos and the stability of dark matter.

The charged-lepton mass matrix is diagonal with the choice of $1_1,1_7,1_4$ representations for $e^c_{1,2,3}$, and $v_2=v_3=0$ for the Higgs symmetry breaking. The Dirac neutrino mass matrix comes from the soft breaking of $\Delta (27)$ in the $N^cN$ mass matrix in the dark sector. Using generalized exchange symmetries with complex conjugation, this is shown to be of the form resulting in cobimaximal mixing, i.e. $\theta _{13} \ne 0$, $\theta _{23} = \pi /4$, $\delta _{CP} = \pm \pi /2$, in agreement with present data for $\delta _{CP} = -\pi /2$.

The dark-matter candidate is either mostly a singlet scalar $\chi _1$ or a Dirac fermion N, both of which have $Z_\chi$ interactions. The bound on $M_{Z_\chi }$ depends on the mass of the dark matter, but is about 34 TeV for $M_N = 150$ GeV.

As with all excursions beyond the SM, only future experiments could decide on whether this proposal makes any sense. It is easily falsifiable by the discovery of $Z_\chi$ below the mass predicted, or that of dark matter not consistent with either $\chi _1$ or N.