1 Introduction

Observations of Type IA Supernova indicate that the Universe undergoes an accelerated expansion [1, 2], which is dominant today (\(\sim \) 68%) [3]. Ordinary matter represents only \(5\%\) of the energy content of the Universe, and the remaining \(27\%\) is the still unknown dark matter (DM). The nature of the dark sector is one of the biggest challenges in the modern cosmology, whose plethora of dark energy (DE) candidates include scalar fields [4,5,6,7,8,9,10,11,12,13,14], vector fields [15,16,17,18,19,20,21], holographic dark energy [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38], models of false vacuum decay [39,40,41,42,43,44,45], modifications of gravity and different kinds of cosmological fluids [46,47,48]. In addition, the two components of the dark sector may interact with each other [25,26,27,28, 43, 48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69], since their densities are comparable and the interaction can eventually alleviate the coincidence problem [70, 71].

When a scalar field is in the presence of a barotropic fluid the relevant evolution equations can be converted into an autonomous system and the asymptotic states of the cosmological models can be analysed. Such approach is well-known, at the background level, for uncoupled dark energy (quintessence, tachyon field and phantom field for instance [72,73,74,75,76]) and coupled dark energy [21, 50, 55, 61, 77,78,79,80,81,82]. On the other hand, cosmological perturbations were only studied using dynamical analysis for \(\varLambda \hbox { CDM}\) [83, 84] and quintessence [84]. The role of cosmological perturbations in uncoupled and coupled quintessence (with diverse forms of interactions between the dark sector) has been investigated in several works [85,86,87,88,89,90,91,92,93,94,95,96], whose aim is to constrain the free parameters of the model using sets of observations. Results from dynamical analysis are also usually employed in such works, as in [97], for instance. Therefore, it is interesting to improve the background analysis in order to understand whether the fixed points are viable to describe each one of the cosmological eras of the Universe or not. This can be done if one takes cosmological perturbations into account. In this paper we go in this direction, analysing interacting quintessence with cosmological perturbations, in the light of dynamical systems theory. Our findings mostly agree with previous results in the literature, where it was used only background equations, for coupled (and uncoupled) quintessence, including the stability of the fixed points. One of those critical points, however, no longer can describe a DE-dominated Universe, when one uses cosmological perturbations.

The rest of the paper is organized as follows. In Sect. 2 we present the basics of the interacting DE and the dynamical analysis theory. In Sect. 3 we present the dynamics of the canonical scalar field, with the correspondent equations for the background and for linear perturbations. We use the dynamical system theory in Sect. 4 to study interacting quintessence at cosmological perturbation level, analysing the critical points and their stabilities. Section 5 is reserved for conclusions. We use Planck units (\(\hbar =c=M_{pl}=1\)) throughout the text.

2 Interacting dark energy and dynamical analysis

We will consider that DE is described by single real scalar field (quintessence) with energy density \(\rho _\phi \) and pressure \(p_\phi \), whose equation of state is \(w_\phi =p_\phi /\rho _\phi \). DE is interacting with DM through a transfer of energy-momentum between them, such that that total energy-momentum is conserved. In the flat Friedmann–Lamaître–Robertson–Walker (FLRW) background with a scale factor a, the continuity equations for both components and for radiation are

$$\begin{aligned} {\dot{\rho }}_\phi +3H(\rho _\phi +p_\phi )&=-\mathscr {Q},\nonumber \\ {\dot{\rho }}_m+3H\rho _m&=\mathscr {Q},\nonumber \\ {\dot{\rho }}_r+4H\rho _r&=0, \end{aligned}$$
(1)

respectively, where \(H={\dot{a}}/a\) is the Hubble rate, \(\mathscr {Q}\) is the coupling between DM and DE and the dot is a derivative with respect to the cosmic time. A positive \(\mathscr {Q}\) corresponds to DE being transformed into DM, while negative \(\mathscr {Q}\) means the transformation in the opposite direction. In principle, the coupling can depend upon several variables \(\mathscr {Q}=\mathscr {Q}(\rho _m,\rho _\phi ,\) \( {\dot{\phi }},H,t,\dots )\), thus we assume here the first form used in the literature \(\mathscr {Q}=Q \rho _m{\dot{\phi }}\) [49, 50], where Q is a positive constant (a negative constant would give similar results). A coupling of the form \(Q \rho _\phi {\dot{\phi }}\) would have no cosmological perturbations, because as we will point out later, DE is expected not to cluster at sub-horizon scales [98]. On the other hand, a coupling \(Q (\rho _\phi +\rho _m){\dot{\phi }}\) was shown not to be viable to describe all three cosmological eras [61].

To deal with the dynamics of the system, we will define dimensionless variables. The new variables are going to characterize a system of differential equations in the form

$$\begin{aligned} X'=f[X], \end{aligned}$$
(2)

where X is a column vector of dimensionless variables and the prime is the derivative with respect to \( \log a\), where we set the present scale factor \(a_0\) to be one. The critical points \(X_c\) are those ones that satisfy \(X'=0\). In order to study stability of the fixed points, we consider linear perturbations Y around them, thus \(X=X_c+Y\). At the critical point the perturbations Y satisfy the following equation

$$\begin{aligned} Y'=\mathscr {J}Y, \end{aligned}$$
(3)

where \(\mathscr {J}\) is the Jacobian matrix. The eigenvalues of \(\mathscr {J}\) determine if the critical points are stable (if all eigenvalues are negative), unstable (if all eigenvalues are positive) or saddle points (if at least one eigenvalue is positive and the others are negative, or vice-versa).

3 Quintessence field dynamics

The real canonical scalar field \(\phi \) is described by the Lagrangian

$$\begin{aligned} \mathscr {L}=-\sqrt{-g}\left( \frac{1}{2}\partial ^\mu \phi \partial _\mu \phi +V(\phi )\right) , \end{aligned}$$
(4)

where \(V(\phi )=V_0 e^{-\lambda \phi }\) is the potential and \(V_0\) and \(\lambda >0\) are constants. A negative \(\lambda \) is obtained if the field is replaced by \(\phi \rightarrow -\phi \), thus we may restrict our attention to a positive \(\lambda \). For a homogeneous field \(\phi \equiv \phi (t)\) in an expanding Universe with FLRW metric and scale factor \(a\equiv a(t)\), the equation of motion becomes

$$\begin{aligned} {\ddot{\phi }}+3 H{\dot{\phi }}+V'(\phi )=-Q \rho _m. \end{aligned}$$
(5)

In the presence of matter and radiation, the Friedmann equations are

$$\begin{aligned} H^2= & {} \frac{1}{3}\left( \frac{{\dot{\phi }}^2}{2}+V(\phi )+ \rho _m+\rho _r\right) , \end{aligned}$$
(6)
$$\begin{aligned} {\dot{H}}= & {} -\frac{1}{2}\left( {\dot{\phi }}^2+\rho _m+\frac{4}{3}\rho _r\right) , \end{aligned}$$
(7)

and the equation of state becomes

$$\begin{aligned} w_\phi =\frac{p_\phi }{\rho _\phi }=\frac{{\dot{\phi }}^2-2 V(\phi )}{{\dot{\phi }}^2+2 V(\phi )}. \end{aligned}$$
(8)

Cosmological perturbations are the roots of structure formation, and they are reached perturbing the energy-momentum tensor and the metric. It is convenient to work in the conformal (Newtonian) gauge, where the density perturbation \(\delta \equiv \delta \rho /\rho \) and the divergence of the velocity perturbation in Fourier space \(\theta \equiv a^{-1}i k^j\delta u_j\) obey the following equations for a general interacting DE model [60]

$$\begin{aligned}&{\dot{\delta }}+\Big [3H(c^2_s-w)-\frac{\mathscr {Q}}{\rho } \Big ]\delta +(1+w)(\theta -3{\dot{\phi }})=-\frac{\delta \mathscr {Q}}{\rho },\nonumber \\&{\dot{\theta }}+\Big [H(1-3w)-\frac{\mathscr {Q}}{\rho }+\frac{{\dot{w}}}{1+w} \Big ]\theta -k^2\phi -\frac{c_s^2}{1+w}k^2\delta =0,\nonumber \\ \end{aligned}$$
(9)

where \(\phi \) is the metric perturbation in Newtonian gauge, \(c_s\equiv \delta p/\delta \rho \) is the sound speed and \( k^i\) are the components of the wave-vector in Fourier space. For radiation the density fluctuations do not cluster, and for quintessence \(c_s=1\) and DE perturbations are expected to be negligible at sub-horizon scales [98], thus they can be neglected. It is interesting, therefore, to analyse only DM perturbations, and to do so it is more convenient to merge Eq. (9) into a second-order differential equation. This is done using the Poisson equation

$$\begin{aligned} k^2\phi =-\frac{3}{2}H^2\varOmega _m\delta _m, \end{aligned}$$
(10)

whose result gives

$$\begin{aligned} {\ddot{\delta }}_m+(2H-Q{\dot{\phi }}){\dot{\delta }}_m-\frac{3}{2}H^2\varOmega _m\delta _m=0. \end{aligned}$$
(11)

Now we may proceed to the dynamical analysis of the system.

Table 1 Critical points (x, y z, \(U_m\)) for quintessence field. \(U_m\) was found only for the viable points that may describe one of the three cosmological eras. The table shows the correspondent equation of state for DE (15), the effective equation of state (16) and the density parameter for DE (13)
Full size table

4 Autonomous system

The new dimensionless variables are defined as

$$\begin{aligned}&x\equiv \frac{{\dot{\phi }}}{\sqrt{6}H}, \quad y\equiv \frac{\sqrt{V(\phi )}}{\sqrt{3}H}, \quad z\equiv \frac{\sqrt{\rho _r}}{\sqrt{3}H}, \quad \lambda \equiv -\frac{V'}{V},\nonumber \\&\varGamma \equiv \frac{VV''}{V'^2},\quad U_m\equiv \frac{\delta '_m}{\delta _m}, \end{aligned}$$
(12)

where the prime is the derivative with respect to \(N\equiv \ln a\).

The DE density parameter is written in terms of these new variables as

$$\begin{aligned} \varOmega _\phi \equiv \frac{\rho _\phi }{3H^2} = x^2+y^2, \end{aligned}$$
(13)

thus the first Friedmann Eq. (6) becomes

$$\begin{aligned} \varOmega _\phi +\varOmega _m+\varOmega _r=1, \end{aligned}$$
(14)

where the matter and radiation density parameter are defined by \(\varOmega _i=\rho _i/(3H^2)\), with \(i=m,r\). From Eqs. (13) and (14) x and y are restricted in the phase plane \(x^2+y^2\le 1\).

The equation of state \(w_\phi \) is written in terms of the dimensionless variables as

$$\begin{aligned} w_\phi =\frac{\varepsilon x^2+-y^2}{\varepsilon x^2+y^2}, \end{aligned}$$
(15)

and the total effective equation of state is

$$\begin{aligned} w_{eff} = \frac{p_\phi +p_r}{\rho _\phi +\rho _m+\rho _r}= x^2-y^2+\frac{z^2}{3}, \end{aligned}$$
(16)

with an accelerated expansion for \(w_{eff} < -1/3\). The dynamical system for the variables x, y, z, \(\lambda \) and \(U_m\) are

$$\begin{aligned} \frac{dx}{dN}= & {} -3x+\frac{\sqrt{6}}{2}y^2\lambda -\frac{\sqrt{6}}{2} Q(1-x^2-y^2-z^2)\nonumber \\&-xH^{-1}\frac{dH}{dN}, \end{aligned}$$
(17)
$$\begin{aligned} \frac{dy}{dN}= & {} -\frac{\sqrt{6}}{2}x y\lambda -yH^{-1}\frac{dH}{dN}, \end{aligned}$$
(18)
$$\begin{aligned} \frac{dz}{dN}= & {} -2z-zH^{-1}\frac{dH}{dN}, \end{aligned}$$
(19)
$$\begin{aligned} \frac{d\lambda }{dN}= & {} -\sqrt{6}\lambda ^2 x\left( \varGamma -1\right) , \end{aligned}$$
(20)
$$\begin{aligned} \frac{d U_m}{dN}= & {} -U_m(U_m+2) +\frac{3}{2}(1-x^2-y^2-z^2)\nonumber \\&+\sqrt{6}QxU_m-U_mH^{-1}\frac{dH}{dN}, \end{aligned}$$
(21)

where

$$\begin{aligned} H^{-1}\frac{dH}{dN}=-\frac{3}{2}(1+ x^2-y^2)-\frac{z^2}{2}. \end{aligned}$$
(22)

4.1 Critical points

The fixed points of the system are obtained by setting \(dx/dN=0\), \(dy/dN=0\), dz / dN, \(d\lambda /dN=0\) and \(dU_m/dN=0\) in Eqs. (17)–(21). When \(\varGamma =1\), \(\lambda \) is constant the potential is \(V(\phi )=V_0e^{-\lambda \phi }\) [72, 73]. The fixed points for coupled [50] or uncoupled quintessence [72] are well-known in the literature, and only the critical points that may satisfactorily represent one of the three cosmological eras (radiation-dominated, matter-dominated or DE-dominated) are shown in Table 1 (see [99] for a review). For those points, the additional critical point \(U_m\) was found.

The eigenvalues of the Jacobian matrix were found for each fixed point in Table 1 and the results are shown in Table 2. The eigenvalues \(\mu _{3c}\) and \(\mu _{4c}\) are

$$\begin{aligned} \mu _{3c,4c}= & {} -\frac{3 \lambda ^2+9 \lambda Q+6 Q^2}{4 (\lambda +Q)^2}\nonumber \\&\pm \frac{\sqrt{3}}{4 (\lambda +Q)}\Big [72-21 \lambda ^2-16 \lambda Q^3 \nonumber \\&-4Q^2 \left( 8 \lambda ^2-15\right) -4 \lambda \left( 4 \lambda ^2-9\right) Q\Big ]^{1/2}. \end{aligned}$$
(23)
Table 2 Eigenvalues and stability of the fixed points
Full size table

The points (a1) and (a2) are the so-called “\(\phi \)-matter-dominated epoch” (\(\phi \hbox {MDE}\)) [50] and they may describe a matter-dominated universe if \(\varOmega _\phi =2Q^2/3\ll 1\). Thus \(\mu _1\) and \(\mu _2\) are negative, while \(\mu _3\) and \(\mu _4\) are always positive. Therefore (a1) and (a2) are saddle points. In the small Q limit, described above, we have \(U_m=1-\frac{4 Q^2}{5}\) for (a1) and \(U_m=-\frac{3}{2}-\frac{Q^2}{5}\) for (a2). The point (a1) correctly describes the growth of the perturbation \(\delta _m\sim a\), with a small correction due to the coupling with DE. On the other hand, the point (a2) does not describe the expected growth of structures.

The radiation-dominated Universe is described by the critical point (b) and matter perturbations do not increase during this epoch (\(U_m=0)\). For this case, the fixed point is unstable, because it has one positive, one negative and one zero eigenvalue [100]. At the background level (without the variable \(U_m\)) (b) is a saddle point, which indicates that the presence of linear cosmological perturbations drives the point away from the unstable equilibrium (i.e. saddle).

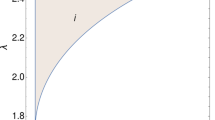
At first glance one might think that the points (c1) and (c2) could describe a matter-dominated universe, when \(Q\ll \lambda \). In this situation, we would have \(U_m=-\frac{1}{4}\left( 1\pm \sqrt{25-\frac{72}{\lambda ^2}}\right) \), which is real for \(\lambda >\frac{6 \sqrt{2}}{5}\). This value for the parameter \(\lambda \) was excluded by cosmological observations more than one decade ago [97, 101], being \(\lambda >1\) ruled out by at least the 3\(\sigma \) level [102]. Without cosmological perturbations the fixed points (c) might represent a DE-dominated Universe, although the match between the coupling constant in this case and the points (a) is difficult. In our case, both points cannot describe the late accelerated expansion of the Universe. The reason is that (c1) is a saddle point, because \(\mu _2\) is always positive while the other eigenvalues can be negative. On the other hand, (c2) could be a stable point if \(\mu _4\) were negative. This condition would be satisfied for the set of values Q and \(\lambda \) shown in Fig. 1, but as we said before, these values of \(\lambda \) are already excluded by current observations. Therefore (c2) is also a saddle point.

Fig. 1
figure 1

Allowed parameter space for Q and \(\lambda \) in order for (c2) to be a stable point. These possible values of \(\lambda \) are ruled out by current cosmological observations [102]

Full size image

Points (d1) and (d2) exist for \(\lambda ^2<6\), they can describe the accelerated expansion of the Universe if \(\lambda ^2<2\) (because \(w_{eff}<-1/3\)) and they are either saddle or stable, depending on the values of Q and \(\lambda \). The point (d1) is an attractor if \(Q<\frac{4-\lambda ^2}{2 \lambda }\), while (d2) is attractor for \(\frac{4-\lambda ^2}{2 \lambda }<Q<\frac{3-\lambda ^2}{\lambda }\). The matter perturbation is constant (\(U_m=0\)) for (d1) or decrease for (d2), indicating that the formation of structures does not happen in the DE-dominated Universe.

5 Conclusions

In this paper we have used dynamical system theory to analyse the evolution of cosmological (matter) perturbations for interacting quintessence. Previous results in the literature [50], regarding the possible fixed points that represent one of each cosmological eras, are maintained (with the exception of point (c), which no longer can describe a DE-dominated Universe) and the viable cosmological transition radiation \(\rightarrow \) matter \(\rightarrow \) DE is achieved considering the sequence of critical points (a1) \(\rightarrow \) (b) \(\rightarrow \) (d1) or (d2). The stability of these points remain similar to previous studies, i.e., to those ones considering only background evolution, for both coupled and uncoupled cases. Future constraints on the parameter \(\lambda \) will elucidate whether quintessence can still be a DE candidate with a exponential potential or not.