Abstract
We improve the determination of the Higgs-boson mass in the MSSM with heavy superpartners, by computing the two-loop threshold corrections to the quartic Higgs coupling that involve both the strong and the electroweak gauge couplings. Combined with earlier results, this completes the calculation of the two-loop QCD corrections to the quartic coupling at the SUSY scale. We also compare different computations of the relation between the quartic coupling and the pole mass of the Higgs boson at the EW scale. We find that the numerical impact of the new corrections on the prediction for the Higgs mass is modest, but comparable to the accuracy of the Higgs-mass measurement at the LHC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Minimal Supersymmetric Standard Model (MSSM) is one of the best-motivated extensions of the Standard Model (SM), and probably the most studied. The Higgs sector of the MSSM consists of two SU(2) doublets, but the model allows for a so-called “decoupling limit” in which a combination of the two doublets has SM-like couplings to matter fermions and gauge bosons – so that its neutral scalar component h can be identified with the Higgs boson discovered at the LHC [1, 2], which itself is broadly SM-like [3] – while the orthogonal combination of doublets is much heavier. An important aspect of the MSSM is the existence of relations between the quartic Higgs couplings and the electroweak (EW) gauge couplings. In the decoupling limit, these relations induce a tree-level prediction \((m_h^2)^{\mathrm{tree}} \approx m_{\scriptscriptstyle Z}^2\cos ^2 2\beta \) for the squared mass of the SM-like scalar, where \(m_{\scriptscriptstyle Z}\) is the Z-boson mass, and the angle \(\beta \) is related to the ratio of the vacuum expectation values (vevs) of the two Higgs doublets by \(\tan \beta =~v_2/v_1\), and determines their admixture into h. Consequently, in the MSSM, the tree-level contribution can only make up for at most half of the squared mass of the observed Higgs boson, \((m_h^2)^{\mathrm{obs}} \approx (125~\mathrm{GeV})^2\) [4]. The rest must arise from radiative corrections. It has been known since the early 1990s [5,6,7,8,9,10] that the most relevant corrections to the Higgs mass are those controlled by the top Yukawa coupling, \(g_t \sim {{\mathcal {O}}}(1)\), which involve the top quark and its superpartners, the stop squarks. These corrections are enhanced by logarithms of the ratio between stop and top masses, and also show a significant dependence on the value of the left–right stop mixing parameter \(X_t\). In particular, for values of \(\tan \beta \) large enough to saturate the tree-level prediction, a Higgs mass around 125 GeV can be obtained with an average stop mass \(M_S\) of about 1–2 TeV when \(X_t/M_S\approx 2\), whereas for vanishing \(X_t\) the stops need to be heavier than 10 TeV.
Over the years, the crucial role of the radiative corrections stimulated a wide effort to compute them with the highest possible precision, in order to keep the theoretical uncertainty of the Higgs-mass prediction under control. By now, that computation is indeed quite advanced: full one-loop corrections [11,12,13,14,15,16] and two-loop corrections in the limit of vanishing external momentum [17,18,19,20,21,22,23,24,25,26,27,28,29,30] are available, and the dominant momentum-dependent two-loop corrections [31,32,33,34,35] as well as the dominant three-loop corrections [36,37,38,39,40,41,42] have also been obtained.Footnote 1 However, when the SUSY scale \(M_S\) is significantly larger than the EW scale (which we can identify, e.g., with the top mass \(m_t\)), any fixed-order computation of \(m_h\) may become inadequate, because radiative corrections of order n in the loop expansion contain terms enhanced by as much as \(\ln ^n(M_S/m_t)\). In the presence of a significant hierarchy between the scales, the computation of the Higgs mass needs to be reorganized in an effective field theory (EFT) approach: the heavy particles are integrated out at the scale \(M_S\), where they only affect the matching conditions for the couplings of the EFT valid below \(M_S\); the appropriate renormalization group equations (RGEs) are then used to evolve those couplings between the SUSY scale and the EW scale, where the running couplings are related to physical observables such as the Higgs-boson mass and the masses of fermions and gauge bosons. In this approach, the computation is free of large logarithmic terms both at the SUSY scale and at the EW scale, while the effect of those terms is accounted for to all orders in the loop expansion by the evolution of the couplings between the two scales. More precisely, large corrections can be resummed to the (next-to)\(^n\)-leading-logarithmic (\(\hbox {N}^n\)LL) order by means of n-loop calculations at the SUSY and EW scales combined with \((n\!+\!1)\)-loop RGEs.
The EFT approach to the computation of the MSSM Higgs mass dates back to the early 1990s [54,55,56], and it has also been exploited in the past [57,58,59,60,61,62,63] to determine analytically the coefficients of the logarithmic terms in the Higgs-mass corrections, by solving perturbatively the appropriate systems of boundary conditions and RGEs. In recent years, after the LHC results pushed the expectations for the SUSY scale into the TeV range, the realization that an accurate prediction for the Higgs mass in the MSSM cannot prescind from the resummation of the large logarithmic corrections brought the EFT computation under renewed focus [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79]. In the simplest scenario in which all of the SUSY particles as well as the heavy Higgs doublet of the MSSM are clustered around a single scale \(M_S\), so that the EFT valid below that scale is just the SM, the state of the art now includes: full one-loop and partial two-loop matching conditions for the quartic Higgs coupling at the SUSY scale, computed for arbitrary values of the relevant SUSY parameters [66, 73]; full three-loop RGEs for all of the parameters of the SM Lagrangian [80,81,82,83,84,85]; full two-loop relations at the EW scale between the running SM parameters and a set of physical observables which include the pole Higgs mass [86,87,88]. The combination of these results allows for a full NLL resummation of the large logarithmic corrections to the Higgs mass, whereas the NNLL resummation can only be considered partial, because in refs. [66, 73] the two-loop matching conditions for the quartic Higgs coupling were computed in the “gaugeless limit” of vanishing EW gauge couplings.Footnote 2
Beyond the pure EFT calculation of the Higgs mass, different “hybrid” approaches to combine the existing “diagrammatic” (i.e., fixed-order) calculations with a resummation of the logarithmic corrections have been proposed [64, 70,71,72]. The aim is to include terms suppressed by powers of \(v^2/M_S^2\,\) (where we denote by v the vev of a SM-like Higgs scalar) up to the perturbative order accounted for by the diagrammatic calculation. In the EFT calculation, those terms can be mapped to the effect of non-renormalizable, higher-dimensional operators, and they are neglected when the theory valid below the matching scale is taken to be the plain SM in the unbroken phase of the EW symmetry. To avoid double counting, the hybrid approaches require a careful subtraction of the terms that are accounted for by both the diagrammatic and the EFT calculations, and indeed a few successive adjustments [74, 75, 79] were necessary to obtain predictions for \(m_h\) that, in the limit of very heavy SUSY masses in which the \({\mathcal {O}}(v^2/M_S^2)\) terms are certainly negligible, show the expected agreement with the pure EFT calculation. The comparison between the predictions of the hybrid and pure EFT calculations, as well as a direct study [73] of the effects of non-renormalizable operators in the EFT, also show that the \({\mathcal {O}}(v^2/M_S^2)\) corrections are significantly suppressed for the values of \(M_S\) that are large enough to allow for \(m_h\approx 125\) GeV. Other recent developments of the EFT approach include: the study of MSSM scenarios in which both Higgs doublets are light, so that the effective theory valid below the SUSY scale is a two-Higgs-doublet model (THDM) [68, 69, 77]; the application of functional techniques to the full one-loop matching of the MSSM onto the SM [92]; the calculation of one-loop matching conditions between the couplings of two generic renormalizable theories [93, 94], which can then be adapted to SUSY (or non-SUSY) models other than the MSSM.
In this paper we focus again on the simplest EFT setup in which the theory valid below the SUSY scale is the SM, and we take a further step towards the full NNLL resummation of the large logarithmic corrections. In particular, we compute the two-loop threshold corrections to the quartic Higgs coupling that involve both the strong and the EW gauge couplings. Combined with the “gaugeless” results of Refs. [66, 73], this completes the calculation of the two-loop threshold corrections that involve the strong gauge coupling. We also discuss the necessary inclusion of contributions beyond the gaugeless limit in the relation between the pole Higgs mass and the \(\overline{\mathrm{MS}}\)-renormalized quartic Higgs coupling at the EW scale, and we compare the results of the full two-loop calculations of that relation given in Refs. [86, 87], respectively. Finally, considering a representative scenario for the MSSM with heavy superpartners, we find that the numerical impact of the new corrections on the prediction for the Higgs mass is modest, but comparable to the accuracy of the Higgs-mass measurement at the LHC.
2 Two-loop matching of the quartic Higgs coupling
In this section we describe our calculation of the two-loop QCD contributions to the matching condition for the quartic Higgs coupling. We consider the setup in which all SUSY particles as well as a linear combination of the two Higgs doublets of the MSSM are integrated out at a common renormalization scale \(Q\approx M_S\), so that the EFT valid below the matching scale is the SM. In our conventions the potential for the SM-like Higgs doublet H contains the quartic interaction term \(\frac{\lambda }{2} \,|H|^4\), and the tree-level squared mass of its neutral scalar component is \((m_h^2)^{\mathrm{tree}} = 2\lambda v^2\), with \(v = \langle H^0 \rangle \approx 174\) GeV. Then the two-loop matching condition for the quartic coupling takes the form
where g and \(g^\prime \) are the EW gauge couplings, \(\beta \) can be interpreted as the angleFootnote 3 that rotates the two original MSSM doublets into a light doublet H and a massive doublet A, and \(\Delta \lambda ^{n\ell }\) is the n-loop threshold correction to the quartic coupling arising from integrating out the heavy particles at the scale Q. The complete result for the one-loop correction \(\Delta \lambda ^{1\ell }\), valid for arbitrary values of all the relevant SUSY parameters, can be found in Refs. [66, 73]. It is computed under the assumptions that \(\lambda \), g and \(g^\prime \) in Eq. (1) are \(\overline{\mathrm{MS}}\)-renormalized parameters of the SM, and that \(\beta \) is defined beyond tree level as described in section 2.2 of Ref. [66], removing entirely the contributions of the off-diagonal wave-function renormalization (WFR) of the Higgs doublets. As to the two-loop correction \(\Delta \lambda ^{2\ell }\), Ref. [66] provided the contributions of \({\mathcal {O}}(g_t^4\,g_s^2)\), where \(g_s\) is the strong gauge coupling, for arbitrary values of all the relevant SUSY parameters; Ref. [73] provided in addition the two-loop contributions involving only the third-family Yukawa couplings, \(g_t\), \(g_b\) and \(g_\tau \), again for arbitrary SUSY parameters, and also discussed some subtleties in the derivation of the \({\mathcal {O}}(g_b^4\,g_s^2)\) contributions from the known results for the \({{\mathcal {O}}}(g_t^4\,g_s^2)\) ones. Altogether, the results of Refs. [66, 73] amounted to a complete determination of \(\Delta \lambda ^{2\ell }\) in the limit of vanishing EW gauge (and first-two-generation Yukawa) couplings. In this paper we take a step beyond this “gaugeless limit” and compute the remaining corrections that involve the strong gauge coupling, namely those of \({{\mathcal {O}}}(g_{t,b}^2\,g^2 g_s^2)\), those of \({\mathcal {O}}(g_{t,b}^2 \, g^{\prime \,2}g_s^2)\) and those involving only gauge couplings, i.e. of \({{\mathcal {O}}}(g^4 g_s^2)\) and \({{\mathcal {O}}}(g^{\prime \,4}g_s^2)\).
We can decompose the “mixed” QCD–EW threshold correction to the quartic Higgs coupling into three terms:
The first term on the r.h.s. of the equation above denotes the contributions of two-loop, one-particle-irreducible (1PI) diagrams with four external Higgs fields involving both strong-interaction vertices (namely squark–gluon, four-squark or quark–squark–gluino vertices) and D-term-induced quartic Higgs–squark vertices proportional to \(g^2\) or to \(g^{\prime \,2}\), and possibly also vertices controlled by the Yukawa couplings. This term can be computed with a relatively straightforward adaptation of the effective-potential approach developed in Refs. [66, 73] for the corresponding calculation in the gaugeless limit. In contrast, the remaining terms on the r.h.s. of Eq. (2) require different approaches. The second term involves the two-loop, \({{\mathcal {O}}}(g_{t,b}^2 \, g_s^2)\) squark contributions to the WFR of the Higgs field, which multiply the tree-level quartic coupling, see Eq. (1), giving rise to \({{\mathcal {O}}}(g_{t,b}^2\,g^2 g_s^2)\) and \({{\mathcal {O}}}(g_{t,b}^2 \, g^{\prime \,2}g_s^2)\) corrections. This term requires a computation of the external-momentum dependence of the two-loop self-energy of the Higgs boson, analogous to the one performed in Refs. [31,32,33,34,35, 53] for the “diagrammatic” case. Finally, the last term on the r.h.s. of Eq. (2) arises from the fact that, while our calculation of the matching condition for the quartic Higgs coupling \(\lambda \) is performed in the \({ \overline{\mathrm{DR}}}\) renormalization scheme assuming the field content of the MSSM, in the EFT valid below the SUSY scale – i.e., the SM – \(\lambda \) is interpreted as an \(\overline{\mathrm{MS}}\)-renormalized quantity. Moreover, we find it convenient to use \(\overline{\mathrm{MS}}\)-renormalized parameters of the SM also for the EW gauge couplings entering the tree-level part of the matching condition, see Eq. (1), and for the top Yukawa coupling entering the one-loop part (but not for the bottom Yukawa coupling, as discussed in Ref. [73]). The corrections arising from the change of renormalization scheme for \(\lambda \) can in turn be extracted from the two-loop self-energy diagrams for the Higgs boson, those arising from the change of scheme and model for the EW gauge couplings require a computation of the external-momentum dependence of the two-loop self-energy of the Z boson, while those arising from the change of scheme and model for the top Yukawa coupling are easier to obtain, being just the product of one-loop terms. In the rest of this section we will describe in more detail our computation of each of the three terms on the r.h.s. of Eq. (2).
2.1 1PI contributions
The 1PI, two-loop contribution to the matching condition for the quartic Higgs coupling can be expressed as
where \(\Delta V^{2\ell ,\,{\tilde{q}}}\) denotes the contribution to the MSSM scalar potential from two-loop diagrams involving the strong gauge interactions of the squarks, and the derivatives are computed at \(H=0\) because we perform the matching between the MSSM and the SM in the unbroken phase of the EW symmetry. Since the strong interactions do not mix different types of squarks, we will now describe the derivation of the stop contribution to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\), and later describe how to translate it into the sbottom contribution and into the contributions of the squarks of the first two generations.
It is convenient to start from the well-known expression for the stop contribution of \({{\mathcal {O}}}(g_s^2)\) to the MSSM scalar potential in the broken phase of the EW symmetry [20],
where \(\kappa = 1/(16\pi ^2)\) is a loop factor, \(C_F=4/3\) and \(N_c=3\) are color factors, the loop integrals I(x, y, z), L(x, y, z) and J(x, y) in Eq. (4) are defined, e.g., in appendix D of Ref. [95], \(m_{\tilde{g}}\) stands for the gluino mass, \(m_{\tilde{t}_1}\) and \(m_{\tilde{t}_2}\) are the two stop-mass eigenstates, and \( \theta _{t}\) denotes the stop mixing angle. The latter is related to the top and stop masses and to the left–right stop mixing parameter by
We recall that \(X_t = A_t - \mu \cot \beta \), where \(A_t\) is the trilinear soft SUSY-breaking Higgs-stop interaction term and \(\mu \) is the Higgs-higgsino mass parameter in the superpotential (in fact, those two parameters enter our results only combined into \(X_t\)). To compute the fourth derivative of the effective potential entering Eq. (3) we express the stop masses and mixing angle as functions of a field-dependent top mass \(m_t = {\hat{g}}_t\,|H|\), where by \({\hat{g}}_t\) we denoteFootnote 4 a SM-like Yukawa coupling related to its MSSM counterpart \({\hat{y}}_t\) by \({\hat{g}}_t = {\hat{y}}_t\sin \beta \), and of a field-dependent Z-boson mass \(m_{\scriptscriptstyle Z}= \hat{g}_{\scriptscriptstyle Z}\,|H|\), where we define \(\hat{g}_{\scriptscriptstyle Z}^2 = ({\hat{g}}^2 + {\hat{g}}^{\prime \,2})/2\). We then obtain
where the last term is obtained from the previous ones by swapping top and Z, and we used the shortcuts
The terms proportional to \(g_t^4\) in the second line of Eq. (6) give rise to the \({{\mathcal {O}}}(g_t^4\,g_s^2)\) contributions to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) already computed in Ref. [66], and we will not consider them further. We will focus instead on the mixed QCD–EW contributions to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) arising from the terms in Eq. (6) that are proportional to \(g_t^2\,g_{\scriptscriptstyle Z}^2\) and to \(g_{\scriptscriptstyle Z}^4\). To obtain the derivatives with respect to \(m_t\) and \(m_{\scriptscriptstyle Z}\) of the stop masses and mixing entering \(\Delta V^{2\ell ,\,{\tilde{t}}}\) we exploit the relations
where
\(\theta _{\scriptscriptstyle W}\) being the Weinberg angle. After taking the required derivatives of \(\Delta V^{2\ell ,\,{\tilde{t}}}\) with respect to \(m_t^2\) and \(m_{\scriptscriptstyle Z}^2\), we use Eq. (5) to make the dependence of \(\theta _t\) on \(m_t\) explicit; we expand the function \(\Phi (m^2_{\tilde{t}_{i}},m_{\tilde{g}}^2,m_t^2)\) entering the loop integrals (see appendix D of Ref. [95]) in powers of \(m_t^2\); we take the limit \(|H|\rightarrow \) 0, leading to \(m_t,m_{\scriptscriptstyle Z}\,\rightarrow 0\); and we identify \(m_{\tilde{t}_1}\) and \(m_{\tilde{t}_2}\) with the soft SUSY-breaking stop mass parameters \(m_{Q_3}\) and \(m_{U_3}\). We remark that, differently from the \({{\mathcal {O}}}(g_t^4\,g_s^2)\) contributions computed in Ref. [66] and the \({{\mathcal {O}}}(g_t^6)\) contributions computed in Ref. [73], the mixed QCD–EW contributions to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) computed here do not contain infrared divergences that need to be canceled out in the matching of the quartic Higgs coupling between MSSM and SM. Also, the terms proportional to \( g_t^2g_{\scriptscriptstyle Z}^2\) and to \(g_{\scriptscriptstyle Z}^4\) in Eq. (6) that involve more than two derivatives of the two-loop effective potential vanish directly when we take the limit \(|H|\rightarrow 0\), thus the mixed QCD–EW contributions to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) can be related as usual to the corresponding two-loop corrections to the Higgs mass.
In order to obtain the contributions to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) from diagrams involving sbottoms, it is sufficient to perform the replacements \(g_t\rightarrow g_b\,\), \(X_t\rightarrow X_b\,\), \(m_{U_3}\rightarrow m_{D_3}\) and \(d_{{\scriptscriptstyle L},{\scriptscriptstyle R}}^t\rightarrow d_{{\scriptscriptstyle L},{\scriptscriptstyle R}}^b\) in the contributions from diagrams involving stops, with
Finally, we recall that our calculation neglects the Yukawa couplings of the first two generations. The contributions to \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) from diagrams involving up-type (or down-type) squarks of the first two generations can be obtained by setting \(g_t =0\) (or \(g_b =0\)) in the contributions from diagrams involving stops (or sbottoms), and replacing the soft SUSY-breaking stop (or sbottom) mass parameters with those of the appropriate generation.
The result for \(\Delta \lambda ^{2\ell ,\mathrm{1{\scriptscriptstyle PI}}}\) with full dependence on all of the input parameters is lengthy and not particularly illuminating, and we make it available upon request – together with all of the other corrections computed in this paper – in electronic form. We show here a simplified result valid in the limit in which all squark masses (\(m_{Q_i},\, m_{U_i},\, m_{D_i},\,\) with \(i=1,2,3\)) as well as the gluino mass \(m_{\tilde{g}}\) are set equal to a common SUSY scale \(M_S\). In units of \(\kappa ^2\,g_s^2\,C_FN_c\), we find
where \((t\rightarrow b)\) denotes terms obtained from the previous ones within square brackets via the replacements \(g_t\rightarrow g_b\) and \(X_t \rightarrow X_b\). We remark in passing that there are no contributions of \({{\mathcal {O}}}(g^2\,g^{\prime \,2}\,g_s^2)\), because the corresponding diagrams involve the trace of the generators of the SU(2) gauge group.
2.2 WFR contributions
Differently from the case of the “gaugeless” corrections computed in Refs. [66, 73], where the quartic Higgs coupling can be considered vanishing at tree level, the mixed QCD–EW corrections include a contribution in which the tree-level coupling is combined with the two-loop WFR of the Higgs field. This reads
where \({\hat{\Pi }}_{hh}^{2\ell ,\,{\tilde{q}}}\) denotes the contribution to the renormalized Higgs-boson self-energyFootnote 5 from two-loop diagrams involving the strong gauge interactions of the squarks, and the derivative is taken with respect to the external momentum \(p^2\). In this case the notation \(H=0\) means that, after having taken the derivative, we take the limit \(v\rightarrow 0\). This implies \(m_q,m_{\scriptscriptstyle Z}\rightarrow 0\) as well as \(p^2\rightarrow 0\) (because \(p^2\) is ultimately set to \(2\lambda v^2\)). Finally, the shift \(\Delta _{\mathrm{{\scriptscriptstyle WFR}}}\) stems from the matching of the one-loop WFR, and will be discussed below.
The relevant two-loop self-energy diagrams are generated with FeynArts [96], using a modified version of the original MSSM model file [97] that implements the QCD interactions in the background field gauge. The color factors are simplified with a private package and the Dirac algebra is handled by TRACER [98]. In order to obtain a result valid in the limit \(v\rightarrow 0\), we performed an asymptotic expansion of the self-energy in the heavy superparticle masses analogous to the one described in section 3 of Ref. [99]. As a useful cross-check of our result, we verified that it agrees with the one that can be obtained by taking appropriate limits in the explicit analytic formulae for the Higgs-boson self-energy given in Refs. [31,32,33].
Our result for the derivative of the two-loop self-energy with full dependence on all of the input parameters is in turn made available upon request. In the simplified scenario of degenerate superparticle masses we find, in units of \(\kappa ^2\,g_s^2\,C_FN_c\),
We remark that there are no contributions proportional to the EW gauge couplings. This is due to the fact that, in the limit of unbroken EW symmetry, the D-term-induced \({{\mathcal {O}}}(g^2)\) and \({\mathcal {O}}(g^{\prime \,2})\) couplings of the Higgs boson to squarks enter only self-energy diagrams that do not depend on the external momentum. We also remark that the derivative of the two-loop self-energy has logarithmic infra-red (IR) divergences in the limit \(p^2\rightarrow 0\), see the last term within square brackets in the third line of Eq. (14). These divergences cancel out in the matching of the Higgs-boson WFR between the MSSM and the SM. Indeed, in the limit \(v\rightarrow 0\) the one-loop contribution of top and bottom quarks to the derivative of the self-energy, which is present both above and below the matching scale, reads
However, the top and bottom Yukawa couplings must be interpreted as the ones of the MSSM above the matching scale, and the ones of the SM below the matching scale. Thus, in the matching between the MSSM and the SM the derivative of the two-loop Higgs self-energy receives the shift
where \(\Delta g_t^{{\tilde{t}},\,g_s^2}\) denotes the one-loop, \({\mathcal {O}}(g_s^2)\) contribution from diagrams involving stops to the difference between the MSSM coupling \({\hat{g}}_t\) and the SM coupling \(g_t\),
and the analogous shift in the bottom Yukawa coupling, \(\Delta g_b^{{\tilde{b}},\,g_s^2}\), can be obtained from Eq. (17) with the replacements \(m_{U_3}\rightarrow m_{D_3}\) and \(X_t\rightarrow X_b\). The loop functions \(\widetilde{F}_6(x)\) and \(\widetilde{F}_9(x,y)\) are defined in the appendix A of Ref. [66]. Using the limits \(\widetilde{F}_6(1)=0\) and \(\widetilde{F}_9(1,1)=1\) it is easy to see that, for degenerate superparticle masses, the shifts in Eq. (16) cancel out entirely the terms within square brackets in the third line of Eq. (14). We have of course checked that the cancellation of the IR divergences in the matching holds even when we retain the full dependence on all of the relevant superparticle masses.
2.3 Contributions arising from the definitions of the couplings
The third contribution to the mixed QCD–EW correction to the quartic Higgs coupling in Eq. (2), which we denoted as \(\Delta \lambda ^{2\ell ,\,\mathrm{{\scriptscriptstyle RS}}}\), collects in fact three separate contributions arising from differences in the renormalization scheme used for the couplings of the MSSM and for those of the EFT valid below the matching scale (i.e., the SM):
The first contribution in the equation above stems from the fact that supersymmetry provides a prediction for the \({ \overline{\mathrm{DR}}}\)-renormalized quartic Higgs coupling, whereas we interpret the parameter \(\lambda \) in the EFT as renormalized in the \(\overline{\mathrm{MS}}\) scheme. The difference between \(\lambda ^{\scriptscriptstyle {\overline{\mathrm{DR}}}}\) and \(\lambda ^{\scriptscriptstyle {\overline{\mathrm{MS}}}}\) contains terms of \({{\mathcal {O}}}(\lambda \,g_t^2\,g_s^2)\) and \({\mathcal {O}}(\lambda \,g_b^2\,g_s^2)\), arising from the dependence on the regularization method of the two-loop quark–gluon contributions to the Higgs WFR, which translate to mixed QCD–EW terms when \(\lambda \) is replaced by its tree-level MSSM prediction. In the limit \(v\rightarrow 0\) we find
where DRED and DREG stand for dimensional reduction and dimensional regularization, respectively. This is again in agreement with the result that can be obtained by taking the appropriate limits in the analytic formulae of Refs. [31,32,33]. The first term on the r.h.s. of Eq. (19) contains an IR divergence for \(p^2\rightarrow 0\), but that term cancels out in the matching between MSSM and SM when the top and bottom Yukawa couplings entering the one-loop quark contribution to the WFR, see Eq. (15), are translated from the \({ \overline{\mathrm{DR}}}\) scheme to the \(\overline{\mathrm{MS}}\) scheme according to
The surviving term on the r.h.s. of Eq. (19) then leads to the following correction to the quartic Higgs coupling:
Supersymmetry connects the tree-level quartic Higgs coupling to the \({ \overline{\mathrm{DR}}}\)-renormalized EW gauge couplings of the MSSM. Since we choose instead to express the tree-level part of the matching condition for \(\lambda \), see Eq. (1), in terms of \(\overline{\mathrm{MS}}\)-renormalized couplings of the SM, the threshold correction \(\Delta \lambda ^{2\ell }\) receives an additional shift, i.e. the second contribution in Eq. (18). The relation between the two sets of EW gauge couplings reads
where the ellipsis denotes one- and two-loop terms that are not of \({{\mathcal {O}}}(g^4\,g_s^2)\) or \({{\mathcal {O}}}(g^{\prime \,4}\,g_s^2)\). We denote by \({\hat{\Pi }}_{{\scriptscriptstyle Z}{\scriptscriptstyle Z}}^{2\ell ,\,q}\) the two-loop quark–gluon contribution to the transverse part of the renormalized Z-boson self-energy, computed either in dimensional reduction or in dimensional regularization, and by \({\hat{\Pi }}_{{\scriptscriptstyle Z}{\scriptscriptstyle Z}}^{2\ell ,\,{\tilde{q}}}\) the contribution from two-loop diagrams involving the strong gauge interactions of the squarks.Footnote 6 The notation \(H=0\) means again the limit \(v\rightarrow 0\), which in this case can be obtained by Taylor expansion in \(m_q^2\) and \(p^2\), since both the squark contribution and the DRED–DREG difference of the quark contribution are free of IR divergences. In units of \(\kappa ^2\,g_s^2\,C_FN_c\) , we find
where the two terms within curly brackets in the first line account for the \({ \overline{\mathrm{DR}}}\)–\(\overline{\mathrm{MS}}\) conversion of \(g^2\) and \(g^{\prime \,2}\), respectively, whereas the remaining terms (where the sum runs over three squark generations) account for their MSSM–SM threshold correction. The function \(F(m_{{\tilde{q}}}^2,m_{\tilde{g}}^2)\) is defined as
We checked that the explicit renormalization-scale dependence of the \({{\mathcal {O}}}(g^4\,g_s^2)\) and \({{\mathcal {O}}}(g^{\prime \,4}\,g_s^2)\) threshold corrections to \(g^2\) and \(g^{\prime \,2}\) is consistent with what can be inferred from the difference between their \(\beta \)-functions in the SM [100] and in the MSSM [101,102,103].
Finally, the third contribution in Eq. (18) arises from the fact that we choose to express the \({{\mathcal {O}}}(g^2\,g_t^2)\) and \({{\mathcal {O}}}(g^{\prime \,2}\,g_t^2)\) terms in the one-loop threshold correction to the quartic Higgs coupling in terms of the \(\overline{\mathrm{MS}}\)-renormalized top Yukawa coupling of the SM. The resulting shift in the two-loop correction reads
where \(\Delta g_t^{{\tilde{t}},\,g_s^2}\) and \(\Delta g_q^{{\scriptscriptstyle \mathrm{reg}},\,g_s^2}\) are the one-loop, \({\mathcal {O}}(g_s^2)\) shifts given in Eqs. (17) and (20), respectively, and
where \(x_{\scriptscriptstyle QU}=m_{Q_3}/m_{U_3}\) and the loop functions \(\widetilde{F}_3(x)\), \(\widetilde{F}_4(x)\) and \(\widetilde{F}_5(x)\) are defined in the appendix A of Ref. [66]. Note that all three functions are equal to 1 for \(x=1\).
2.4 Combining all contributions
We now provide a result that combines all of the contributions discussed in the previous sections, valid in the limit of degenerate superparticle masses \(m_{Q_i}=m_{U_i}=m_{D_i}=m_{\tilde{g}}=M_S\). In units of \(\kappa ^2\,g_s^2\,C_FN_c\) , we find

As a non-trivial check of our final result, we verified that by taking the derivative of the r.h.s. of Eq. (1) with respect to \(\ln Q^2\) we can recover the \({{\mathcal {O}}}(\lambda \,g_t^2\,g_s^2)\) and \({{\mathcal {O}}}(\lambda \,g_b^2\,g_s^2)\) terms of the \(\beta \)-function for the quartic Higgs coupling of the SM [104]:
To this effect, we must combine the explicit scale dependence of our result for \(\Delta \lambda ^{2\ell ,\,\mathrm{{\scriptscriptstyle QCD\text{- }EW}}}\) with the implicit scale dependence of the parameters that enter the tree-level and one-loop parts of the matching condition (for the squark contributions to the latter, see the appendix of Ref. [73]). In particular, we need the terms that involve the strong gauge coupling in the two-loop \(\beta \)-functions of the EW gauge couplings [100],
in the two-loop \(\beta \)-function of \(c_{2\beta }\) [105],
and in the one-loop \(\beta \)-functions of the parameters that enter \(\Delta \lambda ^{1\ell }\),
Note that in Eqs. (29)–(32) we distinguish the (hatted) \({ \overline{\mathrm{DR}}}\)-renormalized couplings of the MSSM from the (unhatted) \(\overline{\mathrm{MS}}\)-renormalized couplings of the SM (however, the distinction is irrelevant for the strong gauge coupling, which enters only the two-loop part of the calculation). Finally, to recover Eq. (28) we need to convert the remaining MSSM Yukawa couplings in the one-loop part of the derivative of \(\lambda \) into their SM counterparts, and exploit in the two-loop part the tree-level MSSM relation to replace \((g^2+g^{\prime \,2})\,c_{2\beta }^2\) with \(4\lambda \).
3 The EW-scale determination of the Higgs mass
A consistent determination of the Higgs mass in the EFT approach requires that the relation between the pole Higgs mass and the \(\overline{\mathrm{MS}}\)-renormalized quartic Higgs coupling at the EW scale be computed at the same perturbative order in the various SM couplings as the SUSY-scale threshold correction \(\Delta \lambda \). In particular, the “gaugeless” calculation of Refs. [66, 73] requires a full determination of the one-loop corrections to the Higgs mass at the EW scale, combined with the two-loop corrections obtained in the limit \(g=g^{\prime }=\lambda =0\). Denoting the scale at which we perform the calculation of the Higgs mass as \(Q_{\mathrm{{\scriptscriptstyle EW}}}\), this approximation implies
where \(G_F\) is the Fermi constant, \(\delta ^{1\ell }\) is the one-loop correction first computed in Ref. [106], and \(\ell _t =~\ln (m_t^2/Q_{\mathrm{{\scriptscriptstyle EW}}})\). The two-loop terms in the second and third lines of Eq. (33) are taken from Ref. [107]. Note that the form of the \({{\mathcal {O}}}(g_t^4\,m_t^2)\) terms implies that the top-quark contribution to \(\delta ^{1\ell }\) is expressed in terms of \(\overline{\mathrm{MS}}\)-renormalized top and Higgs masses. Also, note that Eq. (33) omits for conciseness all corrections involving the bottom and tau Yukawa couplings, which in the SM are greatly suppressed with respect to their top-only counterparts.
In the SUSY-scale calculation of \(\Delta \lambda ^{2\ell }\) described in Sect. 2 we go beyond the gaugeless limit, and we include contributions that involve both the EW gauge couplings and the strong gauge coupling. Strictly speaking, to match the accuracy of that calculation at the EW scale we only need to replace the \({\mathcal {O}}(g_t^2\,g_s^2\,m_t^2)\) terms in Eq. (33) with the complete contributions arising from two-loop diagrams involving quarks and gluons, retaining the dependence on the external momentum in the Higgs self-energy. Explicit formulae for those contributions are provided in Ref. [108]. However, the full two-loop contributions to the relation between the pole Higgs mass, \(\lambda (Q_{\mathrm{{\scriptscriptstyle EW}}})\) and \(G_F\) in the SM are also available [86,87,88]. These contributions can in principle be implemented in our EFT calculation, to prepare the ground for the eventual completion of the NNLL resummation of the large logarithmic corrections. We stress that the inclusion at the EW scale of two-loop corrections whose counterparts are still missing at the SUSY scale cannot be claimed to improve the overall accuracy of the calculation, but it does not degrade it either. Indeed, in the EFT approach the EW-scale and SUSY-scale sides of the calculation are separately free of log-enhanced terms, and the inclusion of additional pieces in only one side does not entail the risk of spoiling crucial cancellations between large corrections.
The results of the full two-loop calculation of Ref. [86] were made public in the form of interpolating formulae. In particular, the relation between the Higgs quartic coupling and the pole Higgs and top masses readsFootnote 7
where the remaining input parameters – namely, the gauge-boson masses, \(G_F\) and \(g_s(m_{\scriptscriptstyle Z})\) – are set to the central values listed in Ref. [86]. Equation (34) can be exploited to treat the measured value of the Higgs mass as an input parameter: it is then possible to evolve \(\lambda \) to the SUSY scale using the RGEs of the SM, and use the threshold condition in Eq. (1) to determine one of the MSSM parameters (e.g., a common mass scale for the stops, or the stop mixing parameter \(X_t\,\), or \(\tan \beta \)) as a function of the others. In alternative, Eq. (34) can be inverted to predict the Higgs mass starting from a full set of MSSM parameters, using the value of \(\lambda (m_t)\) obtained by evolving the \(\lambda (M_S)\) computed in Eq. (1) down to the EW scale. In the latter approach, a phenomenological analysis of the MSSM may well encounter points of the parameter space in which the prediction for the Higgs mass is several GeV away from the measured value. It is then legitimate to wonder about the range of validity of the linear interpolation involved in Eq. (34), which was obtained in a pure-SM context with the (small) uncertainty of the Higgs mass measurement in mind.
Difference (in MeV) between the Higgs mass given as input to the code mr and the Higgs mass obtained by inserting in Eq. (34) the value of \(\lambda (m_t)\) computed by mr, as a function of the input Higgs mass
To test Eq. (34), we compare its predictions against those of the independent two-loop calculation presented in Ref. [87]. The latter is made available in the public code mr [109], which computes the \(\overline{\mathrm{MS}}\)-renormalized parameters of the SM Lagrangian from a set of physical observables that includes \(G_F\) and the pole masses of the Higgs and gauge bosons and of the top and bottom quarks. We start from an input value for the pole Higgs mass ranging between 120 GeV and 130 GeV, feed it into mr, then insert the value of \(\lambda (m_t)\) computed by mr into Eq. (34) to obtain a new prediction for \(m_h\) according to the calculation of Ref. [86]. The remaining input parameters are fixed to the central values considered in Ref. [86]. In Fig. 1 we plot the difference between the initial and final values of \(m_h\), which can be taken as a measure of the discrepancy between the two calculations, as a function of the initial value. In the vicinity of \(m_h= 125\) GeV, where the interpolation involved in Eq. (34) can be expected to be accurate, the two values of \(m_h\) differ by about 20 MeV, i.e. by less than \(0.02\%\). This is well within the theoretical uncertainty estimated in the last term of Eq. (34), which implies a shift in \(m_h\) of about 150 MeV. Such a good numerical agreement is particularly remarkable in view of the fact that the calculations of Refs. [86, 87] differ substantially in what concerns the renormalization of the Higgs vev and the corresponding treatment of the tadpole contributions (they also differ in the treatment of higher-order QCD corrections to the top Yukawa coupling). When we move away from the observed value of the Higgs mass, the discrepancy between the two calculations varies, reaching up to about 120 MeV for the lowest considered value \(m_h=120\) GeV. While such discrepancy remains within the theoretical uncertainty of Eq. (34), the behavior of the blue line in Fig. 1 suggests that, for values of \(m_h\) a few GeV away from the observed one, the linear interpolation loses accuracy and the full dependence on the value of the Higgs mass should be taken into account.
Finally, we performed an analogous test on the \(m_t\) dependence of Eq. (34), keeping the value of the pole Higgs mass that we feed into mr fixed to 125.15 GeV, and varying the pole top mass by \(\pm 2\) GeV around its central value of 173.34 GeV. We find that the difference between the initial value of \(m_h\) and the one obtained by inserting in Eq. (34) the value of \(\lambda (m_t)\) computed by mr varies only by about 10 MeV in the considered range of \(m_t\). This suggests that the linear interpolation of the dependence on the pole top mass in Eq. (34) is not problematic.
4 Impact of the mixed QCD–EW corrections
In this section we investigate the numerical impact of the mixed QCD–EW threshold corrections to the quartic Higgs coupling on the prediction for the Higgs mass in the MSSM with heavy superpartners. We use the code mr [109] to extract – at full two-loop accuracy – the \(\overline{\mathrm{MS}}\)-renormalized parameters of the SM Lagrangian from a set of physical observables, and to evolve them up to the SUSY scale using the three-loop RGEs of the SM. As mentioned in the previous section, in our EFT approach the fact that we combine a full two-loop calculation at the EW scale with an incomplete two-loop calculation at the SUSY scale does not entail the risk of spoiling crucial cancellations between large corrections. Throughout the section we use the world average \(m_t= 173.34\) GeV [110] for the pole top mass, and fix the remaining physical inputs (other than the Higgs mass) to their current PDG values [111], namely \(G_F= 1.1663787 \times 10^{-5}\) \(\hbox {GeV}^{-2}\), \(m_{\scriptscriptstyle Z}= 91.1876\) GeV, \(m_{\scriptscriptstyle W}= 80.385\) GeV, \(m_b= 4.78\) GeV and \(\alpha _s(m_{\scriptscriptstyle Z})=0.1181\).
In order to obtain a prediction for the Higgs mass from a full set of MSSM parameters, we vary the value of the pole mass \(m_h\) that we give as input to mr until the value of the \(\overline{\mathrm{MS}}\)-renormalized SM parameter \(\lambda (Q)\) returned by the code at the SUSY scale \(Q=M_S\) coincides with the MSSM prediction of Eq. (1). In addition to the mixed QCD–EW corrections to the quartic Higgs coupling computed in this paper, we use the results of Refs. [66, 73] for the full one-loop correction \(\Delta \lambda ^{1\ell }\) and for the “gaugeless” part of the two-loop correction \(\Delta \lambda ^{2\ell }\). We recall that, as discussed in Ref. [73], we must also convert the \(\overline{\mathrm{MS}}\)-renormalized bottom Yukawa coupling \(g_b(M_S)\) returned by mr into its \({ \overline{\mathrm{DR}}}\)-renormalized MSSM counterpart, \({\hat{g}}_b(M_S)\), to avoid the occurrence of potentially large \(\tan \beta \)-enhanced terms in \(\Delta \lambda ^{2\ell }\). To this effect, we make use of Eqs. (8), (9), (12) and (13) of Ref. [73].
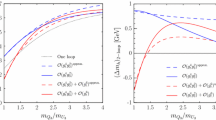
Difference (in MeV) between the predictions for the Higgs mass obtained with and without the inclusion of the mixed QCD–EW corrections to the quartic Higgs coupling, as a function of a common SUSY scale \(M_S\), for \(X_t=\sqrt{6}\,M_S\) (lower, blue lines) or \(X_t=2\,M_S\) (upper, red lines), and \(A_b=A_\tau =A_t\). In each set of lines the solid one is obtained with \(\tan \beta =20\) and the dashed one with \(\tan \beta =5\). The star on each line marks the value of \(M_S\) for which the improved calculation of \(\Delta \lambda ^{2\ell }\) leads to \(m_h= 125.09\) GeV
In Fig. 2 we show the difference (in MeV) between the EFT predictions for the Higgs mass obtained with and without the inclusion of the mixed QCD–EW corrections to the quartic Higgs coupling. We consider a simplified MSSM scenario in which the masses of all superparticles (sfermions, gauginos and higgsinos) as well as the mass of the heavy Higgs doublet are set equal to the common SUSY scale \(M_S\), which we vary between 1 TeV and 20 TeV. The left–right stop mixing parameter is fixed either as \(X_t=\sqrt{6} \,M_S\) (lower, blue lines) or \(X_t=2\,M_S\) (upper, red lines). In each set of lines the solid one is obtained with \(\tan \beta =20\) and the dashed one with \(\tan \beta =5\). The remaining input parameters are the trilinear Higgs–sfermion interaction terms for sbottoms and staus, which we fix as \(A_b=A_\tau =A_t\). We remark that all of the MSSM parameters are interpreted as \({ \overline{\mathrm{DR}}}\)-renormalized quantities expressed at the renormalization scale \(Q=M_S\). The star on each line marks the value of \(M_S\) for which the improved calculation of \(\Delta \lambda ^{2\ell }\) (i.e., including the mixed QCD–EW corrections) leads to the observed value of the Higgs mass, \(m_h= 125.09\) GeV [4].
Values of the common SUSY scale \(M_S\) and of the stop mixing term \(X_t\) that lead to \(m_h= 125.09\) GeV, for \(\tan \beta =20\) and \(A_b=A_\tau =A_t\). The dotted line is obtained including only the one-loop threshold corrections to the Higgs quartic coupling, the dashed line includes the two-loop corrections in the gaugeless limit, and the solid line includes also the effect of the mixed QCD–EW corrections
Figure 2 shows that, in the considered scenario, the mixed QCD–EW corrections computed in this paper are fairly small, shifting the MSSM prediction for \(m_h\) downwards by \({\mathcal {O}}(100)\) MeV. The fact that the corrections are reduced (in absolute value) for larger values of \(M_S\) is partially due to the scale dependence of the relevant couplings: with the exception of \(g^\prime \), they all decrease with increasing \(Q=M_S\). The comparison between the solid and dashed lines in each set shows that the dependence of the mixed QCD–EW corrections on \(\tan \beta \) is rather mild (in contrast, the overall prediction for \(m_h\) depends strongly on \(\tan \beta \), as shown by the relative position of the stars on the solid and dashed lines). Finally, the comparison between the lower (blue) and upper (red) sets of lines shows that the mixed QCD–EW corrections depend rather strongly on the ratio \(|X_t/M_S|\), with smaller ratios leading to smaller corrections. Indeed, we checked that for \(|X_t/M_S| < 1\) the effect of the corrections can be at most of \({{\mathcal {O}}}(10)\) MeV in the considered scenario.
An alternative way to assess the effect of the newly-computed corrections consists in taking the measured value of the Higgs mass as an input parameter, and using the matching condition on the quartic Higgs coupling at the SUSY scale, Eq. (1), to constrain the MSSM parameters. In Fig. 3 we show the values of \(M_S\) and \(X_t\) that lead to \(m_h= 125.09\) GeV, in the simplified scenario with degenerate superparticle and heavy-Higgs masses, for \(\tan \beta =20\) and \(A_b=A_\tau =A_t\). We focus on values of the ratio \(X_t/M_S\) between 2 and 2.5, which allow for SUSY masses around 2 TeV (i.e., roughly at the limit of the HL-LHC reach [112]). Once again, all of the MSSM parameters are interpreted as \({ \overline{\mathrm{DR}}}\)-renormalized quantities expressed at the renormalization scale \(Q=M_S\). The (black) dotted line in Fig. 3 is obtained including only the one-loop threshold corrections to the Higgs quartic coupling, the (blue) dashed line includes the two-loop corrections in the gaugeless limit, and the (red) solid line includes also the effect of the mixed QCD–EW corrections. Unsurprisingly, the comparison between the three lines shows that the mixed QCD–EW corrections are sub-dominant with respect to the two-loop corrections computed in the gaugeless limit. Nevertheless, they can shift the value of \(M_S\) that leads to the observed Higgs mass by \({{\mathcal {O}}}(100)\) GeV in the direction of heavier superparticles.
5 Conclusions
If the MSSM is realized in nature, both the measured value of the Higgs mass and the negative results of the searches for superparticles at the LHC suggest some degree of separation between the SUSY scale and the EW scale. In this scenario, the MSSM prediction for the Higgs mass is subject to potentially large logarithmic corrections, making a fixed-order calculation of \(m_h\) inadequate and calling for an all-orders resummation in the EFT approach.
In this paper we improved the EFT calculation of the Higgs mass in the MSSM, by computing the class of two-loop threshold corrections to the quartic Higgs coupling that involve both the strong and the EW gauge couplings. Combined with the \({{\mathcal {O}}}(g_t^4\,g_s^2)\) and \({\mathcal {O}}(g_b^4\,g_s^2)\) corrections previously provided in Refs. [66, 73], this completes the calculation of the two-loop threshold corrections that involve the strong gauge coupling. Our calculation involves novel complications with respect to the case of the “gaugeless” two-loop corrections of Refs. [66, 73]. While in the latter all two-loop diagrams could be computed in the effective potential approach (i.e., for vanishing external momenta), the mixed QCD–EW corrections include contributions from the \({{\mathcal {O}}}(p^2)\) parts of the two-loop self-energies of the Higgs and gauge bosons. We obtained results for the threshold corrections to the quartic Higgs coupling valid for generic values of all the relevant SUSY parameters, which we make available on request in electronic form. For the sake of illustration, in Sect. 2 we provided explicit formulae in the simplified limit of degenerate superparticle masses.
We remark that our calculation can be trivially adapted also to the split-SUSY scenario in which the gluino is much lighter than the squarks, by taking the limit of vanishing gluino mass in our full results. On the other hand, in scenarios in which the gluino is heavier than the squarks the two-loop corrections to the quartic Higgs coupling contain potentially large terms enhanced by powers of the ratios between the gluino mass and the squark masses. This is a well-known aspect of the \({ \overline{\mathrm{DR}}}\) renormalization of the squark masses and trilinear couplings [24, 67, 73, 113], which could be addressed either by devising an “on-shell” scheme adapted to the heavy-SUSY setup, or by building a tower of EFTs in which the gluino is independently decoupled at a higher scale than the squarks.
In the EFT approach, the inclusion of new threshold corrections to the quartic Higgs coupling at the SUSY scale mandates that corrections of the same perturbative order in the relevant couplings be included in the calculation of the pole Higgs mass at the EW scale. In the simplest heavy-SUSY setup in which the effective theory valid below the SUSY scale is just the SM, we can exploit the full two-loop calculations of the relation between \(m_h\), \(\lambda (Q_{\mathrm{{\scriptscriptstyle EW}}})\) and \(G_F\) presented in Refs. [86,87,88]. In Sect. 3 we compared the results of two of those calculations, Refs. [86, 87], discussing the range of validity of an interpolating formula provided in Ref. [86].
In Sect. 4 we investigated the numerical impact of the mixed QCD–EW corrections to the quartic Higgs coupling. We considered a simplified MSSM scenario with degenerate masses for all superparticles and for the heavy Higgs doublet, focusing on the region of the parameter space in which the prediction for the Higgs mass is close to the observed value and the stop squarks are in principle still accessible at the HL-LHC. We used the code mr [109], based on the calculation of Ref. [87], to extract all of the SM couplings from a set of physical observables and to evolve them up to the SUSY scale, where we compare the value of the quartic Higgs coupling with its MSSM prediction. We found that the impact of the newly-computed two-loop corrections on the prediction for the Higgs mass tends to be small, and it is certainly sub-dominant with respect to the impact of the “gaugeless” two-loop corrections. In the considered scenario, the mixed QCD–EW corrections can shift the prediction for the Higgs mass by \({{\mathcal {O}}}(100)\) MeV, and they can shift the values of the stop masses required to obtain the observed value of \(m_h\) by \({\mathcal {O}}(100)\) GeV.
We stress that the smallness of these effects is in fact a desirable feature of the EFT approach to the calculation of the Higgs mass. While the logarithmically enhanced corrections are accounted for by the evolution of the parameters between the matching scale and the EW scale, and high-precision calculations at the EW scale can be borrowed from the SM, the small impact of new two-loop corrections computed at the SUSY scale suggests that the uncertainty associated to uncomputed higher-order terms should be well under control in the considered scenario. On the other hand, we recall that the accuracy of the measurement of the Higgs mass at the LHC has already reached the level of 100–200 MeV [111] – i.e., it is comparable to the effects of the corrections discussed in this paper – and will improve further when more data are analyzed. If SUSY eventually shows up at the TeV scale, the mass and couplings of the SM-like Higgs boson will serve as precision observables to constrain MSSM parameters that might not be directly accessible by experiment. To this purpose, the accuracy of the theoretical predictions will have to match the experimental one, making a full inclusion of two-loop effects in the Higgs-mass calculation unavoidable. Our results should be viewed as a necessary step in that direction.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Explicit formulae for the corrections computed in this paper are available on request in electronic form.]
Notes
Here and thereafter, we use the shortcuts \(c_\phi \equiv \cos \phi \) and \(s_\phi \equiv \sin \phi \) for a generic angle \(\phi \).
We denote with a hat \({ \overline{\mathrm{DR}}}\)-renormalized couplings of the MSSM, and without a hat \(\overline{\mathrm{MS}}\)-renormalized couplings of the SM. However, in the two-loop part of the corrections the distinction between hatted and un-hatted couplings amounts to a higher-order effect, thus we will drop the hats there to reduce clutter.
For the self-energies of both the Higgs boson and the Z boson, we adopt in this paper the sign convention according to which \(m^2_{\mathrm{pole}}= m^2_{\mathrm{run}} - \Pi (m^2)\). The WFR for the Higgs boson is then \(Z_h = 1 - d\Pi _{hh}(p^2)/dp^2\). Note that this is the opposite of the sign convention adopted in Refs. [31,32,33, 93].
The fact that these mixed QCD–EW corrections should depend only on the quark and squark contributions to the gauge-boson self-energy can be easily inferred by considering the renormalization of the gauge couplings of the leptons.
References
ATLAS Collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). arXiv:1207.7214 [hep-ex]
CMS Collaboration, S. Chatrchyan et al., Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). arXiv:1207.7235 [hep-ex]
ATLAS, CMS Collaboration, G. Aad et al., Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at \( \sqrt{s}=7 \) and 8 TeV. JHEP 08, 045 (2016). arXiv:1606.02266 [hep-ex]
ATLAS, CMS Collaboration, G. Aad et al., Combined measurement of the Higgs boson mass in \(pp\) collisions at \(\sqrt{s}=7\) and 8 TeV with the ATLAS and CMS experiments. Phys. Rev. Lett. 114, 191803 (2015). arXiv:1503.07589 [hep-ex]
Y. Okada, M. Yamaguchi, T. Yanagida, Upper bound of the lightest Higgs boson mass in the minimal supersymmetric standard model. Prog. Theor. Phys. 85, 1–6 (1991)
J.R. Ellis, G. Ridolfi, F. Zwirner, Radiative corrections to the masses of supersymmetric Higgs bosons. Phys. Lett. B 257, 83–91 (1991)
H.E. Haber, R. Hempfling, Can the mass of the lightest Higgs boson of the minimal supersymmetric model be larger than m(Z)? Phys. Rev. Lett. 66, 1815–1818 (1991)
Y. Okada, M. Yamaguchi, T. Yanagida, Renormalization group analysis on the Higgs mass in the softly broken supersymmetric standard model. Phys. Lett. B 262, 54–58 (1991)
J.R. Ellis, G. Ridolfi, F. Zwirner, On radiative corrections to supersymmetric Higgs boson masses and their implications for LEP searches. Phys. Lett. B 262, 477–484 (1991)
A. Brignole, J.R. Ellis, G. Ridolfi, F. Zwirner, The supersymmetric charged Higgs boson mass and LEP phenomenology. Phys. Lett. B 271, 123–132 (1991)
P.H. Chankowski, S. Pokorski, J. Rosiek, Charged and neutral supersymmetric Higgs boson masses: complete one loop analysis. Phys. Lett. B 274, 191–198 (1992)
A. Brignole, Radiative corrections to the supersymmetric charged Higgs boson mass. Phys. Lett. B 277, 313–323 (1992)
A. Brignole, Radiative corrections to the supersymmetric neutral Higgs boson masses. Phys. Lett. B 281, 284–294 (1992)
P.H. Chankowski, S. Pokorski, J. Rosiek, Complete on-shell renormalization scheme for the minimal supersymmetric Higgs sector. Nucl. Phys. B 423, 437–496 (1994). arXiv:hep-ph/9303309
A. Dabelstein, The one loop renormalization of the MSSM Higgs sector and its application to the neutral scalar Higgs masses. Z. Phys. C 67, 495–512 (1995). arXiv:hep-ph/9409375
D.M. Pierce, J.A. Bagger, K.T. Matchev, R.-J. Zhang, Precision corrections in the minimal supersymmetric standard model. Nucl. Phys. B 491, 3–67 (1997). arXiv:hep-ph/9606211
R. Hempfling, A.H. Hoang, Two loop radiative corrections to the upper limit of the lightest Higgs boson mass in the minimal supersymmetric model. Phys. Lett. B 331, 99–106 (1994). arXiv:hep-ph/9401219
S. Heinemeyer, W. Hollik, G. Weiglein, QCD corrections to the masses of the neutral CP-even Higgs bosons in the MSSM. Phys. Rev. D 58, 091701 (1998). arXiv:hep-ph/9803277
S. Heinemeyer, W. Hollik, G. Weiglein, Precise prediction for the mass of the lightest Higgs boson in the MSSM. Phys. Lett. B 440, 296–304 (1998). arXiv:hep-ph/9807423
R.-J. Zhang, Two loop effective potential calculation of the lightest CP even Higgs boson mass in the MSSM. Phys. Lett. B 447, 89–97 (1999). arXiv:hep-ph/9808299
S. Heinemeyer, W. Hollik, G. Weiglein, The Masses of the neutral CP-even Higgs bosons in the MSSM: accurate analysis at the two loop level. Eur. Phys. J. C 9, 343–366 (1999). arXiv:hep-ph/9812472
J.R. Espinosa, R.-J. Zhang, MSSM lightest CP even Higgs boson mass to O(alpha(s) alpha(t)): the effective potential approach. JHEP 03, 026 (2000). arXiv:hep-ph/9912236
J.R. Espinosa, R.-J. Zhang, Complete two loop dominant corrections to the mass of the lightest CP even Higgs boson in the minimal supersymmetric standard model. Nucl. Phys. B 586, 3–38 (2000). arXiv:hep-ph/0003246
G. Degrassi, P. Slavich, F. Zwirner, On the neutral Higgs boson masses in the MSSM for arbitrary stop mixing. Nucl. Phys. B 611, 403–422 (2001). arXiv:hep-ph/0105096
A. Brignole, G. Degrassi, P. Slavich, F. Zwirner, On the O(alpha(t)**2) two loop corrections to the neutral Higgs boson masses in the MSSM. Nucl. Phys. B 631, 195–218 (2002). arXiv:hep-ph/0112177
A. Brignole, G. Degrassi, P. Slavich, F. Zwirner, On the two loop sbottom corrections to the neutral Higgs boson masses in the MSSM. Nucl. Phys. B 643, 79–92 (2002). arXiv:hep-ph/0206101
S.P. Martin, Two loop effective potential for the minimal supersymmetric standard model. Phys. Rev. D 66, 096001 (2002). arXiv:hep-ph/0206136
S.P. Martin, Complete two loop effective potential approximation to the lightest Higgs scalar boson mass in supersymmetry. Phys. Rev. D 67, 095012 (2003). arXiv:hep-ph/0211366
A. Dedes, G. Degrassi, P. Slavich, On the two loop Yukawa corrections to the MSSM Higgs boson masses at large tan beta. Nucl. Phys. B 672, 144–162 (2003). arXiv:hep-ph/0305127
S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, High-precision predictions for the MSSM Higgs sector at O(alpha(b) alpha(s)). Eur. Phys. J. C 39, 465–481 (2005). arXiv:hep-ph/0411114
S.P. Martin, Evaluation of two loop selfenergy basis integrals using differential equations. Phys. Rev. D 68, 075002 (2003). arXiv:hep-ph/0307101
S.P. Martin, Two loop scalar self energies in a general renormalizable theory at leading order in gauge couplings. Phys. Rev. D 70, 016005 (2004). arXiv:hep-ph/0312092
S.P. Martin, Strong and Yukawa two-loop contributions to Higgs scalar boson self-energies and pole masses in supersymmetry. Phys. Rev. D 71, 016012 (2005). arXiv:hep-ph/0405022
S. Borowka, T. Hahn, S. Heinemeyer, G. Heinrich, W. Hollik, Momentum-dependent two-loop QCD corrections to the neutral Higgs-boson masses in the MSSM. Eur. Phys. J. C 74(8), 2994 (2014). arXiv:1404.7074 [hep-ph]
G. Degrassi, S. Di Vita, P. Slavich, Two-loop QCD corrections to the MSSM Higgs masses beyond the effective-potential approximation. Eur. Phys. J. C 75(2), 61 (2015). arXiv:1410.3432 [hep-ph]
R.V. Harlander, P. Kant, L. Mihaila, M. Steinhauser, Higgs boson mass in supersymmetry to three loops. Phys. Rev. Lett. 100, 191602 (2008). arXiv:0803.0672 [hep-ph]
R.V. Harlander, P. Kant, L. Mihaila, M. Steinhauser, Erratum: Higgs boson mass in supersymmetry to three loops. Phys. Rev. Lett. 101, 039901 (2008)
P. Kant, R.V. Harlander, L. Mihaila, M. Steinhauser, Light MSSM Higgs boson mass to three-loop accuracy. JHEP 08, 104 (2010). arXiv:1005.5709 [hep-ph]
R.V. Harlander, J. Klappert, A. Voigt, Higgs mass prediction in the MSSM at three-loop level in a pure \(\overline{{\text{ DR }}}\) context. Eur. Phys. J. C 77(12), 814 (2017). arXiv:1708.05720 [hep-ph]
D. Stöckinger, J. Unger, Three-loop MSSM Higgs-boson mass predictions and regularization by dimensional reduction. Nucl. Phys. B 935, 1–16 (2018). arXiv:1804.05619 [hep-ph]
A .R. Fazio, E .A. Reyes R, The lightest Higgs boson mass of the MSSM at three-loop accuracy. Nucl. Phys. B 942, 164–183 (2019). arXiv:1901.03651 [hep-ph]
E.A. Reyes, A.R. Fazio, Comparison of the EFT hybrid and three-loop fixed-order calculations of the lightest MSSM Higgs boson mass. arXiv:1908.00693 [hep-ph]
A. Pilaftsis, C.E.M. Wagner, Higgs bosons in the minimal supersymmetric standard model with explicit CP violation. Nucl. Phys. B 553, 3–42 (1999). arXiv:hep-ph/9902371
S.Y. Choi, M. Drees, J.S. Lee, Loop corrections to the neutral Higgs boson sector of the MSSM with explicit CP violation. Phys. Lett. B 481, 57–66 (2000). arXiv:hep-ph/0002287
M. Carena, J.R. Ellis, A. Pilaftsis, C.E.M. Wagner, Renormalization group improved effective potential for the MSSM Higgs sector with explicit CP violation. Nucl. Phys. B 586, 92–140 (2000). arXiv:hep-ph/0003180
M. Frank, T. Hahn, S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, The Higgs boson masses and mixings of the complex MSSM in the Feynman-diagrammatic approach. JHEP 02, 047 (2007). arXiv:hep-ph/0611326
S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, The Higgs sector of the complex MSSM at two-loop order: QCD contributions. Phys. Lett. B 652, 300–309 (2007). arXiv:0705.0746 [hep-ph]
W. Hollik, S. Paßehr, Two-loop top-Yukawa-coupling corrections to the Higgs boson masses in the complex MSSM. Phys. Lett. B 733, 144–150 (2014). arXiv:1401.8275 [hep-ph]
W. Hollik, S. Paßehr, Higgs boson masses and mixings in the complex MSSM with two-loop top-Yukawa-coupling corrections. JHEP 10, 171 (2014). arXiv:1409.1687 [hep-ph]
W. Hollik, S. Paßehr, Two-loop top-Yukawa-coupling corrections to the charged Higgs-boson mass in the MSSM. Eur. Phys. J. C 75(7), 336 (2015). arXiv:1502.02394 [hep-ph]
M.D. Goodsell, F. Staub, The Higgs mass in the CP violating MSSM, NMSSM, and beyond. Eur. Phys. J. C 77(1), 46 (2017). arXiv:1604.05335 [hep-ph]
S. Paßehr, G. Weiglein, Two-loop top and bottom Yukawa corrections to the Higgs-boson masses in the complex MSSM. Eur. Phys. J. C 78(3), 222 (2018). arXiv:1705.07909 [hep-ph]
S. Borowka, S. Paßehr, G. Weiglein, Complete two-loop QCD contributions to the lightest Higgs-boson mass in the MSSM with complex parameters. Eur. Phys. J. C 78(7), 576 (2018). arXiv:1802.09886 [hep-ph]
R. Barbieri, M. Frigeni, F. Caravaglios, The supersymmetric Higgs for heavy superpartners. Phys. Lett. B 258, 167–170 (1991)
J.R. Espinosa, M. Quiros, Two loop radiative corrections to the mass of the lightest Higgs boson in supersymmetric standard models. Phys. Lett. B 266, 389–396 (1991)
J.A. Casas, J.R. Espinosa, M. Quiros, A. Riotto, The lightest Higgs boson mass in the minimal supersymmetric standard model. Nucl. Phys. B 436, 3–29 (1995). arXiv:hep-ph/9407389. [Erratum: Nucl. Phys. B 439, 466 (1995)]
H.E. Haber, R. Hempfling, The Renormalization group improved Higgs sector of the minimal supersymmetric model. Phys. Rev. D 48, 4280–4309 (1993). arXiv:hep-ph/9307201
M. Carena, J.R. Espinosa, M. Quiros, C.E.M. Wagner, Analytical expressions for radiatively corrected Higgs masses and couplings in the MSSM. Phys. Lett. B 355, 209–221 (1995). arXiv:hep-ph/9504316
M. Carena, M. Quiros, C.E.M. Wagner, Effective potential methods and the Higgs mass spectrum in the MSSM. Nucl. Phys. B 461, 407–436 (1996). arXiv:hep-ph/9508343
H.E. Haber, R. Hempfling, A.H. Hoang, Approximating the radiatively corrected Higgs mass in the minimal supersymmetric model. Z. Phys. C 75, 539–554 (1997). arXiv:hep-ph/9609331
M. Carena, H.E. Haber, S. Heinemeyer, W. Hollik, C.E.M. Wagner, G. Weiglein, Reconciling the two loop diagrammatic and effective field theory computations of the mass of the lightest CP-even Higgs boson in the MSSM. Nucl. Phys. B 580, 29–57 (2000). arXiv:hep-ph/0001002
G. Degrassi, S. Heinemeyer, W. Hollik, P. Slavich, G. Weiglein, Towards high precision predictions for the MSSM Higgs sector. Eur. Phys. J. C 28, 133–143 (2003). arXiv:hep-ph/0212020
S.P. Martin, Three-loop corrections to the lightest Higgs scalar boson mass in supersymmetry. Phys. Rev. D 75, 055005 (2007). arXiv:hep-ph/0701051
T. Hahn, S. Heinemeyer, W. Hollik, H. Rzehak, G. Weiglein, High-precision predictions for the light CP-even Higgs boson mass of the minimal supersymmetric standard model. Phys. Rev. Lett. 112(14), 141801 (2014). arXiv:1312.4937 [hep-ph]
P. Draper, G. Lee, C.E.M. Wagner, Precise estimates of the Higgs mass in heavy supersymmetry. Phys. Rev. D 89(5), 055023 (2014). arXiv:1312.5743 [hep-ph]
E. Bagnaschi, G.F. Giudice, P. Slavich, A. Strumia, Higgs mass and unnatural supersymmetry. JHEP 09, 092 (2014). arXiv:1407.4081 [hep-ph]
J. Pardo Vega, G. Villadoro, SusyHD: Higgs mass determination in supersymmetry. JHEP 07, 159 (2015). arXiv:1504.05200 [hep-ph]
G. Lee, C.E.M. Wagner, Higgs bosons in heavy supersymmetry with an intermediate \(\text{ m }_{{\rm A}}\). Phys. Rev. D 92(7), 075032 (2015). arXiv:1508.00576 [hep-ph]
E. Bagnaschi, F. Brümmer, W. Buchmüller, A. Voigt, G. Weiglein, Vacuum stability and supersymmetry at high scales with two Higgs doublets. JHEP 03, 158 (2016). arXiv:1512.07761 [hep-ph]
H. Bahl, W. Hollik, Precise prediction for the light MSSM Higgs boson mass combining effective field theory and fixed-order calculations. Eur. Phys. J. C 76(9), 499 (2016). arXiv:1608.01880 [hep-ph]
P. Athron, J.-H. Park, T. Steudtner, D. Stöckinger, A. Voigt, Precise Higgs mass calculations in (non-)minimal supersymmetry at both high and low scales. JHEP 01, 079 (2017). arXiv:1609.00371 [hep-ph]
F. Staub, W. Porod, Improved predictions for intermediate and heavy supersymmetry in the MSSM and beyond. Eur. Phys. J. C 77(5), 338 (2017). arXiv:1703.03267 [hep-ph]
E. Bagnaschi, J. Pardo Vega, P. Slavich, Improved determination of the Higgs mass in the MSSM with heavy superpartners. Eur. Phys. J. C77(5), 334 (2017). arXiv:1703.08166 [hep-ph]
H. Bahl, S. Heinemeyer, W. Hollik, G. Weiglein, Reconciling EFT and hybrid calculations of the light MSSM Higgs-boson mass. Eur. Phys. J. C 78(1), 57 (2018). arXiv:1706.00346 [hep-ph]
P. Athron, M. Bach, D. Harries, T. Kwasnitza, J-h Park, D. Stöckinger, A. Voigt, J. Ziebell, FlexibleSUSY 2.0: extensions to investigate the phenomenology of SUSY and non-SUSY models. Comput. Phys. Commun. 230, 145–217 (2018). arXiv:1710.03760 [hep-ph]
B.C. Allanach, A. Voigt, Uncertainties in the lightest \(CP\) even Higgs boson mass prediction in the minimal supersymmetric standard model: fixed order versus effective field theory prediction. Eur. Phys. J. C 78(7), 573 (2018). arXiv:1804.09410 [hep-ph]
H. Bahl, W. Hollik, Precise prediction of the MSSM Higgs boson masses for low \(\text{ M }_{{{\rm A}}}\). JHEP 07, 182 (2018). arXiv:1805.00867 [hep-ph]
R .V. Harlander, J. Klappert, A .D. Ochoa Franco, A. Voigt, The light CP-even MSSM Higgs mass resummed to fourth logarithmic order. Eur. Phys. J. C 78(10), 874 (2018). arXiv:1807.03509 [hep-ph]
H. Bahl, Pole mass determination in presence of heavy particles. JHEP 02, 121 (2019). arXiv:1812.06452 [hep-ph]
L.N. Mihaila, J. Salomon, M. Steinhauser, Gauge coupling beta functions in the standard model to three loops. Phys. Rev. Lett. 108, 151602 (2012). arXiv:1201.5868 [hep-ph]
K.G. Chetyrkin, M.F. Zoller, Three-loop beta-functions for top-Yukawa and the Higgs self-interaction in the standard model. JHEP 06, 033 (2012). arXiv:1205.2892 [hep-ph]
L.N. Mihaila, J. Salomon, M. Steinhauser, Renormalization constants and beta functions for the gauge couplings of the standard model to three-loop order. Phys. Rev. D 86, 096008 (2012). arXiv:1208.3357 [hep-ph]
A.V. Bednyakov, A.F. Pikelner, V.N. Velizhanin, Yukawa coupling beta-functions in the standard model at three loops. Phys. Lett. B 722, 336–340 (2013). arXiv:1212.6829 [hep-ph]
K.G. Chetyrkin, M.F. Zoller, \(\beta \)-function for the Higgs self-interaction in the standard model at three-loop level. JHEP 04, 091 (2013). arXiv:1303.2890 [hep-ph]. [Erratum: JHEP 09, 155 (2013)]
A.V. Bednyakov, A.F. Pikelner, V.N. Velizhanin, Higgs self-coupling beta-function in the standard model at three loops. Nucl. Phys. B 875, 552–565 (2013). arXiv:1303.4364 [hep-ph]
D. Buttazzo et al., Investigating the near-criticality of the Higgs boson. JHEP 12, 089 (2013). arXiv:1307.3536 [hep-ph]
B.A. Kniehl, A.F. Pikelner, O.L. Veretin, Two-loop electroweak threshold corrections in the standard model. Nucl. Phys. B 896, 19–51 (2015). arXiv:1503.02138 [hep-ph]
S.P. Martin, D.G. Robertson, Standard model parameters in the tadpole-free pure \(\overline{\rm {MS}}\) scheme. arXiv:1907.02500 [hep-ph]
S.P. Martin, Three-loop standard model effective potential at leading order in strong and top Yukawa couplings. Phys. Rev. D 89(1), 013003 (2014). arXiv:1310.7553 [hep-ph]
S.P. Martin, D.G. Robertson, Higgs boson mass in the standard model at two-loop order and beyond. Phys. Rev. D 90(7), 073010 (2014). arXiv:1407.4336 [hep-ph]
S.P. Martin, Four-loop standard model effective potential at leading order in QCD. Phys. Rev. D 92(5), 054029 (2015). arXiv:1508.00912 [hep-ph]
J.D. Wells, Z. Zhang, Effective field theory approach to trans-TeV supersymmetry: covariant matching, Yukawa unification and Higgs couplings. JHEP 05, 182 (2018). arXiv:1711.04774 [hep-ph]
J. Braathen, M.D. Goodsell, P. Slavich, Matching renormalisable couplings: simple schemes and a plot. arXiv:1810.09388 [hep-ph]
M. Gabelmann, M. Mühlleitner, F. Staub, Automatised matching between two scalar sectors at the one-loop level. Eur. Phys. J. C 79(2), 163 (2019). arXiv:1810.12326 [hep-ph]
G. Degrassi, P. Slavich, On the radiative corrections to the neutral Higgs boson masses in the NMSSM. Nucl. Phys. B 825, 119–150 (2010). arXiv:0907.4682 [hep-ph]
T. Hahn, Generating Feynman diagrams and amplitudes with FeynArts 3. Comput. Phys. Commun. 140, 418–431 (2001). arXiv:hep-ph/0012260
T. Hahn, C. Schappacher, The Implementation of the minimal supersymmetric standard model in FeynArts and FormCalc. Comput. Phys. Commun. 143, 54–68 (2002). arXiv:hep-ph/0105349
M. Jamin, M .E. Lautenbacher, TRACER: version 1.1: a mathematica package for gamma algebra in arbitrary dimensions. Comput. Phys. Commun 74, 265–288 (1993)
G. Degrassi, P. Slavich, NLO QCD bottom corrections to Higgs boson production in the MSSM. JHEP 11, 044 (2010). arXiv:1007.3465 [hep-ph]
M .E. Machacek, M .T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 1. Wave function renormalization. Nucl. Phys. B 222, 83–103 (1983)
D.R.T. Jones, Asymptotic behavior of supersymmetric Yang–Mills theories in the two loop approximation. Nucl. Phys. B 87, 127 (1975)
D.R.T. Jones, L. Mezincescu, The beta function in supersymmetric Yang–Mills theory. Phys. Lett. B 136, 242–244 (1984)
S.P. Martin, M.T. Vaughn, Two loop renormalization group equations for soft supersymmetry breaking couplings. Phys. Rev. D 50, 2282 (1994). arXiv:hep-ph/9311340. [Erratum: Phys. Rev. D 78, 039903 (2008)]
M.E. Machacek, M.T. Vaughn, Two loop renormalization group equations in a general quantum field theory. 3. Scalar quartic couplings. Nucl. Phys. B 249, 70–92 (1985)
M. Sperling, D. Stöckinger, A. Voigt, Renormalization of vacuum expectation values in spontaneously broken gauge theories: two-loop results. JHEP 01, 068 (2014). arXiv:1310.7629 [hep-ph]
A. Sirlin, R. Zucchini, Dependence of the quartic coupling H(m) on M(H) and the possible onset of new physics in the Higgs sector of the standard model. Nucl. Phys. B 266, 389–409 (1986)
G. Degrassi, S. Di Vita, J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori, A. Strumia, Higgs mass and vacuum stability in the standard model at NNLO. JHEP 08, 098 (2012). arXiv:1205.6497 [hep-ph]
F. Bezrukov, MYu. Kalmykov, B.A. Kniehl, M. Shaposhnikov, Higgs boson mass and new physics. JHEP 10, 140 (2012). arXiv:1205.2893 [hep-ph]
B.A. Kniehl, A.F. Pikelner, O.L. Veretin, mr: a C++ library for the matching and running of the standard model parameters. Comput. Phys. Commun. 206, 84–96 (2016). arXiv:1601.08143 [hep-ph]
ATLAS, CDF, CMS, D0 Collaboration, First combination of Tevatron and LHC measurements of the top-quark mass. arXiv:1403.4427 [hep-ex]
Particle Data Group Collaboration, M. Tanabashi et al., Review of particle physics. Phys. Rev. D 98(3), 030001 (2018)
HL/HE-LHC Physics Workshop Collaboration, X. Cid Vidal et al., Beyond the standard model physics at the HL-LHC and HE-LHC. arXiv:1812.07831 [hep-ph]
J. Braathen, M.D. Goodsell, P. Slavich, Leading two-loop corrections to the Higgs boson masses in SUSY models with Dirac gauginos. JHEP 09, 045 (2016). arXiv:1606.09213 [hep-ph]
Acknowledgements
We thank Mark Goodsell for useful discussions. The work of S. P. and P. S. is supported in part by French state funds managed by the Agence Nationale de la Recherche (ANR), in the context of the LABEX ILP (ANR-11-IDEX-0004-02, ANR-10-LABX-63) and of the Grant “HiggsAutomator” (ANR-15-CE31-0002). G. D. acknowledges warm hospitality at LPTHE and support from “HiggsAutomator” during the completion of this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Bagnaschi, E., Degrassi, G., Paßehr, S. et al. Full two-loop QCD corrections to the Higgs mass in the MSSM with heavy superpartners. Eur. Phys. J. C 79, 910 (2019). https://doi.org/10.1140/epjc/s10052-019-7417-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7417-9