Bootstrapped Newtonian stars and black holes

Abstract

We study equilibrium configurations of a homogenous ball of matter in a bootstrapped description of gravity which includes a gravitational self-interaction term beyond the Newtonian coupling. Both matter density and pressure are accounted for as sources of the gravitational potential for test particles. Unlike the general relativistic case, no Buchdahl limit is found and the pressure can in principle support a star of arbitrarily large compactness. By defining the horizon as the location where the escape velocity of test particles equals the speed of light, like in Newtonian gravity, we find a minimum value of the compactness for which this occurs. The solutions for the gravitational potential here found could effectively describe the interior of macroscopic black holes in the quantum theory, as well as predict consequent deviations from general relativity in the strong field regime of very compact objects.

1 Introduction and motivation

The true nature of black holes is already problematic in the classical description given by general relativity and notoriously more so once one tries to incorporate the unavoidable quantum physics. Once a trapping surface appears, singularity theorems of general relativity require an object to collapse all the way into a region of vanishing volume and infinite density [1]. At the same time, a point-like source is well known to be classically unacceptable [2,3,4]. One would therefore hope that quantum physics cures this problem, the same way it makes the hydrogen atom stable, by affecting the gravitational dynamics, at least in the strong field regime (where the description of matter likely requires physics beyond the standard model as well [5, 6]).

In light of the above observations, in Ref. [7] we studied an effective equation for the gravitational potential of a static source which contains a gravitational self-interaction term besides the usual Newtonian coupling with the matter density. Following an idea from Ref. [8], this equation was derived in details from a Fierz–Pauli Lagrangian in Ref. [9], and it can therefore be viewed as stemming from the truncation of the relativistic theory at some “post-Newtonian” order (for the standard post-Newtonian formalism, see Ref. [10]). However, since the “post-Newtonian” correction $V_\mathrm{PN}\sim M^2/r^2$ is positive and grows faster than the Newtonian potential $V_\mathrm{N}\sim M/r$ near the surface of the source, one is allowed to consider only matter sources with radius $R\gg R_\mathrm{H}$ in this approximation (where we remark that M is the total ADM mass [11] of the system and

$$\begin{aligned} R_\mathrm{H}\equiv 2\,G_\mathrm{N}\,M \end{aligned}$$

(1.1)

is the gravitational radius of the source.) This consistency condition clearly excludes the possibility to study very compact matter sources and, in particular, those with $R\simeq R_\mathrm{H}$ which are on the verge of forming a black hole. For the ultimate purpose of including such cases and gain some hindsight about the fate of matter which collapses inside a black hole, in Ref. [7] we studied the non-linear equation of the effective theory derived in Ref. [9] at face value, without requiring that the corrections it introduces with respect to the Newtonian potential remain small.

In Ref. [7], we showed that the qualitative behaviour of the complete solutions to that non-linear equation resembles rather closely the Newtonian counterpart. This result, which essentially stems from including a gravitational self-interaction in the Poisson equation, is what we call “bootstrapping” the Newtonian gravity. In fact, including those specific non-linear terms could be viewed as the first step in the perturbative reconstruction of classical general relativity (see, e.g. Refs. [12,13,14]). However, we could also entertain the idea that these terms are meaningful to determine the (mean field) gravitational potential of extremely compact objects if the quantum break-down of classical general relativity occurs at macroscopic scales and general relativity therefore fails at describing (the interior of) black holes [15,16,17,18, 20, 21]. In this case, although its origin lies in the quantum nature of gravity (and matter), if this effective potential applies for macroscopic sources, it does not need to contain explicitly a dependence on the Planck constant $\hbar$ such that general relativistic configurations are (formally) recovered for vanishing $\hbar$.¹ On the other hand, Newtonian physics is recovered (by construction) for sources with small compactness $G_\mathrm{N}\,M/R\sim R_\mathrm{H}/R\ll 1$, and one can therefore consider that the compactness $G_\mathrm{N}\,M/R$ is the parameter measuring deviations from general relativity in the bootstrapped potential.² To be more specific, we expect that the bootstrapped potential admits a description in terms of a quantum state of bound gravitons, like the coherent state that can be used to reproduce the Newtonian potential [8, 9]. The quantum features of the system would hence become apparent only after such a quantum state is constructed explicitly (which we leave for future investigations). Moreover, by studying static sources of uniform density $\rho$ in Ref. [7], we found a finite matter pressure p could support sources of arbitrarily large compactenss $G_\mathrm{N}\,M/R\sim R_\mathrm{H}/R\gg 1$, so that there is no equivalent of the Buchdahl limit [23] of general relativity in the bootstrapped Newtonian gravity. Of course, the pressure becomes the dominant source of energy when $G_\mathrm{N}\,M/R\gg 1$ and, although the strong energy condition $\rho +p>0$ still holds, the dominant energy condition $\rho \ge |p|$ is violated in this regime (see, e.g. Ref. [24]). This suggests that the source of highly compact configurations, such as black holes, must be matter in a quantum state with no purely classical analogue (like Bose–Einstein condensates [15,16,17,18,19,20,21] or degenerate neutron stars). This result is again consistent with the fact that classical general relativistic configurations are expected to become physically relevant only for astrophysical objects with small compactness $R_\mathrm{H}/R\ll 1$.

Since we are mainly interested in investigating static sources which we found can be very compact, a pressure term which prevents the gravitational collapse needs to be included from the onset. For this reason, we here modify the effective theory used in Ref. [7] in order to consistently supplement the matter density with the pressure as sources of the gravitational potential. We then study systems with generic compactness $G_\mathrm{N}\,M/R\sim R_\mathrm{H}/R$, from the regime $R\gg R_\mathrm{H}$, in which we recover the standard post-Newtonian picture, to $R\ll R_\mathrm{H}$ where we find the source is enclosed within a horizon. The latter is defined according to the Newtonian view as the location at which the escape velocity of test particles equals the speed of light. Of course, it should be possible to treat the single microscopic constituents of the source in this test particle approximation and the presence of an horizon therefore refers to their inability to escape the gravitational pull.

Like in Refs. [7, 9], we shall just consider (static) spherically symmetric systems, so that all quantities depend only on the radial coordinate r, and the matter density $\rho =\rho (r)$ will also be assumed homogenous inside the source ($r\le R$) for the sake of simplicity. The pressure will instead be determined consistently from the condition of staticity. The paper is organised as follows: in Sect. 2, we briefly review the derivation of the equation for the potential with the inclusion of a pressure term; in Sect. 3, we solve for the outer and inner potential generated by the homogenous source using appropriate analytical methods for the diverse regimes. In particular, we study intermediate and large compact sources with $R\lesssim R_\mathrm{H}$ as possible candidates for effectively describing collapsed objects which should act as black holes according to general relativity; their horizon structure is then analysed in Sect. 4; we finally comment about our results and possible outlooks in Sect. 5.

2 Bootstrapped theory for the gravitational potential

From Ref. [9], we recall that the non-linear equation for the potential $V=V(r)$ describing the gravitational pull on test particles generated by a matter density $\rho =\rho (r)$ can be obtained starting from the Newtonian Lagrangian

$$\begin{aligned} L_\mathrm{N}[V] = -\,4\,\pi \int _0^\infty r^2 \,{\mathrm{d}}r \left[ \frac{\left( V'\right) ^2}{8\,\pi \,G_\mathrm{N}} +\rho \,V \right] , \end{aligned}$$

(2.1)

where $f'\equiv {\mathrm{d}}f/{\mathrm{d}}r$, and the corresponding equation of motion is the Poisson equation

$$\begin{aligned} r^{-2}\left( r^2\,V'\right) ' \equiv \triangle V = 4\,\pi \,G_\mathrm{N}\,\rho \end{aligned}$$

(2.2)

for the Newtonian potential $V=V_\mathrm{N}$. We can then include the effects of gravitational self-interaction by noting that the Hamiltonian

$$\begin{aligned} H_\mathrm{N}[V] = -L_\mathrm{N}[V] = 4\,\pi \int _0^\infty r^2\,{\mathrm{d}}r \left( -\frac{V\,\triangle V}{8\,\pi \,G_\mathrm{N}} +\rho \,V \right) ,\nonumber \\ \end{aligned}$$

(2.3)

computed on-shell by means of Eq. (2.2), yields the total Newtonian potential energy

$$\begin{aligned} U_\mathrm{N}[V]= & {} 2\,\pi \int _0^\infty {r}^2\,{\mathrm{d}}{r} \,\rho \, V \nonumber \\= & {} \frac{1}{2\,G_\mathrm{N}}\, \int _0^\infty {r}^2 \,{\mathrm{d}}{r}\, V\,\triangle V \nonumber \\= & {} -4\,\pi \int _0^\infty {r}^2 \,{\mathrm{d}}{r}\, \frac{\left( V'\right) ^2}{{8\,\pi \,G_\mathrm{N}}}, \end{aligned}$$

(2.4)

where we used Eq. (2.2) in the second line and assumed that boundary terms vanish at $r=0$ and $r=\infty$ as usual in the last line (for an alternative but equivalent derivation, see Appendix A). One can therefore view the above $U_\mathrm{N}$ as given by the interaction of the matter distribution with the gravitational field or, following Ref. [8] (see also Ref. [25]), as the volume integral of the gravitational current proportional to the gravitational energy $U_\mathrm{N}$ per unit volume $\delta \mathcal {V}=4\,\pi \,r^2\,\delta r$, that is³

$$\begin{aligned} J_V \simeq 4\,\frac{\delta U_\mathrm{N}}{\delta \mathcal {V}} = -\frac{\left[ V'(r)\right] ^2}{2\,\pi \,G_\mathrm{N}}. \end{aligned}$$

(2.5)

As mentioned in the Introduction, in Ref. [7] we found that the pressure p which prevents the system from collapsing becomes very large for compact sources with a size $R\lesssim R_\mathrm{H}$, where $R_\mathrm{H}$ is the gravitational radius of Eq. (1.1). We must therefore add a corresponding potential energy $U_\mathrm{B}$, associated with the work done by the force responsible for the pressure p, such that

$$\begin{aligned} p \simeq -\frac{\delta U_\mathrm{B}}{\delta \mathcal {V}} = J_\mathrm{B} \ . \end{aligned}$$

(2.6)

We will accordingly have to couple the potential field with the energy densities $J_V$ and $J_\mathrm{B}$ and then add the analogous higher order term $J_\rho =-2\,V^2$ which couples with the matter sector, i.e. with the total matter energy density $\rho + p$. Upon including these new source terms, we obtain the total Lagrangian [9]

(2.7)

The parameters $q_V$, $q_\mathrm{B}$ and $q_{\rho }$ play the role of coupling constants⁴ for the three different currents $J_V$, $J_\mathrm{B}$ and $J_\rho$ respectively. They also allow us to control the origin of non-linearities, as we recover the Newtonian Lagrangian (2.1) by setting all of them equal to zero.

The associated effective Hamiltonian is simply given by

$$\begin{aligned} H[V] = -L[V], \end{aligned}$$

(2.8)

and the Euler–Lagrange equation for V reads

$$\begin{aligned}&\left( 1 - 4\,q_V\,V \right) \triangle V = 4\,\pi \,G_\mathrm{N}\left( \rho +q_\mathrm{B}\,p\right) \nonumber \\&\quad - 16\,\pi \,G_\mathrm{N}\,q_{\rho }\,V\,(\rho + p) + 2\,q_V\left( V'\right) ^2. \end{aligned}$$

(2.9)

The latter must be supplemented with the conservation equation that determines the pressure,

$$\begin{aligned} p' = -V'\left( \rho +p\right) , \end{aligned}$$

(2.10)

which can be seen as a correction to the usual Newtonian formula that accounts for the contribution of the pressure to the energy density, or as an approximation for the Tolman–Oppenheimer–Volkoff equation of general relativity.

Although we showed the three parameters $q_\Phi$, $q_\mathrm{B}$ and $q_{\rho }$ explicitly, we shall only consider $q_\Phi =q_\mathrm{B}=q_{\rho }=1$ in the following for the sake of simplicity. In this case, Eq. (2.9) reduces to

$$\begin{aligned} \triangle V = 4\,\pi \,G_\mathrm{N}\left( \rho +p\right) + \frac{2\,\left( V'\right) ^2}{1-4\,V}, \end{aligned}$$

(2.11)

from which we see that the differences with respect to the Poisson Eq. (2.2) are given by the inclusion of the pressure p and the derivative self-interaction term in the right hand side.

3 Homogeneous ball in vacuum

Since we are interested in compact sources, we will consider the simplest case in which the matter density is homogeneous and vanishes outside the sphere of radius $r=R$, that is

$$\begin{aligned} \rho = \rho _0 \equiv \frac{3\, M_0}{4\,\pi \, R^3}\, \Theta (R-r), \end{aligned}$$

(3.1)

where $\Theta$ is the Heaviside step function, and

$$\begin{aligned} M_0 = 4\,\pi \int _0^R r^2\,{\mathrm{d}}r\,\rho (r). \end{aligned}$$

(3.2)

Of course, the uniform density (3.1) is not expected to be compatible with an equation of state, since the pressure $p=p(r)$ must depend on the radial position so as to maintain equilibrium [7]. We also remark that uniform density is not very realistic and is here used just for mathematical convenience and because it is the source for the exact interior Schwarzschild solution [26] in general relativity.⁵

The potential must also satisfy the regularity condition in the centre

$$\begin{aligned} V_\mathrm{in}'(0)=0 \end{aligned}$$

(3.3)

and be smooth across the surface $r=R$, that is

$$\begin{aligned} V_\mathrm{in}(R)= & {} V_\mathrm{out}(R) \equiv V_R \end{aligned}$$

(3.4)

$$\begin{aligned} V'_\mathrm{in}(R)= & {} V'_\mathrm{out}(R) \equiv V'_R, \end{aligned}$$

(3.5)

where we defined $V_\mathrm{in}=V(0\le r\le R)$ and $V_\mathrm{out}=V(R\le r)$.

3.1 Outer vacuum solution

In the vacuum, where $\rho =p=0$, Eq. (2.10) is trivially satisfied and Eq. (2.11) with $q_\Phi =1$ reads

$$\begin{aligned} \triangle V = \frac{2 \left( V'\right) ^2}{1-4\,V}, \end{aligned}$$

(3.6)

which is exactly solved by

$$\begin{aligned} V_\mathrm{out} = \frac{1}{4} \left[ 1-\left( 1+\frac{6\,G_\mathrm{N}\,M}{r}\right) ^{2/3} \right] . \end{aligned}$$

(3.7)

where two integration constants were fixed by requiring the expected Newtonian behaviour in terms of the ADM-like mass M for large r. In fact, the large r expansion now reads

$$\begin{aligned} V_\mathrm{out} \underset{r\rightarrow \infty }{\simeq } -\frac{G_\mathrm{N}\,M}{r} +\frac{G_\mathrm{N}^2\,M^2}{r^2} -\frac{8\,G_\mathrm{N}^3\,M^3}{3\,r^3}, \end{aligned}$$

(3.8)

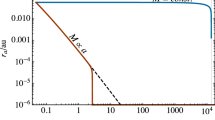
and contains the expected post-Newtonian term $V_\mathrm{PN}$ of order $G_\mathrm{N}^2$ without any further assumptions [9] (see Fig. 1).

From Eq. (3.7), we also obtain

$$\begin{aligned} V_R = V_\mathrm{out}(R) = \frac{1}{4} \left[ 1-\left( 1+\frac{6\,G_\mathrm{N}\,M}{R}\right) ^{2/3} \right] , \end{aligned}$$

(3.9)

and

$$\begin{aligned} V'_R = V_\mathrm{out}'(R) = \frac{G_\mathrm{N}\,M}{R^{2}\left( 1+{6\,G_\mathrm{N}\,M}/R\right) ^{1/3}}, \end{aligned}$$

(3.10)

which we will often use since they appear in the boundary conditions (3.4) and (3.5).

Fig. 1

Potential $V_\mathrm{out}$ (solid line) vs Newtonian potential (dashed line) vs order $G_\mathrm{N}^2$ expansion of $V_\mathrm{out}$ (dotted line) for $r>0$ (all quantities are in units of $G_\mathrm{N}\,M$)

3.2 The inner pressure

We first consider the conservation Eq. (2.10) and notice that, for $0\le r\le R$, we can write it as

$$\begin{aligned} \frac{\left( \rho _0+p\right) '}{\rho _0+p} = -V', \end{aligned}$$

(3.11)

which allows us to express the total effective energy density as

$$\begin{aligned} \rho _0+p = \alpha \,e^{-V}. \end{aligned}$$

(3.12)

The integration constant can be determined by imposing the usual boundary condition

$$\begin{aligned} p(R)=0, \end{aligned}$$

(3.13)

which finally yields

$$\begin{aligned} p = \rho _0 \left[ e^{V_R-V} -1 \right] , \end{aligned}$$

(3.14)

where $V_R$ is given in Eq. (3.9).

3.3 The inner potential

The field equation (2.11) for $0\le r\le R$ and $q_\Phi =1$ becomes

$$\begin{aligned} \triangle V= & {} 4\,\pi \,G_\mathrm{N}\, \rho _0\,e^{V_R-V} + \frac{2\left( V'\right) ^2}{1-4\,V} \nonumber \\= & {} \frac{3\,G_\mathrm{N}\,M_0}{R^3}\,e^{V_R-V} + \frac{2\left( V'\right) ^2}{1-4\,V}, \end{aligned}$$

(3.15)

and we notice that $\rho _0\,e^{V_R}<\rho _0$ since $V_R<0$. The relevant solutions $V_\mathrm{in}$ to Eq. (3.15) must also satisfy the regularity condition (3.3) and the matching conditions (3.4) and (3.5), with $V_R$ and $V'_R$ respectively given in Eq. (3.9) and (3.10). Since Eq. (3.15) is a second order (ordinary) differential equation, the three boundary conditions (3.3), (3.4) and (3.5) will not only fix the potential $V_\mathrm{in}$ uniquely, but also the ratio of the proper mass parameter $G_\mathrm{N}\,M_0/R$ for any given value of the compactness $G_\mathrm{N}\,M/R$.

It is hard to find the complete solution of the above problem for general compactness. An approximate analytic solution to Eq. (3.15) can be found quite straightforwardly only in the regimes of low and intermediate compactness (i.e. for $G_\mathrm{N}\,M/R \ll 1$ and $G_\mathrm{N}\,M/R \simeq 1$). On the other hand, for $G_\mathrm{N}\,M\gg R$, the non-linearity of Eq. (3.15) and the interplay between $M_0$ and the boundary conditions (3.3), (3.4) and (3.5) make it very difficult to find any (approximate or numerical) solutions. In fact, even a slight error in the estimate of $M_0=M_0(M,R)$ can spoil the solution completely. For this reason, we will take advantage of the comparison method [27,28,29,30] which essentially consists in finding two bounding functions $V_\pm$ (upper and lower approximate solutions) such that $E_+(r)<0$ and $E_-(r)>0$ for $0\le r\le R$, where

$$\begin{aligned} E_\pm \equiv \triangle V_\pm - \frac{3\,G_\mathrm{N}\,M_0^{\pm }(M)}{R^3}\,e^{V_R-V_\pm } -\frac{2\left( V_\pm '\right) ^2}{1-4\,V_\pm }. \end{aligned}$$

(3.16)

Comparison theorems then guarantee that the proper solution will lie in between the two bounding functions (see Appendix C for more details⁶), that is

$$\begin{aligned} V_-<V_\mathrm{in}<V_+. \end{aligned}$$

(3.17)

The advantage of this method is twofold. It will serve as a tool for finding approximate solutions in the regime of large compactness and will also allow us to check the accuracy of the approximate analytic solution for low and intermediate compactness.

3.3.1 Small and intermediate compactness

For the radius R of the source much larger or of the order of $G_\mathrm{N}\,M$, an analytic approximation $V_\mathrm{s}$ for the solution $V_\mathrm{in}$ can be found by simply expanding around $r=0$, and turns out to be

$$\begin{aligned} V_\mathrm{s} = V_0 + \frac{G_\mathrm{N}\,M_0}{2\,R^3} \,e^{V_R-V_0}\,r^2. \end{aligned}$$

(3.18)

where $V_0\equiv V_\mathrm{in}(0)<0$ and $V_R$ is given in Eq. (3.9). We remark that the regularity condition (3.3) requires that all terms of odd order in r in the Taylor expansion about $r=0$ must vanish.

We can immediately notice that the above form is qualitatively similar to the Newtonian solution recalled in Appendix B. Like the latter, the present case does not show any singularity in the potential for $r=0$ and the pressure,

$$\begin{aligned} p \simeq \rho _0 \left[ e^{V_R-V_0-B\,r^2} -1 \right] , \end{aligned}$$

(3.19)

is also regular in $r=0$,

$$\begin{aligned} p(0) = \rho _0 \left[ e^{-(V_0-V_R)} -1 \right] >0, \end{aligned}$$

(3.20)

since $V_0<V_R<0$.

The two matching conditions at $r=R$ can now be written as

$$\begin{aligned} \left\{ \begin{array}{l} 2\,R\,(V_R-V_0) \simeq {G_\mathrm{N}\,M_0}\,e^{V_R-V_0}\\ \\ R^2\,V_R'\simeq {G_\mathrm{N}\,M_0}\,e^{V_R-V_0}, \end{array} \right. \end{aligned}$$

(3.21)

One can solve the second equation of the system above for $V_0$ to obtain

$$\begin{aligned}&V_0 = \frac{1}{4}\left[ 1- \left( 1+6\,G_\mathrm{N}\,M/R\right) ^{2/3}\right] \nonumber \\&\quad + \ln \left[ \frac{M_0}{M}\left( 1+6\,G_\mathrm{N}\,M/R\right) ^{1/3}\right] , \end{aligned}$$

(3.22)

which is written in terms of $M_0$ and M. Using the first equation in (3.21), one then finds

$$\begin{aligned} M_0 = \frac{M\,e^{-\frac{G_\mathrm{N}\,M}{2\,R\left( 1+6\,G_\mathrm{N}\,M/R\right) ^{1/3}}}}{\left( 1+6\,G_\mathrm{N}\,M/R\right) ^{1/3}}. \end{aligned}$$

(3.23)

This last expression, along with the one for $V_0$, can be used to write the approximate solution (3.18) in terms of M only as

$$\begin{aligned} V_\mathrm{s} = \frac{R^3\left[ \left( 1{+}6\,G_\mathrm{N}\,M/R\right) ^{1/3}-1\right] {+}2\,G_\mathrm{N}\,M\left( r^2{-}4\,R^2\right) }{4\,R^3\left( 1{+}6\,G_\mathrm{N}\,M/R\right) ^{1/3}},\nonumber \\ \end{aligned}$$

(3.24)

where we remark that this expression contains only the terms of the first two orders in the series expansion about $r=0$.

Fig. 2

Numerical solution to Eq. (3.15) (solid line) vs approximate solution $V_\mathrm{s}=V_+$ in Eq. (3.24) (dotted line) vs lower bounding function $V_-=C\, V_\mathrm{s}$ (dashed line), for $G_\mathrm{N}\,M /R = 1/100$ (top left panel, with $C=1.002$), $G_\mathrm{N}\,M / R= 1/50$ (top central panel, with $C=1.003$) and $G_\mathrm{N}\,M / R= 1/20$ (top right panel, with $C=1.004$). The bottom panels show the region $0 \le r \le R/100$ where the difference between the three potentials is the largest

Fig. 3

Numerical solution to Eq. (3.15) (solid line) vs approximate solution $V_\mathrm{s}=V_-$ in Eq. (3.24) (dotted line) vs upper bounding function $V_+=C\, V_\mathrm{s}$ (dashed line), for $G_\mathrm{N}\,M /R = 1/10$ (top left panel, with $C=0.998$), $G_\mathrm{N}\,M / R= 1/5$ (top central panel, with $C=0.980$) and $G_\mathrm{N}\,M / R= 1$ (top right panel, with $C=0.680$). The bottom panels show the region $0< r < R/100$ where the difference between the three expressions is the largest

Fig. 4

Upper panels: numerical solution $V_\mathrm{n}$ to Eq. (3.15) matched to the exact outer solution (3.7) (solid line) vs approximate solution $V_\mathrm{s}=V_+$ in Eq. (3.24) (dotted line) vs lower bounding function $V_-$ (dashed line) for $G_\mathrm{N}\,M /R = 1/100$ (top left), $G_\mathrm{N}\,M / R= 1/50$ (top middle) and $G_\mathrm{N}\,M / R= 1/20$ (top right). Bottom panels: relative difference $(V_\mathrm{s}-V_\mathrm{n})/V_\mathrm{n}$ (dotted line) vs $(V_--V_\mathrm{n})/V_\mathrm{n}$ (dashed line) in the interior region for $G_\mathrm{N}\,M /R = 1/100$ (bottom left), $G_\mathrm{N}\,M / R= 1/50$ (bottom middle) and $G_\mathrm{N}\,M / R= 1/20$ (bottom right). The negative sign of $(V_\mathrm{s}-V_\mathrm{n})/V_\mathrm{n}$ shows that the approximate solution is an upper bounding function $V_\mathrm{s}=V_+$ in this range of compactness

We can now estimate the accuracy of the approximation (3.18) by means of the comparison method. The plots in Figs. 2 and 3 show that $V_\mathrm{s}$ is already in good agreement with the numerical solution for both small and intermediate compactness and the smaller the ratio $G_\mathrm{N}\,M/R$, the less $V_\mathrm{s}$ differs from the numerical solution. Indeed, the approximate solution $V_\mathrm{s}$ fails in the large compactness regime, which will be studied in the next subsection. The same plots also tell us that $V_\mathrm{s}$ is actually an upper bounding function $V_+$ up to $G_\mathrm{N}\,M /R \simeq 1/20$, but becomes a lower bounding function $V_-$ for higher compactness (this can be verified by showing that it satisfies the required conditions described in Appendix C). The other bounding function ($V_-$ or $V_+$) can be found by simply multiplying $V_\mathrm{s}$ by a suitable constant factor C determined according to the theorem in Appendix C (with $C>1$ for small compactness and $C<1$ for intermediate compactness). This means that the approximate solution (3.18) overestimates the expected true potential $V_\mathrm{in}$ for low compactness, whereas it underestimates $V_\mathrm{in}$ when the compactness grows beyond $G_\mathrm{N}\,M / R \simeq 1/20$. We also note that the gap between the above $V_{-}$ and $V_{+}$ increases for increasing compactness, which signals the need for a better estimate of $M_0=M_0(M)$ in order to narrow this gap and gain more precision for describing the intermediate compactness. The latter regime is particularly useful for understanding objects that have collapsed to a size of the order of their gravitational radius.⁷ We should remark that, in this analysis, we actually employed the comparison method in the whole range $0\le r< \infty$ by defining $V_\pm =C_\pm \,V_\mathrm{out}$, for $r>R$, where $V_\mathrm{out}$ is the exact solution in Eq. (3.7) (see Figs. 4 and 5). This means that we did not require that the lower function $V_-$ (for $G_\mathrm{N}\,M/R \lesssim 1/20$) and the upper function $V_+$ (for $G_\mathrm{N}\,M/R > rsim 1/20$) satisfy the boundary conditions (3.4) and (3.5) at $r=R$. However, since we have the analytical form for $V_\mathrm{out}$ in its entire range of applicability, all that is needed to ensure that $V_\pm$ are the upper and lower bounding functions is for the constants $C_\pm$ which multiply the expression for $V_\mathrm{out}$ to be smaller, respectively larger than one.

Fig. 5

Upper panels: numerical solution $V_\mathrm{n}$ to Eq. (3.15) matched to the exact outer solution (3.7) (solid line) vs approximate solution $V_\mathrm{s}=V_-$ in Eq. (3.24) (dotted line) vs upper bounding function $V_+$ (dashed line) for $G_\mathrm{N}\,M /R = 1/10$ (top left), $G_\mathrm{N}\,M / R= 1/5$ (top middle) and $G_\mathrm{N}\,M / R= 1$ (top right). Bottom panels: relative difference $(V_\mathrm{s}-V_\mathrm{n})/V_\mathrm{n}$ (dotted line) vs $(V_+-V_\mathrm{n})/V_\mathrm{n}$ (dashed line) in the interior region for $G_\mathrm{N}\,M /R = 1/10$ (bottom left), $G_\mathrm{N}\,M / R= 1/5$ (bottom middle) and $G_\mathrm{N}\,M / R= 1$ (bottom right). The negative sign of $(V_\mathrm{s}-V_\mathrm{n})/V_\mathrm{n}$ shows that the approximate solution is a lower bounding function $V_\mathrm{s}=V_-$ in this range of compactness. The rapid growth in modulus of $(V_+-V_\mathrm{n})/V_\mathrm{n}$ with the compactness signals the need of a better estimate of $M=M(M_0)$ for a more accurate description

As stated earlier, the analytic approximation (3.24) works best in the regime of small compactness, in which we can further Taylor expand all quantities to second order in $G_\mathrm{N}\,M/R\ll 1$ to obtain

$$\begin{aligned} V_0 \simeq -\frac{3\, G_\mathrm{N}\, M}{2\, R} \left( 1 - \frac{4\, G_\mathrm{N}\, M}{3\,R} \right) , \end{aligned}$$

(3.25)

and finally use Eq. (3.23) to obtain

$$\begin{aligned} M_0 \simeq M \left( 1 - \frac{5\, G_\mathrm{N}\, M}{2\, R} \right) , \end{aligned}$$

(3.26)

in qualitative agreement with the result of Ref. [7], where however the effect of the pressure on the potential was neglected.

The above expressions for $M_0$ and $V_0$ can be used to write the inner potential (3.18) in a much simpler form in terms of M as

$$\begin{aligned} V_\mathrm{in} \simeq -\frac{3\, G_\mathrm{N}\, M}{2\, R} + \frac{2\, G_\mathrm{N}^2\, M^2}{R^2} + \frac{G_\mathrm{N}\, M\,(R - 2\, G_\mathrm{N}\, M)}{2\, R^4}\, r^2.\nonumber \\ \end{aligned}$$

(3.27)

As expected, the solution for small compactness, which can be useful for describing stars with a radius orders of magnitude larger in size than their gravitational radius, qualitatively tracks the Newtonian case. This can also be seen from Fig. 6. The limitations of the small compactness approximation can be inferred from Eq. (3.27). For $2\,G_\mathrm{N}\,M\equiv R_\mathrm{H}\sim R$ the last term vanishes and $V_\mathrm{in}$ becomes a constant.

Fig. 6

Potential $V_\mathrm{out}$ (solid line) vs approximate solution (3.24) (dotted line) vs Newtonian potential (dashed line), for $G_\mathrm{N}\,M/R =1$ (left panel), $G_\mathrm{N}\,M/R = 1/10$ (center panel) and $G_\mathrm{N}\,M/R = 1/100$ (right panel)

Fig. 7

Pressure obtained from the expansion (3.18) (solid line) vs numerical pressure (dotted line) vs Newtonian pressure (3.28) (dashed line), for $G_\mathrm{N}\,M/R =1/100$ (left panel), $G_\mathrm{N}\,M/R = 1/10$ (center panel) and $G_\mathrm{N}\,M/R = 1$ (right panel)

Finally, it is important to remark that, as opposed to what was done in Ref. [7], the pressure now acts as a source and can be consistently evaluated with the help of Eqs. (3.14) and (3.18). The plots in Fig. 7 clearly show that the pressure can be well approximated by the Newtonian formula in the regime of low compactness, to wit

$$\begin{aligned} p \simeq \frac{3\, G_\mathrm{N}\, M^2\, (R^2 - r^2)}{8\, \pi \, R^6}, \end{aligned}$$

(3.28)

again in qualitative agreement with Ref. [7]. Nevertheless, the same plots indicate that it rapidly departs from the Newtonian expression when we approach the regime of intermediate compactness, while remaining almost identical to the numerical approximation.

3.3.2 Large compactness

For $G_\mathrm{N}\,M/R\gg 1$, rather than employing a Taylor expansion like we did for small compactness, it is more convenient to fully rely on comparison methods [27,28,29,30] and start from the exact solution of the simpler equation

$$\begin{aligned} \psi '' = \frac{3\,G_\mathrm{N}\,M_0}{R^3}\,e^{V_R-\psi }, \end{aligned}$$

(3.29)

which is given by

$$\begin{aligned}&\psi (r;A,B) = -A\left( B+\frac{r}{R}\right) \nonumber \\&\quad +\, 2\,\ln \left[ 1+\frac{3\,G_\mathrm{N}\,M_0}{2\,A^2\,R}\,e^{A\,(B+r/R)+V_R}\right] , \end{aligned}$$

(3.30)

where the constants A, B and $M_0$ can be fixed (for any value of R) by imposing the boundary conditions (3.3), (3.4) and (3.5). Regularity at $r=0$ in particular yields

$$\begin{aligned} M_0 = \frac{2\,A^2\,R}{3\,G_\mathrm{N}}\,e^{-A\,B-V_R}. \end{aligned}$$

(3.31)

Equation (3.5) for the continuity of the derivative across $r=R$ then reads

$$\begin{aligned} A\,\tanh (A/2) = R\,V_R'. \end{aligned}$$

(3.32)

For large compactness, $R\,V_R'\sim (G_\mathrm{N}\,M/R)^{2/3}\gg 1$, and we can approximate the above equation as

$$\begin{aligned} A \simeq R\,V_R'. \end{aligned}$$

(3.33)

The continuity Eq. (3.4) for the potential finally reads

$$\begin{aligned} 2\,\ln \left( 1+e^{R\,V_R'}\right) -R\,V_R'\,(1+B) = V_R, \end{aligned}$$

(3.34)

and can be used to express B in terms of M and R. Putting everything together, we obtain

(3.35)

and

$$\begin{aligned} \frac{M_0}{M}\simeq & {} \frac{G_\mathrm{N}\,M/R}{3\left( 1+6\,G_\mathrm{N}\,M/R\right) ^{2/3} \left\{ 1+\cosh \left[ \frac{G_\mathrm{N}\,M/R}{\left( 1+6\,G_\mathrm{N}\,M/R\right) ^{1/3}}\right] \right\} } \nonumber \\\simeq & {} \frac{1}{3} \left( \frac{2\,G_\mathrm{N}\,M}{9\,R}\right) ^{1/3} e^{-\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}}, \end{aligned}$$

(3.36)

in which we showed the leading behaviours for $G_\mathrm{N}\,M\gg R$. It is important to remark that the condition (3.3) is not apparently satisfied by the above approximate expressions, although it was imposed from the very beginning, which shows once more how complex is to obtain analytical approximations for the problem at hand.

The solutions to the complete equation (3.15) could then be written as

$$\begin{aligned} V_\mathrm{in} = f(r;A,B)\,\psi (r;A,B), \end{aligned}$$

(3.37)

where A, B and $M_0$ should again be computed from the three boundary conditions, so that $V_\mathrm{in}$ eventually depends only on the parameters M and R. Since solving for $f=f(r)$ is not any simpler than the original task, we shall instead just find lower and upper bounds, that is constants $C_\pm$ such that

$$\begin{aligned} C_-<f(r)<C_+, \end{aligned}$$

(3.38)

in the whole range $0\le r\le R$. In particular, we consider the bounding functions

$$\begin{aligned} V_\pm = C_\pm \,\psi (r;A_\pm ,B_\pm ), \end{aligned}$$

(3.39)

where $A_\pm$, $B_\pm$ and $C_\pm$ are constants computed by imposing the boundary conditions (3.3), (3.4) and (3.5) and such that $E_+(r)<0$ and $E_-(r)>0$ for $0\le r\le R$.

In details, we first determine a function $V_C{=}C\,\psi (r;A,B)$ which satisfies the three boundary conditions for any constant C. Equation (3.3) yields the same expression (3.31), whereas the l.h.s. of Eq. (3.32) is just rescaled by the factor C and continuity of the derivative therefore gives the approximate solution

$$\begin{aligned} C\,A \simeq R\,V_R'. \end{aligned}$$

(3.40)

Equation (3.4) for the continuity of the potential likewise reads

$$\begin{aligned} 2\,C\,\ln \left( 1+e^{R\,V_R'/C}\right) -R\,V_R'\,(1+B) = V_R, \end{aligned}$$

(3.41)

Upon solving the above equations one then obtains $V_C=C\,\psi (r;A(M,R,C),B(M,R,C))$ and $M_0{=}M_0(M,R,C)$. For fixed values of R and M, one can then numerically determine a constant $C_+$ such that $E_+<0$ and a constant $C_-<C_+$ such that $E_->0$.

Fig. 8

Left panel: $E_-$ for $C_-=1$. Right panel: $E_+$ for $C_+=1.6$. Both plots are for $G_\mathrm{N}\,M/R=10^3$

Fig. 9

Left panel: approximate inner potentials $V_-$ (dashed line), $\tilde{V}$ (solid line) and $V_+$ (dotted line) for $0\le r\le R$ and exact outer potential $V_\mathrm{out}$ (dotted line) for $r>R$. Right panel: approximate inner potentials $V_-$ (dashed line), $\tilde{V}$ (solid line) and $V_+$ (dotted line) for $0\le r\le R/5$. Both plots are for $G_\mathrm{N}\,M/R=10^3$

Fig. 10

Approximate inner potentials $V_-$ (dashed line), $\tilde{V}$ (solid line) and $V_+$ (dotted line) for $0\le r\le R$ and exact outer potential $V_\mathrm{out}$ (dotted line) for $r>R$ and for $G_\mathrm{N}\,M/R=10^2$ (left panel, with $C_-=1.042$ and $C_+=1.52$) and $G_\mathrm{N}\,M/R=50$ (right panel, with $C_-=1.073$ and $C_+=1.5$)

Fig. 11

Approximate inner potentials $V_-$ (dashed line), $V_\mathrm{lin}$ (solid line) and $V_+$ (dotted line) for $0\le r\le R$. Both plots are for $G_\mathrm{N}\,M/R=10^3$

For example, for the compactness $G_\mathrm{N}\,M/R=10^3$, we can use $C_-\simeq 1$ and $C_+\simeq 1.6$, and the plots of $E_-$ and $E_+$ are shown in Fig. 8. In particular, the minimum value of $|E_+|\simeq 14$. The corresponding potentials $V_\pm$ along with $\tilde{V}=\tilde{C}\,\psi$, where $\tilde{C}=(C_++C_-)/2$, are displayed in Fig. 9. It is easy to see that the three approximate solutions essentially coincide almost everywhere, except near $r=0$ where they start to fan out, albeit still very slightly (the right panel of Fig. 9 shows a close-up of this effect). A similar behaviour is obtained for larger values of $G_\mathrm{N}\,M/R$. For smaller values of the compactness up to $G_\mathrm{N}\,M/R\simeq 50$, the approximation (3.40) is still quite accurate (see Fig. 10), even if the smaller the compactness the bigger the difference between $V_\pm$. Actually, the error in the derivative of the potential at $r=R$ is of the order of $0.01\,\%$ and $0.6\,\%$ for $G_\mathrm{N}\,M/R=10^2$ and $G_\mathrm{N}\,M/R=50$, respectively. In order to obtain a comparable precision for lower compactness, the approximate expression (3.40) should be improved, but we do not need to do that given how accurate is the perturbative expansion employed in Sect. 3.3.1.

From the left panel of Fig. 9, it is clear that for $G_\mathrm{N}\,M/R=10^3$ the potential $V_\mathrm{in}$ is practically linear, except near $r=0$ where it turns into a quadratic shape, in order to ensure the regularity condition (3.3). An approximate expression for the source proper mass $M_0$ in terms of M can then be obtained from the simple linear approximation

$$\begin{aligned} V_\mathrm{lin} \simeq V_R + V'_R\left( r-R\right) , \end{aligned}$$

(3.42)

where $V_R$ and $V_R'$ are given by the usual expressions (3.9) and (3.10), and which is shown in Fig. 11 for $G_\mathrm{N}\,M/R=10^3$. Upon replacing the approximation (3.42) into the Eq. (3.15) for $r=R$, we obtain

$$\begin{aligned} \frac{M_0}{M} \simeq \frac{2\left( 1+5\,G_\mathrm{N}\,M/R\right) }{3\left( 1+6\,G_\mathrm{N}\,M/R\right) ^{4/3}}. \end{aligned}$$

(3.43)

Fig. 12

Pressure evaluated using the approximation $\tilde{V}= \tilde{C}\,\psi$ for $G_\mathrm{N}\,M/R =50$ (left panel), $G_\mathrm{N}\,M/R = 100$ (center panel) and $G_\mathrm{N}\,M/R = 1000$ (right panel). The constant $\tilde{C}=(C_+ + C_-)/2$, where $C_+$ and $C_-$ are the same as in Figs. 9 and 10 for the corresponding cases

The linear approximation is not very useful when it comes to evaluate the maximum value of the pressure, which we expect to occur in the origin at $r=0$, precisely where this approximation must fail. We therefore consider again the approximation $\tilde{V}=\tilde{C}\,\psi$, which replaced into Eq. (3.14) gives rise to the pressure shown in Fig. 12. Since the full expression is very cumbersome, we just show the leading order contribution for large compactness

$$\begin{aligned} p \simeq \frac{M^2\,e^{\frac{1}{2}\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}\left( 3- \frac{5}{\tilde{C}}\right) }}{2\,\pi \,\tilde{C}^2\,(6\,G_\mathrm{N}\,M/R)^{2/3}} \left[ e^{\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}\left( 1- \frac{r}{R}\right) }-1\right] ,\nonumber \\ \end{aligned}$$

(3.44)

which yields

$$\begin{aligned} p(0) \simeq \frac{M^2\,e^{\frac{5}{2}\left( \frac{\tilde{C}-1}{\tilde{C}}\right) \left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}}}{2\,\pi \,\tilde{C}^2\,(6\,G_\mathrm{N}\,M/R)^{2/3}}, \end{aligned}$$

(3.45)

where we find that $\tilde{C}>1$ for $G_\mathrm{N}\,M/R\gg 1$. It is clear from this expression and Fig. 12 how rapidly the pressure grows near the origin when the compactness increases, but still remaining finite and regular everywhere even for very large compactness. In Fig. 13 we can see the comparison of the above approximate expression with the graphs shown in Fig. 12. Of course the biggest the compactness the more rapidly the approximation (3.44) approaches the results of Fig. 12. In Figs. 14 and 15 we instead plot the comparison between the approximation (3.44) with $\tilde{C}=(C_+ +C_-)/2$ and the pressure evaluated from Eq. (3.14) and $V_\pm =C_\pm \,\psi$. The values of $C_-$ and $C_+$ are the same as in Figs. 9 and 10 for the corresponding compactness.

Fig. 13

Comparison between the approximate pressure (12) (dotted line) vs solution of Eq. (3.44) with $\tilde{V}=\tilde{C}\,\psi$ and $\tilde{C}=(C_+ +C_-)/2$ (solid line) for $G_\mathrm{N}\,M /R = 50$ (top left panel), $G_\mathrm{N}\,M / R= 100$ (top central panel), $G_\mathrm{N}\,M / R= 1000$ (top right panel), and the corresponding close-ups in the bottom panels

Fig. 14

Pressure evaluated from $V_-=C_-\,\psi$ (dashed line) vs pressure evaluated from $\tilde{V}=\tilde{C}\,\psi$ (dotted line) for $G_\mathrm{N}\,M/R =50$ (left panel), $G_\mathrm{N}\,M/R = 100$ (center panel) and $G_\mathrm{N}\,M/R = 1000$ (right panel)

Fig. 15

Pressure evaluated from $V_+=C_+\,\psi$ (dashed line) vs pressure evaluated from $\tilde{V}=\tilde{C}\,\psi$ with $\tilde{C}=(C_+ +C_-)/2$ (dotted line) for $G_\mathrm{N}\,M/R =50$ (left panel), $G_\mathrm{N}\,M/R = 100$ (center panel) and $G_\mathrm{N}\,M/R = 1000$ (right panel)

4 Horizon and gravitational energy

The approach we used so far completely neglects any geometrical aspect of gravity. In particular, it is well known that collapsing matter is responsible for the emergence of black hole geometries, providing us with the associated Schwarzschild radius (1.1). In general relativity, this marks the boundary between sources which we consider as stars ($R\gg R_\mathrm{H}$) and black holes ($R\lesssim R_\mathrm{H}$). Moreover, if the pressure is isotropic, stars must have a radius $R>(9/8)\,R_\mathrm{H}$, known as the Buchdahl limit [23], otherwise the necessary pressure diverges.

We found that the pressure is always finite in our bootstrapped picture, hence there is no analogue of the Buchdahl limit. This means that the source can have arbitrarily large compactness, including $R<R_\mathrm{H}$. Lacking precise geometrical quantities, we will follow a Newtonian argument and define the horizon as the value $r_\mathrm{H}$ of the radius at which the escape velocity of test particles equals the speed of light, namely

$$\begin{aligned} 2\,V(r_{\mathrm {H}})= -1, \end{aligned}$$

(4.1)

as in Ref. [7]. Of course, when the source is diluted no horizon should exist and the above definition correctly reproduces this expectation, since that condition is never fulfilled for small compactness (see Figs. 2 and 3). In fact, we can find a limiting lower value for the compactness at which Eq. (4.1) has a solution, by requiring

$$\begin{aligned} 2\, V_\mathrm{in}(r_\mathrm{H}=0) = -1, \end{aligned}$$

(4.2)

which gives $G_\mathrm{N}\,M/R \simeq 0.46$ if we use $V(0) = V_0$ from Eq. (3.22). Upon increasing the compactness, the horizon radius $r_\mathrm{H}$ will increase and eventually approach the radius R of the matter source, which occurs when

$$\begin{aligned} 2\, V_\mathrm{in}(r_\mathrm{H}=R) = 2\, V_\mathrm{out}(R) = -1, \end{aligned}$$

(4.3)

where $V_\mathrm{out}(R) = V_R$ is given by the exact expression in Eq. (3.9). This yields the compactness $G_\mathrm{N}\,M/R \simeq 0.69$ and $r_\mathrm{H}\simeq R \simeq 1.43\, G_\mathrm{N}\,M$. For even larger values of the compactness, the horizon radius will always appear in the outer potential (3.7) and therefore remain fixed at this value in terms of M. We can summarise the situation as follows

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{no\ horizon} &{}\quad \mathrm{for} \ \ G_\mathrm{N}\,M/R \lesssim 0.46 \\ \\ 0< r_{\mathrm {H}}\le R {\simeq } 1.4\,G_\mathrm{N}\,M &{}\quad \mathrm{for} \ \ 0.46 \lesssim G_\mathrm{N}\,M/R {\le } 0.69 \\ \\ r_{\mathrm {H}} \simeq 1.4\,G_\mathrm{N}\,M &{}\quad \mathrm{for} \ \ G_\mathrm{N}\,M/R > rsim 0.69. \end{array} \right. \nonumber \\ \end{aligned}$$

(4.4)

The above values of the compactness further correspond to proper masses

$$\begin{aligned} \frac{M_0}{M} \simeq \left\{ \begin{array}{ll} 0.56 &{}\quad \mathrm{for} \ \ G_\mathrm{N}\,M/R \simeq 0.46 \\ \\ 0.47 &{}\quad \mathrm{for} \ \ G_\mathrm{N}\,M/R \simeq 0.69, \end{array} \right. \end{aligned}$$

(4.5)

so that, when the horizon is precisely at the surface of the source, we have

$$\begin{aligned} r_\mathrm{H}\simeq 1.4\,G_\mathrm{N}\,M \simeq 3\,G_\mathrm{N}\,M_0. \end{aligned}$$

(4.6)

It is also important to remark that the horizon $r_\mathrm{H}$ lies inside the source for a relatively narrow range of the compactness (see Fig. 16 for the corresponding potentials).

Fig. 16

Potentials corresponding to $r_\mathrm{H}=0$ (solid line) and $r_\mathrm{H}=R$ (dashed line)

We can next estimate the gravitational potential energy $U_\mathrm{G}$ from the effective Hamiltonian (2.8) (with $q_{\Phi }=1$). For calculation and conceptual purposes, it is convenient to separate $U_\mathrm{G}$ into three different parts: the “baryon-graviton” contribution, for which the radial integral has only support inside the matter source, given by

$$\begin{aligned} U_\mathrm{BG}= & {} 4\,\pi \int _0^\infty r^2\,{\mathrm{d}}r \left( \rho +p\right) V\left( 1-2\,V\right) \nonumber \\= & {} \frac{3\, M_0}{R^3}\int _0^R r^2\,{\mathrm{d}}r\, e^{V_{R}-V_\mathrm{in}} V_\mathrm{in}\left( 1-2\,V_\mathrm{in}\right) , \end{aligned}$$

(4.7)

where we employed Eq. (3.14); the “graviton-graviton” contribution due to the potential self-interaction inside the source

$$\begin{aligned} U_\mathrm{GG}^\mathrm{in}= & {} \frac{1}{2\,G_\mathrm{N}} \int _0^R r^2\,{\mathrm{d}}r\, \left( V_\mathrm{in}'\right) ^2 \left( 1-4\,V_\mathrm{in}\right) \end{aligned}$$

(4.8)

and outside the source

$$\begin{aligned} U_\mathrm{GG}^\mathrm{out}= & {} \frac{1}{2\,G_\mathrm{N}} \int _R^\infty r^2\,{\mathrm{d}}r\, \left( V_\mathrm{out}'\right) ^2 \left( 1-4\,V_\mathrm{out}\right) , \end{aligned}$$

(4.9)

While the contribution from the outside is exactly given by

$$\begin{aligned} U_\mathrm{GG}^\mathrm{out} = \frac{G_\mathrm{N}\,M^2}{2\,R}. \end{aligned}$$

(4.10)

the inner contributions $U_\mathrm{BG}$ and $U_\mathrm{GG}^\mathrm{in}$ can only be evaluated within the approximations for the potential employed in the previous sections.

Fig. 17

Total gravitational potential energy $U_\mathrm{G}$. Left panel: $U_\mathrm{G}$ in the low compactness regime from the analytic approximations valid in the low and intermediate regime (continuous line) vs $U_\mathrm{G}$ from Eq. (4.11) (dashed line). Center panel: $U_\mathrm{G}$ in the low and intermediate compactness regime. Right panel: $U_\mathrm{G}$ in the high compactness regime

The energy contributions for objects of low compactness $G_\mathrm{N}\,M/R\ll 1$ can be evaluated straightforwardly. Starting from the approximate expression in (3.26) and (3.27) the total energy is calculated to be

$$\begin{aligned} U_\mathrm{G} = U_\mathrm{BG} + U_\mathrm{GG}^\mathrm{in} + U_\mathrm{GG}^\mathrm{out} \simeq -\frac{3\, G_\mathrm{N}\, M^2}{5\,R} + \frac{9\, G_\mathrm{N}^2\, M^3}{7\,R^2}\ ,\nonumber \\ \end{aligned}$$

(4.11)

where we immediately notice the usual newtonian term at the lowest order.

One can also calculate the three components of the gravitational potential energy in the regime of intermediate compactness $G_\mathrm{N}\,M/R\sim 1$, but the explicit expressions would be too cumbersome to display. Instead, the left panel of Fig. 17 shows a comparison in the regime of low compactness between the above expression for $U_\mathrm{G}$ and the one obtained starting from the analytic approximations from Eqs. (3.23) and (3.24), which are valid both for sources of low and intermediate compactness. It can be seen that the two approximations lead to similar results for objects that have low compactness. The center panel also shows the behaviour of $U_\mathrm{G}$ for objects of intermediate compactness. As expected, the gravitational potential energy becomes more and more negative as the density of the source increases.

We conclude with the high compactness regime, in which the increase in modulus of the negative gravitational potential energy is even more dramatic, as shown in the right panel of Fig. 17. To make things easier, we are going to evaluate the contributions (4.7) and (4.8) in the limit $G_\mathrm{N}\,M/R\gg 1$, with the help of the linear approximation (3.42) and (3.43). The leading order in $G_\mathrm{N}\,M/R\gg 1$ then reads

$$\begin{aligned} U_\mathrm{BG} \simeq -\frac{125\,R}{3\,G_\mathrm{N}} e^{\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}} \end{aligned}$$

(4.12)

and

$$\begin{aligned} U_\mathrm{GG}^\mathrm{in} \simeq \frac{5\,G_\mathrm{N}\,M^2}{36\,R}. \end{aligned}$$

(4.13)

One expects that this negative and large potential energy $U_\mathrm{G}$ is counterbalanced by the positive energy (D.11) associated with the pressure (3.44) inside the matter source.

Of course, the total energy of the system should still be given by the ADM-like mass M, which must therefore equal the sum of the matter proper mass $M_0$ and the energy associated with the pressure (see Appendix D for more details about the energy balance).

5 Conclusions and (quantum) outlook

In this work we have fully developed a bootstrapped model of isotropic and homogeneous stars, in which the pressure and density both contribute to the potential describing the gravitational pull on test particles. No equivalent of the Buchdahl limit was found, and the matter source can therefore be kept in equilibrium by a sufficiently large (and finite) pressure for any (finite) value of the compactness $G_\mathrm{N}\,M/R$. When the compactness of the source exceeds a value of order 0.46, a horizon appears inside the source and its radius $r_\mathrm{H}\simeq R$ for $G_\mathrm{N}\,M/R\simeq 0.69$. For larger values of the compactness, the source is entirely inside $r_\mathrm{H}$ and we can consider cases with $r_\mathrm{H} > rsim R$ as representing bootstrapped Newtonian black holes.

When the matter is collapsed further inside the horizon, that is for larger compactness such that $r_\mathrm{H}\gg R$, the gravitational potential energy grows even more negative, and a correspondingly very large pressure p is required in order to support the matter core. In fact, if we assume that black holes have regular inner cores of finite proper mass $M_0$ and thickness R, from Eq. (3.43) we obtain

$$\begin{aligned} \frac{G_\mathrm{N}\,M_0}{R} \sim \left( \frac{G_\mathrm{N}\,M}{R}\right) ^{2/3}, \end{aligned}$$

(5.1)

so that $M_0/M\sim (R/G_\mathrm{N}\,M)^{1/3}$ for $G_\mathrm{N}\,M/R\gg 1$. This means that most of the matter energy must be accounted for by the interactions that give rise to the pressure in very compact sources. Such a huge pressure $p\gg \rho$ violates the dominant energy condition [24] and could only be of purely quantum nature, thus requiring a quantum description of the matter in the source.

Correspondingly, the regular potential we obtained in the present work should be viewed as the mean field description of the quantum state of the (off-shell) gravitons in a (regular⁸) black hole when $R\lesssim r_\mathrm{H}$. It will be therefore a natural development to investigate the quantum features of this potential, as it affects both the quantum state of matter inside the black hole (or falling into it) and the dynamics of the gravitons themselves. Eventually, one would also like to identify the fully quantum state that generates this potential, like it was done for the Newtonian potential in Refs. [9, 33, 34], or in Refs. [40,41,42]. Finally, we would like to remark that, although we found that $M\gg M_0$ for very large compactness, and one could thus infer that matter become almost irrelevant inside a black hole [15,16,17,18,19,20,21], the above picture inherently requires the presence of matter, whose role in black hole physics we believe needs more investigations [35,36,37,38,39].

Appendices

A Gravitational current

We present here an alternative derivation of the gravitational current leading to the same Lagrangian (2.7) of Sect. 2. The starting point will now be the Newtonian energy evaluated on-shell inside a sphere of radius r, that is

$$\begin{aligned} U_\mathrm{N}(r)= & {} 2\,\pi \int _0^r {\bar{r}}^2\,{\mathrm{d}}{\bar{r}} \,\rho (\bar{r})\, V(\bar{r}) \nonumber \\= & {} \frac{1}{2\,G_\mathrm{N}}\, \int _0^r {\bar{r}}^2 \,{\mathrm{d}}{\bar{r}}\, V(\bar{r})\,\triangle V(\bar{r}), \end{aligned}$$

(A.1)

in which we do not perform any integration by parts. We can then define a current $\tilde{J}_V$ proportional to the energy density by deriving $U_\mathrm{N}(r)$ with respect to the volume $\mathcal {V}$, which yields

$$\begin{aligned} \tilde{J}_V \simeq 2\,\frac{{\mathrm{d}}U_\mathrm{N}}{{\mathrm{d}}\mathcal {V}} = \frac{V(r)\,\triangle V(r)}{4\,\pi \,G_\mathrm{N}}. \end{aligned}$$

(A.2)

One can immediately notice that we chose to have a different numerical factor in front of $\tilde{J}_V$ from the one in $J_V$ of Eq. (2.5) in order to keep the same coupling parameter $\tilde{q}_V=q_V$. It is now easy to see that by adding all other sources described in Sect. 2 together with (A.2), we end up with the same Lagrangian (2.7),

$$\begin{aligned} \tilde{L}[V]= & {} L_\mathrm{N}[V] -4\,\pi \int _0^\infty r^2\,{\mathrm{d}}r \nonumber \\&\times \,\left[ q_V\,\tilde{J}_V\,V + q_\mathrm{B}\,J_\mathrm{B}\,V + q_\rho \,J_\rho \left( \rho +p\right) \right] = L[V],\nonumber \\ \end{aligned}$$

(A.3)

where we discarded vanishing boundary terms. In fact, we have

$$\begin{aligned} \int _0^\infty r^2\,{\mathrm{d}}r\,J_V\,V = 2\,\int _0^\infty r^2\,{\mathrm{d}}r\,\tilde{J}_V\,V + \left[ r^2\,V^2\,V'\right] _{r=0}^{r\rightarrow \infty },\nonumber \\ \end{aligned}$$

(A.4)

and the second term in the right hand side vanishes because of the boundary conditions at $r\rightarrow \infty$ and Eq. (3.3) at $r=0$.

B Newtonian solution

We recall that the Newtonian solution of the Poisson equation (2.2) with a homogeneous source of mass $M_0$ and radius R,

$$\begin{aligned} \triangle V_\mathrm{N} = \frac{3\, G_\mathrm{N}\,M_0}{R^3}\,\Theta (R-r), \end{aligned}$$

(B.1)

is given by

$$\begin{aligned} V_\mathrm{N} = \left\{ \begin{array}{lrl} \displaystyle \frac{G_\mathrm{N}\, M_0}{2\,R^3}\left( r^2 - 3\,R^2\right) &{}\quad \mathrm{for} &{} 0\le r<R\\ \\ -\displaystyle \frac{G_\mathrm{N}\,M_0}{r} &{}\quad \mathrm{for} &{} r>R, \end{array} \right. \end{aligned}$$

(B.2)

which is continuous, with continuous first derivative across $r=R$. We also remark that there is one and the same mass parameter $M_0=M$ in the interior and exterior part of the potential.

C Comparison method

We have shown in Sect. 3.3 that a solution to Eq. (3.15) satisfying Eq. (3.17) exists by employing comparison functions [27,28,29] and we recall the fundamentals of this method here for the sake of convenience.

Let us consider an equation of the form

$$\begin{aligned} u''(r) = F(r, u(r), u'(r)), \end{aligned}$$

(C.1)

where F is a real function of its arguments, r varies in the finite interval $[r_1,r_2]$ and a prime denotes the derivative with respect to r. We want to find a solution which further satisfies the general boundary conditions

$$\begin{aligned}&a_1\, u(r_1) - a_2\, u'(r_1) = A_0, \end{aligned}$$

(C.2)

$$\begin{aligned}&b_1\, u(r_2) + b_2\, u'(r_2) = B_0, \end{aligned}$$

(C.3)

with $A_0$, $B_0$, $a_1$, $b_1$ real numbers and $a_2$, $b_2$ non negative real numbers satisfying $a_1^2 + a_2^2 > 0$ and $b_1^2 + b_2^2 > 0$. The theorems in Refs. [27,28,29] guarantee that such a solution $u \in C^2 ([r_1,r_2])$ exists under the following three conditions:

• 1. we can find a lower bounding function

  $$\begin{aligned}&u_-''(r) \ge F(r, u_-(r), u_-'(r)) \end{aligned}$$

  (C.4)
  $$\begin{aligned}&a_1\, u_-(r_1) - a_2\,u_-'(r_1) \le A_0 \end{aligned}$$

  (C.5)
  $$\begin{aligned}&b_1\, u_-(r_2) + b_2\,u_-'(r_2) \le B_0, \end{aligned}$$

  (C.6)

  and an upper bounding function

  $$\begin{aligned}&u_+''(r) \le F(r, u_+(r), u_+'(r)) \end{aligned}$$

  (C.7)
  $$\begin{aligned}&a_1\, u_+(r_1) - a_2\,u_+'(r_1) \ge A_0 \end{aligned}$$

  (C.8)
  $$\begin{aligned}&b_1\,u_+(r_2) + b_2\,u_+'(r_2) \ge B_0 \ ; \end{aligned}$$

  (C.9)

• 2. the function F is continuous on the domain $D = \{(r, u, u')\in [r_1,r_2]\times \mathbb {R}^2\, |\, u_-\le u \le u_+\}$;

• 3. the function F satisfies a Nagumo condition: there exists a continuous and positive function $\phi$ such that

  $$\begin{aligned} \int _0^{\infty } \frac{s\, {\mathrm{d}}s}{\phi (s)} = \infty \end{aligned}$$

  (C.10)

  and, $\forall (t, u, u')\in D$,

  $$\begin{aligned} |F(r, u(r), u'(r))| \le \phi (|u'|). \end{aligned}$$

  (C.11)

Moreover, the solution u will satisfy

$$\begin{aligned} u_- (t)\le u(t) \le u_+ (t). \end{aligned}$$

(C.12)

We can now apply the above general theorem to our problem inside the source, for which $r_1=0$ and $r_2=R$. We first rewrite Eq. (3.15) as

$$\begin{aligned} V''= & {} \frac{3\,G_\mathrm{N}\,M_0}{R^3}\,e^{V_R-V} + \frac{2\left( V'\right) ^2}{1-4\,V} - \frac{2\, V'}{r} \nonumber \\\equiv & {} F(r, V, V'), \end{aligned}$$

(C.13)

and recall the boundary conditions (3.3) and (3.4), that is

$$\begin{aligned}&V'(0) = 0 \end{aligned}$$

(C.14)

$$\begin{aligned}&V(R) = V_{R}. \end{aligned}$$

(C.15)

We can now verify all the requirements of the theorem, and will do so for the case of large compactness analysed in Sect. 3.3.2. The upper and lower bounding functions are therefore $V_\pm$ given in Eq. (3.39) and the domain

$$\begin{aligned} D = \{(r, V, V') \in [0, R]\times \mathbb {R}^2\, |\, V_{-} \le V \le V_{+}\,\}. \end{aligned}$$

(C.16)

Continuity of F on D is easily verified. In fact, the first term on the right hand side of Eq. (C.13) is an exponential of V which is always regular in D. The same is true for the second term considering that $V_\pm < 0$, thus $V<0$ as well. The last term could be tricky but the boundary condition (C.14) require that $V'$ vanishes at $r=0$ at least as fast as r [see the expansion around $r = 0$ in Eq. (3.18)] so that this is also regular in D. Finally, we can choose

$$\begin{aligned} \phi = \underset{D}{\mathrm{max}}(F), \end{aligned}$$

(C.17)

which must be finite given that F is continuous in D.

All of the hypotheses of the theorem hold and a solution to Eq. (3.15) therefore exists and satisfies Eq. (3.17). By imposing the remaining boundary condition (3.5), one can then obtain a relation between $M_0$, which appears in the Eq. (3.15), and M, which appears in the boundary conditions (3.4) and (3.5), for any given value of R.

D Energy balance

In Sect. 4, we only computed the gravitational energy from the Hamiltonian (2.8). The purely baryonic contribution will be given by the proper mass $M_0$ and the pressure energy contribution found again from the newtonian argument (2.6), whereby

$$\begin{aligned} U_\mathrm{B}(R) = D(M,R) - 4\,\pi \int _0^R r^2\,{\mathrm{d}}r\, p(r). \end{aligned}$$

(D.1)

In the newtonian regime, the integration constant D(M, R) can be fixed so as to guarantee that the work done by gravity is equal and opposite to the work done by the forces responsible for the pressure p. In other words, in that case we find D(M, R) by requiring that the gravitational force is conservative. This will also ensure that the total energy related to the Hamiltonian constraint equals the ADM-like mass M of the system, that is

$$\begin{aligned} E = M_0 + U_\mathrm{G} + U_\mathrm{B} = M. \end{aligned}$$

(D.2)

Of course, in the Newtonian case Eq. (D.2) simply reads $E=M_0\equiv M$, as shown in Ref. [7].

In the bootstrapped picture, gravity is not a linear interaction any more and it is not at all obvious that it will still be conservative. A precise energy estimate would therefore require a complete knowledge of the dynamical process which led to the formation of the equilibrium configuration of given ADM-like mass M and radius R. Without that knowledge, we can only assume that the total energy of the equilibrium configuration equals M and fix D(M, R) so that the Hamiltonian constraint (D.2) is satisfied.

With that prescription, we can now evaluate the baryonic contributions. In the low compactness case, we expand all the terms in Eq. (D.2) to order $M^3$, namely

$$\begin{aligned} M_0 \simeq M - \frac{5\,G_\mathrm{N}\,M^2}{2\,R} + \frac{81\,G_\mathrm{N}^2\,M^3}{8\,R^2}, \end{aligned}$$

(D.3)

and the pressure energy

$$\begin{aligned} U_\mathrm{B} \simeq D_s(M,R) - \frac{G_\mathrm{N}\,M^2}{5\,R} + \frac{61\,G_\mathrm{N}^2\,M^3}{70\,R^2}. \end{aligned}$$

(D.4)

Equation (D.2) is then satisfied for

$$\begin{aligned} D_s(M,R) \simeq -\frac{33\,G_\mathrm{N}\,M^2}{10\,R} +\frac{3439\,G_\mathrm{N}^2\,M^3}{280\,R^2} \end{aligned}$$

(D.5)

so that

$$\begin{aligned} U_\mathrm{B} \simeq \frac{31\,G_\mathrm{N}\,M^2}{10\,R} \left( 1 - \frac{6390\,G_\mathrm{N}\,M}{1736\,R} \right) , \end{aligned}$$

(D.6)

which is positive only for small compactness, as its approximation requires.

The high compactness regime of course yields quite different results. To make things easier, we again look at the limiting case of very high compactness, where the linear approximation (3.42) holds, and consider the Hamiltonian constraint (D.2) only at leading order in M. The proper mass in Eq. (3.43) can be simplified further to give

$$\begin{aligned} M_0 \simeq \frac{5\,M}{9\,(6\,G_\mathrm{N}\,M/R)^{1/3}}, \end{aligned}$$

(D.7)

while the pressure energy can be written as

$$\begin{aligned} U_\mathrm{B} \simeq D_b(M,R) - \frac{20\,R^3}{G_\mathrm{N}^3\,M^2} \left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R} \right) ^{2/3} e^{\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R} \right) ^{2/3}}. \end{aligned}$$

(D.8)

Again, we just impose Eq. (D.2) and find

$$\begin{aligned} D_b(M,R)\simeq & {} M + \frac{20\,R^3}{G_\mathrm{N}^3\,M^2} \left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R} \right) ^{2/3} e^{\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R} \right) ^{2/3}} \nonumber \\&+\, \frac{125\,R}{3\,G_\mathrm{N}} e^{\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}}\end{aligned}$$

(D.9)

$$\begin{aligned}&-\, \frac{7\,G_\mathrm{N}\,M^2}{36\,R} - \frac{5\,M}{9\,(6\,G_\mathrm{N}\,M/R)^{1/3}}, \end{aligned}$$

(D.10)

so that

$$\begin{aligned} U_\mathrm{B}\simeq & {} \frac{125\,R}{3\,G_\mathrm{N}} e^{\left( \frac{G_\mathrm{N}\,M}{\sqrt{6}\,R}\right) ^{2/3}}, \end{aligned}$$

(D.11)

which is positive as it should, and precisely counterbalances Eq. (4.12).