1 Introduction

The extreme light infrastructure (ELI) is designed to produce the highest power and intense laser worldwide [1, 2]. It has a potential of reaching ultra-relativistic intensities, challenging the Schwinger limit \(E_\text {s} :=m^2/e \approx 1.32\times 10^{18} \,\mathrm { V\, m^{-1}}\). As laser field approaches this value, vacuum becomes unstable, and a large amount of charged particles produces in pairs, so that laser loses the energy, and its intensity stays within the upper limit. However, Schwinger effect is not only a phenomenon in electromagnetism, but a universal aspect of quantum vacuum in the presence of a \({\mathsf {U}}(1)\) gauge field with a classical background, see e.g. [3,4,5,6,7].

The pair-production rate in the constant electric field had been pioneered by Sauter, Heisenberg and Euler [8, 9], and the corresponding Effect was named after Schwinger [10], who did the calculation based on field-theoretical approaches, see e.g. [11, 12] for a current review. A semiclassical approach called worldline instantons has been introduced more recently to the study of constant and inhomogeneous fields in the small-coupling and weak-field approximations [13, 14], where the production rate, in Wick-rotated Euclidean space, is represented by a worldline path integral. The so-called worldline instantons are the periodic saddle points relevant for a calculation of integral by the steepest descent method. The extension of inhomogeneous fields originates from more practical purpose. As analysed in [14], 1-D dynamic electric fields reduce the critical value of Schwinger effect, such that pair production from vacuum is more close to experimentally observable conditions.

The Schwinger effect at arbitrary coupling in constant field has also been studied in [13] at the weak-field condition, which is considered originally in order to overcome some obstacles from direct application of Schwinger’s approach. However the later observation (e.g. [15]) found that the weak-field condition is broken around the critical field, defined as a point of vacuum cascade, such that the mechanism in weak-field condition loses its prediction for this vacuum phenomenon. Inspired by the similar existence of critical value of electric field in string theory, it is of a possibility to clarify the vacuum cascade in the Coulomb phase beyond the weak-field condition with the help of gauge/gravity duality [7, 16, 17]. This is also known as the Semenoff–Zarembo construction, where the production rate has been obtained by calculating the classical action of a bosonic string, which is attached to a probe D3–brane and coupled to a Kalb–Ramond field.

Since the instanton action in the production rate is equivalent to the string action, which is proportional to the area, calculation of the rate is related to integrating the classical equations of motion for bosonic string in the given external field. In other words, duality converts the problem to evaluating the area of a minimal surface [18, 19] in Euclidean \(\mathrm {AdS}_3\), the boundary of which is assumed to be the trajectory of the worldline on the probe D3–brane. In mathematics, such a Dirichlet problem is known as the Plateau’s problem [20].

In this work, we consider the scalar pair production in a dynamic external field of single-pulse and sinusoidal types at strong coupling and weak-field limit based on the method of worldline instantons, which is explained in Sects. 2 and 3. We first show by a field-theoretical approach, that besides the enhancement due to the dynamics of electric fields, a further contribution to the production rate arises from the Wilson loop, and it becomes dominant in production rate as Keldysh parameter increases. However, such a correction seems to diverge as Keldysh adiabaticity parameter \(\gamma \rightarrow \infty \) based on our estimated formula; and it leads to a contradiction to the weak-field condition, so that near the critical field, the method itself breaks down, and the prediction of a vacuum cascade becomes unclear. To overcome the problem of breaking weak-field condition, we then follow Semenoff and Zarembo’s proposal in Sect. 4, applying the gauge/gravity duality to the Schwinger effect in the Coulomb phase of an \({\mathcal {N}}=4\) supersymmetric Yang–Mills theory. The classical solution of the corresponding string worldsheets are estimated by perturbing the solvable case of a constant external electric field.

2 Worldline instantons at strong coupling

The worldline instanton approach is a semiclassical calculation realised by the worldline path integral representations [21, 22], in which the so-called worldline instanton is a periodic solution of the stationary phase in the path integral. Based on this method, the pair-production rate \(\varGamma \) for a massive scalar QED in the small-coupling and weak-field approximation is computed by [13,14,15]

$$\begin{aligned} V_4 \varGamma = - 2{\mathrm {Im}} \int {\mathcal {D}}x\, \frac{1}{m}\sqrt{\frac{2\uppi }{T_0}}\, {\exp }\mathopen {}\left( -S_{\text {inst}}\right) \mathclose {}, \end{aligned}$$
(1)

where \(V_4\) is the 4-volume, \(T_0\) is a constant, given by

$$\begin{aligned} T_0=\frac{\sqrt{\int ^1_0 \mathrm {d}\tau \, \dot{x}^2}}{m}, \end{aligned}$$
(2)

and \(S_{\text {inst}}\) represents the action of worldline instanton, i.e.

$$\begin{aligned} S_{\text {inst}} = m^2 \sqrt{\int ^1_0 \mathrm {d}\tau \, \dot{x}^2}- \mathrm {i}e \int ^1_0 \mathrm {d}\tau \, B \cdot \dot{x}. \end{aligned}$$
(3)

In Eq. (3), \(B_\mu \) is a classical background field, not to be confused with the fluctuation part of the \({\mathsf {U}}(1)\) gauge field \(A_\mu \), which is also included in the initial setup of path integral, but cancelled due to considerations at small coupling.

The path integral in Eq. (1) can be computed by the stationary phase approximation in weak-field condition

$$\begin{aligned} m\sqrt{\int ^1_0\mathrm {d}u\;\dot{x}^2}\gg 1 \end{aligned}$$
(4)

For more general cases with 1D temporally inhomogeneous fields \(B_1(x_0)\), the worldline instanton is obtained by solving the instanton equation with periodic boundary condition

$$\begin{aligned} x'_1(x_0)=\pm \frac{\mathrm {i}e }{m}\frac{B_1(x_0)}{\sqrt{1+\left( \frac{e B_1(x_0)}{m} \right) ^2}}. \end{aligned}$$
(5)

Thus the pair-production rate can be written as

$$\begin{aligned} \varGamma \sim {\exp }\mathopen {}\left( -\frac{\uppi m^2}{e E} f(\gamma )\right) \mathclose {}, \end{aligned}$$
(6)

where \(f(\gamma )\) is a monotonically decreasing function of Keldysh parameter [23] \(\gamma =m \omega /(e E)\) and calculated by substituting the solution of Eq. (5) into the worldline action with the corresponding background field \(B_\mu \). In addition, the weak-field condition Eq. (4) is of various forms according to different dynamic fields, because it depends on specific instanton solution.

At arbitrary coupling constant but with weak-field condition [13], the production rate is modified by a factor,

$$\begin{aligned} V_4 \varGamma = - 2{\mathrm {Im}} \int {\mathcal {D}}x\, \frac{1}{m}\sqrt{\frac{2\uppi }{T_0}}\, {\exp }\mathopen {}\left( -S_{\text {inst}}\right) \mathclose {} {\langle {W}\rangle }, \end{aligned}$$
(7)

where \({\langle {W}\rangle }\) is the average of \({\mathsf {U}}(1)\) Wilson loop W

$$\begin{aligned} W={\exp }\mathopen {}\left( \mathrm {i}e \oint _C A\cdot \mathrm {d}x\right) \mathclose {}. \end{aligned}$$
(8)

The integral path C is along the 2D trajectory of worldline instanton. In the Feynman gauge of the \({\mathsf {U}}(1)\) field, the Wilson loop becomes [24]

$$\begin{aligned} {\langle {W}\rangle }={\exp }\mathopen {}\left( -\frac{e^2}{8\uppi ^2} {\mathcal {A}}\right) \mathclose {}. \end{aligned}$$
(9)

After simplification, \({\mathcal {A}}\) can be represented via a double contour integrals

$$\begin{aligned} {\mathcal {A}}=\oint _C \oint _C \frac{\mathrm {d}x\cdot \mathrm {d}y}{(x-y)^2}. \end{aligned}$$
(10)

For a constant electric field, the worldline instanton is a circle, and the production rate of a single scalar pair is given by

$$\begin{aligned} \varGamma =\frac{(e E)^2}{(2\uppi )^2} \mathrm {e}^{-\uppi \frac{ E_\text {s}}{E}}, \qquad E_\text {s} :=\frac{m^2}{e}, \end{aligned}$$
(11)

where \(E_\text {s}\) is the Schwinger limit in natural units. Consideration at arbitrary coupling [13] leads to a correction from Eq. (9)

$$\begin{aligned} \varGamma =\frac{(e E)^2}{(2\uppi )^2} \mathrm {e}^{-\uppi \frac{ E_\text {s}}{E}+\frac{e^2}{4}}, \end{aligned}$$
(12)

see also Sect. 3.2. Our aim in the next section is to calculate the Wilson loops in Eq. (9) along two specific worldlines separately. The first one is the worldline instanton in a single-pulse field, whereas the second is in a sinusoidal field. We show that the corrections due to the dynamic fields depend on Keldysh parameter, and the weak-field condition is also broken in these two cases, as noted in e.g. [15].

3 Wilson loops along worldline instanton paths

The Wilson loop in Eq. (9) plays a central role in the case of arbitrary coupling, the integral Eq. (10) standing on the exponent diverges as x approaches y. A regulator \(\varepsilon \) has been introduced in [25], such that Eq. (9) becomes

$$\begin{aligned} {\mathcal {A}}_\varepsilon = \int _{-\uppi }^{\uppi } \mathrm {d}s\,\int _{-\uppi }^{\uppi } \mathrm {d}t\, \frac{ x'(s) \cdot x'(s+t) }{[x(s+t)-x(s)]^2+\varepsilon ^2}, \end{aligned}$$
(13)

where prime indicates derivative with respect to the instanton parameter, and s and t can be understood as angular coordinates for the instanton.

One sees that the integrand in \({\mathcal {A}}_0\) behaves like \(t^{-2}\) as \(t \rightarrow 0\), rendering the integral divergent. Introducing \(\varepsilon \) makes the integral regular, and the divergence can now seen explicitly by expanding the numerator and denominator of the integrand separately. Up to \({O}\mathopen {}\left( t^2\right) \mathclose {}\), the numerator reads

$$\begin{aligned}&x'(s)\cdot x'(s+t) \nonumber \\&\quad = x'(s)^2 + x'(s) \cdot x''(s) t + \frac{1}{2} x'(s) \cdot x'''(s) t^2+O(t^3) \nonumber \\&\quad = x'(s)^2+\frac{1}{2} x'(s) \cdot x'''(s) t^2+O(t^3), \end{aligned}$$
(14)

whereas the denominator becomes

$$\begin{aligned} {\left[ x(s+t)- x(s)\right] }^2+\varepsilon ^2 = \varepsilon ^2 + {x'}\mathopen {}\left( s\right) \mathclose {}^2 t^2 + O(t^4). \end{aligned}$$
(15)

The condition \(x'(s) \cdot x''(s) \equiv 0\) has also been used, because all worldline instantons satisfy \({x'}\mathopen {}\left( s\right) \mathclose {}^2 =a^2\), where a is defined in the same way as in [14]. Hence up to second order of t, one has

$$\begin{aligned} {}^2\!{\mathcal {A}}^{(0)}_\varepsilon&=\int ^{\uppi }_{-\uppi }\mathrm {d}s \, x'(s)^2 \int ^{\uppi }_{-\uppi }\frac{\mathrm {d}t}{x'(s)^2 t^2+\varepsilon ^2} \nonumber \\&=\frac{\uppi }{\varepsilon } \int ^{\uppi }_{-\uppi }\mathrm {d}s\,\sqrt{x'(s)^2}-4+O(\varepsilon ), \end{aligned}$$
(16)

\({}^2\!{\mathcal {A}}^{(1)}_\varepsilon \equiv 0\), and

$$\begin{aligned} {}^2\! {\mathcal {A}}^{(2)}_\varepsilon&= \frac{1}{2}\int ^{\uppi }_{-\uppi }\mathrm {d}s\, x'(s)\cdot x'''(s) \int ^{\uppi }_{-\uppi } \frac{t^2\,\mathrm {d}t}{ x'(s)^2 t^2+\varepsilon ^2}\nonumber \\&=\uppi \int ^{\uppi }_{-\uppi }\mathrm {d}s\, \frac{ x'(s)\cdot x'''(s)}{ x'(s)^2}+O(\varepsilon ). \end{aligned}$$
(17)

One sees that the divergence of \({\mathcal {A}}\) now is removed by introducing a subtraction term

$$\begin{aligned} \updelta \!{\mathcal {A}}=\frac{\uppi }{\varepsilon }\int _{-\uppi }^{\uppi } \mathrm {d}s \sqrt{{x'}\mathopen {}\left( s\right) \mathclose {}^2}, \end{aligned}$$
(18)

which is an example of the perimeter law, depicting the behaviour of the Wilson loop in Euclidean space [24, ch. 82]. Since \({x'}\mathopen {}\left( s\right) \mathclose {}^2 =a^2\) is independent of integration variable, the subtraction term can be worked out as

$$\begin{aligned} \updelta \!{\mathcal {A}}=\frac{2 \uppi ^2 a}{\varepsilon }. \end{aligned}$$
(19)

After subtracting this term from Eq. (13), one obtains the physical \({\mathcal {A}}_{\text {phy}}\) by taking the limit of regularised \({\mathcal {A}}_{\text {reg}}\)

$$\begin{aligned} {\mathcal {A}}_{\text {phy}} :=\lim _{\varepsilon \rightarrow 0}{\mathcal {A}}_{\text {reg}} :=\lim _{\varepsilon \rightarrow 0}{\left( {\mathcal {A}}_\varepsilon -\updelta \!{\mathcal {A}}\right) }. \end{aligned}$$
(20)

The physical Wilson loop is then given by

$$\begin{aligned} {\langle {W}\rangle }_{\text {phy}}= {\exp }\mathopen {}\left( -\frac{e^2}{8\uppi ^2} {\mathcal {A}}_{\text {phy}}\right) \mathclose {}, \end{aligned}$$
(21)

which appears as a factor in the final expression of the production rate.

In our practice with the dynamic fields, \({\mathcal {A}}_\varepsilon \) has yet to be worked out in a closed form, and its estimation is to be discussed in Sect. 3.1.

3.1 Estimation of \({\mathcal {A}}_\varepsilon \) and \({\mathcal {A}}_\text {phy}\)

To derive an approximation of \({\mathcal {A}}_\varepsilon \), one may keep the finite terms in Eqs. (16) and (17), i.e.

$$\begin{aligned} {}^2\! {\mathcal {A}}_{\text {reg}}\approx -4+ \uppi \int ^{\uppi }_{-\uppi }\mathrm {d}s\, {\left[ \frac{ x'(s)\cdot x'''(s)}{ x'(s)^2}\right] }+O(\varepsilon ) \end{aligned}$$
(22)

This will be called a t-expansion up to second order of t, which follows straightforwardly from the separation of divergent term. This method belongs to rational approximation. Furthermore in our application in dynamic fields, this expansion can be worked out in a closed form easily. Also note the \(-4\) term in Eq. (22), which will be mentioned again later with example. The validity of t-expansion is closely related to the uniform convergence of integrand, and demonstrated in Appendix A. If one uses diagonal Padé approximant for integrand rather than t-expansion, the convergence is obvious [26,27,28].

Alternatively, one may also expand the integrand of \({\mathcal {A}}_\epsilon \) with respect to \(\gamma \) for the well-defined point \(\gamma _0\), i.e.

$$\begin{aligned} {\mathcal {A}}_{\varepsilon }= \int ^{\uppi }_{-\uppi }\mathrm {d}s\int ^{\uppi }_{-\uppi }\mathrm {d}t\, \left[ \sum _n f_n(\varepsilon ) {\left( \gamma -\gamma _0\right) }^n\right] \end{aligned}$$
(23)

where \(n\in {\mathbb {Z}}\). This will be called a \(\gamma \)-expansion. If the sequence \(\{f_n(\varepsilon )\}\) is integrable term by term, such that the interchanging summation and integration is valid, then comparing with the similar expansion of \(\updelta \!{\mathcal {A}}\), one obtains the finite terms of each order by

$$\begin{aligned} {\mathcal {A}}^{(n)}_{\text {reg}} = \frac{1}{\varepsilon }\sum _{k=0} F_{n,k}\varepsilon ^k-\frac{2\uppi ^2 a_n}{\varepsilon } \end{aligned}$$
(24)

where \(F_{n,k}\) are coefficients of expansion for \(F_n\) with respect to \(\varepsilon \)

$$\begin{aligned} F_n = \int ^{\uppi }_{-\uppi }\mathrm {d}s\int ^{\uppi }_{-\uppi }\mathrm {d}t\,f_n(\varepsilon ) \end{aligned}$$
(25)

while \(a_n\) are coefficients of expansion for \(a(\gamma )\) with respect to \(\gamma \). Since \(\varepsilon =0\) is the pole of first order for \(A_\varepsilon \) as a function of \(\varepsilon \), \(F_n\) having the same pole of \(\varepsilon \) is obviouse. For those points, where interchanging operation not long stands, this approach fails, e.g. at \(\gamma _0\rightarrow +\infty \). In our application in dynamic fields, this expansion can also be worked out in a closed form at each order. However, the number of terms in the expansion increases exponentially, and the result are obtained by computer algebra system.

Yet another way of estimating \({\mathcal {A}}_\text {phy}\) is numerical integration, in which the regulator \(\varepsilon \) is still needed. There are polynomial contributions of \(\varepsilon \) in the bare term \({\mathcal {A}}_\varepsilon \), and one might think taking a small \(\varepsilon \) would give a good result. However, \({\mathcal {A}}_\varepsilon \) and the counter term \(\updelta \!{\mathcal {A}}\) both diverges like \(\varepsilon ^{-1}\) as \(\varepsilon \rightarrow 0\). A small \(\varepsilon \) leads to a numerically dissatisfying operation, in which two big numbers cancels, yielding a small result and a great loss of significance. This problem becomes catastrophic for the dynamic fields when \(\gamma \rightarrow 0^+\). In order to overcome the potentially catastrophic cancellation, we use linear extrapolation near \(\varepsilon = 0\), in which for each \(\gamma \), \({\mathcal {A}}_\text {reg}\) is numerically calculated for several different values of \(\varepsilon \). The limit of \(\varepsilon \rightarrow 0\) is then obtained by linearly extrapolate the series of results with respect to \(\varepsilon \). In this approach, the error due to extrapolation can also be obtained by estimation of the parameters in linear regression. Furthermore, in our application the numerator and denominator in Eq. (13) scales as \(\gamma ^{-2}\) when \(\gamma \rightarrow +\infty \), so that for a fixed \(\varepsilon \), at large \(\gamma \) the regularised integrand is dominated by the regulator on the denominator. This is overcome by scaling \(\varepsilon \) accordingly, such that the subtraction term in Eq. (13) remains constant with respect to \(\gamma \).

3.2 Constant electric field

For a constant electric field, the worldline instanton is a circle of radius \(R=m/(e E)\), given by [13, 14]

$$\begin{aligned} x_0=R \sin (u), \quad x_1=R \cos (u), \qquad u\in [-\uppi , \uppi ], \end{aligned}$$
(26)

where the zeroth component \(x_0\) denotes the Euclidean time. The instanton action for single pair production is obtained by substituting this solution into Eq. (3), yielding

$$\begin{aligned} S_0 = \frac{\uppi m^2}{e E}. \end{aligned}$$
(27)

The weak-field condition \(m\sqrt{\int ^1_0 \mathrm {d}u\,\dot{x}^2}\gg 1\) [14] implies

$$\begin{aligned} E\ll 2\uppi E_\text {s}, \end{aligned}$$
(28)

where \(E_\text {s}\) is defined in Eq. (11).

On the other hand, the integral in Eq. (13) and the perimeter law in Eq. (18) can be evaluated explicitly as

$$\begin{aligned} {\mathcal {A}}=2 \uppi ^2 {\left( \frac{2 R^2+\varepsilon ^2}{\varepsilon \sqrt{4 R^2+\varepsilon ^2}}-1\right) }, \qquad \updelta \!{\mathcal {A}}=-\frac{2 \uppi ^2 R}{\varepsilon }. \end{aligned}$$
(29)

Hence the regularised Wilson loop for a single scalar pair can be recovered as [13]

$$\begin{aligned} {\langle {W}\rangle }_{\text {reg}}={\exp }\mathopen {}\left( \frac{e^2}{4}\right) \mathclose {}, \end{aligned}$$
(30)

and the production rate is given by

$$\begin{aligned} \varGamma \sim {\exp }\mathopen {}\left( -\frac{\uppi m^2}{e E} + \frac{e^2}{4}\right) \mathclose {}, \end{aligned}$$
(31)

from which the critical field for vacuum cascade can be estimated by

$$\begin{aligned} E_\text {c} = \frac{E_\text {s}}{\alpha } \approx 137 E_\text {s}, \qquad \alpha :=\frac{e^2}{4\uppi }. \end{aligned}$$
(32)

One sees that \(E_\text {c}\) is much greater than the Schwinger limit and breaks the weak field condition in Eq. (28), as have been noted in e.g. [15]. Therefore, the obtained results are not valid when the field goes close to the critical limit, and cannot answer the question whether a vacuum cascade happens near the critical field strength.

3.3 Single-pulse field \(E(t)=E {{\,\mathrm{sech}\,}}^2(\omega t)\)

For a generic 1D dynamic field, we assume that the Wilson loop is of the following form

$$\begin{aligned} {\langle {W(\gamma )}\rangle }={\exp }\mathopen {}\left[ \frac{e^2}{4}\lambda (\gamma )\right] \mathclose {}, \quad \gamma =\frac{m\omega }{e E}, \end{aligned}$$
(33)

where \(\lambda (\gamma )\) is an enhancement factor with respect to the case of a constant external field in Eq. (30). This name of \(\lambda (\gamma )\) is seen to be appropriate from the fact that \(\lambda (\gamma )\) is a monotonically decreasing function and tends to unit at adiabatic limit \(\gamma \rightarrow 0\).

Before applying nonlinear approximation schemes as we discussed in Sect. 3.1 to single-pulse field, we apply it to the case of a constant field. The integrand after t-expansion becomes

$$\begin{aligned} -\frac{R^2 \left( t^2-2\right) }{2 \left( R^2 t^2+\varepsilon ^2\right) } \end{aligned}$$

while the subtracting term Eq. (29) will not change. Then repeating the similar procedure, one gets

$$\begin{aligned} {\widetilde{\lambda }}=1+\frac{2}{\uppi ^2} \end{aligned}$$

which leads to a \(2/\uppi ^2\) deviation compared to Eq. (30). This term comes from \(-4\) in \({}^2\!{\mathcal {A}}^{(0)}\) and does not depend on the specific form of worldline path. Later we will see that this \(2/\uppi ^2\) deviation happens in both cases considered in 2nd-order t-expansion, which is caused by accuracy of estimation method, thus it approaches to zero as the approximation order increases, see Fig. 1. In other words, the emergence of finite terms are expected for each orders, and the higher-order contribution should cancel \(2/\uppi ^2\) from the 2nd-order. Based on this consideration we remove \(2/\uppi ^2\) derivation directly in the final results, which should not be confused with the counter term Eq. (19).

Fig. 1
figure 1

First seven orders of \({\widetilde{\lambda }}_{t^n}\) and their deviation from \(\lambda \) for a constant electric field. Because of symmetry of the integrals, all the odd orders vanish

Full size image

Let us see the first nontrivial example, pair production in the single-pulse field [14, 29]. The instanton has been evaluated explicitly to be

$$\begin{aligned} \begin{aligned} x_0&= \frac{1}{\omega } {\arcsin }\mathopen {}\left[ \frac{\gamma }{\sqrt{1 + \gamma ^2}}\sin (u)\right] \mathclose {},\\ x_1&= \frac{1}{\omega } \frac{1}{\sqrt{1 + \gamma ^2}}\, {{{\,\mathrm{arsinh}\,}}}\mathopen {}\left[ \gamma \cos (u)\right] \mathclose {}, \end{aligned} \end{aligned}$$
(34)

and the worldline action for this path reads

$$\begin{aligned} S_0 = \frac{\uppi m^2}{e E}\frac{2}{1+\sqrt{1+\gamma ^2}}. \end{aligned}$$
(35)

The weak-field condition leads to

$$\begin{aligned} E\ll \frac{2\uppi E_\text {s}}{\sqrt{1+\gamma ^2}}. \end{aligned}$$
(36)

At the nonperturbative region [11] \(\gamma \ll 1\), the weak-field condition reduces to \(E\ll 2\uppi E_\text {s}\). In other words, the dynamics of field also decreases the upper limit of weak-field condition.

Now we turn to the the Wilson loop. The corresponding perimeter law has a closed form

$$\begin{aligned} \updelta \!{\mathcal {A}}=\frac{2 \uppi ^2 \eta }{ \omega \varepsilon }, \qquad \eta =\frac{ \gamma }{ \sqrt{1+\gamma ^2} }. \end{aligned}$$
(37)

With the t-expansion up to \({O}\mathopen {}\left( t^2\right) \mathclose {}\), Eq. (13) reads

$$\begin{aligned} \begin{aligned} {}^2\!{\mathcal {A}}&\approx \frac{\uppi }{\omega \varepsilon \gamma \sqrt{1 + \gamma ^2} } \left\{ -\uppi \omega \varepsilon \gamma {\left( 2 + \gamma ^2\right) }\right. \\&\quad +\Big [\gamma ^2 {\left( \omega ^2 \varepsilon ^2\sqrt{1 + \gamma ^2} +4\right) } +2 \omega ^2 \varepsilon ^2\sqrt{1 + \gamma ^2} \Big ]\\&\left. \quad \times {\arctan }\mathopen {}\left( \frac{\uppi \gamma }{\omega \varepsilon \sqrt{1 + \gamma ^2} }\right) \mathclose {} \right\} . \end{aligned} \end{aligned}$$
(38)

which leads to

$$\begin{aligned} {\widetilde{\lambda }}(\gamma )=\frac{1}{2} {\left( \frac{2 + \gamma ^2}{\sqrt{1 + \gamma ^2}}+\frac{4}{\uppi ^2}\right) }. \end{aligned}$$

One may note that \({\widetilde{\lambda }}\rightarrow 1+2/\uppi ^2\) as \(\gamma \) approaches zero. The \(2/\uppi ^2\) derivation is predicted and has to be subtracted, i.e. the enhancement factor is then in the weak-field condition

$$\begin{aligned} \lambda (\gamma )=\frac{1}{2} {\left( \frac{2 + \gamma ^2}{\sqrt{1 + \gamma ^2}}\right) }. \end{aligned}$$
(39)

This operation guarantees the condition: \(\lambda \rightarrow 1\) as \(\gamma \rightarrow 0\). Since \(\lambda (0)>1\), the factor amplifies the contribution from the Wilson loop in Eq. (30), so that the pair-production rate is no longer exponentially suppressed, see Fig. 2.

Fig. 2
figure 2

The dependence of enhancement factor \(\lambda \) on \(\gamma \) in a single-pulse field, showing a comparison of numerical result with estimation of t-expansion as well as \(\gamma \)-expansions. The shadow indicates the numerical error in extrapolating \(\varepsilon \rightarrow 0^+\) with \(95\%\) confidence

Full size image

Alternatively, the \(\gamma \)-expansion can be worked out as a power series of \(\gamma \), where Eq. (34) has been used by replacing \(\omega = \gamma /R\). After removing the poles at each order of \(\lambda \), one obtains

$$\begin{aligned} \lambda (\gamma )=1+\frac{1}{18} \gamma ^4 - \frac{1}{18} \gamma ^6 + \frac{443}{8640} \gamma ^8 + {O}\mathopen {}\left( \gamma ^{10}\right) \mathclose {}. \end{aligned}$$
(40)

The exponential factor in the production rate is evaluated as

$$\begin{aligned} \varGamma \sim {\exp }\mathopen {}\left( - \frac{\uppi E_\text {s}}{E}\frac{2}{1+\sqrt{1+\gamma ^2}}+\frac{\uppi \alpha }{2} \frac{2 + \gamma ^2}{\sqrt{1 + \gamma ^2}}\right) \mathclose {} \end{aligned}$$
(41)

The first part is the main contribution from instanton action, the second part arises due to the Wilson loop correction from t-expansion. If the critical field is defined as saddle point, at which the exponential suppression is precisely zero, then one could have

$$\begin{aligned} E_\text {c}= \frac{E_\text {s}}{\alpha } \frac{4 \sqrt{\gamma ^2+1}}{\left( \gamma ^2+2\right) \left( \sqrt{\gamma ^2+1}+1\right) } < 137 E_\text {s}. \end{aligned}$$
(42)

On the one hand, as in the case with constant field, Eq. (42) also breaks the weak-field condition at nonperturbative region \(\gamma \ll 1\). On the other hand, in contrast with the case in constant field, the exponential factor of Wilson loop is no longer constant, such that for given E its contribution for production rate becomes dominant as \(\gamma \) increases. In addition, both estimation Eq. (41) (or Eq. (39)) and numerical result seem to be divergent as \(\gamma \) approaches \(+\infty \), even if the pre-exponential factor of Feynman integral were taken into account [30]. It implies that Wilson loop ought to be of a pole at \(\gamma \rightarrow +\infty \), and loses its meaning at this point, where the instanton trajectory collapses to a singular point.

3.4 Sinusoidal field \(E(t)=E \cos (\omega t)\)

The second example is a sinusoidal field [14, 29, 31]. The coordinates of the instanton can be represented by special functions as

$$\begin{aligned} \begin{aligned} x_0&=\frac{1}{\omega } {{{\,\mathrm{arsinh}\,}}}\mathopen {}\left[ \eta \, {{{\,\mathrm{sd}\,}}}\mathopen {}\left( \frac{2 }{\uppi }{K}\mathopen {}\left( \eta ^2\right) \mathclose {} u\bigg |\eta ^2\right) \mathclose {}\right] \mathclose {},\\ x_1&= \frac{1}{\omega } {\arcsin }\mathopen {}\left[ \eta \, {{{\,\mathrm{cd}\,}}}\mathopen {}\left( \frac{2 }{\uppi }{K}\mathopen {}\left( \eta ^2\right) \mathclose {} u\bigg |\eta ^2\right) \mathclose {}\right] \mathclose {}, \end{aligned} \end{aligned}$$
(43)

where \({K}\mathopen {}\left( \cdot \right) \mathclose {}\) is the complete elliptic integral, \({{{\,\mathrm{sd}\,}}}(\cdot )\) and \({{{\,\mathrm{cd}\,}}}(\cdot )\) are Jacobi elliptic functions. The instanton action is given by

$$\begin{aligned} S_0 = \frac{m^2}{e E} \frac{4\sqrt{1+\gamma ^2}}{\gamma ^2} {\left[ {K}\mathopen {}\left( \eta ^2\right) \mathclose {}-{E}\mathopen {}\left( \eta ^2\right) \mathclose {}\right] }. \end{aligned}$$
(44)

Repeating the procedure above, one obtains the corresponding perimeter law in a closed form

$$\begin{aligned} \updelta \!{\mathcal {A}}= \frac{4 \uppi \eta }{\omega \varepsilon } {K}\mathopen {}\left( \eta ^2\right) \mathclose {}. \end{aligned}$$
(45)

The exponent in the t-expansion reads

$$\begin{aligned} \begin{aligned} {\mathcal {A}}&\approx \frac{8 \eta }{\omega \varepsilon } {K}\mathopen {}\left( \eta ^2\right) \mathclose {} {\arctan }\mathopen {}\left[ \frac{2 \eta }{ \omega \varepsilon } {K}\mathopen {}\left( \eta ^2\right) \mathclose {}\right] \mathclose {}\\&\quad +{E}\mathopen {}\left[ {{{\,\mathrm{am}\,}}}\mathopen {}\left( 2 {K}\mathopen {}\left( \eta ^2\right) \mathclose {}|\eta ^2\right) \mathclose {}|\eta ^2\right] \mathclose {}\\&\quad \times {\left\{ \frac{2\omega \varepsilon }{ \eta } {\arctan }\mathopen {}\left[ \frac{2 \eta }{\omega \varepsilon } {K}\mathopen {}\left( \eta ^2\right) \mathclose {}\right] \mathclose {} -4 {K}\mathopen {}\left( \eta ^2\right) \mathclose {}\right\} }, \end{aligned} \end{aligned}$$
(46)

in which \({{{\,\mathrm{am}\,}}}\mathopen {}\left( \cdot \right) \mathclose {}\) is the Jacobi amplitude function. Thus at the week-field approximation \(E\ll 4 E_{\text {s}}{K}\mathopen {}\left( \eta ^2\right) \mathclose {}/\sqrt{1+\gamma ^2}\) [14], one has

$$\begin{aligned} \lambda (\gamma )=\frac{2 }{\uppi ^2} {K}\mathopen {}\left( \eta ^2\right) \mathclose {} {E}\mathopen {}\left[ {{{\,\mathrm{am}\,}}}\mathopen {}\left( 2 {K}\mathopen {}\left( \eta ^2\right) \mathclose {}|\eta ^2\right) \mathclose {}|\eta ^2\right] \mathclose {}. \end{aligned}$$
(47)

Where the deviation \(2/\uppi ^2\) has been subtracted. In this case, \(\lambda (\gamma )\) is also greater than unity and a non-trivial function depending on external field, and it tends to 1 as \(\gamma \) approaches zero. Alternativeszaly, the \(\gamma \)-expansion is implemented by expanding in \(\eta \) first. Removing the divergences in \(\varepsilon \), one obtains

$$\begin{aligned} \lambda = 1 + \frac{\gamma ^4}{72} - \frac{\gamma ^6}{72} + \frac{217 \gamma ^8}{17280} + {O}\mathopen {}\left( \gamma ^{10}\right) \mathclose {}. \end{aligned}$$
(48)

The results are shown in Fig. 3.

Fig. 3
figure 3

The dependence of enhancement factor \(\lambda \) on \(\gamma \) in a sinusoidal field, showing a comparison of numerical result with estimations of t-expansion and fourth-order \(\gamma \)-expansions. The shadow indicates the numerical error in extrapolating \(\varepsilon \rightarrow 0^+\) with \(95\%\) confidence

Full size image

In addition, similar to the example in the last subsection \(\lambda \) is also divergent as \(\gamma \rightarrow \infty \), even if the pre-exponential factor is considered [30]. The exponent factor in the production rate is then given by

$$\begin{aligned} \begin{aligned} \varGamma&\sim \exp \!\bigg \{ - \frac{E_s}{E} \frac{4\sqrt{1+\gamma ^2}}{\gamma ^2} {\left[ {K}\mathopen {}\left( \eta ^2\right) \mathclose {}-{E}\mathopen {}\left( \eta ^2\right) \mathclose {}\right] }\\&\qquad \qquad + \frac{2\alpha }{\uppi } {K}\mathopen {}\left( \eta ^2\right) \mathclose {}{E}\mathopen {}\left( {{{\,\mathrm{am}\,}}}\mathopen {}\left( 2 {K}\mathopen {}\left( \eta ^2\right) \mathclose {}|\eta ^2\right) \mathclose {}|\eta ^2\right) \mathclose {} \bigg \}, \end{aligned} \end{aligned}$$
(49)

For small \(\gamma \), one gets

$$\begin{aligned} E_\text {c} \sim \frac{E_\text {s}}{\alpha } \left( 1-\frac{\gamma ^2}{8}\right) +O(\gamma ^4)<137 E_s, \end{aligned}$$
(50)

which breaks the weak-field condition at nonperturbative region as well.

From above three examples, one may note that, first, the weak-field condition in the non-perturbative ranges \(\gamma <1\) is inevitably broken at strong coupling, which makes the vacuum cascade around the critical field ambiguous [15]; and second, the correction due to the Wilson loop in dynamic fields is a monotonically increasing function with respect to \(\gamma \) and diverges as \(\gamma \rightarrow \infty \).

4 Holographic Schwinger effect with dynamic field

In order to answer the question, if the vacuum cascade for strong coupling happens as the strength of time-dependent field goes close to the critical limit [15], we consider a similar effect in the context of gauge/gravity duality, where the gauge field theory refers to an \({\mathcal {N}}=4\) \({{\mathsf {S}}}{{\mathsf {U}}}(N+1)\) supersymmetric Yang–Mills theory on the 4D boundary of an \(\mathrm {AdS}_5\times S^5\) space, and the quantum gravity is a type IIB superstring theory in the bulk of the \(\mathrm {AdS}_5\times S^5\). The same as the case with constant field, we expect that the string theory could shed some light on the catastrophic vacuum cascade through the duality principle.

According to the Semenoff and Zarembo’s holographic setup [7, 16, 17, 32,33,34], the exponential factor in the production rate of the gauge field is obtained from the superstring counterpart by the area of the string worldsheet attached to a probe D3–brane, i.e.

$$\begin{aligned} \varGamma \sim {\exp }\mathopen {}\left( -S_\text {NG}-S_{B_2}\right) \mathclose {}, \end{aligned}$$
(51)

where \(S_\text {NG}\) is the Nambu–Gotō (NG) action [35, 36]

$$\begin{aligned} S_\text {NG}= T_F \int \mathrm {d}{}^2 \sigma \sqrt{{\left| \det G_{\alpha \beta }\right| }} \end{aligned}$$
(52)

depending on the induced metric

$$\begin{aligned} G_{\alpha \beta } = g_{MN}\frac{\partial x^M}{\partial \sigma ^\alpha } \frac{\partial x^N}{\partial \sigma ^\beta } , \end{aligned}$$
(53)

and \(S_{B_2}\) is the Kalb–Ramond [37] 2-form (or NS–NS, where NS is the abbreviation of Neveu–Schwarz [38]) as an string interaction term,

$$\begin{aligned} S_{B_2} = -T_F \int \mathrm {d}{}^2 \sigma \, B_{MN} \frac{\partial x^M}{\partial \sigma } \frac{\partial x^N}{\partial \tau }. \end{aligned}$$
(54)

In Eqs. (52) and (54), \(\sigma ^\alpha =(\tau , \sigma )\) are the coordinates on the string worldsheet, \(x^M=(x_\nu ,r,\phi _a)\) are the coordinates of the 10-D \(\mathrm {AdS}_5\times S^5\) space with metric \(g_{MN}\), and \(G_{\alpha \beta }\) is the induced metric.

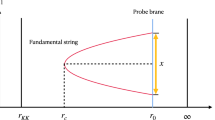
In the Semenoff–Zarembo construction, the worldsheet ends on the probe D3–brane with a boundary, taking the same shape as the worldline instanton. Hence the essential problem is converted to compute the on-shell action of string in Euclidean \(\mathrm {AdS}_5\) with the given boundary. Note that the Nambu–Gotō action is proportional to the worldsheet area, and extremising the area leads to a minimal surface. In other words, calculation of the exponential factor now corresponds to a Plateau’s problem in the framework of gauge/gravity duality.

4.1 Constant electric field

The worldline instanton in a constant field is a circle, thus the worldsheet can be parametrised by

$$\begin{aligned} x_0 = \sigma \cos (\tau ),\qquad x_1 = \sigma \sin (\tau ), \end{aligned}$$
(55)

which is different than the choice in [15], and the two parameterisations have different chirality, i.e. \(\mathrm {sgn}(J)=-1\), where J is the Jacobian. Therefore, the orientation of the Kalb–Ramond coupling is also reversed. The Nambu–Gotō action in our parameterisation becomes

$$\begin{aligned} S_\text {NG}= T_F \int _0^{2\uppi } \mathrm {d}\tau \, \int _{0}^{R} \mathrm {d}\sigma \, \sqrt{{\left| \det G_{\alpha \beta }\right| }}, \end{aligned}$$
(56)

where \(R \equiv \sigma (r_0)\), \(r_0\) is the location of the probe D3–brane. \(r(\sigma )\) can be analytically as [39]

$$\begin{aligned} r = \frac{L^2}{\sqrt{\frac{L^4}{r_0^2}+f(\sigma )}}, \end{aligned}$$
(57)

where \(f(\sigma )=R^2-\sigma ^2=0\) is the worldline instanton on the D3–brane. Substituting it into the Nambu–Gotō action, one obtains

$$\begin{aligned} S_\text {NG}= & {} 2\uppi T_F L^2 \sqrt{\frac{L^4}{r_0^2}+R^2} \int ^{R}_0 \frac{ \sigma \,\mathrm {d}\sigma }{\left( \frac{L^4}{r_0^2}+R^2-\sigma ^2\right) ^{3/2}}\nonumber \\= & {} 2 \uppi L^2 T_F \left( \sqrt{\frac{r_0^2 R^2}{L^2}+1}-1\right) . \end{aligned}$$
(58)

Furthermore, the NS–NS term reads

$$\begin{aligned} S_{B_2}= {\mathrm {sgn}}\mathopen {}\left( J\right) \mathclose {}\int ^{2\uppi }_0 \mathrm {d}\tau \int ^{R}_0\mathrm {d}\sigma \, E_0 \sigma =-\uppi E_0 R^2, \end{aligned}$$
(59)

where R can be fixed by extremising the total action, yielding

$$\begin{aligned} R=\frac{L^2}{r_0}\sqrt{\frac{E_\text {c}^2}{E_0^2}-1},\qquad E_\text {c}=T_F\frac{r_0^2 }{L^2}. \end{aligned}$$
(60)

Where \(E_\text {c}\) is defined as critical values. The exponential factor in the production rate can now be solved as

$$\begin{aligned} \varGamma \sim {\exp }\mathopen {}\left[ -\frac{\sqrt{{\mathfrak {g}}}}{2} {\left( \sqrt{\frac{E_\text {c}}{E_0}} -\sqrt{\frac{E_0}{E_\text {c}}} \right) }^2\right] \mathclose {}, \end{aligned}$$
(61)

in which the string and spacetime parameters have been replaced by the ones of the gauge field via \(T_F=\sqrt{{\mathfrak {g}}}/(2\uppi L^2)\). This is the result obtained in [7] and agrees with the Schwinger’s formula in the weak-field limit.

4.2 Estimation of single-pulse field \(E(t)=E {{\,\mathrm{sech}\,}}^2(\omega t)\)

The instanton path as the worldsheet boundary on the D3–brane in a single-pulse field has been shown in Eq. (34). Thus one can parametrise the worldsheet by using \(\sigma \) and u, i.e.

$$\begin{aligned} \begin{aligned} x_0&= \frac{\sigma }{\gamma }\, {\arcsin }\mathopen {}\left[ \frac{\gamma }{ \sqrt{1+\gamma ^2}} \sin (u)\right] \mathclose {},\\ x_1&= \frac{\sigma }{\gamma \sqrt{1+\gamma ^2}}\, {{{\,\mathrm{arsinh}\,}}}\mathopen {}\left[ \gamma \cos (u)\right] \mathclose {}, \end{aligned} \end{aligned}$$
(62)

where \(\gamma \) is regarded as initial information and not relevant to the scale r. The simplicity of Semenoff–Zarembo construction for constant field led us to speculate that the similar production rates could have been obtained by repeating above procedure. However, it is not anything like worldline instanton, the string worldsheets are not exactly integrable for dynamic fields in our cases. Thus to make an effect estimation, we expand the instanton at adiabatic limit, i.e. \(\gamma \rightarrow 0\),

$$\begin{aligned} \begin{aligned} x_0&\sim \sigma \sin (u)-\sigma \frac{\gamma ^2 }{6} \cos (u) \left[ \cos ^2(u)+3\right] +{O}\mathopen {}\left( \gamma ^4\right) \mathclose {},\\ x_1&\sim \sigma \cos (u)-\sigma \frac{\gamma ^2 }{24} [9 \sin (u)+\sin (3 u)]+{O}\mathopen {}\left( \gamma ^4\right) \mathclose {}, \end{aligned} \end{aligned}$$
(63)

namely the zeroth order of \(\gamma \) is just the circle boundary Eq. (55). Therefore, we will treat the complete worldline boundary as perturbation around the circle. The r component can be estimated by noting that

$$\begin{aligned} r=\frac{L^2 }{\sqrt{ \frac{L^4}{r_0^2} + f(x_0,x_1)}}, \end{aligned}$$
(64)

where \(f(x_0,x_1)=0\) is the instanton path. In a single-pulse field, it reads

$$\begin{aligned} \begin{aligned} f(x_0,x_1)&= \frac{\sigma _0^2 }{2 \gamma ^2} \left[ \gamma ^2+\left( 1 + \gamma ^2\right) {\cos }\mathopen {}\left( \frac{2 \gamma }{\sigma _0}x_0\right) \mathclose {}\right. \\&\quad \left. - {\cosh }\mathopen {}\left( \frac{2 \gamma \sqrt{1 + \gamma ^2} }{\sigma _0}x_1\right) \mathclose {}\right] . \end{aligned} \end{aligned}$$
(65)

In the limit \(\gamma \rightarrow 0\), \(f(x_0,x_1)\) reduces to a circle

$$\begin{aligned} \begin{aligned} f(x_0,x_1)&\sim \sigma _0^2-x_0^2 -x_1^2 +\frac{\gamma ^2 }{3 \sigma _0^2}\left( x_0^2+x_1^2\right) \\&\quad \times \left( -3 \sigma _0^2+x_0^2-x_1^2\right) + {O}\mathopen {}\left( \gamma ^4\right) \mathclose {}. \end{aligned} \end{aligned}$$
(66)

Hence the Nambu–Gotō action is formulated as

$$\begin{aligned} S_{\text {NG}}=S^0_{\text {NG}} -\uppi T_F\frac{ \gamma ^2 r_0 \sigma _0^2 }{\sqrt{\frac{L^4}{r_0^2}+\sigma _0^2}}, \end{aligned}$$
(67)

where \(S^0_{\text {NG}}\) is given in Eq. (58). On the other hand, the NS–NS part right now becomes

$$\begin{aligned} S_{B_2}= S_{B_2}^0 +\frac{3}{2}\uppi E_0 \gamma ^2 \sigma _0^2. \end{aligned}$$
(68)

The \(\sigma _0\) is fixed as the stationary point of the total action,

$$\begin{aligned} \sigma _0\sim \frac{L^2 }{r_0} \sqrt{\frac{E_\text {c}^2}{E_0^2}-1}+\gamma ^2 \frac{ L^2 }{2 r_0 } \frac{\frac{2 E_\text {c}^2}{E_0^2}-1}{\sqrt{\frac{E_\text {c}^2}{E_0^2}-1}} +O\left( \gamma ^3\right) . \end{aligned}$$
(69)

The exponential factor in the production rate with correction up to the second order of \(\gamma \) is

$$\begin{aligned} \begin{aligned} \varGamma&\sim \exp \left[ - \frac{\sqrt{{\mathfrak {g}} } }{2 } \left( \sqrt{\frac{E_0}{E_\text {c}}} -\sqrt{\frac{E_\text {c}}{E_0}} \right) ^2\right. \\&\qquad \qquad \left. -\gamma ^2\frac{ \sqrt{{\mathfrak {g}} } }{4 } \left( \frac{E_\text {c}}{E_0}-\frac{E_0}{E_\text {c}}\right) +{O}\mathopen {}\left( \gamma ^4\right) \mathclose {}\right] . \end{aligned} \end{aligned}$$
(70)

here \({\mathfrak {g}}=g^2_{\text {YM}}N\) denotes the effective coupling at large ’t Hooft limit. In Eq. (70), the first part in the exponent comes from the circular boundary, while the second term arises from the deformation, see Fig. 4.

Fig. 4
figure 4

The exponents of the vacuum decay rate, where the critical field is defined by the maxima, which are emphasised by dots. For constant field, the exponent is given by Eq. (61) and plotted in blue. For single-pulse field in Eq. (70), the colour is red. For sinusoidal field shown in Eq. (79), it is plotted in brown

Full size image

If one defines the critical field as stationary point of exponent, the correction (up to \(O(\gamma ^2)\)) due to the time-dependence of the background field leads a lager critical value comparing with constant field, which is fixed by

$$\begin{aligned} E_0\rightarrow E_{\text {c}}\sqrt{ \frac{2+\gamma ^2}{2-\gamma ^2} } , \end{aligned}$$
(71)

beyond which the decay rate decreases as the similar as Eq. (61). The enhancement up to \(O(\gamma ^2)\) can also be noted from the negative sign of \(\gamma ^2\) in Eq. (70). In other words, the correction plays a role of suppression of pair production.

4.3 Estimation of sinusoidal field \(E(t)=E \cos (\omega t)\)

The worldline instanton in this case can be parametrised as

$$\begin{aligned} \begin{aligned} x_0&=\frac{\sigma }{\gamma }\, {{{\,\mathrm{arsinh}\,}}}\mathopen {}\left[ \eta \, {{{\,\mathrm{sd}\,}}}\mathopen {}\left( \frac{2 }{\uppi }{K}\mathopen {}\left( \eta ^2\right) \mathclose {} u\bigg |\eta ^2\right) \mathclose {}\right] \mathclose {},\\ x_1&= \frac{\sigma }{\gamma }\, {\arcsin }\mathopen {}\left[ \eta \, {{{\,\mathrm{cd}\,}}}\mathopen {}\left( \frac{2 }{\uppi }{K}\mathopen {}\left( \eta ^2\right) \mathclose {} u\bigg |\eta ^2\right) \mathclose {}\right] \mathclose {}, \end{aligned} \end{aligned}$$
(72)

where \(\eta \) has been defined in Eq. (37). The Maclaurin series of Jacobian elliptic functions in \(\gamma \) gives

$$\begin{aligned} \begin{aligned} x_0&\sim \sigma \sin (u)- \sigma \frac{\gamma ^2}{48} [9 \sin (u)\\&\quad +\sin (3 u)+12 u \cos (u)]+{O}\mathopen {}\left( \gamma ^4\right) \mathclose {},\\ x_1&\sim \sigma \cos (u) - \sigma \frac{\gamma ^2}{48} [-12 u \sin (u)\\&\quad +15 \cos (u)+ \cos (3 u)] +{O}\mathopen {}\left( \gamma ^4\right) \mathclose {}. \end{aligned} \end{aligned}$$
(73)

The instanton path on the D3–brane in this case is

$$\begin{aligned} \begin{aligned} f(x_0,x_1)&= \frac{\sigma _0^2 }{2 \gamma ^2 \left( 1 + \gamma ^2\right) } \bigg [\gamma ^4+\left( 1 + \gamma ^2\right) ^2 {\cos }\mathopen {}\left( \frac{2 \gamma }{\sigma _0}x_0\right) \mathclose {}\\&\quad +\left( 21 + \gamma ^2\right) {\cosh }\mathopen {}\left( \frac{2 \gamma }{\sigma _0}x_1\right) \mathclose {}-2(1+ \gamma ^2)\bigg ] \end{aligned} \end{aligned}$$
(74)

and its expansion for small \(\gamma \) reads

$$\begin{aligned} \begin{aligned} f(x_0,x_1)&\sim \sigma _0^2-x_0^2-x_1^2+\gamma ^2\\&\quad \times \left( \frac{x_0^4-x_1^4}{3 \sigma _0^2}-x_0^2-x_1^2\right) +{O}\mathopen {}\left( \gamma ^4\right) \mathclose {}. \end{aligned} \end{aligned}$$
(75)

The second order terms for the Nambu–Gotō action

$$\begin{aligned} \begin{aligned} S_{\text {NG}}^{( 2)}&=\frac{\uppi T_F \gamma ^2}{2 L^4 \sqrt{L^4+r_0^2 \sigma _0^2}}(r_0^4 \sigma _0^4-L^8\\&\quad -2 L^4 r_0^2 \sigma _0^2+L^6 \sqrt{L^4+r_0^2 \sigma _0^2}), \end{aligned} \end{aligned}$$
(76)

and the NS–NS term are

$$\begin{aligned} S_{B_2}^{( 2)} =\uppi \gamma ^2 E_0 \sigma _0^2. \end{aligned}$$
(77)

Up to the second order of \(\gamma \), \(\sigma _0\) is given by

$$\begin{aligned} \sigma _0=\frac{L^2}{r_0} \sqrt{\frac{E_\text {c}^2}{E_0^2}-1} +\gamma ^2\frac{ L^2 }{2 r_0 } \frac{\frac{3 E_\text {c}^4}{2E_0^4}-1}{\sqrt{\frac{E_\text {c}^2}{E_0^2}-1}} +O(\gamma ^4). \end{aligned}$$
(78)

Finally, the exponential factor in the production rate is given by

$$\begin{aligned} \begin{aligned} \varGamma&\sim \exp \left[ - \frac{\sqrt{{\mathfrak {g}} } }{2 } \left( \sqrt{\frac{E_0}{E_\text {c}}} -\sqrt{\frac{E_\text {c}}{E_0}}\right) ^2\right. \\&\left. \qquad \qquad -\gamma ^2\frac{ \sqrt{{\mathfrak {g}} } }{4 } \left( \frac{E_\text {c}^3}{E_0^3} -2\frac{E_\text {c}}{E_0}+1\right) +{O}\mathopen {}\left( \gamma ^4\right) \mathclose {}\right] , \end{aligned} \end{aligned}$$
(79)

see Fig. 4. The critical field should be greater than \(E_\text {c} = T_F r_0^2/L^2\), i.e.

$$\begin{aligned} E_0\rightarrow \frac{\sqrt{1-\gamma ^2+\sqrt{\gamma ^4+4 1 + \gamma ^2}} }{\sqrt{2}}E_{\text {c}} \end{aligned}$$
(80)

and one sees that dynamics of the external field also enhances the critical field as before.

5 Conclusion and discussion

In this paper, the scalar Schwinger effect for dynamic fields at strong coupling and weak-field limit has been studied, by first using the field-theoretical method of worldline instantons. A non-trivial contribution to the production rate is discovered by evaluating the Wilson loop along the instanton path, which depends on the Keldysh adiabaticity parameter \(\gamma \). Thus one may expect that such correction may save the weak-field condition in strong coupling. However after computations, we find that the introduction of the correction term also leads to a contradiction to the weak-field condition near the critical field strength.

We note also that the correction from Wilson loop is a monotonically increasing function with respect to \(\gamma \), which makes the contribution for production rate from Wilson loop become dominant as \(\gamma \) increases. Moreover both t-expansion and numerical calculation suggest a divergent value as \(\gamma \) approaches infinity, even if the pre-exponential factor of Feynman integral is considered. One possible explanation is that the Wilson loop loses its meaning at \(\gamma \rightarrow \infty \), because the instanton trajectory collapses to a singular point.

In order to clarify the vacuum cascade beyond the weak-field condition, in the context of an \({\mathcal {N}}=4\) supersymmetric Yang–Mills theory, the production rate is calculated by the gauge/gravity duality, according to which the instanton action has a string counterpart of the classical string action in Euclidean \(\mathrm {AdS}_3\), where the boundary on the probe D3–brane is given by the instanton path. Thus the problem is converted to solving the classical motion of string with Dirichlet boundary conditions. However the string worldsheets for dynamic fields are not integrable as in the worldline instantons. To provide an explicit estimation, we treat the specific worldsheets as perturbations around the one with circle boundary, which had been solved exactly. Such an expansion is an adiabatic approximation, it is practical and realistic, because only low-frequency laser (comparing with electron mass) is currently operational. The obtained decay rates in the two examples with dynamic fields are similar concave functions as in the case with constant field, but the critical fields increase considerably. In other words, up to \(O(\gamma ^2)\) the correction due to the dynamics of electric field suppresses the pair production, which is opposite to cases of worldline instantons.