Minimally deformed anisotropic model of class one space-time by gravitational decoupling

Abstract

In this article, we have presented a static anisotropic solution of stellar compact objects for self-gravitating system by using minimal geometric deformation techniques in the framework of embedding class one space-time. For solving of this coupling system, we deform this system into two separate system through the geometric deformation of radial components for the source function $\lambda (r)$ by mapping: $e^{-\lambda (r)}\rightarrow e^{-\tilde{\lambda }(r)}+\beta \,g(r)$, where g(r) is deformation function. The first system corresponds to Einstein’s system which is solved by taking a particular generalized form for source function $\tilde{\lambda }(r)$ while another system is solved by choosing well-behaved deformation function g(r). To test the physical viability of this solution, we find complete thermodynamical observable as pressure, density, velocity, and equilibrium condition via. TOV equation etc. In addition to the above, we have also obtained the moment of inertia (I), Kepler frequency (v), compression modulus ($K_e$) and stability for this coupling system. The M–R curve has been presented for obtaining the maximum mass and corresponding radius of the compact objects.

1 Introduction

General Relativity (GR) theory of gravitation has been established by Einstein in 1916 in which gravitational properties spread with the speed of light and the law of physics articulated to be invariant with respect to accelerated observers [1,2,3,4,5]. The main assumptions of Einstein’s theory of gravitation are based on the (i) all events in the universe as a 4-dimensional Riemannian manifold, which is called space-time, (ii) the curvature related with the metric is related to the matter by Einstein’s field equations (EFE). There will be various fields on the space-time which describe the matter content the space-time through energy-momentum tensor $T_{\mu \nu }$. The field equation of GR is non-linear 2nd order partial differential equation of hyperbolic type, which permits clear freedom of change of coordinates. The first solution of EFE describing a self-gravitating, bounded object was obtained by Karl Schwarzschild [6]. This interior solution represents a constant density model with the outer space-time being empty. However, the velocity of sound within the sphere exceeds the velocity of light thus such a model is not realistic. Therefore, this encouraged us to search for physically viable solutions to the Einstein field equations which describe the realistic models. The space-time of Schwarzschild’s exterior solution [7] was obtained in 1916 which describes the gravitational field outside a spherical mass by imposing spherical symmetry on the space-time manifold. The theory of spherical symmetric space-time has been investigated by Takeno (1966) from the point of view of invariant classification, group of motion, conformal transformation and embedding classes, etc.

The method of gravitational decoupling by Minimal Geometric Deformation (MGD) is a great and powerful technique that extends known solutions into more difficult situations. By using this MGD technique, In Ref. [8], Gabbanelli et al. have extended isotropic Durgapal–Fuloria solution in the anisotropic domain while Ovalle and his collaborators [9] have shown that how a spherically symmetric fluid modifies the Schwarzschild vacuum solution and necessity of anisotropy in the fluid. In this connection, several other authors have used the MGD approach to discover the more complex solution which can be seen in the following Refs. [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. The GD was developed by Ovalle [25, 26] as a consequence of the Minimal Geometric Deformation (MGD) [24, 27] (see also Ref. [28]) in the framework of Randall–Sundrum gravity [29, 30]. In Ref. [28], the author extended the Minimal Geometric Deformation approach to investigate a new black hole solution.

The key features of this approach for new solutions to EFE are available in literature as [31]:

I. Considering the energy-momentum tensor $\tilde{T}_{\mu \nu }$ for known metric as a source and extend known solutions of EFE into more complex situations. The new source is coupled with the $\tilde{T}_{\mu \nu }$ associated with the seed solution through a non-dimensional coupling constant $\beta$ which can be written as:

$$\begin{aligned} \tilde{T}_{\mu \nu } \mapsto \hat{T}^{(1)}_{\mu \nu } =\tilde{T}_{\mu \nu }+\beta ^{(1)}{T}^{(1)}_{\mu \nu } \end{aligned}$$

(1)

and then continue to same the process with more sources, like

$$\begin{aligned} \hat{T}^{(1)}_{\mu \nu } \mapsto \hat{T}^{(2)}_{\mu \nu } =\hat{T}^{(1)}_{\mu \nu }+\beta ^{(2)}{T}^{(2)}_{\mu \nu } \end{aligned}$$

(2)

and so on. In this approach, we can spread direct solutions of the Einstein equations related with the simplest gravitational source $\tilde{T}_{\mu \nu }$ into the province of more complex forms of gravitational sources $\tilde{T}_{\mu \nu }=\hat{T}^{(n)}_{\mu \nu }$ .

II. It is noted that we can also use the reverse of the above methodology in order to find an exact solution to Einstein’s field equation. In this procedure, we can split a more difficult energy-momentum tensor $\hat{T}_{\mu \nu }$ into simpler components, say $\tilde{T}^{(i)}_{\mu \nu }$, and then Einstein’s equations have to be solved for each one of these components. In this situation, there will be many solutions corresponding to each component of $\tilde{T}^{(i)}_{\mu \nu }$ associated with the original energy-momentum tensor. At last, we can find the solution of Einstein’s equations for the original energy-momentum tensor $\hat{T}_{\mu \nu }$ by combining all the above individual solution. However, we would like to mention that this procedure works very well as each source satisfies the conservation equation identically, which can be written as

$$\begin{aligned} \nabla _\mu \hat{T}^{\mu \nu }=\nabla _\mu \tilde{T}^{(1){\mu \nu }} = \nabla _\mu \tilde{T}^{(2){\mu \nu }}= \cdots = \nabla _\mu \tilde{T}^{(n){\mu \nu }}=0. \end{aligned}$$

(3)

Now we explain the procedure to explore MGD-decoupling methodology which is as follows: Suppose we have two gravitational sources namely R and S where we will first solve the standard Einstein’s equations corresponding to the source R and then the other set of quasi-Einstein equations are solved for the source S. At last, we combine these two solutions to determine the complete solution for the total system of $R\cup S$. As we know that Einstein’s field equations are non-linear, therefore the above procedure leads a powerful technique to find the solutions and their analysis, especially during the situations that away form trivial cases.

Many analytical solutions were created by Tolman [32], which describe the structure of the interior stellar geometry for the perfect fluid models. However, the anisotropic models where the tangential and radial pressures are unequal, allows a better understanding of the highly-dense matter. Ruderman [33] and Bowers and Liang [34] have been studied the anisotropic fluid distribution that has explored the most updated research. In this continuation Mak and Harko [80] has suggested that anisotropy plays an important role to understand the variation of properties of the dense nuclear matter for a strange star. On the other hand, the presence of anisotropy could be identified through the existence of a solid core or type 3A superfluid [81], pion condensed phase [82], and different kinds of phase transitions [83]. The positive anisotropy inside star provides a realistic star which have been studied by several authors. If we have the anisotropy factor $\varDelta (r) = p_t - p_r > 0$, then anisotropic force inside the stellar system outward-directed which improve the stability and equilibrium criteria, and if the anisotropy factor $\varDelta (r) = p_t - p_r < 0$, then anisotropic force inside the stellar system is directed inward that introduce instability in the system.

Now the finding of the solutions to EFE is a great challenge to meet the requirements of physical acceptability [35,36,37]. Recently Jasim et al. [38] have constructed an anisotropic fluid sphere model by supposing a specific form of the potential metric functions $e^{\lambda }$ and $e^{\nu }$ to EFE with MIT bag EOS in presence of cosmological constant. This model yields a realistic fluid sphere such as PSR 1937 +21. In this connection, an extensive study has been conducted by several authors to understand the role of anisotropy of the interior of stellar objects [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79].

The purpose of this article is to the study of minimally deformed solution for class one space-time by using gravitational decoupling method that gives a generalised solution for anisotropic compact star models. The paper is organized as follows. In Sects. 2 and 3, MGD have been used to scrutinize the interior space-time and field equation to find new embedding class one solution. The non-singularity of the solution has been discussed in Sect. 4 while, in Sect. 5, the boundary condition and determination of constraints have been analyzed. The Sect. 6 is devoted for analysis of the slow rotation approximation, moment of inertia and Kepler frequency. The elastic property of compact stars in Sect. 7 has been studied to focus and determine $K_e$ Âăon compression modulus $K_e$ while, in Sect. 8 the energy conditions have been considered and confirmed at all points in the interior of a star. In Sect. 9, we analyzed the physical features as well as stability of the resulting solution with the help of graphical illustrations considering the equilibrium under various forces, causality, adiabatic index, and Harrison–Zeldovich–Novikov static. We also compared the solution for different values of $\beta$ and analyzed for a well-behaved solution. Finally, we summarize the results in the last section.

2 Interior space-time and field equations with MGD

2.1 Einstein equations for two sources

The action of this modified matter distribution for MGD defined as [26]

$$\begin{aligned} S=S_{EH}+\beta \,S_{1}=\int \left[ {\frac{R}{16\pi }}+\mathscr {L}_M+\beta \,\mathscr {L}_1 \right] \sqrt{-g}~ d^4x \nonumber \\ \end{aligned}$$

(4)

provided $\mathscr {L}_M$ and $\mathscr {L}_1$ are matter fields and additional Lagrangian density due to the extra source respectively. However R denotes the Ricci scalar, g is the determinant of the metric tensor $g_{\mu \nu }$ and $\beta$ is a coupling constant. Now we define the energy-momentum tensor for both Lagrangian matter which are given by

$$\begin{aligned}&\tilde{T}_{\mu \nu }=-\frac{2}{\sqrt{-g}}\,\frac{\delta (\sqrt{-g}\,\mathscr {L}_M)}{\delta g^{\mu \nu }}=-\frac{2\,\partial (\mathscr {L}_M)}{\partial g^{\mu \nu }}+g_{\mu \nu } \mathscr {L}_M \end{aligned}$$

(5)

$$\begin{aligned}&\varTheta _{\mu \nu } = -{2 \over \sqrt{-g}}~{\delta (\sqrt{-g}\mathscr {L}_1) \over \delta g^{\mu \nu }}=-2{\delta \mathscr {L}_1 \over \delta g^{\mu \nu }}+g_{\mu \nu } \mathscr {L}_1. \end{aligned}$$

(6)

By varying the action, (4) with respect to the metric tensor $g^{\mu \nu }$, we get the general equations of motion

$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}g_{\mu \nu } R =-8\pi \,T_{\mu \nu } \end{aligned}$$

(7)

where,

$$\begin{aligned}&T_{\mu \nu }= \tilde{T}_{\mu \nu } + \beta \,\varTheta _{\mu \nu }. \end{aligned}$$

(8)

The symbols used in above equations have their usual meanings. Let us consider the inside of spherical body is filled of an anisotropic fluid matter, therefore in the current situation the stress-energy tensor $\tilde{T}_{\mu \nu }$ takes the following form

$$\begin{aligned} \tilde{T}_{\mu \nu }=(\tilde{\rho }+\tilde{p_t})u_\mu u_\nu -\tilde{p_t}g_{\mu \nu }+\left( \tilde{p_r}-\tilde{p_t}\right) v_\mu v_\nu , \end{aligned}$$

(9)

where the covariant component ${u _{\nu }}$ denote the 4-velocity, fulfilling $u_{\mu }u^{\mu }= -1$ and $u_{\nu }\nabla ^{\mu }u_{\mu }=0$. Here, $\tilde{\rho }$, $\tilde{p_r}$ and $\tilde{p_t}$ represent the matter density and pressures (radial and tangential) for anisotropic matter. It is noted that the presence of this extra source $\varTheta _{\mu \nu }$ in Eq. (8) produce an anisotropies in self gravitating system that can be a scalar, vector or tensor field. We would like to mention here that the Einstein tensor is always divergence free, therefore the stress tensor $T_{\mu \nu }$ in Eq. (7) must satisfy the conservation law,

$$\begin{aligned} \nabla ^{\mu }{T}_{\mu \nu }=0, \end{aligned}$$

(10)

To describe the space-time geometry inside the body for complete system we assume a spherically symmetric line element of the form,

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) \end{aligned}$$

(11)

where $\nu$ and $\lambda$ are functions of the radial coordinate ‘r’ only. Then the Einstein field equations (7) together with the Eqs. (8), (9) and line element (11) give the following set of the equations,

$$\begin{aligned} 8\pi (\tilde{\rho }+\beta \varTheta ^{t}_{t})= & {} {\mathrm{e}^{-\lambda }}\left( {\frac{\lambda ^{{\prime }}}{r}}-\frac{1}{r^2}\right) +\frac{1}{r^2}, \end{aligned}$$

(12)

$$\begin{aligned} 8\pi (\tilde{p}_r-\beta \varTheta ^{r}_{r})= & {} {\mathrm{e}^{-\lambda }} \left( {\frac{\nu ^{{\prime }}}{r}}+\frac{1}{r^2}\right) -\frac{1}{r^2}, \end{aligned}$$

(13)

$$\begin{aligned} 8\pi (\tilde{p}_t-\beta \varTheta ^{\varphi }_{\varphi })= & {} \frac{\mathrm{e}^{-\lambda }}{4} \left( 2 \nu ^{{\prime \prime }}+\nu ^{\prime 2}+2{\frac{\nu ^{{\prime }}-\lambda ^{{\prime }}}{r}}-\nu ^{\prime }\lambda ^{\prime } \right) .\nonumber \\ \end{aligned}$$

(14)

where the effective density ($\rho$), effective radial pressure ($p_r$), effective tangential pressure ($p_t$) and effective anisotropy corresponding to the energy momentum tensor $T_{\mu \nu }$ can be defined as,

$$\begin{aligned}&\rho =\tilde{\rho }+\beta \varTheta ^{t}_{t}, \end{aligned}$$

(15)

$$\begin{aligned}&p_r=\tilde{p}_r-\beta \varTheta ^{r}_{r}, \end{aligned}$$

(16)

$$\begin{aligned}&p_t=\tilde{p}_t-\beta \varTheta ^{\varphi }_{\varphi }, \end{aligned}$$

(17)

$$\begin{aligned}&\varDelta =\tilde{p}_t-\tilde{p}_r+\beta (\varTheta ^{r}_{r}-\varTheta ^{\varphi }_{\varphi }). \end{aligned}$$

(18)

Further, we would like to mention that the linear combination of Eqs. (12)–(14) satisfy the conservation equation for the energy-momentum tensor ${T}^{\mu }_{\nu }={\tilde{T}}^{\mu }_{\nu } + \beta \varTheta ^{\mu }_{\nu }$ with coupling parameter $\beta$ as

$$\begin{aligned}&-\frac{d{\tilde{p}_r}}{dr}-\beta \left[ \frac{{\nu ^\prime }}{2}\,(\varTheta ^t_t-\varTheta ^r_r)-\frac{d \varTheta ^r_r}{dr}+\frac{2}{r}\,(\varTheta ^\varphi _\varphi -\varTheta ^r_r)\right] \nonumber \\&-\frac{{\nu ^\prime }}{2}\,(\tilde{\rho }+\tilde{p}_r)+\frac{2(\tilde{p}_t-\tilde{p}_r)}{r}=0. \end{aligned}$$

(19)

2.2 Gravitational decoupling by MGD approach

Since the system of Eqs. (12)–(14) contains seven unknown functions which are namely p(r), $\rho (r)$, $\nu (r)$, $\lambda (r)$ and three independent components of $\varTheta$. Therefore, this system has infinitely many solutions. Now we will apply the MGD approach to solve this system of equations. In this approach, the system will be converted in the such way that the field equations connected with the source $\varTheta _{\mu \nu }$ will satisfy “effective quasi-Einstein” [namely Eqs. (29)–(31)]. Now we can start by taking a solution of the Eq. (7) for the stress-tensor $\tilde{T}_{\mu \nu }$ which correspond to GR perfect fluid solution [that will be same as the Eqs. (12)–(14) when $\beta \rightarrow 0$] with the line element,

$$\begin{aligned} {d\tilde{s}}^{2}=e^{\tilde{\nu }(r)}{{dt}^{2}}-e^{\tilde{\lambda }(r)}{{dr}^{2}}-{r}^{2}({{d\theta }^{2}}+{{sin}^{2}}\theta {{d\phi }^{2}}), \end{aligned}$$

(20)

where the gravitational potential $e^{\tilde{\lambda }(r)}$ can be defined as,

$$\begin{aligned} e^{-\tilde{\lambda }(r)}=1-\frac{8\pi }{r}\int _0^r{r^2\,\rho (r) dr}=1-\frac{2m(r)}{r} \end{aligned}$$

(21)

here the m(r) represents the Misner–Sharp mass function for the standard general relativity. The influence of the extra source $\varTheta _{\mu \nu }$ on the energy-momentum tensor $\tilde{T}_{\mu \nu }$ can be determined by the geometric deformation via. perfect fluid geometry $\{\tilde{\nu }(r), \tilde{\lambda }(r) \}$ in Eq. (20) as

$$\begin{aligned}&e^{\tilde{\nu }}\rightarrow e^\nu = e^{\tilde{\nu }}+\beta f(r) \end{aligned}$$

(22)

$$\begin{aligned}&e^{-\tilde{\lambda }} \rightarrow e^{-\lambda } = e^{-\tilde{\lambda }}+\beta g(r). \end{aligned}$$

(23)

where f(r) and g(r) are the deformation functions associated with the temporal and radial components of line elements, respectively. It is noted that these deformation functions depend only on radial coordinate while constant $\beta$ is a free parameter. The considered MGD method allows to set $g=0$ or $f=0$, then for this situation the deformation will be performed only on the radial component and other temporal one unaltered (it corresponds to $f=0$). By setting $f=0$ we get

$$\begin{aligned} e^{-\tilde{\lambda }} \rightarrow e^{-\lambda } = e^{-\tilde{\lambda }}+\beta \, g(r) \end{aligned}$$

(24)

This is called as the Minimal Geometric Deformation (MGD) along the radial component of the line element. After plugging the Eq. (24) into field equations (12)–(14), we get two sets of equations as first set corresponding to the standard Einstein field equations for an energy-momentum tensor $\tilde{T}_{\mu \nu }$ which is given as,

$$\begin{aligned}&\frac{1-e^{-\tilde{\lambda }}}{r^{2}}+\frac{e^{-\tilde{\lambda }}\tilde{\lambda }'}{r} = 8\pi \tilde{\rho } \end{aligned}$$

(25)

$$\begin{aligned}&\frac{e^{-\tilde{\lambda }}-1}{r^{2}}+\frac{e^{-\tilde{\lambda }}\tilde{\nu }'}{r} = 8\pi \tilde{p}_{r} \end{aligned}$$

(26)

$$\begin{aligned}&e^{-\tilde{\lambda }}\left( \frac{\tilde{\nu }''}{2}+\frac{\tilde{\nu }'^{2}}{4}-\frac{\tilde{\nu }'\tilde{\lambda }'}{4}+\frac{\tilde{\nu }'-\tilde{\lambda }'}{2r} \right) = 8\pi \tilde{p}_t. \end{aligned}$$

(27)

along with the conservation equation,

$$\begin{aligned} -\frac{d{\tilde{p}_r}}{dr}-\frac{{\nu ^\prime }}{2}\,(\tilde{\rho }+\tilde{p}_r)+\frac{2(\tilde{p}_t-\tilde{p}_r)}{r}=0. \end{aligned}$$

(28)

while second set of equations for the source $\varTheta _{\mu \nu }$, called as quasi-Einstein equations, is given as

$$\begin{aligned}&-{g' \over r}-{g\over r^2}= 8\pi \varTheta ^t_t \end{aligned}$$

(29)

$$\begin{aligned}&-g\left( {\tilde{\nu }' \over r}+{1\over r}\right) = 8\pi \varTheta ^r_r \end{aligned}$$

(30)

$$\begin{aligned}&-{g \over 2}\left( \tilde{\nu }''+{\tilde{\nu }'^2 \over 2}+{\tilde{\nu }' \over r}\right) -{g' \over 2}\left( {\tilde{\nu }' \over 2}+{1\over r}\right) = 8\pi \varTheta ^\phi _\phi . \end{aligned}$$

(31)

The corresponding conservation equation $\nabla ^{\nu }\varTheta _{\mu \nu }=0$ gives,

$$\begin{aligned} \frac{{\nu ^\prime }}{2}\,(\varTheta ^t_t-\varTheta ^r_r)-\frac{d \varTheta ^r_r}{dr}+\frac{2}{r}\,(\varTheta ^\varphi _\varphi -\varTheta ^r_r)=0. \end{aligned}$$

(32)

The above expression is a linear combination of the quasi-Einstein equations. At this stage it is noted that both sources $\tilde{T}_{\mu \nu }$ and $\varTheta _{\mu \nu }$ are individually conserved, which implies that both systems interact only gravitationally.

2.3 Embedding class one condition associated with line element (20)

If the space-time (20) satisfies the Karmarkar [84] condition

$$\begin{aligned} R_{1414}R_{2323} = R_{1212}R_{3434}+R_{1224}R_{1334} \end{aligned}$$

(33)

then the two metric functions $\tilde{\lambda }$ and $\tilde{\nu }$ can be link via

$$\begin{aligned} {\tilde{\lambda }'~ \tilde{\nu }' \over 1-e^{\tilde{\lambda }}} = \tilde{\lambda }'~ \tilde{\nu }'-2\tilde{\nu }''-\tilde{\nu }'^2 \end{aligned}$$

(34)

The above condition implies that the four dimensional space-time (20) is embedded into five dimensional pseudo-Euclidean space i.e. embedding class one solutions. The Karmarkar condition must satisfy the Pandey and Sharma condition [85] $R_{2323}\ne 0$ to describe a class one solution.

On integrating (34) we get

$$\begin{aligned} e^{\tilde{\nu }}=\left( A+B\int \sqrt{e^{\tilde{\lambda }}-1}~dr\right) ^2 \end{aligned}$$

(35)

where A and B are constants of integration.

Using the definition of anisotropy in Eqs. (26) and (27) together with Eq. (35) we express the anisotropic factor, $\tilde{\varDelta }$(r), corresponding to energy-momentum tensor $\tilde{T}_{\mu \nu }$ by some manipulation [64] as

$$\begin{aligned} \tilde{\varDelta }(r) = \tilde{p}_t-\tilde{p}_r={\tilde{\nu }' \over 32 \pi e^{\tilde{\lambda }}} \left[ {2\over r}-{\tilde{\lambda }' \over e^{\tilde{\lambda }}-1} \right] \left[ {\tilde{\nu }' e^{\tilde{\nu }} \over 2\,r\,B^2}-1 \right] . \nonumber \\ \end{aligned}$$

(36)

Here some comments are in order: (i) in this paper, we want to determine a new solution for the field equations (25)–(27) using embedding class one condition. However, it is well known that we can achieve only two kinds of perfect fluid solutions, namely Schwarzschild interior solution (by vanishing of first factor in Eq. (36)) and Kohlar–Chao solution (by vanishing of second factor in Eq. (36)), for embedding class one space-time which have been already discussed in the literature. Therefore, we choose anisotropic matter distribution corresponding to energy momentum tensor $\tilde{T}_{\mu \nu }$ for determining a new solution of embedding class one space-time. (ii) After solving the system (25)–(27), we will solve the quasi-Einstein equations (29)–(31) by taking a suitable form of the deformation function g(r) which we are going to discuss in next section.

3 New embedding class one solution by MGD

Here the field equations (25)–(27) corresponding to energy momentum tensor $\tilde{T}_{ij}$ depends upon two unknown source functions, namely $\tilde{\lambda }$ and $\tilde{\nu }$. Once these source functions are determined then immediately we can obtain the thermodynamical observable like $\tilde{\rho }$, $\tilde{p_r}$ and $\tilde{p_t}$ to describe the complete structure of the proposed model. In this connection, the physical validity of this source function $\tilde{\nu }(r)$ has been proposed by Lake, in which the function should be monotonic increasing function with a regular minimum at $r=0$ that gives a physically viable static spherically symmetric perfect fluid solution of Einstein’s equations which is regular at $r=0$ [86]. On the other hand, the form of another source function $\tilde{\lambda }(r)$ must ensure that $e^{\tilde{\lambda }(r))}=1+O(r^2)$. This form of $\tilde{\lambda }$ gives a sufficient condition for a static perfect fluid solution to be regular at the centre. Therefore in view of above points we consider a new source function $\tilde{\lambda }(r)$, to generate the physical viable solution, of the form as,

$$\begin{aligned} e^{\tilde{\lambda }}= & {} 1+c r^2 e^{nar^2}. \end{aligned}$$

(37)

where c and a are arbitrary parameters with the dimension of  $length^{-2}$ while n is a positive constant. Now form Eq. (37) we observe that $e^{\tilde{\lambda }}\rightarrow 1+O(r^2)$ and regular at centre as $e^{\tilde{\lambda }(0)}=1$. On inserting Eq. (37) into Eq. (35) and integrate we obtain,

$$\begin{aligned} e^{\tilde{\nu }}= & {} \left( A+\frac{B \sqrt{c}}{a n} ~~e^{a n r^2/2}\right) ^2. \end{aligned}$$

(38)

We observe that $\tilde{\nu }(r)$ is regular at centre $r=0$ and positive increasing throughout within the stellar compact object which provides a realistic compact star model. Therefore, the solution of the field equations (25)–(27) can be given by following line element,

$$\begin{aligned} d\tilde{s}^2= & {} \left( A+\frac{B \sqrt{c}}{a n} ~~e^{a n r^2/2}\right) ^2 dt^2 - \left( 1+c r^2 e^{nar^2}\right) ^{-1}dr^2 \nonumber \\&+\, r^2(d\theta ^2 + \sin ^2 \theta ~d\phi ^2). \end{aligned}$$

(39)

Now our next task to find all the components of $\varTheta ^\mu _\nu$ to describe the complete structure of the model. As we see that all these components depend on the deformation function g(r) that requires some restrictions to lead the well-behaved solutions i.e. free of undesired mathematical and physical singularities, and non-decreasing nature, etc. These choices of deformation functions g(r) have been widely considered by authors [87,88,89]. However, we can also be considered other options like as radial pressure associated with $\varTheta ^r_r$ to the mimic radial pressure i.e. $\varTheta ^r_r=p_r$ and density associated with $\varTheta ^t_t$ to mimic energy density i.e. $\varTheta ^t_t=\rho$, or relate only $\varTheta$-sector components through a polytropic, barotropic, or linear equation of state. It is worth mentioning that both later cases are too complicated for determining the deformation function f(r). Therefore, we adopt the first procedure to construct the physically acceptable model then deformation function g(r) has the following form,

$$\begin{aligned}&g(r) = \frac{n c r^2}{c r^2+1}. \end{aligned}$$

(40)

This form was inspired by the property of $e^\lambda$ that it tends to unity if $r\rightarrow 0$ and increasing outward to describe the well-behaved solutions. Then the explicit form of the complete space-time associated with the energy momentum tensor $T_{\mu \nu }$ can be written as

$$\begin{aligned} ds^2= & {} \left( A+\frac{B \sqrt{c}}{a n} ~~e^{a n r^2/2}\right) ^2 dt^2 - r^2(d\theta ^2 + \sin ^2 \theta ~d\phi ^2) \nonumber \\&-\,\left[ \frac{(1+c r^2 e^{nar^2})(c r^2+1)}{(c r^2+1)+\beta n c r^2\,(1+c r^2 e^{nar^2})} \right] dr^2. \end{aligned}$$

(41)

where,

$$\begin{aligned}&e^{\lambda (r)}=\frac{(1+c r^2 e^{nar^2})(c r^2+1)}{(c r^2+1)+\beta n c r^2\,(1+c r^2 e^{nar^2})}, \end{aligned}$$

(42)

$$\begin{aligned}&e^{\nu (r)}=\left( A+\frac{B \sqrt{c}}{a n} ~~e^{a n r^2/2}\right) ^2=e^{\tilde{\nu }(r)}. \end{aligned}$$

(43)

The variation of both gravitational functions are shown in Fig. 1.

Fig. 1

Variation of metric functions with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

Now the density, pressures (radial and transverse), and anisotropy for complete system are given as,

$$\begin{aligned} 8\pi \rho (r)= & {} \frac{1}{r^2} \left[ \frac{2 a n r^2+1}{c r^2 e^{a n r^2}+1}-\frac{2 \left( a n r^2+1\right) }{\left( c r^2 e^{a n r^2}+1\right) ^2}\right. \nonumber \\&\left. -\,\frac{\beta c n r^2 \left( c r^2+3\right) }{\left( c r^2+1\right) ^2}+1 \right] , \end{aligned}$$

(44)

$$\begin{aligned} 8\pi p_r(r)= & {} \frac{c \left( c r^2+1\right) ^{-1} \left( c r^2 e^{a n r^2}+1\right) ^{-1}}{a A n \sqrt{c r^2 e^{a n r^2}}+B c r e^{a n r^2}} \nonumber \\&\bigg [ar A n \sqrt{ce^{a n r^2}} \Big \{e^{a n r^2} \left( c r^2 (\beta n-1)-1\right) \nonumber \\&+\beta n\Big \}+B r e^{a n r^2} \Big \{c n \left[ 2 a r^2 (\beta n+1)+\beta \right] \nonumber \\&+c e^{a n r^2}\left[ c r^2 \left\{ \beta n \left( 2 a n r^2+1\right) -1\right\} -1\right] \nonumber \\&+2 a n\Big \} \bigg ], \end{aligned}$$

(45)

$$\begin{aligned} \varDelta= & {} \frac{c r^2 \left( c r^2+1\right) ^{-2} \left( c r^2 e^{a n r^2}+1\right) ^{-2}}{a A n \sqrt{c r^2 e^{a n r^2}}+B c r e^{a n r^2}} \nonumber \\&\left[ B r \left\{ f_2(r)+f_3(r)\right\} e^{a n r^2}-a A n f_1(r)\right. \nonumber \\&\left. \sqrt{c r^2 e^{a n r^2}} \right] \end{aligned}$$

(46)

$$\begin{aligned} 8\pi p_t (r)= & {} 8\pi p_r+\varDelta \end{aligned}$$

(47)

where,

$$\begin{aligned} f_1(r)= & {} n e^{a n r^2} \left[ a \left( c r^2+1\right) ^2+2 \beta c^2 r^2\right] +c e^{2 a n r^2} \nonumber \\&\left[ \beta c^2 n r^4-\left( c r^2+1\right) ^2\right] +\beta c n \end{aligned}$$

(48)

$$\begin{aligned} f_2(r)= & {} 2 c n e^{a n r^2} \Bigg [\beta c r^2 \left( a n r^2+1\right) \left\{ c \left( a n r^2-1\right) +a n\right\} \nonumber \\&-\,a \left( c r^2+1\right) ^2 \Bigg ] \end{aligned}$$

(49)

$$\begin{aligned} f_3(r)= & {} c^2 e^{2 a n r^2} \Bigg [\beta c n r^4 \left( a n r^2+1\right) \left\{ c \left( a n r^2-1\right) +a n\right\} \nonumber \\&+\,\left( c r^2+1\right) ^2 \Bigg ]+n \left[ a^2 n (c r^2+1) \big \{c r^2 (\beta n+1)\right. \nonumber \\&\left. +\,1\big \}+a \beta c n-\beta c^2 \right] \end{aligned}$$

(50)

Fig. 2

Variation of density with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

Fig. 3

Variation of pressure with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

Fig. 4

Variation of anisotropy with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

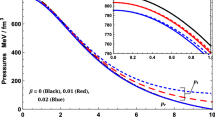
The variations of density, pressure and anisotropy are shown in Figs. 2, 3 and 4.

As we see that the central density is decreasing when n moves from 0.5 to 3.5 while the surface density increases for same n. This implies that the core will be more denser if n increases. However, it will have reverse situation for surface density. On the other hand, the pressure has totally opposite behavior than density. From Fig. 3, it can be observed that central pressure increases with increasing value of n. In this connection, we would like to mention that local anisotropies play an important role in the study of the compact objects. Since positive anisotropy leads the repulsive force which allows to more compact objects while negative anisotropy gives inward force that encourage the compact in collapsing direction. The Fig. 4 shows that the local anisotropy is increasing towards the boundary for each value of n.

The mass, compactness parameter, equation of state parameter and red-shift can be evaluated from

$$\begin{aligned}&m(r) = 4\pi \int r^2 \rho (r)\,dr \nonumber \\&= \frac{r}{2} \left[ 1-\frac{1}{c r^2 e^{a n r^2}+1}+\beta n \left( \frac{1}{c r^2+1}-1\right) \right] \end{aligned}$$

(51)

$$\begin{aligned}&u(r) = {2m(r) \over r} \end{aligned}$$

(52)

$$\begin{aligned}&\omega _r = {p_r \over \rho } ~~;~~\omega _t = {p_t \over \rho } \end{aligned}$$

(53)

$$\begin{aligned}&z(r) = e^{-\nu /2}-1. \end{aligned}$$

(54)

Fig. 5

Variation of pressure to density ratio with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

For a realistic equation of state, the equation state parameters must be less than unity. The variations of equation state parameter and red-shift are shown in Figs. 5 and 6.

Fig. 6

Variation of red-shift with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$   km$^{-2}$ and $\beta =0.01$

4 Non-singularity of the solution

The physical cogency of the solution confirm that the central values of pressure and density must be finite i.e.

$$\begin{aligned}&\rho _c = {3 c (\beta n-1) \over 8\pi }>0, ~~\forall ~~\beta n< 1 ~~\text {and} ~~c<0, \end{aligned}$$

(55)

$$\begin{aligned}&p_{rc} = p_{tc} = \frac{a A c n (\beta n-1)+B \sqrt{c} [2 a n+c (\beta n-1)]}{8\pi (a A n+B \sqrt{c})}. \nonumber \\ \end{aligned}$$

(56)

Also, it needs to ensure that any physical fluid fulfills the Zeldovich’s criterion i.e. $p_{rc}/ \rho _c \le 1$ which implies

$$\begin{aligned} {p_{rc} \over \rho _c} = \frac{a A c n (\beta n-1)+B \sqrt{c} [2 a n+c (\beta n-1)]}{3c(\beta n-1)(a A n+B \sqrt{c})} \le 1. \nonumber \\ \end{aligned}$$

(57)

Now a limitations on B / A arises due to (56) and (57) as

$$\begin{aligned}&{-2acn(\beta n-1) \over 3c^{3/2}(\beta n-1)-\sqrt{c}\{2an+c(\beta n-1)\}} \le {B \over A} \nonumber \\&\quad < {-acn(\beta n-1) \over \sqrt{c}[2an+c(\beta n-1)]}. \end{aligned}$$

(58)

5 Boundary conditions and determination of constants

The line element (2) which describes the interior of the star should join continuously with the exterior Schwarzschild metric, and can be written as

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2m}{r}\right) dt^{2}+\left( 1-\frac{2m}{r}\right) ^{-1}dr^{2} \nonumber \\&+\,r^{2}\big (d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \big ) \end{aligned}$$

(59)

with the radial coordinate r must be greater than 2m.

At the pressure free interface ($r=R$), which needs the equality of corresponding potential functions $e^{\nu }$ and $e^{\lambda }$ across the boundary ($r=R$), to get the following equations [90]

$$\begin{aligned} 1-\frac{2M}{R}= & {} e^{\nu _s} = e^{-\lambda _s}. \end{aligned}$$

(60)

Whereas the extrinsic curvature or the 2nd fundamental form of stars $K_{\mu \nu }=\nabla _\mu r_\nu$, where the unit radial vector $r_\mu$ is normal to any surface of radius r which is also continuous at the interface ($r=R$). This can be stated in terms of Einstein’s tensorial form as [91]

$$\begin{aligned}{}[G_{\mu \nu } r^\nu ]_\varSigma = \lim _{r\rightarrow R^+} (G_{\mu \nu } r^\nu ) - \lim _{r\rightarrow R^-} (G_{\mu \nu } r^\nu )=0. \end{aligned}$$

(61)

By using the field equations and (61) we get

$$\begin{aligned} \left[ 8\pi T_{\mu \nu } r^\nu \right] _\varSigma = 0, \end{aligned}$$

(62)

which implies

$$\begin{aligned}&\left[ 8\pi \left( p_r - \beta ~\varTheta ^1_1 \right) \right] _\varSigma = 0 \nonumber \\&\text{ Or } ~~p_r(R) - \beta ~\varTheta ^1_1(r\rightarrow R^-) = 0. \end{aligned}$$

(63)

On using the boundary conditions (60) and (63) we get

$$\begin{aligned} c= & {} \frac{e^{-a n R^2}}{2 R^4 [2 M+R (\beta n-1)]}\nonumber \\&\times \left[ R^3 e^{a n R^2}-2 M R^2 e^{a n R^2}-2 M R^2-\beta n R^3 \right. \nonumber \\&+R^2 \left\{ \left[ 2 M \left( e^{a n R^2}+1\right) -R e^{a n R^2}+\beta n R\right] ^2 \right. \nonumber \\&\left. \left. -8 M e^{a n R^2} [2 M+R (\beta n-1)] \right\} ^{1/2} \right] \end{aligned}$$

(64)

$$\begin{aligned} A= & {} \sqrt{1-\frac{2 M}{R}}-\frac{B \sqrt{c}~ e^{a n R^2/2}}{a n} \end{aligned}$$

(65)

$$\begin{aligned} B= & {} a n \sqrt{1-\frac{2 M}{R}} \sqrt{c R^2 e^{a n R^2}} \left[ e^{a n R^2} \left\{ c R^2 (\beta n-1)-1\right\} \right. \nonumber \\&\left. +\beta n \right] \left[ cR~e^{a n R^2} \left\{ e^{a n R^2} \left[ c R^2 (\beta n-1)-1\right] +\beta n \right\} \right. \nonumber \\&R e^{a n R^2} \left\{ c n \left[ 2 a R^2 (\beta n+1)+\beta \right] +c e^{a n R^2} \right. \nonumber \\&\left. \left. \left[ c R^2 \left\{ \beta n \left( 2 a n R^2+1\right) -1\right\} -1\right] +2 a n \right\} \right] ^{-1}. \end{aligned}$$

(66)

The observed values of compact stars are providing us the values of M and R, where $a,~n,~\beta$ as free constraints.

6 Slow rotation approximation, moment of inertia and Kepler frequency

The moment of inertia for a uniformly rotating star with angular velocity $\bar{\omega }$ is assumed by [92]

$$\begin{aligned} I = {8\pi \over 3} \int _0^R r^4 (\rho +p_r) e^{(\lambda -\nu )/2} ~{\bar{\omega } \over \varOmega }~dr \end{aligned}$$

(67)

where, the Hartle’s equation has been satisfied for the rotational drag $\bar{\omega }$ [93]

$$\begin{aligned} {d \over dr} \left( r^4 j ~{d\bar{\omega } \over dr} \right) =-4r^3\bar{\omega }~ {dj \over dr} . \end{aligned}$$

(68)

Fig. 7

M–I graphs for $a=0.001$ km$^{-2}$ and $\beta =0.2$

Fig. 8

M–R graphs for non-rotating case with $a=0.001$ km$^{-2}$ and $\beta =0.2$

with $j=e^{-(\lambda +\nu )/2}$ at boundary value $j(R)=1$. The moment of inertia solutions I up to the maximum mass $M_{max}$ have been provided by Bejger and Haensel [94] as

$$\begin{aligned} I = {2 \over 5} \Big (1+x\Big ) {M_{NR}R_{NR}^2}, \end{aligned}$$

(69)

where $x = (M_{NR}/R_{NR})\cdot \mathrm{km/M}_\odot$. The solution so obtained have been plotted mass vs I in Fig. 7 that demonstrated as n increases, the mass and moment of inertia are increasing till up to convinced value of mass and then decreases. From M–R diagram and by comparing Figs. 7 and 8, we have noticed that the mass corresponding to $I_{max}$ and $M_{max}$ are not equal. Actually, the mass corresponding to $I_{max}$ is lesser by $\sim 1.46$% from the $M_{max}$. This occurs to the EoSs due to hyperonization or phase transition to an unusual state without any strong high-density softening[95]. Using this graph we can estimate the maximum moment of inertia for a particular compact star or by matching the observed I with the $I_{\max }$ we can determine the validity of a model.

A rotating compact star can hold higher $M_{max}$ than non-rotating one. The mass relationship between non-rotating and rotating is given by (in the unit $G=C=1$) can be written as (Rotation and accretion powered pulsars P. Ghosh, Singapore 2007, P201)

$$\begin{aligned} M_{R} = M_{NR}+{1 \over 2}I\varOmega _K^2. \end{aligned}$$

(70)

Due to centrifugal force, the radius at the equator increases as some factor as compare to the static one. Cheng and Harko [96] find out the approximate radius formulas for static and rotating stars as $R_{R}/R_{NR} \approx 1.626$. Assuming the compact star is rotating in Kepler frequency $\varOmega _K=(GM_{NR}/R^3_{NR})^{1/2}$ and on using the Cheng–Harko formula we have plotted the M–R for rotating and non-rotating (Fig. 9). The corresponding frequency of rotating can be determined as [97, 98]

$$\begin{aligned} \nu \approx 1.22 \left( {R_{NR} \over 10\,\mathrm{km}}\right) ^{-3/2} \left( {M_{NR} \over M_\odot }\right) ^{1/2}~\text {kHz}. \end{aligned}$$

(71)

Fig. 9

M–R graphs for rotating (R) and non-rotating (NR) cases with $a=0.001$ km$^{-2}$ and $\beta =0.2$

Fig. 10

$\nu$–M graphs for $a=0.001$ km$^{-2}$ and $\beta =0.2$

Fig. 11

Variation of energy conditions (EC) with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

The variation of frequency with mass is shown in Fig. 10.

7 Energy conditions

The energy conditions null energy condition (NEC), dominant energy condition (DEC), weak energy condition (WEC) and strong energy condition (SEC) have to be confirmed at all points in the interior of a star. Therefore, if the following inequalities hold, then the energy conditions will be satisfied simultaneously:

$$\begin{aligned} \text {WEC}&:&T_{\mu \nu }t^\mu t^\nu \ge 0~\text{ or }~\rho \ge 0,~\rho +p_i \ge 0 \end{aligned}$$

(72)

$$\begin{aligned} \text {NEC}&:&T_{\mu \nu }l^\mu l^\nu \ge 0~\text{ or }~ \rho +p_i \ge 0 \end{aligned}$$

(73)

$$\begin{aligned} \text {DEC}&:&T_{\mu \nu }t^\mu t^\nu \ge 0 ~\text{ or }~ \rho \ge |p_i| \end{aligned}$$

(74)

where $T^{\mu \nu }t_\mu \in$ nonspace-like vector.

$$\begin{aligned} \text {SEC} : T_{\mu \nu }t^\mu t^\nu - {1 \over 2} T^\lambda _\lambda t^\sigma t_\sigma \ge 0 ~\text{ or }~ \rho +\sum _i p_i \ge 0. \end{aligned}$$

(75)

where $i\equiv ({ radial}~r, { transverse} ~t),~t^\mu$ and $l^\mu$ are time-like vector and null vector respectively.

With the help of graphical illustrations, the energy conditions have been checked. In Fig. 11, the L.H.S of the above inequalities have been plotted which confirms that all the energy conditions are fulfilled at the interior of stellar object.

8 Stability of the model and equilibrium

8.1 Equilibrium under various forces

The conservation of stress tensor $\nabla _\mu T^\mu _{\nu }=\nabla _\mu \tilde{T}^\mu _\nu +\beta \nabla _\mu \varTheta ^\mu _\nu =0$ leads to Tolman–Oppenheimer–Volkoff equations due to fluid and extra sources [25] as

$$\begin{aligned}&-\frac{\tilde{\nu }}{2}(\tilde{\rho }+\tilde{p}_r)-\frac{d\tilde{p}_r}{dr}+\frac{2}{r}(\tilde{p}_t-\tilde{p}_r)=0 \end{aligned}$$

(76)

$$\begin{aligned}&-{\tilde{\nu }' \over 2} \left[ \varTheta ^t_t-\varTheta ^r_r \right] +{d\varTheta ^r_r \over dr}+{2 \over r} \left[ \varTheta ^r_r-\varTheta ^\phi _\phi \right] =0. \end{aligned}$$

(77)

Fig. 12

Variation of forces in TOV-equation with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

Now the overall TOV-equation becomes

$$\begin{aligned}&-\frac{\tilde{\nu }}{2}(\tilde{\rho }+\tilde{p}_r)-\frac{d\tilde{p}_r}{dr}+\frac{2}{r}(\tilde{p}_t-\tilde{p}_r)-\beta \nonumber \\&\left[ {\tilde{\nu }' \over 2} \left( \varTheta ^t_t-\varTheta ^r_r \right) -{d\varTheta ^r_r \over dr}-{2 \over r} \left( \varTheta ^r_r-\varTheta ^\phi _\phi \right) \right] =0. \end{aligned}$$

(78)

The components for different effective forces due to MGD gravitational decoupling namely gravitational force ($F_g$), hydrostatic force ($F_h$) and anisotropic force ($F_a$) can be defined as,

$$\begin{aligned}&F_g=-\frac{\nu ^{\prime }}{2} \left[ \tilde{\rho }+\tilde{p}+\beta (\varTheta ^t_t-\varTheta ^r_r) \right] , \end{aligned}$$

(79)

$$\begin{aligned}&F_h=-\left( \frac{d\tilde{p_r}}{dr}+\beta \frac{d\varTheta ^r_r}{dr} \right) , \end{aligned}$$

(80)

$$\begin{aligned}&F_a= \frac{2}{r}\left[ (\tilde{p_t}-\tilde{p_r})+\beta \,(\varTheta ^t_t-\varTheta ^r_r)\right] . \end{aligned}$$

(81)

The profile of three different forces are plotted in Fig. 12. From this figure we can observe that the system is in equilibrium position. Moreover, the gravitational force $F_g$ is balanced the system by joint action of anisotropic force $F_a$ and hydrostatic force $F_h$. However, the parameter n plays an important effects on different forces as gravitational force and anisotropic force decreases in magnitude when $n \rightarrow$ 0.5 to 3.5 while hydrostatic force $F_h$ is increasing when n moves from 0.5 to 3.5.

Fig. 13

Variation of sound speed with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

Fig. 14

Variation of stability factor with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001~\mathrm{km}^{-2}$ and $\beta =0.01$

Fig. 15

Variation of adiabatic index with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001~\mathrm{km}^{-2}$ and $\beta =0.01$

8.2 Causality and stability condition

With the help of Causality condition, the stability situation have been analyzed. The causality condition will occurs when the sound velocities (radial $(v_{r}^{2})$ and transverse $(v_{t}^{2})$ are greater than zero and less than 1. The radial velocity and transverse velocity of sound can be achieved as

$$\begin{aligned} v_{r}^{2} = \frac{dp_r}{d\rho },\quad v_{t}^{2} = \frac{dp_r}{d\rho }. \end{aligned}$$

(82)

Figure 13, shows the profile of radial and transverse velocities of sound, which indicates that our model fulfills the causality condition. While Fig. 14 shows the stability condition that proposed by Abreu [99, 100]. i.e. $-1 \le v_t^2-v_r^2 \le 0$.

8.3 Adiabatic index and stability condition

The adiabatic index syndicates the basic features of the EoS on the randomness formulae and consequently contains the link between the relativistic structure of the anisotropic spheres and the EoS of the interior fluid. The stability is linked to the adiabatic index $\varGamma$, which can be written as [101],

$$\begin{aligned} \varGamma _r=\frac{\rho +p_r}{p_r}\frac{dp_r}{d\rho }. \end{aligned}$$

(83)

The stability of a Newtonian sphere condition is $\varGamma _r>4/3$ while, for $\varGamma =4/3$ is the condition for a neutral equilibrium [102]. Due to the regenerative effect of pressure, this condition changes for a relativistic isotropic sphere, which is unstable. For the anisotropic fluid sphere, if the stability depends on the type of anisotropy then the situation becomes more complicated [100, 101]. A recent work by Moustakidis [103] reveals that the critical value of adiabatic index strongly depends on the M / R. The critical value was found to be

$$\begin{aligned} \varGamma _{crit} = {4 \over 3} + {19 \over 42}~{2M \over R}. \end{aligned}$$

(84)

Figure 15, confirms that the model under consideration is stable, due to the adiabatic index is greater than 4/3.

9 Elastic property of compact stars

Assuming neutron stars exhibits isotropic bcc polycrystal structure one can defined the elastic properties via equation of deformation energy as [98]

$$\begin{aligned} \mathscr {E} = {1\over 2} K_e (\nabla \cdot \mathbf{u})^2+\mu \left( u_{ik}-{1\over 3} \delta _{ik}~\nabla \cdot \mathbf{u}\right) ^2 \end{aligned}$$

(85)

where $K_e$ and $\mu$ represents compression and shear modulus respectively. The stress tensor is given by

$$\begin{aligned} \sigma _{ik} = {\partial \mathscr {E} \over \partial u_{ik}} = K_e \delta _{ik} \nabla \cdot \mathbf{u}+2\mu \left( u_{ik}-\frac{1}{3} \delta _{ik}~\nabla \cdot \mathbf{u}\right) \end{aligned}$$

(86)

In this work we will focus on compression modulus $K_e$ which can be determine as $K_e=n_b (\partial p_r / \partial n_b)=\varGamma _r p_r$ [98]. The variation of compression modulus w.r.t. radius and mass are shown in Figs. 16 and 17 respectively.

Fig. 16

$K_e$–M graph r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001 ~\mathrm{km}^{-2}$ and $\beta =0.01$

Fig. 17

Variation of $K_e$ with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001 ~\mathrm{km}^{-2}$ and $\beta =0.01$

Fig. 18

Variation of total mass with central density for $R=9.528~\mathrm{km}, ~a=0.001~\mathrm{km}^{-2}$ and $\beta =0.01$

9.1 Harrison–Zeldovich–Novikov static stability criterion

Harrison et al. [104] and [105] have revealed that the adiabatic index are the same of pulsating star and in slowly deformed matter, which leads to be stable if the mass of the star is increasing with central density i.e. $\partial m /\partial \rho _c > 0$ and unstable if $\partial m /\partial \rho _c < 0$.

Therefore, the mass can be furnished as a function of central density and can be defined as

$$\begin{aligned} m (\rho _c)= & {} \frac{R}{2} \left[ \frac{3-3 \beta n}{3 \beta n-8 \pi \rho _c R^2 e^{a n R^2}-3}-\beta n+\right. \nonumber \\&\left. \frac{\beta n}{\frac{8 \pi \rho _c R^2}{3-3 \beta n}+1}+1\right] \end{aligned}$$

(87)

$$\begin{aligned} {\partial m (\rho _c) \over \partial \rho _c}= & {} \frac{4 \pi R^3}{3-3 \beta n} \left[ \frac{9 (\beta n-1)^2 e^{a n R^2}}{\left( 8 \pi \rho R^2 e^{a n R^2}-3 \beta n+3\right) ^2}-\right. \nonumber \\&\left. \frac{\beta n}{\left( \frac{8 \pi \rho R^2}{3-3 \beta n}+1\right) ^2} \right] \end{aligned}$$

(88)

Its can be verified using the $M-\rho _c$ graph in Fig. 18.

9.2 Effect of coupling parameter $\beta$ on the models

To complete the analysis in detail, we need to observe the effects of $\beta$ on the nature of the solution. To proceed, we are needed to assume a particular value of n and then see the behavior by changing $\beta$. For $n=3$ we have analyzed thoroughly and found that the physically acceptable range of $\beta$ is limited with a range between 0 and 0.7. As $\beta$ increases, the central density and pressure decrease while the anisotropy changes very little. However, the central values of the adiabatic index and sound speed increase with an increase of $\beta$. Therefore, the corresponding equation of state gains its stiffness along with $\beta$ i.e. as the MGD+GTR coupling gets stronger we can obtain a very stiff equation of states, which may explain the current observations of very massive neutron stars (i.e. $M>2M_\odot$). Although, the range of $\beta$ for a physically acceptable solution depends on the assumed values of n.

10 Discussion and conclusion

In this article, we have successfully incorporated the concepts of embedding class one in the gravitational decoupling formalism for the first time. This method makes a simple way of exploring new solutions in MGD, which leads to the new window of re-investigating all the existed embedding class one solutions in MGD formalism and their responses due to the additional source. The paper represents a new embedding class one solution which is deformed minimally by the gravitation decoupling technique. The MGD methodology demonstrated its adaptability in this area, making it an important and acceptable solution for EFE. It is reproduced through the graphical analysis, where the variation of the metric functions with the radial coordinate r, (see Fig. 1) for $M=1.74 M_{\odot }$ and R = 9.528 km considering $a=0.001~\mathrm{km}^{-2}$ and $\beta =0.01$, and the deformation function g(r) as in Eq. (24). The deformation function will be vanished at $r=0$, while $g(r)=n$ as r approaches to infinity. Thus, the metric potential functions are well-behaved at the center and finite and regular throughout of stars. Therefore they are proper to produce new models for anisotropic compact stars.

Figures 2 and 3, shows the behavior of density, pressures(radial and transverse) with respect to $M=1.74\; M_{\odot }$ and $R=9.528$ km considering $a=0.001$ km$^{-2}$ and $\beta =0.01$, which detected that the model is non- singular, furthermore the model is positively finite, and monotone decreasing functions throughout the interior of the star, and achieve their maximum value at the center. Also, radial pressure vanishes at the boundary. The anisotropy factor, which is given in (Fig. 4) with radial coordinate r. However, $\varDelta (0) = 0$ at the center and it is positively increasing away from the center. From Fig. 5, it is clear that the EoS is characterized by the parameters $\omega _r$ and $\omega _t$ relating to radial coordinate r, in which, the EoS factors of the model are less than unity i.e. within the region and demonstrated as a well-behaved model. Figure 6 shows the variations of surface red-shift with radial coordinate r. Thus, the surface of redshift $z(r)\rightarrow 0$ as $r\rightarrow 0$ and subsequently monotonically increasing onto the boundary. For $n= 2$ yields larger moment of inertia $M_{max}$ and $K_e$ (Figs. 7, 8). Also, we have noticed that from Figs. 7 and 8 the $M-I$ graph is more sensitive and/or sharp in the stiffness of equation of states than M–R graph. By using the concepts of Ghosh and Cheng–Harko i.e. Eq. (70) and $R_R/R_{NR} \equiv 1.626$ one can compare the M–R graphs of rotating and non-rotating limits in one frame (Fig. 9), while the variation of frequency with mass for different values of n is shown in Fig. 10. The EC with radial coordinate r for 4U 1608-52 ($M= 1.74M_\odot , R= 9.528$ km) by taking $a=0.001~\mathrm{km}^{2}$ and $\beta = 0.01$ are shown in Fig. 11, which confirms that all EC are fulfilled at the interior of the stellar object. While Fig. 12, shows the profile of three different forces to observe that the system is equilibrium i.e variation of forces in TOV-equation with radial coordinate for 4U 1608-52 ($M= 1.74\; M_\odot , R= 9.528$ km) by taking $a= 0.001$ km$^{-2}$ and $\beta = 0.01$. In the Table 1, we have presented the values of physical parameters for different values of n.

The profile of radial and transverse velocities of sound has been motivated in Fig. 13, which indicates that our model fulfills the causality condition. While (Fig. 14) shows the stability condition proposed by Abreu [99].

Fig. 19

Variation of metric functions ($e^\nu -$solid, $e^{-\lambda }-$dashed), density, pressures ($p_r-$solid, $p_t-$dashed) and equation of state parameters ($\omega _r-$solid, $\omega _t-$dashed) with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001 ~\mathrm{km}^{-2}$ and $n=3$. We are using the same color notation in all the graphs from Figs. 19, 20 and 21 as $\beta =0$ (black), 0.014 (brown), 0.028 (blue), 0.042 (green), 0.056 (red) and 0.07 (cyan)

Fig. 20

Variation of anisotropy, TOV-equation ($F_a-$dashed, $F_g-$small dashed, $F_h-$solid), sound speed ($v_r-$solid, $v_t-$dashed) and stability factor with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001 ~\mathrm{km}^{-2}$ and $n=3$. We are using the same color notation in all the graphs from Figs. 19, 20 and 21 as $\beta =$0 (black), 0.014 (brown), 0.028 (blue), 0.042 (green), 0.056 (red) and 0.07 (cyan)

Fig. 21

Variation of $\varGamma _r$, energy condition (EC) ($p_r+\rho -$solid, $p_t+\rho -$small dashed, $p_r+2p_t+\rho -$dashed), redshift and compression modulus with radial coordinate r for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001 ~\mathrm{km}^{-2}$ and $n=3$. We are using the same color notation in all the graphs from Figs. 19, 20 and 21 as $\beta =0$ (black), 0.014 (brown), 0.028 (blue), 0.042 (green), 0.056 (red) and 0.07 (cyan)

The satisfactions of static stability criterion, modified TOV-equation and Herrera’s cracking method also ensures that the solution is static, equilibrium and stable. Also, we noticed that the system is stable due to the adiabatic index $\varGamma _r$ is greater than 4/3 as shown in (Fig. 15), and is also increasing monotonically outward. The $K_e-M$ graphs (Fig. 16) signifies that as the mass of compact star increases, the compression modulus decreases while the $K_e$ with radial coordinate r graph implies an increasing trend of $K_e$ as r approaches the center i.e .the parameter n increases the stiffness of the corresponding equation of states increases. While in Fig. 17 a variation of $K_e$ with radial coordinate r for 4U 1608-52 ($M= 1.74M_\odot , R= 9.528$ km) by taking $a= 0.001~\mathrm{km}^{-2}$ and $\beta = 0.01$ are motivated for different n. Also, the central values of these physical parameters can be confirmed by the Fig. 18 for $n=2$ than $n= 0.5$. The mass function and compactness effects are able to illustrate the mass growth to choose an appropriate specific mass M. So, the profiles of understanding of the compactness and mass function are shown in Fig. 18. The $m(r)\rightarrow 0$ as $r\rightarrow 0$ and monotonically increasing toward the boundaries.

Table 1 Few interior parameters for 4U 1608-52 ($M=1.74 M_\odot , ~ R=9.528$ km) by taking $a=0.001$ km$^{-2}$ and $\beta =0.01$

The former tendency can be explained as the mass increases the central density also increases which may leads to generation of many interesting particles that unstiffen the equation of state and the compression modulus. The later one is due to the central density is highly dense as compare to the surface that leads to more compression modulus at the core than its surface. As the maximum mass $M_{max}$ increases when n increases, the spinning rate $\nu _{max}$ also increases. We have also compared the nature and behavior of the solution by assuming a particular value of n with different values of $\beta$. For this case, we have found that the central values of density and pressure decreases with increase in $\beta$ (Fig. 19). However, other physical behaviors of solution for different $\beta$ are given in Figs. 20 and 21. On the other hand, the stiffness increases with increase in $\beta$ as the adiabatic index increases and the speed of sound approaches the speed of light. Although, the anisotropy changes in a very small amount when changing the coupling constant $\beta$. The acceptable range of $\beta$ depends upon the chosen value of n. For $n=3$ the possible range lies in $0 \le \beta \le 0.7$. If $\beta > 0.7$, the trend of the density start increase slightly and decreasing near the surface, and the solution start violating causality condition.

Summing up, we can conclude that our models are physically acceptable to describe minimally deformed class one space-time by gravitational decoupling based on the results so obtained.