1 Introduction

Particle physics is experiencing a special period when different big experiments have been carried out and announced remarkable results, especially, after the discovery of a scalar boson (called the Brout-Englert-Higgs boson or, briefly, Higgs boson), which is likely the last puzzle piece filling up the particle content of the standard model [1, 2] (for a review, see, for example, [3]). Thus, the standard model (SM) [4] proves once again to be an excellent model of elementary particles and their interactions as it can explain various phenomena and many its predictions have been confirmed by the experiment. However, there are a number of problems remaining unsolved by the SM and showing that the latter could be just an effective low-energy appearance of a high-energy theory. Neutrino masses and mixing [5,6,7,8,9,10] are one of such problems calling for a modification of the SM. This problem is important not only in particle physics but also in other fields of physics such as nuclear physics, astrophysics and cosmology [11,12,13,14,15]. Many models of neutrino masses and mixing have been proposed but none of them has been recognized as the right model yet. It is why we continue to look for other possibilities leading to building different models beyond the SM. There are several methods for building an extended SM, but the first and, maybe, most-often used one is that of extending the SM gauge group \(SU(3)_c\otimes SU(2)_L \otimes U(1)_Y\) to a larger gauge group. A simpler method is to enlarge only the electro-weak part \(SU(2)_L \otimes U(1)_Y\) of the SM gauge group to, for example, \(SU(3)_L \otimes U(1)_X\) (the 3-3-1 model) [16,17,18,19,20,21,22] or \(SU(4)_L \otimes U(1)_X\) (the 3-4-1 model) [23,24,25,26,27,28]. Below, to simplify notations, the subscript L in \(SU(4)_L\) will be tacit. These models have attracted interest of a number of authors for over 20 years because of their relative simplicity. However, compared with the 3-3-1 model, the 3-4-1 model has been less investigated (one of the reasons might be the 3-4-1 model has a bigger gauge group, thus it is more complicated) but the latter has a richer structure which may provide more chance to explain the beyond SM phenomenology. The 3-4-1 model was first introduced by Voloshin [23, 24] and re-considered later by other authors (see, for example [25,26,27,28]). Originally, this model is characterized by fermions (leptons or quarks) in each family grouped in an SU(4)-quartet (or quartet for short), and its scalar sector composed often of quartets, an SU(4)-decuplet (decuplet) and, sometimes, also an SU(4)-sextet (or the corresponding anti-multiplets). Above, in particular, the term “SU(4)-quartet” means a quartet \(\mathbf {4}\) or anti-quartet \(\mathbf {4}^{*}\). For an anomaly cancellation [29, 30] the model requires an equal number of \(\mathbf {4}\) and \(\mathbf {4}^{*}\) in the fermion sector. One of the possible variants is to choose all the lepton families and one of the quark families, say, the third one, to transform as \(\mathbf {4}\), while the remaining two quark families to transform as \(\mathbf {4}^{*}\), provided that the number of either families or colors is 3 (see, for example [30] for an anomaly-free structure of fermion sector of an 3-4-1 model). Here considering neutrino masses and mixing only, we temporarily put the quark sector aside.

In comparison with the SM (and the 3-3-1 model) the 3-4-1 model has a bigger particle content, including an extended scalar sector, providing more possibilities for solving different problems, in particular, that of neutrino masses and mixing (the price is the introduction of more parameters). Especially, an extended scalar sector may provide a richer structure of neutrino masses. However, the problem of neutrino masses and mixing, so far, has not been investigated very much within the 3-4-1 model, moreover, to our knowledge, such an investigation using a scalar decuplet (decuplet, for short) is still poor, in particular, a seesaw mechanism based on a decuplet has not yet been considered. The present paper is also motivated by noticing that in the 3-4-1 model the VEV configuration of a decuplet can provide a seesaw structure and the seesaw mechanism can be automatically applicable at the leading order by Yukawa coupling to only a single decuplet (with an appropriate VEV), unlike in most of other models, where the seesaw mechanism usually requires more scalar multiplets involved. Another motivation to use a decuplet for generating neutrino masses is that the latter (as well as charged lepton masses) can not be generated directly at the leading order by using quartets which are fundamental representation multiplets of the gauge group SU(4).

As said above, neutrinos are massive but, according to the current particle physics experimental data and cosmological observation constraints [31,32,33,34,35,36], their masses are very tiny, just of the order of \(10^{-1}\) eV, even less. Thus, one must find a way to explain that. One of the most popular ways to generate neutrino small masses is based on the so-called see-saw mechanism (there is a vast literature on this matter but one can see, for example [37,38,39,40] for the type-I see-saw mechanism and [11,12,13,14] for a review on further developments). This mechanism has been applied to the SM and many extended models, in particular, to our knowledge, it was applied for the first time to the 3-3-1 model with right-handed neutrinos by using a scalar \(SU(3)_L\)-sextet in Refs. [41, 42]. The latter papers inspire the present work and a later work, showing that the seesaw mechanism can be applied to the 3-4-1 model with and without a decuplet. One of the feature of the seesaw mechanism is the presence of one or more right-handed neutrinos which are “naturally” introduced in the 3-4-1 model as fundamental representation (quartet) partners of right-handed charged leptons (it is an advantage of this model as in most of other models, except a few ones like those based on the left-right symmetry [38, 43,44,45,46], the right-handed neutrinos are introduced “artificially” by hand). Now let us first make a quick introduction to the 341 model.

The plan of this article is the following. In the next section a concise introduction to the 3-4-1 model with a concentration on its lepton and scalar sectors is presented. Section III is devoted to using an SU(4) decuplet scalar for generation of neurtino masses. Some comments and conclusions are made in the final section.

2 The 3-4-1 model in brief

This extended standard model is based on the gauge group \(SU(3)_c\otimes SU(4) \otimes U(1)_X\). The latter is attractive by several reasons such as in this model two lepton chiralities of each family are unified in a fundamental representation of the SU(4) gauge group and this model, similar to the 331 model, can explain the number of fermion families to be three [20, 21, 29, 30]. Because the subject of the present paper is neutrino masses we will consider only the lepton- and the scalar sectors of the model and leave its gauge- and quark sectors for a future research. As in the case of the 3-3-1 model, the 3-4-1 model, depending on the particle content and their alignment, has several versions. Let us consider one of the possible versions.

2.1 Lepton sector

Many neutrino mass models require the introduction of right-handed neutrinos (the number of which depends on the model considered), here we work in a model with a right-handed neutrino (RHN), say \(N_R^\alpha \), introduced for each family \(\alpha =e,\mu ,\tau \). As usually, these RHN’s are sterile neutrinos being singlets under the electroweak gauge group \(SU(2)_L \otimes U(1)_Y\). One of the main features of the 3-4-1 model is all leptons in each (extended) family are grouped in an SU(4) quartet. An alignment of these quartets can be

$$\begin{aligned} f^a_L = \left[ \begin{array}{c} \nu _L^\alpha \\ l_L^\alpha \\ (N_R^\alpha )^c\\ (l_R^\alpha )^c \end{array}\right] , \quad \alpha =e,\mu ,\tau , \end{aligned}$$
(1)

where \(\nu _L^\alpha \) and \(N_R^\alpha \) are neutrino fields (left- and right handed, respectively), \(l_L^\alpha \) and \(l_R^\alpha \) are charged lepton fields, and \(\alpha \) is a family (flavour) index, while \(F^c\) denotes the charge conjugation of a field F. In this model, \(N_R^\alpha \) are sterile neutrinos by introduction and can be replaced by arbitrary sterile/exotic leptons to make other models. The transformation of \(f^\alpha _L\), being also an \(SU(3)_c\)-singlet and \(U(1)_X\)-neutral, under \(SU(3)_c\otimes SU(4) \otimes U(1)_X\) is summarized as follows

$$\begin{aligned} f^\alpha _L \sim (1,4,0). \end{aligned}$$
(2)

Another alignment of the lepton multiplet,

$$\begin{aligned} f'^\alpha _L = \left[ \begin{array}{c} \nu _L^\alpha \\ l_L^\alpha \\ (l_R^\alpha )^c\\ (N_R^\alpha )^c \end{array}\right] \sim (1,4,0),~~\alpha =e,\mu ,\tau , \end{aligned}$$
(3)

is obtained from the one in (1) by exchanging the positions of the third and the fourth components. Working with which alignment among (1) and (3) is the question of convenience depending on the choice of a gauge symmetry breaking scheme. For example, if we want the 3-4-1 model to be broken to the 3-3-1 model with two neutrinos in a lepton \(SU(3)_L\) triplet [17,18,19] or the minimal 3-3-1 model [20,21,22], we choose the alignment (1) or the alignment (3), respectively. In this paper the alignment (1) is chosen. Other versions of the 3-4-1 model, in which the third and the fourth components of an SU(4) quartet (1) or (3) are occupied by other leptons such as exotic charged leptons and arbitrary sterile neutrinos, could be also considered.

To generate neutrino masses we must introduce an appropriate scalar sector. It can have different structures but below we will work with that containing an SU(4) decuplet.

2.2 Scalar sector

Let us consider a scalar sector of the 3-4-1 model with three quartets,

$$\begin{aligned} \eta= & {} \left[ \begin{array}{c} \eta _1^0 \\ \eta _2^- \\ \eta _3^0\\ \eta _4^+ \end{array} \right] \sim (1,4,0), \quad \rho = \left[ \begin{array}{c} \rho _1^+ \\ \rho _2^0 \\ \rho _3^+\\ \rho _4^{++} \end{array} \right] \sim (1,4,1), \nonumber \\ \chi= & {} \left[ \begin{array}{c} \chi _1^{-} \\ \chi _2^{--} \\ \chi _3^-\\ \chi _4^0 \end{array} \right] \sim (1,4,-1), \end{aligned}$$
(4)

and one decuplet,

$$\begin{aligned} {\varDelta }\sim \left[ \begin{array}{cccc} \varDelta _{11}^0 &{} \varDelta _{12}^- &{} \varDelta _{13}^0 &{} \varDelta _{14}^+\\ \varDelta _{12}^- &{} \varDelta _{22}^{--} &{} \varDelta _{23}^- &{} \varDelta _{24}^0\\ \varDelta _{13}^0 &{} \varDelta _{23}^- &{} \varDelta _{33}^0 &{} \varDelta _{34}^{++}\\ \varDelta _{14}^+ &{} \varDelta _{24}^0 &{} \varDelta _{34}^{++} &{} \varDelta _{44}^+ \end{array} \right] \sim (1,10,0). \end{aligned}$$
(5)

In (5) the normalisation coefficients which can be found by using the kinetic term of \({\varDelta }\) are skipted. Sometimes, the scalar sector is extended with one more quartet similar to \(\eta \), say,

$$\begin{aligned} \xi = \left[ \begin{array}{c} \xi _1^0 \\ \xi _2^- \\ \xi _3^0\\ \xi _4^+ \end{array} \right] \sim (1,4,0), \end{aligned}$$
(6)

in order to resolve a quark mass problem [47] or/and with a (self-conjugate) sextet if a neutrino magnetic moment is included in consideration [23, 24]. Adding the scalar \(\xi \) could be also motivated by the fact that \(\eta \) has two neutral components which may need two independent vacuum (VEV) structures [41, 42]. The scalar sector containing only quartets has been used in different investigations without giving fermion masses at the Yukawa coupling tree levels. The decuplet [23, 24] is introduced to generate charged lepton masses (with the presence of only the sextet some of the charged leptons remain massless) but it seems, it has not been used much for the neutrino mass generation. We will explore the latter in this paper following an idea close to that of [41, 42].

For further use the VEV’s of the scalars are denoted as follows.

$$\begin{aligned} \langle \eta \rangle= & {} \left[ u_1,0, u_3,0 \right] ^T,~~\langle \xi \rangle = \left[ v_1,0,v_3,0 \right] ^T,\nonumber \\ \langle \rho \rangle= & {} \left[ 0,\sigma _2,0,0 \right] ^T, ~~ \langle \chi \rangle = \left[ 0, 0, 0,w_4 \right] ^T, \end{aligned}$$
(7)
$$\begin{aligned} \langle {\varDelta }\rangle= & {} \left[ \begin{array}{cccc} \delta _1 ~&{}~ 0 ~&{}~ \delta _2 ~&{}~ 0\\ 0 ~&{}~ 0 ~&{}~ 0 ~&{}~ \delta _4\\ \delta _2 ~&{}~ 0 ~&{}~ \delta _3 ~&{}~ 0\\ 0 ~&{}~ \delta _4 ~&{}~ 0 ~&{}~ 0 \end{array} \right] . \end{aligned}$$
(8)

For the sake of completeness, a sextet can be also introduced,

$$\begin{aligned} \mathcal{S}\sim \left[ \begin{array}{cccc} 0 &{} -S_{12}^- &{} -S_{13}^0 &{} -S_{14}^+\\ S_{12}^- &{} 0 &{} -S_{23}^-&{} -S_{24}^0\\ S_{13}^0 &{} S_{23}^- &{} 0&{} -S_{34}^+\\ S_{14}^+ &{} S_{24}^0 &{} S_{34}^+&{} 0 \end{array} \right] \sim (1,6,0), \end{aligned}$$
(9)

with the VEV

$$\begin{aligned} \langle \mathcal{S}\rangle = \left[ \begin{array}{cccc} 0 ~&{} 0 &{} -s_1 &{} ~0\\ 0 ~&{} 0 &{} ~0&{} -s_2\\ s_1 ~&{} 0 &{} ~0 &{} ~0\\ 0 ~&{} ~s_2 &{} ~0 &{} ~0 \end{array} \right] . \end{aligned}$$
(10)

Below we will see that to generate neutrino masses (and also masses of other leptons) at the tree level no quartet and sextet but only decuplet is relevant.

3 Decuplet and neutrino mass generation

A neutrino mass generation can be realized by coupling \(\bar{f}_L(f_L)^c\) to scalars transforming under appropriate representations of SU(4). Since both \(\bar{f}_L\) and \((f_L)^c\) transform as an anti-quartet \(\mathbf {4}^{*}\), their product \(\bar{f}_L(f_L)^c\) transforms as \({\mathbf {4}^{*}}\otimes {\mathbf {4}^{*}}\), which in turns can be decomposed as a direct sum of a anti-sextet (which could be self-conjugate) an anti-decuplet: \({\mathbf {4}^{*}}\otimes {\mathbf {4}^{*}}= \mathbf {6}^{*} \oplus \mathbf {10}^{*}\). Therefore, a scalar coupled to \(\bar{f}_L(f_L)^c\) must transform as \(\mathbf {6}\) or \(\mathbf {10}\), thus, it can be a sextet (9) or a decuplet (5). Thus, the Yukawa coupling of \(\bar{f}_L(f_L)^c\) to scalars has the general form (cf. [23, 24])

$$\begin{aligned} -\mathcal{L}_{f\mathcal SD}= Y_{\alpha \beta }^S\bar{f}^\alpha _L({f^\beta _L})^c \mathcal{S} + Y_{\alpha \beta }^\varDelta \bar{f}^\alpha _L({f^\beta _L})^c {\varDelta }, \end{aligned}$$
(11)

where \(Y_{\alpha \beta }\) are coupling coefficients with \(\alpha \) and \(\beta \) being family indices which in general may not coincide with those of the real charged-lepton mass states but it is easy to see that we can work in the basis labeled by the latter, \(\alpha ,\beta =e,\mu ,\tau \), starting from (1). The leptons may get masses when the scalars in (11) develop VEV’s. Since the coupling to the sextet in (11) cannot provide a right lepton mass term it is discarded from consideration here, while the coupling to the decuplet can give lepton-mass-like terms, namely, a charged-lepton mass term if \(\delta _4\ne 0\), and, in some circumstance (see below), a neutrino mass term via a see-saw mechanism. The latter is very important because it can generate small neutrino masses, accompanied, though, by a large mass scale (of heavy hypothesized neutrinos). Thus, for a generation of lepton masses instead of (11) we have

$$\begin{aligned} -\mathcal{L}_{f\varDelta }= Y_{\alpha \beta }^\varDelta \bar{f}^\alpha _L({f^\beta _L})^c {\varDelta }, ~~ \alpha ,\beta =e,\mu ,\tau . \end{aligned}$$
(12)

However, using only the decuplet as in (12) to generate masses of both charged leptons and neutrinos may lead to a wrong correlation between these masses (as the charged lepton- and neutrino mass matrices, which in this case are proportional to the same Yukawa matrix, can be diagonalized by the same unitary matrix, the PMNS matrix is trivial). It why we must use different ways to separately generate charged-lepton- and neutrino masses. Besides the way done via (12), another way of generating lepton masses could be done via an effective coupling of two quartets as follows

$$\begin{aligned} -\mathcal{L^\prime }_{f\varDelta }= \frac{Y_{\alpha \beta }^{\varDelta ^\prime }}{\varLambda }\bar{f}^\alpha _L({f^\beta _L})^c {\varDelta ^\prime }, \end{aligned}$$
(13)

where \(\varDelta ^\prime \) is a decuplet component in the decomposition of a tensor product of two quartets \(\rho \otimes \chi \) or \(\eta \otimes \xi \) according to the rule \({\mathbf {4}}\otimes {\mathbf {4}}= \mathbf {6} \oplus \mathbf {10}\). Depending on which masses (of charged leptons or neutrinos) to be generated \(\rho \otimes \chi \) or \(\eta \otimes \xi \) will be chosen for \({\mathbf {4}}\otimes {\mathbf {4}}\). To express these cases we formally write \(\varDelta _{(1)}^\prime \sim \rho \otimes \chi \) or \(\varDelta _{(2)}^\prime \sim \eta \otimes \xi \). Here again the sextet component \(\mathbf {6}\) in \({\mathbf {4}}\otimes {\mathbf {4}}\) is neglected as it cannot contribute to a lepton mass term. Let us denote a VEV of \(\varDelta ^\prime \), which is either \(\varDelta _{(1)}^\prime \) or \(\varDelta _{(2)}^\prime \), as follows

$$\begin{aligned} \langle {\varDelta ^\prime }\rangle = \left[ \begin{array}{cccc} \delta _1^\prime ~&{}~ 0 ~&{}~ \delta _2^\prime ~&{}~ 0\\ 0 ~&{}~ 0 ~&{}~ 0 ~&{}~ \delta _4^\prime \\ \delta _2^\prime ~&{}~ 0 ~&{}~ \delta _3^\prime ~&{}~ 0\\ 0 ~&{}~ \delta _4^\prime ~&{}~ 0 ~&{}~ 0 \end{array} \right] , \end{aligned}$$
(14)

where

$$\begin{aligned} \delta _1^\prime =\delta _2^\prime =\delta _3^\prime =0, ~\delta _4^\prime =\sigma _2w_4, \end{aligned}$$
(15)

for \(\varDelta ^\prime \sim \rho \otimes \chi \), or

$$\begin{aligned} \delta _1^\prime =u_1v_1, ~\delta _2^\prime =\dfrac{u_1v_2+u_2v_1}{2}, \delta _3^\prime =u_3v_3, ~\delta _4^\prime =0, \end{aligned}$$
(16)

for \(\varDelta ^\prime \sim \eta \otimes \xi \).

Following the latest discussions the lepton masses can be generated by several ways. Let us count two of them. One of the ways is the neutrino masses are generated by either \(\varDelta \) or \(\varDelta _{(2)}^\prime \), then the charged-lepton masses should be generated by an alternative decuplet. Another way is if \(\varDelta \) is involved in the generation of both the neutrino masses and charged-lepton masses, one or all of the decuplets \(\varDelta _{(1)}^\prime \) and \(\varDelta _{(2)}^\prime \) could be required to additionally contribute to the generation of either of these masses to make their total generations different from each other as required above. Here, for one of several possibilities, we will explore the neutrino masses generated by the decuplet \(\varDelta \) (with \(\delta _4=0\)) via (12) and the charged lepton masses generated by \(\varDelta _{(1)}^\prime \) via (13). The general procedure with exchanged roles between a \(\varDelta \) and an appropriate \(\varDelta ^\prime \) is similar and can be investigated separately with a feature that the VEV of \(\varDelta ^\prime \) is adjusted by the VEV’s of quarterts. Since the charged-lepton mass term (13) is independent from the neutrino one (12) we can set at the beginning the charged-lepton mass matrix diagonal, i.e., \(Y_{\alpha \beta }^{\varDelta ^\prime } \sim Y_\alpha ^{\varDelta ^\prime }\delta _{\alpha \beta }\) (here \(\varDelta ^\prime \equiv \varDelta _{(1)}^\prime \)).

In the neutrino subspace, the coupling (12) after \(\varDelta \) acquiring a VEV reads

$$\begin{aligned}&-\mathcal{L}_{M_\nu }= \mathcal{Y}_{\alpha \beta }^\varDelta \left[ \bar{\nu _L}^\alpha , (\bar{N}_R^\alpha )^c \right] \left[ \begin{array}{cccc}\delta _1 &{} \delta _2 \\ \delta _2 &{} \delta _3 \end{array} \right] \left[ \begin{array}{c} (\nu _L^\beta )^c\\ N_R^\beta \\ \end{array}\right] , \end{aligned}$$
(17)
$$\begin{aligned}&\left[ \bar{\nu _L}, (\bar{N}_R)^c \right] ^\alpha \mathcal{M}_{\alpha \beta }\left[ \begin{array}{c} (\nu _L)^c\\ N_R\\ \end{array}\right] ^\beta , \end{aligned}$$
(18)

where the mass matrix \(\mathcal M\) has the form

$$\begin{aligned} \mathcal{M}= \left[ \begin{array}{cccc}{} \mathbf{m_T} &{} \mathbf{m_D} \\ \mathbf{m_D} &{} \mathbf{m_S} \end{array} \right] , \end{aligned}$$
(19)

in which \(\mathbf{m_T}\), \(\mathbf{m_D}\) and \(\mathbf{m_S}\) are \(3\times 3\) matrices with elements

$$\begin{aligned} (\mathbf{m_T})_{\alpha \beta }=Y_{\alpha \beta }^\varDelta \delta _1, ~(\mathbf{m_D})_{\alpha \beta } =Y_{\alpha \beta }^\varDelta \delta _2, ~ (\mathbf{m_S})_{\alpha \beta }=Y_{\alpha \beta }^\varDelta \delta _3, \end{aligned}$$
(20)

The magnitudes of the masses and their ratio depend on not only the Yukawa couplings but also the symmetry breaking’s hierarchy to be discussed below.

The symmetry breaking scheme could be as follows: \(\delta _3\) can break \(SU(3)_L\)-symmetry, thus, SU(4)-symmetry but not \(SU(2)_L\)-symmetry, while \(\delta _2\) can break \(SU(2)_L\)-symmetry and \(\delta _1\) (not necessary to be big) can be very small or zero (to break weakly or not to break a U(1)-symmetry). Thus, we should have

$$\begin{aligned} \delta _3\gg \delta _2\gg \delta _1. \end{aligned}$$
(21)

That means the see-saw mechanism works for (18) leading to the following two eigen matrices

$$\begin{aligned} \mathbf{m}=\mathbf{m_T}-(\mathbf{m_D})^T(\mathbf{m_S})^{-1}{} \mathbf{m_D}, \quad \mathbf{M}=\mathbf{m_S}, \end{aligned}$$
(22)

after converting the mass matrix (19) to a quasi-diagonalized form

$$\begin{aligned} \mathcal{M}_{\mathrm{diag}}= \left[ \begin{array}{cccc}{} \mathbf{m} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{M} \end{array} \right] . \end{aligned}$$
(23)

Following (20) we get the matrix elements, denoted by \(m_{\alpha \beta }\), of the mass matrix \(\mathbf{m}\) of the light neutrinos

$$\begin{aligned} m_{\alpha \beta }=\left[ \delta _1 - {(\delta _2)^2\over \delta _3}\right] Y_{\alpha \beta }^\varDelta . \end{aligned}$$
(24)
Fig. 1
figure 1

Distributions of \(m_{\alpha \beta }\equiv (m_\nu )_{\alpha \beta }\) versus \(sin^2\theta _{13}\) for an NO (on the left) and for an IO (on the right)

Full size image

The eigenvalues \(m_k\), \(k=1,2,3\), of the matrix \(\mathbf{m}\) are the masses of three light active neutrinos (see more below). So far none of the masses \(m_k\) but only the upper bound of their sum is known, \(\sum _k m_k \equiv \sum m_\nu \le 0.12~\hbox {eV}\) [32,33,34,35]. From this bound and the current data on squared mass differences [48] one can derive the bounds \(0\le m_1/\text {eV} \le 0.03\) for a normal neutrino mass ordering (NO) and \(0\le m_3/\text {eV} \le 0.016\) for an inverse neutrino mass ordering (IO). That means \(m_i\) could be of the order of \(10^{-1}~\hbox {eV}\)–\(10^{-2}~\hbox {eV}\) or lower and according to (24) they are related to the strength of the Yukawa couplings. In general the Yukawa couplings are free parameters of the model (to be determined experimentally directly or indirectly) but it is seen from Eq. (20) that they are proportional to \(m_{\alpha \beta }\) which can be calculated numerically using the current experimental data given [48]. Figure 1 shows two-dimensional plots of distributions of \(m_{\alpha \beta }\) versus \(sin^2\theta _{13}\) for both an NO and an IO of the neutrino masses with \(m_1=0.01~\hbox {eV}\) (for an NO) and \(m_3=0.01~\hbox {eV}\) (for an IO), respectively, chosen as testing masses (other values can be chosen, but, at any case, \(m_1\) and \(m_3\) must be in the ranges \(0 \le m_1/\text {eV} \le 0.030 \) for an NO and \(0 \le m_3/\text {eV}\le 0.016\) for an IO, as derived above), while other masses in each mass ordering are constrained by the squared mass differences [48]. Here ten thousand events are created and each \(m_{\alpha \beta }\) is calculated event by event as a function of mixing angles which are random values generated on the base of a Gaussian distribution having the mean (best fit) value and sigmas given in Ref. [48]. From Fig. 1 one can imagine how the Yukawa couplings distribute around their mean values (upto a scale depending on \(\delta _1, \delta _2\) and \(\delta _3\) as shown in (24)). Since the mean values of \(m_{\alpha \beta }\) are of the order of \(10^{-2}~\hbox {eV}\) or smaller (\(m_{\alpha \beta }\le 10^{-2}~\hbox {eV}\)) and \(\delta _2\approx 10^2\) GeV (the electroweak symmetry breaking scale) the range of the Yukawa couplings could be \(Y_{\alpha \beta }^\varDelta \le 10^{-24}\delta _3/eV\) at the seesaw limit \(\delta _1\approx 0\). They are stronger (weaker) for a higher (lower) \(\delta _3\), therefore, an \(SU(4)\times U(1)\)-electroweak phenomenology is sensitive only if \(\delta _3\) is high enough. The distribution shape of \({{\,\mathrm{Tr}\,}}(Y_{\alpha \beta }^\varDelta )\) can be visualized via Fig. 2 showing the distributions of \(\sum m_\nu \) around the mean values \(\overline{\sum } m_\nu \approx 0.07~\hbox {eV}\) (for an NO) and \(\overline{\sum } m_\nu \approx 0.11~\hbox {eV}\) (for an IO). It is seen that these values are still lying within the currently established upper bound \(\sum m_\nu \le 0.12~\hbox {eV}\).

Fig. 2
figure 2

Distribution of \(\sum m_\nu \) versus \(sin^2\theta _{13}\) for an NO (on the left) and for an IO (on the right)

Full size image

If \(m_1> 0.03~\hbox {eV}\) (for an NO) or \(m_3> 0.016~\hbox {eV}\) (for an IO) the sum \(\sum m_\nu \) would exceed 0.12 eV.

Diagonalizing \(Y_{\alpha \beta }\) we get the matrices \(\mathbf{m_T}\), \(\mathbf{m_D}\) and \(\mathbf{m_S}\) diagonalized with eigenvalues

$$\begin{aligned} ({m_T})_k=Y_k^\varDelta \delta _1, ~({m_D})_k=Y_k^\varDelta \delta _2, ~ ({m_S})_k=Y_k^\varDelta \delta _3, \end{aligned}$$
(25)

where, \(k=1,2,3\), numbering the mass eigenvalues and the mass eigenstates. Taking (22) into account this leads to the neutrino mass-states

$$\begin{aligned}&(n_{L})_k = (\nu _L)_k-{(m_D)_k\over (m_S)_k}(N_R^{~c})_k, \nonumber \\&(N_{L})_k = {(m_D)_k\over (m_S)_k}(\nu _L)_k+(N_R^{~c})_k, \end{aligned}$$
(26)

corresponding respectively to the masses

$$\begin{aligned}&m_k= (m_T)_k-{(m_D)_k^2\over (m_S)_k} \equiv \left[ \delta _1-{(\delta _2)^2\over \delta _3}\right] Y^\varDelta _k, \nonumber \\&M_k= (m_S)_k\equiv Y^\varDelta _k \delta _3, \end{aligned}$$
(27)

where the notation \(N_R^{~c}\equiv (N_R)^c\) is used. Note that at \(\delta _1\approx 0\) the ratio \(m_k/M_k\) becomes universal as it depends on neither k nor the coupling coefficients \(Y^\varDelta _k\) but the ratio \(\delta _2/\delta _3\):

$$\begin{aligned} {m_k\over M_k} \approx \left( m_D\over m_S\right) ^2 = \left( \delta _2\over \delta _3\right) ^2. \end{aligned}$$
(28)

That means a ratio can be predicted by knowing the other one. Using (28) we can rewrite (26) in the form

$$\begin{aligned}&(n_L)_k = (\nu _L)_k-\sqrt{m_k\over M_k} ~(N_R^{~c})_k, \nonumber \\&(N_L)_k = \sqrt{m_k\over M_k} ~(\nu _L)_k+(N_R^{~c})_k, \end{aligned}$$
(29)

or

$$\begin{aligned}&(n_L)_k = (\nu _L)_k-{\delta _2\over \delta _3} ~(N_R^{~c})_k, \nonumber \\&(N_L)_k = {\delta _2\over \delta _3} ~(\nu _L)_k+(N_R^{~c})_k. \end{aligned}$$
(30)

Solving the system of Eq. (30) for \((\nu _L)_k\) we get

$$\begin{aligned} (\nu _L)_k = {1\over 1+(\delta _2/ \delta _3)^2}(n_L)_k + {\delta _2/\delta _3\over 1+ (\delta _2/ \delta _3)^2} ~(N_L)_k, \end{aligned}$$
(31)

or, as \(\delta _2\ll \delta _3\),

$$\begin{aligned} (\nu _L)_k \approx (n_L)_k + {\delta _2\over \delta _3}~(N_L)_k. \end{aligned}$$
(32)

In the flavour basis, the neutrinos \((\nu _L)_\alpha \), \(\alpha =e,\mu ,\tau \), have the following general mixing

$$\begin{aligned} (\nu _L)_\alpha \approx ~&\sum _{k=1}^3 U_{\alpha k} (n_L)_k + \sum _{k=1}^3 \varTheta _{\alpha k} ~(N_L)_k, \end{aligned}$$
(33)

where, \(U_{\alpha k}\) is the PMNS matrix, and \(\varTheta _{\alpha k}\approx {\delta _2\over \delta _3}U_{\alpha k}\). That means, the flavour neutrinos in general are mixtures between light active neutrinos and heavy neutrinos which now are objects of increasing intensive search. Since mixing angles with heavy neutrinos are very small they are often neglected but when experiments, especially those searching for heavy neutrinos, become more and more sensitive and precise they should be taken into account.

At the present we do not know the exact bounds of \(m_S\), which can spread from a relatively low scale at keV (or lower) to a very high energy scale near the Planck mass, but we know from the experiment and cosmological constraints [32,33,34,35,36] the upper bound of the active neutrions masses \(m < 10^{-1}eV\). Thus, m / M can be calculated for a given M, for example, \(m/M<10^{-4}\) (that means \(\delta _2/\delta _3<10^{-2}\)) for M at a keV scale and \(m/M<10^{-10}\) (that means \(\delta _2/\delta _3<10^{-5}\)) for M at a GeV scale. The latter estimations do not contradict with the upper bounds of \(|\varTheta |^2\) established for several (current and future) experiments for M of a few GeV’s [49, 50]. As is well known that an existence of Majorana neutrinos violates the lepton number conservation rule.

Fig. 3
figure 3

Scalar-exchanging lepton scattering

Full size image

At the \(SU(2)_L\)-breaking scale \(\delta _2\sim 10^2\) GeV there should be keV heavy neutrinos (\(M\sim 10^3~\hbox {eV}\)) if the \(SU(3)_L\) (or SU(4)) is broken at \(\delta _3\sim 10\) TeV scale. The existence of eV or MeV heavy neutrinos requires the breaking scale \(\delta _3 \sim 10^0\) TeV or \(\delta _3 \sim 10^3\) TeV, respectively. The possible existence of the light heavy neutrinos (with masses, for example, at eV-, keV-, MeV scale) is very interesting not only in particle physical aspect but also in the astro-particle physical and the cosmological aspects (see, for example [42, 51] and references therein).

4 Conclusion

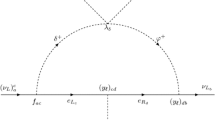
It is well known from the experiment [5,6,7,8,9,10] that neutrinos have masses but they are very small, for example, some combined particle physics data and cosmological probes give an upper bound of the sum of neutrino masses as \(\sum m_\nu < 0.12~\hbox {eV}\) (95% CL) [32,33,34,35,36]. Many theoretical models and mechanisms have been suggested to predict or explain this experimental fact but none of them is completely satisfactory. In this paper we have suggested one more way of neutrino mass generation through spontaneous breaking of an extended \(SU(4)\otimes U(1)_X\) electroweak symmetry by an SU(4)-decuplet scalar acquiring a VEV without using fundamental quartet scalars which cannot generate neutrino masses (and charged-lepton masses) directly. There are limits in which the seesaw mechanism can be realized. Depending on these limits the new (heavy) neutrinos added to the active (light) neutrinos may have masses at different ranges none of which has been so far excluded from the experiment. It should be noted that if the physics of the 3-4-1 model is at around TeV scale, such as that of the LHC and near future accelerators, there may exist light heavy neutrinos (at an eV–keV scale) attracting great interest in particle physics and cosmology (see, for example [51,52,53,54,55]). For \(M_N\) at the order of \(10^2\) GeV considered in Ref. [50] the scale of physics of 3-4-1 model, if existing, would be too high in order to be discovered at the LHC and other present accelerators. The neutrino masses depend on not only the symmetry breaking scales but also Yukawa couplings (to the decuplet) the distribution shapes of which are shown in Figs. 1 and 2 via the model-independent distributions of the neutrino mass matrix elements. Thus, these Yukawa couplings can be determined if the symmetry breaking scales are known and vice versa. More precisely, the Yukawa couplings \(Y_{\alpha \beta }^\varDelta \) and their trace \({{\,\mathrm{Tr}\,}}(Y_{\alpha \beta }^\varDelta )\) can be determined from the distributions in Figs. 1 and 2 upto the factor \(\left[ \delta _1 - \dfrac{(\delta _2)^2}{\delta _3}\right] \). These distributions are derived by using an experimental data for squared mass differences and mixing angles (it means that the PMNS matrix is known) as well as a mass input respecting the mass upper bound \(\sum m_\nu \le 0.12~\hbox {eV}\) and, vice versa, the PMNS matrix can be determined via the model’s parameters fixed by other independent ways, for example, via non-neutrino processes like thoses for S-exchanging L–L scatterings schematically depicted in Fig. 3 (here the symbol “L” stands for a charged lepton and the symbol “S” stands for a scalar from a decuplet). It is a quite long but very interesting work being currently investigated.

As discussed in Ref. [41], besides the seesaw limit \(\delta _1\approx 0\), other limits in the mass term (18) can be considered: the pure Majorana limit (\(m_D=0\)), the Dirac limit (\(m_T=m_S=0\)), the pseudo-Dirac limit (\(m_T\ll m_D\) and \(m_S\ll m_D\)), etc. It can be seen that the pure Majorana limit breaks the present structure of the neutrino mass term to a left-right \(SU(2)_L\otimes SU(2)_R\) structure which can be a subject of a later investigation. We would like to stress that in the present paper the seesaw mechanism is applied, to our knowledge, for the first time to the 3-4-1 model with a scalar decuplet.

Finally, it is worth noting that here we have used a fundamental scalar decuplet for neutrino mass generation but using a decuplet composed of quartets, or using an effective coupling of the latter, is another possibility for generating lepton masses including masses of neutrinos and charged leptons. This research is in progress.