1 Introduction

After the historical direct detection of gravitational waves from a black hole (BH) merger by the LIGO collaboration in 2015 [1], and the first image of the supermassive BH located at the centre of the giant elliptical galaxy Messier 87 (M87) by the Event Horizon Telescope (EHT) project [2] only a few weeks back, there is currently a lot of ongoing research in investigating the properties of BHs in several different contexts. The LIGO direct detection provided us with the strongest evidence so far that BHs do exist in Nature and that they merge, while at the same time it offers us the tools to test strong gravitational fields using radio wave astronomy. However, the LIGO detection has provided us with no information about the horizon of the BH, which after all is its defining property.

The gravitational field produced by a BH is so strong that nothing, not even photons, can escape. Therefore, a BH cannot be seen directly. There is, however, the possibility of seeing a dark shadow of a BH via strong gravitational lensing and photon capture at the horizon, if the BH stands between the observer and nearby light sources. The photons emitted from the source, or of the radiation emitted from an accretion flow around the event horizon of the BH, are expected to create a characteristic shadow-like image, that is a darker region over a brighter background. Indeed, recently the EHT project, a global very long baseline interferometer array observing at a wavelength of \(1.3~\hbox {mm}\), announced and showed the first image of the supermassive BH located at the centre of M87 [3], while the corresponding image from the centre of the Milky Way is yet to come. For instrumentation, data processing and calibration, physical origin of the shadow, etc, see [4,5,6,7,8].

The observation of the shadow probes the spacetime geometry in the vicinity of the horizon, and therefore it tests the existence and properties of the latter [9]. It should be noted, however, that other horizonless compact objects that possess light rings also cast shadows [10,11,12,13,14,15,16,17], and therefore the presence of a shadow does not by itself imply that the object is necessarily a BH. Therefore, strong lensing images and shadows offer us an exciting opportunity not only to detect the nature of a compact object, but also to test whether or not the gravitational field around a compact object is described by a rotating or non-rotating geometry. For a recent brief review on shadows see, [18].

Within the framework of Einstein’s General Relativity [19] the most general BH solution is the Kerr–Newman geometry characterized by its mass, angular momentum and electric charge, see e.g., [20]. Since, however, astrophysical BHs are expected to be electrically neutral, the most interesting cases to be considered are either the Schwarzschild [21] or the Kerr geometry [22]. More rotating BH solutions may be generated starting from non-rotating seed spacetimes applying the Newman–Janis algorithm (NJA), described in [23, 24].

Non-rotating solutions have been obtained in non-standard scenarios, such as polytropic BHs [25, 26] or BHs with quintessencial energy [27], to mention just a few. Over the years the shadow of the Schwarzschild geometry was considered in [28, 29], while the shadow cast by the Kerr solution was studied in [30] (see also [31]). Shadows of Kerr BHs with scalar hair and BH shadows in other frameworks have been considered in [32, 33] and [34,35,36,37,38,39,40,41,42,43,44,45,46,47], respectively.

To explore the physics behind the so-called BH shadows, an alternative tool is provided by the well-known NJA. As already mentioned, this method allows one to pass from a static spherically symmetric BH solution to a rotating one. To be more precise, in the present work we will take a variation of the usual NJA, the only difference being the omission of one of the steps of the NJA, namely the complexification of coordinates [27]. Instead of this, we will follow an “alternate” coordinate transformation, which will be explained in the next section.

In the present work we propose to investigate the shadow of the rotating polytropic BH. The non-rotating, static, spherically symmetric geometry was obtained in [25]. The metric tensor is a solution to Einstein’s field equations with negative cosmological constant, and the thermodynamics of the BH precisely matches that of a polytropic gas. One one hand, as stated in [26], from the point of view of a possible astrophysical tests of the non-rotating polytropic solution, the so-called static radius, which defines the equilibrium region between gravitational attraction and dark energy repulsion, would be of importance [48]. On the other hand, in the rotating case, which will be studied in the present work by using the NJA, the computation of the shadow would constitute a valuable tool in order to confirm or refute theoretical predictions regarding the intimate structure of space and time at the strong field regime.

The plan of our work is the following. After this introduction, we briefly summarize how the NJA works in the next section. In Sect. 3 we study the conditions leading to unstable null trajectories for a general parametrization of a rotating BH while Sect. 4 is devoted to the study of the Hawking temperature and the emission rate of a generic \(3+1\) rotating BH. In Sect. 5 we construct the rotating solution starting from a static and spherically symmetric polytropic BH as the seed geometry and we study some features of the solution as for example horizon and static conditions, causality issues, BH shadow, Hawking temperature and emission rate. Finally we conclude our work in the last section. We adopt the mostly negative metric signature \((+,-,-,-)\), and we choose natural units where \(c=1=G\).

2 Newmann–Janis algorithm without complexification

In this section we review the main aspects on the NJA to generate rotating solutions introduced by Azreg-Aïnou [49] where the author performed modifications in the algorithm with the purpose to avoid the complexification process. As it is well known, the complexification of the radial coordinate in the original NJA to bring the final solution in the Boyer–Linquist coordinates is not unique and depends on how it appears in the metric functions used as a seed to generate a rotating solution. Examples of the above mentioned are

$$\begin{aligned} r^{2}&\rightarrow (r+ia\cos \theta )(r-ia\cos \theta )= r^{2}+a^{2}\cos ^{2}\theta \end{aligned}$$
(1)
$$\begin{aligned} \frac{1}{r}&\rightarrow \frac{1}{2}\bigg (\frac{1}{r+ia\cos \theta }+\frac{1}{r-ia\cos \theta }\bigg )=\frac{r}{r^{2}+a^{2}\cos ^{2}\theta }\end{aligned}$$
(2)
$$\begin{aligned} r^{2}&\rightarrow r\sqrt{(r+ia\cos \theta )(r-ia\cos \theta )}=r\sqrt{r^{2} +a^{2}\cos ^{2}\theta } \end{aligned}$$
(3)

It is worth mentioning that the first two complexification listed above are used to generate the Kerr solution starting from the Schwarzschild metric. Even more, if we only use one of this complexifications, the generated rotating solution will not coincides with form of the Kerr BH.

In order to avoid the ambiguities which arise from complexification procedure, the original protocol must be modified as follows.

As usual, the starting point is a static spherically symmetric metric parametrized as

$$\begin{aligned} ds^{2}=G(r)dt^{2}-\frac{dr^{2}}{F(r)}-H(r)(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(4)

The next step consists in introducing the advanced null coordinates \((u,r,\theta ,\phi )\) defined by

$$\begin{aligned} du=dt-dr/\sqrt{FG}, \end{aligned}$$
(5)

from where, the non-zero components of the inverse metric can be written as \(g^{\mu \nu }=l^{\mu }n^{\nu }+l^{\nu }n^{\mu }-m^{\mu }\bar{m}^{\nu }-m^{\nu }\bar{m}^{\mu }\) with

$$\begin{aligned} l^{\mu }= & {} \delta ^{\mu }_{r} ,\end{aligned}$$
(6)
$$\begin{aligned} n^{\mu }= & {} \sqrt{F/G}\delta ^{\mu }_{u}-(F/2)\delta ^{\mu }_{r} ,\end{aligned}$$
(7)
$$\begin{aligned} m^{\mu }= & {} (\delta ^{\mu }_{\theta }+\frac{i}{\sin \theta }\delta ^{\mu }_{\phi })/\sqrt{2H}, \end{aligned}$$
(8)

and \(l_{\mu }l^{\mu }=m_{\mu }m^{\mu }=n_{\mu }n^{\mu }=l_{\mu }m^{\mu }=n_{\mu }m^{\mu }=0\) and \(l_{\mu }n^{\mu }=-m_{\mu }\bar{m}^{\mu }=1\). Now, introducing the complex transformation

$$\begin{aligned}&r\rightarrow r+ia \cos \theta ,\end{aligned}$$
(9)
$$\begin{aligned}&u\rightarrow u-ia \cos \theta , \end{aligned}$$
(10)

and assuming that

$$\begin{aligned}&G(r)\rightarrow A(r,\theta , a) ,\end{aligned}$$
(11)
$$\begin{aligned}&F(r)\rightarrow B(r,\theta , a) ,\end{aligned}$$
(12)
$$\begin{aligned}&H(r)\rightarrow \varPsi (r,\theta , a) , \end{aligned}$$
(13)

we obtain

$$\begin{aligned} l^{\mu }= & {} \delta ^{\mu }_{r} ,\end{aligned}$$
(14)
$$\begin{aligned} n^{\mu }= & {} \sqrt{B/A}\delta ^{\mu }_{u}-(B/2)\delta ^{\mu }_{r} ,\end{aligned}$$
(15)
$$\begin{aligned} m^{\mu }= & {} (\delta ^{\mu }_{\theta }+ia\sin \theta (\delta ^{\mu }_{u}-\delta ^{\mu }_{r})+\frac{i}{\sin \theta }\delta ^{\mu }_{\phi })/\sqrt{2\varPsi }. \end{aligned}$$
(16)

Using the above transformations, the line element, in the so-called rotating Eddington–Finkelstein coordinates reads

$$\begin{aligned} ds^{2}&=A du^{2}+2\sqrt{\frac{A}{B}}du dr +2a \sin ^{2}\theta \bigg (\sqrt{\frac{A}{B}}-A\bigg )du d\phi \nonumber \\&\quad -2a \sin ^{2}\theta \sqrt{\frac{A}{B}}dr d\phi -\varPsi d\theta ^{2}\nonumber \\&\quad -\sin ^{2}\theta \bigg (\varPsi + a^{2}\sin ^{2}\theta \bigg (2\sqrt{\frac{A}{B}}-A\bigg )\bigg )d\phi ^{2}. \end{aligned}$$
(17)

In order to write the metric (17) in the Boyer–Lindquist coordinates, we proceed to perform the global coordinate transformation

$$\begin{aligned} du= & {} dt+\lambda (r)dr ,\end{aligned}$$
(18)
$$\begin{aligned} d\phi= & {} d\phi +\chi (r)dr , \end{aligned}$$
(19)

where \(\lambda \) and \(\chi \) must depend on r only to ensure the integrability of Eq. (18). As it is well known, in the original NJA the next step in the construction of the rotating metric, consists in complexifying r. However, in order to circumvent the complexification, Azreg–Aïnou (see Ref. [49]) proposed an ansatz for the unknown functions involved. Namely, taking

$$\begin{aligned} \lambda= & {} -\frac{(K+a^{2})}{FH+a^{2}} ,\end{aligned}$$
(20)
$$\begin{aligned} \chi= & {} -\frac{a}{FH+a^{2}} , \end{aligned}$$
(21)

where

$$\begin{aligned} K=\sqrt{\frac{F}{G}}H , \end{aligned}$$
(22)

and

$$\begin{aligned} A(r,\theta )= & {} \frac{FH+a^{2}\cos ^{2}\theta }{(K+a^{2}\cos ^{2}\theta )^{2}}\varPsi ,\end{aligned}$$
(23)
$$\begin{aligned} B(r,\theta )= & {} \frac{FH+a^{2}\cos ^{2}\theta }{\varPsi }, \end{aligned}$$
(24)

the metric (17) takes the Kerr-like form

$$\begin{aligned} ds^{2}= & {} \frac{\varPsi }{\rho ^{2}}\bigg (\frac{\varDelta }{\rho ^{2}}(dt-a \sin ^{2}\theta d\phi )^{2}-\frac{\rho ^{2}}{\varDelta }dr^{2}-\rho ^{2}d\theta ^{2}\nonumber \\&-\frac{\sin ^{2}\theta }{\rho ^{2}}(adt-(K+a^{2})d\phi )^{2})\bigg ), \end{aligned}$$
(25)

with

$$\begin{aligned} \rho ^{2}= & {} K+a^{2}\cos ^{2}\theta ,\end{aligned}$$
(26)
$$\begin{aligned} \varDelta= & {} F H+a^{2} \end{aligned}$$
(27)

where \(a=J/M\), with M, J being the mass and the rotation speed, respectively, of the black hole.

At this point some comments are in order. First, note that the function \(\varPsi (r,\theta ,a)\) remains unknown but it must satisfy the following differential equation

$$\begin{aligned} (K+a^{2}y^{2})^{2}(3\varPsi _{,r}\varPsi _{,y^{2}}-2\varPsi \varPsi _{r,y^{2}})=3a^{2}K_{,r}\varPsi ^{2} \end{aligned}$$
(28)

which corresponds to imposing that the Einstein tensor satisfies \(G_{r\theta }=0\). Second, it can be shown (see appendix A in Ref. [49]) that the metric (25) satisfies Einstein’s field equations \(G_{\mu \nu }=8\pi T_{\mu \nu }\) with the source given by

$$\begin{aligned} T^{\mu \nu }=\epsilon e^{\mu }_{t}e^{\nu }_{t}+p_{r}e^{\mu }_{r}e^{\nu }_{r}+p_{\theta }e^{\mu }_{\theta }e^{\nu }_{\theta }+p_{\phi }e^{\mu }_{\phi }e^{\nu }_{\phi }, \end{aligned}$$
(29)

with

$$\begin{aligned} e^{\mu }_{t}= & {} \frac{(r^{2}+a^{2},0,0,a)}{\sqrt{\rho ^{2}\varDelta }} ,\end{aligned}$$
(30)
$$\begin{aligned} e^{\mu }_{r}= & {} \frac{\sqrt{\varDelta }(0,1,0,0)}{\sqrt{\rho ^{2}}} ,\end{aligned}$$
(31)
$$\begin{aligned} e^{\mu }_{\theta }= & {} \frac{(0,0,1,0)}{\sqrt{\rho ^{2}}} ,\end{aligned}$$
(32)
$$\begin{aligned} e^{\mu }_{\phi }= & {} -\frac{(a\sin ^{2}\theta ,0,0,1)}{\sqrt{\rho ^{2}}\sin \theta }. \end{aligned}$$
(33)

Even more, in order to ensure the consistency of Einstein’s field equations, the unknown \(\varPsi \) must satisfy another constraint, namely

$$\begin{aligned}&(K_{,r}^{2}+K(2-K_{,rr})-a^{2}y^{2}(2+K_{,rr}))\varPsi , \nonumber \\&\quad +(K+a^{2}y^{})(4y^{2}\varPsi _{y^{2}}-K_{,r}\varPsi _{,r})=0. \end{aligned}$$
(34)

Finally, the above expressions can be simplified in the particular case \(G=F\) and \(H=r^{2}\). Indeed, in this case it can be shown that one solution of Eq. (28) is given by

$$\begin{aligned} \varPsi =r^{2}+a^{2}\cos ^{2}\theta , \end{aligned}$$
(35)

and the metric (25) takes the form

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2f}{\rho ^{2}}\right) dt^{2}-\frac{\rho ^{2}}{\varDelta }dr^{2} +\frac{4af \sin ^{2}\theta }{\rho ^{2}}dtd\phi \nonumber \\&-\rho ^{2}d\theta ^{2}-\frac{\varSigma \sin ^{2}\theta }{\rho ^{2}}d\phi ^{2}, \end{aligned}$$
(36)

with

$$\begin{aligned} \rho ^{2}= & {} r^{2}+a^{2}\cos ^{2}\theta ,\end{aligned}$$
(37)
$$\begin{aligned} 2f= & {} r^{2}(1-F) ,\end{aligned}$$
(38)
$$\begin{aligned} \varDelta= & {} -2f+a^{2}+ r^2 , \end{aligned}$$
(39)
$$\begin{aligned} \varSigma= & {} (r^{2}+a^{2})^{2}-a^{2} \varDelta \sin ^{2} \theta . \end{aligned}$$
(40)

It is easy to verify that when \(a=0\) we recover the non rotating black hole solution. It is worth mentioning that the modified NJA here developed allows not only to skip the complexification procedure but to introduce more physical arguments and symmetry properties. Of course, the modified protocol and the standar NJA leads to the same solution as occur in the case of the generation the Kerr BH. However, this modified procedure allows to find rotating solutions in situations in which the original NJ algoritm fails.

3 Null geodesics around the rotating black hole

In this section we implement the standard Hamilton–Jacobi formalism to separate the null geodesic equations in the rotating space-time. Our main goal here is to obtain the celestial coordinates parametrized with the radius of the unstable null orbits and to study the shadow of a generic rotating solution.

Let us start with the Hamilton–Jacobi equations [50]

$$\begin{aligned} \frac{\partial S}{\partial \tau }=\frac{1}{2}g^{\mu \nu }\partial _{\mu }S\partial _{\nu }S, \end{aligned}$$
(41)

where \(\tau \) is the proper time and S is the Jacobi action. As usual, if we assume that Eq. (41) has separable solutions, the action takes the form

$$\begin{aligned} S=-Et+\varPhi \phi +S_{r}(r)+S_{\theta }(\theta ), \end{aligned}$$
(42)

where E and \(\varPhi \) are the conserved energy and angular momentum respectively. Now, replacing (42) in (41) we obtain that

$$\begin{aligned} S_{r}= & {} \int \limits ^{r}\frac{\sqrt{R(r)}}{\varDelta }dr ,\end{aligned}$$
(43)
$$\begin{aligned} S_{\theta }= & {} \int \limits ^{\theta }\sqrt{\varTheta (\theta )}d\theta , \end{aligned}$$
(44)

where

$$\begin{aligned} R(r)&=((r^{2}+a^{2})E-a\varPhi )^{2}-\varDelta (Q+(\varPhi -aE)^{2}) ,\end{aligned}$$
(45)
$$\begin{aligned} \varTheta (\theta )&=Q-(\varPhi ^{2}\csc ^{2}\theta -a^{2}E^{2})\cos ^{2}\theta , \end{aligned}$$
(46)

where Q is the so-called Carter constant. As it is well-known, the unstable photon orbits in the rotating space-time must satisfy the constraints \(R=0\) and \(R'=0\) which lead to

$$\begin{aligned} \left( a^2-a \xi +r^2\right) ^2-\left( a^2+r^2 F\right) \left( (a-\xi )^2+\eta \right)&=0 , \end{aligned}$$
(47)
$$\begin{aligned} 4 \left( a^2-a \xi +r^2\right) -\left( (a-\xi )^2+\eta \right) \left( r F'+2 F\right)&=0, \end{aligned}$$
(48)

where \(\xi =\varPhi /E\) and \(\eta =Q/E^{2}\) correspond to the impact parameters. Hence,

$$\begin{aligned} \xi= & {} -\frac{4 \left( a^2+r^2 F\right) }{a(r F'+2 F)}+a+\frac{r^2}{a}, \end{aligned}$$
(49)
$$\begin{aligned} \eta= & {} \frac{r^3 \left( 8 a^2 F'-r \left( r F'-2 F\right) ^2\right) }{a^2 \left( r F'+2 F\right) ^2}. \end{aligned}$$
(50)

It is worth mentioning that, in the above expressions, r corresponds to the radius of the unstable null orbits.

Now, the apparent shape of the shadow is obtained by using the celestial coordinates which are defined as [51]

$$\begin{aligned} \alpha= & {} \lim \limits _{r_{0}\rightarrow \infty }\left( -r_{0}^{2}\sin \theta _{0}\frac{d\phi }{dr}\bigg |_{(r_{0,\theta _{0}})}\right) , \end{aligned}$$
(51)
$$\begin{aligned} \beta= & {} \lim \limits _{r_{0}\rightarrow \infty }\left( r_{0}^{2}\frac{d\theta }{dr}\bigg |_{(r_{0},\theta _{0})}\right) , \end{aligned}$$
(52)

where \((r_{0},\theta _{0})\) correspond to the coordinates of the observer. Finally, the after calculating the limit in the above expressions, the celestial coordinates read

$$\begin{aligned} \alpha= & {} -\frac{\xi }{\sin \theta _{0}} ,\end{aligned}$$
(53)
$$\begin{aligned} \beta= & {} \pm \sqrt{\eta +a^{2}\cos \theta ^{2}_{0}-\xi ^{2}\cot ^{2}\theta _{0}} \ , \end{aligned}$$
(54)

and the shadow corresponds to the parametric curve of \(\alpha \) and \(\beta \) with r as a parameter.

4 Hawking temperature and emission rate of a rotating black hole

In Ref. [52], the author derived the Hawking temperature of a general four-dimensional rotating BH using the null-geodesic tunneling method developed by Parikh and Wilczek [53,54,55]. In this section we shall summarize the main result obtained in [52].

First of all, the radiated particles are considered as s-waves because for an observer at infinity the radiation is spherically symmetric whether the BH is rotating or not. Now, the tunnelling rate of a s-wave from the inside to the outside of the BH is given by

$$\begin{aligned} \varGamma =\varGamma _{0}e^{-2Im\mathcal {I}}, \end{aligned}$$
(55)

where \(\mathcal {I}\) is the action of the tunnelling particle and \(\varGamma _{0}\) the normalization factor. Moreover, as it is well-known, the emission rate satisfies

$$\begin{aligned} \varGamma =\varGamma _{0}e^{-\beta E}, \end{aligned}$$
(56)

where E is the energy of the emitted particle, \(\beta =2\pi /\kappa \) and \(\kappa \) is the surface gravity of the horizon. Now, from (55) and (56) we arrive to

$$\begin{aligned} \kappa =\frac{\pi E}{Im\mathcal {I}}, \end{aligned}$$
(57)

from where the Hawking temperature can be derived form the standard relation

$$\begin{aligned} T_{H}=\frac{\kappa }{2\pi }. \end{aligned}$$
(58)

In order to obtain an expression of the Hawking temperature in terms of the components of the metric we proceed to consider a generic rotating line element of the form

$$\begin{aligned} ds^{2}= & {} -g_{tt}dt^{2}+g_{rr}dr^{2}+g_{\theta \theta }dr^{2}+g_{\theta \theta }d\theta ^{2}\nonumber \\&+g_{\phi \phi }d\phi ^{2}-2g_{t\phi }dtd\phi . \end{aligned}$$
(59)

It can be demonstrated that (see, Sect. 2 of Ref. [52] for details)

$$\begin{aligned} Im\mathcal {I}=\frac{2\pi E}{\sqrt{G'_{tt}(r_{+},\theta _{0})g^{rr'}(r_{+},\theta _{0})}}, \end{aligned}$$
(60)

where the prime stands for derivative respect to the radial coordinate, \(r_{+}\) is the horizon radius and

$$\begin{aligned} G_{tt}=g_{tt}+2g_{t\phi }\varOmega _{+}-g_{\phi \phi }\varOmega _{+}^{2}, \end{aligned}$$
(61)

with \(\varOmega _{+}\) the angular velocity of the event horizon, which is a constant defined by

$$\begin{aligned} \varOmega _{+}=\frac{g_{t\phi }}{g_{\phi \phi }}\bigg |_{r=r_{+}}. \end{aligned}$$
(62)

Finally, replacing (60) in (57) an using (58), the Hawing temperature takes the form

$$\begin{aligned} T_{H}=\frac{\sqrt{G'_{tt}(r_{+},\theta _{0})g^{rr'}(r_{+},\theta _{0})}}{4\pi }, \end{aligned}$$
(63)

which can be written alternatively as

$$\begin{aligned} T_{H}=\frac{1}{4\pi }\lim \limits _{r\rightarrow r_{+}}\frac{\partial _{r}G_{tt}}{\sqrt{G_{tt}g_{rr}}}. \end{aligned}$$
(64)

Please, notice that the Eq. (64) is a generalization of the standard formula for the Hawking temperature. In particular, when the angular velocity is taken to be zero, we recover the well-known formula, namely:

$$\begin{aligned} T_{H}=\frac{1}{4\pi } \lim \limits _{r\rightarrow r_{+}}\frac{\partial _{r}g_{tt}}{\sqrt{g_{tt}g_{rr}}} . \end{aligned}$$
(65)

In what follows, we shall study the emission rate of a rotating BH. It is well-known that in the high energy regime, the cross-section oscillates around a constant value. For black holes endowed with a photon sphere, the limiting constant value coincides with the geometrical cross-section of this photon sphere [56,57,58,59], and it can be expressed as

$$\begin{aligned} \sigma \approx \pi R_s^2. \end{aligned}$$
(66)

Since the shadow measures the optical appearance of a black hole, it is, in fact, equal to the limiting constant value of the high-energy absorption cross-section. Therefore, although it is possible in principle to perform a complete analysis to compute the exact cross-section through the calculation of all the partial waves, as was done for instance in [60] by Kokkotas et al. in the present work we shall adopt the geometrical approximation following previous works, e.g., [57, 61] and [62], which suffices for our purposes. Indeed, our figure for the emission spectrum, Fig. 3, is very similar qualitatively to Fig. 5 of [61] and [62], and to Fig. 8 of [57]. Following these remarks, we conjecture that the black hole shadow corresponds to its high energy absorption cross-section for the observer located at infinityFootnote 1

In Eq. (66), \(R_{s}\) is the radius of the photon sphere defined by (see, [56])

$$\begin{aligned} R_{s}=\frac{(\alpha _{t}-\alpha _{r})^{2}+\beta _{t}^{2}}{2|\alpha _{t}-\alpha _{r}|}. \end{aligned}$$
(67)

In the previous expression, the quantities \(\alpha _{t},\alpha _{r},\beta _{t}\) correspond to particular values of the celestial coordinates [see Eqs. (53) and (54)] In particular, \(\alpha _{r}\) corresponds to the most right value of \(\alpha \) and the pair \((\alpha _{t},\beta _{t})\) stands for coordinates of the top of the shadow [63]. With all the quantities defined in this section, the emission rate [56, 61, 64,65,66,67,68,69] can be calculated by

$$\begin{aligned} \frac{d^{2}E}{d\omega dt } = \frac{\sigma _{lim}}{e^{\omega / T_H}-1} \frac{\omega ^{3}}{2 \pi ^2}, \end{aligned}$$
(68)

where \(\omega \) represents the frequency of photons. In the next section we obtain the Hawing temperature and the emission rate for a rotating polytropic BH.

5 Rotating polytropic black hole solution

In this section we construct the rotating BH solution from a static and spherically symmetric polytropic BH. Then we shall study some of its physical properties as well as the BH shadow and its emission.

As a starting point, we consider the polytropic BH solution obtained in [25]

$$\begin{aligned} ds^{2}=\mathcal {F}dt^{2}-\mathcal {F}^{-1} d r^{2}-r^{2}d \varOmega ^{2}, \end{aligned}$$
(69)

where \(\mathcal {F}=\left( \frac{r^2}{L^2}-\frac{2 M}{r}\right) \), \(L^{2}=-3/\varLambda \), with \(\varLambda \) being the cosmological constant, and \(d \varOmega ^2 = d \theta ^{2} + \sin ^{2} \theta d \phi ^{2}\) is the line element of the unit two-dimensional sphere. It is worth mentioning that \(\mathcal {F}\) in (69) has the same form of the black string solution found in [70, 71] in the context of plane symmetric solutions of Einstein’s equations [20].

Now, using \(F=G=\frac{r^2}{L^2}-\frac{2 M}{r}\), the line element (36) reads

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{r^{2}}{\rho ^2} \left( 1-\frac{r^2}{L^2}+\frac{2 M}{r}\right) \right) dt^2 -\frac{\rho }{\varDelta }dr^2 - \rho ^2 d\theta ^2\nonumber \\&+\frac{2 a r^{2} \sin ^2\theta }{\rho ^2} \left( 1-\frac{r^2}{L^2}+\frac{2 M}{r}\right) dtd\phi \nonumber \\&-\frac{\varSigma \sin ^2\theta }{\rho ^2}d\phi ^2 , \end{aligned}$$
(70)

with

$$\begin{aligned} \varDelta =a^2+r^2 \left( \frac{r^2}{L^2}-\frac{2 M}{r}\right) . \end{aligned}$$
(71)

At this point some comments are in order. First, the horizons are solutions of \(\varDelta (r_{\pm })=0\) which, in this particular case, corresponds to

$$\begin{aligned} a^2+r_{\pm }^2 \left( \frac{r_{\pm }^2}{L^2}-\frac{2 M}{r_{\pm }}\right) =0. \end{aligned}$$
(72)

It is worth mentioning that from the horizon condition we can obtain a bound on the spin parameter, namely a / M. In this case, the allowed values are constrained by

$$\begin{aligned} \frac{a}{M}<\frac{3^{1/2}}{2^{2/3}}\left( \frac{L}{M}\right) ^{1/3}. \end{aligned}$$
(73)

Note that above result differs from the obtained in the case of the Kerr solution, where the constraint is given by \(a/M<1\). Second, the static limit, namely, the surface from where observers can remain static, corresponds to \(g_{tt}=0\). More precisely,

$$\begin{aligned} \frac{a^2 \cos ^2(\theta )+r_{st}^2 \left( \frac{r_{st}^2}{L^2}-\frac{2 M}{r_{st}}\right) }{a^2 \cos ^2(\theta )+r_{st}^2}=0. \end{aligned}$$
(74)

Note that, the event horizon, \(r_{+}\), coincides with the static radius \(r_{st}\) at the poles \(\theta =0\) and \(\theta =\pi \) as in the Kerr solution. Third, note that causality violation and closed time-like curves are possible if \(g_{\phi \phi }>0\). To be more precise, the condition is

$$\begin{aligned} -\frac{\varSigma \sin ^2(\theta )}{\rho ^2}>0, \end{aligned}$$
(75)

from where, given that \(\sin ^{2}(\theta )/\rho ^2\) is positive, the sign of \(\varSigma \) plays a crucial role in the analysis. What is more, the condition to avoid causality violation and closed time-like curves is to impose \(\varSigma >0\). In the particular case of the rotating polytropic BH, the condition on \(\varSigma \) reads

$$\begin{aligned} a^2 \sin ^2(\theta ) \left( -a^2-\frac{r^4}{L^2}+2 M r\right) +\left( a^2+r^2\right) ^2>0, \end{aligned}$$
(76)

It is worth mentioning that, in contrast to Kerr solution, the causality issues can be avoided for particular choices of the parameters. For example, taking \(a=L\), the above condition reduces to

$$\begin{aligned} L^4+2 L^2 M r \sin ^2\theta +2 L^2 r^2+r^4 \left( 1 - \sin ^2\theta \right) >L^4,\nonumber \\ \end{aligned}$$
(77)

which is trivially satisfied given that all the coefficients involved in the left hand side are positive.

Now, we shall focus our attention in the construction of the BH shadow. Replacing the metric function \(F(r)=-\frac{2M}{r}+\frac{r^{2}}{L^{2}}\) in Eqs. (49) and (50), the impact parameters \((\xi ,\eta )\) associated to the unstable null geodesics around the rotating BH are given by

$$\begin{aligned} \xi= & {} \frac{L^2 r \left( 2 a^2-3 M r\right) }{a \left( L^2 M-2 r^3\right) }+a ,\end{aligned}$$
(78)
$$\begin{aligned} \eta= & {} \frac{L^2 r^3 \left( 4 a^2 \left( L^2 M+r^3\right) -9 L^2 M^2 r\right) }{a^2 \left( L^2 M-2 r^3\right) ^2}, \end{aligned}$$
(79)

from where, assuming \(\theta _{0}=\pi /2\), the celestial coordinates read

$$\begin{aligned} \alpha= & {} -a+ \frac{L^2 r \left( 3 M r-2 a^2\right) }{a \left( L^2 M-2 r^3\right) } ,\end{aligned}$$
(80)
$$\begin{aligned} \beta= & {} \pm \sqrt{\frac{L^2 r^3 \left( 4 a^2 \left( L^2 M+r^3\right) -9 L^2 M^2 r\right) }{a^2 \left( L^2 M-2 r^3\right) ^2}}. \end{aligned}$$
(81)

In Fig. 1 the shadow of the rotating BH is shown for different values of a / M and L / M. In the upper row we also have included the shadow of a Kerr black hole (black solid line). It is noticeable that the size of the silhouette of the polytropic solution increases when a / M and L / M increases. Moreover, it is straightforward that the extra degree of freedom, L / M, of the polytropic solution plays an important role in the description of the shadow. Indeed, the only consequences on the Kerr BH given by the increasing of a / M is a slight shift of the shadow to the right. Note also that the shadow of the polytropic BH undergoes a deformation as a / M increases. Indeed, for \(a/M=1.7\) the silhouette of the polytropic BH losses its symmetry and looks like an oval instead of an ellipse. What is more, this value of a / M is near the upper bound given by Eq. (73) which for \(L/M=\{7,7.5,8\}\) is given by

$$\begin{aligned} \frac{3^{1/3}}{2^{2/3}}\left( \frac{L}{M}\right) ^{1/3}\approx 2. \end{aligned}$$
(82)

In this sense, the shadow of the rotating polytropic BH undergoes a deformation when a / M approach its upper limit as occurs in the Kerr BH case.

Fig. 1
figure 1

Silhouette of the shadow cast by the rotating polytropic BH for \(a/M=0.1\) (left upper panel) with \(L/M=3.7\) (blue line) \(L/M=4\) (gray line) \(L/M=4.3\) (orange line) and \(a/M=0.5\) (right upper panel), \(a/M=1.1\) (left down panel) and \(a/M=1.7\) (right down panel) with \(L/M=7\) (blue line), \(L/M=7.5\) (gray line) and \(L/M=8\) (orange line). The black solid line in the plots of the upper row corresponds to the shadow of the Kerr solution

Full size image
Fig. 2
figure 2

Silhouette of the shadow cast by the rotating polytropic BH for \(L/M=7\) with \(a/M=0.1\) (green), \(a/M=0.4\) (blue), \(a/M=0.7\) (grey), \(a/M=0.9\) (orange). The dashed lines corresponds to the polytropic BH while the solid ones indicate the behaviour of a Kerr solution

Full size image

The dependence of the BH sadow on the angular momentum is shown in Fig. 2. It is worth noticing that the behaviour of the shadow coincides with the usually encountered for increasing values of the angular momentum, namely, the shadow undergoes a shifting to the right and deformation of its shape. However, the shifting and deformation corresponding to the Kerr BH is remarkably greater in comparison to the polytropic solution.

The hawking temperature for this rotating BH is given by

$$\begin{aligned} T_{H}=\frac{-a^2 \left( L^2 (M+r_{+})-2 r_{+}^3\right) +L^2 M r_{+}^2+r_{+}^5}{2 \pi L^2 \left( a^2+r_{+}^2\right) ^2}, \end{aligned}$$
(83)

where \(r_{+}\) is the event horizon radius obtained from the condition (72), which reads

$$\begin{aligned} r_{+}&=\frac{\sqrt{-\frac{2 \root 3 \of {6} a^2 L^2}{d(a,M,L)}+\frac{6 L^2 M}{\sqrt{\frac{\root 3 \of {6} a^2 L^2}{d(a,M,L)}+\frac{1}{2} d(a,M,L)}}-d(a,M,L)}}{2^{5/6} \root 3 \of {3}}\nonumber \\&\quad +\frac{\sqrt{\frac{2 \root 3 \of {6} a^2 L^2}{d(a,M,L)}+d(a,M,L)}}{2^{5/6} \root 3 \of {3}}, \end{aligned}$$
(84)

with

$$\begin{aligned} d(a,M,L)=\root 3 \of {\sqrt{3} \sqrt{27 L^8 M^4-16 a^6 L^6}+9 L^4 M^2}.\nonumber \\ \end{aligned}$$
(85)

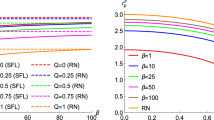
Now, for particular values of the parameters (a, L, M), the Hawking temperature can be computed and \(R_{s}\) can be obtained from Eq. (67). Finally, replacing (83) and (67) in (68), we can study the behaviour of the emission rate as a function of the frequency \(\omega \). The emission rate profile, computed under the previously mentioned geometrical approximation, is depicted in Fig. 3. The solid black line corresponds to the emission of the Kerr black hole which results to be much greater than the emission given by the polytropic solution for the same value of a / M. The detailed behaviour of the emission rate corresponding to the polytropic BH is shown in the zoomed region, where it can be shown that it decreases as L / M growths.

Fig. 3
figure 3

Emission rate of the rotating polytropic BH for \(a/M=0.5\) and \(L/M=7\) (solid blue line), \(L/M=7.5\) (dashed gray line) and \(L/M=8\) (dotted orange line). The solid black line corresponds to the emission of a Kerr BH

Full size image

6 Conclusions

In this work we have reviewed the main aspects related to the Newman–Janis algorithm without complexification, the construction of unstable null orbits and the computation of the Hawking temperature and emission rate for general rotating black holes and we have used these tools to construct a rotating polytropic black hole solution. It is worth mentioning that, to the best of our knowledge, the construction of such a rotating solution has not been considered before. Besides, we have studied some physical properties as the position of the horizons and the static limit which defines the ergosphere as well as the causality condition. We have obtained that, in contrast to the Kerr solution, the causality issues can be avoided for certain choice of the black hole parameters, namely a, M and L. Additionally, we have demonstrated that, in contrast to the Kerr black hole, the bound on the spin parameter a / M can be grater that one because the condition of the appearance of horizons entails that this bound is proportional to L / M. We have also analysed the shadow of the rotating polytropic solution finding that its shape can change while increasing L / M. As a final result, we have studied the emission rate, showing that it decreases for large values of L / M.

Finally, it would be interesting to investigate how the properties of the solution here obtained are modified in light of the so called scale-dependent scenario. In such cases, the coupling constants acquire a dependence on the scale with a free parameter which encodes the quantum features (which is called scale-dependent parameter). Thus, given that the black hole shadows give observational evidence for black holes, we could establish bounds on the aforementioned parameter (see, [72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87]and references therein). We hope to be able to address this issue in a future work.