Bifurcations in Ratra–Peebles quintessence models and their extensions

Abstract

We have used the dynamical system approach in order to investigate the dynamics of cosmological models of the flat Universe with a non-minimally coupled canonical and phantom scalar field and the Ratra–Peebles potential. Applying methods of the bifurcation theory we have found three cases for which the Universe undergoes a generic evolution emerging from either the de Sitter or the static Universe state and finishing at the de Sitter state, without the presence of the initial singularity. This generic class of solutions explains both the inflation and the late-time acceleration of the Universe. In this class inflation is an endogenous effect of dynamics itself.

1 Introduction

The main aim of cosmology is to study the structure and the evolution of the Universe at the large scale. In this context a crucial role plays the notion of a cosmological model obtained from general relativity. If we assume a spacetime with the maximal symmetry of the space-like section of constant time then the evolution of the Universe can be analysed with tools of dynamical systems methods. In principle, there are two advantages of such a treatment of the dynamics. Firstly, evolutionary paths are represented in a geometrical way in the phase space – the space of all states of the system under consideration. Secondly, it gives many possibilities of visualisation how solutions (represented in the phase space by trajectories) depend on the initial conditions. Are they exceptional or typical in the phase space? This question is strictly related to a problem of the stability of solutions.

The right-hand sides of the dynamical system depend not only on the state variables (which form the vector of state) but also on the parameters. These theoretical parameters are present in any effective theory of the Universe. We believe that their interpretation will emerge if we find a more fundamental theory giving us better insight into their nature. Of course, theoretical investigations should be complemented with a statistical estimation of the model parameters from the astronomical and astrophysical data.

From the theoretical point of view, it is important to know how the structure of the phase space changes under variation of model parameters. To such an investigation the bifurcation theory is dedicated. Its methods allow one to obtain some critical (bifurcation) values of the model parameters for which a topological structure of the phase space (modulo homeomorphism preserving the direction of time along trajectories) is not equivalent in the topological sense. If the dynamical system, describing the evolution of the physical system, undergoes the bifurcation at some value of its parameter, one can classify all possible evolutionary paths for all theoretically admissible values of parameters. Hence, in principle, two qualitatively different types can be distinguished. The first case is the model with the parameter at the bifurcation value which describes some state, epoch, of the Universe evolution. In this sense the model is fine-tuned as some exact value of the model parameter is required to describe the Universe dynamics. The second case is a model with other, non-bifurcation values of its parameter. The dynamics of the model is qualitatively indifferent with respect to the choice of the value of the model parameter.

Dynamical systems methods are a powerful tool to analyse the dynamics of physical systems and the application of these methods to analyse the cosmological models is very important as the stability conditions allow one to constrain or even rule out some models [1]. The dynamical analysis can be enriched further with using bifurcation theory methods. Recently, the problem of bifurcations in the FRW cosmology with perfect fluid and the cosmological constant was investigated in the work of Kohli and Haslam [2]. They demonstrated that, as the cosmological constant parameter is varied, expanding de Sitter and contracting de Sitter universes¹ emerge via fold bifurcation. This type of bifurcation occurs in a neighbourhood of the Minkowski spacetime in the phase space. Also, bifurcations play important role in the idea of the Jungle Universe. Following this approach to the study of the dynamics of FRW models filled with different barotropic fluids, the jungle cosmological dynamical system assumes the form of a generalised Lotka–Volterra system where the competitive species are replaced with fluids [3]. The problem of bifurcation is also strictly related to the problem of structural stability which denotes changes of the phase space structure under a small change of right-hand sides of the system [4]. It is also interesting to discover the phenomenon of period-doubling bifurcation in strongly anisotropic Bianchi I quantum cosmology [5].

Basic description of the current acceleration of the Universe is provided by the cosmological constant $\varLambda$, whose natural interpretation is the energy of the quantum vacuum. However, this energy could not be constant during the evolution of the Universe from early epochs to the current state. Hence, in order to include both inflation and late-time acceleration in one model, it is necessary to introduce for example a tool making the vacuum energy dependent on time. Since the action must be covariant, one cannot just use $\varLambda (t)$. The solution is to study a scalar field $\phi$ together with potential $V(\phi )$, driving the evolution of $\phi$. Such a postulate has been suggested for the first time in [6, 7], assuming the power-law form of potential, $V(\phi )\propto \phi ^n$, where $n=\mathrm{const}$ (Ratra–Peebles potential). The scalar field approach for describing the late-time acceleration of the Universe is known under a name of quintessence [8] (for the alternative approach to quintessence see [9]).

On the other hand, the Universe went through an inflation phase in the early epoch of its evolution. Therefore, the cosmological model should solve both the cosmological constant problem (acceleration) and the inflation problem (short exponential expansion).

Instead of considering two scalar fields responsible separately for early inflation and the present acceleration we unify both events using the one scalar field with non-minimal coupling (see also [10,11,12,13,14,15]). Given so many unknown aspects of the universe evolution we undertake the thorough theoretical study of model to determine the possible evolutionary scenarios. Which one, if any, describes the evolution of our Universe is the subject of future empirical and theoretical research in astronomy and cosmology.

Observational constraints on scalar field cosmological models have been recently investigated in [16]. Using Bayesian methods different models of the scalar field cosmology were analysed. The evidence, in the approach where the Bayes information criterion (BIC) was used, indicated that the Ratra–Peebles potential was favoured.

Apart from standard general relativity terms, the additional term $\xi \phi ^2 R$ is considered in the action, describing the coupling between the gravity (represented by the Ricci scalar R) and the scalar field $\phi$, where $\xi$ is the coupling constant. For $\xi =0$ this coupling is minimal, while for $\xi \ne 0$ it is non-minimal. The non-minimal coupling arises from quantum corrections to the scalar field theory [17,18,19] and is necessary for the renormalisation procedure of the scalar field in the curved space [20, 21]. Moreover, a non-minimal coupling of the scalar field to the gravitation is widely used for modelling inflation [22, 23]. The generic cosmological evolution in the scalar field cosmology with non-minimal coupling, which does not possess a singularity, was investigated in [24]. These types of evolution correspond to trajectories starting from an unstable de Sitter state and going to a stable de Sitter state.

We present the analysis of the dynamical system, describing the evolution of the universe with the dark energy as a scalar field with a potential. The application of bifurcation theory methods enables us to fully understand the dynamics of the system, which changes its qualitative properties under the variation of its parameters. The dynamical system under consideration includes both the canonical and the phantom scalar field models, which are distinguished by the value of the discrete parameter $\varepsilon$. We assume the power-law form of the potential, with the exponent n as a model parameter, and the constant non-minimal coupling between the gravity and the scalar field, described by the non-zero parameter $\xi$.

For the purpose of our investigation, we use elements of local bifurcation theory, whose basics we present in Appendix A. We discuss local bifurcations of codimension one, as they appear in models under consideration. For getting more information as regards the bifurcation theory we refer the reader to [25,26,27,28,29].

The first goal of our investigation is to find a model of the universe, the simplest model without the initial singularity, that is in agreement with observational data of acceleration. The problem of non-singular evolution has raised the interests of researchers [24, 30]. The methods applied in the paper enable us to classify all such situations for the model under consideration.

To this aim we explore the range of models that are simple generalization of standard cosmological model LCDM, in order to understand whether the simplest model is highly probable – generic in our terminology. Therefore, we consider the phase space of cosmological models with the scalar field non-minimally coupled to the gravity to understand the full range of cosmological possibilities in epochs that are not necessarily constrained by observations.

In dynamical systems theory, it is well known that the parameter spaces of dynamical systems are stratified into bifurcation regions, with each supporting a different dynamical solution regime. Some can be stable, with different characteristics, such as monotonic stability, periodic damped stability, or multiperiodic damped stability, and some can be unstable, with different characteristics, such as periodic, multiperiodic, or chaotic unstable dynamics. But in general, the existence of bifurcation boundaries is normal and should be expected from most dynamical systems, whether linear or nonlinear. Bifurcation boundaries in parameter space are not the evidence of model defect. While the existence of bifurcation boundaries is well known in economic theory, econometricians using macroeconometric models rarely take bifurcation into consideration, when producing policy simulations. Such models are routinely simulated only at the point estimates of their parameters.

The model under consideration is formulated in terms of dynamical systems with the constant parameter of non-minimal coupling $\xi$. The value of this parameter can be chosen from theoretical reasoning or estimated from empirical data. Because there are different model-dependent estimations of this parameter [22, 31], we are required to consider all values of this parameter indicated by observations. Wang et al. have found recently theoretical constraints on non-minimal coupling from the quantum cosmology [32]. This constraint is $0 \le \xi \le \frac{1}{3}$. It happens that the evolutionary scenarios of the universe (its beginning and future evolution) are different for different values of the parameter $\xi$. In particular, we obtain distinct regimes to reach the de Sitter state, distinct inflation regimes, etc. To obtain the range of parameter values for a given scenario of evolution we can use the bifurcation theory. This theory allows one to stratify the parameter spaces of dynamical systems into bifurcation regions with each supporting a different dynamical solution regime.

There are two advantages of using this theory in physical sciences. First, we identify the range of the model parameter values with possible types of physical evolution of the system. It is especially important given the uncertainty of the model parameter values obtained from empirical studies. Second, we can find the non-generic cases connected with a single value of parameter (the generic cases are for an interval of parameter values). These non-generic cases correspond to parameter values which set up boundaries in the parameter space and separate the regions of generic cases. The non-generic cases can be interesting from the physical point of view, although the problem of fine-tuning arises. However, fine-tuned parameter values are not a defect in cosmology. To be precise, one can distinguish genericity in the sense of typical values of the model parameters, as well as in the sense of initial conditions (the inset is an open set, for example when a critical point is an attractor).

Recently, Mishra and Chakraborty [33] have analysed the model of an interacting f(T) cosmology. They have studied some bifurcation scenarios in which non-hyperbolic critical points are interpreted as phase transitions.

In Sect. 2 we derive the dynamical system from the cosmological equations and the potential function, in terms of dimensionless phase space variables. In Sect. 3 we find equilibria of the dynamical system, analyse their stability properties, designate under which conditions they represent the universe with the equation of state parameter $w_\phi =-1$, find on this basis possible scenarios of the evolution from de Sitter to de Sitter universe (or else from static to de Sitter universe) – which avoids the initial singularity, and which explains the inflation and the late-time acceleration – then we prepare the full analysis of bifurcations of the local stability of equilibria for these scenarios. Section 4 is devoted to the preparation the phase portraits of the system for non-singular scenarios on the Poincaré sphere. Finally, in Sect. 5, we plot the evolution of some physical parameters over the time, within non-singular evolutionary scenarios. In Appendix A a short introduction to bifurcation theory is given.

2 Dynamical equations

The scalar field approach describes the dark energy by the scalar field $\phi$, which is affected by the potential $U(\phi )>0$. The total action is

$$\begin{aligned} S=S_g+S_\phi , \end{aligned}$$

(1)

where

$$\begin{aligned} S_g=\frac{1}{2\kappa ^2}\int {\mathrm {d}}^4x\sqrt{-g}R \end{aligned}$$

(2)

is the Einstein–Hilbert action, and

$$\begin{aligned} S_\phi =-\frac{1}{2}\int {\mathrm {d}}^4x\sqrt{-g}\left[ \varepsilon \nabla ^\alpha \phi \nabla _\alpha \phi +\varepsilon \xi R\phi ^2+2U(\phi )\right] , \end{aligned}$$

(3)

with $\varepsilon =\pm 1$ corresponding to the canonical and the phantom scalar field, respectively, $\kappa ^2=8\pi G$ and $c=\hbar =1$. The parameter $\xi$ is called the coupling parameter; if $\xi \ne 0$, the scalar field is non-minimally coupled to the gravity. Otherwise, the scalar field is minimally coupled to the gravity.

The variation of the total action (1) with respect to the metric tensor $g^{\mu \nu }$ yields the field equation

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=\kappa ^2T_{\mu \nu }^{(\phi )}, \end{aligned}$$

(4)

where the energy–momentum tensor for the non-minimally coupled scalar field is given by

$$\begin{aligned} T_{\mu \nu }^{(\phi )}= & {} \varepsilon \nabla _\mu \phi \nabla _\nu \phi -\frac{1}{2}\varepsilon g_{\mu \nu }\nabla ^\alpha \phi \nabla _\alpha \phi -g_{\mu \nu }\,U(\phi )\nonumber \\&+\,\varepsilon \xi \phi ^2\left( R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R\right) \nonumber \\&+\,\varepsilon \xi \left( g_{\mu \nu }\Box \phi ^2-\nabla _\mu \nabla _\nu \phi ^2\right) , \end{aligned}$$

(5)

while the variation with respect to the scalar field $\phi$ gives the Klein–Gordon equation,

$$\begin{aligned} \Box \phi -\xi R\phi -\varepsilon U_{,\phi }=0, \end{aligned}$$

(6)

where $U_{,\phi }:={\mathrm {d}}U/{\mathrm {d}}\phi$.

We consider the spatially flat ($k=0$) Friedmann–Lemaître–Robertson–Walker (FLRW) metric

$$\begin{aligned} {\mathrm {d}}s^2=-{\mathrm {d}}t^2+a^2(t)\left( {\mathrm {d}}x^2+ {\mathrm {d}}y^2+{\mathrm {d}}z^2\right) , \end{aligned}$$

(7)

where a(t) is the scale factor. This produces the Friedmann equation in the form

$$\begin{aligned} \frac{3}{\kappa ^2}H^2=\rho _\phi =\frac{1}{2}\varepsilon {\dot{\phi }}^2+U+3\varepsilon \xi H^2\phi ^2+6\varepsilon \xi H\phi {\dot{\phi }}, \end{aligned}$$

(8)

the acceleration equation

$$\begin{aligned}&-\frac{1}{\kappa ^2}\big (2\dot{H}+3H^2\big ) =p_\phi = \bigg [\frac{1}{2}\varepsilon {\dot{\phi }}^2(1-4\xi )+6\varepsilon \xi ^2\phi ^2H^2 \nonumber \\&\quad +2\varepsilon \xi H\phi {\dot{\phi }}-U+2\xi \phi U_{,\phi }\bigg ] \bigg / \left[ 1-\varepsilon \kappa ^2\xi \phi ^2(1-6\xi )\right] ,\nonumber \\ \end{aligned}$$

(9)

and the Klein–Gordon equation

$$\begin{aligned} \ddot{\phi }+3H{\dot{\phi }}+6\xi \phi \left( \dot{H}+2H^2\right) +\varepsilon U_{,\phi }=0, \end{aligned}$$

(10)

where $\rho _\phi$ is the energy density and $p_\phi$ is the pressure of the scalar field; the two are connected by the linear barotropic equation of state

$$\begin{aligned} p_\phi =w_\phi \,\rho _\phi , \end{aligned}$$

(11)

where $w_\phi$ is the equation of state parameter.

Let us note that from the Friedmann equation (8) we see that the total energy density of the scalar field consists of the kinetic energy density term $\frac{1}{2}\varepsilon {\dot{\phi }}^2$, the potential energy density term U, and the term related to the gravity–scalar field interaction $3\varepsilon \xi H\phi (H\phi +2{\dot{\phi }})$. Dividing this equation by the critical density $3H^2\kappa ^{-2}$ we obtain an energy conservation equation in the form

$$\begin{aligned} 1=\varOmega _{\phi ,\text {kin}}+\varOmega _{\phi ,\text {pot}}+\varepsilon \kappa ^2\xi \phi \left( \phi +\frac{2{\dot{\phi }}}{H}\right) , \end{aligned}$$

(12)

where

$$\begin{aligned} \varOmega _{\phi ,\text {kin}}:=\frac{\varepsilon \kappa ^2{\dot{\phi }}^2}{6H^2} \end{aligned}$$

(13)

is the scalar field kinetic energy parameter and

$$\begin{aligned} \varOmega _{\phi ,\text {pot}}:=\frac{\kappa ^2U}{3H^2} \end{aligned}$$

(14)

is the scalar field potential energy parameter.

We assume the inverse power-law form of the potential function (known as the Ratra–Peebles potential [6, 7])

$$\begin{aligned} U(\phi )=\frac{M^{n+4}}{\phi ^n}, \end{aligned}$$

(15)

where n is a dimensionless parameter, and $M>0$ is a dimensional constant. The pair of parameter values $\varepsilon =+1$ and $\xi =0$, together with the usage of the power-law form of the potential, refer to the standard Ratra–Peebles quintessence model, while other values constitute extensions of this model.

Let us introduce the following dimensionless real phase space variables:

$$\begin{aligned} u=\frac{{\dot{\phi }}}{H\phi },\quad v=\frac{\sqrt{6}}{\kappa }\frac{1}{\phi }. \end{aligned}$$

(16)

Applying the new variables, we obtain the following condition from the Friedmann equation (8):

$$\begin{aligned} \frac{M^{n+4}}{H^2\phi ^{n+2}}=\frac{1}{2}v^2-\frac{1}{2}\varepsilon u^2-3\varepsilon \xi (1+2u), \end{aligned}$$

(17)

which, in terms of the energy parameters (13)–(14), reads

$$\begin{aligned} 1=\varOmega _{\phi ,\text {kin}}+\varOmega _{\phi ,\text {pot}}+6\varepsilon \xi \frac{1+2u}{v^2}, \end{aligned}$$

(18)

where

$$\begin{aligned} \varOmega _{\phi ,\text {kin}}=\varepsilon \frac{u^2}{v^2} \quad \text{ and }\quad \varOmega _{\phi ,\text {pot}}=\frac{\kappa ^2M^{n+4}}{3H^2\phi ^n}. \end{aligned}$$

(19)

The acceleration equation (9) yields

$$\begin{aligned} \frac{\dot{H}}{H^2}=-\frac{3}{2}(1+w_\phi ), \end{aligned}$$

(20)

where the equation of state parameter, in terms of the new variables, is

$$\begin{aligned} w_\phi= & {} \frac{2}{3}\Big [u^2\left[ 1-\xi (2-n)\right] +4\xi u(2+3\xi n)-\frac{1}{2}\varepsilon v^2(1+2\xi n) \nonumber \\&+\,3\xi \left[ 1+2\xi (1+n)\right] \Big ] \Big / \left[ \frac{1}{3}\varepsilon v^2-2\xi (1-6\xi )\right] . \end{aligned}$$

(21)

The left-hand side of Eq. (20) is equal to $-q-1$, where $q=-\ddot{a}a\dot{a}^{-2}$ is the deceleration parameter; $q<0$ for accelerated expansion (or decelerated contraction) of the universe, and $q>0$ for decelerated expansion (or accelerated contraction) of the universe. Hence, we obtain

$$\begin{aligned} q=\frac{1}{2}(3w_\phi +1), \end{aligned}$$

(22)

which implies that for $w_\phi <-\frac{1}{3}$ the expansion of the universe is accelerated (contraction is decelerated), whereas for $w_\phi >-\frac{1}{3}$ the expansion is decelerated (contraction is accelerated).

Finally, using Eqs. (10), (17) and (20), we obtain the dynamical system, expressed by dimensionless variables (16),

$$\begin{aligned} u'= & {} -\frac{1}{2}u^2(2+n)-\frac{3}{2}u(1+4\xi n)+\frac{1}{2}\varepsilon nv^2 \nonumber \\&-3\xi (1+n) + \frac{6\xi +u}{\frac{1}{3}\varepsilon v^2-2\xi (1-6\xi )} \nonumber \\&\cdot \big \{ u^2 [1-\xi (2-n)] +4\xi u(2+3\xi n) \nonumber \\&-\frac{1}{2}\varepsilon v^2(1+2\xi n)+3\xi [1+2\xi (1+n)] \big \},\nonumber \\ v'= & {} -uv, \end{aligned}$$

(23)

where $f'=\frac{{\mathrm {d}}f}{{\mathrm {d}}\ln a}=H^{-1}\dot{f}$.

Formulae for $w_\phi$ (21) and for $u'$ in the system (23) diverge to infinity as

$$\begin{aligned} v^2\rightarrow 6\varepsilon \xi (1-6\xi ). \end{aligned}$$

(24)

In order to analyse the dynamics at this limit, we can multiply the right-hand sides of the system (23) by the non-negative term $\left[ \frac{1}{3}\varepsilon v^2-2\xi (1-6\xi )\right] ^2$. This operation will produce a dynamical system which will be determined at the limit (24) and will have the same dynamical properties in other points as the previous system² Thus, we obtain the system

$$\begin{aligned} u'= & {} \bigg [ -\frac{1}{2}u^2(2+n)-\frac{3}{2}u(1+4\xi n)+\frac{1}{2}\varepsilon nv^2 \nonumber \\&-3\xi (1+n) \bigg ] \bigg [\frac{1}{3}\varepsilon v^2-2\xi (1-6\xi )\bigg ]^2 \nonumber \\&+(6\xi +u)\left[ \frac{1}{3}\varepsilon v^2-2\xi (1-6\xi )\right] \nonumber \\&\cdot \bigg [u^2 [1-\xi (2-n)]+4\xi u(2+3\xi n) \nonumber \\&-\frac{1}{2}\varepsilon v^2(1+2\xi n)+3\xi [1+2\xi (1+n)]\bigg ], \nonumber \\ v'= & {} -uv\bigg [\frac{1}{3}\varepsilon v^2-2\xi (1-6\xi )\bigg ]^2, \end{aligned}$$

(25)

which is determined also at the limit (24).

From the initial assumptions we have $U(\phi )>0$, equivalent to $\phi >0$, which implies $v>0$. It also implies that the left-hand side of Eq. (17) is greater than zero. It yields the following condition of physicality on variables (u, v):

$$\begin{aligned} \frac{1}{2}v^2-\frac{1}{2}\varepsilon u^2-3\varepsilon \xi (1+2u)>0. \end{aligned}$$

(26)

3 Equilibria, non-singular evolutionary scenarios and bifurcation diagrams of local stability

In this section, we will find the equilibria of the dynamical system derived above, inspect stability of these points and conditions for representing the $w_\phi =-1$ state by them, and we distinguish, on this basis, evolutionary scenarios without singularity, and – finally – prepare bifurcation diagrams for these scenarios.

Table 1 Finite equilibria of the system (25) with existence conditions

Table 2 Eigenvalues, stability type, equation of state parameter $w_\phi$ value and the condition for the $w_\phi =-1$ for equilibria of system (25)

3.1 Equilibria and their stability properties

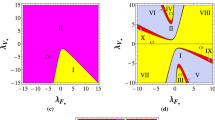
As the phase space (u, v) is infinite, we will investigate firstly the finite region, and then go to the description at infinity. Finite equilibria of the system (25) together with existence conditions (resulting from the fact that $u,v\in {\mathbb {R}}$) are shown in Table 1, while eigenvalues and values of the equation of state parameter $w_\phi$ for the equilibria are summarised in Table 2. Figures 1, 2, 3, 4 and 5 present, in turn, bifurcation diagrams of the local stability of equilibrium points A, B, C and E, whose stability properties depend on values of parameters $\xi$, n and $\varepsilon$. Moreover, in these diagrams, there are formulae for the one-dimensional boundaries separating areas of the local topological equivalence.

We notice from Table 1 that, apart from the equilibrium line F, finite equilibrium points are located only on the axes of phase space. If for a finite point $v=0$ but $u\ne 0$, then $\varepsilon \varOmega _{\phi ,\text {kin}}\rightarrow +\infty$. According to Eq. (18), provided the condition (26) is satisfied, we have $\varOmega _{\phi ,\text {pot}}\rightarrow +\infty$. On the other hand, when $u=0$ and $v\ne 0$, then $\varOmega _{\phi ,\text {kin}}=0$ and $\varOmega _{\phi ,\text {pot}}=1-6\varepsilon \xi v^{-2}$, which is greater than zero when the condition (26) is satisfied.

The region (26) has its boundaries at $v=0$ always at points A and B. The boundary of this region is the limit of the physicality of the system. If $v\ne 0$ we have $H^2\rightarrow +\infty$ and $|{\dot{\phi }}|\rightarrow +\infty$ on this boundary. If the line F exists, the boundary has its extremum on this line at the point $u=-6\xi$. We denote this point as K.

3.2 Non-singular evolutionary scenarios

In this paper, we will be investigating evolutionary scenarios of the universe, starting and finishing at the de Sitter state. The de Sitter universe is the solution to the Einstein field equations which assumes the dynamics of the universe to be dominated by the cosmological constant $\varLambda$, so the matter component (both baryonic and dark) is neglected. In this model, the pressure p and the energy density $\rho$ satisfy

$$\begin{aligned} p_{\mathrm{d}S}=-\rho _{\mathrm{d}S}=-\frac{\varLambda _\text {emergent}}{\kappa ^2}=\mathrm {const}, \end{aligned}$$

(27)

where $\varLambda _\text {emergent}$ is mimicking the parameter $\varLambda$; so the equation of state parameter w is

$$\begin{aligned} w_{\mathrm{d}S}=-1. \end{aligned}$$

(28)

For the spatially flat universe ($k=0$) the scale factor a, within the de Sitter model, depends on time as

$$\begin{aligned} a(t)\propto e^{\pm \sqrt{\frac{\varLambda _\text {emergent}}{3}}{t}}. \end{aligned}$$

(29)

Solutions with the ‘−’ sign in the exponent are frequently called anti-de Sitter states in contrast to the solutions with the ‘$+$’ sign, called de Sitter states. The Hubble function H in this case is equal

$$\begin{aligned} H_{\mathrm{d}S}=\pm \sqrt{\frac{\varLambda _\text {emergent}}{3}}=\mathrm {const} \end{aligned}$$

(30)

where $H_{\mathrm{d}S}$ is a value of H at the critical point representing the de Sitter state.

The emergent de Sitter cosmology enables one to solve cosmological puzzles [34]. It was found that the de Sitter cosmology can emerge from the decaying anti-de Sitter space [35].

By looking at the conditions for the presence of the universe with $w_\phi =-1$ in Table 2 we can distinguish, using bifurcation diagrams (Figs. 1, 2, 3, 4, 5), the sets of parameters for which evolution from the initial (stable in the past) de Sitter to the final (stable) de Sitter state is possible. We can divide these sets into two groups: representing generic evolution and non-generic evolution from an initial state to a final state both having $w_\phi =-1$. The generic evolution takes place, when there exist a family of solutions favouring given conditions, while the non-generic evolution takes place if only one particular solution corresponds to the conditions. For example, when a family of orbits emerges from a stable equilibrium in the past (like an unstable node or a focus) representing the de Sitter state (or in general, the $w_\phi =-1$ state), and then finishes in a stable point also representing the de Sitter state, it is generic evolution. On the other hand, if for example a starting or a final $w_\phi =-1$ point is a saddle, then there exists only one trajectory – a separatrix – which is able to reach this saddle (in the past or in the future, respectively), so the evolution is non-generic. The sets of parameters for which the evolution from the $w_\phi =-1$ state to the $w_\phi =-1$ state occurs are shown in Table 3.

Fig. 1

Bifurcation diagram of the local stability of point A for $\varepsilon =\pm \,1$

Fig. 2

Bifurcation diagram of the local stability of point B for $\varepsilon =\pm \,1$

Fig. 3

Bifurcation diagram of the local stability of point C for $\varepsilon =\pm \,1$

Fig. 4

Bifurcation diagram of the local stability of point E for $\varepsilon =+\,1$

Fig. 5

Bifurcation diagram of the local stability of point E for $\varepsilon =-\,1$

Table 3 Sets of parameters for which the universe undergoes the evolution starting from the state with $w_\phi =-1$ and finishing in the state with $w_\phi =-1$ (non-singular evolution)

3.3 Bifurcation diagrams for non-singular evolutionary scenarios

We will analyse the generic evolutionary scenarios found in this work since they are more interesting than the non-generic ones. Let us start with a discussion of bifurcations for these scenarios. Figures 6, 7 and 8 present bifurcation diagrams of the local stability of equilibria on the $v=0$ nullcline and $u=0$ line under variation of the parameter n for fixed $\xi =\frac{3}{16}$ and $\varepsilon =\pm 1$. This corresponds to generic evolutionary scenarios (a) and (b) in Table 3.

In Fig. 6 we see the occurrence of two transcritical bifurcations on the $v=0$ nullcline. The first takes place for $n=-6$ (it belongs to the general bifurcation condition $n=-4-\sqrt{6\xi (6\xi -1)}/\xi$) and concerns points B and C. For $n<-6$ the point B is a saddle and the point C is an unstable node, while after the ‘collision’ they exchange their stability properties. The second transcritical bifurcation happens for $n=-2$ (belongs to the general condition $n=-4+\sqrt{6\xi (6\xi -1)}/\xi$) and concerns points A and C. The situation looks similar to the previous case: for $n<-2$ the point A is a saddle and the point C is an unstable node, and these properties are exchanged between points after the bifurcation.

Fig. 6

Bifurcation diagram of the local stability of equilibrium points of system (25) on the $v=0$ nullcline under variation of the parameter n for fixed $\xi =\frac{3}{16}$ and $\varepsilon =\pm 1$. Black dots in this diagram denote a non-hyperbolic equilibrium point, while red dots denote an unstable proper node. Grey arrows show the direction of the flow on the nullcline

Fig. 7

Bifurcation diagram of the local stability of equilibrium points of system (25) on the $u=0$ line under variation of the parameter n for fixed $\xi =\frac{3}{16}$ and $\varepsilon =+1$. The black dot in this diagram denotes a non-hyperbolic equilibrium point, while the purple dot denotes a stable degenerate node. Grey arrows show the direction of the flow on the $u=0$ line – arrows directed to the right denote the flow following towards increasing values of u, whereas arrows directed to the left denote the flow following towards decreasing values of u. The flow on the $u=0$ line is perpendicular to this line since on it $v'=0$ in system (25)

Fig. 8

Bifurcation diagram of the local stability of equilibrium points of system (25) on the $u=0$ line under variation of the parameter n for fixed $\xi =\frac{3}{16}$ and $\varepsilon =-1$. Black dots in this diagram denote a non-hyperbolic equilibrium point. Grey arrows show the direction of the flow on the $u=0$ line – arrows directed to the right denote the flow following towards increasing values of u, whereas arrows directed to the left denote the flow following towards decreasing values of u. The flow on the $u=0$ line is perpendicular to this line since on it $v'=0$ in system (25)

The local bifurcation diagram on the $u=0$ line for $\varepsilon =+1$ is shown in Fig. 7. The only transition visible in this diagram refers to the point E which undergoes a change from a stable focus via a stable degenerate node (the purple dot) for $n=-4\frac{4}{7}$ (in general $n=(6-64\xi )/(7\xi )$) into a stable node. In fact, this transition is not a bifurcation, because – despite the fact that flows near nodes and foci are neither orbitally nor smoothly equivalent – they are topologically equivalent, which has been shown in Example 2.1 of [27].

Figure 8 presents the local bifurcation diagram on the $u=0$ line for $\varepsilon =-1$. For $n=-3\frac{5}{9}$ (in general $n=-2/(3\xi )$) another bifurcation appears when the point E coalesces with the neutral line F just to separate again as n exceeds this bifurcation value. Point E passes at this value of n from a saddle into a stable focus, while the line F still remains neutral, but the flow in its neighbourhood near $u=0$ reverses its direction – before the bifurcation the flow follows towards decreasing values of u below the line F and increasing values of u above the line F, while after the bifurcation the flow, below and above the line F, reverses.

Furthermore, combining Figs. 6, 7 and 8, we can notice that a bifurcation takes place also for $n=-4$ in the point $(u,v)=(0,0)$. For $\varepsilon =+1$, as n approaches $-4$ from below, the saddle C on the negative part of the $u=0$ nullcline and the stable node E on the positive part of the $v=0$ axis are approaching the (0, 0) point. They both reach that point for $n=-4$, and then, when n exceeds that value, the point C becomes a stable node (it intercepts the stability from the point E) and is moving towards increasing values of u, while the point E disappears (its coordinates become complex). It is so to speak a combination of the saddle-node and the transcritical bifurcation: the point E behaves as in the saddle-node bifurcation, while the point C behaves as in the transcritical bifurcation. In turn, for $\varepsilon =-1$ the bifurcation is reversed. For $n<-4$ there is only the saddle C on the negative part of $v=0$ axis, which reaches the point (0, 0) for $n=-4$, and when n exceeds $-4$, it appears the saddle E, moving towards increasing values of v, while the point C becomes a stable node (gives its instability to the point E) moving towards increasing values of u. In that case and in the previous case, the point E behaves as in the saddle-node bifurcation and the point C behaves as in the transcritical bifurcation. In general, these transitions take place for all values of $\xi$ different from 0 and $\frac{1}{6}$.

Let us remark that within the range of parameters of the two generic evolutionary scenarios (a) and (b) there does not occur any bifurcation, therefore it is sufficient to prepare only one phase portrait for each scenario and this portrait is representative for the whole set of parameters of a given scenario. Also for the non-generic scenarios (e) and (f), we see no bifurcation.

Bifurcation diagrams on both u and v axes under variation of the parameter $\xi$ are presented in Figs. 9 and 10. The choice of the values of fixed parameters, i.e., $n=-2$ and $\varepsilon =-1$, corresponds to generic evolutionary scenario (c).

Fig. 9

Bifurcation diagram of the local stability of equilibrium points of system (25) on the $v=0$ nullcline under variation of the parameter $\xi$ for fixed $n=-2$ and $\varepsilon =\pm 1$. Black dots in this diagram denote a non-hyperbolic equilibrium point, while red dots denote an unstable proper node. Grey arrows show the direction of the flow on the nullcline

Fig. 10

Bifurcation diagram of the local stability of equilibrium points of system (25) on the $u=0$ line under variation of the parameter $\xi$ for fixed $n=-2$ and $\varepsilon =-1$. The black dot in this diagram denotes a non-hyperbolic equilibrium point, while the purple dot denotes a stable degenerate node. Grey arrows show the direction of the flow on the $u=0$ line – arrows directed to the right denote the flow following towards increasing values of u, whereas arrows directed to the left denote the flow following towards decreasing values of u. The flow on the $u=0$ line is perpendicular to this line since on it $v'=0$ in system (25)

In Fig. 9 we see the occurrence of two pitchfork bifurcations on the $v=0$ nullcline under variation of $\xi$. The first, taking place for $\xi =0$, is subcritical – the stable point C is surrounded by unstable points A and B for $\xi <0$, and at the critical value of $\xi$ they coalesce into one unstable (saddle) point C (this bifurcation emerges in general at $\xi =0$ and $n>-4$). The second pitchfork bifurcation at $\xi =\frac{1}{6}$ appears when all points are unstable – two unstable nodes A and B, surrounding the saddle C, emerge, as $\xi$ exceeds this critical value, from the single saddle C (in general, this bifurcation takes place for $\xi =\frac{1}{6}$ and $n>-4$). Finally, for $\xi =\frac{3}{16}$ (it belongs to the general bifurcation case $n=-4+\sqrt{6\xi (6\xi -1)}/\xi$), there occurs the transcritical bifurcation between points A and C from which, before the bifurcation, the first is an unstable node and the latter is a saddle. Bifurcation at this point can be seen also in Fig. 6; however, there is the parameter n which was varied.

On the line $u=0$, Fig. 10 shows other bifurcations under variation of $\xi$ for fixed $n=-2$ and $\varepsilon =-1$. The saddle D and the neutral line F, which exist for $\xi <0$, coalesce in $\xi =0$. Above this value, D and F disappear and there appears the stable point E; the line F emerges again at $\xi =\frac{1}{6}$. For $\xi =\frac{1}{3}$ the stable point E and the neutral line F coalesce and, as $\xi$ exceeds the bifurcation value, the point E becomes a saddle, while the line F remains neutral, but the flow below and above it reverses.

Combining Figs. 9 and 10 we see that for $\xi =0$, $n=-2$ and $\varepsilon =-1$ all equilibrium points A–F coalesce in $(u,v)=(0,0)$. This coalescence happens for any value of n and $\varepsilon =\pm 1$ at $\xi =0$ and refers to the case of the minimally coupled scalar field. Again, within the range of parameters of the generic scenario (c), we see no bifurcations, which means that one phase portrait will be representative for that case. In turn, the non-generic scenario (g) would require two portraits to be fully represented – the first for $0\le \xi <\frac{1}{6}$ and the second for $\frac{1}{6}\le \xi <\frac{3}{16}$, while in the case of the scenario (h) one portrait would be sufficient.

3.4 Evolution of the field in de Sitter states

Substituting $\dot{H}=0$ to Eq. (9) and using (8), we obtain the condition on $\phi$ for the existence of the de Sitter state,

$$\begin{aligned} \varepsilon {\dot{\phi }}^2(1-2\xi )+2\xi \phi \left( 12\varepsilon \xi H_0^2\phi +4\varepsilon H_0{\dot{\phi }}+U_{,\phi }\right) =0. \end{aligned}$$

(31)

This gives the general formula for the evolution of the field $\phi$ in the de Sitter states,

$$\begin{aligned} {\dot{\phi }}=-\frac{3}{2}H_0\phi -\frac{\varepsilon U_{,\phi }}{4H_0},\quad \text{ for } \xi =\frac{1}{2}\quad \text{ and } H_0\ne 0, \end{aligned}$$

(32)

and

$$\begin{aligned} {\dot{\phi }}= & {} \frac{4\xi H_0\phi \pm \sqrt{2\xi \phi \left[ 4\xi H_0^2\phi (6\xi -1)+\varepsilon U_{,\phi }(2\xi -1)\right] }}{2\xi -1},\nonumber \\&\text{ for } \xi \ne \frac{1}{2}, \end{aligned}$$

(33)

where $H_0=\mathrm{const}$ and $U_{,\phi }=-\frac{nM^{n+4}}{\phi ^{n+1}}$ for the potential (15).

Depending on the rate of change of the field ${\dot{\phi }}$ we can classify inflation into slow-roll or rapid-roll type. The slow-roll approximation assumes that scalar field changes slowly enough towards its equilibrium value that the timescale of this motion is much larger than the cosmic timescale $H^{-1}$ [36, 37]. In order to provide this type of inflation, the following conditions on the potential, expressed in terms of the slow-roll parameters $\epsilon$, $\eta$, have to be satisfied. In the case of the minimal coupling

$$\begin{aligned} \epsilon \ll 1,\quad \text{ where } \epsilon :=\frac{1}{2\kappa ^2}\left( \frac{U_{,\phi }}{U}\right) ^2 \end{aligned}$$

(34)

and

$$\begin{aligned} |\eta |\ll 1,\quad \text{ where } \eta :=\frac{1}{\kappa ^2}\frac{U_{,\phi \phi }}{U}, \end{aligned}$$

(35)

with $U_{,\phi \phi }:={\mathrm {d}}^2U/{\mathrm {d}}\phi ^2$. Chiba and Yamaguchi proposed in [38] the extended slow-roll parameters $\epsilon$, $\eta$, $\delta$ which can be used to articulate the conditions for slow-rolling of the scalar field non-minimally coupled to the gravity

$$\begin{aligned} \epsilon&\ll 1&,\quad \text{ where } \epsilon :=\frac{\varOmega }{2\kappa ^2}\left( \frac{U^\text {eff}_{,\phi }}{U}\right) ^2, \end{aligned}$$

(36)

$$\begin{aligned} |\eta |&\ll 1&,\quad \text{ where } \eta :=\frac{\varOmega U^\text {eff}_{,\phi \phi }}{\kappa ^2U}, \end{aligned}$$

(37)

$$\begin{aligned} |\delta |&\ll 1&,\quad \text{ where } \delta :=\frac{\varOmega _{,\phi }U^{\text {eff}}_{,\phi }}{\kappa ^2U}, \end{aligned}$$

(38)

with $\varOmega :=1-\varepsilon \kappa ^2\xi \phi ^2$ and $U^\text {eff}_{,\phi }:=\varOmega ^2(U/\varOmega ^2)_{,\phi }$ being the effective potential. After substitution, we obtain

$$\begin{aligned} \epsilon= & {} \frac{[(n+4)\varepsilon \kappa ^2\xi \phi ^2-n]^2}{2\kappa ^2\phi ^2(1-\varepsilon \kappa ^2\xi \phi ^2)}, \end{aligned}$$

(39)

$$\begin{aligned} \eta= & {} \frac{n(n+1)}{\kappa ^2\phi ^2}-\varepsilon \xi \left[ 4+n(n+5)+\frac{8}{\varepsilon \kappa ^2\xi \phi ^2-1}\right] , \end{aligned}$$

(40)

$$\begin{aligned} \delta= & {} 2\varepsilon \xi \left( 4+n+\frac{4}{\varepsilon \kappa ^2\xi \phi ^2-1}\right) . \end{aligned}$$

(41)

For the condition $|\xi |\kappa ^2\phi ^2\gg 1$ we obtain the slow-rolling if $\varepsilon \xi <0$ and the parameters (39)–(41) have the form

$$\begin{aligned} \epsilon= & {} -\frac{1}{2}\varepsilon \xi (n+4)^2, \end{aligned}$$

(42)

$$\begin{aligned} \eta= & {} -\varepsilon \xi (n+4)(n+1), \end{aligned}$$

(43)

$$\begin{aligned} \delta= & {} 2\varepsilon \xi (n+4), \end{aligned}$$

(44)

which shows that slow-rolling emerges for $\xi =0$ with any n or for any $\xi$ with $n=-4$. Note that there is no dependence on $\phi$ in (42)–(44).

However, slow-roll is not the only possible type of inflation. Provided the inflation occurs without the slow-rolling of the field we have the rapid-roll inflation [38,39,40]. Within the rapid-roll type of inflation the motion of the scalar field is no more negligible compared to the potential term and we have $|{\dot{\phi }}|\sim H\phi$. For extended rapid-roll parameters, applicable to non-minimal coupling, see [38].

Let us inspect the type of the inflation at equilibria corresponding to initial points of the non-singular evolutionary scenarios, where we expect inflation to occur. The choice of the variables in this work, i.e. $u={\dot{\phi }}/(H\phi )$ and $v\propto 1/\phi$, is convenient for the purpose of investigating the rate of growth of the field ${\dot{\phi }}$. For all non-singular scenarios (a)–(c) inflation takes place at points either A or C, for which it is $v=0$, corresponding to $\phi \rightarrow +\infty$. For scenarios (a) and (b) the evolution starts from an initial de Sitter state at point A, which u coordinate is equal to $u_A=-3/2$, so that ${\dot{\phi }}=-\frac{3}{2}H\phi$, implying $\phi \propto a^{-3/2}$ for this inflation. In the case of scenario (c) inflation takes place at the point C, whose u coordinate depends on the value of $\xi$ and is always negative, lying in the range $-\infty<u_C(\xi )=\frac{2\xi }{4\xi -1}<-\frac{3}{2}$, as one can see in Fig. 9. Thus, we have ${\dot{\phi }}=\frac{2\xi }{4\xi -1}H\phi$ and $\phi \propto a^{2\xi /(4\xi -1)}$. This shows that the basic condition of the slow-rolling of the field, ${\dot{\phi }}^2\ll U$, is violated; strictly speaking, the conditions (36)–(38) are not satisfied. Thus, the inflation, occurring in non-singular scenarios (a)–(c), is of the fast-roll type.

Fig. 11

The phase portrait of system (25) on the Poincaré sphere for the generic scenario (a). Values of parameters are $\xi =\frac{3}{16}$, $n=2$, $\varepsilon =+1$. Purple arrows denote orbits corresponding to the evolution from the $w_\phi =-1$ equilibrium A to the $w_\phi =-1$ equilibrium E, while the blue arrows denote other orbits. Light grey contours correspond to values of the equation of state parameter $w_\phi$. The shaded region is non-physical

On the other hand, note that if a singularity exists, then near a singularity the effects of the potential of the scalar field V can be negligible [41, 42].

4 Phase portraits of the system

Now, we are ready for a discussion of the phase portraits of the system for generic non-singular evolutionary scenarios. Figures 11, 12 and 13 present phase portraits of the system (25) for the evolutionary scenarios (a)–(c). Each of them is representative for its case, as we noticed during the discussion of bifurcation diagrams of equilibria. Portraits have been drawn on the (U, V) plane, which is an orthographic projection of the northern hemisphere $W>0$ and the equator $W=0$ of the unit Poincaré sphere,

$$\begin{aligned} S^2 = \left\{ (U,V,W) \in {\mathbb {R}}^3\ |\ U^2+V^2+W^2 = 1\right\} , \end{aligned}$$

(45)

on which the (u, v) infinite plane had been projected. According to the definition of the Poincaré sphere, the coordinates U, V are expressed by u, v as follows [28]:

$$\begin{aligned} U=\frac{u}{\sqrt{1+u^2+v^2}},\quad V=\frac{v}{\sqrt{1+u^2+v^2}}, \end{aligned}$$

(46)

and the $U^2+V^2=1$ circle corresponds to infinity of the (u, v) plane, i.e., points for which $\sqrt{u^2+v^2}\rightarrow +\infty$.

From an analysis of the flow of the system (25) on the (U, V) plane we obtain the information of the equilibria of the system at infinity; it is summarised in Table 4.

On the $V=0$ line we have, according to Eqs. (18) and (19), the kinetic energy parameter $\varepsilon \varOmega _{\phi ,\text {kin}}\rightarrow +\infty$. Moreover, at the point G, the density of energy related to the gravity–scalar field coupling has the limit $6\varepsilon \xi (1+2u)v^{-2}\rightarrow -\infty \cdot \mathop {\mathrm {sign}}(\varepsilon \xi )$, while at the point H this limit is $+\infty \cdot \mathop {\mathrm {sign}}(\varepsilon \xi )$. On the $V=\sqrt{1-U^2}$ semicircle, if $V\ne 0$, the kinetic energy has a finite value $\varOmega _{\phi ,\text {kin}}=\varepsilon U^2V^{-2}$, and the coupling part of the energy is equal to zero; thus if $\varOmega _{\phi ,\text {kin}}>1$, the point at infinity is non-physical, according to the condition (26). Hence, at points I, J we have $\varOmega _{\phi ,\text {kin}}=\varepsilon$ and $\varOmega _{\phi ,\text {pot}}=1-\varepsilon$.

Fig. 12

The phase portrait of system (25) on the Poincaré sphere for the generic scenario (b). Values of parameters are $\xi =\frac{3}{16}$, $n=-1$, $\varepsilon =-1$. Purple arrows denote orbits corresponding to the evolution from the $w_\phi =-1$ equilibrium A to the $w_\phi =-1$ equilibrium E, while the blue arrows denote other orbits. Light grey contours correspond to values of the equation of state parameter $w_\phi$. The shaded region is non-physical

Fig. 13

The fragment of phase portraits of system (25) on the Poincaré sphere for the generic scenario (b) (on the left) and the generic scenario (c) (on the right). Values of parameters are $\xi =\frac{3}{16}$, $n=-1$, $\varepsilon =-1$ for the (b) scenario, and $\xi =\frac{1}{5}$, $n=-2$, $\varepsilon =-1$ for the (c) scenario. Purple arrows denote orbits corresponding to the evolution from the $w_\phi =-1$ equilibria A (left) or C (right) to the $w_\phi =-1$ equilibrium E, while the blue arrows denote other orbits. Light grey contours correspond to values of the equation of state parameter $w_\phi$. The shaded region is non-physical

Table 4 Equilibrium points of the system (25) at infinity together with existence conditions and values of the equation of state parameter

The phase portrait for the generic scenario (a), taking place for the canonical scalar field ($\varepsilon =+1$) with $\xi =\frac{3}{16}$ and $n>0$, is presented in Fig. 11. Within the physical region (26), the point E, representing the de Sitter universe (as we prove in Sect. 5), is a global attractor to which trajectories from points A ($w_\phi =-1$) and B ($w_\phi =0$) are approaching. The non-singular trajectories (from A to E – marked in purple) can be first either attracted by the saddle C ($w_\phi <-\frac{9}{5}$) or both two saddles I and J in turn ($w_\phi =\frac{1}{4}$ for both) before reaching the final point. As we can see, in this second case, the value $w_\phi =-\frac{1}{3}$ can be exceeded during evolution, which means the sign of $\ddot{a}$ can be changed to negative for a certain time.

The flow for the generic scenario (b), representing the phantom scalar field ($\varepsilon =-1$) for the parameter values $\xi =\frac{3}{16}$ and $-2<n<0$, is shown in Fig. 12, while in the left-hand side of Fig. 13 enlargement of an area of the initial stage of an evolution has been outlined. In this case, evolution from the $w_\phi =-1$ to the $w_\phi =-1$ state also starts at the point A and finishes at the point E (as we show in Sect. 5; in this scenario the state E also corresponds to the de Sitter universe). These orbits are transiting through the line F at the point K; when a trajectory is approaching this point from below (in the sense of the values of the V coordinate), the equation of state parameter $w_\phi \rightarrow -\infty$, and, after exceeding, $w_\phi$ decreases from the limit $+\infty$ – at this point the system undergoes the so-called w-singularity. After passing the point K, orbits are heading towards the stable focus E.

Finally, the flow for the generic scenario (c), for which $\varepsilon =-1$, $\frac{3}{16}<\xi <\frac{1}{4}$, and $n=-2$, is topologically equivalent to the flow for scenario (b), as we can see from bifurcation diagrams – comparing Figs. 8 with 10 and Figs. 6 with 9 we notice that in the range of parameters for scenarios (b) and (c), the relative positions of the equilibria are the same, except the pair of points A and C, which undergo a swap of positions and stability properties while passing between those two scenarios; we cannot, however, say there is a transcritical bifurcation of codimension two between these points, despite that we have to vary values of both $\xi$ and n parameters, because it is enough to change the value of one of these parameters to obtain the same bifurcation. Considering that the non-singular evolution starts from the point A for scenario (b) and from the point C for scenario (c), only the differences between portraits of the cases (b) and (c) are letters marking initial points of this kind of evolution and the shape of the non-physical region described by the condition (26) (it always has a boundary at the point A). The last feature indicates that trajectories from the initial de Sitter point to the point K being attracted on their way by the saddle, which lies on the $V=0$ nullcline, are also physically acceptable in the case (c), in contrast to the case (b). The comparison of differences of phase portraits for the scenarios (b) and (c) has been presented in Fig. 13.

5 Evolution of physical quantities

In this section, we will investigate the evolution of physical quantities, such as H, $\dot{H}+H^2$, $\varOmega _{\phi ,\text {kin}}$, $\varOmega _{\phi ,\text {pot}}$, over the cosmological time t (the proper time of fundamental observers).

Let us notice firstly that the model we use allows us to determine explicitly only $H^2$, ${\dot{\phi }}^2$ and the quotient ${\dot{\phi }}/H$, which means that we are not able to calculate the signs of H and ${\dot{\phi }}$, because the model does not distinguish these signs.³ Knowing that currently $H>0$, we can determine the regions where H goes to negative values by searching for $H^2=0$ points and checking a value of $\dot{H}+H^2$ there.

In order to present the time evolution of the scale factor a and its derivatives, we need to transform Eqs. (17) and (20); thus we obtain, respectively,

$$\begin{aligned} H^2=M^{n+4}\left( \frac{\kappa }{\sqrt{6}}\right) ^{n+2}\frac{2v^{n+2}}{v^2-\varepsilon u^2-6\varepsilon \xi (1+2u)} \end{aligned}$$

(47)

and

$$\begin{aligned} \frac{\ddot{a}}{a}= & {} \dot{H}+H^2 \nonumber \\= & {} -M^{n+4}\left( \frac{\kappa }{\sqrt{6}}\right) ^{n+2}\frac{v^{n+2}(3w_\phi +1)}{v^2-\varepsilon u^2-6\varepsilon \xi (1+2u)}, \end{aligned}$$

(48)

where the overdot symbol ($\dot{\ }$) denotes a derivative with respect to t.

Equation (47) can be used for calculation of the parameter $H_{dS}$ at a critical point on the phase plane (u, v).

The reparameterisation of time for dynamical system (25) gives the new time $\tau$ which is related to t by

$$\begin{aligned} {\mathrm {d}}t={\mathrm {d}}\tau \frac{\left[ \frac{1}{3}\varepsilon v(\tau )^2-2\xi (1-6\xi )\right] ^2}{H[u(\tau ),v(\tau )]}. \end{aligned}$$

(49)

To reconstruct the time t we need to determine the sign of H and integrate the foregoing equation. In this work we assume arbitrarily $\tau =0$ such that $w_\phi (\tau \ge 0)\approx -1$ at least to the third decimal place. Moreover, we put $t(\tau =0)=0$. Having the time t, it is possible to calculate the scale factor directly from the definition of the Hubble function,

$$\begin{aligned} a(t)=\exp \left( \int \limits _0^tH(t'){\mathrm {d}}t'\right) . \end{aligned}$$

(50)

Fig. 14

The evolution of physical quantities over the cosmological time t for the evolutionary scenario (a) with values of parameters $\xi =\frac{3}{16}$, $n=2$, $\varepsilon =+1$. The left column corresponds to orbits passing near the equilibrium point I (plots presented in the left column are for the orbit with the boundary conditions $U(\tau =-3.7)=-0.3$, $V(\tau =-3.7)=0.92$), while the right column corresponds to orbits passing near the equilibrium point C (the plots presented are for the orbit with boundary conditions $U(\tau =-910)=-0.822$, $V(\tau =-910)=0.012$). The time t as well as the quantities H, $H^2$ and $\dot{H}$ have been calculated in units for which $M^{n+4}(\kappa /\sqrt{6})^{n+2}=1$

Let us inspect the value of $H^2$ from Eq. (47) in the limits corresponding to the starting points of non-singular evolutionary scenarios. In the case of scenario (a) the limit of $H^2$ at the point A is always equal to zero, so the initial state corresponds to a static universe. In the scenario (b) this limit at the point A is zero only if $-1<n<0$; for $-2<n<-1$ it diverges to positive infinity for the physical trajectories, while for $n=-1$ (then the point A is the proper node) this limit depends on the direction of the approaching, nevertheless for the physical non-singular trajectories it is finite and is never equal to zero. Thus the initial, asymptotic state A within scenario (b) for $-1<n<0$ represents the static universe, for $n=-1$ it corresponds to the de Sitter universe, while for $-2<n<-1$ it is also of de Sitter type, though with the Hubble function $|H|\rightarrow +\infty$. In the case of scenario (c), the limit of $H^2$ at the initial point C is finite and non-zero throughout the admissible range $\frac{3}{16}<\xi <\frac{1}{4}$; its value decreases monotonically as $\xi$ increases and reaches $H^2\rightarrow +\infty$ as $\xi \rightarrow \frac{3}{16}^+$ (asymptotic transition to scenario (b)) and $H^2\rightarrow 0$ as $\xi \rightarrow \frac{1}{4}$. This implies that the initial state in this scenario represents the de Sitter universe.

Within scenarios (a) for any n and (b) for $-1<n<0$, representing the initially static universe, the scale factor $a=\mathrm{const}>0$ as $t\rightarrow -\infty$. In the case of scenarios (b) for $-2<n\le -1$ and (c) for any $\xi$, representing the universe emerging from the de Sitter state, we have $a\rightarrow 0$ as $t\rightarrow -\infty$.

On the other hand, the limit of $H^2$ at the final state E for all generic scenarios (a)–(c) is finite. It means that the evolution according to each of generic scenarios approaches asymptotically the de Sitter state. The value of $\varLambda _{\text {emergent}}$, according to Eq. (30), in the final states E for scenarios (a) and (b) has the form (depending on n)

$$\begin{aligned} \varLambda _{\text {emergent}}=4^{-(n+1)}M^{n+4}\kappa ^{n+2}(n+4)\left( \frac{3n+12}{|n|}\right) ^{\frac{n}{2}}, \end{aligned}$$

while for scenario (c) this value (as the function of $\xi$) is

$$\begin{aligned} \varLambda _{\text {emergent}}=\frac{M^2}{2\xi }. \end{aligned}$$

In order to find the sign of H along the evolutionary paths, we assume that the passage from negative to positive values of H (or vice versa) can be realised only at the points where $H^2=0$ and we expect that at the final state, which we identify as the late-time acceleration, there is $H>0$. For every generic evolutionary scenario (a)–(c), there is no point on non-singular orbits, for which $H^2=0$. Only at the initial point A for scenarios (a) and (b) the limit of $H^2$ is equal to zero as soon as $n>-1$ (as we showed above). This means that, upon our assumption, all scenarios represent the expanding universe ($H>0$) at any finite time.

We present plots demonstrating the evolution of the equation of state coefficient $w_\phi$ with respect to the cosmological time t along the non-singular orbits and compare it with the time evolution of H, $\dot{H}$ and $H^2+\dot{H}\equiv \frac{\ddot{a}}{a}$ on these orbits. Additionally, we present the diagram of $\varOmega _{\phi ,\mathrm{kin}}$ and $\varOmega _{\phi ,\mathrm{pot}}$ depending on the cosmological time t. It gives us deeper insight into the evolutionary scenarios.

The evolution of physical quantities over the cosmological time t for the evolutionary scenario (a) is presented in Fig. 14. The left column corresponds to an orbit passing near the equilibrium point I, whereas the right column corresponds to an orbit passing near the equilibrium point C. In plots we see the occurrence of initial static state ($w_\phi =-1$, $\dot{H}=0$ and $H=0$ – from the side of $t\rightarrow -\infty$), and the final de Sitter state ($w_\phi =-1$, $\dot{H}=0$ and $H=\mathrm{const}>0$ – from the side of $t\rightarrow +\infty$), between which a non-exponential evolution takes place. For trajectories attracted by the point I it is possible for the universe to undergo a decelerated expansion ($w_\phi >-1/3$, $\dot{H}+H^2=\ddot{a}/a<0$) for a particular interval of time. The kinetic energy density $\varOmega _{\phi ,\text {kin}}$ is changing from $+\infty$ to 0 during the evolution.

The existence of the initial state represented by the static unstable universe can be seen, for example, in the middle right panel of Fig. 14. The corresponding cosmological model starts from the Einstein universe and approaches the de Sitter universe. This evolutionary path is a simple example of what we call the emergent cosmology [43]. It would be interesting to mention that this class of the models is generic in the sense of initial conditions, i.e. a small change of initial conditions does not change this type of evolution – as regards stability with respect to the initial conditions.

Fig. 15

The evolution of physical quantities over the cosmological time t for evolutionary scenarios (b) (in the left) and (c) (in the right). Values of parameters for plots in the left column are $\xi =\frac{3}{16}$, $n=-1$, $\varepsilon =-1$, while for plots in the right column are $\xi =\frac{1}{5}$, $n=-2$, $\varepsilon =-1$. Plots for the scenario (b) have been prepared for the orbit with the boundary conditions $U(\tau =-211)=-0.75$, $V(\tau =-211)=0.27$, whereas plots for the scenario (c) have been prepared for the orbit with the boundary conditions $U(\tau =-110)=-0.767$, $V(\tau =-110)=0.322$. The time t as well as quantities H, $H^2$ and $\dot{H}$ have been calculated in units for which $M^{n+4}(\kappa /\sqrt{6})^{n+2}=1$. For the chosen boundary conditions, the intersection of the orbit with the equilibrium line F (the point of the discontinuity of $w_\phi$) takes place for $t=-6.97936$ in the case of scenario (b) or $t=-6.7425$ in the case of scenario (c)

Figure 15 shows the evolution of the physical quantities over the cosmological time t for the evolutionary scenarios (b) (the left column) and (c) (the right column). Two de Sitter states emerge from both sides of $t\rightarrow \pm \infty$ ($w_\phi =-1$, $\dot{H}=0$, $H=\mathrm{const}>0$). During evolutions (b) and (c), there appears the discontinuity of $w_\phi$, which takes place when the orbit intersects the equilibrium line F. As the solution approaches this line, the equation of state parameter $w_\phi \rightarrow -\infty$. After the solution exceeds line F, $w_\phi$ is decreasing from the limit $+\infty$; there appears the decelerated expansion ($H^2+\dot{H}<0$) for a certain time. The kinetic energy $\varOmega _{\phi ,\text {kin}}$ is changing from $-\infty$ to 0 throughout the evolution.

In Fig. 15, we see the generalised emergent cosmological model. The universe starts from the unstable de Sitter state and approaches the stable de Sitter state through damped oscillations. This class of evolutionary path is generic. Some effects of barotropic matter have been investigated in the context of non-minimally coupled scalar field cosmology, where the vacuum solutions were located on invariant submanifolds [44, 45].

The initial exponential expansion, seen in Fig. 15, which stretches to $t\rightarrow -\infty$, models the inflation in the early universe. This takes place in scenario (b) for $-2<n\le -1$ and in scenario (c) for any allowed value of $\xi$. The second exponential expansion, stretching to $t\rightarrow +\infty$, describes the late-time accelerated expansion on the condition that we add the matter content of the current universe. The full model, taking explicitly the matter component into account, is an interesting aim of further research.

In the model under consideration one can construct observables based on the $H^2$ formula (47) as a function of redshift. The parameters in this formula can be constrained using astronomical and astrophysical data. This will be the subject of our future work.

6 Conclusions

In our studies, we reveal the whole spectrum of the possible qualitative behaviours of the model of cosmology with scalar field non-minimally coupled to the gravity, for the potential of the power-law form. By looking at Figs. 1, 2, 3, 4 and 5 one can see the local stability properties of the system in the vicinity of the equilibria for the full range of values of parameters $(\varepsilon , \xi , n)$, where $\varepsilon =\pm 1$ distinguishes between the canonical ($+1$) and the phantom ($-1$) scalar field, $\xi$ is the coupling constant between the scalar field and the curvature, and n is the exponent in the power-law potential. Different stability properties near equilibria correspond to distinct types of physical evolution of the universe. These regions of topological equivalence are separated with boundaries, being pairs of bifurcation values of parameters $(\xi ,n)$. In Figs. 1, 2, 3, 4 and 5, we present these pairs for all boundaries.

Moreover, we applied this result to find all possible generic scenarios of the evolution of the universe for which the equation of state parameter $w_\phi =-1$ at both the initial and the final state. This value of $w_\phi$ at the initial state indicates the absence of the initial singularity of the universe. There are three generic scenarios of this type, characterised by different sets of parameters $(\varepsilon ,\xi ,n)$. The first of these cases, scenario (a), takes place for the canonical scalar field with the value of the non-minimal coupling parameter $\xi =\frac{3}{16}$ and the exponent appearing in the potential $n>0$, while two other cases, scenarios (b) and (c), respectively, concern the phantom scalar field for $\xi =\frac{3}{16}$ and $-2<n<0$ or for $\frac{3}{16}<\xi <\frac{1}{4}$ and $n=-2$. It occurred that there are two possible physical types of initial states for such kind of evolution – either an unstable static state, taking place for scenario (a) for any n and scenario (b) for $-1<n<0$, or an unstable de Sitter state, for scenario (b) for $-2<n\le -1$ and scenario (c) for any $\xi$. In all scenarios, the universe finishes its evolution at the stable de Sitter state. We identify the initial state with the inflation and the final state with the late-time acceleration – these scenarios realise the quintessential inflation model. Furthermore, analysing bifurcations of equilibria on the (u, v) axes (Figs. 6, 7, 8, 9, 10), we found that each generic scenario (a)–(c) distinguishes the system which possesses the unique qualitative behaviour, as is shown in the phase portraits of these systems (Figs. 11, 12, 13).

We also found the non-generic evolutionary scenarios without the initial singularity, where the evolution either starts at a saddle equilibrium point. This kind of evolution, following a separatrix, corresponds to Starobinsky’s model [46].

We studied the type of inflation in the model. Our conclusion is that in the past there is always realised the fast-roll inflation as soon as $\xi \ne 0$. The physical effect for the non-minimal coupling is that the scalar field decreases monotonically receding this state.

The usage of bifurcation theory methods enabled us to provide a meticulous study of how the dynamics of the cosmological system changes upon a variation of the parameters of the model. From this study, we were able to find evolutionary scenarios corresponding to the universe emerging and finishing its evolution at states with $w_\phi =-1$. The bifurcation analysis was two-stage. First, we extracted sets of parameters for which such a non-singular evolution was possible – in both the generic and the non-generic cases – and afterwards, we investigated how many qualitatively different behaviours appeared within the given scenario.

For example, in the bifurcation diagrams Figs. 1, 2, 3, 4 and 5, if we fix the parameter $\xi$ at the constant value, then we obtain the interval of n (vertical line) divided by bifurcation values separating domains of the topological equivalence, which implies different qualitative behaviour of the model. This shows how the dynamics and how the physics change, depending on the value of n. The detailed analysis of the bifurcation diagrams in Figs. 1, 2, 3, 4 and 5 is contained in Sects. 3.1 and 3.2.

The common feature of all of generic non-singular scenarios, found in this work, is that they lead to the same de Sitter attractor through damped oscillations. In principle, the stable de Sitter case can also be reached via a monotonic evolution without damped oscillation. Such situations happen for the values of parameters $(\varepsilon ,\xi ,n)$ corresponding to the light blue area in Figs. 4 and 5. We do not obtain the evolution that is devoid of the initial singularity for these values of parameters, though. On the other hand, the type of the initial state depends on the value of parameters. The transition from scenario (b) to (c) is realised through merging the saddle point C and the unstable node A; then, increasing the value of $\xi$ from $\frac{3}{16}$, the points separate as C becomes the unstable node, which can be seen in the bifurcation diagram in Fig. 9 in the magnified area.

Wang et al. found the theoretical limit for the value of the non-minimal coupling constant $\xi$ to be $0\le \xi \le \frac{1}{3}$ [32]. On the other hand, we indicated that the scenarios from the de Sitter or the static state to the de Sitter state are valid for $\xi$ in the interval $[\frac{3}{16},\frac{1}{4})$. Therefore, our interval for $\xi$ is contained in this theoretical constraint. In addition, the interval we found accords with the interval found by Hrycyna, who inspected the conditions for unstable states with $w_\phi =-1$ in the asymptotic regime for $\phi \rightarrow +\infty$ in [24].

Appendix A: Elements of applied bifurcation theory

In this appendix, we write basics on the applied bifurcation theory. First, we give the necessary notions of dynamical system theory (necessary from the point of view of bifurcation theory, that is). Then we discuss the definitions related to the topological equivalence of dynamical systems and bifurcations. Finally, we present a basic description of most important types of local bifurcations. We limit the discussion to bifurcations of codimension one in two-dimensional dynamical systems since this is the only kind of bifurcations that appears in our analysis. Definitions 1–9 are quoted from Kuznetsov’s book [27].

1.1 Appendix A.1: Dynamical systems

In deterministic processes, future and past states of a system can be revealed on the basis of its present state and a law describing the evolution. The mathematical formalisation of this fact is the notion of a dynamical system.

A set X of all possible states of a dynamical system is called a state space (or phase space). Usually, one distinguishes finite-dimensional systems defined in $X={\mathbb {R}}^n$ from those defined on manifolds. The state $x_t\in X$ of a system changes with time $t\in T$, where T is a number set. In the case $T={\mathbb {R}}^1$ a system is called a continuous-time dynamical system, while for $T={\mathbb {Z}}$ it is a discrete-time dynamical system.

An evolution law of a dynamical system determines the state $x_t$ of the system at time t, provided the initial state $x_0$ is known. The description of the evolution is given by an evolution operator $\phi ^t$, which is a map

$$\begin{aligned} \phi ^t :X\longmapsto X, \end{aligned}$$

transforming an initial state $x_0\in X$ into some state $x_t\in X$ at time t,

$$\begin{aligned} x_t=\phi ^tx_0. \end{aligned}$$

The deterministic nature of dynamical systems is reflected in the following two properties of the evolution operator. First of all,

$$\begin{aligned} \phi ^0=\mathrm {id}, \end{aligned}$$

(A.1)

where $\mathrm {id}$ is the identity map on X, $\mathrm {id}\;x=x$ for all $x\in X$. The second property is

$$\begin{aligned} \phi ^{t+s}=\phi ^t\circ \phi ^s, \end{aligned}$$

(A.2)

which implies $x_{t+s}=\phi ^t \left( \phi ^sx_0\right)$.

Now we are ready to give the formal definition of the dynamical system, which comes from [27].

Definition 1

A dynamical system is a triple $\{T,X,\phi ^t\}$, where T is a time set, X is a state space, and $\phi ^t:X\mapsto X$ is a family of evolution operators parametrised by $t\in T$ and satisfying properties (A.1) and (A.2).

In the case of continuous-time systems, a family $\left\{ \phi ^t\right\} _{t\in T}$ of evolution operators is called a flow. Moreover, in the cases of both continuous- and discrete-time systems, an orbit $\varGamma$ is an ordered subset of the state space X,

$$\begin{aligned} \varGamma (x_0)= & {} \Big \{x\in X :x=\phi ^tx_0, \\&\text { for all } t\in T \text{ such } \text{ that } \phi ^tx_0 \text { is defined}\Big \}. \end{aligned}$$

Orbits in the state space of a dynamical system compose a phase portrait, which is the geometrical representation of the dynamical system.

Very often one identifies a continuous-time dynamical system with differential equations describing implicitly a law of evolution. Suppose that the state space of a system is $X={\mathbb {R}}^n$. Then the differential equations related to the system are

$$\begin{aligned} \dot{x}=f(x,\alpha ), \end{aligned}$$

(A.3)

where $\dot{x}={\mathrm {d}}x/{\mathrm {d}}t$, the state $x=(x_1,\ldots ,x_n)\in {\mathbb {R}}^n$, $\alpha =(\alpha _1,\ldots ,\alpha _m)\in {\mathbb {R}}^m$ is the parameter vector, and $f:{\mathbb {R}}^n\times {\mathbb {R}}^m\ni (x,\alpha )\mapsto (f_1,\ldots ,f_n)\in {\mathbb {R}}^n$ is a function (a vector field) of the $C^k$ class, with $k\ge 1$. We will frequently refer to dynamical systems without underlining its dependence on the parameter vector $\alpha$. Thus, differential equations have the form

$$\begin{aligned} \dot{x}=f(x). \end{aligned}$$

(A.4)

Let us quote the following three important definitions, taken from [27], which are related to dynamical systems. The first of them is an equilibrium, which is the special case of an orbit.

Definition 2

A point $x^0\in X$ is called an equilibrium (or a fixed point) if $\phi ^tx^0=x^0$ for all $t\in T$.

An equilibrium is thus a point in which the system remains forever. For differential equations (A.4) in an equilibrium $x^0$ we have

$$\begin{aligned} f(x^0)=0. \end{aligned}$$

Subsequent definitions concern the notion of another special kind of orbits – cycles.

Definition 3

A cycle is a periodic orbit, namely a non-equilibrium orbit $L_0$, such that each point $x_0\in L_0$ satisfies $\phi ^{t+T_0}x_0=\phi ^tx_0$ with some $T_0>0$, for all $t\in T$.

Definition 4

A cycle of a continuous-time dynamical system, in a neighbourhood of which there are no other cycles, is called a limit cycle.

1.2 Appendix A.2: Topological equivalence and bifurcations

Before introducing the notion of bifurcation, we should clarify what it means that phase portraits of two dynamical systems have the same qualitative features. For this purpose, let us quote from [27] the definition of topological equivalence of two dynamical systems.

Definition 5

A dynamical system $\{T,{\mathbb {R}}^n,\phi ^t\}$ is called topologically equivalent to a dynamical system $\{T,{\mathbb {R}}^n,\psi ^t\}$ if there is a homeomorphism $h:{\mathbb {R}}^n\mapsto {\mathbb {R}}^n$ mapping orbits of the first system onto orbits of the second system, preserving the direction of time.

Dynamical systems are very often studied in a vicinity of an equilibrium since it is possible to develop useful linear approximations there. Therefore, one may elaborate the topological classification of phase portraits near equilibrium points and hence the need for the following modification of Definition 5.

Definition 6

A dynamical system $\{T,{\mathbb {R}}^n,\phi ^t\}$ is called locally topologically equivalent near an equilibrium $x_0$ to a dynamical system $\{T,{\mathbb {R}}^n,\psi ^t\}$ near an equilibrium $y_0$ if there exists a homeomorphism $h:{\mathbb {R}}^n\mapsto {\mathbb {R}}^n$ that is:

• (i) defined in a small neighbourhood $U\subset {\mathbb {R}}^n$ of $x_0$;

• (ii) satisfies $y_0=h(x_0)$;

• (iii) maps orbits of the first system in U onto orbits of the second system in $V=h(U)\subset {\mathbb {R}}^n$, preserving the direction of time.

Consider the dynamical system (A.3) dependent on parameters $\alpha \in {\mathbb {R}}^m$. As the parameters vary, the phase portrait of the system also varies. This results in two possibilities: either the system remains topologically equivalent to the original one, or its topology changes.

Definition 7

The appearance of topologically nonequivalent phase portrait under variation of parameters is called a bifurcation.

Thus, a bifurcation is a change of the topological type of the system. A value of parameters at which this change happens is called a bifurcation (critical) value.

If a bifurcation occurs when we fix any small neighbourhood of an equilibrium, then it is called a local bifurcation (or a bifurcation of an equilibrium). Otherwise, when a bifurcation cannot be determined by analysing only a small vicinity of an equilibrium, it is a global bifurcation.

It is often convenient to visualise how the occurrence of bifurcations depends on parameters of the system. For this purpose, let us introduce the definition of a bifurcation diagram taken from [27].

Definition 8

A bifurcation diagram of the dynamical system is a stratification of its parameter space induced by the topological equivalence, together with representative phase portraits for each stratum.

In the simplest case, the bifurcation diagram consists of a finite number of regions in the parameter space ${\mathbb {R}}^m$, inside which the phase portrait is topologically equivalent. These regions are separated by bifurcation boundaries, which are smooth submanifolds in ${\mathbb {R}}^m$ (e.g. curves, surfaces).

Definition 9

The codimension of a bifurcation is the difference between the dimension of the parameter space and the dimension of the corresponding bifurcation boundary.

The equivalent and more practical definition says that the codimension is the number of independent conditions determining the bifurcation.

Bifurcations are divided into many types that differ in their course. It is possible to present the most simple differential equations that represent a given type of bifurcation. These equations are called normal forms. In the case of local bifurcations, every dynamical system having a local bifurcation of a specified type is locally topologically equivalent near an equilibrium to the normal form of this type of bifurcation.

1.3 Appendix A.3: Local bifurcations of codimension one in continuous-time systems

Let us introduce most important types of local bifurcations in continuous-time systems of at most two variables. We limit the discussion to bifurcations of codimension one. We present four types of bifurcations. Three of them are bifurcations of the saddle-node family: an elementary saddle-node, a transcritical, and a pitchfork bifurcation, while the last is a Hopf bifurcation.

Fig. 16

Bifurcation diagrams corresponding to the normal forms (A.5)–(A.8). Bifurcations take place in the origin O

Bifurcations of the saddle-node family (also called fold bifurcations) arise as a collision of equilibria, when a real eigenvalue crosses zero in the response to a change of a parameter. In the case of an elementary saddle-node bifurcation, two equilibria – one stable, the other unstable – coalesce and then disappear. In the case of a transcritical bifurcation, two equilibria – one stable, the other unstable – coalesce and then separate again, exchanging their stability properties. Finally, in the case of a pitchfork bifurcation there are two possibilities: in the first of them, called supercritical, three equilibria – one unstable, surrounded by two stable – coalesce into one stable equilibrium, while in the other, called subcritical, three equilibria – one stable, surrounded by two unstable – coalesce into one unstable equilibrium. Normal forms for saddle-node family of bifurcations are

$$\begin{aligned} \text {elementary saddle-node,} \quad \dot{x}= & {} \alpha \pm x^2, \end{aligned}$$

(A.5)

$$\begin{aligned} \text {transcritical,} \quad \dot{x}= & {} \alpha x\pm x^2, \end{aligned}$$

(A.6)

$$\begin{aligned} \text {supercritical pitchfork,} \quad \dot{x}= & {} \alpha x-x^3, \end{aligned}$$

(A.7)

$$\begin{aligned} \text {subcritical pitchfork,} \quad \dot{x}= & {} \alpha x+x^3, \end{aligned}$$

(A.8)

where $\alpha$ is the parameter with the critical value equal to zero. Bifurcation diagrams of the foregoing normal forms are shown in Fig. 16.

A Hopf bifurcation (known also as an Andronov–Hopf bifurcation) arises, when the real parts of two complex and conjugate eigenvalues cross zero. It presents a collision of a stable or unstable equilibrium with a cycle, which shrinks to a point when the collision occurs. The normal form for this kind of bifurcation is

$$\begin{aligned} \dot{x}_1= & {} \alpha x_1-x_2-x_1\left( x_1^2+x_2^2\right) ,\nonumber \\ \dot{x}_2= & {} x_1+\alpha x_2-x_2\left( x_1^2+x_2^2\right) , \end{aligned}$$

(A.9)

which in polar coordinates $(\rho ,\varphi )$ is

$$\begin{aligned} {\dot{\rho }}= & {} \rho (\alpha -\rho ^2),\nonumber \\ {\dot{\varphi }}= & {} 1, \end{aligned}$$

(A.10)

where $\alpha$ is the parameter with the critical value equal to zero.