Direct search constraints on very heavy dark skyrmions

Abstract

In the standard dark matter creation scenario, dark matter arises from freeze-out due to decoupling from the thermal heat bath in the early universe. On the other hand, topological solitons can also emerge during phase transitions through the Kibble–Zurek mechanism or through bubble nucleation. In particular, Murayama and Shu found that the Kibble–Zurek mechanism can produce topological defects up to about 10 PeV, and Bramante et al. had recently pointed out that direct search constraints can be extrapolated to very large masses. Motivated by these observations, we examine direct search constraints for PeV scale dark skyrmions with a Higgs portal coupling to baryons. We find abundance constraints on the combination $g_V^2M_S$ of Skyrme coupling $g_V$ and skyrmion mass $M_S$. We also find that extrapolation of the direct search constraints from XENON1T to very high masses constrains the combination $g_{wh}/g_V^4$ as a function of $M_S$, where $g_{wh}$ is the Higgs portal coupling of the dark skyrmions.

1 Introduction

The dark matter puzzle motivated numerous investigations of the question how dark matter may have been produced in the early universe. Dark matter up to a mass¹ of about 100 TeV [1] can be produced in freeze-out from a thermal heat bath if the dark matter interaction rate with baryons becomes suppressed by the cosmic expansion [4]. Dark matter can also arise in the form of topological defects in phase transitions [5], or due to freeze-in if the interactions were too weak to ever establish thermal equilibrium in the dark sector [6]. Generation during or near the end of inflation is another possibility [7, 8].

Numerous other proposals have been discussed in the literature, but here we would like to focus on direct search constraints on very heavy dark matter from the Kibble–Zurek mechanism [5, 9,10,11]. This is motivated by the observation of Murayama and Shu that this mechanism can produce non-thermal PeV scale dark matter [12], and by the recent observation of Bramante et al. that direct search constraints can be extrapolated to very high mass values [13]. We assume that the dark matter can interact with the baryonic sector through a Higgs portal coupling for the calculation of the pertinent nucleon recoil cross section. We use a skyrmion scenario where the very heavy skyrmions are coherent states of heavy “mesons”, and it is the heavy mesons which couple to baryons through the Higgs portal. The ensuing separation of mass scales ensures that the very heavy dark matter can be non-thermally created as topological defects while the mesons have strong enough coupling to baryons to prevent the mesons’ freeze-out² into a sizable dark matter component. This sets the present model apart from standard thermal Higgs portal models and implies different constraints from direct search experiments.

Higgs portal dark matter from thermal freeze-out has been extensively discussed and is well understood, see e.g. [14, 15] and references there. However, the mechanism of dark matter generation determines what (if any) relation exists between dark matter mass and coupling strength to baryons, thus also determining the relation between dark matter mass and nucleon recoil cross section from the theoretical side of matching to direct search constraints. We are therefore interested in the constraints on topological Higgs portal dark matter which arises through a phase transition in the dark sector without subsequent thermalization and thermal freeze-out.

In particular, a chiral $G=SU_L(2)\times SU_R(2)\rightarrow H=SU_V(2)$ phase transition in the dark sector will create skyrmions from the non-trivial homotopy group $\pi _3(G/H)={\mathbb {Z}}$ which arises from the mappings of compactified ${\mathbb {R}}^3=S^3$ into $S^3$ [16,17,18, 20, 21]. The compactification and the mapping arise from the boundary condition $\lim _{|\varvec{x}|\rightarrow \infty }U(x)=1$ on the fields U(x), which map ${\mathbb {R}}^3\rightarrow S^3$ for fixed time t,

$$\begin{aligned} U(x)= & {} \exp [\mathrm {i}\varvec{w}(x)\cdot \varvec{\sigma }/f_w] \nonumber \\= & {} \cos (|\varvec{w}(x)|/f_w)+\mathrm {i}\hat{\varvec{w}}(x)\cdot \varvec{\sigma }\sin (|\varvec{w}(x)|/f_w). \end{aligned}$$

(1)

Here the $\sigma _i$ are the Pauli matrices of a dark SU(2) isospin symmetry and the vector $\hat{\varvec{w}}=\varvec{w}/|\varvec{w}|$ is the unit vector for the triplet $w_i(x)$ of dark mesons.

The winding number $W=\int d^3\varvec{x}\,W^0$ of the mapping $S^3\rightarrow S^3$ is related to the conserved current (with the convention $\epsilon ^{0123}=-1$)

$$\begin{aligned} W^\mu =\frac{1}{24\pi ^2}\epsilon ^{\mu \nu \rho \sigma }\mathrm {Tr}( \partial _\nu U\!\cdot U^+\!\cdot \partial _\rho U\!\cdot U^+\!\cdot \partial _\sigma U\!\cdot U^+). \end{aligned}$$

(2)

We will denote W as skyrmion number, since the standard designation as “baryon number” is obviously inappropriate: The skyrmions in the dark sector are not baryons, neither in the hadronic sense nor in the cosmologist’s definition of baryonic matter.

The spherically symmetric skyrmions

$$\begin{aligned} \varvec{w}_S(\varvec{x})=w_S(r)\hat{\varvec{x}} \end{aligned}$$

(3)

are stable with skyrmion number $W=\pm 1$ if $w_S(0)=\pm \pi f_w$ [19, 21, 22]. It is therefore natural that skyrmions are discussed as dark matter candidates. Electroweak scale dark skyrmions from a non-standard Higgs sector are constrained to masses up to about 10 TeV [23,24,25,26,27,28]. If the coupling of the skyrmions to baryons is strong enough to thermalize the skyrmions after the phase transition, then their relic abundance is determined by thermal freeze-out [23, 26,27,28]. However, if the skyrmions do not thermalize after the phase transition, then it is the phase transition itself which determines any relic skyrmion abundance. Such a scenario was discussed by Campbell et al. for electroweak skyrmions [24]. Furthermore, Murayama and Shu had pointed out that topological dark matter with masses up to 10 PeV could be generated through the Kibble–Zurek mechanism [12], and indirect signals from very heavy dark skyrmions through Higgs or neutrino portals were discussed in [29].

In the present paper we are interested in direct search constraints on very heavy dark skyrmions, since Bramante et al. had pointed out that limits from existing direct search experiments can principally be extrapolated to very high masses [13]. The non-thermalized dark skyrmions are not constrained by the standard indirect [30,31,32,33,34,35,36,37,38,39,40] and direct [14, 15, 41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56] search analyses for Higgs portal dark matter since the different creation mechanism changes the relation between mass and couplings. However, we can adopt estimates on the ratio $x_c=M_S/T_c$ from hadronic physics. This allows us to constrain the skyrmion parameter $g_V^2 M_S$ from the requirement $\varOmega _S\le \varOmega _{\mathrm {CDM}}$. Direct search constraints from XENON1T then allow us to constrain a combination of the skyrmion coupling and the skyrmion’s Higgs portal coupling as a function of skyrmion mass.

We will review some pertinent aspects of dark skyrmions in Sect. 2 and confirm that skyrmions are good candidates for PeV scale dark matter through a new analysis of their current abundance which takes into account that the Boltzmann equation erases initial conditions for $\varGamma \gtrsim H$ if the reverse process to $S{\overline{S}}$ annihilation is kinematically suppressed. Section 3 discusses constraints on the heavy w mesons which arise from the requirement that the relic very heavy dark skyrmions, but not the heavy w mesons, are the dominant dark matter component. The direct search constraints on PeV scale dark skyrmions are then discussed in Sect. 4. Section 5 summarizes our conclusions.

2 Dark skyrmions from chiral phase transitions

We parametrize chiral symmetry breaking in a dark sector with a Lagrangian

$$\begin{aligned} {\mathcal {L}}={\mathcal {L}}_S+{\mathcal {L}}^{(h)}_{DSM}. \end{aligned}$$

(4)

The fourth order term in the Skyrme Lagrangian

$$\begin{aligned} {\mathcal {L}}_S= & {} \frac{1}{16g_V^2}\mathrm {Tr}[\partial ^\mu U\!\cdot \partial ^\nu U^+\!\cdot (\partial _\mu U\!\cdot \partial _\nu U^+-\partial _\nu U\!\cdot \partial _\mu U^+)] \nonumber \\&-\,\frac{f_w^2}{4}\mathrm {Tr}(\partial _\mu U\!\cdot \partial ^\mu U^+) \end{aligned}$$

(5)

stabilizes skyrmions as topological solitons against Derrick’s theorem [16,17,18, 20, 21]. The coupling constant $g_V$ is usually written as e, but we avoid this notation. The designation $g_V$ is motivated by the observation that the skyrmion coupling can arise from vector dominance due to a hidden local $SU_V(2)$ invariance [18, 57].

The skyrmions (3) can be thought of as coherent excitations of the dark meson fields $\varvec{w}(x)$, and the Skyrme Hamiltonian

$$\begin{aligned} {\mathcal {H}}_S= & {} \frac{1}{16g_V^2}\mathrm {Tr}[\partial _\mu U\!\cdot \partial _\nu U^+\!\cdot (\partial _\nu U\!\cdot \partial _\mu U^+-\partial _\mu U\!\cdot \partial _\nu U^+)] \nonumber \\&+\,\frac{f_w^2}{4}\mathrm {Tr}(\partial _\mu U\!\cdot \partial _\mu U^+) \end{aligned}$$

(6)

defines the mass for the static skyrmion solutions through the energy functional

$$\begin{aligned} E_S=\int \!d^3\varvec{x}\,{\mathcal {H}}_S, \end{aligned}$$

(7)

with the result [18, 21]

$$\begin{aligned} M_S\simeq 73 f_w/g_V. \end{aligned}$$

(8)

Their effective extension can be estimated as $L_S\simeq 1.2/(g_V f_w)$ [58]. The representation (6) for the Skyrme Hamiltonian uses the convention that summation over lower pairs of 4-indices is defined as Euclidean, e.g. $\partial _\mu U\!\cdot \partial _\mu U^+\equiv \partial _0 U\!\cdot \partial _0 U^+ +\varvec{\nabla }U\!\cdot \varvec{\nabla }U^+$.

The Skyrme Lagrangian (5) is symmetric under the chiral symmetry $U(x)\rightarrow L\cdot U(x)\cdot R^+$, but the boundary condition $\lim _{|\varvec{x}|\rightarrow \infty } U(x)=1$ breaks this symmetry to the diagonal subgroup $SU_V(2)$, $U(x)\rightarrow V\cdot U(x)\cdot V^+$. The odd parity pseudo-Goldstone bosons $\varvec{w}(x)$ parametrize the degenerate ground state from the chiral breaking $SU_L(2)\otimes SU_R(2)\rightarrow SU_V(2)$ in the form of a local axial SU(2) transformation (1), i.e. under parity $\mathrm {P}$, $\mathrm {P}\circ U(x)\circ \mathrm {P}=U^{-1}(x)$. Just like for ordinary pions in chiral perturbation theory, the residual $SU_V(2)$ transformation

$$\begin{aligned} \varvec{w}'(x)\cdot \varvec{\sigma }= & {} V\cdot \varvec{w}(x)\cdot \varvec{\sigma }\cdot V^+ \nonumber \\= & {} \exp (\mathrm {i}\varvec{\varphi }\cdot \varvec{\sigma }/2) \cdot \varvec{w}(x)\cdot \varvec{\sigma }\cdot \exp (-\mathrm {i}\varvec{\varphi }\cdot \varvec{\sigma }/2) \end{aligned}$$

implies a standard spin-1 rotation representation on the dark mesons,

$$\begin{aligned} \varvec{w}'(x)= & {} {\underline{R}}(\varvec{\varphi })\cdot \varvec{w}(x) =\exp (\varvec{\varphi }\cdot \underline{\varvec{L}})\cdot \varvec{w}(x) \nonumber \\= & {} \hat{\varvec{\varphi }}(\hat{\varvec{\varphi }}\cdot \varvec{w}(x))+ ({\underline{1}}-\hat{\varvec{\varphi }}\otimes \hat{\varvec{\varphi }})\cdot \varvec{w}(x)\cos \varphi \nonumber \\&-\,\varvec{\varphi }\times \varvec{w}(x)\sin \varphi . \end{aligned}$$

(9)

Here $({\underline{L}}_i)_{jk}=\epsilon _{ijk}$ are the standard SO(3) generators. Adding a mass term for the Goldstone bosons,

$$\begin{aligned} {\mathcal {L}}_{m_w}=\frac{m_w^2f_w^2}{2}\mathrm {Tr}(U-1_2) \end{aligned}$$

(10)

respects the unbroken symmetry and is compatible with the effective Goldstone boson interpretation of the $\varvec{w}$ triplet if $m_w\ll M_S$.

Following Ref. [29] we also include a Higgs coupling for the dark mesons,

$$\begin{aligned} {\mathcal {L}}^{(h)}_{DSM}= & {} \frac{g_{wh}f_w^2}{2}(2H^+(x)H(x)-v_h^2)\mathrm {Tr}(U(x)-1_2) \nonumber \\= & {} g_{wh}f_w^2 v_h\left( h(x)+\frac{h^2(x)}{2v_h}\right) \mathrm {Tr}(U(x)-1_2). \end{aligned}$$

(11)

The exact nature of chiral phase transitions for different chemical potentials and different numbers of underlying fermion flavors is still a matter of investigation. The non-thermal abundance of topological defects from a second order phase transition has been estimated by Muramaya and Shu [12], while Campbell et al. provided an estimate for a first order transition [24].

The finite correlation length $\xi$ from quenching during a second order phase transitions implies that anti-skyrmions and skyrmions with different centers will form with a density of order $\xi ^{-3}$ during the phase transition. The Kibble–Zurek based estimate of Murayama and Shu for the abundance of particle-like topological defects from cosmological phase transitions therefore applies,

$$\begin{aligned} \left. \frac{n_S}{s}\right| _{T=T_c}\simeq 0.006\left( \frac{T_c}{M_{Pl}}\right) ^{1.2}. \end{aligned}$$

(12)

Here $n_S$ denotes the sum of skyrmion and anti-skyrmion densities, and a critical exponent $\nu \simeq 2/3$ was assumed [12]. On the other hand, Campbell et al. assume a first order phase transition in an approximately scale-invariant model with chiral symmetry breaking and a pseudo-dilaton $\chi$. They find an estimate for the skyrmion abundance

$$\begin{aligned} \left. \frac{n_S}{s}\right| _{T=T_c}\simeq 3.2\left( \frac{m_\chi }{v_\chi }\right) ^{3/2}, \end{aligned}$$

(13)

depending on the ratio of dilaton mass to vacuum expectation value $m_\chi /v_\chi$ [24]. We will find that the relic dark skyrmion abundance decouples from the order of the phase transition and the initial skyrmion abundance if $\varGamma (T_c)\gtrsim H(T_c)$ while thermal skyrmion creation is kinematically suppressed.

Numerical simulations indicate that skyrmions annihilate with their classical cross section $\sigma _{S{\overline{S}}}=\pi L_S^2$ into a number $2< \langle N_w\rangle <M_S/m_w$ of $\varvec{w}$ particles [59, 60]. The simulations for hadronic skyrmions actually yield $2< \langle N_w\rangle \lesssim 7$, which is in remarkable agreement with observations of low-energy $p{\overline{p}}$ annihilations. These annihilations produce $5\pm 1$ pions, with pion multiplicities $3\le n_\pi \le 7$ in 99% of measurements [61]. The w-bosons then annihilate into baryons with annihilation cross sections for collision energies which are much larger than the top mass, $\sqrt{s_w}\ge 2m_w\gg m_t$ [29],

$$\begin{aligned} v\sigma _{ww\rightarrow hh}=v\sigma _{ww\rightarrow ZZ} =\frac{1}{2}v\sigma _{ww\rightarrow W^+W^-}=\frac{g_{wh}^2}{4\pi s_w}, \end{aligned}$$

(14)

and

$$\begin{aligned} v\sigma _{ww\rightarrow f{\overline{f}}}=N_c\frac{g_{wh}^2m_f^2}{\pi s_w^2}. \end{aligned}$$

(15)

Their leading order annihilation cross section into Standard Model states is therefore

$$\begin{aligned} v\sigma _{ww}=g_{wh}^2/\pi s_w. \end{aligned}$$

(16)

Both quenching and bubble nucleation delay completion of a phase transition, such that topological defects would be born into a heat bath with lower temperature $T_1$ than their mass, $T_1\lesssim T_c\sim M_S$. Furthermore, we would generically need collision of $\langle N_w\rangle \sim M_S/m_w\gg 2$ $\varvec{w}$ particles to produce an $S{\overline{S}}$ pair, such that these processes are phase-space suppressed with a factor $\exp (-\langle N_w\rangle E_w/T)$. Both of these effects suppress the thermal creation of the dark skyrmions from baryonic matter. Therefore, similar to magnetic monopoles [62], we need to solve the balance equation

$$\begin{aligned} \frac{d}{dt}(n_Sa^3)=-\,\frac{1}{2}n_S^2 a^3 \langle v\sigma _{S{\overline{S}}}\rangle \end{aligned}$$

(17)

with initial conditions given by Eqs. (12) or (13), respectively, to determine the relic skyrmion density today. We encounter a factor 1 / 2 in the skyrmion annihilation rate in equation (17) because $n_S={\tilde{n}}_S+{\tilde{n}}_{{\overline{S}}}\simeq 2{\tilde{n}}_S$ is the sum of skyrmion and anti-skyrmion densities, and the skyrmion annihilation rate is

$$\begin{aligned} \frac{d}{dt}({\tilde{n}}_Sa^3)=-\,{\tilde{n}}_S{\tilde{n}}_{{\overline{S}}} a^3\langle v\sigma _{S{\overline{S}}}\rangle \simeq -\,\frac{1}{4}n_S^2 a^3 \langle v\sigma _{S{\overline{S}}}\rangle . \end{aligned}$$

(18)

The temperature-dependence of $\langle v\sigma _{S{\overline{S}}}\rangle$ depends on how efficiently the dark mesons can couple the skyrmions to the primordial heat bath. The possible range of temperature dependences can be parametrized by

$$\begin{aligned} \langle v\sigma _{S{\overline{S}}}\rangle =\langle v\sigma _{S{\overline{S}}}\rangle _c (T/T_c)^\beta =\langle v\sigma _{S{\overline{S}}}\rangle _c (t_c/t)^{\beta /2}, \end{aligned}$$

(19)

with $0\le \beta \le 1$ [4].

Evolving the skyrmion density from the time $t_c$ of creation to the epoch of radiation-matter equality yields for $t_{eq}\gg t_c$

$$\begin{aligned} n_S(t_{eq}) \simeq \frac{n_S(t_c)}{1+n_S(t_c)(1+\beta )^{-1}\langle v\sigma _{S{\overline{S}}}\rangle _c t_c} \!\left( \frac{t_c}{t_{eq}}\right) ^{3/2}\!. \end{aligned}$$

(20)

Annihilation is negligible at later stages, and we find a relic skyrmion density

$$\begin{aligned} n_S(t_0) \simeq \frac{n_S(t_c)}{1+n_S(t_c)(1+\beta )^{-1}\langle v\sigma _{S{\overline{S}}}\rangle _c t_c} z_c^{-3}, \end{aligned}$$

(21)

where $z_c$ is the redshift at the epoch of the chiral phase transition in the dark sector. This can be expressed in terms of entropy ratios

$$\begin{aligned} z_c^{-3}\simeq \left( \frac{a_c}{a_0}\right) ^3=\frac{s_0}{s_c}=\frac{s_0}{ (2\pi ^2/45)g_{*S}(T_c)T_c^3}. \end{aligned}$$

(22)

The annihilation term in the denominator in Eq. (21) is related to the ratio of the skyrmion reaction rate and the expansion rate at the phase transition,

$$\begin{aligned} n_S(t_c)(1+\beta )^{-1}\langle v\sigma _{S{\overline{S}}}\rangle _c t_c =\varGamma _S(t_c)/2(1+\beta )H(t_c). \end{aligned}$$

(23)

This will be larger than 1 at $t_c$, and we find

$$\begin{aligned} n_S(t_0) \simeq \frac{(1+\beta )}{\langle v\sigma _{S{\overline{S}}}\rangle _c t_c}\frac{s_0}{ (2\pi ^2/45)g_{*S}(T_c)T_c^3}. \end{aligned}$$

(24)

Time and temperature at the phase transition are related by radiation domination,

$$\begin{aligned} t_c T_c^2=\frac{3}{4\pi }M_{Pl}\sqrt{\frac{5}{\pi g_{*\varrho }(T_c)}}. \end{aligned}$$

(25)

Substitution into Eq. (24) yields the relic skyrmion abundance $\varOmega _S h^2=M_S n_S(t_0)/(\varrho _{cr} h^{-2})$,

$$\begin{aligned} \varOmega _S h^2=\frac{6s_0 h^{2}}{M_{Pl}g_{*S}(T_c)\varrho _{cr}}\sqrt{\frac{5}{\pi }g_{*\varrho }(T_c)} \frac{\beta +1}{\langle v\sigma _{S{\overline{S}}}\rangle _c}\frac{M{_S}}{T{_c}}. \end{aligned}$$

(26)

Hadronic physics indicates $5\lesssim x_c\equiv M_S/T_c\lesssim 10$, and therefore we will adopt this range in evaluations of Eq. (26). We can also use a non-relativistic approximation $\langle \sigma v\rangle _c\simeq \pi L_S^2\sqrt{3/x_c}$, $\beta =1/2$. Furthermore, all radiative components are thermalized, $g_{*S}(T_c)=g_{*\varrho }(T_c)$, and we assume that they are dominated by Standard Model degrees of freedom, $g_{*\varrho }(T_c)=112$. This assumption is in agreement with the proposal that the phase transition which generates the dark skyrmions is the last phase transition in the early universe before electroweak symmetry breaking. This yields

$$\begin{aligned} \varOmega _S h^2=\frac{3s_0 h^{2}}{M_{Pl}\varrho _{cr}}\sqrt{\frac{15 x_c^3}{\pi ^3 g_{*\varrho }(T_c)}} \left( \frac{g_V^2M_S}{87.6}\right) ^{\!2}. \end{aligned}$$

(27)

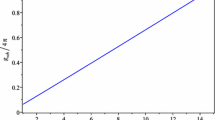
We use current particle data group values [63] for the entropy density $s_0=2891.2\,\mathrm {cm}^{-3}$ and the critical density $\varrho _{cr} h^{-2}=1.05371\times 10^{-5}\,\mathrm {GeV}/\mathrm {cm}^{3}$ to constrain the skyrmion parameter $g_V^2M_S$ from $\varOmega _S h^2\le \varOmega _{\mathrm {CDM}} h^2=0.1186$, see Fig. 1.

Fig. 1

Allowed values of the skyrmion parameter $g_V^2M_S$ for $5\le x_c\equiv M_S/T_c\le 10$

This shows that dark skyrmions can be PeV to multi-PeV scale dark matter for skyrmion couplings $g_V^2\lesssim 1$.

3 Constraints on the heavy dark mesons

We are particularly interested in the very heavy dark skyrmions as the dominant dark matter component, and therefore presume that the heavy w mesons do not contribute to $\varOmega _{CDM}$ at a significant level. I.e. besides $1\,\mathrm {TeV}\le m_w\ll M_S$, we also assume that $g_{wh}$ is sufficiently large to prevent thermal freeze-out of the dark mesons at a level where they would contribute a significant fraction to the dark matter abundance.³ On the other hand, we still assume $g_{wh}<4\pi$ for the perturbative calculation of the Higgs portal annihilation and recoil cross sections. The corresponding domains where $g_{wh}<4\pi$ and $\varOmega _w<0.01\varOmega _{CDM}$, $0.01\varOmega _{CDM}<\varOmega _w<0.1\varOmega _{CDM}$, and $0.1\varOmega _{CDM}<\varOmega _w<\varOmega _{CDM}$, respectively, are indicated in Fig. 2. The small blips near $m_w=4.2$ TeV occur as a consequence of the fact that the top quarks do not contribute to the effective number $g_*(T_f)$ of relativistic degrees of freedom at the freeze-out temperature $T_f$ any more if the thermal dark matter mass drops below that value.

Fig. 2

Regions in the $(m_w,g_{wh})$ plane where the Higgs portal coupling is perturbative and the contribution of thermally created heavy w mesons to dark matter is limited

Since we are interested in observational implications of the very heavy dark skyrmions as the dominant dark matter component, we assume that $\varOmega _w<0.1\varOmega _{CDM}$.

In addition to thermally created heavy dark mesons, annihilation of relic very heavy dark skyrmions will also generate heavy dark mesons, which will then annihilate into Standard Model states following the balance equation

$$\begin{aligned} \frac{dn_w}{dt}=\frac{\langle N_w\rangle }{4} n_S^2 v_{S{\overline{S}}}\pi L_S^2 -n_{w}^2\frac{g_{wh}^2}{6\pi }\langle s_w^{-1}\rangle . \end{aligned}$$

(28)

Energy conservation implies an estimate $\langle N_w\rangle /\langle s_w^{-1}\rangle \simeq 8M_S^2/\langle N_w\rangle$, and detailed balance for those non-thermally created w mesons yields

$$\begin{aligned} \frac{n_w}{n_S}\simeq \frac{\sqrt{48}\pi }{g_{wh}\sqrt{\langle N_w\rangle }}M_S L_Sv_{S{\overline{S}}}. \end{aligned}$$

(29)

This implies for the non-thermal dark w component the estimate

$$\begin{aligned} \frac{\varOmega _w}{\varOmega _S}=\frac{n_w m_w}{n_S M_S}\simeq 6\times 10^2\times \frac{\pi v_{S{\overline{S}}}}{g_{wh}\sqrt{\langle N_w\rangle }} \frac{m_w}{g_V^2 M_S}. \end{aligned}$$

(30)

According to Figs. 1 and 2, $m_w/g_V^2 M_S\sim 10^{-3}$ while $g_{wh}$ is of order 1. Furthermore, we certainly have $v_{S{\overline{S}}}\ll 1$ for the very heavy relic skyrmions, i.e. we can safely assume that the very heavy dark skyrmions are the dominant dark matter component in the model for the parameter ranges identified in Figs. 1 and 2. The “dark mediator bottleneck” that was considered as a generic possibility in Ref. [29] therefore does not materialize in this model.⁴

4 Direct signals from the dark skyrmions

Bramante et al. have pointed out that existing exclusion limits from direct searches can be extrapolated to very high masses [13], and we are particularly interested in direct search constraints on PeV scale dark skyrmions.

To calculate the expected nucleon recoil cross section from virtual Higgs exchange, we consider the skyrmion as a coherent superposition of the $\varvec{w}$ mesons, i.e. we use the coherent state

$$\begin{aligned} |S(t)\rangle= & {} \exp \!\left( -\frac{1}{2}\int \!d^3\varvec{k}\left| \varvec{\zeta }(\varvec{k},t)\right| ^2\right) \nonumber \\&\times \exp \!\left( \int \!d^3\varvec{k}\, \varvec{\zeta }(\varvec{k},t)\cdot \varvec{a}^+(\varvec{k})\right) \!|0\rangle \end{aligned}$$

(31)

with

$$\begin{aligned} \varvec{\zeta }(\varvec{k},t)=\sqrt{\frac{\omega (\varvec{k})}{2}}\varvec{w}_S(\varvec{k}) \exp [\mathrm {i}\omega (\varvec{k})t]. \end{aligned}$$

(32)

Here $\omega ^2(\varvec{k})=\varvec{k}^2+m_w^2$ and $\varvec{w}_S(\varvec{k})$ is the skyrmion in $\varvec{k}$ space,

$$\begin{aligned} \varvec{w}_S(\varvec{k})= & {} \int \!\frac{d^3\varvec{x}}{\sqrt{2\pi }^3}w_S(r)\hat{\varvec{x}} \exp (-\mathrm {i}\varvec{k}\cdot \varvec{x}) \nonumber \\= & {} \sqrt{\frac{2}{\pi }}\hat{\varvec{k}}\int _0^\infty \!dr\,\frac{r}{k}w_S(r)\sin (kr) =\hat{\varvec{k}}w_S(k). \end{aligned}$$

(33)

The state (31,32) has the property to yield the skyrmion as the expecation value of the $\varvec{w}$ meson operator

$$\begin{aligned} \varvec{w}(x)= & {} \int \!\frac{d^3\varvec{k}}{4\sqrt{\pi ^3\omega (\varvec{k})}}\left[ \varvec{a}(\varvec{k})\exp (\mathrm {i}k\cdot x)\right. \nonumber \\&+\left. \varvec{a}^+(\varvec{k})\exp (-\mathrm {i}k\cdot x)\right] , \end{aligned}$$

(34)

i.e.

$$\begin{aligned} \langle S(t)|\varvec{w}(x)|S(t)\rangle =w_S(r)\hat{\varvec{x}}. \end{aligned}$$

(35)

The state (31) and operator (34) are the interaction picture state and operator, respectively,

$$\begin{aligned} |S(t)\rangle= & {} \exp (\mathrm {i}H_0t/\hbar )|S\rangle , \end{aligned}$$

(36)

$$\begin{aligned} \varvec{w}(x)= & {} \exp (\mathrm {i}H_0t/\hbar )\varvec{w}(\varvec{x})\exp (-\mathrm {i}H_0t/\hbar ), \end{aligned}$$

(37)

with $H_0=\int d^3\varvec{k}\hbar \omega (\varvec{k})\varvec{a}^+(\varvec{k})\cdot \varvec{a}(\varvec{k})$. The Schrödinger picture skyrmion state $|S\rangle \equiv |S(0)\rangle$ is of course time-independent for the static skyrmion solution. The time-dependent factor $\exp [\mathrm {i}\omega (\varvec{k})t]$ in $\varvec{\zeta }(\varvec{k},t)$ arises from the shift of the factor from the interaction picture operator $\varvec{a}^+(\varvec{k},t)=\varvec{a}^+(\varvec{k})\exp [\mathrm {i}\omega (\varvec{k})t]$ into the amplitude $\varvec{\zeta }(\varvec{k})$.

The expectation value of the $\varvec{w}$ meson number in the skyrmion state is

$$\begin{aligned} \langle n_w\rangle= & {} \int \!d^3\varvec{k}\left| \varvec{\zeta }(\varvec{k},t)\right| ^2 =\frac{1}{2}\int \!d^3\varvec{k}\,\omega (\varvec{k})\varvec{w}^2_S(\varvec{k}) \nonumber \\= & {} 2\pi \int _0^\infty \!dk\,k^2\omega (k)w^2_S(k). \end{aligned}$$

(38)

This yields for the dark skyrmion-nucleon recoil cross section the estimate

$$\begin{aligned} \sigma _{SN}=\langle n_w\rangle ^2\sigma _{wN}, \end{aligned}$$

(39)

with the nucleon recoil cross section of the $\varvec{w}$ particles (for $m_w\gg m_N$)

$$\begin{aligned} \sigma _{wN}=\frac{1}{\pi }\left( \frac{g_{wh}g_{hN}v_h m_N}{m_h^2 m_w}\right) ^{\! 2}. \end{aligned}$$

(40)

We use the abundance weighted average nucleon mass in stable or long lived Xenon isotopes $m_N=930.6$ MeV in evaluations of Eqs. (39, 40). The coupling constant $g_{hN}$ in Eq. (40) is the effective Higgs-nucleon coupling [64] with a modern value $g_{hN}v_h=289$ MeV [65].

We use the semi-analytic approximation

$$\begin{aligned} \frac{w_S(r)}{f_w}=2\,\mathrm {arccos}\!\left[ 1-\exp \!\left( -\frac{\sqrt{2}}{a}g_Vf_wr\right) \right] , \end{aligned}$$

(41)

$a=0.9451$ [19], for the skyrmion profile in numerical evaluations. This yields Fig. 3 for the skyrmion profile in k space.

Fig. 3

The skyrmion in k space

The $\varvec{w}$ meson number is shown in Fig. 4.

Fig. 4

The $\varvec{w}$ meson number in the coherent state (31,32)

On the other hand, we expect that $\langle n_w\rangle \simeq M_S/m_w$. Fitting this expectation to the result (38) yields estimates $\langle n_w\rangle \simeq 47/gV^2$ and $m_w\simeq 1.3g_Vf_w$.

We can now collect the unknown heavy dark sector parameters in the nucleon recoil cross section in a single parameter, and for future comparisons with collider searches it is useful to express this in terms of the lighter $\varvec{w}$ particles,

$$\begin{aligned} \sigma _{SN}= & {} \frac{1}{\pi }\left( \frac{47 g_{hN}v_h m_N}{m_h^2}\right) ^{\! 2} \left( \frac{g_{wh}}{g_V^2 m_w}\right) ^{\! 2} \nonumber \\= & {} 2.071\times 10^{-7}\times \left( \frac{g_{wh}}{g_V^2 m_w}\right) ^{\! 2}. \end{aligned}$$

(42)

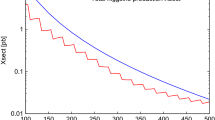
This yields the skyrmion-nucleon recoil cross sections in Fig. 5.

Fig. 5

The skyrmion-nucleon recoil cross section for $1\,\mathrm {TeV}\le \mu _w\equiv g_V^2 m_w/g_{wh}\le 1\,\mathrm {PeV}$

On the other hand, for comparisons with direct dark matter searches it is more useful to express this in terms of the actual dark matter mass $M_S$,

$$\begin{aligned} \sigma _{SN}= & {} \frac{1}{\pi }\left( \frac{47^2 g_{hN}v_h m_N}{m_h^2}\right) ^{\! 2} \left( \frac{g_{wh}}{g_V^4 M_S}\right) ^{\! 2} \nonumber \\= & {} 4.575\times 10^{-4}\times \left( \frac{g_{wh}}{g_V^4 M_S}\right) ^{\! 2}. \end{aligned}$$

(43)

This yields the skyrmion-nucleon recoil cross sections in Fig. 6.

Fig. 6

The skyrmion-nucleon recoil cross section for $100\,\mathrm {TeV}\le \mu _S\equiv g_V^4 M_S/g_{wh}\le 100\,\mathrm {PeV}$

Extrapolation of the XENON1T 1-year constraints to high masses implies $\sigma _{SN}\lesssim 8.3\times 10^{-46}\,\mathrm {cm}^2M_S[\mathrm {TeV}]\times {\mathcal {F}}(M_S)$ [66], where ${\mathcal {F}}(M_S)=|{\mathcal {S}}(1\,\mathrm {TeV})/{\mathcal {S}}(M_S)|^2$ is the corresponding ratio of Helm structure factors squared. Our result (43) then constrains the coupling constant $\eta \equiv g_{wh}/g_V^4$ as a function of dark skyrmion mass. This is displayed in Fig. 7.

Fig. 7

Direct search constraints on very heavy dark skyrmion parameters from the XENON1T 1-year results

The constraints yield $g_V\gtrsim 1.8\times g_{wh}^{1/4}$ for $M_S=100$ TeV and $g_V\gtrsim 0.32\times g_{wh}^{1/4}$ for $M_S=10$ PeV, i.e. an underlying gauge theory to induce the very heavy dark skyrmion model through the BKUYY mechanism [57] could require non-perturbative coupling strength $g_V$ to satisfy direct search constraints at the lower end of the non-thermal dark matter mass range, but very weak gauge coupling $g_V$ would be still possible for higher dark skyrmion masses.

The improved sensitivities of next-generation and next-to-next generation direct search experiments to $g_{wh}/g_V^4$ are displayed in Fig. 8.

Fig. 8

Sensitivities of future direct search experiments for the skyrmion coupling parameter $g_{wh}/g_V^4$

For actual parameters for the next-generation Xenon based experiments, we used XENONnT [67], but the anticipated sensitivities and time scales for LZ [68] and PandaX-4T [69] are comparable. For the DARWIN experiment see [70]. The neutrino floor is too close to the DARWIN limit in the high mass region to resolve on the logarithmic scales used in Fig. 8.

5 Conclusions

In the future, multi-tonne scale direct search experiments with long exposures will provide stronger constraints on very heavy dark matter, and this will eventually also probe the non-thermal dark matter mass range beyond the Griest-Kamionkowski bound around 100 TeV. Indeed, extrapolation from current direct search results already implies constraints for nucleon recoil cross sections at very high masses. It is therefore of interest to develop theoretical models and techniques for nucleon recoils from very heavy dark matter. We find that very heavy dark skyrmions from an early chiral phase transition provide an interesting avenue to theoretical descriptions of dark matter in the PeV mass range. Their non-thermal creation implies that the parameter $x_c=M_S/T_c$ is not determined from a freeze-out condition, but we can use estimates for $x_c$ from hadronic skyrmions. The requirement $\varOmega _S\le \varOmega _{\mathrm {CDM}}$ then constrains the parameter $g_V^2 M_S$ as a function of $x_c$, as shown in Fig. 1. We could also derive an estimate for the nucleon recoil cross section of the dark skyrmions through Higgs exchange (43). Comparison with direct search constraints then limits the parameter $\eta =g_{wh}/g_V^4$ as a function of skyrmion mass $M_S$, as shown in Fig. 7.