Effects of heavy meson loops on higher charmonia radiative transitions

Abstract

Radiative transitions between charmonium states offer an insight into the internal structure of heavy quark bound states within QCD. In this work, we performed a systematically investigation of the radiative transitions of $\psi (nS) \rightarrow \gamma \chi _{cJ}(mP)$ and $\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$ via intermediate charmed meson loop with a non-relativistic effective field theory. We only focus on the line-shape behavior of the distributions via different intermediate meson loops. Our results show that the coupled-channel effects of these decays are relatively weak, while the coupled channel effects has obvious enhancement when the inial (final) states are closed to the thresholds of charmed-mesons pair.

1 Introduction

Heavy quarkonia decays have played an important role in the hadronic physics since the first charmonium $J/\psi$ was discovered in November 1974 [1,2,3]. Until now, experimental progresses of the heavy quarkonia [4] have provided great opportunities for examining many interesting properties of Quantum Chromodynamics (QCD). Meanwhile, many theoretical studies, such as potential models, lattice QCD (LQCD), non-relativistic QCD (NRQCD), QCD sum rules, have been performed [5,6,7]. However, there are still many unresolved problems in charmonium physics [5]. More and more XYZ states have been announced by different experiments [4]. Not all of them can be described by conventional $q{{\bar{q}}}$ quark model [7,8,9,10]. Many investigations on the production and decay of these XYZ states have been carried out in order to understand their nature (see Refs. [11,12,13] for a review).

The X(4140) and X(4274) resonances were firstly observed in $B^+ \rightarrow J/\psi \phi K^+$ decay by CDF Collaboration [14, 15]. Very recently, the LHCb Collaboration confirmed the existence of the X(4140) and X(4274) in the $B^+ \rightarrow J/\psi \phi K^+$ and their quantum numbers are measured to be $J^{PC}=1^{++}$ [16]. In the same process, the LHCb Collaboration also observed two other resonances X(4500) and X(4700) for the first time and their quantum numbers are $J^{PC}=0^{++}$ [17]. After these observations of the LHCb Collaboration, several theoretical explainations, such as tetraquarks, molecular state, rescattering mechanism, have been proposed in order to understand their underlying structures [18,19,20,21,22,23,24,25,26].

The IML transition is regarded as an important nonperturbative transition mechanisms which has a long history [27,28,29] and recently are widely used to study the production and decays of ordinary and exotic states [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. Radiative transitions of charmonium states are of interest largely because they provide one of the few pathways between charmonium states with different quantum numbers. In this work, we will investigate the radiative transitions $\psi (nS)/\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$ via the intermediate charmed meson loops (IML) in a nonrelativistic effective field theory (NREFT).

This paper is organized as follows: In Sect. 2, we will introduce the formulas of the relevant effective lagrangian employed in this work. In Sect. 3, the numerical results are presented. A summary will be given in Sect. 4.

2 Radiative decay

Table 1 The charmed meson loops contributing to $\psi (nS)/\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$. The charmed mesons are listed as [M1, M3, M2]. Flavor labels are dropped for simplicity

Fig. 1

The hadron-level diagrams for $\psi (nS) \rightarrow \gamma \chi _{c0}(mP)$ via intermediate charmed meson loops

In principle, one should include all the possible intermediate-meson-exchange loops in the calculation, however, the break-down of the local quark-hadron duality allows us pick up the leading contributions as a reasonable approximation [29, 30]. The initial charmonium with $J^{PC}=1^{--}$ can couple to either two S-wave charmed mesons in a P-wave, or one S-wave and one P-wave charmed mesons in an S- or D-wave. As is discussed in Ref. [62], the mechanism with an S-wave coupling to the initial $1^{--}$ charmonium will greatly facilitate these similar processes. Therefore, we investigate the meson loops listed in Table 1 as the major contributions to $\psi (nS)/\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$.

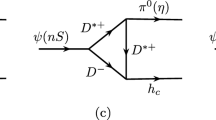
In Table 1, we list the possible charmed meson loops contributing to $\psi (nS)/\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$. There are three charmed mesons in each loop. To be specific, we denote the one connecting the initial charmonium and the photon as M1, the exchanged meson as M2 and one connecting two charmonia as M3. The meson Mi has mass $m_i$. For example, in Fig. 1, we plot all the dominant meson loops contributing to $\psi (nS)\rightarrow \gamma \chi _{c0}(mP)$, M1, M2 and M3 are the $D_1$, ${{\bar{D}}}$ and D, respectively in Fig. 1a.

Table 2 The initial and final charmonium mass spectrum (in unit of GeV) used in this work. The measured masses from the PDG [4], the calculated with screened potential (SP) in Ref. [102], linear potential (LP) in Ref. [67], and the results with SP and LP in [74] are listed

Fig. 2

$M_{\psi (nS)}$-dependence of the rescattering amplitude squared $|{\mathcal {M}}|^2$ of $\psi (nS)\rightarrow \gamma \chi _{cJ}(mP)$. The vertical dash lines indicate a and b: (from left to right)$D_{s1}^+(2460)D_s^-$ and $D_{s1}^+(2460)D_s^{*-}$ threshold, respectively; c $D_{s0}^*(2317)^+D_s^{*-}$ and $D_{s1}^+(2460)D_s^{*-}$ threshold, respectively

Fig. 3

$M_{\chi _{cJ}}$ dependence of the partial widths of $\psi (nS)\rightarrow \gamma \chi _{cJ}$. The vertical dashed lines indicted a: $D^0{\bar{D}}^0$ threshold, $D_s^+D_s^-$ threshold, and $D_s^{*+}D_s^{*-}$ threshold, respectively; b: $D_s^{*+}D_s^-$ threshold; c: $D^{*+}D^{*-}$ and $D_s^{*+}D_s^{*-}$ threshold, $\chi _{c2}$(3P)(NR), respectively

Fig. 4

$M_{\psi (nD)}$-dependence of the partial widths of $\psi (nD)\rightarrow \gamma \chi _{cJ}(mP)$. The vertical dashed lines indicted a and b: $D_1^0(2420){\bar{D}}_0$ threshold, $D_{s1}^+(2536)D_s^-$ and $D_{s1}^+(2536)D_s^{*-}$ threshold, respectively; c: $D_{s1}^+(2536)D_s^{*-}$ threshold

Fig. 5

$M_{\chi _{cJ}}$ dependence of the partial widths of $\psi (nD)\rightarrow \gamma \chi _{cJ}$. The vertical dashed lines indicted a: $D^0{\bar{D}}^0$ threshold, $D_s^+D_s^-$ threshold, and $D_s^{*+}D_s^{*-}$ threshold, respectively; b: $D_s^{*+}D_s^-$; c: $D^{*+}D^{*-}$ and $D_s^{*+}D_s^{*-}$ threshold, respectively

Based on the heavy quark symmetry, the relevant effective Lagrangians used in this work are as follows [63, 64],

$$\begin{aligned} \mathcal {L_S}= & {} {g_S}Tr \left[ {R_{c{\bar{c}}}}{{\bar{S}}_{2i}}{{\bar{H}}_{1i}} \right] + {\text{ H }.c.} , \nonumber \\ \mathcal {L_P}= & {} {g_P}Tr \left[ {P^\mu _{c {\bar{c}}}}{{\bar{H}}_{2i}}\gamma ^\mu {{\bar{H}}_{1i}}\right] + {\text{ H }.c.} , \nonumber \\ \mathcal {L_D}= & {} \frac{g_D}{\sqrt{2}}\{Tr\left[ {J^{\mu \nu }_{c{\bar{c}}}}{{\bar{H}}_{2i}}\gamma ^\nu {{\bar{T}}^\mu _{1i}} \right] \nonumber \\&-Tr\left[ {J^{\mu \nu }_{c{\bar{c}}}}{{\bar{T}}^\mu _{2i}}\gamma ^\nu {{\bar{H}}_{1i}}\right] \} + {\text{ H }.c.} \, , \end{aligned}$$

(1)

with

$$\begin{aligned} {R_{c{\bar{c}}}}= & {} \frac{{1 + \not v}}{2}({\psi ^\mu }{\gamma _\mu } - {\eta _c}{\gamma _5})\frac{{1 - \not v}}{2} \, , \nonumber \\ P^\mu _{c {\bar{c}}}= & {} \frac{1 + \not v}{2}(\chi ^{\mu \alpha }_{c2}\gamma ^{\alpha }+\frac{1}{\sqrt{2}}\epsilon _{\mu \nu \alpha \beta }v^{\alpha }\gamma ^{\beta }\chi ^{\nu }_{c1}\nonumber \\&+\frac{1}{\sqrt{3}}(\gamma ^{\mu }-v^{\mu })\chi _{c0}+h^\mu _c\gamma _5)\frac{1 - \not v}{2} \, \nonumber \\ J^{\mu \nu }_{c {\bar{c}}}= & {} \frac{1 + \not v}{2}(H^{\mu \nu \alpha }_3\gamma _\alpha +\frac{1}{6}(\epsilon ^{\mu \alpha \beta \gamma }v_\alpha \gamma _\beta H^\nu _{2\gamma }\nonumber \\&+\epsilon ^{\nu \alpha \beta \gamma }v_\alpha \gamma _\beta H^\mu _{2\gamma }) \nonumber \\&+\frac{1}{2}\sqrt{\frac{3}{5}}((\gamma ^\mu -v^\mu )H^\nu _1+(\gamma ^\nu -V^\nu )H^\mu _1)\nonumber \\&+\frac{1}{\sqrt{15}}(g^{\mu \nu }-v^\mu v^\nu )\gamma ^\alpha H^\alpha _1+K^{\mu \nu }\gamma _5)\frac{1 - \not v}{2} \end{aligned}$$

(2)

where $v^\mu$ is the heavy quark four-velocity. $H_A$ and $K_A$ are the effective fields of the various members of the multiplets with total spin $J = A$.

The charmed meson doublets are collected into the following superfields [64]:

$$\begin{aligned} H_{1i}= & {} \frac{1 + \not v}{2}[D_i^{*\mu } \gamma _\mu - D_i \gamma _5] \, , \nonumber \\ H_{2i}= & {} [ {{\bar{D}}}_i^\mu \gamma _\mu + {{\bar{D}}}_i\gamma _5]\frac{1 - \not v}{2} \, , \nonumber \\ S_{1i}= & {} \frac{1 + \not v}{2}[D_{1i}^\mu \gamma _\mu \gamma _5 - D_{0i}] \ \nonumber \\ S_{2i}= & {} [{{\bar{D}}}_{0i}-{{\bar{D}}}_{1i}^\mu \gamma _\mu \gamma _5]\frac{1 - \not v}{2} \, , \nonumber \\ T^\mu _{1i}= & {} \frac{1 + \not v}{2}[D^{\mu \nu }_2\gamma _\nu \nonumber \\&-\sqrt{\frac{3}{2}}{\widetilde{D}}_{1\nu }\gamma _5(g^{\mu \nu }-\frac{1}{3}\gamma ^\nu (\gamma ^\mu -v^\mu ))] \, , \nonumber \\ T^\mu _{2i}= & {} [-D^{\mu \nu }_2\gamma _\nu \nonumber \\&-\sqrt{\frac{3}{2}}{\widetilde{D}}_{1\nu }\gamma _5(g^{\mu \nu }+\frac{1}{3}\gamma ^\nu (\gamma ^\mu -v^\mu ))]\frac{1 - \not v}{2} \, , \end{aligned}$$

(3)

where $D^{(*)} = (D^{0(*)},D^{+(*)},D^{+(*)}_s)$, $H_{2i}(S_{2i},T^\mu _{2i})$ is the charged conjugate of $H_{1i}(S_{1i},T^\mu _{1i})$ and i is the light flavor index. Here, we should notice that every heavy field H will contain a factor $\sqrt{m_{H}}$ for normalization in the heavy hadron chiral perturbation theory.

In addition, the lagrangian relevant to the charmed mesons and photon are expressed as [63, 65],

$$\begin{aligned} {\mathcal {L}}_{\gamma }= & {} \frac{e{\widetilde{\beta }}}{4}Tr[{\bar{H}}_{1i}S_{1j}\sigma _{\mu \nu }F_{\mu \nu }Q_{ji}]+ie{\bar{\mu }} Tr[{{\bar{H}}_{1i}T^\mu _{1j}\gamma ^\nu }F_{\mu \nu }{Q_{ji}}] ,\nonumber \\ \end{aligned}$$

(4)

where $F_{\mu \nu } = \partial \mu A_\nu - \partial \nu A_\mu$ is the electromagnetic field tensor, and $Q = diag\{2/3,-1/3,-1/3\}$.

The explicit expression of transition for $\psi (nS) \rightarrow \gamma \chi _{cJ}(nP)$ and $\psi (nD) \rightarrow \gamma \chi _{cJ}(nP)$ amplitudes are given in Appendix.

3 Numerical results

The $\psi (4040)$ and $\psi (4160)$ are widely accepted as the $\psi (3S)$ state [67,68,69,70] and $\psi (2D)$ state [67,68,69], respectively. In Ref. [69], the author argue that the $\psi (4260)$ state can be assigned as 4S charmonium state under the Dirac potential model. The $\psi (4360)$ state was explained as a 3D state from a quark potential model calculation [71], while the $\psi (4360)$ was explained to be the 4S state [69]. In Refs. [62, 67, 68], the $\psi (4415)$ was widely assigning to be the 4S state, while the $\psi (4415)$ is taken to be $\psi (5S)$ state in [73]. The $\psi (4415)$ was also interpreted as 3D or 4D charmonium state depending on different Dirac potential models [69]. In Ref. [71], $\psi (4660)$ was explained as the 5S vector charmonium state. The author proposed that $\psi (4660)$ belongs to the 4D state under potential models [69]. The X(3927) was observed in the $\gamma \gamma \rightarrow D{\bar{D}}$ process by Belle [75] and Babar [76] collaborations, and has been a good candidate for $\chi _{c2}(2P)$ state. In the LP model the calculated mass of $\chi _{c0}(3P)$ is about 4310 MeV [74], which is very close to the mass of X(4350). The higher charmonium states with $J^{PC}=1^{++}$, such as $\chi _{c1}(2P)$, and $\chi _{c1}(3P)$, are still not established. The X(3872) resonance has the same quantum numbers as $\chi _{c1}(2P)$ but with a much lighter mass than potential quark model predictions. The quantum numbers of the charmoniumlike states X(4140) and X(4274) observed by the LHCb Collaboration [16] are determined to be $J^{PC}=1^{++}$. According to the predicted mass from the linear potential model, the X(4274) might be a good candidate of $\chi _{c1}(3P)$. However, within the screened potential model, X(4140) seems to favor the $\chi _{c1}(3P)$ state. The charmonium-like state $X^*(3860)$ observed in the process $e^+e^- \rightarrow J/\psi D{\bar{D}}$ by the Belle collaboration [72] serves as a good candidate for the $\chi _{c0}(2P)$ state. The measured mass and width fit the expectation of the $\chi _{c0}(2P)$ state predicted in the potential models [74].

In Table 2, we list the initial and final charmonium mass spectrum used in this work. Here, we mainly focus on the line-shape behavior of the distributions via different intermediate meson loops.

3.1 $\psi (nS) \rightarrow \gamma \chi _{cJ}(mP)$ radiative decays

In Fig. 2, we present the results for $\psi (nS)$ invariant mass distributions corresponding to these rescattering processes $\psi (nS)\rightarrow \gamma \chi _{cJ}(mP)$ via intermediate charmed meson loops. In our model, the contribution of the IML transitions are considered as unquenched effects. The contributions of IML are only about $10^{-2}$ keVs. In Fig. 2a, one may notice that there are cusps around the thresholds of $D_{s1}^+(2460)D_s^-$ and $D_{s1}^+(2460)D_s^{*-}$, respectively. For the process $\psi (nS)\rightarrow \gamma \chi _{c0}(mP)$ in Fig. 1, there are three subdiagrams: (a) $\{D_1^\prime {\bar{D}}[D]\}$, (b) $\{D_1^\prime {\bar{D}}^*[D^*]\}$, and (c) {$D_0{\bar{D}}^*[D^*]$}. In the heavy quark limit, the amplitudes corresponding to the above three subdiagrams have a simple relation ${\mathcal {M}}_a : {\mathcal {M}}_b : {\mathcal {M}}_c = 3:2:-1$, which implies that the main contribution may come from the $\{D_1^\prime {\bar{D}}[D]\}$ loop. As shown in Fig. 2a, the former cusps stayed at $D_{s1}^+(2460)D_s^-$ threshold are much higher than the later stayed at $D_{s1}^+(2460)D_s^{*-}$ threshold. For $\psi (nS)\rightarrow \gamma \chi _{c1}(mP)$ decays, there are two cusps around the thresholds of $D_{s1}^+(2460)D_s^-$ and $D_{s1}^+(2460)D_s^{*-}$ as shown in Fig. 2b. These two different cusps are of the same order due to ${\mathcal {M}}_{[D_1^\prime ,{{\bar{D}}},D^*]} : {\mathcal {M}}_{[D_1^\prime ,{{\bar{D}}}^*,D]} = 1:1$. The two-particle threshold of $D_{s1}^+(2460)D_s^-$ is very closed to the mass of $\psi (4415)$, so if we take $\psi (4415)$ as the $\psi (4S)$, it maybe the ideal state to produce $\chi _{c0}(mP)$ and $\chi _{c1}(mP)$. In Fig. 2c, the cusps around $D_{s0}^*(2317)^+D_s^{*-}$ are small to stimulate the structure of $\chi _{c2}(mP)$. An obvious threshold enhancement structure appears in the position of $D_{s1}^+(2460)D_s^{*-}$ threshold, which implies that the effects of coupled channels maybe can stimulate the structure of $\chi _{c2}(3P)$ . Theoretically, the contribution from the $D_1^\prime {\bar{D}}^*[D^*]$ and $D_0{\bar{D}}^*[D^*]$ loops should be the same, but we only notice one obvious threshold enhancement structure in Fig. 2c, because the phase space of $D^*_{s0}(2317)\rightarrow D^*_s \gamma$ decay is very small. We also see that the thresholds of $D_{s1}(2460)D_s$, $D_{s1}(2460)D_s^*$, $D_{s0}^*(2317)D_s^*$ are closed to the mass of X(4500) in Fig. 2. In other words, these rescattering amplitude maybe simulate the signal of the structure of X(4500).

In Fig. 3, the numerical results for $\chi _{cJ}$ invariant mass distributions corresponding to these rescattering processes $\psi (nS)\rightarrow \gamma \chi _{cJ}(mP)$ via intermediate meson loops are presented. Notice that there are still several cusps in Fig. 3a which stay around the thresholds of $D^0{\bar{D}}^0$, $D_s^+D_s^-$ and $D_s^{*+}D_s^{*-}$ on the precess of $\psi (nS)\rightarrow \gamma \chi _{c0}$, respectively. The former two cusps seems to be obvious, while the later could be ignored. There are several peaks in Fig. 3b appeared in the position of $\chi _{c1}$(2P)(PDG) and $D_s^{*+}D_s^-$ threshold. Since the mass of $\chi _{c1}$(2P)(PDG) is very closed to the threshold of $D^0{\bar{D}}^{*0}$, the coupled channel effects enhanced. At the same line of $\psi (nS)(\hbox {n} =3,4,5)$, we can conclude that the distributions corresponding to $\chi _{c1}$(2P)(PDG) are much larger than $\chi _{c1}$(2P)(NR). Compared with $\psi (4040), X(4260), X(4360)$, the radiative decay of $\psi (4415)$ and X(4660) maybe more easier to produce $\chi _{c1}$(2P) (PDG) state, especially the $\psi (4415)$ when $M_{\chi _{c1}}$ in the position of $D{\bar{D}}^*$ threshold. Several peaks in Fig. 3c also appeared in the position of $D^{*+}D^{*-}$ and $D_s^{*+}D_s^{*-}$ threshold. We can conclude that X(4660) maybe the ideal scene to generate $\chi _{c2}$(mP) with m =1,2,3 than others. This can be understood the more closed of the mass of X(4660) to $D_1^{\prime }{\bar{D}}^*$ or $D_0{\bar{D}}^{0*}$ threshold, the more easier enhanced of coupled channel effects.

3.2 $\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$ radiative decays

In Fig. 4, we show the numerical results for $\psi (nD)$ invariant mass distributions corresponding to these rescattering processes $\psi (nD)\rightarrow \gamma \chi _{cJ}(mP)$ via intermediate meson loops. Near the threshold of charmed meson pairs, there are obvious enhancement. For the process $\psi (nD)\rightarrow \gamma \chi _{c0}(mP)$, the intermediated charmed meson loops are displayed in Table 1. The amplitudes has the following relationship ${\mathcal {M}}_{D_1{\bar{D}}[D]} : {\mathcal {M}}_{D_1{\bar{D}}^*[D^*]} : {\mathcal {M}}_{D_2{\bar{D}}^*[D^*]}= 6:1:1$ in the heavy quark limit. Therefore when $\sqrt{s} = M_{D_{s1}^+(2536)} + M_{D_s^{*-}}$, we expect that $\chi _{c0}(mP)$ could be observed. There is just one obvious cusps appeared in the position of $D_{s1}^+(2536)D_s^{*-}$ threshold on the process of $\psi (nD)\rightarrow \gamma \chi _{c2}(3P)$ in Fig. 4c. Concerning $\psi (nD)\rightarrow \gamma \chi _{c2}$ via IML , and ${\mathcal {M}}_{ D_1{\bar{D}}^*[D^*]} : {\mathcal {M}}_{D_2{\bar{D}}^*[D^*]} = 5:-1$. It also may because the mass of $\chi _{c2}(3P)$(NR) are much closed to the $D_s^{*+}D_s^{*-}$ threshold than other radiative states, and the threshold of $D_1 {\bar{D}}^*$ or $D_2 {\bar{D}}^*$ mesons are far away from the mass region of $M_{\psi (nD)}$. The mass of X(4660) is extremely closed to $D_{s1}^+(2536)D_s^{*-}$ threshold, so we may search for $\chi _{c2}(3P)$ in the radiative decay of X(4660). Different from Fig. 2b, the strength of Fig. 4b are much larger in the same position of $\psi (nS)$. The cusps stay around the thresholds of $D_1^0(2420){\bar{D}}_0$, $D_{s1}^+(2536)D_s^-$ and $D_{s1}^+(2536)D_s^{*-}$. We notice that there are two anomalous peaks appears in Fig. 4b, whose positions are neither the genuine particles nor the threshold of $D_{sJ}{\bar{D}}_s$. Therefore it is possible that the threshold effects illustrated in Fig. 4b may result in some new resonance. So, our results shows that the coupled-channels effects may be more important when the initial states are close to the thresholds of charmed-mesons pair. It also shows that the decay widths of the excited state $\chi _{c0}$(3P) and $\chi _{c1}$(3P) could be quite small.

The numerical results for $\chi _{cJ}$ invariant mass distributions corresponding to these rescattering processes $\psi (nD)\rightarrow \gamma \chi _{cJ}$ via intermediate meson loops are displayed in Fig. 5. We choose four different masses of $\psi (nD)$ [4, 67]. For $\psi (nD)\rightarrow \gamma \chi _{c0}(mP)$, one notice that there are three cusps around the thresholds of $D^0{\bar{D}}^0$, $D_s^+D_s^-$, and $D_s^{*+}D_s^{*-}$ as shown in Fig. 5a. The largest enhancement at the position of $D^0{\bar{D}}^0$ threshold is for the case of $M_{\psi (nD)}=4.191$ GeV. This is because the intermediate three charmed mesons are almost on-shell, which lead to the largest coupled channel effects. Only a small cusp stays at the $D_s^{*+}D_s^{*-}$ threshold in Fig. 5a. Two obvious peaks in Fig. 5b also appeared in the position of $D^{0}{{\bar{D}}}^{*0}$ and $D_s^{*+}D_s^{-}$ threshold. In Fig. 5c, there are two peaks in the position of $D^{*+}D^{*-}$ and $D_s^{*+}D_s^{*-}$ thresholds for $\psi (nD) \rightarrow \gamma \chi _{c2}(mP)$. Here, one should notice the coupled channels effects and phase space effects will both affect these cusps. For $\psi (4D) \rightarrow \gamma \chi _{c0,1}(mP)$ in Fig. 5a, b, the phase space may affect the cusp strength more important with the increasing mass of $\chi _{c0,1}(mP)$. For $\psi (4D) \rightarrow \gamma \chi _{c2}(mP)$ in Fig. 5c, the coupled channel effects may dominate the cusp strength.

4 Summary

In this work, we have systematically investigated these radiative transitions of $\psi (nS) \rightarrow \gamma \chi _{cJ}(mP)$ and $\psi (nD) \rightarrow \gamma \chi _{cJ}(mP)$ via intermediate charmed meson loop(IML) with NREFT. We present the line-shape behaviors of the distributions via different intermediate meson loops. We only focus on the line-shape behavior of the distributions via different intermediate meson loops. Our results show that the coupled-channel effects of these decays are relatively weak, while the coupled channel effects has obvious enhancement when the inial (final) states are closed to the thresholds of charmed-mesons pair. The coupled-channel effects in the channels of excited states should be testable experimentally in the future.

Appendix: The transitions amplitude

In this appendix, we present the transitions amplitudes for the intermediate meson loops in Table 1. $p_1$, $p_2$, $p_3$ are the four-vector momenta for the initial charmonium, final photon and final charmonia, respectively. $q_1$, $q_2$, and $q_3$ are the four-vector momenta for the intermediate charmed mesons. $\epsilon _1$, $\epsilon _2$ and $\epsilon _3$ are the polarization vectors for the initial stat, final photon, and final charmonium, respectively. The velocity v can be taken as (1, 0, 0, 0) in the static limit. $\epsilon _{\alpha \beta \mu \nu }$ is the antisymmetric Levi-Civita tensor and $\epsilon _{0123}=+1$.

The explicit transition amplitudes for $\psi (nS)(p_1)\rightarrow \gamma (p_2)\chi _{c0}(p_3)$ are given as follows:

$$\begin{aligned}&{\mathcal {M}}_{[D_1,{{\bar{D}}},D]}\nonumber \\&\quad = \frac{\sqrt{3}}{2}g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \frac{1}{q_3^2-m_3^2} \epsilon _{1\alpha } \epsilon ^*_{2\beta } [v\nonumber \\&\qquad \cdot p_2 g^{\alpha \beta }-v^{\beta }p^{\alpha }_2], \nonumber \\&{\mathcal {M}}_{[D_1,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = \frac{2}{2\sqrt{3}}g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1^2} \frac{1}{q_2^2-m_2^2} \frac{1}{q_3^2-m_3^2}\epsilon _{1\alpha } \epsilon ^*_{2\beta } [v\nonumber \\&\qquad \cdot p_2 g^{\alpha \beta }-v^{\beta }p^{\alpha }_2], \nonumber \\&{\mathcal {M}}_{[D_0,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = - \frac{1}{2\sqrt{3}}g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1^2} \frac{1}{q_2^2-m_2^2} \frac{1}{q_3^2-m_3^2} \epsilon _{1\alpha } \epsilon ^*_{2\beta } [v\nonumber \\&\qquad \cdot p_2 g^{\alpha \beta }-v^{\beta }p^{\alpha }_2]. \end{aligned}$$

(5)

The explicit transition amplitudes for $\psi (nS)(p_1) \rightarrow \gamma (p_2) \chi _{c1}(p_3)$ are given as follows:

$$\begin{aligned}&{\mathcal {M}}_{[D_1,{{\bar{D}}},D^*]}\nonumber \\&\quad = \frac{1}{\sqrt{2}}g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _{\alpha \beta \mu \nu } p^{\alpha }_2\epsilon _{1}^\mu \epsilon ^{*\beta }_{2} \epsilon ^{*\nu }_{3}, \nonumber \\&{\mathcal {M}}_{[D_1,{{\bar{D}}}^*,D]}\nonumber \\&\quad = \frac{1}{\sqrt{2}}g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2}\epsilon _{\alpha \beta \mu \nu } p^{\alpha }_2\epsilon _{1}^{\mu } \epsilon ^{*\beta }_{2} \epsilon ^{*\nu }_{3}. \end{aligned}$$

(6)

The explicit transition amplitudes for $\psi (nS)(p_1) \rightarrow \gamma (p_2) \chi _{c2}(p_3)$ are given as follows:

$$\begin{aligned}&{\mathcal {M}}_{[D_1,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = - g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _1^\nu \epsilon ^*_{2\beta }\epsilon ^*_{3\mu \nu } [v^{\beta }p^{\mu }_2 - v\cdot p_2 g^{\beta \mu }], \nonumber \\&{\mathcal {M}}_{[D_0,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = - g_S g_P e{\widetilde{\beta }}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \nonumber \\&\qquad \frac{1}{q_2^2-m_2^2} \frac{1}{q_3^2-m_3^2} \epsilon _1^\nu \epsilon ^*_{2\beta }\epsilon ^*_{3\mu \nu } [v^{\beta }p^{\mu }_2 - v\cdot p_2 g^{\beta \mu }]\, . \end{aligned}$$

(7)

The explicit transition amplitudes for $\psi (nD)(p)\rightarrow \gamma (p_1)\chi _{c0}(p_2)$ are given as follows:

$$\begin{aligned}&{\mathcal {M}}_{[D_1,{{\bar{D}}},D]}\nonumber \\&\quad = -\sqrt{10}g_D g_P e\bar{\mu }Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _{1\alpha } \epsilon ^*_{2\beta } [v^{\beta }p^{\alpha }_2-v\cdot p_2 g^{\alpha \beta }], \nonumber \\&{\mathcal {M}}_{[D_1,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = -\frac{\sqrt{10}}{6}g_D g_P e\bar{\mu }Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _{1\alpha } \epsilon ^*_{2\beta } [v^{\beta }p^{\alpha }_2-v\cdot p_2 g^{\alpha \beta }], \nonumber \\&{\mathcal {M}}_{[D_2,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = -\frac{\sqrt{10}}{6}g_D g_P e\bar{\mu }Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _{1\alpha } \epsilon ^*_{2\beta } [v^{\beta }p^{\alpha }_2-v\cdot p_2 g^{\alpha \beta }] \, . \end{aligned}$$

(8)

The explicit transition amplitudes for $\psi (nD)(p) \rightarrow \gamma (p_1) \chi _{c1}(p_2)$ are given as follows:

$$\begin{aligned}&{\mathcal {M}}_{[D_1,{{\bar{D}}},D^*]}\nonumber \\&\quad = - \sqrt{\frac{5}{3}}g_D g_P e\bar{\mu }Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \frac{1}{q_3^2-m_3^2} \nonumber \\&\qquad \times \epsilon _1^\alpha \epsilon _{2\tau } \epsilon ^{*\nu }_3 \epsilon _{\alpha \beta \mu \nu }[p^{\mu }_2(g^{\beta \tau }-v^{\beta }v^{\tau })+g^{\beta \tau }(p_2^\mu -v\cdot p_2 v^\mu )], \nonumber \\&{\mathcal {M}}_{[D_1,{{\bar{D}}}^*,D]}\nonumber \\&\quad = \sqrt{\frac{5}{3}}g_D g_P e\bar{\mu }Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _1^\alpha \epsilon _{2\tau } \epsilon ^{*\nu }_3 \epsilon _{\alpha \beta \mu \nu }v^{\mu }[v^\tau p_1^\beta -v\cdot p_2 g^{\beta \tau }]. \end{aligned}$$

(9)

The explicit transition amplitudes for $\psi (nD)(p) \rightarrow \gamma (p_1) \chi _{c2}(p_2)$ are given as follows:

$$\begin{aligned}&{\mathcal {M}}_{[D_1,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = \frac{5}{\sqrt{30}} g_D g_P e{{\bar{\mu }}}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _1^\alpha \epsilon ^*_{2\beta }\epsilon ^*_{3\alpha \mu } [v\cdot p_2 g^{\beta \mu }-v^{\beta }p^{\mu }_2], \nonumber \\&{\mathcal {M}}_{[D_2,{{\bar{D}}}^*,D^*]}\nonumber \\&\quad = - \frac{1}{\sqrt{30}} g_D g_P e{{\bar{\mu }}}Q\int \frac{d^4q_2}{(2\pi )^4}\frac{1}{q_1^2-m_1} \frac{1}{q_2^2-m_2^2} \nonumber \\&\qquad \frac{1}{q_3^2-m_3^2} \epsilon _1^\alpha \epsilon ^*_{2\beta }\epsilon ^*_{3\alpha \mu } [v\cdot p_2 g^{\beta \mu }-v^{\beta }p^{\mu }_2] \, . \end{aligned}$$

(10)

The charmonium spectrum and their strong decays into open-charm meson pairs are investigated in Refs. [74, 104]. Here the coupling constants $g_S$, $g_P$, and $g_D$ may be determined by the relevant data of Refs. [74, 104]. Recently, the $\psi (4415)$ is widely accepted to be $\psi (4S)$ state. With $\Gamma _{\psi (4415)\rightarrow DD_1}=12$ MeV and $\Gamma _{\psi (4415)\rightarrow D^*D_0}=8.7$ MeV, we get $g_S\simeq 0.36 {\text{ G }eV}^{-1/2}$. With $M_{\chi _{c0}(2P)}=3.869$ GeV and $\Gamma _{\chi _{c0}(2P) \rightarrow D{\bar{D}}}=22.3$ MeV calculated in LP model [74, 104], we get $g_P \simeq 1.28 \, {\text{ G }eV}^{-1/2}$. We get $g_D\simeq 0.30 {\text{ G }eV}^{-1/2}$ with $M_{\psi (3D)}=4.486$ GeV and $\Gamma _{\psi (3D) \rightarrow DD_1}=9.8$ MeV. The coupling constants ${\tilde{\beta }}$ is relevant to radiative decay rates of the charmed mesons and can be extracted according to the experimental data. We take the values of $|{\tilde{\beta }}|=0.42$ $\hbox {GeV}^{-1}$ estimated in Ref. [65]. There is no experimental measurement on the radiative decays of the P-wave charmed mesons. We take the ${\bar{\mu }} \simeq 0.47$ $\hbox {GeV}^{-1}$ with the help of the predictions of $\Gamma (D_1^0 \rightarrow D^{(*)0}\gamma )$ [66].