Abstract
The TOTEM experiment at the LHC has performed the first measurement at \(\sqrt{s} = 13\,\mathrm{TeV}\) of the \(\rho \) parameter, the real to imaginary ratio of the nuclear elastic scattering amplitude at \(t=0\), obtaining the following results: \(\rho = 0.09 \pm 0.01\) and \(\rho = 0.10 \pm 0.01\), depending on different physics assumptions and mathematical modelling. The unprecedented precision of the \(\rho \) measurement, combined with the TOTEM total cross-section measurements in an energy range larger than \(10\,\mathrm{TeV}\) (from 2.76 to \(13\,\mathrm{TeV}\)), has implied the exclusion of all the models classified and published by COMPETE. The \(\rho \) results obtained by TOTEM are compatible with the predictions, from other theoretical models both in the Regge-like framework and in the QCD framework, of a crossing-odd colourless 3-gluon compound state exchange in the t-channel of the proton–proton elastic scattering. On the contrary, if shown that the crossing-odd 3-gluon compound state t-channel exchange is not of importance for the description of elastic scattering, the \(\rho \) value determined by TOTEM would represent a first evidence of a slowing down of the total cross-section growth at higher energies. The very low-|t| reach allowed also to determine the absolute normalisation using the Coulomb amplitude for the first time at the LHC and obtain a new total proton–proton cross-section measurement \(\sigma _{\mathrm{tot}} = (110.3 \pm 3.5)\,\mathrm{mb}\), completely independent from the previous TOTEM determination. Combining the two TOTEM results yields \(\sigma _{\mathrm{tot}} = (110.5 \pm 2.4)\,\mathrm{mb}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The TOTEM experiment at the LHC has measured the differential elastic proton–proton scattering cross-section as a function of the four-momentum transfer squared, t, down to \(|t| = 8\times 10^{-4}\,\mathrm{GeV^2}\) at the centre-of-mass energy \(\sqrt{s} = 13\,\mathrm{TeV}\) using a special \(\beta ^* = 2.5\,\mathrm{km}\) optics. This allowed to access the Coulomb-nuclear interference (CNI) and to determine the \(\rho \) parameter, the real-to-imaginary ratio of the forward hadronic amplitude, with an unprecedented precision.
Measurements of the total proton–proton cross-section and \(\rho \) have been published in the literature from the low energy range of \(\sqrt{s} \sim 10\,\mathrm{GeV}\) up to the LHC energy of \(8\,\mathrm{TeV}\) [1]. Such experimental measurements have been parametrised by a large variety of phenomenological models in the last decades, and were analysed and classified by the COMPETE collaboration [2].
It is shown in the present paper that none of the above-mentioned models can describe simultaneously the TOTEM \(\rho \) measurement at \(13\,\mathrm{TeV}\) and the ensemble of the total cross-section measurements by TOTEM ranging from \(\sqrt{s} = 2.76\) to \(13\,\mathrm{TeV}\) [3,4,5,6]. The exclusion of the COMPETE published models is quantitatively demonstrated on the basis of the p-values reported in this work. Such conventional modelling of the low-|t| nuclear elastic scattering is based on various forms of Pomeron exchanges and related crossing-even scattering amplitudes (not changing sign under crossing, cf. Section 4.5 in [7]).
Other theoretical models exist both in terms of Regge-like or axiomatic field theories [8] and of QCD [9,10,11] – they are capable of predicting or taking into account several effects confirmed or observed at LHC energies: the existence of a sharp diffractive dip in the proton–proton elastic t-distribution also at LHC energies [12], the deviation of the elastic differential cross-section from a pure exponential [4], the deviation of the elastic diffractive slope, B, from a linear \(\log (s)\) dependence as a function of the centre-of-mass energy [6], the variation of the nuclear phase as a function of t, the large-|t| power-law behaviour of the elastic t-distribution with no oscillatory behaviour and the growth rate of the total cross-section as a function of \(\sqrt{s}\) at LHC energies [6]. These theoretical frameworks foresee the possibility of more complex t-channel exchanges in the proton–proton elastic interaction, including crossing-odd scattering amplitude contributions (changing sign under crossing).
The crossing-odd contributions relevant for high energies (where secondary Reggeons are expected to be negligible [13]) were associated with the concept of the Odderon (the crossing-odd counterpart of the Pomeron [14]) invented in the 70’s [15, 16] and later confirmed as an essential QCD prediction [9,10,11, 17, 18]. They are quantified in QCD (see e.g. Refs. [19, 20]) where they are represented (in the most basic form) by the exchange of a colourless 3-gluon compound state in the t-channel in the non-perturbative regime (|t| ranging from 0 up to roughly the diffractive dip and bump). Such a state would naturally have \(J^{PC}=1^{-}\) quantum numbers and is predicted by lattice QCD with a mass of about 3 to \(4\,\mathrm{GeV}\) (also referred to as vector glueball) [21, 22] as required by the s-t channel duality [23]. For completeness, an exchange of a 3-gluon state may also be crossing even, e.g. in case the state evolves (collapses) into 2 gluons [24,25,26]. However hereafter, unless specified differently, we will refer only to crossing-odd 3-gluon exchanges – the crossing-even 3-gluon exchanges will be included in the Pomeron amplitude as a sub-leading contribution (suppressed by \(\alpha _{\mathrm{s}}\) with respect to the 2-gluon exchanges).
Experimental searches for a 3-gluon compound state have used various channels. In central production the 3-gluon state emitted by one proton may fuse with a Pomeron (photon) emitted from the other proton (electron/positron) and create a detectable meson system [26, 27]. However, such processes are dominated by pomeron–photon (photon–photon) fusion, making the observation of a 3-gluon state difficult. In elastic scattering at low energy [28], the observation of 3-gluon compound state is complicated by the presence of secondary Regge trajectories influencing the potential observation of differences between the proton–proton and proton–antiproton scattering. At high energy (gluonic-dominated interactions) [29], one could investigate for both proton–proton and proton–antiproton scattering the diffractive dip, where the imaginary part of the Pomeron amplitude vanishes; however there are no measurements nor facilities allowing a comparison at the same fixed \(\sqrt{s}\) energy.
The Coulomb-nuclear interference at the LHC is an ideal laboratory to probe the exchange of a virtual odd-gluons compound state, because it selects the required quantum numbers in the t-range where the interference terms cannot be neglected with respect to the QED and nuclear amplitudes squared. The highest sensitivity is reached in the t-range where the QED and nuclear amplitudes are of similar magnitude, thus this has been the driving factor in designing the acceptance requirements then achieved via the \(2.5\,\mathrm{km}\) optics of the LHC. The \(\rho \) parameter being an analytical function of the nuclear phase at \(t=0\), it represents a sensitive probe of the interference terms into the evolution of the real and imaginary parts of the nuclear amplitude.
Consequently theoretical models have made sensitive predictions via the evolution of \(\rho \) as a function of \(\sqrt{s}\) to quantify the effect of the possible 3-gluon compound state exchange in the elastic scattering t-channel [20, 30]. Those, currently non-excluded, theoretical models systematically require significantly lower \(\rho \) values at \(13\,\mathrm{TeV}\) than the predicted Pomeron-only evolution of \(\rho \) at \(13\,\mathrm{TeV}\), consistently with the \(\rho \) measurement reported in the present work.
The confirmation of this result in additional channels would bring, besides the evidence for the existence of the QCD-predicted 3-gluon compound state, theoretical consequences such as the generalization of the Pomeranchuk theorem (i.e. the total cross-section of proton–proton and proton–antiproton asymptotically having their ratio converging to 1 rather than their difference converging to 0).
On the contrary, if the role of the 3-gluon compound state exchange is shown insignificant, the present TOTEM results at \(13\,\mathrm{TeV}\) would imply by the dispersion relations the first experimental evidence for total cross-section saturation effects at higher energies, eventually deviating from the asymptotic behaviour proposed by many contemporary models (e.g. the functional saturation of the Froissart compound [31]).
The two effects, crossing-odd contribution and cross-section saturation, could both be present without being mutually exclusive.
Besides the extraction of the \(\rho \) parameter, the very low |t| elastic scattering can be used to determine the normalisation of the differential cross-section – a crucial ingredient for measurement of the total cross-section, \(\sigma _{\mathrm{tot}}\). In its ideal form, the normalisation can be determined as the proportionality constant between the Coulomb cross-section known from QED and the data measured at such low |t| that other than Coulomb cross-section contributions can be neglected. This “Coulomb normalisation” technique opens the way to another total cross-section measurement at \(\sqrt{s} = 13\,\mathrm{TeV}\), completely independent of previous results. This publication presents the first successful application of this method to LHC data.
Section 2 of this article outlines the experimental setup used for the measurement. The properties of the special beam optics are described in Sect. 3. Section 4 gives details of the data-taking conditions. The data analysis and reconstruction of the differential cross-section are described in Sect. 5. Section 6 presents the extraction of the \(\rho \) parameter and \(\sigma _{\mathrm{tot}}\) from the differential cross-section. Physics implications of these new results are discussed in Sect. 7.
2 Experimental apparatus
The TOTEM experiment, located at the LHC Interaction Point (IP) 5 together with the CMS experiment, is dedicated to the measurement of the total cross-section, elastic scattering and diffractive processes. The experimental apparatus, symmetric with respect to the IP, detects particles at different scattering angles in the forward region: a forward proton spectrometer composed of detectors in Roman Pots (RPs) and the magnetic elements of the LHC and, to measure at larger angles, the forward tracking telescopes T1 and T2. A complete description of the TOTEM detector instrumentation and its performance is given in [32, 33]. The data analysed here come from the RPs only.
A RP is a movable beam-pipe insertion which houses the tracking detectors that are thus capable of approaching the LHC beam to a distance of less than a millimetre, and to detect protons with scattering angles of only a few microradians. The proton spectrometer is organised in two arms: one on the left side of the IP (LHC sector 45) and one on the right (LHC sector 56), see Fig. 1. In each arm, there are two RP stations, denoted “210” (about \(210\,\mathrm{m}\) from the IP) and “220” (about \(220\,\mathrm{m}\) from the IP). Each station is composed of two RP units, denoted “nr” (near to the IP) and “fr” (far from the IP). The presented measurement is performed with units “210-fr” (approximately \(213\,\mathrm{m}\) from the IP) and “220-fr” (about \(220\,\mathrm{m}\) from the IP). The 210-fr unit is tilted by \(8^\circ \) in the transverse plane with respect to the 220-fr unit. Each unit consists of 3 RPs, one approaching the outgoing beam from the top, one from the bottom, and one horizontally. Each RP houses a stack of 5 “U” and 5 “V” silicon strip detectors, where “U” and “V” refer to two mutually perpendicular strip orientations. The special design of the sensors is such that the insensitive area at the edge facing the beam is only a few tens of micrometres [34]. Due to the \(7\,\mathrm{m}\) long lever arm between the two RP units in one arm, the local track angles can be reconstructed with an accuracy of about \(2.5\,\mathrm{\mu rad}\).
Since elastic scattering events consist of two collinear protons emitted in opposite directions, the detected events can have two topologies, called “diagonals”: 45 bottom–56 top and 45 top–56 bottom, where the numbers refer to the LHC sector.
This article uses a reference frame where x denotes the horizontal axis (pointing out of the LHC ring), y the vertical axis (pointing against gravity) and z the beam axis (in the clockwise direction).
3 Beam optics
The beam optics relate the proton kinematical states at the IP and at the RP location. A proton emerging from the interaction vertex \((x^*\), \(y^*)\) at the angle \((\theta _x^*,\theta _y^*)\) (relative to the z axis) and with momentum \(p\,(1+\xi )\), where p is the nominal initial-state proton momentum and \(\xi \) denotes relative momentum loss, is transported along the outgoing beam through the LHC magnets. It arrives at the RPs in the transverse position
relative to the beam centre. This position is determined by the optical functions, characterising the transport of protons in the beam line and controlled via the LHC magnet currents. The effective length \(L_{x,y}(z)\), the magnification \(v_{x,y}(z)\) and the dispersion \(D_{x,y}(z)\) quantify the sensitivity of the measured proton position to the scattering angle, the vertex position and the momentum loss, respectively. Note that for elastic collisions the dispersion terms \(D\,\xi \) can be ignored because the protons do not lose any momentum. The values of \(\xi \) only account for the initial state momentum offset (\(\approx 10^{-3}\)) and variations (\(\approx 10^{-4}\)). Due to the collinearity of the two elastically scattered protons and the symmetry of the optics, the impact of \(D\,\xi \) on the reconstructed scattering angles is negligible compared to other uncertainties.
The data for the analysis presented here have been taken with a new, special optics, the \(\beta ^{*} = 2500\,\mathrm{m}\), specifically developed for measuring low-|t| elastic scattering and conventionally labelled by the value of the \(\beta \)-function at the interaction point. It maximises the vertical effective length \(L_{y}\) and minimises the vertical magnification \(|v_{y}|\) at the RP position \(z = 220\,\)m (Table 1). This configuration is called “parallel-to-point focussing” because all protons with the same angle in the IP are focussed on one point in the RP at 220 m. It optimises the sensitivity to the vertical projection of the scattering angle – and hence to |t| – while minimising the influence of the vertex position. In the horizontal projection the parallel-to-point focussing condition is not fulfilled, but – similarly to the \(\beta ^{*} = 1000\,\)m optics used for a previous measurement [5] – the effective length \(L_{x}\) at \(z = 220\,\)m is sizeable, which reduces the uncertainty in the horizontal component of the scattering angle. The very high value of \(\beta ^*\) also implies very low beam divergence which is essential for accurate measurement at very low |t|.
Event rates from run 5321 as a function of time. The blue and green graphs give rates of fully reconstructed events in the two diagonal configurations relevant for elastic scattering. The red graph shows a rate of high-multiplicity events in a single RP (bottom pot in sector 45 and unit 210-fr) where no track can be reconstructed. For the other RPs this rate evolution was similar
4 Data taking
The results reported here are based on data taken in September 2016 during a sequence of dedicated LHC proton fills (5313, 5314, 5317 and 5321) with the special beam properties described in the previous section.
The vertical RPs approached the beam centre to only about 3 times the vertical beam width, \(\sigma _{y}\), thus roughly to \(0.4\,\mathrm{mm}\). The exceptionally close distance was required in order to reach very low |t| values and was possible due to the low beam intensity in this special beam operation: each beam contained only four or five colliding bunches and one non-colliding bunch, each with about \(5\times 10^{10}\) protons.
The horizontal RPs were only needed for the track-based alignment and therefore placed at a safe distance of \(8\,\sigma _{x} \approx 5\) mm, close enough to have an overlap with the vertical RPs.
The collimation strategy applied in the previous measurement [5] with carbon primary collimators was first tried, however, this resulted in too high beam halo background. To keep the background under control, a new collimation scheme was developed, with more absorbing tungsten collimators closest to the beam in the vertical plane, in order to minimise the out-scattering of halo particles. As a first step, vertical collimators TCLA scraped the beam down to \(2\,\sigma _{y}\), then the collimators were retracted to \(2.5\,\sigma _{y}\), thus creating a \(0.5\,\sigma _{y}\) gap between the beam edge and the collimator jaws. A similar procedure was performed in the horizontal plane: collimators TCP.C scraped the beam to \(3\,\mathrm{\sigma _{x}}\) and then were retracted to \(5.5\,\mathrm{\sigma _{x}}\), creating a \(2.5\,\mathrm{\sigma _x}\) gap. With the halo strongly suppressed and no collimator producing showers by touching the beam, the RPs at \(3\,\sigma _{y}\) were operated in a background-depleted environment for about one hour until the beam-to-collimator gap was refilled by diffusion, as diagnosed by the increasing shower rate (red graph in Fig. 2). When the background conditions had deteriorated to an unacceptable level, the beam cleaning procedure was repeated, again followed by a quiet data-taking period.
The events collected were triggered by a double-arm proton trigger (coincidence of any RP left of IP5 and any RP right of IP5) or a zero-bias trigger (random bunch crossings) for calibration purposes.
In total, a data sample with an integrated luminosity of about \(0.4\,{\mathrm{nb}}^{-1}\) was accumulated in which more than 7 million of elastic event candidates were tagged.
5 Differential cross-section
The analysis method is very similar to the previously published one [5]. The only important difference stems from using different RPs for the measurement: unit 210-fr instead of 220-nr as in [5] since the latter was not equipped with sensors anymore. Due to the optics and beam parameters the unit 210-fr has worse low-|t| acceptance, further deteriorated by the tilt of the unit (effectively increasing the RP distance from the beam). Consequently, in order to maintain the low-|t| reach essential for this study, the main analysis (denoted “2RP”) only uses the 220-fr units (thus 2 RPs per diagonal). Since not using the 210-nr units may, in principle, result in worse resolution and background suppression, for control reasons, the traditional analysis with 4 units per diagonal (denoted “4RP”) was pursued, too. In Sect. 5.5 the “2RP” and “4RP” will be compared showing a very good agreement. In what follows, the “2RP” analysis will be described unless stated otherwise.
Section 5.1 covers all aspects related to the reconstruction of a single event. Section 5.2 describes the steps of transforming a raw t-distribution into the differential cross-section. The t-distributions are analysed separately for each LHC fill and each diagonal, and are only merged at the end as detailed in Sect. 5.3. Section 5.4 describes the evaluation of systematic uncertainties and Sect. 5.5 presents several comparison plots used as systematic cross checks.
5.1 Event analysis
The event kinematics are determined from the coordinates of track hits in the RPs after proper alignment (see Sect. 5.1.2) using the LHC optics (see Sect. 5.1.3).
5.1.1 Kinematics reconstruction
For each event candidate the scattering angles of both protons (one per arm) are first estimated separately. In the “2RP” analysis, these formulae are used:
where L and R refer to the left and right arm, respectively, and x and y stand for the proton position in the 220-fr unit. This one-arm reconstruction is used for tagging of elastic events, where the left and right arm protons are compared.
Once a proton pair has been selected, both arms are used to reconstruct the kinematics of the event
Thanks to the left-right symmetry of the optics and elastic events, this combination leads to cancellation of the vertex terms (cf. Eq. (1)) and thus to improvement of the angular resolution (see Sect. 5.1.4).
Finally, the scattering angle, \(\theta ^*\), and the four-momentum transfer squared, t, are calculated:
where p denotes the beam momentum.
In the “4RP” analysis, the same reconstruction as in [5] is used which allows for stronger elastic-selection cuts, see Sect. 5.2.1.
5.1.2 Alignment
TOTEM’s usual three-stage procedure (Section 3.4 in [33]) for correcting the detector positions and rotation angles has been applied: a beam-based alignment prior to the run followed by two offline methods. The first method uses straight tracks to determine the relative position among the RPs by minimising track-hit residuals. The second method exploits the symmetries of elastic scattering to determine the positions of RPs with respect to the beam. This determination is repeated in 20-minute time intervals to check for possible beam movements.
The alignment uncertainties have been estimated as \(25\,\mathrm{\mu m}\) (horizontal shift), \(100\,\mathrm{\mu m}\) (vertical shift) and \(2\,\mathrm{m rad}\) (rotation about the beam axis). They are larger than in some previous TOTEM publications (e.g. Ref. [32]) due to the lower instantaneous luminosity with \(\beta ^* = 2.5\,\mathrm{km}\) and thus smaller statistics in every alignment time interval. Propagating the uncertainties through Eq. (3) to reconstructed scattering angles yields \(0.50\,\mathrm{\mu rad}\) (\(0.35\,\mathrm{\mu rad}\)) for the horizontal (vertical) angle. RP rotations induce a bias in the reconstructed scattering angles:
where the proportionality constants c and d have zero mean and standard deviations of 0.013 and 0.00039, respectively.
5.1.3 Optics
It is crucial to know with high precision the LHC beam optics between IP5 and the RPs, i.e. the behaviour of the spectrometer composed of the various magnetic elements. The optics calibration has been applied as described in [35]. This method uses RP observables to determine fine corrections to the optical functions presented in Eq. (1).
In each arm, the residual errors induce a bias in the reconstructed scattering angles:
where the biases \(b_x\) and \(b_y\) have uncertainties of \(0.17\,\mathrm{\%}\) and \(0.15\,\mathrm{\%}\), respectively, and a correlation factor of \(-0.90\). To evaluate the impact on the t-distribution, it is convenient to decompose the correlated biases \(b_x\) and \(b_y\) into eigenvectors of the covariance matrix:
where the factors \(\eta _{1,2,3}\) have zero mean and unit variance. The fourth eigenmode has a negligible contribution and therefore is not explicitly listed.
5.1.4 Resolution
Two kinds of resolution can be distinguished: the resolution of the single-arm angular reconstruction, Eq. (2), used for selection cuts and near-edge acceptance correction, and the resolution of the double-arm reconstruction, Eq. (3), used for the unsmearing correction of the final t-distribution. Since the single-arm reconstruction is biased by the vertex term in the horizontal plane, the corresponding resolution is significantly worse than the double-arm reconstruction.
The single-arm resolution can be studied by comparing the angles reconstructed from the left and right arm, see an example in Fig. 3. The width of the distributions was found to grow slightly during the fills, compatible with the effect of beam emittance growth. The typical range was from 10.0 to \(14.5\,\mathrm{\mu rad}\) for the horizontal projection and from 0.36 to \(0.38\,\mathrm{\mu rad}\) for the vertical. The associated uncertainties were 0.3 and 0.007, respectively. As illustrated in Fig. 3, the shape of the distributions is very close to Gaussian, especially at the beginning of each fill.
Since in the vertical plane the resolution is driven by the beam divergence, the double-arm resolution can simply be scaled from the single-arm value: \(\sigma (\theta ^*_y) = (0.185 \pm 0.010)\,\mathrm{\mu rad}\) where the uncertainty accounts for the full variation in time. In the horizontal plane the estimation is more complex due to several contributing smearing mechanisms. Therefore, a MC study was performed with two extreme sets of beam divergence, vertex size and sensor resolution values. These parameters were tuned within the “4RP” analysis where they are accessible thanks to the additional information from the 210-fr units. The study yielded \(\sigma (\theta ^*_x) = (0.29 \pm 0.04)\,\mathrm{\mu rad}\) where the uncertainty accounts for the full time variation.
5.2 Differential cross-section reconstruction
For a given t bin, the differential cross-section is evaluated by selecting and counting elastic events:

where \(\varDelta t\) is the width of the bin, \({\mathcal {N}}\) is a normalisation factor and the other symbols stand for various correction factors: \({\mathcal {U}}\) for unfolding of resolution effects, \({\mathcal {B}}\) for background subtraction, \({\mathcal {A}}\) for acceptance correction and \({\mathcal {E}}\) for detection and reconstruction efficiency.
5.2.1 Event tagging
Within the “2RP” analysis one may apply the cuts requiring the reconstructed-track collinearity between the left and the right arm, see Table 2. The correlation plots corresponding to these cuts are shown in Fig. 4.
In order to limit the selection inefficiency, the thresholds for the cuts are set to \(4\,\mathrm{\sigma }\). Applying the cuts at the \(5\,\mathrm{\sigma }\)-level would yield about \(0.1\,\mathrm{\%}\) more events almost uniformly in every |t|-bin. This kind of inefficiency only contributes to a global scale factor, which is irrelevant for this analysis because the normalisation is taken from a different data set (cf. Sect. 5.2.6).
In the “4RP” analysis, thanks to the additional information from the 210-fr units, more cuts can be applied (cf. Table 2 in [36]). In particular the left-right comparison of the reconstructed horizontal vertex position, \(x^*\), and the vertical position-angle correlation in each arm. Furthermore, since the single-arm reconstruction can disentangle the contributions from \(x^*\) and \(\theta ^*_x\), the angular resolution is better compared with the “2RP” analysis and consequently cut 1 in the “4RP” analysis is more efficient against background.
Correlation plots for the elastic event selection cuts presented in Table 2 (“2RP” analysis), showing events from the LHC fill 5313 and with diagonal topology 45 bottom–56 top. The solid black lines delimit the signal region within \(\pm 4\,\mathrm{\sigma }\)
5.2.2 Background
As the RPs were very close to the beam, one may expect an enhanced background from coincidence of beam halo protons hitting detectors in the two arms. Other background sources (pertinent to any elastic analysis) are central diffraction and pile-up of two single diffraction events.
The background rate (i.e. impurity of the elastic tagging) is estimated in two steps, both based on distributions of discriminators from Table 2 plotted in various situations, see an example in Fig. 5. In the first step, diagonal data are studied under several cut combinations. While the central part (signal) remains essentially constant, the tails (background) are suppressed when the number of cuts is increased. In the second step, the background distribution is interpolated from the tails into the signal region. The form of the interpolation is inferred from non-diagonal RP track configurations (45 bottom–56 bottom or 45 top–56 top), artificially treated like diagonal signatures by inverting the y coordinate sign in the arm 45. These non-diagonal configurations cannot contain any elastic signal and hence consist purely of background which is expected to be similar in the diagonal and non-diagonal configurations. This expectation is supported by the agreement of the tails of the red, blue and green curves in the figure. Since the non-diagonal distributions are flat, the comparison of the signal-peak size to the amount of interpolated background yields an order-of-magnitue estimate of \(1 - {\mathcal {B}} = {\mathcal {O}}(10^{-3})\).
Distributions of discriminator 1, i.e. the difference between the horizontal scattering angle reconstructed from the right and the left arm. Data from LHC fill 5314. Black and red curves: data from diagonal 45 bottom–56 top, the different colours correspond to various combinations of the selection cuts (see numbering in Table 2). Blue and green curves: data from anti-diagonal RP configurations, obtained by inverting track y coordinate in the left arm. The vertical dashed lines represent the boundaries of the signal region (\(\pm 4\,\mathrm{\sigma }\))
The t-distribution of the background can also be estimated by comparing data from diagonal and anti-diagonal configurations, as illustrated in Fig. 6. The ratio background / (signal + background) can be obtained by dividing the blue or green histograms by the red or magenta histograms. Consequently, the background correction factor, \({\mathcal {B}}\), is estimated to be \(0.9975 \pm 0.0010\) at \(|t| = 0.001\,\mathrm{GeV^2}\), \(0.9992 \pm 0.0003\) at \(|t| = 0.05\,\mathrm{GeV^2}\) and \(0.998 \pm 0.001\) at \(|t| = 0.2\,\mathrm{GeV^2}\). The uncertainty comes from statistical fluctuations in the histograms and from considering different diagonals and anti-diagonals.
5.2.3 Acceptance correction
The acceptance for elastic protons is limited mostly by two factors: sensor coverage (relevant for low \(|\theta ^*_y|\)) and LHC beam aperture (at \(|\theta ^*_y| \approx 100\,\mathrm{\mu rad}\)). Since the 210-fr unit is tilted with respect to the 220-fr unit, the thin windows around sensors do not overlap perfectly. Therefore there are phase space regions where protons need to traverse thick walls of 210-fr RP before being detected in 220-fr RP. This induces reduced detection efficiency difficult to determine precisely. Consequently these regions (close to the sensor edge facing the beam) have been excluded from the fiducial region used in the analysis, see the magenta lines in Fig. 7.
Distribution of scattering angle projections \(\theta _y^*\) vs. \(\theta _x^*\), data from LHC fill 5317. The upper (lower) part comes from the diagonal 45 bottom–56 top (45 top–56 bottom). The red horizontal lines represent cuts due to the LHC apertures, the magenta lines cuts due to the RP edges. The dotted circles show contours of constant scattering angle \(\theta ^* = 50\), 100 and \(150\,\mathrm{\mu rad}\). The parts of the contours within acceptance are emphasized in thick black
The correction for the above phase-space limitations includes two contributions – a geometrical correction \({\mathcal {A}}_{\mathrm{geom}}\) reflecting the fraction of the phase space within the acceptance and a component \({\mathcal {A}}_{\mathrm{fluct}}\) correcting for fluctuations around the acceptance boundaries:
The calculation of the geometrical correction \({\mathcal {A}}_{\mathrm{geom}}\) is based on the azimuthal symmetry of elastic scattering, experimentally verified for the data within acceptance. As shown in Fig. 7, for a given value of \(\theta ^*\) the correction is given by:
The correction \({\mathcal {A}}_{\mathrm{fluct}}\) is calculated analytically from the probability that any of the two elastic protons leaves the region of acceptance due to the beam divergence. The beam divergence distribution is modelled as a Gaussian with the spread determined by the method described in Sect. 5.1.4. This contribution is sizeable only close to the acceptance limitations. Data from regions with corrections larger than 2 are discarded.
The full acceptance correction, \({\mathcal {A}}\), has a value of 12 in the lowest-|t| bin and decreases smoothly towards about 2.1 at \(|t| = 0.2\,\mathrm{GeV^2}\). Since a single diagonal cannot cover more than half of the phase space, the minimum value of the correction is 2.
The uncertainties related to \({\mathcal {A}}_{\mathrm{fluct}}\) follow from the uncertainties of the resolution parameters: standard deviation and distribution shape, see Sect. 5.1.4. Since \({\mathcal {A}}_{\mathrm{geom}}\) is calculated from a trivial trigonometric formula, there is no uncertainty directly associated with it. However biases can arise indirectly from effects that break the assumed azimuthal symmetry like misalignments or optics perturbations already covered above.
5.2.4 Inefficiency corrections
Since the overall normalisation will be determined from another dataset (see Sect. 5.2.6), any inefficiency correction that does not alter the t-distribution shape does not need to be considered in this analysis (trigger, data acquisition and pile-up inefficiency discussed in [36, 37]). The remaining inefficiencies are related to the inability of a RP to resolve the elastic proton track.
One such case is when a single RP does not detect and/or reconstruct a proton track, with no correlation to other RPs. This type of inefficiency, \({\mathcal {I}}_1\), is evaluated within the “4RP” analysis by removing the studied RP from the tagging cuts, repeating the event selection and calculating the fraction of recovered events. A typical example is given in Fig. 8, showing that the efficiency decreases gently with the vertical scattering angle. This dependence is reproduced with MC simulations and originates from the fact that protons with larger \(|\theta _y^*|\) hit the RPs further from their edge and therefore the potentially created secondary particles have more chance to be detected. Since the RP detectors cannot resolve multiple tracks (non-unique association between “U” and “V” track candidates), the presence of a secondary particle track prevents from using the affected RP in the analysis. The \({\mathcal {I}}_1\) inefficiency includes several sources: nuclear scattering, delta rays, etc. As shown by the MC studies, only some of them give edge effects, that’s why they are at about \(0.5\,\mathrm{\%}\) level.
Single-RP uncorrelated inefficiency for the 220-fr bottom RP in the right arm. The rapid drop at \(\theta _y^* \approx 4\,\mathrm{\mu rad}\) is due to acceptance effects at the sensor edge. The red lines represent a linear fit of the efficiency dependence on the vertical scattering angle (solid) and its extrapolation to the regions affected by acceptance effects (dashed)
Proton interactions in a RP affecting simultaneously another RP downstream represent another source of inefficiency. The contribution from these correlated inefficiencies, \({\mathcal {I}}_2\), is determined by evaluating the rate of events with high track multiplicity (\(\gtrsim \) 5) in both 210-fr and 220-fr RP units. Events with high track multiplicity simultaneously in the top and bottom RP of the 210-fr units are discarded as such a shower is likely to have started upstream from the RP station and thus be unrelated to the elastic proton interacting with detectors. The value, \({\mathcal {I}}_2 \approx (1.5 \pm 0.7)\,\mathrm{\%}\), is compatible between left/right arms and top/bottom RP pairs and compares well to Monte-Carlo simulations (e.g. section 7.5 in [38]).
The full correction is calculated as
The first term in the parentheses sums the contributions from the diagonal RPs used in the analysis. In the “2RP” analysis it increases from about 6.9 to \(8.5\,\mathrm{\%}\) from the lowest to the highest \(|\theta _y^*|\), with an uncertainty of about \(0.4\,\mathrm{\%}\). For the “4RP” analysis, since more RPs contribute, the sum is greater: from 10.5 to \(13.0\,\mathrm{\%}\) between the lowest to the highest \(|\theta _y^*|\).
5.2.5 Unfolding of resolution effects
Thanks to the very good resolution (see Sect. 5.1.4), the following iterative procedure can be safely used to evaluate the correction for resolution effects.
- 1.
The differential cross-section data are fitted by a smooth curve.
- 2.
The fit is used in a numerical-integration calculation of the smeared t-distribution (using the resolution parameters determined in Sect. 5.1.4). The ratio between the smeared and the non-smeared t-distributions gives a set of per-bin correction factors.
- 3.
The corrections are applied to the observed (yet uncorrected) differential cross-section yielding a better estimate of the true t-distribution.
- 4.
The corrected differential cross-section is fed back to step 1.
As the estimate of the true t-distribution improves, the difference between the correction factors obtained in two successive iterations decreases. When the difference becomes negligible, the iteration stops. This is typically achieved after the second iteration.
The final correction \({\mathcal {U}}\) is significantly different from 1 only at very low |t| (where a rapid cross-section growth occurs, see Fig. 9). The relative effect is never greater than \(0.4\,\mathrm{\%}\).
Several fit parametrisations were tested, however yielding negligible difference in the final correction \({\mathcal {U}}\) for \(|t| \lesssim 0.3\,\mathrm{GeV^2}\). Figure 9 shows the case for two of those.
For the uncertainty estimate, the uncertainties of the \(\theta _x^*\) and \(\theta _y^*\) resolutions (see Sect. 5.1.4) as well as fit-model dependence have been taken into account. Altogether, the uncertainty is smaller than \(0.1\,\mathrm{\%}\).
Differential cross-section from Table 3 with statistical (bars) and systematic uncertainties (bands). The yellow band represents all systematic uncertainties, the green one all but normalisation. The bands are centred around the bin content. Inset: a low-|t| zoom of cross-section rise due to the Coulomb interaction
5.2.6 Normalisation
The normalisation factor \({\mathcal {N}}\) is determined by requiring the integrated nuclear elastic cross-section to be \(\sigma _{\mathrm{el}} = 31.0\,\mathrm{mb}\) as obtained by TOTEM from a \(\beta ^* = 90\,\mathrm{m}\) dataset at the same energy [6]. The elastic cross-section is extracted from the data in two parts. The first part sums the \(\mathrm{d}\sigma /\mathrm{d}t\) histogram bins for \(0.01< |t| < 0.5\,\mathrm{GeV^2}\). The second part corresponds to the integral over \(0< |t| < 0.01\,\mathrm{GeV^2}\) of an exponential fitted to the data on the interval \(0.01< |t| < 0.05\,\mathrm{GeV^2}\).
The uncertainty of \({\mathcal {N}}\) is dominated by the \(5.5\,\mathrm{\%}\) uncertainty of \(\sigma _{\mathrm{el}}\) from Ref. [6].
5.2.7 Binning
The bin sizes are set according to the t resolution. Three different binnings are considered in this analysis: “dense” where the bin size is as large as the standard deviation of |t|, “medium” with bins twice as large and “coarse” with bins three times larger than the standard deviation of |t|.
5.3 Data merging
After analysing the data in each diagonal and LHC fill separately, the individual differential cross-section distributions are merged. This is accomplished by a per-bin weighted average, with the weight given by inverse squared statistical uncertainty. The final cross-section values are listed in Table 3 and are visualised in Fig. 10. The figure clearly shows a rapid cross-section rise below \(|t| \lesssim 0.002\,\mathrm{GeV^2}\) which, as interpreted later, is an effect due to the electromagnetic interaction.
5.4 Systematic uncertainties
The following sources of systematic uncertainties have been considered.
Alignment: shifts in \(\theta ^*_{x,y}\) (see Sect. 5.1.2). Both left-right symmetric and anti-symmetric modes have been considered. In the vertical plane, both contributions correlated and uncorrelated between the diagonals have been considered.
Alignment x-y tilts and optics: mixing between \(\theta ^*_{x}\) and \(\theta ^*_{y}\) (see Sect. 5.1.2). Both left-right symmetric and anti-symmetric modes have been considered.
Optics uncertainties: scaling of \(\theta ^*_{x,y}\) (see Sect. 5.1.3). The three relevant modes in Eq. (6) have been considered.
Background subtraction (see Sect. 5.2.2): the t-dependent uncertainty of the correction factor \({\mathcal {B}}\).
Acceptance correction (see Sect. 5.2.3): the uncertainty of resolution parameters, non-gaussianity of the resolution distributions, left-right asymmetry of the beam divergence.
Inefficiency corrections (see Sect. 5.2.4): for the uncorrelated inefficiency \({\mathcal {I}}_1\) both uncertainties of the fitted slope and intercept have been considered. For the correlated inefficiency \({\mathcal {I}}_2\) the uncertainty of its value has been considered.
The beam-momentum uncertainty: considered when the scattering angles are translated to t, see Eq. (4). The uncertainty was estimated by LHC experts as \(0.1\,\mathrm{\%}\) [39] in agreement with a previous assessment by TOTEM (Section 5.2.8. in [4]).
Unsmearing (see Sect. 5.2.5): uncertainty of resolution parameters and model dependence of the fit.
Normalisation (see Sect. 5.2.6): overall multiplicative factor.
Relative variation of the final differential cross-section due to systematic uncertainties (medium binning). The colourful histograms represent the leading uncertainties, each of them corresponds to a \(1\,\mathrm{\sigma }\) bias, cf. Eq. (12). The envelope is determined by summing all considered contributions (except normalisation) in quadrature for each |t| value
Collection of cross-check plots (medium binning, only statistical uncertainties are plotted). Top left: comparison of results from the two diagonals, data from all LHC fills. Top right: comparison of results from time periods after and before beam cleanings, data from all LHC fills and both diagonals. Bottom left: comparison of results from “2RP” and “4RP” analyses, data from all LHC fills and both diagonals. Bottom right: comparison of results obtained from two different data-takings at the same energy but with different optics. The blue histogram is taken from Ref. [6]
For each error source, its effect on the |t|-distribution is evaluated with a Monte-Carlo simulation. It uses a fit of the final differential cross-section data to generate the true t-distribution and, in parallel, builds another t-distribution where the systematic error at \(1\,\mathrm{\sigma }\) level is introduced. The difference between the two t-distributions gives the systematic effect on the differential cross-section. This procedure is formally equivalent to evaluating
where \(\delta q\) corresponds to a \(1\,\mathrm{\sigma }\) bias in the quantity q responsible for a given systematic effect.
The systematic uncertainty corresponding to the final differential cross-section merged from all the analysed LHC fills and both diagonals is propagated according to the same method as applied to the data, see Sect. 5.3. To be conservative, the systematic errors are assumed fully correlated among the four analysed LHC fills. The correlations between the two diagonals are respected for each systematic effect. This is particularly important for the vertical (mis)-alignment, as already noted in Ref. [5]. The relative position between the top and bottom RPs is known precisely from track-based alignment (see Sect. 5.1.2) and the leading component of residual misalignment is thus between the beam and a RP. Furthermore, whenever the beam was closer to a top RP, it would be further away from the corresponding bottom RP and vice versa. Consequently, the effect of the misalignment is predominantly anti-correlated between the diagonals. While the misalignment uncertainty in the lowest |t| bin reaches about \(7\,\mathrm{\%}\) for a single diagonal, once the diagonals are merged the impact drops to about \(1.2\,\mathrm{\%}\).
The leading uncertainties (except normalisation) are shown in Fig. 11. At low |t| they include the vertical alignment (left-right symmetric, top-bottom correlated) and the uncertainty of the vertical beam divergence. At higher |t| values, the uncertainties are dominated by the beam momentum and optics uncertainties (mode 3 in Eq. (7)). These leading effects are listed in Table 3 which can be used to approximate the covariance matrix of systematic uncertainties:
where i and j are bin indices (row numbers in Table 3) and the sum goes over the leading error contributions q (five rightmost columns in the table).
5.5 Systematic cross-checks
Compatible results have been obtained by analysing data subsets of events from different bunches, different diagonals (Fig. 12, top left), different fills and different time periods – in particular those right after and right before the beam cleanings (Fig. 12, top right). Figure 12, bottom left, shows that both analysis approaches, “2RP” and “4RP”, yield compatible results. The relatively large difference between the diagonals at very low |t| (Fig. 12, top left) is fully within the uncertainty due to the vertical misalignment, see Sect. 5.4.
Figure 12, bottom right, shows an excellent agreement between the data from this analysis and previous results obtained with \(\beta ^* = 90\,\mathrm{m}\) optics [6].
Differential cross-section at higher |t| values as determined in the “2RP” analysis (black points) with a fit (red line) used for the evaluation of the CNI effects. The fit also allows for a first dip-bump characterisation at \(13\,\mathrm{TeV}\): the dip is located at \(|t| \approx 0.47\,\mathrm{GeV^2}\), the bump at \(|t|\approx 0.62\,\mathrm{GeV^2}\) and the bump/dip cross-section ratio is about 1.8 (a more recent and precise quantification can be found in Ref. [41]). For comparison: at \(7\,\mathrm{TeV}\) the dip was found at \(0.53\,\mathrm{GeV^2}\) [12] and the bump/dip ratio \(1.7\pm 0.1\) (local polynomial fit of the data in Table 5 in Ref. [36])
6 Determination of \(\rho \) and total cross-section
The value of the \(\rho \) parameter can be extracted from the differential cross-section thanks to the effects of Coulomb-nuclear interference (CNI). Explicit treatment of these effects allows also for a conceptually more accurate determination of the total cross-section.
Our modelling of the CNI effects is summarised in Sects. 6.1, 6.2 and 6.3 describe data fits and results. In Sect. 6.2 the differential cross-section normalisation is fixed by the \(\beta ^* = 90\,\mathrm{m}\) data [6] (see Sect. 5.2.6). In Sect. 6.3 the normalisation is adjusted or entirely determined from the \(\beta ^* = 2500\,\mathrm{m}\) data presented in this publication. This allows for different or even completely independent total cross-section determination with respect to Ref. [6].
6.1 Coulomb-nuclear interference
A detailed overview of different CNI descriptions was given in Ref. [5], Section 6. Here we briefly summarise the choices used for the presented analysis.
The Coulomb amplitude can be derived from QED. In the one-photon approximation it yields the cross-section
where \(\alpha \) is the fine-structure constant and \({\mathcal {F}}\) represents an experimentally determined form factor. Several form factor determinations have been considered (by Puckett et al., Arrington et al. and Borkowski et al., see summary in [42]) and no difference in results has been observed.
Motivated by the observed differential cross-section, at low |t| the modulus of the nuclear amplitude is parametrised as
The \(b_1\) parameter is responsible for the leading exponential decrease, the other \(b_n\) parameters can describe small deviations from the leading behaviour. Since the calculation of CNI may, in principle, involve integrations (e.g. Eq. (17)), it is necessary to extend the nuclear amplitude meaningfully to higher |t| values, too. In that region, we fix the amplitude to a function that describes well the dip–bump structure observed in the data, see the red curve in Fig. 13. In order to avoid numerical problems, the intermediate |t| region is modelled with a continuous and smooth interpolation between the low and high-|t| parts. It has been checked that altering the high-|t| part within reasonable limits has negligible impact on the results.
Several parametrisations have been considered for the phase of the nuclear amplitude. Since one of the main goals of this analysis is to compare the newly obtained \(\rho \) value with those at lower energies, we have focused on parametrisations similar to past analyses. Consequently we have considered phases with slow variation at low |t|: constant, Bailly and standard from Ref. [5]. No dependence of the results on this choice was observed and therefore only the constant phase
will be retained in what follows. A more complete exploration is planned for a forthcoming TOTEM publication, including phases leading to a peripheral description of elastic scattering – where the impact-parameter distribution peaks at values significantly larger than zero, cf. Section 6.1.3 in [5].
We have used the most general interference formula available in the literature – the “KL” formula [43]:
which is numerically almost identical to the formula by Cahn [44] as shown in Ref. [5]. The CNI effects were calculated by the computer code from Ref. [42].
6.2 Data fits with fixed normalisation
The fits of the data from Table 3 have been carried out with the standard least-squares method, minimising
where \(\varDelta \) is a vector of differences between the differential cross-section data and a fit function \(\mathrm{d}\sigma ^{\mathrm{C+N}}/\mathrm{d}t\) evaluated at the representative point \(t^{\mathrm{rep}}\) of each bin [40]. The minimisation is repeated several times, and the representative points are updated between iterations. The covariance matrix \(\mathsf {V}\) has two components. The diagonal of \(\mathsf {V}_{\mathrm{stat}}\) contains the statistical uncertainty squared from Table 3, \(\mathsf {V}_{\mathrm{syst}}\) includes all systematic uncertainty contributions except the normalisation, see Eq. (13). For improved fit stability, the normalisation uncertainty is not included in the \(\chi ^2\) definition. In order to propagate this uncertainty to the fit results, the fit is repeated with the normalisation adjusted by \(+5.5\,\mathrm{\%}\) and \(-5.5\,\mathrm{\%}\). For each fit parameter the mean deviation from the fit result with no normalisation adjustment is taken as the effect of normalisation uncertainty, which is then added quadratically to the uncertainty reported by the fit with no bias.
The complete fit procedure has been validated with a Monte-Carlo study confirming that it has negligible bias. It also indicates the composition of the fit parameter uncertainties. For example, for a fit with \(N_b = 1\) using data in the “coarse binning” up to \(|t| = 0.07\,\mathrm{GeV^2}\), the \(\rho \) uncertainty due to the statistical uncertainties is about 0.004, due to the systematic uncertainties is about 0.003 and due to the normalisation uncertainty is about 0.009.
The fits have been found to have negligible dependence on the binning used (see Sect. 5.2.7), the choice of electromagnetic form factor (see text below Eq. (14)), the high-|t| nuclear amplitude (see text below Eq. (15)), the choice of the nuclear amplitude phase (see text above Eq. (16)), the number of fit iterations and the choice of start parameter values for the \(\chi ^2\) minimisation.
Since the extracted value of \(\rho \) may depend on the assumed fit parametrisation etc., an exploration with various fit configurations has been performed: several degrees of the hadronic modulus polynomial, \(N_b = 1, 2, 3\), and different sub-samples of the data, constraining them by a maximal value of |t|, \(|t|_{\mathrm{max}}\). For the latter, two values have been chosen. \(|t|_{\mathrm{max}} = 0.15\,\mathrm{GeV^2}\) corresponds to the largest interval before the differential cross-section accelerates its decrease towards the dip. It is the largest interval where application of parametrisation from Eq. (15) is sensible. The other choice, \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\), reflects an interval where purely-exponential (\(N_b = 1\)) nuclear amplitude is expected to provide a good fit. A summary of the fit results is shown in Table 4. The fit with \(N_b = 1\) on the larger |t| range has bad quality, thus the \(\rho \) value is not displayed. This shows that the data are not compatible with a pure exponential, similarly to the previous observation at \(\sqrt{s} = 8\,\mathrm{TeV}\) [4, 5]. Except for this case, all other fit configurations yield good quality and \(\rho \) values constrained to a narrow range.
Details of fit with \(N_b = 3\) and \(|t|_{\mathrm{max}} = 0.15\,\mathrm{GeV^2}\). The fit parameters read: \(a = (648\pm 34)\,\mathrm{mb/GeV^2}\), \(b_1 = (10.64 \pm 0.08)\,\mathrm{GeV^{-2}}\), \(b_2 = (4.1 \pm 1.1)\,\mathrm{GeV^{-4}}\), \(b_3 = (10.3 \pm 4.9)\,\mathrm{GeV^{-6}}\) and \(\rho = 0.10 \pm 0.01\)
The extreme cases in Table 4, combination \(N_b=1\) with \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\) and \(N_b=3\) with \(|t|_{\mathrm{max}} = 0.15\,\mathrm{GeV^2}\) have important meanings. In the latter, the largest possible sample is used and maximum flexibility is given to the fit. In that sense, this fit corresponds to the best \(\rho \) determination considered. Also, in this case the fit data include many points where the CNI effects are limited. Consequently, the fit can “learn” the trend of the nuclear component and “impose it” in the region of strong CNI effects. Conversely, the fit configuration \(N_b=1\) with \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\) includes data with sizeable CNI effects. This complementarity explains why these two cases give the extreme values of \(\rho \) in Table 4. Fit details for these two configurations are shown in Figs. 14 and 15.
Dependence of the \(\rho \) parameter on energy. The \({\mathrm{pp}}\) (blue) and \(\mathrm{p}{{\bar{\mathrm{p}}}}\) (green) data are taken from PDG [45]. TOTEM measurements are marked in red. The two points at \(13\,\mathrm{TeV}\) correspond to the two selected fit cases discussed in text: the lhs. point to the combination \(N_b = 3\) and \(|t|_{\mathrm{max}} = 0.15\,\mathrm{GeV^2}\) while the rhs. point to \(N_b = 1\) and \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\)
The fit configuration \(N_b=1\) with \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\) has another important meaning. Considering the shrinkage of the “forward-cone”, this |t| range is similar to the one used in the UA4/2 analysis [46]. This fact may suggest why UA4/2 could not observe deviations of the differential cross-section from pure exponential: the |t| range was too narrow, as it would be for the present data, had the acceptance stopped at \(|t| = 0.07\,\mathrm{GeV^2}\), see Fig. 15. Beyond the |t| range, this fit combination shares more similarities with the UA4/2 fit (and in general with many other past experiments): purely exponential fit and assumption of constant hadronic phase. Moreover, as shown in Ref. [5], the “KL” interference formula [43] used in this report gives for this fit configuration very similar \(\rho \) results as the “SWY” interference formula [47] used in many past data analyses. From this point of view this fit combination corresponds to the most fair comparison to previous \(\rho \) determinations and their extrapolations, as e.g. in Fig. 16. It is worth noting that this fit configuration yields a \(\rho \) value incompatible at the level of about \(4.7\,\mathrm{\sigma }\) with the preferred COMPETE model (blue curve in the figure).
Further tests were performed in order to probe the stability of the \(\rho \) extraction. Since at higher |t| values the effects of CNI are limited, one may conceive a two-step fit: first, use only the higher |t| data to determine the parameters of the hadronic modulus, cf. Eq. (15), and second, optimise only \(\rho \) with all the data but the hadronic modulus fixed from the first step. Figure 14 indicates that for the first step one needs to include points down to about \(|t| = 0.04\,\mathrm{GeV^2}\) in order to describe correctly the concavity of the data. Performing the two-step fit with \(N_b=3\) and with ansatz \(\rho = 0.10\) (or 0.14) yields, at the end, \(\rho = 0.103\) (or 0.116). Although there is a non-zero \(\rho \) difference (CNI effects cannot be fully neglected at higher |t|), these tests demonstrate the trend of the data towards \(\rho \approx 0.10\). A logical counterpart of the procedure just described would be to give the higher-|t| data less weight. In its extreme, where the higher-|t| data are not used at all, this has already been covered by fits with \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\) discussed above, also showing the preference for lower \(\rho \) values.
Constraints to the relation between \(\rho \) and \(\sigma _{\mathrm{el}}\) derived from this data set (red line) and from Ref. [6] (blue line)
Figure 17 illustrates a small correction due to a conceptual improvement in combining the data from this publication and from Ref. [6]. The latter assumes certain values of \(\rho \) in order to evaluate cross-section estimates which are in turn used in this analysis (see Sect. 5.2.6) to estimate \(\rho \). This circular dependence can be resolved by considering simultaneously the \(\rho \) dependence of \(\sigma _{\mathrm{el}}\) in Ref. [6] (blue line) and the \(\sigma _{\mathrm{el}}\) dependence of \(\rho \) determined in this analysis (red line). The latter is done as linear interpolation of \(\rho \) values extracted assuming \(\sigma _{\mathrm{el}} = 30.9\) and \(31.1\,\mathrm{mb}\). The linear dependence is confirmed with Monte-Carlo studies. The solution consistent with both datasets (the crossing of the red and blue curves) brings negligible correction to \(\rho \) and \(-0.03\,\mathrm{\%}\) correction to the value of \(\sigma _{\mathrm{el}}\) published in Ref. [6] for \(\rho =0.10\).
For each of the fits presented above, the total cross-section can be derived via the optical theorem:
the results are listed in Table 4.
6.3 Data fits with variable normalisation
Beyond the determination of the \(\rho \) parameter, the very low |t| data offer a normalisation method, too. Suppose that the nuclear amplitude in Eq. (17) were negligible, then the normalisation of the differential cross-section could be performed with respect to the Coulomb amplitude, known from QED. While such an extreme situation does not occur within the available dataset, Table 3, the lowest |t| points receive large contribution from the Coulomb amplitude and can thus be used for normalisation adjustment or determination. In practice, we extend the fit function in Eq. (17) with parameter \(\eta \)
which represents normalisation adjustments with respect to the \(\beta ^* = 90\,\mathrm{m}\) result [6] (corresponding to \(\eta = 1\)).
In turn, the normalisation can be determined from the \(\beta ^* = 90\,\mathrm{m}\) data (Ref. [6] and Sect. 5.2.6), from the \(\beta ^* = 2500\,\mathrm{m}\) data (this publication) or their combination. This is formalised in the following three approaches.
approach 1: normalisation from \(90\,\mathrm{m}\) data, results presented in the previous section (in particular Table 4),
approach 2: normalisation estimated with \(2500\,\mathrm{m}\) data under the constraint (mean and standard deviation) from the \(90\,\mathrm{m}\) data,
approach 3: normalisation estimated only from \(2500\,\mathrm{m}\) data.
Illustration of approach 3, single fit. The data come from Table 3, the normalisation uncertainty is not shown as it is not relevant for this fit
Since the Coulomb normalisation is performed at very low |t|, the presentation in this section will focus on fits with \(N_b = 1\). Fits with \(N_b = 3\) were tested, too, without significant changes in the results. For the sake of simplicity, only the medium binning will be used in this section. The previous section has shown that results do not depend on the choice of binning.
Since the nuclear-amplitude component cannot be neglected even at the lowest |t| points of the available dataset, Table 3, the normalisation determination must be performed with care. It has been found preferable to make the fits in sequence of three steps, using dedicated and physics-motivated fit configurations for each parameter. The parameters of the nuclear amplitude are determined from a “golden nuclear |t| range” where |t| is large enough for CNI effects to be small while |t| is small enough for the \(N_b = 1\) parametrisation to be suitable. For example, analysing Eq. (17) one can find that CNI effects modify the nuclear cross-section by less than \(1\,\mathrm{\%}\) for \(|t| \gtrsim 0.007\,\mathrm{GeV^2}\). This range agrees with what is empirically found when trying to go as low as possible in |t| with the nuclear range without finding significant deviations from the exponential with \(N_b = 1\) either due to the destructive interference with the Coulomb interaction or due to the non-exponentiality of the nuclear amplitude [4]. In the nuclear range, the CNI effects can be ignored (charging the residual effects on systematics), making the fit independent of the interference modelling. The normalisation \(\eta \), in contrary, is determined from the lowest |t| points which are the only ones having sensitivity to the Coulomb-amplitude component. The \(\rho \) parameter is derived from a |t| range where CNI effects are significant, thus including at least the complement of the nuclear range, \(|t| \lesssim 0.007\,\mathrm{GeV^2}\). Note that overlapping |t| ranges are used for determination of \(\eta \) and \(\rho \).
In detail, approach 2 was implemented via the following sequence of fits.
Step a (determination of \(b_1\)): fit over range \(0.005< |t| < 0.07\,\mathrm{GeV^2}\), the CNI effects are ignored. The fit gives a p-value of 0.75.
Step b (determination of \(\eta \)): fit over range \(|t| < 0.0015\,\mathrm{GeV^2}\), with \(b_1\) fixed from step a. The overall \(\chi ^2\) receives an additional term \((\eta - 1)^2/ \sigma _\eta ^2\), \(\sigma _\eta = 0.055\), which reflects the constraint from the \(\beta ^* = 90\,\mathrm{m}\) data. The fit gives negligible average pull and yields a p-value of 0.11.
Step c (determination of \(\rho \) and a): fit over range \(|t| < 0.07\,\mathrm{GeV^2}\), with \(b_1\) fixed from step a and \(\eta \) fixed from step b. The fit gives a p-value of 0.73.
The \(\rho \) and total cross-section results are listed in Table 5. \(\eta \) was found to be 1.005 thus deviating by a fraction of sigma (\(\sigma _\eta = 0.055\)) from the \(\beta ^* = 90\,\mathrm{m}\) normalisation.
Total (red), inelastic (blue) and elastic (green) cross-section as a function of energy, \(\sqrt{s}\). The data are taken from Ref. [6] (and references therein) and Table 5. At \(\sqrt{s} = 13\,\mathrm{TeV}\), three total cross-section points are shown: left filled corresponds to approach 3, right filled to Ref. [6] and central hollow to the average in Eq. (21)
Approach 3 was implemented via the following sequence of fits.
Step a (determination of \(\eta a^2\) and \(b_1\)): fit over range \(0.0071< |t| < 0.026\,\mathrm{GeV^2}\). The CNI effects are ignored, therefore the fit is only sensitive to the product \(\eta a^2\), cf. Eqs. (20) and (15). The fit yields a p-value of 0.91.
Step b (determination of \(\eta \)): fit over range \(|t| < 0.0023\,\mathrm{GeV^2}\), with \(b_1\) and product \(\eta a^2\) fixed from step a. Since \(\eta \) is determined and the product \(\eta a^2\) is fixed, a is also determined in this step. The fit gives negligible average pull and yields a p-value of 0.14.
Step c (determination of \(\rho \)): fit over range \(|t| < 0.0071\,\mathrm{GeV^2}\), with \(b_1\) fixed from step a and \(\eta \) and a fixed from step b. The fit yields a p-value of 0.23.
The \(\rho \) and total cross-section results are listed in Table 5. \(\eta \) was found to be 1.020 thus deviating by less than half a sigma (\(\sigma _\eta \)) from the \(\beta ^* = 90\,\mathrm{m}\) normalisation.
As a test we tried approach 3 implementation with a single fit over \(|t| < 0.05\,\mathrm{GeV^2}\), where all parameters (\(\eta \), a, \(b_1\) and \(\rho \)) are free and initialised to the values obtained in the previous paragraph. As anticipated above, such fit might have encountered problems due to non-optimal parameter sensitivities on the available |t| range, however, the results listed in Table 5 are reasonable. \(\eta \) was found to be 1.05 thus deviating by less than a sigma (\(\sigma _\eta \)) from the \(\beta ^* = 90\,\mathrm{m}\) normalisation. The fit quality is good: p-value of 0.70, see also the illustration in Fig. 18. The single fit is also able to show the correlations between the fitted parameters. As expected, \(\eta \) and a are essentially fully anticorrelated. Both \(\eta \) and a are strongly correlated with \(\rho \) with correlation coefficients of about 0.85, whereas the correlation of these parameters to \(b_1\) is weak, the correlation coefficient is about 0.4. Finally the correlation coefficient between \(\rho \) and \(b_1\) is in between with a correlation coefficient about 0.6. These correlations confirm the necessity of the step-wise determination of the parameters using the ranges with most sensitivity for the parameter concerned to minimize the influence of the value of the other parameters to the determination.
The uncertainties for the fits presented above were determined with the following procedure. The experimentally determined \(\mathrm{d}\sigma /\mathrm{d}t\) histogram was modified by adding randomly generated fluctuations reflecting the statistical, systematic and normalisation uncertainties (see Sect. 5.4). This was done 100 times with different random seeds. Each of the modified histograms was fitted by the above sequences, yielding fit parameter samples to determine the parameter fluctuations, i.e. uncertainties. Histogram modifications resulting in excessive parameter deviations from the unmodified fit (\(\varDelta \rho > 0.05\) or \(\varDelta \sigma _\mathrm{tot} > 10\,\mathrm{mb}\)) were disregarded since such cases would not be accepted in the analysis. This estimation method gives consistent results with Sect. 6.2 (for approach 1) and \(\chi ^2\)-based estimate (from approach 3, single fit). The \(\rho \) and \(\sigma _{\mathrm{tot}}\) uncertainties were cross-checked and adjusted by varying one of the variables with its uncertainty at a time for the steps where several variables were determined.
Table 5 compares \(\rho \) and total cross-section results from Ref. [6] and the approaches described above. All the results are consistent within the estimated uncertainties. The top two rows use the same normalisation, which is a decisive component for the total cross-section value. The larger \(\sigma _{\mathrm{tot}}\) obtained in this publication can be attributed to the methodological difference: the destructive Coulomb-nuclear interference is explicitly subtracted here. The \(\sigma _{\mathrm{tot}}\) determinations from Ref. [6] and approach 3 are completely independent, both in terms of data and method, and can therefore be combined for uncertainty reduction. The weighted average yields:
which corresponds to \(2.2\,\mathrm{\%}\) relative uncertainty.
Figure 19 compares selected total cross-section measurements at \(\sqrt{s} = 13\,\mathrm{TeV}\) with past measurements.
Predictions of COMPETE models [48] for \({\mathrm{pp}}\) interactions. Each model is represented by one line (see legend). The red points represent the reference TOTEM measurements. The \(\sigma _{\mathrm{tot}}\) point at \(13\,\mathrm{TeV}\) corresponds to the weighted average in Eq. (21). The two \(\rho \) points at \(13\,\mathrm{TeV}\) correspond to the two cases discussed in Sect. 6.2: the left point to the fit with \(N_b=3\) and \(|t|_{\mathrm{max}} = 0.15\,\mathrm{GeV^2}\), the right point to \(N_b=1\) and \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\)
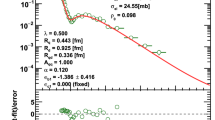
Predictions of the model by Nicolescu et al. (dashed blue curve from [30], solid blue curve from [51]) and the Durham model [20] (including crossing-odd contribution from [19]) compared to the reference TOTEM measurements (red markers). The \(\sigma _{\mathrm{tot}}\) point at \(13\,\mathrm{TeV}\) corresponds to the weighted average in Eq. (21). The two \(\rho \) points at \(13\,\mathrm{TeV}\) correspond to the two cases discussed in Sect. 6.2: the left point to the fit with \(N_b=3\) and \(|t|_{\mathrm{max}} = 0.15\,\mathrm{GeV^2}\), the right point to \(N_b=1\) and \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\). For the Durham model the black curve corresponds to the prediction without a colourless 3-gluon t-channel exchange. The magenta and green curves refer to the \({\mathrm{pp}}\) predictions including a 3-gluon exchange with proton coupling equivalent to 0.8 and \(1.3\,\mathrm{mb}\), respectively
7 Discussion of physics implications
One very comprehensive (and therefore representative) study of the pre-LHC data is by the COMPETE collaboration [2]. In total 256 models, all without crossing-odd components relevant for high energies, were considered to describe \(\sigma _{\mathrm{tot}}\) and \(\rho \) data for various reactions (\({\mathrm{pp}}\), \(\mathrm{p}\pi \), \({\mathrm{pK}}\), etc.) and the corresponding particle-antiparticle reactions. Out of these models, 23 were found to give a reasonable description of the data [48]. Extrapolations from these models are confronted with newer TOTEM measurements in Fig. 20, which shows that they are grouped in 3 bands. Each band is plotted in a different colour and has a different level of compatibility with the data. As argued above, the \(13\,\mathrm{TeV}\) fit with \(N_b=1\) and \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\) (rightmost point in the figure) corresponds to the most fair comparison to past analyses and is therefore used to evaluate the compatibility with the COMPETE models. The \(8\,\mathrm{TeV}\) \(\rho \) point is not included in this calculation since it does not bring any information due to its large uncertainty. The \(\sigma _{\mathrm{tot}}\) measurements can be, to a large extent, regarded as independent: they used data from different LHC fills at different energies, different beam optics, often different RPs, often different analysis approaches (fit parametrisation, treatment of CNI) and often they were analysed by different teams. The only correlation comes from using common normalisation at a given collision energy. Consequently, two compatibility evaluations were made: using all \(\sigma _{\mathrm{tot}}\) points from Fig. 20 and using their subset with a single point per energy. These two results thus provide upper and lower bounds for the actual compatibility level. The observations can be summarised as follows.
The blue band is compatible (p-value 0.990 to 0.995) with the \(\sigma _{\mathrm{tot}}\) data, but incompatible (p-value \(3\times 10^{-6}\)) with the \(\rho \) point.
The magenta band is incompatible (p-value \(1\times 10^{-5}\) to \(5\times 10^{-4}\)) with the \(\sigma _{\mathrm{tot}}\) data and incompatible (p-value \(9\times 10^{-3}\)) with the \(\rho \) point.
The green band is incompatible (p-value \(3\times 10^{-18}\) to \(5\times 10^{-12}\)) with the \(\sigma _{\mathrm{tot}}\) data, but compatible (p-value 0.4) with the \(\rho \) point.
In summary, none of the COMPETE models is compatible with the ensemble of TOTEM’s \(\sigma _{\mathrm{tot}}\) and \(\rho \) measurements.
Another, even less model-dependent, relation between \(\sigma _{\mathrm{tot}}\) and \(\rho \) can be obtained from dispersion relations [7, 49]. If only the crossing-even component of the amplitude is considered, it can be shown that \(\rho \) is proportional to the rate of growth of \(\sigma _{\mathrm{tot}}\) with energy. Therefore, the low value of \(\rho \) determined in Sect. 6 indicates that either the total cross-section growth should slow down at higher energies or that there is a need for an odd-signature object being exchanged by the protons. While at lower energies such contributions may naturally come from secondary Reggeons, their contribution is generally considered negligible at LHC energies due to their Regge trajectory intercept lower than unity.
A variety of odd-signature exchanges relevant at high energies have been discussed in literature, within different frameworks and under different names, see e.g. the reviews [17, 26]. The “Odderon” was introduced within the axiomatic theory [8, 15, 30] as an amplitude contribution responsible for \(\mathrm{p}{{\bar{\mathrm{p}}}}\) vs. \({\mathrm{pp}}\) differences in the total cross-section as well as in the differential cross-section, particularly in the dip region. Crossing-odd trajectories (with \(J=1\) at \(t=0\)) were also studied within the framework of Regge theory as a counterpart of the crossing-even Pomeron. It has also been shown that such an object should exist in QCD, as a colourless compound state of three reggeised gluons with quantum numbers \(J^{PC} = 1^{--}\) (see e.g. [24]). The binding strength among the 3 gluons is greater than the strength of their interaction with other particles. There is also evidence for such a state in QCD lattice calculations, known under the name “vector glueball” (see e.g. [21]). Such a state, on one hand, can be exchanged in the t-channel and contribute, e.g., to the elastic-scattering amplitude. On the other hand it can be created in the s-channel and thus be observed in spectroscopic studies. QCD-like studies based on the AdS/CFT correspondence show that the Odderon emerges on equally firm footing as the Pomeron [50].
There are multiple ways how an odd-signature exchange component may manifest itself in observable data. Focussing on elastic scattering at the LHC (unpolarised beams), there are 3 regions often argued to be sensitive. In general, the effects of an odd-signature exchange (3-gluon compound) are expected to be much smaller than those of even-signature exchanges (2-gluon compound). Consequently, the sensitive regions are those where the contributions from 2-gluon exchanges cancel or are small. At very low |t| the 2-gluon amplitude is expected to be almost purely imaginary, while a 3-gluon exchange would make contributions to the real part and therefore \(\rho \) is a very sensitive parameter. The effects on \(\rho \) in \({\mathrm{pp}}\) and \(\mathrm{p}{{\bar{\mathrm{p}}}}\) are opposite so that for \({\mathrm{pp}}\) the odd-signature exchange component is expected to decrease the \(\rho \) value and for \(\mathrm{p}{{\bar{\mathrm{p}}}}\) to increase its value, see e.g. [30]. Another such example is the dip, often described as the imaginary part of the amplitude crossing zero, thus ceding the dominance to the real part to which a 3-gluon exchange may contribute. In agreement with such predictions, the observed dips in \(\mathrm{p}{{\bar{\mathrm{p}}}}\) scattering are shallower than those in \({\mathrm{pp}}\). At \(\sqrt{s} = 53\,\mathrm{GeV}\), there are data showing a very significant difference between the \({\mathrm{pp}}\) and \(\mathrm{p}{{\bar{\mathrm{p}}}}\) dip [28]. The interpretation of this difference is, however, complicated due to non-negligible contribution from secondary Reggeons. These are not expected to give sizeable effects at the Tevatron energies (see e.g. [13]), which thus gives weight to the D0 observation of a very shallow dip in \(\mathrm{p}{{\bar{\mathrm{p}}}}\) elastic scattering [52] compared to the very pronounced dip measured by TOTEM at \(7\,\mathrm{TeV}\) [12]. The \({\mathrm{pp}}\) vs. \(\mathrm{p}{{\bar{\mathrm{p}}}}\) dip difference is also predicted to be energy-dependent which presents another experimental observable (see e.g. [53]). Sometimes the high-|t| region is also argued to be sensitive to 3-gluon exchanges. Actually the original “Odderon” concept was general to include any crossing-odd contribution. Beside the solution discussed earlier, a solution to the Odderon equation exists in QCD for a leading order 3-free-gluons approximation. In fact in the large-|t| range (perturbative QCD) models (e.g. [54]) predict coherent exchange of 3 individual gluons as opposed to the 3-gluon compound state exchanged at low |t| (non-perturbative QCD).
Figure 21 compares the TOTEM data with two compatible models: by Nicolescu et al. [51] and the extended Durham model [20] (original model [55] plus crossing-odd contribution from [19]). The 2007 version of the Nicolescu model (dashed blue) is based only on pre-LHC data and predicts \(\sigma _{\mathrm{tot}}\) overestimating the TOTEM measurements – as argued in Ref. [51] it might be due to the ambiguities in prolonging the amplitudes in the non-forward region. The 2017 version (solid blue) includes also LHC measurements up to \(13\,\mathrm{TeV}\) and describes the \(\sigma _{\mathrm{tot}}\) data well. Both versions yield similar results for \(\rho \), with a pronounced energy dependence. This comes from the fact that the crossing-odd component is almost negligible at \(\sqrt{s} \approx 500\,\mathrm{GeV}\) but very significant at \(13\,\mathrm{TeV}\). Conversely, in the Durham model the effect is sizeable at \(\sqrt{s} \approx 500\,\mathrm{GeV}\) and gently diminishes with energy. The Durham model also predicts a mild energy dependence of the \(\rho \) parameter. Therefore, precise \(\rho \) measurements at \(\sqrt{s} \approx 900\,\mathrm{GeV}\) and \(14\,\mathrm{TeV}\) would be valuable for discrimination between these models. For both models, the inclusion of a crossing-odd exchange component was essential to reach the agreement between the data and model. In particular, the Durham model without such a contribution (black line) is not so well compatible (p-value 0.02) with the (rhs.) \(\rho \) point obtained with \(N_b=1\) and \(|t|_{\mathrm{max}} = 0.07\,\mathrm{GeV^2}\).
8 Summary
The measurement of elastic differential cross-section disfavours the purely-exponential low-|t| behaviour at \(\sqrt{s} = 13\,\mathrm{TeV}\), similarly to the previous observation at \(8\,\mathrm{TeV}\). Thanks to the very low-|t| reach, the first extraction of the \(\rho \) parameter at \(\sqrt{s} = 13\,\mathrm{TeV}\) was made by exploiting the Coulomb-nuclear interference. The fit with conditions similar to past experiments yields \(\rho = 0.09 \pm 0.01\), one of the most precise \(\rho \) determinations in history. The fit over the maximum of data points and with maximum reasonable flexibility of the fit function gives \(\rho = 0.10 \pm 0.01\).
Also thanks to the very low |t| reach, it was possible to apply the “Coulomb normalisation” technique for the first time at the LHC and obtain another total cross-section measurement \(\sigma _{\mathrm{tot}} = (110.3 \pm 3.5)\,\mathrm{mb}\) completely independent from the previous TOTEM measurement at \(\sqrt{s} = 13\,\mathrm{TeV}\) [6] but well compatible with it. Since these two measurements are independent, it is possible to calculate the weighted average yielding \(\sigma _{\mathrm{tot}} = (110.5 \pm 2.4)\,\mathrm{mb}\).
The updated collection of TOTEM’s \(\sigma _{\mathrm{tot}}\) and \(\rho \) data presents a stringent test of model descriptions. For an indicative example, none of the models considered by the COMPETE collaboration is compatible with both \(\sigma _{\mathrm{tot}}\) and \(\rho \).
For both models found to be consistent with TOTEM’s data, the inclusion of a crossing-odd 3-gluon-state exchange in the t-channel was essential for reaching the good agreement with the data.
If it is demonstrated in future that the crossing-odd exchange component is unimportant for elastic scattering, the low \(\rho \) value determined in this publication represents the first experimental evidence for slowing down of the total cross-section growth at higher energies, leading to a deviation from most current model expectations.
We observe significant incompatibilities between \({\mathrm{pp}}\) and \(\mathrm{p} {{\bar{\mathrm{p}}}}\) differential cross-section (in the non-perturbative t-range): this implies experimental evidence of crossing-odd exchange in the t-channel, hence of a colourless C-odd 3-gluon compound state exchange [24, 25].
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All data analysed during this study are included in this published article and will be uploaded to the HepData database (https://www.hepdata.net/).]
References
Particle Data Group, C. Patrignani et al., Chin. Phys. C 40, 100001 (2016)
COMPETE Collaboration, J. Cudell et al., Phys. Rev. Lett. 89, 201801 (2002)
TOTEM Collaboration, G. Antchev et al., Europhys. Lett. 101, 21004 (2013)
TOTEM Collaboration, G. Antchev et al., Nucl. Phys. B 899, 527 (2015)
TOTEM Collaboration, G. Antchev et al., Eur. Phys. J. C 76, 661 (2016)
TOTEM Collaboration, G. Antchev et al., CERN preprint CERN-EP-2017-321 (2017). arXiv:1712.06153 [hep-ex]
V. Barone, E. Predazzi, High-Energy Particle Diffraction (Springer, Berlin, 2002)
P. Gauron, L. Lukaszuk, B. Nicolescu, Phys. Lett. B 294, 298 (1992)
J. Bartels, Nucl. Phys. B 175, 365 (1980)
J. Kwieciǹski, M. Praszałowicz, Phys. Lett. B 94, 413 (1980)
T. Jaroszewicz, J. Kwieciǹski, Z. Phys. C 12, 167 (1982)
TOTEM Collaboration, G. Antchev et al., Europhys. Lett. 95, 41001 (2011)
W. Broniowski et al., Phys. Rev. D 98, 074012 (2018)
E. Levin, (1998). arXiv:hep-ph/9808486
L. Lukaszuk, B. Nicolescu, Lett. Nuovo Cim. 8, 405 (1973)
D. Joynson et al., Nuovo Cim. A 30, 345 (1975)
M.A. Braun, (1998). arXiv:hep-ph/9805394
B.L. Ioffe, V.S. Fadin, L.N. Lipatov, Quantum Chromodynamics: Perturbative and Nonperturbative Aspects (Cambridge University Press, Cambridge, 2010)
E. Levin, M. Ryskin, Phys. Rep. 189, 268 (1990)
V.A. Khoze, A.D. Martin, M.G. Ryskin, Phys. Rev. D 97, 034019 (2018)
C.J. Morningstar, M. Peardon, Phys. Rev. D 60, 034509 (1999)
Y. Chen et al., Phys. Rev. D 73, 014516 (2006)
G. Veneziano, Nuovo Cim. A 57, 190 (1968)
J. Bartels, L. Lipatov, G. Vacca, Phys. Lett. B 477, 178 (2000)
J. Bartels et al., Eur. Phys. J. C Part. Fields 20, 323 (2001)
C. Ewerz, (2003). arXiv:hep-ph/0306137
H1 Collaboration, C. Adloff et al., Phys. Lett. B 544, 35 (2002)
A. Breakstone et al., Phys. Rev. Lett. 54, 2180 (1985)
K. Akiba et al., J. Phys. G 43, 110201 (2016)
R. Avila, P. Gauron, B. Nicolescu, Eur. Phys. J. C 49, 581 (2007)
M. Froissart, Phys. Rev. 123, 1053 (1961)
TOTEM Collaboration, G. Anelli et al., JINST 3, S08007 (2008)
TOTEM Collaboration, G. Antchev et al., Int. J. Mod. Phys. A 28, 1330046 (2013)
G. Ruggiero et al., Nucl. Instrum. Methods. A604, 242 (2009)
TOTEM Collaboration, G. Antchev et al., New J. Phys. 16, 103041 (2014)
TOTEM Collaboration, G. Antchev et al., Europhys. Lett. 101, 21002 (2013)
TOTEM Collaboration, G. Antchev et al., Phys. Rev. Lett. 111, 012001 (2013)
H. Niewiadomski, Reconstruction of Protons in the TOTEM Roman Pot Detectors at the LHC, PhD thesis, Manchester U., Manchester, 2008, Presented on 11 Sep (2008)
E. Todesco, J. Wenninger, Phys. Rev. Accel. Beams 20, 081003 (2017)
G.D. Lafferty, T.R. Wyatt, Nucl. Instrum. Methods A355, 541 (1995)
TOTEM, G. Antchev et al., (2018). arXiv:1812.08283
J. Kašpar, Comput. Phys. Commun. 185, 1081 (2014). http://elegent.hepforge.org/
V. Kundrát, M. Lokajíček, Z. Phys. C 63, 619 (1994)
R. Cahn, Z. Phys. C 15, 253 (1982)
Particle Data Group, K. Nakamura et al., J. Phys. G 37, 075021 (2010)
UA4/2 Collaboration, C. Augier et al., Phys. Lett. B 316, 448 (1993)
G.B. West, D. Yennie, Phys. Rev. 172, 1413 (1968)
COMPETE Collaboration, Benchmarks For the Forward Observables (2002). http://nuclth02.phys.ulg.ac.be/compete/publications/benchmarks_details/. Accessed 6 Dec 2017
I.M. Dremin, JETP Lett. 97, 571 (2013)
R.C. Brower, M. Djurić, C.I. Tan, J. High Energy Phys. 2009, 063 (2009)
E. Martynov, B. Nicolescu, Phys. Lett. B 778, 414 (2018)
D0 Collaboration, V.M. Abazov et al., Phys. Rev. D 86, 012009 (2012)
A. Ster, L. Jenkovszky, T. Csörgő, Phys. Rev. D 91, 074018 (2015)
A. Donnachie, P. Landshoff, Z. Phys. C 2, 55 (1979)
V.A. Khoze, A.D. Martin, M.G. Ryskin, Eur. Phys. J. C 74, 2756 (2014)
Acknowledgements
This work was supported by the institutions listed on the front page and also by the Magnus Ehrnrooth foundation (Finland), the Waldemar von Frenckell foundation (Finland), the Academy of Finland, the Finnish Academy of Science and Letters (The Vilho, Yrjö and Kalle Väisälä Fund), the OTKA NK 101438 and the EFOP-3.6.1-16-2016-00001 Grants (Hungary) and the grant MNiSW DIR/WK/2018/13 by the Polish Ministry of Science and Higher Education. Individuals have received support from Nylands nation vid Helsingfors universitet (Finland), from the MŠMT ČR (Czech Republic) and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences and the NKP-17-4 New National Excellence Program of the Hungarian Ministry of Human Capacities.
Author information
Authors and Affiliations
Corresponding author
Additional information
M. Lo Vetere: Deceased.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Antchev, G., Aspell, P., Atanassov, I. et al. First determination of the \({\rho }\) parameter at \({\sqrt{s} = 13}\) TeV: probing the existence of a colourless C-odd three-gluon compound state. Eur. Phys. J. C 79, 785 (2019). https://doi.org/10.1140/epjc/s10052-019-7223-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7223-4