Abstract
I argue that the ten dimensional non-supersymmetric tachyonic superstrings may serve as good starting points for the construction of viable phenomenological vacua. Thus, enlarging the space of possible solutions that may address some of the outstanding problems in string phenomenology. A tachyon free six generation Standard–like Model is presented, which can be regarded as an orbifold of the \(SO(16)\times E_8\) heterotic–string in ten dimensions. I propose that any \((2,\,0)\) heterotic–string in four dimensions can be connected to a \((2,\,2)\) one via an orbifold or by interpolations and provide some evidence for this conjecture. It suggests that any Effective Field Theory (EFT) model that cannot be connected to a \((2,\,2)\) theory is necessarily in the swampland, and will simplify the analysis of the moduli spaces of \((2,\,0)\) string compactifications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
String theory provides a viable framework to explore the unification of all the fundamental matter and interactions. While string theory produces a consistent theory of perturbative quantum gravity, it accommodates consistently the gauge and matter structures of the subatomic regime, including the chirality property of the electroweak interactions. No other contemporary theory achieves this feat. Yet it is expected that the string character of this basic theory is only exhibited at energy scales that are far removed from those accessible to present day experiments. In that respect one would have to rely on the effective, point-like, field theory limit of the string construction in order to confront the theory with experiment. For that purpose it is vital to be able to identify the smooth effective field theory (EFT) limit corresponding to particular string theory vacua. To date this identification is only possible in limited cases [1], and entail mostly the analysis of various supergravity theories that are EFT limits of the corresponding string theories. The picture is murky in both directions, as for the most part one does not know whether an actual supergravity theory has an origin in a string construction. Furthermore, while supersymmetry is a beautiful theoretical construction, it is not clear whether nature makes use of it. It is therefore important to explore alternatives from the point of view of the worldsheet string theory.
To date investigation of non-supersymmetric string models were primarily conducted in the context of the tachyon free \(SO(16)\times SO(16)\) ten dimensional heterotic string theory [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. This construction can be obtained as an orbifold of the ten dimensional supersymmetric \(E_8\times E_8\) heterotic–string, and can be connected to it by interpolations in a compactified dimension [4, 5]. It is well known that string theory gives rise to additional vacua in ten dimensions that are tachyonic [2,3,4, 6]. However, the tachyonic modes may be projected out by Generalised GSO projections. Therefore, from the point of view of the worldsheet string theory, these string vacua may serve as viable starting points for the construction of phenomenological string models and offer novel perspectives on some outstanding issues in string phenomenology. Furthermore, they may reveal alternative symmetries to those provided by spacetime supersymmetry. An example is the Massive Boson–Fermion Degeneracy of [22,23,24].
In this paper I explore this possibility. For general reference I first examine the constructions of such models in ten dimensions. The discussion then reverts to the construction of phenomenological models in four dimensions that can be regarded as compactifications of the ten dimensional vacua. I present a six generation tachyon free model with standard–like gauge group, as well as a three generation model that does, however, contain two tachyonic states. I discuss the reduction of the number of generations to three generations and the prospect of generating such tachyon free models.
Additionally, the moduli spaces of (2, 0) heterotic–string vacua is discussed. This class of compactifications is vast with little understanding of the relation between the worldsheet constructions and their smooth effective field theory limits. I conjecture that all (2, 0) heterotic–string vacua can be related to those with (2, 2) worldsheet supersymmetry by an orbifold or by an interpolation and offer some evidence for this conjecture, as well as some counter arguments. If the conjecture is correct it can serve as an enormous simplifying tool for the analysis of the moduli spaces of (2, 0) string compactifications. In the very least it can serve as a classifying criteria between the vacua that can be regarded as descending from (2, 2) vacua and those that do not.
2 Ten dimensional vacua
We start our discussion with the \(E_8\times E_8\) heterotic–string in ten dimensions. Its partition function is given by
where the level–one SO(2n) characters are given by
In the following I omit the prefactor due to the uncompactified dimensions. The ten dimensional \(SO(16)\times SO(16)\) heterotic–string is obtained by applying the orbifold projection
where F is the spacetime fermion number, taking \(S_8\rightarrow -S_8 \) and \(F_{z_1,z_2}\) are the fermion numbers of the two \(E_8\) factors, taking \(S_{16}^{1,2}\rightarrow -S_{16}^{1,2}\). The partition function of the \(SO(16)\times SO(16)\) heterotic–string is therefore given by
Examining the partition function in Eq. (4) it is noted that the would–be tachyonic term, \(O_8 \left( \overline{C}_{16} {{\overline{V}}}_{16} + {{\overline{V}}}_{16} \overline{C}_{16}\right) \) only produces massive physical states. Upon compactifications to lower dimensions, in general, tachyonic states will appear in the spectrum, but may be projected in special cases. In that respect, we may consider the ten dimensional tachyonic vacua and similarly project the tachyons in special cases.
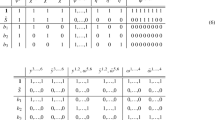
In the free fermion formulation [25,26,27] the vacua are specified in terms of boundary condition basis vectors and one-loop Generalised GSO (GGSO) phases. The \(E_8\times E_8\) and \(SO(16)\times SO(16)\) models are specified in terms of a common set of basis vectors
where I adopted the conventional notation used in the phenomenological free fermionic constructions [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. The basis vector \(\mathbb {1}\) is required by the consistency rules [25,26,27] and generates a model with an SO(32) gauge group from the Neveu-Schwarz (NS) sector. The spacetime supersymmetry generator is given by the combination
The choice of GGSO phase \(C{z_1\atopwithdelims []z_2}=\pm 1\) then selects between the \(E_8\times E_8\) or \(SO(16)\times SO(16)\) heterotic–string vacua in ten dimensions. The relation in Eq. (6) dictates that in ten dimensions the breaking pattern \(E_8\times E_8\rightarrow SO(16)\times SO(16)\) is correlated with the breaking of spacetime supersymmetry. Equation (6) does not hold in lower dimensions.
To consider the tachyonic ten dimensional vacua we can start with the \(E_8\times E_8\) partition function and apply the orbifold
the resulting partition function is now given by
produces the partition function of the \(SO(16)\times E_8\) non-supersymmetric and tachyonic heterotic–string vacuum. It is noted that the term \(O_8{{\overline{V}}}_{16}{{\overline{O}}}_{16}\) in the partition function gives rise to a tachyonic state in the vectorial 16 representation of SO(16). All of the non-supersymmmetric tachyonic string vacua in ten dimensions were classified in Refs. [2, 3, 6]. It was further shown that all the ten dimensional vacua can be connected by interpolations in lower dimensions or by orbifolds [4, 5].
In the free fermion construction all the ten dimensional are specified in terms of boundary condition basis vectors and GGSO phases [25,26,27]. The \(SO(16)\times E_8\) vacuum is generated by the basis vectors \(\{{\mathbb {1}}, z_1\}\) from Eq. (5), irrespective of the choices of the GGSO phases. Other ten dimensional vacua can similarly be generated by replacing the \(z_1\) basis vectors with \(z_1=\{{{{\bar{\phi }}}}^{1,\dots , 4}\}\) and additional similar \(z_i\) basis vectors with utmost two overlapping periodic fermions. All these vacua are in principle connected by interpolations or orbifolds along the lines of Ref. [4], and, in general, will contain tachyons in their spectrum. Our interest here is rather in the possibility of constructing tachyon free phenomenological vacua, starting from the tachyonic ten dimensional vacua. The lesson to draw from the ten dimensional exercise is that these models can be constructed by removing the ten dimensional vector \(S={\mathbb {1}}+z_1+z_2\) from the basis of the phenomenological four dimensional models.
3 Lower dimensional constructions
We can similarly consider compactifications of either of the models to lower dimensions, e.g. for the \(E_8\times E_8\) heterotic–string
where for each circle,
and
In the case of one compactified dimension, the \(Z_+\) partition function is
Applying the orbifold projection
where \(\delta x^9 = x_9 +\pi R\), in \(Z_+^{9d}\) produces the \(Z_-^{9d}\) partition function given by
The partition function of the free fermion model \(\{1,S,z_1,z_2\}\), with \(1+S+z_1+z_2=\{y^1 ,\omega ^1~| ~{\bar{y}}^1,{\bar{\omega }}^1\}\), is given by
In terms of the SO(2n) characters shown in Eq. (2) we have
and
where the orbifold operation is [55]
where \(F_L^{\mathrm{int}}\) acts in the 9th dimension. The observation here is that in lower dimensions we can couple the projection of the spinorial states from the sectors \(z_1\) and \(z_2\) with an action in an internal dimension, thus breaking \(E_8\times E_8\rightarrow SO(16)\times SO(16)\) without breaking supersymmetry. We can similarly consider the compactifications to four dimensions on an SO(12) lattice that corresponds to the enhanced lattice at the free fermionic point. The two partition functions are given by
and
and are connected by the orbifold [56]
with
where \(F_{\mathrm{L}}\) is the fermion number for the “left” component in the expression of the internal lattice i.e., the nontrivial action of this operator is \(F_{\mathrm{L}} S_{12}=- S_{12}\) and \(F_\mathrm{L} C_{12}=- C_{12}\). The projection in (21) and (22) is defined at the free fermionic point and can be generalised to an arbitrary point in the moduli space. The important point to note is that all these supersymmetric and non-supersymmetric vacua can be interpolated by compactifications to lower dimensional vacua [19, 20]. Reversing the order of the projections we can consider them as compactifications of the non-supersymmetric \(SO(16)\times SO(16)\) heterotic–string that are connected by interpolations to the supersymmetric vacua on the boundary of the moduli space. Similar constructions and interpolations can be implemented for the other ten dimensional string vacua.
To construct phenomenological four dimensional vacua that correspond to compactification of the ten dimensional tachyonic vacua, we can investigate the phenomenological free fermionic models. This class of heterotic–string models correspond to \(Z_2\times Z_2\) orbifold of six dimensional toroidal lattices [57,58,59,60]. From the analysis of the ten dimensional vacua we learn that the construction of the tachyonic ten dimensional vacua amounts to removing the vector combination S from the allowed combination of basis vectors. To construct a non-supersymmetric phenomenological four dimensional model, we can start with \(SO(16)\times SO(16)\) ten dimensional model and explore the compactifications to four dimensions on \(Z_2\times Z_2\) orbifolds. This was pursued in Ref. [21], and a general discussion of the tachyonic producing sectors was presented. In general, in addition to the tachyon that arise in the Neveu–Schwarz \({\mathbf {0}}\) sector, the models contain numerous additional tachyon producing sectors. Those were classified in Ref. [21]. For specific choices of the GGSO phases, phenomenological tachyon free models can be constructed [21]. The alternative is to explore compactifications of the ten dimensional tachyonic vacua. As discussed in Sect. 2 this amounts to removing the vector S from the additive group in these constructions.
Phenomenological free fermionic heterotic–string models were constructed by pursuing two methodologies. The first, which is referred to as NAHE–based models, was followed by using a common subset of boundary condition basis vectors, the so-called NAHE-set [61, 62], that was first used in the construction of the flipped SU(5) (FSU5) heterotic–string model [28] and subsequently employed in the construction of the Standard-like Models (SLM) [29,30,31,32,33]; Pati–Salam (PS) [34, 35]; Left–Right Symmetric (LRS) [36, 37]; \(SU(4)\times SU(2)\times U(1)\) (SU421) [38, 39]; models. The NAHE-set is a common set of five basis vectors, \(\{{\mathbb {1}}, S, b_1, b_2, b_3\}\), where S is the spacetime supersymmetry generator, discussed above, and \(b_1\), \(b_2\) and \(b_3\) are the three twisted sectors of the \(Z_2\times Z_2\) orbifold. The different phenomenological models are constructed by adding three or four additional boundary condition basis vectors to the NAHE-set [28,29,30,31,32,33,34,35,36,37,38,39]. The second method entails a systematic classification of toroidal \(Z_2\times Z_2\) orbifolds for the different SO(10) subgroups. The method was initially developed for the classification of vacua with an SO(10) GUT group [41,42,43,44] and subsequently employed for the classification of PS [47,48,49]; FSU5 [51, 52]; SLM [53]; and LRS [54] models. The method works with a fixed set of basis vectors and the enumeration of the models is achieved by varying the independent GGSO phases of the one-loop partition function, i.e. the set of basis vectors that generate the SO(10) models is given by
where \(i = 1,\ldots ,6\) and the fermions which appear in the basis vectors have periodic (Ramond) boundary conditions, whereas those not included have antiperiodic (Neveu-Schwarz) boundary conditions. Additional vectors are added to the set in (23) to generate the models with the various SO(10) subgroups [47,48,49, 51,52,53,54]. The GGSO phases \(C{v_i\atopwithdelims []v_{j}}\) with \(i>j\) span the space of vacua, corresponding to \(2^{n(n-1)/2}\) string models.
The basis vector S coincides with the vector combination in Eq. (6) and generates \({N} = 4\) spacetime supersymmetry, with SO(44) gauge symmetry. The \(e_i\) vectors break the gauge symmetry to \(SO(32)\times U(1)^6\) and maintain the \({N}=4\) supersymmetry. These vectors correspond to all possible internal symmetric shifts of the six internal bosonic coordinates. The vectors \(b_1\) and \(b_2\) corresponds to \({Z}_2 \times {Z}_2\) orbifold twists. They break the spacetime supersymmetry to \({N}=1\), and the gauge symmetry to \(SO(10)\times U(1)^3 \times SO(16)\). Addition of the basis vectors \(z_1\) and \(z_2\) breaks the hidden SO(16) gauge group to \(SO(8)\times SO(8)\).
The reduction of spacetime supersymmetry to \(N=0\) can ensue by projecting the remaining supersymmetry from the S basis vector. Setting \(c{S\atopwithdelims []v_i}=-\delta _{v_i}\) guarantees the existence of \(N=1\) supersymmetry, and therefore the reduction to \(N=0\) is obtained by relaxing this condition. The products \(S\cdot e_i= 0\) and \(S\cdot z_i= 0\) entail that the \(\{e_i, z_1, z_2\}\) basis vectors act as projectors on the S-sector. They can project all the gravitinos from the S-sector, hence inducing the breaking from \(N=4\) to \(N=0\) spacetime supersymmetry.
Non-supersymmetric NAHE-based models as well as those models generated by the set in Eq. (23) can be represented as compactifications of the ten dimensional \(SO(16)\times SO(16)\) heterotic–string. Similar to the ten dimensional case the untwisted tachyonic state is projected out by the basis vector S. However, unlike the case of the ten dimensional model, the sectors that can produce additional tachyonic states proliferate. In the context of the three generation free fermionic models these sectors were classified in Ref. [21]. In general, the construction of realistic non-supersymmetric models without any tachyonic states is exceedingly hard. The reason is precisely due to the proliferation of tachyon producing sectors that arise due to the breaking of the string symmetries to smaller symmetries. In the free fermionic construction this is manifested by the larger number of independent basis vectors that are required in the construction of the quasi–realistic three generation models. Examples of rare tachyon free cases can be found [21], and one can even search for such models with suppressed cosmological constant [7,8,9,10,11,12,13,14,15,16,17,18].
As noted in the ten dimensional case compactifiations of the ten dimensional tachyonic vacua amounts to removing the vector S from the set of basis vectors, e.g. the set \(\{{\mathbb {1}}, z_1,z_2\}\) produces a non supersymmetric model with \(SU(2)^6\times SO(12)\times E_8\times E_8\) or \(SU(2)^6\times SO(12)\times SO(16)\times SO(16)\). In this case the untwisted tachyonic state in general reappear. It is noted also that the left–moving vector bosons remain in the spectrum, and are projected out by the additional NAHE-set basis vectors. We can start to explore such models by starting with a reduced NAHE-set that does not include the S-vector. This set is given by

The set of basis vectors in Eq. (24) produces a non supersymmetric model with 96 multiplets in the 16 spinorial representation of SO(10). The four dimensional gauge symmetry is \(SO(10)\times SO(6)^3\times E_8\). The model contain an untwisted tachyonic state in the vectorial 10 representation of SO(10). This tachyonic state is entirely projected out in the FSU5 and SLM type models, but not in the PS or LRS models. Similar to the case of the non-supersymmetric models in Ref. [21], whether or not a model contains tachyons is highly model dependent. The model defined by the set of basis vectors
with the set of GGSO projection coefficients given by

produces a tachyon free SLM model with
observable and hidden gauge groups, where the hidden sector gauge symmetry is generated by vector bosons that arise in the Neveu–Schwarz sector and the sector \(\zeta ={\mathbb {1}}+b_1+b_2+b_3\). The model contains six chiral generations in the spinorial 16 representation of SO(10), decomposed under the gauge group in Eq. (27), from the sectors \(b_1\), \(b_2\) and \(b_3\). The doubling of the number of generations compared to the NAHE–based models occurs because of the removal of the S projection, with the result that the chirality of the \(\chi ^{ij}\) worldsheet fermions in the sectors \(b_1\), \(b_2\) and \(b_3\) is not fixed and consequently the number of generations is doubled. I discuss below how this can be remedied. The model contains three pairs of untwisted Higgs doublets \(h_1, {{{\bar{h}}}}_1\), \(h_2, {{{\bar{h}}}}_2\), \(h_3, {{{\bar{h}}}}_3\), that couple to the twisted states from the sectors \(b_1\), \(b_2\) and \(b_3\) and produce a leading mass term for the top quark mass. Additional electroweak Higgs doublet representation are obtained from the sector \(b_1+b_2+\alpha +\beta \). In that respect, the flavour structure in the model is similar to that of other NAHE–based Standard-like Models [63, 64]. The untwisted Neveu–Schwarz sector and the sectors \(\beta \pm \gamma \); \(\alpha \pm \gamma \); \(\alpha +\beta \); \(b_2+b_3+\beta \pm \gamma \oplus \zeta \); \(b_2+b_3+\alpha +2\gamma \); \(b_1+b_3+\alpha \pm \gamma \oplus \zeta \); \(b_1+b_3+\alpha +2\gamma \); \(b_1+b_2+\alpha +2\gamma \); \(b_1+b_2+\alpha +\beta \), produce spacetime bosons, whereas the sectors \(b_1\); \(b_2\); \(b_3\); \(b_1+2\gamma \oplus \zeta \); \(b_2+2\gamma \oplus \zeta \); \(b_3+2\gamma \oplus \zeta \); \(b_2\pm \gamma \); \(b_1+b_2+b_3+2\gamma \), produce spacetime fermions. Here the notation \(\oplus \zeta \) denotes the states that transform under the hidden non-Abelian group factors, that are obtained from a given sector and the given sector \(\oplus \zeta \). The \(U(1)_{1,2,3}\) symmetries are anomalous. Thus the model contains one anomalous U(1) combination that can be canceled by a generalised Green-Schwarz mechanism [65]. The entire spectrum of the model will be presented elsewhere.
As discussed above the model defined by Eqs. (25, 26) gives rise to six chiral generation due to the removal of the S projection on the states from the sectors \(b_1\), \(b_2\) and \(b_3\). The consequence is that the chirality of the worldsheet fermions \(\chi ^{ij}\) in these sectors is not fixed, hence doubling the number of generations compared to the NAHE-based three generation models. This situation can be remedied by including a basis vector that mimics the projection of the S vector, but without generating spacetime gravitinos, which is achieved by modifying the boundary conditions of the right–moving worldsheet fermions in the basis vector S. An example of a vector that achieves this feat is given by
with the choice of GGSO projection coefficients
the resulting model contains three generation of chiral fermions from the sectors \(b_1\), \(b_2\) and \(b_3\). The vector \({{\mathcal {S}}}\) in Eq. (29) does not give rise to any massless gravitinos and therefore the model is non supersymmetric. Vector bosons contributing to the hidden sector gauge group arise again in the untwisted NS-sector and the \(\zeta \)-sector, generating an \(SU(3)\times SU(2)\times U(1)^5\) hidden sector gauge group, whereas the observable gauge group coincides with the one in Eq. (27). The model does, however, contain two tachyonic states from the sector \({{\mathcal {S}}}+b_1+b_2+b_3+\alpha +\beta +2\gamma \), that are neutral under the observable gauge symmetry and charged under the hidden sector gauge group. A systematic search for similar tachyon free three generation models can be pursued by using the free fermionic classification method with or without a modified \({{\mathcal {S}}}\) sector and there is no a priori reason to assume that they do not exist. The situation in that respect is similar to the proliferation of gauge symmetry enhancing sectors in these models, but typically there exist configurations of free phases in which all the enhancing vector bosons are projected out.
4 Connectedness of (2, 0) and (2, 2) string vacua
In Sect. 3 I argued that the ten dimensional tachyonic string vacua may serve as good starting points for the construction of viable four dimensional string models. These are not the traditional string vacua that are explored in Effective Field Theory (EFT) studies of string compactifications, which are focused on the approximate supergravity limit of the supersymmetric string models. As the basis vector S is the generator of spacetime supersymmetry, these EFT limits are those that would be characterised as effective limits of string vacua that contain the basis vector S, in the different ten dimensional string theories, e.g. in the Type II superstring and heterotic–string. It is noted that the worldsheet perspective may afford alternative starting points for the exploration of the phenomenological application of string theory.
The heterotic–string is particularly appealing from the point of view of the Standard Model data, as it accommodates the embedding of the chiral matter states in the spinorial 16 representation of SO(10). The supersymmetric string compactifications in four dimensions may have (2, 2) worldsheet supersymmetry or (2, 0), where the first case correspond to heterotic–string vacua with \(E_6\) gauge symmetry in four dimensions, whereas the second case correspond to vacua in which the \(E_6\) symmetry is broken to \(SO(10)\times U(1)\) and its subgroups. While the moduli spaces of the (2, 2) string theories, and their EFT limits, are fairly well understood [1], that is not the case for those with (2, 0) worldsheet supersymmetry. Understanding the moduli spaces of (2, 0) string vacua and their EFT limits is an important problem in string phenomenology. It is therefore of interest to explore whether string theory can offer some guidance from a worldsheet perspective.
It is known that the ten dimensional vacua are connected via orbifolds or by interpolations in lower dimensions [4, 5, 66]. The interpolation among string vacua was also studied in the context of four dimensional phenomenological string vacua [19, 20]. It has further been proposed that the different superstring theories can be seen to be contained in the bosonic string [67]. In this section I propose that all (2, 0) heterotic–string vacua can be connected to (2, 2) heterotic–string vacua via orbifolds or via interpolations. I present some evidence for this conjecture that stems from the classification of fermionic \(Z_2\times Z_2\) orbifolds and the observation of spinor–vector duality in the space of these compactifications. It should be noted that this claim is unexpected from the point of view of the effective field theory description of string vacua. Indeed, some constructions have been presented that do not seem to have an underlying (2, 2) structure [68].
We can again turn to the free fermionic models to seek guidance. We can consider the extended NAHE–set basis with the vectors \(\{{\mathbb {1}}, S, b_1, b_2, b_3, z_1 \}\) [69,70,71]. As discussed above the subset \(\{{\mathbb {1}}, S, z_1= {\mathbb {1}}+b_1+b_2+b_3, z_2 \}\) generates a model with \(N=4\) spacetime supersymmetry with \(S0(12)\times SO(16)\times SO(16)\) or \(SO(12)\times E_8\times E_8\) four dimensional gauge group, depending on the GGSO phase \(C{z_1\atopwithdelims []z_2}\), corresponding to the partition functions in Eq. (19) and (20), respectively. Applying the \(Z_2\times Z_2\) twists produces a model with \(N=1\) spacetime supersymmetry and \(SO(4)^3\times SO(10)\times U(1)^3\) or \(SO(4)^3\times E_6\times U(1)^2\) gauge symmetries. The untwisted internal moduli space is identical in the two cases and consists of three Kähler and three complex moduli [72]. In the fermionic language the exactly marginal operators corresponding to the moduli fields take the form of worldsheet Thirring interactions [73,74,75]. The untwisted moduli fields correspond to untwisted scalar fields that parametrise this moduli space [72]. The vacuum with the enhanced \(E_6\) symmetry has (2, 2) worldsheet symmetry, whereas in the vacuum with SO(10) symmetry the right–moving \(N=2\) worldsheet supersymmetry is broken. In the \(E_6\) case the twisted sector produces 24 representations in the 27 representation of \(E_6\). In these models these states decompose under \(E_6\rightarrow SO(10)\times U(1)\) in the following way. The spinorial 16 representations are obtained from the sectors \(b_1\), \(b_2\) and \(b_3\), whereas the vectorial 10 representations of SO(10) are obtained from the sectors \(b_j+z_1\), \(j=1,2,3\). In addition to the vectorial 10 representations the sectors \(b_j+z_1\), \(j=1,2,3\) produce the 24 copies of: the SO(10) singlets in the 27 representation of \(E_6\); an additional singlet that correspond to the twisted moduli; and additional 8 \(E_6\) real singlets, giving a total of 32 real states. Correspondingly, in the SO(10) models the (2, 2) worldsheet supersymmetry is broken. The breaking is induced by the same GGSO phase of the \(N=4\) spacetime supersymmetric vacuum, namely \(C{z_1\atopwithdelims []z_2}=-1\). The sectors \(b_j\) still produce the 24 copies of the 16 spinorial representation of SO(10). However, the sectors \(b_j+z_1\) now produce 24 copies in the 16 vectorial representation of the hidden SO(16) gauge group. The total number of physical states from the sectors \(b_j\oplus b_j+z_1\) is therefore preserved and is again 32. However, the simple identification of the twisted moduli is obscured. The two models are, however, connected by the discrete map \(C{z_1\atopwithdelims []z_2}=+1\rightarrow -1\) in the fermionic worldsheet language. In the orbifold language the map is between two distinct Wilson lines [76], i.e. it is part of the \(N=4\) moduli space.
The \(Z_2\times Z_2\) on the SO(12) lattice produces 24 fixed points [57,58,59,60, 69,70,71]. The \(Z_2\times Z_2\) at a generic point in the moduli space has 48 fixed. The number of 48 fixed points is reduced to 24 by acting with a freely acting shift on the six dimensional torus. The freely acting shift that reproduces the SO(12) lattice at the free fermionic point is a generalisation of the one given in Eq. (22), and involves a non-geometric asymmetric shift of both the momenta and winding modes [56]. This asymmetric shift correspond to the fact that the SO(12) lattice is realised with a non-trivial antisymmetric B–tensor field, at the free fermionic point in the moduli space [57,58,59,60, 69,70,71]. The moduli space correspond to the \(N=4\) moduli space, which is parametrised by the six dimensional metric G, the anti–symmetric tensor B, and the Wilson lines W.
A general classification of the \(Z_2\times Z_2\) orbifolds with SO(10) GUT symmetry using the free fermion methodology was performed in [41,42,43,44]. Two relevant observation were made. The first is that the enumeration of the vacua with different numbers of generations only depends on the GGSO phases of the subset of basis vectors that preserve the \(N=4\) spacetime supersymmetry. Hence, the enumeration only depends on the moduli fields of the \(N=4\) toroidal compactifications. At this level the moduli space is connected by continuous interpolations. The action of the \(Z_2\times Z_2\) orbifolds, which breaks \(N=4\rightarrow N=1\) spacetime supersymmetry, merely projects to different number of generations, but the information is predetermined by the data of the \(N=4\) toroidal lattice. The \(Z_2\times Z_2\) orbifold action also projects some of the moduli fields. The transformations between the different vacua at the \(N=1\) level are therefore discrete, rather than continuous.
The second observation in the fermionic classification of the \(Z_2\times Z_2\) orbifolds is the existence of a global symmetry in the space of (2, 0) string compactifications, under the exchange of spinor and vector representation of the SO(10) GUT group, dubbed spinor–vector duality [42,43,44,45,46, 76]. This duality can be interpreted as a discrete remnant of the enhanced \(E_6\) symmetry, just as T–duality is a discrete remnant of the enhanced symmetry at the self–dual point [77]. The vacuum at the \(E_6\) enhanced symmetry point, which possesses (2, 2) worldsheet supersymmetry, is self–dual under the spinor–vector duality. The spectral flow operator of the right–moving \(N=2\) worldsheet supersymmetry is the operator that mixes between the spinorial and vectorial SO(10) states in the 27 representation of \(E_6\). In the SO(10) vacua, in which the right–moving worldsheet supersymmetry is broken, the spectral flow operator induces the map between the dual vacua. Now, from the point of view of the fermionic or orbifold constructions, the order of the \(N=4\) deformation Eq. (22), or the \(Z_2\times Z_2\) orbifold, does not matter. Thus, the (2, 0) vacua can be interpreted as orbifold deformations of the (2, 2) vacua. It is further noted that this picture generalises to string compactifications with interacting CFTs [78]. The existence of similar symmetries is expected to be a general property of (2, 0) heterotic–string vacua with an SO(10) GUT symmetry.
String compactifications with (2, 0) worldsheet supersymmetry, in general, do not need to possess an SO(10) GUT symmetry. The right–moving gauge symmetry may remain entirely unbroken; it can be broken to smaller subgroups; or it can be realised as a higher level Kac–Moody algebra [79,80,81]. In the case of the ten dimensional theories, it was argued in [4] that all the ten dimensional theories are indeed connected by interpolations or orbifolds. In the same vein, we may hypothesise that the variety of four dimensional theories are similarly connected. Given that a large class descend from the underlying \(N=4\) toroidal space, there exist an uplift from the \(N=1\) theory to the \(N=4\) theory, which is the inverse of the modding out procedure of the breaking from \(N=4\) to \(N=1\). In the \(N=4\) theory, the moduli space is continuous, so we expect that indeed all the (2, 0) can be connected by interpolations or by orbifolds to the (2, 2) theories. In the very least, we see that some classes of (2, 0) compactifications, e.g. those with an SO(10) GUT symmetry, can be seen to arise as deformations of those with (2, 2) worldsheet supersymmetry, and investigation of their moduli spaces can be facilitated by analysing this deformation. Furthermore, if we regard the SO(10) embedding of the Standard Model spectrum as phenomenologically desirable, these cases are the ones that may be physically relevant. Given that the spinor–vector duality extends to worldsheet compactifications with interacting CFTs [78], gives reason to hypothesise that the same structure extends, albeit in a more intricate way, to string vacua with interacting internal CTFs.
5 Discussion and conclusion
The validation of the Standard Model as providing viable parametrisation of all sub-atomic observable phenomena, reinforces the possibility that further insight into the Standard Model parameters can only be obtained by fusing it with gravity. Among contemporary quantum gravity approaches, string theory is unique because its internal consistency requirements mandates the existence of the matter and gauge structures that are the bedrock of the Standard Model. By that string theory provide the arena to develop a phenomenological approach to quantum gravity. However, given that the string scale is far removed from experimentally accessible scales, it is likely that string theory will only provide some initial values for the Standard Model parameters, and their confrontation with experimental data will be performed by utilising effective field theory methods. An example of this line of thought is the calculation of the top and bottom quarks Yukawa couplings and the resulting prediction of the top quark mass [82, 83], which is obtained by evolving the string extracted parameters to the experimentally accessible scale. Relating string vacua to their effective field theory smooth limit is therefore an important problem in string phenomenology, which at present is only understood in limited cases [1, 84,85,86]. Improving the understanding of the effective field theory limit of string vacua is therefore an important problem in string phenomenology. To date relating string vacua to low energy observables relies exclusively on the effective supergravity limit. An important question is therefore to explore to what extent is supersymmetry a necessary component in the construction of viable string models. Non-supersymmetric non-tachyonic vacua were constructed in the past as compactifications of the \(SO(16)\times SO(16)\) heterotic–string in ten dimensions. However, worldsheet string theory may offer the alternative of staring with a tachyonic ten dimensional vacuum and projecting the tachyons with the GGSO projections. In this paper, I constructed one such six generation model with SLM gauge symmetry and discussed the reduction to three generations. Such models are particularly interesting from the point of view of the MSDS constructions that do not utilise the S basis vector, which is common to the supersymmetric and \(SO(16)\times SO(16)\) constructions. Whether an actual tachyon free three generation model can be constructed remains to be seen, but it is clear that if it exists, it will have very special structure, rather than generic. Furthermore, the possibility to freeze all moduli, aside from the dilaton, in fermionic \(Z_2\times Z_2\) orbifolds [87], offers the prospect of a such a model that is not connected to a tachyonic point anywhere in the moduli space.
Additionally, I proposed that from the worldsheet perspective all heterotic–string vacua with (2, 0) worldsheet supersymmetry can be connected to those with (2, 2) via orbifolds or interpolations. If correct, it will facilitate the understanding of the moduli spaces of (2, 0) heterotic–string compactifications. The evidence relies on the connectivity of the \(N=4\) moduli space and the existence of global symmetries, such as the spinor–vector duality, in the space to (2, 0) heterotic–string compactifications. In the very least it can serve as a useful classification criteria between (2, 0) vacua that can, and those that cannot, be connected via orbifolds or interpolations to those with (2, 2) worldsheet supersymmetry. An affirmative conclusion will support the suggestion [88] that while string vacua are distinct from the point of view of the low energy field theory, they are equivalent from the string worldsheet point of view. From the worldsheet string perspective different string vacua merely exchange massive and massless states. The preservation of the total number of massless states, distributed among the different group factors, hints that the quantum gravity consistency requirements only care about the total number of massless degrees of freedom, rather than about the transformation properties under the low scale effective field theory gauge group.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The research area of this paper is theoretical. It relates to the general data provided by the particle Standard Model rather than those a specific particle experiment.]
References
L.J. Dixon, V. Kaplunovsky, J. Louis, Nucl. Phys. B 329, 27 (1990)
L.J. Dixon, J.A. Harvey, Nucl. Phys. B 274, 93 (1986)
L. Alvarez-Gaume, P.H. Ginsparg, G.W. Moore, C. Vafa, Phys. Lett. B 171, 155 (1986)
P.H. Ginsparg, C. Vafa, Nucl. Phys. B 289, 414 (1986)
H. Itoyama, T.R. Taylor, Phys. Lett. B 186, 129 (1987)
H. Kawai, D.C. Lewellen, S.H.H. Tye, Phys. Rev. D 34, 3794 (1986)
K.R. Dienes, Phys. Rev. Lett. 65, 1979 (1990)
K.R. Dienes, Phys. Rev. D 42, 2004 (1990)
S. Abel, K.R. Dienes, Phys. Rev. D 91, 126014 (2015)
M. Blaszczyk, S. Groot Nibbelink, O. Loukas, F. Ruehle, JHEP 1510, 166 (2015)
S. Groot Nibbelink, E. Parr, Phys. Rev. D 94, 041704 (2016)
I. Florakis, J. Rizos, Nucl. Phys. B 913, 495 (2016)
I. Florakis, arXiv:1611.10323
S. Groot Nibbelink et al, arXiv:1710.09237
S. Abel, K.R. Dienes, E. Mavroudi, Phys. Rev. D 97, 126017 (2018)
T. Coudarchet, H. Partouche, Nucl. Phys. B 933, 134 (2018)
A. Abel, E. Dudas, D. Lewis, H. Partouche, arXiv:1812.09714
H. Itoyama, S. Nakajima, arXiv:1905.10745
A.E. Faraggi, M. Tsulaia, Phys. Lett. B 683, 314 (2010)
B. Aaronson, S. Abel, E. Mavroudi, Phys. Rev. D 95, 106001 (2017)
J.M. Ashfaque, P. Athanasopoulos, A.E. Faraggi, H. Sonmez, Eur. Phys. J. C76, 208 (2016)
C. Kounnas, Fortsch. Phys. 56, 1143 (2008)
I. Florakis, C. Kounnas, Nucl. Phys. B 820, 237 (2009)
I. Florakis, C. Kounnas, N. Toumbas, Nucl. Phys. B 834, 273 (2010)
I. Antoniadis, C. Bachas, C. Kounnas, Nucl. Phys. B 289, 87 (1987)
H. Kawai, D.C. Lewellen, S.H.-H. Tye, Nucl. Phys. B 288, 1 (1987)
I. Antoniadis, C. Bachas, Nucl. Phys. B 298, 586 (1988)
I. Antoniadis, J. Ellis, J. Hagelin, D.V. Nanopoulos, Phys. Lett. B 231, 65 (1989)
A.E. Faraggi, D.V. Nanopoulos, K. Yuan, Nucl. Phys. B 335, 347 (1990)
A.E. Faraggi, Phys. Lett. B 278, 131 (1992)
A.E. Faraggi, Nucl. Phys. B 387, 239 (1992)
G.B. Cleaver, A.E. Faraggi, D.V. Nanopoulos, Phys. Lett. B 455, 135 (1999)
A.E. Faraggi, E. Manno, C.M. Timirgaziu, Eur. Phys. J. C 50, 701 (2007)
I. Antoniadis, G.K. Leontaris, J. Rizos, Phys. Lett. B 245, 161 (1990)
G.K. Leontaris, J. Rizos, Nucl. Phys. B 554, 3 (1999)
G.B. Cleaver, A.E. Faraggi, C. Savage, Phys. Rev. D 63, 066001 (2001)
G.B. Cleaver, D.J. Clements, A.E. Faraggi, Phys. Rev. D 65, 106003 (2002)
G.B. Cleaver, A.E. Faraggi, S.E.M. Nooij, Nucl. Phys. B 672, 64 (2003)
A.E. Faraggi, H. Sonmez, Phys. Rev. D 91, 066006 (2015)
A. Gregori, C. Kounnas, J. Rizos, Nucl. Phys. B 549, 16 (1999)
A.E. Faraggi, C. Kounnas, S.E.M. Nooij, J. Rizos, Nucl. Phys. B 695, 41 (2004). arXiv:hep-th/0311058
A.E. Faraggi, C. Kounnas, J. Rizos, Phys. Lett. B 648, 84 (2007)
A.E. Faraggi, C. Kounnas, J. Rizos, Nucl. Phys. B 774, 208 (2007)
A.E. Faraggi, C. Kounnas, J. Rizos, Nucl. Phys. B 799, 19 (2008)
T. Catelin-Julian, A.E. Faraggi, C. Kounnas, J. Rizos, Nucl. Phys. B 812, 103 (2009)
C. Angelantonj, A.E. Faraggi, M. Tsulaia, JHEP 1007, 4 (2010)
B. Assel, C. Christodoulides, A.E. Faraggi, C. Kounnas, J. Rizos, Phys. Lett. B 683, 306 (2010)
B. Assel, C. Christodoulides, A.E. Faraggi, C. Kounnas, J. Rizos, Nucl. Phys. B 844, 365 (2011)
C. Christodoulides, A.E. Faraggi, J. Rizos, Phys. Lett. B 702, 81 (2011)
L. Bernard et al., Nucl. Phys. B 868, 1 (2013)
A.E. Faraggi, J. Rizos, H. Sonmez, Nucl. Phys. B 886, 202 (2014)
H. Sonmez, Phys. Rev. D 93, 125002 (2016)
A.E. Faraggi, J. Rizos, H. Sonmez, Nucl. Phys. B 927, 1 (2018)
A.E. Faraggi, G. Harries, J. Rizos, Nucl. Phys. B 936, 472 (2018)
A.E. Faraggi, E. Manno, Eur. Phys. J. C66, 465 (2010)
A.E. Faraggi, Phys. Lett. B 544, 207 (2002)
A.E. Faraggi, Phys. Lett. B 326, 62 (1994)
E. Kiritsis, C. Kounnas, Nucl. Phys. B 503, 117 (1997)
A.E. Faraggi, S. Forste, C. Timirgaziu, JHEP 0608, 057 (2006)
P. Athanasopoulos, A.E. Faraggi, S. Groot Nibbelink, V.M. Mehta, JHEP 1604, 038 (2016)
A.E. Faraggi, D.V. Nanopoulos, Phys. Rev. D 48, 3288 (1993)
A.E. Faraggi, Int. J. Mod. Phys. A 14, 1663 (1999)
A.E. Faraggi, E. Halyo, Phys. Lett. B 307, 305 (1993)
A.E. Faraggi, E. Halyo, Nucl. Phys. B 416, 63 (1994)
M. Dine, N. Seiberg, E. Witten, Nucl. Phys. B 289, 589 (1987)
P. Ginsparg, Phys. Rev. D 35, 648 (1987)
A. Casher, F. Englert, H. Nicolai, A. Taormina, Phys. Lett. B 162, 121 (1985)
M. Bertolini, R. Plesser, JHEP 1809, 067 (2018)
A.E. Faraggi, Nucl. Phys. B 407, 57 (1993)
A.E. Faraggi, Eur. Phys. J. C 49, 803 (2007)
G. Cleaver, A.E. Faraggi, Int. J. Mod. Phys. A 14, 2335 (1999)
A.E. Faraggi, Nucl. Phys. B 728, 83 (2005)
J. Bagger, D. Nemeschansky, N. Seiberg, S. Yankielowicz, Nucl. Phys. B 289, 53 (1987)
D. Chang, A. Kumar, Phys. Rev. D 38, 1893 (1988)
D. Chang, A. Kumar, Phys. Rev. D 38, 3734 (1988)
A.E. Faraggi, I. Florakis, T. Mohaupt, M. Tsulaia, Nucl. Phys. B 848, 332 (2011)
A. Giveon, M. Porrati, E. Rabinovici, Phys. Rep. 244, 77 (1994) (For review and references, see e.g.)
P. Athanasoupoulos, A.E. Faraggi, D. Gepner, Phys. Lett. B 735, 357 (2014)
D.C. Lewellen, Nucl. Phys. B 337, 61 (1990)
S. Chaudhuri, S.W. Chung, G. Hockney, J.D. Lykken, Nucl. Phys. B 456, 89 (1995)
K.R. Dienes, J. March-Russell, Nucl. Phys. B 479, 113 (1996)
A.E. Faraggi, Phys. Lett. B 274, 47 (1992)
A.E. Faraggi, Nucl. Phys. B 487, 55 (1997)
S. Groot Nibbelink, M. Trapletti, M. Walter, Phys. Lett. B 652, 124 (2007)
S. Groot Nibbelink, T.W. Ha, M. Trapletti, Phys. Rev. D 77, 026002 (2008)
S. Groot Nibbelink, D. Klevers, F. Ploger, M. Trapletti, P.K.S. Vaundrevange, JHEP 0804, 60 (2008)
G.B. Cleaver, A.E. Faraggi, E. Manno, C. Timirgaziu, Phys. Rev. D 78, 046009 (2008)
A.E. Faraggi, Fortsch. Phys. 59, 1139 (2011)
Acknowledgements
I would like to thank Costas Bachas, Doron Gepner and Dan Israel for useful discussions. I would like to thank the Galileo Galilei Institute for Theoretical Physics and INFN for hospitality and partial support during the workshop “String Theory from a worldsheet perspective”; and the CERN Theoretical Physics division for hospitality, where part of this work was conducted.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Faraggi, A.E. String phenomenology from a worldsheet perspective. Eur. Phys. J. C 79, 703 (2019). https://doi.org/10.1140/epjc/s10052-019-7222-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7222-5