Polarization transfer in hyperon decays and its effect in relativistic nuclear collisions

Abstract

We calculate the contribution to the polarization of $\Lambda$ hyperons in relativistic nuclear collisions at high energy from the decays of $\Sigma ^{*}(1385)$ and $\Sigma ^0$, which are the predominant sources of $\Lambda$ production besides the primary component, as a function of the $\Lambda$ momentum. Particularly, we estimate the longitudinal component of the mean spin vector as a function of the azimuthal angle in the transverse plane, assuming that primary $\Sigma ^{*}$ and $\Sigma ^0$ polarization follow the predictions of local thermodynamic equilibrium in a relativistic fluid. Provided that the rapidity dependence around midrapidity of polarization is negligible, we find that this component of the overall spin vector has a very similar pattern to the primary one. Therefore, we conclude that the secondary decays cannot account for the discrepancy in sign between experimental data and hydrodynamic model predictions of the longitudinal polarization of $\Lambda$ hyperons recently measured by the STAR experiment at RHIC.

1 Introduction

The evidence of global polarization of $\Lambda$ hyperons in relativistic nuclear collisions [1] is having a remarkable impact in this field. Indeed, the global polarization turns out to be in a very good quantitative agreement with the combined predictions of thermodynamics and hydrodynamics  [2,3,4,5]. These predictions are based on the assumption that local thermodynamic equilibrium is achieved at some early stage of the process (Quark Gluon Plasma - QGP – formation) and maintained until hadronization, where the fluid basically breaks up into a kinetic hadronic system. Thermodynamics provides that particles at hadronization are polarized if the thermal vorticity tensor $\varpi$ (see below for definition) is non-vanishing while the hydrodynamic model predicts $\varpi$ at the hadronization once initial conditions of QGP are set.

The model is very successful for the global polarization, that is for the mean spin vector of the $\Lambda$ hyperon, which is parallel to the overall angular momentum of the colliding nuclei, at several energies. This model also predicts the mean spin vector as a function of momentum of the $\Lambda$ hyperon [2,3,4, 6]. Particularly, it was observed that the longitudinal – that is, along the beam line – component of the $\Lambda$ mean spin vector shows a very similar pattern to that of the azimuthal particle spectra, the so-called elliptic flow [3, 7]. This feature and more characteristics of the longitudinal component of the polarization were analyzed and discussed in Refs. [8, 9].

The oscillations of the longitudinal polarization of $\Lambda$ as a function of the azimuthal angle have indeed been observed by the STAR experiment [12], yet with a flipped sign with respect to the thermodynamic-hydrodynamic calculations [8]. Interestingly, the sign prediction was confirmed in an AMPT-based calculation of the thermal vorticity pattern at hadronization [13] as well as in a single-freeze out scenario [11]. Furthermore, the STAR experiment has measured the azimuthal dependence of the component of the mean spin vector at $\sqrt{s_{_\mathrm{NN}}} = 200\ \hbox {GeV}$ [14] along the total angular momentum axis and found that it is markedly different from the predictions of the model [2,3,4, 10], exhibiting a maximum along the reaction plane and a minimum in the orthogonal direction.

There might be many reasons for these discrepancies and different options have been lately discussed in literature: non-equilibrium of spin degrees of freedom and the consequent need of developing a spin kinetic theory [15,16,17,18,19,20]; introduction of a spin potential breaking the equivalence of stress-energy and spin tensors [21,22,23]; final-state hadronic potentials [24] and others. However, before invoking alternative theoretical scenarios, it is desirable to consider and possibly rule out the simplest mechanisms and the simplest among the simplest – at least conceptually – is resonance decay. It should be stressed that the calculations of the polarization pattern in $\Lambda$ momentum space in the thermodynamic-hydrodynamic framework were made only for primary particles, namely those directly emitted from the hadronizing source. However, most $\Lambda$’s are secondary, i.e., decay products of higher lying states and so one wonders whether the contribution of the secondaries could modify the polarization pattern of the primaries and account for the experimental observations.

In a previous work [25], the decay contribution to global polarization was calculated for several channels and found to be just a slight cumulative correction to the primary component [4]. In this work, we extend this calculation differentially in momentum space, thereby answering the above question.

The paper is organized as follows: in Sect. 2, a formalism is developed for single particle spin density matrix and the relevant mean spin vector by assuming no interaction between the final hadrons. In Sect. 3, we derive the formalism for reduced spin density matrix and polarization transfer in two-body decays, which are then applied to the concrete cases contributing to $\Lambda$ polarization: $\Sigma ^{*} \rightarrow \Lambda \pi$ in Sect. 3.1 and $\Sigma ^0 \rightarrow \Lambda \gamma$ Sect. 3.2. For polarization transfer, momentum average over the Mother particle distribution should also be involved, which is presented in Sect. 4. The numerical results are presented in Sect. 5, which is followed by brief conclusions and discussions in Sect. 6.

1.1 Notations and conventions

In this paper, we use the natural units with $\hbar =c=k_B=1$.

The Minkowskian metric tensor is $\mathrm{diag}(1,-1,-1,-1)$; for the Levi-Civita symbol we use the convention $\epsilon ^{0123}=1$. Operators in Hilbert space will be denoted by a large upper hat, e.g. ${\widehat{T}}$; while unit vectors with a small upper hat, e.g. $\hat{v}$. Vector and tensor products are denoted by “$\cdot$” and “ : ”, respectively, e.g. $b \cdot {\widehat{P}}=b_{\mu }{\widehat{P}}^{\mu }$ and $\varpi : {\widehat{J}}=\varpi _{\mu \nu }{\widehat{J}}^{\mu \nu }$, where summation over repeated indices is understood.

The summation convention is also implemented for the angular momentum component indices: if the indices show more than once as superscripts or subscripts in the formula, they should be summed over all possible values. For example, we should sum over m in the numerator of (17) and over $m,\lambda _1$ and $\lambda _2$ in the denominator as $|D^j(\varphi _{*},\theta _{*},0)^{m}_{\lambda }|^2 =D^j(\varphi _{*},\theta _{*},0)^{m \,*}_{\lambda _1-\lambda _2}D^j (\varphi _{*},\theta _{*},0)^{m}_{\lambda _1-\lambda _2}$.

The following conventions are used for the energy-momentum variables: the variables in the Mother particle’s rest frame will be labelled by a subscript “$*$”. In general, the four-momentum of the Mother in the laboratory frame is denoted by a capital “P” and with a “p” for the Daughter particles, which will be emphasised further when needed. Finally, the three-momentum is denoted by the roman font, i.e., “P” and “p” for the Mother and Daughter, respectively.

2 Spin density matrix

A crucial ingredient for our calculation is the spin density matrix at local thermodynamic equilibrium for hadrons at particlization stage. The definition of the spin density matrix for free particles with four-momentum p in Quantum Field Theory (QFT) is as follows:

$$\begin{aligned} \Theta (p)_{\sigma \sigma '} = \frac{\mathrm{tr}({\widehat{\rho }}\, a^{\dagger } (p)_{\sigma '}a(p)_{\sigma })}{\sum _{\tau } \mathrm{tr}({\widehat{\rho }}\, a^{\dagger }(p)_{\tau } a(p)_{\tau })}, \end{aligned}$$

(1)

where $a(p)_{\sigma }$ are destruction operators of the particle with momentum p in the spin state $\sigma$ and ${\widehat{\rho }}$ is the density operator representing the state of the field. As it is known, the meaning of $\sigma$ depends on the choice of the so-called standard Lorentz transformation [p] taking the unit time vector into the direction of the four-momentum p of the massive particle [26]. For most common choices, $\sigma$ is either the third component of the spin in the rest frame [27] or the helicity [28]; (see also Ref. [29]) we will use the latter throughout, corresponding to the transformation:

$$\begin{aligned} {[}p] = \mathsf{R}(\varphi ,\theta ,0) \mathsf{L}_z(\xi ) =\mathsf{R}_z(\varphi ) \mathsf{R}_y(\theta ) \mathsf{L}_z(\xi ), \end{aligned}$$

(2)

where $\mathsf{L}_z(\xi )$ is a Lorentz boost along the z axis with hyperbolic angle $\xi$ ($\cosh \xi = \varepsilon /m$) and $\mathsf{R}(\varphi ,\theta ,0)$ is a rotation with the Euler angles $\varphi ,\theta ,0$ associated to the spherical coordinates of the momentum $\mathbf{p}$.

From the spin density matrix (1), one can readily determine the mean spin vector by utlizing the decomposition of this vector operator on the space-like orthonormal vector basis $n_i(p) =[p](\hat{e}_i)$ [25, 26] associated with the particle momentum p:

$$\begin{aligned} S^{\mu }(p)= & {} \sum _{i=1}^3 D^S(\mathsf{J}^i)_{\sigma \sigma '} \Theta (p)_{\sigma '\sigma } n_i(p)^{\mu } \nonumber \\= & {} \sum _{i=1}^3 \mathrm{tr}(D^S(\mathsf{J}^i) \Theta (p)) [p](\hat{e}_i)^{\mu }\nonumber \\= & {} \sum _{i=1}^3 [p]^{\mu }_i \mathrm{tr}(D^S(\mathsf{J}^i) \Theta (p)), \end{aligned}$$

(3)

where $\mathsf{J}^i$ are the angular momentum generators, $D^S(\mathsf{J})$ their irreducible representation matrices of spin S and $\hat{e}_i$ is the i-th vector of the orthonormal basis. It should be stressed that, in spite of its appearance, the mean spin vector (3) is independent of the particular choice of the standard Lorentz transformation [p]. Indeed, the spin density matrix (1) also depends on the conventional choice of the standard Lorentz transformation – the definition of the spin variables $\sigma$, and this compensates the dependence on the matrix elements $[p]^{\mu }_i$ (see Appendix A).

The angular momentum generators $\mathsf{J}$ and the boost generators $\mathsf{K}$ are the vector components of the anti-symmetric tensor generators of the Lorentz transformations. In covariant form,

$$\begin{aligned} D^S(\mathsf{J}^{\lambda }) = -\frac{1}{2} \epsilon ^{\lambda \mu \nu \rho } D^S(J_{\mu \nu })\hat{t}_{\rho }, \quad D^S(\mathsf{K}^{\lambda }) = D^S(J^{\nu \lambda })\hat{t}_{\nu } , \end{aligned}$$

(4)

implying the decomposition:

$$\begin{aligned} D^S(J_{\mu \nu }) = \epsilon _{\mu \nu \rho \sigma } D^S(\mathsf{J}^{\rho }) \hat{t}^{\sigma } + D^S(\mathsf{K}_{\nu })\hat{t}_{\mu } - D^S(\mathsf{K}_{\mu })\hat{t}_{\nu }, \end{aligned}$$

(5)

where $\hat{t}$ is the unit time vector with components (1, 0, 0, 0), which implies $\lambda \ne 0$ in (4). Thereby, the Eq. (3) can be rewritten with the full range of indices:

$$\begin{aligned} S^{\mu }(p) = [p]^{\mu }_{\nu } \mathrm{tr}(D^S(\mathsf{J}^{\nu }) \Theta (p)). \end{aligned}$$

(6)

The calculation of the spin density matrix (1) for a general spin is not an easy task in QFT. Even for the simplest non-trivial case of a density operator involving the angular momentum, an exact solution is not known. However, it is possible to find an explicit exact solution for single relativistic quantum particles neglecting quantum statistics, i.e. quantum field effects. In this case, the general equilibrium density operator ${\widehat{\rho }}$ reads:

$$\begin{aligned} {\widehat{\rho }}= \frac{1}{Z} \exp \left[ -b \cdot {\widehat{P}}+ \frac{1}{2} \varpi : {\widehat{J}}\right] , \end{aligned}$$

where b is a constant time-like four-vector and $\varpi$ a constant anti-symmetric tensor which turns out to be the thermal vorticity [30, 31]; ${\widehat{P}}$ and ${\widehat{J}}$ are the conserved total four-momentum and total angular momentum-boosts operators, respectively. Viewing the system as a set of non-interacting distinguishable particles, we can write:

$$\begin{aligned} {\widehat{P}}= \sum _{i} {\widehat{P}}_i, \quad {\widehat{J}}= \sum _i {\widehat{J}}_i, \end{aligned}$$

and consequently,

$$\begin{aligned} {\widehat{\rho }}= \otimes _i {\widehat{\rho }}_i \quad \mathrm{with} \; {\widehat{\rho }}_i =\frac{1}{Z_i} \exp \left[ -b \cdot {\widehat{P}}_i + \frac{1}{2} \varpi : {\widehat{J}}_i \right] . \end{aligned}$$

By using Poincaré group algebra, it can be shown that each ${\widehat{\rho }}_i$ can be factorized as [34]:

$$\begin{aligned} {\widehat{\rho }}_i = \frac{1}{Z_i} \exp \left[ -\tilde{b} \cdot {\widehat{P}}_i \right] \exp \left[ \frac{1}{2} \varpi : {\widehat{J}}_i\right] , \end{aligned}$$

where

$$\begin{aligned} \tilde{b}_{\mu } = \sum _{k=0}^{\infty } \frac{i^k}{(k+1)!} \underbrace{\left( \varpi _{\mu \nu _1} \varpi ^{\nu _1\nu _2} \cdots \varpi _{\nu _{k-1}\nu _k} \right) }_{\text {k times}} b^{\nu _k}. \end{aligned}$$

Then, for a single particle with momentum p, the spin density matrix can be expressed as:

$$\begin{aligned} \Theta (p)_{\sigma \sigma '} = \frac{\langle {p,\sigma }| {\widehat{\rho }}_i |{p,\sigma '}\rangle }{\sum _{\tau } \langle {p,\tau }| {\widehat{\rho }}_i |{p,\tau }\rangle }. \end{aligned}$$

(7)

To derive the explicit form for (7), we use an analytic continuation technique: we first determine $\Theta (p)$ for imaginary $\varpi$ and then continue the function to real values. If $\varpi$ is imaginary, $\exp [\varpi :{\widehat{J}}/2] \equiv {\widehat{\Lambda }}$ is just a unitary representation of a Lorentz transformation, and then one can use the well known relations in group theory to obtain:

$$\begin{aligned} \Theta (p)_{\sigma \sigma '} {=} \frac{\langle {p,\sigma }| {\widehat{\Lambda }}|{p,\sigma '}\rangle }{\sum _{\tau } \langle {p,\tau }| {\widehat{\Lambda }}|{p,\tau }\rangle } {=}\frac{2\varepsilon \delta ^3(\mathbf{p} {-} \mathbf{\Lambda (p)}) W(p)_{\sigma \sigma '}}{2\varepsilon \delta ^3(\mathbf{p} - \mathbf{\Lambda (p)}) W(p)_{\tau \tau }}. \end{aligned}$$

(8)

where $\mathbf{\Lambda (p)}$ stands for the spacial part of the four-vector $\mathsf{\Lambda }(p)$. In (8), W(p) is the Wigner rotation, that is:

$$\begin{aligned} W(p) = D^S([\mathsf{\Lambda }p]^{-1} \mathsf{\Lambda } [p]), \end{aligned}$$

where $D^S$ stands for the finite-dimensional representation of dimension $2S+1$, the so-called $(0,2S+1)$ representation [28] of the SO(1,3)-SL(2,C) matrices in the argument.¹ We have also used the covariant normalization of states:

$$\begin{aligned} \langle {p,\sigma }|{p, \sigma '}\rangle = 2 \varepsilon \delta ^3(\mathbf{p}-\mathbf{p}') \delta _{\sigma \sigma '}. \end{aligned}$$

Altogether, we have:

$$\begin{aligned} \Theta (p)_{\sigma \sigma '} = \frac{D^S([p]^{-1} \mathsf{\Lambda } [p])_{\sigma \sigma '}}{\mathrm{tr}(D^S(\mathsf{\Lambda }))}, \end{aligned}$$

which seems to be an appropriate form to be analytically continued to real $\varpi$. However, it is not satisfactory yet as the continuation to real $\varpi$, that is²

$$\begin{aligned} D^S(\mathsf{\Lambda }) = \exp \left[ - \frac{i}{2} \varpi : \Sigma _S\right] \rightarrow \exp \left[ \frac{1}{2} \varpi : \Sigma _S\right] \end{aligned}$$

does not give rise to a hermitian matrix for $\Theta (p)$ as it should. This problem can be fixed by taking into account that W(p) is the representation of a rotation, hence unitary. We can thus replace W(p) with $(W(p) + W(p)^{-1\dagger })/2$ in (8) and, by using the property of of SL(2,C) representations $D^S(A^{\dagger }) = D^S(A)^{\dagger }$ [26] we obtain:

$$\begin{aligned} \Theta (p) = \frac{D^S([p]^{-1} \mathsf{\Lambda } [p]) +D^S\left( [p]^{\dagger } \mathsf{\Lambda }^{-1 \dagger }[p]^{-1\dagger }\right) }{\mathrm{tr}\left( D^S(\mathsf{\Lambda })+D^S(\mathsf{\Lambda })^{-1 \dagger }\right) }, \end{aligned}$$

which will give a hermitian result because the analytic continuation of $\Lambda ^{-1\dagger }$ reads:

$$\begin{aligned} D^S\left( \mathsf{\Lambda }^{-1\dagger }\right) \rightarrow \exp \left[ \frac{1}{2} \varpi : \Sigma _S^{\dagger }\right] . \end{aligned}$$

Therefore, the final expression of the spin density matrix is:

$$\begin{aligned} \Theta (p) = \frac{D^S\left( [p]^{-1} \exp [(1/2) \varpi : \Sigma _S] [p]\right) +D^S\left( [p]^{\dagger } \exp \left[ (1/2) \varpi : \Sigma ^{\dagger }_S\right] [p]^{-1\dagger }\right) }{\mathrm{tr}\left( \exp [(1/2) \varpi : \Sigma _S] + \exp \left[ (1/2)\varpi : \Sigma _S^{\dagger }\right] \right) }, \end{aligned}$$

(9)

which is manifestly hermitian.

The expression (9) can be further simplified. By taking the above matrices as SO(1,3) transformations and using known relations in group theory, we have

$$\begin{aligned}&{[}p]^{-1} \exp \left[ \frac{1}{2} \varpi : J \right] [p] =\exp \left[ \frac{1}{2} \varpi ^{\mu \nu } [p]^{-1} J_{\mu \nu } [p] \right] \\&\quad =\exp \left[ \frac{1}{2} \varpi ^{\mu \nu } [p]^{-1\alpha }_{\mu } {[}p]^{-1^{\beta }}_{\nu } J_{\alpha \beta }\right] . \end{aligned}$$

We can now apply the Lorentz transformation [p] to the tensor $\varpi$:

$$\begin{aligned} \varpi ^{\mu \nu } [p]^{-1\alpha }_{\mu } [p]^{-1 \beta }_{\nu } =\varpi ^{\alpha \beta }_{*}(p) \end{aligned}$$

(10)

to realize that $\varpi _{*}^{\alpha \beta }$ are the components of the thermal vorticity tensor in the rest-frame of the particle with four-momentum p. Note that these components are obtained by back-boosting with [p], which is not a pure Lorentz boost in the helicity scheme. Finally, (9) becomes

$$\begin{aligned}&\Theta (p) \nonumber \\&\quad = \frac{D^S(\exp [(1/2) \varpi _{*}(p) : \Sigma _S]) +D^S\left( \exp [(1/2) \varpi _{*}(p) : \Sigma ^{\dagger }_S]\right) }{\mathrm{tr}\left( \exp [(1/2) \varpi : \Sigma _S] + \exp [(1/2) \varpi : \Sigma _S^{\dagger }]\right) }. \end{aligned}$$

(11)

The thermal vorticity $\varpi$ is usually $\ll 1$; in this case, the spin density matrix can be expanded in power series around $\varpi =0$. Taking into account that $\mathrm{tr}(\Sigma _S)=0$, we have:

$$\begin{aligned} \Theta (p)^{\sigma }_{\sigma '} \simeq \frac{\delta ^{\sigma }_{\sigma '}}{2S+1} + \frac{1}{4(2S+1)} \varpi _{*}(p)^{\alpha \beta }(\Sigma _{S{\alpha \beta }} +\Sigma _{S{\alpha \beta }}^{\dagger })^{\sigma }_{\sigma '} \end{aligned}$$

to first order in $\varpi$. We can now use (5) to decompose $\Sigma _{S\mu \nu } = D^S(J_{\mu \nu })$ and take advantage of a known feature of the $D^S$ representation, namely that $D^S(\mathsf{J}^i)$ are hermitian matrices while $D^S(\mathsf{K}^i)$ are anti-hermitian, to find

$$\begin{aligned} \Theta (p)^{\sigma }_{\sigma '} \simeq \frac{\delta ^{\sigma }_{\sigma '}}{2S+1} + \frac{1}{2(2S+1)} \varpi _{*}(p)^{\alpha \beta } \epsilon _{\alpha \beta \rho \nu } D^S(\mathsf{J}^{\rho })^{\sigma }_{\sigma '} \hat{t}^{\nu }. \end{aligned}$$

(12)

By plugging (12) into (6), we get:

$$\begin{aligned} S^{\mu }(p)&= [p]^{\mu }_{\kappa } \frac{1}{2(2S+1)} \varpi _{*}(p)^{\alpha \beta } \epsilon _{\alpha \beta \rho \nu } \mathrm{tr}\left( D^S(\mathsf{J}^{\rho }) D^S(\mathsf{J}^{\kappa }) \right) \hat{t}^{\nu } \nonumber \\&= - \frac{1}{2(2S+1)}\frac{S(S+1)(2S+1)}{3} [p]^{\mu }_{\kappa } \varpi _{*}(p)^{\alpha \beta }\epsilon _{\alpha \beta \rho \nu } g^{\rho \kappa } \hat{t}^{\nu } \nonumber \\&= - \frac{1}{2}\frac{S(S+1)}{3} [p]^{\mu }_{\rho } \varpi _{*}(p)_{\alpha \beta } \epsilon ^{\alpha \beta \rho \nu } \hat{t}_{\nu } \nonumber \\&= - \frac{1}{2m} \frac{S(S+1)}{3} \varpi _{\alpha \beta } \epsilon ^{\alpha \beta \mu \nu } p_{\nu }, \end{aligned}$$

(13)

where, in the last equality, we have boosted the vector to the laboratory frame by using the Eq. (10).

For a fluid made of distinguishable particles, $\varpi$ becomes a local function [31], so that the expression (13) gives rise to the integral average:

$$\begin{aligned} S^{\mu }(p)= - \frac{1}{2m}\frac{S(S+1)}{3} \epsilon ^{\mu \alpha \beta \nu } p_{\nu }\frac{\int d\Sigma _{\lambda } p^{\lambda } f(x,p) \varpi _{\alpha \beta }(x)}{\int d\Sigma _{\lambda } p^{\lambda } f(x,p)} \end{aligned}$$

(14)

with f(x, p) the distribution function. The latter is basically the same formula obtained in Refs. [25, 31].

3 Spin density matrix and polarization transfer in two-body decays

Consider a massive particle, henceforth named “Mother” and denoted by “M”, with spin j and third component m in its rest frame decaying into two particles, henceforth named “Daughters” and denoted by “$D_1$” and “$D_2$”. In the Mother rest frame, the magnitude of the momentum of the Daughters is fixed:

$$\begin{aligned} \mathrm{p}_{*}=\mathrm{p}_{*D}\equiv \frac{1}{2 m_M }\prod _{s,t=\pm }({m}_M +s\,m_{D_1}+t\,m_{D_2})^{1/2} \end{aligned}$$

(15)

due to energy-momentum conservation, where $m_M$ is the mass of the Mother, and $m_{D_1}$, $m_{D_2}$ are the mass of the Daughters. As long as the decay is unobserved, the contribution of the decayed state to the quantum superposition reads, in the helicity basis [26, 28, 29],

$$\begin{aligned} |{p_{*} j m \lambda _1 \lambda _2}\rangle \propto T^j(\lambda _1,\lambda _2) \int \mathrm{d}\Omega _{*} D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } |{\mathbf{p}_{*} \lambda _1\lambda _2}\rangle , \end{aligned}$$

(16)

where $\mathrm{d}\Omega _{*} = \sin \theta _{*} \mathrm{d}\theta _{*} \mathrm{d}\varphi _{*}$ is the infinitesimal solid angle corresponding to the momentum direction of Daughter 1; $D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda }$ is the complex conjugate of the rotation matrix element in the representation j with components m and $\lambda =\lambda _1 - \lambda _2$; and $T^j(\lambda _1,\lambda _2)$ are the reduced helicity transition amplitudes.

Once a measurement of the momentum of either decay particle is made and a momentum $\mathbf{p}_{*}$ is found, according to quantum mechanics, the pure state gets reduced to a mixed one with density operator:

$$\begin{aligned} {\widehat{\rho }}(\mathbf{p}_{*}) = \frac{T^j(\lambda _1,\lambda _2) T^j(\lambda '_1,\lambda '_2)^{*} D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } D^j(\varphi _{*},\theta _{*},0)^{m}_{\lambda '} |{\mathbf{p}_{*} \lambda _1\lambda _2}\rangle \langle {\mathbf{p}_{*} \lambda '_1 \lambda '_2}|}{|T^j(\lambda _1,\lambda _2)|^2 |D^j(\varphi _{*},\theta _{*},0)^{m}_{\lambda }|^2 \langle {\mathbf{p}_{*} \lambda _1 \lambda _2}|{\mathbf{p}_{*} \lambda _1 \lambda _2}\rangle }. \end{aligned}$$

(17)

This is indeed the density operator in spin space for the two-Daughter system in the Mother’s rest frame, for a given spin state m of the Mother. However, the spin state of the Mother is itself a density operator of the sort (11) in the laboratory frame. This means that the decayed state is not simply (16), rather the one with the density operator:

$$\begin{aligned} \sum _{m,n=-j}^j \Theta ^m_{n} |{p_{*} jm \lambda _1 \lambda _2}\rangle \langle {p_{*} j n \lambda _1' \lambda _2'}|, \end{aligned}$$

hence the overall density operator of the Daughters reads explicitly:

$$\begin{aligned} {\widehat{\rho }}(\mathbf{p}_{*}) \propto&T^j(\lambda _1,\lambda _2) T^j(\lambda '_1,\lambda '_2)^{*} D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } \Theta ^m_n \nonumber \\&\times D^j(\varphi (\varphi _{*},\theta _{*},0)^{n}_{\lambda '} |{\mathbf{p}_{*} \lambda _1\lambda _2}\rangle \langle {\mathbf{p}_{*} \lambda '_1 \lambda '_2}|. \end{aligned}$$

(18)

By using the density operator (18), we can write down the normalized spin density matrix of the Daughters in the Mother rest frame as:

$$\begin{aligned}&\Theta _{D \, \lambda '_1 \lambda '_2}^{\; \; \lambda _1 \lambda _2}\nonumber \\&\quad =\frac{T^j(\lambda _1,\lambda _2) T^j(\lambda '_1,\lambda '_2)^{*} D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } \Theta ^m_n D^j(\varphi _{*},\theta _{*},0)^{n}_{\lambda '}}{|T^j(\lambda _1,\lambda _2)|^2 D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } \Theta ^m_n D^j(\varphi _{*},\theta _{*},0)^{n}_{\lambda }}, \end{aligned}$$

(19)

whence the mean spin vector of the Daughter 1 can be obtained from the Eq. (6) as

$$\begin{aligned} S^{\mu }_1(\mathbf{p}_{*}) = [p_{*}]^{\mu }_{\nu } D^{S_1} (\mathsf{J}^{\nu })_{\lambda _1}^{\lambda '_1} \Theta _{D \, \lambda '_1 \lambda _2}^{\; \; \lambda _1 \lambda _2}. \end{aligned}$$

(20)

Then, in general, the mean spin vector of the Daughters depends on the spin density matrix of the Mother $\Theta$, which is a $(2j+1)\times (2j+1)$ hermitian matrix with trace 1 hence depending on $(2j+1)^2-1$ real parameters. For this reason, in principle, the mean spin vector of the Daughter does not just depend on the mean spin vector of the Mother (3 real parameters), except for $j=1/2$ but it involves more variables, a well known fact in the literature [32, 33]. Nevertheless, in the case of relativistic nuclear collisions and QGP with small thermal vorticity, the spin density matrix of the primary Mothers can be approximated by the (12) which

eventually entails that the mean spin vector of the Daughters depends only on the mean spin vector of the Mother, like in the spin-1/2 case, as we will see.

Let us implement the approximation (12) for $\Theta ^m_n$ in the (19) to obtain its first order expansion in thermal vorticity. The first term in (12) is proportional to the identity and selects $m=n$ in (19), then one is left with:

$$\begin{aligned} D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } D^j(\varphi _{*},\theta _{*},0)^{m}_{\lambda '} = \delta ^{\lambda }_{\lambda '} \end{aligned}$$

due to the unitarity of the $D^j$’s. On the other hand, the second term in the (12) gives rise to the following product of three matrices:

$$\begin{aligned}&D^j(\varphi _{*},\theta _{*},0)^{m \, *}_{\lambda } D^j(\mathsf{J}^{\rho })^m_n D^j(\varphi _{*},\theta _{*},0)^{n}_{\lambda '}\\&\quad =D^j(\varphi _{*},\theta _{*},0)^{-1 \, \lambda }_{m} D^j(\mathsf{J}^{\rho })^m_n D^j(\varphi _{*},\theta _{*},0)^{n}_{\lambda '}, \end{aligned}$$

which, according to a well known relation in group representation theory, equals

$$\begin{aligned} \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho }_{\tau } D^j(\mathsf{J}^{\tau })^{\lambda }_{\lambda '}, \end{aligned}$$

(21)

where the rotation $\mathsf{R}$ transforms the z-axis unit vector $\hat{\mathbf{k}}$ into the momentum $\mathbf{p}_{*}$ of the decayed particle. Altogether, we can rewrite the (19) as:

$$\begin{aligned}&\Theta _{D \, \lambda '_1 \lambda _2}^{\; \; \lambda _1 \lambda _2} \simeq \frac{T^j(\lambda _1,\lambda _2) T^j(\lambda '_1,\lambda '_2)^{*} \left[ \delta ^{\lambda }_{\lambda '} + (1/2) \varpi _{*}(P)^{\alpha \beta } \epsilon _{\alpha \beta \rho \nu } D^j(\mathsf{J}^{\tau })^{\lambda }_{\lambda '} \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho }_{\tau } {\hat{t}}^{\nu } \right] }{\sum _{\lambda _1,\lambda _2} |T^j(\lambda _1,\lambda _2)|^2}, \end{aligned}$$

(22)

where P is the momentum of the Mother in the laboratory frame.

We are now in a position to work out (20) by using the spin density matrix in the Eq. (22). For strong and electromagnetic decays with parity conservation, it is readily found that the first term containing $\delta ^{\lambda }_{\lambda '}$ does not give any contribution to the mean spin vector because $\lambda _2=\lambda _2'$ implies $\lambda _1 = \lambda '_1$ and one is left with a vanishing trace of $D^{S1}(\mathsf{J}^{\nu })$ in (20). Conversely, the second term in (22) yields a finite non-vanishing result:

$$\begin{aligned}&S^{\mu }_1(\mathbf{p}_{*}) = \frac{1}{2} \varpi _{*}(P)^{\alpha \beta } \epsilon _{\alpha \beta \rho \nu } {\hat{t}}^{\nu }\nonumber \\&\qquad \times \frac{T^j(\lambda _1,\lambda _2) T^j(\lambda '_1,\lambda _2)^{*}[p_{*}]^{\mu }_{\kappa } D^{S_1}(\mathsf{J}^{\kappa })_{\lambda _1}^{\lambda '_1} D^j(\mathsf{J}^{\tau })^{\lambda }_{\lambda '} \mathsf{R}(\varphi _{*}, \theta _{*},0)^{\rho }_{\tau }}{\sum _{\lambda _1,\lambda _2} |T^j(\lambda _1,\lambda _2)|^2} \nonumber \\&\quad = - \frac{3}{j(j+1)} S_{*M}(P)_{\rho }\nonumber \\&\qquad \times \frac{T^j(\lambda _1,\lambda _2) T^j(\lambda '_1,\lambda _2)^{*} {[}p_{*}]^{\mu }_{\kappa } D^{S_1}(\mathsf{J}^{\kappa })_{\lambda _1}^{\lambda '_1} D^j(\mathsf{J}^{\tau })^{\lambda }_{\lambda '} \mathsf{R}(\varphi _{*}, \theta _{*},0)^{\rho }_{\tau }}{\sum _{\lambda _1,\lambda _2} |T^j (\lambda _1,\lambda _2)|^2},\nonumber \\ \end{aligned}$$

(23)

where we have used (13) to express the formula in terms of the mean spin vector of the Mother in its rest frame $S_{*M}(P)$. In the next subsections, we will work out two specific relevant decays: $\Sigma ^{*} \rightarrow \Lambda \pi$ and $\Sigma \rightarrow \Lambda \gamma$.

3.1 $\Sigma ^{*} \rightarrow \Lambda \pi$

In this case, $\lambda _2=0$, $j=3/2$ and $S_1 = 1/2$ in (23), and $T(1/2,0)=T(-1/2,0)$ because of parity invariance [25]. Hence, there is only one independent helicity amplitude which cancels out in the (23) and we have:

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*})= & {} - \frac{3}{2j(j+1)}\\&\times S_{*M}(P)_{\rho }[p_{*}]^{\mu }_{\kappa } D^{1/2}(\mathsf{J}^{\kappa })_{\lambda _1}^{\lambda '_1} D^{3/2} (\mathsf{J}^{\tau })^{\lambda _1}_{\lambda '_1} \mathsf{R}(\varphi _{*}, \theta _{*},0)^{\rho }_{\tau } \\= & {} - \frac{3}{2j(j+1)} \\&\times S_{*M}(P)_{\rho } [p_{*}]^{\mu }_{\kappa } \mathrm{tr}( D^{1/2}(\mathsf{J}^{\kappa }) D^{3/2}_\mathrm{RED}(\mathsf{J}^{\tau })) \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho }_{\tau }, \end{aligned}$$

where $D^{3/2}_\mathrm{RED}$ is the reduced $2\times 2$ matrix formed with the elements labelled by the indices $\lambda =\pm 1/2$. Since

$$\begin{aligned} D^{3/2}_\mathrm{RED}(\mathsf{J}^1)) = \sigma _1, \quad D^{3/2}_\mathrm{RED} (\mathsf{J}^2)) = \sigma _2, \quad D^{3/2}_\mathrm{RED}(\mathsf{J}^3)) = \frac{\sigma _3}{2}, \end{aligned}$$

where the $\sigma$’s are the Pauli matrices, the mean spin vector becomes:

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*})&=- \frac{3}{2j(j+1)} S_{*M}(P)_{\rho } [p_{*}]^{\mu }_{\kappa } C_{\tau } \mathrm{tr}(\sigma _{\kappa } \sigma _{\tau }) \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho }_{\tau } \\&= \frac{3}{j(j+1)} S_{*M}(P)_{\rho } [p_{*}]^{\mu }_{\kappa } C_{\tau } g^{\kappa \tau } \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho }_{\tau } \\&= \frac{3}{j(j+1)} S_{*M}(P)_{\rho } [p_{*}]^{\mu }_{\tau } C_{\tau } \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho \tau }, \end{aligned}$$

with

$$\begin{aligned} C_{\tau } = (1/2,1/2,1/2,1/4) = \frac{1}{2} - \frac{1}{4} \delta _{\tau }^3. \end{aligned}$$

Note that we set $C_0 = 1/2$ instead of the obvious 0 as the multiplying matrix element $\mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho 0}$ always vanishes.

In the helicity scheme, the matrix $[p_{*}]$ can be expanded according to (2) and so, taking advantage of the orthogonality of rotations $\mathsf{R}$, we have

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*})= & {} \frac{3}{j(j+1)} S_{*M}(P)_{\rho } C_{\tau } \mathsf{R}(\varphi _{*},\theta _{*},0)^{\mu }_{\nu } \mathsf{L}_z (\xi )^{\nu }_{\tau } \mathsf{R}^{-1}(\varphi _{*},\theta _{*},0)^{\tau \rho } \\= & {} \frac{3}{2j(j+1)} \left[ L_{\hat{\mathbf{p}}_{*}}(\xi )^{\mu }_{\rho } S_{*M}(P)^{\rho } \right. \\&\left. - \frac{1}{2} S_{*M}(P)_{\rho }\mathsf{R} (\varphi _{*},\theta _{*},0)^{\mu }_{\nu } \mathsf{L}_z (\xi )^{\nu }_3 \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho 3} \right] , \end{aligned}$$

where $L_{\hat{\mathbf{p}}_{*}}(\xi )$ is the pure Lorentz boost transforming $\hat{t}$ into the direction of $\hat{\mathbf{p}}_{*}$ in the Mother’s rest frame. The Lorentz transformation can be expanded as well by using the momentum of the Daughter:

$$\begin{aligned}&\mathsf{R}(\varphi _{*},\theta _{*},0)^{\mu }_{\nu } \mathsf{L}_z (\xi )^{\nu }_3 \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho 3} \nonumber \\&\quad = \mathsf{R}(\varphi _{*},\theta _{*},0)^{\mu }_3 \mathsf{L}_z (\xi )^3_3 \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho 3}\nonumber \\&\qquad + \mathsf{R}(\varphi _{*},\theta _{*},0)^{\mu }_0 \mathsf{L}_z (\xi )^0_3 \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho 3} \nonumber \\&\quad = - \cosh \xi \, \hat{\mathbf{p}}_{*}^{\mu } \hat{\mathbf{p}}_{*}^{\rho } - \sinh \xi \, \hat{\mathbf{p}}_{*}^{\rho } \delta ^{\mu }_0\nonumber \\&\quad = - \frac{\varepsilon _{*}}{m_{\Lambda }} \hat{\mathbf{p}}_{*}^{\mu } \hat{\mathbf{p}}_{*}^{\rho } - \frac{\mathrm{p}_{*}}{m_{\Lambda }} \hat{\mathbf{p}}_{*}^{\rho } \delta ^{\mu }_0, \end{aligned}$$

(24)

so that the spin vector becomes:

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*})= & {} \frac{3}{2j(j+1)} \left[ \phantom {\left. -\frac{\varepsilon _{*}}{2m_{\Lambda }} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \hat{\mathbf{p}}_{*}^{\mu } - \frac{\mathrm{p}_{*}}{2m_{\Lambda }} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \delta ^{\mu }_0 \right] } \mathsf{L}_{\hat{\mathbf{p}}_{*}}(\xi )^{\mu }_{\rho } S_{*M}(P)^{\rho }\right. \\&\left. -\frac{\varepsilon _{*}}{2m_{\Lambda }} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \hat{\mathbf{p}}_{*}^{\mu } - \frac{\mathrm{p}_{*}}{2m_{\Lambda }} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \delta ^{\mu }_0 \right] , \end{aligned}$$

where $m_{\Lambda }$ is the mass of the $\Lambda$. With the help of the known formulae of pure Lorentz boosts, we get:

$$\begin{aligned} S^0_{\Lambda }(\mathbf{p}_{*})= & {} \frac{3}{2j(j+1)} \left[ \frac{1}{m_{\Lambda }} \mathbf{p}_{*} \cdot \mathbf{S}_{*M} - \frac{1}{2m_{\Lambda }} \mathbf{S}_{*M} \cdot \mathbf{p}_{*} \right] \\= & {} \frac{3}{2j(j+1)} \frac{1}{2m_{\Lambda }} \mathbf{S}_{*M} \cdot \mathbf{p}_{*} , \\ \mathbf{S}_{\Lambda }(\mathbf{p}_{*})= & {} \frac{3}{2j(j+1)}\\&\times \left[ \mathbf{S}_{*M} + \frac{\mathbf{p}_{*} \cdot \mathbf{S}_{*M}}{(\varepsilon _{*}+ m_{\Lambda })m_{\Lambda }} \mathbf{p}_{*} -\frac{\varepsilon _{*}}{2m_{\Lambda } \mathrm{p}_{*}^2} \mathbf{S}_{*M} \cdot \mathbf{p}_{*} \mathbf{p}_{*} \right] \\= & {} \frac{3}{2j(j+1)} \left[ \mathbf{S}_{*M} + \frac{\varepsilon _{*} -2m_{\Lambda }}{2m_{\Lambda } \mathrm{p}_{*}^2} \mathbf{S}_{*M} \cdot \mathbf{p}_{*} \mathbf{p}_{*} \right] . \end{aligned}$$

Finally, the spin vector is boosted to the $\Lambda$ rest frame and we use $j=3/2$ to obtain the spin three-vector as:

$$\begin{aligned} \mathbf{S}_{0\Lambda }(\mathbf{p}_{*})= & {} \mathbf{S}_{\Lambda }(p_{*}) -S^0_{\Lambda }(p_{*}) \frac{\mathbf{p}_{*}}{\varepsilon _{*}+m_{\Lambda }}\nonumber \\= & {} \frac{2}{5} \left[ \mathbf{S}_{*M} - \frac{1}{2} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \hat{\mathbf{p}}_{*} \right] . \end{aligned}$$

(25)

This result is in full agreement with the global mean spin vector of the $\Lambda$ from polarized $\Sigma ^{*}$ decay derived in Ref. [25]. Indeed, by setting $\mathbf{S}_{*M} = S_{*M} \hat{\mathbf{k}}$ without loss of generality and integrating over $\mathrm{d}\Omega _{*}/4 \pi$ to average out the angular dependence in (25), we get:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda } \rangle = \frac{1}{3} \mathbf{S}_{*M}. \end{aligned}$$

which is precisely the result found in Ref. [25].

3.2 $\Sigma ^0 \rightarrow \Lambda \gamma$

In this case, $j=1/2$, $S_1 = 1/2$, and $|\lambda _2| = 1$ as the second particle is a photon. These numbers imply that $\lambda _2 =2 \lambda _1$, $\lambda '_1=\lambda _1$ and $\lambda = \lambda _1 -\lambda _2 = - \lambda _1$ [25]. Furthermore, because of parity conservation, there is only one independent helicity amplitude which cancels out and (23) becomes:

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*})= & {} - \frac{3}{2j(j+1)} S_{*M}(P)_{\rho }[p_{*}]^{\mu }_{\kappa }\nonumber \\&\times D^{1/2}(\mathsf{J}^{\kappa })^{\lambda _1}_{\lambda _1} D^{1/2} (\mathsf{J}^{\tau })_{-\lambda _1}^{-\lambda _1} \mathsf{R}(\varphi _{*}, \theta _{*},0)^{\rho }_{\tau }. \end{aligned}$$

(26)

The combination

$$\begin{aligned} D^{1/2}(\mathsf{J}^{\kappa })_{-\lambda _1}^{-\lambda _1} D^{1/2} (\mathsf{J}^{\tau })^{\lambda _1}_{\lambda _1} = C_{\tau } g^{\kappa \tau } \end{aligned}$$

vanishes except for $\kappa =\tau =3$ with

$$\begin{aligned} C_{\tau } = (0,0,0,1/2) = \frac{1}{2} \delta ^3_{\tau }, \end{aligned}$$

then we can rewrite (26) as:

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*})= & {} -\frac{3}{2j(j+1)} S_{*M}(P)_{\rho }[p_{*}]^{\mu }_{\kappa } C_{\tau } g^{\kappa \tau } \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho }_{\tau }\\= & {} -\frac{3}{4j(j+1)} S_{*M}(P)_{\rho } [p_{*}]^{\mu }_{\tau } \delta ^3_{\tau } \mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho \tau } \\= & {} -\frac{3}{4j(j+1)} S_{*M}(P)_{\rho } [p_{*}]^{\mu }_3 \mathsf{R} (\varphi _{*},\theta _{*},0)^{\rho 3} \\= & {} -\frac{3}{4j(j+1)} S_{*M}(P)_{\rho } \mathsf{R}(\varphi _{*},\theta _{*},0)^{\mu }_{\nu } \mathsf{L}_3(\xi )^{\nu }_3\\&\times \,\mathsf{R}(\varphi _{*},\theta _{*},0)^{\rho 3}. \end{aligned}$$

By plugging the (24), we find

$$\begin{aligned} S^{\mu }_{\Lambda }(\mathbf{p}_{*}) = - \frac{3}{4j(j+1)} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \left( \frac{\varepsilon _{*}}{m_{\Lambda }} \hat{\mathbf{p}}_{*}^{\mu } + \frac{\mathrm{p}_{*}}{m_{\Lambda }} \delta ^{\mu }_0 \right) , \end{aligned}$$

which yields the three-component spin vector:

$$\begin{aligned} \mathbf{S}_{0\Lambda }(\mathbf{p}_{*}) = \mathbf{S}_{\Lambda }(p_{*}) - S^0_{\Lambda }(p_{*}) \frac{\mathbf{p}_{*}}{\varepsilon _{*}+m_{\Lambda }} = - \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \, \hat{\mathbf{p}}_{*} \end{aligned}$$

(27)

after boosting back to the $\Lambda$ rest frame. Similar to the $\Sigma ^{*}$ case, this equation is again in full agreement with the average spin vector of the $\Lambda$ from polarized $\Sigma ^0$ decay [25].

4 Momentum average and longitudinal polarization

So far, we have derived the formulae for the polarization transfer in two-body decays in terms of the mean spin vectors of particles in their rest frames – what experiments can actually measure – for some given momentum of the $\Lambda$ in the Mother’s rest frame. However, we are more interested in the polarization vector inherited by the $\Lambda$ as a function of the $\Lambda$ momentum $\mathbf{p}$ in the laboratory frame. Besides, Mother particles have a momentum distribution and we have to fold our result therewith in order to compare with the experimental results.

Let $\mathbf{P}$ be the momentum of the Mother in the laboratory frame and $n(\mathbf{P})$ its un-normalized momentum spectrum, such that ${\int \mathrm{d}^3 \mathrm{P} \; n(\mathbf{P})}$ yields the total number of the Mother. One would then define the mean spin vector of the $\Lambda$ for a specific decay as:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle = \frac{\int \mathrm{d}^3 \mathrm{P} \; n(\mathbf{P}) \, \mathbf{S}_{0\Lambda }(\mathbf{p}_{*})}{\int \mathrm{d}^3 \mathrm{P} \; n(\mathbf{P})}, \end{aligned}$$

where $\mathbf{S}_{0\Lambda }(\mathbf{p}_{*})$ is given by either (25) or (27) and $\mathbf{p}_{*}$ is a function of $\mathbf{p}$ and $\mathbf{P}$ because it is related to $\mathbf{p}$ by a Lorentz transformation. Since the magnitude of $\mathbf{p}_{*}$ is fixed, the three components of $\mathbf{P}$ are not completely independent for a given $\mathbf{p}$. This can be seen from the Lorentz transformation relation:

$$\begin{aligned} \varepsilon _{*} = \frac{\varepsilon _M}{m_M} \varepsilon -\frac{1}{m_M} \mathbf{P} \cdot \mathbf{p} = \sqrt{\mathrm{p}^2_{*D} + m^2_{\Lambda }}, \end{aligned}$$

where $\varepsilon = \sqrt{\mathrm{p}^2 + m_{\Lambda }^2}$ and $\mathrm{p}_{*D}$ is given by the (15). To implement this constraint, one should multiply both the numerator and denominator of the above equation by a $\delta (\mathrm{p}_{*}-\mathrm{p}_{*D})$ so that:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle =\frac{\int \mathrm{d}^3 \mathrm{P} \; n(\mathbf{P}) \, \mathbf{S}_{0\Lambda }(\mathbf{p}_{*}) \delta (\mathrm{p}_{*} - \mathrm{p}_{*D})}{\int \mathrm{d}^3 \mathrm{P} \; n(\mathbf{P}) \delta (\mathrm{p}_{*} - \mathrm{p}_{*D})}. \end{aligned}$$

Now, it is convenient to change the integration variable from $\mathbf{P}$ to $\mathbf{p}_{*}$ to take advantage of the straightforward $\delta$ integration and this can indeed be done by using Lorentz boosts (see Appendix A):

$$\begin{aligned} \mathbf{P}= & {} 2 m_M \frac{(\varepsilon _{*} + \varepsilon )(\mathbf{p} - \mathbf{p}_{*})}{(\varepsilon _{*} + \varepsilon )^2-(\mathbf{p} - \mathbf{p}_{*})^2}\nonumber \\= & {} m_M \frac{(\varepsilon _{*} + \varepsilon )(\mathbf{p} - \mathbf{p}_{*})}{m_{\Lambda }^2 + \varepsilon \varepsilon _{*} +\mathbf{p}\cdot \mathbf{p}_{*}} \implies \hat{\mathbf{P}} = \frac{\mathbf{p} - \mathbf{p}_{*}}{\Vert \mathbf{p} - \mathbf{p}_{*}\Vert }, \end{aligned}$$

(28)

After this change of variable, the integration in $\mathrm{d}\mathrm{p}_{*}$ is trivial and we are left with the solid angle integration:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle= & {} \frac{\int \mathrm{d}^3 \mathrm{p}_{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \, \mathbf{S}_{0\Lambda }(\mathbf{p}_{*}) \delta (\mathrm{p}_{*} - \mathrm{p}_{*D})}{\int \mathrm{d}^3 \mathrm{p}_{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf P}{\partial \mathbf{p}_{*}} \right| \, \delta (\mathrm{p}_{*} - \mathrm{p}_{*D})}\nonumber \\= & {} \frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \, \mathbf{S}_{0\Lambda }(\mathbf{p}_{*})}{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf P}{\partial \mathbf{p}_{*}} \right| \,}, \end{aligned}$$

(29)

where the absolute value of the determinant of the Jacobian reads (see Appendix A):

$$\begin{aligned} \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| =\frac{m_M^3(\varepsilon _{*} + \varepsilon )^2 \left[ (\varepsilon _{*} +\varepsilon )^2 - (\varepsilon \varepsilon _{*} + \mathbf{p}\cdot \mathbf{p}_{*}+m_{\Lambda }^2) \right] }{\varepsilon _{*}(\varepsilon \varepsilon _{*} +\mathbf{p}\cdot \mathbf{p}_{*}+m_{\Lambda }^2)^3}. \end{aligned}$$

(30)

The $\mathbf{S}_{0\Lambda }(\mathbf{p}_{*})$ in Eqs. (25) and (27) are now to be used in the (29) to obtain the expressions of the mean spin of the $\Lambda$ inherited in the decays of $\Sigma ^{*}$ and $\Sigma ^0$ produced in the nuclear collision:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle =&\frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \, \frac{2}{5} \left[ \mathbf{S}_{*M} - \frac{1}{2} \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \hat{\mathbf{p}}_{*} \right] }{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \,} \; \Sigma ^{*} \rightarrow \Lambda \pi , \nonumber \\ \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle =&- \frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf P}{\partial \mathbf{p}_{*}} \right| \, \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \hat{\mathbf{p}}_{*}}{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \,} \quad \Sigma ^0 \rightarrow \Lambda \gamma , \end{aligned}$$

(31)

As it can be seen, the contribution to the $\Lambda$ polarization is proportional to the mean spin vector of the Mother, just like the global polarization, but in a more complicated fashion than simple vector collinearity.

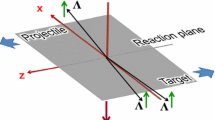
Because of the symmetries of the system of colliding nuclei in peripheral collisions (total reflection and rotation around the total angular momentum axis), the components of the polarization vector should exhibit a symmetry pattern in momentum space (see also discussion in Ref. [8]). Particularly, they can be expanded in Fourier series as a function of the momentum azimuthal angle and, because of those symmetries, the leading harmonics are [3, 8, 13, 35]

$$\begin{aligned} S_{*Mx}&\simeq \frac{2j(j+1)}{3} \left[ h_1(\mathrm{P}_T,Y) \sin \varphi _M + h_2(\mathrm{P}_T,Y) \sin 2 \varphi _M \right] , \nonumber \\ S_{*My}&\simeq \frac{2j(j+1)}{3} \nonumber \\&\quad \times \left[ g_0(P_T,Y) + g_1(\mathrm{P}_T,Y) \cos \varphi _M + g_2(\mathrm{P}_T,Y) \cos 2 \varphi _M \right] , \nonumber \\ S_{*Mz}&\simeq \frac{2j(j+1)}{3} f_2(\mathrm{P}_T,Y) \sin 2 \varphi _M, \end{aligned}$$

(32)

where Y is the rapidity of the Mother. The coefficient ${2j(j+1)/3}$ in front is meant to remove from the functions f, g, h their trivial dependence on the spin, according to the Eq. (13). The aforementioned symmetries imply that $h_1$ and $g_1$ are odd functions of Y whereas $g_0, f_2, g_2, h_2$ are even. The hydrodynamic model supplied with the usual initial conditions [3, 35] predicts the magnitude of the functions f, g, h and particularly their signs to be:

$$\begin{aligned} g_0< 0, \quad h_2< 0, \quad g_2 > 0, \quad f_2 < 0 , \end{aligned}$$

in a right-handed reference frame with x-axis on the reaction plane and y-axis in the direction opposite to the total angular momentum. We can decompose the momenta in cylindrical or spherical coordinates and use the rightmost equality in Eq. (28),

$$\begin{aligned} \mathbf{P} ={}&\mathrm{P}_T \cos \varphi _M \hat{\mathbf{i}} + \mathrm{P}_T \sin \varphi _M \hat{\mathbf{j}} + \mathrm{P}_z \hat{\mathbf{k}}, \nonumber \\ \mathbf{p}={}&\mathrm{p}_T \cos \varphi \hat{\mathbf{i}} + \mathrm{p}_T \sin \varphi \hat{\mathbf{j}} + \mathrm{p}_z \hat{\mathbf{k}},\nonumber \\ \mathbf{p}_{*}={}&\mathrm{p}_{*} \sin \theta _{*} \cos \varphi _{*} \hat{\mathbf{i}} + \mathrm{p}_{*} \sin \theta _{*} \sin \varphi _{*} \hat{\mathbf{j}} + \mathrm{p}_{*} \cos \theta _{*} \hat{\mathbf{k}}, \end{aligned}$$

(33)

where the trigonometric functions can be expressed in terms of the momenta of the $\Lambda$ as:

$$\begin{aligned}&\sin 2 \varphi _M \nonumber \\&\quad = \frac{ \mathrm{p}_{*}^2 \sin ^2\theta _{*} \sin 2 \varphi _{*} {+} \mathrm{p}_T^2 \sin 2\varphi {-} 2 \mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \sin (\varphi _{*} {+}\varphi )}{\mathrm{p}_{*}^2 \sin ^2\theta _{*}{+}\mathrm{p}_T^2 -2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos (\varphi _{*} -\varphi )}\nonumber \\&\quad ={\mathcal {A}}(\theta _{*},\psi )\sin 2\varphi +{\mathcal {B}}(\theta _{*},\psi ) \cos 2\varphi , \nonumber \\&\cos 2 \varphi _M \nonumber \\&\quad = \frac{\mathrm{p}_{*}^2 \sin ^2\theta _{*} \cos 2 \varphi _{*} {+} \mathrm{p}_T^2 \cos 2\varphi {-} 2 \mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos (\varphi _{*} {+}\varphi )}{\mathrm{p}_{*}^2 \sin ^2\theta _{*}{+}\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos (\varphi _{*} -\varphi )}\nonumber \\&\quad ={\mathcal {A}}(\theta _{*},\psi )\cos 2\varphi - {\mathcal {B}}(\theta _{*},\psi ) \sin 2\varphi , \nonumber \\&\sin \varphi _M \nonumber \\&\quad = \frac{\mathrm{p}_T \sin \varphi - \mathrm{p}_{*} \sin \theta _{*} \sin \varphi _{*}}{\sqrt{\mathrm{p}_{*}^2 \sin ^2\theta _{*}+\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos (\varphi _{*} -\varphi )}}\nonumber \\&\quad ={\mathcal {C}}(\theta _{*},\psi )\sin \varphi +{\mathcal {D}}(\theta _{*},\psi ) \cos \varphi , \nonumber \\&\cos \varphi _M \nonumber \\&\quad = \frac{\mathrm{p}_T \cos \varphi - \mathrm{p}_{*} \sin \theta _{*} \cos \varphi _{*}}{\sqrt{\mathrm{p}_{*}^2 \sin ^2\theta _{*}+\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos (\varphi _{*} -\varphi )}}\nonumber \\&\quad = {\mathcal {C}}(\theta _{*},\psi )\cos \varphi - {\mathcal {D}}(\theta _{*},\psi )\sin \varphi \end{aligned}$$

(34)

with the variable $\psi = \varphi _{*} - \varphi$ and the auxiliary functions:

$$\begin{aligned} {\mathcal {A}}(\theta _{*},\psi )= & {} {\mathrm{p}_{*}^2\sin ^2\theta _{*} \cos 2 \psi - 2 \mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos \psi +\mathrm{p}_T^2 \over \mathrm{p}_{*}^2 \sin ^2\theta _{*}+\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos \psi },\nonumber \\ {\mathcal {B}}(\theta _{*},\psi )= & {} {\mathrm{p}_{*}^2 \sin ^2\theta _{*} \sin 2\psi - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \sin \psi \over \mathrm{p}_{*}^2 \sin ^2\theta _{*}+\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos \psi }, \nonumber \\ {\mathcal {C}}(\theta _{*},\psi )= & {} {\mathrm{p}_T - \mathrm{p}_{*} \sin \theta _{*} \cos \psi \over \sqrt{\mathrm{p}_{*}^2 \sin ^2\theta _{*}+\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos \psi }},\nonumber \\ {\mathcal {D}}(\theta _{*},\psi )= & {} {- \mathrm{p}_{*} \sin \theta _{*} \sin \psi \over \sqrt{\mathrm{p}_{*}^2 \sin ^2\theta _{*}+\mathrm{p}_T^2 - 2\mathrm{p}_{*} \mathrm{p}_T \sin \theta _{*} \cos \psi }}. \end{aligned}$$

(35)

The integration over the solid angle $\mathrm{d}\Omega _{*}$ in (31) can be replaced by an integration over $\psi$:

$$\begin{aligned} \int \mathrm{d}\Omega _{*}= & {} \int _0^{\pi } \mathrm{d}\theta _{*} \sin \theta _{*} \int _{0}^{2\pi } \mathrm{d}\varphi _{*} \\= & {} \int _0^{\pi } \mathrm{d}\theta _{*} \sin \theta _{*} \int ^{2\pi -\varphi }_{-\varphi }\!\mathrm{d}\psi {=} \int _0^{\pi }\!\mathrm{d}\theta _{*}\!\sin \theta _{*} \int _{-\pi }^{\pi }\!\mathrm{d}\psi , \end{aligned}$$

where the last equality is owing to the $2\pi$-periodic in $\psi$ of all integrand functions.

We now specialize to the case of midrapidity $\Lambda$’s, that is, with $\mathrm{p}_z = \mathbf{p} \cdot \hat{\mathbf{k}} = 0$. The spectrum function $n(\mathbf{P})$ depends on the specific model of the collision, but it must be even in $\cos \theta _M$ because of the symmetries of the colliding system, and, to the approximation of neglecting elliptic flow, isotropic in $\varphi _M$, that is depending only on $\mathrm{P}_T$ to a very good approximation. From (28) we have:

$$\begin{aligned} \mathrm{P}_T = m_M \frac{(\varepsilon _{*} + \varepsilon ) \sqrt{\mathrm{p}_{*}^2 \sin ^2\theta _{*} + \mathrm{p}_T^2 - 2\mathrm{p}_T \mathrm{p}_{*} \sin \theta _{*} \cos \psi }}{m_{\Lambda }^2 + \varepsilon \varepsilon _{*} + \mathrm{p}_T \mathrm{p}_{*} \sin \theta _{*} \cos \psi }, \end{aligned}$$

(36)

which implies that the Mother spectrum function is even in $\cos \theta _{*}$ and even in $\psi$. For mid-rapidity $\Lambda$ with $\mathrm{p}_z=0$, it ensues from (28) that:

$$\begin{aligned} \hat{\mathbf{P}} \cdot \hat{\mathbf{k}}= & {} \cos \theta _M = - \frac{\mathrm{p}_{*} \cos \theta _{*}}{\Vert \mathbf{p} - \mathbf{p}_{*}\Vert } \nonumber \\= & {} - \frac{\mathrm{p}_{*}\cos \theta _{*}}{\sqrt{ \mathrm{p}_{*}^2+\mathrm{p}_T^2-2\mathrm{p}_T \mathrm{p}_{*} \sin \theta _{*}\cos \psi }}, \end{aligned}$$

(37)

so the Mother spectrum function must be an even function of $\cos \theta _{*}$ as well. Moreover, the rapidity Y is an odd function of $\cos \theta _{*}$ and an even function of $\psi$ because:

$$\begin{aligned} M_T \sinh Y = \sqrt{\mathrm{P}_T^2 + m_M^2} \sinh Y = \mathbf{P} \cdot \hat{\mathbf{k}} = \mathrm{P}_T \tan \theta _M \end{aligned}$$

in view of the Eqs. (36) and (37). Similarly, it can be shown that the determinant of the Jacobian (30) is also even in $\psi$ and $\cos \theta _{*}$.

We now focus on the polarization along the beam, i.e., $\langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle \cdot \hat{\mathbf{k}}$. Formulae (31) can then be written in a compact form as:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle \cdot \hat{\mathbf{k}} =\frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \, \left[ A~S_{*M z} + B~( \mathbf{S}_{*M} \cdot \hat{\mathbf{p}}_{*} \cos \theta _{*}) \right] }{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \,} \end{aligned}$$

with A and B depending on the specific decay, namely:

$$\begin{aligned} A = \frac{2}{5} \quad B = -\frac{1}{5} \quad \mathrm{for}\; \Sigma ^{*}, \quad A = 0 \quad B = - 1 \quad \mathrm{for}\; \Sigma ^0. \end{aligned}$$

(38)

We thus have:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle \cdot \hat{\mathbf{k}}=\frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \, \left[ S_{*M z} \left( A + B \cos ^2 \theta _{*} \right) + \frac{B}{2} \left( S_{*M x} \cos \varphi _{*} \sin 2 \theta _{*} + S_{*M y} \sin \varphi _{*} \sin 2 \theta _{*} \right) \right] }{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \,}. \end{aligned}$$

(39)

To work out Eq. (39) one has to use (32), then (34) and (35). The symmetry features in $\theta _{*}$ and $\psi$ simplify the computation because, as the spectrum and the determinant are even functions of $\cos \theta _{*}$, and the coefficients ${\mathcal {A}},{\mathcal {B}}, {\mathcal {C}},{\mathcal {D}}$ in (35) as well, only few terms survive the integration in $\theta _{*}$. Particularly, the terms proportional to functions which are rapidity-even such as $g_0, h_2, g_2$ vanish as they multiply the odd function $\sin 2 \theta _{*}$. Besides, since:

$$\begin{aligned} {\mathcal {A}}(\theta _{*},-\psi )= & {} {\mathcal {A}}(\theta _{*},\psi ) \quad {\mathcal {B}}(\theta _{*},-\psi ) = -{\mathcal {B}}(\theta _{*},\psi ) \end{aligned}$$

(40)

$$\begin{aligned} {\mathcal {C}}(\theta _{*},-\psi )= & {} {\mathcal {C}}(\theta _{*},\psi ) \quad {\mathcal {D}}(\theta _{*},-\psi ) = -{\mathcal {D}}(\theta _{*},\psi ) \end{aligned}$$

(41)

all combinations involving odd functions in $\psi$ will vanish after integration. We are thus left with the following function as integrand:

$$\begin{aligned}&f_2 (\mathrm{P}_T,Y) \left( A + B \cos ^2 \theta _{*} \right) {\mathcal {A}}(\theta _{*},\psi ) \sin 2 \varphi \nonumber \\&\quad + \frac{B}{4} \left[ h_1(\mathrm{P}_T,Y) + g_1(\mathrm{P}_T,Y) \right] \nonumber \\&\quad \times \left[ \mathcal {C}(\theta _{*},\psi ) \cos \psi -\mathcal {D}(\theta _{*},\psi )\sin \psi \right] \sin 2\theta _{*} \sin 2\varphi , \end{aligned}$$

(42)

which, as expected, is altogether proportional to $\sin 2 \varphi$, like for the primary hyperons.

At sufficiently high energy, because of approximate longitudinal boost invariance, we expect all of the functions g, h, f in Eq. (32) to be very weakly dependent on rapidity. As a consequence, since $h_1$ and $g_1$ are rapidity-odd, they should vanish at $Y=0$, hence negligible compared to $f_2$ and $g_2$. Therefore, we can approximate the longitudinal component of the transferred spin as:

$$\begin{aligned}&\langle \mathbf{S}_{0\Lambda }(\mathbf{p}_T) \rangle \cdot \hat{\mathbf{k}}\nonumber \\&\quad \simeq \sin 2 \varphi \, \frac{2j(j+1)}{3} \nonumber \\&\qquad \times \frac{\int _0^{\pi } \mathrm{d}\theta _{*} \sin \theta _{*} \int _{-\pi }^{\pi } \mathrm{d}\psi \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \, f_2 (\mathrm{P}_T) \left( A + B \cos ^2 \theta _{*} \right) {\mathcal {A}}(\theta _{*},\psi )}{\int _0^{\pi } \mathrm{d}\theta _{*} \sin \theta _{*} \int _{-\pi }^{\pi } \mathrm{d}\psi \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}_{*}} \right| \,} \nonumber \\&\quad \equiv \sin 2 \varphi \, \frac{2j(j+1)}{3} f_2 ({\mathrm{p}}_T)_\mathrm{M \rightarrow \Lambda }. \end{aligned}$$

(43)

Putting all contributions together, including primaries:

$$\begin{aligned}&\langle \langle \mathbf{S}_{0\Lambda }(\mathbf{p}_T) \rangle \cdot \hat{\mathbf{k}}\rangle \nonumber \\&\quad = {1\over 2}F_2^\mathrm{Tot}(\mathrm{p}_T)\sin 2 \varphi \nonumber \\&\quad \equiv \frac{1}{2} \left[ F_2 (\mathrm{p}_T) + F_2 ({\mathrm{p}}_T)_\mathrm{\Sigma ^{*} \rightarrow \Lambda } + F_2 ({\mathrm{p}}_T)_\mathrm{\Sigma ^0 \rightarrow \Lambda } \right] \sin 2 \varphi , \end{aligned}$$

(44)

Fig. 1

Left panel: longitudinal polarization coefficients $F_2(\mathrm{p}_T)$ of the $\Lambda$. Primary and secondary components, weighted with the production fractions are shown together with the resulting sum (solid line). Right panel: comparison between the total polarization coefficient $F_2^\mathrm{Tot}(\mathrm{p}_T)$ of the $\Lambda$ and the one $f_2(\mathrm{p}_T)$ of only primary $\Lambda$’s [8]

with

$$\begin{aligned}&F_2 (\mathrm{p}_T) = X_p f_2 (\mathrm{p}_T), \\&F_2 ({\mathrm{p}}_T)_\mathrm{\Sigma ^{*} \rightarrow \Lambda }=5 X_{\Sigma ^{*}} f_2 ({\mathrm{p}}_T)_\mathrm{\Sigma ^{*} \rightarrow \Lambda },\\&F_2 ({\mathrm{p}}_T)_\mathrm{\Sigma ^0 \rightarrow \Lambda } = X_{\Sigma ^0} f_2 ({\mathrm{p}}_T)_\mathrm{\Sigma ^0 \rightarrow \Lambda } , \end{aligned}$$

where X’s are the $\Lambda$ number fractions from the different contributing channels: primary $X_p$ and secondary $X_{\Sigma ^{*}}$, $X_{\Sigma ^0}$.

Likewise, it is possible to calculate the component of the overall mean spin vector along different directions, notably the total angular momentum direction, conventionally $-y$. Unlike the longitudinal component, it involves at least two of the functions in Eq. (32), that is $g_0$ and $g_2$ (see Appendix B); this makes numerical computation more difficult than longitudinal component and we do not carry it out here, leaving it to future work.

5 Numerical computation and results

We are now in a position to evaluate the contribution of the secondary $\Lambda$’s to the whole longitudinal polarization by using (44), under the assumption of no re-interaction which means no loss of mean polarization due to final state elastic rescattering of hadrons. The fractions of primary and secondary $\Lambda$’s can be estimated by means of the statistical hadronization model. At the hadronization temperature $T=164\ \hbox {MeV}$ and baryon chemical potential of 30 MeV for $\sqrt{s_{_\mathrm{NN}}} =200\ \hbox {GeV}$ [36], these fractions turn out to be $X_p= 0.243$, $X_{\Sigma ^{*}} = 0.359$ and $X_{\Sigma ^0}=0.275$ with a primary fraction of $\Sigma ^{*}$ of virtually 100% and of $\Sigma ^0$ around 60%, which has been used as a further factor in our computations. Furthermore, at this temperature the quantum statistics effects are negligible for all of these particles and the distinguishable particle approach used in this paper is an excellent approximation.

The other ingredients in (44) are the two-body transfer functions $F_2$’s which require, according to (43), the primary $f_2$’s of the Mother $\Sigma ^{*}$ and $\Sigma ^0$ as well as their momentum spectrum $n(\mathbf{P})$. The primary $f_2$ functions depend mostly on the thermal vorticity and weakly on the mass of the hadrons through the Fermi-Dirac distribution function (see (45)), hence it is a very good approximation to take the same function for all involved hyperons, that is, $\Lambda$, $\Sigma ^0$ and $\Sigma ^{*}$. A fit to the $f_2(\mathrm{p}_T)$ function of the primary $\Lambda$’s obtained in Ref. [8] yields:

$$\begin{aligned} f_2(p_T)= & {} -7.71 \times 10^{-3} p_T^2 + 3.32 \times 10^{-3} p_T^3 \\&-4.71 \times 10^{-4} p_T^4 \end{aligned}$$

with $\mathrm{p}_T$’s units $\mathrm{GeV}$. The functions $F_2(\mathrm{p}_T)$ for primary and secondary decay contributions are shown in Fig. 1, and the associated polarizations are shown in Fig. 2 where we choose $\mathrm{p}_T=2~\mathrm{GeV}$ as an example.

As far as the momentum spectrum is concerned, because of its appearance in both numerator and denominator of (43), it is plausible that the dependence on its shape is very mild. For the purpose of an approximate calculation, we have assumed a spectrum of the following form:

$$\begin{aligned} n(\mathbf{P}) \propto \frac{1}{\cosh Y} \mathrm{e}^{-M_T/T_s} =\frac{m_M}{E} \mathrm{e}^{-M_T/T_s}, \end{aligned}$$

(45)

where Y is the rapidity of the mother, E its energy, the transverse mass $M_T = \sqrt{\mathrm{P}_T^2 + m_M^2}$ and $T_s$ is a phenomenological parameter describing the slope of the transverse momentum spectrum. We have checked that the final results are very weakly dependent on $T_s$ within a realistic range between 0.2 and 0.8 $\mathrm{GeV}$.

Fig. 2

Left panel: the azimuthal angle dependence of the longitudinal polarization $P^z = \langle \mathbf{S}_{0\Lambda } \rangle \cdot \hat{\mathbf{k}}/S = 2 \langle \mathbf{S}_{0\Lambda } \rangle \cdot \hat{\mathbf{k}}$ of the $\Lambda$. Primary and secondary components, weighted with the production fractions are shown together with the resulting sum (solid line) at fixed transverse momentum $\mathrm{p}_T=2~\mathrm{GeV}$ and slope parameter $T_s=0.3~\mathrm{GeV}$. Right panel: comparison between the total polarization of the $\Lambda$ including secondary contributions with that of only primary $\Lambda$’s [8]

The results are shown in Figs. 1 and 2. It can be seen that the weighted sum of all the $f_2$ components gives rise to almost the same result as for the primary $\Lambda$ alone. This is somewhat surprising because the signs of the components originated from $\Sigma ^{*}$ and $\Sigma ^0$ differ in sign and magnitude. In fact, the quasi-coincidence observed on the right panels of the figures is seemingly an accidental result of the combinations of magnitudes of the various terms and the fractions X in Eq. (44). There are missing contributions from secondary $\Sigma ^0$ and more resonances decaying into $\Lambda$, but their weight in $\Lambda$ production is altogether limited compared to the computed one and definitely not able to flip the sign of $f_2$ in Fig. 1.

6 Summary and conclusions

In summary, we have studied the contribution to the polarization of $\Lambda$ hyperons from the decays of $\Sigma ^{*}$ and $\Sigma ^0$, which are the main sources of secondary $\Lambda$’s in nuclear collisions. Particularly, we have studied the corrections to the primary pattern of the longitudinal component (i.e. along the beam line) of the spin vector and found out that, provided that polarization is weakly dependent on rapidity, its cumulative effect is small compared to almost all previous calculations with only primary contribution. This is apparently the result of an accidental combination of primary and secondary fractions, and of the spins of $\Sigma ^{*}$ and $\Sigma ^0$. Since other contributions to $\Lambda$ production are almost negligible, we conclude that hadronic decays cannot account for the observed discrepancy between the experimental results and the predictions of the thermodynamic-hydrodynamic model on the longitudinal polarization of the $\Lambda$ at $\sqrt{s_{_\mathrm{NN}}} = 200\ \hbox {GeV}$ [12].

Appendices

Appendix A: Lorentz transformation and Jacobian determinant

In this Appendix, we derive Eqs. (28) and (30) in Sect. 4. Let $p^{\mu }=(\varepsilon , \mathbf{p})$ and $p_{*}^{\mu }=(\varepsilon _{*} , \mathbf{p}_{*})$ be the four-momenta of the $\Lambda$ in the laboratory frame and Mother rest frame, respectively, and $P^{\mu }=(\varepsilon _M, \mathbf{P})$ the four-momentum of the Mother in the laboratory frame. The pure Lorentz boost transforming the momentum of the $\Lambda$ from laboratory to Mother rest frame reads:

$$\begin{aligned} \varepsilon _{*}&= \gamma (\varepsilon - \mathbf{V}\cdot \mathbf{p}), \end{aligned}$$

(A1)

$$\begin{aligned} \mathbf{p}_{*}&= \mathbf{p} + \left[ \frac{\gamma -1}{\Vert \mathbf{V}\Vert ^2}{} \mathbf{V} \cdot \mathbf{p} - \gamma ~\varepsilon \right] \mathbf{V} , \end{aligned}$$

(A2)

where $\mathbf{V}=\mathbf{P}/\varepsilon _M$ is the velocity of the Mother and $\gamma =\varepsilon _M/m_M$ the corresponding Lorentz factor. Hence, (A1) and (A2) can also be written as:

$$\begin{aligned} \varepsilon _{*}&= {1\over m_M} (\varepsilon _M\varepsilon - \mathbf{P}\cdot \mathbf{p}) \end{aligned}$$

(A3)

$$\begin{aligned} \mathbf{p}_{*}&= \mathbf{p} + \left[ \frac{\mathbf{P} \cdot \mathbf{p}}{m_M (\varepsilon _M + m_M)} -\frac{\varepsilon }{m_M} \right] \mathbf{P} , \end{aligned}$$

(A4)

By solving the Eq. (A3) to get the $\mathbf{P} \cdot \mathbf{p}$, we can rewrite (A4) as:

$$\begin{aligned} \mathbf{p}_{*} = \mathbf{p} + \left[ \frac{\varepsilon _M\varepsilon - m_M \varepsilon _{*}}{m_M(\varepsilon _M+m_M)} - \frac{\varepsilon }{m_M} \right] \mathbf{P} = \mathbf{p} - \frac{\varepsilon _{*} + \varepsilon }{\varepsilon _M+m_M} \mathbf{P}, \end{aligned}$$

(A5)

We now move $\mathbf{p}$ to the left-hand side and take the square

$$\begin{aligned} \Vert \mathbf{p}_{*} - \mathbf{p} \Vert ^2={}&\frac{(\varepsilon _{*} +\varepsilon )^2}{(\varepsilon _M+m_M)^2} \Vert \mathbf{P} \Vert ^2 \\ ={}&\frac{\varepsilon _M-m_M}{\varepsilon _M+m_M}(\varepsilon _{*} + \varepsilon )^2, \end{aligned}$$

where the relativistic dispersion relation has been used in the latter equality. Therefore, the energy of the Mother can be obtained by solving the above equation:

$$\begin{aligned} \varepsilon _M=m_M \frac{(\varepsilon _{*} + \varepsilon )^2 + \Vert \mathbf{p}_{*} - \mathbf{p} \Vert ^2}{(\varepsilon _{*} + \varepsilon )^2 - \Vert \mathbf{p}_{*} - \mathbf{p} \Vert ^2}, \end{aligned}$$

(A6)

which, when substituted into (A5) yields the momentum of the Mother as a function of the momenta in both QGP and Mother frames:

$$\begin{aligned} \mathbf{P}= 2m_M \frac{(\varepsilon _{*} + \varepsilon )(\mathbf{p} -\mathbf{p}_{*} )}{(\varepsilon _{*} + \varepsilon )^2 -\Vert \mathbf{p}-\mathbf{p}_{*} \Vert ^2}. \end{aligned}$$

The above equation is the expression needed to change the integration variable from $\mathbf{P}$ to $\mathbf{p}_{*}$ by keeping $\mathbf{p}$ fixed. The Jacobian of the transformation reads

$$\begin{aligned} \frac{\partial \mathrm{P}_i}{\partial \mathrm{p}_{*j}}= & {} \frac{2m_M}{D^2} \left\{ \left[ (\mathrm{p}_{i}-\mathrm{p}_{*i})\frac{\mathrm{p}_{*j}}{\varepsilon _{*}} -(\varepsilon _{*} + \varepsilon )\delta _{ij} \right] D \right. \\&\left. - 2N_i \left[ (\varepsilon _{*} + \varepsilon ) \frac{\mathrm{p}_{*j}}{\varepsilon _{*}} + (\mathrm{p}_j - \mathrm{p}_{*j}) \right] \right\} \end{aligned}$$

where:

$$\begin{aligned} D&= (\varepsilon _{*} + \varepsilon )^2-\Vert \mathbf{p}_{*} - \mathbf{p}\Vert ^2 , \\ N_i&= (\varepsilon _{*} + \varepsilon )(\mathrm{p}_i-\mathrm{p}_{*i} ). \end{aligned}$$

After some algebraic manipulations, the determinant of the Jacobian can be computed and turns out to be:

$$\begin{aligned} \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}} \right| =\frac{m_M^3(\varepsilon _{*} + \varepsilon )^2 \left[ (\varepsilon _{*} + \varepsilon )^2 - (\varepsilon \varepsilon _{*} + \mathbf{p} \cdot \mathbf{p}_{*}+m_{\Lambda }^2) \right] }{\varepsilon _{*}(\varepsilon \varepsilon _{*} + \mathbf{p}\cdot \mathbf{p}_{*}+m_{\Lambda }^2)^3} \end{aligned}$$

with $m_{\Lambda }$ the mass of the Daughter, that is Eq. (30).

Appendix B: Transferred polarization along angular momentum direction

Herein, we work out the component of the spin vector of the secondary $\Lambda$ along the angular momentum, conventionally opposite to the y axis direction, from (31):

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle \cdot \hat{\mathbf{j}} =\frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}} \right| \, \left[ S_{*M y} \left( A + B \sin ^2 \varphi _{*} \sin ^2 \theta _{*} \right) + \frac{B}{2} \left( S_{*M z} \sin \varphi _{*} \sin 2 \theta _{*} + S_{*M x} \sin 2 \varphi _{*} \sin ^2 \theta _{*} \right) \right] }{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}} \right| \,}, \end{aligned}$$

where we have replaced the expressions of the components of the Mother’s spin vector according to Eqs. (32). As $h_1(\mathrm{P}_T,Y)$ and $g_1(\mathrm{P}_T,Y)$ are odd functions of Y, hence changing sign under the transformation $\theta _{*}\rightarrow \pi -\theta _{*}$, Eqs. (32), (34) and (35) imply that the terms proportional to $h_1(\mathrm{P}_T,Y), g_1(\mathrm{P}_T,Y)$ vanish after integration in $\theta _{*}$. Likewise, the term proportional to $f_2(\mathrm{P}_T,Y)$, which is an even function under the above transformation, vanishes upon integration over $\theta _{*}$ because it is multiplied by a factor $\sin 2 \theta _{*}$ which is odd. Therefore, we are left with:

$$\begin{aligned} \langle \mathbf{S}_{0\Lambda }(\mathbf{p}) \rangle \cdot \hat{\mathbf{j}} ={2j(j+1)\over 3} \frac{\int \mathrm{d}\Omega _{*} \; n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}} \right| \, I(\theta _{*},\varphi _{*})}{\int \mathrm{d}\Omega _{*} n(\mathbf{P}) \left| \frac{\partial \mathbf{P}}{\partial \mathbf{p}} \right| \,}, \end{aligned}$$

where the integrand in the numerator is

$$\begin{aligned} I (\theta _{*},\varphi _{*})= & {} (g_0 + g_2 \cos 2 \varphi _M)\\&\times \left( A + \frac{B}{2}(1-\cos 2\varphi _{*}) \sin ^2 \theta _{*} \right) \\&+ \frac{B}{2} h_2 \sin 2 \varphi _M\sin ^2 \theta _{*} \sin 2\varphi _{*}. \end{aligned}$$

The term

$$\begin{aligned} g_0\left( A + \frac{B}{2} \sin ^2 \theta _{*} \right) \end{aligned}$$

contributes to the global polarization and is not of special interest here. The remaining part of the integrand function I, after replacing $\varphi _{*} = \varphi + \psi$ reads:

$$\begin{aligned}&g_2 \left( A + \frac{B}{2}(1-\cos 2 \varphi \cos 2 \psi + \sin 2 \varphi \sin 2 \psi ) \sin ^2 \theta _{*} \right) \nonumber \\&\quad \times \cos 2 \varphi _M-\frac{B}{2} g_0 \sin ^2 \theta _{*} \cos 2 \varphi \cos 2 \psi \nonumber \\&\quad +\frac{B}{2} g_0 \sin ^2 \theta _{*} \sin 2 \varphi \sin 2 \psi +\frac{B}{2} h_2 \sin ^2 \theta _{*} \nonumber \\&\quad \times (\cos 2 \varphi \sin 2 \psi + \sin 2 \varphi \cos 2 \psi ) \sin 2 \varphi _M . \end{aligned}$$

(B1)

The term

$$\begin{aligned} g_0 \frac{B}{2} \sin ^2 {\theta _{*}} \sin 2 \varphi \sin 2 \psi \end{aligned}$$

does not contribute after integration as it gives rise to an odd function in $\psi$.

We can now plug in the (34) to rewrite (B1) as:

$$\begin{aligned}&g_2 \left( A + \frac{B}{2}(1-\cos 2 \varphi \cos 2 \psi + \sin 2 \varphi \sin 2 \psi ) \sin ^2 \theta _{*} \right) \\&\quad \times ({\mathcal {A}} \cos 2 \varphi - {\mathcal {B}} \sin 2 \varphi ) -\frac{B}{2} g_0 \sin ^2 \theta _{*} \cos 2 \psi \cos 2 \varphi \\&\quad + \frac{B}{2} h_2 \sin ^2 \theta _{*} (\cos 2 \varphi \sin 2 \psi + \sin 2 \varphi \cos 2 \psi ) \\&\quad \times ({\mathcal {A}} \sin 2 \varphi + {\mathcal {B}} \cos 2 \varphi ). \end{aligned}$$

Taking into account that Eq. (4041) and that the odd combinations in $\psi$ vanish after integration, the effective integrand function is reduced to:

$$\begin{aligned}&g_2 \left[ \left( A + \frac{B}{2}(1-\cos 2 \varphi \cos 2 \psi ) \sin ^2 \theta _{*} \right) {\mathcal {A}} \cos 2 \varphi \right. \\&\quad \left. -\frac{B}{2}{\mathcal {B}}\sin 2 \psi \sin ^2 \theta _{*} \sin ^2 2 \varphi \right] {-} \frac{B}{2} g_0 \sin ^2 \theta _{*} \cos 2 \psi \cos 2 \varphi \\&\quad +\frac{B}{2} h_2 \sin ^2 \theta _{*} ({\mathcal {A}} \cos 2 \psi \sin ^2 2 \varphi + {\mathcal {B}}\sin 2 \psi \cos ^2 2 \varphi ). \end{aligned}$$

Finally, by rearranging all the terms and utilizing double-angle trigonometric relationships, we can put the expression in terms of different simple trigonometric functions of $\varphi$:

$$\begin{aligned}&\left[ g_2 \left( A + \frac{B}{2}\sin ^2 \theta _{*} \right) {\mathcal {A}} -\frac{B}{2} g_0 \sin ^2 \theta _{*} \cos 2 \psi \right] \\&\qquad \times \cos 2 \varphi + \frac{B}{2} \sin ^2 \theta _{*} {\mathcal {A}} \cos 2 \psi (h_2\sin ^2 2 \varphi -g_2\cos ^2 2 \varphi ) \\&\qquad + \frac{B}{2} \sin ^2 \theta _{*}{\mathcal {B}}\sin 2 \psi (h_2\cos ^2 2 \varphi -g_2\sin ^22 \varphi ) \\&\quad = \left[ \frac{B}{4} (h_2-g_2) \sin ^2 \theta _{*} ({\mathcal {A}} \cos 2 \psi +{\mathcal {B}}\sin 2 \psi )\right] \\&\qquad +\left[ g_2 \left( A + \frac{B}{2}\sin ^2 \theta _{*} \right) {\mathcal {A}} {-}\frac{B}{2}g_0\sin ^2\theta _{*}\cos 2\psi \right] \cos 2\varphi \\&\qquad - \left[ \frac{B}{4} (h_2+g_2) \sin ^2 \theta _{*}({\mathcal {A}} \cos 2 \psi -{\mathcal {B}}\sin 2 \psi )\right] \cos 4 \varphi . \end{aligned}$$

The first term contributes to the global polarization, whereas the second and the third are the expected leading azimuthal modulations of this component.