1 Introduction

During last two decades, several observations like type Ia Supernovae, Cosmic Microwave Background (CMB) radiations, large scale structure (LSS), Sloan Digital Sky Survey (SDSS), Wilkinson Microwave Anisotropy Probe (WMAP), Planck observations [1,2,3,4,5,6,7,8,9,10,11,12] suggest that our Universe is experiencing an accelerated expansion due to some unknown exotic fluid which generates sufficient negative pressure, known as dark energy (DE). Although a long-time debate has been done on this well-reputed and interesting issue of modern cosmology, we still have little knowledge about DE. The most appealing and simplest candidate for DE is the cosmological constant \(\Lambda \). Since the source of the DE still now unknown, so several candidates of the DE models have been proposed in the literatures where the scalar field plays a significant role in cosmology as they are sufficiently complicated to produce the observed dynamics. Recently many cosmological models have been constructed by introducing dark energies such as quintessence, Phantom, Tachyon, k-essence, dilaton, Hessence, DBI-essence, ghost condensate, quintom, Chaplygin gas models, interacting dark energy models [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. A review on dynamics of dark energy has been studied in Ref. [31]. Another approach to explore the accelerated expansion of the universe is the modified theories of gravity. The main candidates of modified gravity includes brane world models, DGP brane, LQC, Brans–Dicke gravity, Gauss–Bonnet gravity, Horava–Lifshitz gravity, f(R) gravity, f(T) gravity, f(G) gravity etc [32,33,34,35,36,37,38,39,40,41,42,43,44]. Also for recent reviews on the issue of dark energy and modified gravity theories, see, for instance, [45,46,47,48,49,50,51].

Motivated by high energy physics, the scalar field models play an significant role to explain the nature of DE due to its simple dynamics [52, 53]. In the very early epoch of the Universe, it is strongly believed that the universe had a very rapid exponential growth during a very short era (which is known as inflation). During this era, there was a single canonical scalar field called inflaton [5] which has a canonical kinetic energy term in the Lagrangian density. The simplest form of the canonical scalar field is known as quintessence field, which alone cannot explain the phantom crossing. Also the canonical scalar field cannot fully explain several cosmological natures of the Universe. So non-canonical scalar field was proposed to solve several important cosmological problems [54, 55]. For instance, the non-canonical scalar field can resolve the coincidence problem [56]. So it is reasonable to consider the non-canonical scalar field as a viable cosmological model of DE candidate. In general, the non-canonical scalar field involves higher order derivatives term of a scalar field in the Horndeski Lagrangian [57]. For instance, the k-essence is one of the simple form of a non-canonical scalar field model. In the present work, we will consider non-canonical scalar field model with general form of k-essence Lagrangian [58,59,60,61,62,63,64].

The idea of fractal effects in the Einstein’s equations is another approach to cosmic acceleration in a gravity theory. Calcagni [65, 66] discussed the quantum gravity phenomena and different cosmological properties in fractal universe. Fractal features of quantum gravity and Cosmology in D-dimensions have also been investigated. Also it has been discussed the properties of a scalar field model at classical and quantum level. The Multi-scale gravity and cosmology have been studied in [67]. Karami et al. [68] have investigated the holographic, new agegraphic and ghost dark energy models in the framework of fractal cosmology. Lemets et al. [69] have studied the interacting dark energy models in the fractal universe with the interaction between dark energy and dark matter. Sheykhi et al. [70] have analyzed the thermodynamical properties on the apparent horizon in the fractal universe. Chattopadhyay et al. [71] have discussed some special forms of holographic Ricci dark energy in fractal Universe. Halder et al. [72] have presented a comparative study of different entropies in fractal Universe. Maity and Debnath [73] have studied the co-existence of modified Chaplygin gas and other dark energies in the framework of fractal Universe. Jawad et al. [74] have studied the implications of pilgrim dark energy models in the fractal Universe. Das et al. [75] have described cosmic scenario in the framework of fractal Universe. Sardi et al. [76] have studied an interacting new holographic dark energy in the framework of fractal cosmology.

In the present work, we consider the non-canonical scalar field model in the background of effective fractal spacetime. We shall extend the work of Ref. [63] in the framework of D-dimensional fractal spacetime by considering more general power law form of kinetic term. We shall try to obtain the observationally viable model to describe the nature of the equation of state (EoS) parameter \(w_{\phi }(z)\) for the scalar field and the deceleration parameter q(z) which are functions of redshift z. To describe the DE evolutions, we will choose four kinds of well known parametrizations models for different choices of \(w_{\phi }(z)\). We found the best fit values and confidence contours of two parameters for different forms of \(w_{\phi }\) by considering the observational data analysis of SNIa, BAO, CMB and Hubble. The paper is organized as follows: in Sect. 2, we discuss a general non-canonical scalar field model in the framework of non-flat model of D-dimensional fractal Universe. By suitable choice of the function \(f(\phi )\), we obtain potential function \(V(\phi )\) and Hubble parameter in terms of z and EoS parameter \(w_{\phi }(z)\). Then we choose four kinds of EoS parameter \(w_{\phi }(z)\) to obtain H(z). In Sect. 3, we provide the joint data analysis mechanism for the observations of SNIa, BAO, CMB and Hubble. Finally we discuss the results of the work in Sect. 4.

2 Non-canonical scalar field model in fractal universe

In the fractal Universe [65], the space and time co-ordinates scale are satisfying \([x^{\mu }]=-1,~\mu =0,1,\ldots , D-1\), where D is the topological dimension of the embedding space-time. Also in the action for the fractal Universe [65, 75], the standard measure can be replaced by a non-trivial measure which appears in Lebesgue–Stieltjes integrals: \(d^{D}x \rightarrow d\varrho (x)\) with \([\varrho ]=-D\alpha ,~\alpha \ne 1\), where \(\alpha \) describes the fraction of states. Here the measure is considered as general Borel \(\varrho \) on a fractal set. So in D dimensions, \((M, \varrho )\) denotes the metric space-time where M is equipped with measure \(\varrho \). Here the probability measure \(\varrho \) is a continuous function with \(d\varrho (x)=(d^{D}x) v(x)\), which is the Lebesgue–Stieltjes measure and v is known as the weight function or fractal function.

In the Einstein’s gravity, the total action for the scalar field model in effective fractal space-time is given by [65]

$$\begin{aligned} S=S_{g}+S_{sf}+S_{m} \end{aligned}$$
(1)

where the ansatz for the gravitational action is

$$\begin{aligned} S_{g}=\frac{1}{2\kappa ^{2}}\int d\varrho (x)\sqrt{-g}~(R-\omega \partial _{\mu }v\partial ^{\mu }v)~, \end{aligned}$$
(2)

the scalar field action is given by

$$\begin{aligned} S_{sf}=\int d\varrho (x)\sqrt{-g}~{{\mathcal {L}}}(\phi ,X) \end{aligned}$$
(3)

and the matter action is given by

$$\begin{aligned} S_{m}=\int d\varrho (x)\sqrt{-g}~{{\mathcal {L}}}_{m} \end{aligned}$$
(4)

Here g is the determinant of the dimensionless metric \(g_{\mu \nu }\), \(\kappa ^{2}=8\pi G\) is Newton’s constant, R is the Ricci scalar and the term proportional to \(\omega \) (fractal parameter) has been added because v (fractal function), like the other geometric quantity \(g_{\mu \nu }\), is dynamical. Also \(\mathcal{L}(\phi ,X)\) is the Lagrangian density for scalar field \(\phi \), \(X(=\frac{1}{2}\partial _{\mu }\phi \partial ^{\mu }\phi )\) is the kinetic term, \({{\mathcal {L}}}_{m}\) is the matter Lagrangian.

In the general form of non-canonical scalar field model, the Lagrangian density can be expressed as [58, 63]

$$\begin{aligned} {{\mathcal {L}}}(\phi ,X)=f(\phi )X\left( \kappa ^{4}X \right) ^{n-1}-V(\phi ) \end{aligned}$$
(5)

where \(f(\phi )\) is the arbitrary function and \(V(\phi )\) is the corresponding potential for the non-canonical scalar field \(\phi \). For \(n=1\) and \(f(\phi )=1\), it reduces to usual canonical scalar field Lagrangian. For \(n=1\) and \(f(\phi )=-1\), we get the phantom scalar field model. For \(f(\phi )=1\), it reduces to particular form of general non-canonical scalar field model [55].

The expressions for the energy density \(\rho _{\phi }\) and pressure \(p_{\phi }\) associated with the non-canonical scalar field \(\phi \) are given by

$$\begin{aligned} \rho _{\phi }= & {} 2X~\frac{\partial {{\mathcal {L}}}}{\partial X}-\mathcal{L}=(2n-1)2^{-n}\kappa ^{4(n-1)}f(\phi ){\dot{\phi }}^{2n}+V(\phi )\nonumber \\ \end{aligned}$$
(6)
$$\begin{aligned} p_{\phi }= & {} \mathcal{L}=2^{-n}\kappa ^{4(n-1)}f(\phi ){\dot{\phi }}^{2n}-V(\phi ) \end{aligned}$$
(7)

Now we consider the line-element for D-dimensional non-flat Friedmann–Robertson–Walker (FRW) universe as

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)\left[ \frac{dr^{2}}{1-kr^{2}}+r^{2}d\Omega ^{2}_{D-2} \right] \end{aligned}$$
(8)

where a(t) is the scale factor and \(k~(=0,\pm 1)\) is the curvature scalar.

Taking the variation of the action given in (1) with respect to the D-dimensional FRW metric \(g_{\mu \nu }\), we obtain the Friedmann equations in a fractal universe as [65, 73]

$$\begin{aligned} \left( \frac{D}{2}-1\right) H^{2}+\frac{k}{a^{2}}+H\frac{{\dot{v}}}{v}-\frac{1}{2}\frac{\omega }{D-1}{\dot{v}}^{2} =\frac{\kappa ^{2}}{D-1}~\rho \end{aligned}$$
(9)

and

$$\begin{aligned}&(D-2)\left( {\dot{H}}+H^{2}-H\frac{{\dot{v}}}{v}+\frac{\omega }{D-1}{\dot{v}}^{2} \right) -\frac{\Box v}{v}\nonumber \\&\quad =-\frac{\kappa ^{2}}{D-1}~[(D-3)\rho +(D-1)p] \end{aligned}$$
(10)

where \(H(=\frac{{\dot{a}}}{a})\) is the Hubble parameter and \(\Box v\) (where \(\Box \) is the D’Alembertian operator) is defined by

$$\begin{aligned} \Box v=\frac{1}{\sqrt{-g}}~\partial ^{\mu }(\sqrt{-g}~\partial _{\mu }v) \end{aligned}$$
(11)

which can be simplified to the following form:

$$\begin{aligned} \Box v=-[\ddot{v}+(D-1)H{\dot{v}}] \end{aligned}$$
(12)

Here the total energy density is \(\rho =\rho _{m}+\rho _{\phi }\) and total pressure is \(p=p_{m}+p_{\phi }\) where \(\rho _{m}\) and \(p_{m}\) are respectively energy density and pressure for matter. The continuity equation for fractal Universe is given by

$$\begin{aligned} {\dot{\rho }}+\left[ (D-1)H+\frac{{\dot{v}}}{v}\right] (\rho +p)=0 \end{aligned}$$
(13)

Since the fractal function v is time dependent, so we can choose the power law form of of v in terms of the scale factor as \(v=v_{0}a^{\beta }\) where \(v_{0}\) and \(\beta \) are positive constants [70,71,72,73,74,75,76]. The parameter \(\beta \) is related to the Hausdorff dimension of the physical space-time. So the Eqs. (9), (10) and (13) reduce to

$$\begin{aligned}&\left[ \frac{D}{2}-1+\beta -\frac{\omega v_{0}^{2}\beta ^{2}a^{2\beta }}{2(D-1)}\right] H^{2}+\frac{k}{a^{2}}\nonumber \\&\quad =\frac{\kappa ^{2}}{D-1}~(\rho _{m}+\rho _{\phi })~, \end{aligned}$$
(14)
$$\begin{aligned}&(D-2+\beta ){\dot{H}}+\left[ (D-2)\left( 1-\beta +\frac{\omega v_{0}^{2}\beta ^{2}a^{2\beta }}{D-1} \right) \nonumber \right. \\&\left. \qquad +\beta ^{2}+(D-1)\beta \right] H^{2} \nonumber \\&\quad =-\frac{\kappa ^{2}}{D-1}~[(D-3)(\rho _{m}+\rho _{\phi })+(D-1)(p_{m}+p_{\phi })]\nonumber \\ \end{aligned}$$
(15)

and

$$\begin{aligned} ({\dot{\rho }}_{m}+{\dot{\rho }}_{\phi })+(\beta +D-1)H(\rho _{m}+\rho _{\phi }+p_{m}+p_{\phi })=0\nonumber \\ \end{aligned}$$
(16)

Now we assume that the matter and scalar field are separately conserved. So the conservation equations for matter and scalar field are given by

$$\begin{aligned} {\dot{\rho }}_{m}+(\beta +D-1)H(\rho _{m}+p_{m})=0 \end{aligned}$$
(17)

and

$$\begin{aligned} {\dot{\rho }}_{\phi }+(\beta +D-1)H(\rho _{\phi }+p_{\phi })=0 \end{aligned}$$
(18)

Solving Eq. (17), we get the expression of energy density of matter as

$$\begin{aligned} \rho _{m}(z)=\rho _{m0}(1+z)^{(\beta +D-1)(1+w_{m})} \end{aligned}$$
(19)

where \(\rho _{m0}\) is the present value of the energy density, \(w_{m}=\frac{p_{m}}{\rho _{m}}\) is the constant equation of state parameter for matter and \(z~(=\frac{1}{a}-1)\) is the redshift (choosing \(a_{0}=1\)).

From Eqs. (6) and (7), we obtain the the potential \(V(\phi )\) and \(f(\phi )\) as in the following forms:

$$\begin{aligned} V(\phi )=\frac{1}{2n}[1-(2n-1)w_{\phi }]\rho _{\phi } \end{aligned}$$
(20)

and

$$\begin{aligned} f(\phi ){\dot{\phi }}^{2n}=\frac{2^{n}}{2n\kappa ^{4(n-1)}}(1+w_{\phi })\rho _{\phi } \end{aligned}$$
(21)

Now we obtain the equation of state parameter \(w_{\phi }\) for scalar field as

$$\begin{aligned} w_{\phi }=\frac{p_{\phi }}{\rho _{\phi }}=\frac{\kappa ^{4(n-1)}f(\phi ){\dot{\phi }}^{2n} -2^{n}V(\phi )}{(2n-1)\kappa ^{4(n-1)}f(\phi ){\dot{\phi }}^{2n}+2^{n}V(\phi )} \end{aligned}$$
(22)

Now integrating Eq. (18), we obtain [63]

$$\begin{aligned} \rho _{\phi }(z)=\rho _{\phi 0}~exp\left( (\beta +D-1)\int _{0}^{z}\frac{1+w_{\phi }(z)}{1+z}~dz \right) \end{aligned}$$
(23)

where \(\rho _{\phi 0}\) is the present value of energy density for scalar field. To solve the scalar field \(\phi \), we assume [63]

$$\begin{aligned} f(z)=\left( \frac{f_{0}}{H}\right) ^{2n} \end{aligned}$$
(24)

where \(f_{0}\) is constant. In Ref. [63], the authors have assumed \(n=2\) and studied the features of the model. From equation (21), we obtain

$$\begin{aligned} \phi (z)=\phi _{0}+\frac{\sqrt{2}}{f_{0}(2n)^{\frac{1}{2n}}\kappa ^{\frac{2(n-1)}{n}}}\int _{0}^{z} \frac{(1+w_{\phi }(z))^{\frac{1}{2n}}\rho _{\phi }(z)^{\frac{1}{2n}}}{1+z}~dz\nonumber \\ \end{aligned}$$
(25)

where \(\phi _{0}\) is the present value of \(\phi \). From Eq. (20), we obtain the potential function as

$$\begin{aligned} V(z)= & {} \frac{\rho _{\phi 0}}{2n}[1-(2n-1)w_{\phi }(z)]~\nonumber \\&exp\left( (\beta +D-1)\int _{0}^{z}\frac{1+w_{\phi }(z)}{1+z}~dz \right) \end{aligned}$$
(26)

From Eq. (14), we obtain [63]

$$\begin{aligned} H^{2}(z)=\frac{\xi H_{0}^{2}\left[ \Omega _{m0}(1+z)^{(\beta +D-1)(1+w_{m})}+\Omega _{\phi 0}~exp\left( (\beta +D-1)\int _{0}^{z}\frac{1+w_{\phi }(z)}{1+z}~dz \right) -\Omega _{k0}(1+z)^{2}\right] }{\left[ \xi +\omega v_{0}^{2}\beta ^{2}-\omega v_{0}^{2}\beta ^{2}(1+z)^{-2\beta }\right] } \end{aligned}$$
(27)

where \(H_{0}\) is the present value of the Hubble parameter, \(\xi =(D-1)(D-2+2\beta )-\omega v_{0}^{2}\beta ^{2}\), \(\Omega _{m0}=\frac{2\kappa ^{2}\rho _{m0}}{\xi H_{0}^{2}}\) and \(\Omega _{\phi 0}=\frac{2\kappa ^{2}\rho _{\phi 0}}{\xi H_{0}^{2}}\) and \(\Omega _{k0}=\frac{2(D-1)k}{\xi H_{0}^{2}}\) are present value of the density parameters of matter, scalar field and curvature scalar respectively satisfying \(\Omega _{m0}+\Omega _{\phi 0}-\Omega _{k0}=1\). The deceleration parameter q(z) can be written as

$$\begin{aligned} q(z)=-\frac{\ddot{a}}{aH^{2}}=-1+\frac{(1+z)}{2H^{2}}~\frac{dH^{2}}{dz} \end{aligned}$$
(28)

Since expression of H(z) is given in Eq. (27), so q(z) can be expressed in term of z analytically. Now we see that the functions \(\rho _{\phi }(z),~\phi (z),~V(z),f(z),~H(z),~q(z)\) completely depend on the EoS parameter function \(w_{\phi }(z)\) with number of constant parameters. In the next subsections, we will consider different well known parameterization forms of \(w_{\phi }(z)\) and investigate the natures of Hubble parameter, deceleration parameter, scalar field and its potential in different models.

2.1 Model I : linear parameterization

The equation of state parameter for linear parametrization is [77] \(w_{\phi }(z)=w_0+{w_1}z\), where \(w_0\) and \(w_1\) are constants in which \(w_{0}\) represents the present value of \(w_{\phi }(z)\). The energy density of the model then gives rise to

$$\begin{aligned} \rho _{\phi }(z)=\rho _{\phi 0}(1+z)^{(\beta +D-1)(1+w_0-{w_1})}e^{(\beta +D-1){w_1}z} \end{aligned}$$
(29)

From Eq. (27), the Hubble parameter can be expressed as

$$\begin{aligned} H^{2}(z)=\frac{\xi H_{0}^{2}\left[ \Omega _{m0}(1+z)^{(\beta +D-1)(1+w_{m})}+\Omega _{\phi 0}~(1+z)^{(\beta +D-1)(1+w_0-{w_1})}e^{(\beta +D-1){w_1}z}-\Omega _{k0}(1+z)^{2}\right] }{\left[ \xi +\omega v_{0}^{2}\beta ^{2}-\omega v_{0}^{2}\beta ^{2}(1+z)^{-2\beta }\right] } \end{aligned}$$
(30)

2.2 Model II : Chevallier–Polarski–Linder (CPL) parameterization

In the Chevallier–Polarski–Linder (CPL) Parameterization model, the equation of state parameter is given by [78, 79] \(w_{\phi }(z)=w_0+{w_1}\frac{z}{1+z}\). Here again \(w_0\) and \(w_1\) are constants in which \(w_{0}\) represents the present value of \(w_{\phi }(z)\). With these, the expressions of energy density becomes

$$\begin{aligned} \rho _{\phi }=\rho _{\phi 0}(1+z)^{(\beta +D-1)(1+w_0+{w_1})}e^{-\frac{(\beta +D-1){w_1}z}{1+z}} \end{aligned}$$
(31)

From Eq. (27), the Hubble parameter can be written as

$$\begin{aligned} H^{2}(z)=\frac{\xi H_{0}^{2}\left[ \Omega _{m0}(1+z)^{(\beta +D-1)(1+w_{m})}+\Omega _{\phi 0}~(1+z)^{(\beta +D-1)(1+w_0+{w_1})}e^{-\frac{(\beta +D-1){w_1}z}{1+z}}-\Omega _{k0}(1+z)^{2}\right] }{\left[ \xi +\omega v_{0}^{2}\beta ^{2}-\omega v_{0}^{2}\beta ^{2}(1+z)^{-2\beta }\right] } \end{aligned}$$
(32)

2.3 Model III : Jassal–Bagla–Padmanabhan (JBP) parameterization

For the Jassal–Bagla–Padmanabhan (JBP) parameterization model, the equation of state parameter is [80] \(w_{\phi }(z)=w_0+{w_1}\frac{z}{(1+z)^2}\), where \(w_0\) and \(w_1\) are constants in which \(w_{0}\) represents the present value of \(w_{\phi }(z)\). The following expression is subsequently obtained as

$$\begin{aligned} \rho _{\phi }=\rho _{\phi 0}(1+z)^{(\beta +D-1)(1+w_0)}e^{\frac{(\beta +D-1){w_1}z^2}{2(1+z)^2}} \end{aligned}$$
(33)

From Eq. (27), the Hubble parameter can be written as

Fig. 1
figure 1

Variations of \(w_{0}\) and \(w_{1}\) in the joint analysis (SNIa+BAO+CMB+Hubble) for the linear parameterization (Model I). We plot the graphs for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black) contours for (\(w_{0},~w_{1}\)) by fixing the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3,\omega =0.2, v_{0}=0.5,f_{0}=2,n=3,H_{0}=72,\Omega _{m0}=0.3,\Omega _{k0}=0.05\)

Full size image
Fig. 2
figure 2

Variation of H(z) with the variation of z (Model I) by considering the best fit values \(w_{0}=-0.737,w_{1}=0.173\)

Full size image
Fig. 3
figure 3

Variation of q(z) with the variation of z (Model I) by considering the best fit values \(w_{0}=-0.737,w_{1}=0.173\)

Full size image
Fig. 4
figure 4

Variation of f(z) with the variation of z (Model I) by considering the best fit values \(w_{0}=-0.737,w_{1}=0.173\)

Full size image
Fig. 5
figure 5

Variation of \(\phi (z)\) with the variation of z (Model I) by considering the best fit values \(w_{0}=-0.737,w_{1}=0.173\)

Full size image
$$\begin{aligned} H^{2}(z)=\frac{\xi H_{0}^{2}\left[ \Omega _{m0}(1+z)^{(\beta +D-1)(1+w_{m})}+\Omega _{\phi 0}~(1+z)^{(\beta +D-1)(1+w_0)}e^{\frac{(\beta +D-1){w_1}z^2}{2(1+z)^2}}-\Omega _{k0}(1+z)^{2}\right] }{\left[ \xi +\omega v_{0}^{2}\beta ^{2}-\omega v_{0}^{2}\beta ^{2}(1+z)^{-2\beta }\right] } \end{aligned}$$
(34)
Fig. 6
figure 6

Variation of V(z) with the variation of z (Model I) by considering the best fit values \(w_{0}=-0.737,w_{1}=0.173\)

Full size image
Fig. 7
figure 7

Variation of \(f(\phi )\) with the variation of \(\phi \) for the linear parameterization (Model I)

Full size image

2.4 Model IV: Efstathiou parametrization

Here, in Efstathiou parametrization model, the equation of state parameter takes the form [81, 82] \(w_{\phi }(z)=w_0+w_1~log(1+z)\), where again \(w_0\) and \(w_1\) are constants in which \(w_{0}\) represents the present value of \(w_{\phi }(z)\). This gives rise to the following expression

$$\begin{aligned} \rho _{\phi }=\rho _{\phi 0}(1+z)^{(\beta +D-1)(1+w_0)}e^{\frac{(\beta +D-1)w_1}{2}[log(1+z)]^2} \end{aligned}$$
(35)

From Eq. (27), the Hubble parameter can be written as

$$\begin{aligned} H^{2}(z)=\frac{\xi H_{0}^{2}\left[ \Omega _{m0}(1+z)^{(\beta +D-1)(1+w_{m})}+\Omega _{\phi 0}~(1+z)^{(\beta +D-1)(1+w_0)}e^{\frac{(\beta +D-1)w_1}{2}[log(1+z)]^2}-\Omega _{k0}(1+z)^{2}\right] }{\left[ \xi +\omega v_{0}^{2}\beta ^{2}-\omega v_{0}^{2}\beta ^{2}(1+z)^{-2\beta }\right] } \end{aligned}$$
(36)

3 Observational data analysis technique

In this section, we shall discuss the mechanism for fitting the theoretical models with the recent observational data sets from the type Ia supernova (SN Ia), the baryonic acoustic oscillations (BAO) and the cosmic microwave background (CMB) data survey.

3.1 Data sets

  • SNIa data set: Here we assume 580 data points of type Ia supernovae with redshift ranging from 0.015 to 1.414. Using this data set, the \(\chi ^{2}\) function is given by [63, 83]

Fig. 8
figure 8

Variation of \(V(\phi )\) with the variation of \(\phi \) for the linear parameterization (Model I)

Full size image
$$\begin{aligned} \chi ^{2}_{SN}=A_{SN}-\frac{B_{SN}^{2}}{C_{SN}} \end{aligned}$$
(37)

where

$$\begin{aligned} A_{SN}= & {} \sum _{i=1}^{580}\frac{[\mu _{th}(z_{i})-\mu _{obs}(z_{i})]^{2}}{\sigma ^{2}(z_{i})}~, \end{aligned}$$
(38)
$$\begin{aligned} B_{SN}= & {} \sum _{i=1}^{580}\frac{[\mu _{th}(z_{i})-\mu _{obs}(z_{i})]}{\sigma ^{2}(z_{i})}~, \end{aligned}$$
(39)

and

$$\begin{aligned} C_{SN}=\sum _{i=1}^{580}\frac{1}{\sigma ^{2}(z_{i})} \end{aligned}$$
(40)

Here the distance modulus \(\mu (z)\) for any SNIa at a redshift z is given by

$$\begin{aligned} \mu (z)=5~ log_{10}\left[ (1+z)\int _{0}^{z}\frac{dz'}{E(z')}\right] +\mu _{0} \end{aligned}$$
(41)
Fig. 9
figure 9

Variations of \(w_{0}\) and \(w_{1}\) in the joint analysis (SNIa+BAO+CMB+Hubble) for the CPL parameterization (Model II). We plot the graphs for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black) contours for (\(w_{0},~w_{1}\)) by fixing the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3, \omega =0.2, v_{0}=0.5,f_{0}=2,n=3,H_{0}=72,\Omega _{m0}=0.3, \Omega _{k0}=0.05\)

Full size image
Fig. 10
figure 10

Variation of H(z) with the variation of z (Model II) by considering the best fit values \(w_{0}=-0.797,w_{1}=0.499\)

Full size image
Fig. 11
figure 11

Variation of q(z) with the variation of z (Model II) by considering the best fit values \(w_{0}=-0.797,w_{1}=0.499\)

Full size image
Fig. 12
figure 12

Variation of f(z) with the variation of z (Model II) by considering the best fit values \(w_{0}=-0.797,w_{1}=0.499\)

Full size image

where \(\mu _{0}\) is a nuisance parameter which should be marginalized. Also \(\mu _{th}\) represents the theoretical distance modulus, while \(\mu _{obs}\) is the theoretical distance modulus and \(\sigma \) is the standard error associated with the data point and \(E(z)=H(z)/H_{0}\) is the normalized Hubble parameter.

  • SNIa + BAO data set: Eisenstein et al. [84] proposed the Baryon Acoustic Oscillation (BAO) peak parameter. The BAO signal has been directly detected at a scale \(\sim \) 100 MPc by SDSS survey. We shall investigate the parameters of the prescribed models using the BAO peak joint analysis for the redshift which has the range \(0< z < z_{1}\) where \(z_1 = 0.35\). For the SDSS data sample, \(z_{1}\) is called the typical redshift which has been used in the early times [85]. The BAO peak parameter can be defined in the following form:

    $$\begin{aligned} {{\mathcal {A}}}=\frac{\sqrt{\Omega _m}}{E(z_1)^{1/3}}\left( \frac{\int _{0}^{z_1}\frac{dz}{E(z)}}{z_1}\right) ^{2/3} \end{aligned}$$
    (42)

where

$$\begin{aligned} \Omega _m=\Omega _{m0} (1+z_1)^3 E(z_1)^{-2} \end{aligned}$$
(43)

Using SDSS data set [84], the value of \({{\mathcal {A}}}\) is \(0.469 \pm 0.017\) for flat model of the FRW universe. Now for BAO analysis, the \(\chi ^2\) function can be written as in the following form

$$\begin{aligned} \chi ^2_{BAO}=\frac{({{\mathcal {A}}}-0.469)^2}{(0.017)^2} \end{aligned}$$
(44)
Fig. 13
figure 13

Variation of \(\phi (z)\) with the variation of z (Model II) by considering the best fit values \(w_{0}=-0.797,w_{1}=0.499\)

Full size image
Fig. 14
figure 14

Variation of V(z) with the variation of z (Model II) by considering the best fit values \(w_{0}=-0.797,w_{1}=0.499\)

Full size image
Fig. 15
figure 15

Variation of \(f(\phi )\) with the variation of \(\phi \) for the CPL parameterization (Model II)

Full size image
Fig. 16
figure 16

Variation of \(V(\phi )\) with the variation of \(\phi \) for the CPL parameterization (Model II)

Full size image

  • SNIa + BAO + CMB data set: For Cosmic Microwave Background (CMB), the shift parameter of CMB power spectrum peak is given by [86, 87]

    $$\begin{aligned} {{\mathcal {R}}}=\sqrt{\Omega _m} \int _{0}^{z_2} \frac{dz'}{E(z')} \end{aligned}$$
    (45)

where \(z_2\) is the value of the redshift at the surface of last scattering. The WMAP data gives the value \({{\mathcal {R}}}=1.726 \pm 0.018 \) at the redshift \(z=1091.3\). For CMB measurement, the \(\chi ^2\) function can be defined as

$$\begin{aligned} \chi ^2_{CMB}=\frac{({{\mathcal {R}}}-1.726)^2}{(0.018)^2} \end{aligned}$$
(46)

  • Hubble data set: Here we use the observed Hubble data set by Stern et al. [88] at different redshifts at 12 data points [89, 90]. The \(\chi ^2\) function is given by

    $$\begin{aligned} \chi ^2_{H}=\sum _{i=1}^{12} \frac{\left( H(z_{i})-H_{obs}(z_{i})\right) ^2}{\sigma ^{2}(z_{i})} \end{aligned}$$
    (47)

    where the redshift of these data falls in the region \(0<z<1.75\).

The total joint data analysis (SNIa+BAO+CMB+Hubble) for the \(\chi ^2\) function is defined by

$$\begin{aligned} \chi ^2_{Tot}=\chi ^2_{SN}+\chi ^2_{BAO}+\chi ^2_{CMB}+\chi ^{2}_{H} \end{aligned}$$
(48)

The best fit values of the model parameters can be determined by minimizing the corresponding Chi-square value which is equivalent to the maximum likelihood analysis.

Fig. 17
figure 17

Variations of \(w_{0}\) and \(w_{1}\) in the joint analysis (SNIa+BAO+CMB+Hubble) for the JBP parameterization (Model III). We plot the graphs for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black) contours for (\(w_{0},~w_{1}\)) by fixing the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3, \omega =0.2, v_{0}=0.5,f_{0}=2,n=3,H_{0}=72,\Omega _{m0}=0.3, \Omega _{k0}=0.05\)

Full size image
Fig. 18
figure 18

Variation of H(z) with the variation of z (Model III) by considering the best fit values \(w_{0}=-0.754,w_{1}=0.261\)

Full size image
Fig. 19
figure 19

Variation of q(z) with the variation of z (Model III) by considering the best fit values \(w_{0}=-0.754,w_{1}=0.261\)

Full size image
Fig. 20
figure 20

Variation of f(z) with the variation of z (Model III) by considering the best fit values \(w_{0}=-0.754,w_{1}=0.261\)

Full size image
Fig. 21
figure 21

Variation of \(\phi (z)\) with the variation of z (Model III) by considering the best fit values \(w_{0}=-0.754,w_{1}=0.261\)

Full size image
Fig. 22
figure 22

Variation of V(z) with the variation of z (Model III) by considering the best fit values \(w_{0}=-0.754,w_{1}=0.261\)

Full size image
Fig. 23
figure 23

Variation of \(f(\phi )\) with the variation of \(\phi \) for the JBP parameterization (Model III)

Full size image
Fig. 24
figure 24

Variation of \(V(\phi )\) with the variation of \(\phi \) for the JBP parameterization (Model III)

Full size image
Fig. 25
figure 25

Variations of \(w_{0}\) and \(w_{1}\) in the joint analysis (SNIa+BAO+CMB+Hubble) for the Efstathiou parameterization (Model IV). We plot the graphs for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black) contours for (\(w_{0},~w_{1}\)) by fixing the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3, \omega =0.2, v_{0}=0.5,f_{0}=2,n=3,H_{0}=72,\Omega _{m0}=0.3, \Omega _{k0}=0.05\)

Full size image
Fig. 26
figure 26

Variation of H(z) with the variation of z (Model IV) by considering the best fit values \(w_{0}=-0.766,w_{1}=0.307\)

Full size image
Fig. 27
figure 27

Variation of q(z) with the variation of z (Model IV) by considering the best fit values \(w_{0}=-0.766,w_{1}=0.307\)

Full size image
Fig. 28
figure 28

Variation of f(z) with the variation of z (Model IV) by considering the best fit values \(w_{0}=-0.766,w_{1}=0.307\)

Full size image
Fig. 29
figure 29

Variation of \(\phi (z)\) with the variation of z (Model IV) by considering the best fit values \(w_{0}=-0.766,w_{1}=0.307\)

Full size image
Fig. 30
figure 30

Variation of V(z) with the variation of z (Model IV) by considering the best fit values \(w_{0}=-0.766,w_{1}=0.307\)

Full size image

3.2 Data fittings and numerical results

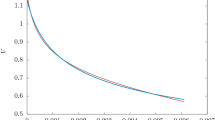
  • Model I (Linear): For this model, using SNIa+BAO+CMB+Hubble joint analysis, we found the minimum value of \(\chi ^{2}_{Tot}=7.104\) and the best fit values of the parameters \(w_{0}=-0.738\) and \(w_{1}=0.174\) where we have fixed the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3,\omega =0.2, v_{0}=0.5,f_{0}=2,n=3,\Omega _{m0}=0.3,\Omega _{k0}=0.05\) and \(H_{0}=72\) km \(\hbox {s}^{-1}\) \(\hbox {MPc}^{-1}\). We have plotted the contours of (\(w_{0},~w_{1}\)) in Fig. 1 for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black). Now taking best fit values of the parameters \(w_{0}\) and \(w_{1}\), we have drawn the Hubble parameter H(z) vs redshift z in Fig. 2 and the deceleration parameter q(z) vs z in Fig. 3. We have seen that the Hubble parameter and deceleration parameter decrease over the expansion of time. The deceleration parameter q(z) has a sign flip from positive to negative, so our model generates deceleration phase to acceleration phase of the Universe. Also at the present value of \(z=0\), the deceleration parameter q is negative, so at present our Universe is undergoing the acceleration phase. The function f(z), non-canonical scalar field \(\phi (z)\) and its potential V(z) have been drawn in Figs. 4, 5 and 6 respectively. We have seen that f(z) and \(\phi (z)\) increase as z decreases but V(z) first increases and then decreases as z decreases. Also \(f(\phi )\) and \(V(\phi )\) in terms of scalar field \(\phi \) have been drawn in Figs. 7 and 8 respectively. Here \(f(\phi )\) increases but \(V(\phi )\) first increases and then decreases as \(\phi \) increases.

  • Model II (CPL): Due to joint analysis of SNIa+BAO+CMB+Hubble, we have found the minimum value of \(\chi ^{2}_{Tot}=7.042\) and the best fit values of the parameters \(w_{0}=-0.796\) and \(w_{1}=0.498\) where we have fixed the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3,\omega =0.2, v_{0}=0.5,f_{0}=2,n=3,\Omega _{m0}=0.3,\Omega _{k0}=0.05\) and \(H_{0}=72\) km \(\hbox {s}^{-1}\) \(\hbox {MPc}^{-1}\). We have plotted the contours of the parameters (\(w_{0},~w_{1}\)) in Fig. 9 for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black). Now taking best fit values of the parameters \(w_{0}\) and \(w_{1}\), we have drawn the Hubble parameter H(z) vs redshift z in Fig. 10 and the deceleration parameter q(z) vs z in Fig. 11. We have seen that the Hubble parameter first decreases and then increases and deceleration parameter decreases over the evolution of the Universe. The deceleration parameter q(z) has a sign flip from positive to negative levels. The function f(z), non-canonical scalar field \(\phi (z)\) and its potential V(z) have been drawn in Figs. 12, 13 and 14 respectively. We have seen that f(z) first increases and thereafter decreases and \(\phi (z)\) increase as z decreases but V(z) first decreases and then increases as z decreases. Also \(f(\phi )\) and \(V(\phi )\) in terms of scalar field \(\phi \) have been drawn in Figs. 15 and 16 respectively. Here \(f(\phi )\) sharply increases but \(V(\phi )\) decreases as \(\phi \) increases.

  • Model III (JBP): For this model, by investigating the SNIa+BAO+CMB+Hubble joint analysis, we have found the minimum value of \(\chi ^{2}_{Tot}=7.088\) and the best fit values of the parameters \(w_{0}=-0.755\) and \(w_{1}=0.262\) where we have fixed the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3,\omega =0.2, v_{0}=0.5,f_{0}=2,n=3,\Omega _{m0}=0.3,\Omega _{k0}=0.05\) and \(H_{0}=72\) km \(\hbox {s}^{-1}\) \(\hbox {MPc}^{-1}\). We have plotted the contours of (\(w_{0},~w_{1}\)) in Fig. 17 for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black). Now taking best fit values of the parameters \(w_{0}\) and \(w_{1}\), we have drawn the Hubble parameter H(z) vs redshift z in Fig. 18 and the deceleration parameter q(z) vs z in Fig. 19. We have seen that the Hubble parameter first decreases and then increases and deceleration parameter decreases as z decreases. The deceleration parameter q(z) has a sign flip from positive to negative and passes phantom barrier. The function f(z), non-canonical scalar field \(\phi (z)\) and its potential V(z) have been drawn in Figs. 20, 21 and 22 respectively. We have seen that f(z) and \(\phi (z)\) increase as z decreases but V(z) first decreases and then sharply increases as z decreases. Also \(f(\phi )\) and \(V(\phi )\) in terms of scalar field \(\phi \) have been drawn in Figs. 23 and 24 respectively. Here \(f(\phi )\) sharply increases but \(V(\phi )\) decreases as \(\phi \) increases.

  • Model IV (Efstathiou): Using SNIa+BAO+CMB+Hubble joint analysis, we have found the minimum value of \(\chi ^{2}_{Tot}=7.072\) and the best fit values of the parameters \(w_{0}=-0.765\) and \(w_{1}=0.308\) where we have fixed the other parameters \(\beta =-0.5,D=5,w_{m}=-0.3,\omega =0.2, v_{0}=0.5,f_{0}=2,n=3,\Omega _{m0}=0.3,\Omega _{k0}=0.05\) and \(H_{0}=72\) km \(\hbox {s}^{-1}\) \(\hbox {MPc}^{-1}\). We have plotted the contours of (\(w_{0},~w_{1}\)) in Fig. 25 for different confidence levels 66% (solid, blue), 90% (dashed, red) and 99% (dashed, black). Now taking best fit values of the parameters \(w_{0}\) and \(w_{1}\), we have drawn the Hubble parameter H(z) vs redshift z in Fig. 26 and the deceleration parameter q(z) vs z in Fig. 27. We have seen that the Hubble parameter first decreases and thereafter slightly increases and deceleration parameter decreases and crosses the phantom barrier. The function f(z), non-canonical scalar field \(\phi (z)\) and its potential V(z) have been drawn in Figs. 28, 29 and 30 respectively. We have seen that f(z) first increases and then slightly decreases and \(\phi (z)\) increase as z decreases but V(z) first decreases and then sharply increases as z decreases. Also \(f(\phi )\) and \(V(\phi )\) in terms of scalar field \(\phi \) have been drawn in Figs. 31 and 32 respectively. Here \(f(\phi )\) sharply increases but \(V(\phi )\) decreases as \(\phi \) increases.

Fig. 31
figure 31

Variation of \(f(\phi )\) with the variation of \(\phi \) for the Efstathiou parameterization (Model IV).

Full size image
Fig. 32
figure 32

Variation of \(V(\phi )\) with the variation of \(\phi \) for the Efstathiou parameterization (Model IV)

Full size image

4 Discussions and concluding remarks

In this work, we have studied non-canonical scalar field model in the non-flat D-dimensional fractal Universe on the condition that the matter and scalar field are separately conserved. To get the solutions of potential V, scalar field \(\phi \), function f, densities, Hubble parameter and deceleration parameter, the fractal function has been chosen in the form \(v\propto a^{\beta }\). In the Lagrangian for general form of non-canonical scalar field model, the kinetic term \(\propto f(\phi )X^{n}\) and the function f has been suitable chosen in the form \(f\propto H^{-2n}\). For \(n=2\), the non-canonical scalar field model has been discussed in Ref. [63]. We have chosen four types of parametrizations forms of equation of state parameter \(w_{\phi }(z)\). We have analyzed best fit values of the unknown parameters (\(w_{0},w_{1}\)) of the parametrizations models due to the joint data analysis (SNIa+BAO+CMB+Hubble). Since we have interested to consider the D-dimensional fractal Universe, so for instance, for graphical representations, we have assumed \(D=5\) which is higher than 4-dimensions and analyzed the physical parameters in this respect. To get graphical analysis, throughout the paper, we have chosen all other parameters, \(\beta =-0.5,w_{m}=-0.3,\omega =0.2, v_{0}=0.5,f_{0}=2,n=3,\Omega _{m0}=0.3,\Omega _{k0}=0.05\) and \(H_{0}=72\) km \(\hbox {s}^{-1}\) \(\hbox {MPc}^{-1}\). For model I, the the best fit values of the parameters are obtained as \((w_{0},w_{1})=(-0.738,0.174)\). For model II, the the best fit values of the parameters are \((w_{0},w_{1})=(-0.796,0.498)\). For model III, the the best fit values of the parameters are \((w_{0},w_{1})=(-0.755,0.262)\) and also for model IV, the the best fit values of the parameters are obtained as \((w_{0},w_{1})=(-0.765,0.308)\). We have also plotted the contours of (\(w_{0},~w_{1}\)) for different confidence levels 66%, 90% and 99% for all these models. For all of the parametrized models, we have shown that the deceleration parameter q undergoes a smooth transition from its deceleration phase (\(q > 0\)) to an acceleration phase (\(q < 0\)). For all the models, we have shown in graphically that the potential function \(V(\phi )\) always decreases and the function \(f(\phi )\) always increases as \(\phi \) increases.